Multiple zeta-star values for indices of infinite length

Minoru Hirose Institute for Advanced Research, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8602, Japan [email protected] , Hideki Murahara The University of Kitakyushu, 4-2-1 Kitagata, Kokuraminami-ku, Kitakyushu, Fukuoka, 802-8577, Japan [email protected] and Tomokazu Onozuka Institute of Mathematics for Industry, Kyushu University 744, Motooka, Nishi-ku, Fukuoka, 819-0395, Japan [email protected]

Abstract.

In this paper, we consider infinite-length versions of multiple zeta-star values. We give several explicit formulas for the infinite-length versions of multiple zeta-star values. We also discuss the analytic properties of the map from indices to the infinite-length versions of multiple zeta-star values.

Key words and phrases:

Multiple zeta(-star) values; Indices of infinite length

2020 Mathematics Subject Classification:

Primary 11M32

1. Main result

The multiple zeta-star value is the convergent series

\zeta^{\star}(k_{1},\dots,k_{r})=\sum_{n_{1}\geq\cdots\geq n_{r}\geq 1}\frac{1}{n_{1}^{k_{1}}\cdots n_{r}^{k_{r}}}

for $(k_{1},\dots,k_{r})\in\mathbb{Z}_{\geq 1}^{r}$ with $k_{1}\geq 2$ and has been studied variously, along with the multiple zeta values. In this paper, we consider the infinite length version of the multiple zeta-star values.

Definition 1.1.

For $(k_{1},k_{2},\dots)\in\mathbb{Z}_{\geq 1}^{\infty}$ with $k_{1}\geq 2$ , we define multiple zeta-star values for indices of infinite length by

\displaystyle\zeta^{\star}(k_{1},k_{2},\dots)

\displaystyle=\sum_{m_{1}\geq m_{2}\geq\cdots\geq 1}\frac{1}{m_{1}^{k_{1}}m_{2}^{k_{2}}\cdots}\qquad(=\lim_{r\rightarrow\infty}\zeta^{\star}(k_{1},\dots,k_{r})),

where the summation is over the all decreasing sequence $(m_{j})_{j=1}^{\infty}$ of positive integers such that $\lim_{r\to\infty}m_{r}=1$ .

We will see later that the above sum converges except for the case where $k_{1}=2$ and $k_{j}=1$ for all $j>1$ (see Section 3). First, we will show some formulas for the multiple zeta-star values for indices of infinite length. Let $\{k\}^{r}$ denote the $r$ times repetition of the $k$ , e.g., $(\{k\}^{3})=(k,k,k)$ . We use the summation symbol $\sum^{\prime}$ in an extended meaning of $\sum$ , i.e., $\sum^{\prime}{\!}_{j=a}^{b-1}$ means $-\sum_{j=b}^{a-1}$ if $b<a$ , 0 if $b=a$ , $\sum_{j=a}^{b-1}$ if $b>a$ .

Theorem 1.2.

We have the following equalities:

(1)

For $k_{1},\dots,k_{r}\in\mathbb{Z}_{\geq 1}^{r}$ with $k_{1}\geq 2$ ,

$\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}+1,\{1\}^{\infty})=\zeta^{\star}(k_{1},\dots,k_{r}).$

(2)

For $k_{1},\dots,k_{r}\in\mathbb{Z}_{\geq 1}^{r}$ with $k_{1}\geq 2$ ,

	$\displaystyle\zeta^{\star}(k_{1},\dots,k_{r},\{2\}^{\infty})$
	$\displaystyle=(-1)^{k_{1}+\cdots+k_{r}}\left(2-2\sum_{s=1}^{r}\sideset{}{{}^{\prime}}{\sum}_{j=2}^{k_{s}-1}(-1)^{k_{1}+\cdots+k_{s-1}+j}\zeta^{\star}(k_{1},\dots,k_{s-1},j)\right).$

(3)

For $k\geq 2$ ,

$\zeta^{\star}(\{k\}^{\infty})=\prod_{m=2}^{\infty}\left(\frac{m^{k}}{m^{k}-1}\right)=\prod_{c^{k}=1}\Gamma(2-c).$
(4)

For $n\geq 2$ ,

$\zeta^{\star}(\{2,\{1\}^{n-2}\}^{\infty})=n.$
(5)

For $n\geq 1$ ,

$\zeta^{\star}(\{\{2\}^{n},1\}^{\infty})=2\prod_{c^{2n+1}=1}\frac{\Gamma(2-c)}{\Gamma(2+c)}.$

(6)

For $n\geq 0$ ,

\displaystyle\zeta^{\star}(\{\{2\}^{n},3,\{2\}^{n},1\}^{\infty})=2\prod_{s\in\{\pm 1\}}\prod_{c^{2n+2}=s}\Gamma(2-c)^{-s}\Gamma\left(1-\frac{c}{2}\right)^{2s}.

Example 1.3.

We have the following equalities:

(1)

$\zeta^{\star}(\{4\}^{\infty})=\frac{8\pi}{e^{\pi}-e^{-\pi}},$
(2)

$\zeta^{\star}(3,\{2\}^{\infty})=2\zeta(2)-2,$
(3)

$\zeta^{\star}(\{3,1\}^{\infty})=\frac{4(e^{\pi}+1)}{\pi(e^{\pi}-1)},$
(4)

$\zeta^{\star}(\{2\}^{\infty})=2,$
(5)

$\zeta^{\star}(\{2,1\}^{\infty})=3$ .

Second, let us define $Z^{\star}:[0,1]\to[1,\infty]$ by $Z^{\star}(0)=1$ and

Z^{\star}\left(\sum_{j=1}^{\infty}\frac{1}{2^{k_{1}+\cdots+k_{j}}}\right)=\zeta^{\star}(k_{1}+1,k_{2},k_{3},\dots),

where $k_{1},k_{2},\dots\in\mathbb{Z}_{\geq 1}$ . The function $Z^{\star}$ contains information of all multiple zeta-star values for indices of infinite length (see Figure 1 for the graph of $Z^{\star}$ ).

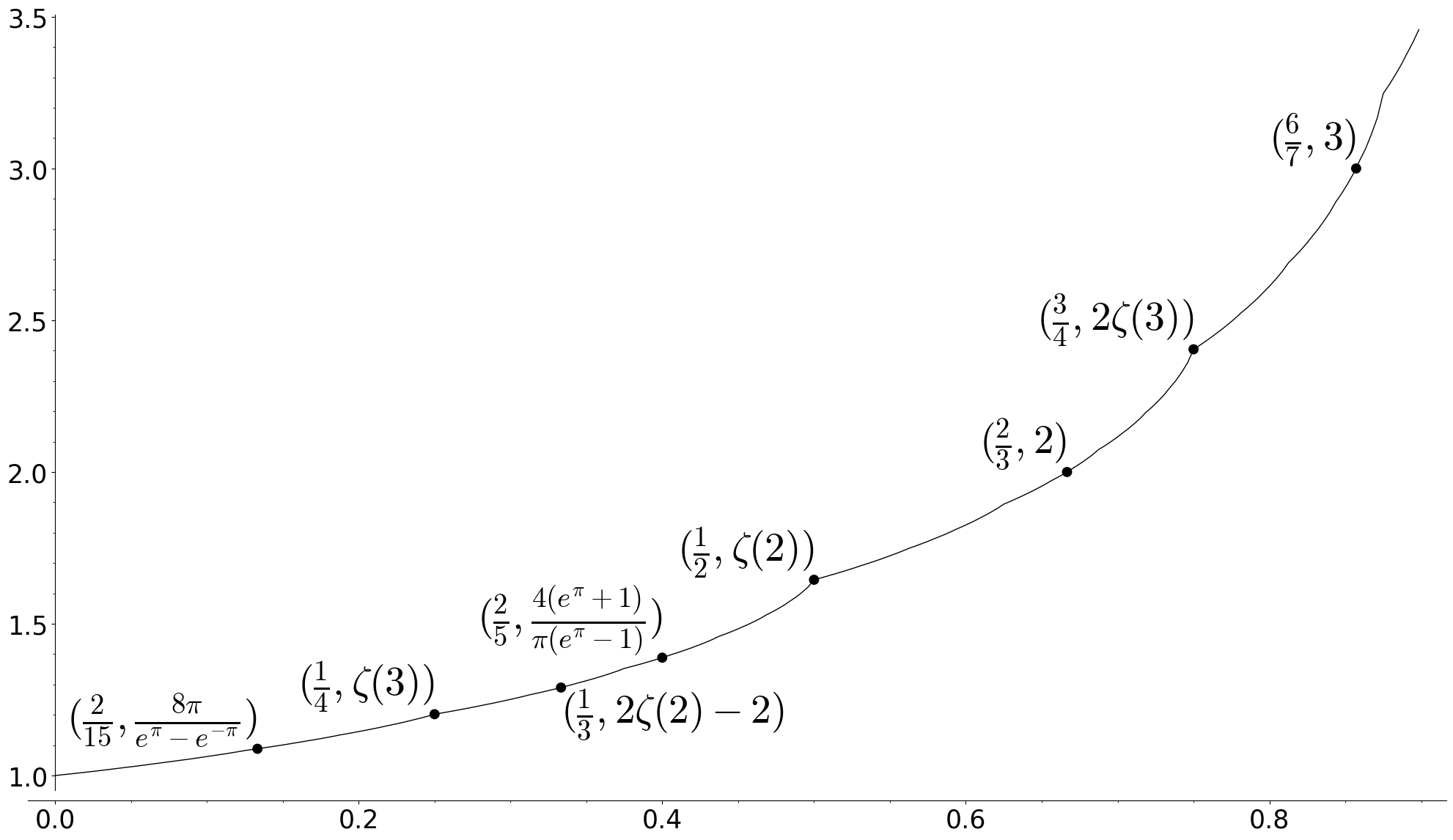
Refer to caption — Figure 1. The graph and some special values of $Z^{\star}$ .

Given two indices $(k_{1},k_{2},\dots)$ and $(l_{1},l_{2},\dots)$ , we say that the former is lexicographically smaller than the latter if there exists $j$ such that $k_{i}=l_{i}$ and $k_{j}<l_{j}\;(i\in\{1,\dots,j-1\})$ .

Theorem 1.4.

$Z^{\star}$ is a continuous and bijective function, or equivalently, the map

(k_{1},k_{2},k_{3},\dots)\mapsto\zeta^{\star}(k_{1}+1,k_{2},k_{3},\dots)

gives an order-reversing bijection between $(\mathbb{Z}_{\geq 1}^{\infty},\prec)$ and $(1,\infty]$ where $\prec$ is the lexicographic order.

Remark 1.5.

The order structure for the set of multiple zeta values is studied by Kumar [1].

Remark 1.6.

Li, independently of our study, obtained the same results as Theorem 1.2 (1), (4), Theorem 1.4, and further studied related topics. For more details, see [2].

Theorem 1.7.

The map $Z^{\star}$ is not differentiable on some dense set. More precisely, we have the followings:

(1)

The map $Z^{\star}$ is right-differentiable at $z$ for $0\leq z<1$ .
(2)

The map $Z^{\star}$ is left-differentiable at $z$ if $z\not\in\{1-\frac{1}{2^{n}}\mid n>0\}$ .
(3)

The map $Z^{\star}$ is not left-differentiable at $z$ if $z\in\{1-\frac{1}{2^{n}}\mid n>0\}$ .
(4)

The left-differential $\partial_{-}Z^{\star}(z)$ is equal to the right-differential $\partial_{+}Z^{\star}(z)$ if $z\in(0,1)\setminus\left\{\frac{a}{2^{n}}\mid 0<a<2^{n},n>0\right\}$ .
(5)

The left-differential $\partial_{-}Z^{\star}(z)$ is greater than the right differential $\partial_{+}Z^{\star}(z)$ if $z\in\left\{\frac{a}{2^{n}}\mid 0<a<2^{n}-1,n>0\right\}$ .

The proof of Theorem 1.7 will be given in Theorems 4.7, 4.8, 4.10, and 5.5 (see also Remark 4.9).

2. Special values

Lemma 2.1.

For $k_{1},\dots,k_{r},l\in\mathbb{Z}_{\geq 1}$ with $k_{1}>1$ , we have

\zeta^{\star}(k_{1},\dots,k_{r},\{l\}^{\infty})=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\prod_{s=2}^{m_{r}}\frac{s^{l}}{s^{l}-1}.

Proof.

It follows from the following calculation:

	$\displaystyle\zeta^{\star}(k_{1},\dots,k_{r},\{l\}^{\infty})$
	$\displaystyle=\lim_{R\to\infty}\sum_{m_{1}\geq\cdots\geq m_{r}\geq n_{1}\geq\cdots\geq n_{R}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}n_{1}^{l}\cdots n_{R}^{l}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\lim_{R\to\infty}\sum_{m_{r}\geq n_{1}\geq\cdots\geq n_{R}\geq 1}\frac{1}{n_{1}^{l}\cdots n_{R}^{l}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\lim_{R\to\infty}\sum_{c_{1}+\cdots+c_{m_{r}}=R}\prod_{s=1}^{m_{r}}\frac{1}{s^{lc_{s}}}\qquad(c_{s}\coloneqq\#\{j:n_{j}=s\})$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\sum_{c_{2},\dots,c_{m_{1}}=0}^{\infty}\prod_{s=2}^{m_{r}}\frac{1}{s^{lc_{s}}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\prod_{s=2}^{m_{r}}\sum_{c=0}^{\infty}\frac{1}{s^{lc}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\prod_{s=2}^{m_{r}}\frac{s^{l}}{s^{l}-1}.\qed$

Proof of Theorem 1.2 (1).

By Lemma 2.1, we have

	$\displaystyle\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}+1,\{1\}^{\infty})$	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r-1}^{k_{r-1}}m_{r}^{k_{r}+1}}\prod_{s=2}^{m_{r}}\frac{s}{s-1}$
		$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}$
		$\displaystyle=\zeta^{\star}(k_{1},\dots,k_{r}).\qed$

Proof of Theorem 1.2 (2).

Let $L(k_{1},\dots,k_{r})$ (resp. $R(k_{1},\dots,k_{r})$ ) be the left (resp. right) hand side of the theorem. By Lemma 2.1, we have

	$\displaystyle L(k_{1},\dots,k_{r})$	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\prod_{m=2}^{m_{r}}\frac{m^{2}}{m^{2}-1}$
		$\displaystyle=2\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r-1}^{k_{r-1}}}\cdot\frac{1}{m_{r}^{k_{r}-1}(m_{r}+1)}.$

Thus,

	$\displaystyle L(k_{1},\dots,k_{r},a)+L(k_{1},\dots,k_{r},a+1)$
	$\displaystyle=2\sum_{m_{1}\geq\cdots\geq m_{r}\geq n\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}}\cdot\frac{1}{n+1}\left(\frac{1}{n^{a-1}}+\frac{1}{n^{a}}\right)$
	$\displaystyle=2\sum_{m_{1}\geq\cdots\geq m_{r}\geq n\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r}^{k_{r}}n^{a}}$
	$\displaystyle=2\zeta^{\star}(k_{1},\dots,k_{r},a).$

On the other hand, by definition,

R(k_{1},\dots,k_{r},a)+R(k_{1},\dots,k_{r},a+1)=2\zeta^{\star}(k_{1},\dots,k_{r},a).

Thus we have

L(k_{1},\dots,k_{r},a)+L(k_{1},\dots,k_{r},a+1)=R(k_{1},\dots,k_{r},a)+R(k_{1},\dots,k_{r},a+1).

Furthermore, we have

	$\displaystyle L(k_{1},\dots,k_{r},2)$	$\displaystyle=L(k_{1},\dots,k_{r}),$
	$\displaystyle R(k_{1},\dots,k_{r},2)$	$\displaystyle=R(k_{1},\dots,k_{r}),$

and $L(2)=2=R(2)$ . Thus the claim follows by induction. ∎

Proof of Theorem 1.2 (3).

We have

\displaystyle\zeta^{\star}(\{k\}^{\infty})=\sum_{m_{1}\geq m_{2}\geq\cdots\geq 1}\frac{1}{m_{1}^{k}m_{2}^{k}\cdots}=\prod_{m=2}^{\infty}\sum_{s=0}^{\infty}\frac{1}{m^{ks}}=\prod_{m=2}^{\infty}\frac{m^{k}}{m^{k}-1}.

Since

m^{k}-1=\prod_{c^{k}=1}(m-c),

we have

	$\displaystyle\prod_{m=2}^{\infty}\frac{m^{k}}{m^{k}-1}$	$\displaystyle=\lim_{n\to\infty}\prod_{m=2}^{n}\prod_{c^{k}=1}\frac{m}{m-c}$
		$\displaystyle=\prod_{c^{k}=1}\lim_{n\to\infty}\prod_{m=2}^{n}\frac{2+(m-2)}{2-c+(m-2)}.$

Using

\Gamma(x)=\lim_{n\to\infty}\frac{n^{x}n!}{x(x+1)\cdots(x+n)},

we obtain

\displaystyle\prod_{m=2}^{\infty}\frac{m^{k}}{m^{k}-1}=\prod_{c^{k}=1}\frac{\Gamma(2-c)}{\Gamma(2)}=\prod_{c^{k}=1}\Gamma(2-c).

Proof of Theorem 1.2 (4).

It is known that $\zeta^{\star}(\{2,\{1\}^{n-2}\}^{a},1)=n\zeta(an+1)$ (see [3] and [5]). Thus, we have

\zeta^{\star}(\{2,\{1\}^{n-2}\}^{\infty})=\lim_{a\to\infty}\zeta^{\star}(\{2,\{1\}^{n-2}\}^{a},1)=n.\qed

Proof of Theorem 1.2 (5).

Using [4, Theorem 1.2], we have

	$\displaystyle\zeta^{\star}(\{\{2\}^{n},1\}^{d})$	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{d}\geq 1}\frac{2^{\#\{m_{1},\dots,m_{d}\}}}{m_{1}^{2n+1}\cdots m_{d}^{2n+1}}$
		$\displaystyle=\sum_{\begin{subarray}{c}(c_{1},c_{2},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}\\ \sum_{m=1}^{\infty}c_{m}=d\end{subarray}}\prod_{\begin{subarray}{c}m\geq 1\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}},$

where we put $c_{m}=\#\{j:m_{j}=m\}$ . Then

\displaystyle\zeta^{\star}(\{\{2\}^{n},1\}^{d})=\sum_{\begin{subarray}{c}(c_{2},c_{3},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}\\ \sum_{m=2}^{\infty}c_{m}=d\end{subarray}}\prod_{\begin{subarray}{c}m\geq 2\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}}+2\sum_{\begin{subarray}{c}(c_{2},c_{3},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}\\ \sum_{m=2}^{\infty}c_{m}<d\end{subarray}}\prod_{\begin{subarray}{c}m\geq 2\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}}.

Since

\displaystyle\lim_{d\to\infty}\sum_{\begin{subarray}{c}(c_{2},c_{3},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}\\ \sum_{m=2}^{\infty}c_{m}=d\end{subarray}}\prod_{\begin{subarray}{c}m\geq 2\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}}=0

and

	$\displaystyle\lim_{d\to\infty}\sum_{\begin{subarray}{c}(c_{2},c_{3},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}\\ \sum_{m=2}^{\infty}c_{m}<d\end{subarray}}\prod_{\begin{subarray}{c}m\geq 2\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}}$	$\displaystyle=\sum_{(c_{2},c_{3},\dots)\in\mathbb{Z}_{\geq 0}^{\infty}}\prod_{\begin{subarray}{c}m\geq 2\\ c_{m}\geq 1\end{subarray}}\frac{2}{m^{(2n+1)c_{m}}}$
		$\displaystyle=\prod_{m=2}^{\infty}\left(1+2\sum_{c=1}^{\infty}\frac{1}{m^{(2n+1)c}}\right),$

we have

\displaystyle\zeta^{\star}(\{\{2\}^{n},1\}^{\infty})

\displaystyle=2\prod_{m=2}^{\infty}\frac{m^{2n+1}+1}{m^{2n+1}-1}.

We obtain the result by a similar calculation as in the proof of Theorem 1.2 (3). ∎

Proof of Theorem 1.2 (6).

Using the equation [4, Theorem 4.8 (2-c-2-1)] with $c_{1}=\cdots=c_{r}=3$ and $a_{1}=\cdots=a_{r}=b_{1}=\cdots=b_{r}=n$ , we have

\zeta^{\star}(\{\{2\}^{n},3,\{2\}^{n},1\}^{d})=\sum_{m_{1}\geq\cdots\geq m_{2d}\geq 1}\frac{(-1)^{m_{1}+\cdots+m_{2d}}2^{\#\{m_{1},\dots,m_{2d}\}}}{m_{1}^{2n+2}\cdots m_{2d}^{2n+2}}.

Using this equality, we have

	$\displaystyle\lim_{d\to\infty}\zeta^{\star}(\{\{2\}^{n},3,\{2\}^{n},1\}^{d})$	$\displaystyle=2\prod_{m=2}^{\infty}\left(1+2\left(\frac{(-1)^{m}}{m^{2n+2}}+\frac{(-1)^{2m}}{m^{2(2n+2)}}+\cdots\right)\right)$
		$\displaystyle=2\prod_{m=2}^{\infty}\left(1+\frac{2}{(-1)^{m}m^{2n+2}-1}\right)$
		$\displaystyle=2\prod_{m=2}^{\infty}\left(\frac{m^{2n+2}+(-1)^{m}}{m^{2n+2}-(-1)^{m}}\right).$

Then we find

	$\displaystyle\lim_{d\to\infty}\zeta^{\star}(\{\{2\}^{n},3,\{2\}^{n},1\}^{d})$	$\displaystyle=2\prod_{m=2}^{\infty}\left(\frac{m^{2n+2}-1}{m^{2n+2}+1}\right)\times\prod_{m=2:\mathrm{even}}^{\infty}\left(\frac{m^{2n+2}+1}{m^{2n+2}-1}\right)^{2}$
		$\displaystyle=2\prod_{m=2}^{\infty}\left(\frac{m^{2n+2}-1}{m^{2n+2}+1}\right)\times\prod_{m=1}^{\infty}\left(\frac{m^{2n+2}+(1/2)^{2n+2}}{m^{2n+2}-(1/2)^{2n+2}}\right)^{2}.$

By a similar calculation as in Proof of Theorem 1.2 (3), we get

	$\displaystyle\lim_{d\to\infty}\zeta^{\star}(\{\{2\}^{n},3,\{2\}^{n},1\}^{d})$	$\displaystyle=2\frac{\prod_{c^{2n+2}=1}\Gamma(2-c)^{-1}\Gamma(1-\frac{c}{2})^{2}}{\prod_{c^{2n+2}=-1}\Gamma(2-c)^{-1}\Gamma(1-\frac{c}{2})^{2}}$
		$\displaystyle=2\prod_{s\in\{\pm 1\}}\prod_{c^{2n+2}=s}\Gamma(2-c)^{-s}\Gamma\left(1-\frac{c}{2}\right)^{2s}.\qed$

3. Order property and continuity of the zeta-star map

In this section, we will give a proof of Theorem 1.4.

Lemma 3.1.

For positive integers $a,b,A$ with $A\geq 2$ , we have

	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{m_{1}^{2}m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}\leq\sum_{n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(n_{1}-1)n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}},$
	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(m_{1}-1)m_{1}^{2}m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}$
	$\displaystyle\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq\left(\frac{A+1}{2A}\right)^{a}\sum_{n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(n_{1}-1)n_{1}^{k_{1}+1}n_{2}^{k_{2}}\cdots n_{b}^{k_{b}}}.$

Proof.

We have

	L.H.S. of the first equality
	$\displaystyle\leq\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(m_{1}-1)m_{1}m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\left(\frac{1}{m_{1}-1}-\frac{1}{m_{1}}\right)\cdot\frac{1}{m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}$
	$\displaystyle=\sum_{m_{2}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(m_{2}-1)m_{2}m_{3}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}.$

Repeating the similar calculations, we obtain the first result. As for the second equality, we have

	L.H.S. of the second equality
	$\displaystyle\leq\frac{A+1}{A}\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(m_{1}-1)m_{1}(m_{1}+1)m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}$
	$\displaystyle=\frac{A+1}{A}\sum_{m_{1}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{2}\left(\frac{1}{m_{1}(m_{1}-1)}-\frac{1}{m_{1}(m_{1}+1)}\right)\cdot\frac{1}{m_{2}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}$
	$\displaystyle=\frac{A+1}{2A}\sum_{m_{2}\geq\cdots\geq m_{a}\geq n_{1}\geq\cdots\geq n_{b}\geq A}\frac{1}{(m_{2}-1)m_{2}^{2}m_{3}\cdots m_{a}n_{1}^{k_{1}}\cdots n_{b}^{k_{b}}}.$

By repeating the above procedure, we obtain the second result. ∎

Proof that the map $\zeta^{\star}$ is order-reversing.

Let ${\bf k}=(k_{1},k_{2},\dots)\in\mathbb{Z}_{\geq 1}^{\infty}$ and ${\bf k}^{\prime}=(k_{1}^{\prime},k_{2}^{\prime},\dots)\in\mathbb{Z}_{\geq 1}^{\infty}$ . Put ${\bf k}_{+}=(k_{1}+1,k_{2},k_{3},\dots)$ for ${\bf k}$ and ${\bf k}^{\prime}_{+}$ in the same manner. Assume that ${\bf k}\prec{\bf k^{\prime}}$ by the lexicographic order. Then there exists $r\geq 1$ such that $k_{i}=k_{i}^{\prime}$ for $1\leq i<r$ and $k_{r}<k_{r}^{\prime}$ . Then

	$\displaystyle\zeta^{\star}({\bf k}_{+})$	$\displaystyle=\sum_{m_{1}\geq m_{2}\geq\cdots}\frac{1}{m_{1}^{k_{1}+1}m_{2}^{k_{2}}m_{3}^{k_{3}}\cdots}$
		$\displaystyle>\sum_{m_{1}\geq m_{2}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}+1}m_{2}^{k_{2}}\cdots m_{r}^{k_{r}}}$
		$\displaystyle=\zeta^{\star}(k_{1}+1,k_{2},\dots,k_{r})$

and

	$\displaystyle\zeta^{\star}({\bf k}^{\prime}_{+})$	$\displaystyle\leq\zeta^{\star}(k_{1}+1,k_{2},\dots,k_{r-1},k_{r}^{\prime},\{1\}^{\infty})$
		$\displaystyle=\zeta^{\star}(k_{1}+1,k_{2},\dots,k_{r-1},k_{r}^{\prime}-1)\leq\zeta^{\star}(k_{1}+1,k_{2},\dots,k_{r}).$

Thus, we have $\zeta^{\star}({\bf k}_{+})>\zeta^{\star}({\bf k}^{\prime}_{+})$ , i.e., $\zeta^{\star}$ is an order-reversing map. ∎

Proof that $\zeta^{\star}({\bf k})$ is convergent for ${\bf k}\neq(2,\{1\}^{\infty})$ .

Let ${\bf k}=(k_{1},k_{2},\dots)\in\mathbb{Z}_{\geq 1}^{\infty}$ with $k_{1}\geq 2$ and ${\bf k}\neq(2,\{1\}^{\infty})$ . Then there exists $n\geq 2$ such that $(\{2,\{1\}^{n-2}\}^{\infty})\prec{\bf k}$ . Thus, by Theorem 1.2 (4), $\zeta({\bf k})\leq\zeta(\{2,\{1\}^{n-2}\}^{\infty})=n$ , which implies the convergence of $\zeta({\bf k})$ . ∎

Proof that the map $Z^{\star}$ is continuous.

Let ${\bf k}=(k_{1},k_{2},\dots)\in\mathbb{Z}_{\geq 1}^{\infty}$ with $k_{1}\geq 2$ . We need to show that for any $\epsilon>0$ , there exists ${\bf l}$ and ${\bf l}^{\prime}$ such that

	$\displaystyle{\bf k}\prec{\bf k}^{\prime}\prec{\bf l}$	$\displaystyle\implies\zeta^{\star}({\bf k})-\zeta^{\star}({\bf k}^{\prime})<\epsilon,$
	$\displaystyle{\bf l}^{\prime}\prec{\bf k}^{\prime}\prec{\bf k}$	$\displaystyle\implies\zeta^{\star}({\bf k}^{\prime})-\zeta^{\star}({\bf k})<\epsilon.$

Since the sequence $\left(\zeta^{\star}(k_{1},\dots,k_{n})\right)_{n=1}^{\infty}$ is bounded and monotone increasing, there exist $r\geq 1$ such that

\zeta^{\star}(k_{1},\dots,k_{r})>\zeta^{\star}({\bf k})-\epsilon.

Thus

\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}+1,\{1\}^{\infty})>\zeta^{\star}({\bf k})-\epsilon.

By taking ${\bf l}=(k_{1},\dots,k_{r-1},k_{r}+1,\{1\}^{\infty})$ , we obtain the first line.

Now we will show the second line. We first show the claim for indices with a finite number of elements greater than or equal to $2$ . Let ${\bf k}=(k_{1},\dots,k_{r},\{1\}^{\infty})$ with $k_{r}\geq 2$ . Since

	$\displaystyle\lim_{a\to\infty}\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}-1,a+1,\{1\}^{\infty})$
	$\displaystyle=\lim_{a\to\infty}\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r-1}^{k_{r-1}}m_{r}^{k_{r}-1}}\sum_{s=1}^{m_{r}}\frac{1}{s^{a}}$
	$\displaystyle\leq\lim_{a\to\infty}\zeta(a)\sum_{m_{1}\geq\cdots\geq m_{r}\geq 1}\frac{1}{m_{1}^{k_{1}}\cdots m_{r-1}^{k_{r-1}}m_{r}^{k_{r}-1}}$
	$\displaystyle=\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}-1)$
	$\displaystyle=\zeta^{\star}({\bf k}),$

there exist $n\geq 1$ such that

\zeta^{\star}(k_{1},\dots,k_{r-1},k_{r}-1,n+1,\{1\}^{\infty})<\zeta^{\star}({\bf k})+\epsilon.

Thus, the claim holds for indices with a finite number of elements greater than or equal to $2$ .

Assume that there exists infinitely many $j$ such that $k_{j}>1$ .

{\bf k}=(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots)\qquad(a_{j}\geq 2,b_{j}\geq 0).

We need to show the existence of $s$ such that

\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots,a_{s-1},\{1\}^{b_{s-1}},a_{s}-1)<\zeta^{\star}({\bf k})+\epsilon.

Note that

	$\displaystyle\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots,a_{s-1},\{1\}^{b_{s-1}},a_{s}-1)-\zeta^{\star}({\bf k})$
	$\displaystyle<\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots,a_{s-1},\{1\}^{b_{s-1}},a_{s}-1)$
	$\displaystyle\quad-\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots,a_{s-1},\{1\}^{b_{s-1}},a_{s})$
	$\displaystyle\leq\zeta^{\star}(2,\{1\}^{b},2,\{1\}^{r-2},1)-\zeta^{\star}(2,\{1\}^{b},2,\{1\}^{r-2},2),$

where $b=b_{1}$ and $r=b_{2}+\cdots+b_{s-1}+s-1$ . Then we have

	$\displaystyle\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots,a_{s-1},\{1\}^{b_{s-1}},a_{s}-1)-\zeta^{\star}({\bf k})$
	$\displaystyle<\sum_{m\geq n_{1}\geq\cdots\geq n_{b+r}\geq 1}\frac{1}{m^{2}n_{1}\cdots n_{b}n_{b+1}^{2}n_{b+2}\cdots n_{b+r-1}}\left(\frac{1}{n_{b+r}}-\frac{1}{n_{b+r}^{2}}\right)$
	$\displaystyle=\sum_{m\geq n_{1}\geq\cdots\geq n_{b+r}\geq 2}\frac{1}{m^{2}n_{1}\cdots n_{b}n_{b+1}^{2}n_{b+2}\cdots n_{b+r-1}}\left(\frac{1}{n_{b+r}}-\frac{1}{n_{b+r}^{2}}\right)$
	$\displaystyle\leq\sum_{m\geq n_{1}\geq\cdots\geq n_{b+r}\geq 2}\frac{1}{m^{2}n_{1}\cdots n_{b}n_{b+1}^{2}n_{b+2}\cdots n_{b+r}}$
	$\displaystyle\leq\left(\frac{3}{4}\right)^{r-1}\sum_{n_{b+r}\geq 2}\frac{1}{(n_{b+r}-1)n_{b+r}^{2}}.$

Here, we used Lemma 3.1 for the last inequality. Thus, for any $\epsilon>0$ , there exists $s$ such that

\zeta^{\star}(a_{1},\{1\}^{b_{1}},a_{2},\{1\}^{b_{2}},\dots a_{s-1},\{1\}^{b_{s-1}},a_{s}-1)<\zeta^{\star}({\bf k})+\epsilon.

This finishes the proof. ∎

4. Analytic properties of the zeta-star map

This section investigates the differential of $Z^{\star}$ . Hereinafter, we understand $0^{0}=1$ .

Lemma 4.1.

For $z=\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ , we have

Z^{\star}(z)=\sum_{m_{1}\geq m_{2}\geq\cdots\geq 1}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}.

Proof.

Note that $a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots$ vanishes except for the case $m_{j}=m_{j+1}$ for all $j$ such that $a_{j}=0$ . The case where there exists infinitely many $j$ such that $a_{j}=1$ follows from the definition of $Z^{\star}$ . The case $z=0$ also follows from the definition of $Z^{\star}$ . The other case follows from Theorem 1.2 (1), e.g., when $a_{j}=\delta_{j,1}$ ,

	$\displaystyle Z^{\star}\left(\frac{1}{2}+\frac{0}{4}+\frac{0}{8}+\cdots\right)$	$\displaystyle=Z^{\star}\left(\frac{0}{2}+\frac{1}{4}+\frac{1}{8}+\cdots\right)=\zeta^{\star}(3,\{1\}^{\infty})$
		$\displaystyle=\zeta^{\star}(2)=\sum_{m_{1}\geq m_{2}\geq\cdots\geq 1}\frac{1^{m_{1}-m_{2}}0^{m_{2}-m_{3}}0^{m_{3}-m_{4}}}{m_{1}^{2}m_{2}m_{3}m_{4}\cdots}.\qed$

Lemma 4.2.

For $z=\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ , we have

Z^{\star}(z)=1+\frac{z}{2}+\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\left(z-\sum_{i=1}^{d-1}\frac{a_{i}}{2^{i}}\right).

Proof.

It follows from the following calculation

	$\displaystyle Z^{\star}(z)$	$\displaystyle=\sum_{m_{1}\geq m_{2}\geq\cdots\geq 1}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}$
		$\displaystyle=\sum_{1\leq d\leq e}\sum_{\begin{subarray}{c}m_{1}\geq\cdots\geq m_{d}\geq 3\\ 2=m_{d+1}=\cdots=m_{e}\\ 1=m_{e+1}=m_{e+2}=\cdots\end{subarray}}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}+\sum_{2\geq m_{1}\geq m_{2}\geq\cdots}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}.$

Here,

	$\displaystyle\sum_{1\leq d\leq e}\sum_{\begin{subarray}{c}m_{1}\geq\cdots\geq m_{d}\geq 3\\ 2=m_{d+1}=\cdots=m_{e}\\ 1=m_{e+1}=m_{e+2}=\cdots\end{subarray}}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}$
	$\displaystyle=\sum_{d=1}^{\infty}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)\sum_{e=d}^{\infty}\frac{a_{d}a_{e}}{2^{e-d}}$
	$\displaystyle=\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\left(z-\sum_{i=1}^{d-1}\frac{a_{i}}{2^{i}}\right)$

and

	$\displaystyle\sum_{2\geq m_{1}\geq m_{2}\geq\cdots}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}^{2}m_{2}m_{3}\cdots}$
	$\displaystyle=1+\frac{1}{2}\sum_{\begin{subarray}{c}2\geq m_{1}\geq m_{2}\geq\cdots\\ m_{1}\neq 1\end{subarray}}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}m_{2}m_{3}\cdots}$
	$\displaystyle=1+\frac{1}{2}\sum_{e=1}^{\infty}\sum_{\begin{subarray}{c}2=m_{1}=\cdots=m_{e}\\ 1=m_{e+1}=m_{e+2}=\cdots\end{subarray}}\frac{a_{1}^{m_{1}-m_{2}}a_{2}^{m_{2}-m_{3}}\cdots}{m_{1}m_{2}m_{3}\cdots}$
	$\displaystyle=1+\frac{1}{2}\sum_{e=1}^{\infty}\frac{a_{e}}{2^{e}}$
	$\displaystyle=1+\frac{z}{2}.\qed$

Lemma 4.3.

For $s\geq 1$ , we have

\sum_{m_{1}\geq\cdots\geq m_{s}\geq 3}\frac{1}{m_{1}^{4}m_{2}\cdots m_{s}}=O\left(\frac{s}{3^{s}}\right).

Proof.

For $x>0$ , put

F_{s}(x)=\sum_{m_{1}\geq\cdots\geq m_{s}\geq 3}\frac{1}{m_{2}\cdots m_{s}}\begin{cases}\frac{1}{m_{1}(m_{1}-1)(m_{1}-2)(m_{1}-3)}&\text{if }m_{1}>3,\\ x&\text{if }m_{1}=3.\end{cases}

Note that

	$\displaystyle\sum_{m=n}^{\infty}\frac{1}{m(m-1)(m-2)(m-3)}$	$\displaystyle=\frac{1}{3}\sum_{m=n}^{\infty}\left(\frac{1}{(m-1)(m-2)(m-3)}-\frac{1}{m(m-1)(m-2)}\right)$
		$\displaystyle=\frac{1}{3(n-1)(n-2)(n-3)}.$

Then

	$\displaystyle F_{s}(x)$	$\displaystyle=\sum_{\begin{subarray}{c}m_{2}\geq\cdots\geq m_{s}\geq 3\\ m_{2}>3\end{subarray}}\frac{1}{m_{2}\cdots m_{s}}\sum_{m_{1}=m_{2}}^{\infty}\frac{1}{m_{1}(m_{1}-1)(m_{1}-2)(m_{1}-3)}$
		$\displaystyle\quad+\quad\sum_{\begin{subarray}{c}m_{2}\geq\cdots\geq m_{s}\geq 3\\ m_{2}=3\end{subarray}}\frac{1}{m_{2}\cdots m_{s}}\left(\sum_{m_{1}=4}^{\infty}\frac{1}{m_{1}(m_{1}-1)(m_{1}-2)(m_{1}-3)}+x\right)$
		$\displaystyle=\frac{1}{3}\sum_{\begin{subarray}{c}m_{2}\geq\cdots\geq m_{s}\geq 3\\ m_{2}>3\end{subarray}}\frac{1}{m_{3}\cdots m_{s}}\cdot\frac{1}{m_{2}(m_{2}-1)(m_{2}-2)(m_{2}-3)}$
		$\displaystyle\quad+\frac{1}{3}\sum_{\begin{subarray}{c}m_{2}\geq\cdots\geq m_{s}\geq 3\\ m_{2}=3\end{subarray}}\frac{1}{m_{3}\cdots m_{s}}\left(\frac{1}{18}+x\right)$
		$\displaystyle=\frac{1}{3}F_{s-1}\left(x+\frac{1}{18}\right).$

Thus we have

F_{s}(x)=\frac{1}{3^{s-1}}F_{1}\left(x+\frac{s-1}{18}\right).

Hence we get

\displaystyle\sum_{m_{1}\geq\cdots\geq m_{s}\geq 3}\frac{1}{m_{1}^{4}m_{2}\cdots m_{s}}\leq F_{s}\left(\frac{1}{18}\right).

This finishes the proof. ∎

Lemma 4.4.

Let $a_{j}\in\{0,1\}$ for $1\leq j\leq d-1$ . Assume that $\sum_{i=1}^{t}(1-a_{i})\geq 2$ for some $t\leq d-1$ , then

\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}=O\left(\frac{d-t}{3^{d-t}}\right).

Proof.

From the assumption, let $a_{u}=a_{v}=0\;(u<v\leq t)$ and $a_{1}=\cdots=a_{u-1}=a_{u+1}=\cdots=a_{v-1}$ =1. Then

	L.H.S.	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{u}^{m_{u}-m_{u+1}}a_{v}^{m_{v}-m_{v+1}}a_{v+1}^{m_{v+1}-m_{v+2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}$
		$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{u}=m_{u+1}\geq\cdots\geq m_{v}=m_{v+1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{v+1}^{m_{v+1}-m_{v+2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}.$

Using Lemma 3.1, we have

L.H.S.

\displaystyle\leq\frac{3}{2}\sum_{m_{v+1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{v+1}^{m_{v+1}-m_{v+2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{v+1}^{4}m_{v+2}\cdots m_{d}}.

By Lemma 4.3, we obtain the result. ∎

Lemma 4.5.

Let $z=\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ and assume that $\sum_{i=1}^{t}(1-a_{i})\geq 2$ . Then we have

Z^{\star}(z)=1+\frac{z}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\left(z-\sum_{i=1}^{d-1}\frac{a_{i}}{2^{i}}\right)+O\left(\frac{r-t}{3^{r-t}}\right).

Proof.

Since

z-\sum_{i=1}^{d-1}\frac{a_{i}}{2^{i}}\leq\sum_{i=d}^{\infty}\frac{1}{2^{i}}=2^{1-d},

we have

	$\displaystyle\sum_{d=r+1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\left(z-\sum_{i=1}^{d-1}\frac{a_{i}}{2^{i}}\right)$
	$\displaystyle\leq 2\sum_{d=r+1}^{\infty}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)$
	$\displaystyle\leq 2\sum_{d=r+1}^{\infty}O\left(\frac{d-t}{3^{d-t}}\right)$

by Lemma 4.4. Note that in the above equality, the $O$ -constants are independent of $d$ . By Lemma 4.2, we get the result. ∎

Lemma 4.6.

Let $x=\sum_{j=1}^{\infty}a_{j}/2^{j}$ with $a_{j}\in\{0,1\}$ and $y=\sum_{j=1}^{\infty}b_{j}/2^{j}$ with $b_{j}\in\{0,1\}$ . Assume that $a_{j}=b_{j}$ for $j=1,\dots,r$ . Furthermore, assume that $\sum_{i=1}^{t}(1-a_{i})\geq 2$ with $t\leq r$ . Then

Z^{\star}(x)-Z^{\star}(y)=(x-y)\left(\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\right)+O\left(\frac{r-t}{3^{r-t}}\right).

Proof.

By Lemma 4.5, the proof is clear. ∎

Theorem 4.7.

Let $z=\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ . Assume that $\sum_{j=1}^{\infty}a_{j}=\infty$ and $\sum_{j=1}^{t}(1-a_{j})\geq 2$ for some $t$ . Then

\partial_{-}Z^{\star}(z):=\lim_{x\to z-0}\frac{Z^{\star}(z)-Z^{\star}(x)}{z-x}=\frac{1}{2}+\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}.

Thus, $Z^{\star}$ is left-differentiable at $z$ if $z\not\in\{1-\frac{1}{2^{n}}\mid n>0\}$ .

Proof.

Take $0<x<z$ and put $x=\sum_{j=1}^{\infty}\frac{b_{j}}{2^{j}}$ . Let $p=p(x)$ be the minimal integer such that $(a_{p},b_{p})=(1,0)$ . Put

y=\sum_{j=1}^{p}\frac{a_{j}}{2^{j}}=\sum_{j=1}^{p-1}\frac{a_{j}}{2^{j}}+\frac{1}{2^{p+1}}+\frac{1}{2^{p+2}}+\cdots.

Furthermore, let $r$ be the maximal integer such that

a_{p+1}=a_{p+2}=\cdots=a_{r}=0

and

b_{p+1}=b_{p+2}=\cdots=b_{r}=1.

Then by Lemma 4.6, we have

Z^{\star}(z)-Z^{\star}(y)=(z-y)\left(\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\right)+O\left(\frac{r-t}{3^{r-t}}\right)

and

Z^{\star}(y)-Z^{\star}(x)=(y-x)\left(\frac{1}{2}+\sum_{d=1}^{r}b_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{b_{1}^{m_{1}-m_{2}}\cdots b_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\right)+O\left(\frac{r-t}{3^{r-t}}\right).

From the intermediate value theorem, there exists a real number $u(x)$ between

\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}

and

\frac{1}{2}+\sum_{d=1}^{r}b_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{b_{1}^{m_{1}-m_{2}}\cdots b_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}

such that

Z^{\star}(z)-Z^{\star}(x)=(z-x)u(x)+O\left(\frac{r-t}{3^{r-t}}\right).

Since

	$\displaystyle z-x$	$\displaystyle\geq\frac{1}{2^{p}}-\frac{1}{2^{p+1}}-\cdots-\frac{1}{2^{r}}-\sum_{j=r+2}^{\infty}\frac{1}{2^{j}}$
		$\displaystyle=\frac{1}{2^{r+1}},$

we have

\frac{Z^{\star}(z)-Z^{\star}(x)}{z-x}=u(x)+O\left(r(2/3)^{r}3^{t}\right).

By the condition $\sum_{j=1}^{\infty}a_{j}=\infty$ , we have $\lim_{x\to z-0}p(x)=\infty$ and thus

\lim_{x\to z-0}u(x)=\frac{1}{2}+\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d},

which completes the proof. ∎

Theorem 4.8.

Let $z=\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ and assume that $\sum_{j=1}^{\infty}(1-a_{j})=\infty$ . Then

\partial_{+}Z^{\star}(z):=\lim_{x\to z+0}\frac{Z^{\star}(z)-Z^{\star}(x)}{z-x}=\frac{1}{2}+\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}.

Thus, $Z^{\star}$ is right-differentiable at $z$ for any $0\leq z<1$ .

Proof.

Take $x\in(z,1)$ and put $x=\sum_{j=1}^{\infty}\frac{b_{j}}{2^{j}}$ . Let $p=p(x)$ be the minimal integer such that $(a_{p},b_{p})=(0,1)$ . Put

y=\sum_{j=1}^{p}\frac{b_{j}}{2^{j}}=\sum_{j=1}^{p-1}\frac{b_{j}}{2^{j}}+\frac{1}{2^{p+1}}+\frac{1}{2^{p+2}}+\cdots.

Furthermore, let $r$ be the maximal integer such that

a_{p+1}=a_{p+2}=\cdots=a_{r}=1

and

b_{p+1}=b_{p+2}=\cdots=b_{r}=0.

Then by Lemma 4.6, we have

Z^{\star}(x)-Z^{\star}(y)=(x-y)\left(\frac{1}{2}+\sum_{d=1}^{r}b_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{b_{1}^{m_{1}-m_{2}}\cdots b_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\right)+O\left(\frac{r-t}{3^{r-t}}\right)

and

Z^{\star}(y)-Z^{\star}(z)=(y-z)\left(\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}\right)+O\left(\frac{r-t}{3^{r-t}}\right).

From the intermediate value theorem, there exists a real number $u(x)$ between

\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}

and

\frac{1}{2}+\sum_{d=1}^{r}b_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{b_{1}^{m_{1}-m_{2}}\cdots b_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}

such that

Z^{\star}(z)-Z^{\star}(x)=(z-x)u(x)+O\left(\frac{r-t}{3^{r-t}}\right).

Since

	$\displaystyle\|z-x\|$	$\displaystyle\geq\frac{1}{2^{p}}-\frac{1}{2^{p+1}}-\cdots-\frac{1}{2^{r}}-\sum_{j=r+2}^{\infty}\frac{1}{2^{j}}$
		$\displaystyle=\frac{1}{2^{r+1}},$

we have

\frac{Z^{\star}(z)-Z^{\star}(x)}{z-x}=u(x)+O\left(r(2/3)^{r}3^{t}\right).

By the condition $\sum_{j=1}^{\infty}(1-a_{j})=\infty$ , we have $\lim_{x\to z+0}p(x)=\infty$ and thus

\lim_{x\to z+0}u(x)=\frac{1}{2}+\sum_{d=1}^{\infty}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d},

which completes the proof. ∎

Remark 4.9.

By Theorems 4.7 and 4.8, if $z$ admits a $2$ -adic expansion $\sum_{j=1}^{\infty}\frac{a_{j}}{2^{j}}$ satisfying $\sum_{j=1}^{\infty}a_{j}=\sum_{j=1}^{\infty}(1-a_{j})=\infty$ , then $\partial_{+}Z^{\star}(z)=\partial_{-}Z^{\star}(z)$ . This implies Theorem 1.7 (4).

Theorem 4.10.

For $z=\sum_{j=1}^{r}\frac{a_{j}}{2^{j}}$ with $a_{j}\in\{0,1\}$ and $a_{r}=1$ , we have

\partial_{+}Z^{\star}(z)=\frac{1}{2}+\sum_{d=1}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}

and

\partial_{-}Z^{\star}(z)=\partial_{+}Z^{\star}(z)+\sum_{m_{1}\geq\cdots\geq m_{r}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{r-1}^{m_{r-1}-m_{r}}}{m_{1}^{2}m_{2}\cdots m_{r}}2^{r}(m_{r}-2)\qquad(z\neq 1-1/2^{r}).

Proof.

The first statement is just a special case of Theorem 4.8. Since

z=\sum_{j=1}^{r-1}\frac{a_{j}}{2^{j}}+\frac{1}{2^{r+1}}+\frac{1}{2^{r+2}}+\cdots,

we have

	$\displaystyle\partial_{-}Z^{\star}(z)$	$\displaystyle=\frac{1}{2}+\sum_{d=1}^{r-1}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}$
		$\displaystyle\quad+\sum_{d=r+1}^{\infty}\left(\sum_{m_{1}\geq\cdots\geq m_{r}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{r-1}^{m_{r-1}-m_{r}}}{m_{1}^{2}m_{2}\cdots m_{r}}\sum_{m_{r}=m_{r+1}\geq\cdots\geq m_{d}\geq 3}\frac{1}{m_{r+1}\cdots m_{d}}\right)2^{d}$

by Lemma 4.7. Since

\displaystyle\frac{2^{r+1}}{m_{r}}\prod_{n=3}^{m_{r}}\sum_{c=0}^{\infty}\left(\frac{2}{n}\right)^{c}=\frac{2^{r+1}}{m_{r}}\prod_{n=3}^{m_{r}}\frac{n}{n-2}=2^{r}(m_{r}-1),

the third term equals

	$\displaystyle\sum_{p=0}^{\infty}\left(\sum_{m_{1}\geq\cdots\geq m_{r}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{r-1}^{m_{r-1}-m_{r}}}{m_{1}^{2}m_{2}\cdots m_{r}}\frac{1}{m_{r}}\sum_{m_{r}\geq n_{1}\geq\cdots\geq m_{p}\geq 3}\frac{1}{n_{1}\cdots n_{p}}\right)2^{p+r+1}\qquad(p=d-r-1)$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{r}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{r-1}^{m_{r-1}-m_{r}}}{m_{1}^{2}m_{2}\cdots m_{r}}\cdot\frac{2^{r+1}}{m_{r}}\prod_{n=3}^{m_{r}}\sum_{c=0}^{\infty}\left(\frac{2}{n}\right)^{c}$
	$\displaystyle=\sum_{d=r}^{r}a_{d}\left(\sum_{m_{1}\geq\cdots\geq m_{d}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{d-1}^{m_{d-1}-m_{d}}}{m_{1}^{2}m_{2}\cdots m_{d}}\right)2^{d}+\sum_{m_{1}\geq\cdots\geq m_{r}\geq 3}\frac{a_{1}^{m_{1}-m_{2}}\cdots a_{r-1}^{m_{r-1}-m_{r}}}{m_{1}^{2}m_{2}\cdots m_{r}}2^{r}(m_{r}-2).$

Thus the theorem is proved. ∎

5. Divergence of left-differential

In this section, we give a proof of Theorem 1.7 (3).

Lemma 5.1.

Fix $r\geq 1$ . Then we have

\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}\leq\frac{1}{(n-1)\cdots(n-r)r^{s}}

for all $s\geq 1$ and $n\geq r+1$ . Furthermore, there exists $C_{r}\in\mathbb{R}_{>0}$ such that

\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}\geq\frac{1}{(n-1)\cdots(n-r)r^{s}}-\frac{C_{r}}{(n-1)\cdots(n-r)(n-r-1)(r+1)^{s}}

for all $s\geq 1$ and $n\geq r+2$ .

Proof.

The first claim follows from

	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$
	$\displaystyle\leq\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}(m_{1}-1)\cdots(m_{1}-r)m_{2}\cdots m_{s}}$
	$\displaystyle=\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{r}\left(\frac{1}{(m_{1}-1)\cdots(m_{1}-r)}-\frac{1}{m_{1}(m_{1}-1)\cdots(m_{1}-r+1)}\right)\frac{1}{m_{2}\cdots m_{s}}$
	$\displaystyle=\sum_{m_{2}\geq\cdots\geq m_{s}\geq n}\frac{1}{r}\cdot\frac{1}{(m_{2}-1)\cdots(m_{2}-r)}\cdot\frac{1}{m_{2}\cdots m_{s}}$
	$\displaystyle=\cdots$
	$\displaystyle=\frac{1}{(n-1)\cdots(n-r)r^{s}}.$

There exists $C_{r}\in\mathbb{R}_{>0}$ such that

\frac{1}{m^{r+1}}\geq\frac{1}{m(m-1)\cdots(m-r)}-\frac{C_{r}}{m(m-1)\cdots(m-r-1)}

for all $m\geq r+2$ . Then, the second claim follows from

	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$
	$\displaystyle\geq\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}(m_{1}-1)\cdots(m_{1}-r)m_{2}\cdots m_{s}}$
	$\displaystyle\quad-C_{r}\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}(m_{1}-1)\cdots(m_{1}-r-1)m_{2}\cdots m_{s}}$
	$\displaystyle=\frac{1}{(n-1)\cdots(n-r)r^{s}}-\frac{C_{r}}{(n-1)\cdots(n-r)(n-r-1)(r+1)^{s}}.\qed$

Lemma 5.2.

Fix $r\geq 1$ . Then there exists $D_{r}\in\mathbb{R}_{>0}$ such that

\frac{1}{r!r^{s}}-\frac{sD_{r}}{(r+1)^{s}}\leq\sum_{m_{1}\geq\cdots\geq m_{s}\geq r+1}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}\leq\frac{1}{r!r^{s}}

for all $s\geq 1$ .

Proof.

We have

	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{s}\geq r+1}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$	$\displaystyle=\sum_{i=0}^{s}\sum_{\begin{subarray}{c}m_{1}\geq\cdots\geq m_{i}\geq r+2\\ m_{i+1}=\cdots=m_{s}=r+1\end{subarray}}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$
		$\displaystyle\geq\sum_{i=1}^{s}\frac{1}{(r+1)^{s-i}}\sum_{m_{1}\geq\cdots\geq m_{i}\geq r+2}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{i}},$

and by the second claim of the previous lemma,

	$\displaystyle\geq\sum_{i=1}^{s}\frac{1}{(r+1)^{s-i}}\left(\frac{1}{(r+1)!r^{i}}-\frac{C_{r}}{(r+1)!(r+1)^{i}}\right)$
	$\displaystyle=\frac{1}{r!r^{s}}-\frac{1}{(r+1)!(r+1)^{s-1}}-\frac{sC_{r}}{(r+1)!(r+1)^{s}}$

This proves the lower bound for the inequality, and the upper bound follows from the first claim of the previous lemma. ∎

Lemma 5.3.

Fix $r\geq 1$ . Then there exists $E_{r}\in\mathbb{R}_{>0}$ such that

\displaystyle\frac{s-E_{r}}{r!r^{s}}

\displaystyle\leq\sum_{m_{1}\geq\cdots\geq m_{s}\geq r}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}-\frac{1}{r^{r+s}}\leq\frac{s}{r!r^{s}}

for all $s\geq 1$ .

Proof.

We have

	$\displaystyle\sum_{m_{1}\geq\cdots\geq m_{s}\geq r}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$	$\displaystyle=\frac{1}{r^{r+s}}+\sum_{i=1}^{s}\sum_{\begin{subarray}{c}m_{1}\geq\cdots\geq m_{i}\geq r+1\\ m_{i+1}=\cdots=m_{s}=r\end{subarray}}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}$
		$\displaystyle=\frac{1}{r^{r+s}}+\sum_{i=1}^{s}\frac{1}{r^{s-i}}\sum_{m_{1}\geq\cdots\geq m_{i}\geq r+1}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{i}}.$

Here, by the previous lemma,

\frac{1}{r!r^{i}}-\frac{iD_{r}}{(r+1)^{i}}\leq\sum_{m_{1}\geq\cdots\geq m_{i}\geq r+1}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{i}}\leq\frac{1}{r!r^{i}}.

Furthermore,

\sum_{i=1}^{s}\frac{1}{r^{s-i}}\left(\frac{1}{r!r^{i}}\right)=\frac{s}{r!r^{s}}

and

	$\displaystyle\sum_{i=1}^{s}\frac{1}{r^{s-i}}\left(\frac{iD_{r}}{(r+1)^{i}}\right)$	$\displaystyle=D_{r}r\left(r^{1-s}+r^{-s}-r(r+1)^{-s}-(s+1)(r+1)^{-s}\right)$
		$\displaystyle\leq D_{r}r\left(\frac{r+1}{r^{s}}\right).$

Putting $E_{r}=D_{r}r(r+1)r!$ , we obtain the lemma. ∎

By Lemmas 5.1 and 5.3, we have

\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}\asymp_{r}\begin{cases}\frac{1}{(n-1)\cdots(n-r)r^{s}}&n>r\\ \frac{s}{r^{s}}&n=r.\end{cases}

Thus we have the following:

Lemma 5.4.

Fix $r\geq 1$ . We have

\displaystyle\sum_{n=r}^{\infty}\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{r+1}m_{2}\cdots m_{s}}\asymp\frac{s}{r^{s}}

for all $s\geq 1$ .

Theorem 5.5.

Fix $p>0$ and put $z=1-\frac{1}{2^{p}}$ . Then for $h=\frac{1}{2^{q}}$ with $q>p$ , we have

\displaystyle\frac{Z^{\star}(z)-Z^{\star}(z-h)}{h}

\displaystyle\asymp q.

Thus, $Z^{\star}$ is not left-differentiable at $1-\frac{1}{2^{p}}$ .

Proof.

We only consider the case $q>p+1$ . Note that

z=\sum_{\begin{subarray}{c}k=1\\ k\neq p\end{subarray}}^{\infty}\frac{1}{2^{k}}\quad\text{ and }\quad z-h=\sum_{\begin{subarray}{c}k=1\\ k\neq p,q\end{subarray}}^{\infty}\frac{1}{2^{k}}.

By definition, we have

Z^{\star}(z)=\sum_{\begin{subarray}{c}m_{1}\geq m_{2}\geq\cdots\geq 1\\ m_{p}=m_{p+1}\end{subarray}}\frac{1}{m_{1}^{2}m_{2}m_{3}\cdots}

and

Z^{\star}(z-h)=\sum_{\begin{subarray}{c}m_{1}\geq m_{2}\geq\cdots\geq 1\\ m_{p}=m_{p+1},m_{q}=m_{q+1}\end{subarray}}\frac{1}{m_{1}^{2}m_{2}m_{3}\cdots}.

Then we have

	$\displaystyle Z^{\star}(z)-Z^{\star}(z-h)$	$\displaystyle=\sum_{\begin{subarray}{c}m_{1}\geq m_{2}\geq\cdots\geq 1\\ m_{p}=m_{p+1},m_{q}>m_{q+1}\end{subarray}}\frac{1}{m_{1}^{2}m_{2}m_{3}\cdots}$
		$\displaystyle\asymp\sum_{\begin{subarray}{c}m_{1}\geq m_{2}\geq\cdots\geq 1\\ m_{p}=m_{p+1},m_{q}>m_{q+1}\end{subarray}}\frac{1}{m_{1}(m_{1}-1)m_{2}m_{3}\cdots}$
		$\displaystyle=\sum_{\begin{subarray}{c}m_{p}\geq m_{p+1}\geq\cdots\geq 1\\ m_{p}=m_{p+1},m_{q}>m_{q+1}\end{subarray}}\frac{1}{m_{p}(m_{p}-1)m_{p+1}m_{p+2}\cdots}$
		$\displaystyle=\sum_{\begin{subarray}{c}m_{p+1}\geq\cdots\geq 1\\ m_{q}>m_{q+1}\end{subarray}}\frac{1}{m_{p+1}^{2}(m_{p+1}-1)m_{p+2}m_{p+3}\cdots}.$

Similar to the proof of Lemma 2.1, we have

	$\displaystyle Z^{\star}(z)-Z^{\star}(z-h)$
	$\displaystyle\asymp\sum_{m_{p+1}\geq\cdots\geq m_{q}\geq 2}\frac{1}{m_{p+1}^{2}(m_{p+1}-1)m_{p+2}m_{p+3}\cdots m_{q}}\sum_{m_{q}>m_{q+1}\geq m_{q+2}\cdots}\frac{1}{m_{q+1}m_{q+2}\cdots}$
	$\displaystyle=\sum_{m_{p+1}\geq\cdots\geq m_{q}\geq 2}\frac{1}{m_{p+1}^{2}(m_{p+1}-1)m_{p+2}m_{p+3}\cdots m_{q}}\prod_{m=2}^{m_{q}-1}\frac{m}{m-1}$
	$\displaystyle=\sum_{m_{p+1}\geq\cdots\geq m_{q}\geq 2}\frac{m_{q}-1}{m_{p+1}^{2}(m_{p+1}-1)m_{p+2}m_{p+3}\cdots m_{q}}$
	$\displaystyle\asymp\sum_{m_{p+1}\geq\cdots\geq m_{q}\geq 2}\frac{1}{m_{p+1}^{3}m_{p+2}m_{p+3}\cdots m_{q-1}}.$

Hence we get

	$\displaystyle Z^{\star}(z)-Z^{\star}(z-h)$	$\displaystyle\asymp\sum_{n=2}^{\infty}\sum_{m_{p+1}\geq\cdots\geq m_{q-1}\geq n}\frac{1}{m_{p+1}^{3}m_{p+2}m_{p+3}\cdots m_{q-1}}$
		$\displaystyle=\sum_{n=2}^{\infty}\sum_{m_{1}\geq\cdots\geq m_{s}\geq n}\frac{1}{m_{1}^{3}m_{2}m_{3}\cdots m_{s}},$

where $s=q-p-1>0.$ By Lemma 5.4, we find

\displaystyle Z^{\star}(z)-Z^{\star}(z-h)

\displaystyle\asymp\frac{s}{2^{s}}\asymp qh,

which completes the proof. ∎

Acknowledgements

This work was supported by JSPS KAKENHI Grant Numbers JP18K13392, JP19K14511, JP22K03244, and JP22K13897.

References

[1] K. Kumar, Order Structure and Topological Properties of the Set of Multiple Zeta Values, Int. Math. Res. Notices 2016, 1541–1562.
[2] J. Li, The topology of the set of multiple zeta-star values, arXiv:2309.07569.
[3] Y. Ohno and N. Wakabayashi, Cyclic sum of multiple zeta values, Acta Arithmetica 123 (2006), 289–295.
[4] J. Zhao, Identity families of multiple harmonic sums and multiple zeta (star) families, J. Math. Soc. Japan 68 (2016), 1669–1694.
[5] S.A. Zlobin, Generating functions for the values of a multiple zeta function, Vestnik Moskov. Univ. Ser. I Mat. Mekh. no. 2 (2005), 55–59; Moscow Univ. Math. Bull. 60 (2005), 44–48 (English transl.).

Multiple zeta-star values for indices of infinite length

Abstract.

Key words and phrases:

2020 Mathematics Subject Classification:

1. Main result

Definition 1.1.

Theorem 1.2.

Example 1.3.

Theorem 1.4.

Remark 1.5.

Remark 1.6.

Theorem 1.7.

2. Special values

Lemma 2.1.

Proof.

Proof of Theorem 1.2 (1).

Proof of Theorem 1.2 (2).

Proof of Theorem 1.2 (3).

Proof of Theorem 1.2 (4).

Proof of Theorem 1.2 (5).

Proof of Theorem 1.2 (6).

3. Order property and continuity of the zeta-star map

Lemma 3.1.

Proof.

Proof that the map ζ⋆\zeta^{\star} is order-reversing.

Proof that ζ⋆​(𝐤)\zeta^{\star}({\bf k}) is convergent for 𝐤≠(2,{1}∞){\bf k}\neq(2,\{1\}^{\infty}).

Proof that the map Z⋆Z^{\star} is continuous.

4. Analytic properties of the zeta-star map

Lemma 4.1.

Proof.

Lemma 4.2.

Proof.

Lemma 4.3.

Proof.

Lemma 4.4.

Proof.

Lemma 4.5.

Proof.

Lemma 4.6.

Proof.

Theorem 4.7.

Proof.

Theorem 4.8.

Proof.

Remark 4.9.

Theorem 4.10.

Proof.

5. Divergence of left-differential

Lemma 5.1.

Proof.

Lemma 5.2.

Proof.

Lemma 5.3.

Proof.

Lemma 5.4.

Theorem 5.5.

Proof.

Acknowledgements

References

Proof that the map $\zeta^{\star}$ is order-reversing.

Proof that $\zeta^{\star}({\bf k})$ is convergent for ${\bf k}\neq(2,\{1\}^{\infty})$ .

Proof that the map $Z^{\star}$ is continuous.