Multiple stellar populations in Asymptotic Giant Branch stars of Galactic Globular Clusters
Abstract
Multiple stellar populations (MPs) are a distinct characteristic of Globular Clusters (GCs). Their general properties have been widely studied among main sequence, red giant branch (RGB) and horizontal branch (HB) stars, but a common framework is still missing at later evolutionary stages.
We studied the MP phenomenon along the AGB sequences in 58 GCs, observed with the Hubble Space Telescope in ultraviolet (UV) and optical filters. By using UV-optical color-magnitude diagrams, we selected the AGB members of each cluster and identified the AGB candidates of the metal-enhanced population in type II GCs. We studied the photometric properties of AGB stars and compared them to theoretical models derived from synthetic spectra analysis.
We observe the following features: i) the spread of AGB stars in photometric indices sensitive to variations of light-elements and helium is typically larger than that expected from photometric errors; ii) the fraction of metal-enhanced stars in the AGB is lower than in the RGB in most of the type II GCs; iii) the fraction of 1G stars derived from the chromosome map of AGB stars in 15 GCs is larger than that of RGB stars; v) the AGB/HB frequency correlates with the average mass of the most helium-enriched population.
These findings represent a clear evidence of the presence of MPs along the AGB of Galactic GCs and indicate that a significant fraction of helium-enriched stars, which have lower mass in the HB, does not evolve to the AGB phase, leaving the HB sequence towards higher effective temperatures, as predicted by the AGB-manqué scenario.
1 Introduction
A peculiar feature of the chemical composition of stars belonging to Milky Way Globular Clusters (GCs) is the significant variation of light-elements such as helium, carbon (C), nitrogen (N), oxygen (O) and sodium (Na), observed only in a tiny fraction of the Galactic bulge (%, Schiavon et al., 2017) and halo field stars (%, Martell et al., 2011).
In few GCs, stars also show difference in magnesium (Mg) and aluminum (Al) content. The observed chemical variations are not random but follow trends defined by the anti-correlation C-N, O-Na, and Mg-Al. In particular, every GC includes two main stellar groups: 1G, composed of stars with halo-like chemical composition; 2G composed of stars depleted in C and O, and enhanced in N, Na and helium with respect to 1G. When observed in color-magnitude diagrams (CMDs) obtained by combining ultraviolet (UV) and optical observations, 1G and 2G stars lie on distinct sequences, called multiple stellar populations (MPs). The current framework of MPs in Galactic GCs largely derives from the study of the spectroscopic and photometric properties of red giant branch (RGB) stars (e.g. Milone et al., 2017; Lagioia et al., 2018; Marino et al., 2019). In a limited number of GCs it has also been possible to clearly identify MPs in fainter stars, thanks to the detection of split main sequences in CMDs (Anderson, 1997; D’Antona et al., 2005; Piotto et al., 2007; Milone et al., 2013, 2015a; Bellini et al., 2017b, e.g.).
The study of MPs at later evolutionary stages, is more problematic. In the case of horizontal branch (HB) stars, both age-metallicity and helium-mass loss degeneracy hamper a proper understanding of the impact that chemical variations have on the color distribution of core helium-burning stars in CMDs (see e.g. Sandage & Wildey, 1967; Fusi Pecci et al., 1993; Catelan et al., 2001; Tailo et al., 2020). This indetermination propagates to the subsequent evolutionary phase, the asymptotic giant branch (AGB), where the uncertain definition of the sub-populations distribution is further amplified by statistical fluctuations due to the fast evolutionary timescale of AGB stars (Greggio & Renzini, 1990).
A viable solution to this issue is provided by the direct spectroscopic determination of the atmospheric abundance of the light proton-capture tracing MPs (Sneden et al., 2000). In this context, early studies found evidence of significant difference in CN band strength between RGB and AGB stars in NGC 5904 (M 5) and NGC 6752, with the latter being biased toward the CN-weak populations Norris et al. (see 1981); Smith & Norris (see 1993). The same disproportion in CN-band distribution was also detected later in NGC 1851 AGB stars (Campbell et al., 2012). More recently, works based on high-resolution determination of abundance of Na, a light element not involved in internal mixing processes during the RGB evolution (Kraft, 1994; Carretta et al., 2009), confirmed the lack of Na-rich stars in the AGB of some GCs.
For instance, the Na content of 20 AGB stars of NGC 6752 analyzed by Campbell et al. (2013), was found to be lower than dex, corresponding to the abundance threshold separating 1G and 2G RGB stars (Carretta et al., 2012; Milone et al., 2013). Later on, through the analysis of new spectroscopic data of the same sample of stars, Lapenna et al. (2016) confirmed a relative lack of 2G members among NGC 6752 AGB stars, with none of them associated to the most Na- and helium-rich cluster population (Carretta et al., 2012; Milone et al., 2013). Interestingly, this finding seems to confirm the theoretical scenario predicted for the evolution of the hot HB stars of NGC 6752 (Villanova et al., 2009; Cassisi et al., 2014; Tailo et al., 2019b). Indeed, hot HB stars with tiny hydrogen-rich atmospheres, usually associated to the most helium-rich GC population(s) (e.g. D’Antona et al., 2002; Milone et al., 2018), would skip the early-AGB phase, characterized by a progressive expansion and cooling of the HB star envelope, and instead evolve to higher temperatures and luminosities until they reach the white-dwarf cooling sequence. The shell helium-burning phase of these stars is therefore called AGB-manqué (Greggio & Renzini, 1990).
A confirmation of this prediction would come from the recent spectroscopic analysis of the AGB stars of NGC 2808, a GC cluster known for its extended (and complex) HB morphology, linked to one of the largest internal helium variations observed among Galactic GCs (Y, with Y = helium mass fraction, Milone et al., 2015a). Indeed, Marino et al. (2017) identified three groups of AGB stars with distinct Na abundance, following the typical Na-O anti-correlation trend observed for the cluster RGB stars, with the distribution skewed towards lower Na RGB values (see also Wang et al., 2016), thus implying that the extremely helium-enhanced cluster stars evolved as AGB manqué.
However, a similar outcome has been found in NGC 6121 (M 4) which, at the contrary of NGC 2808, is not populated by extremely hot HB stars (Marino et al., 2008; Villanova et al., 2012) and shows a rather small internal helium enrichment (Y Milone et al., 2018). As in the previous case, Marino et al. (2017) and Wang et al. (2017) found that the Na-poor and Na-rich cluster AGB star roughly cover the lowest two thirds of the [Na/Fe] abundance range occupied by the cluster RGB stars, thus suggesting that part of the 2G cluster stars could not reach the AGB phase (MacLean et al., 2016).
Dispersion in Mg-Al abundance has also been employed to explore MPs in the AGB stars of GCs with different HB morphology. For instance, Lapenna et al. (2015) found no Al-rich stars among the AGB stars of NGC 6266 (M 62), a result indicating the total lack of of 2G AGB stars and compatible with the large helium variation detected from main sequence stars color difference by Milone (2015). Conversely, in their spectroscopic analyses, García-Hernández et al. (2015) and Masseron et al. (2019) found a similar spread in the AGB and RGB stars of NGC 5024 (M 53), NGC 5272 (M 3), NGC 6205 (M 13), NGC 6341 (M 92), NGC 7078 (M 15), and NGC 7089 (M 2).
In principle, spectroscopic discrepancies might be reduced by claiming either zero-point offsets in the abundances obtained from different datasets or with different reduction techniques (see e.g. Campbell et al., 2017), or the adoption of arbitrary thresholds for the selection of typical abundances in 1G and 2G AGB stars (Marino et al., 2017). However, an effective solution to the “AGB problem”, namely the unexpected high fraction of 2G stars avoiding the AGB phase (Campbell et al., 2013), requires an homogeneous definition of the observational properties of these stars in large samples of GCs. In this regard, photometry represents an ideal tool because it provides the necessary multiplexing capability. For instance, Gratton et al. (2010) adopted a statistical approach to analyze the relation between the parameter , namely the numerical fraction of AGB-to-HB stars in a GC (Caputo et al., 1989), and the minimum mass along the HB, for a sample of 21 clusters. They found that blue-extended HB-morphology clusters attain values smaller than the rest of GCs. This result would be consistent with the AGB-manqué prediction.
Another approach is represented by the study of MPs through the use of filter combinations that trace the different chemical content of stars through the variation of their flux at different wavelengths. The two main solutions adopted so far are the index or pseudo-color = , sensitive to C, N, O stellar content thanks to the specific pass-band of the F275W, F336W, and F438W filters, available at the UV and Visual (UVIS) channel of the Wide Field Planetary Camera 3 (WFC3) on board Hubble Space Telescope (HST Milone et al., 2015b), and = , sensitive to the content of N, O, and helium through the F814W filter. From the previous definitions it follows that the latter index is not as sensitive as the former to the presence of MPs. Its lower accuracy is, however, counterbalanced by two clear upsides: the existence of a corresponding ground-based version = (Marino et al., 2008; Monelli et al., 2013) and, as a consequence, the possibility of being used in the post-HST era (Lagioia et al., 2019a).
The measurement of the color spread of stars in both previous combinations, usually referred to as width, , provides a general view of the total chemical variations in the host GCs, and can be employed for a direct comparison of the MP properties in GCs with different age, mass, and metallicity, as already done in extensive studies of MPs in Galactic and extra-galactic GCs, by using the width of RGB stars (Milone et al., 2017; Lagioia et al., 2019b). In principle, therefore, the same approach can also be adopted with AGB stars. Indeed, few recent works have clearly shown that AGB stars are spread over color intervals comparable to those observed for RGB stars, like in the case of NGC 7089 (Milone et al., 2015b), NGC 2808 (Milone et al., 2015a), and NGC 6121 (Lardo et al., 2017; Marino et al., 2019). Moreover, the direct comparison between AGB and RGB star width in any given cluster could provide a solid evidence of missing MPs in AGB phase (Marino et al., 2017).
The quantity , although representing a direct evidence of GC internal chemical variations, cannot provide the necessary resolution for the study of the detailed chemical composition of a cluster. A powerful tool has been recently introduced to overcome this problem: the so-called chromosome map (ChM, Milone et al., 2015b, a, 2017). This photometric diagram correlates the spread of stars in two different color combinations, each one sensitive to different features of the spectrum of a star. The most comprehensive ChM compilation published so far (Milone et al., 2017) includes all the 57 GCs observed in the HST UV Legacy Survey (Piotto et al., 2015) and has provided the most detailed glimpse into the complex composition of Galactic GCs. In particular, the ChM combines the information of the with the large-baseline color , that is sensitive to metallicity and helium variations. In this context, the recent analysis by Marino et al. (2017) has shown that the ChM of the AGB stars of NGC 2808 present a degree of complexity comparable with that visible in the ChM of RGB stars (Milone et al., 2015b), with three distinct groups corresponding to as many different spectroscopic abundances. It is unfortunately not as easy to obtain the ChM of AGB stars as for the RGB for plain evolutionary reasons. Indeed, the AGB evolutionary timescale is about ten times faster than that of RGB stars brighter than HB stars (Greggio & Renzini, 1990). It follows that only a limited number of GCs can provide the necessary statistical significance for a detailed MP study.
All the aforementioned findings represent a clear signature that chemical variations are also a common property of AGB stars, and offer a compelling motivation for the extension of the MP analysis to a larger sample of clusters, which is the purpose of the present work. For this reason, we decided to analyze the observational properties of the AGB stars of all the clusters observed in the HST UV Legacy Survey (Piotto et al., 2015), in the same photometric bands adopted for the study of MPs along the RGB (Milone et al., 2017).
Section 2 of the present paper describes the methodology for the selection of the AGB and RGB samples in each analyzed cluster, the identification of AGB stars belonging to the metal-rich population (hereafter called anomalous) in type II GCs, and the measurement of the color spread, or width, of the selected sample in specific photometric indices. Section 3 reports the computation of appropriate evolutionary models for the comparison between observed width and theoretical predictions. Section 4 illustrates the relation existing between the AGB and RGB width. Section 5 show the procedure for the construction of the ChM of clusters with well populated AGB samples, and the analysis of population ratios. Section 6 describes the relation between the frequency of AGB stars and chemical enrichment in GCs. Finally, Section 7 provides a summary of the analysis and a description of the contribution of this work to the MP phenomenology in GCs.
2 Data reduction and analysis
The dataset analyzed in this work comprises a total of 58 clusters, including the 57 GCs observed in the UV Legacy Survey of Galactic GCs (Piotto et al., 2015), and the distant Galactic cluster NGC 2419 (Zennaro et al., 2019). All the 57 UV Legacy Survey GCs have been observed in the WFC3/UVIS broad-bands F275W, F336W, and F438W, and complemented with the F606W and F814W observations collected for the ACS Survey of Galactic GCs (Sarajedini et al., 2007). A complete description of the image database, exposure times, and reduction techniques is reported in Piotto et al. (2015); Milone et al. (2018) and Nardiello et al. (2018). Details about database and reduction procedure of NGC 2419 data are provided in the recent paper by Zennaro et al. (2019), to which we refer the interested reader.
In a nutshell, the photometry of every cluster has been derived by analyzing the images with the suite Kitchen Sync 2 (see Sabbi et al., 2016; Bellini et al., 2017a), originally developed by J. Anderson for the analysis of ACS images (Anderson et al., 2008). The suite is comprised of FORTRAN routines which recursively analyze the pixel values on the images and apply a local-peak finding algorithm. In each analyzed image, a selection of relatively bright stars is used to model a grid of spatially-variable point spread functions (PSF), which represent the best-fit model for stars detected at different locations on the chip.
The position and flux of stars with different luminosity are determined with two different approaches. For bright stars, position and flux are independently determined in each single exposure and then averaged, while for faint stars an average position is computed from all the images where a star is detected, and then the flux is determined at that position by using the best-fit PSF.
Finally, stellar positions are corrected for geometrical distortion by using the solution of Bellini & Bedin (2009) and Bellini et al. (2011). Instrumental magnitudes are calibrated to the VEGAMAG system as in Bedin et al. (2005).
A selection of well-measured stars has been performed by using the parameters of photometric quality produced by the reduction software as in Milone et al. (2009). The photometry of clusters affected by significant differential reddening has been also corrected as in Milone et al. (2012a). Finally, the cluster membership has been established on the basis of relative proper motions as done in Milone et al. (2018).
2.1 Identification of AGB stars
A reliable identification of the AGB stars in each GC is a critical step in our analysis. The procedure detailed below is based on the observational features of AGB stars at different wavelengths.
The AGB phase begins at the onset of helium-shell burning. In low mass stars, this phase is characterized by an electron-degenerate CO core whose mass increases as the helium shell moves outwards. During the first evolutionary stages, referred as early-AGB (EAGB), the of the low mass AGB stars steadily decreases while the luminosity increases, until they asymptotically reach the typical values of RGB stars. From this moment on, EAGB stars evolve by increasing their luminosity and decreasing , with values slightly higher than those of RGB stars, eventually becoming colder and brighter than the brightest RGB stars near the AGB tip (see e.g. Kamath et al., 2012).
In optical CMDs, variations between stars are visible as color differences. At relatively high luminosities, random photometric errors are of the order, or even larger, than the color differences corresponding to the small temperature differences between AGB and RGB stars, thus making it challenging to identify stars at different evolutionary stages. On the other side, since the UV flux of EAGB stars is significantly higher than that of RGB stars at similar luminosities, the two sequences appear well distinct in far UV-optical CMDs (Lagioia et al., 2015, and references therein). Such a behavior is shown in Figure 1, where we plotted the vs. CMD (panel a) and the vs. CMD (panel b) of the brightest stars of the Galactic GC NGC 5024. In the first CMD, at mag, we can distinguish two sequences of stars, running almost parallel in the bottom-left – top right direction, separated by a color gap of less than 1 mag: the bluest and brightest sequence is populated by AGB stars, while the reddest by RGB stars. We can also recognize, at colors bluer than mag, the presence of a third group, mainly composed of HB stars. The distinct location of these three stellar groups in the UV-optical CMD allows a straightforward separation of the diagram into different regions, whose boundaries, marked by the dotted lines in the plot, have been used to assign an evolutionary status to the plotted stars. For the sake of clarity, we decided to represent AGB, RGB, and HB stars as red, dark-gray, and light-gray colored points, respectively. In passing, we notice that in this CMD, the increasing F336W luminosity trend of RGB stars is reversed at mag because of the increasing importance of line blanketing by metals for the coldest spectral type stars at UV wavelengths (see Buzzoni et al., 2010, and references therein).

In the optical CMD of panel (b), we plotted with the same color code the previously selected AGB, RGB and HB stars of NGC 5024. As mentioned before, the determination of the AGB evolutionary membership in optical CMDs is thwarted by the small (less than 0.05 mag) color differences between AGB and RGB stars. We notice, however, that in this CMD all the AGB stars selected in the UV-optical CMD of panel (a) are bluer (hotter) than RGB stars at the same luminosity, thus demonstrating that our method produces a reliable selection of bona-fide AGB stars.
Nonetheless, the selection procedure may also result in few ambiguous attributions that are addressed by checking the location of equivocal cases in CMDs obtained by using different band combinations. In the case of NGC 5024, for instance, we can identify two of such stars. One star, marked by the black triangle, that appears to be an AGB star in the CMD of panel (a) and (b), lies almost beyond the red RGB boundary in the vs. CMD displayed in panel (c). Another star, marked with a square, lies at the border of the RGB region in the CMD of panel (a), and appears as an AGB in the optical CMD of panel (b). However in panel (c) the same star has a color too blue with respect to the rest of AGB stars. This comparison led us to exclude both the previous candidate AGBs from the NGC 5024 AGB sample.
The above procedure has been applied to identify the AGB candidates in every cluster of our dataset except for a group of ten peculiar GCs. These clusters, that in the extensive analysis of Milone et al. (2017) have been classified as type II GCs, as opposed to the rest of clusters classified as type I, show a significant internal variation of [Fe/H] and heavy elements (Marino et al., 2019, and references therein). The photometric signature of this feature is revealed by the presence of a secondary RGB sequence, redder than main one(s) in the color (see Figs. 10–18 in Milone et al., 2017). This group of RGB stars is usually referred to as anomalous population.
In the case of type II CMDs, our selection method may result in a spurious bias that would exclude some AGB members belonging to the anomalous population. To show this, we plot in panel (d) of Fig. 1, the vs. CMD of the type II GC NGC 7089 (M 2). As for NGC 5024, we defined three regions containing the majority of cluster AGB, RGB, and HB stars, plotted with the previously adopted color code. In the RGB region, we can see a sparse group of stars fainter than the bulk of other RGBs, composed by the cluster anomalous population. However, in the vs. CMD displayed in panel (e), the two RGB sequences are indistinguishable. As a consequence, also the anomalous AGB stars will attain the same colors of the other cluster AGB members. For this reason, we empirically defined a region, indicated by the dashed line, that includes all the stars with location compatible with the AGB phase. We observe that six stars classified as RGB members in the UV-optical CMD, and marked with an open starred symbol, fall in this region. We see that three of them lie along the main RGB sequence in the UV-optical CMD of panel (d), two have F336W magnitudes typical of the anomalous RGB sequence, while the remaining one lies at the border of the RGB region. Their location in both the CMDs indicate that they are probable candidates of the AGB anomalous population and, therefore, they have been merged to the cluster AGB sample.
Interestingly, in the optical CMD we observe a star, that we marked with an open circle, having two peculiar features: i) it is mag bluer than AGB stars at the same luminosity; ii) it has , thus lying beyond the displayed limits of the UV-optical CMD of panel (d). The bluer optical color and the strong UV flux suggest that this star is a post-EAGB candidate, namely a star with very small hydrogen-rich envelope, that fails to reach the thermal-pulse AGB phase, leaving off the asymptotic branch towards higher (Greggio & Renzini, 1990). We notice that the presence of a small mass envelope is also connected with an higher mass loss during the RGB evolution, which is in turn linked to higher helium content in stars (Tailo et al., 2019a). Milone et al. (2018) found that the maximum internal helium variation, , of NGC 7089 is as high as , therefore corroborating the hypothesis on the peculiar nature of this star.
The method described above has been used for the selection of the sample of AGB stars in all the others type II clusters, namely NGC 362, NGC 1261, NGC 1851, NGC 5139 (), NGC 5286, NGC 6715 (M 54), NGC 6388, and NGC 6934.
The total number of AGB stars, , identified in each cluster, has been reported in Table 1 together with the total number of RGB stars, , brighter than the faintest AGB candidate in F814W band. We notice that since no AGB stars have been found in NGC 5053 and NGC 6121, the corresponding entries are empty. In all the other 56 GCs, ranges from 1 (NGC 6397) to 161 (NGC 6441). Among them, 21 GCs have . Since statistical significance is an important factor in the determination of the photometric properties of AGB stars, we empirically assumed as a lower limit for the inclusion of a GC in the following analysis.
It is important here to stress the fact that the procedure for the selection of the AGB candidates in type II GCs can results in a not complete definition of the sample of their anomalous population. A better understanding of this phenomenon requires, however, a deeper evaluation of the fraction of stars left out by the adopted selection method, as done in the following section.
2.2 Completeness of the AGB identifications in type II clusters
In the previous section we have seen that in the vs. CMD, the AGB sequence of the anomalous population on type II GCs intersects the RGB sequence. This implies that part of the anomalous AGB population can be left out by our selection procedure. To prevent this issue, we have also seen that we can take advantage of the color, where the AGB sequences of all the cluster stellar populations occupy the same region. Conversely, optical colors are far from ideal for selecting AGB and RGB stars because the separation of the two evolutionary sequences is comparable with the typical photometric error at their characteristic luminosities. This implies that optical CMDs will only provide a partial solution to the aforementioned issue.
It is therefore necessary to evaluate the maximum fraction of anomalous AGB stars missed by our selection procedure. To this purpose, we performed a series of simulations where we constructed artificial CMDs composed by stellar populations with different iron abundance. To build the artificial CMDs, we took advantage of appropriate evolutionary models from the MESA 111http://waps.cfa.harvard.edu/MIST/ database (Choi et al., 2016). In particular, we used isochrones of 13.5, 12.5, and 11.5 Gyr at different [Fe/H] values, ranging from to dex in steps of 0.15 dex. For each grid point, we simulated two artificial CMDs with [Fe/H] and 0.30 dex. The age and metallicity interval roughly covers the entire range spanned by the studied Type II GCs, while the observed average difference in [Fe/H] content between metal-rich and metal-poor stars in these clusters is smaller than dex (Marino et al., 2019, and references therein).
Figure 2 shows an example of our simulations obtained from 12.5 Gyr isochrones with [Fe/H] and [Fe/H], to which we will refer as metal-poor and metal-rich population, respectively. Each simulated population is composed of stars with a random flat distribution of initial masses higher than that of the corresponding model’s turn-off. Artificial magnitudes have been obtained by interpolation on the initial mass values of the isochrone. To each simulated magnitude has been assigned a random error based on a Gaussian distribution with the typical dispersion of our observations. The resulting vs. and vs. artificial CMDs are displayed in the left and right panel of the figure, where for the sake of clarity we decided to plot only 50,000 stars in each simulated population. Moreover, we marked the interval corresponding to the location of the EAGB phase with a dashed line. In particular we used the blue color for the metal-poor population, and the red color for the metal-rich one.
The left diagram shows that the metal-rich AGB sequence intersects the metal-poor RGB one, so that the most evolved metal-rich AGBs appear fainter than the brightest metal poor RGBs, in F336W band. This fact clearly indicates that the adopted AGB selection method can leave out part of the bright metal-rich AGB population. In order to estimate the fraction of missed stars, we performed the following steps: i) we tagged as input AGB members the simulated stars with initial mass falling in the interval defined by the upper and lower limit of the model EAGB range; ii) as done for the observations, we defined by eye a region delimiting the probable AGB candidates, as indicated by the black box in both the diagrams; iii) we flagged as AGB members the stars falling in either box-delimited region; iv) we compared the number of recovered and input AGB stars to estimate the fraction of lost AGB stars. By applying the above procedure for different combinations of age and metallicity, we found that the maximum fraction of missed AGB stars of the metal-rich stellar population is % when [Fe/H] and % when [Fe/H], corresponding respectively to a completeness of % and %, as reported in the right panel. The missed stars are mostly composed by AGB stars at later evolutionary stages. Our simulations also show that a small fraction (%) of metal-poor stars is left out by our selection: this derives from the non-perfect location and extension of the AGB-delimiting region. We can therefore consider 1% as the random error associated to our completeness estimates.
The most significant variations of completeness have been observed for the most metal-poor and metal-rich bins of the analyzed metallicity range, and for . In the first case the completeness of the metal-rich population is %, while it reduces to nearly zero for the most metal-rich bin, where the metal-rich AGB is all fainter and redder than the metal-poor RGB. We emphasize however that none of the type II GCs in our GC database has metallicity lower than dex, and that for the most metal-rich Type II studied GC, namely NGC 6388 (, Harris, 1996, 2010 update), the internal iron variation is negligible (see Carretta & Bragaglia, 2018). Finally, we notice that similar results have been obtained by using models of 13.5 and 11.5 Gyr.
Our analysis indicates that the maximum fraction of anomalous AGB stars missed by our selection procedure is negligible when the metallicity difference between the anomalous and other GC stars is smaller than dex. This fraction rapidly increases, becoming significant at metallicity differences larger than dex. Moreover, in the interval considered in our simulations, cluster age has a negligible effect on the results.

2.3 AGB candidates of the anomalous population in type II clusters
In this section we seek AGB candidates of the anomalous population in type II clusters (Milone et al., 2017). To do this we take advantage of their vs CMD. Indeed, as shown by Milone et al. (2017), this diagram represents an efficient tool to separate populations with different metallicity in GCs.

Figure 3 shows the vs CMDs of the ten Type II GCs included in our database, arranged from the less to the most metal-rich. In each CMD, we marked with red points the AGB candidates found through the selection procedure described in Sect. 2.1. We see that in all the CMDs the majority of AGB members occupy the uppermost portion of the diagram, except for a group of few stars that have F336W luminosities comparable with or lower than that of RGB stars at the same colors. As seen in the previous section, this indicates that they are likely to be members of the AGB anomalous population. However, since our AGB selection procedure is mainly based on the location of stars in the vs CMD, some of the AGB stars not belonging to the anomalous population may attain colors similar to those of RGB stars in the narrower color-baseline vs CMD. According to this consideration, we identified as the most probable members of the anomalous AGB population, only those AGB stars fainter-redder than the main RGB, while the AGBs lying at the blue border of the main RGB sequence have been excluded. In the case of NGC 5139 and NGC 6388, since no clear separation is visible between the different cluster RGB sequences, we decided to flag as anomalous AGBs all the stars redder - fainter than the blue limit of the main RGB sequence. Since the majority of anomalous AGB candidates in NGC 6388 attain similar colors, we decided to use a wider panel in order to stretch the horizontal scale of the plot. In each panel, the selected anomalous AGB candidates have been marked with an open starred symbol in each CMD. We notice that in two clusters, namely NGC 1261 and NGC 6934, no anomalous AGBs were found, while only one anomalous AGB candidate has been identified in NGC 6656, which is one of the clusters with the highest fraction () of anomalous population RGB stars among those analyzed by Milone et al. (2017). On the other side, the highest number of AGB candidates have been detected in the three massive GCs NGC 5139 (9) NGC 6388 (11), and NGC 6715 (8).
Figure 4 shows the relation between the fraction of anomalous candidate AGBs, , as a function of the fraction of anomalous RGB stars determined by Milone et al. (2017). For each cluster , the error associated to the estimate of the fraction of anomalous AGBs has been obtained by performing 50,000 simulations of values randomly distributed in the interval . For each simulation, we evaluated the fraction of simulated values smaller than the -th value. Finally the 68th percentile of the resulting distribution has been taken as the error associated to the anomalous AGB fraction. The black dashed line in the plot marks the identity relation.
We see that in six GCs the fraction of anomalous RGBs is significantly higher than that of the AGBs, thus suggesting that part of their anomalous population does not reach the asymptotic branch. In NGC 362 and NGC 7089 the fraction of anomalous AGBs is higher, but consistent within one sigma with that of RGB stars. We also notice that these two clusters are among the Type II GCs with the lowest fraction of anomalous RGB stars (respectively % and %; Milone et al., 2017). As a consequence, small random statistical fluctuations can significantly affect the estimate of their fraction of anomalous AGBs.

2.4 Determination of the AGB and RGB width
The photometric footprint of the presence of MPs in GCs is represented by the color spread of stars, observed in CMDs where specific color combinations, sensitive to the content variation of light-elements and helium, are used. The two main choices adopted so far are the index and : the first mostly traces chemical differences in O, N, and C, while the second in N, C and helium.
The vs. pseudo-CMDs of the brightest stars in all the analyzed GCs, sorted in ascending order of metallicity, are displayed in Figures 5, 6, 7, 8, 9, 10 and 11. For the sake of convenience we decided to not show also the vs. pseudo-CMDs of our targets. In each CMD, the gray points represent the cluster RGB and HB stars, while the red points the AGB candidates. The black error bars on the left side of each panel indicate the typical photometric errors of the AGB stars.
A quick look at the CMDs shows that the AGB sequences are much wider than the spread expected from observational errors alone in all the analyzed GCs, except in eight clusters, namely NGC 7099, NGC 4590, NGC 5466, NGC 6397, NGC 6809, NGC 6535, NGC 6218, and NGC 6496, that have a poorly populated sequence of AGB stars with a spread comparable with the pseudo-color error. On the other hand, the poorly populated AGB sequence of NGC 2298, NGC 5897, NGC 6541, NGC 6144, NGC 3201, NGC 288, NGC 6717, NGC 6362, NGC 6352, NGC 6838, and NGC 6366 displays a clear spread. The pseudo-color broadening observed in the CMDs clearly show that MPs are a common characteristic of the analyzed GCs.







A deeper view into the properties of MPs can be obtained through the analysis of their color extension. Figure 12 illustrates the procedure for the measurement of the width of the AGB and the upper RGB stars of NGC 7089. Panel (a) shows the vs. pseudo-CMD of the brightest cluster stars, where gray and red points represent respectively RGB/HB members and AGB candidates. We also highlighted the anomalous AGB stars of the clusters with the usual red starred symbol. So we did with the post-EAGB candidate, marked with a black starred symbol. Stars in this diagram follow an almost vertical trend along all the displayed magnitude interval until mag, where they move towards bluer colors because of the effect of line blanketing, as seen in the previous section. As such, all the AGB/RGB stars brighter than this threshold have been excluded from the following computation. We therefore defined a magnitude interval, delimited by the long-dashed horizontal lines, extended from the brightest to the faintest cluster AGB star, not belonging to the cluster anomalous AGB sample, which has been discarded in the following procedure. We then divided this luminosity range in three magnitude bins, delimited by the dotted horizontal lines. For each bin i, we measured the 80th percentile of the pseudo-color distribution of the AGB and of the RGB star sample, indicated respectively by open circles and triangles. Then, we linearly interpolated these points along the magnitude values attained by the AGB and by the RGB stars included in the selected magnitude interval. The interpolation line was then used to ‘verticalize’ the CMD of the AGB stars (panel b) and of the RGB stars (panel c). In these two diagrams, the abscissa of each star, , and , corresponds to the difference between its pseudo-color and the pseudo-color of the interpolating function at the same F814W magnitude, whose abscissa is now identically equal to zero. Finally, we computed the 10th and the 90th percentile of the distribution, marked by the red (gray) short-dashed vertical lines in panel b (c), and took the absolute difference between these two values as the width of the cluster AGB (RGB) stars, .
The same method was applied to obtain the pseudo-color width of the cluster AGB (RGB) stars, , as shown in panel (d), (e) and (f) of Fig. 12. In this case we used the 20th percentile distribution of the AGB (RGB) stars in the selected magnitude interval, as shown in panel (d). Since the x-axis interval of the diagrams in panel (b), (c), (e), and (f) spans 1 mag, we can see that the observed width of the cluster AGB (RGB) stars in the is about a factor of two smaller than that measured in the pseudo-color .
The error in the determination of the width of the AGB and RGB stars, in both the pseudo-colors, has been estimated by performing 10,000 bootstrapping tests on random sampling with replacement. Each test was carried out by generating a simulated sample containing sequential copies of the and . Then a random sub-sample composed of a number of stars equal to the observed one was extracted and the resulting width computed. The 68.27th percentile of the distribution of simulated measurements was taken as the standard error of the observed width.
The procedure described so far has been applied to measure the AGB and RGB width of the other clusters. Since the number of detected AGB stars varies from one cluster to another, as well as the covered F814W magnitude interval, the number of adopted bins has been changed accordingly from a minimum of 2 to a maximum of 3. The AGB members of NGC 6304 are oddly distributed in magnitude, with the majority of them spanning a very narrow interval. For this reason, it has not been possible to get a reliable estimate of their pseudo-color extension, and the cluster has not been included in the analysis described in the forthcoming section.

Photometric errors also affect the observed pseudo-color spread by introducing a spurious contribution to the intrinsic width of the cluster AGB and RGB stars. To estimate this additional spread we took advantage of the photometric errors previously determined, to simulate an artificial pseudo-color distribution and measure the corresponding width, with the same procedure used for the observations. The simulated width values have been subtracted in quadrature from the corresponding observed width values to obtain the intrinsic widths , , and . We have reported the AGB and RGB intrinsic width together with the corresponding error at columns 4 and 5, and 6 and 7, respectively for the pseudo-color and .
The listed and values indicate that the intrinsic color spread of AGB stars in all the clusters with more than 9 AGB members, is larger than that expected from photometric errors alone. This finding, based on the largest database of GCs analyzed so far, provides a clear indication that AGB sequences of the 35 analyzed GCs host multiple stellar populations.
| ID | ||||||
|---|---|---|---|---|---|---|
| NGC 104 | 29 | 71 | ||||
| NGC 288 | 3 | 6 | - | - | - | - |
| NGC 362 | 29 | 87 | ||||
| NGC 1261 | 31 | 69 | ||||
| NGC 1851 | 38 | 75 | ||||
| NGC 2298 | 7 | 15 | - | - | - | - |
| NGC 2419 | 83 | 373 | ||||
| NGC 2808 | 83 | 196 | ||||
| NGC 3201 | 3 | 4 | - | - | - | - |
| NGC 4590 | 7 | 15 | - | - | - | - |
| NGC 4833 | 16 | 50 | ||||
| NGC 5024 | 32 | 112 | ||||
| NGC 5053 | 0 | - | - | - | - | - |
| NGC 5139 | 31 | 53 | ||||
| NGC 5272 | 15 | 71 | ||||
| NGC 5286 | 69 | 138 | ||||
| NGC 5466 | 8 | 15 | - | - | - | - |
| NGC 5897 | 5 | 12 | - | - | - | - |
| NGC 5904 | 15 | 54 | ||||
| NGC 5927 | 17 | 52 | ||||
| NGC 5986 | 38 | 98 | ||||
| NGC 6093 | 35 | 117 | ||||
| NGC 6101 | 11 | 17 | ||||
| NGC 6121 | 0 | - | - | - | - | - |
| NGC 6144 | 7 | 12 | - | - | - | - |
| NGC 6171 | 13 | 16 | ||||
| NGC 6205 | 14 | 66 | ||||
| NGC 6218 | 4 | 21 | - | - | - | - |
| NGC 6254 | 10 | 25 | ||||
| NGC 6304 | 11 | 28 | - | - | - | - |
| NGC 6341 | 15 | 64 | ||||
| NGC 6352 | 4 | 11 | - | - | - | - |
| NGC 6362 | 5 | 14 | - | - | - | - |
| NGC 6366 | 2 | 3 | - | - | - | - |
| NGC 6388 | 158 | 268 | ||||
| NGC 6397 | 1 | 2 | - | - | - | - |
| NGC 6441 | 161 | 246 | ||||
| NGC 6496 | 2 | 11 | - | - | - | - |
| NGC 6535 | 3 | 9 | - | - | - | - |
| NGC 6541 | 8 | 27 | - | - | - | - |
| NGC 6584 | 11 | 27 | ||||
| NGC 6624 | 15 | 33 | ||||
| NGC 6637 | 29 | 54 | ||||
| NGC 6652 | 8 | 15 | - | - | - | - |
| NGC 6656 | 10 | 70 | ||||
| NGC 6681 | 12 | 23 | ||||
| NGC 6715 | 84 | 248 | ||||
| NGC 6717 | 7 | 14 | - | - | - | - |
| NGC 6723 | 23 | 39 | ||||
| NGC 6752 | 11 | 29 | ||||
| NGC 6779 | 14 | 27 | ||||
| NGC 6809 | 3 | 10 | - | - | - | - |
| NGC 6838 | 6 | 6 | - | - | - | - |
| NGC 6934 | 23 | 56 | ||||
| NGC 6981 | 14 | 22 | ||||
| NGC 7078 | 34 | 192 | ||||
| NGC 7089 | 68 | 216 | ||||
| NGC 7099 | 6 | 14 | - | - | - | - |
3 Impact of light elements on the colors of AGB stars
To qualitatively investigate the typical effects of changing the abundances of He, C, N, and O on the colors and magnitudes of AGB stars, we combined isochrones and synthetic spectra of AGB stars with appropriate chemical compositions. We used the evolutionary code ATON 2.0 (Ventura et al., 1998; Mazzitelli et al., 1999; Ventura et al., 2009) to calculate 12 Gyr-old isochrones with [Fe/H], [/Fe] but different RGB mass loss, helium content and C, N, and O abundance (see D’Antona et al., 2002; Tailo et al., 2019b, 2020, for details).
We first investigated the effect of helium and mass-loss variations on the AGBs. We calculated an isochrone with pristine helium content (Y), [C/Fe]=0.0, [N/Fe]=0.0 and [O/Fe]=0.4 and RGB mass loss . Moreover, we derived two helium-enhanced isochrones with Y with the same C, N and O content as above and different mass losses of and . Finally, we computed three isochrones with Y, [C/Fe]=0.5, [N/Fe]=1.21 and [O/Fe]=0.1 and .
To account for the effect of C, N and O variations on the studied isochrones, we extended the procedure by Milone et al. (2012b, 2018) to the AGB. We identified five points along each isochrone with [C/Fe]=0, [N/Fe]=0 and [O/Fe]=0.4 and extracted their and gravity (). We used ATLAS12 and SYNTHE computer programs (e.g. Castelli, 2005; Kurucz, 2005; Sbordone et al., 2007, 2011) to calculate a spectrum with [C/Fe]=0.0, [N/Fe]=0.0, and [O/Fe]=0.4 (reference spectrum) and a spectrum with enhanced nitrogen [N/Fe]=1.21 and depleted carbon and oxygen ([C/Fe] and [O/Fe]). All spectra are computed over the wavelength interval between 2000 Å and 10,000 Å and are convoluted with the throughput of the F275W, F336W, F438W WFC3/UVIS filters and the F606W and F814W ACS/WFC filters used in this paper.
As an example, the uppermost panel of Figure 13 compares the spectra of two AGB stars with Y=0.25, , K and . The red spectrum is representative of 1G star and has [C/Fe]=0.0, [N/Fe]=0.0 and [O/Fe]=0.4, whereas the C, N, O content of the blue spectrum resembles 2G stars ([C/Fe]=0.5, [N/Fe]=1.21 and [O/Fe]=0.1). We calculate the magnitude difference between each point of the two spectra as -2.5 times the logarithm of their flux ratio and plot this quantity as a function of the wavelength. For comparison, we over-plotted the transmission curves of the five filters used in this paper. Clearly, the 2G spectrum provides F336W magnitude fainter than the 1G ones, mostly due to the NH band around 3,600 Å. 2G stars also exhibit brighter F275W and F438W magnitudes, as a consequence of the strength of the OH and CH molecular bands, respectively. Hence, C, N, and O variations in the spectra of AGB stars show a qualitative behavior similar to that observed in RGB stars (e.g. Milone et al., 2012b).
Synthetic spectra are convoluted with the throughput of the five filters used in this paper to derive the corresponding magnitudes. The magnitude differences between the comparison and the reference spectrum are added to the corresponding magnitudes of the isochrones with 1G-like chemical composition to derive the corresponding isochrones enhanced in N and depleted in C and O.



4 Comparison between AGB and RGB width
The photometric width as standard measurement of the amount of internal chemical variations gives us the ability to compare the properties of MPs across the entire parameter-space spanned by GCs. In this regard, recent works have demonstrated that a significant correlation exists between the spread of RGB in the indices and , and cluster’s metallicity and mass (Milone et al., 2017; Lagioia et al., 2019a). For this reason we decided to study the relation between the AGB and RGB width.
In the top panel of Figure 14, we plot vs. of the 35 clusters, listed in Table 1, for which the measurement of the relative quantities is available. In the diagram, each point has been color-coded according to the corresponding cluster’s metallicity [Fe/H] (Harris, 1996, 2010 update), mapped to the color scale reported in the legend. We see that the two represented quantities follow, on average, a positive correlation. In order to provide a reference for the comparison, we overplotted three lines representing the identity relation (dashed line), and the relations and (top and bottom dotted lines). We observe that the majority of GCs (27 out of 35 GCs) have AGB width smaller than the RGB width, and that among them, 7 GCs have , with the remarkable cases of NGC 2419, NGC 5139 (), and NGC 6752, the three GCs with the smallest AGB/RGB width ratio. On the other hand, NGC 6341 and NGC 5927 are the only two clusters lying above the line. Their relatively large error bars, however, do not allow to draw strong conclusions. The color distribution seems to suggest the presence of a mild monotonic trend between the AGB intrinsic width and metallicity, with the most metal-rich clusters having on average larger width values.
The bottom panel displays the scatter plot of vs. . As before, we also overplotted the same three reference lines. We observe that all the clusters lie within the region defined by the and lines, with the clusters quite uniformly distributed above and below the identity relation line. Only two clusters, namely NGC 6341 and NGC 6752, have AGB/RGB width ratios larger than 1.5. While the first cluster shows a behavior similar to that observed in the previous case, that of NGC 6752 is reversed. However, we highlight the fact that the AGB width estimate of this cluster has been derived from a relatively low number of stars (11) and, as a consequence, it is poorly constrained, as also indicated by its large error bars. Therefore, again, no firm conclusion can be achieved about these two GCs. We finally notice the absence of any trend with metallicity in this color combination.
The relation between AGB and RGB width visible in both the diagrams clearly indicates that none of the observed clusters have a mono-populated AGB sequence. The trend visible in the top panel shows that, on average, the AGB width is smaller than the RGB width. In the hypothesis that in each cluster all the stellar populations in the RGB evolve to the AGB, we would expect to observe AGB widths comparable with or larger than those of the corresponding RGB stars. The displayed trend instead, indicates that the AGB width is on average smaller than the RGB width. This finding clearly suggests that in the majority of clusters a significant fraction of 2G stars does not evolve to the AGB, as predicted by the AGB-manqué scenario. Our finding, based on a large sample of GCs, provides a robust evidence of the existence of this phenomenon.
We emphasize that the displayed trend may include some spurious scatter due to the specific evolutionary conditions of each different cluster: mass loss has, indeed, an important effect on the color spread of AGB stars, as seen in the previous section. This implies that a precise evaluation of the chemical variations corresponding to every AGB width measurement can be obtained through the comparison between observations and theoretical models, suitably tailored to the specific properties of each analyzed cluster. However, a one-to-one comparison between the AGB and RGB width of each cluster is beyond the purpose of the present analysis.

5 The chromosome maps of AGB stars
The analysis of the AGB width presented in the previous section provides a strong indication about the presence of MPs along the AGB of the analyzed GCs, as well as of the partial depletion of MPs due to the evolution of the most chemically-enriched stars as AGB-manqué. To further investigate this phenomenon, we exploited the ChM of AGB stars. The construction of the ChM of the GCs analyzed in the present work, shown in Figure 15 for the template cluster NGC 2808, is based on the method introduced by Milone et al. (2015a) and extended to the AGB by Marino et al. (2017). In the figure, panel (a) displays the portion of the vs. pseudo-CMD of the cluster, zoomed on the AGB stars. AGB stars are represented as red points, while all the other visible stars, mainly composed by bright RGBs, as light-gray points. As described in Section 2.4, we excluded the brightest AGB cluster stars, which are shown as light-red points. Long-dashed horizontal lines delimit the selected luminosity interval. The left and right dashed black curves represent, respectively, the 4th and 96th percentile of the pseudo color-distribution of the AGB stars. They have been obtained by dividing the entire luminosity interval in 4 bins and then computing, for each bin, the color corresponding to the 4th and 96th percentile of the color distribution. We then applied a boxcar-average smoothing to the observed distribution points and finally fit the resulting pseudo-colors by a cubic spline along the central magnitude of the bins. We then performed a double-normalization by subtracting to the pseudo-color of each star, the corresponding value along the 96th percentile fit curve, and dividing the result by the distance between the point of the 4th and 96th fit curve at the same magnitude (see equation 1 and 2 in Milone et al., 2017). The ratio has been finally multiplied by the factor , corresponding to the intrinsic width of the AGB stars. This quantity is defined as the observed distance between the fit curves at a reference luminosity equal to 5 mag brighter than the main-sequence turn-off in F814W band, minus the contribution due to the photometric error, as described in the previous section.
The luminosity of the main sequence turn-off has been determined by applying the naive estimator method (Silverman, 1986). This procedure consists in subdividing a pre-selected F814W magnitude range centered on the turn-off region of the CMD, in a number of magnitude bins. For each bin the median color and magnitude of stars is computed. The same algorithm is applied in sequence by shifting the first bin magnitude by an fraction of the bin width. The magnitude and color of all median points are then boxcar-average smoothed. Finally the bluest color of the interpolating function is taken as the value. We found mag. The result of the double normalization is a new quantity called . The same procedure has been applied to the vs. CMD displayed in panel (b). We found in this case mag and obtained the new quantity .
Panel (c) displays the ChM, namely the vs. diagram of the AGB stars of NGC 2808. A glance at the distribution of the stars immediately shows that in this cluster, the AGB stars are not evenly distributed but rather clustered in at least four distinct groups (see Marino et al., 2017, for comparison). In order to understand if the observed scatter can be accounted to the photometric error, we derived the ChM expected for a mono-populated cluster. In this case the scatter is mostly due to the observational errors. The center of the resulting distribution has been arbitrarily shifted at coordinates = . It appears as an ellipse flattened along the horizontal direction, with a major semi-axis of mag. We see that the vertical extension of the AGB ChM is mag, therefore about four times larger than that of the error distribution.
The density diagram plotted in panel (d) further confirms the presence of discrete stellar populations. It shows indeed two main groups of stars at coordinates and , and two other less populated groups at and . With the aim of properly assigning a membership to each star in the various groups, we built the histogram distribution of AGB stars along the y-axis and x-axis. The results are shown in panel (e) and (f), respectively. Each histogram has been obtained by splitting the horizontal and vertical intervals in bins of mag, and computing the number of clusters falling in each bin at steps equal to half bin width. This choice mitigates the arbitrary decision of a given bin width. In the histogram of panel (e), we can recognize three distinct sections, centered at = mag. The histogram of the last section shows a secondary split at mag, in agreement with the density map in panel (d). The histogram in panel (f) shows two main peaks at = mag and mag. Therefore, we used the vertical histogram distribution to subdivide the ChM into three groups, that we named 1G (magenta points), (azure points) and (blue points). The nomenclature follows the subdivision adopted by Marino et al. (2017). For the sake of clarity, we used a different color code for the three groups of stars. We finally cross-matched the three AGB spectroscopic targets by Marino et al. (2017), and marked them with a black starred symbol in the ChM of panel (c). We see that these stars, which have different O and Na abundance, belong to the different groups identified in the AGB ChM, thus providing the definitive confirmation that 1G, , and , correspond to distint stellar populations with different light-element abundance
A detailed interpretation of the MP composition of the cluster AGB star can be obtained by comparing the present ChM with that obtained from the analysis of RGB stars (Milone et al., 2017). Since ChM are built from the measurement of the spread of stars in specific color combinations, such a comparison is ultimately connected to that of the widths. However, as already mentioned before, this implies a precise evaluation of the factors affecting the evolutionary path of post-HB stars, which is not the purpose of the present analysis. Notwithstanding, we decided to perform a crude comparison by assuming that the effect of the presence of 1G and 2G stars in the extension of the ChM of AGB and RGB stars is comparable. Therefore, we decided to scale-up the width of the RGB stars in and (see Milone et al., 2017, Table 2) to that of the AGB stars derived in this work. The scaled RGB ChM is represented by the gray points plotted on background in panel (c).
Interestingly, we observe that the AGB ChM broadly reproduces the overdensities corresponding to the sub-populations observed in the RGB ChM. In particular we observe a similar elongation between the AGB and RGB 1G populations, with three AGB stars ( mag) attaining values bluer than the blue tail of the RGB stars. On the other side and AGB stars appear to follow the same trend of the sub-groups C and D of the 2G RGB population (see Marino et al., 2017). We also notice the presence of a blue tail in the group, that overlaps the location of the extreme helium-enhanced cluster (E) population ( Milone et al., 2015a). This appears to be in contrast with the predictions of evolutionary models of very helium-rich stars, which must avoid the AGB phase (e.g. Chantereau et al., 2016). Of course, spectroscopic investigation is mandatory to understand whether these AGB stars are the counterparts of RGB and MS stars with extreme helium abundances, or if they have intermediate helium content but have experienced severe RGB mass loss.
For reference we also computed the histogram distribution of the ChM of the photometric errors. The corresponding orange-shaded histograms appears to be spread over an interval visibly narrower than the sub-structures visible in both the ChM histogram distribution in panel (e) and (f).

We used the same procedure to build the ChM of all the other GCs with in our database (see column 2 of Table 1). The heterogeneous F814W magnitude distribution of the AGB stars of NGC 104 and NGC 6637, in the CMDs used to build their ChM, did not allow to obtain reliable estimate of the AGB widths. For this reason, these two GCs have been excluded from the following analysis.
We ended up with a sample of 14 GCs including NGC 362, NGC 1261, NGC 1851, NGC 2419, NGC 5024, NGC 5139, NGC 5286, NGC 5986, NGC 6093, NGC 6388, NGC 6441, NGC 6715, NGC 7078 and NGC 7089. The ChMs of these GCs, sorted by increasing metallicity, are displayed in Figure 16. In the ChMs of type II GCs we also highlighted the anomalous AGB stars with the usual red starred symbol. As for NGC 2808, in each panel we plotted on background the scaled-up ChM of the corresponding cluster RGB stars. In passing we note that we have also derived the ChM of the RGB stars of NGC 2419 for the first time in this paper. For the sake of comparison, the probable 1G and 2G RGB members of each cluster Milone et al. (2017) have been colored, respectively, in light-green and magenta, except for NGC 2419 and NGC 6441, for which it is not possible to obtain a straightforward population classification of their RGB stars. In all the type II GCs diagrams, the anomalous RGB stars are represented as grey points.
In the majority of GCs, the distribution of the AGB stars does not appear clustered in separate groups, except for NGC 7078, NGC 1261, NGC 362 and perhaps NGC 6388, where we can recognize a subdivision that resembles that of the overlapped RGB ChM. We also notice that, similarly to what is observed in the RGB ChM, the anomalous AGB stars in type II GCs lie on the rightmost part of the diagram.
The ChMs of Fig. 16 clearly show that, in each GC, the observed color spread is not compatible with the presence of a single population. Moreover they show that the MPs in the AGB can be associated to the different groups visible in the RGB ChMs.


5.1 Population ratios
A quantitative estimate of the fraction of stars that skipped the AGB phase can be obtained from the comparison of the ration between 2G stars in the AGB and RGB. To identify the different groups of stars in the AGB we decided to adopt the subdivision of the RGB ChM as a guideline for membership definition: all the AGB stars falling in the area occupied by the RGB 1G (2G) stars have then been flagged as 1G (2G) in the AGB. In type II GCs, the anomalous AGB stars have been considered as part of the 2G sample.
This crude selection allowed us to estimate the population ratio of the 1G AGB stars of NGC 2808 and 12 out of 14 GCs displayed in Fig. 16. Indeed, as mentioned in the previous section, it is not possible to derive a clear subdivisions of the RGB populations of NGC 2419 and NGC 6441 from their ChMs. The resulting 1G fractions, , are listed in Table 2. The error of each observed population ratio has been obtained with the same method used for the estimate of the anomalous AGB fraction, described in Sect. 2.3. We see that the values range from in NGC 5139 and NGC 5286 to in NGC 7078. For comparison, we have also reported the fraction of 1G RGB stars, , from Milone et al. (2017, see their Table 2).
In the left panel of Figure 17 we plot the vs of the clusters in Table 2. For reference, we also plotted a dashed line marking the identity relation. We observe that four GCs, namely NGC 7089, NGC 6388, NGC 1261, and NGC 6093 are consistent, within the errors, with an equal proportion 1G stars in both the evolutionary phases. Four clusters, namely NGC 5139, NGC 2808, NGC 6715, and NGC 7078, definitely exhibit a shortage of 2G AGB stars: all these GCs have, indeed, a very prominent hot HB component, expected to skip the EAGB and evolve instead along the AGB-manqué channel. We also see that NGC 5286 has an higher fraction of 1G RGB stars.
In the right panel of Fig. 17 we plot the difference between the fraction of 1G AGB and RGB stars as a function of the maximum internal helium enrichment, , determined by Milone et al. (2018). We observe a clear direct correlation between the two quantities. The trend suggests that in the GCs with the most helium-enriched 2G component, the fraction of 1G AGB stars is higher. These results represent a further, independent confirmation of the predictions of the AGB-manqué scenario.

As a simple experiment, we decided to verify to which extent the differences observed between 1G AGB and RGB population ratios can be reconciled if the stars evolved as AGB-manqué are included in the 2G population of the AGB. To this aim, we sought AGB-manqué candidates in the analyzed GCs by looking at their UV CMDs. An example is shown in Figure 18, that displays the vs. CMD of four GCs with extended HB morphology: NGC 2808, NGC 7078, NGC 6715, and NGC 7089. The AGB members of each cluster have been represented as red points.
Since AGB-manqué stars have very thin envelopes, their evolution will be entirely spent at higher than K, approaching luminosities typical of post-EAGB stars (Greggio & Renzini, 1990). According to this, we expect to observe AGB-manqué stars to lie at the bluest end of the HB, with luminosities comparable to those EAGB stars. Therefore, we empirically selected as AGB-manqué candidates the stars occupying the bluest portion of the CMD, with F336W magnitudes brighter than the group of stars at the hottest end of the HB, which are mainly composed by EHB stars (e.g. Tailo et al., 2015). We marked the candidate stars with a blue starred symbol. We cannot exclude the possible presence of few bright Blue Stragglers in the selected samples. Moreover, they could also potentially include post-EAGB and/or post-AGB stars, although the probability to observe one of these stars in a cluster is very low, because of their very rapid evolution timescale ( yr) (D’Cruz et al., 1996; Schiavon et al., 2012). The low incidence of these stars, however, does not affect our conclusions.
We identified 23 AGB-manqué candidates in NGC 2808, 9 in NGC 5139, 8 in NGC 6388, 30 in NGC 6715, 8 in NGC 7078, and 10 in NGC 7089. If the AGB-manqué candidates represented the total fraction of lost stars of the 2G population of these GCs, we would then observe a smaller fraction of 1G AGB stars, that is for NGC 2808, for NGC 5139, for NGC 6388 and NGC 6715, for NGC 7078, and for NGC 7089, and relative errors comparable with the previous ones.
The red points in the left panel of Fig. 17 mark the new location in the plot of the previous six GCs. We see that, in this case, NGC 6388, NGC 6715, and NGC 7089 would be consistent, within one sigma, with the same fraction of 1G AGB and RGB stars. We also notice that the fraction of 1G AGB stars in NGC 6715 is slightly higher than the RGB one, and this is probably due to some spurious additional contribution in the AGB-manqué count if this cluster, which has a strong contamination from the background stars of the Sagittarius Dwarf spheroidal galaxy. On the other hand, the new population ratios of NGC 5139, NGC 2808 and NGC 7078 would be consistent with the same fraction of 1G RGB stars only within about two sigma. We notice that since in both the AGB-manqué and EAGB phase stars are burning helium in a shell, the shell helium burning should run for the same time, therefore by adding the AGB-manqué candidates, the AGB ratio should become equal to the RGB ratio. While the fact that the anomalous population of NGC 5139 spans an extreme interval of metallicity ( dex; e.g. Johnson et al., 2009; Marino et al., 2011), could potentially mitigate the observed discrepancy in this cluster, the relative predominance of 1G AGB stars in the other two GCs could be reconciled either by assuming a shorter evolutionary timescale of the AGB-manqué stars. Indeed, since the major difference between AGB-manqué and normal AGB stars is their core mass within the hydrogen-helium discontinuity, the shorter timescale of the former would derive from the fact that these stars are the progeny of hot (extreme) HB stars, that experience almost no core-mass increase, as opposed to the precursors of standard AGBs, namely normal HB stars, which instead undergo a steady increase of the core mass (Greggio & Renzini, 1990).


| ID | aaFrom Milone et al. (2017). | |||
|---|---|---|---|---|
| NGC 362 | 10 | 18 | ||
| NGC 1261 | 9 | 22 | ||
| NGC 1851 | 15 | 23 | ||
| NGC 2808 | 34 | 41 | ||
| NGC 5024 | 12 | 19 | ||
| NGC 5139 | 7 | 23 | ||
| NGC 5286 | 15 | 52 | ||
| NGC 5986 | 11 | 25 | ||
| NGC 6093 | 11 | 23 | ||
| NGC 6388 | 40 | 114 | ||
| NGC 6715 | 29 | 53 | ||
| NGC 7078 | 23 | 10 | ||
| NGC 7089 | 19 | 47 |
6 AGB frequency and multiple populations
The study of the AGB frequency relative to HB stars plays an important role in the context of MPs. In particular, since AGB-manqé stars are the progeny of HB stars with mass lower than (Moehler et al., 2019; Prabhu et al., 2020), which are associated with the most helium-rich stellar component in a cluster (D’Antona et al., 2002; Tailo et al., 2020), differences in internal helium variations between clusters can affect the AGB/HB ratio. This prediction is quantified by the evolutionary parameter (Caputo et al., 1989), namely the number ratio between AGB and HB stars, which is proportional to the ratio between the lifetime of stars in these two evolutionary phases. According to theoretical predictions, should not be higher than about 0.2 (Cassisi et al., 2014).
To explore this phenomenon, we took advantage of a large database of homogeneously defined AGB samples in GCs, determined in the present work, and of the independent measurements of maximum internal helium variations, , obtained by (Milone et al., 2018). For each GC, we determined the frequency of AGB stars relative to HB stars, , by counting HB members in the corresponding vs. CMD. The error of each frequency measurement has been estimated with the same method used in Section 2.3). With the purpose of limiting spurious outcomes due to the stochastic fluctuations, we decided to limit the following analysis to the 36 GCs in our database with , for which we report the corresponding frequency values Table 3.
| ID | |
|---|---|
| NGC 104 | |
| NGC 362 | |
| NGC 1261 | |
| NGC 1851 | |
| NGC 2419 | |
| NGC 2808 | |
| NGC 4833 | |
| NGC 5024 | |
| NGC 5139 | |
| NGC 5272 | |
| NGC 5286 | |
| NGC 5904 | |
| NGC 5927 | |
| NGC 5986 | |
| NGC 6093 | |
| NGC 6101 | |
| NGC 6171 | |
| NGC 6205 | |
| NGC 6254 | |
| NGC 6304 | |
| NGC 6341 | |
| NGC 6388 | |
| NGC 6441 | |
| NGC 6584 | |
| NGC 6624 | |
| NGC 6637 | |
| NGC 6656 | |
| NGC 6681 | |
| NGC 6715 | |
| NGC 6723 | |
| NGC 6752 | |
| NGC 6779 | |
| NGC 6934 | |
| NGC 6981 | |
| NGC 7078 | |
| NGC 7089 |
In the left panel of Figure 19 we plot of and for these GCs, where color, size and shape of each point map, respectively, metallicity (Harris, 1996, 2010 update), present-day mass (Baumgardt & Hilker, 2018), and cluster’s type (Marino et al., 2019), as indicated in the legend. The diagram shows a scattered distribution, with all the GCs having frequency values smaller than except NGC 6171, which has . We observe that the bulk of GCs does not seem to follow any clear trend. It is necessary to consider that the AGB of type II GCs can suffer a significant depletion of anomalous population stars, as seen in Section 2.3. Hence, the resulting shortage of AGB stars in these GCs would importantly affect the observed AGB/HB frequency meaning in a way difficult to predict. This implies in turn that no strong conclusions can be derived for these GCs.
On the other side, if we limit our analysis to type I GCs with , therefore excluding the two massive GCs NGC 2808, NGC 2419, which are the type I clusters with the highest internal helium variation ( Milone et al., 2018), and among the GCs with the most complex MP pattern (Milone et al., 2015a; Zennaro et al., 2019), the majority of points display an inverse monotonic trend, with smaller AGB frequencies attained by clusters with higher internal helium variations. This impression is confirmed by the high value of the Spearman’s coefficient () reported in the bottom right corner. Finally we notice that the distribution of points shows no correlation with the cluster metallicity.
Finally, we verified that the analysis of the AGB/RGB frequency shows a similar trend, resulting therefore in the same conclusions. For the sake of convenience we decided to not show the corresponding plot.
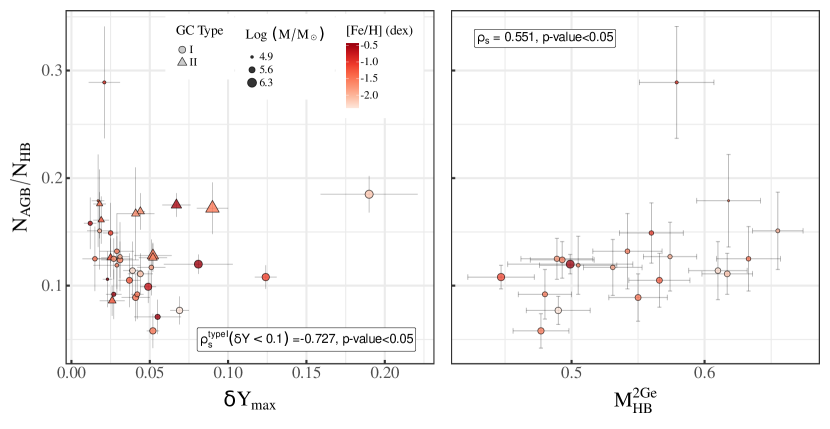
Another way of investigating AGB depletion and helium enrichment is through the analysis of the relation between observed frequency and minimum mass along the HB. Gratton et al. (2010) showed that a direct correlation exists between minimum mass along the HB and the numeric frequency of AGB stars relative to the RGB, with lower frequencies attained by clusters with smaller minimum HB mass. In the right panel of Figure 19 we plot vs , where the latter quantity indicates the average mass of the HB stars belonging to the most helium-enriched population, recently determined by Tailo et al. (2020), available for 20 type I GCs in our database. Color and size of each points follows the convention adopted in the left panel. With the exception of the outlier NGC 6171, we observe a clear correlation, that confirms the expectation of the AGB-manqé scenario of lower AGB frequencies in clusters with smaller minimum mass in the HB (Prabhu et al., 2020). The mild monotonic trend is also indicated by the value of the Spearman’s coefficient, , In passing we also notice that clusters with higher total mass have, on average, smaller minimum HB mass, while no clear trend is visible with metallicity.
The two plots in Figure 19 indicate, in general, a mild correlation between frequency of AGB stars and internal helium variations in clusters, which is in turn directly related to the mass of their hottest HB stars. The lack of a strong evidence of correlation is potentially connected to the fact that the parameters ruling the distribution of HB stars are degenerate. For instance, at a given helium enrichment, we would expect more massive HB stars in slightly younger GCs, thus a smaller proportion of AGB-manqué. The same conclusion would also be true for clusters of the same age, but different metallicity.
7 Summary and conclusions
MPs are a common property of Galactic GCs. They have been widely characterized along main sequence, RGB and HB stars in large samples of clusters (e.g. Anderson, 1997; D’Antona et al., 2005; Piotto et al., 2007; Milone et al., 2017; Lagioia et al., 2019b; Marino et al., 2019; Dondoglio et al., 2021; Tailo et al., 2020). A coherent picture at later evolutionary stages is, however, still missing.
Recent spectroscopic analyses revealed that a lower fraction of 2G stars is found to populate the AGB of some clusters, like NGC 6752 (Campbell et al., 2013; Lapenna et al., 2016), NGC 6121 (Marino et al., 2017; MacLean et al., 2016, M 4), NGC 6205 (Lapenna et al., 2015, M 62) and NGC 2808 (Marino et al., 2017). Although no univocal consensus has been achieved on the interpretation of the results, the lack of a more or less significant fraction of 2G stars corresponds to the predictions of the AGB-manqué scenario (Greggio & Renzini, 1990), according to which the most helium-enriched stars have envelope masses too low in the HB phase, so they do not evolve towards the Hayashi track as a normal AGB star, but rather towards higher temperatures until they reach the white-dwarf cooling sequence.
In order to shed new light to this problem we decided to analyze the photometric properties of the AGB stars in the largest sample of GCs analyzed so far, composed by 58 objects observed by HST in UV and optical bands (Sarajedini et al., 2007; Piotto et al., 2015). Suitable combinations of filters allow to disentangle MPs in CMDs and study their properties in statistically significant samples of stars. Through a procedure that exploits CMDs in different color combinations we selected the most probable AGB candidates in every analyzed cluster. Then, we derived their properties through the analysis of their photometric features and comparison with theoretical models. Our methods and findings are summarized in the following:
-
1.
we investigated AGB stars in type II GCs and identified, for the first time, AGB stars associated with their metal-rich (anomalous) stellar populations. The fraction of anomalous AGB stars with respect to the total number of AGB stars is significantly lower than the corresponding fraction of stars in the anomalous RGB, with NGC 7089 and NGC 362 possible exceptions;
-
2.
we constructed the vs. CMD of the bright stars of 56 GCs with at least one AGB detection. We find that the AGB sequences of at least 48 clusters exhibit larger pseudo-color spread than that expected from photometric errors alone. Hence, they host multiple stellar populations. In eight clusters, namely NGC 7099, NGC 4590, NGC 5466, NGC 6218, NGC 6397, NGC 6496, NGC 6535, and NGC 6809, there is no evidence of intrinsic broadening among AGB stars with similar luminosity. However, the small number of AGB stars in these clusters prevents us from any conclusion on the presence of MPs among their AGB. We conclude that in none of the studied clusters all 2G stars avoid the AGB phase;
-
3.
we used synthetic spectra with appropriate chemical composition and theoretical stellar models from the Roma database (Ventura et al., 1998; Mazzitelli et al., 1999) to derive, for the first time, isochrones of 1G and 2G AGB stars. We show that 2G stars define AGB sequences with smaller values of and bluer colors than 1G stars with the same luminosity. The flux difference is mostly due to NH molecular bands that affect the spectral region covered by the F336W filter and the OH and CN molecules enclosed by the F275W and F438W filters, respectively. Since 2G stars are enhanced in N and depleted in C and O, they have fainter F336W and brighter F275W and F438W magnitudes than 1G stars with the same luminosity. Moreover, 2G stars are helium enhanced with respect to the 1G, hence they have colors bluer than 1G stars at the same luminosity. In addition to the content of helium, C, N, and O, the amount of mass loss experienced during the RGB phase affects the colors of AGB stars. In particular, an increase in mass loss can dramatically shift to the blue the AGB sequences;
-
4.
we measured the intrinsic width of AGB stars in the pseudo-colors for 35 GCs with , and compared it with the corresponding quantity obtained from RGB stars. We observe that the intrinsic width of AGB stars is on average smaller than that of RGB. This finding suggests that a substantial part of the RGB stars in these GCs does not evolve to the AGB;
-
5.
we constructed the ChM of 15 GCs with well populated AGB sequence and identified their 1G and 2G AGB stars: this allowed us to derive the fraction of 1G stars along the AGB. On average, AGB stars host fractions of 1G stars larger than in the RGB, and NGC 2808, NGC 5139, NGC 6715, and NGC 7078 and are the clusters with the most pronounced differences. This result is consistent with the AGB-manqué scenario where part of 2G stars skips the AGB phase (Campbell et al., 2013) due to their typical mass lower than that of 1G stars. Indeed, 2G stars are enhanced in helium (Lagioia et al., 2018; Milone et al., 2018) and lose more mass in the RGB phase compared to the 1G (Tailo et al., 2019a, 2020). This scenario is corroborated by the evidence from this paper and from Gratton et al. (2010) that the frequency of AGB/HB stars of the type I GCs correlates with the minimum mass of HB stars; the AGB frequency of type I GCs with also anti-correlates with the maximum helium abundance of 2G stars.
References
- Anderson (1997) Anderson, A. J. 1997, PhD thesis
- Anderson et al. (2008) Anderson, J., King, I. R., Richer, H. B., et al. 2008, The Astronomical Journal, 135, 2114, doi: 10.1088/0004-6256/135/6/2114
- Baumgardt & Hilker (2018) Baumgardt, H., & Hilker, M. 2018, Monthly Notices of the Royal Astronomical Society, 478, 1520, doi: 10.1093/mnras/sty1057
- Bedin et al. (2005) Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, Monthly Notices of the Royal Astronomical Society, 357, 1038, doi: 10.1111/j.1365-2966.2005.08735.x
- Bellini et al. (2011) Bellini, A., Anderson, J., & Bedin, L. R. 2011, Publications of the Astronomical Society of the Pacific, 123, 622, doi: 10.1086/659878
- Bellini et al. (2017a) Bellini, A., Anderson, J., Bedin, L. R., et al. 2017a, The Astrophysical Journal, 842, 6, doi: 10.3847/1538-4357/aa7059
- Bellini & Bedin (2009) Bellini, A., & Bedin, L. R. 2009, Publications of the Astronomical Society of the Pacific, 121, 1419, doi: 10.1086/649061
- Bellini et al. (2017b) Bellini, A., Milone, A. P., Anderson, J., et al. 2017b, The Astrophysical Journal, 844, 164, doi: 10.3847/1538-4357/aa7b7e
- Buzzoni et al. (2010) Buzzoni, A., Patelli, L., Bellazzini, M., Pecci, F. F., & Oliva, E. 2010, Monthly Notices of the Royal Astronomical Society, 403, 1592, doi: 10.1111/j.1365-2966.2009.16223.x
- Campbell et al. (2017) Campbell, S. W., MacLean, B. T., D’Orazi, V., et al. 2017, Astronomy and Astrophysics, 605, A98, doi: 10.1051/0004-6361/201731101
- Campbell et al. (2012) Campbell, S. W., Yong, D., Wylie-de Boer, E. C., et al. 2012, The Astrophysical Journal Letters, 761, L2, doi: 10.1088/2041-8205/761/1/L2
- Campbell et al. (2013) Campbell, S. W., D’Orazi, V., Yong, D., et al. 2013, Nature, 498, 198, doi: 10.1038/nature12191
- Caputo et al. (1989) Caputo, F., Castellani, V., Chieffi, A., Pulone, L., & Tornambe, Jr., A. 1989, The Astrophysical Journal, 340, 241, doi: 10.1086/167387
- Carretta & Bragaglia (2018) Carretta, E., & Bragaglia, A. 2018, Astronomy and Astrophysics, 614, A109, doi: 10.1051/0004-6361/201832660
- Carretta et al. (2009) Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, Astronomy and Astrophysics, 505, 139, doi: 10.1051/0004-6361/200912097
- Carretta et al. (2012) Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & D’Orazi, V. 2012, The Astrophysical Journal Letters, 750, L14, doi: 10.1088/2041-8205/750/1/L14
- Cassisi et al. (2014) Cassisi, S., Salaris, M., Pietrinferni, A., Vink, J. S., & Monelli, M. 2014, Astronomy and Astrophysics, 571, A81, doi: 10.1051/0004-6361/201424540
- Castelli (2005) Castelli, F. 2005, Memorie della Societa Astronomica Italiana Supplementi, 8, 25
- Catelan et al. (2001) Catelan, M., Ferraro, F. R., & Rood, R. T. 2001, The Astrophysical Journal, 560, 970, doi: 10.1086/323049
- Chantereau et al. (2016) Chantereau, W., Charbonnel, C., & Meynet, G. 2016, Astronomy and Astrophysics, 592, A111, doi: 10.1051/0004-6361/201628418
- Choi et al. (2016) Choi, J., Dotter, A., Conroy, C., et al. 2016, The Astrophysical Journal, 823, 102, doi: 10.3847/0004-637X/823/2/102
- D’Antona et al. (2005) D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, The Astrophysical Journal, 631, 868, doi: 10.1086/431968
- D’Antona et al. (2002) D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, Astronomy and Astrophysics, 395, 69, doi: 10.1051/0004-6361:20021220
- D’Cruz et al. (1996) D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, The Astrophysical Journal, 466, 359, doi: 10.1086/177515
- Dondoglio et al. (2021) Dondoglio, E., Milone, A. P., Lagioia, E. P., et al. 2021, The Astrophysical Journal, 906, 76, doi: 10.3847/1538-4357/abc882
- Fusi Pecci et al. (1993) Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, The Astronomical Journal, 105, 1145, doi: 10.1086/116500
- García-Hernández et al. (2015) García-Hernández, D. A., Mészáros, S., Monelli, M., et al. 2015, The Astrophysical Journal Letters, 815, L4, doi: 10.1088/2041-8205/815/1/L4
- Gratton et al. (2010) Gratton, R. G., D’Orazi, V., Bragaglia, A., Carretta, E., & Lucatello, S. 2010, Astronomy and Astrophysics, 522, A77, doi: 10.1051/0004-6361/201015405
- Greggio & Renzini (1990) Greggio, L., & Renzini, A. 1990, The Astrophysical Journal, 364, 35, doi: 10.1086/169384
- Harris (1996) Harris, W. E. 1996, The Astronomical Journal, 112, 1487, doi: 10.1086/118116
- Johnson et al. (2009) Johnson, C. I., Pilachowski, C. A., Michael Rich, R., & Fulbright, J. P. 2009, The Astrophysical Journal, 698, 2048, doi: 10.1088/0004-637X/698/2/2048
- Kamath et al. (2012) Kamath, D., Karakas, A. I., & Wood, P. R. 2012, The Astrophysical Journal, 746, 20, doi: 10.1088/0004-637X/746/1/20
- Kraft (1994) Kraft, R. P. 1994, Publications of the Astronomical Society of the Pacific, 106, 553, doi: 10.1086/133416
- Kurucz (2005) Kurucz, R. L. 2005, Memorie della Societa Astronomica Italiana Supplementi, 8, 14
- Lagioia et al. (2015) Lagioia, E. P., Dalessandro, E., Ferraro, F. R., et al. 2015, The Astrophysical Journal, 800, 52, doi: 10.1088/0004-637X/800/1/52
- Lagioia et al. (2019a) Lagioia, E. P., Milone, A. P., Marino, A. F., Cordoni, G., & Tailo, M. 2019a, The Astronomical Journal, 158, 202, doi: 10.3847/1538-3881/ab45f2
- Lagioia et al. (2019b) Lagioia, E. P., Milone, A. P., Marino, A. F., & Dotter, A. 2019b, The Astrophysical Journal, 871, 140, doi: 10.3847/1538-4357/aaf729
- Lagioia et al. (2018) Lagioia, E. P., Milone, A. P., Marino, A. F., et al. 2018, Monthly Notices of the Royal Astronomical Society, 475, 4088, doi: 10.1093/mnras/sty083
- Lapenna et al. (2015) Lapenna, E., Mucciarelli, A., Ferraro, F. R., et al. 2015, The Astrophysical Journal, 813, 97, doi: 10.1088/0004-637X/813/2/97
- Lapenna et al. (2016) Lapenna, E., Lardo, C., Mucciarelli, A., et al. 2016, The Astrophysical Journal Letters, 826, L1, doi: 10.3847/2041-8205/826/1/L1
- Lardo et al. (2017) Lardo, C., Salaris, M., Savino, A., et al. 2017, Monthly Notices of the Royal Astronomical Society, 466, 3507, doi: 10.1093/mnras/stw3374
- MacLean et al. (2016) MacLean, B. T., Campbell, S. W., De Silva, G. M., et al. 2016, Monthly Notices of the Royal Astronomical Society, 460, L69, doi: 10.1093/mnrasl/slw073
- Marino et al. (2008) Marino, A. F., Villanova, S., Piotto, G., et al. 2008, Astronomy and Astrophysics, 490, 625, doi: 10.1051/0004-6361:200810389
- Marino et al. (2011) Marino, A. F., Milone, A. P., Piotto, G., et al. 2011, The Astrophysical Journal, 731, 64, doi: 10.1088/0004-637X/731/1/64
- Marino et al. (2017) Marino, A. F., Milone, A. P., Yong, D., et al. 2017, The Astrophysical Journal, 843, 66, doi: 10.3847/1538-4357/aa7852
- Marino et al. (2019) Marino, A. F., Milone, A. P., Renzini, A., et al. 2019, Monthly Notices of the Royal Astronomical Society, 487, 3815, doi: 10.1093/mnras/stz1415
- Martell et al. (2011) Martell, S. L., Smolinski, J. P., Beers, T. C., & Grebel, E. K. 2011, Astronomy and Astrophysics, 534, A136, doi: 10.1051/0004-6361/201117644
- Masseron et al. (2019) Masseron, T., García-Hernández, D. A., Mészáros, S., et al. 2019, Astronomy and Astrophysics, 622, A191, doi: 10.1051/0004-6361/201834550
- Mazzitelli et al. (1999) Mazzitelli, I., D’Antona, F., & Ventura, P. 1999, Astronomy and Astrophysics, 348, 846
- Milone (2015) Milone, A. P. 2015, Monthly Notices of the Royal Astronomical Society, 446, 1672, doi: 10.1093/mnras/stu2198
- Milone et al. (2009) Milone, A. P., Bedin, L. R., Piotto, G., & Anderson, J. 2009, Astronomy and Astrophysics, 497, 755, doi: 10.1051/0004-6361/200810870
- Milone et al. (2012a) Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012a, Astronomy and Astrophysics, 540, A16, doi: 10.1051/0004-6361/201016384
- Milone et al. (2012b) —. 2012b, The Astrophysical Journal, 744, 58, doi: 10.1088/0004-637X/744/1/58
- Milone et al. (2013) Milone, A. P., Marino, A. F., Piotto, G., et al. 2013, The Astrophysical Journal, 767, 120, doi: 10.1088/0004-637X/767/2/120
- Milone et al. (2015a) —. 2015a, The Astrophysical Journal, 808, 51, doi: 10.1088/0004-637X/808/1/51
- Milone et al. (2015b) —. 2015b, Monthly Notices of the Royal Astronomical Society, 447, 927, doi: 10.1093/mnras/stu2446
- Milone et al. (2017) Milone, A. P., Piotto, G., Renzini, A., et al. 2017, Monthly Notices of the Royal Astronomical Society, 464, 3636, doi: 10.1093/mnras/stw2531
- Milone et al. (2018) Milone, A. P., Marino, A. F., Renzini, A., et al. 2018, Monthly Notices of the Royal Astronomical Society, 481, 5098, doi: 10.1093/mnras/sty2573
- Moehler et al. (2019) Moehler, S., Landsman, W. B., Lanz, T., & Miller Bertolami, M. M. 2019, Astronomy and Astrophysics, 627, A34, doi: 10.1051/0004-6361/201935694
- Monelli et al. (2013) Monelli, M., Milone, A. P., Stetson, P. B., et al. 2013, Monthly Notices of the Royal Astronomical Society, 431, 2126, doi: 10.1093/mnras/stt273
- Nardiello et al. (2018) Nardiello, D., Libralato, M., Piotto, G., et al. 2018, Monthly Notices of the Royal Astronomical Society, 481, 3382, doi: 10.1093/mnras/sty2515
- Norris et al. (1981) Norris, J., Cottrell, P. L., Freeman, K. C., & Da Costa, G. S. 1981, The Astrophysical Journal, 244, 205, doi: 10.1086/158698
- Piotto et al. (2007) Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, The Astrophysical Journal Letters, 661, L53, doi: 10.1086/518503
- Piotto et al. (2015) Piotto, G., Milone, A. P., Bedin, L. R., et al. 2015, The Astronomical Journal, 149, 91, doi: 10.1088/0004-6256/149/3/91
- Prabhu et al. (2020) Prabhu, D. S., Subramaniam, A., & Sahu, S. 2020, arXiv e-prints, 2012, arXiv:2012.05732
- Sabbi et al. (2016) Sabbi, E., Lennon, D. J., Anderson, J., et al. 2016, The Astrophysical Journal Supplement Series, 222, 11, doi: 10.3847/0067-0049/222/1/11
- Sandage & Wildey (1967) Sandage, A., & Wildey, R. 1967, The Astrophysical Journal, 150, 469, doi: 10.1086/149350
- Sarajedini et al. (2007) Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, The Astronomical Journal, 133, 1658, doi: 10.1086/511979
- Sbordone et al. (2007) Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, Astronomy and Astrophysics, 465, 815, doi: 10.1051/0004-6361:20066385
- Sbordone et al. (2011) Sbordone, L., Salaris, M., Weiss, A., & Cassisi, S. 2011, Astronomy and Astrophysics, 534, A9, doi: 10.1051/0004-6361/201116714
- Schiavon et al. (2012) Schiavon, R. P., Dalessandro, E., Sohn, S. T., et al. 2012, The Astronomical Journal, 143, 121, doi: 10.1088/0004-6256/143/5/121
- Schiavon et al. (2017) Schiavon, R. P., Zamora, O., Carrera, R., et al. 2017, Monthly Notices of the Royal Astronomical Society, 465, 501, doi: 10.1093/mnras/stw2162
- Silverman (1986) Silverman, B. W. 1986, Monographs on Statistics and Applied Probability
- Smith & Norris (1993) Smith, G. H., & Norris, J. E. 1993, The Astronomical Journal, 105, 173, doi: 10.1086/116418
- Sneden et al. (2000) Sneden, C., Ivans, I. I., & Kraft, R. P. 2000, Memorie della Societa Astronomica Italiana, 71, 657
- Tailo et al. (2019a) Tailo, M., D’Antona, F., Caloi, V., et al. 2019a, Monthly Notices of the Royal Astronomical Society, 486, 5895, doi: 10.1093/mnras/stz1273
- Tailo et al. (2019b) Tailo, M., Milone, A. P., Marino, A. F., et al. 2019b, The Astrophysical Journal, 873, 123, doi: 10.3847/1538-4357/ab05cc
- Tailo et al. (2015) Tailo, M., D’Antona, F., Vesperini, E., et al. 2015, Nature, 523, 318, doi: 10.1038/nature14516
- Tailo et al. (2020) Tailo, M., Milone, A. P., Lagioia, E. P., et al. 2020, Monthly Notices of the Royal Astronomical Society, 498, 5745, doi: 10.1093/mnras/staa2639
- Ventura et al. (2009) Ventura, P., Caloi, V., D’Antona, F., et al. 2009, Monthly Notices of the Royal Astronomical Society, 399, 934, doi: 10.1111/j.1365-2966.2009.15335.x
- Ventura et al. (1998) Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, Astronomy and Astrophysics, 334, 953
- Villanova et al. (2012) Villanova, S., Geisler, D., Piotto, G., & Gratton, R. G. 2012, The Astrophysical Journal, 748, 62, doi: 10.1088/0004-637X/748/1/62
- Villanova et al. (2009) Villanova, S., Piotto, G., & Gratton, R. G. 2009, Astronomy and Astrophysics, 499, 755, doi: 10.1051/0004-6361/200811493
- Wang et al. (2016) Wang, Y., Primas, F., Charbonnel, C., et al. 2016, Astronomy and Astrophysics, 592, A66, doi: 10.1051/0004-6361/201628502
- Wang et al. (2017) —. 2017, Astronomy and Astrophysics, 607, A135, doi: 10.1051/0004-6361/201730976
- Zennaro et al. (2019) Zennaro, M., Milone, A. P., Marino, A. F., et al. 2019, Monthly Notices of the Royal Astronomical Society, 487, 3239, doi: 10.1093/mnras/stz1477