Multi-task manifold learning for small sample size datasets
Abstract
In this study, we develop a method for multi-task manifold learning. The method aims to improve the performance of manifold learning for multiple tasks, particularly when each task has a small number of samples. Furthermore, the method also aims to generate new samples for new tasks, in addition to new samples for existing tasks. In the proposed method, we use two different types of information transfer: instance transfer and model transfer. For instance transfer, datasets are merged among similar tasks, whereas for model transfer, the manifold models are averaged among similar tasks. For this purpose, the proposed method consists of a set of generative manifold models corresponding to the tasks, which are integrated into a general model of a fiber bundle. We applied the proposed method to artificial datasets and face image sets, and the results showed that the method was able to estimate the manifolds, even for a tiny number of samples.
keywords:
Multi-task unsupervised learning , Multi-level modeling , Small sample size problem , manifold disentanglement , Meta-learning1 Introduction
To model a high-dimensional dataset, it is often assumed that the data points are distributed in a low-dimensional nonlinear subspace, that is, a manifold. Such manifold-based methods are useful in data visualization and unsupervised modeling, and have been applied in many fields [1, 2]. A common problem of the manifold-based approach is that it requires a sufficient number of samples to capture the overall shape of the manifold. If there are only a few samples in a high-dimensional space, the samples cover the manifold very sparsely, and then it is difficult to estimate the manifold shape. This is referred to as the small sample size problem in the literature [3].
As a typical example, we consider a face image dataset because face images of a person are modeled by a manifold [4, 5]. To estimate the face manifold of a person, we need many photographs with various expressions or various poses. However, it is typically difficult to obtain such an exhaustive image set for a single person. If we only have a limited number of facial expressions for the person, it seems almost impossible to estimate a face manifold in which many unknown expressions are contained. Thus, we use multi-task learning; if we can utilize face images of many other people, an exhaustive dataset is no longer necessary.
In the single-task scenario, the aim of manifold learning is to map a dataset to a low-dimensional latent space by modeling the data distribution by a manifold. Thus, in the multi-task scenario, the aim is to map a set of datasets to a common low-dimensional space. For this purpose, multiple manifold learning tasks are executed in parallel, with transferring the information between tasks. Therefore, the success of multi-task learning depends on what and how information is transferred between tasks.
In this study, we use a generative manifold model approach, which is a class of manifold learning methods. Particularly, we chose the method that models a manifold by kernel smoothing, that is, kernel smoothing manifold model (KSMM). Therefore, our target is to develop a multi-task KSMM (MT-KSMM), which works for small sample size datasets. Additionally, MT-KSMM also aims to estimate a general model, which can be applied to new tasks. Thus, our target method covers meta-learning of manifold models [6].
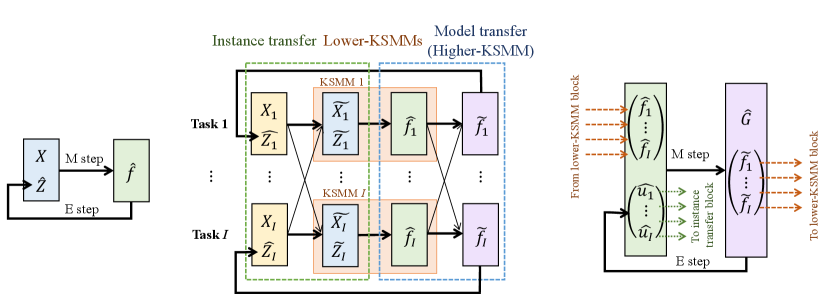
In the proposed method, we introduce two different types of information transfer between tasks: instance transfer and model transfer. For the instance transfer, the given datasets are merged among the similar tasks, whereas for the model transfer, the estimated manifold models are regularized so that they get closer among the similar tasks. To execute these information transfers, we introduce an extra KSMM into MT-KSMM, whereby the manifold models of tasks are integrated into a general model of a fiber bundle. In addition, the extra KSMM also estimates the similarities between tasks, by which the amount of information transfer is controlled. Thus the extra KSMM works as the command center which governs the KSMMs for tasks. Hereafter, the extra KSMM is referred to as the higher-order KSMM (higher-KSMM, in short), whereas the KSMMs for tasks are referred to as the lower-KSMMs. Thus, the key ideas of this work are (1) using two styles of information transfer alternately, and (2) using the hierarchical structure consisting of the lower-KSMMs and the higher-KSMM.
The remainder of this paper is structured as follows: We introduce related work in Section 2, and describe the theoretical framework in Section 3. We present the proposed method in Section 4 and experimental results in Section 5. In Section 6, we discuss the study from the viewpoint of information geometry, and in the final section, we present the conclusion.
2 Related work
2.1 Multi-task unsupervised learning
Multi-task learning is a paradigm of machine learning that aims to improve performance by learning similar tasks simultaneously [7, 8]. Many studies have been conducted on multi-task learning, particularly in supervised learning settings. By contrast, few studies have been conducted on multi-task unsupervised learning. Some studies on multi-task clustering have been reported [9, 10, 11, 12].
To date, few studies have been conducted on dimensionality reduction, subspace methods, and manifold learning. To the best of our knowledge, a study on multi-task principal component analysis (PCA) is the only research that is expressly aimed at the multi-task learning of subspace methods [13]. In multi-task PCA, the given datasets are modeled by linear subspaces, which are regularized so that they are closed to each other on the Grassmannian manifold.
Regarding nonlinear subspace methods, to the best of our knowledge, the most closely related work is the higher-order self-organizing map (SOM2, which is also called the ‘SOM of SOMs’) [14, 15]. Although SOM2 is designed for multi-level modeling rather than multi-task learning, the function of SOM2 can also be regarded as multi-task learning. SOM2 is described in detail below.
2.2 Multi-level modeling
Multi-level modeling (or hierarchical modeling) aims to obtain higher models of tasks in addition to modeling each task [16]. Although multi-level modeling does not aim to improve the performance of individual tasks, the research areas of multi-level modeling and multi-task learning overlap. In fact, multi-level modeling is sometimes adopted as an approach for multi-task learning [17, 18, 19].
As in the case of multi-task learning, most studies conducted on multi-level modeling have considered supervised learning, particularly linear models. Among the multi-level unsupervised modeling approaches, SOM2 aims to model a set of self-organizing maps (SOMs) using a higher-order SOM (higher-SOM) [14, 15]. In SOM2, the lower-order SOMs (lower-SOMs) model each task using a nonlinear manifold, whereas the higher-SOM models those manifolds by another nonlinear manifold in function space. As a result, the entire dataset is represented by a product manifold, that is, a fiber bundle. Thus, the manifolds represented by the lower-SOMs are the fibers, whereas the higher-SOM represents the base space of the fiber bundle. Additionally, the relations between tasks are visualized in the low-dimensional space of the tasks, in which similar tasks are arranged nearer to each other and different tasks are arranged further from each other.
The learning algorithm of SOM2 is not a simple cascade of SOMs. The higher and lower-SOMs learn in parallel and affect each other. Thus, whereas the higher-SOM learns the set of lower models, the lower-SOMs are regularized by the higher-SOM so that similar tasks are represented by similar manifolds. Thus, SOM2 has many aspects of multi-task learning. In fact, SOM2 has been applied to several areas of multi-task learning, such as unsupervised modeling of face images of various people [20], nonlinear dynamical systems with latent state variables [21, 22], shapes of various objects [23, 24], and people of various groups [25, 26]. In this sense, SOM2 is one of the earliest works on multi-task unsupervised learning for nonlinear subspace methods.
Although SOM2 works like multi-task learning, it is still difficult for it to estimate manifolds when the sample size is small. Additionally, SOM2 has several limitations that originate from SOM, such as poor manifold representation caused by the discrete grid nodes. In this study, we try to overcome these limitations of SOM2 by replacing SOM with KSMM. Then we extend it for multi-task learning so that it estimates the manifold shape more accurately, even for a small sample size.
2.3 Meta-learning
Recently, the concept of meta-learning has been gaining importance [6]. Meta-learning aims to solve unseen future tasks efficiently through learning multiple existing tasks. This is in contrast to multi-task learning, which aims to improve the learning performance of existing tasks. Because MT-KSMM aims to obtain a general model that can represent future tasks in addition to existing tasks, our aim covers both multi-task learning and meta-learning. Similar to the cases of multi-task learning and multi-level learning, meta-learning of unsupervised learning has rarely been performed. Particularly, to the best of our knowledge, meta-learning in an unsupervised manner of unsupervised learning has not been reported, except SOM2. In this sense, SOM2 is a method in a unique position. In this study, we aim to develop a novel method for multi-task, multi-level, and meta-learning of manifold models based on SOM2.
2.4 Generative manifold modeling
Nonlinear methods for dimensionality reduction are roughly categorized into two groups. The first group is methods that project data points from high-dimensional space to low-dimensional space. Most dimensionality reduction methods, including many manifold learning approaches, are classified in this group. By contrast, the second group explicitly estimates the mapping from low-dimensional latent space to the manifold in high-dimensional visible space [27]. Thus a nonlinear embedding is estimated by this group. Because new samples on the manifold can be generated by using the estimated embedding, we refer to the second group as generative manifold modeling in this study. An advantage of generative manifold model is that it does not suffer from the pre-image problem and the out-of-sample extension problem [28]. Thus, by generating new samples between the given data points, generative manifold model completes the manifold shape entirely. Additionally, because the embedding is explicitly estimated, generative manifold model allows the direct measurement of the distance between two manifolds in function space. These are the reasons that we chose the generative manifold model approach.
The representative methods of generative manifold modeling are generative topographic mapping (GTM) [29], the Gaussian process latent variable model (GPLVM) [30, 27], and unsupervised kernel regression (UKR) [31], which originate from the SOM [32]. To estimate the embedding and the latent variables, GPLVM and GTM employ the Bayesian approach that use a Gaussian process, whereas UKR and SOM employ the non-Bayesian approach that use a kernel smoother. Additionally, GPLVM and UKR represent the manifold in a non-parametric manner, whereas GTM and SOM represent it in parametric manner. In this study, we use a parametric kernel smoothing approach like the original SOM, for ease of information transfer between tasks.
2.5 Unsupervised manifold alignment
In nonlinear subspace methods, there is always arbitrariness in the determination of the coordinate system of the latent space. For example, any orthogonal transformation of the latent space yields an equivalent result. Additionally, any nonlinear distortion along the manifold is also allowed.
In single-task learning, such arbitrariness is not a problem, but it causes serious problems in multi-task learning. Because the coordinate system of the latent space is determined differently for each task, the learning results become incompatible between tasks. Therefore, it prevents knowledge transfer between tasks.
To solve this problem, we need to know the correspondences between two different manifolds, or we need to regularize them so that they share the same coordinate system. This is known as the manifold alignment problem, which is challenging to solve under the unsupervised condition [33]. This is one reason why the multi-task subspace method is difficult. In the case of multi-task PCA, they escaped this problem by mapping them to a Grassmannian manifold [13]; however, this approach is only possible for the linear subspace case. Therefore, manifold alignment is an unavoidable problem, which is challenged in this study.
3 Problem formulation
In this section, we first describe generative manifold modeling in the single-task case, and then we present the problem formulation of the multi-task case. The notation used in this paper is described in Appendix A, and the symbol list is presented in Table 2.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
3.1 Problem formulation for single-task learning
First, we describe the problem formulation for the single-task case (Figure 1 (a)). Let and be high-dimensional visible space and low-dimensional latent space, respectively, and let be the observed sample set, where . In the case of a face image dataset, is the set of face images of a single person with various expressions or poses, and is the sample latent variable corresponding to , which represents the intrinsic property of the image, such as the expression or pose. The main purpose of manifold learning is to map to by assuming that sample set is modeled by a manifold , which is homeomorphic to . Thus, a homeomorphism can be defined, by which is projected to . Note that actual samples are not distributed in exactly because of observation noise. Thus, the observed sample is represented as , where is observation noise. Generative manifold modeling not only aims to estimate the sample latent variables , but also to estimate the embedding explicitly. Thus, the probabilistic generative model is estimated as . Because is expected to be a smooth continuous mapping, we assume that is a member of a reproducing kernel Hilbert space (RKHS) .
3.2 Problem formulation for multi-task learning
Now we formulate the problem in which we have tasks. Thus, we have sample sets , where . For example, in the case of face image datasets, we have image sets of people, with expressions or poses for each person. We denote the entire sample set by , where . We also denote the entire sample set by matrix . In the same manner, is the latent variable set of task , which corresponds to , whereas the entire latent variable set is represented as . Additionally, let be the task index of sample , and let be the index set of samples that belong to task . To simplify the explanation, we consider the case in which each dataset has the same number of samples (sample per task: S/T), that is, .
Similar to the single-task case, we assume that is modeled by manifolds , which are all homeomorphic to the common latent space . Thus, we can define a smooth embedding for each task, where (Figure 1 (b)). By considering the observation noise, we represent the probability distribution of task by . In this study, the individual embedding is referred to as the task model.
To apply multi-task learning, the given tasks need to have some similarities or common properties. We make the following two assumptions on the similarities of tasks. First, the sample latent variable represents the intrinsic property of the sample, which is independent of the task. Thus, if and are mapped to the same , they are regarded as having the same intrinsic property, even if . For example, if both and are face images of different people with the same expression (e.g., smiling), they should be mapped to the similar , even if the images look different. Using this assumption, the distance between two manifolds and can be defined using the norm as
| (1) |
where is the measure of , which is common to all tasks. In this study, we define the measure as , where is the prior of .
Second, we assume that the set of task models is also distributed in a nonlinear manifold embedded into RKHS (Figure 1 (c)). Thus, is defined by a nonlinear smooth embedding , where is the low-dimensional latent space for tasks. Under this assumption, all tasks are assigned to the task latent variables , so that . It also means that if and are similar, then and . As a result, the entire model distribution is represented as
| (2) |
where is defined as , and is the embedded product manifold of into (Figure 1 (d)). In this study, is referred to as the general model. Using the general model, each task model is expected to be .
We can describe this problem formulation using the terms of the fiber bundle. Suppose that is the total space of the fiber bundle, where . Then we can define a projection so that , where is now referred to as the base space. Thus, the samples that belong to the same task are all projected to the same . Under this scenario, becomes a fiber bundle, and each task manifold is regarded as a fiber. Additionally, we can define another projection , which satisfies . Such a formulation using the fiber bundle has been proposed in some studies [14, 34].
Under this scenario, our aim is to determine the general model in addition to the task model set , and to estimate the latent variables of samples and tasks . Considering compatibility with SOM, we assume that the latent spaces are square spaces and , and the priors and are the uniform distribution on and 111Rigorously speaking, we need to consider the border effect in the case of compact latent space, such as . In this study, we ignore such a border effect for ease of implementation. Such an approximation is common in SOM and its variations.. The difficulty of learning depends on S/T (i.e., ) and the number of tasks . Particularly, we are interested in the case in which S/T is too small to capture the manifold shape, whereas we have a sufficient number of tasks for multi-task learning.
4 Proposed method
In this section, we first describe the single task of manifold modeling, which is called KSMM. Then we describe the information transfer among the tasks. Finally, we present the multi-task KSMM, that is, MT-KSMM. In this section, we outline the derivation of the MT-KSMM algorithm, and in Appendix B, we describe the details.
4.1 Kernel smoothing manifold modeling (KSMM)
We chose KSMM as a generative manifold modeling method, which estimates the embedding using a kernel smoother. Thus, our aim is to develop the multi-task KSMM, that is, MT-KSMM. KSMM is a theoretical generalization of SOM, which has been proposed in many studies [35, 36, 37, 38, 39]. The main difference between SOM and KSMM is that the former discretizes the latent space to regular grid nodes, whereas the latter treats it as continuous space. According to previous studies, the cost function of KSMM is given by
| (3) |
where is the non-negative smoothing kernel defined on , which is typically [38]. If we regard as the probability density that represents the uncertainty of , the cost function (3) equals the cross-entropy between the data distribution and the model distribution (ignoring the constant), which are given by
| (4) | ||||
| (5) |
Thus, , where ‘’ means that both hands are equal except the constant, and denotes the cross-entropy.
The KSMM algorithm is the expectation maximization (EM) algorithm in the broad sense [38, 39], in which the E and M steps are iterated alternately until the cost function (3) converges (Figure 2 (a)). In the E step, the cost function (3) is optimized with respect to , whereas is fixed as follows:
| (6) | ||||
| (7) |
where and represent the estimators of and , respectively222In this study, the (tentative) estimators are denoted by hat when we need to indicate expressly. We also denote the information transfer result by tilde .. The latent variable estimation obtained by (7) is used in the original SOM [32] and some similar methods [31]. Note that we can rewrite (7) as
which means the maximum log-likelihood estimator. We optimize (7) using SOM-like grid search to avoid local minima for early loops of iterations, and then they are updated by the gradient method in the later loops.
By contrast, in the M step, (3) is optimized with respect to , whereas is fixed, as follows:
| (8) |
The solution of (8) is given by the kernel smoothing of samples as
| (9) |
These E and M steps are executed repeatedly until the cost function (3) converges. In the proposed method, embedding is represented parametrically using orthonormal bases. The details are provided in Section 4.5.
There are several reasons why we chose kernel smoothing-based manifold modeling rather than Gaussian process-based modeling. First, because KSMM is a generalization of SOM, it is easy to extend SOM2 to MT-KSMM naturally. Second, because the information transfers are made by the non-negative mixture of datasets or models, a kernel smoother can be used consistently through the method. Third, because the kernel smoother acts as an elastic net that connects the data points [40, 41], the kernel smoothing of task models is expected to solve the unsupervised manifold alignment problem by minimizing the distance between manifolds. Finally, as far as we examined, kernel smoothing-based manifold modeling is more stable and less sensitive to sample variations than the Gaussian process. This property seems to be desirable for multi-task learning, particularly when the sample size is small.
(a) KSMM (b) MT-KSMM (c) Higher-KSMM
4.2 Information transfer between tasks
For multi-task learning, the information about each task needs to be transferred to other tasks. Generally, there are three major approaches: feature-based, parameter-based, and instance-based [8]. To summarize, the feature-based approach transfers or shares the intrinsic representation between tasks, the parameter-based approach transfers the model parameters between tasks, and the instance-based approach shares the datasets among the tasks. In the proposed method, we use two information transfer styles: model transfer, which corresponds to the parameter-based approach, and instance transfer, which corresponds to the instance-based approach. Although we do not use the feature-based approach explicitly in the proposed method, we can regard the latent space , which is common to all tasks, as the intrinsic representation space shared among the tasks. Therefore, the proposed method is related to all information transfer styles of multi-task learning.
In instance transfer, samples of a task are transferred to other tasks, and form a weighted mixture of samples. Thus, if task is a neighbor of task in the task latent space , the sample set is merged with the target set as an auxiliary sample set with a larger weight. By contrast, if task is far from task in , then is merged with with a small (or zero) weight. We denote the weight of sample in source task with respect to the target task by (). Typically is defined as
| (10) |
where determines the neighborhood size for data mixing, and is the estimator of the task latent variable . Then we have the merged dataset , where indicates that is a member of with weight . Similarly, the latent variable set is also merged with the same weight as . The data distribution corresponding to the merged dataset becomes
| (11) |
where . Eq. (11) means that the data distributions are smoothed by kernel before the task models are estimated. By creating a weighted mixture of samples, we can avoid the small sample set problem.
By contrast, in model transfer, each task model is modified so that it becomes similar to the models of the neighboring tasks, as follows:
| (12) |
where . Eq. (12) means the kernel smoothing of the task models . Thus, the model distribution becomes
| (13) |
Note that (12) and (13) are integrated as
| (14) |
Therefore, the log of model distributions is smoothed by kernel after the task models are estimated.
4.3 Architecture of multi-task KSMM (MT-KSMM)
When we have datasets (i.e., tasks), we need to execute KSMMs in parallel. To execute the multi-task learning of KSMMs, the proposed method MT-KSMM introduces two key ideas. The first idea is to use both instance transfer and model transfer, and the second idea is to introduce the higher-KSMM, which integrates the manifold models estimated by the KSMMs for tasks (i.e., the lower-KSMMs).
As described in 4.1, KSMM estimates from and in the M step, whereas is estimated from and in the E step. The first key idea is to use the merged dataset that is obtained by instance transfer instead of using the original dataset . Thus, is estimated from and . Similarly, to estimate the latent variables , the proposed method uses the embedding that is obtained using model transfer instead of using directly (Figure 2 (b)).
To execute instance transfer and model transfer, we need to determine the similarities between tasks. For this purpose, the proposed method introduces the higher-KSMM (Figure 2 (c)). Thus, the higher-KSMM estimates the latent variables of tasks , by which the similarities between tasks are determined. Another important role of the higher-KSMM is to make the model transfer by estimating the general model from the task models .
After introducing these two key ideas, the entire architecture of MT-KSMM consists of three blocks: the instance transfer block, lower-KSMM block, and higher-KSMM block (i.e., the model transfer block) (Figure 2 (b)). The aim of the lower-KSMM is to estimate the task models for each task from the merged dataset . Without considering information transfer, the cost function of the lower KSMM for task is given by
| (15) |
However, the minimization of the cost function is affected by the information transfer at every iteration of the EM algorithm. Thus, before executing the M step, are merged by the instance transfer as , whereas before executing the E step, is replaced by as a result of model transfer.
By contrast, the aim of the higher-KSMM is to estimate the general model by regarding the task models as the dataset. Thus, the cost function (without considering the influence of other blocks) is given by
| (16) |
This cost function equals the cross-entropy between and as
where
Note that is determined by and , regarding as the input data. Therefore, is not determined by the observed samples naively; thus,
The lower and higher-KSMMs do not simply optimize the cost functions (15) and (16) in parallel. The estimated task models are fed forward to the higher-KSMM from the lower-KSMM as the dataset, whereas the estimated general model is fed back from the higher to the lower as a result of model transfer, so that . Additionally, the estimated task latent variables are also fed back from the higher-KSMM to the instance transfer block, whereby the merged datasets are updated. Such a hierarchical optimization process satisfies the concept of meta-learning [6].
4.4 MT-KSMM algorithm
The MT-KSMM algorithm is described as follows (also see Algorithm 1).
- Step 0:
-
Initialization
For the first loop, the latent variables and are initialized randomly.
- Step 1:
-
Instance transfer
- Step 2:
-
M step of the lower-KSMM
Task models are updated so that the cost function of the lower-KSMM is minimized as
for each task . The solution is given by the kernel smoothing of the merged sample set as follows:
(17) Then we have the model distribution set by (5).
- Step 3:
-
M step of the higher-KSMM
The general model is updated so that the cost function of the higher-KSMM is minimized as
The solution is given by
(18) Then we have the entire model distribution using (2). This process is regarded as model transfer.
- Step 4:
-
E step of the higher-KSMM
- Step 5:
-
E step of the lower-KSMM
Finally, the sample latent variables are updated so that the log-likelihood is maximized as
(20)
These five steps are iterated until the calculation converges. During the iterations, the length constant of the smoothing kernels and are gradually reduced just like the ordinary SOM.
4.5 Parametric representation of embeddings
To apply the gradient method, we represent embedding parametrically using orthonormal basis functions defined on the RKHS (e.g., normalized Legendre polynomials), such as
where is the basis set and is the coefficient matrix. In the case of single-task KSMM, the estimator of the coefficient matrix is determined as
| (21) |
where
| (22) | ||||
| (23) |
and
| (24) | ||||
| (25) |
Similarly, in MT-KSMM, the coefficient matrices of the task models are estimated as
| (26) |
where
| (27) | ||||
| (28) | ||||
| (29) | ||||
| (30) |
Thus, (17) is replaced by (26)–(30). Note that becomes a tensor of order 3. For the higher-KSMM, the general model is represented as
| (31) |
where is the coefficient tensor and represents the tensor–matrix product, where is the basis set for the higher-KSMM. The coefficient tensor is estimated as
| (32) | ||||
| (33) | ||||
| (34) |
where
| (35) | ||||
| (36) |
Thus, (18) is replaced by (32)–(36). Note that the computational cost of the proposed method with respect to the data size is for the lower-KSMMs and for the higher-KSMM. Therefore, the computation cost is proportional to both the data size and number of tasks .
5 Experimental results
5.1 Experiment protocol
To demonstrate the performance of the proposed method, we applied the method to three datasets. The first was an artificial dataset generated from two-dimensional (2D) manifolds, and the second and third were face image datasets of multiple subjects with various poses and expressions, respectively.
To examine how the information transfer improved performance, we compared methods that used different transfer styles, and KSMM was used for all methods as the common platform. Thus, (1) MT-KSMM (the proposed method) used both instance transfer and model transfer, (2) KSMM2 (the preceding method) used model transfer only, and (3) single-task KSMM did not transfer information between tasks333It is not able to examine the case of using instance transfer only because the task latent variable cannot be estimated without using the higher-KSMM, which also makes the model transfer.. KSMM2 is a modification of the preceding method SOM2 that replaces the higher and lower-SOMs with KSMMs. Note that this modification improves the performance of SOM2 by eliminating the quantization error. Similarly, single-task KSMM can be regarded as a SOM with continuous latent space.
In the experiment, we trained the methods on a set of tasks by changing S/T. After training was complete, we evaluated the performance both qualitatively and quantitatively using the test data. We used two types of test data: test data of existing tasks and test data of new tasks. The former evaluates the generalization performance for new data of existing tasks that have been learned, and the latter evaluates the generalization performance for new unknown tasks.
We assessed the learning performance quantitatively using two approaches: the root mean square error (RMSE) of the reconstructed samples and the mutual information (MI) between the true and estimated sample latent variables. RMSE (smaller is better) evaluates accuracy in the visible space without considering the compatibility of the sample latent variables, whereas MI (larger is better) evaluates accuracy in the latent space , and considers how consistent the sample latent variables are between tasks. We evaluated both RMSE and MI for the test data of existing tasks and new tasks. For existing tasks, we used the task latent variable that was estimated in the training phase, whereas was estimated by minimizing (19) for each new task.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
5.2 Artificial datasets
We examined the performance of the proposed method using an artificial dataset. We used 2D saddle shape hyperboloid manifolds embedded in 10-dimensional (10D) visible space. The data generation model is given by
| (37) |
where and are the latent variables generated by the uniform distribution and is a seven-dimensional zero vector. is 10D Gaussian noise , where . We generated 300 manifolds (i.e., tasks) by changing , each of which had 100 samples. For training, 200 out of 300 tasks were used for training, each of which had S/T, and the other samples were used as test data. Thus, samples of 100 tasks were used as test data for new tasks.
A representative result is shown in Figure 3. In this case, each task had only two samples for training (2 S/T). Thus, it was impossible to estimate the 2D manifold shape using single-task learning (Figure 3 (d)). Despite this, the proposed algorithm estimated manifold shapes successfully (Figure 3 (b)), although the border area of the manifolds was shrunk because of missing data. Compared with the proposed method, KSMM2 performed poorly in capturing the manifold shapes (Figure 3 (c)).

| Saddle shape | Convex | Triangle | Sine | |||
|---|---|---|---|---|---|---|
| RMSE | MT-KSMM | |||||
| Existing tasks | KSMM2 | |||||
| KSMM | ||||||
| MT-KSMM | ||||||
| New tasks | KSMM2 | |||||
| KSMM | ||||||
| MI | MT-KSMM | |||||
| Existing tasks | KSMM2 | |||||
| KSMM | ||||||
| MT-KSMM | ||||||
| New tasks | KSMM2 | |||||
| KSMM |
Figure 4 (a) and (b) show the RMSE and MI for the test data of existing tasks when S/T was changed. The results show that MT-KSMM performed better than the other methods, particularly when S/T was small. As S/T increased, all methods reduced the RMSE. By contrast, in the case of MI, the performance of single-task KSMM did not improve, even when a sufficient number of training samples was provided. Because no information was transferred between tasks in single-task KSMM, the manifolds were estimated independently for each task. Consequently, the sample latent variables were estimated inconsistently between tasks.
Figure 4 (c) and (d) show the RMSE and MI for the test data for new tasks. We generated 100 new tasks using (37), each of which had 100 samples. Then we estimated the task latent variable and sample latent variable using the trained model. For new tasks, MT-KSMM also demonstrated excellent performance, which suggests that it has high generalization ability.
We further evaluated the performance using other artificial datasets, which are shown in Figure 5. In this experiment, we used 400 tasks and 3 S/T for training. As shown in the figure, MT-KSMM succeeded in modeling the continuous change of manifold shapes. In the case of the triangular manifold (b), MT-KSMM succeeded in capturing the rotation of triangular shapes. In the case of sine manifolds, all manifolds intersected on the same line, and the data points on the intersection could not be distinguished between tasks. Despite this, MT-KSMM succeeded in modeling the continuous change of the manifold shape. Table 1 summarizes the experiment on artificial datasets. For all cases, MT-KSMM consistently demonstrated the best performance among the three methods.

(a)

(b)


 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |

 |
 |
| (a) | (b) |
 |
 |
 |
|
| (a) | (b) | (c) |
5.3 Face image dataset A: various poses
We applied the proposed method to a face image dataset with various poses444http://robotics.csie.ncku.edu.tw/Databases/FaceDetect_PoseEstimate.htm. The dataset consisted of the face images of 90 subjects taken from various angles. We used 25 images per subject, which were taken every from to . The face parts were cut out from the original images with pixels and a Gaussian filter was applied to remove noise. In the experiment, we used the face images of 80 subjects for the training tasks and the remaining images of 10 subjects for the test tasks. In this experiment, the dimensions of the sample latent space and the task latent space were 1 and 2, respectively.
Figure 6 shows the reconstructed images for an existing task (a) and new task (b). In this case, only two images per subject were used for training (i.e., 2 S/T). In the case of the existing task (Figure 6 (a)), we used only left face images of the subject for training, but MT-KSMM supplemented the right face images by mixing the images of other subjects. As a result, MT-KSMM successfully modeled the continuous pose change555We make a brief comment about image quality. Because the manifolds were represented as a linear combination of training data, it was unavoidable that the reconstructed images became cross-dissolved images of the training images, particularly when the number of training data was small. To reconstruct more realistic images, it is necessary to use more training images, and/or to implement prior knowledge into the method, but this is out of scope for this study.. By contrast, KSMM2 and single-task KSMM failed to model the pose change. This ability of MT-KSMM was also observed for new tasks, for which no image was used for training. As Figure 6 (b) shows, MT-KSMM reconstructed face images of various angles, whereas KSMM2 and single-task KSMM failed.
Figure 7 shows the sample latent variables estimated by MT-KSMM. The estimated latent variables were consistent with the actual pose angles for both existing tasks (below the dashed line) and new test tasks (above the dashed line). Thus, the face manifolds were aligned for all subjects, so that the latent variable represented the same property regardless of the task difference.
By changing the task latent variable and fixing the sample latent variable , various faces in the same pose were expected to appear. Figure 8 shows the generated face images using MT-KSMM when was changed. The results indicate that MT-KSMM worked as expected. In terms of the fiber bundle, the manifolds of various poses (Figure 6) corresponds to the fibers, whereas the manifold that consisted of various subjects corresponds to the base space (Figure 8).
Figure 9 shows the RMSE and MI for the test data for existing tasks ((a) and (b)) and new tasks ((c) and (d)). In this evaluation, RMSE was measured using the error between the true image and reconstructed image, and MI was measured between the true pose angle and sample latent variable . Like the case of the artificial dataset, MT-KSMM performed better than the other methods, particularly when the number of training data was small.
5.4 Face image dataset B: various expressions
 |
 |
| (a) | (b) |
 |
We applied the proposed method to another face image dataset, in which subjects displayed various expressions [42, 43]. The dataset consisted of image sequences, which ranged from a neutral expression to a distinct expression. We chose 96 subjects from the dataset, each of which had 30 images. Eighty subjects were used for training as existing tasks and the remaining 16 subjects are used for testing as new tasks. In the dataset, the sequences were labeled according to the emotion type, but the label information was not used for training.
The face image data that we used were pre-processed as follows: From each face image, 64 landmark points, such as eyes and lip edges, were extracted, and 2D coordinates were obtained from the image. Thus, each face image was transformed into 128-dimensional vector data. To separate the emotional expression from the face shape, the landmark vectors were subtracted from the vector of the neutral expressions. Thus, for all subjects, the origin was the neutral expression. To learn the dataset, the 2D latent space was used for both and .
Figure 12 shows the reconstructed images for an existing task, trained using 2 S/T. Although only two images were used for training (‘surprise’ and ‘anger’ for this subject), MT-KSMM reconstructed other expressions successfully, whereas KSMM2 and single-task KSMM failed.
MT-KSMM was expected to generate images expressing various emotions according to the sample latent variable , whereas it was expected to generate images of various expression styles of the same emotion type according to the task latent variable . Figure 12 shows the images generated by MT-KSMM, suggesting that the proposed method successfully represented the faces as expected. In terms of the fiber bundle, Figure 12 (a) represents a fiber, whereas Figure 12 (b) shows the base space.
Figure 12 shows the estimated sample latent variables . The results indicate that MT-KSMM (Figure 12 (a)) roughly classified the face images according to the expression, whereas the KSMM2 and single-task KSMM did not demonstrate such a classified representation of emotion types in the latent space. Finally, we evaluated the RMSE of the reconstructed images (Figure 13). Again, MT-KSMM performed better than the other methods for both existing and new tasks.

(a)

(b)
5.5 Application to multi-task supervised learning
Although the proposed method was designed for multi-task manifold learning, the concepts of instance transfer and model transfer can be applied to other learning paradigms. Figure 14 shows two toy examples of multi-task regression. In this experiment, 400 tasks were generated by slanted sinusoidal functions , where and are the input and output, respectively; is the task latent variable; and are fixed parameters. There were 2 S/T, which were generated by the uniform random input.
In the first case (Figure 14 (a)), the input was distributed in uniformly. For this dataset, the latent variable was simply replaced by the input , whereas the corresponding output was regarded as the observed data . Thus, Step 5 in Algorithm 1 was omitted. As shown in Figure 14 (a), the proposed method successfully estimated the continuous change of sinusoidal functions from small sample sets.
The proposed method can be applied to multi-task regression when domain shifts occur. In the second case (Figure 14 (b)), the input distribution also changed according to the task latent variable . For this case, MT-KSMM was directly applied by regarding each input–output pair as the training sample of MT-KSMM; thus, . Although the border area was shrunk because of the absence of training samples, MT-KSMM successfully captured the continuous change of the function shapes, as well as the change of the input domain. Note that the estimation of the input distribution was also difficult for the small sample case.
6 Discussion
The key idea of the proposed method is to use two types of information transfer: instance transfer and model transfer. We discuss how these transfers work from the viewpoint of information geometry. We also discuss the problem formulation of multi-task manifold learning from the viewpoint of optimal transport.
6.1 From the information geometry viewpoint
Generative manifold model can be regarded as an infinite Gaussian mixture model (GMM) in which the Gaussian components are arranged continuously along the nonlinear manifold. Like the ordinary GMM, the EM algorithm can be used to solve it [38, 39]. We first depict the single-task KSMM case from the information geometry viewpoint (Figure 15 (a)) and then describe the multi-task case (Figure 15 (b)).
6.1.1 Single-task case
Information geometry is geometry in statistical space , which consists of all possible probability distributions. In our case, is the space that consists of all joint probabilities of and , that is, .
When both and are given, we assume that the data distribution is represented as
Thus, the data distribution corresponds to a point in . Because dataset is known, whereas the latent variables are unknown, the set of data distributions for all possible becomes a data manifold . Therefore, estimating from means determining the optimal point in the data manifold .
It should be noted that there is arbitrariness with respect to the coordinate system of . For example, if the coordinate system of is rotated or nonlinearly distorted, we obtain another equivalent solution of . Therefore, there is an infinite number of equivalent data distributions with respect to (indicated for the depth direction in Figure 15 (a)). Additionally, when the number of samples is small, is far from the true distribution, and there is a large variation depending on the sample set .
Similarly, we can consider a manifold consisting of all possible model distributions. In this study, we represent a model distribution as
where . Thus, the set of all possible model distributions forms a model manifold , which is homeomorphic to . Therefore, estimating from means determining the optimal point in . Like the case of data distribution, there is also arbitrariness with respect to the coordinate system of .
The aim of KSMM is to minimize the cross-entropy between and , that is, minimize the Kullback–Leibler (KL) divergence 666Rigorously speaking, the self-entropy of needs to be considered because it also depends on .. The KSMM algorithm is the EM algorithm by which KL-divergence is minimized with respect and alternately. From the information geometry viewpoint, the optimal solutions and are given as the nearest points of two manifolds and . To determine the optimal pair , projections between two manifolds are executed iteratively. Thus, in the M step, is projected to , whereas in the E step, is projected to . These two projections are referred to as m-projection and e-projections (Figure 15 (a)). m- and e-projections are executed repeatedly until and converge to the nearest points of and [44]. We note again that there are infinite solution pairs because of the arbitrariness of the coordinate system of .
6.1.2 Information transfers
As shown in (11), the data distribution set is mixed by the instance transfer as
| (38) |
where
Then we have . In information geometry, Eq. (38) is called the m-mixture of the data distribution set . Therefore, the instance transfer is translated as the transfer by the m-mixture in terms of information geometry.
By contrast, as shown in (14), the log of the model distributions are mixed by the model transfer as
| (39) |
where
Then we have . Eq. (39) is called the e-mixture of model distributions in information geometry. Therefore, the model transfer is translated as the transfer by the e-mixture. It has been shown that the e-mixture transfer improves multi-task learning in estimating the probability density [45].
6.1.3 Multi-task case
Based on the above discussion, the learning process of MT-KSMM can be interpreted as follows (Figure 15 (b)): Suppose that we have data distributions . In Step 1, are mapped to using instance transfer (i.e., m-mixture transfer). However, MT-KSMM not only models the given tasks, but can also model unknown tasks. Therefore, we have a data distribution for any :
As a result, we have a smooth manifold in , which is homeomorphic to . Manifold is obtained by the kernel smoothing of the data distributions in the m-mixture manner. We refer to this process as m-smoothing. Thus, the instance transfer can be translated as m-smoothing, which generates the manifold .
In Step 2, manifold is projected to by the m-projection (26), and we obtain the model distribution set in . Then, in Step 3, we obtain a manifold from :
Because manifold is obtained by the kernel smoothing of in the e-mixture manner, we refer to this process as e-smoothing. Thus, the model transfer is now regarded as e-smoothing, which generates the manifold in . In the manifold , the model distributions of unknown tasks are also represented.
After e-smoothing, in Steps 4 and 5, the latent variables and are estimated by the e-projection, by which is updated. Thus, the MT-KSMM algorithm is depicted as the bidirectional m- and e-projections of and , which are generated by m- and e-smoothing, respectively.
It is worth noting that m-smoothing tends to make the distributions broader, whereas e-smoothing tends to make them narrower. Thus, if either m- or e-smoothing is used alone, it will not work as expected, particularly when S/T is small. Therefore, the combination of m- and e-smoothing is essentially important for multi-task manifold modeling. Additionally, e-smoothing plays another important role in MT-KSMM. By performing e-smoothing, the neighboring models come closer to each other in , and their coordinate systems also come closer to each other. As a result, the manifolds are aligned between the tasks, and the latent variables acquire a consistent representation.
To summarize, the MT-KSMM algorithm consists of the following steps: (Step 1) By m-smoothing, we obtain manifold from the data distribution set . This process is the instance transfer. (Step 2) is projected to by m-projection, and we obtain the model distribution set . (Step 3) By e-smoothing, we obtain manifold from . This process is the model transfer. (Steps 4 and 5) is projected to by e-projection, and latent variables and are updated.
In this discussion, we described the learning process of MT-KSMM from the viewpoint of information geometry. We discussed the depiction of two manifolds and in , which are generated by m- and e-smoothing, respectively, and are projected alternately by m- and e-projections, respectively. We believe that such geometrical operations are the essence of the two information transfer styles in multi-task manifold modeling.
6.2 From the optimal transport viewpoint
In this study, we assumed that the latent space was common to all tasks. For example, for the face image set, we expected the latent variable to represent the pose or expression of the face image regardless of which task it belonged to. Thus, if we had two manifolds and , and the corresponding embeddings and , we considered that and would represent the same intrinsic property, even if . Based on this assumption, information was transferred between tasks. However, some questions arise. The first question is how we can know whether latent variables that belong to different tasks represent the same intrinsic property. The second question is how we can regularize multi-task learning so that the latent variables represent the common intrinsic property. Note that the intrinsic property is unknown. Therefore, we need to redefine the objective of multi-task manifold learning without using such ambiguous terms.
In this study, we defined the distance between two manifolds and as (1). Thus, to measure the distance, the corresponding embeddings and need to be provided. However, because there is arbitrariness with respect to the coordinate system of , there are many equivalent embeddings that generate the same manifold. Therefore, if are not specified, the distance between two manifolds cannot be determined uniquely. In such a case, it is natural to choose the pair that minimizes (1). Thus, the distance is defined as
| (40) |
where is a set of embeddings, which yield the equivalent data distribution on ; that is, for any , they satisfy , where . Such a distance between manifolds (40) becomes the optimal transport distance between and . Based on this, we can say that manifolds are aligned with respect to the coordinate system induced by , if and only if minimizes (40). Additionally, if two manifolds are aligned, we assume that the latent variable represents the intrinsic property that is independent of the task.
Now we recall the problem formulation in terms of the fiber bundle (Figure 1 (d)), in which each task manifold is regarded as a fiber. Then we can consider the integral of the transport distance between fibers along the base space , which equals the length of manifold (Figure 1 (c)). When all task manifolds are aligned with neighboring ones, the total length of manifold is expected to be minimized. As already described, SOM (in addition to KSMM) works like an elastic net. Therefore, roughly speaking, the higher-KSMM tends to shorten the length of manifold , whereby the task manifolds are gradually aligned. Therefore, in MT-KSMM, the transport distance along the base space is implicitly regularized to be optimized. It would be worth trying to implement such optimal transport-based regularization in the objective function explicitly, and this is our future work. The underlying learning theory from the optimal transport viewpoint would be also an important issue in the future.
7 Conclusion
In this paper, we proposed a method for multi-task manifold learning by introducing two information transfers: instance transfer and model transfer. Throughout the experiments, the proposed method, MT-KSMM performed better than KSMM2 and single-task KSMM. Because in the comparison we consistently used KSMM as a platform for manifold learning, we can conclude that these results were only caused by differences in the manner of information transfer between tasks. Thus, the combination of instance transfer and model transfer are effective for multi-task manifold learning, particularly when the sample per task is small. It should be noted that KSMM2 (i.e., the preceding method SOM2) learns appropriately when sufficient samples are provided. Because KSMM2 uses model transfer only, we can also conclude that instance transfer is necessary for the small sample size case. By contrast, model transfer is necessary for manifold alignment, whereby the latent variables are estimated consistently across tasks, representing the same intrinsic feature of the data.
The proposed method projects the given data into the product space of the task latent space and sample latent space, in which the intrinsic feature of the data content is represented by the sample latent variables, whereas the intrinsic feature of the data style is represented by the task latent variable. For example, in the case of the face image set, ‘content’ refers to the expressed emotions and ‘style’ refers to the individual difference in the manner of expressing emotions. Such a learning paradigm is referred to as content–style disentanglement in the recent literature [46]. Therefore, the proposed method is not only multi-task manifold learning under the small sample size condition, but also has the ability to perform content–style disentanglement under the condition where data are observed partially for each style. Because recent studies on content–style disentanglement implement the autoencoder (AE) platform [47], which typically requires a larger number of samples, applying the proposed information transfers to an AE would be a challenging theme in future work.
Acknowledgements
We thank S. Akaho, PhD, from National Institute of Advanced Industrial Science and Technology of Japan, who gave us important advice for this study. This work was supported by JSPS KAKENHI [grant number 18K11472, 21K12061, 20K19865]; and ZOZO Technologies Inc. We thank Maxine Garcia, PhD, from Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript.
References
- [1] X. Huo, X. Ni, A. K. Smith, A survey of manifold-based learning methods, in: T. W. Liao, E. Triantaphyllou (Eds.), In Recent Advances in Data Mining of Enterprise Data, World Scientific, 2007, Ch. 15, pp. 691–745.
- [2] R. Pless, R. Souvenir, A survey of manifold learning for images, IPSJ Transactions on Computer Vision and Applications 1 (2009) 83–94. doi:10.2197/ipsjtcva.1.83.
- [3] S.-J. Wang, H.-L. Chen, X.-J. Peng, C.-G. Zhou, Exponential locality preserving projections for small sample size problem, Neurocomputing 74 (17) (2011) 3654–3662. doi:10.1016/j.neucom.2011.07.007.
- [4] C. Shan, S. Gong, P. McOwan, Appearance manifold of facial expression, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 3766 LNCS (2005) 221–230. doi:10.1007/11573425\_22.
- [5] Y. Chang, C. Hu, R. Feris, M. Turk, Manifold based analysis of facial expression, Image and Vision Computing 24 (6) (2006) 605–614. doi:10.1016/j.imavis.2005.08.006.
-
[6]
T. Hospedales, A. Antoniou, P. Micaelli, A. Storkey,
Meta-learning
in neural networks: A survey, IEEE Transactions on Pattern Analysis and
Machine Intelligence (2021).
doi:10.1109/TPAMI.2021.3079209.
URL https://www.scopus.com/inward/record.uri?eid=2-s2.0-85105850460&doi=10.1109%2fTPAMI.2021.3079209&partnerID=40&md5=91a28d509d70e45dadbe80985f2a7b93 - [7] R. Caruana, Multitask learning, Machine Learning 28 (1) (1997) 41–75. doi:10.1023/A:1007379606734.
- [8] Y. Zhang, Q. Yang, An overview of multi-task learning, National Science Review 5 (1) (2018) 30–43. doi:10.1093/nsr/nwx105.
- [9] Z. Zhang, J. Zhou, Multi-task clustering via domain adaptation, Pattern Recognition 45 (1) (2012) 465–473. doi:10.1016/j.patcog.2011.05.011.
- [10] X.-L. Zhang, Convex discriminative multitask clustering, IEEE Transactions on Pattern Analysis and Machine Intelligence 37 (1) (2015) 28–40. doi:10.1109/TPAMI.2014.2343221.
- [11] X. Zhang, X. Zhang, H. Liu, X. Liu, Multi-task clustering through instances transfer, Neurocomputing 251 (2017) 145–155. doi:10.1016/j.neucom.2017.04.029.
- [12] X. Zhang, X. Zhang, H. Liu, X. Liu, Partially related multi-task clustering, IEEE Transactions on Knowledge and Data Engineering 30 (12) (2018) 2367–2380. doi:10.1109/TKDE.2018.2818705.
- [13] I. Yamane, F. Yger, M. Berar, M. Sugiyama, Multitask principal component analysis, Journal of Machine Learning Research 63 (2016) 302–317.
- [14] T. Furukawa, SOM of SOMs, Neural Networks 22 (4) (2009) 463–478. doi:10.1016/j.neunet.2009.01.012.
- [15] T. Furukawa, SOM of SOMs: Self-organizing map which maps a group of self-organizing maps, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 3696 LNCS (2005) 391–396. doi:10.1007/11550822\_61.
- [16] R. Dedrick, J. Ferron, M. Hess, K. Hogarty, J. Kromrey, T. Lang, J. Niles, R. Lee, Multilevel modeling: A review of methodological issues and applications, Review of Educational Research 79 (1) (2009) 69–102. doi:10.3102/0034654308325581.
- [17] A. Zweig, D. Weinshall, Hierarchical regularization cascade for joint learning, no. PART 2, 2013, pp. 1074–1082.
- [18] L. Han, Y. Zhang, Learning multi-level task groups in multi-task learning, Vol. 4, 2015, pp. 2638–2644.
- [19] L. Han, Y. Zhang, Learning tree structure in multi-task learning, Vol. 2015-August, 2015, pp. 397–406. doi:10.1145/2783258.2783393.
- [20] J. Jiang, L. Zhang, T. Furukawa, A class density approximation neural network for improving the generalization of fisherface, Neurocomputing 71 (16-18) (2008) 3239–3246. doi:10.1016/j.neucom.2008.04.042.
- [21] T. Ohkubo, K. Tokunaga, T. Furukawa, RBFSOM: An efficient algorithm for large-scale multi-system learning, IEICE Transactions on Information and Systems E92-D (7) (2009) 1388–1396. doi:10.1587/transinf.E92.D.1388.
- [22] T. Ohkubo, T. Furukawa, K. Tokunaga, Requirements for the learning of multiple dynamics, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 6731 LNCS (2011) 101–110. doi:10.1007/978-3-642-21566-7\_10.
- [23] S. Yakushiji, T. Furukawa, Shape space estimation by SOM2, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 7063 LNCS (PART 2) (2011) 618–627. doi:10.1007/978-3-642-24958-7\_72.
- [24] S. Yakushiji, T. Furukawa, Shape space estimation by higher-rank of SOM, Neural Computing and Applications 22 (7-8) (2013) 1267–1277. doi:10.1007/s00521-012-1004-4.
- [25] H. Ishibashi, R. Shinriki, H. Isogai, T. Furukawa, Multilevel–multigroup analysis using a hierarchical tensor SOM network, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 9949 LNCS (2016) 459–466. doi:10.1007/978-3-319-46675-0\_50.
- [26] H. Ishibashi, T. Furukawa, Hierarchical tensor SOM network for multilevel-multigroup analysis, Neural Processing Letters 47 (3) (2018) 1011–1025. doi:10.1007/s11063-017-9643-1.
- [27] N. Lawrence, Probabilistic non-linear principal component analysis with gaussian process latent variable models, Journal of Machine Learning Research 6 (2005).
- [28] K. Bunte, M. Biehl, B. Hammer, A general framework for dimensionality-reducing data visualization mapping, Neural Computation 24 (3) (2012) 771–804. doi:10.1162/NECO\_a\_00250.
- [29] C. Bishop, M. Svensén, C. Williams, GTM: The generative topographic mapping, Neural Computation 10 (1) (1998) 215–234. doi:10.1162/089976698300017953.
- [30] N. Lawrence, Gaussian process latent variable models for visualisation of high dimensional data, 2004.
- [31] P. Meinicke, S. Klanke, R. Memisevic, H. Ritter, Principal surfaces from unsupervised kernel regression, IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (9) (2005) 1379–1391. doi:10.1109/TPAMI.2005.183.
- [32] T. Kohonen, Self-organized formation of topologically correct feature maps, Biological Cybernetics 43 (1) (1982) 59–69. doi:10.1007/BF00337288.
- [33] C. Wang, S. Mahadevan, Manifold alignment without correspondence, 2009, pp. 1273–1278.
- [34] T. Daouda, R. Chhaibi, P. Tossou, A.-C. Villani, Geodesics in fibered latent spaces: A geometric approach to learning correspondences between conditions (2020). arXiv:2005.07852.
- [35] S. Luttrell, Self-organisation: A derivation from first principles of a class of learning algorithms, 1989, pp. 495–498. doi:10.1109/ijcnn.1989.118288.
- [36] Y. Cheng, Convergence and ordering of kohonen’s batch map, Neural Computation 9 (8) (1997) 1667–1676. doi:10.1162/neco.1997.9.8.1667.
- [37] T. Graepel, M. Burger, K. Obermayer, Self-organizing maps: Generalizations and new optimization techniques, Neurocomputing 21 (1-3) (1998) 173–190. doi:10.1016/S0925-2312(98)00035-6.
- [38] T. Heskes, Self-organizing maps, vector quantization, and mixture modeling, IEEE Transactions on Neural Networks 12 (6) (2001) 1299–1305. doi:10.1109/72.963766.
- [39] J. Verbeek, N. Vlassis, B. Kröse, Self-organizing mixture models, Neurocomputing 63 (SPEC. ISS.) (2005) 99–123. doi:10.1016/j.neucom.2004.04.008.
- [40] R. Durbin, D. Willshaw, An analogue approach to the travelling salesman problem using an elastic net method, Nature 326 (6114) (1987) 689–691. doi:10.1038/326689a0.
- [41] A. Utsugi, Hyperparameter selection for self-organizing maps, Neural Computation 9 (3) (1997) 623–635. doi:10.1162/neco.1997.9.3.623.
- [42] T. Kanade, J. Cohn, Y. Tian, Comprehensive database for facial expression analysis, 2000, pp. 46–53. doi:10.1109/AFGR.2000.840611.
- [43] P. Lucey, J. Cohn, T. Kanade, J. Saragih, Z. Ambadar, I. Matthews, The extended cohn-kanade dataset (ck+): A complete dataset for action unit and emotion-specified expression, 2010, pp. 94–101. doi:10.1109/CVPRW.2010.5543262.
- [44] S.-i. Amari, Information geometry of the em and em algorithms for neural networks, Neural Networks 8 (9) (1995) 1379–1408. doi:10.1016/0893-6080(95)00003-8.
- [45] K. Takano, H. Hino, S. Akaho, N. Murata, Nonparametric e-mixture estimation, Neural Computation 28 (12) (2016) 2687–2725. doi:10.1162/NECO\_a\_00888.
- [46] H. Kazemi, S. Iranmanesh, N. Nasrabadi, Style and content disentanglement in generative adversarial networks, 2019, pp. 848–856. doi:10.1109/WACV.2019.00095.
- [47] J. Na, W. Hwang, Representation learning for style and content disentanglement with autoencoders, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 12047 LNCS (2020) 41–51. doi:10.1007/978-3-030-41299-9\_4.
| For problem formulation (single task case) | |
|---|---|
| High-dimensional visible data space with dimension | |
| Low-dimensional latent space with dimension | |
| Observed dataset containing samples, where | |
| Latent variable set of samples, where | |
| Manifold representing the data distribution | |
| Embedding from to , referred to as the model | |
| Prior of | |
| Probabilistic generative model of and | |
| Inverse variance (precision) of observation noise | |
| For problem formulation (multi-task case) | |
| Dataset of the th task containing samples | |
| Entire dataset of tasks, where | |
| design matrix consisting of the entire dataset of tasks | |
| Number of tasks | |
| Task to which sample belongs | |
| Sample set belonging to task | |
| Manifold of task | |
| Embedding from to , referred to as the task model | |
| Function space (RKHS) consisting of embeddings from to | |
| Low-dimensional latent space for tasks with dimension | |
| Task manifold embedded into | |
| Latent variable set for tasks, where | |
| Embedding from to | |
| Embedding from to , referred to as the general model | |
| Prior of | |
| Probabilistic generative model of task | |
| Probabilistic generative model of , , and | |
| For KSMM (single task case) | |
| Non-negative smoothing kernel with length constant | |
| Tentative estimators of latent variables | |
| Tentative estimator of mapping | |
| Joint empirical distribution of and under and are given | |
| Basis functions for a parametric representation | |
| Coefficient matrix to represent parametrically | |
| Multi-task case (MT-KSMM) | |
| Function that determines the weight of the instance transfer from task to | |
| Length constant of | |
| Merged dataset of task obtained by instance transfer | |
| is a weighted set where denotes the weight of | |
| Merged latent variable set obtained by instance transfer | |
| Number of merged sample sets of task | |
| Task model after model transfer is executed | |
| Joint empirical distribution after instance transfer is executed | |
| Generative model for the th task after model transfer is executed | |
| Smoothing kernel for the higher-KSMM with length constant | |
| Basis function for the higher-KSMM | |
| Coefficient matrix to represent task model parametrically | |
| Coefficient tensor consisting of | |
| Coefficient tensor to represent general model parametrically | |
Appendix A Symbols and notation
In this paper, scalars and functions are usually written in italics (e.g., , , and ). Indices and their upper limits are written in lowercase and uppercase italics, respectively (e.g., and ). Sets are also written in uppercase italics (e.g., and ). Vectors and matrices are written in lowercase and uppercase boldface, respectively (e.g., and ), whereas tensors are written in uppercase boldface and underlined (e.g., . Continuous spaces and manifolds are written in cursive script (e.g., and ).
The list of symbols used in this paper is shown in Table 2.
Appendix B Details of the equation derivation
B.1 Derivation of the KSMM algorithm
The cost function of KSMM is given by (3). First, we show that this cost function equals the cross-entropy between (4) and (5), except the constant. The cross-entropy is given by
Note that, in this study, we assume that the prior is a uniform distribution. Thus,
and we obtain the cost function (3). We apply the expectation of the square error for the normal distribution:
To estimate the latent variables, we need to minimize the cost function (3) with respect to each as (6). Because is obtained by kernel smoothing, can be considered sufficiently smooth to be locally approximated as linear. By considering the first-order Taylor expansion, the square error is approximated as a quadratic function centered on the minimum point. Because is symmetric around , the minimum point of (6) equals the minimum point of (7).
B.2 Derivation of the MT-KSMM algorithm
B.3 Derivation of the parametric representation of KSMM
Using the orthonormal basis set , we represent the mapping parametrically as
where . In this case, the cost function (3) becomes
If we differentiate with respect to , then
Because the stationary point of should satisfy , we have the following equation:
| (41) | |||
| (42) |
The left-hand side (41) becomes
where and is an matrix. By contrast, the right-hand side (42) becomes
Because holds, the estimator of is given by
| (43) |
Thus, we have (26). In the KSMM algorithm, the tentative estimator of latent variables is used instead of .
B.4 Derivation of the parametric representation of MT-KSMM
Similar to the non-parametric case, we obtain the parametric representation of MT-KSMM by a straightforward extension, but a tensor–matrix product is required in the notation.
First, we introduce some tensor operations. Suppose that is an matrix, and let be the vector representation of . Thus, is an -dimensional vector obtained by flattening . When we have such matrices , the entire matrix set is represented as a matrix . Note that is an matrix, which is also denoted by in tensor notation. We further suppose that is a linear transformation, where is an matrix, whereas is an matrix. Using the tensor–matrix product, this linear transformation is denoted by , which means in element-wise notation, where is a tensor of order three and size . Similarly, means .
Using the above notation, the parametric representation of MT-KSMM becomes as follows: For the lower-KSMMs, we estimate the coefficient matrix as for each task ; using this, the task model is represented as . Consequently, the entire coefficient matrices become a tensor of order three and size . By flattening using , can also be represented by a matrix . Because we use an orthonormal basis set , the metric in function space equals the Euclidean metric in the ordinary vector space of the coefficient matrices. Thus, we consider that are equivalent to , including the metric.
The higher-KSMM estimates by regarding the task model set as a dataset. Thus, in the parametric representation, the aim of the higher-KSMM is to estimate a function , where is the latent variable of tasks. By regarding as a data matrix and applying (43), we have
| (44) |
where and are defined in (33) and (34), respectively. Using tensor–matrix product notation, (44) is denoted by .