Multi-state Swap Test Algorithm

The concept of quantum computing was proposed by Richard Feynman in the early 1980s[1] and David Deutsch later gave a quantum algorithm solution to a toy issue[2]. In recent years, Quantum algorithms and their applications in fields like encryption[3],database search[4], quantum simulation[5], optimization problems[6] and linear systems of equations[7] (refer to [8] for more information) have proved spectacular. For certain problems, these quantum algorithms outperform classical algorithms in terms of speed. Typically, quantum algorithms are described using quantum circuits, which are made up of a sequence of quantum gates that can handle quantum bits. When dealing with quantum circuits, it’s important to measure the similarity or overlap between two states $\left|\phi\right\rangle$ and $\left|\psi\right\rangle$, which can be denoted by $\left|{\left\langle{\phi,\psi}\right\rangle}\right|^{2}$[9].

Swap Test is a well-known quantum circuit, which uses a controlled-swap (CSWAP) gate and an ancillary qubit to estimate the inner product $\left|{\left\langle{\phi,\psi}\right\rangle}\right|^{2}$ of two states $\left|\phi\right\rangle,\left|\psi\right\rangle$[10][11]. It has attracted interest as a fundamental primitive and its efficient implementation on near-term quantum computers is a hot research issue at the moment. In[12], L. Cincio et al. presented a machine learning approach for discovering short-depth algorithm to compute states overlap, whose performance is better than the linear scaling of Swap Test. In [13], M. Fanizza et al. studied the estimation of overlap between two unknown pure quantum states in a finite-dimensional system, given $M$ and $N$ copies of each type. They demonstrated that allowing for general collective measurements on all copies can yield a more precise estimate. In [14], U. Chabaud et al. proposed a strategy for a programmable projective measurement device, which may be interpreted as an optimal Swap Test when only one copy of one state and $M-1$ of the other is available. There are many applications that require state overlap computation thus making Swap Test appears as a subroutine in these applications. For instance, it is used to measure entanglement and indistinguishabiliy for quantum states[11][15], and also common in quantum supervised learning to measure the distances of quantum states[16][17][18]. What’s more, proofs-of-concept in implementations of quantum computers[19][20] call for this Swap Test as well.

Consider the case when there are $n$ quantum states$\left|{\phi_{1}}\right\rangle,\left|{\phi_{2}}\right\rangle,...,\left|{\phi_{n}}\right\rangle$ and the Swap Test can only assess the overlap of two at a time. In order to obtain the overlap $\left|{\left\langle{\phi_{i}}\right|\left.{\phi_{j}}\right\rangle}\right|^{2}$ between arbitrary two states $\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle(i,j=1,2,...,m;i\neq j)$, there is a trivial solution which requires $\frac{{n(n-1)}}{2}$ Swap Tests and $\frac{{n(n-1)}}{2}$ ancillary qubits. In [21], X. Gitiaux et al. extended two-state Swap Test to $n$ quantum states $\left|{\phi_{1}}\right\rangle,\left|{\phi_{2}}\right\rangle,...,\left|{\phi_{n}}\right\rangle$. They built a unitary ${\rm U}_{4}$ circuit with three ancillaries, three controlled-swap (CSWAP) gates, and one Swap Test to compute overlap for four states. Based on the ${\rm U}_{4}$ circuit, they developed a recursive algorithm to generalize a circuit which can estimate overlaps between $n$ quantum states at a time. The circuit requires $O(n)$ CSWAP gates and $O(\log n)$ ancillary qubits.

In this paper, following the idea of [21], we design a new circuit ${\rm U}_{4}$ with two ancillaries, two controlled-swap(CSWAP) gates , and two simple Swap Test. We also present two rules to swap four groups of quantum states. Based on the swap rules and our ${\rm U}_{4}$, a circuit to calculate the overlap between different pairs of $n$ arbitrary input states are presented. Our circuit requires $n\log_{2}n$ CSWAP gates and $2(n-1)$ ancillary qubits.

The paper is organized as follows: some correlative preliminaries are introduced in Section 2; a multi-state Swap Test algorithm is proposed in Section 3; In Section 4, the simulation of 8-state Swap Test algorithm on IBM Quantum Experience’s platform is described. And the correctness and performance of the algorithm are analyzed in section 5. A brief discussion and a summary are given in Section 6.

Suppose that there are $n$ quantum states $|{\phi_{1}}\rangle,|{\phi_{2}}\rangle,...,|{\phi_{n}}\rangle$. An algorithm to construct one circuit to take all $n$ input states at once and get the overlap of arbitrary two input states in $|{\phi_{1}}\rangle,|{\phi_{2}}\rangle,...,|{\phi_{n}}\rangle$ is presented.

Two swap rules are designed as follows: $N(N=2^{2},2^{3},...,2^{k})$ quantum states can be divided into four groups $G_{1},G_{2},G_{3},G_{4}$. $Rule1$ is to exchange the states of 2nd and 3rd group in turn and get $G_{1},G_{3},G_{2},G_{4}$; $Rule2$ is to exchange the states of 2nd and 4th group in turn and get $G_{1},G_{4},G_{3},G_{2}$. The multi-state Swap Test algorithm based on the two swap rules is as follows:

(1) Constructing a circuit ${\rm U}_{4}$ to estimate the overlap of any two of the 4 states quantum states $|{\phi_{1}}\rangle,|{\phi_{2}}\rangle,|{\phi_{3}}\rangle,|{\phi_{4}}\rangle$. In ${\rm U}_{4}$, there are two ancillary qubits $s_{1},s_{2}$ and four input qubits $q_{1},q_{2},q_{3},q_{4}$. The initial states are $s_{1}s_{2}=|+\rangle|+\rangle$ and $q_{1}q_{2}q_{3}q_{4}=|{\phi_{1}}\rangle|{\phi_{2}}\rangle|{\phi_{3}}\rangle|{\phi_{4}}\rangle$. $q_{1}q_{2}q_{3}q_{4}$ are divided into four groups $G_{1}=q_{1};G_{2}=q_{2};G_{3}=q_{3};G_{4}=q_{4}$. There are also two CSWAP gates, where $s_{1}(s_{2})$ is the control qubit to swap two groups $G_{2},G_{3}(q_{2},q_{4})$ according to $rule1(rule2)$. Two simple Swap Test for two quantum states are places at the end of ${\rm U}_{4}$ to measure the overlap for $q_{1},q_{2}$ and $q_{3},q_{4}$. The ${\rm U}_{4}$ is shown in Fig.(9).

The swap results between $s_{1},s_{2}$ and $q_{1},q_{2},q_{3},q_{4}$ are shown in Table.(2).

According to the Table.(2), if $s_{1}s_{2}=\left|{0}{0}\right\rangle$, the overlap of $\left|{\phi_{1}\phi_{2}}\right\rangle$ and $\left|{\phi_{3}\phi_{4}}\right\rangle$ can be obtained through two simple Swap Test; if $s_{1}s_{2}=\left|{0}{1}\right\rangle$, the overlap of $\left|{\phi_{1}\phi_{3}}\right\rangle$ and $\left|{\phi_{2}\phi_{4}}\right\rangle$ can be obtained through two simple Swap Test; if $s_{1}s_{2}=\left|{1}{0}\right\rangle$, the overlap of $\left|{\phi_{1}\phi_{4}}\right\rangle$ and $\left|{\phi_{3}\phi_{2}}\right\rangle$ can be obtained through two simple Swap Test.

(2) Constructing a circuit ${\rm U}_{8}$ to estimate the overlap of any two quantum states in $\left|{\phi_{1}}\right\rangle,\left|{\phi_{2}}\right\rangle,\left|{\phi_{3}}\right\rangle,\left|{\phi_{4}}\right\rangle,\left|{\phi_{5}}\right\rangle,\left|{\phi_{6}}\right\rangle,\left|{\phi_{7}}\right\rangle,\left|{\phi_{8}}\right\rangle$. In ${\rm U}_{8}$, there are four ancillary qubits $s_{1},s_{2},s_{3},s_{4}$ and eight input qubits $q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7},q_{8}$. The initial states are $s_{1}s_{2}s_{3}s_{4}=\left|+\right\rangle\left|+\right\rangle\left|+\right\rangle\left|+\right\rangle$ and $q_{1}q_{2}q_{3}q_{4}q_{5}q_{6}q_{7}q_{8}=\left|{\phi_{1}}{\phi_{2}}{\phi_{3}}{\phi_{4}}{\phi_{5}}{\phi_{6}}{\phi_{7}}{\phi_{8}}\right\rangle$. $q_{1}q_{2}q_{3}q_{4}q_{5}q_{6}q_{7}q_{8}$ are divided into four groups $G_{1}=q_{1}q_{2};G_{2}=q_{3}q_{4};G_{3}=q_{5}q_{6};G_{4}=q_{7}q_{8}$. There are also eight CSWAP gates. $s_{1}(s_{2})$ is a control qubit on two CSWAP gates to swap $G_{2},G_{3}(G_{2},G_{4})$ according to $rule1(rule2)$. And $s_{3},q_{1},q_{2},q_{3},q_{4}$ can be seen as inputs of ${\rm U}_{4}$ and $s_{4},q_{5},q_{6},q_{7},q_{8}$ can also be seen as inputs of ${\rm U}_{4}$. Four simple Swap Test for two quantum states are places at the end of ${\rm U}_{8}$ to measure the overlap for $q_{1},q_{2}$ and $q_{3},q_{4}$. The ${\rm U}_{8}$ is shown in Fig.(10).

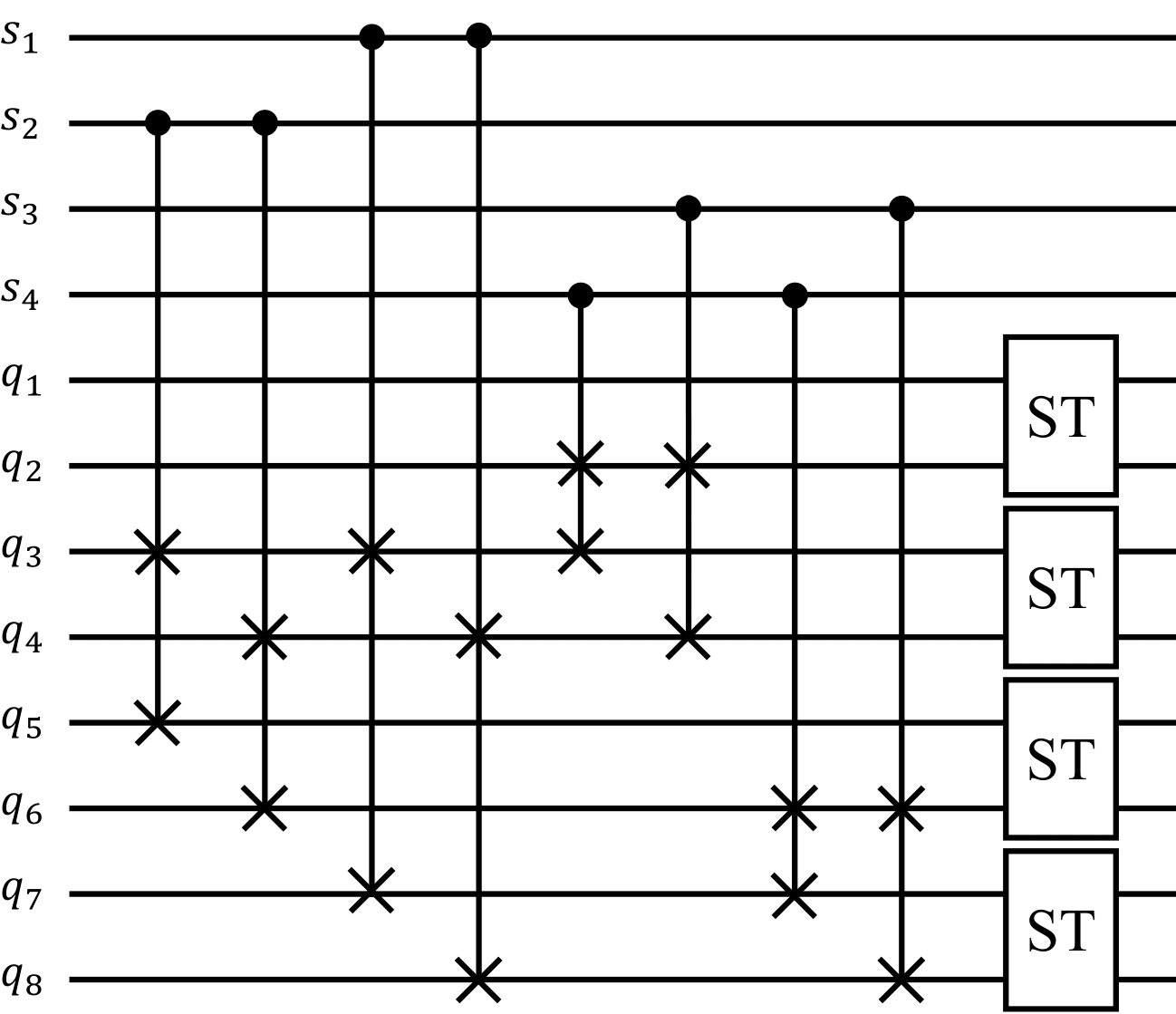
The swap results between $s_{1},s_{2},s_{3},s_{4}$ and $q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7},q_{8}$ are shown in Table.(3).

(3) Constructing a circuit ${\rm U}_{m}$ to estimate any two quantum states’ overlap for $m$ states $\left|{\phi_{1}}\right\rangle,\left|{\phi_{2}}\right\rangle,...\left|{\phi_{m}}\right\rangle$. If $2^{k-1}<m\leq 2^{k}$, $2^{k}-m$ $\left|0\right\rangle$ are added into $m$ states. In ${\rm U}_{n}(n=2^{k})$, there are $2(k-1)$ ancillary qubits $s_{1},s_{2},...,s_{2(k-1)}$ and $2^{k}$ input states $q_{1},q_{2},...,q_{2^{k}}$. The initial states are $s_{i}=\left|+\right\rangle$ and $q_{i}=\left|{\phi_{i}}\right\rangle(i=1,2,...,2^{k})$. $q_{1},q_{2},...,q_{2^{k}}$ are divided into four groups $G_{1}=q_{1},q_{2},...,q_{2^{k-2}},G_{2}=q_{2^{k-2}+1},q_{2^{k-2}+2},...,q_{2(2^{k-2})},G_{3}=q_{2(2^{k-2})+1},q_{2(2^{k-2})+2},...,q_{3(2^{k-2})},G_{4}=q_{3(2^{k-2})+1},q_{3(2^{k-2})+2},...,q_{2^{k}}.$ There are also $(k-1)2^{k-1}$ CSWAP gates in ${\rm U}_{n}$. $s_{1}(s_{2})$ is a control qubit on $\frac{{2^{k}}}{4}$ CSWAP gates to swap the states in $G_{2},G_{3}(G_{2},G_{4})$ according to $rule1(rule2)$. Then the $2^{k-1}$ inputs of $G_{1}G_{2}(G_{3}G_{4})$ can be used to construct a circuit ${\rm U}_{2^{k-1}}$. After recursively constructing round by round, $s_{(2(k-1)-\frac{{2^{k}}}{4}+i)},q_{4n-3},q_{4n-2},q_{4n-1},q_{4n}(i=1,2,...,\frac{{2^{k}}}{4})$ can be used as inputs of ${\rm U}_{4}$. $2^{k-1}$ simple Swap Test for two quantum states are places at the end of ${\rm U}_{2^{k}}$ to measure the overlap for $(q_{1},q_{2})$, $(q_{3},q_{4})$,…,$(q_{2^{k}-1},q_{2^{k}})$.

In this section, 8 random states $|\phi_{i}\rangle(i=1,2,...,8)$ are chosen as an example of a multi-state Swap Test algorithm and then the correctness of the algorithm on this example is verified by experiments on IBM quantum cloud platform.

For arbitrary two states $\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle(i,j=1,2,...,8;i\neq j)$, the exact overlap is denoted by $o(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)$, which can be calculated by the definition of overlap $\left|{\left\langle{\phi,\psi}\right\rangle}\right|^{2}$; And the estimated overlap is denoted by $\widehat{o}(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)$, which can be obtained by executing simulated experiments.

The simulated quantum circuit on IBM quantum cloud platform for 8-state Swap Test algorithm is given in Fig.(11), where $q_{0}q_{1}q_{2}q_{3}$ are the auxiliary control qubits that corresponds to $s_{1}s_{2}s_{3}s_{4}$, $q_{4}q_{5}q_{6}q_{7}q_{8}q_{9}q_{10}q_{11}$ are the initial states that corresponds to $|\phi_{1}\rangle|\phi_{2}\rangle|\phi_{3}\rangle|\phi_{4}\rangle|\phi_{5}\rangle|\phi_{6}\rangle|\phi_{7}\rangle|\phi_{8}\rangle$ and $q_{12}q_{13}q_{14}q_{15}$ are the result qubits of simple two-state Swap Test. The initial states $q_{0}q_{1}q_{2}q_{3}$ are $\left|+\right\rangle\left|+\right\rangle\left|+\right\rangle$. Pair of normalized random numbers are generated by Python random package and the initial states $q_{4}q_{5}q_{6}q_{7}q_{8}q_{9}q_{10}q_{11}$ in the experiment are $|\phi_{1}\rangle=[0.0864,0.9963]$,$|\phi_{2}\rangle=[0.8391,0.5440]$,$|\phi_{3}\rangle=[0.2202,0.9755]$,$|\phi_{4}\rangle=[0.5486,0.8361]$,$|\phi_{5}\rangle=[0.2607,0.9654]$,$|\phi_{6}\rangle=[0.4164,0.9091]$,$|\phi_{7}\rangle=[0.9981,0.0609]$,$|\phi_{8}\rangle=[0.4658,0.8849]$. And the measurement results of this implementation through IBM Quantum Experience (QISKIT) are given in Fig.(12),with 8192 runs. Meanwhile, the measurement times of $q_{0}q_{1}q_{2}q_{3}q_{12}q_{13}q_{14}q_{15}$ is shown in Appendix A.

The estimated overlap of $\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle(i,j=1,2,...,8;i\neq j)$ can be obtained according to the relation of $s_{1},s_{2},s_{3},s_{4}$ and $q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7},q_{8}$ in Table.2 and Appendix A. For example, $s_{1},s_{2},s_{3},s_{4}=\left|{0010}\right\rangle$ and $s_{1},s_{2},s_{3},s_{4}=\left|{0011}\right\rangle$, the measurement result of $q_{15}$ is related to estimate values of $\left\langle{\phi_{6}}\right|\left.{\phi_{7}}\right\rangle$. After counting times of $q_{15}=\left|1\right\rangle$ $t_{1}=403$ and the times of $q_{15}=\left|0\right\rangle$ $t_{0}=601$, $\widehat{o}(|{\phi_{6}}\rangle,|{\phi_{7}}\rangle)={\frac{{2t_{0}}}{{t_{0}+t_{1}}}-1}=0.4441$. The exact overlap of arbitrary two states $o(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)$ and the estimated overlap of arbitrary two states $\widehat{o}(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)(i,j=1,2,...,8;i\neq j)$ is shown in Table.(4).

The scatter diagram is shown in Fig.(13), where the estimate overlap value $\widehat{o}(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)$ is X-axis and the exact overlap value $o(\left|{\phi_{i}}\right\rangle,\left|{\phi_{j}}\right\rangle)$ is Y-axis. It can be seen from Fig.(13) that most of the points fall near the diagonals of the picture, i.e. the line $y=x$, indicating that the estimate overlap results are close to the exact overlap results.

9 data sets of the initial states $D_{1},D_{2},D_{3},D_{4},D_{5},D_{6},D_{7},D_{8},D_{9}$ are generated by Python random package to be simulated in this experiment and their initial values are shown in Appendix B. And the scatter diagrams of estimated overlaps and exact overlaps of these 9 sets are shown in Fig.(14), where the estimated overlaps is X-axis and the exact overlaps is Y-axis. It can be seen from Fig.6 that most of the points fall near the diagonals of the picture, i.e., the line $y=x$, indicating that the estimated overlaps are close to the exact overlaps.

In this section, we analyze the correctness and performance of our multi-state Swap Test algorithm in theory.