Multi-resonant open-access microcavity arrays for light matter interaction

Laser ablation is a widely employed process in the fabrication of open-access optical cavity mirrors, used to carve near-spherical depressions into a glass substrate [32]. It requires intense laser irradiation to induce localised evaporation, leaving a concave feature suitable for the creation of a cavity mirror of tight curvature. Low scattering losses are ensured by sustaining laser illumination for a period of milliseconds, establishing a molten layer which is smoothed by the action of surface tension. The interplay of the evaporative and molten processes is largely governed by the characteristics of this laser exposure sequence, allowing one to shape the mirror geometry. However, as a thermal process it is notoriously difficult to both predict and finely control, thereby requiring ablation systems to support the rapid characterisation of fabricated surface topographies and allow the empirical derivation of desired pulse sequences.

The laser ablation system developed for the fabrication of our cavity mirrors is based upon an architecture reported by Takahashi et al., used in the fabrication of fibre-tip mirrors with markedly low ellipticity [33]. In broad similarity with the reported system, our apparatus uses a 10.6 $\mu$m CO₂ pulsed laser focused to a beam radius of approximately 100 $\mu$m onto the target substrate. Circular polarisation is ensured to reduce feature ellipticity, albeit with an inherent ellipticity of 0.6 remaining in the beam profile itself. Pulse shaping is performed by modulating the duty cycle of the laser, creating exposure durations of 5-150 ms of optical powers of 1-4 W. Fluctuations in the laser power are reduced to $<0.5$% by the inclusion of an optical isolator and with the implementation of electronic feedback to the laser. However, persistent variation was observed in fabricated feature geometries, which was notably reduced by constructing each depression from many repeated exposures.

To provide support for tapered mirror substrates, key alterations were made to the Takahashi approach, particularly for substrate mounting and surface reconstruction. Schematics of this beamline are shown in Fig. 2. This apparatus accepts a broad range of geometries for both glass substrates and optical fibres, mounted by bespoke adaptors into a $\varnothing$1" cylindrical fixture. In turn, the target substrate is installed into a stepper motorised rotation mount (Thorlabs K10CR1/M), used to set the facet orientation of the target substrate with respect to axis of ellipticity in the addressing laser. This is secured onto a six-axis translation stage (Thorlabs MAX609L/M & DRV001), including stepper motors and closed-loop piezoelectric transducers in each Cartesian axis. Stepper motor translations are applied in the plane of the laser propagation axis to build arrays of features, similar to [34], over a region of 4 mm $\times$ 4 mm. An example of such an array, fabricated on a standard planar $\varnothing$1/2" cylindrical substrate, is shown in Fig. 3.

Employing the procedure reported in [35], each ablation feature is constructed from a pattern of laser exposures, with piezoelectric translation performed between each shot. By careful shaping of the micro-pattern, this method is demonstrated to enhance feature diameter, tailor ellipticity and bring fabricated features closer to a spherical profile. In our system the maximum pattern size is 30 $\mu$m $\times$ 30 $\mu$m, limited by the range of the piezoelectric translation stage. By way of example, for the $93.2\mu$m diameter mirror discussed in Section 2.3, the micro-pattern consisted of 81 ablation sites repeated 5 times, with exposure power of 3.8W and duration increasing from 120ms to 130ms.

For rapid surface reconstruction, the infrared beamline could be electronically switched to a white light Michelson interferometer by motorised flip mounts (Thorlabs MFF101/M). This allowed the target substrate to remain stationary between ablation and reconstruction, with a transition time of $<1$ s. Following standard techniques [36], the surface profile of the target substrate is measured in the static interference pattern produced with a planar reference substrate. For enhanced resolution, the profile can also be obtained by scanning the path length of one interferometric arm and observing the coherence envelope imposed by the illumination source. This gives a measure of feature curvature, diameter and ellipticity, each crucial in the production of cavity geometries of choice.

Bulk substrates allow the cavity mode to freely expand into the glass so that it can emerge from the substrate with its polarisation and transverse mode profile preserved to then be manipulated with external mode-matching optics. This facilitates the injection of laser light for cavity stabilisation and the capture of intra-cavity generated photons. To allow for better compatibility of such mirrors with atom or ion traps, the substrates are often coned or tapered such that the end facet is 0.1-0.3 mm in diameter, which is comparable to the end facet of an optical fibre. The taper angle must be sufficiently shallow to contain the emanating cavity mode, while permitting open-access for emitter loading and persistent localisation. For neutral atoms, this may require support of a tightly focused optical dipole trap, without excessive illumination of the cavity mirrors. In this case, the taper angle must be sharp and the dimensions of the facet restricted. For ions, perturbation of the trapping potential by the dielectric mirror surfaces creates a limit on trapping lifetime, thus imposing a similar motivation to constrain the size of the substrate facet [30]. For the case of a cavity array, a further consideration of the facet size comes in the layout and quantity of the desired features.

For this work, a range of cavity mode geometries and array layouts were explored, requiring a conservative taper angle and the ability to tailor the facet size. Fig. 4 shows the tapered substrates, with interferometric images of sample facets given as Fig. 5. The substrates were shaped from UV-Fused Silica by a commercial optics manufacturer (Knight Optical UK Ltd.), leaving a pointed tip on the substrate. We polished this tip to the desired facet geometry using a motorised random orbital plate and 20 nm grit paper. Eventually the surface was subjected to thermal annealing inherent to laser ablation in order to ensure a satisfactory surface roughness of approximately 3Å. The experimental verification of this is given in Section 2.3.

Performing ablation on the tapered mirror substrates introduced experimental complexities not observed with fibre-tip facets. The geometry of the generated ablation features was observed to depend both on the chosen exposure parameters and the facet size. This follows from the modified heat transport in the bulk substrate during the ablation process, likely causing varying peak temperatures and surface tension. This made it difficult to develop an ablation pulse sequence for a desired mirror geometry using a reference glass, before applying it to an arbitrarily shaped pyramidal facet. While some variability was observed in cavity mirror geometry across an array fabricated on reference glass, nominally attributed to laser power fluctuation and cross-talk between the translational axes of the flexure stage, the heat transport considerations suggested above were the dominant source of feature variation. Similar challenges were experienced in the fabrication of the closely spaced cavity arrays, where the creation of one mirror depression would modify the geometry of those ablated next to it. Further, when facet sizes approached the 125$\mu$m diameter standard of single-mode fibre-tips, the anisotropy of the substrate around the ablation site was seen to induce minor feature warping. Since the warping had the tendency to modify mirror ellipticity, when formed into a cavity it has the potential to induce or alter birefringence [37]. This can limit the fidelity of remote entanglement generation in a quantum network [38]. To create single-feature cavities with a mirror diameter similar to the substrate facet, restoring cylindrical symmetry to the facet may indeed be advantageous. However, as illustrated in Fig. 5, expanding the facet size removes this issue. This allowed the mirror features to be located such that their periphery was well separated from the substrate edge and neighbouring array mirrors, with nominally 100$\mu$m between ablation sites.

We experimentally verify the optical quality of the tapered mirrors and demonstrate reflective losses within standard limits for ablative processing and thus suitability for the construction of high-finesse cavities. Dielectric coating of the tapered substrates was performed by a commercial supplier (Laseroptik GmbH) using ion beam sputtering. The coating, consisting of quarter wave stacks of Ta₂O₅ and SiO₂, had a design wavelength of 780 nm and was specified for minimal transmission. To evaluate the mirror quality, we are interested in scattering losses arising from the features’ surface roughness, absorption losses in the dielectric coating and residual transmission. Where possible, we ascribe these losses to aspects of mirror manufacturing process, acting as key feedback for future production cycles.

The mirror reflectivity was determined via the cavity finesse, using its common definition as the ratio of free spectral range to linewidth [39]:

where $R_{i,j}$ are mirror reflectivities, $\mathcal{L}_{i,j}$ are scattering and absorption losses summed for each mirror and $\mathcal{T}_{i,j}$ is their transmission. $\Delta\omega_{\textrm{fsr}}$ is the free spectral range of the cavity and $\Delta\omega_{\textrm{c}}$ is the full-width at half maximum of its resonance line shape. This ratio is measured via laser spectroscopy, addressing the cavity with a laser while scanning its length. The laser wavelength was chosen to correspond to the design wavelength of the dielectric stack in order to minimise transmission losses. The laser has a linewidth of a few hundred kilohertz, significantly smaller than the expected cavity linewidth. Sidebands of frequency $\Delta\nu_{\textrm{SB}}=100$ MHz were applied to the laser. The cavity length was modified by driving a piezoelectric transducer with a constant voltage gradient. Over short time intervals at the centre of the scan range it is reasonable to assume that the mirrors have a constant velocity. Therefore, $\Delta\omega_{\textrm{c}}$ can be determined from the ratio of the time taken to cross the main cavity resonance feature, $\Delta t_{2\kappa}$, to the time taken to move between resonance with the sidebands, $\Delta t_{\textrm{SB}}$:

However, such an approach is not suitable for the determination of free spectral range owing to the nonlinearity of piezoelectric extension being significant over the translational distance of the free spectral range. In order to compensate for the non-linear expansion, we rely upon the resolution of higher order modes. For each mode, coordinates of $(t,2\Delta\nu_{\textrm{SB}}/\Delta t_{\textrm{SB}})$ are fitted, mapping the nonlinear rate of cavity resonance frequency change. The integral under this curve, taken between two consecutive fundamental mode resonances, then gives a robust measure of free spectral range.

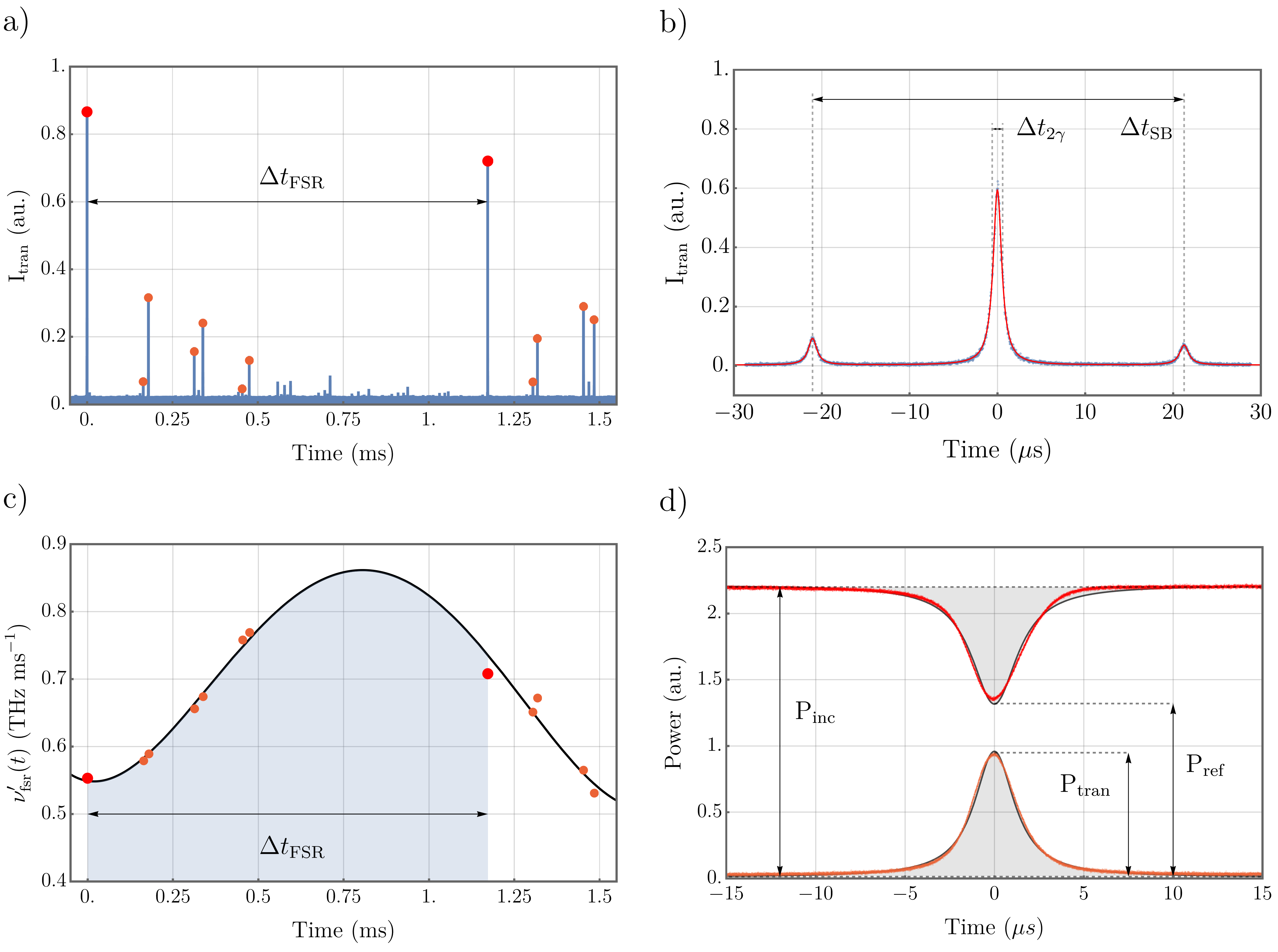
The properties of new mirrors are determined by measuring the finesse in this manner, pairing them with a reference mirror of known characteristics. An illustration of the geometry of this cavity is given as Figure 4c). Two types of super-polished reference mirrors were used, coated for different transmission values, with each being of 50mm radius of curvature and optically characterised by the manufacturer (Research Electro-Optics, Inc.). Following the labelling convention of Figure 5, pyramidal mirrors a) and b) were characterised using a reference mirror with $\mathcal{L}=2$ppm and $\mathcal{T}=0.5$ppm, giving finesse values of $146500\pm 3400$ and $156500\pm 7200$ respectively, corresponding to pyramidal losses of $\mathcal{L}_{a}+\mathcal{T}_{a}=40.4\pm 1.0$ and $\mathcal{L}_{b}+\mathcal{T}_{b}=37.7\pm 1.8$. Pyramidal mirrors b) and the top right feature of c) were characterised using a reference mirror with $\mathcal{L}=2$ppm and $\mathcal{T}=38.3$ppm, giving finesse values of $79300\pm 4100$ and $77000\pm 3800$ respectively, corresponding to pyramidal losses of $\mathcal{L}_{b}+\mathcal{T}_{b}=38.9\pm 4.1$ and $\mathcal{L}_{c}+\mathcal{T}_{c}=41.3\pm 4.0$. All errors are calculated statistically.

To determine the transmission of the pyramidal mirror coating and thus isolate their incoherent loss rate, we compare the transmitted optical power from the cavity to the back-reflected power on resonance, following the technique of [40]. For pyramidal mirror b) paired with the high transmission reference mirror, this gave $\mathcal{T}_{b}=1.8\pm 0.4$ppm. This highlights that low transmission rates are achievable for the presented design, which may be useful in experiments where directionality of the photonic emission is desired. This can be achieved by constructing the cavity with one mirror with low transmission and another mirror with high transmission, engineered by simply modifying the number of layers in the dielectric stack. Assuming each mirror possesses similar transmission, from the above characterisations we can therefore estimate that the pyramidal mirror possesses scattering and absorption losses of $35.9\pm 1.8$ppm. These losses outweigh the transmission substantially, which is a well-known issue in most cavity implementations using laser-ablated or FIB machined mirrors. However, in combination with low-loss superpolished mirror of 40ppm transmission, our new cavities do nonetheless transmit about half the light from the cavity to outside free-running modes.

In an ideal cavity array, the mirror surfaces have parallel normal axes, such that when paired with an equivalent substrate, the optical modes sit at the centre of each mirror. Any misalignment of these axes, caused by error in ablation beam pointing or underlying curvature of the initial substrate facet, may cause the cavity modes to migrate towards the mirror periphery. To ensure that any such error does not degrade cavity finesse, good optical quality should be achieved across the entire mirror. In combination with atomic force microscopy (AFM) analysis, surface homogeneity was indicated in the finesse measurements described above, via the constant linewidth of several of the higher order modes.

Prior to the application of a reflective coating, scattering losses were predicted by AFM analysis (NaniteAFM, Nanosurf). This highlighted the important role of thermal annealing, clearly visible in Fig 7a). RMS surface roughness was determined over a central area of 2.5$\mu$m $\times$ $2.5\mu$m as $\sigma_{rms}=0.33\pm 0.01$ nm (see Fig.7b)). Using a demonstrated model [41], this corresponds to scattering losses of $29\pm 1$ ppm, leaving approximately 7ppm to be associated with coating absorption. Absorption of cavity locking light can be known to generate thermal instability of an optical cavity around resonance, especially for FFPCs, but no such effect was observed in the probing of cavity linewidth performed above. Overall, these values are competitive with other laser machined mirrors, for which losses in the range $\mathcal{L}=20-35$ ppm were achieved [42, 12, 27, 18, 43]. In realising an optical quality and geometrical range similar to FFPCs, we outline scope to achieve the favourable atom-cavity coupling parameters observed in such systems. For the $S_{1/2}\Longleftrightarrow P_{3/2}$ transition of Rubidium atoms we estimate the cooperativity to range from 60 for cavities made from mirrors with radius of curvature of 1200 $\mu$m to 150 for cavities made from mirrors with radius of curvature of 500 $\mu$m (assuming a Finesse of 78,000). For the $P_{1/2}\Longleftrightarrow D_{3/2}$ transition of Ca⁺ ions, the cooperativities are estimated to range from 5 and 11 for the respective cavities.