MonoNeRF: Learning a Generalizable Dynamic Radiance Field
from Monocular Videos
Abstract
In this paper, we target at the problem of learning a generalizable dynamic radiance field from monocular videos. Different from most existing NeRF methods that are based on multiple views, monocular videos only contain one view at each timestamp, thereby suffering from ambiguity along the view direction in estimating point features and scene flows. Previous studies such as DynNeRF disambiguate point features by positional encoding, which is not transferable and severely limits the generalization ability. As a result, these methods have to train one independent model for each scene and suffer from heavy computational costs when applying to increasing monocular videos in real-world applications. To address this, We propose MonoNeRF to simultaneously learn point features and scene flows with point trajectory and feature correspondence constraints across frames. More specifically, we learn an implicit velocity field to estimate point trajectory from temporal features with Neural ODE, which is followed by a flow-based feature aggregation module to obtain spatial features along the point trajectory. We jointly optimize temporal and spatial features in an end-to-end manner. Experiments show that our MonoNeRF is able to learn from multiple scenes and support new applications such as scene editing, unseen frame synthesis, and fast novel scene adaptation. Codes are available at https://github.com/tianfr/MonoNeRF.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/93209e73-9224-4358-a6de-1795df6c7d61/x1.png)
1 Introduction
Novel view synthesis [6] is a highly challenging problem. It facilitates many important applications in movie production, sports event, and virtual reality. The long standing problem recently has witnessed impressive progress due to the neural rendering technology [28, 26, 9]. Neural Radiance Field (NeRF) [28, 55, 22, 27, 47, 52, 53] shows that photo-realistic scenes can be represented by an implicit neural network. Concretely, taken as a query the position and viewing direction of the posed image, the network outputs the color of each pixel by volume rendering method. Among these approaches, it is supposed that the scene is static and can be observed from multiple views at the same time. Such assumptions are violated by numerous videos uploaded to the Internet, which usually contain dynamic foregrounds, recorded by the monocular camera.
More recently, some studies aim to explore how to learn dynamic radiance field from monocular videos [10, 13, 21, 50, 51, 41]. Novel view synthesis from monocular videos is a challenging task. As foreground usually dynamically changes in a video, there is ambiguity in the view direction to estimate precise point features and dense object motions (i.e., scene flow [45]) from single views. In other words, we can only extract the projected 2D intra-frame local features and inter-frame optical flows, but fail to obtain precise 3D estimations. Previous works address this challenge by representing points as 4D position features (coordinate and time), so that the learned positional encoding provides specific information for each 3D point in the space [10, 13, 21, 50, 51, 41]. Based on positional encoding, these methods make efforts on exploiting scene priors [12, 49, 50] or adding spatio-temporal regularization [10, 13, 21, 51] to learn a more accurate dynamic radiance field.
However, while positional encoding successfully disambiguates 3D points from monocular 2D projections, it severely overfits to the training video clip and is not transferable. Therefore, existing positional encoding based methods have to optimize one independent model for each dynamic scene. With the fast increase of monocular videos in reality, they suffer from heavy computational costs and lengthy training time to learn from multiple dynamic scenes. Also, the lack of generalization ability limits further applications of scene editing which requires interaction among different scenes. A natural question is raised: can we learn a generalizable dynamic radiance field from monocular videos?
In this paper, we provide a positive answer to this question. The key challenge of this task is to learn to extract generalizable point features in the 3D space from monocular videos. While independently using 2D local features and optical flows suffers from ambiguity along the ray direction, they provide complementary constraints to jointly learn 3D point features and scene flows. On the one hand, for the sampled points on each ray, optical flow provides generalizable constraints that limit the relations of their point trajectories. On the other hand, for the flowing points on each estimated point trajectory, we consider that they should share the same point features. We estimate each point feature by aggregating their projected 2D local features, and design feature correspondence constraints to correct unreasonable trajectories.
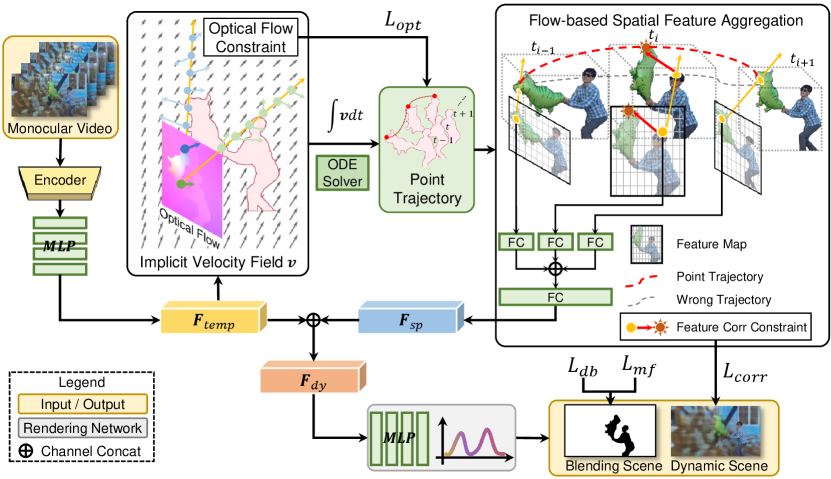
To achieve this, we propose MonoNeRF to build a generalizable dynamic radiance field for multiple dynamic scenes. We hypothesize that a point moving along its trajectory over time keeps the consistent point feature. Our method concurrently predicts 3D point features and scene flows with point trajectory and feature correspondence constraints in monocular video frames. More specifically, we first propose to learn an implicit velocity field that encodes the speed from the temporal feature of each point. We supervise the velocity field with optical flow and integrate continuous point trajectories on the field with Neural ODE [5]. Then, we propose a flow-based feature aggregation module to sample spatial features of each point along the point trajectory. We incorporate the spatial and temporal features as the point feature to query the color and density for image rendering and jointly optimize point features and trajectories in an end-to-end manner. As shown in Figure 1, experiments demonstrate that our MonoNeRF is able to render novel views from multiple dynamic videos and support new applications such as scene editing, unseen frame synthesis, and fast novel scene adaption. Also, in the widely-used setting of novel view synthesis on training frames from single videos, our MonoNeRF still achieves better performance than existing methods despite that cross-scene generalization ability is not required in this setting.
2 Related Work
Novel view synthesis for static scenes. The long standing problem of novel view synthesis aims to construct new views of a scene from multiple posed images. Early works needed dense views captured from the scene [19, 14]. Recent studies have shown great progress by explicitly representing 3D scenes as neural representations [26, 28, 9, 7, 52, 25, 18, 39]. However, these methods train a separate model for each scene and need various training time for optimization. PixelNeRF [55] and MVSNeRF [4] proposed feature-based methods that directly render new scenes from the encoded features. Additionally, many researchers studied the generalization and decomposition abilities of novel view synthesis model [3, 38, 29, 15, 1, 18, 42]. Compared with these methods, our method studies the synthesis and generalization ability of dynamic scenes.
Space-time view synthesis from monocular videos. With the development of neural radiance field in static scenes, recent studies started to address the dynamic scene reconstruction problem [21, 51, 10, 20, 31, 33]. In monocular videos, a key challenge is that there exist multiple scene constructions implying the same observed image sequences. Previous approaches addressed this challenge by using 3D coordinates with time as point features and adding scene priors or spatio-temporal regularization. Scene priors such as shadow modeling [50], human shape prior [49, 23], and facial appearance [12] are object-specific and closer to special contents. Spatio-temporal regularization such as depth and flow regularization [10, 13, 21, 51] and object deformations [41] are more object-agnostic, but weaker in applying consistency restriction to dynamic foregrounds. In this paper, we study the challenge by constraining point features.
Scene flow for reconstruction. Scene flow firstly proposed by [45] depicts the motion of each point in the dynamic scene. Its 2D projection i.e., optical flow contributes to many downstream applications such as video super-resolution [46], video tracking [43], video segmentation [44], and video recognition [2]. Several methods studied the scene flow estimation problem based on point cloud sequences [30, 24]. However, estimating scene flow from an observed video is an ill-posed problem. In dynamic scene reconstruction, previous works [21, 13] established discrete scene flow for pixel consistency in observation time. In this way, the flow consistency in observed frames can only be constrained, leading to ambiguity in non-observed time. Du et al. [10] proposed to build the continuous flow field in a dynamic scene. Compared to these methods, we study the generalization ability of the flow field in different scenes.
3 Approach
In this section, we introduce the proposed model that we term as MonoNeRF. We first present the overview of our model and then detail the approach of each part. Lastly, we introduce several strategies for optimizing the model.
3.1 MonoNeRF
MonoNeRF aims to model generalizable radiance field of dynamic scenes. Our method takes multiple monocular videos as input and uses optical flows, depth maps, and binary masks of foreground objects as supervision signals. Those signals could be generated by pretrained models automatically. We build the generalizable static and dynamic fields for backgrounds and foregrounds separately. For generalizable dynamic field, we suppose that spatio-temporal points flow along their trajectories and hold consistent features over time. We first extract video features by a CNN encoder and generate the temporal feature vectors based on the extracted features. Then, we build an implicit velocity field from the temporal feature vectors to estimate point trajectories. Next, we exploit the estimated point trajectories as indexes to find the local image patches on each frame and extract the spatial features from the patches with the proposed flow-based feature aggregation module. Different from NeRF [28] that uses scene-agnostic point positions to render image color, we aggregate the scene-dependent spatial and temporal features as the final point features to render foreground scenes with volume rendering. Finally, we design the optical flow and feature correspondence constraints for jointly learning point features and trajectories. For generalizable static field, we suppose backgrounds are static and each video frame is considered as a different view of the background. Since some background parts may be occluded by the foreground, we design an effective strategy to sample background point features. In the end, we combine the generalizable static and dynamic fields for rendering free-point videos.
3.2 Generalizable Dynamic Field
In this section, we introduce our generalizable dynamic field that renders novel views of dynamic foregrounds. We denote a monocular video as consisting of frames . For each frame , is the observed timestamp and is the projection transform from the world coordinate to the 2D frame pixel coordinate. As Figure 2 shows, given a video , we exploit a video encoder to extract the video feature vector represented as and generate the temporal feature vector with a multiple layer perceptron (MLP) : . We build the implicit velocity field based on .
Implicit velocity field. We suppose points are moving in the scene and represent a spatio-temporal point as including the 3D point position and time . We define as the continuous point trajectory and denotes the position of point at timestamp . We further define the velocity field which includes the 3D velocity of each point. The relationship between point velocity and trajectory is specified as follows,
| (1) |
is conditioned on and implemented by an MLP : . We calculate the point trajectory at an observed timestamp with Neural ODE [5],
| (2) |
We take as an index to query the spatial feature.
Flow-based spatial feature aggregation. We employ to project on and find the local image patch indexed by the projected position . We extract the feature vector from the patch with the encoder and a fully connected layer ,
| (3) |
In practice, is implemented by using to extract the frame-wise feature map of and sampling the feature vector at with bilinear interpolation. The spatial feature vector is then calculated by incorporating with a fully connected layer ,
| (4) |
Finally, we incorporate and as the point feature vector ,
| (5) |
We build the generalizable dynamic field based on .
Dynamic foreground rendering. Taking a point and its feature vector as input, our generalizable dynamic radiance field : predicts the volume density , color and blending weight of the point. We follow DynNeRF [13] and utilize to judge whether a point belongs to static background or dynamic foreground. We exploit volume rendering to approximate each pixel color of an image. Concretely, given a ray starting from the camera center along the direction through a pixel, its color is integrated by
| (6) |
where are the bounds of the volume rendering depth range and is the accumulated transparency. We simplify and here and in the following sections. Next we present the optical flow and feature correspondence constraints that jointly supervise our model.
Optical flow constraint. We supervise with the optical flow . In practice, it can only approximate the backward flow and forward flow between two consecutive video frames [40]. We hence estimate the point backward and forward trajectory variations during the period that the point passes between two frames and calculate optical flows by integrating the trajectory variations of each point along camera rays. Formally, given a ray through a pixel on the frame at time , for each point on the ray i.e., the trajectory variations back to and forward to are obtained by the following equation,
| (7) |
We follow previous works [21, 13] and exploit the volume rendering to integrate pseudo optical flows and by utilizing the estimated volume density of each point,
| (8) |
where denotes we use to project 3D trajectory variations on the image plane of . We supervise the pseudo flows by the ground truth flows,
| (9) |
In this way, the relation of point trajectories along a ray is limited by the optical flow supervision.
Feature correspondence constraint. According to Section 3.1, a point moving along the trajectory holds the same feature and represents the consistent color and density. For each ray at the current time through a pixel of , we warp the ray from the neighboring observed timestamps and as and separately by using (7),
| (10) |
where . We render the pixel color from the point features not only along the ray at the time , but also along the wrapped rays at and at . The predicted pixel color is rendered by using (6) and supervised by the ground truth colors ,
| (11) |
The feature correspondence constraint is defined as
| (12) |
supervises the predicted color and point features .
3.3 Generalizable Static Field
As mentioned in Section 3.1, for some background parts occluded by the changing foreground in the current view, their features implying the foreground cannot infer the correct background information. However, the occluded parts could be seen in non-occluded views with correct background features. To this end, given a point position , the background point feature vector is produced by
| (13) |
where is a fully connected layer and denotes the image encoder. and are the non-occluded frame and corresponding projection transform respectively. denotes that we find the local image patch at and extract the feature vectors with an image encoder similar to . Since there is no prior in which frames they can be exposed, we apply a straightforward yet effective strategy by randomly sampling one frame from the other frames in the video. We represent the static scene as a radiance field to infer the color and density by using an MLP : . The expected background color is given by
| (14) |
where . We employ foreground masks to optimize the static field by supervising the pixel color in each video frame in the background regions (where ),
| (15) |
where represents the ground truth color.
| PSNR / LPIPS | Jumping | Skating | Truck | Umbrella | Balloon1 | Balloon2 | Playground | Average |
|---|---|---|---|---|---|---|---|---|
| NeRF [28] | 20.58 / 0.305 | 23.05 / 0.316 | 22.61 / 0.225 | 21.08 / 0.441 | 19.07 / 0.214 | 24.08 / 0.098 | 20.86 / 0.164 | 21.62 / 0.252 |
| NeRF [28] + time | 16.72 / 0.489 | 19.23 / 0.542 | 17.17 / 0.403 | 17.17 / 0.752 | 17.33 / 0.304 | 19.67 / 0.236 | 13.80 / 0.444 | 17.30 / 0.453 |
| Yoon et al. [54] | 20.16 / 0.148 | 21.75 / 0.135 | 23.93 / 0.109 | 20.35 / 0.179 | 18.76 / 0.178 | 19.89 / 0.138 | 15.09 / 0.183 | 19.99 / 0.153 |
| Tretschk et al. [41] | 19.38 / 0.295 | 23.29 / 0.234 | 19.02 / 0.453 | 19.26 / 0.427 | 16.98 / 0.353 | 22.23 / 0.212 | 14.24 / 0.336 | 19.20 / 0.330 |
| Li et al. [21] | 24.12 / 0.156 | 28.91 / 0.135 | 25.94 / 0.171 | 22.58 / 0.302 | 21.40 / 0.225 | 24.09 / 0.228 | 20.91 / 0.220 | 23.99 / 0.205 |
| NeuPhysics [34] | 20.16 / 0.205 | 25.13 / 0.166 | 22.62 / 0.212 | 21.02 / 0.426 | 16.68 / 0.238 | 22.54 / 0.265 | 15.10 / 0.367 | 20.48 / 0.282 |
| DynNeRF [13] | 24.23 / 0.144 | 28.90 / 0.124 | 25.78 / 0.134 | 23.15 / 0.146 | 21.47 / 0.125 | 25.97 / 0.059 | 23.65 / 0.093 | 24.74 / 0.118 |
| MonoNeRF | 24.26 / 0.091 | 32.06 / 0.044 | 27.56 / 0.115 | 23.62 / 0.180 | 21.89 / 0.129 | 27.36 / 0.052 | 22.61 / 0.130 | 25.62 / 0.106 |

3.4 Optimization
The final dynamic scene color combines the colors from the generalizable dynamic and static fields,
| (16) |
where
| (17) |
and applies the reconstruction loss,
| (18) |
Next we design several strategies to optimize our model.
Point trajectory discretization. While point trajectory can be numerically estimated by the continuous integral (2) with Neural ODE solvers [5], it needs plenty of time for querying each point trajectory. To accelerate the process, we propose to partition into evenly-spaced bins and suppose the point velocity in each bin is a constant. The point trajectory can be estimated by the following equation,
| (19) |
where .


| Balloon2 / Truck | PSNR | SSIM | LPIPS |
|---|---|---|---|
| NeRF [28] | 20.33 / 20.26 | 0.662 / 0.669 | 0.224 / 0.256 |
| NeRF [28] + time | 20.22 / 20.26 | 0.661 / 0.639 | 0.218 / 0.256 |
| NeuPhysics [34] | 19.45 / 20.24 | 0.478 / 0.517 | 0.343 / 0.285 |
| DynNeRF [13] | 19.99 / 20.33 | 0.641 / 0.621 | 0.291 / 0.273 |
| MonoNeRF | 21.30 / 23.74 | 0.669 / 0.702 | 0.204 / 0.174 |
Depth-blending restriction. To calculate the blending weights within a foreground ray in the generalizable dynamic field, only the points in close proximity to the estimated ray depth are regarded as foreground points, whereas points beyond this range are excluded. We penalize the blending weights of non-foreground points in foreground rays. Specifically, given a ray through a pixel and the pixel depth , We penalize the blending weights of the points on the ray out of the interval ,
| (20) |
where is the blending weight at the position . controls the surface thickness of the dynamic foreground.
Mask flow loss. We further constrain the consistency of point features by minimizing blending weight variations along trajectories,
| (21) |
where denotes the blending weight at .
4 Experiments
In this section, we conducted experiments on the Dynamic Scene dataset [54]. We first tested the performance of synthesizing novel views from single videos, and then we tested the generalization ability from multiple videos. In the end, we carried out ablation studies on our model.
4.1 Experimental Setup
Dataset. We used the Dynamic Scene dataset [54] to evaluate the proposed method. Concretely, it contains 9 video sequences that are captured with 12 cameras by using a camera rig. We followed previous works [21, 13] and derived each frame of the video from different cameras to simulate the camera motion. All the cameras capture images at 12 different timestamps . Each training video contains twelve frames sampled from the camera at time followed DynNeRF [13]. We used COLMAP [36, 37] to approximate the camera poses. It is assumed intrinsic parameters of all the cameras are the same. DynamicFace sequences were excluded because COLMAP fails to estimate camera poses. All video frames were resized to 480270 resolution. We generated the depth, mask, and optical flow signals from the depth estimation model [35], Mask R-CNN [16], and RAFT [40].
| PSNR / LPIPS | Umbrella | Balloon2 | Average |
|---|---|---|---|
| w/o. | 20.59 / 0.256 | 22.79 / 0.159 | 21.57 / 0.230 |
| w/o. | 22.75 / 0.175 | 24.85 / 0.098 | 23.80 / 0.137 |
| w/o. | 22.81 / 0.181 | 25.09 / 0.143 | 23.95 / 0.162 |
| Ours | 23.44 / 0.169 | 25.44 / 0.093 | 24.44 / 0.131 |
Implementation details. We followed pixelNeRF [55] and used ResNet-based MLPs as our implicit velocity field and rendering networks and . For generalizable dynamic field, we utilized Slowonly50 [11] pretrained on Kinetics400 [2] dataset as the encoder with the frozen weights. We removed the final fully connected layer in the backbone and incorporated the first, second, and third feature layers for querying . We simplified (4) that at time is sampled from . For generalizable static field, we used ResNet18 [17] pretrained on ImageNet [8] as the encoder . We extracted a feature pyramid from video frames for querying . The vector sizes of , , , and are 256. Please refer to the supplementary material for more details.

| PSNR / LPIPS | Training frames | Unseen frames | Unseen videos |
|---|---|---|---|
| w/o. | 22.76 / 0.148 | 20.69 / 0.348 | 21.68 / 0.345 |
| w/o. | 22.95 / 0.135 | 20.95 / 0.354 | 21.67 / 0.342 |
| w/o. | 21.75 / 0.230 | 19.79 / 0.371 | 21.81 / 0.337 |
| w/o. random | 17.30 / 0.435 | 16.93 / 0.512 | 20.28 / 0.353 |
| Ours | 23.02 / 0.130 | 21.30 / 0.304 | 22.63 / 0.277 |
4.2 Novel View Synthesis from Single Video
In this section, we trained the models from single monocular videos, where existing methods are applicable to this setting. Specifically, we first tested the performance on training frames, which is the widely-used setting to evaluate video-based NeRFs. Then, we tested the generalization ability on unseen frames in the video, where other existing methods are not able to transfer well to the unseen motions.
Novel view synthesis on training frames. To evaluate the synthesized novel views, we followed DynNeRF [13] and tested the performance by fixing the view to the first camera and changing time. We reported the PSNR and LPIPS [56] in Table 1. We evaluated the performance of Li et al. [21], Tretschk et al. [41], NeuPhysics [34], and Chen et al. [13] from the official implementations. Even without the need of generalization ability, our method achieves better results.
Novel view synthesis on unseen frames. We split the video frames into two groups: four front frames were used for training and the rest of eight unseen frames were utilized to render novel views. Figure 4 shows that our model successfully renders new motions in the unseen frames, while DynNeRF [13] only interpolates novel views in the training frames. The reported PSNR, SSIM [48], and LPIPS scores in Table 2 quantitatively verify the superiority of our model.
4.3 Novel View Synthesis from Multiple Videos
In the section, we tested the novel view synthesis performance on multiple dynamic scenes. It is worth noting that as existing methods can only learn from single monocular videos, they are not applicable to the settings that need to train on multiple videos. Then, we evaluated the novel scene adaption ability on several novel monocular videos. Lastly, we conducted a series of scene editing experiments.
Novel view synthesis on training videos. We selected Balloon2 and Umbrella scenes to train our model. As shown in Figure 3 and Table 3, our model could distinguish foregrounds from two scenes and perform well with . Specifically, it predicts generalizable scene flows with and renders more accurate details with .

Novel view synthesis on unseen videos. We explored the generalization ability of our model by pretraining on the Balloon2 scene and fine-tuning the pretrained model on other scenes. Figure 5 presents the results of four unseen videos: Playground, Skating, Truck, and Balloon1. We also pretrained DynNeRF [13] on the Balloon2 scene for a fair comparison. While DynNeRF only learns to render new scenes from scratch, our model transfers to scenes with correct dynamic motions. By further training with 500 steps, our model achieves better image rendering quality and higher LPIPS scores, which takes about 10 minutes.
Scene editing. As Figure 6 shows, our model further supports many scene editing applications by directly processing point features without extra training. Changing background was implemented by exchanging the static scene features between two scenes. Moving, scaling, duplicating and flipping foreground were directly applied by operating video features in dynamic radiance field. The above applications could be combined arbitrarily.
4.4 Ablation Study
We conducted a series of experiments to examine the proposed , , , random sampling strategy, and trajectory discretization method. We show in Figure 7 that deblurs the margin of the synthesized foreground in novel views, keeps the blending consistency in different views for delineating the foreground more accurately, The random sampling strategy successfully renders static scene without dynamic foreground, and backgrounds of two scenes are mixed without . We also show the numeric comparisons of , and random sampling strategy in Table 4. In Table 5, our discretization method reaches comparable results with ODE solvers [5] and achieves higher performance with the increase of .
5 Conclusion
In this paper, we study the generalization ability of novel view synthesis from monocular videos. The challenge is the ambiguity of 3D point features and scene flows in the viewing directions. We find that video frame features and optical flows are a pair of complementary constraints for learning 3D point features and scene flows. To achieve this, we propose a generalizable dynamic radiance field called MonoNeRF. We estimate point features and trajectories from the video features extracted by a video encoder and render dynamic scenes from points features. Experiments show that our model could learn a generalizable radiance field for dynamic scenes, and support many scene editing applications.
Acknowledgements. This work was supported by the National Key Research and Development Program of China under Grant No. 2020AAA0108100, the National Natural Science Foundation of China under Grant No. 62206147 and 61971343. The authors would like to thank the Shanghai Artificial Intelligence Laboratory for its generous support of computational resources.
References
- [1] Shengqu Cai, Anton Obukhov, Dengxin Dai, and Luc Van Gool. Pix2NeRF: Unsupervised conditional -GAN for single image to neural radiance fields translation. In CVPR, pages 3971–3980, 2022.
- [2] Joao Carreira and Andrew Zisserman. Quo vadis, action recognition? a new model and the kinetics dataset. In CVPR, pages 6299–6308, 2017.
- [3] Eric Chan, Marco Monteiro, Petr Kellnhofer, Jiajun Wu, and Gordon Wetzstein. pi-GAN: Periodic implicit generative adversarial networks for 3D-aware image synthesis. In CVPR, 2021.
- [4] Anpei Chen, Zexiang Xu, Fuqiang Zhao, Xiaoshuai Zhang, Fanbo Xiang, Jingyi Yu, and Hao Su. MVSNeRF: Fast generalizable radiance field reconstruction from multi-view stereo. In ICCV, pages 14124–14133, 2021.
- [5] Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David K Duvenaud. Neural ordinary differential equations. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, editors, NeurIPS, volume 31, 2018.
- [6] Shenchang Eric Chen and Lance Williams. View interpolation for image synthesis. In Proceedings of the 20th annual conference on Computer graphics and interactive techniques, pages 279–288, 1993.
- [7] Xingyu Chen, Qi Zhang, Xiaoyu Li, Yue Chen, Ying Feng, Xuan Wang, and Jue Wang. Hallucinated neural radiance fields in the wild. In CVPR, pages 12943–12952, 2022.
- [8] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. ImageNet: A large-scale hierarchical image database. In CVPR, pages 248–255, 2009.
- [9] Kangle Deng, Andrew Liu, Jun-Yan Zhu, and Deva Ramanan. Depth-supervised NeRF: Fewer views and faster training for free. In CVPR, June 2022.
- [10] Yilun Du, Yinan Zhang, Hong-Xing Yu, Joshua B. Tenenbaum, and Jiajun Wu. Neural radiance flow for 4d view synthesis and video processing. In ICCV, 2021.
- [11] Christoph Feichtenhofer, Haoqi Fan, Jitendra Malik, and Kaiming He. SlowFast networks for video recognition. In ICCV, pages 6201–6210, 2019.
- [12] Guy Gafni, Justus Thies, Michael Zollhöfer, and Matthias Nießner. Dynamic neural radiance fields for monocular 4d facial avatar reconstruction. In CVPR, pages 8649–8658, June 2021.
- [13] Chen Gao, Ayush Saraf, Johannes Kopf, and Jia-Bin Huang. Dynamic view synthesis from dynamic monocular video. In ICCV, 2021.
- [14] Steven J Gortler, Radek Grzeszczuk, Richard Szeliski, and Michael F Cohen. The lumigraph. In ACM SIGGRAPH, pages 43–54, 1996.
- [15] Jiatao Gu, Lingjie Liu, Peng Wang, and Christian Theobalt. StyleNeRF: A style-based 3D aware generator for high-resolution image synthesis. In ICLR, 2022.
- [16] Kaiming He, Georgia Gkioxari, Piotr Dollar, and Ross Girshick. Mask r-cnn. In ICCV, Oct 2017.
- [17] Kaiming He, X. Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. CVPR, pages 770–778, 2016.
- [18] Wonbong Jang and Lourdes Agapito. CodeNeRF: Disentangled neural radiance fields for object categories. In ICCV, pages 12949–12958, October 2021.
- [19] Marc Levoy and Pat Hanrahan. Light field rendering. In ACM SIGGRAPH, 1996.
- [20] Tianye Li, Mira Slavcheva, Michael Zollhöfer, Simon Green, Christoph Lassner, Changil Kim, Tanner Schmidt, Steven Lovegrove, Michael Goesele, Richard Newcombe, and Zhaoyang Lv. Neural 3D video synthesis from multi-view video. In CVPR, pages 5521–5531, June 2022.
- [21] Zhengqi Li, Simon Niklaus, Noah Snavely, and Oliver Wang. Neural scene flow fields for space-time view synthesis of dynamic scenes. In CVPR, 2021.
- [22] Lingjie Liu, Jiatao Gu, Kyaw Zaw Lin, Tat-Seng Chua, and Christian Theobalt. Neural sparse voxel fields. In NeurIPS, volume 33, 2020.
- [23] Lingjie Liu, Marc Habermann, Viktor Rudnev, Kripasindhu Sarkar, Jiatao Gu, and Christian Theobalt. Neural actor: Neural free-view synthesis of human actors with pose control. ACM Trans. Graph.(ACM SIGGRAPH Asia), 2021.
- [24] Xingyu Liu, Charles R Qi, and Leonidas J Guibas. Flownet3D: Learning scene flow in 3D point clouds. In CVPR, pages 529–537, 2019.
- [25] Yuan Liu, Sida Peng, Lingjie Liu, Qianqian Wang, Peng Wang, Theobalt Christian, Xiaowei Zhou, and Wenping Wang. Neural rays for occlusion-aware image-based rendering. In CVPR, 2022.
- [26] Ricardo Martin-Brualla, Noha Radwan, Mehdi S. M. Sajjadi, Jonathan T. Barron, Alexey Dosovitskiy, and Daniel Duckworth. NeRF in the Wild: Neural radiance fields for unconstrained photo collections. In CVPR, 2021.
- [27] Ben Mildenhall, Peter Hedman, Ricardo Martin-Brualla, Pratul P. Srinivasan, and Jonathan T. Barron. NeRF in the dark: High dynamic range view synthesis from noisy raw images. In CVPR, pages 16169–16178, 2022.
- [28] Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. NeRF: Representing scenes as neural radiance fields for view synthesis. In ECCV, 2020.
- [29] Michael Niemeyer and Andreas Geiger. GIRAFFE: Representing scenes as compositional generative neural feature fields. In CVPR, pages 11453–11464, June 2021.
- [30] Michael Niemeyer, Lars Mescheder, Michael Oechsle, and Andreas Geiger. Occupancy Flow: 4D reconstruction by learning particle dynamics. In ICCV, 2019.
- [31] Julian Ost, Fahim Mannan, Nils Thuerey, Julian Knodt, and Felix Heide. Neural scene graphs for dynamic scenes. In CVPR, pages 2856–2865, June 2021.
- [32] Keunhong Park, Utkarsh Sinha, Jonathan T. Barron, Sofien Bouaziz, Dan B Goldman, Steven M. Seitz, and Ricardo Martin-Brualla. Nerfies: Deformable neural radiance fields. ICCV, 2021.
- [33] Albert Pumarola, Enric Corona, Gerard Pons-Moll, and Francesc Moreno-Noguer. D-NeRF: Neural Radiance Fields for Dynamic Scenes. In CVPR, 2020.
- [34] Yi-Ling Qiao et al. Neuphysics: Editable neural geometry and physics from monocular videos. In NeurIPS, 2022.
- [35] René Ranftl, Katrin Lasinger, David Hafner, Konrad Schindler, and Vladlen Koltun. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE TPAMI, 44(3):1623–1637, 2022.
- [36] Johannes Lutz Schönberger and Jan-Michael Frahm. Structure-from-Motion Revisited. In CVPR, 2016.
- [37] Johannes Lutz Schönberger, Enliang Zheng, Marc Pollefeys, and Jan-Michael Frahm. Pixelwise View Selection for Unstructured Multi-View Stereo. In ECCV, 2016.
- [38] Katja Schwarz, Yiyi Liao, Michael Niemeyer, and Andreas Geiger. GRAF: Generative radiance fields for 3D-aware image synthesis. In NeurIPS, 2020.
- [39] Pratul P. Srinivasan, Boyang Deng, Xiuming Zhang, Matthew Tancik, Ben Mildenhall, and Jonathan T. Barron. NeRV: Neural reflectance and visibility fields for relighting and view synthesis. In CVPR, 2021.
- [40] Zachary Teed and Jia Deng. RAFT: Recurrent All-Pairs field transforms for optical flow. In Andrea Vedaldi, Horst Bischof, Thomas Brox, and Jan-Michael Frahm, editors, ECCV, pages 402–419, 2020.
- [41] Edgar Tretschk, Ayush Tewari, Vladislav Golyanik, Michael Zollhöfer, Christoph Lassner, and Christian Theobalt. Non-rigid neural radiance fields: Reconstruction and novel view synthesis of a dynamic scene from monocular video. In ICCV, pages 12939–12950, 2021.
- [42] Alex Trevithick and Bo Yang. GRF: Learning a general radiance field for 3D scene representation and rendering. In ICCV, 2021.
- [43] Emanuele Trucco and Konstantinos Plakas. Video tracking: a concise survey. IEEE Journal of oceanic engineering, 31(2):520–529, 2006.
- [44] Yi-Hsuan Tsai, Ming-Hsuan Yang, and Michael J Black. Video segmentation via object flow. In CVPR, pages 3899–3908, 2016.
- [45] S. Vedula, S. Baker, P. Rander, R. Collins, and T. Kanade. Three-dimensional scene flow. In ICCV, volume 2, pages 722–729 vol.2, 1999.
- [46] Longguang Wang, Yulan Guo, Li Liu, Zaiping Lin, Xinpu Deng, and Wei An. Deep video super-resolution using HR optical flow estimation. IEEE TIP, 29:4323–4336, 2020.
- [47] Peng Wang, Lingjie Liu, Yuan Liu, Christian Theobalt, Taku Komura, and Wenping Wang. NeuS: Learning neural implicit surfaces by volume rendering for multi-view reconstruction. In NeurIPS, 2021.
- [48] Zhou Wang, A.C. Bovik, H.R. Sheikh, and E.P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE TIP, 13(4):600–612, 2004.
- [49] Chung-Yi Weng, Brian Curless, Pratul P. Srinivasan, Jonathan T. Barron, and Ira Kemelmacher-Shlizerman. HumanNeRF: Free-viewpoint rendering of moving people from monocular video. In CVPR, pages 16210–16220, June 2022.
- [50] Tianhao Wu, Fangcheng Zhong, Andrea Tagliasacchi, Forrester Cole, and Cengiz Öztireli. D2NeRF: Self-supervised decoupling of dynamic and static objects from a monocular video. In NeurIPS, 2022.
- [51] Wenqi Xian, Jia-Bin Huang, Johannes Kopf, and Changil Kim. Space-time neural irradiance fields for free-viewpoint video. In CVPR, pages 9421–9431, 2021.
- [52] Yuanbo Xiangli, Linning Xu, Xingang Pan, Nanxuan Zhao, Anyi Rao, Christian Theobalt, Bo Dai, and Dahua Lin. BungeeNeRF: Progressive neural radiance field for extreme multi-scale scene rendering. In ECCV, 2022.
- [53] Qiangeng Xu, Zexiang Xu, Julien Philip, Sai Bi, Zhixin Shu, Kalyan Sunkavalli, and Ulrich Neumann. Point-NeRF: Point-based neural radiance fields. CVPR, 2022.
- [54] Jae Shin Yoon, Kihwan Kim, Orazio Gallo, Hyun Soo Park, and Jan Kautz. Novel view synthesis of dynamic scenes with globally coherent depths from a monocular camera. In CVPR, June 2020.
- [55] Alex Yu, Vickie Ye, Matthew Tancik, and Angjoo Kanazawa. pixelNeRF: Neural radiance fields from one or few images. In CVPR, 2021.
- [56] Richard Zhang, Phillip Isola, Alexei A. Efros, Eli Shechtman, and Oliver Wang. The unreasonable effectiveness of deep features as a perceptual metric. In CVPR, June 2018.
| parameter | ||||||
|---|---|---|---|---|---|---|
| value | 1 | 0.02 | 4 | 0.01 | 1 | 0.03 |
Appendix A Implementation Details
In this section, we present specific implementation details of our model and each experimental setting. The entire model was trained on a NVIDIA A100 GPU with a total batch size of 1024 rays. The learning rate is 0.0005 without decaying. The initial training time is about 3 hours.
A.1 Generalizable Dynamic Field
We trained the generalizable dynamic field in an end-to-end manner. The overall loss function is
| (22) |
The hyper-parameter values of all loss functions are listed in Table 6. is the blending thickness as described in the in the paper. We used the Slowonly50 network in SlowFast [11] as the video encoder , which was pretrained on the Kinetics400 [2] dataset, and removed all the temporal pooling layers in the network. We froze the weights of the pretrained model. The temporal features are the latent vectors of size 256 extracted by the encoder and fused by , and the spatial features of each point were extracted prior to the first 3 spatial pooling layers, which were upsampled using bilinear interpolation, concatenated in the channel dimension and fused with the fully connected layers to form latent vectors of size 256. To incorporate the point feature into NeRF [28] network, we followed pixelNeRF [55] to use multi-layer perceptron (MLP) with residual modulation [17] as our basic block. We employed 4 residual blocks to implement our implicit velocity field, and another 4 residual blocks as the rendering network.

| NeRF [28] + time | DynNeRF [13] | MonoNeRF | |
| PSNR / LPIPS | 23.80 / 0.684 | 25.80 / 0.671 | 27.77 / 0.501 |
A.2 Generalizable Static Field
We used ResNet18 [17] as the image encoder , which was pretrained on ImageNet [8]. The point features in generalizable static field were incorporated prior to 4 pooling layers in ResNet18, which were upsampled and concatenated to form latent vectors of size 256 aligned to each point. We also used MLP with residual modulation as basic architecture for static rendering network. To train the generalizable static field, we used the segmentation mask preprocessed by DynNeRF [13] and optimized the static field by using the image pixels that belong to static background.
A.3 Novel View Synthesis on Unseen Frames
Novel view synthesis on unseen frames aims to test the generalizable ability of our model on unseen motions in a fixed static scene. We used the first 4 frames to train our generalizable dynamic field, and evaluated the performance on the rest 8 frames for each scene. The training step was set to 40000 in this setting.
A.4 Novel View Synthesis on Unseen Videos
Novel view synthesis on unseen videos aims to test the generalizable ability of our model on novel dynamic scenes. We pretrained our model on Balloon2 scene and finetuned the model on other scenes with the pretrained parameters. The pretraining step on Balloon2 scene was set to 20000. We used the official model [13] trained on Balloon2 scene for a fair comparison. The initial training time is about 3 hours for one scene, and the finetuning time is about 10 minutes.
A.5 Scene Editing
All the scene editing operations are conducted directly on the extracted backbone features without extra training. Changing background was conducted by exchanging the extracted image features in static field in our model. Moving foreground was implemented by moving the video features in the dynamic field at the corresponding position. Scaling foreground was implemented by scaling the video features in the dynamic field. Duplicating foreground was conducted by copying the video features to the corresponding position. Flipping foreground was applied by flipping the video features. Since the above operations are independent to each other, they can be combined in an arbitrary way.