Monolayer V₂MX₄: A New Family of Quantum Anomalous Hall Insulators

Introduction. The discovery of the quantum anomalous Hall (QAH) effect set a remarkable example for understanding topological states of quantum matter in condensed matter physics and material science Hasan and Kane (2010); Qi and Zhang (2011); Tokura et al. (2019); Wang and Zhang (2017); Bernevig et al. (2022); Chang et al. (2023). Such a state is characterized by a topologically nontrivial insulating bulk with a finite Chern number $\mathcal{C}$ Thouless et al. (1982); Haldane (1988) but gapless chiral edge states, which is promising for the realization of dissipationless electronic devices Zhang and Zhang (2012); Wang et al. (2013) and topological computation Qi et al. (2010); Wang et al. (2015a); Lian et al. (2018). The QAH effect has been observed first in magnetically doped topological insulators (TI) Chang et al. (2013, 2015); Mogi et al. (2015); Bestwick et al. (2015); Watanabe et al. (2019), and subsequently in the intrinsic magnetic TI MnBi₂Te₄ Deng et al. (2020), in the moiré graphene Serlin et al. (2020) and moiré transition metal dichalcogenide Li et al. (2021), but only at low temperature (below $5$ K). Such low critical temperature is a weighty obstacle for practical applications, for example the quantum resistance standard Okazaki et al. (2022). Seeking new QAH insulator materials You et al. (2019); Sun et al. (2020a); Li et al. (2020); Xuan et al. (2022); Sun et al. (2020b); Li et al. (2022); Jiang et al. (2023) with preferably large bulk gaps has become an important goal in topological material research.

Physically, the basic mechanism for the QAH effect is band inversion of the spin polarized bands Liu et al. (2008), where both the spin-orbit coupling (SOC) and ferromagnetism are sufficiently strong. From the materials perspective, strong SOC prefers heavy elements, while the ferromagnetism favors transition metal elements preferably with 3$d$ electrons. Thus the challenge in searching for large-gap QAH insulator materials is to synergize the seemingly conflicting requirement of SOC and ferromagnetism. Indeed, the inhomogeneities in magnetic TI Yu et al. (2010); Wang et al. (2015b); Zhang et al. (2019); Li et al. (2019); Otrokov et al. (2019) from magnetic dopants Chong et al. (2020) and defects Garnica et al. (2022) drastically suppress the exchange gap by several order of magnitude, which fundamentally limits the exactly quantized anomalous Hall effect to very low temperatures. Therefore, finding stoichiometric 2D magnetic materials for QAH effect preferably in monolayer with versatile tunability is highly desired.

Here we predict a series of large-gap QAH insulators in monolayer V₂MX₄ ($M=$ W, Mo; $X=$ S, Se), based on density functional theory (DFT) calculations and tight-binding model. The Vienna ab initio simulation package Kresse and Furthmüller (1996) is employed by using the Perdew-Burke-Ernzerhof Perdew et al. (1996) generalized-gradient approximation. We perform $\text{DFT}+\text{Hubbard}$ $U$ calculations Dudarev et al. (1998). The predicted topology was further verified by Heyd-Scuseria-Ernzerhof (HSE) hybrid functional with band gap listed in Table 1 Krukau et al. (2006). These materials have the ferromagnetic (FM) ground state with Chern number $\mathcal{C}=-1$ and extraordinarily large bulk gaps ($\sim 0.2$ eV). We find the large topological gap originates from the deep band inversion between V $d_{xz},d_{yz}$ orbitals and $M$ $d_{z^{2}}$ orbital. The rich choice of candidate materials in Table 1 indicates that the physics here is generic with the space group $P$-$42m$.

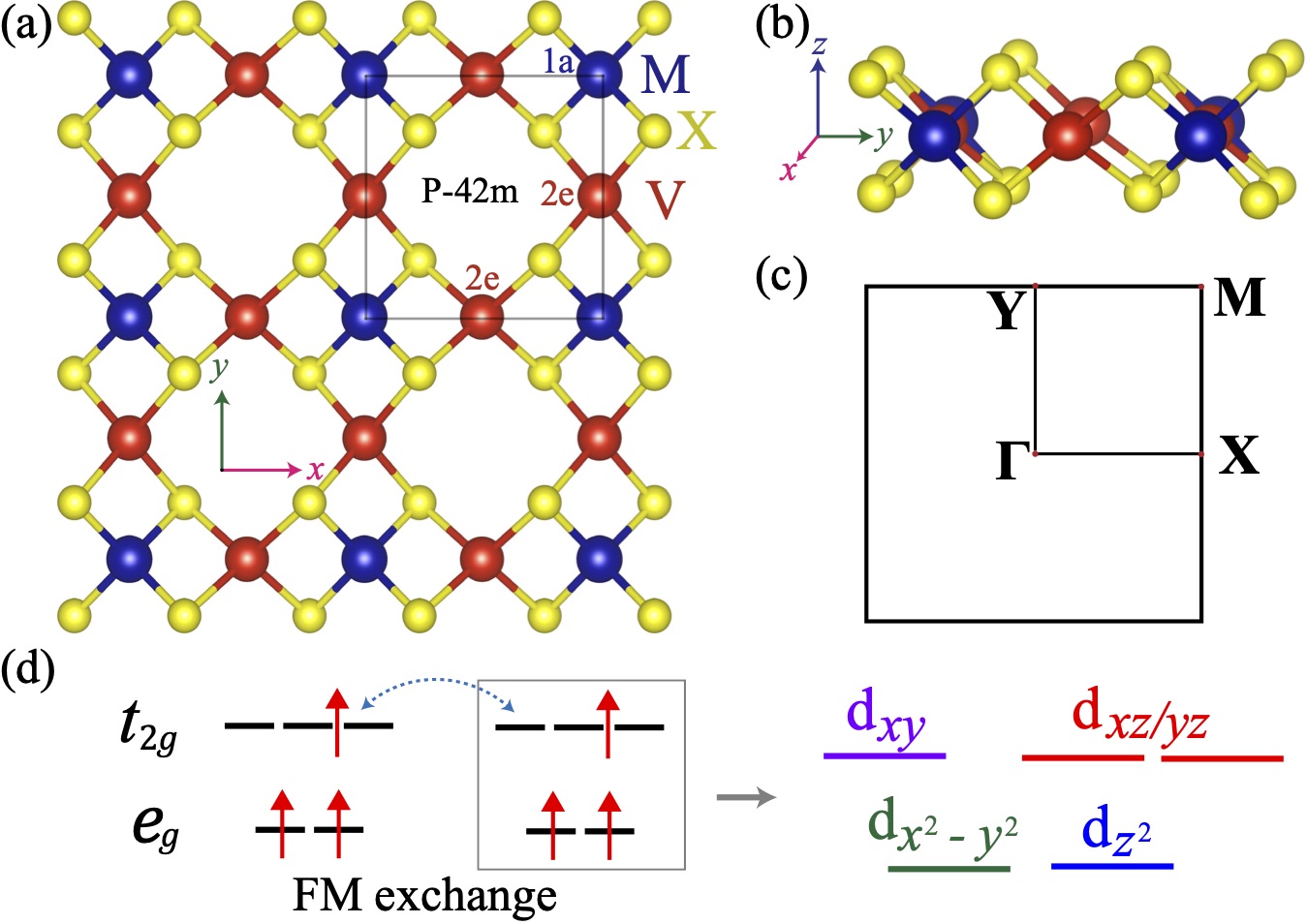
Structure and magnetic properties. The monolayer V₂MX₄ has a tetragonal lattice with the space group $P$-$42m$ (No. 111). As shown in Fig. 1(a), each primitive cell includes three (i.e., one V${}_{2}M$ and two $X_{2}$) atomic layers, where each V or $M$ atom is surrounded by four $X$ atoms forming a distorted edge-sharing tetrahedron. These QAH materials are obtained from high-throughput screening of insulating V₂MX₄ with $M$ from group 5 and 6, and $X$ from group 16. Their lattice constants are listed in Table 1. The dynamical and thermal stability of monolayer V₂MX₄ are confirmed by first-principles phonon and molecular dynamics calculations sup , respectively. We will mainly discuss V₂WS₄ with similar results for other materials in this class. In reality, Cu${}_{2}\textit{MX}_{4}$ and Ag${}_{2}\textit{MX}_{4}$ with the same structure have been experimentally synthesized Crossland et al. (2005); Gan and Schwingenschlögl (2014); Hu et al. (2016); Zhan et al. (2018); Wu et al. (2019); Lin et al. (2019), which implies high probability to fabricate V₂MX₄. Meanwhile, the van der Waals nature of these materials implies the experimental feasibility to exfoliate monolayer from bulk sample.

First-principles calculations show V${}_{2}MX_{4}$ listed in Table 1 have strong FM ground state with an out-of-plane easy axis sup . The underlying mechanism of FM can be elucidated from orbital occupation. The magnetic moments are mainly provided by V ($\approx 2.6\mu_{B}$) rather than W ($\approx 0.4\mu_{B}$). The fractional magnetic moment is due to band inversion between V $d_{xz,yz}$ orbitals and W $d_{z^{2}}$ orbital (Fig. 3(a)). Thus the magnetism is from V atoms. The tetrahedral crystal field splits V $3d$ orbitals into doublet $e_{g}(d_{x^{2}-y^{2}},d_{z^{2}})$ and triplet $t_{2g}(d_{xy},d_{xz},d_{yz})$ orbitals (Fig. 1(d)). The energy of $e_{g}$ stays lower with respect to $t_{2g}$, because the latter point towards the negatively charged ligands. Thus each V atom is in the $e^{2}_{g}t_{2g}^{1}$ configuration with the magnetic moment of $3\mu_{B}$ according to the Hund’s rule, which is close to the DFT calculations. The FM exchange coupling between neighboring V atoms is strongly enhanced by Hund’s rule interaction due to empty $t_{2g}$ orbitals Khomskii (2004). Furthermore, the predicted Curie temperature for monolayer V₂MX₄ is much higher than that of MnBi₂Te₄.

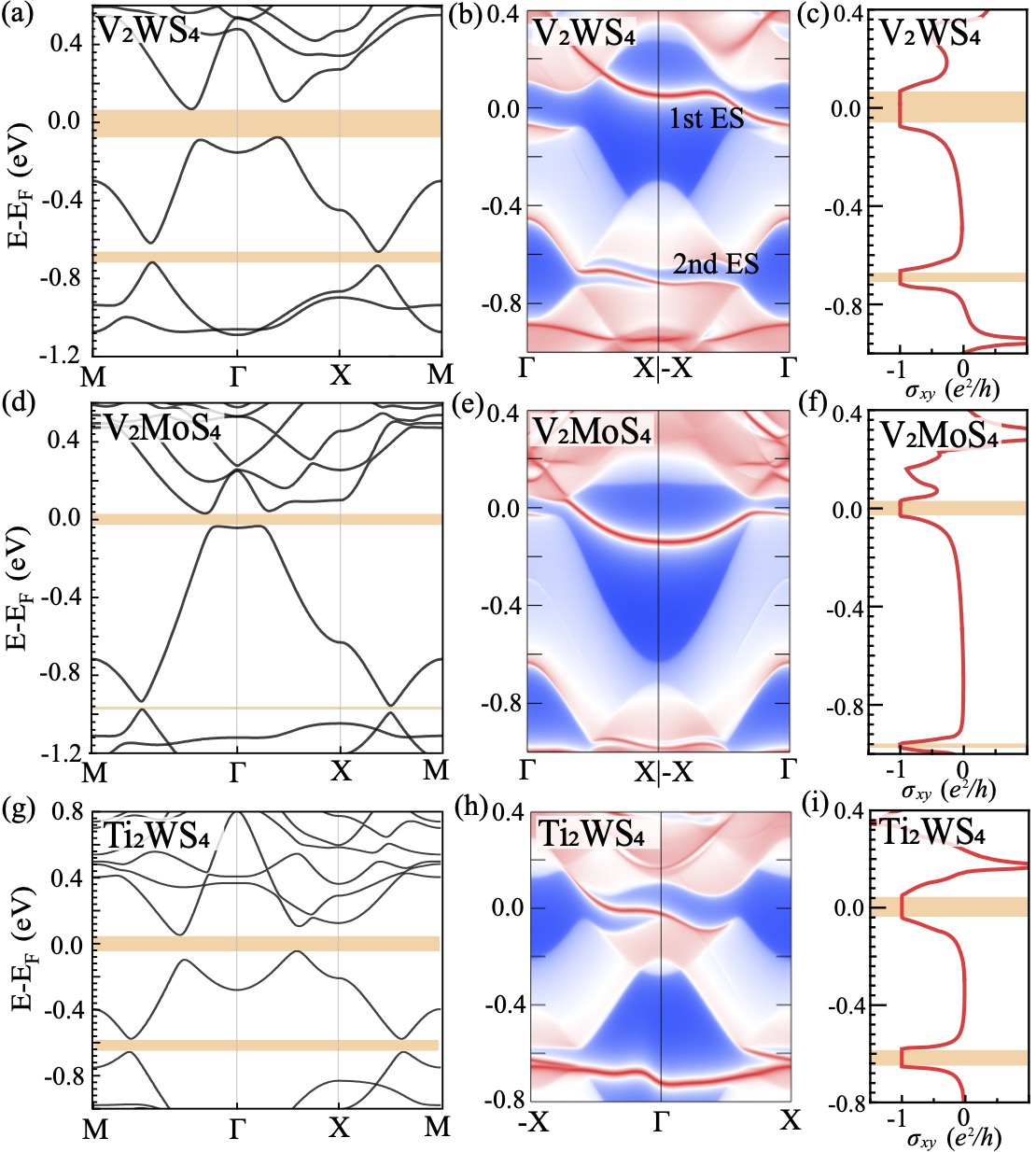
Electronic structures. Fig. 2(a) and Fig. 3(a) display the electronic structure of monolayer V₂WS₄ with and without SOC, respectively. There are two band inversions between different spin polarized bands, both of which are further gapped by SOC. Specifically, one is near the Fermi energy $E_{F}$ between spin up bands contributed by $d_{xy},d_{yz}$ orbitals of V and spin down band by $d_{z^{2}}$ orbital of W, the other is about $0.7$ eV below $E_{F}$ between V $d_{xy},d_{yz}$ spin up bands and W $d_{x^{2}-y^{2}}$ spin down band. There also exists a spin polarized quadratic band touching at $\Gamma$ point from $d_{xy},d_{yz}$ orbitals of V above $E_{F}$, with the nontrivial gap opened by SOC Wang and Wang (2021). The anomalous Hall conductance $\sigma_{xy}$ versus $E_{F}$ is calculated in Fig. 2(c), which displays a quantized value of $-e^{2}/h$ near both $E_{F}$ and $E_{F}-0.7$ eV. This indicates the topological nontrivial bands with $\mathcal{C}=-1$ below $E_{F}-0.7$ eV, which is consistent with single chiral edge states dispersing within the bulk gap as in the edge local density of states (Fig. 2(b)). Interestingly, there also exists an occupied 2nd chiral edge state which is $0.7$ eV below $E_{F}$, which can be measured by scanning tunneling microscope. By replacing W by the same group element Mo, V₂MoS₄ monolayer has similar band structure and same topological properties as shown in Fig. 2(d)-2(f). The topological gap of monolayer V₂W$X_{4}$ is larger than that of V₂Mo$X_{4}$, which is due to enhanced SOC from heavier elements and deeper band inversion.

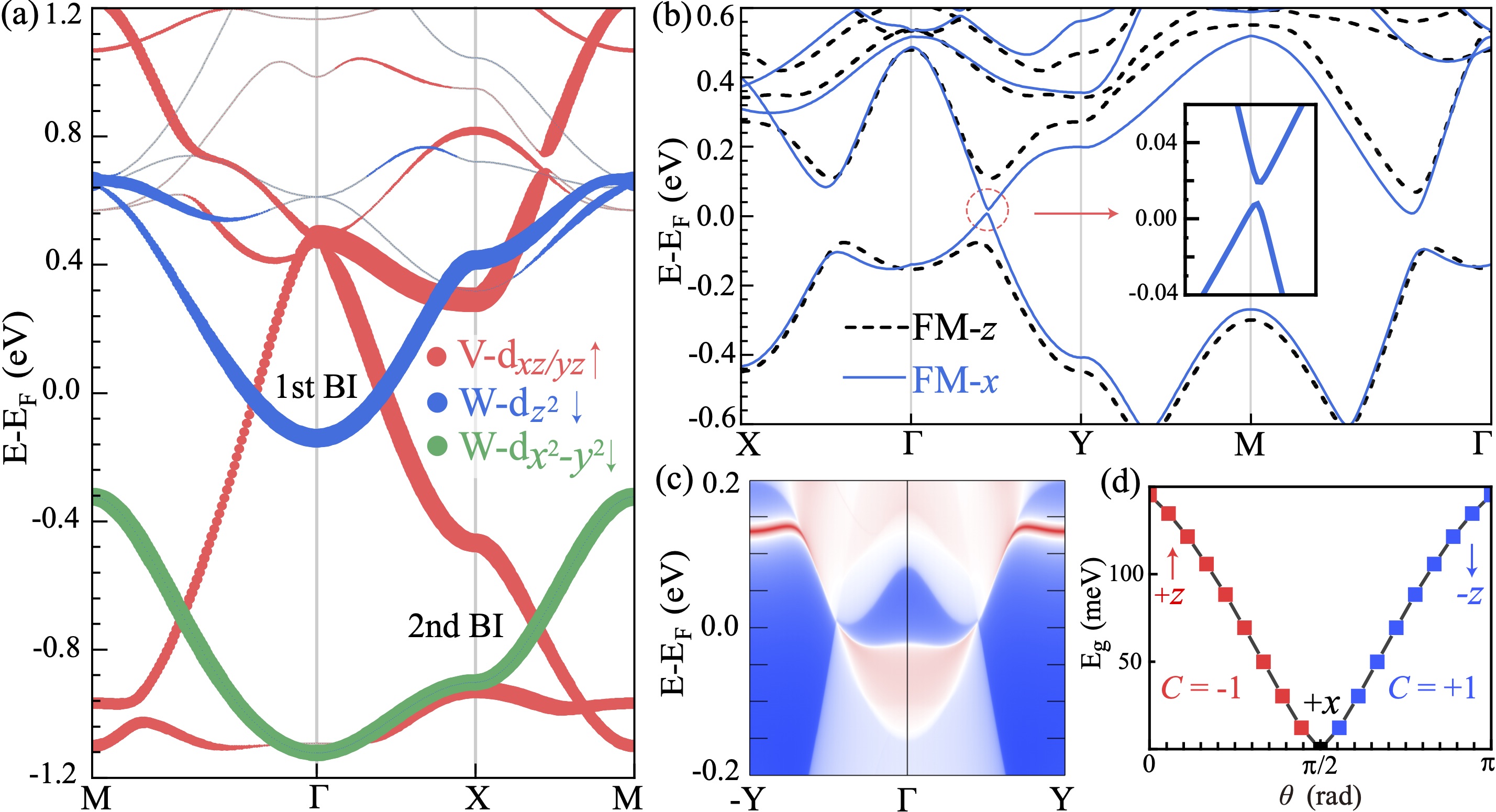
The topological gap strongly depends on spin orientations. Fig. 3(b) shows the band structure for the in-plane ferromagnetism along $x$-axis. The symmetries of the system reduces to $C_{2x}$ and $C_{2z}\mathcal{T}$, where $\mathcal{T}$ is time-reversal. One can see the gap along $\Gamma$-Y decreases but not closes, for there is no symmetry to guarantee a gapless point. Along the high symmetry lines, there is a small negative indirect gap between valence top along $\Gamma$-Y and conduction bottom along $\Gamma$-M. The Chern number of valence bands are calculated to be $\mathcal{C}=0$, which is guaranteed by $C_{2z}\mathcal{T}$. Similar to $\mathcal{IT}$, $\sigma_{xy}$ is odd under $C_{2z}\mathcal{T}$ in 2D materials, which ensures $\mathcal{C}=0$ when ferromagnetism is completely along any in-plane direction. This is consistent with the edge local density of state calculation in Fig. 3(c), where there is no chiral edge state. The FM-$x$ state is trivial without any kinds of topology, which is checked by the band representation of $C_{2x}$ (i.e., symmetry indicator). Then by varying the spin orientation from $+z$ to $+x$, then to $-z$ axis, the band gap monotonically decreases to close, and negative then reopens, which is accompanied by the topological phase transitions from $\mathcal{C}=-1$ to $\mathcal{C}=0$ and then to $\mathcal{C}=1$ in Fig. 3(d). The gap varies approximately in relation as $E_{g}\propto S\cos(\theta+\theta_{0})\approx\langle S_{z}\rangle$, with $\theta_{0}\approx 0.1$ sup . This simply means the topologically nontrivial gap is opened by SOC related to $\langle S_{z}\rangle$ component, while the trivial gap is associated with $\langle S_{x}\rangle$ component.

The intimate relationship between band gap and spin orientation implies that the electronic structure is renormalized by magnon excitations. In FM-$z$ ground state, the magnons contribution to magnetization is $\langle S_{z}\rangle=S-\int d^{2}\mathbf{k}n_{B}(\epsilon_{\mathbf{k}})/(2\pi)^{2}$, where $n_{B}(\epsilon_{\mathbf{k}})\equiv 1/[\exp(\epsilon_{\mathbf{k}}/k_{B}T)-1]$ is the Bose distribution, $\epsilon_{\mathbf{k}}$ is magnon dispersion. Taking V₂WS₄ as an example, $S=3/2$ and the magnon gap is estimated to be $5.34$ meV. Thus when $T<58$ K, the magnon is absent; when $T\lesssim 200$ K, the reduction in $\langle S_{z}\rangle$ from magnon excitation is less than $6\%$ compared to $\langle S_{z}\rangle=3/2$ sup . Therefore, the large topological gap of ground state still holds in the presence of magnon excitation. It is worth mentioning that when temperature is close to $T_{c}$, the significant thermal spin fluctuation will decrease $\langle S_{z}\rangle$ and topological gap dramatically.

Tight-binding model and origin of topology. To reveal the origin of $\mathcal{C}=-1$ topology in the electronic structure, we perform the symmetry analysis of the band irreducible representation and construct a tight-binding model to recover the essential topological physics. The first and second band inversions occur at $\Gamma$ and M point, respectively. Naively, one may simply count the angular momentum difference locally at the band inversion point to be the Chern number change as in the conventional $s$-$p$ band inversion. However, this is incorrect due to band inversion from the opposite spin polarization here. For example, at M point for second band inversion, only spin contributes to the angular momentum difference, which implies the lowest band ($d^{\downarrow}_{x^{2}-y^{2}}$ from W) should have $\mathcal{C}=1$, this is contrary to the first principles calculations of $\mathcal{C}=-1$.

Then we construct a concrete tight-binding model including $d^{\uparrow}_{xz},d^{\uparrow}_{yz}$ of V and $d_{z^{2}}^{\downarrow},d_{x^{2}-y^{2}}^{\downarrow}$ of W to decipher the origin of topology. There are two V in an unit cell, and $d_{xz},d_{yz}$ orbitals of each V are non-degenerate. However, $d_{xz}$ of one V and $d_{yz}$ of the other V are degenerate, which are related to each other by $S_{4z}$. Therefore, for the low energy physics, we only need to consider $d^{\uparrow}_{xz},d^{\uparrow}_{yz}$ from two V, respectively and $d_{z^{2}}^{\downarrow},d_{x^{2}-y^{2}}^{\downarrow}$ of W, namely a four orbitals model. The Hamiltonian is obtained by considering the nearest-neighbor and next-nearest-neighbor hopping with SOC included, where the explicit forms are in Supplementary Materials sup . As shown in Fig. 4(a) and 4(b), the band structure and the corresponding irreducible representations of high symmetry points (listed in Table 2) in DFT calculation (Fig. 2(a) and Fig. 3(a)) are rebuilt in our tight-binding model.

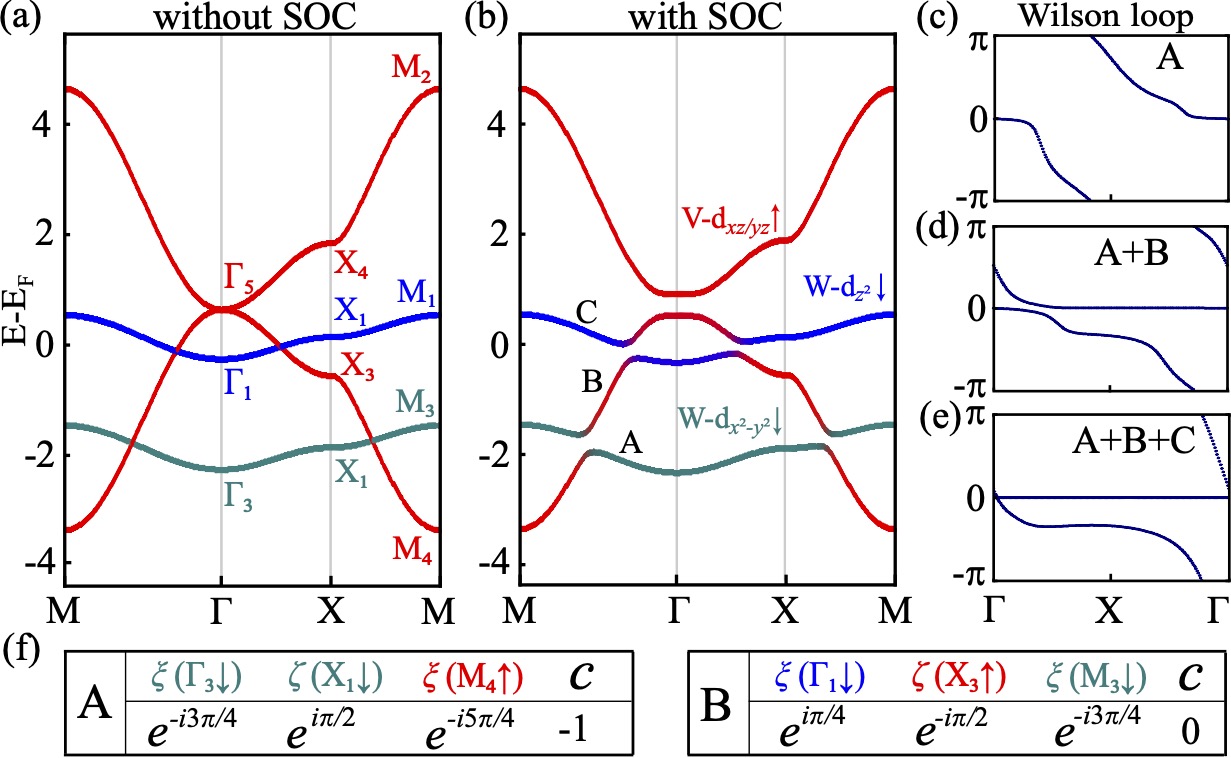
The symmetry generators of space group $P$-$42m$ are $S_{4z}$, $C_{2z}$ and $C_{2x}$. For tight-binding model of V₂MX₄, $\mathcal{I}$ can be viewed as $C_{2z}$ due to lacking of $z$ direction. Then $S_{4z}$ becomes $C^{3}_{4z}$, namely, the system is effectively $C_{4z}$ invariant. The Chern number of band in a $S_{4}$ invariant system is shown to be Fang et al. (2012); sup ,

Here $F=1$ for spinful case. $\xi_{j}(k)$ is the eigenvalue of $S_{4z}$ at the $S_{4z}$-invariant $\Gamma$ and M points of the $j$-th band, $\zeta_{j}(k)$ is the eigenvalue of $C_{2z}$ at the $C_{2z}$-invariant X point on the $j$-th band. Now the band topology can be diagnosed by the symmetry information listed in Table 2. The eigenvalues and Chern numbers for lowest (A) and second lowest band (B) are calculated in Fig. 4(f). All of these are consistent with the Wilson loop calculations for the lowest one and two bands shown in Fig. 4(c) and 4(d). The quadratic band touching at $\Gamma_{5}$ is from degenerate $d_{xz},d_{yz}$, which have an effective angular momentum $\ell_{z}=\pm 1$, and SOC opens a topologically nontrivial gap Wang and Wang (2021). Thus the Chern number summation of lowest three bands is only determined by the sign of SOC. As shown in Fig. 4(e), the total Chern number of the lowest three bands is $\mathcal{C}=-1$, namely, both bands B and C have $\mathcal{C}=0$, and the only nontrivial $\mathcal{C}=-1$ is carried by band A, which is consistent with first principles calculations. If we artificially reverse the sign of SOC, then the Chern number of the lowest three bands are $(\mathcal{C}_{A},\mathcal{C}_{B},\mathcal{C}_{C})=(-1,0,2)$. Now we fully understand that the topology in this system is not only from gapping the degenerate $d_{xz},d_{yz}$ orbitals of V by SOC, but also the band inversions from them and W $d_{z^{2}}$ and $d_{x^{2}-y^{2}}$.

Here we analyze the origin of the large topological gap. The topological gap is from SOC term as $\lambda_{\text{so}}\bm{\ell}\cdot\mathbf{s}=\lambda_{\text{so}}(\ell_{+}s_{-}+\ell_{-}s_{+})/2+\lambda_{\text{so}}\ell_{z}s_{z}$, where $\lambda_{\text{so}}$ is atomic SOC strength. The nontrivial gap is opened by combining the first term with orbital hopping and hybridization. For spin polarized band inversion in QAH, two bands are inverted at certain high-symmetry point in the Brillouin zone, and topological gap $E_{g}$ opens at a finite wave vector $\delta k$ away from the band inversion point due to orbital hybridization with $E_{g}\propto\lambda^{\prime}\delta k$, where $\lambda^{\prime}$ is the hybridization strength. For spin polarized band inversion with same spin such as MnBi₂Te₄ Zhang et al. (2019); Li et al. (2019), $\lambda^{\prime}\propto\lambda_{\text{so}}^{2}$, namely second-order process. In V₂MX₄, the band inversion are between opposite spin polarized bands, $\lambda^{\prime}\propto\lambda_{\text{so}}$, thus a lower-order process with greater strength in gap opening. Meanwhile, these materials have deep band inversion with large $\delta k$. Therefore, both $\lambda^{\prime}$ and $\delta k$ are enhanced in V₂MX₄ and lead to large topological gap.

Material generalization. The key for the $\mathcal{C}=-1$ phase here is rooted in the spin polarized quadratic band touching of $d_{xz},d_{yz}$ orbitals at $\Gamma$ point, where $S_{4z}$ ensures their degeneracy. With SOC and certain orbital occupations, QAH phase can be realized. In fact, the model and analysis from $d$ orbitals above are quite general, and also apply to monolayer Ti₂WX₄ ($X=$ S, Se) with the same lattice structure of $P$-$42m$ symmetry and similar $d$-orbital projected band structure and irreducible representations sup . Ti₂WX₄ has the FM ground state, and the magnetism is from Ti atom. Interestingly, the bandwidth of $d_{z^{2}}$ orbital is much narrower than that of $d_{xz},d_{yz}$ orbitals in Ti. Each Ti atom is in the $e_{g}^{1}t_{2g}^{1}$ configuration with the magnetic moment close to $2\mu_{B}$ according to the Hund’s rule. The $e_{g}$-$t_{2g}$ kinetic exchange leads to strong ferromagnetism Jiang et al. (2023). Meanwhile, similar two band inversions occur between $d^{\uparrow}_{xy},d^{\uparrow}_{yz}$ bands of Ti and $d^{\downarrow}_{z^{2}}$ band of W first at $E_{F}$, and $d^{\downarrow}_{x^{2}-y^{2}}$ band of W then below $E_{F}$. By adding SOC, the nontrivial topology from quadratic band touching of $d_{xz},d_{yz}$ at $\Gamma$ is now transmitted to the bands below $E_{F}$, leading to the $\mathcal{C}=-1$ QAH phase (Fig. 2(g)-(i)). We point out that Ti $d$-orbitals contribute both of topology and magnetism, nevertheless the physics is quite different from KTiSb class of compounds, where the topology is from band inversion from $d_{xz},d_{yz}$ and $d_{z^{2}}$ at $M$ point Jiang et al. (2023).

Discussions. The topological band structures in these materials have interesting thickness dependence. Bilayer V₂WS₄ has AA or AB stacking. The magnetic ground state is $A$-type AFM with the out-of-plane easy axis in AB stacking, which is FM within each layer but AFM between the adjacent layer. The $t_{2g}$-$t_{2g}$ exchange of V atoms between neighbor layers via $p$ orbitals of ligand is AFM due to Goodenough-Kanamori-Anderson rule Khomskii (2004). The system has a full band gap and gapped helical edge state, namely $\mathcal{C}=0$, which can be simply viewed as stacking of two QAH with opposite Chern number along $z$-axis. The FM-$z$ state of bilayer also has a full gap but with $\mathcal{C}=-2$. We further calculate the trilayer case and obtain AFM ground state with an uncompensated FM layer along $z$ axis, and the system is a $\mathcal{C}=-1$ QAH insulator sup . Therefore, we expect $\mathcal{C}$ will oscillate between $-1$ and $0$ depending on odd and even layers of multilayer, as long as it has a full band gap.

The quantized $\sigma_{xy}$ and vanishing longitudinal conductivity of QAH insulator imply a quantized Kerr/Faraday rotation Ikebe et al. (2010); Shimano et al. (2013), when the frequency satisfies $\omega\ll E_{g}/\hbar$. However, such a quantized magnetooptical effect has not been achieved in existing QAH systems yet due to the small band gap Okada et al. (2016); Mogi et al. (2022). Here the topologically nontrivial Chern bands in V₂MX₄ lies far below and above $E_{F}$, which provides an intriguing but rare platform for exploring giant Kerr rotation from the optical transitions between Chern bands, even possibly in the optical frequency range.

In summary, our work uncover large gap $\mathcal{C}=-1$ QAH phase with interesting interplay between magnetism and topology solely from $d$ orbitals, which applies to a large class of ternary chalcogenide in space group $P$-$42m$. The rich choice of candidate materials indicate the physics is quite general. We hope the theoretical work here could aid the search for new QAH insulators in transition metal compounds.