33institutetext: Department of Computer Science and Engineering, Indian Institute of Information Technology, Sri City, Andhra Pradesh, India
[email protected], [email protected], [email protected]
Moment Centralization based Gradient Descent Optimizers for Convolutional Neural Networks
Abstract
Convolutional neural networks (CNNs) have shown very appealing performance for many computer vision applications. The training of CNNs is generally performed using stochastic gradient descent (SGD) based optimization techniques. The adaptive momentum-based SGD optimizers are the recent trends. However, the existing optimizers are not able to maintain a zero mean in the first-order moment and struggle with optimization. In this paper, we propose a moment centralization-based SGD optimizer for CNNs. Specifically, we impose the zero mean constraints on the first-order moment explicitly. The proposed moment centralization is generic in nature and can be integrated with any of the existing adaptive momentum-based optimizers. The proposed idea is tested with three state-of-the-art optimization techniques, including Adam, Radam, and Adabelief on benchmark CIFAR10, CIFAR100, and TinyImageNet datasets for image classification. The performance of the existing optimizers is generally improved when integrated with the proposed moment centralization. Further, The results of the proposed moment centralization are also better than the existing gradient centralization. The analytical analysis using the toy example shows that the proposed method leads to a shorter and smoother optimization trajectory. The source code is made publicly available at https://github.com/sumanthsadhu/MC-optimizer.
1 Introduction
Deep learning has become very prominent to solve the problems in computer vision, natural language processing, and speech processing [17]. Convolutional neural networks (CNNs) have been exploited to utilize deep learning in the computer vision area with great success to deal with the image and video data [15], [22], [9], [24], [1], [19]. The CNN models are generally trained using the stochastic gradient descent (SGD) [3] based optimization techniques where the parameters of the model are updated in the opposite direction of the gradient. The performance of any CNN model is also sensitive to the chosen SGD optimizer used for the training. Hence, several SGD optimizers have been investigated in the literature.
The vanilla SGD algorithm suffers from the problem of zero gradients at local minimum and saddle regions. The SGD with momentum (SGDM) uses the accumulated gradient, i.e., momentum, to update the parameters instead of the current gradient [25]. Hence, it is able to update the parameters in the local minimum and saddle regions. However, the same step size is used by SGDM for all the parameters. In order to adapt the step size based on the gradient consistency, AdaGrad [8] divides the learning rate by the square root of the accumulated squared gradients from the initial iteration. However, it leads to a vanishing learning rate after some iteration as the squared gradient is always positive. In order to tackle the learning rate diminishing problem of AdaGrad, RMSProp [10] uses a decay factor on the accumulated squared gradient. The idea of both SGDM and RMSProp is combined in a very popular Adam gradient descent optimizer [13]. Basically, Adam uses a first order moment as the accumulated gradient for parameter update and a second order moment as the accumulated squared gradient to control the learning rate. A rectified adam (Radam) [18] performs the rectification in Adam to switch to SGDM to improve the precision of the convergence of training. Recently, Adabelief optimizer [27] utilizes the residual of gradient and first order moment to compute the second order moment which improves the training at saddle regions and local minimum. Other notable recent optimizers include diffGrad [6], AngularGrad [20], signSGD [2], Nostalgic Adam [11], and AdaInject [7].
The above mentioned optimization techniques do not utilize the normalization of the moment for smoother training. However, it is evident that normalization plays a very important role in the training of deep learning models, such as data normalization [23], batch normalization [12], instance normalization [5], weight normalization [21], and gradient normalization [4]. The gradient normalization is also utilized with SGD optimizer in [26]. However, as the first order moment is used for the parameter updates in adaptive momentum based optimizers, we proposed to perform the normalization on the accumulated first order moment. The contributions of this paper can be summarized as follows:
-
•
We propose the concept of moment centralization to normalize the first order moment for the smoother training of CNNs.
-
•
The proposed moment centralization is integrated with Adam, Radam, and Adabelief optimizers.
-
•
The performance of the existing optimizers is tested with and without the moment centralization.
The rest of the paper is structured as follows: Section 2 presents the proposed moment centralization based SGD optimizers; Section 3 summarizes the experimental setup, datasets used and CNN models used; Section 4 illustrates the experimental results, comparison and analysis; and finally Section 5 concludes the paper.
2 Proposed Moment Centralization based SGD Optimizers
In this paper, a moment centralization strategy is proposed for the adaptive momentum based SGD optimizers for CNNs. The proposed approach imposes the explicit normalization over the first order moment in each iteration. The imposed zero mean distribution helps the CNN models for a smoother training. The proposed moment centralization is generic and can be integrated with any adaptive momentum based SGD optimizer. In this paper, we use it with state-of-the-art optimizers, including Adam [13], Radam [18] and Adabelief [27]. The Adam optimizer with moment centralization is termed AdamMC. Similarly, the Radam and Adabelief optimizers with moment centralization are referred to as RadamMC and AdabeliefMC, respectively. In this section, we explain the proposed concept with Adam, i.e., AdamMC.
Let a function represents a CNN model having parameters for image classification. Initially, the parameters are initialized randomly and updated using backpropagation of gradients in the subsequent iterations of training. During the forward pass of training, the CNN model takes a batch of images () containing images as the input and returns the cross-entropy loss as follows:
| (1) |
where is the softmax probability of given input image for the correct class level . Note that the class level is represented by the one-hot encoding in the implementation. During the backward pass of the training, the parameters are updated based on the gradient information. Different SGD optimizers utilize the gradient information differently for the parameter update. The adaptive momentum based optimizers such as Adam are very common in practice which utilizes the first order and second order momentum which is the exponential moving average of gradient and squared gradient, respectively. Hence, we explain the proposed concept below with the help of Adam optimizer.
Consider to be the gradient of an objective function w.r.t. the parameter , i.e., in the iteration of training, where represents the parameter values obtained after iteration. The first order moment () in the iteration is computed as follows,
| (2) |
where is the first order moment in iteration and is a decay hyperparameter. Note that the distribution of first order moments is generally not zero centric which leads to the update in a similar direction for the majority of the parameters. In order to tackle this problem, we propose to perform the moment centralization by normalizing the first order moment with zero mean as follows,
| (3) |
The second order moment () in the iteration is computed as follows,
| (4) |
where is the second order moment in iteration and is a decay hyperparameter. Note that we do not perform the centralization of second order moments as it may lead to a very inconsistent effective learning rate.
The first and second order moments suffer in the initial iteration due to very small values leading to very high effective step size. In order to cope up with this bias, Adam [13] has introduced a bias correction as follows,
| (5) |
where and are the bias corrected first and second order moment, respectively. Finally, the parameter update in iteration is performed as follows,
| (6) |
where is the updated parameter, is the parameter after iteration, is the learning rate and is a very small constant number used for numerical stability to avoid the division by zero. The steps of Adam optimizer without and with the proposed moment centralization concept are summarized in Algorithm 1 (Adam) and Algorithm 2 (AdamMC), respectively. The changes in the AdamMC are highlighted in blue color. Similarly, we also incorporate the moment centralization concept with Radam [18] and Adabelief [27] optimizers. The steps for Radam, RadamMC, Adabelief, and AdabeliefMC are illustrated in Algorithm 3, 4, 5, and 6, respectively.
3 Experimental Setup
All experiments are conducted on Google Colab GPUs using the Pytorch 1.9 framework. We want to emphasise that our Moment Centralization (MC) approach does not include any additional hyper-parameters. To incorporate MC into the existing optimizers, only one line of code is required to be included in the code of existing adaptive momentum based SGD optimizers, with all other settings remaining untouched.
3.1 CNN Models Used
We use VGG16 [22] and ResNet18 [9] CNN models in the experiments to validate the performance of the proposed moment centralization based optimizers, including AdamMC, RadamMC and AdabeliefMC. The VGG16 is a plain CNN model with sixteen learnable layers. It uses three fully connected layers towards the end of the network. It is one of the popular CNN models utilized for different computer vision tasks. The ResNet18 is a directed acyclic graph-based CNN model which utilizes the identity or residual connections in the network. The identity connection improves the gradient flow in the network during backpropagation and helps in the training of a deep CNN model.
3.2 Datasets Used
We test the performance of the proposed moment centralization optimizers on three benchmark datasets, including CIFAR10, CIFAR100 [14] and TinyImageNet111http://cs231n.stanford.edu/tiny-imagenet-200.zip [16]. The CIFAR10 dataset consists of 60,000 images from 10 object categories with 6,000 images per category. The 5,000 images per category are used for the training and the remaining 1,000 images per category are used for testing. Hence, the total number of images used for training and testing in CIFAR10 data is 50,000 and 10,000, respectively. The CIFAR100 contains the same 60,000 images of CIFAR10, but divides the images into 100 object categories which is beneficial to test the performance of the optimizers for fine-grained classification. The TinyImageNet dataset is part of the full ImageNet challange. It contsists of 200 object categories. Each class has 500 images for training. However, the test set consists of 10,000 images. The dimension of all the images is 64x64 in color in TinyImageNet dataset.
3.3 Hyperparameter Settings
All the optimizers in the experiment share the following settings. The decay rates of first and second order moments and are and , respectively. The first and second order moments (, ) are initialized to . The training is performed for 100 epochs with learning rate for the first 80 epochs and for the last 20 epochs. The weight initialization is performed using random numbers from a standard normal distribution.
| CNN Model | VGG16 Model | ResNet18 Model | ||||
| Optimizer | Adam | AdamGC | AdamMC | Adam | AdamGC | AdamMC |
| Run1 | 92.49 | 92.43 | 92.49 | 93.52 | 91.82 | 93.42 |
| Run2 | 92.52 | 90.64 | 92.26 | 93.49 | 93.43 | 93.37 |
| Run3 | 92.70 | 92.15 | 92.56 | 93.95 | 91.18 | 93.3 |
| MeanStd | 92.570.11 | 91.740.96 | 92.440.16 | 93.650.26 | 92.141.16 | 93.360.06 |
| Optimizer | Radam | RadamGC | RadamMC | Radam | RadamGC | RadamMC |
| Run1 | 92.79 | 92.16 | 93.33 | 94.02 | 93.67 | 94.00 |
| Run2 | 93.30 | 92.92 | 93.33 | 92.85 | 93.76 | 93.69 |
| Run3 | 92.80 | 92.58 | 93.36 | 94.06 | 93.7 | 94.08 |
| MeanStd | 92.960.29 | 92.550.38 | 93.340.02 | 93.640.69 | 93.710.05 | 93.920.21 |
| Optimizer | Adabelief | AdabeliefGC | AdabeliefMC | Adabelief | AdabeliefGC | AdabeliefMC |
| Run1 | 92.91 | 92.71 | 93.07 | 93.86 | 93.74 | 93.78 |
| Run2 | 92.67 | 93.04 | 92.94 | 92.31 | 93.88 | 93.72 |
| Run3 | 92.85 | 92.83 | 92.91 | 93.98 | 93.73 | 93.56 |
| MeanStd | 92.810.12 | 92.860.17 | 92.970.09 | 93.380.93 | 93.780.08 | 93.690.11 |
| CNN Model | VGG16 Model | ResNet18 Model | ||||
| Optimizer | Adam | AdamGC | AdamMC | Adam | AdamGC | AdamMC |
| Run1 | 67.74 | 67.68 | 68.47 | 71.4 | 73.74 | 74.48 |
| Run2 | 67.51 | 67.73 | 69.43 | 71.47 | 73.34 | 73.92 |
| Run3 | 67.96 | 68.26 | 68.01 | 71.64 | 73.58 | 74.64 |
| MeanStd | 67.740.23 | 67.890.32 | 68.640.72 | 71.50.12 | 73.550.2 | 74.350.38 |
| Optimizer | Radam | RadamGC | RadamMC | Radam | RadamGC | RadamMC |
| Run1 | 69.56 | 70.31 | 70.89 | 73.54 | 73.75 | 74.31 |
| Run2 | 70.05 | 69.81 | 70.57 | 73.15 | 73.07 | 74.61 |
| Run3 | 69.82 | 70.26 | 70.35 | 73.41 | 73.88 | 74.48 |
| MeanStd | 69.810.25 | 70.130.28 | 70.600.27 | 73.370.2 | 73.570.44 | 74.470.15 |
| Optimizer | Adabelief | AdabeliefGC | AdabeliefMC | Adabelief | AdabeliefGC | AdabeliefMC |
| Run1 | 70.84 | 70.85 | 71.44 | 74.05 | 73.69 | 74.38 |
| Run2 | 70.71 | 71.17 | 70.83 | 74.11 | 73.95 | 74.86 |
| Run3 | 70.37 | 70.56 | 70.84 | 74.3 | 73.74 | 74.74 |
| MeanStd | 70.640.24 | 70.860.31 | 71.040.35 | 74.150.13 | 73.790.14 | 74.660.25 |
| CNN Model | VGG16 Model | ResNet18 Model | ||||
| Optimizer | Adam | AdamGC | AdamMC | Adam | AdamGC | AdamMC |
| Run1 | 42.38 | 45.02 | 43.50 | 49.08 | 53.90 | 53.02 |
| Run2 | 41.92 | 43.00 | 41.06 | 49.00 | 53.60 | 53.62 |
| Run3 | 42.72 | 44.42 | 39.22 | 49.00 | 52.54 | 54.10 |
| MeanStd | 42.340.4 | 44.151.04 | 41.262.15 | 49.030.05 | 53.350.71 | 53.580.54 |
| Optimizer | Radam | RadamGC | RadamMC | Radam | RadamGC | RadamMC |
| Run1 | 43.86 | 45.94 | 47.22 | 49.84 | 51.62 | 53.40 |
| Run2 | 44.10 | 45.86 | 47.48 | 50.50 | 51.54 | 52.72 |
| Run3 | 45.18 | 45.80 | 47.26 | 50.78 | 51.92 | 52.88 |
| MeanStd | 44.380.70 | 45.870.07 | 47.320.14 | 50.370.48 | 51.690.20 | 53.000.36 |
| Optimizer | Adabelief | AdabeliefGC | AdabeliefMC | Adabelief | AdabeliefGC | AdabeliefMC |
| Run1 | 47.32 | 47.84 | 47.22 | 51.82 | 52.02 | 53.04 |
| Run2 | 49.12 | 47.60 | 52.86 | 46.78 | 51.80 | 53.08 |
| Run3 | 47.16 | 47.94 | 48.34 | 51.04 | 51.56 | 53.78 |
| MeanStd | 47.871.09 | 47.790.17 | 49.472.99 | 49.882.71 | 51.790.23 | 53.300.42 |
4 Experimental Results and Analysis
In order to demonstrate the improved performance of the optimizers with the proposed moment centralization, we conduct the image classification experiments using VGG16 [22] and ResNet18 [9] CNN models on CIFAR10, CIFAR100 and TinyImageNet datasets [14] and report the classification accuracy. The results are compared with the corresponding optimization method without using moment centralization. Moreover, the results are also compared with the corresponding optimization method with the gradient centralization [26]. We repeat all the experiments three times with independent initializations and consider the mean and standard deviation for the comparison purpose. All results are evaluated with the same settings as described above.
The classification accuracies on the CIFAR10, CIFAR100 and TinyImagenet datasets are reported in Table 1, Table 2, and Table 3, respectively. It is noticed from these results that the optimizers with moment centralization (i.e., AdamMC, RadamMC, and AdabeliefMC) outperform the corresponding optimizers without moment centralization (i.e., Adam, Radam, and Adabelief, respectively) and with gradient centralization (i.e., AdamGC, RadamGC, and AdabeliefGC, respectively) in most of the scenario. The performance of the proposed AdamMC optimizer is also comparable with Adam on the CIFAR10 dataset, where AdamGC (i.e., Adam with gradient centralization [26]) fails drastically. It’s also worth mentioning that the classification accuracy using the proposed optimizers is very consistent in different trials with a reasonable standard deviation in the results, except on TinyImageNet dataset using VGG16 model.



The accuracy plot w.r.t. epochs is depicted in Fig. 1 on CIFAR100 dataset for different optimizers. Note that the learning rate is set to 0.001 for first 80 epochs and 0.0001 for last 20 epochs. It is noticed in all the plots that the performance of the proposed optimizers boosts significantly and outperforms other optimizers when the learning rate is dropped. It shows that the proposed moment centralization leads to better regularization and reaches closer to minimum.



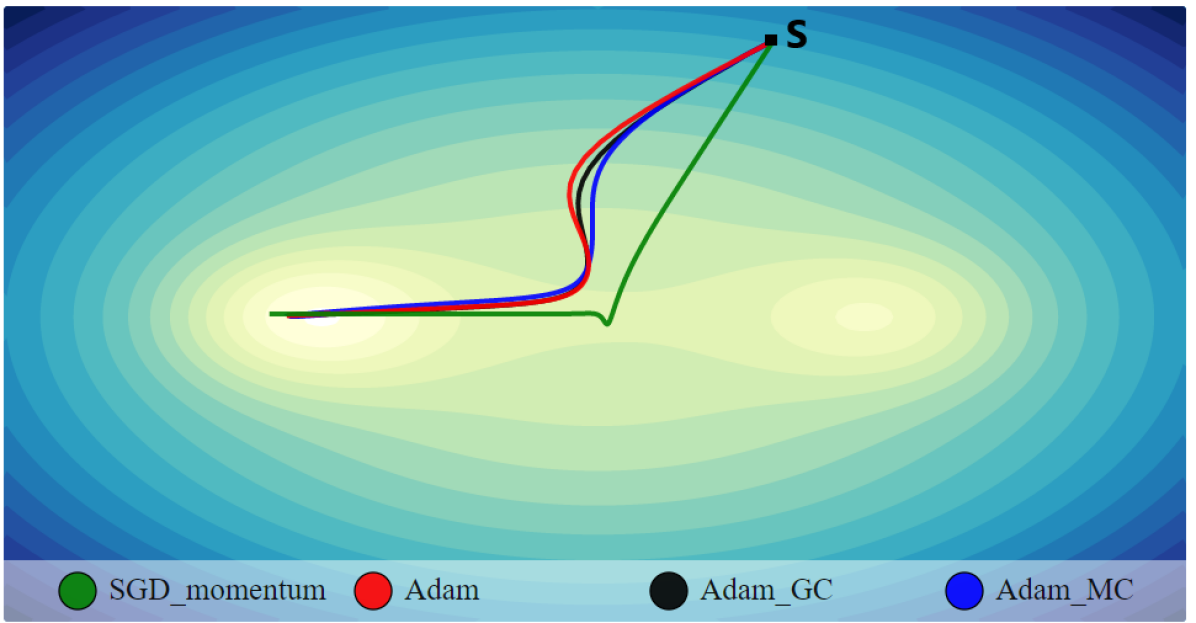
In order to justify the improved performance of the proposed Adam_MC method, we show the convergence plot in terms of the optimization trajectory in Fig. 2 with random intializations for following toy example:
| (7) |
It is a quadratic ‘bowl’ with two gaussian looking minima at (1, 0) and (-1, 0), respectively. It can be observed in Fig. 2(a) that the Adam_MC optimizer leads to a shorter path and faster convergence to reach minimum as compared to other optimizers. Figure 1 illustrates how the moment centralization for Adam, RAdam, and Adabelief achieved higher accuracy after the 80th epoch than without. This demonstrates that optimizers with MC variation have faster convergence speed than without. The SGD shows much oscillations near the local minimum. In Fig. 2(b), Adam and Adam_GC depict fewer turns as compared to SGD with momentum, while Adam_MC exhibits smoother updates. In Fig. 2(c-d), Adam_MC leads to less oscillations throughout its course as compared to other optimizers. Hence, it is found that the proposed optimizer leads to shorter and smoother path as compared to other optimizers.
5 Conclusion
In this paper, a moment centralization is proposed for the adaptive momentum based SGD optimizers. The proposed approach explicitly imposes the zero mean constraints on the first order moment. The moment centralization leads to better training of the CNN models. The efficacy of the proposed idea is tested with state-of-the-art optimizers, including Adam, Radam, and Adabelief on CIFAR10, CIFAR100 and TinyImageNet datasets using VGG16 and ResNet18 CNN models. It is found that the performance of the existing optimizers is improved when integrated with the proposed moment centralization in most of the cases. Moreover, the moment centralization outperforms the gradient centralization in most of the cases. Based on the findings from the results, it is concluded the moment centralization can be used very effectively to train the deep CNN models with improved performance. It is also observed that the proposed method leads to shorter and smoother optimization trajectory. The future work includes the exploration of the proposed idea on different types of computer vision applications.
References
- [1] Basha, S.S., Ghosh, S., Babu, K.K., Dubey, S.R., Pulabaigari, V., Mukherjee, S.: Rccnet: An efficient convolutional neural network for histological routine colon cancer nuclei classification. In: 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV). pp. 1222–1227. IEEE (2018)
- [2] Bernstein, J., Wang, Y.X., Azizzadenesheli, K., Anandkumar, A.: signsgd: Compressed optimisation for non-convex problems. In: International Conference on Machine Learning. pp. 560–569 (2018)
- [3] Bottou, L.: Large-scale machine learning with stochastic gradient descent. In: Proceedings of the COMPSTAT, pp. 177–186 (2010)
- [4] Chen, Z., Badrinarayanan, V., Lee, C.Y., Rabinovich, A.: Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. In: International Conference on Machine Learning. pp. 794–803. PMLR (2018)
- [5] Choi, S., Kim, T., Jeong, M., Park, H., Kim, C.: Meta batch-instance normalization for generalizable person re-identification. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 3425–3435 (2021)
- [6] Dubey, S.R., Chakraborty, S., Roy, S.K., Mukherjee, S., Singh, S.K., Chaudhuri, B.B.: diffgrad: an optimization method for convolutional neural networks. IEEE transactions on neural networks and learning systems 31(11), 4500–4511 (2019)
- [7] Dubey, S., Basha, S., Singh, S., Chaudhuri, B.: Curvature injected adaptive momentum optimizer for convolutional neural networks. arXiv preprint arXiv:2109.12504 (2021)
- [8] Duchi, J., Hazan, E., Singer, Y.: Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research 12(Jul), 2121–2159 (2011)
- [9] He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 770–778 (2016)
- [10] Hinton, G., Srivastava, N., Swersky, K.: Neural networks for machine learning. Lecture 6a overview of mini-batch gradient descent course (2012)
- [11] Huang, H., Wang, C., Dong, B.: Nostalgic adam: Weighting more of the past gradients when designing the adaptive learning rate. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. pp. 2556–2562 (2019)
- [12] Ioffe, S., Szegedy, C.: Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: International conference on machine learning. pp. 448–456. PMLR (2015)
- [13] Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. In: International Conference on Learning Representations (2015)
- [14] Krizhevsky, A., Hinton, G., et al.: Learning multiple layers of features from tiny images. Tech Report (2009)
- [15] Krizhevsky, A., Sutskever, I., Hinton, G.E.: Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 25, 1097–1105 (2012)
- [16] Le, Y., Yang, X.: Tiny imagenet visual recognition challenge. CS 231N 7(7), 3 (2015)
- [17] LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature 521(7553), 436–444 (2015)
- [18] Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., Han, J.: On the variance of the adaptive learning rate and beyond. In: International Conference on Learning Representations (2019)
- [19] Repala, V.K., Dubey, S.R.: Dual cnn models for unsupervised monocular depth estimation. In: International Conference on Pattern Recognition and Machine Intelligence. pp. 209–217. Springer (2019)
- [20] Roy, S., Paoletti, M., Haut, J., Dubey, S., Kar, P., Plaza, A., Chaudhuri, B.: Angulargrad: A new optimization technique for angular convergence of convolutional neural networks. arXiv preprint arXiv:2105.10190 (2021)
- [21] Salimans, T., Kingma, D.P.: Weight normalization: A simple reparameterization to accelerate training of deep neural networks. Advances in neural information processing systems 29, 901–909 (2016)
- [22] Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. In: International Conference on Learning Representations (2015)
- [23] Singh, D., Singh, B.: Investigating the impact of data normalization on classification performance. Applied Soft Computing 97, 105524 (2020)
- [24] Srivastava, Y., Murali, V., Dubey, S.R.: Hard-mining loss based convolutional neural network for face recognition. In: International Conference on Computer Vision and Image Processing. pp. 70–80. Springer (2020)
- [25] Sutskever, I., Martens, J., Dahl, G., Hinton, G.: On the importance of initialization and momentum in deep learning. In: Proceedings of the International Conference on Machine Learning. pp. 1139–1147 (2013)
- [26] Yong, H., Huang, J., Hua, X., Zhang, L.: Gradient centralization: A new optimization technique for deep neural networks. In: European Conference on Computer Vision. pp. 635–652. Springer (2020)
- [27] Zhuang, J., Tang, T., Ding, Y., Tatikonda, S.C., Dvornek, N., Papademetris, X., Duncan, J.: Adabelief optimizer: Adapting stepsizes by the belief in observed gradients. Advances in Neural Information Processing Systems 33 (2020)