Molecular Impurities as a Realization of Anyons on the Two-Sphere

The study of quasiparticles with fractional statistics, called anyons, has been an active field of research in the past decades. This field has gained a lot of attention, due to the possible usage of these quasiparticles in quantum computation Kitaev (2003); Lloyd (2002); Freedman et al. (2003); Nayak et al. (2008). In contrast to bosons and fermions, anyons acquire a phase $e^{i\pi\alpha}$ under the exchange of two particles, where the statistics parameter $\alpha$ is not necessarily an integer. The integer cases $\alpha=0$ and $\alpha=1$ represent bosons and fermions, respectively. For non-integer $\alpha$, the transformation law $\Psi\rightarrow e^{i\pi\alpha}\Psi$ under the exchange of two particles, can only be realized by allowing the wave function $\Psi$ to be multivalued. The idea is that the multiple values keep book of the different possible ways the particles could “braid” around each other. Due to the triviality of the braid group in $3+1$ dimensions, anyons are a purely low-dimensional phenomenon.

Although anyons are predicted to be realized in the fractional quantum Hall effect (FQHE) Tsui et al. (1982); Laughlin (1983); Arovas et al. (1984); Thouless et al. (1982); Kane and Mele (2005); Fu et al. (2007); Haldane (1988); Lundholm and Rougerie (2016), they have not yet been unambiguously detected in experiment. Indeed there has been a recent upsurge in interest concerning the realization of anyons in experimentally feasible systems Cooper and Simon (2015); Zhang et al. (2014, 2015); Morampudi et al. (2017); Umucalılar et al. (2018); Correggi et al. (2019). For instance, it has been recently shown in Refs. Yakaboylu and Lemeshko (2018); Yakaboylu et al. (2020) how these quasiparticles emerge from impurities in standard condensed matter systems. Nevertheless, all these works focus on the particles moving on the two-dimensional plane, i.e., on $\mathbb{R}^{2}$. Since the theory of anyons and their statistical behavior are strongly dependent on the geometry and topology of the underlying space, investigations on curved spaces reveal novel features of quantum statistics Thouless and Wu (1985); Einarsson (1990, 1991); Pithis and Ruiz Euler (2015); Ouvry and Polychronakos (2019); Tononi and Salasnich (2019); Tononi et al. (2020); Polychronakos and Ouvry (2020). In particular, theoretical discussions for systems having various geometry and topology have widened our understanding of the FQHE  Haldane (1983); Laughlin (1983).

In the present Letter, we explore the possibility of emerging fractional statistics for particles restricted to move on the sphere, $\mathbb{S}^{2}$, instead of on the plane. We show that such quasiparticles naturally arise from a system of molecular impurities exchanging angular momentum with a many-particle bath. In the regime of low energies, we identify the spectrum of this system with that of anyons. This does not only allow us to realize anyons on the sphere, but also to open up various numerical approaches to investigate the spectrum of $N$ anyons on the sphere. To illustrate this, we present the spectrum of two anyons on the sphere in the presence of a Dirac monopole field, extending the recent result of Ref. Ouvry and Polychronakos (2019); Polychronakos and Ouvry (2020). Furthermore, the anyonic behavior of molecular impurities suggests that a novel type of exclusion principle holds, which concerns the alignment of the molecules, instead of the exchange of their actual position.

We start by considering a system of $N$ free anyons on the two-sphere. The Hamiltonian is given by the sum of the Laplacian of the $j$th particle on the sphere: $H_{\text{0}}=-\sum_{j=1}^{N}\nabla_{j}^{2}$, which acts on a multivalued wave function $\Psi$. By performing a singular gauge transformation, $\Psi\rightarrow e^{i\beta}\Psi$, one can get rid of the multivaluedness Wu (1984); Mund and Schrader (1993); Lee and Oh (1994); Oh (1996); Rao (2016) and the free anyon Hamiltonian on the sphere $H_{\text{0}}$ becomes equivalent to

which now acts on single valued bosonic (fermionic) wave functions. Here anyons are depicted as bosons (fermions) interacting with the magnetic gauge field $A$, which explains that the calculation of the anyonic spectra is very hard Lundholm (2017). Note that $A=\nabla\beta$ is an almost pure gauge field, up to the singularities of $\beta$, where the particles meet, and it can be found as the variational solution of the Chern-Simons (CS) Lagrangian $L_{\mathbb{S}^{2}}=\sum_{j}\left(A\cdot\dot{q}_{j}+A_{0}\right)-(4\pi\alpha)^{-1}\int_{\mathbb{S}^{2}}\mathrm{d}\Omega\ A\wedge\mathrm{d}A$, where $q_{j}$ is the position of the nonrelativistic point particle coupled to the CS field, $A_{0}$ the time component of the gauge field, and $\wedge$ the wedge product. For anyons on the plane, one can always find a single magnetic potential $A$ as a solution. However, due to the non trivial homology of $\mathbb{S}^{2}$, the CS Lagrangian on the sphere can only be solved in two different stereographic coordinate charts: north and south patches, $A^{N}$ and $A^{S}$. As they should be a single object in the overlap patch, we require them to be gauge equivalent. This equivalence is given by the Dirac quantization condition (DQC) $(N-1)\alpha\in\mathbb{Z}$ Lee and Oh (1994); Oh (1996).

In what follows, in order to simplify our expressions, we represent the stereographic coordinates $(x,y)$ as a complex number, $z=x+iy$. In these coordinates, we define the gauge transformation $F=e^{i\beta}$, with $\beta(z_{1},..,z_{N})=-i\alpha\underset{j<k}{\sum}\log\left(\frac{z_{j}-z_{k}}{|z_{j}-z_{k}|}\right)$. The connections (gauge fields) are $A_{\bar{z}_{j}}=iD_{\bar{z}_{j}}\beta=-\frac{\alpha(1+|z_{j}|^{2})}{2}\sum_{k\neq j}\left(\bar{z}_{j}-\bar{z}_{k}\right)^{-1}$ and $A_{z_{j}}=iD_{z_{j}}\beta=\frac{\alpha(1+|z_{j}|^{2})}{2}\sum_{k\neq j}\left(z_{j}-z_{k}\right)^{-1}$, where we encode the contribution from the metric on $\mathbb{S}^{2}$ in the differential operators $D_{\bar{z}_{j}}=(1+|z_{j}|^{2})\partial_{\bar{z}_{j}}$ and $D_{z_{j}}=(1+|z_{j}|^{2})\partial_{z_{j}}$ Comtet et al. (1992). In the language of connections, $F$ represents the holonomy of $A$, and it is discontinuous along the lines which connect the particles with the north (south) pole, usually called the Dirac lines. Without loss of generality, we consider the north pole, which corresponds to the choice of $z_{j}=\cot(\theta_{j}/2)\exp(i\varphi_{j})$, with spherical coordinates $\theta_{j}$ and $\varphi_{j}$. These lines represent the magnetic potential in the singular gauge, by assigning the particle an additional phase factor whenever it crosses them. The DQC makes sure that the Dirac lines are invisible, in the sense that one cannot distinguish between the theory where the lines run to the north pole and theories where they run to any other point. This means that our system is rotational invariant, up to gauge equivalences.

The anyon Hamiltonian in our stereographic coordinate system is written as

Direct calculations to investigate the spectra of $H_{\mathrm{anyon}}$ turn out to be problematic, when the spectrum is calculated from the bosonic end. This is due to that the matrix elements of $A_{z_{j}}A_{\bar{z}_{j}}$ for certain bosonic states are singular, which is similar to the case of anyons on the plane Yakaboylu et al. (2020). We can overcome this difficulty with the similarity transformation $H^{\prime}_{\mathrm{anyon}}=e^{\alpha\sum_{j<k}\log|z_{j}-z_{k}|}H_{\mathrm{anyon}}e^{-\alpha\sum_{j<k}\log|z_{j}-z_{k}|}$. The advantage is that one of the two magnetic potentials vanishes in this pseudo-gauge and the Hamiltonian simplifies to

where the non-zero magnetic potential is $A^{\prime}_{z_{j}}=2A_{z_{j}}$. Note that $H^{\prime}_{\mathrm{anyon}}$ is self-adjoint in a weighted $L^{2}$ space. As we discuss below, while the first form of the anyon Hamiltonian (2) allows us to realize anyons in natural quantum impurity setups, the Hamiltonian (3) provides powerful numerical techniques to calculate the spectra of anyons on the sphere within the simplified impurity models.

We will now consider a general impurity problem of $N$ bosonic or fermionic impurities on $\mathbb{S}^{2}$ interacting with some Fock space $\mathcal{F}$. Within the Bogoliubov-Fröhlich theory Fröhlich (1954); Bogolyubov (1947); Pitaevskii and Stringari (2016), the impurity Hamiltonian is

where $b_{v}^{\dagger},b_{v}$ are the bosonic creation and annihilation operators in $\mathcal{F}$, $\omega_{v}$ is the energy of the mode $v$, and $\lambda_{v}(z_{1},..,z_{N})$ and $\beta_{v}(z_{1},..,z_{N})$ describe the interaction of the impurities with the Fock space, depending on their coordinates $z_{1},..,z_{N}$. In the limit of $\omega_{v}\rightarrow\infty$ (the adiabatic limit), one can justify that the lowest spectrum of $H_{\mathrm{imp}}$ is described by the Born-Oppenheimer (BO) approximation; see Ref Yakaboylu et al. (2020) for an analysis of this assumption in the planar case. The projection of the Hamiltonian to the smaller Hilbert space manifests itself as a minimal coupling of the otherwise free particles with effective magnetic potentials $A_{z_{1}},..,A_{z_{N}}$ and a scalar potential $\Phi$.

Following Ref Yakaboylu et al. (2020), we first apply the transformation $S(z_{1},..,z_{N})=e^{-i\sum_{v}\beta_{v}b_{v}^{\dagger}b_{v}}$ to Eq. (4), and then project the transformed Hamiltonian onto the coherent state $\ket{\phi(z_{1},..,z_{N})}=e^{-\sum_{v}\frac{\lambda_{v}}{\omega_{v}}(b^{\dagger}_{v}-b_{v})}\ket{0}$. The emerging magnetic potential in complex coordinates is then given by

Let us consider the specific choice $\beta_{v}(z_{1},..,z_{N})=-ip_{v}\underset{j<k}{\sum}\log\left(\frac{z_{j}-z_{k}}{|z_{j}-z_{k}|}\right)$, which results in $A^{\mathrm{imp}}_{z_{j}}=\frac{\alpha(1+|z_{j}|^{2})}{2}\sum_{k\neq j}\left(z_{j}-z_{k}\right)^{-1}$ with $\alpha(z_{1},..,z_{N})=\sum_{v}p_{v}\left(\frac{\lambda_{v}}{\omega_{v}}\right)^{2}$. We thus see that $A^{\mathrm{imp}}_{\bar{z}_{j}}$ is the sought CS gauge field and obeys the DQC if $\alpha(z_{1},..,z_{N})$ is a constant and satisfies $(N-1)\alpha\in\mathbb{Z}$. We emphasize, however, that for the values of $\alpha$ which do not satisfy the DQC, the impurity Hamiltonian (4) is still well-defined. The only difference for these values is that the theory is no longer fully rotational invariant, but, instead, it is invariant under rotation around the $z$ axis. In other words, the Dirac lines, which emerge together with the statistical gauge field, are not invisible Park et al. (1994) and they puncture the sphere. These features have drastic effects on the physical realization of anyons on the sphere in terms of quantum impurities, in comparison to emergent anyons on the plane studied in Ref. Yakaboylu et al. (2020).

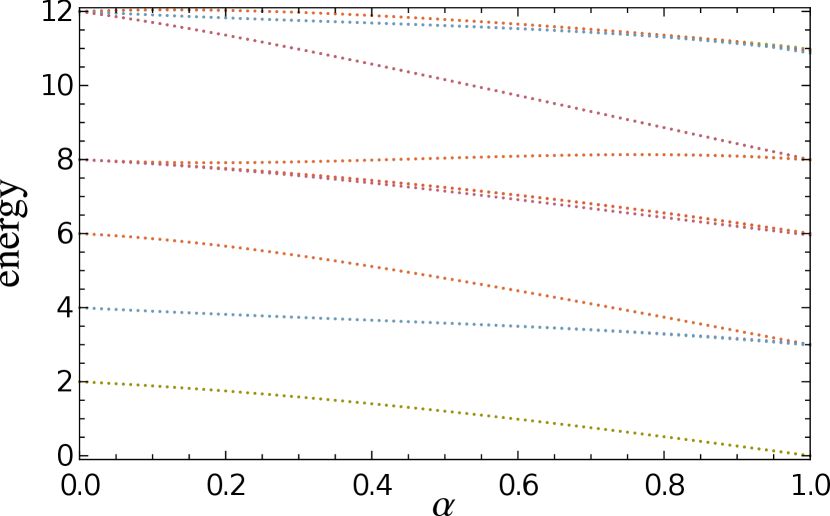
In general, the impurity Hamiltonian (4) corresponds to interacting anyons due the presence of the scalar potential $\Phi$. An impurity Hamiltonian whose lowest-energy spectrum is governed by the anyon Hamiltonian in the pseudo-gauge (3), however, describes free anyons, as the scalar potential vanishes with $A_{\bar{z}}=0$. Although such an impurity Hamiltonian is not Hermitian and may be harder to realize experimentally, considered as a toy model its non-Hermiticity is harmless for our purposes and it opens up simple numerical approaches to calculate the spectra of anyons on the sphere.

Our numerical tools work for an arbitrary number of particles. Nevertheless, we will here study only the two-anyon case, since the computational effort strongly scales with the number of particles. Furthermore, we investigate impurities interacting with a Dirac monopole field $B$. This allows us to investigate the spectrum for all values of $\alpha$, as the DQC in the presence of a Dirac monopole field is $2B-(N-1)\alpha\in\mathbb{Z}$ Ouvry and Polychronakos (2019); Polychronakos and Ouvry (2020). Accordingly, we consider the following simple model

where $H_{B}=H_{0}+\sum^{2}_{j=1}A^{B}_{z_{j}}D_{\bar{z}_{j}}$ describes the bosonic or fermionic particles interacting with the Dirac monopole field $B$ generated by the gauge field $A^{B}_{z_{j}}=2B\bar{z}_{j}$, $p$ is an integer, and we subtracted the vacuum energy, $-\omega\alpha/p$, of the pure Fock space part of the Hamiltonian.

One could calculate the lowest spectrum of $H^{\prime}_{\mathrm{imp}}$ by diagonalizing the matrix $\bra{S(A);n}H^{\prime}_{\mathrm{imp}}\ket{S^{\prime}(A^{\prime});n^{\prime}}$, where $\ket{S(A)}=\ket{Y_{l_{1},m_{1}}\otimes_{S(A)}Y_{l_{2},m_{2}}}$ are the impurity basis with $Y_{l,m}$ being the spherical harmonics, $\otimes_{S(A)}$ the (anti-)symmetric tensor product, and $\ket{n}$ the $n$-particle state in the Fock space. Instead of this direct diagonalization technique, we first diagonalize the Fock space part of the Hamiltonian with the displacement operator. The anyon Hamiltonian (3) in the presence of a Dirac monopole field, which emerges in the limit of $\omega\to\infty$, is, then, given by

see Supplemental Material for the derivation. We underline that a similar form of the Hamiltonian (7) for anyons on the plane has been previously introduced in Ref. Yakaboylu et al. (2020), where the second term of the right hand side was written in terms of composite bosons/fermions for an even integer $p$. Extending this approach we use here Bose-Fermi mixtures which enable us to set $p=1$. Within such a simple choice Eq. (7) can be written as the following matrix equation

where the elements of the matrices are given by $E_{\mathrm{bos}}=\bra{S}H_{0}\ket{S^{\prime}}$, $E_{\mathrm{fer}}=\bra{A}H_{0}\ket{A^{\prime}}$, $W_{S}=\bra{S}\sum^{2}_{j=1}\bar{z}_{j}D_{\bar{z}_{j}}\ket{S^{\prime}}$, and $Z^{-1}=\bra{S}z_{1}-z_{2}\ket{A}$. As the latter two terms are straightforward to calculate numerically, and the matrix $Z$ can be obtained by taking the (pseudo)inverse of $Z^{-1}$, Eq. (8) opens up a powerful route to calculate the anyonic spectrum. The spectrum from the fermionic end in terms of the relative statistics parameter can be calculated simply with the replacement of the basis $\ket{S(A)}\to\ket{A(S)}$ in Eq. (8).

As an example, we compute the eigenvalues for $\alpha$ ranging from $0$ to $1$. For an easier comparison with the result existing in Ref. Polychronakos and Ouvry (2020), we calculate the spectrum from the fermionic end. The result presented in Fig. 1 is consistent with the one shown in Ref. Polychronakos and Ouvry (2020), where the spectrum was calculated only for the subset of energy levels with unit total angular momentum.

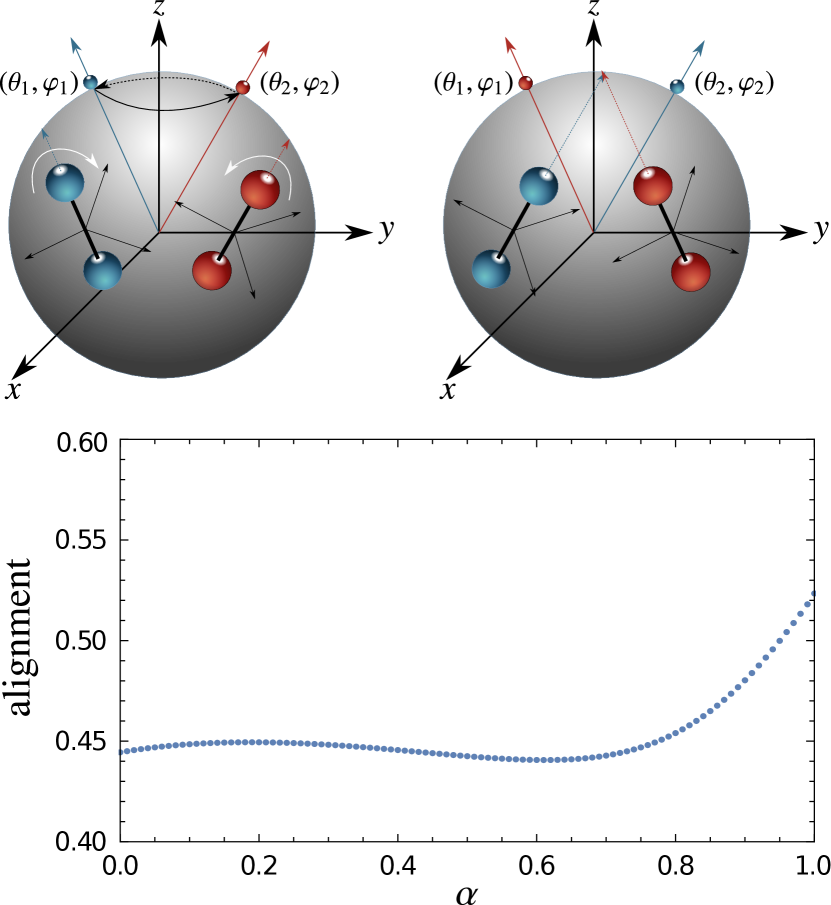
The general form of the impurity Hamiltonian (4) allow us also to physically realize anyons on the sphere in terms of quantum impurities. The kinetic energy of the particles on the sphere, which is given by the Laplacian, $-\left(D_{z_{j}}-\bar{z}_{j}\right)D_{\bar{z}_{j}}$, can be realized as the angular momentum operator $\boldsymbol{L}_{j}^{2}$. The latter can be considered as the Hamiltonian of linear molecules, which enables us to map rotation of molecules to motion of point particles on the sphere. Consequently, instead of point-like impurities, which have been considered for the planar case in Ref. Yakaboylu et al. (2020), we consider here linear molecules and explore the angular momentum exchange with the bath. Such a realization exposes a novel correlation between molecular impurities. Specifically, the exchange of the particles on the sphere corresponds to a change in the alignment of the molecules, but not the exchange of the molecules themselves, see Fig. 2 (Top). Therefore, the emerging statistical interaction manifests itself in the alignment of molecules.

To illustrate this in a transparent way, we consider the simple impurity Hamiltonian (6) in the absence of the Dirac monopole. We investigate the alignment $\langle\left(\cos\theta_{1}-\cos\theta_{2}\right)^{2}\rangle$ as a function of the statistics parameter for two molecules. In Fig. 2 (Bottom) we present the alignment for the ground state, which is obtained from Eq. (8) for the case of $B=0$. We note that the Hamiltonian is still well-defined for the values of $\alpha$ which do not satisfy the DQC as we discussed before. Thus, the alignment of the molecules could be used as an experimental measure of the statistics parameter. Such a measurement can be performed, for instance, within the technique of laser-induced molecular alignment Friedrich and Herschbach (1995); Lemeshko et al. (2013). Further discussion of the alignment of molecules as a consequence of the statistical interaction will be the subject of future work.

A physical realization of the interaction between the molecules and a bath is also natural in the physics of impurities. Indeed, it was shown that the molecular impurities rotating in superfluid helium can be described within an impurity problem Schmidt and Lemeshko (2015, 2016); Lemeshko and Schmidt (2016). The resulting quasiparticle, which is called the angulon, represents a quantum impurity exchanging orbital angular momentum with a bath of quantum oscillators, and serves as a reliable model for the rotation of molecules in superfluids Lemeshko (2017). Therefore, we consider the following angulon Hamiltonian Yakaboylu et al. (2018); Li et al. (2019)

where $\hat{b}^{\dagger}_{k,l,m}$ and $\hat{b}_{k,l,m}$ are the bosonic creation and annihilation operators written in the spherical basis Schmidt and Lemeshko (2015), $q_{i}=(\theta_{i},\varphi_{i})$ are the angular coordinates representing the molecular rotation of the $i$-th molecule, $V$ is a confining potential, and H.c. stands for Hermitian conjugate. Note that the coupling terms might depend on the intermolecular distance, as well. For heavy molecules the BO approximation can be justified with a gapped dispersion $\omega_{k,l,m}$. Furthermore, following our previous reasoning and Eq. (5), if the impurity-bath coupling satisfies the relation $i\sum_{k,l,m}\left(\frac{\lambda_{k,l,m}}{\omega_{k,l,m}}\right)^{2}D_{z_{j}}\beta_{k,l,m}=A_{z_{j}}$, the lowest-energy spectrum of the two linear molecules immersed in the bath coincide with the spectrum of two anyons on the sphere. In principle, such an interaction is feasible with the state-of-art techniques in the physics of superfluid helium as well as ultracold molecules.

In order to present a simple and intuitive realization, we first neglect the intermolecular distance. This enables us to define the interaction term simply as $\lambda_{k,l,m}(q_{1},q_{2})e^{-i\beta_{k,l,m}(q_{1},q_{2})}=u_{k,l}\sum_{j=1}^{2}Y_{l,m}(q_{j})$ with the impurity-bath coupling $u_{k,l}$. For a physical configuration, we consider molecular impurities in superfluid helium nanodroplets. The corresponding coupling captures the details of the molecule-helium interaction. For the form of the coupling and the relevant parameters we refer the reader to Supplemental Material and Ref. Cherepanov and Lemeshko (2017); Cherepanov et al. (2019), where the model has been used in order to describe angulon instabilities and oscillations observed in the experiment. Furthermore, the dispersion relation of superfluid helium allows us to achieve a gapped dispersion at the roton minimum $\omega_{r}$ Lemeshko and Schmidt (2016). Following the experimental realization proposed in Ref. Yakaboylu et al. (2020) for anyons on the plane, we also couple the impurities to an additional constant magnetic field and rotate the whole system at the cyclotron frequency $\Omega$, which breaks time reversal symmetry so that anyons can emerge on the lowest-energy spectrum.

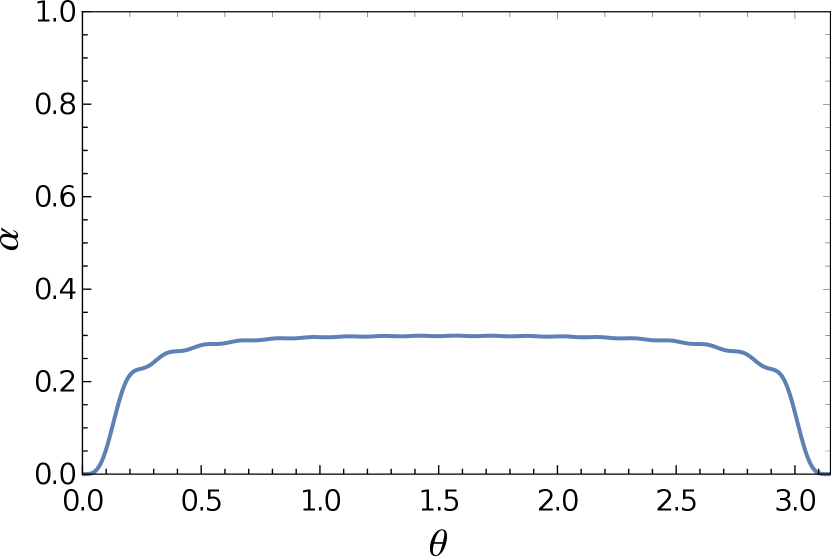
A priori, the emerging statistics parameter $\alpha=\alpha(\theta)$ depends on the relative angle $\theta$ between the points $q_{1}$ and $q_{2}$. However, with a careful choice of the model parameters, $\alpha$ becomes approximately constant with the condition $\Omega\,l_{\text{max}}/\omega_{r}\gg 1$, see Supplemental Material. The condition imposes that the cyclotron frequency should be at the order of the roton minimum. This implies that molecular impurities should be subjected to a strong magnetic field at the order of $M\omega_{r}$ with $M$ being the mass of the molecules. The $\theta$ dependence of $\alpha$ is demonstrated in Fig. 3. In general, the statistics parameter does not satisfy the DQC. Therefore, the molecular impurities correspond to anyons interacting with the magnetic potential depicted by the Dirac lines, with broken rotational symmetry. We also note that with the additional confining potential, $V$, the particles are confined to one of the half spheres so that the statistics parameter becomes accessible to the experiment.

Thus, we see that a system of two linear molecules exchanging angular momentum with a many-particle bath can give rise to a system of quasiparticles with anyonic statistics, and can be realized by considering molecular impurities in superfluid helium droplets. It would be interesting to continue this approach and investigate, whether one can generalize the results above e.g. to non-Abelian Chern-Simons particles with the help of a higher order Born-Oppenheimer approximation.

in 1,…,5 See pages \x of SupplementalMaterial12.pdf