Moiré band theory for M-valley twisted transition metal dichalcogenides

Introduction— Moiré materials, artificial two-dimensional (2D) crystals with large lattice constants created by forming moiré patterns in layered 2D materials, have emerged in recent years [1] as a successful platform for experimental and theoretical discovery. Moiré materials are strictly speaking quasicrystals, but when the constituent layers are semiconductors or semimetals the electronic states near the Fermi energy are accurately described by emergent Hamiltonians that have only the moiré periodicity [2, 3]. Because their effective Hamiltonians are periodic, moiré materials support low-energy Bloch bands, which can have a small bandwidth and be topologically nontrivial. Moreover, the large lattice constants allow the number of electrons per moiré unit cell to be tuned over large ranges with electrical gates - effectively moving through an artificial periodic table without chemical doping. Materials of this type therefore serve as flexible tunable quantum systems in which strong-correlation and topological electron physics can be studied, often together.

The moiré materials that have been studied experimentally to date are almost exclusively formed from either graphene or group VI transition metal dichalcogenide (TMD) 2D layers [1, 4]. Accordingly, there has been a focus on developing theoretical models to describe the low-energy electronic states in these specific materials [5, 2, 6, 7, 8, 9, 10, 11]. In generic weakly coupled multilayer materials, the electronic states near the Fermi energy are formed from the Bloch states near the Fermi energy of the constituent crystalline layers, which in graphene and group VI TMDs usually have crystal momenta near $K$ or $\Gamma$ points in their respective triangular lattice Brillouin zones (BZ). In moiré materials, Bloch states with crystal momenta that are near distinct low-energy momenta (the set of which we denote $\mathcal{K}\subset\text{BZ}$) decouple and separate periodic models emerge, one associated with each low-energy point (valley) $\bm{k}_{*}\in\mathcal{K}$ [3]. Most attention has been given to developing models for $K$-valley materials. Since there are two inequivalent $K$-points related by time-reversal symmetry in triangular lattices, the valley-projected moiré band Hamiltonians break time-reversal symmetry. This property is the root cause [12, 13, 14, 9, 15, 16] of the anomalous Hall effect and magnetic circular dichroism, and of the integer and fractional quantum anomalous Hall effects seen [17, 18, 19, 20, 21, 22, 23, 24] in these materials.

In this Letter, we propose that bilayers of group IV and IVB TMDs with small twist angles or differences in lattice constant are realistic candidate moiré materials and derive moiré band models for their low-energy conduction states using Hafnium diselenide (HfS₂) twisted homobilayers as a representative example. In HfS₂, the valence band maximum (VBM) is at the $\Gamma$ point and the conduction band minima (CBM) are at the three inequivalent $M$ points [25, 26] in both bulk and single-layer limits. We focus here on the CBM states in homobilayers and use Wannier function (WF) [27] processed density function theory (DFT) [28] to construct the moiré band model. The current model applies to HfS₂ twisted homobilayers with $n$-type electrostatic doping. Generalizations to other materials, to heterobilayers, and to multilayers are straightforward although the symmetry considerations discussed below are altered. We find that the valley-projected moiré bands are time-reversal invariant, implying that they cannot support an anomalous Hall effect or magnetic circular dichroism, and that they are strongly anisotropic. Thus, interaction-induced spontaneous valley polarization will manifest experimentally by anisotropy in transport.

Moiré band models via the local displacement scheme— The local displacement approach [3] is an approximation scheme that can be used to construct accurate periodic effective models of the low-energy electronic states of semiconductor bilayers that have small relative twist angles ($\theta$) and/or lattice constant ratios ($\lambda$) close to one, and weak coupling between layers. This approach employs a family of Bloch Hamiltonians $H(\bm{\mathsf{d}})$ of (fictitious) crystalline insulator bilayers – constructed as aligned stacks of the quasicrystal’s constituent layers, but with lattice constants (of the top layer, for instance) that are artificially adjusted (if necessary) so that the top and bottom layers are characterized by the same Bravais lattice $\Lambda$ ¹¹1For every $\bm{\mathsf{d}}\in\mathbb{R}^{2}$ the Bloch Hamiltonian $H(\bm{r},\bm{p}(\bm{r});\bm{\mathsf{d}})$ of the bilayer is $\Lambda$-periodic in $\bm{r}$ where $\Lambda$ is the Bravais lattice of the (arbitrarily chosen) bottom layer. The vertical separation between layers is fixed at each $\bm{\mathsf{d}}$ by minimizing energy. Therefore, we can (and will) choose the real-space Bravais lattice to be independent of $\bm{\mathsf{d}}$. The same is true of the unit cell $\Omega_{uc}$ (BZ) of $\Lambda$ ($\Lambda^{*}$). – parameterized by an in-plane relative displacement $\bm{\mathsf{d}}\in\mathbb{R}^{2}$ between layers. If $H(\bm{\mathsf{d}})$ has time-reversal symmetry, then a set of WFs, denoted by $\ket{W_{I,\bm{R}}(\bm{\mathsf{d}})}$, can be constructed [30] for the set of isolated energy bands just above (below) the band gap at charge neutrality ²²2That $H(\bm{\mathsf{d}})$ has time-reversal symmetry is not a necessary criterion, but is valid in HfS₂ bilayers and simplifies our discussion. We also assume that at each $\bm{k}\in\text{BZ}$ the set of isolated conduction (valence) bands remains energetically isolated from all other bands as $\bm{\mathsf{d}}$ is varied. Again, this is not necessary, but is convenient and valid in HfS₂ bilayers.. We will assume that these WFs can be chosen such that the label $I$ decomposes into layer and orbital labels $I=(l,\alpha_{l})$, where $l=\mathfrak{b}$ and $l=\mathfrak{t}$ identify bottom and top layers, respectively; indeed, the identification of layer as a degree of freedom is essential and the main advantage of a Wannier-based approach. This type of Wannier construction is natural in weakly coupled bilayers and succeeds in HfS₂ bilayers. We denote the $\bm{\mathsf{d}}$-dependent WF matrix elements by $\bra{W_{(l,\alpha_{l}),\bm{R}}(\bm{\mathsf{d}})}H(\bm{\mathsf{d}})\ket{W_{(l^{\prime},\beta_{l^{\prime}}),\bm{R}^{\prime}}(\bm{\mathsf{d}})}$ and their Bloch Fourier transforms by

$\displaystyle H^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{\mathsf{d}})\equiv\bra{\tilde{\psi}_{(l,\alpha_{l}),\bm{k}}(\bm{\mathsf{d}})}H(\bm{\mathsf{d}})\ket{\tilde{\psi}_{(l^{\prime},\beta_{l^{\prime}}),\bm{k}}(\bm{\mathsf{d}})}.$

(1)

Here $\ket{\tilde{\psi}_{(l,\alpha_{l}),\bm{k}}(\bm{\mathsf{d}})}$ are Bloch-type vectors defined by the WFs and are smooth over the BZ and $\Lambda^{*}$-periodic in $\bm{k}$. These momentum-space Wannier matrix elements evaluated at valley-center momenta $\bm{k}_{*}\in\mathcal{K}$ provide the microscopic data needed to construct the moiré band models.

We assume that the WFs track smoothly with $\bm{\mathsf{d}}$ so that $W_{(l,\alpha),\bm{R}}(\bm{r};\bm{\mathsf{d}}+\bm{\mathsf{a}})=W_{(l,\alpha),\bm{R}}(\bm{r}-\delta_{l,\mathfrak{t}}\bm{\mathsf{a}};\bm{\mathsf{d}})$ after relative translation of layers by $\bm{\mathsf{a}}\in\mathbb{R}^{2}$. It follows that

$\displaystyle\ket{\tilde{\psi}_{(l,\alpha),\bm{k}}(\bm{\mathsf{d}}+\bm{\mathsf{a}})}\approx e^{-i\delta_{l,\mathfrak{t}}\bm{k}\cdot\bm{\mathsf{a}}}\ket{\tilde{\psi}_{(l,\alpha),\bm{k}}(\bm{\mathsf{d}})},$

(2)

and therefore that

$\displaystyle\bar{H}^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{\mathsf{d}})\equiv e^{i\bm{k}\cdot(\delta_{l^{\prime},\mathfrak{t}}-\delta_{l,\mathfrak{t}})\bm{\mathsf{d}}}H^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{\mathsf{d}})$

(3)

is $\Lambda$-periodic in $\bm{\mathsf{d}}$ and admits a Fourier series expansion with coefficients given by

$\displaystyle\bar{H}^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{G})=\frac{1}{\Omega_{uc}}\int_{\Omega_{uc}}e^{i\bm{G}\cdot\bm{\mathsf{d}}}\bar{H}^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{\mathsf{d}})\;d\bm{\mathsf{d}}$

(4)

for $\bm{G}\in\Lambda^{*}$.

There are two elements to the local displacement scheme. First we replace $\bm{\mathsf{d}}$ in each WF matrix element by $\bm{d}(\bm{R})\equiv\lambda R^{z}_{\theta}(\bm{R})-\bm{R}$, where $\bm{R}$ is the lattice site of a WF in that matrix element and $\bm{d}(\bm{R})$ is its local displacement ³³3The quasicrystal has top (bottom) layer Bravais lattice $\Lambda_{t}$ ($\Lambda_{b}$) and we arbitrarily choose $\Lambda\equiv\Lambda_{b}$. By definition, $\Lambda_{t}=\lambda R_{\theta}^{z}(\Lambda_{b})$ and the operator $\bm{d}:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ encodes the local displacement of bottom layer lattice site $\bm{R}\in\Lambda_{b}$ via $\lambda R^{z}_{\theta}(\bm{R})\equiv\big{(}\bm{R}+\bm{d}(\bm{R})\big{)}\in\Lambda_{t}$. for twist angle $\theta$ and lattice scaling factor $\lambda$ [3]. $R^{z}_{\theta}:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ is a linear function of position that encodes counter-clockwise rotation by $\theta$ about the surface-normal direction $\hat{\bm{e}}_{z}$. Note that this replacement coarse grains position from the lattice points $\Lambda$ to continuous space. At this stage we are neglecting in-plane strain relaxation relative to rigid rotation, which can be important, but this correction can be conveniently added, as we discuss below. Secondly we replace $\bm{k}$ in the $l=l^{\prime}$, $\bm{G}\neq\bm{0}$ and the $l\neq l^{\prime}$ terms by their value at the nearby $\bm{k}_{*}\in\mathcal{K}$ – the wavevector of the CBM at the center of the valley of interest. Both elements are justified [3] for sufficiently long moiré periods because the $\bm{k}$ dependence of the Hamiltonian at each $\bm{\mathsf{d}}$ occurs on the scale of $\Lambda$.

With these approximations, the local displacement (LD) Hamiltonian $H_{\text{LD}}(\bm{k}_{*})$ for valley $\bm{k}_{*}\in\mathcal{K}$ acts in an envelope function space [33] that is the direct product of layer, Wannier orbital (within each layer), and continuous position subspaces, and its eigenstates are spinors with layer and Wannier orbital indices. Using a momentum-space representation for the position degree of freedom one obtains

	$\displaystyle\bra{l,\alpha_{l},\bm{k}}H_{\text{LD}}(\bm{k}_{*})\ket{l^{\prime},\beta_{l^{\prime}},\bm{k}^{\prime}}$
	$\displaystyle=\delta_{l,l^{\prime}}\Big{(}\delta\big{(}\bm{k}^{\prime}-\bm{k}\big{)}\bar{H}^{l,\alpha_{l}}_{l,\beta_{l}}(\bm{k};\bm{G}=\bm{0})$
	$\displaystyle\qquad\qquad+\sum_{\bm{G}\in\Lambda^{*}\setminus\{\bm{0}\}}\delta\big{(}\bm{k}^{\prime}-\bm{k}-\tilde{\bm{G}}\big{)}\bar{H}^{l,\alpha_{l}}_{l,\beta_{l}}(\bm{k}_{*};\bm{G})\Big{)}$
	$\displaystyle+(1-\delta_{l,l^{\prime}})\sum_{\bm{G}\in\Lambda^{*}}\delta\big{(}\bm{k}^{\prime}-\bm{k}+(-1)^{l,\mathfrak{t}}\tilde{\bm{k}}_{*}-\tilde{\bm{G}}\big{)}\bar{H}^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k}_{*};\bm{G}).$		(5)

Here $\bm{G}\in\Lambda^{*}$, $\tilde{\bm{G}}\equiv\lambda R^{z}_{-\theta}(\bm{G})-\bm{G}$ is a vector in the moiré reciprocal lattice $\Lambda_{\text{M}}^{*}$ ⁴⁴4The set $\Lambda_{\text{M}}^{*}\equiv\{\lambda R_{-\theta}(\bm{G})-\bm{G}:\bm{G}\in\Lambda^{*}\}\subset\mathbb{R}^{2}$ equipped with addition is a Bravais lattice. This is called the moiré reciprocal lattice and its dual, the moiré lattice, is given by $\Lambda_{\text{M}}=\{\bm{r}\in\mathbb{R}^{2}:\bm{d}(\bm{\mathfrak{r}})\in\Lambda\}$., $\tilde{\bm{k}}_{*}\equiv\lambda R^{z}_{-\theta}(\bm{k}_{*})-\bm{k}_{*}$, and $\bm{k},\bm{k}^{\prime}$ are extended from BZ to $\mathbb{R}^{2}$. Because the layer separations in the van der Waals crystals from which moiré materials can be successfully fabricated are always much larger than the lattice constants within layers, sizable values for $\bar{H}^{l,\alpha_{l}}_{l^{\prime},\beta_{l^{\prime}}}(\bm{k};\bm{G})$ are expected for $\bm{G}$ only in the first few shells of $\Lambda^{*}$, implying that the lowest energy moiré bands involve pockets of momentum space that are small compared to the Brillouin zone size. This property justifies the valley-decoupling that occurs in the local displacement approximation and also justifies an expansion of $\bar{H}^{l,\alpha_{l}}_{l,\beta_{l}}(\bm{k};\bm{G}=\bm{0})$ around the CBM $\bm{k}_{*}$ that is parameterized by an effective mass tensor. A key property of $M$-valley TMDs is that their effective mass tensors are anisotropic.

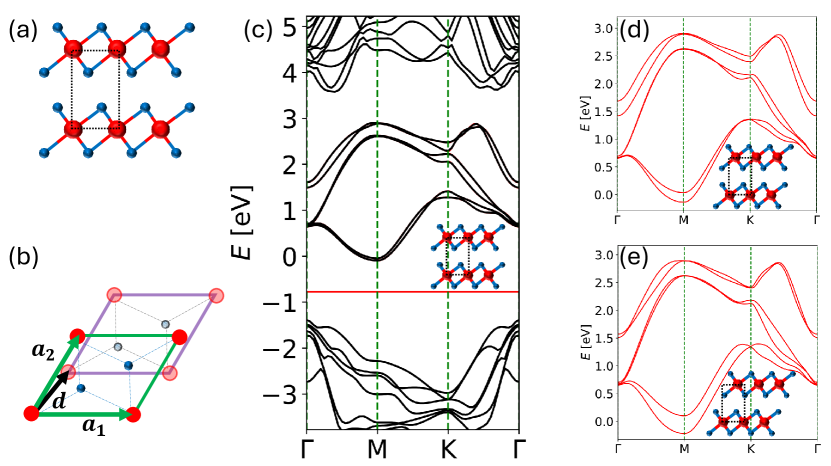
$\bm{\mathsf{d}}$-dependence of HfS₂ crystalline bilayer bands— As illustrated in Fig. 1, monolayer HfS₂ has a triangular lattice $\Lambda$ with Hf ions located at Bravais lattice sites around which S ions form octahedral cages [25]. Trigonal monolayers and AA-stacked ⁵⁵5By AA-stacked we mean that top and bottom layer have identical orientation. bilayers (with any $\bm{\mathsf{d}}$) have a center of inversion symmetry that leads to a Kramers spin-degeneracy at each $\bm{k}\in\text{BZ}$. For HfS₂ bilayers, we find that spin-orbit interactions have negligible impact on the six spin-degenerate low-energy conduction bands ⁶⁶6DFT bandstructure calculations for HfS₂ monolayers that employ different pseudo-potentials can result in more significant, albeit still small, SOI in the low-energy conduction bands (see, e.g., Fig. 9 of Ref. [44]). Ultimately, what is most relevant for our study is the energetics of the doubly-degenerate lowest energy conduction bands near M, and for these states SOI has almost no impact., which remain energetically isolated from all other bands throughout the BZ and vary weakly with $\bm{\mathsf{d}}$ (see Supplementary Material and Fig. 1), demonstrating the weak interlayer coupling needed for the accuracy of local displacement moiré band models. Within each $s_{z}$ spin sector, the low-energy conduction bands are accurately described throughout the BZ by a six-orbital tight-binding Hamiltonian $H_{\text{TB}}(\bm{\mathsf{d}})$. The conduction band minima occur near the three $M$ points ($\mathcal{K}\equiv\{\bm{M}_{1},\bm{M}_{2},\bm{M}_{3}\}$).

In principle, we could construct a moiré band model with three orbitals plus spin in each layer by retaining all orbitals needed for the Wanner processing. We find however that near each $\bm{M}_{\nu}\in\mathcal{K}$, the two lowest energy bands are separated from the other four bands retained in the tight-binding model by $\approx 2$ eV. This motivates the construction of a simpler and more physically transparent model with only layer and spin degrees of freedom that still accounts for the higher energy bands perturbatively. To do so we re-express the $6\times 6$ matrix $\mathcal{H}_{\text{TB}}(\bm{k};\bm{\mathsf{d}})$, which has elements $H^{l,\alpha_{l},s_{z}}_{l^{\prime},\beta_{l^{\prime}},s_{z}}(\bm{k};\bm{\mathsf{d}})$, in the basis of the Bloch energy eigenvectors at the relevant valley center $\bm{M}_{\nu}\in\mathcal{K}$ and at an arbitrary reference displacement $\bm{\mathsf{d}}_{0}=\bm{0}$. Rewritten in this basis, $\mathcal{H}_{\text{TB}}(\bm{k};\bm{\mathsf{d}})$ takes the form

$\displaystyle\mathcal{H}_{\bm{M}_{\nu}}(\bm{k};\bm{\mathsf{d}})=\begin{pmatrix}\mathcal{H}_{\text{lowE}}(\bm{k};\bm{\mathsf{d}})&T(\bm{k};\bm{\mathsf{d}})\\ T^{\dagger}(\bm{k};\bm{\mathsf{d}})&\mathcal{H}_{\text{highE}}(\bm{k};\bm{\mathsf{d}})\end{pmatrix},$

(6)

where $\mathcal{H}_{\text{lowE}}(\bm{k};\bm{\mathsf{d}})$ is a $2\times 2$ matrix, $\mathcal{H}_{\text{highE}}(\bm{k};\bm{\mathsf{d}})$ is a $4\times 4$ matrix and $T(\bm{k};\bm{\mathsf{d}})$ is a $2\times 4$ matrix. $\mathcal{H}_{\text{lowE}}(\bm{k};\bm{\mathsf{d}})$ is the low-energy sector (of the isolated low-energy conduction bands near $\bm{M}_{\nu}$) and $\mathcal{H}_{\text{highE}}(\bm{k};\bm{\mathsf{d}})$ is the high-energy sector. Defining the zero of energy at the low-energy sector eigenvalues (which are approximately equal), to second-order in perturbation theory ⁷⁷7See, e.g., Appendix B of Ref. [45] and Ref. [46]. we obtain

$\displaystyle\mathcal{H}^{\bm{M}_{\nu}}_{\text{eff}}(\bm{k};\bm{\mathsf{d}})$

$\displaystyle=\mathcal{H}_{\text{lowE}}(\bm{k};\bm{\mathsf{d}})-T^{\dagger}(\bm{k};\bm{\mathsf{d}})\mathcal{H}_{\text{highE}}^{-1}(\bm{k};\bm{\mathsf{d}})T(\bm{k};\bm{\mathsf{d}}).$

(7)

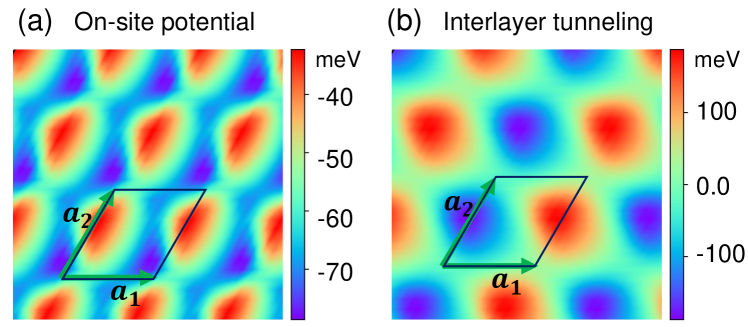
When we diagonalize the matrix (7), we find that its eigenvectors are even and odd combinations of Bloch-type states in top and bottom layers at all values of $\bm{\mathsf{d}}$: $\ket{\phi^{\bm{M}_{\nu}}_{\pm,\bm{k}}(\bm{\mathsf{d}})}=\ket{\tilde{\phi}^{\bm{M}_{\nu}}_{b,\bm{k}}(\bm{\mathsf{d}})}\mp\ket{\tilde{\phi}^{\bm{M}_{\nu}}_{t,\bm{k}}(\bm{\mathsf{d}})}$, where $\ket{\tilde{\phi}^{\bm{M}_{\nu}}_{l,\bm{k}}(\bm{\mathsf{d}})}=\sum_{\alpha=1}^{3}C^{\bm{M}_{\nu}}_{\alpha}(\bm{k},\bm{\mathsf{d}})\ket{\tilde{\psi}_{(l,\alpha,s_{z}),\bm{M}_{\nu}}(\bm{\mathsf{d}}_{0})}$. When transformed back to a layer representation, the average of the eigenvalues can be interpreted as potentials that are identical in each layer and half the difference as a real tunneling amplitude between layers. These properties are expected since each $\bm{M}_{\nu}\in\mathcal{K}$ is time-reversal invariant and the system has inversion symmetry which implies that top and bottom intralayer potentials are identical and interlayer tunneling amplitude is real-valued. The $\bm{\mathsf{d}}$-dependence of the intralayer potential $\Delta_{l}(\bm{M}_{\nu};\bm{\mathsf{d}})$ and of the interlayer tunneling $\Delta_{T}(\bm{M}_{\nu};\bm{\mathsf{d}})$ for valley $\bm{M}_{1}=\bm{b}_{1}/2$ is plotted in Fig. 2. In Table 1 we list all sizable Fourier components of $\Delta_{l}(\bm{M}_{1};\bm{\mathsf{d}})$ and of $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};\bm{\mathsf{d}})\equiv e^{i\bm{M}_{1}\cdot\bm{\mathsf{d}}}\Delta_{T}(\bm{M}_{1};\bm{\mathsf{d}})$ for top-to-bottom tunneling (recall Eq. (3)). As anticipated only a small number of parameters are needed to define the moiré band model for valley $\bm{M}_{1}$. The valley-projected Hamiltonians for other valleys are related to that for valley $\bm{M}_{1}$ by the $C_{3}$ rotational symmetry of HfS₂, as we now describe.

The spatial symmetries of HfS₂ bilayers constrain the form of the Hamiltonian matrix elements $H^{i,\alpha_{i},s_{z}}_{j,\beta_{j},s_{z}}(\bm{k};\bm{\mathsf{d}})$ and therefore also of the effective masses $m_{a,l}^{\bm{M}_{\nu}}$ (defined precisely below), $\Delta_{l}(\bm{M}_{\nu};\bm{\mathsf{d}})$, and $\Delta_{T}(\bm{M}_{\nu};\bm{\mathsf{d}})$. In bulk, each Hf ion location in 1T-HfS₂ has $D_{3d}$ point group symmetry. This point group symmetry is inherited in the bilayer with $\bm{\mathsf{d}}=\bm{0}$ (albeit no longer about Hf sites) and, in fact, its elements have counterparts in bilayers with general $\bm{\mathsf{d}}$, namely: (a) a spatial inversion symmetry, which implies that the effective masses are layer independent ($m_{a,\mathfrak{b}}^{\bm{M}_{\nu}}=m_{a,\mathfrak{t}}^{\bm{M}_{\nu}}$), the potentials are layer independent ($\Delta_{\mathfrak{b}}(\bm{M}_{\nu};\bm{\mathsf{d}})=\Delta_{\mathfrak{t}}(\bm{M}_{\nu};\bm{\mathsf{d}})$), and the tunneling is real ($\Delta_{T}(\bm{M}_{\nu};\bm{\mathsf{d}})=\Delta_{T}^{*}(\bm{M}_{\nu};\bm{\mathsf{d}})$). (Here and below we use that $\bm{M}_{\nu}$ is equivalent to $-\bm{M}_{\nu}$); (b) a symmetry that involves the rotation of the top layer by $\Theta=2\pi n/3$ for $n\in\mathbb{Z}$ about the surface-normal $\hat{\bm{e}}_{z}$ relative to the bottom layer, which implies $m_{a,l}^{\bm{M}_{\nu}}=m_{a,l}^{R^{z}_{\Theta}(\bm{M}_{\nu})}$ ⁸⁸8“$\parallel$” and “$\perp$” on LHS and RHS are with respect to $\bm{M}_{\nu}$ and $R^{z}_{\Theta}(\bm{M}_{\nu})$, respectively. and $\Delta_{\mu}(\bm{M}_{\nu};\bm{\mathsf{d}})=\Delta_{\mu}(R^{z}_{\Theta}(\bm{M}_{\nu});R^{z}_{\Theta}(\bm{\mathsf{d}}))$ for $\mu\in\{b,t,T\}$; and (c) three symmetries that involve a total rotation by $\pi$ about in-plane axes $\hat{\bm{e}}_{i}$ ($i\in\{\text{A,B,C}\}$, which are parallel to one of the three lines connecting nearest-neighbor Hf ions and positioned at midway between the layers) followed by $\bm{\mathsf{d}}\rightarrow-R^{i}_{\pi}(\bm{\mathsf{d}})$, which for the $\bm{M}_{1}=\bm{b}_{1}/2$ valley implies $\Delta_{\mathfrak{b}}(\bm{M}_{1};\bm{b}_{2})=\Delta_{\mathfrak{t}}(\bm{M}_{1};-\bm{b}_{1}-\bm{b}_{2})$, $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};\bm{0})=\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};-\bm{b}_{1})^{*}$, $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};\bm{b}_{2})\in\mathbb{R}$, $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};-\bm{b}_{1}-\bm{b}_{2})\in\mathbb{R}$, $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};\bm{b}_{1}+\bm{b}_{2})=\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};-\bm{b}_{1}+\bm{b}_{2})^{*}$. Since $s_{z}$ spin sectors are identical, time-reversal symmetry implies $\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};\bm{G})=\bar{\Delta}_{\mathfrak{t}}^{\mathfrak{b}}(\bm{M}_{1};-\bm{G}-\bm{b}_{1})^{*}$. This is a minimal set of symmetry relations which explains the most prominent structure of Fig. 2 via Table 1.

Two-orbital anisotropic moiré band model— We now address the position-independent (intralayer $\bm{G}=\bm{0}$) term in the moiré band Hamiltonian of Eq. (5), which is obtained by averaging the intralayer Hamiltonian matrix elements over $\bm{\mathsf{d}}$. When described at parabolic order, the effective mass tensor has eigenvectors in the $\bm{k}$-space directions parallel ($a=\,\parallel$) and perpendicular ($a=\,\perp$) to $\bm{M}_{\nu}$, which we have denoted above by $m_{a,l}^{\bm{M}_{\nu}}$. The effective mass eigenvalues are weakly dependent on $\bm{\mathsf{d}}$ and approximated here by their spatial averages ⁹⁹9Position-dependent effective masses can be included in the moiré band Hamiltonian when needed.. The explicit form of the plane-wave representation two-orbital continuum model Hamiltonian is

	$\displaystyle\bra{l,\bm{\mathfrak{q}}+\tilde{\bm{G}}}H_{\text{LD}}\ket{l^{\prime},\bm{\mathfrak{q}}^{\prime}+\tilde{\bm{G}^{\prime}}}=$
	$\displaystyle\delta_{l,l^{\prime}}\delta\big{(}\bm{\mathfrak{q}}^{\prime}-\bm{\mathfrak{q}}\big{)}\Big{(}\delta_{\tilde{\bm{G}}^{\prime},\tilde{\bm{G}}}\sum_{a\in\{\parallel,\perp\}}\frac{\hbar^{2}}{2m_{a,l}^{\bm{M}_{\nu}}}\big{(}\mathfrak{q}^{a}+\tilde{G}^{a}\big{)}^{2}$
	$\displaystyle\qquad\qquad\qquad\quad+\Delta_{l}(\bm{M}_{\nu};\tilde{\bm{G}}^{\prime}-\tilde{\bm{G}})\Big{)}$
	$\displaystyle+(1-\delta_{l,l^{\prime}})\delta\big{(}\bm{\mathfrak{q}}^{\prime}-\bm{\mathfrak{q}}+(-1)^{l,\mathfrak{t}}\tilde{\bm{k}}_{*}\big{)}\bar{\Delta}_{l^{\prime}}^{l}(\bm{M}_{\nu};\tilde{\bm{G}}^{\prime}-\tilde{\bm{G}}),$		(8)

where $k^{\parallel}\equiv\bm{k}\cdot\hat{\bm{M}}_{\nu}$, $k^{\perp}\equiv\bm{k}\cdot(\hat{\bm{e}}_{z}\crossproduct\hat{\bm{M}}_{\nu})$, and $\hat{\bm{M}}_{\nu}\equiv\bm{M}_{\nu}/|\bm{M}_{\nu}|$.

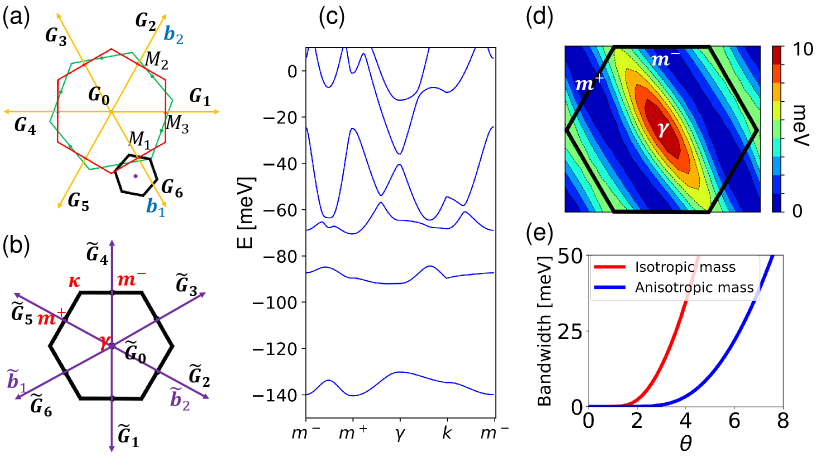
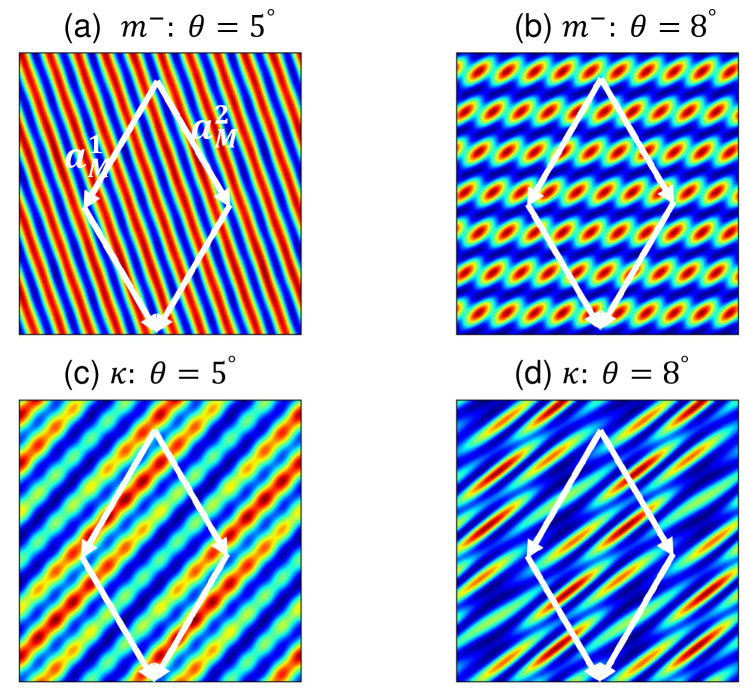
Our findings for the $\bm{M}_{1}$ valley are summarized in Fig. 3 and additional plots are included in the Supplementary Materials. The effective masses in HfS₂ crystal bilayers are highly anisotropic as evidenced in Fig. 1(c)–(e); $m_{\parallel,l}^{\bm{M}_{\nu}}/m_{\perp,l}^{\bm{M}_{\nu}}\approx 9$. As shown in Figs. 3(c) and (d), this leads in the $\bm{M}_{1}$ valley to moiré bands that are significantly much more dispersive along the $\perp\bm{M}_{\nu}$ direction which is along the $\tilde{\bm{b}}_{1}$ direction in the moiré BZ (the $m^{-}$ to $m^{+}$ line), and less dispersive along the direction parallel to $\bm{M}_{1}$ (the $\kappa$ to $\gamma$ line). In real space (see Fig. 4), the eigenfunctions in the lowest energy moiré conduction band are more localized close to favored positions along the large mass directions. Up to an overall scaling factor related to variation in bandwidth, the shape of that band is qualitatively independent of $\theta$ for small twist angles (see Supplementary Material). Fig. 4 shows that the spatial distribution of flat-band charge is more momentum dependent within a band than in the case of atomic crystals, which have strong attractive Coulombic potentials centered on nuclear positions. This property is shared with other moiré material systems and implies that interaction effects can shape not only the widths of bands but also their shapes as band filling factors change.

Valleys at time-reversal invariant momenta and inversion symmetry together imply $\Delta_{T}(\bm{M}_{\nu};\bm{\mathsf{d}})$ is real-valued and top and bottom intralayer potentials are identical. Therefore, the previously defined [40] layer pseudo-spin map $\Delta$ is characterized by degree $0$. Layer textures can be induced in real and momentum space by applying electrostatic gate fields between layers, but these can never yield Chern bands because of time-reversal symmetry. This implies that the Hall conductivity within each valley vanishes and therefore cannot be used as a harbinger of interaction-induced spontaneous valley polarization, as commonly seen in graphene multilayers and $K$-valley group VI TMDs. However, unlike in those materials, the valley-projected bands in t(HfS₂)/HfS₂ are highly anisotropic and a rotational symmetry implies that the high and low mass directions (in the crystal BZ) are rotated between valleys.

Discussion— In this Letter we employ the WF-based local displacement scheme [3] to construct a moiré band model of the low-energy electronic conduction states in t(HfS₂)/HfS₂, a prototypical group IV TMD homobilayer. This approach provides a universal moiré band Hamiltonian that applies at all small twist angles by evaluating displacement-dependent corrections to the Hamiltonian that are small on the atomic scale but significant on the moiré scale. We have neglected in-plane strain relaxation, but this can be included by modifying the mapping $\bm{d}:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ between lattice sites and position from the linear form that applies for rigid rotations [41]. Although strain effects can be important for a quantitatively accurate moiré bandstructure, the novel qualitative aspects of these moiré materials is due to time-reversal invariant valley momenta and effective mass anisotropy, which will persist in the presence of strain relaxation. We find that the low-energy conduction bands are determined mainly by interlayer tunneling terms in each valley-projected moiré band Hamiltonian that are peaked near metal on chalcogen layer configurations and have a typical size $\sim 100$ meV, and secondarily by intralayer potential variations that are identical in the two layers and vary by $\sim 30$ meV over the moiré unit cell. The tunneling amplitudes are real because of time-reversal invariance in each valley and this implies that the moiré band Hamiltonian separates into even and odd layer-parity sectors.

Monolayer HfS₂ has anisotropic dispersion near its conduction band minimum and this leads to valley-projected moiré bands that are also anisotropic. We find that the lowest energy moiré conduction bands are narrow and isolated, the established recipe for interesting strong correlation physics, with bandwidths below $1$ meV for $\theta\lesssim 4^{\circ}$. At much smaller twist angles we expect classical lattice-gas physics in which hopping between sites plays no role. It appears therefore that the interesting range of twist angles is larger than in the well-studied $K$-valley moiré systems. Spin-valley flavor magnetism appears likely to be as common in $M$-valley TMDs as it is in $K$-valley TMDs, and this can lead to insulating states at integer band fillings $\nu$, smaller than the filling $\nu=6$ at which the lowest band is filled. The mismatch in shape between Fermi surface contours in different valleys favors valley polarization over inter-valley coherence [42]. Anisotropy in transport is therefore a likely signature of strong correlation physics in $M$-valley TMDs. It seems likely that the strongly anisotropic bands may bring the tendency toward density-wave states and other aspects of quasi-one-dimensional material physics to the moiré platform.

Acknowledgments— We are grateful to Andrei Bernevig, Dumitru Călugăru, Yi Jiang, Haoyu Hu, Hanqi Pi and collaborators for insightful discussions near the conclusion of this work. We acknowledge HPC resources provided by the Texas Advanced Computing Center at The University of Texas at Austin. This work was supported by a Simons Foundation Collaborative Research Grant and by Robert A. Welch Foundation Grant F-2112.

Note Added— As this manuscript was being prepared for publication we learned of a closely related study by Călugăru et al. [43] which reaches similar conclusions.