11email: [email protected] 22institutetext: Departamento de Física Universidad de Oviedo, C. Federico García Lorca 18, E–33007 Oviedo, Spain 33institutetext: Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), C. Independencia 13, 33004 Oviedo, Spain
33email: [email protected]
Modelling radio luminosity functions of radio-loud AGN by the cosmological evolution of supermassive black holes.
Abstract
Aims. We develop a formalism to model the luminosity functions (LFs) of radio-loud active galactic nuclei (AGN) at GHz frequencies by the cosmological evolution of the supermassive black hole (SMBH) hosted in their nuclei. The mass function and Eddington ratio distributions of SMBHs computed in a previous work published by one of the authors have been taken as the starting point for this analysis.
Methods. Our approach is based on physical and phenomenological relations that allow us to statistically calculate the radio luminosity of AGN cores, corrected for beaming effects, by linking it with the SMBH at their centre, through the fundamental plane of black hole activity. Moreover, radio luminosity from extended jets and lobes is also computed through a power-law relationship that reflects the expected correlation between the inner radio core and the extended jets and lobes. By following a classification scheme well established in the field, radio-loud AGN are further divided into two classes, characterized by different accretion modes onto the central BH. If the Eddington ratio, , is they are called low-kinetic (LK) mode AGN; if , they are called high-kinetic (HK) mode AGN, this critical value roughly corresponding to the transition between radiatively inefficient and efficient accretion flows. The few free parameters used in the present model are determined by fitting two different types of observational data sets: local (or low-redshift) LFs of radio-loud AGN at 1.4 GHz and differential number counts of extragalactic radio sources at 1.4 and 5 GHz.
Results. Our present model fits well almost all published data on LFs of LK mode AGN and of the total AGN population up to redshifts and also in the full range of luminosities currently probed by data. On the other hand, it tends to underestimate some recent measures of the LF of HK mode AGN at low redshifts, but only at low radio luminosities. All in all, the good performance of our model in this redshift range is remarkable, considering that all the free parameters used but the fraction of HK mode AGN are redshift independent. The present model is also able to provide a very good fit to almost all data on number counts of radio-loud sources at 1.4 and 5 GHz.
Key Words.:
Radio continuum: galaxies – Galaxies: active – Galaxies: evolution – Galaxies: luminosity function, mass function – quasars: supermassive black holes.1 Introduction
Active galactic nuclei (AGN) have been of particular interest over the past decade due to the crucial role they play in galaxy formation and evolution. They are associated with the accretion of material on supermassive black holes (SMBHs), with masses that vary from millions to billions of solar masses.
Depending on their mode of accretion, AGN are typically divided into two main categories (for a review, see e.g. Heckman & Best 2014). The first category, called quasar-mode or radiative-mode AGN, consists of objects that efficiently convert the potential energy of the gas accreted by the SMBH in the form of radiation. Radiatively efficient accretion flows in SMBHs are usually described by a standard geometrically-thin, optically-thick accretion disc (Shakura & Sunyaev 1973). Powerful jets are present in a small fraction of radiative-mode AGN. The second category (called radio-mode or jet-mode AGN) is apparently associated with a mode of accretion where most of the released energy is in kinetic form. The geometrically-thin accretion disc is replaced by a geometrically-thick structure in which the inflow time is much shorter than the radiative cooling time. These are called advection-dominated or radiatively inefficient accretion flows (ADAFs or RIAFs; e.g., Narayan & Yi 1994, 1995; Quataert & Narayan 1999). One of their characteristic properties is that they are capable of launching two-sided jets.
The transition between the two modes of accretion seems to occur at a critical value of the Eddington ratio of (Maccarone et al. 2003; Jester 2005). The observed dichotomy between Fanaroff & Riley (1974) class I (FR I) and II (FR II) radio galaxies confirms this hypothesis: the line separating low-power FR I and high-power FR II galaxies in a plot of AGN radio luminosity against host galaxy optical luminosity is interpreted as a threshold in accretion rate and corresponds to (Ghisellini & Celotti 2001; Xu et al. 2009; Ghisellini et al. 2009). However, this interpretation has been questioned in some recent analyses (Gendre et al. 2013; Vardoulaki et al. 2020). A similar dichotomy is observed for Galactic black holes in X-ray binaries, where the transition between spectral states is observed at the same , and radio emission in high-accreting systems is substantially suppressed (e.g. Maccarone et al. 2003).
Radio galaxies can be also classified based on emission line strengths and line flux ratios, as low-excitation and high-excitation. The former population of radio galaxies has been historically associated with jet-mode AGN, while the latter forms a small sub-population of radiative-mode AGN that produce powerful jets. Best & Heckman (2012) showed that, in the nearby Universe, the low-excitation population typically has a low accretion rate, below one per cent of the Eddington rate, whereas high-excitation radio galaxies predominately accrete above this value.
In this paper we follow the nomenclature used in Merloni & Heinz (2008) to distinguish AGN with different accretion modes (based on their analogies with Galactic black holes in X-ray binaries). If the accretion rate is below the critical ratio , AGN are said to be in low-kinetic (LK) mode (corresponding to jet-mode AGN defined above). LK mode AGN are typically radio-loud objects and can be associated with FR I radio galaxies, with the only possible exception of LINERs, which are likely members of the radio-mode population but with rather modest radio luminosities. On the other hand, AGN accreting above this critical value () can be observed in two different states: high-kinetic (HK) mode AGN, or high-radiative (HR) mode AGN, depending on the presence or lack of powerful jets. AGN in HR mode, which are the majority of high-accreting SMBHs, are radio-quiet and will be not considered in the following analysis. HK mode AGN are instead radio-loud objects and can be roughly associated with FR II radio galaxies (see e.g. Heckman & Best 2014).
Table 1 shows the expected correspondence of the Merloni & Heinz classification with common AGN classes, and summarizes the main properties. We recall that HK mode AGN are characterized by radiatively efficient accretion flows and by the presence of powerful radio jets, which are probably produced by rapidly-spinning black holes (Yuan & Narayan 2014). Type-1 and type-2 AGN are also included in the table. These two classes are defined according to their optical spectra: type-1 AGN show both broad and narrow lines, while type-2 AGN only narrow lines. The lack of broad emission lines is typically associated with the presence of obscuration along the line of sight. However, at least a fraction of type-2 AGN appear to be unobscured and intrinsically lacking a broad-line region. They appear to be low-luminosity and low accretion rate AGN (e.g. Trump et al. 2011; Hickox & Alexander 2018).
The observed emission from AGN-powered radio sources includes radiation from classical extended jets and double lobes, and from the compact radio component (jet core) that are more directly associated with the energy generation and collimation near central SMBHs. According to the unification model (see e.g. Urry & Padovani 1995), the appearance of radio sources, including their spectra, depends primarly on their axis orientation relative to the observer. A line of sight close to the source jet-axis offers a view of the compact base of the approaching jet. Its radio emission is Doppler-boosted and presents the typical flat spectrum111Radio sources are typically divided according to their spectral index between 1.4 and 5 GHz (we adopt the convention ). They are classified as flat-spectrum sources if and steep-spectrum otherwise. associated with optically-thick sources; they are generally called blazars. In the case of a side-on view, the observed emission is dominated by the extended optically-thin components with a steeper spectrum. In general, however, at an intermediate angle of view, radio sources (i.e. classical steep-spectrum radio sources, usually associated with giant elliptical galaxies and, at lower luminosities, with starburst or less active galaxies) can have a significant contribution from both components.
The radio luminosity function (LF) is an important and common tool for understanding the evolution of AGN over cosmic time. In recent years, a large effort has been made on studying and modelling the evolution of radio LFs, by exploiting large-area multi-wavelength surveys (e.g. Massardi et al. 2010; Rigby et al. 2011; Smolčić et al. 2017b; Yuan et al. 2017; Malefahlo et al. 2020), including the use of cosmological simulations (e.g. Bonaldi et al. 2019; Thomas et al. 2020). The evolution of the radio AGN population is also expected to be strictly connected to the SMBH accretion history, being the radio emission of AGN core directly dependent on the central black hole mass, spin, and accretion rate (see e.g. Heckman & Best 2014). Recently, following this idea, empirical or semi-analitic models of the radio AGN LF were developed based on the growth of SMBHs across cosmic time (Saxena et al. 2017; Weigel et al. 2017; Griffin et al. 2019).
In this work, we attemp to model the LF of the radio-loud AGN population at GHz frequencies based on the SMBHs evolution. The starting point of the work is the SMBH mass functions (MFs) and Eddington ratio distributions computed by Tucci & Volonteri (2017). In Section 2 we develop the formalism to link these quantities to the radio LF of radio-loud AGN populations. AGN in LK and HK mode are studied separately, due to the different accretion rate behaviour and radio properties. In Section 3 we present the observational data used to determine free parameters of the model, which are computed in Section 4 where model predictions are also compared to observations. Finally, in Section 5 we summarize our main findings and possible future developments.
Throughout this paper we adopt a flat Lambda cold dark matter (\textLambdaCDM) cosmology with and H.
| Nomenclature | Eddington | Radio | morphology | emission lines | blazars | ||
|---|---|---|---|---|---|---|---|
| ratio | emission | () | |||||
| Low Kinetic | jet mode | radio loud | FRI & FRII | low excitation | type-2 | BL Lac | |
| High Kinetic | radiative mode | radio loud | FRII | high excitation | type-1 & 2 | FSRQ | |
| High Radiative | radiative mode | radio quiet | – | type-1 & 2 | – | ||
2 From mass functions of active SMBHs to radio luminosity functions of AGN
In this section we describe how to link the radio emission of AGN, both from jet cores and from extended jets and lobes, with SMBH physical properties such as mass and accretion rate. Based on the evolution of the mass function and the accretion rate of active SMBHs predicted by Tucci & Volonteri (2017), we estimate the luminosity function of radio-loud AGN at GHz frequencies from redshift 0 to 4. We proceed as follows:
-
•
The intrinsic radio emission from the AGN jet core is linked to the SMBH mass and X-ray luminosity through the fundamental plane relation of BH activity (Sect. 2.1).
-
•
Beaming effects of relativistic jets are taken into account in order to calculate the observed core luminosity (Sect. 2.3).
-
•
The extended radio emission from AGN jets and lobes is obtained from the intrinsic core luminosity using an empirical power-law relation. Both are expected to be related to the bulk kinetic power of jets (Sect. 2.4).
- •
Hereafter we adopt a simple power-law spectrum for AGN-powered radio sources in the 1–5 GHz frequency range (i.e. ) with for flat-spectrum sources and for steep-spectrum ones, respectively.
2.1 Intrinsic luminosity function of radio jet cores
Theoretical arguments have shown that the amount of synchrotron radiation emitted from a scale-invariant jet depends both on the black hole mass and the accretion rate (Falcke & Biermann 1995; Heinz & Sunyaev 2003). The first observational evidence of this dependency was the discovery of the fundamental plane (FP) of black hole activity, which is the relationship between X-ray luminosity, radio luminosity, and black hole mass for low accretion rate black holes, connecting Galactic black holes in X-ray binaries and AGN (Merloni et al. 2003; Falcke et al. 2004). In the FP relation the X-ray emission is considered to be a tracer of the accretion rate, while the radio luminosity is used as a probe for the AGN jet. Many authors have since confirmed the existence of a black hole FP relationship (Körding et al. 2006; Merloni & Heinz 2007; Gültekin et al. 2009; Plotkin et al. 2012; Saikia et al. 2015).
According to the FP relation, the radio luminosity of AGN cores is related to the X-ray luminosity and the black hole (BH) mass, , by (e.g. Merloni et al. 2003; Falcke et al. 2004; Plotkin et al. 2012)
| (1) |
where is the intrinsic (i.e. unbeamed) core luminosity at 5 GHz; is the (unabsorbed) X-ray luminosity in the 2–10 keV band (both in unit of erg s-1); and , and are the correlation coefficients of the FP relation.
The observed correlation coefficients can be compared with the values predicted by theoretical models. These coefficients depend roughly on the accretion flow (if it is radiatively efficient or inefficient) and on the dominant physical process that originates the observed X-rays. Several components can potentially contribute to the X-ray emission: synchrotron and synchrotron self-Compton radiation from the jet; emission from the accretion flow; and inverse Compton scattering of soft disc photons on hot electrons of the corona. Merloni et al. (2003) show how different theoretical models for emission processes can be directly translated into predictions of the FP coefficients in the cases where X-rays are predominantly originated by optically thin synchrotron jet emission or by inverse Compton scattering.
For sources at low accretion rates, the FP relation is well established. Different authors (Merloni et al. 2003; Falcke et al. 2004; Gültekin et al. 2009; Plotkin et al. 2012) have determined it with reasonable agreement of the correlation parameters (with some exceptions; e.g. Bongiorno et al. 2012) and in agreement with theoretical expectations for radiatively inefficient accretion flow models (in particular with the advection dominated accretion flow, ADAF, solution; Merloni et al. 2003). Regardless of the physical explanation, this scaling relation implies that the same mechanism governing the accretion and ejection processes from black holes holds over approximately nine orders of magnitude in mass. For low accretion rate (or LK mode) AGN we adopt the correlation coefficients obtained by Merloni & Heinz (2007, 2008) based on the Merloni et al. (2003) data: , , and , with an intrinsic scatter of 0.6 dex.
When high accretion rate sources are included in the FP relation, the inferred coefficients change and the intrinsic scatter increases. Li et al. (2008) and Dong et al. (2014) explored the FP for samples of radiatively efficient black holes. Dong et al. (2014) considered X-ray binaries and radio-quiet type-1 AGN with Eddington ratio higher than 1%. The correlation coefficients they found are different with respect to low-accretion AGN and compatible with those expected from radiatively efficient accretion disc models: the slope with the X-ray luminosity is steeper () and a small anti-correlation with the black hole mass () is found. Very similar results are also found in Li et al. (2008), but only for radio-loud broad-line AGN; their sample also includes radio-quiet broad-line AGN that provide results in agreement with the FP of LK mode sources.
Because of the larger uncertainty in the FP relation for HK mode AGN, the correlation coefficients are not fixed in the model as for LK mode AGN, but considered as free parameters.
It is more convenient for us to write the FP relation (Eq. 1) in terms of the Eddington ratio (i.e. the ratio of the bolometric luminosity to the Eddington luminosity erg s-1, ) as
| (2) |
where , and is the bolometric correction (from Marconi et al. 2004). Standard radio monochromatic luminosities are now considered in Eq. 2 (in units of erg s-1 Hz-1).
We impose a continuity condition in the FP relationship at the transition of the LK and HK mode regimes (i.e. at the critical accretion rate of ). Under this condition we can write HK mode FP parameters as a function of LK mode ones:
| (3) |
where . The first equation is obtained by requiring the continuity condition to be valid for each SMBH mass. Thus, if the FP relation is fixed for LK mode AGN, only the coefficient is needed to compute .
Once the FP relationship is established it is easy to extract the intrinsic luminosity function of AGN cores at 5 GHz (i.e. 222Hereafter luminosity functions, mass functions, and Eddington ratio distributions are always defined by logarithmic intervals. The redshift dependence is ignored at the moment.) as a function of the mass function and the Eddington ratio distribution of active SMBHs. For sources in the mode (with or ) we have
| (4) | |||||
where is the fraction of LK mode AGN that are radio-loud, and is the fraction of HK mode AGN of the total AGN population accreting at above the critical ratio, . For simplicity, we assume the same mass function for LK and HK mode AGN. The quantity is the core luminosity estimated from the FP relation for a given SMBH with mass and Eddington ratio . The integrals on and account for the intrinsic scatter in the FP relation, which is assumed to have a Gaussian distribution with dispersion . The integral limits and depend on the accretion mode: for sources in the LK mode and for those in the HK mode. Below the Eddington ratio of , SMBHs are typically classified as inactive and behave as radio-quiet AGN. Finally, the minimum mass in the SMBH mass function is fixed to . The contribution of less massive BHs is still very uncertain and expected to be negligible in the luminosity–flux density range we are investigating (see e.g. Koliopanos 2017; Greene et al. 2019).
2.2 Mass function and Eddington ratio distribution of active SMBHs


Tucci & Volonteri (2017) studied the evolution of the SMBH population, total and active, via the continuity equation, backwards in time from z = 0 to z = 4. Type-1 and type-2 AGN are differentiated in that model with different Eddington ratio distributions, chosen on the basis of observational estimates; a log-normal distribution is employed for type-1 AGN, and a power-law distribution with an exponential cut-off at super-Eddington luminosities is employed for type-2 AGN (see Fig. 1). Tucci & Volonteri (2017) showed that the evolution of the AGN MF is well constrained by the quasar bolometric luminosity function333The authors used the function from Hopkins et al. (2007)., with small dependence on the average radiative efficiency, the Eddington ratio distribution, and the local mass function of SMBHs. The model contains information on the main physical quantities that determine the intrinsic properties of SMBHs (i.e. mass and accretion rate).
In the following analysis we use the AGN MF provided by Tucci & Volonteri (2017) for an average radiative efficiency of , and the Eddington ratio distribution defined in their Eq. 12. Their evolution in redshift is shown in Fig. 1. We can see from the Eddington ratio distribution that at low redshift most type-2 AGN accrete at very low rates, while the distribution of type-1 AGN peaks at . When the redshift increases, the distribution for type-2 AGN flattens, and that for type-1 AGN becomes sharper and peaked at . Looking at the MF, the number density of low-mass AGN decreases by more than an order of magnitude between and 4, while for massive AGN () the number density peaks at redshifts 1–2 and then rapidly decreases up to . We have verified that using the AGN MFs that result from and 0.1 (the other two main cases considered in that paper) does not have any relevant impact on our final results.
In Fig. 2 we show the intrinsic radio luminosity functions of AGN cores at 5 GHz in the LK and HK mode as a function of redshift, obtained by Eq. 4. For LK mode AGN, using the FP relation of Merloni & Heinz (2008), the core LFs present a peak at luminosities of – erg s-1 Hz-1. The rapid decrease below these luminosities is probably due to the cuts in the AGN MF at and in the Eddington ratio distribution at . The core LF also shows a significant decrease in amplitude at , due to the strong evolution of the low-mass AGN MF observed in Fig. 1. At the same time the fraction of high-lumiosity objects increases with redshift, due to the combined effect of a higher average Eddington ratio and a flatter AGN MF.
A quite different behaviour is instead observed in Fig. 2 for HK mode AGN. The intrinsic core luminosity is computed now using , 444These values correspond to the best-fit model found in the following analysis., and the continuity condition for the FP relation. As expected, HK mode AGN are much less numerous than LK mode AGN, but more luminous. The peak in the LF is found from to erg s-1 Hz-1, at increasing luminosities with increasing redshift. We observed an important evolution of the LF. Going to high redshifts, HK mode AGN become more numerous and typically brighter by 2–3 orders of magnitude than local ones. Again, this increase in number and in luminosity with redshift of HK mode AGN reflects the evolution of the mass density and of the Eddington ratio distributions for massive (type-1) AGN from the Tucci & Volonteri (2017) model.


2.3 Beaming effects and observed AGN core luminosities
Radio-loud AGN are characterized by the presence of relativistic jets that emit synchrotron radiation. The observed luminosities of AGN core jets are affected by Doppler beaming effects and can be significantly different from their intrinsic values. Here we derive the relation between intrinsic and observed AGN core LF, given a distribution of the Lorentz factor . We assume the simple model in which each AGN contains two identical, straight, and oppositely directed jets with bulk flow velocity in units of the speed of light. Jets are randomly oriented such that if represents the angle between the jet axis and the line of sight, is uniformly distributed between 0 and 1. Finally, according to current models of the emission in inner cores of AGN, in the optically thick regime the spectrum of core emission is assumed to be a power law with index (see e.g. Blandford & Königl 1979).
The observed luminosity () of AGN core jets is related to the intrinsic luminosity () via the formula
| (5) |
The Lorentz factor is related to the bulk velocity by and . The exponent depends on the emission model assumed for AGN jets and is for continuous jets or for discrete moving sources (see e.g. Urry & Padovani 1995). We take as reference value , which is probably more appropriate for the continuous jet emission associated with flat-spectrum cores of AGN. The contribution of opposite-directed jets can be safely ignored in Eq. 5 because it only affects the shape of the very faint end of the beamed core LF (Lister 2003).
We take a power-law distribution for the Lorentz factor of AGN jets, with . This distribution provides the best fit to the apparent speed distribution in AGN jets (Lister & Marscher 1997; Lister 2003; Liu & Zhang 2007). The AGN population contains a wide range of apparent jet speeds, which is inconsistent with a single-valued intrinsic speed distribution, and extends from 0 to about 35c (Kellermann et al. 2004; Cohen et al. 2007; Lister et al. 2009). Because the maximum value of the apparent velocity sets the approximate value of the maximum Lorentz factor (Vermeulen & Cohen 1994), we adopt and . For the slope of the distribution we take the best-estimated value (i.e. ) from Liu & Zhang (2007), which is in agreement with the results of Lister & Marscher (1997) and Lister (2003). We have verified that changing from 1.3 to 2 (i.e. the interval indicated by data on the apparent velocities of jets) has little impact on our results.
These analyses are typically based on complete samples of radio-loud AGN, including BL Lacs, flat-spectrum radio quasars, and radio galaxies, objects with very different intrinsic luminosity values. Lister & Marscher (1997) investigated a possible correlation between and the intrinsic luminosity of the AGN jet in the form of . They found that observational data do not require such a correlation, and simple models with independent of provide as good fits to the data as – dependent models. Based on this outcome and for the sake of simplicity, we consider the Lorentz factor to be independent of the intrinsic luminosity of the AGN jet, and we use the same distribution for AGN in LK and HK mode.
Given the Lorentz factor distribution, the observed LF of AGN core jets, , can be estimated from the intrinsic LF by
| (6) |
where the conditional probability, , to observe an object with a core luminosity if the intrinsic core luminosity is , is
| (7) | |||||
The limits of the integration are fixed by the condition that and , where . We find that and . Moreover, the conditional probability is zero if or . We can then write the observed luminosity function as
| (8) |
where
| (9) |
Using the intrinsic core LFs computed in the previous section, Fig. 2 shows the observed LFs after applying the beaming correction. We expect an important Doppler boosting of the AGN luminosity when the line of sight is close to the jet axis (i.e. ). This effect is observed as an increase in the high-lumiosity tail of the intrinsic core LFs. On the other hand, when the angle of view is the observed luminosity can be strongly reduced, as observed in the LFs at the lowest luminosities. The global effect of beaming is therefore a broadening of LFs at low and high luminosities.
2.4 Radio luminosity of AGN from extended jets and lobes
The luminosity of AGN cores can be strongly suppressed by debeamed effects when they are observed at angles with respect to the jet axis. In these cases the emission from extended jets and lobes is expected to dominate over the core, and AGN will show the typical steep spectra ().
It is well established that the extended radio luminosity of AGN is correlated with the bulk kinetic power of the jet, and hence linked to the AGN central engine (e.g. Rawlings & Saunders 1991; Willott et al. 1999). A commonly used relation in converting radio luminosity to jet power is that presented by Willott et al. (1999). Based on the minimum energy condition to estimate the energy stored in the radio lobes, Willott et al. (1999) derived a relation between the jet kinetic power and the radio luminosity of FR II radio sources of the form .
Different methods to estimate the jet kinetic power, independently of the radio lobe luminosity, have been developed and used to test the Willott et al. (1999) relation, finding a good agreement with it (O’Dea et al. 2009; Daly et al. 2012; Godfrey & Shabala 2013).
For FR I galaxies the conversion of mechanical power to observed radio luminosity is more complex due to their strong interactions with the enviroment. These sources are known to be decelerated to sub-relativistic speeds during the propagation in the intergalactic medium. The Willott et al. (1999) relation has also been calibrated against FR I sources by studying cavities and bubbles produced by jets in the intergalactic medium (see e.g. Rafferty et al. 2006; Hardcastle et al. 2007; Bîrzan et al. 2008; Cavagnolo et al. 2010). These authors found a relation similar to that of FR II sources.
On the other hand, the radio core emission is expected to be a good tracer of the kinetic jet power. According to the standard model of the synchrotron jet emission (Blandford & Königl 1979), the core luminosity should present a dependence on the kinetic jet power of the form . Heinz & Sunyaev (2003) showed that in scale-invariant jet models with radiatively inefficient accretion modes the flat-spectrum core emission follows the relation . This relation was observationally confirmed by Merloni & Heinz (2007) from a sample of 15 nearby AGN for which the average kinetic power was determined based on the observed X-ray cavities.
We therefore expect a direct link between the intrinsic core luminosity of AGN and the luminosity of their extended jets and lobes. Based on the above discussion, we assume a power-law relationship between them (i.e. in logarithmic scale):
| (10) |
According to the expected relations between kinetic jet power and radio luminosity from jet core and extended jets and lobes (Willott et al. 1999; Blandford & Königl 1979), the power-law index is estimated to be 555This value is calculated by considering the above relations: and ..
Assuming a Gaussian distributed scatter around the previous relation (with variance ), the conditional probability to have an extended jet–lobe luminosity from an AGN with a given core luminosity is
| (11) |
where is the luminosity estimated from Eq. 10. The values of , , and are considered as free parameters of the model and different for LK and HK mode AGN.
Given the intrinsic core LF of AGN , the LF associated with the extended jet–lobe luminosity, , can be written as
| (12) |
2.5 Radio luminosity function of radio-loud AGN
At this point we have all we need to estimate the LF of radio-loud AGN at radio frequencies and in the redshift range of –4, starting from the intrinsic core LF at 5 GHz. The following formulas are valid for AGN in LK and in HK mode.
The observed AGN radio luminosity is the sum of the beamed core emission () plus the extended emission from jets and lobes (): . Both core and extended luminosities are related to the intrinsic core luminosity. In the previous sections we provided these relations at 5 GHz.
The total LF inferred at a radio frequency can be written as
| (13) |
Assuming that AGN core and extended emissions scale with frequency as a power law of indices and , respectively, we have that the total luminosity at frequency is related to the 5 GHz core and extended luminosities as
| (14) |
where and are at 5 GHz. The conditional probability depends on the conditional probabilities and at 5 GHz in the following way:
| (15) | |||||
Inserting Eq. 15 in Eq. 13 and using Eq. 7 and 11 for and respectively, we find
| (16) | |||||
where
| (17) |
We can also estimate the LF for flat- and steep-spectrum sources separately. For flat-spectrum sources (and in an equivalent way for steep-spectrum sources) the LF is
| (18) |
where is the conditional probability that an object is classified as flat-spectrum having a total luminosity at frequency and an intrinsic core luminosity at 5 GHz.
The observational condition for a source to be flat-spectrum is that the flux density at 1.4 GHz is . In terms of luminosity666The relation between luminosity and observed flux density at frequency is , where is the luminosity distance and the source redshift., taking into account the K-correction and the contributions from the flat-spectrum core and from the extended steep-spectrum lobes, the condition at 5 GHz becomes with
| (19) |
assuming and .
2.6 Number counts
Differential number counts, , defined as the number of sources per unit area with flux density within , are the typical observables from large-area radio surveys. Observed number counts are projected counts over a large range of redshifts and can be written as the integral along redshift of the radio luminosity function
| (22) | |||||
where is the comoving volume and
| (23) |
with .
3 Data sets
In this section we review observational data on LFs and number counts of radio-loud AGN at frequencies from a few hundred MHz to a few GHz. Low-redshift LFs at 1.4 GHz and number counts at 1.4 and 5 GHz are used to constrain the free parameters of the model. Other available data, including LFs at high redshifts () and number counts at , are taken as a cross-check of the consistency of the model.
3.1 Observational data on radio luminosity functions
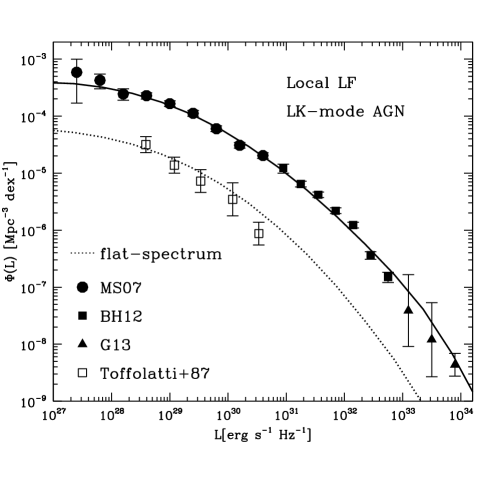
Accurate measurements of radio LFs are mainly restricted to the local Universe or at low redshifts, . The local LF of radio-loud AGN has been achieved at 1.4 GHz by the combination of the NRAO VLA Sky Survey (NVSS; Condon et al. 1998) and the Faint Images of the Radio Sky at Twenty cm (FIRST; Becker et al. 1995) survey with recent large-area spectroscopic surveys (e.g. Machalski & Godlowski 2000; Sadler et al. 2002; Mauch & Sadler 2007; Best & Heckman 2012; van Velzen et al. 2012). In particular, Mauch & Sadler (2007) determined the local LF from a sample of NVSS sources associated with galaxies brighter than mag in the 6 degree Field Galaxy Survey (6dFGS, Jones et al. 2004). Through visual examination of 6dF spectra they were able to distinguish between star-forming galaxies and radio-loud AGN. The latter population is found to be 40 per cent of the sample, corresponding to objects. More recently, using a much larger sample of radio-loud AGN ( objects) constructed by combining the seventh data release of the Sloan Digital Sky Survey (SDSS, York et al. 2000) with the NVSS and the FIRST survey, Best & Heckman (2012, hereafter BH12) found very good agreement with the Mauch & Sadler (2007) local LF at radio luminosities erg s-1Hz-1 (see Figure 3). At lower luminosities their LF flattens below the Mauch & Sadler (2007) estimates. This is likely due to the incompleteness of the BH12 sample, whose flux limit is 5 mJy, corresponding to a radio luminosity of erg s-1Hz-1 at redshift .
Using the wide range of emission line measurements available, BH12 classified radio sources in low-excitation and high-excitation objects and derived the local LF at 1.4 GHz for the two populations separately. More recently, Pracy et al. (2016, hereafter P16) also derived the radio luminosity function for the two populations of radio galaxies by using an optical spectroscopic survey of radio galaxies identified from matched FIRST sources and SDSS images. Their local luminosity function for the radio-loud AGN population is in good agreement with the BH12 estimates at erg s-1Hz-1. Nonetheless, the P16 LF for high-excitation AGN has a steeper slope than the BH12 value, and significantly exceeds it at low luminosities (see Figure 3). P16 explain the discrepancy as being due to the stricter method employed by BH12 to identify AGN with respect to star-forming galaxies. Gendre et al. (2013) derived the local radio LF for high-power low- and high-excitation sources, using the Combined NVSS-FIRST Galaxy catalogue (CoNFIG), extending measurements up to erg s-1Hz-1. As displayed in Figure 3, the local LF presented by Gendre et al. (2013) is in very good agreement with the estimate of P16. On the other hand, it shows an excess at the highest luminosities in comparison with BH12, especially for HK mode AGN.
According to previous data, low-excitation (or LK mode) sources clearly dominate the local LF at low and intermediate luminosities, up to erg s-1Hz-1, with a fraction of high-excitation (or HK mode) AGN . The two populations become roughly equal in number at erg s-1Hz-1. Hoever, these results are not confirmed by recent findings from Butler et al. (2019, hereafter B19). They use Australia Telescope Compact Array (ATCA) observations of the XMM extragalactic survey south field (ATCA XXL-S). Differently to previous analyses, they first identify high-excitation AGN (both radio-loud and radio-quiet) based on multi-wavelength information; the remaining sources are then divided into low-excitation AGN and star-forming galaxies. B19 found a comparable contribution of high- and low-excitation AGN to the total AGN LF in the whole luminosity range. Their high-excitation LF is significantly larger than estimates from P16 (by a factor 2–5) and BH12 (by one order of magnitude; see Fig. 3). These discrepancies are attributed again to the different classification criteria used to identify star-forming galaxies and AGN (see the discussion in their Section 4.3.2), and to differences in the optical and radio depths probed by the samples.
The fact that three studies (Best & Heckman 2012; Pracy et al. 2016; Butler et al. 2019) employ different methods and/or criteria to separate radio-loud AGN and star-forming galaxies, and that they find quite different results that are not consistent with each other, indicates the difficulty and the uncertainties present in the classification procedure. In the following analysis we decide to use both the BH12 and P16 measurements for the model fitting. On the other hand, due to the larger uncertainties associated with them and some discrepancies in the local AGN LF with previous estimates (a factor of 3–4 between ; see Fig. 3), the B19 data will be considered only for comparison.
Only a few studies attempted to disentangle the contributions of sources with different spectral classes to the local LF (Toffolatti et al. 1987; Stickel et al. 1991; Dunlop & Peacock 1990; Padovani et al. 2007; Mao et al. 2017). At 1.4 GHz steep-spectrum sources are the dominant population, while flat-spectrum sources are found to be less than 10 per cent. Determinations of the local and low-redshift LF of flat-spectrum sources are provided by Toffolatti et al. (1987) and Padovani et al. (2007). These are based on small samples, and cover different ranges of luminosities, below and above erg s-1Hz-1, respectively. Estimates from Padovani et al. (2007) are obtained from a sample of BL Lac objects with average redshift of 0.26 and assuming no evolution, while Toffolatti et al. (1987) used flat-spectrum sources at . The two LFs join almost smoothly with each other (see Fig. 11).
The evolution of the radio LF with redshift has been studied by different authors (e.g. Sadler et al. 2007; Donoso et al. 2009; Smolčić et al. 2009; Yuan & Wang 2012; McAlpine et al. 2013; Best et al. 2014; Padovani et al. 2015; Smolčić et al. 2017b; Ceraj et al. 2018), typically out to . For example, Smolčić et al. (2009) derived the LF for low radio power AGN ( erg s-1Hz-1) from a sample of the VLA–COSMOS survey in four redshift bins in the range , finding a modest evolution of the LF. This result was confirmed by Donoso et al. (2009), using a catalogue of AGN at constructed from the cross-correlation of the NVSS/FIRST survey with the MegaZ–LRG of luminous red galaxies from the SDSS. While the comoving number density of low-luminosity AGN increases only by a factor between and 0.55, this factor reaches values of more than 10 at erg s-1Hz-1.
Best et al. (2014) and Pracy et al. (2016) investigated the evolution of radio-loud AGN in the radiative and jet mode (or high- and low-excitation mode) separately out to . They showed that the space density values of the two AGN populations have quite different evolutions with redshift: the space density of radiative-mode AGN strongly increases from the local Universe to by a factor of 4–7, while jet-mode AGN have a slower evolution or no evolution depending on radio luminosity. In agreement with this, Butler et al. (2019) found a weak positive evolution in low-excitation mode AGN, and a stronger one in high-excitation mode AGN (although weaker than in previous works). This is consistent with the mild evolution seen in the total radio luminosity function at low radio power and the more rapid evolution of luminous radio galaxies, already observed in previous analyses.
| BH12-based | P16-based | |||
| AGN | Dataa | Luminosityb | Dataa | Luminosityb |
| MS07 | MS07 | |||
| radio-loud | BH12 | (30.6, 33) | P16 | (28.2, 33.5) |
| G13 | G13 | |||
| MS07 | MS07 | |||
| LK mode | BH12 | (30.6, 33) | P16 | (28.2, 33.5) |
| G13 | G13 | |||
| HK mode | BH12 | [29.45, 33) | P16 | [28.8, 33.5) |
| G13 | G13 | |||
-
a
See Fig. 3 for the meaning of acronyms.
-
b
Luminosities are given in [erg s-1Hz-1]).
3.2 Luminosity functions used in the model determination
Radio luminosity functions provide essential information for the determination of free parameters of the model. To this end, we use the local luminosity function of the total AGN population and of LK and HK mode sub-classes, as discussed in detail in the previous subsection, along with the total LF at measured by Donoso et al. (2009, see Fig. 14). We leave instead higher redshift data for a consistency check of model results.
We execute the model fitting procedure with two different sets of data for the local LF, one based on the BH12 estimates and the other on the P16 estimates. In Table 2 we summarize the data employed with the corresponding luminosity range. It is important to note that the total LF from MS07 is also used for the LK mode LF at very low luminosities in the hypothesis that at those luminosities the contribution of HK mode AGN is negligible. Moreover, BH12 measurements for the total and LK mode LF are used only for erg s-1Hz-1, due to incompleteness issues of the sample at lower luminosities (see previous subsection). On the contrary, we include in the analysis all the BH12 estimates for HK mode AGN, taking into account that our model tends to underestimate HK mode space densities from BH12 at erg s-1Hz-1 (see next sections).
In addition, we also consider the following data, all at 1.4 GHz:
- •
- •



3.3 Number counts from large-area surveys
Relevant information on the evolution of the space density of radio-loud AGN can be provided by observed number counts that gather radio sources in a large range of redshifts, up to , with a peak at redshifts 1–2 (see e.g. Massardi et al. 2010).
Thanks to large-area radio surveys, number counts of radio sources have been accurately estimated at frequencies from hundreds of MHz to a few GHz and more (for a review, see e.g. de Zotti et al. 2010; and the more recent measurements from Smolčić et al. 2017a; Butler et al. 2018; Ocran et al. 2020).
For the model determination we employ number counts at 1.4 and 4.8 GHz. These are mainly based on the NVSS at 1.4 GHz, and on the Northern Green Bank GB6 survey (Gregory et al. 1996) and Kuehr et al. (1981) at 4.8 GHz. We use number counts only for flux densities mJy. At sub-mJy flux densities the relative number of star-forming galaxies and radio-quiet AGN becomes increasingly important (see e.g. Massardi et al. 2010, and references therein). We do not include number counts at frequencies larger than 5 GHz or smaller than 1.4 GHz. The assumption of a single-slope power law spectrum for the core or lobe AGN emission can be considered valid only in a small range of frequencies (see discussion in Sect. 4.5).
Finally, we include in the analysis the estimates of number counts for flat-spectrum sources at 4.8 GHz from Tucci et al. (2011), obtained by combining different surveys between 1.4 and 20 GHz, by extrapolating the spectral energy distribution of flat-spectrum radio sources as discussed in that paper.
4 Constraining model parameters
In Sect. 2 we describe how to compute the LF of radio-loud AGN starting from the evolution of the SMBH mass function and the Eddington ratio distribution. This method implies the use of phenomenological and theoretical relations that connect SMBH properties, such as mass and accretion rate, to the AGN luminosity at radio wavelengths. In most of the cases, these relations are not well established and free parameters are consequently introduced in the model. Observational measurements of radio LFs and number counts, described in the previous section, are exploited to determine these free parameters and, at the same time, to test the reliability of the model.
Active galactic nuclei in the LK mode are typically less luminous than HK mode objects, but are much more numerous, and they are expected to dominate radio LFs at very low redshifts (). On the other hand, AGN in the HK mode are expected to give the main contribution to number counts observed from large-area surveys at GHz frequencies at mJy, with a broad redshift distribution peaking at (Brookes et al. 2008; Massardi et al. 2010).
We decided to proceed separately for the two populations of AGN. Firstly, we determined the free parameters for LK mode AGN by fitting the local LF for this class of objects, which is well measured by observations. Then, we used the information on number counts and on HK mode and total LFs to constrain the parameters of HK mode AGN.
Uncertainties on observational LFs typically include only statistical errors. As shown in Fig. 3, at some luminosities they are so small that they are probably underestimated or dominated by systematic errors (Massardi et al. 2010; Best & Heckman 2012). For example, Massardi et al. (2010) adopted an error of at least 0.2 dex for the MS07 and Donoso et al. (2009) LFs to determine the parameters of their evolutionary model. In order to avoid that few observational data with unrealistic small uncertainties weigh too heavily in the fitting procedure, we decided to fix a minimum error value for the observational data used in the analysis; we adopted, conservatively, an error of at least 0.05 dex for LFs and 0.02 dex for number counts.
Hereafter, we mainly focus on results obtained from the BH12-based set of local LFs, as described in Table 2. Model predictions are, however, almost independent of which of the two local LF sets is employed in the analysis. We discuss the results using the P16-based data set in Sect. 4.4.



4.1 Results for AGN in the LK mode
As already stated above, for AGN in the LK mode we adopt the FP correlation coefficients provided by Merloni & Heinz (2008): , and , with an intrinsic scatter of 0.6 dex. We also assume that all LK mode AGN are radio-loud (i.e. ). The presence of jets is commonly associated with this class of objects (Merloni & Heinz 2008), in analogy with the low, hard state of black hole X-ray binaries in which radio emission is always detected.
The only free parameters for this AGN population are the coefficients , , and of Eqs. 10 and 11 that connect the intrinsic core luminosity to the extended emission from jets and lobes. It is important to keep in mind that these parameters are independent of redshift, and that the time evolution of the LF for LK mode AGN is fully regulated by the evolution of the SMBH mass function and accretion rate (see Sections 2.2 and 2.4).
In order to prevent a too large number of very bright sources, we impose an exponential cut-off in the values of the intrinsic scatter and (see Eq. 4 and 11) at high intrinsic core luminosities, with a minimum value of 0.2:
| (24) |
The cut-offs on and have an impact on luminosity functions only at and erg s-1 Hz-1, respectively, and on number counts at the jansky level. We apply the same cut-offs also to HK mode AGN.
We use a Markov chain Monte Carlo (MCMC) method to determine the three model parameters by fitting the BH12-based local LF for low-excitation AGN and the local LF for flat-spectrum sources in the luminosity range dominated by LK mode AGN (i.e. erg s-1 Hz-1). We find a very tight linear relation between and (see Fig. 4), meaning that only one of them is a real free parameter of the model, with ranging from 1.3 to 1.45 and from to . We therefore directly determine from , using the linear relation displayed in Fig. 4 and Table 3.
The fit is then repeated using and as the only free parameters. In Fig. 5 we show the probability density function (PDF) of the two parameters. We find a significant correlation between the two parameters. The best-fit model is obtained for and , while the median values (plus the 68% confidence levels) of the marginalized PDFs are and .
As shown in Fig. 5, the model parameters can be in a large range of values, preserving an almost equivalent ability to fit the data. Changing the parameters at the 1 or 2 level around the median has little impact on the LK mode local LF. Differences are more relevant for number counts, as shown in Appendix A. Therefore, we tested the impact of different LK mode models when HK mode AGN are also included and total LFs and number counts are fitted. We consider, in particular, five sets of parameters (shown as large points in Fig. 5): the set that provides the best results will be adopted as our reference model for LK mode AGN in the following analysis. This corresponds to (see Appendix A and the red point in Fig. 5).
As shown in Fig. 6, the model is able to provide a very good fit to the local luminosity function, even for flat-spectrum sources (see also Fig.11). We also compare our predictions with observational estimates of the LK mode LF at from Best et al. (2014), finding again a good match.

In order to check the hypothesis of , we also included the fraction of radio-loud LK mode AGN among the free parameters. We do not find any significant improvement in the fit and a large fraction of radio-loud AGN () is required from the data.
Using Eq. 12 we can compute the LF associated with the extended jet–lobe AGN emission, starting from the intrinsic core LF (Fig. 7). With respect to the core LF, the peak of the extended jet–lobe LF is shifted to fainter luminosities by around two orders of magnitude. Nevertheless, at high luminosities, the space density for this LF is larger than that associated with the intrinsic core emission and close to the beamed value, as an effect of the large dispersion in the intrinsic core-extended jet–lobe luminosity relation.
4.2 Model parameters for AGN in the HK mode
The number of free parameters for AGN in the HK mode increases substantially. First of all, the FP relation is not as well established as for LK mode AGN, although there are indications that a correlation is still present for this population of sources. We assume that this relation (Eq. 1) is still valid for HK mode AGN but with unknown coefficients. We impose the continuity condition at and, as shown in Eq. 3, the only free parameter is . The dispersion in the FP relation is fixed to 0.6, as for LK mode AGN. Other free parameters are the coefficients of the relation between extended and core luminosity (Eq. 10), and , plus the scatter in the relation, . Finally, differently from LK mode AGN, the fraction of high-accreting SMBHs that are radio-loud (i.e. in the HK mode) is quite uncertain and probably redshift dependent. We parametrize this fraction as a function of redshift as
| (25) |
where is the fraction of HK mode AGN at redshift zero. Both and are free parameters of the model. We impose the condition that at , in agreement with estimates from the literature (Rafter et al. 2009; Kratzer & Richards 2015; Kellermann et al. 2016).
To summarize, we end up with six free parameters (, , , , , and ). They can be determined thanks to the wide and composite amount of data to be fitted. Given the LFs and number counts of LK mode AGN, we can compare model predictions with the local LF for the total population of radio-loud AGN and for HK mode AGN777Unless expressly stated otherwise, in the following subsections we are considering the BH12-based data set for the local LFs.; the LF for flat-spectrum sources at and erg s-1 Hz-1; the LF for radio-loud AGN at redshift ; differential number counts at 1.4 and 5 GHz (at mJy); and differential number counts of flat-spectrum sources at 5 GHz.
Roughly speaking, redshift-independent parameters from FP and core-extended luminosity relations determine the shape of LFs at different redshifts, the shape and the ratio of number counts at 1–5 GHz, while their normalizations are fixed mainly by the fraction of HK mode AGN.
As before, we use a MCMC method to compute the best-fit parameters of the model and to estimate model uncertainties. Some caveats should be taken into account. Firstly, as already seen for LK mode AGN, the parameters show a large degeneracy and correlation with each other. Consequently, the likelihood of the model parameters presents not a single minimum but multiple local minima with comparable values of . Moreover, predicted LFs and number counts are very sensitive to small variations in the model parameters. For example, results are sensitive to variations of and lower than 1%, and to variations of and of the order of few per cent. The MCMC inizialization cannot be chosen randomly, but the input parameter set has to be firstly tuned, especially for strongly correlated parameters, otherwise the MCMC algorithm will not be able to converge to a minimum.
| BH12-based | LK mode AGN | |||||||||
| best model | (0.62)a | (0.55)a | (8.6)a | (0.6)a | (1.42)b | –13.95 | 0.81 | – | – | 33 |
| median | ||||||||||
| P16-based | ||||||||||
| best model | (0.62)a | (0.55)a | (8.6)a | (0.6)a | (1.50)b | –16.40 | 0.84 | – | – | 61 |
| median | ||||||||||
| BH12-based | HK mode AGN | |||||||||
| best model | 1.70 | (–0.57)c | (-30)c | (0.6)a | (0.78)d | 7.73 | 0.79 | 0.61 | 2.08 | 212 |
| median | ||||||||||
| P16-based | ||||||||||
| best model | 1.52 | (–0.46)c | (–30)c | (0.6)a | (0.93)d | 2.76 | 0.82 | 2.81 | 1.27 | 315 |
| median | ||||||||||



As a starting point, we tried to reduce the number of free parameters looking for very tight linear correlations between parameters, as was done for LK mode AGN. We proceeded in the following way. We ran the MCMC algorithm with different input parameter sets, covering a large range of possible values for the input parameters. We find that MCMC chains converge to local minima that depend on the inizialization of parameters. A strong linear relation is found between and (see Fig. 8), similarly to LK mode AGN. The correlation is valid over a very large range of values for , from 0 to 10. We decided therefore to fix the parameter using the linear fit displayed in Fig. 8 and Table 3.
The MCMC method was then run again with the remaining parameters. The results are now less sensitive to the initialization and the algorithm is able to converge to the global minimum starting from any reasonable parameter set. In Fig. 9 we show the marginalized PDFs of the parameters, while in Table 3 we report the best-fit model, the median, and the uncertainties of the parameters, and in Table 4 the of the fit to the different data sets. We still find a significant correlation among the parameters, and in particular between , , and . The power-law index is found between 0.6 and 0.95, very close to the theoretical expectation of 0.8 (see discussion in Sect. 2.4), while the parameter covers a large range of values, between 2 and 14. This means that the normalization coefficient in the core and extended luminosity relation can vary by more than ten orders of magnitude. It is interesting to compare this result with the range of values for LK mode AGN: []. AGN in LK and HK mode therefore have quite a different relationship between core and extended luminosity: using the best-fit models, for an intrinsic core luminosity of (in erg s-1 Hz-1) we get for HK mode AGN and for LK mode AGN. We conclude therefore that the model typically predicts a much stronger contribution of extended jets and lobes for the former AGN class.
The FP parameter is found between 1.5 and 1.9, about three times larger than the value used for LK mode AGN, and (unlike LK mode AGN) the intrinsic core luminosity is anti-correlated with the SMBH mass. These results are in good agreement with observational constraints of the FP relation for high-accretion AGN (Dong et al. 2014).
The fraction of HK mode AGN is between 0.5 and 1 per mil at , and it steeply increases with redshift, with ranging from 1.8 to 2.4 (increasing , decreases). Models predict therefore a very low fraction of high-accreting AGN in the HK mode, especially in the local Universe, with per cent at –1, between 0.4–1 per cent at and 1–2.4 per cent at (see Fig. 10).
| Data set | BH12-based | P16-based | ||
|---|---|---|---|---|
| Luminosity Function | ||||
| LK mode | ||||
| local | 19 | 25 | 17 | 55 |
| flat-spectrum (z=0.1) | 5 | 8 | 5 | 6 |
| HK mode | ||||
| local | 15 | 16 | 13 | 76 |
| Total population | ||||
| local | 19 | 37 | 17 | 42 |
| 10 | 4 | 10 | 16 | |
| flat-spectrum (z=0.3) | 10 | 14 | 10 | 12 |
| Number Counts | ||||
| 1.4 GHz | 62 | 102 | 62 | 114 |
| 5 GHz | 24 | 31 | 24 | 43 |
| 5 GHz flat-spectrum | 9 | 9 | 9 | 12 |
| All data | 173 | 244 | 167 | 376 |









4.3 Model fits to observational data
Figures 11 and 13 provide a visual check of the model fits to observational data, and in particular to the fits used in the parameters determination (corresponding to the BH12-based data set for the local LFs). In these figures, along with the best-fit model, we also consider lower and upper limit cases that should provide a rough estimate of uncertainties in model predictions. As the upper limit we take a model with %, , and , while as the lower limit a model with %, , and .
In Fig. 11 we consider the local LF at 1.4 GHz for the total population of radio-loud AGN and for HK mode AGN. The former is quite well reproduced by the model in the whole luminosity range in which data are available.
It is more interesting to focus on HK mode AGN. The best-fit model provides a good fit to the BH12 HK mode space densities at erg s-1Hz-1, whereas it tends to underestimate BH12 estimates at lower luminosities. A better agreement is found for models that predict a relatively large local fraction of HK mode AGN (%). Model predictions of the HK mode local LF always show a maximum at erg s-1Hz-1 and a decrease at lower luminosities. On the contrary, BH12 measurements seem to keep increasing while moving to low luminosities (we recall that the first points in the BH12 HK mode LF should be considered as lower limits).
The local LF for flat-spectrum sources is also consistent with observational data (Toffolatti et al. 1987; Padovani et al. 2007) over the seven orders of magnitudes covered by them. It is interesting to note how model predictions for the local LF of flat-spectrum HK mode sources can vary at low to intermediate luminosities according to the parameter set used. At erg s-1Hz-1, the upper and lower cases differ by about two orders of magnitude. This is due to the dependence of the extended jet–lobe LF on the (or ) parameter. As shown in Fig. 12, changing the value of from 0.78 to 1.25, the peak of the LF moves from to erg s-1Hz-1. With low values of , therefore, extended emission from jets and lobes is typically fainter and the number of flat-spectrum sources increases.
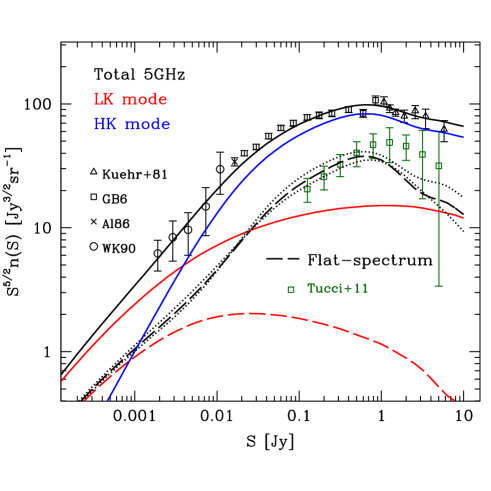
Finally, models provide a very good fit to number counts of the AGN population at 1.4 GHz and at 5 GHz, and of the flat-spectrum sources at 5 GHz, as shown in Fig. 13. Number counts are dominated by AGN in HK mode starting from flux densities mJy. There are no relevant differences among model predictions using different parameter sets, mainly due to the strong constraints imposed by number counts at 1.4 GHz at Jy. Some scatter is observed, but only at the jansky level for flat-spectrum sources.
Smolčić et al. (2017a) provided separate estimates of number counts for low- to moderate-luminosity AGN (analogous to LK mode) and moderate- to high-luminosity AGN (mostly analogous to HK mode). Very remarkably, although these data are not considered for the fit, the agreement between these number counts and the predictions of our current models is excellent (as displayed in the left panel of Fig. 13).
4.4 Model parameters using the P16-based data set
Model parameters are also determined using the P16-based data set (see Table 3). With respect to the BH12-based one, the main change is the much higher fraction of HK mode AGN found at low to intermediate luminosities in the local LF. The P16 and BH12 measurements of the LK mode and total local LF are instead consistent with each other, at least for erg s-1Hz-1 (see Fig 3).
For LK mode AGN, the model predicts a quite similar local LF at intermediate to high luminosities, indepedent of the data set, with some differences only at low luminosities ( erg s-1Hz-1). In terms of parameters, from the P16 data set is about 20 per cent smaller with respect to the BH12-based case.
The impact of the different HK mode local LF is quite significant on the model. As expected, the most affected parameter is the local fraction of HK mode AGN, whose best-fit value is now about five times the BH12-based one (i.e. per mil). The evolution of the HK mode fraction is softer than before, as shown in Fig. 10, and compatible with previous results at high redshifts. The best-fit values for the parameters and are smaller than the BH12-based results, especially , but still compatible with them at the 2 level. The predicted number counts are instead very similar to the BH12-based ones due to the strong constraints imposed by observational data. The larger found for the P16-based best-fit model is mainly due to the poor fit to the HK mode local LF (see Table 4).
Remarkably, at low luminosities the predicted local LF for HK mode AGN is still consistent with the BH12 data, and significantly underestimates the P16 measurements (see Fig.11). This can be understood by the following remarks. The BH12-based model predicts a number density of HK mode AGN of Mpc-3 at , while, based on the P16 LF, it should be roughly of the order of Mpc-3 (taking into account only sources with erg s-1Hz-1). The model can increase the local number density by increasing the local fraction of HK mode AGN (). Because the local number density of SMBHs with is from the Tucci & Volonteri (2017) mass function, should be of the order of 0.1, which is more than 30 times larger than the best-fit value. Such a high level of HK mode AGN is probably difficult to conciliate with the observed number counts, which set quite stringent constraints on the space density of the HK mode AGN population at .
We can conclude that our model indeed predicts a small fraction of HK mode AGN at low to intermediate luminosities (–0.3% locally), independently of the observational data considered for the local HK mode LF. We verify this by (arbitrarily) reducing the uncertainties in the P16 HK mode estimates in order to give a high relevance to these data in the fitting procedure. As a result, not very differently from before, we find a good fit to the P16 HK mode space densities only at erg s-1Hz-1, but not at lower luminosities, where the predicted HK mode LF is still well below the P16 estimates.
4.5 Comparing model predictions with more observational data
The model allows us to compute the AGN LF at redshifts up to , and number counts at frequencies that are outside the 1–5 GHz range. In Figures 14–16 we compare predictions of our best-fit (BH12-based) model with observational data that are not used in the fitting process (with the only exception for the Donoso et al. data). This is an important check of the reliability of model forecasts outside the redshift and frequency ranges where the model is defined.
In Figure 14 we can compare the time evolution of the modeled AGN LF with observations, from redshift up to . The model shows quite good agreement with most of the data at , over a large range of luminosities, from to erg s-1Hz-1. At high redshifts, observational measurements become more difficult to carry out and present larger uncertainties; however, the general trend of data is well reproduced by the model at all redshifts. Some dicrepancies are shown with the data of Smolčić et al. (2017b) at erg s-1Hz-1. They steeply increase as the luminosity decreases, much more than predicted by the model. As discussed by Bonaldi et al. (2019), however, the LF of radio-loud AGN estimated by Smolčić et al. (2017b) might be contaminated by the presence of radio-quiet AGN whose emission is dominated by the star formation of host galaxies.
Focusing on HK mode AGN only, the modelled LF increases from redshift 0 to at all (but especially at high) luminosities (see Fig. 14 and 15). For example, at the LF is larger than the local one by a factor 5 and 20 at and erg s-1Hz-1, respectively. This is due to the strong increase in the fraction of HK mode AGN going back in time and to the evolution of the Tucci & Volonteri (2017) mass function for high-accreting SMBHs. At higher redshifts, contrary to LK mode AGN, the HK mode LF still keeps increasing at high luminosities, while almost no evolution is found at intermediate to low luminosities, making the shape of the HK mode LFs quite flat from to erg s-1Hz-1. The relevance of HK mode AGN become more and more important for the LF with the increase in the redshift, and they are the dominant mode at () erg s-1Hz-1 at (3).
The evolution of the HK mode LF can be compared with observational data up to (Fig. 15). This is very consistent with data from Best et al. (2014) at , and partially consistent with Pracy et al. (2016) at . On the other hand, as already discussed for the local LF, the model underestimates estimates of Butler et al. (2019) at low redshifts. The discrepancy seems to substantially reduce going to higher redshifts, and we find a good match in the bin.
In principle, luminosity functions and number counts can be estimated by the model also at frequencies outside the 1–5 GHz interval. However, this is a critical operation. The model assumes a power-law spectrum with constant slope for flat- and steep-spectrum sources. This approximation is valid in a small range of frequencies, but clearly fails when spectra are extrapolated over a large interval. This is particularly true at high frequencies: flat-spectrum sources become the most relevant population and their spectral index at GHz are typically poorly correlated with the 1–5 GHz one (see e.g. Sadler et al. 2008; Tucci et al. 2008; Massardi et al. 2016).
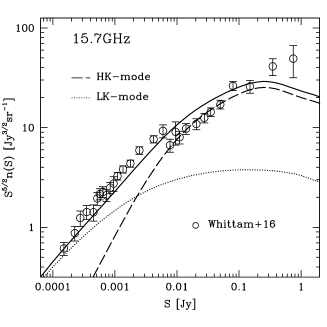
Accurate measurements of number counts of radio-loud AGN are available at 150 and 610 MHz. At 610 MHz the model is still able to provide a good fit of the data, as shown in Fig. 16. On the contrary, if we consider number counts at 150 MHz, we need to introduce a significant steepening of the average spectral index used for steep-spectrum sources, from to , in order to get the proper normalization. This steepening is consistent with the average spectral index found by Ocran et al. (2020) for radio-loud AGN that is . On the other hand, using the GLEAM 4 Jy sample, White et al. (2020) found a median spectral index of between 151 and 1400 MHz, with a steepening only within the GLEAM band (). This may indicate that the extrapolation of model predictions to frequencies as low as 150 MHz requires a more accurate method than a simple steepening of the average spectral index.
Finally, in Fig. 16 we compare model predictions to number counts from the Ninth Cambridge (9C) and Tenth Cambridge (10C) radio surveys at 15.7 GHz (AMI Consortium et al. 2011; Whittam et al. 2016a). They cover almost four orders of magnitude in flux density, from 0.1 mJy to 1 Jy (low flux densities covered by the 10C survey and high flux densities by the 9C survey). At Jy, where the two surveys overlap, number counts seem to present a break in normalization: the 9C number counts have a slope similar to the 10C value, but with a normalization lower by a factor of . The model follows the same overall slope of the observed number counts, but with a normalization that falls between the two different ones determined by the 10C and 9C surveys. We note, however, that these predictions are extrapolations using the 1–5 GHz average spectral indices, which are probably not suitable at higher frequencies. In addition, HK and LK mode AGN could have a different spectral behaviour between 5 and 20 GHz, as suggested by Sadler et al. (2014) and Whittam et al. (2016b).

4.6 Predictions on cosmic evolution of radio-loud AGN
Based on our best-fit model for LK and HK mode AGN, we can compute the AGN number and luminosity density as a function of redshift, up to , as follows:
| (26) |
In Fig. 17 we show the evolution of the number and luminosity density for the two AGN populations, and for their sub-class of flat-spectrum sources. We consider three different lower limits in the integral, , , and erg s-1Hz-1 (while the upper limit is fixed to erg s-1Hz-1). As discussed above and clearly shown in the figure, LK and HK mode AGN are expected to have a quite different cosmic evolution. LK mode AGN are much more numerous at all redshifts, but they are typically faint objects (the fraction of objects brighter than erg s-1Hz-1 is always %). The number density steadily decreases with redshift (except flat-spectrum sources that show a peak at –2), while the luminosity density peaks at . This implies a luminosity-dependent evolution for this class of AGN.
On the other hand, HK mode AGN show strong evolution until redshift 1.5, and modest or no evolution after that. However, the very flat slope in the number and luminosity density at high redshifts (), observed in Fig. 17, has to be taken with some caution. The model becomes less predictive at these redshifts (i.e. when the contribution to number counts is less important). In addition, the evolution of the fraction of high-accreting HK mode AGN has been described by a simple power law of redshift. Although it can be satisfactory in most of the range, this parametrization can fail at the highest redshifts when this fraction may stop growing or even decrease. Finally, most HK mode AGN are brighter than erg s-1Hz-1, and ten per cent or more have erg s-1Hz-1. No significant differences in the cosmic evolution of flat- and steep-spectrum sources are observed for HK mode AGN.

Model predictions of the number density evolution of steep-spectrum sources can be compared with results from Rigby et al. (2015) (see Fig. 18). They extend the analysis of Rigby et al. (2011) including fainter objects from the Subaru/XMM-Newton Deep Field, and covering the luminosity range of erg s-1Hz-1. The number density of steep-spectrum sources was estimated in five luminosity bins, using a grid-based modelling that takes into account source counts, redshift samples and local LFs, without any assumptions about the LF shape and high-redshift behaviour. The model seems to roughly match the Rigby et al. estimates in all the bins, apart from an excess of bright ( erg s-1Hz-1) sources at low redshifts.
5 Conclusions
In this paper we have developed a formalism to link the luminosity function of radio-loud AGN at GHz frequencies with the cosmological evolution of SMBHs. Our approach is based on physical and phenomenological relations that allow us to connect in a statistical way radio emission of AGN cores with SMBHs at their centre, through the fundamental plane of black hole activity, and radio emission from extended jets and lobes, through a power law relation because radio core and extended emission are both a good tracers of the kinetic jet power.
This formalism allows us to model the evolution of the luminosity function of radio-loud AGN. They are divided into two classes according to the measured Eddington ratio, , greater or smaller than the critical value 0.01 (LK mode and HK mode AGN, respectively). This critical value should correspond to the transition between radiatively inefficient and efficient accretion flows, and explain the observed dichotomies, for example, between FRI and FRII radio galaxies, low- and high-excitation AGN, and BL Lacs and flat-spectrum radio quasars.
The model takes as input the evolution of mass function and Eddington ratio distributions of SMBHs. We used the ones provided by Tucci & Volonteri (2017) at redshifts from 0 to 4. The model is also characterized by a remarkably limited number of free parameters, which mainly arise from uncertainties in the relations discussed above: after fixing tightly linearly correlated parameters, there are only two free parameters associated with LK mode AGN and five with HK mode AGN. We adopted a Markov chain Monte Carlo method to fix the free parameters of the model by fitting two different types of observational data sets: local (or low-redshift) LFs at 1.4 GHz of AGN populations, and differential number counts at 1.4 and 5 GHz. The model is able in general to provide a very good fit to them. This is especially relevant for 1.4 GHz number counts that are very accurately determined in the flux density range 1–100 mJy. The model is also in perfect agreement with number counts of LK and HK mode AGN estimated by Smolčić et al. (2017a) at that frequency (data that are not used in constraining the parameters of the model; see Section 4).
Moreover, our model predictions have been compared to the recent data on LFs of radio-loud AGN in the whole redshift range . Although they were not used in determining the free parameters of the model, we find again a very satisfactory fit of these data. In particular, the modelled AGN evolution seems to reproduce the observed one in the full range of luminosities covered by data, at least up to . In addition, the predicted evolution of the number density of steep-spectrum sources agrees quite well with the estimates from Rigby et al. (2015). The good performance of the model at these redshifts is remarkable, considering that all the free parameters but the fraction of HK mode AGN are redshift independent. An important role in driving the correct AGN evolution is given by the SMBH mass functions and Eddington ratio distributions provided as input to the model.
The AGN evolution with cosmic time obtained from the model is quite different for the two classes of AGN and dependent on the luminosity. The space density of AGN in LK mode typically declines with redshift, with the only exception of bright objects that positively evolves at . This produces a total luminosity density that peaks at –1.5. On the other hand, HK mode AGN show a positive evolution up to –2, weaker at low luminosities and stronger at high luminosities. At higher redshifts the evolution becomes very modest or null. The total number and luminosity density consequently keep increasing up to and then remain almost constant up to .
The main uncertainty in the model comes from the LF of HK mode AGN at low redshifts. The local LF for this class was recently estimated by three works (Best & Heckman 2012; Pracy et al. 2016; Butler et al. 2019) using different criteria to distinguish AGN and star-forming radio galaxies. Their results show a quite big discrepancy in the space density of HK mode AGN at low/intermediate luminositites ( erg s-1Hz-1): from a few per cent of the total (Best & Heckman 2012) to ten per cent (Pracy et al. 2016) or more (Butler et al. 2019). Such disagreement is probably due to misclassifications of faint sources. Independently of which observational data are taken into account, however, our model predicts a very low space density of HK mode AGN at low to intermediate luminosities, in agreement with the Best & Heckman (2012) measurements. The local fraction of high-accreting AGN in HK mode is expected to be very small, of the order of a few per mil or less, with a strong evolution with redshift. It is interesting to note (and in support of the goodness of the model) that at redshift , where the contribution of star-forming galaxies is negligible, model predictions closely agree with observational estimates. This is true even for the Butler et al. (2019) measurements that locally display the greatest differences from our model. Moreover, locally, a larger fraction of faint AGN in HK mode is probably incompatible with the positive evolution observed for this class of AGN and with the constraints imposed by the measured number counts.
Coefficients in the fundamental plane relation for HK mode AGN has been considered unknown by the model and determined by the fitting procedure. The model finds a positive correlation between the intrinsic core radio luminosity and the X-ray luminosity, steeper than the one observed for LK mode AGN, and in agreement with theoretical expectations for radiatively efficient accretion flows (e.g. Merloni et al. 2003). On the other hand, an anti-correlation is found between the intrinsic core radio luminosity and the SMBH mass that is consistent with estimates of Dong et al. (2014).
Observational data are not yet able to provide strong constraints on the coefficients of the relation between the luminosity of AGN intrinsic cores and of extended jets and lobes. Assuming a power-law relationship between them, we find a large degeneracy between the normalization and the power-law index of the relation. In addition, the normalization parameter can vary by orders of magnitude in the model, providing an equally good fit to the data (both for HK and LK mode AGN). In order to remove this degeneracy and to narrow the allowed parameters range, more information about different AGN sub-populations would be required; for example, accurate estimates of the local luminosity function of HK mode AGN at erg s-1Hz-1 could provide a better determination of their fraction, and significantly reduce the uncertainty on the core and extended emission relation. Similarly, estimates of the local luminosity function for flat-spectrum radio quasars and BL Lacs separately could give a relevant improvement in the parameter determination.
Finally, we have extrapolated model predictions outside the frequency range of 1–5 GHz. The comparison with the currently determined number counts at a few hundred MHz and 15 GHz show again the good performance of the model, although at 150 MHz the average spectral index of steep-spectrum sources has to be increased to fit the observed number counts. As a consequence, we expect that a more accurate modelling of AGN spectra for compact and extended emissions is required when a large range of frequencies is considered.
Predictions of the best-fit models for LFs and number counts of LK and HK mode AGN are available at the following webpage: https://www.astro.unige.ch/~tucci/AGNradioLF/.
Acknowledgements.
The authors thank the anonymous referee for the constructive remarks, which have improved the quality of the manuscript. MT warmly thanks M. Volonteri for the long discussions about SMBHs and AGN that allowed this work to be carried out, and M. Spinelli for the helpful discussion on MCMC methods. LT acknowledges the Spanish Ministerio de Ciencia, Innovación y Universidades for partial financial support under projects PGC2018-101814-B-I00 and PGC2018-101948-B-I00. Part of the analysis was performed using the cluster Yggdrasil of the University of Geneva.References
- Altschuler (1986) Altschuler, D. R. 1986, A&AS, 65, 267
- AMI Consortium et al. (2011) AMI Consortium, Davies, M. L., Franzen, T. M. O., et al. 2011, MNRAS, 415, 2708
- Becker et al. (1995) Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559
- Best & Heckman (2012) Best, P. N. & Heckman, T. M. 2012, MNRAS, 421, 1569
- Best et al. (2014) Best, P. N., Ker, L. M., Simpson, C., Rigby, E. E., & Sabater, J. 2014, MNRAS, 445, 955
- Bîrzan et al. (2008) Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859
- Blandford & Königl (1979) Blandford, R. D. & Königl, A. 1979, ApJ, 232, 34
- Bonaldi et al. (2019) Bonaldi, A., Bonato, M., Galluzzi, V., et al. 2019, MNRAS, 482, 2
- Bongiorno et al. (2012) Bongiorno, A., Merloni, A., Brusa, M., et al. 2012, MNRAS, 427, 3103
- Brookes et al. (2008) Brookes, M. H., Best, P. N., Peacock, J. A., Röttgering, H. J. A., & Dunlop, J. S. 2008, MNRAS, 385, 1297
- Butler et al. (2018) Butler, A., Huynh, M., Delhaize, J., et al. 2018, A&A, 620, A3
- Butler et al. (2019) Butler, A., Huynh, M., Kapińska, A., et al. 2019, A&A, 625, A111
- Cavagnolo et al. (2010) Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066
- Ceraj et al. (2018) Ceraj, L., Smolčić, V., Delvecchio, I., et al. 2018, A&A, 620, A192
- Cohen et al. (2007) Cohen, M. H., Lister, M. L., Homan, D. C., et al. 2007, ApJ, 658, 232
- Condon et al. (1998) Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693
- Daly et al. (2012) Daly, R. A., Sprinkle, T. B., O’Dea, C. P., Kharb, P., & Baum, S. A. 2012, MNRAS, 423, 2498
- de Zotti et al. (2010) de Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&A Rev., 18, 1
- Dong et al. (2014) Dong, A.-J., Wu, Q., & Cao, X.-F. 2014, ApJ, 787, L20
- Donoso et al. (2009) Donoso, E., Best, P. N., & Kauffmann, G. 2009, MNRAS, 392, 617
- Dunlop & Peacock (1990) Dunlop, J. S. & Peacock, J. A. 1990, MNRAS, 247, 19
- Falcke & Biermann (1995) Falcke, H. & Biermann, P. L. 1995, A&A, 293, 665
- Falcke et al. (2004) Falcke, H., Körding, E., & Markoff, S. 2004, A&A, 414, 895
- Fanaroff & Riley (1974) Fanaroff, B. L. & Riley, J. M. 1974, MNRAS, 167, 31P
- Franzen et al. (2016) Franzen, T. M. O., Jackson, C. A., Offringa, A. R., et al. 2016, MNRAS, 459, 3314
- Garn et al. (2008) Garn, T., Green, D. A., Riley, J. M., & Alexand er, P. 2008, MNRAS, 387, 1037
- Gendre et al. (2013) Gendre, M. A., Best, P. N., Wall, J. V., & Ker, L. M. 2013, MNRAS, 430, 3086
- Ghisellini & Celotti (2001) Ghisellini, G. & Celotti, A. 2001, A&A, 379, L1
- Ghisellini et al. (2009) Ghisellini, G., Maraschi, L., & Tavecchio, F. 2009, MNRAS, 396, L105
- Godfrey & Shabala (2013) Godfrey, L. E. H. & Shabala, S. S. 2013, ApJ, 767, 12
- Greene et al. (2019) Greene, J. E., Strader, J., & Ho, L. C. 2019, arXiv e-prints, arXiv:1911.09678
- Gregory et al. (1996) Gregory, P. C., Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427
- Griffin et al. (2019) Griffin, A. J., Lacey, C. G., Gonzalez-Perez, V., & Lagos, C. d. P. 2019, arXiv e-prints, arXiv:1912.09490
- Gültekin et al. (2009) Gültekin, K., Cackett, E. M., Miller, J. M., et al. 2009, ApJ, 706, 404
- Hardcastle et al. (2007) Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849
- Heckman & Best (2014) Heckman, T. M. & Best, P. N. 2014, ARA&A, 52, 589
- Heinz & Sunyaev (2003) Heinz, S. & Sunyaev, R. A. 2003, MNRAS, 343, L59
- Hickox & Alexander (2018) Hickox, R. C. & Alexander, D. M. 2018, ARA&A, 56, 625
- Hopkins et al. (2007) Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731
- Hurley-Walker et al. (2017) Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146
- Intema et al. (2011) Intema, H. T., van Weeren, R. J., Röttgering, H. J. A., & Lal, D. V. 2011, A&A, 535, A38
- Jester (2005) Jester, S. 2005, ApJ, 625, 667
- Jones et al. (2004) Jones, D. H., Saunders, W., Colless, M., et al. 2004, MNRAS, 355, 747
- Kellermann et al. (2016) Kellermann, K. I., Condon, J. J., Kimball, A. E., Perley, R. A., & Ivezić, Ž. 2016, ApJ, 831, 168
- Kellermann et al. (2004) Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539
- Koliopanos (2017) Koliopanos, F. 2017, in XII Multifrequency Behaviour of High Energy Cosmic Sources Workshop (MULTIF2017), 51
- Körding et al. (2006) Körding, E., Falcke, H., & Corbel, S. 2006, A&A, 456, 439
- Kratzer & Richards (2015) Kratzer, R. M. & Richards, G. T. 2015, AJ, 149, 61
- Kuehr et al. (1981) Kuehr, H., Witzel, A., Pauliny-Toth, I. I. K., & Nauber, U. 1981, A&AS, 45, 367
- Li et al. (2008) Li, Z.-Y., Wu, X.-B., & Wang, R. 2008, ApJ, 688, 826
- Lister (2003) Lister, M. L. 2003, ApJ, 599, 105
- Lister et al. (2009) Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874
- Lister & Marscher (1997) Lister, M. L. & Marscher, A. P. 1997, ApJ, 476, 572
- Liu & Zhang (2007) Liu, Y. & Zhang, S. N. 2007, ApJ, 667, 724
- Maccarone et al. (2003) Maccarone, T. J., Gallo, E., & Fender, R. 2003, MNRAS, 345, L19
- Machalski & Godlowski (2000) Machalski, J. & Godlowski, W. 2000, A&A, 360, 463
- Malefahlo et al. (2020) Malefahlo, E., Santos, M. G., Jarvis, M. J., White, S. V., & Zwart, J. T. L. 2020, MNRAS, 492, 5297
- Mao et al. (2017) Mao, P., Urry, C. M., Marchesini, E., et al. 2017, ApJ, 842, 87
- Marconi et al. (2004) Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169
- Massardi et al. (2016) Massardi, M., Bonaldi, A., Bonavera, L., et al. 2016, MNRAS, 455, 3249
- Massardi et al. (2010) Massardi, M., Bonaldi, A., Negrello, M., et al. 2010, MNRAS, 404, 532
- Mauch & Sadler (2007) Mauch, T. & Sadler, E. M. 2007, MNRAS, 375, 931
- McAlpine et al. (2013) McAlpine, K., Jarvis, M. J., & Bonfield, D. G. 2013, MNRAS, 436, 1084
- Merloni & Heinz (2007) Merloni, A. & Heinz, S. 2007, MNRAS, 381, 589
- Merloni & Heinz (2008) Merloni, A. & Heinz, S. 2008, MNRAS, 388, 1011
- Merloni et al. (2003) Merloni, A., Heinz, S., & di Matteo, T. 2003, MNRAS, 345, 1057
- Narayan & Yi (1994) Narayan, R. & Yi, I. 1994, ApJ, 428, L13
- Narayan & Yi (1995) Narayan, R. & Yi, I. 1995, ApJ, 452, 710
- Ocran et al. (2020) Ocran, E. F., Taylor, A. R., Vaccari, M., Ishwara-Chand ra, C. H., & Prandoni, I. 2020, MNRAS, 491, 1127
- O’Dea et al. (2009) O’Dea, C. P., Daly, R. A., Kharb, P., Freeman, K. A., & Baum, S. A. 2009, A&A, 494, 471
- Padovani et al. (2015) Padovani, P., Bonzini, M., Kellermann, K. I., et al. 2015, MNRAS, 452, 1263
- Padovani et al. (2007) Padovani, P., Giommi, P., Landt, H., & Perlman, E. S. 2007, ApJ, 662, 182
- Plotkin et al. (2012) Plotkin, R. M., Markoff, S., Kelly, B. C., Körding, E., & Anderson, S. F. 2012, MNRAS, 419, 267
- Pracy et al. (2016) Pracy, M. B., Ching, J. H. Y., Sadler, E. M., et al. 2016, MNRAS, 460, 2
- Quataert & Narayan (1999) Quataert, E. & Narayan, R. 1999, ApJ, 520, 298
- Rafferty et al. (2006) Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216
- Rafter et al. (2009) Rafter, S. E., Crenshaw, D. M., & Wiita, P. J. 2009, AJ, 137, 42
- Rawlings & Saunders (1991) Rawlings, S. & Saunders, R. 1991, Nature, 349, 138
- Rigby et al. (2015) Rigby, E. E., Argyle, J., Best, P. N., Rosario, D., & Röttgering, H. J. A. 2015, A&A, 581, A96
- Rigby et al. (2011) Rigby, E. E., Best, P. N., Brookes, M. H., et al. 2011, MNRAS, 416, 1900
- Sadler et al. (2007) Sadler, E. M., Cannon, R. D., Mauch, T., et al. 2007, MNRAS, 381, 211
- Sadler et al. (2014) Sadler, E. M., Ekers, R. D., Mahony, E. K., Mauch, T., & Murphy, T. 2014, MNRAS, 438, 796
- Sadler et al. (2002) Sadler, E. M., Jackson, C. A., Cannon, R. D., et al. 2002, MNRAS, 329, 227
- Sadler et al. (2008) Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2008, MNRAS, 385, 1656
- Saikia et al. (2015) Saikia, P., Körding, E., & Falcke, H. 2015, MNRAS, 450, 2317
- Saxena et al. (2017) Saxena, A., Röttgering, H. J. A., & Rigby, E. E. 2017, MNRAS, 469, 4083
- Shakura & Sunyaev (1973) Shakura, N. I. & Sunyaev, R. A. 1973, A&A, 500, 33
- Smolčić et al. (2017a) Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017a, A&A, 602, A2
- Smolčić et al. (2017b) Smolčić, V., Novak, M., Delvecchio, I., et al. 2017b, A&A, 602, A6
- Smolčić et al. (2009) Smolčić, V., Zamorani, G., Schinnerer, E., et al. 2009, ApJ, 696, 24
- Stickel et al. (1991) Stickel, M., Padovani, P., Urry, C. M., Fried, J. W., & Kuehr, H. 1991, ApJ, 374, 431
- Thomas et al. (2020) Thomas, N., Dave, R., Jarvis, M. J., & Angles-Alcazar, D. 2020, arXiv e-prints, arXiv:2010.11225
- Toffolatti et al. (1987) Toffolatti, L., Franceshini, A., de Zotti, G., & Danese, L. 1987, A&A, 184, 7
- Trump et al. (2011) Trump, J. R., Impey, C. D., Kelly, B. C., et al. 2011, ApJ, 733, 60
- Tucci et al. (2008) Tucci, M., Rubiño-Martin, J. A., Rebolo, R., et al. 2008, MNRAS, 386, 1729
- Tucci et al. (2011) Tucci, M., Toffolatti, L., de Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57
- Tucci & Volonteri (2017) Tucci, M. & Volonteri, M. 2017, A&A, 600, A64
- Urry & Padovani (1995) Urry, C. M. & Padovani, P. 1995, PASP, 107, 803
- van Velzen et al. (2012) van Velzen, S., Falcke, H., Schellart, P., Nierstenhöfer, N., & Kampert, K.-H. 2012, A&A, 544, A18
- Vardoulaki et al. (2020) Vardoulaki, E., Jiménez Andrade, E. F., Delvecchio, I., et al. 2020, arXiv e-prints, arXiv:2009.10721
- Vermeulen & Cohen (1994) Vermeulen, R. C. & Cohen, M. H. 1994, ApJ, 430, 467
- Šlaus et al. (2020) Šlaus, B., Smolčić, V., Novak, M., et al. 2020, A&A, 638, A46
- Weigel et al. (2017) Weigel, A. K., Schawinski, K., Caplar, N., et al. 2017, ApJ, 845, 134
- White et al. (1997) White, R. L., Becker, R. H., Helfand, D. J., & Gregg, M. D. 1997, ApJ, 475, 479
- White et al. (2020) White, S. V., Franzen, T. M. O., Riseley, C. J., et al. 2020, Publications of the Astronomical Society of Australia, 37
- Whittam et al. (2016a) Whittam, I. H., Riley, J. M., Green, D. A., et al. 2016a, MNRAS, 457, 1496
- Whittam et al. (2016b) Whittam, I. H., Riley, J. M., Green, D. A., & Jarvis, M. J. 2016b, MNRAS, 462, 2122
- Willott et al. (1999) Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017
- Wrobel & Krause (1990) Wrobel, J. M. & Krause, S. W. 1990, ApJ, 363, 11
- Xu et al. (2009) Xu, Y.-D., Cao, X., & Wu, Q. 2009, ApJ, 694, L107
- York et al. (2000) York, D. G., Adelman, J., Anderson, John E., J., et al. 2000, AJ, 120, 1579
- Yuan & Narayan (2014) Yuan, F. & Narayan, R. 2014, ARA&A, 52, 529
- Yuan & Wang (2012) Yuan, Z. & Wang, J. 2012, ApJ, 744, 84
- Yuan et al. (2017) Yuan, Z., Wang, J., Zhou, M., Qin, L., & Mao, J. 2017, ApJ, 846, 78
Appendix A Model predictions for LK mode AGN from different parameter sets
| model | |||||
|---|---|---|---|---|---|
| 1 | -9.17 | 1.24 | 1.15 | 35 | 240 |
| 2 | -10.86 | 1.30 | 1.05 | 32 | 230 |
| 3 | -12.37 | 1.36 | 0.94 | 31 | 228 |
| 4 | -13.95 | 1.42 | 0.81 | 33 | 212 |
| 5 | -15.41 | 1.47 | 0.64 | 36 | 224 |


As discussed in Sect. 4.1, model parameters for LK mode AGN are strongly correlated, and fixing one of the two between or is almost sufficient to define the model for that AGN population. The range of possible values for these two parameters is quite large, and very good fits to observational data are found for and . In this Appendix, we discuss how a different set of parameters can quantitatively affect the predicted LFs and number counts of LK mode AGN.
Along with the best-fit model (corresponding to Model 3 of Table 5), we select four other sets of parameters that cover the full range of possible parameter values (see Fig. 4 and Table 5). In Fig. 19 we show the results for the five different models in terms of the local LF and number counts. The local LFs (both total and flat-spectrum) are very similar at the luminosities covered by observations, with some differences only at higher luminosities.
The choice of the parameter set is more relevant for number counts. The shape of number counts is slightly dependent on the parameters: models with lower values of tend to have steeper number counts at sub-Jy–Jy levels and lower counts at mJy levels. Moreover, they predict significantly fewer flat-spectrum sources.
Differences in number counts can have a significant impact on the model performance when the full radio-loud AGN population is considered (i.e. LK mode plus HK mode AGN). Although they are not large, we find some changes in the accuracy of the global fit when using the five parameter sets for LK mode sources: the global best fit is obtained using Model 4 with that is taken as our reference model for LK mode AGN.