Modeling Incomplete Conformality during Atomic Layer Deposition in High Aspect Ratio Structures

As with most ALD modeling approaches [1], our model assumes that the processes are limited by the reactive transport of a single reactant species. For clarity, our discussion focuses on the H₂O-limited regime during ALD of Al₂O₃. However, the same insights are valid for the TMA-limited case and to similar reactants. We employ a first-order Langmuir surface model, combined with diffusive reactant transport for the calculation of the surface coverage $\theta$, building upon the model first proposed by Yanguas-Gil and Elam [8] by considering reversible kinetics and the impact of gas-phase diffusivity [6, 9, 16].

The following reaction pathways for an impinging water flux $\Gamma_{\mathrm{H_{2}O}}$ ($\mathrm{m^{-2}\,s^{-1}}$) are considered, represented in Fig. 1: Adsorption-reflection, mediated by a $\theta$-dependent sticking coefficient $\beta(\theta)=\beta_{0}(1-\theta)$, and desorption, given by an evaporation flux $\Gamma_{\mathrm{ev}}$ ($\mathrm{m^{-2}\,s^{-1}}$). In the original model [8] as well as in subsequent developments [22, 10, 23], irreversible kinetics are assumed, i.e., $\Gamma_{\mathrm{ev}}=0$. However, other works have highlighted the necessity of considering the reaction reversibility, leading to the following equation for the time evolution of $\theta$ at each surface point $\vec{r}$ [6, 9, 16]:

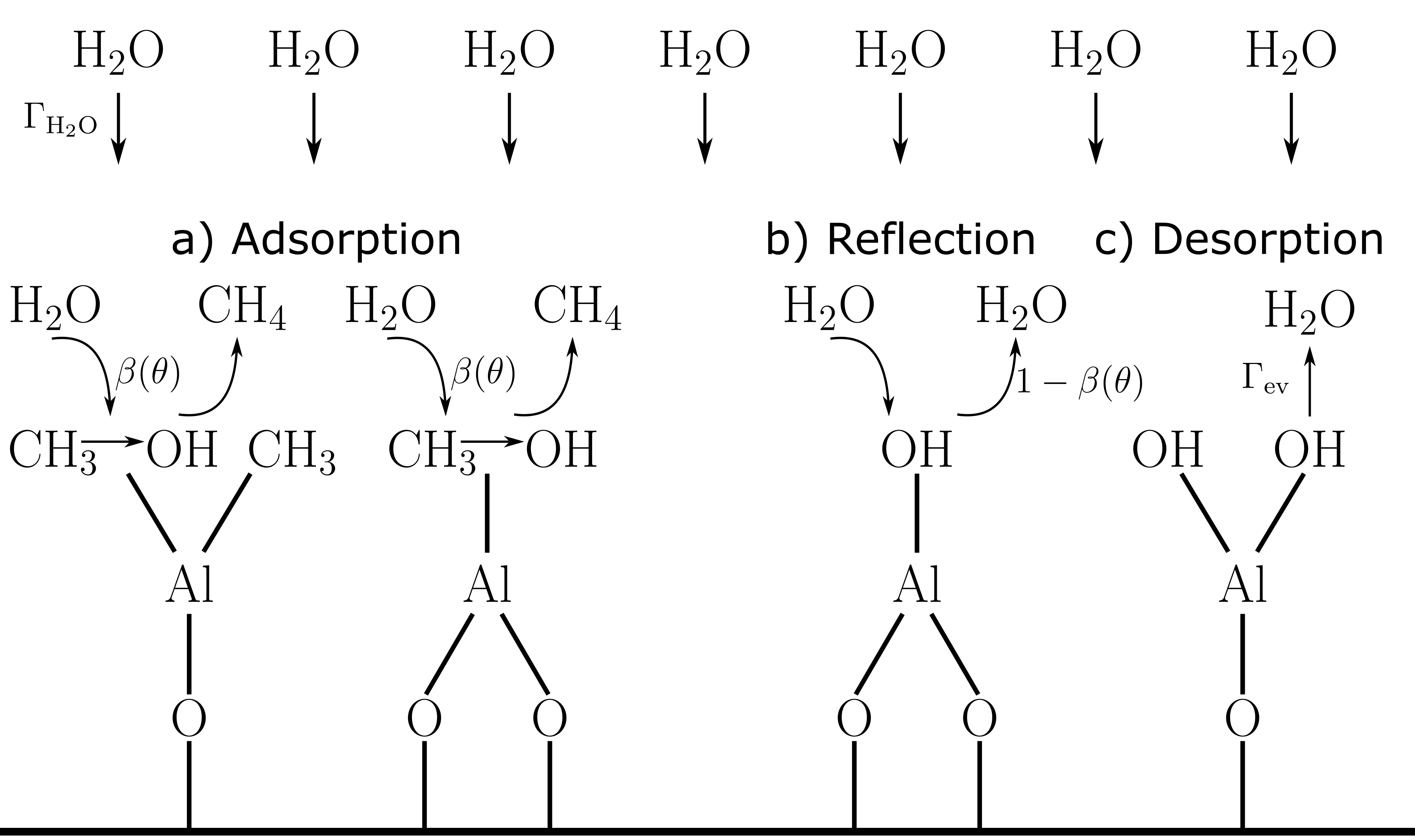
Equation (1) describes an empirical model with two phenomenological parameters: $\beta_{0}$ and $\Gamma_{\mathrm{ev}}$. The surface site area $s_{0}$ ($\mathrm{m^{2}}$) can be estimated with a “billiard ball” approximation from the deposited film density $\rho$ ($\mathrm{kg\,m^{-3}}$) and GPC (Å) [9]. In contrast to the steady-state assumption applied in, e.g., plasma etching simulations [19], we solve (1) up to the reactor pulse time $t_{p}$ ($\mathrm{s}$) using the forward Euler method with $N_{t}$ total time steps. The purge step is not considered.

A requirement for determining $\theta(\vec{r})$ is finding the distribution of the reactant flux $\Gamma_{\mathrm{H_{2}O}}(\vec{r})$. This calculation is challenging given that the $\beta(\theta)$ changes not only across the surface but also after the solution of each step of (1). Although powerful methods such as the Boltzmann transport equation [6], the lattice Boltzmann model [24], or Monte Carlo ray tracing can be used [11, 15], they require substantial computational resources.

To alleviate the computational burden, we assume a preferential transport direction, i.e., that the flux is equal on all surfaces at the same $z$ coordinate. This allows to calculate the flux using the continuity equation assuming diffusive flow in a cylinder of diameter $d$ ($\mu\mathrm{m}$) and length $L$ ($\mu\mathrm{m}$), with adsorption losses, given by a 1D differential equation [8, 25]:

In (2), $\bar{v}$ ($\mathrm{m\,s^{-1}}$) is the thermal speed and $\Gamma_{0}$ ($\mathrm{m^{-2}\,s^{-1}}$) is the flux of the reactant species inside the reactor, which can be calculated using the kinetic theory of gases [26] from the reactor temperature $T$ ($\mathrm{{}^{\circ}C}$), reactant molar mass $M_{A}$ ($\mathrm{kg\,mol^{-1}}$), and partial pressure $p_{A}$ ($\mathrm{mTorr}$). The frozen surface approximation is employed [8], that is, transport is assumed to reach equilibrium on a much faster timescale than the chemical evolution of the surface (i.e., $d\Gamma_{\mathrm{H_{2}O}}/dt=0$ even though $d\theta/dt\neq 0$). This approximation is generally accepted as valid for microscopic structures [25]. This equation is solved with a central finite differences scheme for each step of the solution of (1).

The system composed of (1) and (2) is, in essence, a re-statement of the established Yanguas-Gil and Elam model [8] with two main differences. First, the reversibility of the reactions is considered in (1). Also, the diffusivity $D$ ($\mathrm{m^{2}\,s}^{-1}$) is considered explicitly, which enables to combine Knudsen diffusion with gas-phase diffusion through the Bosanquet interpolation formula, which is discussed in the following paragraph. Both of these physical-chemical phenomena have been incorporated into modeling by previous studies either separately [6, 12] or jointly [9, 16]. However, such models, most notably the approach taken by Ylilammi et al. [9] and its subsequent expansion [16], rely on a different set of approximations for the calculation of the flux distribution inside the structure and do not compute a solution to (2). In their work, the frozen surface approximation is not employed and the partial pressure distribution, which is equivalent to the reactant flux distribution, is directly approximated as two separate regions, one linear and another exponentially decaying.

As previously indicated, $D$ can be calculated by considering two individual contributions: One stemming from reactant-wall collisions, i.e., the Knudsen diffusivity $D_{\mathrm{Kn}}$, and another stemming from reactant-reactant collisions, i.e., the gas-phase diffusivity $D_{A}$. Historically, Knudsen diffusion has been defined in terms of a long cylindrical tube [27] of diameter $d$, leading to the following expression for the diffusivity [17]:

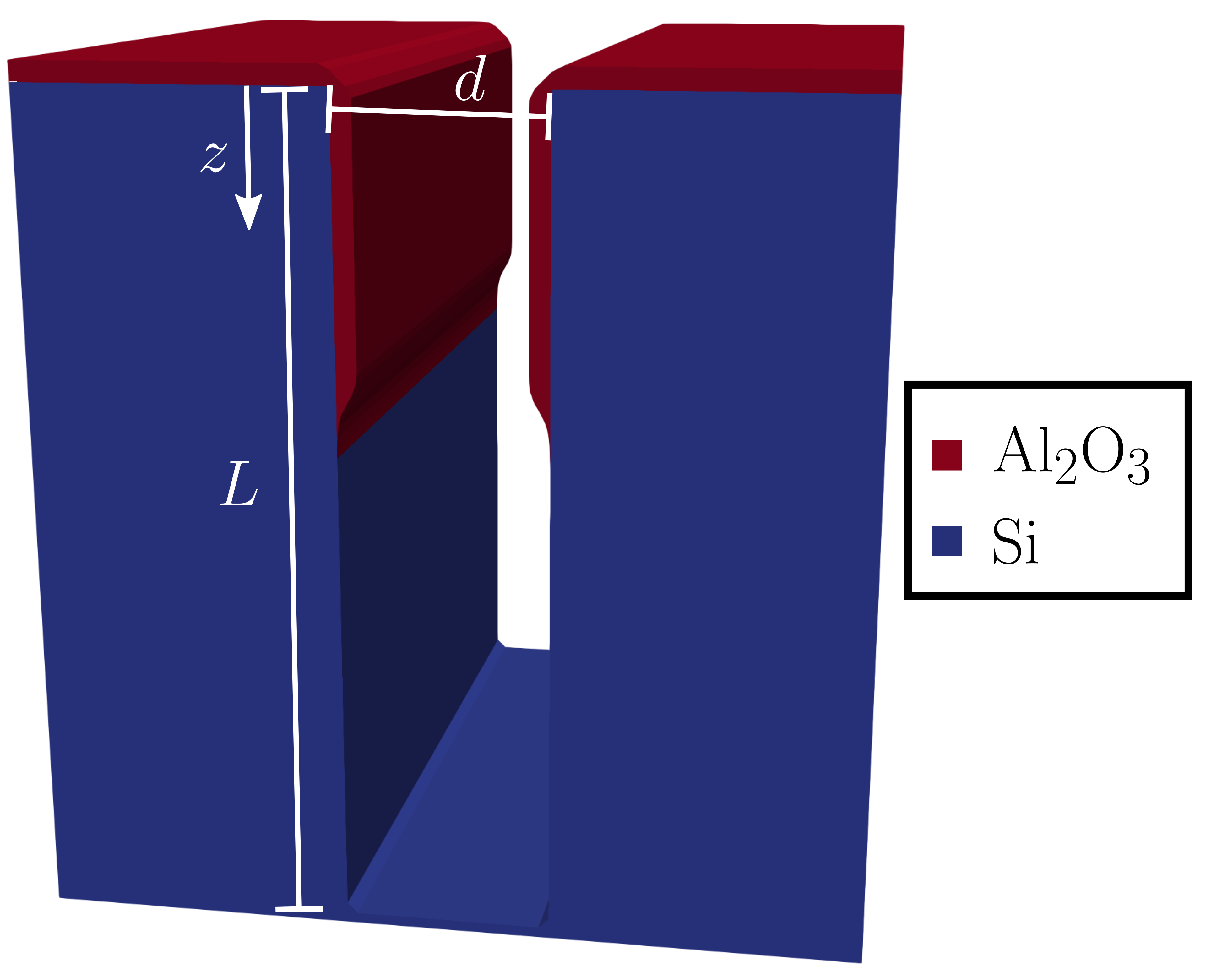
Therefore, when structures other than a long cylindrical tube are considered, some kind of mapping between the involved geometry and the standard cylinder must be provided. The development of such mappings has been the source of much controversy since the inception of the theory [28], leading to many lingering misconceptions (e.g., incorrect conductance values for square tubes). A further discussion of these misconceptions is outside of the scope of the presented research, instead, the simplified hydraulic diameter approximation is employed [9]. That is, the diameter $d$ in (2) and (3) is replaced with $d\to h_{d}\cdot d$, where $h_{d}$ is the hydraulic diameter factor and $d$ is a relevant physical dimension. For example, for a wide rectangular trench with opening $d$ (c.f. Fig. 3), $h_{d}$ is estimated to be $2$ [1, 9].

Equation (3) is valid when reactant-wall collisions are more likely than reactant-reactant collisions (i.e., Knudsen number $\mathrm{Kn}>10$). Should the rate of particle-particle collisions be comparable, i.e., $1<\mathrm{Kn}<10$, $D$ can be approximated with the Bosanquet interpolation formula [17]:

In (4), $D_{A}$ is the conventional Chapman-Enskog gas-phase diffusivity [26] calculated from the particle hard-sphere diameter $d_{A}$ ($\mathrm{pm}$). In this work, we assume only Knudsen diffusivity ($D_{A}\to\infty$), except when otherwise indicated.

In Fig. 2, the impact of the parameters $\beta_{0}$ and $\Gamma_{\mathrm{ev}}$ in the required $t_{p}$ for achieving $95\%$ saturation is presented. We define saturation as the final state of the surface coverage in the steady state, i.e., $d\theta_{\mathrm{sat}}(\vec{r})/dt=0$. Since this situation is only reached on the limit $t_{p}\to\infty$, we identify a relevant time as the pulse time necessary to reach $0.95\cdot\theta_{\mathrm{sat}}$. In addition, as $\theta_{\mathrm{sat}}$ is defined on the entire structure, the coverage value at the bottom of the structure, i.e., $\theta_{\mathrm{sat}}(z{=}L)$, is chosen as the representative value for analysis, since it is where the impact of the flux restriction is the largest.

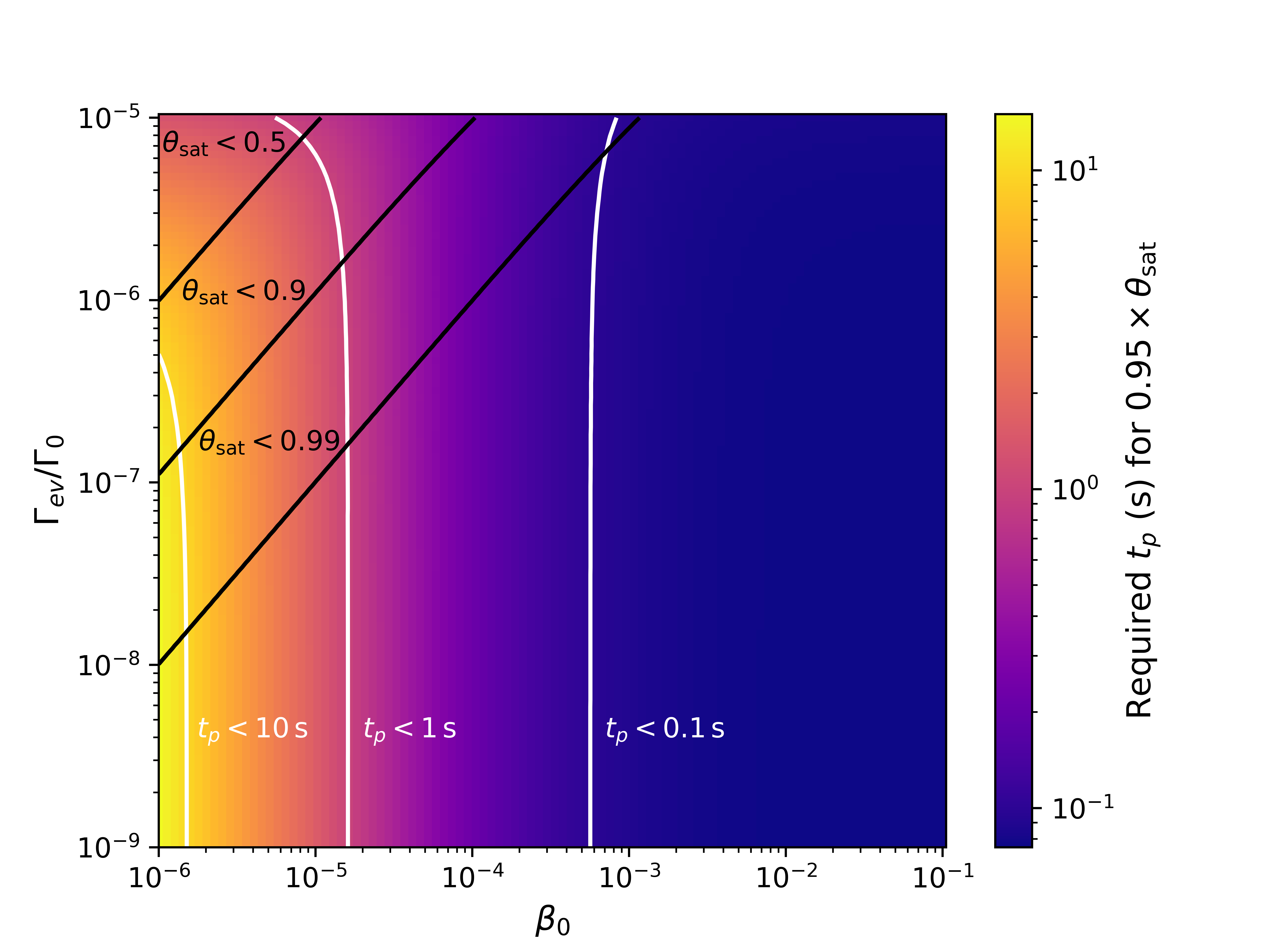
From Fig. 2, we observe that $\beta_{0}$ has the most influence on the saturation time. Instead of directly impacting $t_{p}$, $\Gamma_{\mathrm{ev}}$ greatly affects the maximum coverage achievable at the bottom of the structure. Therefore, it strictly limits the maximum aspect ratio achievable by a certain reactor configuration and must be considered in the design of novel technologies. In addition, previous work has shown that a high value of $\Gamma_{\mathrm{ev}}$ can impact the thickness profile particularly in the transition between a region with high growth to one with low growth [16].

In order to calculate the time evolution of the thickness profiles during the fabrication process in a manner compatible with simulation of further processing steps and DTCO, we employ the established level-set method [18, 19] as implemented in ViennaLS [20] and in Silvaco’s Victory Process [21]. In this method, the surface is described as the zero level-set of a 3D function $\phi(\vec{r})$ which evolves in time according to the level-set equation

where $V(\vec{r})$ is a scalar velocity field describing how the surface should evolve over time, i.e., how a material is grown or etched. An illustration of a simulated 3D trench geometry after ALD of Al₂O₃ is shown in Fig. 3.

The methodology presented in Section 2.1 is limited to calculating $\theta(\vec{r})$. However, it is not straightforward to map $\theta(\vec{r})$ into $V(\vec{r})$. Growth rates can be calculated cycle-by-cycle by evolving the surface by the molecular layer thickness [15], however, this imposes a performance penalty since the grid resolution must be small enough to capture the individual molecular layer and $\theta(\vec{r})$ must be calculated $N_{\mathrm{cycles}}$ times. This calculation repeats even though the geometry changes minimally between sequential cycles.

In order to capture a realistic ALD process with hundreds or thousands of cycles, a more efficient approach is required, bundling multiple cycles into the surface evolution step. For this, we introduce an artificial time $t^{*}=N_{\mathrm{cycles}}/C$ where $C$ is a numerical constant. It is important to note that $t^{*}$ is unrelated to $t_{p}$, since the latter is only required for the calculation of $\theta(\vec{r})$. In essence, to maintain unit consistency with 5, the time variable $t^{*}$ represents a bundle of multiple ALD cycles. Thus, the velocity field becomes

The constant $C$ can be chosen by considering the involved number of cycles such that $t^{*}\approx 1$. In fact, the choice of $C$ plays a limited role in the determination of the bundling. Instead, in the involved level-set based topography simulators, $V(\vec{r})$ is assumed to be constant during each time step $\Delta t$ of the solution of (5). According to the Courant-Friedrichs-Lewy (CFL) condition [18], the time step is limited to allow an evolution of at most one grid spacing $\Delta x$, i.e., $\Delta t<\Delta x/\max{|V(\vec{r})|}$. After each time step, the geometrical inputs of (2), namely $d$ and $L$, are updated. Thus, for (6) to be physically meaningful, $\Delta x$ must be small enough such that the a change in the geometry of its magnitude does not significantly impact $\theta(\vec{r})$.

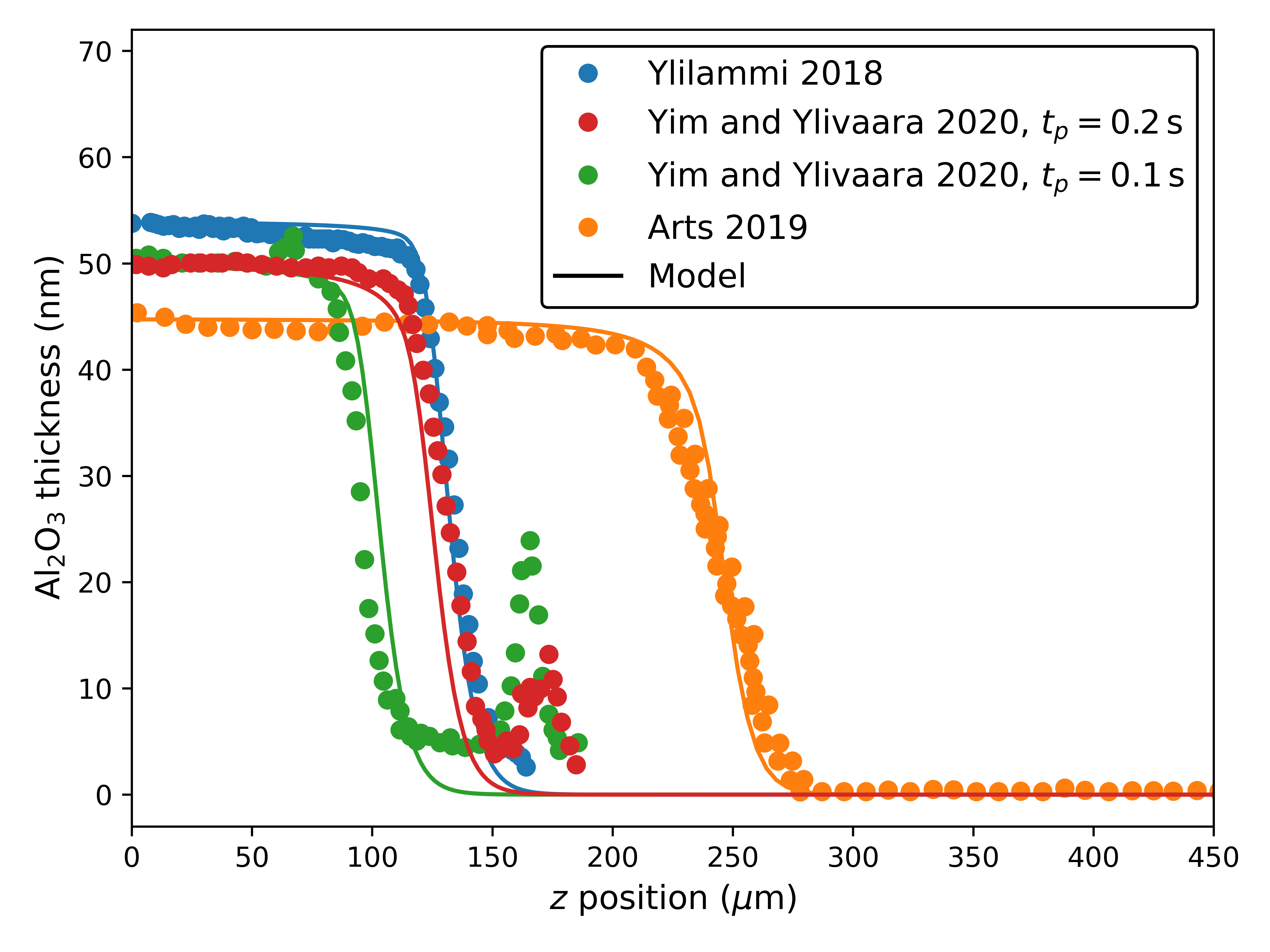
We calibrate our model to measured thickness profiles of Al₂O₃ in the H₂O-limited regime. Arts et al. [13] report film thicknesses in lateral HAR trench-like structures ($d=0.5\,\mu\mathrm{m}$, $L=5000\,\mu\mathrm{m}$) with an H₂O dose of approximately $750\,\mathrm{mTorr}{\cdot}\mathrm{s}$ after $400$ ALD cycles with a GPC of $1.12\,\text{\r{A}}$ at three calibrated substrate temperatures $T$ ($150\,\mathrm{{}^{\circ}C}$, $220\,\mathrm{{}^{\circ}C}$, and $310\,\mathrm{{}^{\circ}C}$). We estimate $t_{p}$ to be $0.1\,\mathrm{s}$. We were unable to reproduce the reported penetration depths with realistic values of density [29] in the calculation of $s_{0}$ [9] using the “billiard ball” approximation. Therefore, we treat $s_{0}$ as another parameter to be estimated, for which we obtain the value of $3.36\cdot 10^{-19}\,\mathrm{m^{2}}$. The parameters for each $T$ were obtained by manual adjustment and visual comparison to the experimental data and are provided in Table 1. The model comparison to experimental data is given in Fig. 4. The authors of the original work also estimate $\beta_{0}$ from the slope at $50\%$ height, and those values are reported in Table 1.

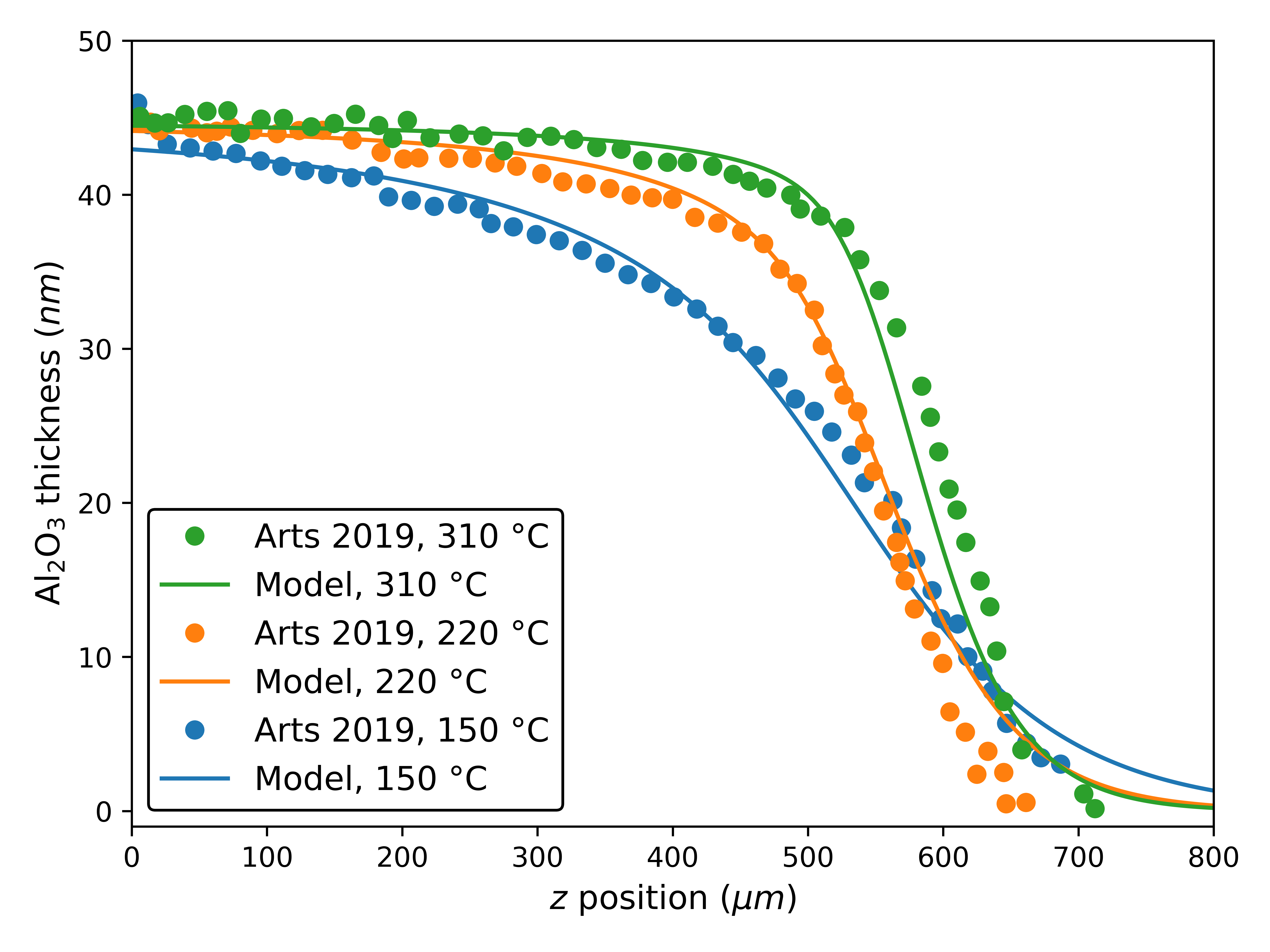
In Fig. 4, we note a good agreement between our topography simulations using the combined model for surface coverage and the reported experimental profiles. The estimated values of $\beta_{0}$ are also generally consistent with the estimated ranges from the original work, which is expected since it also relies on first-order Langmuir kinetics. However, we expect that our methodology provides a more accurate estimate, including on the discrepant value at $150\,\mathrm{{}^{\circ}C}$, since we consider the entire profile and we include $\Gamma_{\mathrm{ev}}$. Nonetheless, it is possible that we overestimate $\Gamma_{\mathrm{ev}}$ since we do not consider the purge step. The reduction in thickness and the less abrupt transition between the region with high growth for that profile is strong evidence of the important role of reversible reactions, which is supported by other modeling studies [16].

Due to the availability of data at different substrate temperatures, we perform an indicative Arrhenius analysis, shown in Fig. 5. In Fig. 5 (a), we observe that the $\beta_{0}$ increases and $\Gamma_{\mathrm{ev}}$ decreases with increasing $T$. This suggests that the increase in temperature not only makes the reaction more efficient but also, counter-intuitively, reduces the reversibility of the reaction. This is the cause of the negative value of $E_{A}$ on the Arrhenius fit of $\Gamma_{\mathrm{ev}}$, which is not itself the true activation energy of the reaction. Instead, we interpret the value of $E_{A}$ from the linear fit of $\beta_{0}$ ($0.178\,\mathrm{eV}$) as that representing the energy barrier involved in the reaction, since it is the one which must be overcome on a clean surface (i.e., $\theta{=}0$). Although this value is lower than first-principle studies suggest ($1.101\,\mathrm{eV}$) [30], it is consistent with a recent experimental analysis exploring a two-stage reaction, where $E_{A}$ is estimated as $0.166\pm 0.02\,\mathrm{eV}$ [31]. This two-stage reaction is a possible cause of failure of the “billiard ball” approximation for $s_{0}$.

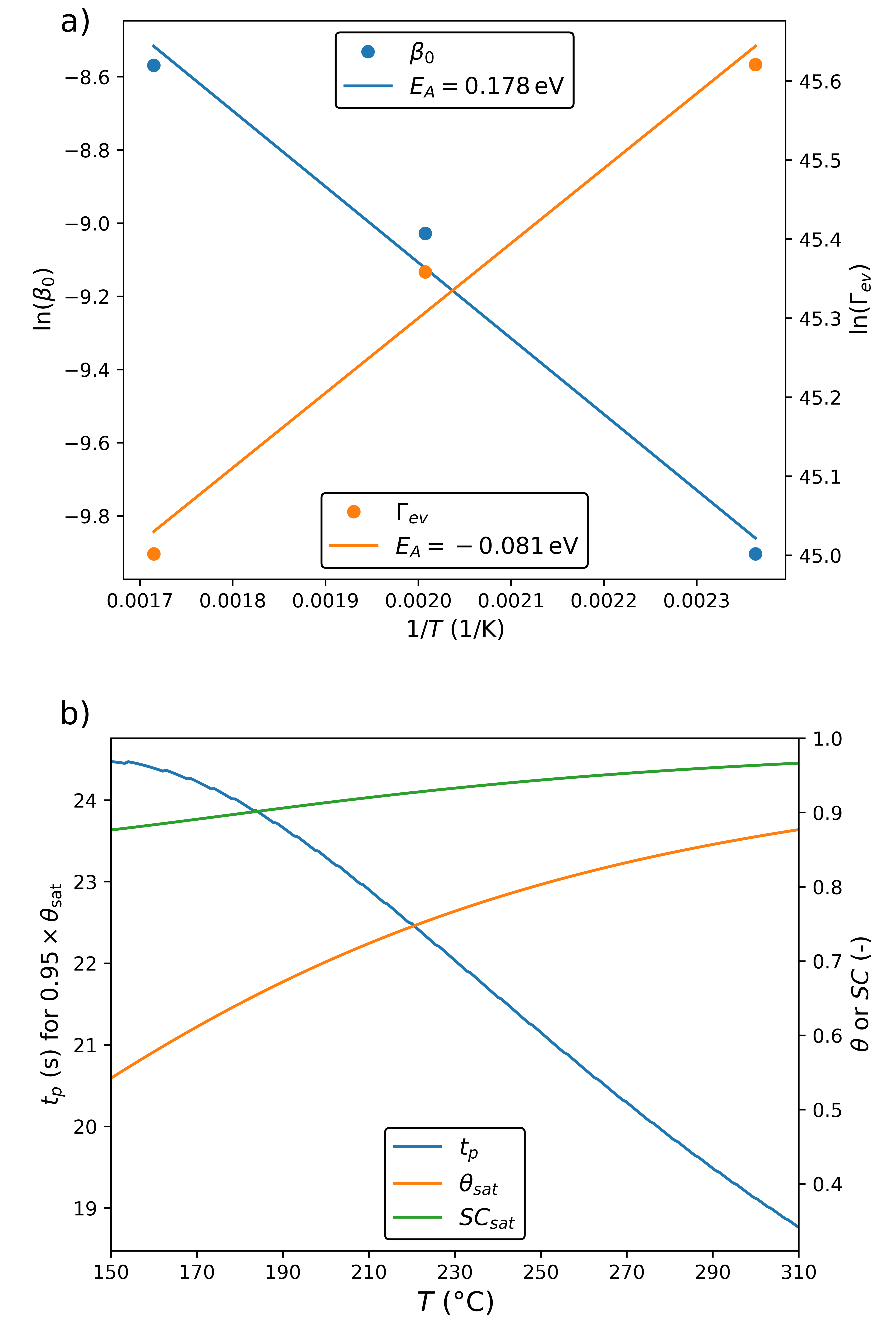
From the fitted Arrhenius relationships, both model parameters ($\beta_{0}$ and $\Gamma_{\mathrm{ev}}$) can be expressed as functions of the single physical variable $T$. Thus, the parameter analysis from Fig. 2 can be reduced from three to two dimensions, as shown in Fig. 5 (b). We observe that the saturation $t_{p}$ reduces and $\theta_{\mathrm{sat}}$ at $z=L$ increases with higher temperatures, as is expected from a more thermodynamically favorable reaction. However, in many experimental situations $\theta$ is not easily measurable. Instead, the step coverage ($\mathrm{SC}$) is commonly measured [25]. After saturation, i.e. $d\theta/dt=0$, we estimate the step coverage to be $\mathrm{SC}_{\mathrm{sat}}=\theta_{\mathrm{sat}}({z=L})/\theta_{\mathrm{sat}}({z=0})$. Interestingly, we note that $\mathrm{SC}_{\mathrm{sat}}$ is high and nearly constant for the entire tested temperature range even though $\theta_{\mathrm{sat}}$ has a larger variation. Thus, we expect that, at low temperatures, the film quality could be low due to the presence of defects such as vacancies and voids.

Similarly to Section 3.1, the model is manually calibrated to published thickness profiles of Al₂O₃ in the TMA-limited regime. Due to the comparatively higher complexity of TMA, this step has received more research attention, therefore, we are able to simultaneously apply our model to multiple independent experiments in similar lateral HAR structures ($d=0.5\,\mu\mathrm{m}$) [9, 13, 32]. All available reactor and film parameters were taken directly from the original publications. The unavailable data was estimated as follows: For Ylilammi et al. [9] (and footnotes from [32]), we estimate $p_{A}=325\,\mathrm{mTorr}$; for Arts et al. [13], $t_{p}=0.4\,\mathrm{s}$ and $\rho_{\mathrm{Al_{2}O_{3}}}=3000\,\mathrm{kg}/\mathrm{m^{3}}$; and for Yim and Ylivaara et al. [32], $p_{A}=160\,\mathrm{mTorr}$.

Since all reported thickness profiles were obtained on a restricted range of set temperatures ($275\,^{\circ}\mathrm{C}$ in [13], $300\,^{\circ}\mathrm{C}$ otherwise), we manually calibrate our model to all profiles with the same parameter set presented in Table 2, including the estimates of $\beta_{0}$ from the original works. The disparity is likely due to the effect of $\Gamma_{\mathrm{ev}}$, which is corroborated by the most similar value being that from [9], whose approach also considers reversible kinetics.

The comparison to the published measured profiles is provided in Fig. 6, showing good agreement. This is strong evidence for the hypothesis discussed in Section 2.1 that the model parameters are determined by the reactor setup, most importantly the reactor $T$. The peaks shown in the experimental data from [32] are disregarded since they are reported to be spurious interactions with the pillars sustaining the structure.

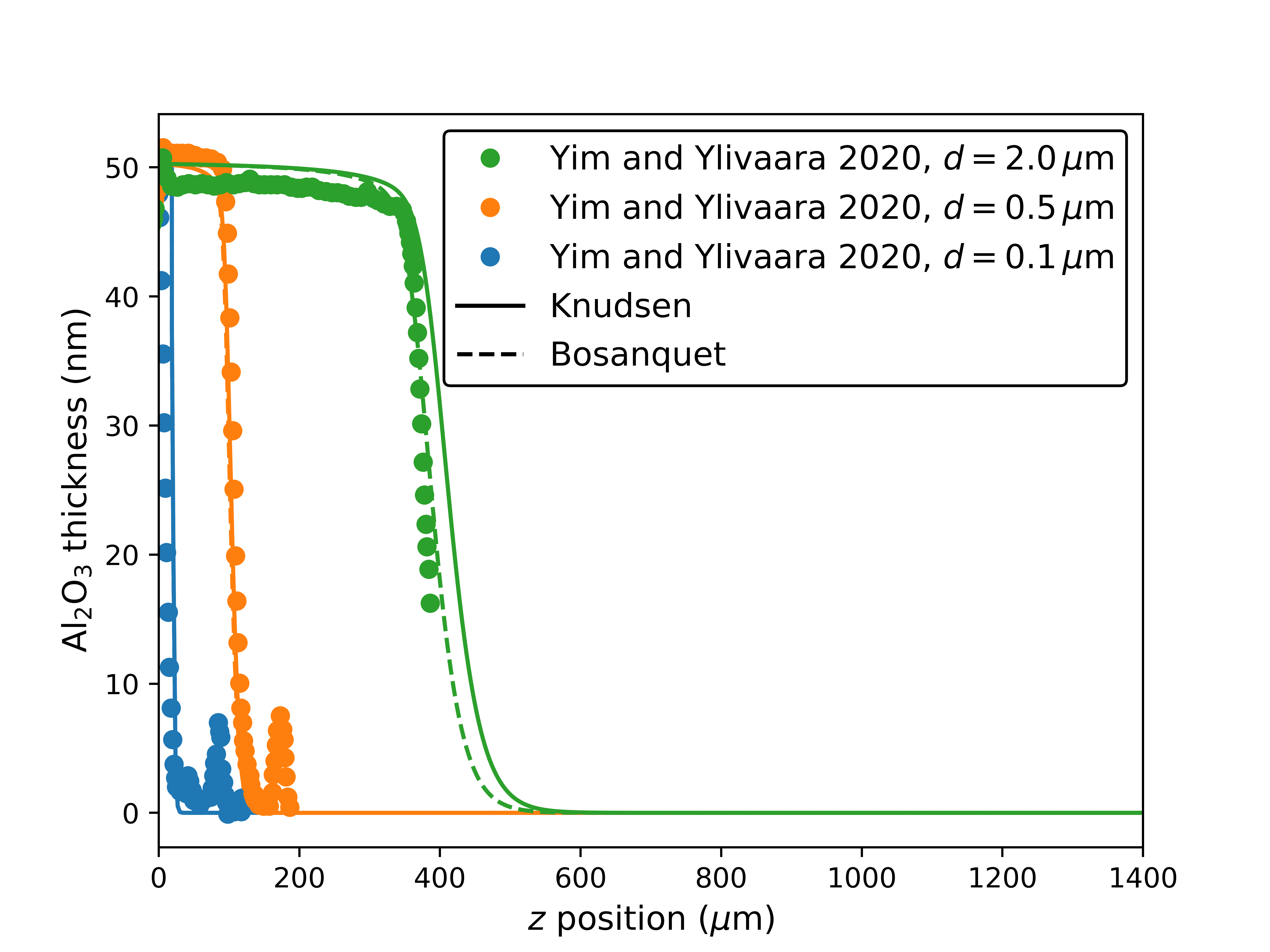
We reproduce additional experiments by Yim and Ylivaara et al. [32] in lateral HAR structures with different initial openings $d$, shown in Fig. 7. The discrepancy in the structure with $d=0.1\,\mu\mathrm{m}$ is due to the limits of our model when the opening becomes fully constricted. In this situation, the approximation that the entire geometry can be represented by an evolving but single value of $d$ starts to fail. One additional limitation is the failure of the hydraulic diameter approximation in a constricted structure, since it is not rigorously justified and has significant discrepancies with regards to established results [28]. For the structure with opening $d=2.0\,\mu\mathrm{m}$, pure Knudsen diffusivity is no longer valid, since $\mathrm{Kn}\approx 8.9$. We recover accuracy by using (4) (marked “Bosanquet”) which is calculated using the hard-sphere diameters of TMA $d_{\mathrm{TMA}}=591\,\mathrm{pm}$ and of nitrogen (N₂, the carrier gas) $d_{\mathrm{N_{2}}}=374\,\mathrm{pm}$ [9].