Model for independent particle motion
Abstract
Independent particle model in nuclear physics assumes that the nucleon in the nucleus moves in the average (mean field) potential generated by all other nucleons. This chapter gives a short overview of basic features of the independent particle motion in atomic nuclei and its theoretical realization in the framework of shell models for spherical, deformed and rotating nuclei as well as in more sophisticated approaches such as microscopic+macroscopic model and density functional theories. Independent particle motion of nucleons leads to global and single-particle consequences. The global ones manifest themselves in the shell structure and its consequences for global structure of nuclear landscape, the existence of superheavy nuclei and the superdeformation at high spin are briefly reviewed. The latter shows itself in the single-particle properties such as energies, alignments and densities; their manifestations are illustrated on specific examples.
1 Introduction
The basic idea of the independent particle model is that nucleon (proton or neutron) moves in an average (mean field) nuclear potential and this motion is independent of motion of other nucleons. This allows to replace the complicated solution of the problem of interacting particles ( is total number of nucleons in the nucleus) with much simpler problem of noninteracting particles in the mean field potential. This mean field potential can be either designed in a phenomenological way or calculated fully self-consistently from effective interaction. As discussed in this chapter, many properties of the nuclei have been described with high accuracy within such frameworks and many new phenomena (for example, superheavy nuclei and superdeformation at high spin) have been predicted theoretically and later observed experimentally. Independent particle model in its different realizations provides also the basis [mean field] for the models which take into account residual interactions such as pairing, vibrations, particle-vibration coupling etc. These interactions are typically included either by adding respective terms to the version of independent particle model or by the modification of the formalism.
The basic features of independent particle model, its realization in the shell model variants, microscopic+macroscopic model and covariant density functional theory will be discussed in this chapter. In addition, some manifestations of the independent particle motion emerging from the shell structure and single-particle properties will be considered. In no way, this chapter should be considered as ”all-inclusive”: it only scratches the surface of huge body of experimental and theoretical results. More comprehensive and detailed reviews on specific phenomena/theoretical approaches are quoted in respective sections. In addition, some aspects of the independent particle motion are discussed in the books Bohr1975 ; RS.80 ; Casten-book ; NilRag-book .
2 Independent particle model
The solution of the many-body nuclear problem for a nucleus consisting of nucleons ( protons and neutrons) requires the solution of the eigenvalue problem Bohr1975 ; RS.80
| (1) |
The Hamiltonian of the system could be either in non-relativistic (Schrödinger equation) or relativistic (Dirac equation) forms. It contains the kinetic and potential energy contributions from each nucleon
| (2) |
and includes two-body interaction between - and -th nucleons.
The total wave function of the nucleus in the state with quantum numbers has to be expressed in terms of the ones of the individual nucleons . Here , and are position, spin and isospin variables, respectively. For simplicity, in further discussion will represent all independent variables of the -th nucleon. Total wave function of the system of the particles has to be antisymmetric with respect of the exchange of the coordinates of two particles. Thus, a many-body state is written in the form of the Slater determinant RS.80
| (7) |
The factor is due to normalization. The choice of the single-particle wavefunctions defines the type of the many-body state. It is important to remember that the single-particle spectrum is infinite one. Thus, in practical applications respective Hilbert space is truncated most frequently based on energy considerations.
In nuclear systems it is possible to recast Eq. (1) in the form
| (8) |
where is the residual two-body interaction and is the single-particle hamiltonian. This recast essentially means that the part of original two-body interaction is moved to the single-particle hamiltonian . The latter can be chosen in such a way that the contribution of residual interaction becomes rather small or even negligible.
Independent particle model corresponds to the situation when second term in Eq. (8) is neglected. Thus, the nuclear Hamiltonian is a sum of single-particle terms
| (9) |
and eigenvalue problem is reduced to
| (10) |
where stand for the single-particle energy.
Independent particle model allows to reduce the nuclear many-body problem from complicated two-body treatment to much simpler one-body one. It also relies on the use of the single-particle potentials. Independent particle model corresponds to the description of a nucleus in terms of noninteracting particles in the orbitals of these single-particle potentials which itself are produced by all the nucleons. Thus, nucleons move essentially free in these potentials. In this model, the ground state is formed by filling all the single-particle states located below the Fermi level. The excitation of the particle from occupied state below this level to an empty one above it leads to an excited state. This process is called as a particle-hole excitation.
The justifications for an independent particle model have been discussed in a number of publications Bohr1975 ; Casten-book . The mean free path between collisions of the constituent nucleons is large compared to the average distance between them and in some cases it could be larger than the dimensions of the nucleus. As a consequence, the interactions between nucleons contribute mostly to the smoothly varying average potential in which the particles moves independently. One can arrive to the same conclusion by taking into account the fact that the nucleons occupy only approximately 1% of the volume of the nucleus. This estimate follows from the consideration of nucleons as hard spheres of radius fm. This value of corresponds to the half of the closest distance which two nucleons can approach each other due to infinite repulsion (see discussion in Sec. 2-5b of Ref. Bohr1975 ). For such value of , nuclear matter behaves close to the free gas of nucleons with very rare head-on collisions of nucleons. The Pauli principle and the weakness of strong nuclear interaction when compared with characteristic kinetic energies of nucleons inside the nucleus are other contributing factors for the justification of independent particle model Bohr1975 ; Casten-book .
3 Spherical shell model
The discussion of previous section clearly illustrates the need for the introduction of the single-particle potential. This one-body potential can be introduced either in phenomenological or in a fully self-consistent ways. In the former case, one deals with phenomenological Nilsson, Woods-Saxon or folded Yukawa potentials. Self-consistent single-particle potentials are formed as a result of the solution of the many-body nuclear problem within non-relativistic and relativistic density functional theories (DFTs); note that these potentials are not treated separately from the rest of the nuclear many-body problem.

To illustrate the major physics aspects behind these potentials and for pedagogical reasons, the harmonic oscillator (HO) potential and its modifications relevant for nuclear physics problems will be considered here. The single-particle hamiltonian of the nucleon with mass entering into Eq. (9) is given by
| (11) |
where the central potential
| (12) |
is pure HO potential representing one-body (mean) potential (field). This hamiltonian in spherical coordinates is given by
| (13) |
and the wave function representing the solution of the eigenvalue problem is separable in angular (, ) and radial () coordinates: ). Here, and are radial and angular [given by spherical harmonics] wave functions, respectively. Note that the latter is the eigenfunction of the angular momentum operator :
| (14) |
The solutions of the hamiltonian with only central potential included are shown in the left column of Fig. 1. The spectrum of single-particle states, characterized by principal quantum number , is equidistant in energy with high degree of the degeneracy of the single-particle states.
The realistic nuclear potential is located somewhat between pure HO and square well potentials. To correct for that a centrifugal potential has to be added to ; it is usually parametrized as NilRag-book ; N.55 ; RNS.78 :
| (15) |
Within the shell this term leads to a lowering in energy of high- states relatively to low- ones and to a removal of the degeneracy between the states (see middle panel of Fig. 1).
In addition, there is a coupling between spin () and orbital motion of the single particle which, in general, is given by the following interaction term:
| (16) |
Here indicates the spin-orbit potential which may be different from the central one and is the coupling constant of spin-orbit interaction. In the case of harmonic oscillator potential this term can be further simplified to . The presence of spin-orbit potential leads to the lowering and rising in energy of the and states emerging from the state with a given orbital angular momentum (see right column in Fig. 1). Only with this interaction included, it is possible to reproduce experimentally observed shell closures at particle numbers 2, 8, 20, 28, 50, 82 and 126 Bohr1975 ; Casten-book ; RNS.78 . Note that the single-particle state is completely defined by a set of quantum numbers .
The combined potential
| (17) |
is usually called as modified oscillator (MO) or Nilsson potential. This potential is defined by three parameters , and for each kind of nucleons ( or ). defines the radius of respective matter distribution, simulates the surface diffuseness depth, and is the strength of spin-orbit interaction. The Coulomb potential is not directly included into the MO potential but it is effectively accounted by the differences of the above mentioned parameters in the proton and neutron subsystems.
Although the MO potential is still extensively used in nuclear structure studies, more realistic treatment of the single-particle degrees of freedom is achieved by means of the Woods-Saxon (WS) GISF.73 ; CDNSW.87 ; BDNO.89 and folded Yukawa (FY) MN.81 ; DPB.16 potentials. This is because they have more realistic shape of the potential (thus eliminating the need for ) and explicitly include the Coulomb interaction. Their structure is illustrated below for the WS potential
| (18) |
where central potential is given by
| (19) |
with being the potential depth, the surface thickness and the nuclear radius (with typical value of fm). Here represents the Coulomb potential. However, numerical realization of these potentials is more complicated as compared with the MO potential. The detailed comparison of the WS and MO potentials is presented in Ref. BDNO.89 .
4 Deformed shell model
In deformed nuclei, the shape of the nuclear surface is generally parametrized by means of a multipole expansion of the radius in terms of the shape parameters RS.80 ; a typical parametrization is
| (20) |
where are the deformation parameters and is the radius of the sphere with the same volume. For axially symmetric nuclear shapes and quadrupole deformation is dominant RS.80 ; CAFE.77 . For simplicity, higher multipolarity deformations such as octupole , hexadecapole , … are not taken into account in the present discussion. Note that in the literature different parametrizations of the deformations of the single-particle potential exist (see discussion in Refs. NilRag-book ; CAFE.77 ).
There are two facts which affect the consideration of single-particle potentials in deformed nuclei N.55 . First, this potential should follow the nuclear density distribution. Second, in deformed nuclei the oscillator frequencies ( and ) are different along different principal axis of nuclear ellipsoid. As a result, the central potential of Eq. (12) is modified in the following way:
| (21) |
Since nuclear matter is highly incompressible, the change of the shape of the nucleus from spherical to ellipsoidal should not modify the volume of the nucleus. This is accounted by the volume-conservation condition
| (22) |
Assuming axial symmetry around the axis, i.e. , the central potential can be rewritten as
| (23) |
where stands for the quadrupole deformation of the potential (the measure of the deviation from spherical shape). Thus, the hamiltonian of the Nilsson model becomes
| (24) | |||||
Note that for simplicity only general outline of the Nilsson model is provided here N.55 . Technical details of the solution of the Nilsson potential are discussed in Refs. NilRag-book ; N.55 ; BDNO.89 . Note also that there are generalizations of the Woods-Saxon and folded Yukawa potentials to deformed shapes GISF.73 ; CDNSW.87 ; MN.81 ; DPB.16 ; CAFE.77 .
As a result, the focus here is on the consequences of the breaking of spherical symmetry on the single-particle states. They are usually illustrated by means of the Nilsson diagrams which show the evolution of the energies of deformed single-particle states as a function of deformation (see, for example, Figs. 3 and 5 in Ref. N.55 , Figs. 8.3 and 8.5 in Ref. NilRag-book and Fig. 3 in Ref. PhysRep-SBT for such diagrams obtained with the Nilsson potential). The general structure (and frequently fine details) of the Nilsson diagrams obtained in phenomenological single-particle potentials and in self-consistent models are very similar. This clearly indicates that the former have deep microscopic roots. Thus, the results obtained in covariant density functional theory presented in Fig. 2 are used here to illustrate the impact of deformation on the single-particle states.


Several major features emerge on transition from spherical to deformed shapes. First, it removes the degeneracy of the spherical subshells and deformed single-particle states are only two-fold degenerate. Second, the deformed single-particle states are defined by approximate Nilsson quantum numbers (note they are frequently shown in inverted order of ). Here, () stands for the projection of the total (orbital) single-particle angular momentum on the axis of symmetry, is the principal quantum number and is the number of nodes of the wavefunction along the symmetry axis. Note that the parity of the state is defined by . For prolate shapes, the deformed orbitals emerging from a given spherical -subshell are split in such a way that the state with is always lowest in energy while that with is the highest one. The states with intermediate values are arranged in such a way that the energies of two neighboring deformed states satisfy the condition (see Fig. 2).The order of the states is inverted for the oblate shapes NilRag-book ; N.55 . Third, as a consequence of these modifications of the single-particle states with deformation, spherical shell gaps disappear and new deformed gaps, which are comparable in size with minor shell gaps at spherical shape, appear. These gaps are encircled in Fig. 2).
4.1 Cranked shell model
Rotation is the phenomenon which appears in all branches of physics, from galaxies down to atomic nuclei. In the latter, it is a collective phenomenon in which many nucleons define a nuclear deformation and contribute to rotational motion. Note that contrary to classical mechanics, a collective rotation along the symmetry axis of nuclear density distribution is forbidden in quantum mechanics.
The simplest way to describe the properties of rotating nuclei in a microscopic way is to use the cranking-model approximation suggested by Inglis Ing.54 ; Ing.56 . Over the years this model has been successfully applied to the description of different phenomena in rotating nuclei NilRag-book ; PhysRep-SBT ; VDS.83 ; Szybook ; MPZZ.13 . The consideration here is restricted to one-dimensional cranking in which the nuclear field is rotated externally with a constant angular velocity around a principal axis usually defined as the -axis. This is done in order to outline the basic features of this model.

The basic idea of the cranking model is that a nucleus with angular momentum can be described in terms of an intrinsic state at rest in a rotating frame. In the one-dimensional cranking approximation for collective rotation, the total cranking Hamiltonian (or Routhian) for a system of independent particles is given by
| (25) |
where is the total Hamiltonian in the laboratory system, is the -component of the total angular momentum and is the single-particle Hamiltonian in the rotating system
| (26) |
with being the single-particle Hamiltonian in the laboratory system and the -component of the single-particle angular momentum. In Eq. (25), the sum extends over the occupied proton and neutron orbitals. The term in Eq. (25) is analogous to the Coriolis and centrifugal forces in classical mechanics.
Then the total energy in the laboratory system is given as
| (27) |
and the total spin by
| (28) |
where are the single-particle eigenfunctions in the rotating system and the corresponding eigenvalues (single-particle routhians). The approximation used in Eq. (28) is valid only in the limit of high spin ().
The evolution of the single-particle states in rotating potential is shown in Fig. 3. There are several important features. First, the time-reversal symmetry is broken in rotating potential and two-fold degeneracy of deformed single-particle states, which exist in non-rotating nuclei, is removed. As a consequence, each single-particle orbital has additionally to be characterized by signature quantum number (either or ) NilRag-book ; PhysRep-SBT ; VDS.83 . This quantum number is a consequence of the fact that full cranking Hamiltonian is invariant with respect to a rotation through an angle around the cranking axis (-axis)
| (29) |
The eigenvalues of are , where is the signature exponent quantum number. Alternatively, one can define signature quantum number as . Signature quantum number () of a single-particle orbital could take the or values. Similar to parity, this classification of the single-particle states is an important tool for identifying the nucleon orbitals in the rotating nuclear potential.
Second, the coupling between the different single-particle orbitals increases with increasing rotational frequency. As illustrated in Fig. 3 this leads to the change of the dominant Nilsson components of the wavefunction. Third, the slope of the orbitals in Fig. 3 corresponds to the single-particle alignment NilRag-book ; VDS.83
| (30) |
for the case of cranking at fixed deformation. Note that single-particle routhians are always plotted at fixed deformation in phenomenological potentials. In contrast, they are given along the equilibrium deformation path in the DFT calculations. Thus, the condition (30) is only approximately satisfied in the latter case provided that deformation changes with increasing rotational frequency are modest. Note that in general depends on signature and this dependence is especially pronounced for the single-particle orbitals with low value of .
The knowledge of single-particle alignments is extremely useful for an understanding of physical situation and interpretation of experimental data. For example, high- or high- intruder orbitals (such as those with Nilsson labels and ) have large values of and, as a consequence, they are strongly downsloping with increasing rotational frequency (see Fig. 3). Large energy splitting between two signature partner orbitals of a given single-particle state appear for the states with but no such splitting exist for the states with large value of . For example, this is a case for the state for which a large signature splitting between the branches leads to a formation of large gap at MeV which is absent at MeV (see Fig. 3).
The advantage of the cranking model is that it provides a microscopic description of rotating nuclei, where the total angular momentum is described as a sum of single-particle angular momenta, and thus collective and ‘non-collective’ rotations can be treated on the same footing. On the other hand, there are limitations. The cranking-model approximation is semiclassical, because the rotation is imposed externally. The model also breaks the rotational invariance, since a fixed rotation axis is used. These latter limitations are not very important for very fast rotation . Another shortcoming of the cranking model is that the wave functions are not eigenstates of the angular momentum operator, which can lead to difficulties; for example, a proper calculation of electromagnetic transition probabilities requires the use of projection techniques RS.80 . Furthermore, the cranking model is a poor approximation in the crossing region of two weakly interacting bands, but this difficulty can be overcome by the removal of such crossings PhysRep-SBT .
4.2 Spatial densities of the single-particle states
The total density of the nucleus is defined as the sum of the single-particle densities of occupied states
| (31) |
which are given by
| (32) |
for the th single-particle state. The single-particle wave function can be expanded into basis states
| (33) |
where represents the set of quantum numbers defining the basis state and the expansion coefficients. Of special interest are the cases when this expansion is dominated by a single basis state () since then the nodal structure of the wave function of the state and consequently its single-particle density will be predominantly defined by this basis state. This takes place either at spherical shape or at extremely elongated nuclear shapes typical for rod shape structures or megadeformation (MD) AA.18 .

In the latter case, the wave function defined by asymptotic Nilsson quantum number is expanded into the basis states characterized by NilRag-book ; AA.18 . For extremely elongated shapes in light nuclei this expansion is dominated by a single basis state AA.18 . This is illustrated in Fig. 4 which shows the single-particle densities of indicated states at the deformation typical for the MD shapes. They are characterized by axial or nearly axially symmetric spheroidal/ellipsoidal like density clusters formed for the single-particle states with the Nilsson quantum numbers, doughnut density distributions for the states, multiply (two for and three for ) ring shapes for the Nilsson states with and 3. Fig. 4 clearly indicates the importance of the deformation which has two critical effects. First, it leads to the formation of density clusters with specific nodal structure and to the separation of the clusters in space. Second, it lowers the energies of the Nilsson states of the type which favors the -clusterization and leads to the configurations in which all occupied single-particle states have this type of structure.




It is impossible to experimentally measure the single-particle density distributions in rotating nuclei. That is a reason why contrary to the single-particle energies and alignments they have not been used as fingerprints of independent particle motion. However, they are important for an understanding of the -clusterization and the evolution of extremely elongated shapes in light nuclei such as ellipsoidal and rod shapes and nuclear molecules AA.18 ; A.18 . The examples of total neutron densities of later two types of nuclear shapes are provided in Fig. 5. A rod-shaped nuclear configuration in 12C is built from a linear chain of three -clusters and could be well understood from the summation of the single-particle densities of occupied single-particle states AA.18 (see also Refs. IMIO.11 ; YIM.14 ; ZIM.15 for additional discussion of rod-shaped nuclei built on linear chains of the particles). Rod-shaped configurations appear also in heavier nuclei such as 42Ca and 44Ti AA.18 . However, their densities are more uniform since the -clusterization is suppressed by the occupation of the single-particle orbitals which have either doughnut or ring type single-particle density distributions (see Fig. 4 and Refs. AA.18 ; EKLV.18 ). Nuclear molecules are characterized by the formation of the neck between two nuclear fragments: the configuration of 36Ar is an example of such structure (see Fig. 5).
A knowledge of the nodal structure of the single-particle densities of the states allows to understand the microscopic mechanism of the transition between different nuclear shapes. For example, in order to build nuclear molecules from typical ellipsoidal density distributions one has to move matter from the neck (equatorial region) into the polar one. This can be achieved by means of specific particle-hole excitations which move the particles from (preferentially) doughnut type orbitals or from the orbitals which have a density ring in an equatorial plane into the orbitals (preferentially of the type) building the density mostly in the polar regions of the nucleus AA.18 ; A.18 .
Another example of important role of the single-particle density of the states is seen in so-called “bubble” structures of the ground states of spherical nuclei. This is due to a specific radial nodal structure of the wavefunctions of the single-particle states (see Fig. 6.2 in Ref. NilRag-book ): only () states build the density in the center of the nucleus. On the contrary, the states do not participate in the building of the densities in the center of the nucleus due to presence of the centrifugal barrier (see also Fig. 2 in Ref. KLRL.17 ). The impact of this feature is especially pronounced in proton subsystem of 34Si KLRL.17 ; GGKNPOGV.09 . Left panel of Fig. 6 shows the evolution of the proton densities in the isotones. The 40Ca, 38Ar and 36S nuclei in which the proton orbital is occupied show similar proton density patterns with the density peak at the center. In contrast, the emptying of the proton orbital in 34Si leads to a considerable depletion of the proton density in the central region of nucleus. This “bubble” phenomenon has been indirectly confirmed in experiment Bubble-exp .
Similar depletion of the density in the central region of the nucleus exist also in superheavy nuclei (see Refs. AF.05-dep ; BRRMG.99 ; SNR.17 and right panel of Fig. 6). However, the mechanism of its creation is different as compared with the one active in 34Si since the emptying of the states is not possible in such nuclei. It relies on the fact that the filling of low-/high- orbitals builds the density in the central/surface region of the nucleus AF.05-dep ; BRRMG.99 ). Thus, starting from the flat density distribution in 208Pb (which is experimentally verified, see Fig. 2.4 in Ref. NilRag-book ) one can build “bubble”-type structure in the superheavy nucleus by occupying predominantly high- orbitals outside the 208Pb core AF.05-dep . It was suggested in Ref. SNR.17 that the depletion of density in central region is mostly due to Coulomb interaction. This, however, contradicts to the observation that spherical superheavy nuclei with have significantly smaller depletion of the density in the central region as compared with the one AF.05-dep .
5 Microscopic+macroscopic models
The ”shell model” concepts discussed above assume some fixed mean field properties which do not depend on nucleonic configuration. In addition, they require the use of deformation parameters in the case of deformed and cranked shell models which have to be defined either from experimental data or from higher level model.
To overcome these deficiencies the microscopic+macroscopic (mic+mac) model has been suggested in 1960s Strut67 ; Nil69 ; Brack72 which can be considered as an approximation to the Hartree-Fock approach Brack72 . In this model the total energy of the nucleus is separated into two parts, a macroscopic part and a microscopic part ,
| (34) |
The macroscopic energy is defined by some version of the liquid-drop model while the microscopic energy is obtained from quantal shell corrections calculated from a phenomenological potential using the Strutinsky prescription Strut67 . The shape of the nuclear surface is parametrized by means of a multipole expansion of the radius in terms of the shape parameters (see Eq. (20)). Then the equilibrium deformation in a specific nucleonic configuration is determined by a minimization of the total energy with respect to the shape parameters.
For a simplicity, only the basic features of the mic-mac method for the rotating nuclei are outlined here since the case of no rotation is easy to obtain by dropping respective terms. The total nuclear energy at a specific deformation and spin is given as a sum of the rotating liquid drop energy and the shell energy
| (35) |
The shell energy is defined as the difference between the discrete and smoothed (indicated by ) single-particle energy sums,
| (36) |
with both terms evaluated at the same spin value . The smoothed sum is calculated using the Strutinsky procedure Strut67 . Then the total nuclear energy and equilibrium deformation of specific nucleonic configuration can be calculated as a function of spin (defined via Eq. (28)). By considering numerous configurations, defined by the occupation of single-particle orbitals with the specific sets of quantum numbers such as parity, signature etc, one can build comprehensive spectra of multiply rotational bands and compare them with experimental data.
Note that in the mic+mac approach the moment of inertia, defined from smoothed single-particle quantities, has to be renormalized to a rotating liquid behavior. The renormalization of the moment of inertia is especially important in the Nilsson potential because of the -term but it is also required in the Woods-Saxon potential because the potential radius is often different from the nuclear matter radius (see Ref. PhysRep-SBT and references therein).
The consideration above is restricted to the situation of no pairing correlations. The experience and detailed studies show that this is quite accurate approximation at high spins PhysRep-SBT ; VALR.05 . However, the pairing correlations play an important role at low and medium spins. In the mic+mac approaches they are usually taken into account at the BCS level by adding pairing energy term PD.03 ; CRBLLP.08 ; MSIS.16
| (37) |
The mic+mac model is simpler than self-consistent approaches and it is also substantially cheaper in numerical calculations. Despite approximations and simplifications employed by this method, it provides an accurate description of the ground state energies and deformations as well as fission barrier heights PD.03 ; MSIS.16 and rotational properties of multiply bands in different nuclei PhysRep-SBT ; CRBLLP.08 .
6 Self-consistent approaches: covariant density functional theory
There are several types of self-consistent density functional theories (DFTs) based either on the non-relativistic Shrödinger equation with finite range Gogny or zero range Skyrme forces or on the relativistic Dirac equation. The latter is called as covariant density functional theory (CDFT) VALR.05 and its brief outline will be presented here. It was very successful in the description of many physical phenomena (see reviews in Refs. VALR.05 ; MTZZLG.06 ; NVR.11 ; RDFNS.16 ). The detailed reviews of the Skyrme and Gogny DFTs are presented in Refs. BHP.03 ; PM.14 .
There are several classes of the CDFT models and, for simplicity, only meson-exchange (ME) models will be considered here. In these models the nucleus is described as a system of Dirac nucleons interacting via the exchange of mesons with finite masses leading to finite-range interactions. The starting point of the ME models is a standard Lagrangian density GRT.90
| (38) | |||||
which contains nucleons described by the Dirac spinors with the mass and several effective mesons characterized by the quantum numbers of spin, parity, and isospin. The Lagrangian (38) contains as parameters the meson masses , , and and the coupling constants , , and . is the charge of the protons and it vanishes for neutrons. The coupling constants are density dependent in the density dependent meson exchange (DDME) class of covariant energy density functionals (CEDFs) TW.99 ; DD-ME2 . In contrast, they are constant in the so-called non-linear (NL) CEDFs in which the density dependence is introduced via the powers of the -meson BB.77 :
| (39) |
The solution of these Lagrangians leads to the relativistic Hartree-Bogoliubov (RHB) equations VALR.05 . They are illustrated below on the example of the cranked RHB (CRHB) equations for the fermions in the rotating frame (in one-dimensional cranking approximation) CRHB
| (40) |
where () are chemical potentials defined from the average particle number constraints for protons and neutrons; and are quasiparticle Dirac spinors; denotes the quasiparticle energies; and is the angular momentum component entering into the Coriolis term . Here, is the Dirac Hamiltonian for the nucleon with mass
| (41) |
which contains an attractive scalar potential
| (42) |
a repulsive vector potential
| (43) |
and a magnetic potential
| (44) |
These equations are solved numerically in triaxial harmonic oscillator basis and signature basis is used for the single-particle states. The CRHB framework is applicable to the description of both rotating nuclei in the paired regime and one-/two-quasiparticle configurations in rotating and non-rotating nuclei. An approximate particle number projection by means of the Lipkin-Nogami (LN) method is also used in it CRHB but its discussion is omitted for simplicity. The CRHB+LN calculations have been successful in the description of rotating nuclei in paired regime VALR.05 ; CRHB ; AO.13 and one-quasiparticle configurations in odd- nuclei (see discussion of Fig. 12 below). Moreover, the CRHB framework can be either reduced to unpaired regime, leading to so-called cranked relativistic mean field (CRMF) approach KR.89 ; ALR.98 , or upgraded to the 2- and 3-dimensional cranking approximation MPZZ.13 . By putting it can also be applied to the description of non-rotating nuclei, but more specialized versions of the RHB computer codes (without cranking and signature basis) designed for triaxial, axially symmetric and spherical shapes also exist Niksic2014_CPC185-1808 .
It turns out that without any assumptions on the form of the single-particle potential self-consistent calculations generate single-particle properties (energies, alignments) which in general are similar to those obtained in phenomenological potentials. This is illustrated in Fig. 9 below which compares the single-particle spectra of the superheavy nucleus obtained with phenomenological folded Yukawa (FY) potential, non-relativistic Skyrme functionals SkP, SkM*, SLy6, SLy7, SkI1, SkI4 and Sk3, and CEDFs NL3, NL-Z, NL-Z2 and NL-VT1. The Nilsson diagrams obtained in the RHB calculations with the CEDF NL3* (see Fig. 2) show a lot of similarities with those obtained in the Woods-Saxon potential (see, for example, Figs. 3 and 4 in Ref. CAFE.77 ). The behavior of the single-particle states in the rotating potential obtained in the Woods-Saxon potential (see Fig. 3) is very similar to that obtained in the CRMF calculations (see Fig. 4 in Ref. ALR.98 ). However, there is a principal difference in the physical mechanisms related to the single-particle degrees of freedom between two types of approaches and it is related to time-odd mean fields DD.95 ; AR.00-to . They are absent in phenomenological potentials but are present in self-consistent models. For example, in the CRHB framework they are related to the terms which break time-reversal symmetry, namely, a magnetic potential (see Eq. (44)) and the the Coriolis term . In the DFT approaches, time-odd mean fields modify single-particle energies AA.10 ; SDMMNSS.10 , single-particle alignments AR.00-to and have large impact on rotational properties of nuclei DD.95 ; AR.00-to .
7 Manifestation of independent particle motion in non-rotating and rotating nuclei
When considering the manifestations of independent particle motion one should separate the effects which emerge from the shell structure (as a coherent effect of motion of many particles) and those from individual motion of the particles. The configuration-mixing interactions [which are accumulated in residual interaction term of the Hamiltitonian given by Eq. (8)] such as pairing and the coupling to the low-lying collective vibrational degrees of freedom act destructively on the individual properties of the single-particle orbitals. In contrast, the global effects emerging from the underlying shell structure are not that much affected by these residual interactions. Thus, a global shell structure at spin zero, the superdeformation at high spin and the existence of superheavy nuclei are considered as the examples of such effects.
Then the physical properties which sensitively depend on the single-particle features of individual orbitals are discussed. First, the energies of experimental and calculated one-quasiparticle states in non-rotating deformed nuclei are compared. Then, the analysis is extended to rotating nuclei at low and medium spins. The rotation acts as a tool to significantly reduce the role of pairing interaction SGBGV.89 ; NWJ.89 ; AF.05 . Thus, nuclear systems at very high spins in which the impact of pairing is negligible are considered and the single-particle and polarization effects due to the occupation of specific orbitals are analyzed. In addition, the phenomenon of band termination is discussed as an example of the competition of the collective and single-particle degrees of freedom.
7.1 Global shell structure at spin zero

The state-of-the-art view on the nuclear landscape is shown in Fig. 7. It is based on the results of the calculations presented in Refs. AA.21 ; AARR.14 ; AATG.19 . The bands (shown by gray color) of spherical nuclei along proton and neutron numbers 8, 20, 28, 50 and 82 (as well as for neutron number ) are seen in this figure. They are due to large spherical shell gaps at these particle numbers which provide an extra stability of the nuclei. Note that these bands are more pronounced in neutron subsystem. Outside of these bands of spherical nuclei, the ground states of the nuclei are either oblate or prolate being in typical range of quadrupole deformations . Similar structures and features are also obtained in non-relativistic calculations of Refs. MSIS.16 ; DGLGHPPB.10 ; Eet.12 but they are restricted to the nuclei below . In general, existing experimental data confirms these model predictions SP.08 but there may be some differences between specific model and experiment.
With increasing proton number these classical features disappear and only toroidal shapes are calculated as the lowest in energy. This region (shown in white color between two black lines in Fig. 7) is penetrated only by three islands (shown in gray color) of potentially stable spherical hyperheavy nuclei. Their existence is due to substantial proton and 186 and neutron , 308, and 406 spherical shell gaps AA.21 and substantial fission barriers around spherical minima AA.21 ; AATG.19 . However, these states are highly excited with respect of minima corresponding to toroidal shapes. They could become the ground states if relevant toroidal minima are unstable with respect of so-called sausage deformations AA.21 ; Wong.73 .
Thus, the richness of nuclear structure seen in experimentally known part of nuclear landscape is replaced by a more uniform structure of the nuclear landscape in the region of hyperheavy ( nuclei dominated by toroidal nuclei AA.21 ; AATG.19 . This transition from compact ellipsoidal-like shapes to non-compact toroidal shapes is driven by the enhancement of the role of Coulomb interaction with increasing AATG.19 . Thus, the former shapes become either unstable against fission or energetically unfavored in hyperheavy nuclei.
Single-particle degrees of freedom play also an important role in the definition of the boundaries of nuclear landscape. For example, the position of two-neutron drip line of ellipsoidal nuclei depends sensitively on the single-particle energies of high- states located in the vicinity of neutron continuum threshold AARR.15 . The transition from ellipsoidal to toroidal shapes drastically modifies the underlying single-particle structure and as a result lowers the energy of the Fermi level for protons AA.21 . As a consequence, a substantial shift of the two-proton drip line from its expected position for ellipsoildal shapes (shown by dashed orange line in Fig. 7) towards more proton-rich nuclei for toroidal shapes (shown by solid line in Fig. 7) takes place AA.21 .
7.2 Superheavy nuclei
With increasing proton number beyond the fission barriers provided by the liquid drop become rather small and then for higher they disappear (see Fig. 10.6 in Ref. NilRag-book ). It turns out that the existence of the heaviest nuclei with is primarily determined by shell effects due to the quantum-mechanical motion of protons and neutrons inside the nucleus SGK.66 ; Meld-67 ; OU.15 ; GMNORSSSS.19 ; AALMZ.21 . In these nuclei the heights of fission barriers are entirely determined by the shell corrections and they would not exist without shell effects. These effects also play a central role for the production, stability and spectroscopy of superheavy nuclei.
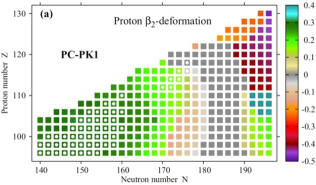

Although state-of-the-art theoretical models provide a reasonable description of many aspects of the physics of superheavy nuclei, they face substantial challenges in the prediction of the location of next spherical shell closures BRRMG.99 ; SP.07 ; OU.15 ; GMNORSSSS.19 ; AALMZ.21 ; AANR.15 . These challenges are illustrated in Fig. 8 which shows the map of calculated ground state quadrupole deformations obtained with two covariant energy density functionals. The predictions of these two functionals are drastically different in the vicinity of the and lines. The PC-PK1 functional predicts wide bands of spherical nuclei in the chart along and . In contrast, in the calculations with DD-PC1, the band along does not exist and narrower band along is seen only for . These discrepancies are due to modest differences in the single-particle properties of these functionals and related differences in the competition of shell effects at spherical and deformed shapes AANR.15 . Note that the width of the band of spherical nuclei in the chart along a specific particle number corresponding to a shell closure indicates the impact of this shell closure on the structure of neighboring nuclei.

There is a wide variety of the predictions for proton and neutron spherical shell closures in superheavy nuclei obtained in different models. These are proton numbers at and 126 and neutron numbers at and 184 (see Fig. 9 and Refs. BRRMG.99 ; SP.07 ; GMNORSSSS.19 ; AANR.15 . However, in the CDFT the could be eliminated as a potential candidate when the deformation effects are taken into account AANR.15 and the nuclei become deformed in a number of functionals when both deformation and correlations beyond mean field effects are considered SALM.19 . The challenges the models face in the prediction of spherical shell closures are due to two factors. At present, self-consistent models do not provide a spectroscopic quality of the description of the single-particle spectra DABRS.15 . In contrast, the phenomenological potentials better describe single-particle spectra in known nuclei (see Ref. SP.07 and references therein) but they fail to incorporate self-consistency effects (such as a depletion of the density in central region of nucleus) which are important in superheavy nuclei (see discussion of Fig. 6).
Fig. 8 illustrates that only for a few experimentally known and 118 nuclei the CDFT predictions differ. In general, with possible exception of these high- isotopic chains, existing experimental data on superheavy nuclei are described with comparable level of accuracy by all existing models GMNORSSSS.19 ; AALMZ.21 ; AANR.15 . This is undeniable success of independent particle model the global consequences of which (shell structure) led to the predictions of superheavy nuclei in 1960s within relatively simple models SGK.66 ; Meld-67 . Experimental data collected over these years fully confirmed these predictions and some differences in the predictions of next spherical shell closures are secondary to this success. This field or research (both experimental and theoretical) remains extremely active which is illustrated by recent reviews OU.15 ; GMNORSSSS.19 ; AALMZ.21 . However, at present available experimental data does not allow to give a preference to the predictions of one or another model and to decide where next (if any) proton and neutron spherical shell closures are located or whether there is an island of spherical superheavy nuclei.
7.3 Superdeformation at high spin
Fig. 7 shows that the ground states of the nuclei in experimentally known part of the nuclear chart are characterized by quadrupole deformation which is located typically in the range . Strutinsky has predicted excited minimum with in the second (superdeformed, SD) potential well of potential energy curves of deformed nuclei in Ref. Strut67 . At low spin such minima are located at high excitation energies, but they can be brought down to the yrast line by fast rotation since it favors extremely deformed shapes. This was confirmed later in the mic+mac calculations of Ref. Ander.76 which predicted the doubly magic SD band in 152Dy with 2:1 semi-axis ratio. The existence of the SD bands is due to the shell effects associated with large proton and neutron SD shell gaps. For example, in the region of superdeformation these shell effects are produced by large proton and neutron SD shell gaps which exist both in phenomenological potentials (see Fig. 3 in this paper and Refs. NWJ.89 ; Rag.93 ) and in the DFT calculations ALR.98 .
The phenomenon of superdeformation at high spin has been confirmed experimentally by the observation of the first SD band in 152Dy in 1986 Twin . From that time, a significant amount of experimental data on the SD bands in different mass regions has been collected Firestone.2002 . The mic+mac and DFT-based cranked approaches rather well describe experimental observables such as dynamic and kinematic moments of inertia and transitional quadrupole moments of these bands (see Refs. CRHB ; ALR.98 ; NWJ.89 ; Rag.93 and references quoted therein). The calculations also reveal a substantial dependence of these physical observables on the occupation of high- intruder orbitals; here stands for the principal quantum number of dominant component of the wave function. For example, they strongly depend on the number of occupied protons and neutrons in the region of superdeformation. This region is also of special interest since pairing is negligible in the majority of the SD bands. As a consequence, it provides one of the best examples of independent particle motion in nuclear physics (see detailed discussion in the last section).
7.4 The phenomenon of band termination

One of clear manifestations of the independent particle motion is the phenomenon of band termination PhysRep-SBT ; HFMSAD.72 ; WKW.80 . It definitely reveals the fact that each single-particle orbital occupied in nucleonic configuration possesses a limited and state-dependent angular momentum. Of special interest are so-called smooth terminating bands which show a continuous transition from high collectivity at low and medium spin values to a pure particle-hole (terminating) state at the maximum spin which can be built within the configuration PhysRep-SBT ; RJFSW.95 . Note that this feature of finite multi-fermion systems has so far only been observed and studied in atomic nuclei. In the terminating state, the symmetry axis coincides with the rotation axis. Since collective rotation along the symmetry axis is forbidden in quantum mechanics, no further angular momentum can be brought into the system with the same occupation of single-particle orbitals and thus this state represents the termination of the rotational band.
The phenomenon of band termination has been observed in several regions of nuclear chart (see review in Ref. PhysRep-SBT ). However, the best examples of smooth terminating bands are seen in the region in which the nuclei have several valence particles and holes outside the 100Sn core. A classical example of terminating bands in 109Sb PhysRep-SBT ; RJFSW.95 is considered here in order to illustrate the major features of smooth band termination. A critical feature of these bands is the fact that their dynamic moments of inertia gradually decrease with increasing rotational frequency to unusually low values (near 1/3 of rigid-body value) at the highest observed frequencies. This is definite indication of significant suppression of pairing correlations PhysRep-SBT making this type of rotational structures as one of the best examples of independent particle motion.
Fig. 10 compares the experimental and calculated energies of rotational bands with respect of rigid rotor reference , where is the moment of inertia parameter. The calculations are performed in configuration-dependent cranked Nilsson-Strutinsky approach (CNS) approach PhysRep-SBT ; BR.85 . The configurations relatively to the 100Sn core are labelled using the shorthand notation , where is the total signature of the configuration (only sign is shown) and , and are the numbers of proton holes in the orbitals, of protons in the orbitals and of neutrons in the orbitals, respectively. One can see that the CNS calculations without pairing very well reproduce experimental data. Some discrepancies seen at low spin are due to the neglect of pairing.
The CNS calculations suggest that rotational bands of interest are near prolate at low spin and thus they involve collective rotation about an axis perpendicular to the symmetry axis. With increasing spin the valence nucleons gradually align their spin vectors with the axis of rotation via the Coriolis interaction. This causes the nuclear shape to gradually trace a path through the triaxial () plane, toward the non-collective oblate shape at (see left panel of Fig. 11). After the available spin is exhausted, consistent with the Pauli principle, the band terminates. This gradual change from collective near-prolate to non-collective oblate () shape leads to a gradual decrease of transition quadrupole moment which agrees with available experimental data (see right panel in Fig. 11). The termination spins, which depend on the configuration, are well defined property for terminating bands and they confirm the termination process. For example, the detailed structure of the (band 1) terminating state in 109Sb is . Note that fully self-consistent cranked relativistic mean field calculations confirm this physical picture VALR.05 . However, due to technical reasons it is difficult to follow smooth terminating bands up to their terminating states in such calculations.


7.5 Single-particle states in deformed nuclei
Non-rotating nuclei
The detailed comparison of experimental and theoretical information on the properties of specific individual states can shed additional light on the validity in independent particle motion in atomic nuclei. In non-rotating nuclei, such information is provided by the energies of the single-particle states, their densities and by the transitions between the single-particle states. However, such densities are not accessible experimentally and calculated transition probabilities are prone to substantial theoretical errors. One could imagine that spherical nuclei would provide the cleanest and simplest set of data on the single-particle properties. It turns out that this is not a case because of substantial residual interaction due to (quasi)particle-vibration (quasiparticle-phonon) coupling. As a consequence, the wavefunctions of the states in the spherical nuclei are not of pure single-particle nature since they are substantially polluted by the vibrational admixtures MBBD.85 ; AL.15 ; CCSB.14 .


The impact of the quasiparticle-vibration coupling is reduced in deformed nuclei since the part of such correlations is accounted at the level of deformed mean field. Indeed, the admixtures of the phonons to the structure of the ground and low-lying states in deformed rare-earth and actinide odd-mass nuclei is relatively small (especially, when compared with spherical open shell nuclei AL.15 ) according to the quasiparticle-phonon model ABNSW.88 ; SSMJ.15 . Thus, deformed nuclei can provide a better and cleaner examples of independent particle motion.


Fig. 12 compares experimental and calculated energies of one-quasiparticle states in odd- 249Bk and 251Cf nuclei. The results of the calculations with non-relativistic Skyrme (SLy4, UNEDF2), Gogny (D1S, D1M) and covariant (NL1, NL3*) energy density functionals are shown in this figure. These are fully self-consistent calculations which means that the total energies of the nucleonic configurations with blocked -th single-particle state of interest are obtained within Hartree-Fock-Bogoliubov or RHB frameworks RS.80 . Then the ground state is associated with nucleonic configuration which has the lowest energy and the energies of the excited states are defined as . Note that in Fig. 12 the particle and hole states are plotted at and , respectively. This is done in order to facilitate the comparison of these self-consistent results with the Nilsson diagrams.
One can see that the energies of some deformed one-quasiparticle states are rather well described in specific functionals, but others deviate appreciably from the experiment. The detailed comparison of experimental data with calculations is presented in Ref. DABRS.15 . Considering an average level of the accuracy of the description of experimental data, it is difficult to give a clear preference to one or another functional. At present, a systematic analysis of the accuracy of the reproduction of the single-particle spectra in deformed nuclei is available only in the RHB framework AS.11 and smaller in scope (only for the Rb, Yb and Nb isotopic chains) analysis is carried out in the HFB calculations with Gogny forces (see Ref. RSR.11 and references therein). These investigations reveal two sources of inaccuracies in the description of the energies of the single-particle states, namely, low effective mass leading to a stretching of the energy scale of the calculated results as compared with experimental ones and incorrect relative positions of some single-particle states DABRS.15 ; AS.11 . On the absolute scale these deficiencies are not large especially considering the fact that no (or very limited) information on single-particle degrees of freedom has been taken into account in the fitting protocols of covariant (non-relativistic) energy density functionals. The accounting of quasiparticle-vibration coupling (QVC) improves the agreement with experiment by both improving the description of the energies of individual states and increasing the density of the single-particle states in the vicinity of the Fermi level. This was illustrated for the 251Cf nucleus in the RHB+QVC framework in Ref. ZBNLRS.22 .
In general, phenomenological potentials provide better description of the energies of the single-particle states in deformed odd- nuclei because they are fitted to this type of experimental data CDNSW.87 ; BDNO.89 ; BR.85 . However, such accuracy is obtained at the cost of neglect of self-consistency effects AS.11 and effective incorporation of the effects of particle-vibration coupling ZBNLRS.22 .
Rotating nuclei in the pairing regime
As discussed earlier the rotation of the nuclei can generate substantial modifications of the single-particle energies and provides single-particle alignments as a new measure of the single-particle properties. This leads to a new and very robust probes of the single-particle structure since some pairs of the orbitals emerging from a given non-rotating state show significant signature splitting (see, for example, the and pairs of the orbitals in Fig. 3) while other pairs (such as and in Fig. 3) show no signature splitting.
These features can be used for a reliable interpretation of experimental data. This is demonstrated in Fig. 13 which compares experimental Routhians with calculated ones for selected set of rotational bands in odd-neutron 163Er nucleus. The excitation energies are taken relative to a reference configuration which is the ground state (-) configuration in even-even nucleus. Experimental Routhian is well approximated by the Harris expression
| (45) |
with MeV-1 and MeV-3 extracted from the ground state band in 164Er. The calculations are performed in the cranked shell model (CSM) BF.79 which employs fixed mean-field parameters for the Nilsson potential and pairing. The parameters of its reference are adjusted to the calculated Routhian of the -configuration. The quasiparticle orbitals, on which rotational bands are build, are labelled by the letters of the alphabet A, B, C , D (for high- intruder states) and E, F, G, … (for normal parity states) [see Ref. F.18 for details of this labelling convention]. One can see that this relatively simple model can describe rather well experimentally observed features such as (i) large signature splitting in the pair of bands A/B, (ii) the lack or small amount of signature splitting in the pairs of bands E/F, X/Y and G/H, (iii) the presence of paired band crossing at MeV in the E/F, G/H and C bands which reflects itself in the change of the slope of the Routhians as a function of rotational frequency and (iv) the absence of paired band crossing in the A/B and X/Y pairs. The latter is due to the fact that the occupation of either of these orbitals blocks paired band crossing in neutron subsystem.
Over the years huge amount of experimental data on rotating nuclei has been accumulated and more sophisticated theoretical tools have been developed and successfully applied for the description of rotating nuclei both in paired and unpaired regimes. They go beyond the basic assumption of the CSM on the constancy of the mean and pairing fields and take into account their configuration dependence either on the level of mic+mac model or on a fully self-consistent level. These include cranked Nilsson-Strutinsky approach PhysRep-SBT ; CRBLLP.08 , cranked approaches based on the Skyrme and Gogny DFTs MDD.00 ; ER.94 ; DBH.01 and CDFT AO.13 ; KR.89 ; ZHA.20 and others.
7.6 Single-particle and polarization effects due to the occupation of single-particle orbitals
The addition or removal of particle(s) to the nucleonic configuration modifies the total physical observables. But it also creates the polarization effects on the physical properties (both in time-even and time-odd channels) of initial configuration. The comparison of relative properties of two configurations can shed important light both on the impact of the added/removed particle(s) in specific orbital(s) on physical observable of interest and on the related polarization effects. In addition, the comparison with experimental data on such properties can provide a measure of the accuracy of the description of single-particle properties in model calculations.
| Band | Configuration | (b) | (b) | |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 149Gd(1) | [NL1] | [NL1] | ||
| [SkP] | ||||
| [SkM*] | ||||
| 151Tb(1) | [NL1] | [NL1] | ||
| [SkP] | ||||
| [SkM*] | ||||
| 151Dy(1) | [NL1] | [NL1] | ||
| [SkP] | ||||
| [SkM*] |
Let us consider an example of rotational bands in the regime of weak pairing. The relative properties of different physical observables such as relative charge quadrupole moments
| (46) |
and relative effective alignments Rag.93
| (47) |
are defined as the differences between either charge quadrupole moments or the spins of the bands A and B at the same rotational frequency with the band being a reference band.
They provide sensitive probes of the single-particle motion and polarization effects induced by the occupation of specific single-particle orbitals. In addition, the experimental values of relative charge quadrupole moments are to a large degree free from the uncertainties due to stopping powers which impact the absolute values of these moments. The probes the differences in time-even mean fields generated by the addition or removal of particle(s) from the configuration of the reference band ALR.98 ; SDDN.96 .
The effective alignment depends both on the alignment properties of single-particle orbital(s) by which the two bands differ and on the polarization effects (both in time-even and time-odd channels of the DFTs) induced by the particles in these orbitals ALR.98 . It can also be used to investigate experimentally the structure of the underlying single-particle orbitals in the configurations of interest ALR.98 ; Rag.93 . Note that additivity principle for the single-particle observables has been tested for the first time on the example of effective alignments of superdeformed bands in the mass region Rag.93 .

The comparison of experimental and calculated values for a selected set of superdeformed bands in the nuclei near 152Dy is presented in Table 1 (for a more extensive set of data see Table 2 in Ref. SDDN.96 ). One can see that these quantities (column 3) are well described in model calculations (columns 4 or 5). In addition, the additivity rule of quadrupole moments SDDN.96 which states that relative quadrupole moments of two configurations can be well approximated by the sum of individual contributions of -th particles to the charge quadrupole moment defined with respect of core SD configuration in 152Dy
| (48) |
is rather well fulfilled both in relativistic and non-relativistic DFT calculations (compare columns 4 and 5 in Table 1 and see Ref. SDDN.96 ). This means that the polarization effects due to individual particles or holes are largely independent.
Experimental and calculated values for single-particle orbitals active in the vicinity of the SD shell closures in the region of superdeformation are compared in Fig. 14. The calculations are carried out within the cranked relativistic mean field ALR.98 and the cranked Nilsson-Strutinsky Rag.93 approaches. The CRMF calculations reproduce in average the experimental values better than the CNS approach. This indicates that alignment properties of single-particle orbitals and their polarization effects are correctly accounted for in the CRMF approach. The discrepancy between the CRMF calculations and experiment seen in Fig. 14a at MeV is most likely due to the fact that pairing correlations play some role at low rotational frequency in the 149Gd(1) band.
It is necessary to point on principal differences in the description of these relative observables in the DFT and mic+mac based approaches. The relative quadrupole moments are self-consistently described in the DFT based approaches ALR.98 ; SDDN.96 ; MADLN.07 . In contrast, the effective single-particle quadrupole moments in the mic+mac method are not uniquely defined because of the lack of self-consistency between the microscopic and macroscopic contributions KRA.98 . In the mic+mac models (for example, CNS) polarization effects caused by time-odd fields are neglected and therefore is predominantly defined by the alignment properties of the active single-particle orbitals Rag.93 . On the contrary, they play an important role in the DFT models DD.95 ; AR.00-to .
Similar studies of relative properties of rotational bands have been performed in different regions of nuclear chart AF.05 ; MADLN.07 ; KRA.98 ). For example, a statistical analysis of significant number of rotational configurations in the region of superdeformation confirms the additivity principle for quadrupole moments and effective alignments MADLN.07 . This justifies the use of an extreme single-particle model in an unpaired regime typical of high angular momentum. Note that the basic idea behind the additivity principle for one-body operators is rooted in the independent particle model.
8 Conclusions
The concept of independent particle motion is the foundation of the absolute majority of the nuclear structure models. It leads to verifiable consequences such as shell structure and individual single-particle properties of nucleons. Both mic+mac and DFT models are used nowadays for the description of numerous aspects of low energy nuclear phenomena. The former allows significant flexibility (such as the calculation of large number of the nucleonic configurations in a single nucleus as it is done in the CNS approach PhysRep-SBT ) but lacks self-consistency. This neglect of self-consistency limits the applicability of the mic+mac models to ellipsoidal nuclei with similar density distributions in proton and neutron subsystems. In contrast, the DFT models are fully self-consistent which makes them applicable to very exotic nuclear shapes including clustered, ”bubble” and toroidal ones. However, the calculation of many nucleonic configurations in a given nucleus involving one or several blocked single-particle states still remains a challenge especially in the formalism which includes pairing. At present, the use of these two theoretical frameworks should be considered as complimentary.
The validity of independent particle model has been confirmed by experimental observation of superheavy nuclei and the phenomenon of superdeformation at high spin; these observations were motivated by model predictions. They together with global structure of the nuclear landscape are the consequences of underlying shell structure, which emerges from independent particle motion of the nucleons in the nucleus. The energies and alignments of the single-particle states serve as a clear fingerprint of individual properties of the single-particle orbitals. Signature splitting properties are of particular value since either their large values or no splittings help in the identification of the single-particle states involved in the structure of observed experimental bands. The experimental features seen at extremely high spins where the pairing correlations are negligible provide the best [at the level of single-particle states] examples of independent particle motion; these are found in smooth terminating bands of the mass region and in superdeformed bands of the mass region.
9 Acknowledgments
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Award No. DE-SC0013037. I would like to thank I. Debes and J. Dudek for the creation of improved quality Fig. 3. Useful discussions with I. Ragnarsson are greatly appreciated.
References
- (1) A. Bohr and B. R. Mottelson, Nuclear Structure, vol. 1, (W. A. Benjamin, Inc., 1969).
- (2) P. Ring and P. Schuck, The Nuclear Many-Body Problem (Springer-Verlag, Berlin, 1980)
- (3) R. F. Casten, Nuclear Structure from a Simple Perspective, (Oxford University Press, 1990).
- (4) S. G. Nilsson and I. Ragnarsson, Shapes and shells in nuclear structure, (Cambridge University Press, 1995).
- (5) S. G. Nilsson, Binding states of individual nucleons in strongly deformed nuclei, Mat.-Fys. Medd.-K.Dan. Vidensk. Selsk. 29, no. 16 (1955).
- (6) I. Ragnarsson, S. G. Nilsson and R. K. Sheline, Shell structure in nuclei, Phys. Rep. 45, 1 (1978).
- (7) F. A. Gareev, S. P. Ivanova, V. G. Soloviev and S. I. Fedotov, Single-particle energies and wave functions of the Saxon-Woods potentials and nonrotational states of odd-mass nuclei in the region , Phys. Elem. Part. and Atom. Nuclei, v. 4., part 2 (1973).
- (8) S. Cwiok, J. Dudek, W. Nazarewicz, J. Skalski, and T. Werner, Single-particle energies, wave functions, quadrupole moments and -factors in an axially deformed Woods-Saxon potential with applications to the two-centre-type nuclear problems, Comp. Phys. Comm. 46, 379 (1987).
- (9) R. Bengtsson, J. Dudek, W. Nazarewicz and P.Olanders, A systematic comparison between the Nilsson and Woods-Saxon deformed shell model potentials, Phys. Scripta 39, 196 (1989).
- (10) P. Möller and J. R. Nix, Nuclear mass formula with a Yukawa-plus-exponential macroscopic model and a folded-Yukawa single-particle potential, Nucl. Phys. A 361, 117 (1981).
- (11) A. Dobrowolski, K. Pomorski and J. Bartel, Solving the eigenvalue problem of the nuclear Yukawa-folded mean-field Hamiltonian, Comp. Phys. Comm. 199, 118 (2016).
- (12) R.R. Chasman, I. Ahmad, A.M. Friedman and J.R. Erskine, Survey of single-particle states in the mass region , Rev. Mod. Phys. 49, 833 (1977).
- (13) A.V. Afanasjev, D.B. Fossan, G.J. Lane and I. Ragnarsson, Termination of Rotational Bands: Disappearance of Quantum Many-body Collectivity, Phys. Rep. 322, 1 (1999).
- (14) J. Dobaczewski, A.V. Afanasjev, M.Bender, L.M.Robledo, and Yue Shi, Properties of nuclei in the nobelium region studied within the covariant, Skyrme, and Gogny energy density functionals, Nucl. Phys. A 944, 388 (2015).
- (15) D. R. Inglis, Particle derivation of nuclear rotation properties associated with a surface wave, Phys. Rev. 96, 1059 (1954).
- (16) D.R. Inglis, Nuclear moments of inertia due to nucleon motion in a rotating well, Phys. Rev. 103, 1786 (1956).
- (17) M.J.A. de Voigt, J. Dudek, Z. Szymański, High-spin phenomena in atomic nuclei, Rev. Mod. Phys. 55, 949 (1983).
- (18) Z. Szymański, Fast Nuclear Rotation, (Claredon Press, Oxford, 1983).
- (19) J. Meng, J. Peng S.-Q.- Zhang, P.-W. Zhao, Progress on tilted axis cranking covariant density functional theory for nuclear magnetic and antimagnetic rotation, Front. of Phys. 8, 55 (2013).
- (20) J. Robin, Th. Byrski, G. Duchêne, F. A. Beck, D. Curien, N. Dubray, J. Dudek, A. Gó ź dź, A. Odahara, N. Schunck, N. Adimi, D. E. Appelbe, P. Bednarczyk, A. Bracco, B. Cederwall, S. Courtin, D. M. Cullen, O. Dorvaux,S. Ertück, G. de France, B. Gall, P. Joshi, S. L. King, A. Korichi, K. Lagergren, G. Lo Bianco, S. Leoni, A. Lopez-Martens, S. Lunardi, B. Million, A. Nourredine, E. Pachoud, E. S. Paul, C. Petrache, I. Piqueras, N. Redon, A. Saltarelli, J. Simpson, O. Stezowski, R. Venturelli, J. P. Vivien, and K. Zuber, Extended investigation of superdeformed bands in 151,152Tb nuclei, Phys. Rev. C 77, 014308 (2008).
- (21) A.V. Afanasjev and H. Abusara, From cluster structures to nuclear molecules: The role of nodal structure of the single-particle wave functions, Phys. Rev. C, 97, 024329 (2018).
- (22) A.V. Afanasjev, Cluster structures, ellipsoidal shapes and nuclear molecules in light nuclei, EPJ Web of Conf. 194, 06001 (2018).
- (23) K. Karakatsanis, G.A. Lalazissis, P. Ring, and E. Litvinova, Spin-orbit splittings of neutron states in isotones from covariant density functionals and their extensions, Phys. Rev. C 95, 034318 (2017).
- (24) A.V. Afanasjev and S. Frauendorf, Central depression in nuclear density and its consequences for the shell structure of superheavy nuclei, Phys. Rev. C 71, 024308 (2005).
- (25) T. Ichikawa, J.A.Maruhn, N. Itagaki, and S.Ohkubo, Linear Chain Structure of Four- Clusters in , Phys. Rev. Lett. 107, 112501 (2011).
- (26) J. M. Yao, N. Itagaki, and J. Meng, Searching for a linear-chain structure in excited states of with covariant density functional theory, Phys. Rev. C 90, 054307 (2014).
- (27) P.W. Zhao, N. Itagaki, and J. Meng, Rod-shaped Nuclei at Extreme Spin and Isospin, Phys. Rev. Lett. 115, 022501 (2015).
- (28) J.-P. Ebran, E. Khan, R.-D. Lasseri, and D. Vretenar, Single-particle spatial dispersion and clusters in nuclei, Phys. Rev. C 97, 061301(R) (2018).
- (29) M. Grasso, L. Gaudefroy, E. Khan, and T. Nikšić, J. Piekarewicz, O. Sorlin, N. Van Giai, and D. Vretenar, Nuclear “bubble” structure in , Phys. Rev. C 79, 034318 (2009).
- (30) A. Mutschler, A. Lemasson, O. Sorlin, D. Bazin, C. Borcea, R. Borcea, Z. Dombrádi, J.-P. Ebran, A. Gade, H. Iwasaki, E. Khan, A. Lepailleur, F. Recchia, T. Roger, F. Rotaru, D. Sohler, M. Stanoiu, S.R. Stroberg, J. A. Tostevin, M. Vandebrouck, D. Weisshaar and K. Wimmer, A proton density bubble in the doubly magic 34Si nucleus, Nature Phys. 13, 152 (2017).
- (31) M. Bender, K.Rutz, P.-G. Reinhard, J.A. Maruhn and W. Greiner, Shell structure of superheavy nuclei in self-consistent mean-field models, Phys. Rev. C 60, 034304 (1999).
- (32) A. Sobiczewski and K. Pomorski, Description of structure and properties of superheavy nuclei, Prog. Part. Nucl. Phys. 58, 292 (2007).
- (33) B. Schuetrumpf, W. Nazarewicz, W. and P.-G. Reinhard, Central depression in nucleonic densities: Trend analysis in the nuclear density functional theory approach, Phys. Rev. C 96, 024306 (2017).
- (34) V.M. Strutinsky, Shell effects in nuclear masses and deformation energies, Nucl. Phys. A 95, 420 (1967).
- (35) S.G. Nilsson, C.F. Tsang, A. Sobiczewski, Z. Szymański, S. Wycech, C. Gustafsson, I.-L. Lamm, P. Möller, On the nuclear structure and stability of heavy and superheavy elements, B. Nilsson, Nucl. Phys. A 131, 1 (1969).
- (36) M. Brack, J. Damgaard, A.S. Jensen, H.C. Pauli, V.M. Strutinsky, C.Y. Wong, Funny Hills: The shell-correction approach to nuclear shell effects and its application to the fission process, Rev. Mod. Phys. 44 (1972) 320.
- (37) D. Vretenar, A.V. Afanasjev, G.A. Lalazissis and P. Ring, Relativistic Hartree-Bogoliubov Theory: Static and Dynamic Aspects of Exotic Nuclear Structure, Phys. Rep. 409, 101 (2005).
- (38) K. Pomorski and J. Dudek, Nuclear liquid-drop model and surface-curvature effects, Phys. Rev. C 67, 443161 (2003).
- (39) B. G. Carlsson, I. Ragnarsson, R. Bengtsson, E. O. Lieder, R. M. Lieder, and A. A. Pasternak, Triaxial shape with rotation around the longest principal axis in 142Gd, Phys. Rev. C78, 034316 (2008).
- (40) J. Meng, H. Toki, S. G. Zhou, S. Q. Zhang, W. H. Long and L. S. Geng, Relativistic continuum Hartree-Bogoliubov theory for ground state properties of exotic nuclei, Prog. Part. Nucl. Phys. 470 (2006).
- (41) T. Nikšić, D. Vretenar and P. Ring, Relativistic nuclear energy density functionals: mean-field and beyond, Prog. Part. Nucl. Phys. 66, 519 (2011).
- (42) Relativistic Density Functional for Nuclear Structure, (World Scientific Publishing Co), Edited by Jie Meng, Int. Rev. Nucl. Phys. 10 (2016).
- (43) M. Bender, P.-H. Heenen and P.-G. Reinhard, Self-consistent mean-field models for nuclear structure, Rev. Mod. Phys. 75, 121 (2003).
- (44) S. Peru and M. Martini, Mean field based calculations with the Gogny force: Some theoretical tools to explore the nuclear structure, Eur. Phys. J A50, 88 (2014).
- (45) Y. K. Gambhir, P. Ring, and A. Thimet, Relativistic mean field theory for finite nuclei, Ann. Phys. (NY) 198, 132 (1990).
- (46) S. Typel and H. H. Wolter, Relativistic mean field calculations with density dependent meson-nucleon coupling, Nucl. Phys. A656, 331 (1999).
- (47) G.A. Lalazissis, T.Nikšić, D. Vretenar and P. Ring, New relativistic mean-field interaction with density-dependent meson-nucleon couplings, Phys. Rev. C 71, 024312 (2005).
- (48) J. Boguta and R. Bodmer, Relativistic calculation of nuclear matter and the nuclear surface, Nucl. Phys. A292, 413 (1977).
- (49) A.V. Afanasjev, P. Ring and J. König, Cranked relativistic Hartree-Bogoliubov theory: formalism and application to the superdeformed bands in the region, Nucl. Phys. A676, 196 (2000).
- (50) A. V. Afanasjev and O. Abdurazakov, Pairing and rotational properties of actinides and superheavy nuclei in covariant density functional theory, Phys. Rev. C 88, 014320 (2013).
- (51) W. Koepf and P. Ring, A relativistic description of rotating nuclei: the yrast line of 20Ne, Nucl. Phys. A 493, 61 (1989).
- (52) A.V. Afanasjev, G. Lalazissis and P. Ring, Relativistic mean field theory in rotating frame: Single-particle properties at superdeformation, Nucl. Phys. A 634, 395 (1998).
- (53) T. Nikšić and N. Paar and D. Vretenar and P. Ring, DIRHB - a relativistic self-consistent mean-field framework for atomic nuclei, Comp. Phys. Comm. 185, 1808 (2014).
- (54) J. Dobaczewski and J. Dudek, Time-odd components in the mean field of rotating superdeformed nuclei, Phys. Rev. C 52, 1827 (1995).
- (55) A.V. Afanasjev and P. Ring, Time-odd mean fields in the rotating frame: Microscopic nature of nuclear magnetism, Phys. Rev. C 62, 031302(R), (2000).
- (56) A. V. Afanasjev and H. Abusara, Time-odd mean fields in covariant density functional theory: nonrotating systems, Phys. Rev. C, 81, 014309 (2010).
- (57) N. Schunck, J. Dobaczewski, J. McDonnell, J. Moré, W. Nazarewicz, J. Sarich and M. V. Stoitsov, One-quasiparticle states in the nuclear energy density functional theory, Phys. Rev. C 81, 024316 (2010).
- (58) Y.R. Shimizu, J.D. Garrett, R. A. Broglia, M. Gallardo and E. Vigezzi, Pairing fluctuations in rapidly rotating nuclei, Rev. Mod. Phys. 61, 131 (1989).
- (59) W. Nazarewicz, R. Wyss and A. Johnson, Structure of superdeformed bands in the mass region, Nucl. Phys. A 503, 285 (1989).
- (60) A.V. Afanasjev and S. Frauendorf, Description of rotating nuclei in terms of isovector pairing, Phys. Rev. C 71, 064318 (2005).
- (61) S.E. Agbemava and A.V. Afanasjev, Hyperheavy spherical and toroidal nuclei: The role of shell structure, Phys. Rev. C 103 034323 (2021).
- (62) S.E. Agbemava, A.V. Afanasjev, D.Ray and P.Ring, Global performance of covariant energy density functionals: Ground state observables of even-even nuclei and the estimate of theoretical uncertainties, Phys. Rev. C 89, 054320 (2014)
- (63) S.E. Agbemava, A.V. Afanasjev, A. Taninah, and A. Gyawali, Extension of the nuclear landscape to hyperheavy nuclei, Phys. Rev. C 99, 034316 (2019).
- (64) P. Möller, A.J. Sierk, T. Ichikawa and H. Sagawa, Nuclear ground-state masses and deformations: FRDM(2012), Atomic Data and Nuclear Data Tables, 109-110, 1 (2016).
- (65) J.-P. Delaroche, M. Girod, J. Libert, H. Goutte, S. Hilaire, S. Peru, N. Pillet and G.F. Bertsch, Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction, Phys. Rev. C 81, 014303 (2010).
- (66) J. Erler, N. Birge, M. Kortelainen, W. Nazarewicz, E. Olsen, A.M. Perhac and M. Stoitsov, The limits of the nuclear landscape, Nature, 486, 509 (2012).
- (67) O. Sorlin and M.-G. Porquet, Nuclear magic numbers: New features far from stability, Prog. Part. Nucl. Phys. 61, 602 (2008).
- (68) C. Y. Wong, Toroidal and spherical bubble nuclei, Ann. Phys. 77, 279 (1973).
- (69) A.V. Afanasjev, S.E. Agbemava, D. Ray and P. Ring, Neutron drip line: Single-particle degrees of freedom and pairing properties as sources of theoretical uncertainties, Phys. Rev. C 91, 014324 (2015).
- (70) A. Sobiczewski, F.A. Gareev, and B.N. Kalinkin, Closed shells for and in a diffuse potential well, Phys. Lett. 22, 500 (1966).
- (71) H. Meldner, Predictions of new magic regions and masses for super-heavy nuclei from calculations with realistic shell model single particle Hamiltonians, Ark. Fys. 36, 593 (1967).
- (72) Yu.Ts. Oganessian and V.K. Utyonkov, Super-heavy element research, Rep. Prog. Phys. 78, 036301 (2015)
- (73) S.A. Giuliani, Z. Matheson, W. Nazarewicz, E. Olsen, P.-G. Reinhard, J. Sadhukhan, B. Schuetrumpf, N. Schunck, and P. Schwerdtfeger, Colloquium: Superheavy elements: Oganesson and beyond, Rev. Mod. Phys. 91, 011001 (2019).
- (74) G.G. Adamian, N.V. Antonenko, H. Lenske, L. A. Malov and Shan-Gui Zhou, Self-consistent methods for structure and production of heavy and superheavy nuclei, Eur. Phys. J A57, 89 (2021).
- (75) S.E. Agbemava, A,V. Afanasjev, T. Nakatsukasa, and P. Ring, Covariant density functional theory: Reexamining the structure of superheavy nuclei, Phys. Rev. C 92, 054310 (2015).
- (76) Z. Shi, A.V. Afanasjev, Z.P. Li, and J. Meng, Superheavy nuclei in a microscopic collective Hamiltonian approach: The impact of beyond-mean-field correlations on ground state and fission properties, Phys. Rev. C 99, 064316 (2019).
- (77) G. Andersson, S.E. Larsson, G.Leander, P. Möller, S.G. Nilsson, I. Ragnarsson, S. Åberg, R. Bengtsson, J. Dudek, B. Nerlo-Pomorska, K.Pomorski and Z.Szymański, Nuclear shell structure at very high angular momentum, Nucl. Phys. A 268, 205 (1976).
- (78) P.J. Twin, B.M. Nyakó, A.H. Nelson, J. Simpson, M.A. Bentley, H.W. Cranmer-Gordon, P.D. Forsyth, D. Howe, A.R. Mokhtar, J.D. Morrison, J.F. Sharpey-Schafer and G. Sletten, Observation of a Discrete-Line Superdeformed Band up to in , Phys. Rev. Lett. 57, 811 (1986).
- (79) I. Ragnarsson, Orbital and spin assignment of SD bands in the Dy/Gd region — identical bands, Nucl. Phys. A 557 (1993) 167c.
- (80) B. Singh, R. Zywina and R.B. Firestone, Table of superdeformed nuclear bands and fission isomers, Nucl. Data Sheets 97, 241 (2002).
- (81) O. Häusser, A.J. Ferguson, A.B. Mcdonald, I.M.Szöghy, T.K. Alexander and D.L.Disdier, High spin states in 20Ne from 16O() scattering, Nucl. Phys. A 179, 465 (1972).
- (82) A. Watt, D. Kelvin and R. R. Whitehead, Shell-model calculations in the shell: X. Termination of rotational bands, J. Phys. G 6, 35 (1980)
- (83) I. Ragnarsson, V.P. Janzen, D.B. Fossan, N.C. Schmeing, R. Wadsworth, Smooth termination of collective rotational bands, Phys. Rev. Lett. 74 (1995) 3935
- (84) T. Bengtsson and I. Ragnarsson, Rotational bands and particle-hole excitations at very high spin, Nucl. Phys. A 436, 14 (1985).
- (85) C. Mahaux, P. F. Bortignon, R. A. Broglia and C. H. Dasso, Dynamics of the shell model, Phys. Rep. 120, 1 (1985).
- (86) A.V. Afanasjev and E. Litvinova, Impact of collective vibrations on quasiparticle states of open-shell odd-mass nuclei and possible interference with the tensor force, Phys. Rev. C 92, 044317 (2015).
- (87) L.-G. Cao, G. Colò, H. Sagawa and P. F. Bortignon, Properties of single-particle states in a fully self-consistent particle-vibration coupling approach, Phys. Rev. C 89, 044314 (2014).
- (88) B. A. Alikov, K. N. Badalov, V. O. Nesterenko, A. V. Sushkov, and J. Wawryszczuk, On the role of the Coriolis and quasiparticle-phonon interactions in describing E1 transition probabilitues in odd Eu and Tb isotopes, Z. Phys. A 331, 265 (1988).
- (89) N. Y. Shirikova, A. V. Sushkov, L. A. Malov, and R. V. Jolos, Structure of the low-lying states of the odd-neutron nuclei with , Eur. Phys. J. A 51, 21 (2015).
- (90) S. Frauendorf, Beyond the Unified Model, Phys. Scr. 93, 043003 (2018).
- (91) A.V. Afanasjev and S. Shawaqfeh, Deformed one-quasiparticle states in covariant density functional theory, Phys. Lett. B 706, 177 (2011).
- (92) R. Rodriguez-Guzman, P. Sarriguren, and L. M. Robledo, Shape evolution in yttrium and niobium neutron-rich isotopes, Phys. Rev. C 83, 044307 (2011).
- (93) Y. Zhang, A. Bjelc̆ić, T. Niks̆ić, E. Litvinova, P. Ring, and P. Schuck, A many-body approach to superfluid nuclei in axial geometry, submitted to Phys. Rev. C., see also nuclear theory arXiv:2104.14513.
- (94) R. Bengtsson and S. Frauendorf, Quasiparticle spectra near the yrast line, Nucl. Phys. A 327, 139 (1979).
- (95) H. Molique, J. Dobaczewski and J. Dudek, Superdeformed bands in and neighboring nuclei predicted within the Hartree-Fock method, Phys. Rev. C 61, 044304 (2000).
- (96) J.L. Egido and L.M. Robledo, High spin properties of the Er and Yb isotopes with the Gogny force, Nucl. Phys. A 570, 69 (1994).
- (97) T. Duguet, P. Bonche and P.-H. Heenen, Rotational properties of 252,253,254No: influence of pairing correlations, Nucl. Phys. A 679, 427 (2001).
- (98) Z.-H. Zhang, M. Huang and A.V. Afanasjev, Rotational excitations in rare-earth nuclei: A comparative study within three cranking models with different mean fields and treatments of pairing correlations. Phys. Rev. C 101, 054303 (2020).
- (99) W. Satuła, J. Dobaczewski, J. Dudek, and W. Nazarewicz, Additivity of quadrupole moments in superdeformed bands: single-particle motion at extreme conditions. Phys. Rev. Lett. 77 (1996) 5182.
- (100) M. Matev, A. V. Afanasjev, J. Dobaczewski, G. A. Lalazissis, and W. Nazarewicz, Additivity of effective quadrupole moments and angular momentum alignments in nuclei, Phys. Rev. C 76, 034304 (2007).
- (101) L.B. Karlsson, I. Ragnarsson and S. Åberg, Polarization effects in superdeformed nuclei, Nucl. Phys. 639, 654 (1998).
- (102) A.V. Afanasjev and P. Ring, Superdeformations in relativistic and non-relativistic mean field theories, Phys. Scripta. T 88, 10 (2000).