MixTEA: Semi-supervised Entity Alignment with Mixture Teaching
Abstract
Semi-supervised entity alignment (EA) is a practical and challenging task because of the lack of adequate labeled mappings as training data. Most works address this problem by generating pseudo mappings for unlabeled entities. However, they either suffer from the erroneous (noisy) pseudo mappings or largely ignore the uncertainty of pseudo mappings. In this paper, we propose a novel semi-supervised EA method, termed as MixTEA, which guides the model learning with an end-to-end mixture teaching of manually labeled mappings and probabilistic pseudo mappings. We firstly train a student model using few labeled mappings as standard. More importantly, in pseudo mapping learning, we propose a bi-directional voting (BDV) strategy that fuses the alignment decisions in different directions to estimate the uncertainty via the joint matching confidence score. Meanwhile, we also design a matching diversity-based rectification (MDR) module to adjust the pseudo mapping learning, thus reducing the negative influence of noisy mappings. Extensive results on benchmark datasets as well as further analyses demonstrate the superiority and the effectiveness of our proposed method.
1 Introduction
Entity alignment (EA) is a task at the heart of integrating heterogeneous knowledge graphs (KGs) and facilitating knowledge-driven applications, such as question answering, recommender systems, and semantic search Gao et al. (2018). Embedding-based EA methods Chen et al. (2017); Wang et al. (2018); Sun et al. (2020a); Yu et al. (2021); Xin et al. (2022a) dominate current EA research and achieve promising alignment performance. Their general pipeline is to first encode the entities from different KGs as embeddings (latent representations) in a uni-space, and then find the most likely counterpart for each entity by performing all pairwise comparison. However, the pre-aligned mappings (i.e., training data) are oftentimes insufficient, which is challenging for supervised embedding-based EA methods to learn informative entity embeddings. This happens because it is time-consuming and labour-intensive for technicians to manually annotate entity mappings in the large-scale KGs.
To remedy the lack of enough training data, some existing efforts explore alignment signals from the cheap and valuable unlabeled data in a semi-supervised manner. The most common semi-supervised EA solution is using the self-training strategy, i.e., iteratively generating pseudo mappings and combining them with labeled mappings to augment the training data. For example, Zhu et al. (2017) propose IPTransE which involves an iterative process of predicting on unlabeled data and then treats the predictions above an elaborate threshold (confident predictions) as pseudo mappings for retraining. To further improve the accuracy of pseudo mappings, Sun et al. (2018) design a heuristic editing method to remove wrong alignment by considering one-to-one alignment constraint, while Mao et al. (2020) and Cai et al. (2022) utilize a bi-directional iterative strategy to determine pseudo mapping if and only if the two entities are mutually nearest neighbors of each other. Despite the encouraging results, existing semi-supervised EA methods still face the following problems: (1) Uncertainty of pseudo mappings. Prior works have largely overlooked the uncertainty of pseudo mappings during semi-supervised training. Revisiting the self-training process, the generation of pseudo mappings is either black or white, i.e., an entity pair is either determined as a pseudo mapping or not. While in fact, different pseudo mappings have different uncertainties and contribute differently to model learning Zheng and Yang (2021). (2) Noisy pseudo mapping learning. The performance of semi-supervised EA methods depends heavily on the quality of pseudo mappings, while these pseudo mappings inevitably contain much noise (i.e., False Positive mappings). Even worse, adding them into the training data would misguide the subsequent training process, thus causing error accumulation and further hurting the alignment performance.
To tackle the aforementioned limitations, in this paper, we propose a simple yet effective semi-supervised EA solution, termed as MixTEA. To be specific, our method is based on a Teacher-Student architecture Tarvainen and Valpola (2017), which aims to generate pseudo mappings from a gradually evolving teacher model and guides the learning of a student model with a mixture teaching of labeled mappings and pseudo mappings. We explore the uncertainty of pseudo mappings via probabilistic pseudo mapping learning rather than directly adding “reliable” pseudo mappings into the training data, which lends us to flexibly learn from pseudo mappings with different uncertainties. To achieve that, we propose a bi-directional voting (BDV) strategy that utilizes the consistency and confidence of alignment decisions in different directions to estimate the uncertainty via the joint matching confidence score (converted to matching probability after a softmax). Meanwhile, a matching diversity-based rectification (MDR) module is designed to adjust the pseudo mapping learning, thus reducing the influence of noisy mappings. Our contributions are summarized as follows:
(I) We propose a novel semi-supervised EA framework, termed as MixTEA111https://github.com/Xiefeng69/MixTEA, which guides the model’s alignment learning with an end-to-end mixture teaching of manually labeled mappings and probabilistic pseudo mappings.
(II) We introduce a bi-directional voting (BDV) strategy which utilizes the alignment decisions in different directions to estimate the uncertainty of pseudo mappings and design a matching diversity-based rectification (MDR) module to adjust the pseudo mapping learning, thus reducing the negative impacts of noise mappings.
(III) We conduct extensive experiments and thorough analyses on benchmark datasets OpenEA Sun et al. (2020b). The results demonstrate the superiority and effectiveness of our proposed method.
2 Related Works
2.1 Embedding-based Entity Alignment
While the recent years have witnessed the rapid development of deep learning techniques, embedding-based EA approaches obtain promising results. Among them, some early studies Chen et al. (2017); Sun et al. (2017) are based on the knowledge embedding methods, in which entities are embedded by exploring the fine-grained relational semantics. For example, MTransE Chen et al. (2017) applies TransE Bordes et al. (2013) as the KG encoder to embed different KGs into independent vector spaces and then conducts transitions via designed alignment modules. However, they need to carefully balance the weight between the encoder and alignment module in one unified optimization problem. Due to the powerful structure learning capability, Graph Neural Networks (GNNs) like GCN Kipf and Welling (2017) and GAT Veličković et al. (2018) have been employed as the encoder with Siamese architecture (i.e., shared-parameter) for many embedding-based models. GCN-Align Wang et al. (2018) applies Graph Convolution Network (GCN) for the first time to capture neighborhood information and embed entities into a unified vector space, but it suffers from the structural heterogeneity of different KGs. To mitigate this issue and improve the structure learning, AliNet Sun et al. (2020a) adopts multi-hop aggregation with a gating mechanism to expand neighborhood ranges for better structure modeling, and KE-GCN Yu et al. (2021) combines GCN and knowledge embedding methods to jointly capture the rich structural features and relation semantics of entities. More recently, IMEA Xin et al. (2022a) designs a Transformer-like architecture to encode multiple structural contexts in a KG while capturing alignment interactions across different KGs.
In addition, some works further improve the EA performance by introducing the side information about entities, such as entity names Zhang et al. (2019), attributes Liu et al. (2020), and literal descriptions Yang et al. (2019). Afterward, a series of methods were proposed to integrate knowledge from different modalities (e.g., relational, visual, and numerical) to obtain joint entity representation for EA Chen et al. (2020); Liu et al. (2021); Lin et al. (2022). However, these discriminative features are usually hard to collect, noise polluted, and privacy sensitive Pei et al. (2022).
2.2 Semi-supervised Entity Alignment
Since the manually labeled mappings used for training are usually insufficient, many semi-supervised EA methods have been proposed to take advantage of labeled mappings and the large amount of unlabeled data for alignment, which can provide a more practical solution in real scenarios. The mainstream solutions focus on iteratively generating pseudo mappings to compensate for the lack of training data. IPTransE Zhu et al. (2017) applies threshold filtering-based self-training to yield pseudo mappings but it fails to obtain satisfactory performance since it brings much noise data, which would misguide the subsequent training. Besides, it is also hard to determine an appropriate threshold to select “confident” pseudo mappings. KDCoE Chen et al. (2018) performs co-training of KG embedding model and literal description embedding model to gradually propose new pseudo mappings and thus enhance the supervision of alignment learning for each other. To further improve the quality of pseudo mappings, BootEA Sun et al. (2018) designs an editable strategy based on the one-to-one matching rule to deal with matching conflicts and MRAEA Mao et al. (2020) proposes a bi-directional iterative strategy which imposes a mutually nearest neighbor constraint. Inspired by the success of self-training, RANM Cai et al. (2022) proposes a relation-based adaptive neighborhood matching method for entity alignment and combines a bi-directional iterative co-training strategy, making become a natural semi-supervised model. Moreover, CycTEA Xin et al. (2022b) devises an effective ensemble framework to enable multiple alignment models (called aligners) to exchange their reliable entity mappings for more robust semi-supervised training, but it requires high complementarity among different aligners.
3 Problem Statement
A knowledge graph (KG) is formalized as , where and refer to the set of entities and the set of relations, respectively. is the set of triples, where , , and denote head entity (subject), relation, tail entity (object), respectively. Given a source KG , a target KG , and a small set of pre-aligned mappings (called training data) , where means equivalence relationship, entity alignment (EA) task pairs each source entity via nearest neighbor (NN) search to identify its corresponding target entity :
| (1) |
where denotes distance metrics (e.g., Manhattan or Euclidean distance). Moreover, to mitigate the inadequacy of training data, semi-supervised EA methods make effort to explore more potential alignment signals over the vast unlabeled entities, i.e., and , which denote the unlabeled entity set of source KG and target KG, respectively.

4 Proposed Method
In this section, we present our proposed semi-supervised EA method, called MixTEA, in Figure 1. MixTEA follows the teacher-student training scheme. The teacher model is performed to generate probabilistic pseudo mappings on unlabeled entities and student model is trained with an end-to-end mixture teaching of manually labeled mappings and probabilistic pseudo mappings. Compared to previous methods that require filtering pseudo mappings via thresholds or constraints, the end-to-end training gradually improves the quality of pseudo mappings, and the more and more accurate pseudo mappings in turn benefit EA training.
4.1 KG Encoder
We first introduce the KG encoder (denoted as ) which utilizes neighborhood structures and relation semantics to embed entities from different KGs into a unified vector space. We randomly initialize the trainable entity embeddings and relation embeddings , where and are the dimension of entities and relations, respectively.
Structure modeling. Structural features are crucial since equivalent entities tend to have similar neighborhood contexts. Besides, leveraging multi-range neighborhood structures is capable of providing more alignment evidence and mitigating the structural heterogeneity issue. In this work, we apply Graph Attention Network (GAT) Veličković et al. (2018) to allow an entity to selectively aggregate its surrounding information via attentive mechanism and we then recursively capture multi-range structural features by stacking layers:
| (2) |
| (3) |
where represents transposition, means concatenation, and a are the layer-specific transformation parameter and attention transformation vector, respectively. means the neighbor set of (including itself by adding a self-connection), and indicates the learned importance of entity to entity . denotes the entity embedding matrix at -th layer with . is the nonlinear function and we use ELU here.
Relation modeling. Relation-level information which carries rich semantics is vital to align entities in KGs because two equivalent entities may share overlapping relations. Considering that relation directions, i.e., outward () and inward (), have delicate impacts on characterizing the given target entity , we use two mean aggregators to gather outward and inward relation semantics separately to provide supplementary features for heterogeneous KGs:
| (4) |
| (5) |
where and are the sets of outward and inward relations of entity , respectively.
Weighted concatenation. After capturing the contextual information of entities in terms of neighborhood structures and relation semantics, we concatenate intermediate features for entity to obtain the final entity representation:
| (6) |
where and is the trainable attention vector to adaptively control the flow of each feature. We feed w to a softmax before multiplication to ensure that the normalized weights sum to 1.
4.2 Alignment Learning with Mixture Teaching
In the following, we will introduce mixture teaching, which is reached by the supervised alignment learning and probabilistic pseudo mapping learning in an end-to-end training manner.
Teacher-student architecture. Following Mean Teacher Tarvainen and Valpola (2017), we build our method which consists of two KG encoders with identical structure, called student model and teacher model , respectively. The student model constantly updates its parameters supervised by the manually labeled mappings as standard and the teacher model is updated via the exponential moving average (EMA) Tarvainen and Valpola (2017) weights of the student model. Moreover, the student model also learns from the pseudo mappings generated by the teacher model to further improve its performance, in which the uncertainty of pseudo mappings is formalized as calculated matching probabilities. Specifically, we update the teacher model as follows:
| (7) |
where denotes model weights, and is a preset momentum hyperparameter that controls the teacher model to update and evolve smoothly.
Supervised alignment learning. In order to make equivalent entities close to each other and unmatched entities pull away from each other in a unified space, we apply a margin-based alignment loss Wang et al. (2018); Mao et al. (2020); Yu et al. (2021) supervised by pre-aligned mappings:
| (8) | ||||
where is a hyperparameter of margin, is to ensure non-negative output, denotes the set of negative entity mappings, and means L2 distance (Euclidean distance). Negative mappings are sampled according to the cosine similarity of two entities Sun et al. (2018).
Probabilistic pseudo mapping learning. As mentioned above, the teacher model is responsible for generating probabilistic pseudo mappings for the student model to provide more alignment signals and thus enhance the alignment performance. Benefiting from the EMA update, the predictions of the teacher model can be seen as an ensemble version of the successive student models’ predictions. Therefore it is more robust and stable for pseudo mapping generation. Moreover, bi-directional iterative strategy Mao et al. (2020) reveals the asymmetric nature of alignment directions (i.e., source-to-target and target-to-source), which can produce pseudo mappings based on the mutually nearest neighbor constraint. Inspired by this, we propose a bi-directional voting (BDV) strategy which fuses alignment decisions in each direction to yield more comprehensive pseudo mappings and model their uncertainty via the joint matching confidence score. Concretely, after encoding, we can first obtain the similarity matrix by performing pairwise similarity calculation between the unlabeled source and target entities as follows:
| (9) |
where denotes cosine similarity function. and represent similarity matrices in different directions between source and target entities, and is the transposition of (i.e., . Next, for each matrix, we pick up the entity pair which has the maximum predicted similarity in each row as the pseudo mapping and then we combine the results of the pseudo mappings in different directions weighted by their last Hit@1 scores on validation data to obtain the final pseudo mapping matrix:
| (10) |
| (11) |
| (12) |
where is the function that converts the similarity matrix to a one-hot matrix (i.e., the only position with a value 1 at each row of the matrix indicates the pseudo mapping). In this manner, we arrive at the final pseudo mapping matrix generated by the teacher model, in which each pseudo-mapping is associated with a joint matching confidence score (the higher the joint matching confidence, the less the uncertainty). Different from the bi-directional iterative strategy, we use the voting consistency and matching confidence of alignment decisions in different directions to facilitate uncertainty estimation. Specifically, given an entity pair (, ), its confidence is 1 when and only when both directions unanimously vote this entity pair as a pseudo mapping, otherwise its confidence is in the interval (0,1) when only one direction votes for it and 0 when no direction votes for it (i.e., this entity pair will not be regarded as a pseudo mapping).
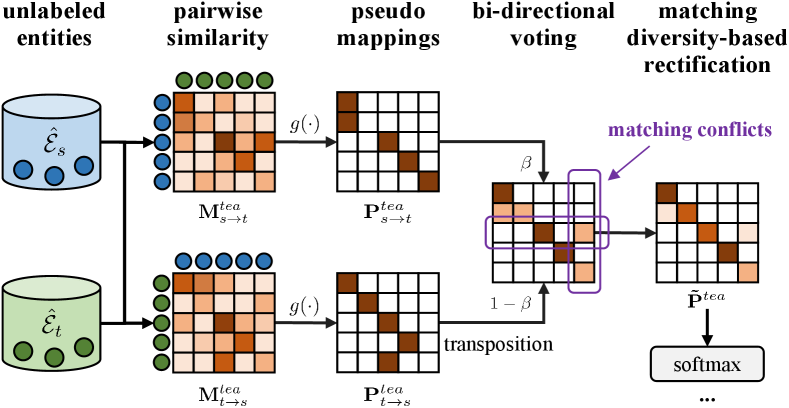
In addition, the ideal predictions of EA need to satisfy the one-to-one matching constraint Suchanek et al. (2011); Sun et al. (2018), i.e., a source entity can be matched with at most one target entity, and vice versa. However, the joint decision voting process inevitably yields matching conflicts due to the existence of erroneous (noisy) mappings. Inspired by Gal et al. (2016), we further propose a matching diversity-based rectification (MDR) module to adjust the pseudo mapping learning, thus mitigating the influence of noisy mappings dynamically. We denote (i.e., ) as the similarity matrix calculated based on the student model and define a Cross-Entropy (CE) loss between and rectified by matching diversity:
| (13) |
| (14) |
where denotes the rectified pseudo mapping matrix. To be specific, the designed rectification term (Eq. (13)) measures how much a potential pseudo mapping deviates (in terms of joint matching confidence score) from other competing pseudo mappings in and . The larger the deviation, the greater the penalty for this pseudo mapping, and vice versa. Notably, both and are fed into a softmax to be converted to probability distributions before CE to implement probabilistic pseudo mapping learning. Besides, an illustrative example of generating the probabilistic pseudo mapping matrix is provided in Figure 2.
Optimization. Finally, we minimize the following combined loss function (final objective) to optimize the student model in an end-to-end training manner:
| (15) |
where is a ramp-up weighting coefficient used to weight between the supervised alignment learning (i.e., ) and pseudo mappings learning (i.e., ). In the beginning, the optimization is dominated by and during the ramp-up period, will gradually participate in the training to provide more alignment signals. The overall optimization process is outlined in Algorithm 1 (Appendix A), where the student model and the teacher model are updated alternately, and the final student model is utilized for EA inference (Eq. (1)) on test data.
5 Experimental Setup
5.1 Data and Evaluation Metrics
We evaluate our method on the 15K benchmark dataset (V1) in OpenEA Sun et al. (2020b) since the entities thereof follow the degree distribution in real-world KGs. The brief information of experimental data is shown in Table 3 (Appendix B). It contains two cross-lingual settings, i.e., EN-FR-15K (English-to-French) and EN-DE-15K (English-to-German), and two monolingual settings, i.e., D-W-15K (DBPedia-to-Wikidata) and D-Y-15K (DBPedia-to-YAGO). Following the data splits in OpenEA, we use the same split setting where 20%, 10%, and 70% pre-aligned mappings are utilized for training, validation, and testing, respectively.
Entity alignment is a typical ranking problem, where we obtain a target entity ranking list for each source entity by sorting the similarity scores in descending order. We use Hits@k (=1, 5) and Mean Reciprocal Rank (MRR) as the evaluation metrics Sun et al. (2020b); Xin et al. (2022a). Hits@k is to measure the alignment accuracy, while MRR measures the average performance of ranking over all test samples. The higher the Hits@k and MRR, the better the alignment performance.
5.2 Baseline Methods
We choose the methods from the related work as baselines and divide them into two classes below:
- •
-
•
Semi-supervised methods. These methods aim to explore alignment signals from unlabeled entities, such as (1) IPTransE Zhu et al. (2017), (2) SEA Pei et al. (2019), (3) KDCoE Chen et al. (2018), (4) BootEA Sun et al. (2018), (5) MRAEA Mao et al. (2020), (6) RANM Cai et al. (2022) and (7) GAEA Xie et al. (2023).
As our method and the above baselines only contain a single model and mainly rely on structural information, for a fair comparison, we do not compare with ensemble-based frameworks (e.g., CycTEA Xin et al. (2022b)) and models infusing side information from multi-modality (e.g., EVA Liu et al. (2021), RoadEA Sun et al. (2022)). For the baseline RANM, we remove the name channel to guarantee a fair comparison.
5.3 Implementation Details
All the experiments are performed in PyTorch on an NVIDIA GeForce RTX 3090 GPU. Following OpenEA Sun et al. (2020b), we report the average results of five-fold cross-validation. The embedding dimensions of entities and relations are set to 256 and 128, respectively, the number of GAT layer is 2, the margin is 2.0, and the momentum is 0.9. In the EA inference phase, we use Cosine distance as the distance metric and apply Faiss222https://github.com/facebookresearch/faiss to perform NN search efficiently. The default alignment direction is from left to right, e.g., in D-W-15K, we regard DBpedia as the source KG and seek to find the counterparts of source entities in the target KG Wikidata. The details of hyperparameter settings are shown in Appendix C.
6 Experimental Results
6.1 Performance Comparison
Table 1 reports the experimental results of all the methods on the OpenEA 15K datasets. Even utilizing only the structure information, KE-GCN and IMEA achieve inspiring performance by exploring the rich structural contexts. However, they are hard to further improve the performance because suffer from the lack of enough training data. We also observe that some semi-supervised EA methods (e.g., IPTransE and SEA) fail to outperform these structure-based EA methods, reflecting the fact that both encoder design and semi-supervised strategy are important components of facilitating high-accuracy EA. IPTransE obtains unsatisfactory alignment results since it produces many noise pseudo mappings during the self-training process but does not design an appropriate mechanism to eliminate the influence of noise. Besides, the performance of KDCoE is unstable. According to Sun et al. (2020b), this is because many entities lack textual descriptions, thus preventing the model from finding complementary mappings for co-training from the textual description embedding model. BootEA and MRAEA are competitive baselines in semi-supervised EA domain. Nevertheless, BootEA needs a carefully fine-tuned confidence threshold to filter pseudo mappings, which often leads to unstability, while MRAEA and RANM still follows the data augmentation paradigm, which ignores the uncertainty of pseudo mappings and is prone to cause error accumulation. Although GAEA learns representations of vast unseen entities via contrastive learning, its performance is unstable. The bottom part of Table 1 shows our method consistently achieves the best performance in all tasks with a small standard deviation (std.). More precisely, our model surpasses state-of-the-art baselines averagely by 3.1%, 3.3%, and 3.5% in terms of Hit@1, Hit@5, and MRR, respectively.
6.2 Ablation Study
To verify the effectiveness of our method, we perform the ablation study with the following variant settings: (1) w/o removes the relation modeling. (2) w/o removes probabilistic pseudo mapping learning. (3) w/o BDV only considers EA decisions in the default alignment direction to generate pseudo mappings instead of applying the bi-directional voting strategy (i.e., ). (4) w/o MDR removes matching diversity-based rectification module in pseudo mappings learning. (5) w/o B&M denotes that the complete model deletes both BDV and MDR module.
The ablation results are shown in Table 2. We can observe that the complete model achieves the best experimental results, which indicates that each component in our model design contributes to the performance improvement. Removing relation modeling from entity representation causes performance drops, which identifies the relation semantics can help in enriching the expressiveness of entity representations. W/o caused the most significant performance degradation, especially in monolingual settings, showing the crucial role of the pseudo mapping learning in general. The results of w/o BDV and w/o MDR suggest that the bi-directional voting strategy and matching diversity-based rectification module can do benefit to improving the quality of pseudo mapping learning. W/o B&M also demonstrates that the combination of BDV and MDR can further improve the alignment performance. Although w/o BDV only takes EA decisions in one direction into account, it still inevitably brings matching conflicts since NN search neglects the inter-dependency between different EA decisions. Compared to w/o B&M, the MDR in w/o BDV has a certain positive effect, which indicates that our proposed MDR can be applied to other pseudo mapping generation algorithms and help the models to train better.
6.3 Auxiliary Experiments

(a) EN-DE-15K

(b) D-W-15K
Training visualization. To inspect our method comprehensively, we also plot the test Hit@1 curve throughout the training epochs in Figure 3. KG Encoder (th=0.9) represents the KG Encoder described in Sec. 4.1 applying the self-training with threshold=0.9 to generate pseudo mappings every 20 epochs. We control the same experimental settings to remove the performance perturbations induced by different parameters. From Figure 3, we observe that our method converges quickly and achieves the best and most stable alignment performance. The performance of the KG Encoder gradually decreases in the later stages since it gets stuck in overfitting to the limited training data. Although self-training brings some performance gains after data augmentation in the early stages, the performance drops dramatically in the later stages. This is because it involves many noise pseudo mappings and causes error accumulation as the self-training continues. In the later stages, self-training has difficulty in further generating new mappings while existing erroneous mappings constantly misguide the model training, thus hurting the performance.
Hyperparameter analysis. We design hyperparameter experiments to investigate the performance varies with some hyperparameters. Due to the space limitation, these experimental results and analyses are listed in Appendix D.
7 Conclusion
In this paper, we propose a novel semi-supervised EA framework, termed as MixTEA, which guides the model learning with an end-to-end mixture teaching of manually labeled mappings and probabilistic pseudo mappings. Meanwhile, we propose a bi-directional voting (BDV) strategy and a matching diversity-based rectification (MDR) module to assist the probabilistic pseudo mapping learning. Experimental results on benchmark datasets show the effectiveness of our proposed method.
Limitations
Although we have demonstrated the effectiveness of MixTEA, there are still some limitations that should be addressed in the future: (1) Currently, we only utilize structural contexts which are abundant and always available in KGs to embed entities. However, when side information (e.g., visual contexts, literal contexts) is available, MixTEA needs to be extended into a more comprehensive EA framework and ensure that it does not become over-complex in the teacher-student architecture. Therefore, how to involve this side information is our future work. (2) Vanilla self-training iteratively generates pseudo mappings and adds them to the training data, where the technicians can perform spot checks during model training to monitor the quality of pseudo mappings. While MixTEA computes probabilistic pseudo mapping matrix and performs end-to-end training, thus making it hard to provide explicit entity mappings for the technicians to check their correctness. Therefore, it is imperative to design a strategy to combine the self-training and probabilistic pseudo mapping learning to enhance the interpretability and operability.
Ethics Statement
This work does not involve any discrimination, social bias, or private data. Therefore, we believe that our study complies with the ACL Ethics Policy.
Acknowledgments
We thank the anonymous reviewers for their comments. This work is supported by the National Natural Science Foundation of China No. 62172428.
References
- Bordes et al. (2013) Antoine Bordes, Nicolas Usunier, Alberto Garcia-Durán, Jason Weston, and Oksana Yakhnenko. 2013. Translating embeddings for modeling multi-relational data. In Proceedings of the 26th International Conference on Neural Information Processing Systems-Volume 2, pages 2787–2795.
- Cai et al. (2022) Weishan Cai, Wenjun Ma, Lina Wei, and Yuncheng Jiang. 2022. Semi-supervised entity alignment via relation-based adaptive neighborhood matching. IEEE Transactions on Knowledge and Data Engineering.
- Chen et al. (2020) Liyi Chen, Zhi Li, Yijun Wang, Tong Xu, Zhefeng Wang, and Enhong Chen. 2020. Mmea: entity alignment for multi-modal knowledge graph. In Knowledge Science, Engineering and Management: 13th International Conference, KSEM 2020, Hangzhou, China, August 28–30, 2020, Proceedings, Part I 13, pages 134–147. Springer.
- Chen et al. (2018) Muhao Chen, Yingtao Tian, Kai-Wei Chang, Steven Skiena, and Carlo Zaniolo. 2018. Co-training embeddings of knowledge graphs and entity descriptions for cross-lingual entity alignment. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pages 3998–4004.
- Chen et al. (2017) Muhao Chen, Yingtao Tian, Mohan Yang, and Carlo Zaniolo. 2017. Multilingual knowledge graph embeddings for cross-lingual knowledge alignment. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, pages 1511–1517.
- Gal et al. (2016) Avigdor Gal, Haggai Roitman, and Tomer Sagi. 2016. From diversity-based prediction to better ontology & schema matching. In Proceedings of the 25th International Conference on World Wide Web, pages 1145–1155.
- Gao et al. (2018) Yuqing Gao, Jisheng Liang, Benjamin Han, Mohamed Yakout, and Ahmed Mohamed. 2018. Building a large-scale, accurate and fresh knowledge graph. KDD-2018, Tutorial, 39:1939–1374.
- Kipf and Welling (2017) Thomas N Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations.
- Lin et al. (2022) Zhenxi Lin, Ziheng Zhang, Meng Wang, Yinghui Shi, Xian Wu, and Yefeng Zheng. 2022. Multi-modal contrastive representation learning for entity alignment. In Proceedings of the 29th International Conference on Computational Linguistics, pages 2572–2584.
- Liu et al. (2021) Fangyu Liu, Muhao Chen, Dan Roth, and Nigel Collier. 2021. Visual pivoting for (unsupervised) entity alignment. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pages 4257–4266.
- Liu et al. (2020) Zhiyuan Liu, Yixin Cao, Liangming Pan, Juanzi Li, and Tat-Seng Chua. 2020. Exploring and evaluating attributes, values, and structures for entity alignment. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 6355–6364.
- Mao et al. (2020) Xin Mao, Wenting Wang, Huimin Xu, Man Lan, and Yuanbin Wu. 2020. Mraea: an efficient and robust entity alignment approach for cross-lingual knowledge graph. In Proceedings of the 13th International Conference on Web Search and Data Mining, pages 420–428.
- Pei et al. (2019) Shichao Pei, Lu Yu, Robert Hoehndorf, and Xiangliang Zhang. 2019. Semi-supervised entity alignment via knowledge graph embedding with awareness of degree difference. In The World Wide Web Conference, pages 3130–3136.
- Pei et al. (2022) Shichao Pei, Lu Yu, Guoxian Yu, and Xiangliang Zhang. 2022. Graph alignment with noisy supervision. In Proceedings of the ACM Web Conference 2022, pages 1104–1114.
- Suchanek et al. (2011) Fabian M Suchanek, Serge Abiteboul, and Pierre Senellart. 2011. Paris: Probabilistic alignment of relations, instances, and schema. Proceedings of the VLDB Endowment (PVLDB), 5(3):157–168.
- Sun et al. (2017) Zequn Sun, Wei Hu, and Chengkai Li. 2017. Cross-lingual entity alignment via joint attribute-preserving embedding. In The Semantic Web–ISWC 2017: 16th International Semantic Web Conference, Vienna, Austria, October 21–25, 2017, Proceedings, Part I 16, pages 628–644. Springer.
- Sun et al. (2022) Zequn Sun, Wei Hu, Chengming Wang, Yuxin Wang, and Yuzhong Qu. 2022. Revisiting embedding-based entity alignment: A robust and adaptive method. IEEE Transactions on Knowledge and Data Engineering.
- Sun et al. (2018) Zequn Sun, Wei Hu, Qingheng Zhang, and Yuzhong Qu. 2018. Bootstrapping entity alignment with knowledge graph embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pages 4396–4402.
- Sun et al. (2020a) Zequn Sun, Chengming Wang, Wei Hu, Muhao Chen, Jian Dai, Wei Zhang, and Yuzhong Qu. 2020a. Knowledge graph alignment network with gated multi-hop neighborhood aggregation. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 222–229.
- Sun et al. (2020b) Zequn Sun, Qingheng Zhang, Wei Hu, Chengming Wang, Muhao Chen, Farahnaz Akrami, and Chengkai Li. 2020b. A benchmarking study of embedding-based entity alignment for knowledge graphs. In Proceedings of the VLDB Endowment.
- Tarvainen and Valpola (2017) Antti Tarvainen and Harri Valpola. 2017. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Proceedings of the 31st International Conference on Neural Information Processing Systems, pages 1195–1204.
- Veličković et al. (2018) Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. 2018. Graph attention networks. In International Conference on Learning Representations.
- Wang et al. (2018) Zhichun Wang, Qingsong Lv, Xiaohan Lan, and Yu Zhang. 2018. Cross-lingual knowledge graph alignment via graph convolutional networks. In Proceedings of the 2018 conference on empirical methods in natural language processing, pages 349–357.
- Xie et al. (2023) Feng Xie, Xiang Zeng, Bin Zhou, and Yusong Tan. 2023. Improving knowledge graph entity alignment with graph augmentation. In Advances in Knowledge Discovery and Data Mining: 27th Pacific-Asia Conference on Knowledge Discovery and Data Mining, PAKDD 2023, Osaka, Japan, May 25–28, 2023, Proceedings, Part II, pages 3–14.
- Xin et al. (2022a) Kexuan Xin, Zequn Sun, Wen Hua, Wei Hu, and Xiaofang Zhou. 2022a. Informed multi-context entity alignment. In Proceedings of the 15th ACM International Conference on Web Search and Data Mining, pages 1197–1205.
- Xin et al. (2022b) Kexuan Xin, Zequn Sun, Wen Hua, Bing Liu, Wei Hu, Jianfeng Qu, and Xiaofang Zhou. 2022b. Ensemble semi-supervised entity alignment via cycle-teaching. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 36, pages 4281–4289.
- Yang et al. (2019) Hsiu-Wei Yang, Yanyan Zou, Peng Shi, Wei Lu, Jimmy Lin, and Xu Sun. 2019. Aligning cross-lingual entities with multi-aspect information. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 4431–4441.
- Yu et al. (2021) Donghan Yu, Yiming Yang, Ruohong Zhang, and Yuexin Wu. 2021. Knowledge embedding based graph convolutional network. In Proceedings of the Web Conference 2021, pages 1619–1628.
- Zeng et al. (2021) Weixin Zeng, Xiang Zhao, Jiuyang Tang, and Changjun Fan. 2021. Reinforced active entity alignment. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, pages 2477–2486.
- Zhang et al. (2019) Qingheng Zhang, Zequn Sun, Wei Hu, Muhao Chen, Lingbing Guo, and Yuzhong Qu. 2019. Multi-view knowledge graph embedding for entity alignment. In Proceedings of the 28th International Joint Conference on Artificial Intelligence.
- Zheng and Yang (2021) Zhedong Zheng and Yi Yang. 2021. Rectifying pseudo label learning via uncertainty estimation for domain adaptive semantic segmentation. International Journal of Computer Vision, 129(4):1106–1120.
- Zhu et al. (2017) Hao Zhu, Ruobing Xie, Zhiyuan Liu, and Maosong Sun. 2017. Iterative entity alignment via joint knowledge embeddings. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, pages 4258–4264.
Appendix A Pseudocode of Training Procedure
Appendix B Dataset Statistics
| Datasets | #Ent. | #Rel. | #Tri. | |
|---|---|---|---|---|
| EN-FR-15K | English | 15000 | 267 | 47334 |
| French | 15000 | 210 | 40864 | |
| EN-DE-15K | English | 15000 | 215 | 47676 |
| German | 15000 | 131 | 50419 | |
| D-W-15K | DBPedia | 15000 | 248 | 38265 |
| Wikidata | 15000 | 169 | 42746 | |
| D-Y-15K | DBPedia | 15000 | 165 | 30292 |
| YAGO | 15000 | 28 | 26638 | |
Appendix C Hyperparameter Details
We tune the hyperparameters for our proposed MixTEA. The setting values and search ranges of hyperparameters are described in Table 4.
| Hyperparameters | Value/Search range |
|---|---|
| The number of GAT layer | [1, 2, 3, 4] |
| Momentum parameter | [0.9, 0.99, 0.999] |
| Margin | [1, 2, 3] |
| Negative sample size | [10, 20, 30] |
| Embedding dimension | [128, 256] |
| Embedding initialization | Xavier |
| Learning rate | 0.005 |
Appendix D Hyperparameter Analysis
The impact of different GAT layers. We vary the number of GAT layer from 1 to 4 and the quantitative results are illustrated in Figure 4 (a). =1 results in poor alignment performance due to the limited structural modeling power. The best performance is achieved when =2, except for the D-Y-15K task. Increasing will not bring further performance improvement, we infer that there is overfitting or oversmoothing during neighborhood aggregation. In D-Y-15K, the optimal performance is obtained when =4. The possible reason is that in D-Y-15K, the two KGs have relatively sparse structure information (as shown in Table 3 in Appendix B), therefore they need to capture more alignment evidence from distant neighbors.

(a) the number of GAT layers

(b) momentum parameter
The impact of momentum parameter. We investigate the momentum parameter in [0, 0.9, 0.99] and the results in EN-DE-15K and D-W-15K tasks are presented in Figure 4 (b). We found that our method maintains good performance under different momentum settings, demonstrating that our method is insensitive to . In addition, a proper such as 0.9 brings certain performance improvements, which indicates that the EMA update manner can facilitate the teacher model to yielding stable and robust pseudo mappings.