Mittag-Leffler stability of complete monotonicity-preserving schemes for time-dependent coefficients sub-diffusion equations
Abstract
A key characteristic of the anomalous sub-solution equation is that the solution exhibits algebraic decay rate over long time intervals, which is often refered to the Mittag-Leffler type stability. For a class of power nonlinear sub-diffusion models with variable coefficients, we prove that their solutions have Mittag-Leffler stability when the source functions satisfy natural decay assumptions. That is the solutions have the decay rate as , where , are positive constants, and . Then we develop the structure preserving algorithm for this type of model. For the complete monotonicity-preserving (-preserving) schemes developed by Li and Wang (Commun. Math. Sci., 19(5):1301-1336, 2021), we prove that they satisfy the discrete comparison principle for time fractional differential equations with variable coefficients. Then, by carefully constructing the fine the discrete supersolution and subsolution, we obtain the long time optimal decay rate of the numerical solution as , which is fully agree with the theoretical solution. Finally, we validated the analysis results through numerical experiments.
keywords:
time-dependent coefficient sub-diffusion equations, -preserving schemes, Mittag-Leffler type stability, discrete comparison principle.Declarations of interest: none.
1 Introduction
A typical application of time fractional equations is to describe various anomalous diffusion models, namely sub-diffusion and super-diffusion phenomena. For the standard diffusion process, which is usually described by the classical heat equation, where the mean square displacement (MSD) of particles is a linear function of time, i.e., . 111As usual, our notation here represents the asymptotic limit , where represents a general positive constant, which may take different values in different places, but is always independent of or . We also use the standard notation to represent a certain asymptotic order, for example means . However, many actual model data indicate that the MSD of anomalous diffusion processes may have a form , where . Based on random walk theory, we can rigorously derive fractional diffusion equations, where Caputo derivatives are typically used in the time direction instead of classical first-order derivatives [3, 8]. Specifically, when , it is referred to as the sub-diffusion process.
For the time fractional order model, its solutions exhibit asymptotic behavior completely different from the standard diffusion equation over a long time interval. In fact, solutions to time fractional equations typically have algebraic decay rates, while standard first-order equations have exponential decay rates. This can be seen from the simple example below. Consider the fractional ODE: with , where the Caputo fractional derivative of order is defined by [8]. The solution is given by , where is the Mittag-Leffler funciton. When , we have by the asymptotic expansion formula of Mittag-Leffler funciton. This long-term algebraic decay rate is commonly referred to as Mittag-Leffler stability. Another surprising result is presented in [19], which shows that for the fractional ODE: with and , the solution has the asymptotic decay rate .
Once we have the above two results and combine appropriate energy methods, we can obtain the long-term decay rate estimation of the standard -norm for the solution of linear or some nonlinear anomalous diffusion model. See for example [4, 10, 19, 2]. Currently, most of these analyses are focused on constant coefficient equations. However, the anomalous diffusion problems can be both constant coefficients and variable coefficients. Compared with constant coefficient equations, the variable coefficient equations are appropriate for modeling of anomalous diffusive processes in turbulent media. For instance, modeling sub-diffusive transport inside a fractured porous media [6]. Diffusion representation of tracer particles in heterogeneous biological ambient fluids [1]. In particular, the application of the time dependence coefficient is a new perspective of coupling the spatial and temporal variables, which avoids the divergence caused by the long tail of the temporal probability distribution at a fixed time [5]. For more information on the application of variable coefficients to more complex physical and biological systems, see also [3, 5, 7].
The aim of this paper is to study both theoretically and numerically the long time Mittag-Leffler stability of the solutions for a class of nonlinear anomalous diffusion models with time-dependent coefficients
| (1) |
where , , , and is a bounded domain with smooth boundary . And can be linear or nonlinear operator, some typical examples including the Laplace operator ; the -Laplace operator with and the mean curvature operator . Following [4, 16],we assume that satisfies the following structural assumption
| (2) |
where , and . One can verify that the above example of indeed satisfies the elliptical structure assumption [4, 14]. The non-zero source terms and satisfies the decay estimate
| (3) |
Let be the solution of (1). Under the above assumptions, we can establish the long-term estimation of , i.e. Mittag-Leffler stability, by combining the energy method with the long-term estimation of time fractional ODEs. For the homogeneous linear constant coefficient equation with and , we can apply standard eigenvalue and eigenfunction pairs methods to obtain that . For the constant coefficient nonlinear equation with and satisfying (2), it is shown that ; see [16, 4, 2]. And for the homogeneous varying coefficient nonlinear equation with and satisfying (2), the asymptotic estimate for weak solution is obtained in [14], from which can see from that the time-dependent factor has a direct impact on the long-term decay rate of the solution.
At present, most numerical methods for time fractional equations focus on the reduction in numerical convergence rate caused by weak singularity of the solution near the initial moment. Various effective techniques have been developed to restore high-order convergence of numerical methods; see [13, 11, 15, 9]. From the perspective of the structure-preserving algorithm, we naturally hope that the numerical solution can preserve the long-term optimal decay rate of the sub-diffusion equation, that is, establish numerical Mittag-Leffler stability. At present, there are relatively few research results on qualitative analysis of numerical solutions to anomalous diffusion equations, especially long-term behavior analysis. For the linear time fractional evolutional equation, the numerical ML stability, i.e. is established in [18] through singularity analysis of the generating function of the numerical solution, where is the numerical approximation of at . For the constant coefficient nonlinear equation with and satisfying (2), the numerical ML stability as was recently established in [17], using the discrete comparison principle and the method of constructing fine discrete sup and sub solutions. The key to success here lies in a class of time fractional derivative structure-preserving discrete schemes, namely the -preserving schemes developed in [12]. The discrete coefficients of this type of numerical method have many excellent properties.
The objective of this article is twofold.
- 1.
-
2.
We establish the numerical ML stability for (1) based on the -preserving schemes and show that . Firstly, we prove that the -preserving schemes also satisfies the discrete comparison principle for variable coefficient equations. Then, applying this result, we construct discrete sup and sub solutions with variable coefficients to obtain the expected optimal numerical decay rate estimate. Our work in this article extend the results in [17] from homogeneous constant coefficient equations to non-homogeneous, variable coefficient equations.
The rest of this article is organized as follows. In Section 2, we derive the long time decay rate of continuous solutions for (1) and provide detailed proofs of the estimates. In Section 3, we recall -preserving schemes on uniform mesh with time step size and their main properties. In Section 4, we establish the discrete numerical ML stability for (1). We first derive the discrete comparison principle of -preserving schemes for a class of time-dependent fractional ODEs. Then, by constructing discrete sub and sup solution we show the numerical ML stability for fractional non-homogeneous, variable coefficient ODEs. Then, by establishing a variable coefficient discrete energy inequality, we obtain the estimate of the long-term decay rate of the numerical solution of (1). Finally, we present several typical numerical examples to illustrate and verify the optical numerical decay rate in Section 5.
2 Decay estimate for nonlinear models with time-dependent coefficients
Consider the time-dependent coefficients fractional ODE, which highlight the influence of :
| (4) |
where , , and . The decay result concerning (4) reads as follows.
Note that when , the fractional ODE (4) is reduced to the power nonlinear equation and its solution has decay rate [16]. Further, when and , it becomes fractional linear ODE and the solution has the decay rate . Our first result below is to extend the estimation of the long-term decay rate of homogeneous equation (4) to non-homogeneous cases with source terms.
The proof the Mittag-Leffler stability of fractional ODEs in [16, 14] is mainly based on the comparison principle and the construction of appropriate barrier functions.
Lemma 2.2 (Fractional comparison principle).
It is noted that in (4), the nonlinear function is positive and nondecreasing, which allows the utilization of Lemma 2.2 to prove Lemma 2.1. Now we extend Lemma 2.1 to non-homogeneous cases with source terms.
Theorem 2.1.
Consider the fractional ODE: with and assume that satisfies for some . Then there exists constants , such that the solution satisfies
| (6) |
Our main idea of proof is as follows: by constructing new fine upper and lower solutions, we can control the source function and obtain inequality of the corresponding homogeneous equation, which can be applied to Lemma 2.2.
Proof.
By the assumption , we have
| (7) |
Define .
I. Construct a subsolution. Consider the function
| (8) |
where
Using the definition of , it is easy to find that is monotonically decreasing. Now we show that is a sub solution for over the interval . For , by noting and , we have
On the other hand, for we have . Therefor,
By the definitions of , and noting that , we confirm that
then
| (9) |
Hence, combining (7), (2) and (9), we have
II. Construct a supersolution. Define by means of
Let us consider the monotonically decreasing function
| (10) |
For , we have
| (11) |
Next, observe that for , we may thus estimate as follows
It follows from the definition that and . Hence, we have for .
Finally, suppose that , we obtain
By definition of , we also have , which yields for . In summary, we get that
As an immediate application of Theorem 2.1, we can derive the long-term decay rate for for the solution of the time fractional PDE model (3) by combination of appropriate energy estimate.
Corollary 2.1.
3 -preserving numerical methods
From the perspective of structural preservation algorithms, it is natural to develop structural preservation algorithms for time fractional order equations, so that numerical solutions can accurately preserve the long-term optimal decay rate of the solution in Lemma 2.1 for nonlinear fractional ODEs and in Corollary 2.1 for nonlinear fractional PDEs. That is to develop numerical Mittag-Leffler stability for the model (1).
The Caputo fractional derivative has a convolutional structure, so we consider that its numerical approximation also has a corresponding discrete convolution structure, which takes the form of
| (14) |
where and denotes the numerical approximation of on the uniform meshes with step size . The weight coefficients can be computed explicitly. The two most popular methods are Grünwald-Letnikov scheme and L1 method, both of which can be seen as fractional extensions of the classical backward Euler scheme.
Example 3.1.
For L1 method, the weight satisfies
and consequently .
Example 3.2.
For the Grünwald-Letnikov scheme, the weights are the -th coefficients of the generating function . Therefore,
By using Riemann-Liouville fractional integration, the initial value problem of the Caputo derivative can be transformed into the corresponding Volterra integral equation, which also has a convolutional structure and its kernel function is for . The standard kernel function is a very important class of completely monotonic () functions 222A function is said to be completely monotone if for all and . . Based on the basic idea of preserving structure algorithm, the -preserving numerical methods for Riemann-Liouville fractional integration is developed in [12]. The new concept and framework of -preserving numerical methods has many excellent properties in the discrete coefficients. This kind of numerical methods has recently been successfully applied to a class of nonlinear anomalous diffusion models [17]. It is proved in [12] that for -preserving numerical methods the weights and have the convenient properties
| (15) |
These properties imply that there exist constants , which are independent of , sunch that
| (16) |
It is easy to verify the Grünwald-Letnikov scheme and L1 method in the above two examples are -preserving and their coefficients meet the above properties. See more details in [12].
4 Numerical Mittag-Leffler stability
In the section, we study the numerical Mittag-Leffler stability for -preserving numerical methods for nonlinear sub-diffusion models with variable coefficients. Specifically, we prove that for the -preserving schemes, its numerical solution has a long-term optimal decay rate that is completely consistent with the corresponding continuous equation. Our proof mainly consists of the following three steps. Firstly, we establish the discrete comparison principle for variable coefficient equations. Then we apply this result to homogeneous equations with variable coefficients and establish the Mittag-Leffler stability of numerical solutions. Finally, for general non-homogeneous equations with source terms, we also establish the numerical Mittag-Leffler stability.
4.1 Discrete fractional comparison principle
We have the following discrete fractional comparison principle, which extend the results of [12].
Lemma 4.1.
Let be the -preserving discrete operator defined in (14). Assume the function is nondecreasing and . Suppose that the sequences , , satisfy and
Then for all . We call a discrete subsolution for and a discrete supsolution.
Proof.
Define the sequence for with . Then we get that . Because is nondecreasing and and for any , we further get that
| (17) |
Define the indicator function
| (18) |
Multiplying the inequality (17) by gives
It’s easy to see . Let with . Since for and , we have
That is for all . For , because of and , one has . Meanwhile, we know from the definition of , which yields that . Following a similar method, we can easily obtain for all . This implies that for all , i.e., . The argument for is similar. ∎
4.2 Numerical Mittag-Leffler stability for homogeneous equations
With the above preparation, we can now prove our first result, which is the numerical Mittag-Leffler stability of nonlinear homogeneous equations with variable coefficients. We focus here on the direct impact of the coefficient factor on the long-term optimal decay rate.
Theorem 4.1.
The main method we prove here is to construct appropriate discrete upper and lower solutions and such that they all have the same long-term asymptotic decay rate , and then obtain the desired result using the discrete comparison principle.
Proof.
I. Construction of the discrete subsolution Set for . Define the sequence
| (21) |
where , and are three parameters to be determined. Below, we will make appropriate choices for these three parameters to ensure that:
(i) the sequence is monotonically decreasing and positive;
(ii) satisfies that .
We divide the proof into several steps.
Step 1. is monotonically decreasing. From (21) we know that is monotonically increasing with respect to for and , . Therefore, in order for to be positive and monotonically decreasing if and only if . That is
| (22) |
Step 2. is a discrete subsolution for . For , it follows from (14) that
By the properties (15), we have the estimate
which yields that . Therefore, in order to make a discrete lower solution, we only need to select parameters such that
Hence, we can take such that
| (23) |
Step 3. is a discrete subsolution for . For , we have
Note that can be rewritten as Hence, recalling that for , we have
In view of and , we get that
Since is monotonically decreasing, so
Thus We just need to select parameters such that That is
| (24) |
Step 4. Parameters selection relying only on data. We now choose appropriate parameters to ensure that all three inequalities (22), (23) and (24) hold simultaneously. We can choose
| (25) |
According to the above definition, we can easily see that inequality (23) and (24) hold. Let’s verify that (22) is also valid. In fact, we have
Then . Those analysis shows that is a subsolution to with decay rate .
II. Construction of the discrete supersolution. Define the function
| (26) |
Then take for . The parameters and are two parameters to be determined. Below, we will make appropriate choices for these two parameters to ensure that:
(i) the sequence is monotonically decreasing and positive;
(ii) satisfies that .
We also divide the proof into several steps.
Step 1. is monotonically decreasing. Obviously when , is monotonically decreasing on . In order for is monotonic for all , we just need . That is . Now we take to make the required inequality holds.
Step 2. is a discrete supersolution for . From (26), we have
| (27) |
Step 3. is a discrete supersolution for . Considering separately the cases and . Note that for and put . Hence . With this formula, the discretisation (14) can be rewritten as
| (28) |
where we use the fact for . Note that and for , which leads to for . Now it follows from (28) that
By (16) and , one has so
| (29) |
where and on imply that . By the definition of and , there is
| (30) |
In order for is a discrete supsolution, we only need
| (31) |
Therefor, we can take such that
| (32) |
Step 4. is a discrete supersolution for . Let , so and . From (28), one has
| (33) |
Using and the same method as that in the case of , one has
| (34) |
Note that implies that and . Now by the definition of , we have
On the other hand, can be bounded by Since and the definitions of , then
| (35) |
4.3 Numerical Mittag-Leffler stability for non-homogeneous equations
Our goal here is study the decay estimates of numerical solutions to the non-homogeneous fractional ODE: with , where all the parameters and satisfy the same conditions as Theorem 2.1. Hence, Theorem 4.2 below is the discrete version of Theorem 2.1.
Theorem 4.2.
Consider the time -preserving scheme for the fractional ODE given by
| (40) |
On the uniform mesh , the numerical solution satisfies
| (41) |
where the positive constants , are independent of and .
The proof strategy is somewhat similar to the Theorem 2.1. Under the assumption of source function , we can control the additional terms brought by the source function. Of course, compared to the case of homogeneous equations, this requires more precise estimation and better discrete upper and lower solutions. Due to the detailed proof of Theorem 4.1 on homogeneous equations, we will only provide an overview of the proof of this theorem here.
Proof.
From satisfying the decay estimate , we know that
Our current strategy is to construct appropriate discrete sub solution and sup solution such that
| (42) |
I. Discrete subsolution. Define
where and . Then define the monotonically decreasing sequence
| (43) |
For , we have
| (44) | ||||
For , by the definition of , and we have
| (45) | ||||
Noting that , we get that
II. Discrete supersolution. Define the function
| (46) |
where . Then we define the sequence for .
For , we have and
Next, suppose that , one has
| (47) | ||||
By the definition of , we have . Noting that , we obtain .
Finally, suppose that . We have
| (48) | ||||
It follows from the definition of that . Hence, we get that by the fact .
In summary, the above analysis indicates that the discrete sub solution and sup solution satisfy the inequality (42). Hence, it follows from Theorem 4.1 that , which leads to the required results by the construction of and .
∎
4.4 Numerical Mittag-Leffler stability for time fractional PDEs
Consider the time semi-discretization of the initial boundary value problem (1) by -preserving schemes
| (49) |
where is the approximation of at . Now we hope to apply the estimation of fractional ODE obtained above and combine appropriate energy methods to establish the long-term optimal decay rate of the numerical solution , that is, to establish a discrete version of Corollary 2.1.
The following -norm inequality of -preserving schemes is crucial. It can be seen as a discrete version of the -norm inequality (13), which once again reveals the good structural preservation characteristics of -preserving schemes.
Lemma 4.2.
Theorem 4.3.
5 Numerical experiments
In this section, we present some numerical experiments to confirm our theoretical analysis. Assume that the numerical solutions has the long-time decay rate as . Then we can define the the index function as
| (51) |
which is the numerical observation decay rate approximates the theoretical predictions decay rate with order . See more details in [17].
5.1 Nonlinear F-ODEs with time-dependent coefficients
In this test, consider the scalar model (4): with initial value and , which has an optimal numerical decay rates predicted by Theorem 4.1.
Here we take , and the parameter . Table 1 and Table 2 respectively show the polynomial decay rate of the numerical solution computed by Grünwald-Letnikov scheme for various parameters of and . We also plot the log-log relation of the numerical solution and in Figure 1 with various parameters. It can be seen from those data and Figure that the numerical solutions are monotone and positive and are completely consistent with our theoretical prediction, i.e. .
| 2.801315 | 1.400861 | 0.700384 | 0.348185 | 0.172802 | |
| 2.800657 | 1.400434 | 0.700247 | 0.348575 | 0.173056 | |
| 2.800438 | 1.400291 | 0.700191 | 0.348764 | 0.173191 | |
| 2.800328 | 1.400219 | 0.700158 | 0.348883 | 0.173282 | |
| 2.800263 | 1.400176 | 0.700137 | 0.348967 | 0.173348 | |
| 2.8 | 1.4 | 0.7 | 0.35 | 0.175 |
| 2.001509 | 1.001087 | 0.502494 | 0.250823 | 0.124179 | |
| 2.000754 | 1.000559 | 0.501724 | 0.250673 | 0.124242 | |
| 2.000503 | 1.000379 | 0.501393 | 0.250602 | 0.124278 | |
| 2.000378 | 1.000288 | 0.501199 | 0.250556 | 0.124303 | |
| 2.000302 | 1.000232 | 0.501067 | 0.250524 | 0.124322 | |
| 2 | 1 | 0.5 | 0.25 | 0.125 |
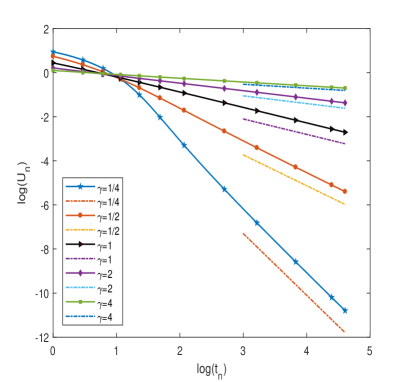
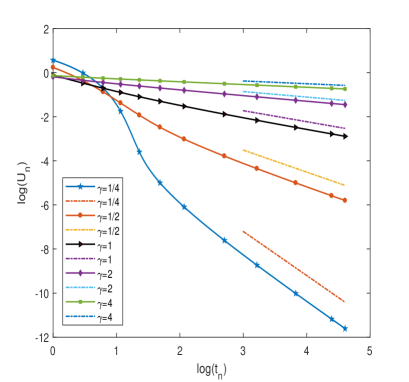
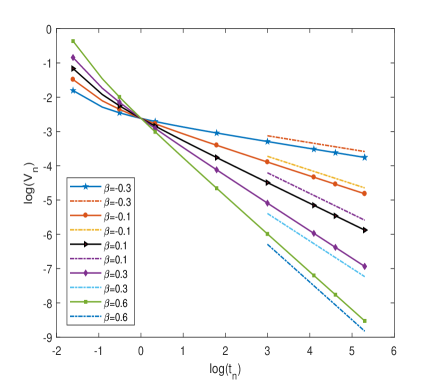
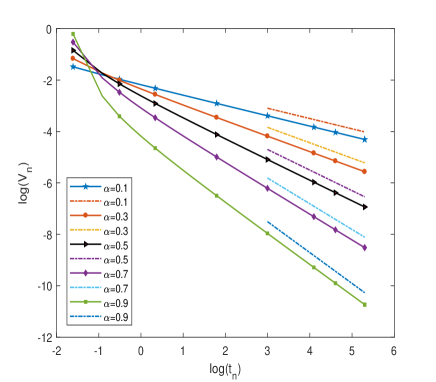
5.2 Time fractional PDEs with time-dependent coefficients
Consider the time fractional partial differential equation:
| (52) |
where is Laplace operator. One has the Poincaré inequality for some positive constant , i.e., the structural assumption (2) holds true for . Therefore, we can obtain that the decay rate of the true solution is .
In this example, we take and the initial value . The linear finite element in space and Grünwald-Letnikov scheme in time are employed to solve the problem (52) with time step size . Table 3 and Table 4 presents the results of the decay rate for numerical solutions with , and , to problem (52). Both log-log picture presented in Figure 2 show the evolution of has decay rate , which are also completely consistent with our theoretical prediction
| 0.203591 | 0.403624 | 0.603672 | 0.803713 | 1.103757 | |
| 0.201189 | 0.401221 | 0.601252 | 0.801270 | 1.101281 | |
| 0.200701 | 0.400732 | 0.600756 | 0.800768 | 1.100773 | |
| 0.200491 | 0.400521 | 0.600542 | 0.800551 | 1.100554 | |
| 0.200375 | 0.400404 | 0.600423 | 0.800430 | 1.100432 | |
| 0.2 | 0.4 | 0.6 | 0.8 | 1.1 |
| 0.400381 | 0.601848 | 0.803713 | 1.005938 | 1.208512 | |
| 0.400083 | 0.600622 | 0.801270 | 1.002020 | 1.202882 | |
| 0.400029 | 0.600372 | 0.800768 | 1.001218 | 1.201734 | |
| 0.400008 | 0.600265 | 0.800551 | 1.000872 | 1.201240 | |
| 0.400000 | 0.600205 | 0.800430 | 1.000679 | 1.200965 | |
| 0.4 | 0.6 | 0.8 | 1 | 1.2 |
References
- [1] M. Bologna, A. Svenkeson, B. J. West, and P. Grigolini. Diffusion in heterogeneous media: An iterative scheme for finding approximate solutions to fractional differential equations with time-dependent coefficients. J. Comput. Phys., 293:297–311, 2015.
- [2] T. Boudjeriou. Decay estimates and extinction properties for some parabolic equations with fractional time derivatives. Fract. Calc. Appl. Anal., 27:393–432, 2024.
- [3] F. S. Costa, E. C. Oliveira, and A. R. G. Plata. Fractional diffusion with time-dependent diffusion coefficient. Rep. Math. Phys., 87:59–79, 2021.
- [4] S. Dipierro, E. Valdinoci, and V. Vespri. Decay estimates for evolutionary equations with fractional time-diffusion. J. Evol. Equ., 19:435–462, 2019.
- [5] K. S. Fa and E. K. Lenzi. Time-fractional diffusion equation with time dependent difussion coefficient. Phys. Rev. E (3), 72:011107, 2005.
- [6] D. Hernández and E. C. Herrera-Hernández. Non-local diffusion models for fractured porous media with pressure tests applications. Adv. Water Resour., 149:103854, 2021.
- [7] J. Hristov. Subdiffusion model with time-dependent diffusion coefficient: Integral-balance solution and analysis. Therm. Sci., 21:69–80, 2017.
- [8] B. Jin. Fractional differential equations: An approach via fractional derivatives. Springer, Cham, 2021.
- [9] Bangti Jin and Zhi Zhou. Numerical treatment and analysis of time-fractional evolution equations, volume 214. Springer Nature, 2023.
- [10] J. Kemppainen and R. Zacher. Long-time behavior of non-local in time Fokker-Planck equations via the entropy method. Math. Models Methods Appl. Sci., 29:209–235, 2019.
- [11] Natalia Kopteva. Error analysis of the L1 method on graded and uniform meshes for a fractional-derivative problem in two and three dimensions. Math. Comp., 88(319):2135–2155, 2019.
- [12] L. Li and D. L. Wang. Complete monotonicity-preserving numerical methods for time fractional odes. Commun. Math. Sci., 19:1301–1336, 2021.
- [13] H. L. Liao, W. McLean, and J. W. Zhang. A discrete gronwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J. Numer. Anal., 57(1):218–237, 2019.
- [14] A. G. Smadiyeva and B. T. Torebek. Decay estimates for the time-fractional evolution equations with time-dependent coefficients. Proc. R. Soc. A, 479:381–397, 2023.
- [15] Martin Stynes. A survey of the L1 scheme in the discretisation of time-fractional problems. Numer. Math. Theor. Meth. Appl., 15:1173–1192, 2022.
- [16] V. Vergara and R. Zacher. Optimal decay estimates for time-fractional and other nonlocal subdiffusion equations via energy methods. SIAM J. Math. Anal., 47:210–239, 2015.
- [17] D. L. Wang and M. Stynes. Optimal long-time decay rate of numerical solutions for nonlinear time-fractional evolutionary equations. SIAM J. Numer. Anal., 61:2011–2034, 2023.
- [18] D. L. Wang and J. Zou. Mittag-Leffler stability of numerical solutions to time fractional odes. Numer. Algorithms, 92:2125–2159, 2023.
- [19] R. Zacher. Boundedness of weak solutions to evolutionary partial integro-differential equations with discontinuous coefficients. J. Math. Anal. Appl., 348:137–149, 2008.