Mitigating radio frequency interference in CHIME/FRB real-time intensity data

Masoud Rafiei-Ravandi Department of Physics, McGill University, 3600 rue University, Montréal, QC H3A 2T8, Canada McGill Space Institute, McGill University, 3550 rue University, Montréal, QC H3A 2A7, Canada Perimeter Institute for Theoretical Physics, 31 Caroline Street N, Waterloo, ON N25 2YL, Canada Department of Physics and Astronomy, University of Waterloo, Waterloo, ON N2L 3G1, Canada Kendrick M. Smith Perimeter Institute for Theoretical Physics, 31 Caroline Street N, Waterloo, ON N25 2YL, Canada Masoud Rafiei-Ravandi [email protected]

Abstract

Extragalactic fast radio bursts (FRBs) are a new class of astrophysical transient with unknown origins that have become a main focus of radio observatories worldwide. FRBs are highly energetic ( $\sim 10^{36}$ – $10^{42}$ erg) flashes that last for about a millisecond. Thanks to its broad bandwidth (400–800 MHz), large field of view ( $\sim$ 200 sq. deg.), and massive data rate (1500 TB of coherently beamformed data per day), the Canadian Hydrogen Intensity Mapping Experiment / Fast Radio Burst (CHIME/FRB) project has increased the total number of discovered FRBs by over a factor 10 in 3 yr of operation. CHIME/FRB observations are hampered by the constant exposure to radio frequency interference (RFI) from artificial devices (e.g., cellular phones, aircraft), resulting in $\sim$ 20% loss of bandwidth. In this work, we describe our novel technique for mitigating RFI in CHIME/FRB real-time intensity data. We mitigate RFI through a sequence of iterative operations, which mask out statistical outliers from frequency-channelized intensity data that have been effectively high-pass filtered. Keeping false-positive and false-negative rates at very low levels, our approach is useful for any high-performance surveys of radio transients in the future.

High energy astrophysics (739), Radio telescopes (1360), Radio transient sources (2008)

1 introduction

The search for extragalactic fast radio bursts (FRBs) has become a central undertaking for radio telescopes worldwide. FRBs are brief ( $\sim$ millisecond) flashes of radio signal with unknown origins. To date, over 750 FRBs have been discovered (see, e.g., CHIME/FRB Catalog 1 in CHIME/FRB Collaboration, 2021).¹¹1Catalogs of known FRBs are available on https://www.herta-experiment.org/frbstats (Spanakis-Misirlis, 2021) and https://www.wis-tns.org (Petroff & Yaron, 2020). This includes 25 repeating sources that emit multiple bursts sporadically over long ( $\sim$ days to months) time intervals, and about 20 (repeating and nonrepeating) sources that are localized to host galaxies (for a recent review, see Petroff et al., 2022).

The FRB arrival time $t$ at the observing frequency $\nu$ is delayed proportional to $\nu^{-2}$ , owing to the dispersion of radio waves in the intervening cold plasma along the line of sight. The delay is measured by the dispersion measure (DM), which sets the proportionality constant in the dispersion relation. FRBs are found by integrating the total intensity $I(t,\nu)$ across frequency along different dispersion profiles and searching for sharp peaks in the time profiles in the ( $t,\mbox{DM}$ ) space.

Most FRBs have been discovered by the Canadian Hydrogen Intensity Mapping Experiment / Fast Radio Burst (CHIME/FRB) instrument (CHIME/FRB Collaboration, 2018), which is equipped with an incoherent dedispersion search engine (out to a maximum DM of 13,000 pc cm^-3) operating constantly between 400 and 800 MHz. CHIME/FRB is one of the four digital backends that are connected to the CHIME telescope, which has a large field of view ( $\sim$ 200 deg²). The CHIME telescope and its digital backends (CHIME Collaboration, 2022) are located at the Dominion Radio Astrophysical Observatory (DRAO), which is in a radio-quiet area in the Okanagan Valley, British Columbia, Canada. Despite being regulated by local and federal governments, the CHIME radio bandwidth is exposed to a broad range of anthropogenic signals from various sources nearby (e.g., cellular phones) and far away (e.g., aircraft and satellites) that interfere with daily observations of astrophysical phenomena. If not mitigated properly, even a very short ( $\sim$ 10 ms) blip of radio frequency interference (RFI) could trigger thousands of false positives in the CHIME/FRB instrument.

RFI can be very unpredictable in the $(t,\nu)$ space. Several RFI mitigation techniques have been effective in the past. Most notably, impulsive RFI could be masked through an iterative threshold-based scheme (see, e.g., the SumThreshold algorithm in Offringa et al., 2010a, b) or a statistical estimator such as the spectral kurtosis (see, e.g., Nita & Gary, 2010a, b; Taylor et al., 2019). Periodic RFI could be detected more robustly in the harmonic space of intensity (see, e.g., Maan et al., 2021). In addition, large-scale RFI variations could be removed by fitting a baseline (see, e.g., Eatough et al., 2009; Zhang et al., 2022). Furthermore, general RFI patterns could be flagged through machine-learning algorithms (see, e.g., Akeret et al., 2017; Czech et al., 2018; Yang et al., 2020). In this work, we describe our strategy for mitigating RFI in the CHIME/FRB data. CHIME/FRB science requirements combined with its data rate (1500 TB/day) introduced computational challenges that led to the design and development of extremely optimized software from scratch.

As a brief overview, CHIME/FRB masks RFI through a long sequence of iterative operations in a real-time pipeline. These operations have been fine-tuned in order to account for the computational cost while simultaneously minimizing the false-positive and false-negative rates. The pipeline computes a time-varying RFI mask for the frequency-channelized intensity data, so that RFI can be suppressed prior to the dedispersion transform. This technique is the first step in our RFI mitigation and is the only one that works directly with the intensity data to lower the number of false positives from $\sim 10^{5}$ to a few per day, while detecting FRBs at an unprecedented rate (CHIME/FRB Collaboration, 2021). Despite being designed for a specific instrument, our algorithms could in principle be applied to other real-time searches of radio transients such as pulsar surveys.

The paper is organized as follows. We present an overview of the CHIME/FRB software pipeline in §2. In §3, we present a detailed account of our RFI mitigation strategy. We discuss results, unsolved problems, and potential opportunities for improvement in §4. Throughout, we adopt the CHIME/FRB data as a running example.

2 CHIME/FRB pipeline

The CHIME/FRB instrument (CHIME/FRB Collaboration, 2018) has multiple processing levels (denoted by L1, L2, etc.) that have been running constantly except during upgrade cycles and emergency shutdowns since mid-2018 (for a full discussion of telescope up time, see CHIME Collaboration, 2022). In L0 (the CHIME FX correlator, containing 256 processing nodes; also see CHIME Collaboration, 2022), frequency-channelized data are coherently arranged in an array of $4\times 256$ digitally formed beams. In L1 (the real-time FRB search engine, running on 128 processing nodes, each with two 10-core Intel E5-2630v4 CPUs and 128 GB of RAM), beamformed packets are assembled into a time series of total intensity samples. Then, RFI is mitigated by generating a mask (zeros and ones), which is subsequently used for detrending (or effectively high-pass filtering) and dedispersing the intensity (see Figure 1). Once the intensity is dedispersed, L1b groups and ranks astrophysical vs. RFI-triggered events based on their signal-to-noise ratio (S/N), arrival time, DM, and sky location. Next, L2/L3 labels sources “Galactic” or “extragalactic” and depending on this and on, e.g., S/N, decides what action to take (e.g., whether to store buffered intensity data). Finally, metadata are stored in a database (L4).

Refer to caption — Figure 1: CHIME/FRB L1 data for a single beam, containing a pulsar transit along with RFI. Top panel: raw intensity with persistent RFI between 600 and 650 MHz. The relatively low-intensity region centered at $\sim$ 750 MHz corresponds to the long-term evolution (LTE) band, which is usually active. Multiple scatterings of radio waves off the feed structure cause the systematic “ripple” effect with a period of $\approx$ 30 MHz across the bandwidth (CHIME Collaboration, 2022). Black regions indicate missing data. Middle panel: detrended intensity, including the missing data and RFI mask (black regions) prior to the dedispersion transform (see Figure 2). Dispersed sweeps ( $\propto\nu^{-2}$ ) across the bandwidth, particularly visible in the 600–400 MHz range at $\approx$ 2.2 second intervals, are signals from a nearby pulsar. Bottom panel: dedispersion space of events, including the pulsar (green and yellow dots at DM $\lesssim 100$ pc cm^-3). The RFI event at ( $t\approx 128.8$ s, DM $\approx 6500$ pc cm^-3) has a low signal-to-noise ratio ( $7\leq{\rm S/N}<10$ ) and is below the detection threshold.

We define a “false positive” as an event with nonastrophysical origin (e.g., RFI, thermal noise, and faulty calibration) and S/N $\geq$ 10 that passes through L1–L4 and is classified as an astrophysical candidate. We emphasize that the main CHIME/FRB search is carried out over the dedispersion space. Resembling FRBs by randomly lining up as $\nu^{-2}$ in the intensity space, RFI has been by far the largest contributing factor to the CHIME/FRB false positives, which could easily overwhelm L2–L4 pipelines. In addition, unmasked RFI could reduce the true-positive rate. The L1 system computes a running estimate of the variance of intensity, and unmasked RFI could contaminate this estimate, lowering the overall system sensitivity, severely impacting the true-positive rate for various selection criteria. As such, we mitigate false positives in all levels of the intensity pipeline: L1 masks raw intensity data without incorporating beam information, while L1b–L3 employ machine-learning classifiers to discriminate between true and false positives after sky localization utilizing ancillary information about the system performance and environment. This paper focuses on the RFI mitigation prior to the dedispersion transform in L1.

The L1 software package contains multiple object-oriented code libraries with distinct purposes. For instance, “ch_frb_io”²²2ch_frb_io: https://github.com/CHIMEFRB/ch_frb_io assembles L0 data packets into a stream of 1 s chunks of masked intensity data,³³3Intensity values are floating-point numbers between 0 and 256. Initial masks contain zeros and ones that correspond to bad and good intensity data, respectively. which are then fed into “rf_pipelines”⁴⁴4rf_pipelines: https://github.com/kmsmith137/rf_pipelines for RFI mitigation. Figure 2 shows the high-level logic of the RFI mitigation pipeline as configured and implemented for CHIME/FRB.

Each box in the diagram represents an operation (or “transform”) whose input and output arrays are represented as arrows. All arrays are 2D arrays indexed by ( $t,\nu$ ), which are processed in 4 s chunks (see §3). The “intensity stream” continuously emits arrays of the intensity $I_{t\nu}$ and mask $M_{t\nu}$ that are downsampled from 16k to 1k frequency channels as follows:

	$\displaystyle I_{t\nu}$	$\displaystyle=$	$\displaystyle\frac{\mathop{\textstyle\sum}\limits_{n=0}^{15}{M_{t,16\nu+n}\,I_{t,16\nu+n}}}{\mathop{\textstyle\sum}\limits_{n=0}^{15}{M_{t,16\nu+n}}}$		(1)
	$\displaystyle M_{t\nu}$	$\displaystyle=$	$\displaystyle\frac{1}{16}\mathop{\textstyle\sum}\limits_{n=0}^{15}{M_{t,16\nu+n}}\,,$		(2)

where the masks are treated as nonbinary weights. Next, downsampled data are processed inside the “subpipeline” in order to update the mask, which is then upsampled from 1k to 16k frequency channels for mitigating RFI in the raw intensity data. We upsample arrays by copying and tiling elements along the downsampled axis (e.g., upsampling the 1D array $[0,0.5,1]$ by a factor 2 yields $[0,0,0.5,0.5,1,1]$ ). This down/upsampling logic is essential for minimizing the computational cost while maintaining a robust yet coarse-grained estimate of time-varying RFI patterns across the CHIME/FRB bandwidth at 1 ms time resolution. In §3, we take a deep dive into the core of our RFI mitigation algorithm inside the “subpipeline.”

Using the upsampled mask, we detrend and dedisperse the raw intensity with 16k frequency channels. Thus, the dedispersion transform continuously receives a set of (detrended intensity, RFI mask) arrays with 16k frequency channels as input. Then, the dedispersion transform replaces masked regions⁵⁵5The dedispersion transform can be configured to expand the boundaries of masks in order to suppress potentially unmasked residuals from highly active RFI in neighboring frequency and time samples. This is the last line of defense against RFI-triggered false positives in L1. of intensity arrays by an estimate of the running variance based on a white noise model for the input intensity values and a slowly varying function for the variance of unmasked intensity along the time axis. In addition, the running variance is adopted for normalizing dedispersed events to S/N. Finally, the dedispersion transform outputs a 4D array (DM, scattering measure, spectral index, time) of coarse-grained trigger statistics, where the coarse-graining is done by taking the maximum over time and DM.

The entire chain of L1 operations is fixed in the CHIME/FRB instrument; a slight modification in the algorithm requires a system-wide reconfiguration and restart.⁶⁶6CHIME/FRB L1 configuration files are available in ch_frb_rfi: https://github.com/mrafieir/ch_frb_rfi Although very rare, such reconfigurations are necessary when RFI starts to show up in a newly allocated radio band, e.g., owing to the 5G network. To that end, we alert system operators⁷⁷7The instrument is monitored daily by members of the CHIME/FRB collaboration. to save several hours of intensity data during active RFI. Using the saved data, we attempt to reproduce the culprit for a close visual inspection. We can often find a simple hotfix that will suppress the new RFI effectively (see §3.3).

3 RFI transform chains

The “subpipeline” (see Figure 2) contains a sequence of over 100 transforms for masking RFI. This long chain of operations is constructed mainly by iterating over the clipping and detrending transforms, which are described in §3.1 and §3.2, respectively. We took the iterative approach based on the observation that RFI contaminates the probability distribution function (PDF) of intensity (and its higher moments) through statistical outliers (e.g., 5 $\sigma$ deviations from the mean of intensity in a specific frequency channel) that can be masked incrementally.

While our clipping and detrending transforms can generally recognize and suppress RFI through the upsampled mask, they can also leave some residuals that induce false positives after the final round of detrenders. For example, unmasked narrowband RFI could cause a series of ripples in the detrended intensity along the frequency axis. Under the right circumstances, these ripples could induce false positives downstream. Therefore, we need to account for such residual-induced false positives as well as RFI-triggered false positives throughout the L1 pipeline (see, e.g., Figure 4). In addition, we require an overall latency of $\sim$ 10 s for reporting events in real time. This is to facilitate detection of counterparts using other telescopes, achieved through automated real-time alerts (Zwaniga, 2021). Also, our baseband (voltage) recording system (Michilli et al., 2021) imposes an upper bound (4 s) on the size of intensity chunks in the L1 ring buffers.

Figure 3 illustrates the CHIME/FRB RFI transform chain nested inside the subpipeline.

The simplest form of RFI transforms is a static mask, which constantly eliminates a set of known frequency channels exhibiting intense RFI. We place the static mask at the very beginning of our chain in order to minimize residuals, which can easily distort the intensity PDF.

Following the static mask, clipping transforms or “clippers” take the streaming chunk of intensity data and mask out statistical outliers dynamically. These outliers could be deviations from the mean or standard deviation (stdv) of the intensity PDF along an arbitrary axis (i.e., time and/or frequency). Then, a sequence of detrending transforms or “detrenders” remove large-scale intensity variations (along time and frequency) from the data. Next, a second round of clipping transforms is applied to the modified intensity PDF. We note that both the mask and intensity data stream are updated throughout this process inside the subpipeline. However, only the mask is upsampled and passed to the last round of detrenders prior to the dedispersion over 16k frequency channels. The last round of detrenders is required for the CHIME/FRB dedispersion transform, which assumes a zero baseline for the incoming intensity data stream. Finally, the upsampled mask ( $\sim$ 20% loss of bandwidth on average) and detrended intensity data are passed to the dedispersion transform.

Ideally, the specific configuration of RFI transform chains would be determined through a global minimization problem, which would aim at minimizing the computational cost along with the false-positive and false-negative rates. In actuality, we configured the CHIME/FRB RFI transform chain empirically; although not necessarily optimal, we configured transforms through trial and error using hundreds of hours of intensity acquisitions.⁸⁸8Other than with the real-time pipeline, L1 can be run in an offline mode with saved intensity data. The remainder of this section contains a detailed account of the RFI transform chains.

3.1 Clipping transform chain

CHIME/FRB beamformed intensity data are constructed by summing squared voltages $\langle V_{a}(\nu)V_{b}^{*}(\nu^{\prime})\rangle$ from the CHIME antennas $a$ and $b$ (see, e.g., Masui et al., 2019). In the absence of RFI, we expect the raw voltages to be Gaussian distributed (Fridman & Baan, 2001) and hence the intensity to be $\chi^{2}$ distributed. In CHIME/FRB, we developed two different types of transforms for masking statistical outliers in the intensity data: intensity and standard deviation (stdv) clipping transforms.

Let $I_{t\nu}$ represent the 2D array of possibly downsampled masked intensity, which is a function of time ( $t$ ) and frequency ( $\nu$ ). Then, the intensity clipping transform updates the mask $M_{t\nu}$ by zeroing out elements that satisfy

\left|I_{t\nu}-\bar{I}_{t\nu}\right|\geq\left(\sigma_{c}\mbox{Var}(I)_{t\nu}^{1/2}\right),

(3)

where the threshold level $\sigma_{c}$ is a configurable constant, and the mean intensity array $\bar{I}_{t\nu}$ and variance array $\mbox{Var}(I)_{t\nu}$ are computed based on the initial intensity $I_{t\nu}$ along a specific axis in time and/or frequency in two stages as follows:

I_{t\nu}\xrightarrow[\rm internally]{\rm clip}\left[\bar{I}_{t^{\prime}\nu^{\prime}},\mbox{Var}(I)_{t^{\prime}\nu^{\prime}}\right]\xrightarrow{{\rm reshape}}\left[\bar{I}_{t\nu},\mbox{Var}(I)_{t\nu}\right],

(4)

where the indices $t^{\prime}$ and $\nu^{\prime}$ refer to arrays with a reduced length, e.g., computing the mean along the time axis of an array with shape ( $N_{t},N_{\nu}$ )=(4k, 16k) results in a new array with shape ( $N_{t^{\prime}},N_{\nu^{\prime}}$ )=(1, 16k). In Equation (4), the first stage is the computation of the masked mean and variance along an axis:

	$\displaystyle\bar{I}_{t^{\prime}\nu^{\prime}}$	$\displaystyle=$	$\displaystyle\frac{\mathop{\textstyle\sum}\limits_{m=0}^{D_{t}-1}\,\mathop{\textstyle\sum}\limits_{n=0}^{D_{\nu}-1}{M_{xy}\,I_{xy}}}{\mathop{\textstyle\sum}\limits_{m=0}^{D_{t}-1}\,\mathop{\textstyle\sum}\limits_{n=0}^{D_{\nu}-1}{M_{xy}}}$		(5)
	$\displaystyle\mbox{Var}(I)_{t^{\prime}\nu^{\prime}}$	$\displaystyle=$	$\displaystyle\frac{\mathop{\textstyle\sum}\limits_{m=0}^{D_{t}-1}\,\mathop{\textstyle\sum}\limits_{n=0}^{D_{\nu}-1}M_{xy}{\left(I_{xy}-\bar{I}_{xy}\right)^{2}}}{\mathop{\textstyle\sum}\limits_{m=0}^{D_{t}-1}\,\mathop{\textstyle\sum}\limits_{n=0}^{D_{\nu}-1}{M_{xy}}},$		(6)

where the indices $x\equiv tD_{t}+m$ and $y\equiv\nu D_{\nu}+n$ are defined with the downsampling factors $D_{t}\equiv N_{t^{\prime}}/N_{t}$ and $D_{\nu}\equiv N_{\nu^{\prime}}/N_{\nu}$ along the time and frequency axis, respectively. Here, the possibly downsampled mask $M_{xy}$ is treated as nonbinary weights. In addition, an intensity clipping transform can have an internal iteration that temporarily masks out intensity outliers $n_{c,{\rm in}}$ times prior to the final computation of mean and variance. We configure the internal iteration by the threshold parameter $\sigma_{c,{\rm in}}$ . Whether internal or external, every clipping iteration helps improve the RFI mask by recognizing more statistical outliers and hence reshaping the masked intensity PDF to a robust $\chi^{2}$ distribution in real time. In the second stage, we reshape these masked arrays by copying and tiling elements along the reduced axis. This recovers the initial shape of input intensity data, enabling the final element-wise operation in Equation (3).

Likewise, the stdv clipping transform masks RFI along the time or frequency axis using the following criterion:

\left|J_{t^{\prime}\nu^{\prime}}-\overline{J_{t^{\prime}\nu^{\prime}}}\right|\geq\left(\sigma_{c}\mbox{Var}(J_{t^{\prime}\nu^{\prime}})^{1/2}\right),

(7)

where the masked array $J_{t^{\prime}\nu^{\prime}}\equiv\mbox{Var}(I)_{t^{\prime}\nu^{\prime}}$ with no internal clipping, and the mean of variance $\overline{J_{t^{\prime}\nu^{\prime}}}$ and variance of variance $\mbox{Var}(J_{t^{\prime}\nu^{\prime}})$ are scalar. Unlike the intensity clippers, the stdv clippers “reshape” the running mask to match its shape ( $N_{t^{\prime}},N_{\nu^{\prime}}$ ) with the initial intensity $I_{t\nu}$ only after executing Equation (7).

Table 1 lists the CHIME/FRB clipping transform chain, which is iterated $n_{c}$ times before and after the intensity detrenders, i.e., the clipping transform chain is a nested loop inside an outer loop over detrenders. The first three stdv clippers are along the time axis, and have a 3 $\sigma$ threshold with no down/upsampling factors. Then, two stdv clippers are applied along the frequency axis, with a 3 $\sigma$ threshold and no down/upsampling factors. Next, two intensity clippers are applied at a 5 $\sigma$ threshold. Finally, two intensity clippers are applied with downsampling factors of 16 and 2 along the time and frequency axis, respectively. The downsampling logic helps expand the mask and hence prevent intensity leakage over RFI-contaminated regions.

$i$	type	$\sigma_{c}$	$\sigma_{c,{\rm in}}$	$n_{c,{\rm in}}$	axis	$N_{t}$	$D_{t}$	$D_{\nu}$
1	stdv	3	$-$	$-$	$t$	4096	1	1
2	stdv	3	$-$	$-$	$t$	4096	1	1
3	stdv	3	$-$	$-$	$t$	4096	1	1
4	stdv	3	$-$	$-$	$\nu$	4096	1	1
5	stdv	3	$-$	$-$	$\nu$	4096	1	1
6	intensity	5	5	9	$\nu$	4096	1	1
7	intensity	5	5	9	$t$	4096	1	1
8	intensity	5	3	9	$(t,\nu)$	4096	16	2
9	intensity	5	3	9	$\nu$	4096	16	2

Table 1: Clipping transform chain for dynamically masking RFI in the CHIME/FRB intensity stream. The index

i

specifies the position of each transform in the chain. The intensity and standard deviation (stdv) transforms clip statistical outliers at the threshold level

\sigma_{c}

from the mean (see Equations 3 and 7). In addition, the intensity clipping transform has an internal iteration which allows for temporarily masking outliers at the

\sigma_{c,{\rm in}}

level prior to the final clipping operation. The number of internal iterations is set by the parameter

n_{c,{\rm in}}

N_{t}

is the total number of 1 ms time samples in an intensity chunk that each transform processes in real time. In each transform, the incoming chunks are downsampled (and consequently final coarse-grained masks are upsampled) by the two factors

D_{t}

and

D_{\nu}

along the time and frequency axis, respectively (see, e.g., Equations 5 and 6). Operations along the axis

(t,\nu)

are carried out over the 2D array of intensity values.

Since RFI is a non-Gaussian process (Fridman & Baan, 2001; Mirhosseini, 2020), we expect RFI-triggered false positives to appear more distinctly at higher statistical moments of the intensity. Therefore, we place the stdv transforms at the very beginning of the clipping transform chain. Additionally, we refrain from downsampling the intensity in the beginning, since coarse-grained masks lack precision in containing only regions with RFI. In the case of intensity clippers, internal iterations are effective in decontaminating PDFs at a low computational cost. On the other hand, RFI residuals can hide behind internal masks and hence contaminate the stream if $\sigma_{c,{\rm in}}$ and $n_{c,{\rm in}}$ are not set properly. Finally, we mask typically along the time axis first, since RFI tends to arrive in constant frequency bands. Furthermore, we maximize the chunk size $N_{t}$ , which is constrained mainly by the latency requirement for the CHIME/FRB baseband recording system. We find empirically that by iterating the clipping transform chain (Table 1) six times before and after a chain of detrenders (see §3.2), we are able to sufficiently suppress RFI while detecting real pulsars in CHIME/FRB intensity acquisitions.⁹⁹9We initially designed the RFI transform chain through the analysis of incoherent beam data (400–800 MHz, $N_{\nu}$ =1k) from the CHIME Pathfinder (Bandura et al., 2014) and single-beam data (400–800 MHz, $N_{\nu}$ =16k) from the Galt 26 m telescope. These instruments share the same RFI environment with CHIME/FRB at DRAO. The current configuration is based on seven different production-level transform chains that were designed to either mitigate new sources of RFI or adapt to other pipeline requirements (e.g., constraining the buffer size $N_{t}$ for the baseband recording system) sporadically since the first CHIME/FRB commissioning in mid-2018.

3.2 Detrending transform chain

The CHIME/FRB intensity stream exhibits large-scale variations from RFI, forward gains, and digital beamforming (Ng et al., 2017) as functions of the time, frequency, and sky location. Such baseline variations distort the intensity PDF, causing the clipping and dedispersion transforms to fail. We mitigate this effect by introducing a chain of detrending transforms in the pipeline. Detrending transforms remove a best-fit model with the polynomial degree $\alpha$ from the masked intensity array $I_{t\nu}$ along an axis (see, e.g., Eatough et al., 2009). This real operation is a computationally low-cost alternative to a high-pass filter in the harmonic space of intensity.

Table 2 lists the CHIME/FRB detrending transform chain, which contains two types of transforms: the polynomial (based on Legendre polynomials) and spline detrenders, both of which make use of the Cholesky decomposition for efficient computation of the best-fit coefficients. We designed the main RFI transform chain in the subpipeline such that detrenders are sandwiched between clipping transforms (see Figure 3). In other words, the detrending transform chain is an outer loop with $n_{d}$ iterations, each of which contains $n_{c}$ inner iterations over the clipping transform chain. We emphasize that subpipeline detrenders do not affect the intensity stream, which is fed into the dedispersion transform (see Figure 2). Subpipeline detrenders work in tandem with clipping transforms in order to generate a mask that mitigates RFI contamination in the detrended downsampled intensity chunks.

$j$	type	$\alpha$	axis	$N_{t}$
1	polynomial	4	$t$	4096
2	spline	12	$\nu$	4096

Table 2: Detrending transform chain for the CHIME/FRB intensity stream. The index

j

specifies the position of each transform in the chain. Each transform fits a model with the polynomial degree

\alpha

to intensity arrays of width

N_{t}

(number of 1 ms time samples) along one “axis”. Then, the model is subtracted from data in order to account for large-scale variations due to RFI and instrumental systematics.

The CHIME/FRB subpipeline currently has only a single iteration ( $n_{d}=1$ ) of the detrending transform chain. We detrend the raw intensity after generating the RFI mask; using the upsampled mask with 16k frequency channels, we apply the same detrending transform chain to the raw intensity ( $N_{\nu}=16$ k) prior to the dedispersion transform, which assumes input data with a zero mean. In addition to modifying the intensity values, detrenders can modify the running mask (e.g., by masking an entire chunk) in corner cases where numerical instabilities, e.g., owing to highly active RFI, cause a failure in converging on a robust solution. Therefore, the upsampled RFI mask is subject to further modification in the last round of detrenders between the subpipeline and dedispersion transform (see Figure 2).

3.3 Auxiliary transforms

Thus far, we have described our RFI mitigation technique, which is tailored to recognize statistical outliers within a distribution of intensity values. Assuming unlimited computational resources, we find empirically that any changes in our standard transform chain parameters (e.g., Table 1) could result in either masking excessively or RFI residuals downstream. However, the CHIME/FRB RFI environment is dynamic; unknown RFI appears suddenly at DRAO from time to time. In particular, we have been experiencing a series of “RFI storms” since late-2020 (see, e.g., Figures 4 and 5). Such unusually intense events could escape the entire clipping transform chain, consequently triggering $\sim$ 1 million false positives in a single day of operation. Although new radio transmitters and reflective aircraft¹⁰¹⁰10Aircraft-triggered RFI typically escapes the L1 pipeline, causing a few thousand subthreshold ( $7\leq{\rm S/N}<10$ ) false positives in a day (see, e.g., Figures 4 and 5). We eliminate these events in the downstream pipelines. could cause such high numbers of false positives, the exact source of RFI storms and their spectral properties are still an unsolved puzzle.

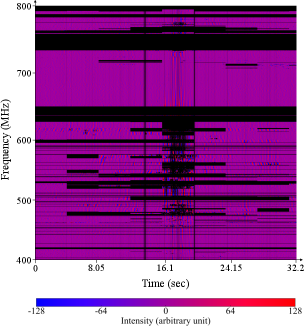
If highly active RFI persists for a few weeks, then we start saving intensity data to disk for offline inspection. If the culprit is static in frequency, e.g., newly allocated radio bands, then we update our static mask. If the culprit is dynamic, e.g., abrupt changes in the running variance across irregular time intervals, then we might need to increase the number of clipping iterations ( $n_{c}$ ) in order to account for a period of highly active RFI.

Another low-budget solution would be to append a few “auxiliary” transforms to the main RFI chain. Table 3 lists an auxiliary transform chain that we have designed for the CHIME/FRB pipeline. The chain contains two identical transforms that operate along the frequency axis with a relatively large downsampling factor along the time axis ( $D_{t}=256$ ), potentially resulting in expanding the mask widely over the time axis. Such mask expanding transforms can suppress RFI residuals around edges of RFI-contaminated regions that are localized in time. On the other hand, modifying the running L1 configuration with such coarse-grained masks could introduce a time-varying bias into the instrumental selection function. Therefore, we generally avoid using the auxiliary transform chain (Table 3) as a hotfix in the CHIME/FRB pipeline.

$k$	type	$\sigma_{c}$	$\sigma_{c,{\rm in}}$	$n_{c,{\rm in}}$	axis	$N_{t}$	$D_{t}$	$D_{\nu}$
1	stdv	3	$-$	$-$	$\nu$	4096	256	2
2	stdv	3	$-$	$-$	$\nu$	4096	256	2

Table 3: Auxiliary transform chain for enhancing the CHIME/FRB RFI mask under severe RFI conditions. The index

k

specifies the position of each transform in the chain. The other parameters are described in Table 1.

4 Discussion

The CHIME/FRB L1 pipeline is currently the leading search engine for detecting FRBs, which are usually immersed in an influx of RFI-triggered false positives. We mitigate RFI in a sequence of iterative operations that are fine-tuned empirically based on statistics of intensity values in real time. In this paper, we focus on false positives that arise in the 2D dedispersion space ( $t,\mbox{DM}$ ). However, the L1 dedispersion transform generates a 4D trigger array indexed by (DM, scattering measure, spectral index, $t$ ), presenting an opportunity for masking RFI in other dimensions.

Our RFI mitigation strategy is an attempt to minimize the overall computational cost, false-positive and false-negative rates for the CHIME/FRB instrument. This problem could be generalized to the continuous domain, where binary rates are replaced by ranges of parameters in the selection function of our instrument. For instance, we could lower our false-positive rate significantly by adding more clipping transforms with $\sigma_{c}<3$ to the RFI transform chain. This would introduce a significant bias in our sensitivity for detecting bright FRBs. In other words, any solution to the RFI problem places a set of constraints on the instrumental selection function in the continuous domain of FRB parameters (see, e.g., §3.2). On the other hand, our injection system, which injects synthetic FRB signals in real time into the pipeline allows us to characterize such biases in principle (Merryfield et al., 2022).

In this work, we have presented a customized set of operations that probably does not correspond to an optimal solution for the CHIME/FRB RFI environment. We could in principle replace our trial-and-error strategy by an automated pipeline, e.g., based on machine-learning techniques, that would solve the minimization problem more accurately. Such a systematic approach would enable us to impose user-defined constraints on the instrumental selection function for varying choices of RFI environment. In addition, the L1 pipeline could learn from downstream pipelines through an automated feedback mechanism; assuming that L1 could undergo a soft restart, we could modify the transform chain on-the-fly in order to account for sudden changes in the RFI environment. On the other hand, a time-varying transform chain might not lead to a well-characterized instrumental selection function. We defer the study and development of these features to future work.

Our algorithms have proven to be successful in maintaining a low false-positive rate, while allowing for the detection of astrophysical events. Despite being effective, our current detrenders operate independently along a single axis (time or frequency) that may not fully capture 2D variations of RFI across the intensity plane ( $t,\nu$ ). In addition, detrending along the frequency axis can remove significant signal from intrinsically wide bursts at low DMs, severely impacting the true-negative rate and completeness (see Figures 16 and 18 in CHIME/FRB Collaboration, 2021). Furthermore, we note that CHIME/FRB RFI mitigation and incoherent dedispersion routines were designed based on the assumption that FRBs are isolated events in time. However, this assumption might not be valid for repeating and multicomponent FRBs with $\lesssim 1$ s separation between events (CHIME/FRB Collaboration, 2022). Additionally, FRBs could be immersed in transits of bright pulses from Galactic sources such as PSR B0329+54, which could impact the running variance. Given the complexity of these multivariate problems, we characterize the CHIME/FRB selection function through systematic FRB injections into real data (CHIME/FRB Collaboration, 2021; Merryfield et al., 2022).

CHIME/FRB intensity data have provided us with a unique opportunity to investigate a multitude of RFI-related problems that might be of interest to other experiments such as the upcoming Hydrogen Intensity and Real-time Analysis Experiment (Crichton et al., 2022) and the Canadian Hydrogen Observatory and Radio-transient Detector (Vanderlinde et al., 2019). Here, we list a few unsolved problems for future exploration:

•

What is the source of RFI storms? How can we suppress them without masking excessively?
•

Most RFI storms tend to trigger false positives at high DMs (see, e.g., Figure 5). Given the CHIME/FRB L1 pipeline, would this be expected statistically? Could this be due to a design flaw in our RFI transform chain?
•

$\sim$ 10% of CHIME/FRB multibeam-detected FRB candidates seem to exhibit a false negative in at least one beam. Given that neighboring beams are expected to share the same RFI environment, what factors could contribute to such nondetections?
•

Technically, we could have multiple subpipelines with different downsampling factors in series. Would this be useful for enhancing the mask over narrowband RFI?

We hope to build on this work in the future to answer some of these problems as the CHIME/FRB instrument continues to observe the radio sky.

We acknowledge that CHIME is located on the traditional, ancestral, and unceded territory of the Syilx/Okanagan people. We are grateful to the staff of the Dominion Radio Astrophysical Observatory, which is operated by the National Research Council of Canada. CHIME is funded by a grant from the Canada Foundation for Innovation (CFI) 2012 Leading Edge Fund (Project 31170) and by contributions from the provinces of British Columbia, Québec, and Ontario. The CHIME/FRB Project is funded by a grant from the CFI 2015 Innovation Fund (Project 33213) and by contributions from the provinces of British Columbia and Québec, and by the Dunlap Institute for Astronomy and Astrophysics at the University of Toronto. Additional support was provided by the Canadian Institute for Advanced Research (CIFAR), McGill University and the McGill Space Institute thanks to the Trottier Family Foundation, and the University of British Columbia. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research & Innovation. K.M.S. was supported by an NSERC Discovery Grant and a CIFAR fellowship. We thank Sabrina Berger, Alice Curtin, Vicky Kaspi, Dustin Lang, Emily Petroff, Ziggy Pleunis, and Shriharsh Tendulkar for comments on the manuscript.

References

Akeret et al. (2017) Akeret, J., Chang, C., Lucchi, A., & Refregier, A. 2017, Astronomy and Computing, 18, 35, doi: 10.1016/j.ascom.2017.01.002
Bandura et al. (2014) Bandura, K., Addison, G. E., Amiri, M., et al. 2014, Ground-based and Airborne Telescopes V, 9145, 914522, doi: 10.1117/12.2054950
CHIME Collaboration (2022) CHIME Collaboration. 2022, The Astrophysical Journal Supplement Series, 261, 29, doi: 10.3847/1538-4365/ac6fd9
CHIME/FRB Collaboration (2018) CHIME/FRB Collaboration. 2018, The Astrophysical Journal, 863, 48, doi: 10.3847/1538-4357/aad188
CHIME/FRB Collaboration (2021) —. 2021, The Astrophysical Journal Supplement Series, 257, 59, doi: 10.3847/1538-4365/ac33ab
CHIME/FRB Collaboration (2022) —. 2022, Nature, 607, 256, doi: 10.1038/s41586-022-04841-8
Crichton et al. (2022) Crichton, D., Aich, M., Amara, A., et al. 2022, Journal of Astronomical Telescopes, Instruments, and Systems, 8, 011019, doi: 10.1117/1.JATIS.8.1.011019
Czech et al. (2018) Czech, D., Mishra, A., & Inggs, M. 2018, Astronomy and Computing, 25, 52, doi: 10.1016/j.ascom.2018.07.002
Eatough et al. (2009) Eatough, R. P., Keane, E. F., & Lyne, A. G. 2009, Monthly Notices of the Royal Astronomical Society, 395, 410, doi: 10.1111/j.1365-2966.2009.14524.x
Fridman & Baan (2001) Fridman, P. A., & Baan, W. A. 2001, Astronomy and Astrophysics, 378, 327, doi: 10.1051/0004-6361:20011166
Maan et al. (2021) Maan, Y., van Leeuwen, J., & Vohl, D. 2021, A&A, 650, A80, doi: 10.1051/0004-6361/202040164
Masui et al. (2019) Masui, K. W., Shaw, J. R., Ng, C., et al. 2019, The Astrophysical Journal, 879, 16, doi: 10.3847/1538-4357/ab229e
Merryfield et al. (2022) Merryfield, M., Tendulkar, S. P., Shin, K., et al. 2022, arXiv e-prints, arXiv:2206.14079, doi: 10.48550/arXiv.2206.14079
Michilli et al. (2021) Michilli, D., Masui, K. W., Mckinven, R., et al. 2021, The Astrophysical Journal, 910, 147, doi: 10.3847/1538-4357/abe626
Mirhosseini (2020) Mirhosseini, A. 2020, Master’s thesis, University of British Columbia. https://open.library.ubc.ca/collections/24/items/1.0394838
Ng et al. (2017) Ng, C., Vanderlinde, K., Paradise, A., et al. 2017, XXXII International Union of Radio Science General Assembly & Scientific Symposium (URSI GASS) 2017, 4, doi: 10.23919/URSIGASS.2017.8105318
Nita & Gary (2010a) Nita, G. M., & Gary, D. E. 2010a, PASP, 122, 595, doi: 10.1086/652409
Nita & Gary (2010b) —. 2010b, MNRAS, 406, L60, doi: 10.1111/j.1745-3933.2010.00882.x
Offringa et al. (2010a) Offringa, A. R., de Bruyn, A. G., Biehl, M., et al. 2010a, MNRAS, 405, 155, doi: 10.1111/j.1365-2966.2010.16471.x
Offringa et al. (2010b) Offringa, A. R., de Bruyn, A. G., Zaroubi, S., & Biehl, M. 2010b, arXiv e-prints, arXiv:1007.2089, doi: 10.48550/arXiv.1007.2089
Petroff et al. (2022) Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2022, The Astronomy and Astrophysics Review, 30, 2, doi: 10.1007/s00159-022-00139-w
Petroff & Yaron (2020) Petroff, E., & Yaron, O. 2020, Transient Name Server AstroNote, 160, 1
Spanakis-Misirlis (2021) Spanakis-Misirlis, A. 2021, Astrophysics Source Code Library, ascl:2106.028. https://ui.adsabs.harvard.edu/abs/2021ascl.soft06028S
Taylor et al. (2019) Taylor, J., Denman, N., Bandura, K., et al. 2019, Journal of Astronomical Instrumentation, 8, 1940004, doi: 10.1142/S225117171940004X
Vanderlinde et al. (2019) Vanderlinde, K., Liu, A., Gaensler, B., et al. 2019, Canadian Long Range Plan for Astronomy and Astrophysics White Papers, 2020, 28, doi: 10.5281/zenodo.3765414
Yang et al. (2020) Yang, Z., Yu, C., Xiao, J., & Zhang, B. 2020, MNRAS, 492, 1421, doi: 10.1093/mnras/stz3521
Zhang et al. (2022) Zhang, C.-P., Xu, J.-L., Wang, J., et al. 2022, Research in Astronomy and Astrophysics, 22, 025015, doi: 10.1088/1674-4527/ac3f2d
Zwaniga (2021) Zwaniga, A. 2021, Master’s thesis, McGill University. https://escholarship.mcgill.ca/concern/theses/p8418s91c