ifaamas \acmConference[AAMAS ’22]Proc. of the 21st International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2022)May 9–13, 2022 OnlineP. Faliszewski, V. Mascardi, C. Pelachaud, M.E. Taylor (eds.) \copyrightyear2022 \acmYear2022 \acmDOI \acmPrice \acmISBN \acmSubmissionID171 \affiliation \institutionNanyang Technological University \countrySingapore \affiliation \institutionNanyang Technological University \countrySingapore \affiliation \institutionNanyang Technological University \countrySingapore \affiliation \institutionNanyang Technological University \countrySingapore \affiliation \institutionNanyang Technological University \countrySingapore \affiliation \institutionNanyang Technological University \countrySingapore
Mis-spoke or mis-lead: Achieving Robustness in Multi-Agent Communicative Reinforcement Learning
Abstract.
Recent studies in multi-agent communicative reinforcement learning (MACRL) have demonstrated that multi-agent coordination can be greatly improved by allowing communication between agents. Meanwhile, adversarial machine learning (ML) has shown that ML models are vulnerable to attacks. Despite the increasing concern about the robustness of ML algorithms, how to achieve robust communication in multi-agent reinforcement learning has been largely neglected. In this paper, we systematically explore the problem of adversarial communication in MACRL. Our main contributions are threefold. First, we propose an effective method to perform attacks in MACRL, by learning a model to generate optimal malicious messages. Second, we develop a defence method based on message reconstruction, to maintain multi-agent coordination under message attacks. Third, we formulate the adversarial communication problem as a two-player zero-sum game and propose a game-theoretical method -MACRL to improve the worst-case defending performance. Empirical results demonstrate that many state-of-the-art MACRL methods are vulnerable to message attacks, and our method can significantly improve their robustness.
Key words and phrases:
Multi-Agent Reinforcement Learning; Robust Reinforcement Learning; Adversarial Reinforcement Learning1. Introduction
Cooperative multi-agent reinforcement learning (MARL) has achieved remarkable success in a variety of challenging problems, such as urban systems Singh et al. (2020), coordination of robot swarms Hüttenrauch et al. (2017) and real-time strategy video games Vinyals et al. (2019). To tackle the problems of scalability and non-stationarity in MARL, the framework of centralized training with decentralized execution (CTDE) is proposed Oliehoek et al. (2008); Kraemer and Banerjee (2016), where decentralized policies are learned in a centralized manner so that they can share experiences, parameters, etc., during training. Despite the advantages, CTDE-based methods still perform unsatisfactorily in scenarios where multi-agent coordination is necessary, mainly due to partial observability in decentralized execution. To mitigate partial observability, many multi-agent communicative reinforcement learning (MACRL) methods have been proposed, which allow agents to exchange information such as private observations, intentions during the execution phase. MACRL greatly improves multi-agent coordination in a wide range of tasks Foerster et al. (2016); Sukhbaatar et al. (2016); Jiang and Lu (2018); Das et al. (2019); Wang et al. (2019, 2020); Kim et al. (2021).
Meanwhile, adversarial machine learning has received extensive attention Huang et al. (2011); Barreno et al. (2010). Adversarial machine learning demonstrates that machine learning (ML) models are vulnerable to manipulation Goodfellow et al. (2017); Gleave et al. (2020). As a result, ML models often suffer from performance degradation when under attack. For the same reason, many practical applications of ML models are at high risk. For instance, researchers have shown that, by placing a few small stickers on the ground at an intersection, self-driving cars can be tricked into making abnormal judgements and driving into the opposite lane Tencent (2019). Maliciously designed attacks on ML models can have serious consequences.
Unfortunately, despite great importance, adversarial problems, especially adversarial inter-agent communication problems, remain largely uninvestigated in MACRL. Blumenkamp et al. show that, by introducing random noise in communication, agents are able to deceive their opponents in competitive games Blumenkamp and Prorok (2020). However, the attacks are not artificially designed and therefore inefficient. Besides, cooperative cases, where communication is more crucial, are neglected. They also fail to propose an effective defence, but merely retrain the models to adapt to the attacks. Mitchell et al. propose to generate weights of Attention models Vaswani et al. (2017) through Gaussian process for defending against random attacks in attention-based MACRL Mitchell et al. (2020). However, the applicability of this approach is unsatisfactory, being limited to attention-based MACRL, and its performance on maliciously designed attacks is unclear.
In this paper, we systematically explore the problem of adversarial communication in MACRL, where there are malicious agents that attempt to disrupt multi-agent cooperation by manipulating messages. Our contributions are in three aspects. First, we propose an effective learning approach to model the optimal attacking scheme in MACRL. Second, to defend against the adversary, we propose a two-stage message filter which works by first detecting the malicious message and then recovering the message. The defending scheme can greatly maintain the coordination of agents under message attacks. Third, to address the problem that the message filter can be exploited by learnable attackers, we formulate the attack-defense problem as a two-player zero-sum game and propose -MACRL, based on a game-theoretical framework Policy-Space Response Oracle (PSRO) Lanctot et al. (2017); Muller et al. (2019), to approximate a Nash equilibrium policy in the adversarial communication game. -MACRL improves the defensive performance under the worst case and thus improves the robustness. Empirical experiments demonstrate that many state-of-the-art MACRL algorithms are vulnerable to attacks and our method can significantly improve their robustness.
2. Preliminaries and Related Work
Multi-Agent Communicative Reinforcement Learning. There has been extensive research on encouraging communication between agents to improve performance on cooperative or competitive tasks. Among the recent advances, some design communication mechanisms to address the problem of when to communicate Kim et al. (2019); Singh et al. (2018); Jiang and Lu (2018); other lines of works, e.g., TarMac Das et al. (2019), focus on who to communicate. These works determine the two fundamental elements in communication, i.e., the message sender and the receiver. Apart from the two elements, the message itself is another element which is crucial in communication, i.e., what to communicate: Jaques et al. propose to maximize the social influence of messages Jaques et al. (2019). Kim et al. encode messages such that they contain the intention of agents Kim et al. (2021). Some other works learn to send succinct messages to meet the limitations of communication bandwidth Wang et al. (2019); Zhang et al. (2020b); Wang et al. (2020). Despite significant progress in MACRL, if some agents are adversarial and send maliciously designed messages, multi-agent coordination will rapidly disintegrate as these messages propagate.
Adversarial Training. Adversarial training is a prevalent paradigm for training robust models to defend against potential attacks Goodfellow et al. (2017); Szegedy et al. (2014). Recent literature has considered two types of attacks Carlini and Wagner (2017); Papernot et al. (2017); Tramèr et al. (2018): black-box attack and white-box attack. In black-box attack, the attacker does not have access to information about the attacked deep neural network (DNN) model; whereas in white-box attack, the attacker has complete knowledge, e.g., the architecture, the parameters and potential defense mechanisms, about the DNN model. We consider the black-box attack in our problem formulation, because the setting of the white-box attack is too idealistic and may not be applicable to many realistic adversarial scenarios. In adversarial training, the attacker tries to attack a DNN by corrupting the input via -norm () attack Goodfellow et al. (2017). The attacker carefully generates artificial perturbations to manipulate the input of the model. In doing so, the DNN will be fooled into making incorrect predictions or decisions. The attacker finds the optimal perturbation by optimizing:
where is the input, is the DNN model, is a metric to measure the distance between the outputs of the DNN model w/ and w/o being attacked, is used to measure that for the inputs.
Adversarial Reinforcement Learning (RL). Recent advances in adversarial machine learning motivate researchers to investigate the adversarial problem in RL Gleave et al. (2020); Lin et al. (2017); Xu et al. (2021). SA-MDP Zhang et al. (2020a) characterizes the problem of decision making under adversarial attacks on state observations. Lin et al. propose two tactics of attacks, i.e., the strategically-timed attack and the enchanting attack, which attack by injecting noise to states and luring the agent to a designated target Lin et al. (2017). Gleave et al. consider the problem of taking adversarial actions that change the environment and consequentially change the observation of agents Gleave et al. (2020). ATLA Zhang et al. (2021) propose to train the optimal adversary to perturb state observations and improve the worst-case agent reward. The settings of these works are different from ours: we consider the multi-agent scenario and restrict the attacking approach to adversarial messages, which makes the detection of anomalies difficult. Tu et al. propose to attack on multi-agent communication Tu et al. (2021). However, their focus is on the representation-level, whereas we focus on the policy-level. Recently, there are some works considering a similar setting as ours Blumenkamp and Prorok (2020); Mitchell et al. (2020). However, they either focus on random attacks in specific competitive games or the defence of specific communication methods.

3. Achieving Robustness in MACRL
In this section, we propose our method for achieving robustness in MACRL. We begin by proposing the problem formulation for adversarial communication in MACRL. Then, we introduce the method to build the optimal attacking scheme in MACRL. Next, we propose a learnable two-stage message filter to defend against possible attacks. Finally, we propose to formulate the attack-defense problem as a two-player zero-sum game, and design a game-theoretic method -MACRL to approximate a Nash equilibrium policy for the defender. In this way, we can improve the worst-case performance of the defender and thus enhance robustness.
3.1. Problem Formulation: Adversarial Communication in MACRL
An MACRL problem can be modeled by Decentralised Partially Observable Markov Decision Process with Communication (Dec-POMDP-Com) Oliehoek et al. (2016), which is defined by a tuple . denotes the state of the environment and is the message space. Each agent chooses an action at a state , giving rise to a joint action vector, . is a Markovian transition function. Every agent shares the same joint reward function , and is the discount factor. Due to partial observability, each agent has individual partial observation , according to the observation function Each agent holds two policies, i.e., action policy and message policy , both of which are conditioned on the action-observation history and incoming messages aggregated by the communication protocol .
In adversarial communication where there are malicious agents, we assume that each malicious agent holds the third private adversarial policy, , which generates adversarial message based on its action-observation history , received messages and the message intended to be sent. Malicious agents could send messages by convexly combining their original messages with adversarial messages, i.e., , or simply summing up the messages, i.e., . To reduce the likelihood of being detected, apart from the adversarial policy , malicious agents strictly follow their former action policy and message policy, trying to behave like benign agents. Fig. 1(a) presents the overall attacking procedure. The agent (attacker) is malicious and tries to generate adversarial message to disrupt cooperation. The adversarial message sent by agent together with normal messages sent by other agents (denoted by ) are processed by the communication protocol (algorithm-related), generating a contaminated incoming message for a benign agent . From agent ’s perspective, under such attack, the estimated Q-values will change. If the action with the highest Q-value shifts, agent will make incorrect decisions, leading to suboptimality. To perform an effective attack in MACRL, we propose to optimize the adversarial policy by minimizing the joint accumulated rewards, i.e., . We make two assumptions to make the adversarial communication problem both practical and tractable.
Assumption 1.
(Byzantine Failure Kirrmann (2015)) Agents have imperfect information on who are malicious.
Assumption 2.
(Concealment) Malicious agents do not communicate or cooperate with each other when performing attacks in order to be covert.
To defend against the attacker, as in Fig. 1(b), we propose to cascade a learnable defender to the communication protocol module. The defender performs a transformation from to to reconstruct the contaminated messages, to avoid distributing the contaminated message directly to agent . With such transformation, the benign agent can estimate the Q-value for each action more properly and reduce the probability of selecting sub-optimal actions.
3.2. Learning the Attacking Scheme
To model the attack scheme in adversarial communication, we use a deep neural network (DNN) , parameterized by , to generate adversarial messages for a malicious agent. The adversarial policy is a multivariate Gaussian distribution whose parameters are determined by the DNN , i.e., where is a fixed covariance matrix. The reason of using Gaussian distribution as the prior is that it is the maximum entropy distribution under constraints of mean and variance. Each malicious agent generates adversarial messages by sampling from its adversarial policy. The optimization objective of the adversarial policy is to minimize the accumulated team rewards subject to a constraint on the distance between and . We utilize Proximal Policy Optimization (PPO) Schulman et al. (2017) to optimize the adversarial policy by maximizing the following objective:
| (1) |
where , is the policy in the previous learning step, is the clipping ratio, and is the advantage function. Let denotes the input of the value function and we define the reward of the attacker to be negative team reward, then where is the value function, denotes the next step state, and is the immediate reward. We learn the value function by minimizing .
3.3. Defending against Adversarial Communication
We can train a DNN to model the attack scheme in adversarial communication. However, the defence of that is non-trivial because i) benign agents have no prior knowledge on which agents are malicious; ii) the malicious agents can inconsistently pretend to be cooperative or non-cooperative to avoid being detected; and iii) recovering useful information from the contaminated messages is difficult. To address these challenges, we design a two-stage message filter for the communication protocol to perform defence. The message filter works by first determining the messages that are likely to be malicious and then recovering the potential malicious messages before distributing them to the corresponding agents. As in Fig. 2, the message filter consists of an anomaly detector and a message reconstructor . The anomaly detector, parameterized by , outputs the probability that each incoming message needs to be recovered, i.e., , where denotes a binomial distribution, denotes the message sent by agent . We perform sampling from the generated distributions to determine the anomaly messages 111We abuse to represent that messages are fed into in batch.. Here, is an indicator that records whether a message is predicted to be malicious or not. The predicted malicious messages are recovered by the reconstructor separately. The recovered message and other normal messages are aggregated and determine the messages that each agent will receive.

The optimization objective of the message filter is to maximize the joint accumulated rewards under attack, i.e., , where is the team reward after performing the defending strategy. We utilize PPO to optimize the strategy. To mitigate the local optima induced by unguided exploration in large message space, we introduce a regularizer which is optimized under the guidance of the ground-truth labels of messages (whether they are malicious). For the reconstructor, we train it by minimizing the distance between the messages before and after being attacked. To improve the tolerance of the reconstructor to errors made by the detector, apart from malicious messages, we also use benign messages as training data, in which case the reconstructor is an identical mapping. Formally, the two-stage message filter is optimized by maximizing the following function:
| (2) |
where , is the advantages which are estimated similarly as in the attack, is the one-hot ground-truth labels of messages, is the messages that have not been attacked. , and are hyperparameters.
3.4. Achieving Robust MACRL
Despite the defensive message filter, the effectiveness of the defence system can rapidly decrease if malicious agents are aware of the defender and adjust their attack schemes. To mitigate this, we formulate the attack-defence problem as a two-player zero-sum game (malicious agents are controlled by the attacker) and improve the performance of the defender in the worst case. We define the adversarial communication game by a tuple , , where is the joint policy space of the players ( and denote the policy space of the defender and the attacker respectively), is the utility function which is used to calculate utilities for the attacker and the defender given their joint policy . The utility of the defender is defined as the expected team return. The adversarial communication game is zero-sum, i.e., the utility of the defender must be the negative of the utility of the attacker for . The solution concept of the adversarial communication game is Nash equilibrium (NE) and we can approach an NE by optimizing the following MaxMin objective:
| (3) |
where is the best response policy of the defender, i.e., .

We propose -MACRL to optimize the objective in the adversarial communication game. -MACRL is developed based on Policy-Space Response Oracle (PSRO) Lanctot et al. (2017), a deep learning-based extension of the classic Double Oracle algorithm McMahan et al. (2003). The workflow of -MACRL is depicted in Fig. 3. At each iteration, -MACRL keeps a population (set) of policies , e.g., and . We can evaluate the utility table for the current iteration and calculate a Nash equilibrium for the game restricted to policies in by, for example, linear programming, replicator dynamics, etc. denotes the meta-strategy which is an arbitrary categorical distribution. Next, we calculate the best response policy to the NE in this restricted game for each player (player denotes the opponent of player , ), e.g., and . We extend the population by adding the best response policies to the policy set: for . After extending the population, we complete the utility table and perform the next iteration. The algorithm converges if the best response policies are already in the population. Practically, -MACRL approximates the utility function by having each policy in the population playing with each other policy in and tracking the average utilities. The approximation of the best response policies is performed by maximizing and for the attacker and the defender, where the full expressions of the two objectives are described in Eq. 1 and Eq. 2, respectively.
The overall algorithm of -MACRL is presented in Algorithm 1. We first initialize the meta-game and the mixed strategies (line 1 and line 1). Then, at each step, we train the attacker and the defender alternately by letting them best respond to their corresponding opponent (line 1). Next, the learned new policy is added to the policy set for the two players respectively (line 1). After extending the policy set, we can check the convergence (line 1) and calculate the missing entries in (line 1). Finally, we solve the new meta-game (line 1) and repeat the iteration.
4. Experiments
We conduct extensive experiments on a variety of state-of-the-art MACRL algorithms to answer: Q1: Are MACRL methods vulnerable to message attacks and whether the two-stage message filter is able to consistently recover multi-agent coordination? Q2: Whether -MACRL is able to improve the robustness of MACRL algorithms under message attacks? Q3: Whether our method is able to scale to scenarios where there are multiple attackers? Q4: Which components contribute to the performance of the method and how does the proposed method work? We first categorize existing MACRL algorithms and then select representative algorithms to perform the evaluation. All experiments are conducted on a server with 8 NVIDIA Tesla V100 GPUs and a 44-core 2.20GHz Intel(R) Xeon(R) E5-2699 v4 CPU.
4.1. Experimental Setting
MACRL methods are commonly categorized by whether they are implicit or explicit Oliehoek et al. (2016); Ahilan and Dayan (2021). In implicit communication, the actions of agents influence the observations of the other agents. Whereas in explicit communication, agents have a separate set of communication actions and exchange information via communication actions. In this paper, we focus on explicit communication because in implicit communication, to carry out an attack, the attacker’s behaviour is often bizarre, making the attack trivial and easily detectable. We consider the following three realistic types of explicit communication:
-
•
Communication with delay (CD): Communication in real world is usually not real-time. We can model this by assuming that it takes one or a few time steps for the messages being received by the targeted agents Sukhbaatar et al. (2016).
-
•
Local communication (LC): Messages sometimes cannot be broadcast to all agents due to communication distance limitations or privacy concerns. Therefore, agents need to learn to communicate locally, affecting only those agents within the same communication group Das et al. (2019); Böhmer et al. (2020).
- •
Following the above taxonomy, we select some representative state-of-the-art algorithms to perform evaluation222Sweeping the whole list of algorithms for each category is impossible and unnecessary since there have been a lot of algorithms proposed and algorithms in each category usually share common characteristics.. As in Table 1, we select CommNet Sukhbaatar et al. (2016), TarMAC Das et al. (2019) and NDQ Wang et al. (2019) for CD, LC and CC respectively. A brief introduction to each of the chosen algorithms is provided in Appendix A. We evaluate in the following environments, which are similar to those in the paper that first introduced the algorithms:
| Categories | Methods | Environments |
| CD | CommNet Sukhbaatar et al. (2016) | Predator Prey (PP) Böhmer et al. (2020) |
| LC | TarMAC Das et al. (2019) | Traffic Junction (TJ) Sukhbaatar et al. (2016) |
| CC | NDQ Wang et al. (2019) | StarCraft II (SCII) Samvelyan et al. (2019) |
Predator Prey (PP). There are 3 predators, trying to catch 6 prey in a grid. Each predator has local observation of a sub-grid centered around it and can move in one of the 4 compass directions, remain still, or perform catch action. The prey moves randomly and is caught if at least two nearby predators try to catch it simultaneously. The predator will obtain a team reward at 10 for each successful catch and will be punished for each losing catch action. There are two tasks with and , respectively. A prey will be removed from the grid after it being caught. An episode ends after 60 steps or all preys have been caught.
Traffic Junction (TJ). In TJ, there are cars and the aim of each car is to complete its pre-assigned route. Each car can observe of a region around it, but is free to communicate with other cars. The action space for each car at every time step is {gas, brake}. The reward function is , where is the number of time steps since the activation of the car, and is a collision penalty. Cars become available to be sampled and put back to the environment with new assigned routes once they complete their routes.
StarCraft II (SCII). We consider SMAC Samvelyan et al. (2019) combat scenarios where the enemy units are controlled by StarCraft II built-in AI (difficulty level is set to hard), and each of the ally units is controlled by a learning agent. The units of the two groups can be asymmetric. The action space contains no-op, move[direction], attack[enemy id], and stop. Agents receive a globally shared reward which calculates the total damage made to the enemy units at each time step. We conduct experiments on four SMAC tasks: 3bane_vs_hM, 4bane_vs_hM, 1o_2r_vs_4r and 1o_3r_vs_4r. More details about the tasks are in Appendix B.
For each of the tasks, we first train the chosen MACRL methods to obtain the action policy and the message policy for each agent. After that, we randomly select an agent to be malicious and train its adversarial policy to examine whether MACRL methods are vulnerable to message attacks. Then we perform defence by training the message filter, during which the adversarial policy of the malicious agent is fixed but keeps working. To show that a single message filter is brittle and can be easily exploited if the attacker adapts to it, we freeze the learned message filter and retrain the adversarial policy. Finally, we integrate the message filter into the framework of -MACRL and justify if -MACRL is helpful to improve the robustness. All experiments are carried out with five random seeds and results are shown with a 95% confidence interval.
4.2. Recovering Multi-Agent Coordination
We first evaluate the performance of our attacking method on the three selected MACRL algorithms. Then we try to recover multi-agent coordination for the attacked algorithms by applying the message filter.

CommNet. The experiments for CommNet are conducted on predator prey (PP) Böhmer et al. (2020). We set the punishment as and to create two PP tasks with different difficulties. As in Fig. 4, at the beginning of the attack, the performance of CommNet does not have obvious decrease, indicating that injecting random noise into the message is hard to disrupt agent coordination. As we gradually train the adversarial policy, there is a significant drop in the test return, with 40% and 33% decreases in the task of and , respectively. Multi-agent cooperation has been severely affected due to the malicious messages. When the test return decreases to preset thresholds, i.e., 23 for and 20 for , we freeze the adversarial policy network and start to train the message filter. As shown in the blue curves in Fig 4, with the message filter, test return steadily approaches the converged value of CommNet (red line), indicating that the message filter can effectively recover multi-agent coordination under attack.
| Easy | Hard | |
| TarMAC | ||
| TarMAC w/ | ||
| TarMAC w/ |
TarMAC. We conduct message attack and defence on the Traffic Junction (TJ) environment Sukhbaatar et al. (2016). There are two modes in TJ, i.e., easy and hard. The easy task has one junction of two one-way roads on a grid with . In the hard task, its map has four junctions of two-way roads on a grid and . As shown in Table 2, under attack, the success rate of TarMAC decreases in both the easy and the hard scenarios, demonstrating the vulnerability of TarMAC under malicious messages. After that, we equip TarMAC with the defender, then its performance improves considerably, demonstrating the merit of the message filter.

NDQ. We further examine the adversarial communication problem in NQD. We perform evaluation on two StarCraft II Multi-Agent Challenge (SMAC) Samvelyan et al. (2019) scenarios, i.e., and , in which the communication between cooperative agents is necessary Wang et al. (2019). As presented in Fig. 5, under attack, the test win rate of NDQ decreases dramatically, demonstrating that NDQ is also vulnerable to message attacks. After applying the message filter as the defender, we can find the test win rate quickly reaches to around in and in , demonstrating that, once again, our defence methods succeed in restoring multi-agent coordination under message attacks.

4.3. Improving Robustness with -MACRL
We have demonstrated that many state-of-the-art MACRL algorithms are vulnerable to message attacks, and after applying the message filter, multi-agent coordination can be recovered. In this part, we integrate the message filter into the framework of -MACRL and show that the robustness of MACRL algorithms can be significantly improved with -MACRL.
Exploiting the message filter. We first show that a single message filter is brittle and can be easily exploited if the attacker adapts to it. We perform experiments on CommNet by freezing the message filter and retraining the adversarial policy. As depicted in Fig. 6, the test return of the team gradually decreases as the training proceeds, with around 30% and 20% decreases in the task of and respectively. We also conduct experiments on NDQ and similar phenomenon is observed (see Appendix D). We conclude that even though the designed message filter is able to recover multi-agent cooperation under message attacks, its performance can degrade if faced with an adaptive attacker.
| Methods | Scenarios | ||
| CommNet | |||
| TarMAC | Easy | ||
| Hard | |||
| NDQ | 3bane_vs_hM | ||
| 1o_2r_vs_4r |
Improving robustness. To illustrate the improvement in robustness, we make comparisons between the defender trained by -MACRL and the vanilla defending method. For the defender trained with -MACRL, a population of attack policies are learned together with the defender, whose policy is also a mixture of sub-policies. In the vanilla training method, only a single defending policy is trained for the defender. We use the expected utility value (the accumulated team return) as the metric to compare the performance of the defender. Specifically, the larger the expected utility, the better the robustness. We denote the expected utility of the defender trained by -MACRL as and the result for the vanilla one as . As shown in Table 3, -MACRL consistently outperforms the vanilla method over all the algorithms and environments. The improvement of expected utilities indicates that the defender trained by -MACRL is more robust. Intuitively, the defender benefits from exploring a wider range of the policy space with -MACRL, which enables the defender to maintain multi-agent coordination when faced with attacks.
4.4. Scaling to Multiple Attackers
To examine the performance of the method in scenarios where there is more than one attacker, we conduct experiments on NDQ in two new challenge tasks: 4bane_vs_hM and . In the former maps, i.e., 3bane_vs_hM and , there are only three agents in the team, making multiple attackers unreasonable. To mitigate this, we create 4bane_vs_hM and based on 3bane_vs_hM and by increasing one more agent to the team. We randomly sample two agents to be malicious. According to our assumptions (agents have no knowledge about who are malicious and malicious agents cannot communicate with each other), we can directly apply the attacking method to each of the malicious agents. As shown in Fig. 7, the attackers can quickly learn effective adversarial policies with less learning steps. On the other hand, the message filter can still successfully recover multi-agent cooperation under multiple attackers, though it takes much more learning steps to converge. We further evaluate the effectiveness of -MACRL on the two tasks and consistent results are observed: trained with -MACRL, the agents can obtain larger expected utilities. More results on other algorithms and environments are provided in Appendix D.

| Methods | Scenarios | ||
| NDQ | 4bane_vs_hM | ||
| 1o_3r_vs_4r |
4.5. Ablation Study and Analysis
We have shown that by integrating the message filter into the framework of -MACRL, the robustness of MACRL algorithms can be improved. However, the performance of -MACRL directly is affected by the message filter. In this part, we will take a deeper look at how the message filter works.


Which components contribute to the performance? The message filter consists of two components: the anomaly detector and the message reconstructor. Here, we alternatively disable these two components in the message filter to study how they contribute to the performance. We run experiments on three scenarios, with each scenario corresponding to an MACRL algorithm. Following the former training procedure, we first train the original MACRL algorithm to obtain the action policy and the message policy; then we sample an attacker and train its adversarial policy by PPO; next we freeze the policy of the attacker and train the message filter (with the anomaly detector or the reconstructor disabled). As in Fig. 8, if we disable the message reconstructor in the message filter and replace it with a random message generator, after being attacked, multi-agent coordination is hard to be recovered, demonstrating the importance of the reconstructor. We further disable the anomaly detector and randomly choose an agent to reconstruct its message, as in Fig. 9, the defending performance is also poor. The ablation illustrates that both the anomaly detector and the reconstructor are critical in the message filter.

How does the proposed method work? Now we take a deeper look at how the message filter works. We conduct experiments on NDQ in the task. There are three agents in the team, of which agent is the attacker and the others, namely agent and agent , are benign agents. As shown in Fig. 10 (a)-(c), the action space of each agent contains eight elements. White cells in Q values correspond to illegal actions at the current state, and the action with red Q value is optimal, e.g., of agent . When attacked by the agent , the optimal action of agent shifts from to , leading to sub-optimality. After applying the message filter, the decision of agent is corrected to . We further examine the messages received by agent and agent . As in Fig. 10 (d)-(e), the attacked messages are quite different from the original messages, while after applying the message filter, the distance between the original messages and the reconstructed messages becomes closer.
5. Conclusion
In this paper, we systematically examine the problem of adversarial communication in MACRL. The problem is of importance but has been largely neglected before. We first provide the formulation of adversarial communication. Then we propose an effective method to model message attacks in MACRL. Following that, we design a two-stage message filter to defend against message attacks. Finally, to improve robustness, we formulate the adversarial communication problem as a two-player zero-sum game and propose -MACRL to improve the robustness. Experiments on a wide range of algorithms and tasks show that many state-of-the-art MACRL methods are vulnerable to message attacks, while our algorithm can consistently recover multi-agent cooperation and improve the robustness of MACRL algorithms under message attacks.
References
- (1)
- Ahilan and Dayan (2021) Sanjeevan Ahilan and Peter Dayan. 2021. Correcting Experience Replay for Multi-Agent Communication. ICLR (2021).
- Barreno et al. (2010) Marco Barreno, Blaine Nelson, Anthony D Joseph, and J Doug Tygar. 2010. The security of machine learning. Machine Learning 81, 2 (2010), 121–148.
- Blumenkamp and Prorok (2020) Jan Blumenkamp and Amanda Prorok. 2020. The emergence of adversarial communication in multi-agent reinforcement learning. CoRL (2020).
- Böhmer et al. (2020) Wendelin Böhmer, Vitaly Kurin, and Shimon Whiteson. 2020. Deep coordination graphs. In ICML. 980–991.
- Carlini and Wagner (2017) Nicholas Carlini and David Wagner. 2017. Towards evaluating the robustness of neural networks. In 2017 IEEE Symposium on Security and Privacy (SP). 39–57.
- Das et al. (2019) Abhishek Das, Théophile Gervet, Joshua Romoff, Dhruv Batra, Devi Parikh, Mike Rabbat, and Joelle Pineau. 2019. Tarmac: Targeted multi-agent communication. In ICML. 1538–1546.
- Foerster et al. (2016) Jakob N Foerster, Yannis M Assael, Nando de Freitas, and Shimon Whiteson. 2016. Learning to communicate with Deep multi-agent reinforcement learning. In NeurIPS. 2145–2153.
- Gleave et al. (2020) Adam Gleave, Michael Dennis, Cody Wild, Neel Kant, Sergey Levine, and Stuart Russell. 2020. Adversarial Policies: Attacking Deep Reinforcement Learning. In ICLR.
- Goodfellow et al. (2017) Ian Goodfellow, Nicolas Papernot, Sandy Huang, Yan Duan, Pieter Abbeel, and Jack Clark. 2017. Attacking machine learning with adversarial examples. OpenAI. https://blog. openai. com/adversarial-example-research (2017).
- Huang et al. (2011) Ling Huang, Anthony D Joseph, Blaine Nelson, Benjamin IP Rubinstein, and J Doug Tygar. 2011. Adversarial machine learning. In Proceedings of the 4th ACM Workshop on Security and Artificial Intelligence. 43–58.
- Hüttenrauch et al. (2017) Maximilian Hüttenrauch, Adrian Šošić, and Gerhard Neumann. 2017. Guided deep reinforcement learning for swarm systems. arXiv preprint arXiv:1709.06011 (2017).
- Jaques et al. (2019) Natasha Jaques, Angeliki Lazaridou, Edward Hughes, Caglar Gulcehre, Pedro Ortega, DJ Strouse, Joel Z Leibo, and Nando De Freitas. 2019. Social influence as intrinsic motivation for multi-agent deep reinforcement learning. In ICML. 3040–3049.
- Jiang and Lu (2018) Jiechuan Jiang and Zongqing Lu. 2018. Learning attentional communication for multi-agent cooperation. In NeurIPS. 7254–7264.
- Kim et al. (2019) Daewoo Kim, Sangwoo Moon, David Hostallero, Wan Ju Kang, Taeyoung Lee, Kyunghwan Son, and Yung Yi. 2019. Learning to schedule communication in multi-agent reinforcement learning. ICLR (2019).
- Kim et al. (2021) Woojun Kim, Jongeui Park, and Youngchul Sung. 2021. Communication in multi-Agent reinforcement learning: Intention Sharing. ICLR (2021).
- Kingma and Ba (2014) Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
- Kirrmann (2015) Hubert Kirrmann. 2015. Fault Tolerant Computing in Industrial Automation. Switzerland: ABB Research Center.
- Kraemer and Banerjee (2016) Landon Kraemer and Bikramjit Banerjee. 2016. Multi-agent reinforcement learning as a rehearsal for decentralized planning. Neurocomputing 190 (2016), 82–94.
- Lanctot et al. (2017) Marc Lanctot, Vinicius Zambaldi, Audrūnas Gruslys, Angeliki Lazaridou, Karl Tuyls, Julien Pérolat, David Silver, and Thore Graepel. 2017. A unified game-theoretic approach to multiagent reinforcement learning. In NeurIPS. 4193–4206.
- Lin et al. (2017) Yen-Chen Lin, Zhang-Wei Hong, Yuan-Hong Liao, Meng-Li Shih, Ming-Yu Liu, and Min Sun. 2017. Tactics of adversarial attack on deep reinforcement learning agents. In IJCAI. 3756–3762.
- McMahan et al. (2003) H Brendan McMahan, Geoffrey J Gordon, and Avrim Blum. 2003. Planning in the presence of cost functions controlled by an adversary. In ICML. 536–543.
- Mitchell et al. (2020) Rupert Mitchell, Jan Blumenkamp, and Amanda Prorok. 2020. Gaussian Process Based Message Filtering for Robust Multi-Agent Cooperation in the Presence of Adversarial Communication. arXiv preprint arXiv:2012.00508 (2020).
- Muller et al. (2019) Paul Muller, Shayegan Omidshafiei, Mark Rowland, Karl Tuyls, Julien Perolat, Siqi Liu, Daniel Hennes, Luke Marris, Marc Lanctot, Edward Hughes, et al. 2019. A generalized training approach for multiagent learning. In ICLR.
- Oliehoek et al. (2016) Frans A Oliehoek, Christopher Amato, et al. 2016. A Concise Introduction to Decentralized POMDPs. Vol. 1. Springer.
- Oliehoek et al. (2008) Frans A Oliehoek, Matthijs TJ Spaan, and Nikos Vlassis. 2008. Optimal and approximate Q-value functions for decentralized POMDPs. JAIR 32 (2008), 289–353.
- Papernot et al. (2017) Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. 2017. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security. 506–519.
- Paszke et al. (2019) Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. 2019. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In NeurIPS. 8026–8037.
- Samvelyan et al. (2019) Mikayel Samvelyan, Tabish Rashid, Christian Schroeder de Witt, Gregory Farquhar, Nantas Nardelli, Tim G. J. Rudner, Chia-Man Hung, Philiph H. S. Torr, Jakob Foerster, and Shimon Whiteson. 2019. The StarCraft multi-agent challenge. CoRR abs/1902.04043 (2019).
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347 (2017).
- Singh et al. (2018) Amanpreet Singh, Tushar Jain, and Sainbayar Sukhbaatar. 2018. Learning when to communicate at scale in multiagent cooperative and competitive tasks. ICLR (2018).
- Singh et al. (2020) Arambam James Singh, Akshat Kumar, and Hoong Chuin Lau. 2020. Hierarchical Multiagent Reinforcement Learning for Maritime Traffic Management. In AAMAS. 1278–1286.
- Sukhbaatar et al. (2016) Sainbayar Sukhbaatar, Arthur Szlam, and Rob Fergus. 2016. Learning multiagent communication with backpropagation. In NeurIPS. 2252–2260.
- Szegedy et al. (2014) Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. 2014. Intriguing properties of neural networks. In ICLR.
- Tencent (2019) Keen Security Lab Tencent. 2019. Experimental Security Research of Tesla Autopilot. (2019). https://keenlab.tencent.com/en/whitepapers/Experimental_Security_Research_of_Tesla_Autopilot.pdf
- Tramèr et al. (2018) Florian Tramèr, Alexey Kurakin, Nicolas Papernot, Ian Goodfellow, Dan Boneh, and Patrick McDaniel. 2018. Ensemble adversarial training: attacks and defenses. In ICLR.
- Tu et al. (2021) James Tu, Tsunhsuan Wang, Jingkang Wang, Sivabalan Manivasagam, Mengye Ren, and Raquel Urtasun. 2021. Adversarial attacks on multi-agent communication. arXiv preprint arXiv:2101.06560 (2021).
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In NeurIPS. 5998–6008.
- Vinyals et al. (2019) Oriol Vinyals, Igor Babuschkin, Wojciech M Czarnecki, Michaël Mathieu, Andrew Dudzik, Junyoung Chung, David H Choi, Richard Powell, Timo Ewalds, Petko Georgiev, et al. 2019. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 575, 7782 (2019), 350–354.
- Wang et al. (2020) Rundong Wang, Xu He, Runsheng Yu, Wei Qiu, Bo An, and Zinovi Rabinovich. 2020. Learning efficient multi-agent communication: An information bottleneck approach. In ICML. 9908–9918.
- Wang et al. (2019) Tonghan Wang, Jianhao Wang, Chongyi Zheng, and Chongjie Zhang. 2019. Learning Nearly Decomposable Value Functions Via Communication Minimization. In ICLR.
- Xu et al. (2021) Hang Xu, Rundong Wang, Lev Raizman, and Zinovi Rabinovich. 2021. Transferable environment poisoning: Training-time attack on reinforcement learning. In AAMAS. 1398–1406.
- Zhang et al. (2021) Huan Zhang, Hongge Chen, Duane S Boning, and Cho-Jui Hsieh. 2021. Robust reinforcement learning on state observations with learned optimal adversary. In ICLR.
- Zhang et al. (2020a) Huan Zhang, Hongge Chen, Chaowei Xiao, Bo Li, Mingyan Liu, Duane Boning, and Cho-Jui Hsieh. 2020a. Robust deep reinforcement learning against adversarial perturbations on state observations. In NeurIPS. 21024–21037.
- Zhang et al. (2020b) Sai Qian Zhang, Jieyu Lin, and Qi Zhang. 2020b. Succinct and robust multi-agent communication with temporal message control. arXiv preprint arXiv:2010.14391 (2020), 17271–17282.
Appendix A Introduction to the selected MACRL algorithms
In this section, we introduce the selected MACRL algorithms for evaluation:
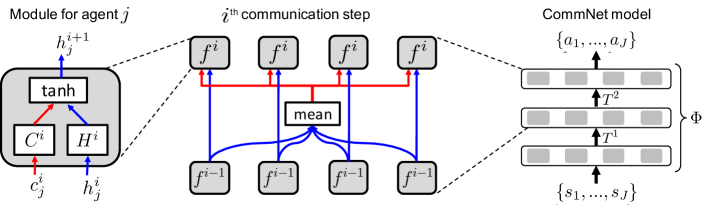
CommNet Sukhbaatar et al. (2016) is a simple yet effective multi-agent communicative algorithm where incoming messages of each agent are generated by averaging the messages sent by all agents in the last time step. We present the architecture of CommNet in Fig. 13.
TarMAC Das et al. (2019) extends CommNet by allowing agents to pay attention to important parts of the incoming messages via Attention Vaswani et al. (2017) network. Concretely, each agent generates signature and query vectors when sending message. In the message receiving phase, attention weights of incoming messages are calculated by comparing the similarity between the query vector and the signature vector of each incoming message. Then a weighted sum over all incoming messages is performed to determine the message an agent will receive for decentralized execution. The architecture of TarMAC is in Fig. 14.
NDQ Wang et al. (2019) achieves nearly decomposable Q-functions via communication minimization. Specifically, it trains the communication model by maximizing mutual information between agents’ action selection and communication messages while minimizing the entropy of messages between agents. Each agent broadcasts messages to all other agents. The sent messages are sampled from learned distributions which are optimized by mutual information. The overview of NDQ is in Fig. 15.
Appendix B The SMAC maps


For the SCII environments, we conduct experiments on the following four maps to examine the attack and defence on NDQ:
3bane_vs_hM: 3 Banelings try to kill a Hydralisk assisted by a Medivac. 3 Banelings together can just blow up the Hydralisk. Therefore, to win the game, 3 Banelings ally units should not give the Hydralisk changes to rest time when the Medivac can restore its health.
4bane_vs_hM: Similar to 3bane_vs_hM, the main difference in 3bane_vs_hM is there are 4 Banelings.
1o_2r_vs_4r: Ally units consist of 1 Overseer and 2 Roaches. The Overseer can find 4 Reapers and then notify its teammates to kill the invading enemy units, the Reapers, in order to win the game. At the start of an episode, ally units spawn at a random point on the map while enemy units are initialized at another random point. Given that only the Overseer knows the position of the enemy unit, the ability to learn to deliver this message to its teammates is vital for effectively winning the combat.
1o_3r_vs_4r: Similar to 1o_2r_vs_4r, the main difference in 1o_3r_vs_4r is there are 1 Overseer and 3 Roaches.
Appendix C Hyperparameters
We train all the selected MACRL methods with the same hyperparameters as in the corresponding papers, to reproduce the performances. We use Adam Kingma and Ba (2014) optimizer with a learning rate of 0.001 to train the attacker model as well as the anomaly detector and the message reconstructor. We use the default hyperparameters of Adam optimizer. , and are all 0.001. The clip ratio in PPO is . The attacker model contains 3 linear layers and each layer has 64 neurons with ReLU activation. Same deep neural networks are used in the anomaly detector and the message reconstructor. We use PyTorch Paszke et al. (2019) to implement all the deep neural network models.
Appendix D Additional Results
We train an adaptive attacker in NDQ to exploit the message filter. As in Fig. 12, the test won rate decrease significantly, illustrating that a single message filter is brittle and can easily be exploited.

We also conduct experiments of multi attackers on the original environments. Two agents are selected randomly to be malicious. As in Table. 5, outperforms the vanilla method in most of the tasks, demonstrating the effectiveness of our method.
| Methods | Scenarios | ||
| CommNet | |||
| TarMAC | Easy | ||
| Hard | |||
| NDQ | 3bane_vs_hM | ||
| 1o_2r_vs_4r |