Minimax Weight Learning for Absorbing MDPs111This research is supported by National Key R&D Program of China (Nos. 2021YFA1000100 and 2021YFA1000101) and Natural Science Foundation of China (No. 71771089)
Abstract
Reinforcement learning policy evaluation problems are often modeled as finite or discounted/averaged infinite-horizon Markov Decision Processes (MDPs). In this paper, we study undiscounted off-policy evaluation for absorbing MDPs. Given the dataset consisting of i.i.d episodes under a given truncation level, we propose an algorithm (referred to as MWLA in the text) to directly estimate the expected return via the importance ratio of the state-action occupancy measure. The Mean Square Error (MSE) bound of the MWLA method is provided and the dependence of statistical errors on the data size and the truncation level are analyzed. The performance of the algorithm is illustrated by means of computational experiments under an episodic taxi environment
keywords:
Absorbing MDP, Off-policy, Minimax weight learning, Policy evaluation, Occupancy measure1 Introduction
Off-policy evaluation (OPE) in reinforcement learning refers to the estimation of the expected returns of target policies using data collected by possibly different behavior policies. It is particularly important in situations where implementing new strategies is expensive, risky, or even dangerous, such as medicine (Murphy et al., 2001), education (Mandel et al., 2014), economics (Hirano et al., 2003), recommender systems (Li et al., 2011), and more. Currently available OPE procedures are mostly based on direct importance sampling (IS) techniques, which suffer from high variances that exponentially increase over the time horizon, known as ”the curse of horizon” (Jiang and Li, 2016; Li et al., 2015).
A promising idea recently proposed uses marginalized importance sampling (MIS) to alleviate the curse of horizon, but raises a new problem of how to estimate the maginalized importance ratios. For instance, in the case of an infinite-horizon discounted Markov Decision Process (MDP), Liu et al. (2018) compute the importance weights based on the state distribution by solving a minimax optimization problem, and propose a method to estimate the expected return. Moreover, Uehara et al. (2020) propose a Minimax Weight Learning (MWL) algorithm that directly estimates the ratio of the state-action distribution without relying on the specification of the behavior policy.
In many real practices, such as robotic tasks, the environments will terminate at certain random times when they evolve into certain states. In such situations, it is no longer appropriate to model the environments using only finite-time or infinite-time MDPs. Instead, MDPs with absorbing states are suitable, where the absorption reflects the termination of the processes. Furthermore, from a theoretical perspective, absorbing MDPs extend the framework of infinite-horizon discounted MDP processes (Altman, 1999) but the reverse does not hold (see Section 2.1 for more details).
The theory of absorbing MDPs has been extensively studied and is well understood. For example, the knowledge of the times required to reach the absorbing states, depending on both the state and the actions, can be found in Chatterjee et al. (2008) and Iida and Mori (1996) and the minimization of the expected undiscounted cost until the state enters the absorbing set in various applications (such as pursuit problems, transient programming, and first pass problems) are investigated by Eaton and Zadeh (1962), Derman (1970), Kushner (1971)), among others. Other research efforts include the stochastic shortest path problem (Bertsekas and Tsitsiklis, 1991), the control-to-exit time problem (Kesten and Spitzer, 1975; Borkar, 1988), among a vast number of others.
In the context of learning when the underlying distributions are unknown, however, while many benchmark environments are indeed episodic and have random horizons, such as board games (a game terminates once the winner is determined), trips through a maze, and dialog systems (a session terminates when the conversation is concluded) (Jiang, 2017), there are only limited efforts specifically contributed to absorbing MDPs. In this paper, we propose an MWL algorithm for offline RL involving absorbing MDPs, referred to as MWLA hereafter. Our proposed approach tackles two key challenges.
The first challenge pertains to the Data structure. While an infinite horizon MDP can be treated as an ergodic Markov chain under suitable assumptions, the same assumption is not always valid for absorbing MDPs due to their indefinite horizons and varying episode lengths, of which some can be quite short. Therefore, assuming that the collected data consists of i.i.d. tuples , which is crucial for the MWL method, is not always natural. Instead, we propose working with data that consists of trajectories, where each data point represents a single trajectory.
The second challenge arises from the random episodic length and the expected undiscounted total rewards. In absorbing MDPs, the length of an episode is indefinite, and it may not be always practical to observe extremely long episodes fully, due to various reasons, such as their length or cost. To address this issue, a simple but practical choice is to truncate long episodes with a level . If the expected total rewards are discounted with , it is easy to see that we can control the errors resulting from such truncations by sufficiently small . However, with the expected undiscounted total rewards, how to quantify the errors is unclear up to now for absorbing MDPs.
Our proposed MWLA algorithm deals with truncated episode data, and we provide a theoretical analysis of the errors resulting from episode truncation. As a result, it aids us in gaining a better understanding of the effects of episode truncation and identifying an appropriate truncation level under which the errors caused by truncation can be deemed acceptable.
Specifically, in this paper, we derive an estimate of the expected undiscounted return of an absorbing MDP and establish an upper bound for the MSE of the MWLA algorithm. The bound consists of three parts: errors due to statistics, approximation and optimization, respectively. The statistical error depends on both the truncation level and data size. Moreover, we present a uniform bound on MSE by means of an optimization with respect to the truncation level when the truncation level is relatively large. We also demonstrate the effectiveness of our algorithm through numerical experiments in the episodic taxi environment.
The remainder of this paper is organized as follows: Section 2 introduces the model formulation and specifies some basic settings. The MWLA algorithm and its theoretical guarantees without knowledge of behavior policies are presented in Section 3. Additionally, we discuss a parallel version of MWLA, referred to MSWLA, for absorbing MDP with a known behavior policy in Remark 3.2. In Section 4, under the assumption that the data consists of i.i.d. episodes, MSE bound for the MWLA method is provided in Theorems 4.1 and 4.2. Specifically, when the function classes are VC classes, compared with Theorem 9 in Uehara et al. (2020), it is found that our statistical error is related to the truncation length . The related work is discussed in Section 5, providing more details to clarify their connection to and differences between the current work. In Section 6, a computer experiment is reported under the episodic taxi environment, compared with on-policy, naive-average, and MSWLA methods, where estimates of returns and their MSEs are given under different episode numbers and truncation lengths. All theoretical proofs and the pseudo-code of the algorithm are deferred to the Appendix.
2 Basic setting
An MDP is a controllable rewarded Markov process, represented by a tuple of a state space , an action space , a reward distribution mapping a state-action pair to a distribution over the set of real numbers with an expectation value , a transfer probability function and an initial state distribution .
In this paper, a policy refers to a time-homogeneous mapping from to the family of all distributions over , executed as follows. Starting with an initial state , at any integer time , an action is sampled, a scalar reward is collected, and a next state is then assigned by the environment. The space is assumed enumerable and is bounded. The probability distribution generated by under a policy and an initial distribution is denoted by , and is used for its expectation operation. When the initial state , the probability distribution and expectation are indicated by and respectively, so that and The notation and are also used to indicate the probability and expectation generated by starting from the state-action couple and subsequently the following policy .
An absorbing state, represented by , is a state such that and for all . It is assumed that there is only one unique absorbing state. For a trajectory, denote by the terminal time, where and throughout the paper signifies “defined as”. An MDP is absorbing if for all states and all policies . Denote by the non-absorbing states. We make the following assumption on .
Assumption 2.1.
.
Write for the collection of all functions mapping a couple to a real number. Introduce a functional on by
and for any functions , let . Note that implicitly depends on the initial distribution .
The expected return under a policy is given by
| (1) |
which depends only on the transition probability and the mean reward function rather than the more detailed reward distribution functions.
For any , taking the indicator function as a particular mean reward function, i.e., collecting a unit reward at and zero otherwise, gives rise to the occupancy measure
| (2) |
where by Assumptions 2.1. Conceptually, can also be retrieved from Chapmann-Kolmogorov equations
| (3) |
Conversely, with the measure , we can retrieve the expected return
as an integration of the mean reward function with respect to the occupancy measure. In addition, a simple recursive argument shows that
A direct result of this equality is a family of equations
| (4) |
Denote by . Then the system of equations (4) can equivalently be rewritten as
| (5) |
Remark 2.1.
MDP models with absorbing states to maximize expected return (1) fundamentally differ from the usually analyzed discounted MDPs with infinite time-horizon. Here two points are discussed:
-
1.
In the perspective of probability theory, MDP models with absorbing states to maximize the expected returns generalize infinite-horizon MDPs that maximize discounted expected return. To see it, consider an infinite-horizon discounted MDP . To create a new model with an absorbing state, we introduce a new state such that , define
keep the action space the same, and introduce a reward function by . The optimal policy of and are the same because the two models share the same Bellman optimality equation(a similar argument is discussed in Section 10.1 of Altman (1999)).
In the context of learning, and are essentially two different models because one generally needs to estimate the unknown parameter (the probability of transitioning to the absorbing state or the unknown discount factor) in , whereas is known in .
-
2.
In general, an MDP with absorbing states to maximize expected return is not necessarily translated to an MDP to maximize expected discounted return. For example, one can consider the case when the transition probability of a state to the absorbing state under a policy depends on the state.
3 Minimax Weight Learning for absorbing MDP (MWLA)
Let
| (6) |
be a representative episode of an absorbing MDP with probability distribution and its i.i.d. copies, respectively. The objective is to estimate the expected return by using the dataset of i.i.d. trajectories , each of which is a realization of truncated at a prespecified time step , i.e.
The algorithm developed here, as indicated by the title “Minimax Weight Learning for Absorbing MDP” of this section and referred to as MWLA below is an extension of Uehara et al. (2020)’s Minimax Weight Learning (MWL) algorithm for infinite-horizon discounted MDPs. Their method uses a discriminator function class to learn the importance weight (defined in equation (7) below) on state-action pairs. One of their important tools is the (normalized) discounted occupancy, which can be approximated well using the given discount factor and the suitable dataset (for example, the dataset consisting of i.i.d. tuples ). However, in our setting, the normalized occupancy is not applicable since the reward is not discounted. Our method is essentially based on the occupancy measure defined in equation (2).
For any , let
| (7) |
Observe that
provided that implies . By replacing , and with their estimates , and , respectively, a plug-in approach suggests that can be simply estimated by
| (8) |
in which the crucial step is to estimate .
From equality (5), we formally introduce an error function
| (9) | |||||
so that Conversely, by taking a family of particular functions , as what has been done in (2), the uniqueness of the solution to this system of equations can be derived, as what is in the following Theorem.
Note that if and only if , we can safely work with the system of equations , where and throughout the remainder of the paper, of a vector or a matrix denotes its Eclidean norm.
Theorem 3.1.
The function is the unique bounded solution to the system of equations , provided that the following conditions hold:
-
1.
The occupancy measure is the unique solution to the system of equations of ,
(10) -
2.
implies for all .
Theorem 3.1 simply states that
| (11) |
In real applications, is approximated by
where is a working class of , and treated as discriminators. For artificially designed , the class is only required to be bounded because it may be computationally inefficient to require for .
For any , define a function by . The theorem below, with a novel relationship between and the error function , will be helpful in bounding the estimation error of occupancy measure ratio by means of the mini-max loss via the discriminator class chosen properly.
Theorem 3.2.
The error function allows for the expressions
| (12) |
Consequently,
-
1.
and
-
2.
.
Here denotes the supremum norm.
The MWLA algorithm to estimate is now ready to be described as follows. Firstly, for all , define the trajectory-specific empirical occupancy measures and rewards by
| (13) |
and
Secondly, for any , introduce an empirical error function
| (14) | |||||
so that an estimate of is then defined by
Putting them into equation (8), the expected return is consequently estimated by
| (15) |
Remark 3.1.
Compared to the MWL algorithm in Uehara et al. (2020), the MWLA algorithm described above utilizes truncated episodes instead of the tuples. Consequently, the accuracy of the estimation depends on two factors: the data size and the truncation level . Therefore, it is crucial to comprehend how errors vary at different levels of and . This will aid us in gaining a better understanding of the effects of episode truncation and identifying an appropriate truncation level under which the errors caused by truncation can be deemed acceptable. A detailed analysis on this matter is presented in the next section.
Below is an example of the MWLA algorithm applied to absorbing tabular MDPs.
Example 3.1.
Write and for the tabular model. Note that any matrix defines a map by . Take the function classes and . For every , denote by the -dimensional unit column vector with at its -th component, and let . For and and , the empirical error is
where
is an matrix, is the vectorized by columns and is an -vector. Therefore,
Therefore, the estimate is with the least square solution to the equation .
Remark 3.2 (A variant for known ).
If we define , then and from (5), we have that
For a given target policy , simply denote by , so that the equation above can be rewritten as
where .
With this equation, if the behavior policy is known, we can construct a corresponding estimate of the value function based on the minimax optimization problem:
For convenience, we refer to the method as MSWLA (marginalized state weight learning for absorbing MDPs) algorithm which is essentially an extension of the method discussed in Liu et al. (2018). By similar arguments in Example 3.1, in the tabular case where and the function classes and are , the empirical error function for the MSWLA algorithm is for any , where
, and for any , is the -dimensional column vector whose -th entry is and other elements are .
4 MSE bound of the estimated return
Denote by the commonly known Q-function and the unique positive solution to the equation Let us now analyze the error bound of with respect to the number of episodes and the truncation level , measured by the mean squared error (MSE) as provided in the following theorems.
The following technical assumption is necessary, which is also supposed in Uehara et al. (2020) as Assumption 2.
Assumption 4.1.
There exists a constant , such that .
Theorem 4.1.
Suppose that
-
1.
there exists a common envelop of and , i.e. , for all , , satisfying
(16) -
2.
and have finite pseudo-dimensions and , respectively;
- 3.
-
4.
;
-
5.
there exists such that .
Then we have the following:
-
1.
When , there exists a constant independent of and , such that
-
2.
When , there exists a constant independent of and , such that
Especially, if and , then
Theorem 4.2.
Suppose the assumptions in Theorem 4.1 hold and but .
-
(1)
When , there exists a constant independent of , such that
-
(2)
When , there exists a constant independent of , such that
Obviously, the additional term becomes when in the closure of under the metric .
Theorems 4.1 and 4.2 provide upper bounds for the MSE of the MWLA algorithm for a few situations. They are expressed as functions of two key parameters: the truncation level and the number of the episodes . When is small (i.e., ), the estimate errors composed of four parts: the pure truncation term , a crossing term arising from the sampling randomness, an approximation error , and an optimization error . While the first two errors stem from the randomness of the statistics, the other two result from the degree of closeness of the two function classes and to and , respectively. For a large (i.e., ), however, the pure truncation term and the mixing term can be dominated by an -free term . This indicates simply that MWLA algorithm can avoid the curse of the horizon.
In the following are more remarks on the results.
Remark 4.1.
Consider the case . For the infinite horizon MDP with i.i.d. tuples , the error bound of the MWL method consists of a statistical error and an approximation error , where is the Rademacher complexity of the function class
as given in Theorem 9 of Uehara et al. (2020). Let , be the VC-subgraph dimension (i.e. pseudo-dimension) of respectively. Because (Corollary 1 of Uehara et al., 2021), the statistical error is dominated by . For MWLA with i.i.d. episodes, the MSE bound also consists of an approximation error and a statistical error. When , the statistical error is bounded by , including an extra factor in form.
Remark 4.2.
Remark 4.3.
Remark 4.4.
With an MSE bound, a confidence interval of the error of the estimation can be derived easily by Markov’s inequality. That is, if and , then
As a result, for any given and , one can easily retrieve a sample complexity or , such that if or .
5 Connections to related work
Research on off-policy evaluation (OPE) for MDPs with infinite and fixed finite horizons can be classified into two categories according to whether the behavior policy is known.
When the behavior policy is known, IS is a commonly used method that reweights rewards obtained by behavior policies, according to its likelihood ratio of the evaluation policy over the behavior to provide unbiased estimates of the expected returns. However, the IS method suffers from exponentially increasing variance over the time horizon because the ratio is computed as a cumulative product of the importance weight over action at each time step (Precup, 2000). To reduce that extremely high variance, a series of OPE methods have been proposed based on IS. For example, the weighted importance sampling (WIS) method, the stepwise importance sampling method, and the doubly robust(DR) method can reduce the variance to certain degree (Cassel et al., 1976; Robins et al., 1994; Robins and Rotnitzky, 1995; Bang and Robins, 2005). However, the exponential variance of IS-based methods cannot be significantly improved when the MDP has high stochasticity (Jiang and Li, 2016).
The MIS method proves a promising improvement over IS by successfully avoiding the trouble of exponential variance. For example, for a finite-horizon inhomogeneous MDP, compared to weighting the whole trajectories, Xie et al. (2019) uses a ratio with to reweight the rewards in order to achieve a lower variance. In an infinite horizon setting, based on a discounted stationary distribution, Liu et al. (2018) proposes using the ratio with . The ratio is then estimated by a minimax procedure with two function approximators: one to model a weight function , and the other to model , as a discriminator class for distribution learning.
For the case of unknown behavior policies, Hanna et al. (2019) show that the IS method with an estimated behavior policy has a lower asymptotic variance than the one with a known behavior strategy. The fitted -iteration, which uses dynamic programming to fit directly from the data, can overcome the curse of dimensionality, with a cost of assuming that the function class contains and is closed under the Bellman update , so as to avoid a high bias, see Ernst et al. (2005) and Le et al. (2019). Uehara et al. (2020) propose the MWL algorithm by estimating marginalized importance weight . A Dualdice algorithm is further proposed to estimate the discounted stationary distribution ratios (Nachum et al., 2019a; Nachum et al., 2019b; Nachum and Dai, 2020) where the error function can be considered as a derivative of the error function (loss function in their terminology) in Uehara et al. (2020). Jiang and Huang (2020) combine MWL and MQL into a unified value interval with a unique type of double robustness, if either the value-function or the importance-weight class is correctly specified, the interval is valid, and its length measures the misspecification of the other class.
In reinforcement learning, while many benchmark environments are indeed episodic and have random horizons, such as board games (a game terminates once the winner is determined), trips through a maze, and dialog systems (a session terminates when the conversation is concluded) (Jiang, 2017), there are only limited efforts specifically contributed to absorbing MDPs. Researchers often take absorbing MDPs as special cases of finite-horizon MDPs, by padding all trajectories with absorbing states (with random lengths) to the same length. Another way to handle absorption practically is to use the infinite-horizon setup (with a sufficiently large discount factor), and whenever a trajectory terminates, we imagine it continuous infinitely at absorbing states. However, when the random horizons are not bounded and the random episodes are not observed completely, especially, accompanied by the undiscounted rewards, new issues will arise. For example, how do the unobserved trajectories affect the results? As our results show this problem is by no means trivial, which is essentially neglected when we simply apply the two ways mentioned above.
The current paper deals with the OPE for absorbing MDPs through the MWLA algorithm, a variant of the MWL to fit the random horizon and truncated episodic data modeled by absorbing MDPs, using episodic data rather than the -tuple data. In addition, we explicitly analyze the dependence of the error bound of the MSE on the truncation level and data size and derive the uniform bound of the MSE by optimization when the truncation level is relatively large.
6 Experiments
In this section, we present several computational experiments that showcase the performance of the MWLA and other relevant algorithms. We first describe the experimental settings and subsequently report and discuss the results.
6.1 Setting
The environment we employ is a version of Dietterich (2000)’s Taxi, a two-dimensional setup that simulates a taxi moving along a grid world, as indicated by Figure 1. The four corners are marked as R(ed), B(lue), G(reen), and Y(ellow). Initially, the taxi randomly chooses a corner to wait for a passenger, who appears or disappears with a probability at each of the four corners, and that passenger wishes to be transported to one of the four corners (also chosen randomly). The taxi must pick up the passenger and drops him off at his destination. An episode ends once a passenger is successfully dropped off at his destination.

There are a total of 2000 states (), made from 25 taxi locations, passenger appearance status, and 5 taxi status (empty or one of 4 destinations with a passenger). There are four navigation actions that move the taxi one square North, South, East, or West, respectively. Each action yields a deterministic movement. Only 3 and 2 actions can be taken when the taxi is at the boundary and the corner, respectively. The taxi receives a reward of -1 at every time step when a passenger is picked up in Taxi, 0 if the passenger is successfully dropped off at the right place and -2 at each time step if the taxi is empty.
As in Liu et al. (2018), we first run a Q-learning with a soft-max action preference with 400,000 iterations to produce the target policy and then run 60,000 iterations to produce another auxiliary policy , of which both are regularized such that the probability of crossing any boundary of the grid is . The behaviors are then formed by with . The true expected return of the target policy is approximated by a set of on-policy Monte-Carlo trajectories, truncated at to assure that the majority of the trials have stopped at the absorbing state before time step .
6.2 Results
Reported here are the experiment results for MWLA, MSWLA, an on-policy, IS, and a naive averaging baseline algorithm. The on-policy algorithm (referred to as On-Policy below) estimates the expected return by the direct average over a set of trajectories generated by the target policy itself, and the naive average baseline algorithm (referred to as Naive Average below) does it by a direct average over a different set of trajectories generated by the behavior policy, all truncated at . We also show the results of MWL applied to another set of simulated data.
The first experiment is on the MSEs of the five methods under , , , and trajectories and a set of truncation levels . A total of duplicates for every parameter combination are generated with different random seeds. The results are visualized in Figures 2 (for ) and 3 (for ), where every graph corresponds to a single episode size in the upper panels, and a single truncation level in the lower panels. The MSEs of MWLA and MSWLA all decrease at the beginning and then vary slowly when the truncation level increases. MWLA is better than MSWLA to a moderate degree, and both are significantly lower than the on-policy, IS, and naive averaging baseline algorithms.

Agend: The horizontal axis indicates the truncation levels and the vertical the logarithm
of the MSEs.

Agend: The horizontal axis indicates the number of trajectories and the vertical the MSE,
both are scaled in logarithm.

Agend: The horizontal axis indicates the truncation level and the vertical the logarithm
of the MSEs.
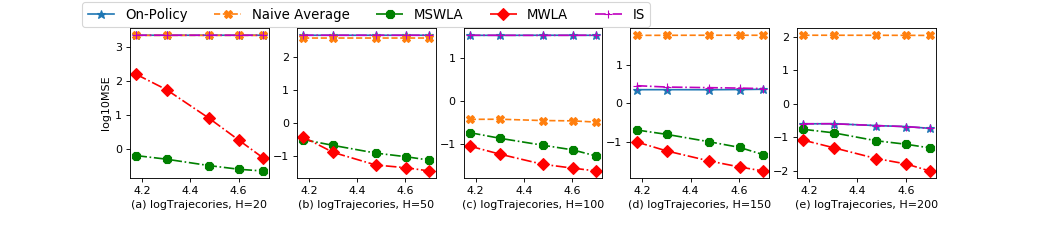
Agend: The horizontal axis indicates the number of trajectories and the vertical the MSE,
both are scaled in logarithm.
The averaged estimated returns are also provided, see Figure 4, together with twice the standard errors of the estimates , corresponding to the 95% confidence intervals, where N=100 is the number of duplicates, is the estimated return of the -th duplicate, and is the sample standard deviation of . The estimates by MSWLA and MWLA both approach the expected returns as the numbers of trajectories get large. MSWLA has slightly smaller biases than MWLA but significantly larger fluctuations, giving rise to a higher MSE, as indicated by Figures 2 and 3, even in the final graph in the bottom panel, with a quite small deviation of the averaged estimated returns from the expected return for the largest data size due to the randomness of the data.


Agend: 1. The horizontal axis indicates the number of trajectories and the vertical the MSE,
both are scaled in logarithm. 2. The blue lines represent the true expected returns.
The final experiment is to examine the performance of the MWL by Uehara et al. (2020) algorithm to estimate the expected undiscounted returns of absorbing MDPs by treating them as a special case of infinite-horizon MDPs with a subjectively designed large discount factor . The experiment is carried out under the policy mixing ratio , truncation levels and , and numbers of trajectories , , , , . We also produce duplicates for every parameter combination to empirically evaluate the MSEs. Two methods are employed to estimate the expected returns. One is the direct MWLA with trajectory data as above. The other is the MWL algorithm under large discount factors , , and , where the data consisting of all the tuples obtained by breaking the trajectories and the MSEs are computed using the errors between the estimates and the true expected (undiscounted) return. Here, we need to note that the MWL algorithm really estimates some quantity that is a function of the artificially associated discount factor and the target policy . The error between and the true value thus depends on the policy and, more importantly, the discount fact also, so that there could exist some optimal , the value of which is certainly unknown to the agent because so is the MDP model , to minimize and thus the MSE. The MSE result is empirically depicted in Figure 5, where the horizontal axis is again indicated by the logarithm of the trajectory numbers.


Agend: The horizontal axis indicates the number of trajectories and the vertical the MSE,
both are scaled in logarithm.
From the figure, we clearly have the following observations:
-
1.
The MSEs are almost constant for the number of trajectories we experimented with, quite possibly implying that, compared with the variance, bias contributes the most to an MSE.
-
2.
The MSEs of the MWL algorithm vary over different , meaning that different gives rise to different errors of the MWL algorithm to the true value (caused mainly by the bias according to the previous item).
-
3.
It appears that is optimal in our experiment. However, it is unclear how to identify an optimal theoretically, even approximately.
-
4.
MWLA significantly performs better than MWL, which we attribute to the unbiasedness of the MWLA by taking .
7 Conclusions and discussions
This paper addresses an OPE problem for absorbing MDPs. We propose the MWLA algorithm as an extension of the MWL algorithm by Uehara et al. (2020). This MWLA algorithm proceeds with episodic data subject to truncations. The expected return of a target policy is estimated and an upper bound of its MSE is derived, in which the statistical error is related to both data size and truncation level. We also briefly discuss the MSWLA algorithm for situations where behavior policies are known. The numerical experiments demonstrate that the MWLA method has a lower MSE as the number of episodes and truncation length increase, significantly improving the accuracy of policy evaluation.
Conceptually, one can estimate the corresponding state-action value function using estimated expected return, for example, by fitted-Q evaluation. The double robust (DR) estimation algorithm, which integrates learning weights and state-action value functions , is an effective and robust approach. It is now still unclear if a DR variant of the MWLA algorithm can be developed.
In statistics, confidence intervals are important to quantify the uncertainty of the point estimates. Recent work in the RL area includes Shi et al. (2021), who propose a novel deeply-debiasing procedure to construct efficient, robust, and flexible confidence intervals for the values of target policies for infinite-horizon discounted MDPs and Dai et al. (2020), who develops a CoinDICE algorithm for calculating confidence intervals. It would be interesting to combine these methods with MWLA for absorbing MDPs.
Moreover, we would like to note that policy optimization is one of the crucial goals of RL. The policy optimization based on the MWL algorithms has been analyzed by Liu et al. (2019) that proposes an off-policy policy gradient optimization technique for infinite-horizon discounted MDP by using MSWL to correct state distribution shifts for the i.i.d. tuple data structure, and Huang and Jiang (2020) that investigates the convergence of two off-policy policy gradient optimization algorithms based on state-action density ratio learning, among others. Therefore, it is important and possible to explore how the MWLA approach can be used in off-policy optimization for absorbing MDPs.
Finally, it should be noted that the state-action space considered in this paper is discrete. This choice is based on the fact that the absorbing MDPs with discrete state-action space are prevalent in real-world applications. Moreover, our theoretical analysis heavily relies on the discrete feature of the state-action space as evidenced by e.g., the proof of Lemma B.4 in Appendix. For cases involving continuous state-action spaces, it is quite common practice to employ approximations by e.g. linear or deep neural networks, so it would need additional efforts and considerations to extend the framework to continuous state-action spaces.
Acknowledgments
The authors thank the editors and referees for their helpful comments and suggestions.
\zihao5\heitiReference
- Altman (1999) Eitan Altman. Constrained Markov decision processes: stochastic modeling. Routledge, 1999.
- Bang and Robins (2005) Heejung Bang and James M Robins. Doubly robust estimation in missing data and causal inference models. Biometrics, 61(4):962–973, 2005.
- Bertsekas and Tsitsiklis (1991) Dimitri P Bertsekas and John N Tsitsiklis. An analysis of stochastic shortest path problems. Mathematics of Operations Research, 16(3):580–595, 1991.
- Borkar (1988) Vivek S Borkar. A convex analytic approach to markov decision processes. Probability Theory and Related Fields, 78(4):583–602, 1988.
- Cassel et al. (1976) Claes M Cassel, Carl E Särndal, and Jan H Wretman. Some results on generalized difference estimation and generalized regression estimation for finite populations. Biometrika, 63(3):615–620, 1976.
- Chatterjee et al. (2008) Debasish Chatterjee, Eugenio Cinquemani, Giorgos Chaloulos, and John Lygeros. Stochastic control up to a hitting time: optimality and rolling-horizon implementation. arXiv preprint arXiv:0806.3008, 2008.
- Dai et al. (2020) Bo Dai, Ofir Nachum, Yinlam Chow, Lihong Li, Csaba Szepesvári, and Dale Schuurmans. Coindice: Off-policy confidence interval estimation. Advances in neural information processing systems, 33:9398–9411, 2020.
- Derman (1970) Cyrus Derman. Finite state markovian decision processes. Technical report, 1970.
- Dietterich (2000) Thomas G Dietterich. Hierarchical reinforcement learning with the maxq value function decomposition. Journal of artificial intelligence research, 13:227–303, 2000.
- Eaton and Zadeh (1962) Jo H Eaton and LA Zadeh. Optimal pursuit strategies in discrete-state probabilistic systems. 1962.
- Ernst et al. (2005) Damien Ernst, Pierre Geurts, and Louis Wehenkel. Tree-based batch mode reinforcement learning. Journal of Machine Learning Research, 6:503–556, 2005.
- Hanna et al. (2019) Josiah Hanna, Scott Niekum, and Peter Stone. Importance sampling policy evaluation with an estimated behavior policy. In International Conference on Machine Learning, pages 2605–2613. PMLR, 2019.
- Hirano et al. (2003) Keisuke Hirano, Guido W Imbens, and Geert Ridder. Efficient estimation of average treatment effects using the estimated propensity score. Econometrica, 71(4):1161–1189, 2003.
- Huang and Jiang (2020) Jiawei Huang and Nan Jiang. On the convergence rate of density-ratio basedoff-policy policy gradient methods. In Neural Information Processing Systems Offline Reinforcement Learning Workshop, 2020.
- Iida and Mori (1996) Tetsuo Iida and Masao Mori. Markov decision processes with random horizon. Journal of the Operations Research Society of Japan, 39(4):592–603, 1996.
- Jiang (2017) Nan Jiang. A theory of model selection in reinforcement learning. PhD thesis, 2017.
- Jiang and Huang (2020) Nan Jiang and Jiawei Huang. Minimax value interval for off-policy evaluation and policy optimization. Advances in Neural Information Processing Systems, 33:2747–2758, 2020.
- Jiang and Li (2016) Nan Jiang and Lihong Li. Doubly robust off-policy value evaluation for reinforcement learning. In International Conference on Machine Learning, pages 652–661. PMLR, 2016.
- Kesten and Spitzer (1975) Harry Kesten and Frank Spitzer. Controlled markov chains. The Annals of Probability, pages 32–40, 1975.
- Kushner (1971) HJ Kushner. Introduction to stochastic control. holt, rinehart and wilson. New York, 1971.
- Le et al. (2019) Hoang Le, Cameron Voloshin, and Yisong Yue. Batch policy learning under constraints. In International Conference on Machine Learning, pages 3703–3712. PMLR, 2019.
- Li et al. (2011) Lihong Li, Wei Chu, John Langford, and Xuanhui Wang. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms. In Proceedings of the fourth ACM international conference on Web search and data mining, pages 297–306, 2011.
- Li et al. (2015) Lihong Li, Rémi Munos, and Csaba Szepesvári. Toward minimax off-policy value estimation. In Artificial Intelligence and Statistics, pages 608–616. PMLR, 2015.
- Liu et al. (2018) Qiang Liu, Lihong Li, Ziyang Tang, and Dengyong Zhou. Breaking the curse of horizon: Infinite-horizon off-policy estimation. Advances in Neural Information Processing Systems, 31, 2018.
- Liu et al. (2019) Yao Liu, Adith Swaminathan, Alekh Agarwal, and Emma Brunskill. Off-policy policy gradient with state distribution correction. arXiv preprint arXiv:1904.08473, 2019.
- Mandel et al. (2014) Travis Mandel, Yun-En Liu, Sergey Levine, Emma Brunskill, and Zoran Popovic. Offline policy evaluation across representations with applications to educational games. In AAMAS, volume 1077, 2014.
- Murphy et al. (2001) Susan A Murphy, Mark J van der Laan, James M Robins, and Conduct Problems Prevention Research Group. Marginal mean models for dynamic regimes. Journal of the American Statistical Association, 96(456):1410–1423, 2001.
- Nachum and Dai (2020) Ofir Nachum and Bo Dai. Reinforcement learning via fenchel-rockafellar duality. arXiv preprint arXiv:2001.01866, 2020.
- Nachum et al. (2019a) Ofir Nachum, Yinlam Chow, Bo Dai, and Lihong Li. Dualdice: Behavior-agnostic estimation of discounted stationary distribution corrections. Advances in Neural Information Processing Systems, 32, 2019a.
- Nachum et al. (2019b) Ofir Nachum, Bo Dai, Ilya Kostrikov, Yinlam Chow, Lihong Li, and Dale Schuurmans. Algaedice: Policy gradient from arbitrary experience. arXiv preprint arXiv:1912.02074, 2019b.
- Pollard (2012) David Pollard. Convergence of stochastic processes. Springer Science & Business Media, 2012.
- Precup (2000) Doina Precup. Eligibility traces for off-policy policy evaluation. Computer Science Department Faculty Publication Series, page 80, 2000.
- Robins and Rotnitzky (1995) James M Robins and Andrea Rotnitzky. Semiparametric efficiency in multivariate regression models with missing data. Journal of the American Statistical Association, 90(429):122–129, 1995.
- Robins et al. (1994) James M Robins, Andrea Rotnitzky, and Lue Ping Zhao. Estimation of regression coefficients when some regressors are not always observed. Journal of the American statistical Association, 89(427):846–866, 1994.
- Sen (2018) Bodhisattva Sen. A gentle introduction to empirical process theory and applications. Lecture Notes, Columbia University, 11:28–29, 2018.
- Shi et al. (2021) Chengchun Shi, Runzhe Wan, Victor Chernozhukov, and Rui Song. Deeply-debiased off-policy interval estimation. In International Conference on Machine Learning, pages 9580–9591. PMLR, 2021.
- Uehara et al. (2020) Masatoshi Uehara, Jiawei Huang, and Nan Jiang. Minimax weight and q-function learning for off-policy evaluation. In International Conference on Machine Learning, pages 9659–9668. PMLR, 2020.
- Uehara et al. (2021) Masatoshi Uehara, Masaaki Imaizumi, Nan Jiang, Nathan Kallus, Wen Sun, and Tengyang Xie. Finite sample analysis of minimax offline reinforcement learning: Completeness, fast rates and first-order efficiency. arXiv preprint arXiv:2102.02981, 2021.
- Xie et al. (2019) Tengyang Xie, Yifei Ma, and Yu-Xiang Wang. Towards optimal off-policy evaluation for reinforcement learning with marginalized importance sampling. Advances in Neural Information Processing Systems, 32, 2019.
Appendix
Appendix A Proof of Theorems in Section 3
A.1. Proof of Theorem 3.1.
It suffices to prove the uniqueness. Note that, for all ,
By the condition that is the unique solution to (10), it follows that , i.e. .
A.2. Proof of Theorem 3.2.
With any policy , associate a one-step forward operator on , defined by
| (17) |
Then, is linear over . Moreover, the state-action function with respect to
| (18) | |||||
and, by definition (9) of , the error function
| (19) |
By Theorem 3.1, we can further change the form of as
| (20) |
By the definition, is the Q-function of the reward under the policy . Therefore, Equation (18) states that
It then follows from putting the above into (20) that, for every ,
This gives the first equality of Equation (12). The second can be examined similarly by considering the function to instead .
We prove the remainder results in what follows.
(1). As a result of the first equality of part (1),
so that
provided that , The desired result (2) is thus proved.
(3). If then, substitute for in the second equality of part (1) gives ruse to
The proof is thus complete.
Appendix B Proof of Theorems in Section 4
To begin with, the following two results are quoted for easy reference later on. Denote by a set generated by a function class and a data set . Then the empirical -covering number refers to the smallest number of balls of radius required to cover , where, the distance is computed by the empirical -norm
Lemma B.1.
(Pollard, 2012) Let be a permissible class of functions and are i.i.d. samples from some distribution . Then, for any given ,
| (21) |
For a class of functions on a measurable space equiped with a probability measure , the covering numbers refers to the smallest number of balls of radius required to cover , where distances are measured in terms of the -norm for all . The covering number can then be bounded in terms of the function class’s pseudo-dimension:
Lemma B.2.
(Sen, 2018) Suppose that is a class of functions with measurable envelope (i.e. for any ) and has a finite pseudo-dimension . Then, for any , and any probability measure such that ,
where is a universal constant and .
Recall that in Theorem 4.1, we address that the functional classes and have finite pseudo-dimensions and , , and there exists a function satisfying that , for all , and . In addition, we assume that there exists such that . Besides them, we also remind here that our data consist of i.i.d samples from under the behavior policy . The proof of Theorem 4.1 proceeds in the following 3 parts: decomposition, evaluation, and optimization.
B.1. Decomposition
First decompose the estimate defined in equation (15) as
| (22) |
where
and
Because , it follows that
where is defined in (14) and we have used the fact that
Using the fact
we further have
| (23) |
where
Substituting (13) into the expression of in (14), it follows that
where is assumed. Similarly,
Define
and
where is a constant specified later in B.2. Then
| (24) | |||||
B.2. Evaluation
For any , let , where is the minimum integer no less than . Obviously, and
B.2.1. The upper bound of
An upper bound of is derived via a sequence of auxiliary results.
Lemma B.3.
With the constant , for any ,
Proof. For any and ,
Recall the notation . Due to the assumption (1) in Theorem 4.1, and are bounded by , respectively,
Therefore,
| (25) | |||||
where the equality follows from the i.i.d. property of trajectories. By further the inequality for every ,
| (26) |
and
| (27) |
substituting (26) and (27) into (25) leads to the desired result.
Lemma B.4.
There exists a constant independent of such that for ,
Proof. For a representative trajectory of the form (6), denote by
We have that
It is easy to see that . Denote by The distance in can be bounded by
Note that, in our setting,
where at the second inequality, we use the assumption (16). Let be the probability on such that . We get that
The same arguments imply that
As a result,
Note that . Due to the assumption (2) in Theorem 4.1, from Lemma B.2 we get that
Taking , we have
where By Pollard’s tail inequality (Lemma B.1),
| (28) |
For any , let . Then, by (28), we have that
which implies the desired result.
Lemma B.5.
There exists a constant independent of such that for ,
Proof. By (24),
| (29) | |||||
Note that for any ,
| (30) | |||||
where the last inequality comes from the assumption (5) in Theorem 4.1 and the setting of . Substituting (30) into (29) and applying Lemma B.3 and Lemma B.4, we get that
where . Since , it follows from (29) that
where . Let
we can readily get the desired result.
B.2.2. The upper bounds of and
Lemma B.6.
Denote by . We have that
Proof.
Define a truncated occupancy measure Then
and hence
where the last inequality follows from Hölder’s inequality. Invoking the bounds from and , we get that
where the first inequality is due to and the second inequality follows from the fact that are i.i.d and have expectation . Observing that
we obtain that
Since and , we arrive at the conclusion.
Lemma B.7.
We have that
Proof. Noting that
applying the Hölder inequality, we have that
Therefore,
Because are i.i.d and follows distribution and is independent of , it follows that
When is given, is the sum of random variables who are independent with the same distribution . Hence
Therefore
which implies the desired result, since .
B.3. Optimization
Based on the above discussion, we get that for any truncation level and such that ,
where the first inequality follows from (22) and the simple inequality , the second inequality follows from (23) and the last inequality is due to Lemma B.5-Lemma B.7. Letting
we have that, for any truncation level and ,
| (31) |
where
for . Note that
which combining the fact and implies that there exists a unique such that
which implies and hence for all ,
Moreover, is decreasing for while increasing for .
Lemma B.8.
For any , and there exists constants such that
Proof. From , we know that is a solution of
Note that is increasing on and
We have that .
To prove the second assertion, we note that
On the other hand, when ,
for . Noting that for all , we can find a constant such that
for all and . Moreover, when ,
Consequently, there exists a constant such that
Now we are at the position to finish the proof of Theorem 4.1.
Appendix C Algorithm Supplement
Algorithm 1 summarizes the pseudo-codes of our MWLA algorithm applied to the taxi environment in Section 6.
The algorithm needs the following notation:
represents absorbing state set,
The idea of the algorithm is explained in Example 3.1. Here, for the convenience of computations, we set
We also introduce a regularization factor which helps us find the unique solution of the constrained quadratic programming problem . When is sufficient small, the solution is an approximation of where is the Moore-Penrose pseudo-inverse of . In our experiments, is set to be .