MIMO-OFDM-Based Massive Connectivity With Frequency Selectivity Compensation

We use bold capital letters like $\mathbf{X}$ for matrices and bold lowercase letters $\mathbf{x}$ for vectors. $(\cdot)^{T}$ and $(\cdot)^{H}$ are used to denote the transpose and the conjugate transpose, respectively. We use ${\rm diag}(\mathbf{x})$ for the diagonal matrix created from vector $\mathbf{x}$, ${\rm diag}(\mathbf{x}_{1},...,\mathbf{x}_{N})$ for the block diagonal matrix with the $n$-th block being vector $\mathbf{x}_{n}$, and ${\rm diag}(\mathbf{X}_{1},...,\mathbf{X}_{N})$ for the block diagonal matrix with the $n$-th block being matrix $\mathbf{X}_{n}$. We use ${\rm vec}(\mathbf{X})$ for the vectorization of matrix $\mathbf{X}$ and $\otimes$ for the Kronecker product. $||\mathbf{X}||_{F}$ and $||\mathbf{x}||_{2}$ are used to denote the Frobenius norm of matrix $\mathbf{X}$ and the $l_{2}$ norm of vector $\mathbf{x}$, respectively. Matrix $\mathbf{I}$ denotes the identity matrix with an appropriate size. For a random vector $\mathbf{x}$, we denote its probability density function (pdf) by $p(\mathbf{x})$. $\delta(\cdot)$ denotes the Dirac delta function and $\delta[\cdot]$ denotes the Kronecker delta function. The pdf of a complex Gaussian random vector $\mathbf{x}\in\mathbb{C}^{N}$ with mean $\mathbf{m}$ and covariance $\mathbf{C}$ is denoted by $\mathcal{CN}(\mathbf{x};\mathbf{m},\mathbf{C})={\rm exp}(-(\mathbf{x}-\mathbf{m})^{H}\mathbf{C}^{-1}(\mathbf{x}-\mathbf{m}))/(\pi^{N}|\mathbf{C}|)$.

The remainder of this paper is organized as follows. In Section II, we introduce the existing system models. Furthermore, we propose the block-wise linear system model and demonstrate its superiority. In Section III, we formulate a Bayesian inference problem to address the ADD and CE problem. In Section IV, we propose the Turbo-MP algorithm, describe the pilot design, and analyze the algorithm complexity. In Section V, we apply the EM algorithm to learn the prior parameters. Moreover, we show how Turbo-MP is unfolded into a neural network. In Section VI, we present the numerical results. In Section VII, we conclude this paper.

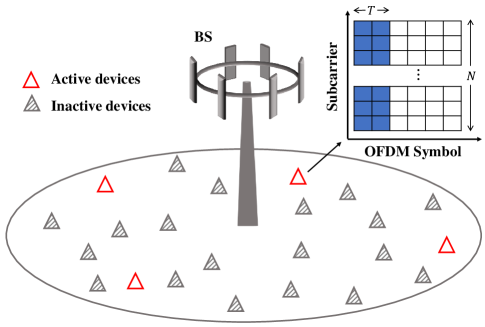
Consider a MIMO-OFDM-based grant-free NOMA system as shown in Fig. 1, where a frequency band of $N$ adjacent OFDM subcarriers are allocated for mMTC. $N$ is usually much less than the total number of available subcarriers in the considered OFDM system. This frequency allocation strategy follows the idea of narrow-band internet-of-things [24] and network slicing [25]. Then the allocated bandwidth is used to support $K$ single-antenna devices to randomly access an $M$-antenna base station (BS). In each time instance, only a small subset of devices are active. To characterize such sporadic transmission, the device activity is described by an indicator function $\alpha_{k}$ as

with $p(\alpha_{k}=1)=\lambda$ where $\lambda\ll 1$.

We adopt a multipath block-fading channel, i.e., the multipath channel response remain constant within the coherence time. Denote the channel frequency response on the $n$-th subcarrier from the $k$-th device at $m$-th BS antenna by

where $\Delta f$ is the OFDM subcarrier spacing; $L_{k}$ is the number of channel taps of the $k$-th device; $\rho_{k,l}$ and $\tau_{k,l}$¹¹1Strictly speaking, the differences of the tap delay at different BS antennas are absorbed in $\beta_{k,m,l}$ are respectively the $l$-th tap power and tap delay of the $k$-th device; $\beta_{k,m,l}\sim\mathcal{CN}(\beta_{k,m,l};0,1)$ is the normalized complex gain and assumed to be independent for any $k,m,l$ [26]. Then the channel frequency response can be expressed in a matrix form as

Let $a_{k,n}^{(t)}$ be the pilot symbol of the $k$-th device transmitted on th $n$-th subcarrier at the $t$-th OFDM symbol, and $T$ be the number of OFDM symbols for pilot transmission. Then we construct a block diagonal matrix $\mathbf{\Lambda}_{k}\in\mathbb{C}^{TN\times N}$ with the $n$-th diagonal block being $[a_{k,n}^{(1)},...,a_{k,n}^{(T)}]^{T}$, i.e.,

Assume the cyclic-prefix (CP) length $L_{cp}>\tau_{k,l},\forall k,l$. After removing the CP and applying the discrete Fourier transform (DFT), the system model in the frequency domain is described as

where $\mathbf{Y}\in\mathbb{C}^{TN\times M}$ is the observation matrix; $\mathbf{N}$ is an additive white Gaussian noise (AWGN) matrix with its elements independently drawn from $\mathcal{CN}(0,\sigma_{N}^{2})$. In [16, 17, 18], CS algorithms were proposed based on (8) to achieve the CE on every OFDM subcarrier.

Define the time-domain channel matrix of the $k$-th device as $\tilde{\mathbf{H}}_{k}\in\mathbb{C}^{N\times M}$. Note that $\tilde{\mathbf{H}}_{k}$ can be represented as the IDFT of $\mathbf{G}_{k}$, i.e,

where $\mathbf{F}\in\mathbb{C}^{N\times N}$ is the DFT matrix with the $(n_{1},n_{2})$-th element being $1/\sqrt{N}\cdot{\rm exp}(-j2\pi n_{1}n_{2}/N)$. Similarly, $\mathbf{G}_{k}$ is represented as $\mathbf{G}_{k}=\mathbf{F}\tilde{\mathbf{H}}_{k}$. Substituting $\mathbf{G}_{k}=\mathbf{F}\tilde{\mathbf{H}}_{k}$ into (8), we obtain

where $\tilde{\mathbf{H}}=[\tilde{\mathbf{H}}_{1}^{T},...,\tilde{\mathbf{H}}_{K}^{T}]^{T}$ is the channel matrix in the time domain. It is known that the channel delay spread is usually much smaller than $N$, i.e., some rows of $\tilde{\mathbf{H}}_{k}$ are zeros. Besides, due to the sporadic transmission of the devices, $\tilde{\mathbf{H}}_{k}$ is an all-zero matrix if device $k$ is inactive. In this case, CS algorithms such as Vector AMP [10, 9] and Turbo-CS [12, 20] can be used to recover $\tilde{\mathbf{H}}$ from observation $\mathbf{Y}$ by exploiting the sparsity of $\tilde{\mathbf{H}}$. However, path delay is generally not an integer multiple of the sampling interval, resulting in the energy leakage problem of the IDFT transform (9) which severely compromises the sparsity of $\tilde{\mathbf{H}}$. An illustration of the energy leakage problem is given in Fig. 2(b).

For narrow-band mMTC [1], the variations of the channel frequency response across the subcarriers are typically slow and limited, which inspires us to develop an alternative channel model to efficiently leverage the correlation in the frequency domain. In specific, we propose a block-wise linear channel model. We divide the $N$ continuous subcarriers into $Q$ sub-blocks. In each sub-block $q$, a linear function is used as the approximation of the channel frequency response:

where $h_{k,q,m}$ and $c_{k,q,m}$ represent the mean and slope of the linear function in the $q$-th sub-block, respectively; $\Delta_{k,n_{q},m}$ is the error term due to model mismatch; and $l_{q}=(q-\frac{1}{2})N/Q$ is the midpoint of $n_{q}$. Intuitively, $h_{k,q,m}$ can be seen as the mean-value of the channel response in the $q$-th sub-block, and $c_{k,q,m}$ is used to characterize the change of the channel response for the compensation of the frequency-selectivity. For the $k$-th device, we define the matrix $\mathbf{H}_{k}\in\mathbb{C}^{Q\times M}$ and $\mathbf{C}_{k}\in\mathbb{C}^{Q\times M}$ as

The reason for introducing $\alpha_{k}$ in (15)-(19) is that the channel estimation and device activity detection can be jointly achieved by recovering $\mathbf{H}_{k}$ and $\mathbf{C}_{k}$.

Define $\mathbf{E}_{1}={\rm diag}(\mathbf{1}_{N/Q},...,\mathbf{1}_{N/Q})\in\mathbb{R}^{N\times Q}$ with $\mathbf{1}_{N/Q}$ being an all-one vector of length $N/Q$ and $\mathbf{E}_{2}={\rm diag}(\mathbf{d},...,\mathbf{d})\in\mathbb{R}^{N\times Q}$ with $\mathbf{d}=[-\frac{N}{2Q}+1,...,\frac{N}{2Q}]^{T}$. Then the block-wise linear approximation of the channel frequency response $\mathbf{G}_{k}$ is given by

where $\mathbf{\Delta}_{k}\in\mathbb{C}^{N\times M}$ is the error matrix from the $k$-th device with the $(n,m)$-th element $\Delta_{k,n,m}$ in (II-B). Substituting (20) into (8) with some manipulations, we obtain the block-wise linear system model as

where $\mathbf{A}=[\mathbf{\Lambda}_{1}\mathbf{E}_{1},...,\mathbf{\Lambda}_{K}\mathbf{E}_{1}]\in\mathbb{C}^{TN\times QK}$ and $\mathbf{B}=[\mathbf{\Lambda}_{1}\mathbf{E}_{2},...,\mathbf{\Lambda}_{K}\mathbf{E}_{2}]\in\mathbb{C}^{TN\times QK}$ are the pilot matrices; $\mathbf{H}=[\mathbf{H}_{1}^{T},...,\mathbf{H}_{K}^{T}]^{T}\in\mathbb{C}^{QK\times M}$ is the channel mean matrix; $\mathbf{C}=[\mathbf{C}_{1}^{T},...,\mathbf{C}_{K}^{T}]^{T}\in\mathbb{C}^{QK\times M}$ is the channel compensation matrix; $\mathbf{W}$ is the summation of the AWGN and the error terms from model mismatch as

Following the central limit theorem, for a large devices number $K$, $\mathbf{W}$ can be modeled as an AWGN matrix with mean zero and variance $\sigma_{w}^{2}$. We note that with $Q=N$ and $\mathbf{C}=\mathbf{0}$, system model (21) reduces to the model (8) in [16, 17, 18] where the channel response on every subcarrier needs to be estimated exactly. Furthermore, we adjust the sub-block number $Q$ to strike a balance between the number of channel variables to be estimated and the model accuracy. An example is shown in Fig. 2 where the channel response in the frequency domain and its block-wise linear approximation is given in Fig. 2(a). It is seen that sub-block number $Q=4$ is sufficient to ensure that the block-wise linear model approximates the frequency-domain channel response very well. This implies that, with model (21), only $2Q$ variables need to be estimated for each device at each BS antenna. Compared to the channel response in the time domain as shown in Fig. 2(b), it is clear that the number of unknown variables $2Q$ is much less than the number of corresponding non-zero taps. In the remainder of the paper, we focus on the estimation algorithm design based on model (21). In the simulation section, we will show that our algorithm designed based on (21) significantly outperforms the existing approaches based on (8) and (II-A).

The factor graph representation of $p(\mathbf{H},\mathbf{C},\boldsymbol{\alpha}|\mathbf{Y})$ is shown in Fig. 3, based on which Turbo-MP is established. In the factor graph, the likelihood and prior as in (III) are treated as the factor nodes (grey rectangles), while the random variables are treated as the variable nodes (blank circles). In specific, Turbo-MP consists of four modules referred to as Module A, B, C, and D, respectively. Module A is to obtain the estimates of the channel mean matrix $\mathbf{H}$ and the channel compensation matrix $\mathbf{C}$ by exploiting the likelihood $\prod_{m}p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$. Modules B and C are to obtain the estimates of $\mathbf{H}$ and $\mathbf{C}$ by exploiting the priors $\prod_{k}p(\mathbf{H}_{k}|\alpha_{k})$ and $p(\mathbf{C}_{k}|\alpha_{k})$, respectively. Module D is to obtain the estimate of $\alpha_{k}$ by exploiting the prior $p(\alpha_{k})$. The estimates are passed between modules in each Turbo-MP iteration like turbo decoding [29]. For example, the output of Module B is used as the input of Module A, and vice versa. The four modules are executed iteratively until convergence. The derivation of Turbo-MP algorithm follows the sum-product rule [22] and the principle of Turbo-CS [12, 20].

In Module A, $\mathbf{h}_{m}$ and $\mathbf{c}_{m}$ at antenna $m=1,..,M$ are estimated separately by exploiting the likelihood $\prod_{m}p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$ and the messages from Modules B and C. In specific, denote the message from variable node $\mathbf{h}_{m}$ to factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$ by $\mathcal{M}_{\mathbf{h}_{m}\to\mathbf{y}_{m}}(\mathbf{h}_{m})$ and the message from variable node $\mathbf{c}_{m}$ to factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$ by $\mathcal{M}_{\mathbf{c}_{m}\to\mathbf{y}_{m}}(\mathbf{c}_{m})$. Following the principle of Turbo-CS [12, 20], we assume that the above two messages are Gaussian, i.e., $\mathcal{M}_{\mathbf{h}_{m}\to\mathbf{y}_{m}}(\mathbf{h}_{m})\sim\mathcal{CN}(\mathbf{h}_{m};\mathbf{h}_{m}^{A,pri},v_{\mathbf{h}_{m}}^{A,pri}\mathbf{I})$ and $\mathcal{M}_{\mathbf{c}_{m}\to\mathbf{y}_{m}}(\mathbf{c}_{m})\sim\mathcal{CN}(\mathbf{c}_{m};\mathbf{c}_{m}^{A,pri},v_{\mathbf{c}_{m}}^{A,pri}\mathbf{I})$. Note that the algorithm starts with $\mathbf{h}_{m}^{A,pri}=\mathbf{0}$, $\mathbf{c}_{m}^{A,pri}=\mathbf{0}$, $v_{\mathbf{h}_{m}}^{A,pri}=\lambda\vartheta_{\mathbf{H}}$, and $v_{\mathbf{c}_{m}}^{A,pri}=\lambda\vartheta_{\mathbf{C}}$. From the sum-product rule, the belief of $h_{k,q,m}$ at factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$ is

In the above, $\mathbf{y}_{m}$ is the subscript is the shorthand for factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$; $/h_{k,q,m}$ denotes the set includes all elements in $\mathbf{h}_{m}$ except $h_{k,q,m}$. Then we define the belief of $\mathbf{h}_{m}$ at factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m},\mathbf{c}_{m})$ as

Combing (IV-B) and (27), the message $\mathcal{M}_{\mathbf{y}_{m}}(\mathbf{h}_{m})$ is also Gaussian with the mean $\mathbf{h}_{m}^{A,post}$ and variance $v_{\mathbf{h}_{m}}^{A,pri}$. From [20, Eq. 11], the mean $\mathbf{h}_{m}^{A,post}$ is expressed as

where $\mathbf{\boldsymbol{\Sigma}}_{m}$ is the covariance matrix given by

To reduce the computational complexity of channel inverse ${\boldsymbol{\Sigma}}_{m}^{-1}$, we require that $\mathbf{A}$ is partial orthogonal [12], i.e., $\mathbf{A}\mathbf{A}^{H}=KP\mathbf{I}$, where $P$ is the average power of the pilot symbol. (The design of $\mathbf{A}$ to guarantee partial orthogonality is presented in IV-F.) In addition, it is easy to verify $\mathbf{B}=\mathbf{D}\mathbf{A}$ where the diagonal matrix $\mathbf{D}={\rm diag}\big{(}[\mathbf{d}^{T},...,\mathbf{d}^{T}]^{T}\otimes\mathbf{(}\mathbf{1}_{T})^{T}\big{)}\in\mathbb{R}^{TN\times TN}$ with $\mathbf{1}_{T}$ being an all-one vector of length $T$. Then the expression of $\mathbf{\boldsymbol{\Sigma}}_{m}$ is simplified to

Then the variance $v_{\mathbf{h}_{m}}^{A,post}$ is given by

where ${\Sigma}_{m,i,i}$ is the $(i,i)$-th element of ${\boldsymbol{\Sigma}}_{m}$. We note that (IV-B) and (31) also corresponds to the linear minimum mean-square error (LMMSE) estimator [28, Chap. 11] given the observation $\mathbf{y}_{m}$, the mean $\mathbf{h}_{m}^{A,pri},\mathbf{c}_{m}^{A,pri}$and the variance $v_{\mathbf{h}_{m}}^{A,pri},v_{\mathbf{c}_{m}}^{A.pri}$.

From the sum-produce rule, the extrinsic message from factor node $p(\mathbf{y}_{m}|\mathbf{h}_{m}\mathbf{c}_{m})$ to variable node $\mathbf{h}_{m}$ is calculated as

Given the Gaussian messages $\mathcal{M}(\mathbf{h}_{m})$ and $\mathcal{M}_{\mathbf{h}_{m}\to\mathbf{y}_{m}}(\mathbf{h}_{m})$, the extrinsic message is also Gaussian as

where the variance $v_{\mathbf{h}_{m}}^{A,ext}$ and the mean $\mathbf{h}_{m}^{A,ext}$ are respectively given by

The calculation to obtain the belief of $\mathbf{c}_{m}$ is similar. We have the Gaussian belief $\mathcal{M}(\mathbf{c}_{m})$ with its mean and variance respectively given by

where $D_{i,i}$ is the $(i,i)$-th element of $\mathbf{D}$. Then we obtain the extrinsic message $\mathcal{M}_{\mathbf{y}_{m}\to\mathbf{c}_{m}}(\mathbf{c}_{m})\sim\mathcal{CN}(\mathbf{c}_{m};\mathbf{c}_{m}^{A,ext},v_{\mathbf{c}_{m}}^{A,ext}\mathbf{I})$ with its mean and variance as follows:

In Module B, each $\mathbf{H}_{k},\forall k$ is estimated individually by exploiting the prior $p(\mathbf{H}_{k}|\alpha_{k})$ and the messages from Modules A and D. In specific, given the message $\mathcal{M}_{\mathbf{y}_{m}\to\mathbf{h}_{m}}(\mathbf{h}_{m})\sim\mathcal{CN}(\mathbf{h}_{m};\mathbf{h}_{m}^{A,ext},v_{\mathbf{h}_{m}}^{A,ext}\mathbf{I})$ from module A, we have

For description convenience, the factor node $p(\mathbf{H}_{k}|\alpha_{k})$ is replaced by $f_{k}^{B}$. Then the message from variable node $\mathbf{H}_{k}$ to factor node $p(\mathbf{H}_{k}|\alpha_{k})$ is expressed as

where $\mathbf{H}_{k}^{B,pri}\in\mathbb{C}^{Q\times M}$ with the $(q,m)$-th element $h_{k,q,m}^{B,pri}=h_{k,q,m}^{A,ext}$ and $\mathbf{V}^{B}={\rm diag}([v_{\mathbf{h}_{1}}^{B,pri},...,v_{\mathbf{h}_{M}}^{B,pri}]^{T}\otimes\mathbf{1}_{Q}^{T})$ with $\mathbf{1}_{Q}$ being an all-one vector of length $Q$.

Combing the Bernoulli Gaussian prior $p(\mathbf{H}_{k}|\alpha_{k})$, Gaussian message $\mathcal{M}_{\mathbf{H}_{k}\to f_{k}^{B}}(\mathbf{H}_{k})$ and Bernoulli message $\mathcal{M}_{\alpha_{k}\to f^{B}_{k}}(\alpha_{k})$ in (IV-E), the belief of $\mathbf{H}_{k}$ at factor node $f_{k}^{B}$ is Bernoulli Gaussian and expressed as

where

We note that the mean of ${\rm vec}(\mathbf{H}_{k})$ with respect to $\mathcal{M}_{f_{k}^{B}}(\mathbf{H}_{k})$ is

Define $l=(m-1)Q+q$. The variance of the $(q,m)$-th element of $\mathbf{H}_{k}$ with respect to $\mathcal{M}_{f_{k}^{B}}(\mathbf{H}_{k})$ is

Recall that the relationship between $\mathbf{H}_{k}$ and $\mathbf{h}_{m}$ is described as $[\mathbf{H}_{1}^{T},...,\mathbf{H}_{K}^{T}]^{T}=[\mathbf{h}_{1},...,\mathbf{h}_{M}]$. Through such relationship, we obtain $\mathbf{h}_{m}^{B,post}$. Following [12, 20], the variance ${v}_{\mathbf{h}_{m}}^{B,post}$ is approximated by

Then the belief of $\mathbf{h}_{m}$ at Module B is defined as

The above Gaussian belief assumption is widely used in message passing based iterative algorithms such as Turbo-CS [12], approximate message passing (AMP) [13] and expectation propagation (EP) [30]. Such treatment may loses some information but facilities the message updates. (Strictly speaking, the belief of the variable corresponds to a factor node instead of a Module. However, the belief of $\mathbf{h}_{m}$ is associated with $K$ factor nodes $p(\mathbf{H}_{k}|\alpha_{k}),\forall k$, making the expression cumbersome. For convenience, we use the definition $\mathcal{M}_{B}(\mathbf{h}_{m})$.)

From the sum-product rule, we have $\mathcal{M}_{\mathbf{h}_{m}\to B}(\mathbf{h}_{m})={\mathcal{M}_{\mathbf{y}_{m}\to\mathbf{h}_{m}}(\mathbf{h}_{m})}$. Then the extrinsic message is calculated as

Given the Gaussian messages $\mathcal{M}_{B}(\mathbf{h}_{m})$ and $\mathcal{M}_{\mathbf{h}_{m}\to B(\mathbf{h}_{m})}$, the extrinsic message is also Gaussian with its variance and mean respectively given by

where $\mathbf{h}_{m}^{B,ext}$ and ${v}_{\mathbf{h}_{m}}^{B,ext}$ are respectively used as the input mean and variance of $\mathbf{h}_{m}$ for Module A, i.e., $\mathbf{h}_{m}^{A,pri}=\mathbf{h}_{m}^{B,ext}$ and ${v}_{\mathbf{h}_{m}}^{A,pri}={v}_{\mathbf{h}_{m}}^{B,ext}$. Then we have

Similarly to the process in Module B, each $\mathbf{C}_{k},\forall k$ in module C is estimated individually by exploiting the prior $p(\mathbf{C}_{k}|\alpha_{k})$ and the messages from Modules A and D. For description convenience, $f_{k}^{C}$ is used to replace factor node $p(\mathbf{C}_{k}|\alpha_{k})$. The message from variable node $\mathbf{C}_{k}$ to factor node $p(\mathbf{C}_{k}|\alpha_{k})$ is expressed as

where $\mathbf{C}_{k}^{C,pri}\in\mathbb{C}^{Q\times M}$ with its $(q,m)$-th element $c_{k,q,m}^{C,pri}=c_{k,q,m}^{A,ext}$ and $\mathbf{V}^{C}={\rm diag}([v_{\mathbf{c}_{1}}^{C,pri},...,v_{\mathbf{c}_{M}}^{C,pri}]^{T}\otimes\mathbf{1}_{Q}^{T})$.

With the Bernoulli Gaussian prior $p(\mathbf{C}_{k}|\alpha_{k})$, Gaussian message $\mathcal{M}_{\mathbf{C}_{k}\to f_{k}^{C}}(\mathbf{C}_{k})$ and message $\mathcal{M}_{\alpha_{k}\to f^{C}_{k}}(\alpha_{k})$ in (IV-E), the belief of $\mathbf{C}_{k}$ at factor node $f_{k}^{C}$ is Bernoulli Gaussian and expressed as