Milnor Invariants
From classical links to surface-links, and beyond

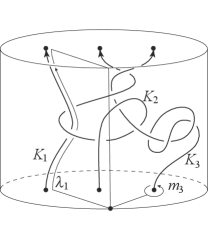
Let $n$ be a positive integer. An $n$-component link is a union of $n$ simple closed curves in 3-space. In particular, a 1-component link is called a knot. For example, in Figure 1, $K_{1}\cup K_{2}$ is a $2$-component link. A link is trivial if it bounds a disjoint union of disks. Two links are equivalent if there is a ‘continuous deformation’ (more precisely, an ambient isotopy) between them.

Let $D^{2}$ be the unit disk and $D^{1}$ the diameter on the $x$-axis with same orientation as the $x$-axis. An $n$-string link is a union of $n$ simple curves in the cylinder $D^{2}\times[0,1]$ such that the $i$th component runs from $p_{i}\times\{0\}$ to $p_{i}\times\{1\}$ for each $i=1,...,n$, where $p_{1},...,p_{n}$ are points on $D^{1}$ that are arranged in order along the orientation of $D^{1}$. For example, in Figure 2, $K_{1}\cup K_{2}\cup K_{3}$ is a $3$-string link.

Two strings links are equivalent if there is a continuous deformation between them fixing the boundary of $D^{2}\times[0,1]$. An $n$-string link is trivial if it is equivalent to the $n$-string link $\bigcup_{i=1}^{n}(p_{i}\times[0,1])$.

For an $n$-component link $L=K_{1}\cup\cdots\cup K_{n}$, let $G(L)$ be the fundamental group of the complement of $L$. As illustrated in Figure 1, for each component $K_{i}$, we choose a pair of elements $m_{i}$ and $\lambda_{i}$ in $G(L)$, that are called an $i$th meridian and an $i$th longitude respectively,¹¹1While we skip the detailed definition, in this article it is enough to know that meridians and longitudes are special elements in $G(L)$ that depend on the link. and we call the pair $(G(L),\{m_{i},\lambda_{i}\}_{i})$ a peripheral system of $L$. It is known that the peripheral systems up to certain equivalence give the classification of links [23, Theorem 6.1.7]. Hence investigating the equivalence classes of peripheral systems is nothing more than investigating the equivalence classes of links. As we will see below, Milnor invariants are invariants derived from peripheral systems.

Since $G(L)$ is non-commutative, classifying peripheral systems is as difficult as classifying links. Therefore we consider the natural projection

$$\rho_{2}:G(L)\longrightarrow N_{2}(L)=G(L)/\Gamma_{2}G(L),$$

where $\Gamma_{2}G(L)=[G(L),G(L)]$ is the commutator subgroup²²2$[X,Y]$ is the subgroup generated by the set $\{xy^{-1}x^{-1}y~{}|~{}x\in X,y\in Y\}$ of $G(L)$. We remark that $N_{2}(L)$ is a free abelian group generated by $\rho_{2}(m_{1}),...,\rho_{2}(m_{n})$. Hence each $\rho_{2}(\lambda_{k})~{}(k=1,...,n)$ can be written as

$$\rho_{2}(\lambda_{k})=\sum_{i\in\{1,...,n\}\setminus\{k\}}\mu_{L}(ik)\rho_{2}(m_{i}).$$

The integer coefficient $\mu_{L}(ik)$ of $\rho_{2}(m_{i})$ is called a (length-2) Milnor invariant of $L$.

More generally, for an integer $q\geq 2$ we consider the natural projection

$$\rho_{q}:G(L)\longrightarrow N_{q}(L)=G(L)/\Gamma_{q}G(L),$$

where for a group $G$, we define $\Gamma_{1}G=G$ and $\Gamma_{q}G=[\Gamma_{q-1}G,G]$. It is known that $N_{q}(L)$ is a nilpotent group generated by $\rho_{q}(m_{1}),...,\rho_{q}(m_{n})$, and it is called the $q$th nilpotent group of $L$ (or the $q$th nilpotent quotient of $G(L)$). Taking the Magnus expansion $E(\rho_{q}(\lambda_{k}))$, we have an integer $\mu_{L}(I)$ with respect to each sequence $I=i_{1},...,i_{s}k~{}(s<q)$ with length $s+1$. Here the Magnus expansion $E(\rho_{q}(\lambda_{k}))$ is a formal power series in non-commutative variables $X_{1},...,X_{n}$ given by

$$E(\rho_{q}(m_{i}))=1+X_{i},~{}E(\rho_{q}(m_{i}^{-1}))=1-X_{i}+X_{i}^{2}-X_{i}^{3}+\cdots\hskip 10.00002pt(i=1,2,\ldots,n).$$

We denote the integer coefficient of $X_{i_{1}}\cdots X_{i_{s}}$ in $E(\rho_{q}(\lambda_{k}))$ by $\mu_{L}(i_{1}...i_{s}k)$. And we define $\mu_{L}(k)=0$.

The Magnus expansion has the following property.

For a link $L$, the numbers $\mu_{L}(I)$ are determined by a peripheral system $(G(L),\{m_{i},\lambda_{i}\}_{i})$. But $(G(L),\{m_{i},\lambda_{i}\}_{i})$ is not uniquely determined by $L$, and $\mu_{L}(I)$ (of length at least 3) are not invariants for $L$. So, for a sequence $I$ with length at most $q$, we define

$$\Delta_{L}(I):=\gcd\left\{\mu_{L}(J)~{}\vline~{}\begin{array}[]{l}J\textrm{ is a sequence obtained from $I$ by deleting at least one}\\ \textrm{index and permuting the resulting sequence cyclicly}\end{array}\right\},$$

and take the residue class $\overline{\mu}_{L}(I)$ of $\mu_{L}(I)$ modulo $\Delta_{L}(I)$, which is an invariant for $L$ and is called a Milnor $\overline{\mu}$-invariant.³³3A length-$2$ Milnor invariant $\mu_{L}(ik)$ is equal to the linking number $\mathrm{lk}(K_{i},K_{k})$ between $K_{i}$ and $K_{k}$. Hence Milnor invariants are regarded as a generalization of linking number. V.G. Turaev [35] and R. Porter [36] characterized Milnor invariants by means of Massey product. Moreover, T. Cochran [12] gave a geometric characterization for Milnor invariants as linking numbers of intersections between Seifert surfaces for links, which are closed related to Massey product. K. Murasugi [34] showed that Milnor invariants are given by linking numbers of branched covering space. We note that if the length of $I$ is $2$, then $\Delta_{L}(I)=0$, and hence $\overline{\mu}_{L}(I)=\mu_{L}(I)$. The length of the sequence $I$ is called the length of Milnor invariant $\overline{\mu}_{L}(I)$. It seems that Milnor invariants depend on $q$, but it is known that Milnor invariants of length at most $q$ are equal to those obtained from $\rho_{q+1}$. Therefore for any sequence $I$ with length at most $q$, Milnor invariant $\overline{\mu}_{L}(I)$ is independent of $q$.

As in the case of links, we obtain the integer $\mu_{L}(I)$ for a string link $L$. In this case, the meridians and the longitudes are uniquely chosen as illustrated in Figure 2. Hence for all $I$, $\mu_{L}(I)$ are invariants for $L$, and they are called Milnor $\mu$-invariants.

Milnor invariants for string links are defined by N. Habegger and X.S. Lin [20]. Their definition is different from that in the previous section. In this section, we present the idea of the definition by Habegger and Lin.

Set $D_{\varepsilon}=D^{2}\times\{\varepsilon\}~{}(\varepsilon\in\{0,1\})$. For an $n$-string link $L\subset D^{2}\times[0,1]$, by Stallings Theorem [41, Theorem 5.1], the inclusion map

$$D_{\varepsilon}\setminus L\hookrightarrow D^{2}\times[0,1]\setminus L$$

induces the isomorphism

$$\varphi_{q}^{\varepsilon}:\pi_{1}(D_{\varepsilon}\setminus L)/\Gamma_{q}\pi_{1}(D_{\varepsilon}\setminus L)\longrightarrow N_{q}(L)$$

for each $q$. Hence we have an isomorphism

$$\varphi_{q}:=(\varphi_{q}^{1})^{-1}\circ\varphi_{q}^{0}:\pi_{1}(D_{0}\setminus L)/\Gamma_{q}\pi_{1}(D_{0}\setminus L)\longrightarrow\pi_{1}(D_{1}\setminus L)/\Gamma_{q}\pi_{1}(D_{1}\setminus L).$$

Since $\pi_{1}(D_{\varepsilon}\setminus L)(=\pi_{1}(D^{2}\setminus\{p_{1},...,p_{n}\}))$ is the free group $F$ generated by the meridians $m_{1},...,m_{n}$, we have the automorphism

$$\varphi_{q}:F/\Gamma_{q}F\longrightarrow F/\Gamma_{q}F.$$

It follows from the definition of $\varphi_{q}$ that $\varphi_{q}(\rho_{q}(m_{i}))=\rho_{q}(\lambda_{i}^{-1}m_{i}\lambda_{i})$. This means that $\varphi_{q}$ ‘contains’  the information of Milnor $\mu$-invariants for $L$. In fact, $\varphi_{q}$ can be regarded as Milnor invariants of length at most $q-1$, see Proposition 2.4.

We summarize the properties of Milnor invariants that are deeply related to the topics in this article.

1. (1)

   (J. Milnor [32], J. Stallings [41], A. J. Casson [6])  Milnor invariants are isotopy invariants for links [32], and moreover link concordance invariants [41], [6].

2. (2)

   (K. Habiro [21]) Milnor invariants with length at most $k$ are $C_{k}$-equivalence invariants, where the $C_{k}$-equivalence is an equivalence relation generated by local moves, $C_{k}$-moves, defined by Habiro [21].

3. (3)

   (J. Milnor [31], N. Habegger and X.S. Lin [20])  For any sequence $I$ consisting of non repeated indices, $\overline{\mu}(I)$ is link-homotopy invariant [31], where link-homotopy is an equivalence relation generated by changing crossings between strands of the same component. It is known that $L$ is link-homotopic to a trivial link if and only if $\overline{\mu}_{L}(I)=0$ for any non-repeated sequence $I$ [31], and that the $\mu(I)$’s classify string links up to link-homotopy [20].⁴⁴4This follows from [20, Theorem 1.7], which is not stated in terms of Milnor invariants.

A link $L$ is an object in 3-space, but it can actually be ‘drawn’  on the plane, so we may regard it as a figure on the plane. We call this figure a diagram of $L$. In general, a link diagram is a union of closed curves on the plane with finitely many crossings, where each crossing has an ‘over/under information’. Likewise, we can define a string link diagram as a union of curves on the rectangle $D^{1}\times[0,1]$ such that the $i$th component runs from $p_{i}\times\{0\}$ to $p_{i}\times\{1\}$. A crossing is locally the intersection of two orthogonal line segments, and the point with over (resp. under) information is called over crossing (resp. under crossing), where formally we assume that over and under crossings are distinct points on distinct line segments, see Figure 3.

Two (string) link diagrams are equivalent if one is deformed into the other by a combination of continuous deformations (fixing the boundary) and the three local moves R1, R2, R3 in Figure 4, called Reidemeister moves.

The following theorem shows that the classification of links is nothing more than the classification of link diagrams.

While all crossings of link diagrams have over/under informations, we extend the concept of link diagrams by considering diagrams that formally allow crossings without over/under informations as on the left side of Figure 3. A diagram containing crossings without over/under information does not correspond to any link in 3-space. It is an ‘imaginary’ link, so it is called a virtual link diagram. A crossing without over/under information is called a virtual crossing. On the other hand, a crossing with an over/under information is called a classical crossing. For convenience, we also allow the case where there are no virtual crossings in a virtual link diagram. From now on, when we emphasize that link diagrams contain only classical crossings, we call them classical link diagrams.

For virtual link diagrams, we define five local moves as follows. The first four moves in Figure 5 are called virtual Reidemeister moves (VR1,VR2,VR3,VR4), and the last move is called OC move (Overcrossings Commute).

The residue classes of the set of virtual link diagrams modulo continuous deformations, Reidemeister moves, virtual Reidemeister moves and OC moves is called welded links.⁵⁵5The residue classes modulo continuous deformations, Reidemeister moves and virtual Reidemeister moves are called virtual links. Here we never treat virtual links. We define welded string links in a similar way.

The Reidemeister moves, the virtual Reidemeister moves, and the OC move are called the welded moves. As an important property of welded links, the following theorem is known.

This theorem implies that there is a natural injection from the equivalence classes of classical links to welded links, i.e., we can say

‘classical links can be embedded in welded links.’

In this sense, as we mentioned in introduction, the relationship between ‘classical links’ and ‘welded links’  is similar to the relationship between ‘real numbers’ and ‘complex numbers’.

For an $n$-component virtual link diagram $L$, we choose $n$ points $p_{1},...,p_{n}$ on $L$ such that each $p_{i}$ is on the $i$th component of $L$ and disjoint from the crossings of $L$. The pair $(L,\mathbf{p})$ of $L$ and $\mathbf{p}=(p_{1},...,p_{n})$ is called a based virtual link diagram. Two based virtual link diagrams are equivalent if one is deformed into the other by a combination of continuous deformations, moves as illustrated in Figure 6, and welded moves that do not contain base points. The residue classes of the set of based virtual link diagrams modulo this equivalence relation is called based welded links. Based welded links are ‘between’  welded string links and welded links. In fact we have the following sequence of surjections:

$$\{\text{welded string links}\}\twoheadrightarrow\{\text{based welded links}\}\twoheadrightarrow\{\text{welded links}\}.$$

One advantage of considering based welded links is that peripheral systems can be uniquely defined (as explained in the next section). This means that, like string links, based welded links are very ‘suitable’  objects for defining Milnor invariants. In the next section, we define Milnor invariants for based welded links, and by using this definition, we define Milnor invariants for welded string links and for welded links.

A diagram of a (based/string) welded link means a representative of the welded link, i.e., a virtual link diagram. However, since it is tedious to distinguish them, the welded link (i.e. the residue class) and its diagram (i.e. a representative) are often identified. From now on we simply call based welded link diagrams based diagrams.

For a based diagram $(L,\mathbf{p})$, $L$ is divided into several segments by its base points and under-crossings. These segments are called the arcs of $L$. Let $a_{i0}$ be the outgoing arc from the base point $p_{i}$, and let $a_{i1},...,a_{i{r_{i}}}$ be the other arcs of the $i$th component of $L$ that appear after $a_{i0}$ in order, when traveling around the $i$th component from $p_{i}$ along the orientation, where $r_{i}+1$ is the number of arcs of the $i$th component ($i=1,...,n)$, see Figure 7. Note that $a_{ir_{i}}$ is the ingoing arc to $p_{i}$

The group $G(L,\mathbf{p})$ of $(L,\mathbf{p})$ is the quotient group of the free group $\widetilde{F}$ with generating set $\{a_{ij}\}_{i,j}$ modulo the following relations

$$R_{ij}=a_{i(j-1)}u_{ij}^{\varepsilon(ij)}a_{ij}^{-1}u_{ij}^{-\varepsilon(ij)}~{}~{}(1\leq i\leq n,~{}1\leq j\leq r_{i}),$$

where $u_{ij}$ denote the arc containing the over crossing between the arcs $a_{i(j-1)}$ and $a_{ij}$ as illustrated in Figure 7, and $\varepsilon(ij)\in\{-1,1\}$ is the sign of the crossing involving $a_{i(j-1)},a_{ij}$ and $u_{ij}$; in the figure, if the orientation of $u_{ij}$ is from up to down, then $\varepsilon(ij)=+1$, otherwise $\varepsilon(ij)=-1$.

For each $i$, the two elements $a_{i0}$ and

$$\lambda_{i}=a_{i0}^{-w_{i}}u_{i1}^{\varepsilon(i1)}u_{i2}^{\varepsilon(i2)}\cdots u_{ir_{i}}^{\varepsilon(ir_{i})}~{}(\text{where $w_{i}$ is the sum of signs $\varepsilon(il)$ for all $u_{il}\subset K_{i}$})$$

of $G(L,\mathbf{p})$ are called the $i$th meridian and the $i$th longitude respectively. As in the case of classical links, the pair $(G(L,\mathbf{p}),\{a_{i0},\lambda_{i}\}_{i})$ is called the peripheral system of $(L,\mathbf{p})$. We note that the peripheral system of $G(L,\mathbf{p})$ is uniquely determined from the diagram $(L,\mathbf{p})$.

We consider the natural projection

$$\rho_{q}:G(L,\mathbf{p})\longrightarrow N_{q}(L,\mathbf{p})=G(L,\mathbf{p})/\Gamma_{q}G(L,\mathbf{p}).$$

We remark that $N_{q}(L,\mathbf{p})$ is a nilpotent group generated by $\rho_{q}(a_{i0})=\alpha_{i}~{}(i=1,...,n)$, and it is called the $q$th nilpotent group of $(L,\mathbf{p})$ (or the $q$th nilpotent quotient of $G(L,\mathbf{p})$). Hence each $\rho_{q}(\lambda_{k})$ can be written as a word of $\alpha_{1},...,\alpha_{n}$. Moreover, it is known that for the free group $F$ with generating set $\{\alpha_{i}~{}|~{}(i=1,...,n)\}$, we have

$$N_{q}(L,\mathbf{p})\cong F/\Gamma_{q}F,$$

see Theorem 2.6. As in the case of string links (see the last paragraph in Section 1.2), by taking the Magnus expansion $E(\rho_{q}(\lambda_{k}))$, we have integers $\mu_{(L,\mathbf{p})}(i_{1},...,i_{s}k)~{}(s<q)$, which are invariants for the based diagram $(L,\mathbf{p})$. Since the condition $s<q$ is not essential, we have invariants for all sequences. We call them Milnor $\mu$-invariants for based welded links.

For a welded string link $S$, by identifying both ends $p_{i}\times\{0\},p_{i}\times\{1\}$ of $S$ to a point $p_{i}~{}(i=1,...,n)$, we obtain a based diagram $(L,\mathbf{p})$. Then we define $\mu_{S}(I):=\mu_{(L,\mathbf{p})}(I)$ for all sequences $I$, and call them Milnor $\mu$-invariants for the welded string link $S$. For a welded link $L$, by choosing a set $\mathbf{p}$ of base points on $L$, we have a based diagram $(L,\mathbf{p})$. And we define Milnor $\overline{\mu}$-invariants $\overline{\mu}_{L}(I)$ for the welded link $L$ for all sequences $I$ as the residue classes of $\mu_{(L,\mathbf{p})}(I)$ modulo $\Delta_{(L,\mathbf{p})}(I)$, where

$$\Delta_{(L,\mathbf{p})}(I):=\gcd\left\{\mu_{(L,\mathbf{p})}(J)~{}\vline~{}\begin{array}[]{l}J\textrm{ is a sequence obtained from $I$ by deleting at least }\\ \textrm{one index and permuting the resulting sequence cyclicly}\end{array}\right\}.$$

As the names ‘invariants’  suggest, Milnor invariants for welded string links and welded links are invariants under their equivalence relations respectively.

For each $k(=1,...,n)$, since $\rho_{q}(a_{kr_{k}})=(\rho_{q}(\lambda_{k}))^{-1}\alpha_{k}\rho_{q}(\lambda_{k})$, we have the automorphism

$$\varphi_{q}=\varphi_{q}(L,\mathbf{p}):F/\Gamma_{q}F\longrightarrow F/\Gamma_{q}F,~{}\alpha_{k}\longmapsto\rho_{q}(a_{kr_{k}}).$$

By applying the five lemma to the natural exact sequence

$$1\rightarrow\Gamma_{q-1}F/\Gamma_{q}F\hookrightarrow F/\Gamma_{q}F\twoheadrightarrow F/\Gamma_{q-1}F\rightarrow 1,$$

we can see that $\varphi_{q}(L,\mathbf{p})$ is an isomorphism. As in the case of classical string links, $\varphi_{q}(L,\mathbf{p})$ can be regarded as the Milnor invariants of $(L,\mathbf{p})$ of length at most $q-1$. In fact, by using Proposition 1.1, we have the following proposition.

A map $f$ from the set of arcs of a diagram $(L,\mathbf{p})$ to a group $X$ is called an $X$-coloring of $(L,\mathbf{p})$ if $f$ satisfies

$$f(a_{ij})=f(u_{j})^{-\varepsilon(j)}f(a_{i(j-1)})f(u_{j})^{\varepsilon(j)},$$

for each classical crossing involving $a_{i(j-1)},a_{ij}$ and $u_{j}$ (see Figure 7). Let $(L^{\prime},\mathbf{p}^{\prime})$ be a diagram obtained from $(L,\mathbf{p})$ by a single welded move. Then it is easily seen that there is an $X$-coloring of $(L^{\prime},\mathbf{p}^{\prime})$ which coincides with $f$ for the arcs not contained in the disk where the welded move is applied.

Let $\widetilde{N}$ be the normal closure of $\widetilde{F}$ that contains $\{R_{ij}\}_{i,j}$, and let $A(L,\mathbf{p})$ be the set of arcs $\{a_{ij}\}_{i,j}$ of $(L,\mathbf{p})$. Then by compositing the natural projection

$$A(L,\mathbf{p})\subset\widetilde{F}\twoheadrightarrow\widetilde{F}/\widetilde{N}=G(L,\mathbf{p})$$

and $\rho_{q}$, we have the map

$$\phi_{q}:A(L,\mathbf{p})\longrightarrow F/\Gamma_{q}F(\cong N_{q}(L,\mathbf{p})).$$

Since $\phi_{q}$ is an $(F/\Gamma_{q}F)$-coloring of $(L,\mathbf{p})$ and uniquely determined by $(L,\mathbf{p})$, $\phi_{q}(a_{kr_{k}})$ is an invariant for $(L,\mathbf{p})$. Moreover since $\varphi_{q}(\alpha_{k})=\phi_{q}(a_{kr_{k}})$, $\phi_{q}$ determines the automorphism $\varphi_{q}$ of the nilpotent group of $(L,\mathbf{p})$. By Proposition 2.4, these $(F/\Gamma_{q}F)$-colorings can also be regarded as Milnor invariants of length at most $q-1$.

Here we show how to calculate Milnor invariants of based diagrams. This is simply a rewriting of the method given by Milnor [32] for classical links into one for based diagrams.

Let $(L,\mathbf{p})$ be a based diagram. For the $i$th component $K_{i}$ illustrated in Figure 7, we put

$$v_{ij}=u_{i1}^{\varepsilon(i1)}\cdots u_{ij}^{\varepsilon(ij)}.$$

(Note that $\lambda_{i}=a_{i0}^{-w_{i}}v_{ir_{i}}$.) Let $F$ be the free group generated by $a_{i0}=\alpha_{i}~{}(i=1,...,n)$. Then, for a positive integer $q$, we define inductively a homomorphism

$$\eta_{q}=\eta_{q}(L,\mathbf{p}):\widetilde{F}\longrightarrow F(\subset\widetilde{F})$$

as follows:⁷⁷7While $\eta_{q}$ is essentially the same as defined in [32], in [32] $a_{i0}\cup a_{ir_{i}}$ is treated as a single arc.

$$(\mathrm{i})~{}\eta_{1}(a_{ij})=\alpha_{i};~{}~{}~{}(\mathrm{ii})~{}\eta_{q+1}(a_{i0})=\alpha_{i},~{}\eta_{q+1}(a_{ij})=\eta_{q}(v_{ij}^{-1})\alpha_{i}\eta_{q}(v_{ij})\hskip 10.00002pt(1\leq j\leq r_{i}).$$

The map $\eta_{q}$ is called Chen-Milnor map [10],[32]. The following lemma can be easily shown by induction on $q$.

Since $N_{q}(L,\mathbf{p})=(\widetilde{F}/\widetilde{N})/\Gamma_{q}(\widetilde{F}/\widetilde{N})\cong\widetilde{F}/\Gamma_{q}\widetilde{F}\cdot\widetilde{N}$, by the lemma above, we have the following theorem.

By Proposition 1.1 (2) and Theorem 2.6, we have the following corollary.

The $W_{k}$-concordance is an equivalence relation that combines two equivalence relations, $W_{k}$-equivalence and welded-concordance, which are explained in the next section. The $W_{k}$-equivalence can be seen as a welded version of $C_{k}$-equivalence, an equivalence relation on classical links defined by Habiro [21].

B. Colombari [13] showed the following theorem.

The content of this section is due to [29]. Our main purpose here is to introduce the definition of $W_{k}$-equivalence. Before explaining $W_{k}$-equivalence, some preparation is necessary. From now on, in order to deal with diagrams of (based) welded links and welded string links simultaneously, for convenience, we assume that they are contained in the disk.

Two $n$-component diagrams $L$ and $L^{\prime}$ are welded-concordant if one can be deformed into the other by a sequence of welded equivalence and the birth/death and saddle moves of Figure 16, such that, for each $i\in\{1,\cdots,n\}$, the number of birth/death moves is equal to the number of saddle moves, in the deformation from the $i$th component of $L$ into the $i$th component of $L^{\prime}$. In the case of based diagrams, the move of Figure 6 is also required, and each local move does not include base points.

It is shown that Milnor invariants for diagrams are welded-concordance invariants [11].

In this subsection, we give a sketch of proof of Theorem 3.1 using a special $W$-tree presentation called ascending presentation.

Let $(V,T)$ be a $W$-tree presentation of a based diagram $(L,\mathbf{p})$. Note that $V$ is also a based diagram. The $W$-tree presentation $(V,T)$ is ascending⁹⁹9This notion was first defined in [1], in the context of Gauss diagrams. if, when running around each component of $V$ from the base point along the orientation, all tails of $T$ appear before all heads of $T$. A based diagram is ascendable if it has an ascending presentation.