Mid-infrared spectrally-uncorrelated biphotons generation from doped PPLN: a theoretical investigation
Abstract
We theoretically investigate the preparation of mid-infrared (MIR) spectrally-uncorrelated biphotons from a spontaneous parametric down-conversion process using doped LN crystals, including MgO doped LN, ZnO doped LN, and In2O3 doped ZnLN with doping ratio from 0 to 7 mol%. The tilt angle of the phase-matching function and the corresponding poling period are calculated under type-II, type-I, and type-0 phase-matching conditions. We also calculate the thermal properties of the doped LN crystals and their performance in Hong-Ou-Mandel interference. It is found that the doping ratio has a substantial impact on the group-velocity-matching (GVM) wavelengths. Especially, the GVM2 wavelength of co-doped InZnLN crystal has a tunable range of 678.7 nm, which is much broader than the tunable range of less than 100 nm achieved by the conventional method of adjusting the temperature. It can be concluded that the doping ratio can be utilized as a degree of freedom to manipulate the biphoton state. The spectrally uncorrelated biphotons can be used to prepare pure single-photon source and entangled photon source, which may have promising applications for quantum-enhanced sensing, imaging, and communications at the MIR range.
I Introduction
The mid-infrared (MIR) wavelength range (approximately 2-20 m) is of great interest to a variety of scientific and technological applications in sensing, imaging, and communications Tournie and Cerutti (2019); Ebrahim-Zadeh and Sorokina (2008). Firstly, this range contains strong absorption bands of a variety of gases, leads to essential applications in gas sensing El Shamy et al. (2020) and environmental monitoring Chen et al. (2020). Secondly, the MIR region covers the atmospheric transmission window between 3 m and 5 m. This region with relatively high transparency is beneficial for atmospheric monitoring and free-space communications Bellei et al. (2016). Thirdly, room temperature objects emit light at MIR wavelengths, resulting in novel applications in infrared thermal imaging Tittl et al. (2015); Mancinelli et al. (2017). Fourthly, with the rapid development of optical fiber communications, there is a growing demand to expand the communication wavelengths into the MIR region to increase the communication bandwidth Soref (2015).
All these practical applications mentioned above are based on strong light sources in the MIR region. However, the advantages of the MIR range have not been fully exploited using quantum technology. In order to further improve the sensitivity in those applications, one promising approach is to utilize a single-photon source or entangled photon source in the MIR region. Spontaneous parametric down-conversion (SPDC) is one of the widely used methods to prepare biphotons, which can be used to produce single-photon source and entangled photon source. Previously, several theoretical and experimental works have been dedicated to the development of single or entangled photon source in MIR range from an SPDC process. In 2016, Lee et al. calculated the extended phase-matching properties of periodically poled potassium niobate (PPKN) for single-photon generation at the MIR range Lee et al. (2016). In 2017, Mancinelli et al. performed coincidence measurements on twin photons generated from periodically poled lithium niobate (PPLN) at 3.1 m Mancinelli et al. (2017). In 2018, McCracken, et al. numerically investigated the mid-infrared single-photon generation in a range of novel nonlinear materials, including PPLN, PPKTP, GaP, GaAs, CdSiP2, and ZnGeP2 McCracken et al. (2018). In 2019, Rosenfeld et al. experimentally prepared MIR photon pairs in a four-wave mixing process from a silicon-on-insulator waveguide at around 2.1 m Rosenfeld et al. . In 2020 Kundys et al. numerically studied the reconfigurable MIR single-photon sources based on functional ferroelectrics, i.e., PMN-0.38PT crystal at 5.6 m Kundys et al. (2020). In the same year, Prabhakar et al. experimentally demonstrated the entangled photons generation and Hong-Ou-Mandel interference at 2.1 m from PPLN crystals Prabhakar et al. (2020).
Many biphoton sources have been demonstrated in the previous studies Lee et al. (2016); Mancinelli et al. (2017); McCracken et al. (2018); Kundys et al. (2020); Prabhakar et al. (2020); however, from the experimental point of view, it is still lack of high-quality biphotons source at the MIR range, especially the spectrally uncorrelated biphotonsMosley et al. (2008a); Grice et al. (2001); U’Ren et al. (2006); Graffitti et al. (2018); Laudenbach et al. (2016). The biphotons generated from an SPDC process are generally spectrally correlated due to the energy and momentum conservation laws. However, it is necessary to utilize biphotons with no spectral correlations to obtain the heralded pure-state single photon for many quantum information processing (QIP) protocols, such as quantum computation Walmsley and Raymer (2005), boson sampling Broome et al. (2013), and quantum teleportation Valivarthi et al. (2016), measurement-device-independent quantum key distribution Valivarthi et al. (2017). In quantum sensing, a high-NOON state, which provides high accuracy for phase-sensitive measurements, should be prepared from spectrally uncorrelated biphotons Nagata et al. (2007); Yabuno et al. (2012). Therefore, spectrally uncorrelation of photon pairs from SPDC is indispensable for the future development of quantum information at the MIR range.
In this work, we investigate the generation of spectrally uncorrelated biphotons from PPLN crystals at MIR range. PPLN has the merits of large nonlinear coefficient and wide transparency range (0.4 m 5 m) Nikogosyan (2005); Liu et al. (2017); Yang et al. (2020); Wang et al. (2020). Another unique advantage of PPLN is that its intrinsical group-velocity-matched (GVM) wavelengths are in the MIR range, and the spectrally uncorrelated biphoton state can be engineered at the GVM wavelengths Mosley et al. (2008a); Jin et al. (2018).
In addition, we also consider the manipulation of the biphoton state by adding different dopants in PPLN. Traditionally, PPLN is doped with different dopants to improve its properties. For example, by doping Mg and Zr, the damage resistance can be improved from visible to ultraviolet region Kong et al. (2020); by doping Zn, the electro-optical coefficients can be improved Abdi et al. (1999); by doping Fe, the photorefractive properties can be improved Zhang et al. (1998). Especially, doping rare-earth elements (e.g., Tm, Er, Dy, Tb, Gd, Pr) makes PPLN a right candidate for lasers and quantum memories Palatnikov et al. (2006); Dutta et al. (2020). It is natural to deduce that doping can also be utilized as a degree of freedom to manipulate the single photons state at the MIR range. Therefore, we study the spectrally uncorrelated biphotons generation from doped PPLN in this work. Specifically, we investigated the GVM wavelengths, the tilt angle, the poling period, the thermal properties and the HOM interferences of biphtons generated from three kinds of doped LN crystals, including MgLN [MgO( mol%)LiNbO3], ZnLN [ZnO( mol%)LiNbO3], and InZnLN [In2O3( mol%)ZnO(5.5 mol%)LiNbO3, with from 0 to 7].
II Theory
The biphoton state generated from SPDC can be expressed as Mosley et al. (2008b)
| (1) |
where is the angular frequency, is the creation operator, and the subscripts and indicate the signal and idler photon. The joint spectral amplitude (JSA) can be calculated as the product of the pump envelope function (PEF) and the phase-matching function (PMF) :
| (2) |
A PEF with a Gaussian-distribution can be written as
| (3) |
where is the center angular frequency of the pump; is the bandwidth of the pump, and the subscript indicates the pump photon. The full-width at half-maximum (FWHM) is FWHMω = 2.
If we choose wavelengths as the variables, the PEF can be rewritten as
| (4) |
where is the central wavelength of the pump; The FWHM of the pump at intensity level is FWHMλ = . For , FWHM.
The PMF function can be written as
| (5) |
where is the length of the crystal, and is the wave vector. is the poling period and can be calculated by
| (6) |
The angle between the ridge direction of PMF and the horizontal axis is determined by Jin et al. (2013a)
| (7) |
where is the group velocity.
The shape of the JSA is determined by the following three GVM conditions Edamatsu et al. (2011); Jin et al. (2019).
The GVM1 condition ( 0∘):
| (8) |
The GVM2 condition ( 90∘):
| (9) |
The GVM3 condition ( 45∘):
| (10) |
The purity can be calculated by performing Schmidt decomposition on :
| (11) |
where and are the two orthogonal basis vectors in the frequency domain, and is a set of non-negative real numbers that satisfy the normalization condition . The purity p is defined as:
| (12) |
GVM wavelengths are important parameters for nonlinear crystals. The maximal purities under GVM1, GVM2, and GVM3 conditions are around 0.97, 0.97, and 0.82, respectively Edamatsu et al. (2011).
Note the three GVM conditions in Eqs.(8-10) are also called fully-asymmetric GVM or symmetric GVM conditions in Ref. Graffitti et al. (2018). In fact, the spectrally-pure state can be prepared for any angle between 0 and 90 degrees, independently from the PDC-type (type-0, type-I, or type-II) and wavelength degeneracy (degenerated or non-degenerated). Perfectly separable JSA can be achieved only with Gaussian pump and Gaussian PMF (via domain engineering techniques), as proven in Ref. Quesada and Brańczyk (2018). However, the three GVM conditions listed in Eqs.(8-10) with the degenerated wavelengths are the most widely used cases in the experiments Jin et al. (2020); Cai et al. (2020); Duan et al. (2020). Especially, the GVM3 condition has a symmetric distribution along the anti-diagonal direction, i.e., , which is the prerequisite condition for high-visibility HOM interferences. Therefore, we mainly focus on the type-II phase-matching condition in the calculation below.

III Calculation and simulation
In this section, we first calculate the angle in the range of 0 and 90 degrees, and the corresponding poling period under type-II, type-I, and type-0 phase-matching conditions. Then, we consider the thermal properties, and the HOM interferences for the doped PPLN crystals under the type-II phase-matching condition. The Sellmeier equations for these crystals are chosen from Refs. Schlarb and Betzler (1994); Schlarb et al. (1995, 1996), where the Sellmeier equations are parameterized by the dopant concentration. The PPLN crystals are negative uniaxial crystals , where is the refractive index of the ordinary (extraordinary) ray.
III.1 Angle and poling period for type-II phase-matching condition
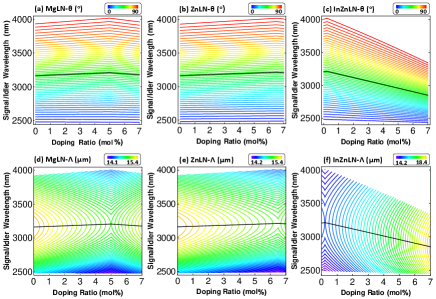
In the calculation below, we consider type-II phase-matched () SPDC in a collinear configuration with wavelength degenerated or non-degenerated (. In the type-II phase-matching condition, we set the pump and the signal as o-ray, and the idler as e-ray. Figure 1(a-c) shows the tilt angle as a function of the doping ratio ( mol %) and signal/idler (degenerated) wavelength. For MgLN in Fig. 1(a), on the line of , the GVM1 wavelength increased monotonically, i.e., from 2478.6 nm at to 2472.7 nm at . For , the GVM2 wavelength increased non-monotonically from 3931.4 nm () to the maximal value of 4016.6 nm (), and then decreased to 3961.6 nm (). For , the GVM3 wavelength also increased non-monotonically, i.e., increased from 3163.6 nm () to 3207.6 nm (), and then decreased to 3177.1 nm ().
For ZnLN in Fig. 1(b), on the line of , the GVM1 wavelength increased monotonically from 2478.6 nm at to 2485.8 nm at . On the line of , the GVM2 wavelength start from 3931.4 nm at , and reach a maximal value of 4019.3 nm at , and then decreased to 4009.0 nm at . On the line of , the GVM3 wavelength is 3163.6 nm, 3213.6 nm, and 3208.2 nm, at , 6.5, and 7, respectively.
| Crystal Name | MgLN | ZnLN | InZnLN |
|---|---|---|---|
| at 0 mol% (nm) | 2478.6 | 2478.6 | 2484.3 |
| at 7 mol% (nm) | 2472.7 | 2485.8 | 2436.9 |
| (nm) | 5.9 | -7.2 | 47.4 |
| at 0 mol% (nm) | 3931.4 | 3931.4 | 4006.0 |
| at 7 mol% (nm) | 3961.6 | 4009.0 | 3342.9 |
| Maximum of | 4016.6 | 4019.3 | 4021.6 |
| (nm) | -85.2 | -87.9 | 678.7 |
| at 0 mol% (nm) | 3163.6 | 3163.6 | 3205.9 |
| at 7 mol% (nm) | 3177.1 | 3208.2 | 2850.4 |
| Maximum of | 3207.6 | 3213.6 | 3213.9 |
| (nm) | -44.0 | -50.0 | 363.5 |
For InZnLN in Fig. 1(c), the GVM1 () wavelength decreased monotonically from 2484.3 nm at to 2436.9 nm at . The GVM2 () wavelength increased non-monotonically: start from 4006.0 nm at and reach a maximal value of 4021.6 nm at , and then decreased to 3342.9 nm at . The GVM3 () wavelength also increased non-monotonically, the wavelengths are 3205.9 nm, 3213.9 nm, and 2850.4 nm at , 0.2, and 7, respectively. Figure 1(d-f) shows the poling period for each crystal. is 14.1 m to 15.4 m for MgLN, 14.2 m to 15.4 m for ZnLN, and 14.2 m to 18.4 m for InZnLN. For comparison, we also list the wavelength of GVM1, GVM2, and GVM3 at different doping ratios in Tab. 1. It can be discovered in Tab. 1 that the co-doped crystal, InZnLN, has a large tunable wavelength range of 678.7 nm. This feature is essential for quantum state engineering at the MIR wavelength range.
Next, we consider the wavelength non-degenerated cases for a fixed doping ratio, i.e., MgO( mol%):LiNbO3, ZnO( mol%): LiNbO3, and In2O3( mol%): ZnO(5.5 mol%): LiNbO3. Figure 2(a-c) shows the angle as a function of the pump and the signal wavelengths for MgLN, ZnLN, InZnLN, with the same doping ratio of 5 mol%. On the line of (), the signal wavelength decreases (increases) monotonically with the increase of the pump wavelength. On the line of , the signal wavelength changes non-monotonically. Figure 2(d-f) shows the corresponding poling period , ranging from 5.0 m to 18.0 m for the three crystals.


III.2 Angle and poling period for type-I and type-0 phase-matching conditions
It is also possible to prepare spectrally pure states under the type I and type-0 phase-matching conditions, as long as the angle is between 0∘ and 90∘. Type-0 and type-I PDC in PPLN are routinely used in many quantum optics experiments, e.g., in biphoton states generation and frequency conversion Brecht et al. (2015); Ansari et al. (2018). Figure 3(a-c) shows the angle as a function of the pump and the signal wavelengths under type-I () phase-matching condition. The pump wavelength is in the range of 300-900 nm and the signal is in the range of 500-5000 nm. Figure 3(d-f) shows the corresponding poling period , ranging from 9.3 m to 79.0 m. For wavelengths near the degenerated case, the poling period is larger than the case of far from the degenerated condition. The of InZnLN is larger than the values of MgLN and ZnLN.
Figure 4(a-c) shows the case for type-0 () phase-matching condition. The pump wavelength is in the range of 600-1500 nm, and the signal is in the range of 700-5000 nm. The corresponding poling period is between 13.6 m to 27.7 m, as shown in Fig. 4(d-f). The three crystals have a similar performance under the type-0 phase matching-condition.


| Crystal Name | MgLN | ZnLN | InZnLN |
| at 20 (nm) | 2474.6 | 2483.7 | 2450.7 |
| 20-120 (nm) | -2.8 | -2.8 | -2.8 |
| at 20 (nm) | 4019.7 | 4002.5 | 3557.3 |
| 20-120 (nm) | 75.9 | 78.1 | 87.3 |
| at 20 (nm) | 3209.3 | 3203.8 | 2960.2 |
| 20-120 (nm) | 39.7 | 40.5 | 41.1 |
| at 20 (m) | 14.1 | 14.2 | 16.6 |
| at 20 (m) | 14.4 | 14.5 | 16.7 |
| at 20 (m) | 15.0 | 15.1 | 17.2 |
| References | Schlarb and Betzler (1994) | Schlarb et al. (1995) | Schlarb et al. (1996) |
III.3 Thermal properties
In this subsection, we investigate the thermal properties of the doped PPLN crystals. Temperature is a crucial parameter for quasi-phase-matched (QPM) crystals, since the phase-matching conditions in the QPM crystals are mainly controlled by temperature in the experiments. Using the temperature-dependent Sellmeier equations in Refs. Schlarb and Betzler (1994); Schlarb et al. (1995, 1996), we can calculate the GVM wavelength as a function of the temperature. We first consider the case of MgLN with different doping ratios, and then we compare MgLN with ZnLN and InZnLN at a fixed doping ratio. Figure 5(a) shows the case of GVM1 wavelength, which increases linearly with the increase of temperature. When the temperature increases from 20 to 120, the GVM wavelength increases by about 2.8 nm for all the doping ratio from 0 to 7 mol%. Figure 5(b) and (c) show the cases of GVM2 and GVM3 wavelengths, which decrease by about 78 nm and 40 nm respectively when the temperature increases from 20 to 120. By comparing Figs. 5(a), (b), and (c), it can be concluded that the GVM2 wavelength is the most sensitive one to the temperature increase, i.e., decreases by about 78 nm. In contrast, GVM1 is not so sensitive, i.e., only increase by 2.8 nm.
Next, we consider the thermal properties of other doped LN crystals. We compare the case of Mg(5 mol%)LN, Zn(5 mol%)LN, and In(5 mol%)Zn(5.5 mol%)LN in Fig. 6 and Tab. 2. The most apparent feature in Fig. 6 and Tab. 2 is that the signal/idler wavelength changes linearly. The wavelength difference between 20 and 120 , , is almost the same for three different crystals, i.e., , , and are about 2.8 nm, 78 nm, and 40 nm, respectively. This phenomenon implies that the thermal-related GVM wavelength is not dominated by the doped elements, but by the main component, LiNbO3. The calculated the poling period of the three crystals at 20 are in the range of 14-15 m, which can be realized with the current technology. Note that the thermal expansion of the LN crystals are not considered in the calculation, since such data are not available in the references.
III.4 Hong-Ou-Mandel interference


In this subsection, we consider the possible future applications of the spectrally-uncorrelated biphotons in Hong-Ou-Mandel interference Hong et al. (1987); Brańczyk (2017), which is the foundation for many QIP applications such as quantum computation Walmsley and Raymer (2005), boson sampling Broome et al. (2013), and quantum teleportation Valivarthi et al. (2016). Figure 7 shows the JSA of the biphotons generated from 5 mol% MgO doped PPLN under GVM1, GVM2, and GVM3 conditions. The spectral ranges for Figs. 7(a-c) are 60 nm, 130 nm, and 40 nm, respectively. The dimension of each JSA matrix is 200200. Note the photon bandwidths shown in Fig. 7 are just examples. In fact, the bandwidth is strongly dependent on the pulse duration and the crystal length, and the same photon purity can be achieved at different combinations of pump pulse and crystal length. The biphotons under GVM1 and GVM2 conditions (see Fig. 7(a, b)) can be used for HOM interference between two independent sources, with a typical experimental setup shown in Refs. Mosley et al. (2008a); Jin et al. (2013b). In the experiment, two signals and are sent to a beamsplitter for interference and then detected by two single-photon detectors, while two idlers and are directly sent to single-photon detectors for heralding the signals. The four-fold coincidence probability as a function of the delay time can be described by Ou (2007); Mosley et al. (2008a); Jin et al. (2015)
| (13) |
where and are the JSAs from the first and the second crystals. Figure 8(a, b) are the simulated HOM interference curves between two heralded signals or two heralded idlers from two independent MgLN sources, with the JSA shown in Fig. 7(a). Without using any narrow bandpass filters, visibility can achieve 96.8%. It can be deduced from Eq.( 13) that the visibility, in this case, is determined by the purity (JSA separability) of the heralded signal photons Mosley et al. (2008a). The bandwidth of the HOM dip depends on the photon bandwidth, which is determined by the crystal length and the pulse duration. If we change the crystal length to be 50 mm, the corresponding HOM dips are 0.64 ps for two signals, and 8.4 ps for two idlers.
The biphotons under the GVM3 condition (see Fig. 7(c)) can be used for HOM interference between the signal and the idler photons from the same SPDC source, with a typical setup shown in Hong et al. (1987); Prabhakar et al. (2020). In the experiment, the signal and the idler are sent to a beamsplitter for interference and then detected by two single-photon detectors. The two-fold coincidence probability as a function of is given by Grice (1997); Ou (2007); Jin et al. (2015):
| (14) |
The green curve in Fig. 8(c) is the simulated HOM interference pattern between a signal and an idler from the same Mg(5 mol%)LN crystal at 24.5∘C, with the JSA shown in Fig. 8(c). Under this condition, the visibility is as high as 100%. By fixing the poling period and changing the doping ratio to 4.90 mol%, 4.95 mol%, 5.05 mol%, and 5.10 mol%, the interference patterns oscillate, as shown in Fig. 8(c). By changing the temperature to 22.5∘C, 23.5∘C, 25.5∘C and 26.5∘C, the interference patterns also oscillate, as shown in Fig. 8(d).
IV Discussions
We notice that LN crystal has several different growing methods, and each method has a different effect on the Sellmeier equations. The MgLN, ZnLN, and InZnLN crystals investigated in the Calculation and Simulation section were grown using the Czochralski technique from a congruent melt (mole ratio Li/Nb 0.942) Schlarb and Betzler (1994); Schlarb et al. (1995, 1996). As shown in Fig. 1, 0 mol% Zn doped LN (i.e., pure LN) has the GVM1, GVM2, GVM3 wavelengths of 2478.6 nm, 3931.4 nm , and 3163.6 nm, respectively. In contrast, the pure LN grown from the stoichiometric melt (mole ratio Li/Nb 1) Hobden and Warner (1966) has the GVM1, GVM2, GVM3 wavelengths of 2681.0 nm, 4653.6 nm, and 3595.8 nm, respectively. Further, using the Sellmeier equations from Ref. Zelmon et al. (1997), the pure LN grown from the congruent melt (mole ratio Li/Nb 0.937) has the GVM1, GVM2, GVM3 wavelengths of 2678.5 nm, 4361.7 nm, and 3499.1 nm, respectively. These differences are mainly caused by different growing methods. In addition, the LN crystal can also be doped with other elements, which also affect the Sellmeier equations. For example, NdMgLN crystal (grown by the Czochralski technique from a congruent melt in Ref. Kitaeva et al. (1998) has the GVM1, GVM2, GVM3 wavelengths of 2615.3 nm, 4562.5 nm, and 3511.5 nm, respectively. We also investigated ErMgLN and MgTiLN crystal Zhang et al. (2009); Yongmao et al. (1992). However, they do not satisfy the three kinds of GVM conditions. In this calculation, the maximal doping ratio we considered is 7 mol%. In fact, this ratio can still be improved, and we anticipate the wavelength tunability can be further improved at a larger doping ratio.
In this work, limited by the available Sellmeier equations, we only investigate the LN crystals doped with Mg, Zn, In, and Nd. In the future, it is promising to explore more LN crystals doped with different chemical elements and with different doping ratios. Another promising direction is investigating the spectrally pure single-photon state generation from doped PPLN waveguide Cheng et al. (2019); Sun et al. (2019); Niu et al. (2020) or doped PPLN film Ge et al. (2018), which has the merits of higher nonlinear efficiency, easier for integration and microminiaturization. In Fig. 7, the purities are 0.968, 0.963, and 0.826, respectively, and this purity can be further improved to near 1 using the custom poling technique Brańczyk et al. (2011); Cui et al. (2019).
In the section of Calculation and Simulation, we only show the configuration of in the type-II phase-matching condition. In fact, we also investigate the configuration of . Although the GVM2 wavelength under this configuration is in the telecom wavelength, the effective nonlinear coefficient, unfortunately, is zero. The reason is analyzed in detail in the Appendix.
For future applications, spectrally uncorrelated biphotons can be used to prepare pure single-photons and entangled photons which can be applied for sensing, imaging, and communication with a quantum-enhanced performance at MIR region. As shown in the section of Calculation and simulation, all the poling periods of the doped PPLN crystals are above 5 m, which can be easily fabricated using the off-the-shelf technology. So, the MIR-band single-photon source calculated in the work is ready for fundamental research and industry applications, so as to promote the second quantum revolution.
V Conclusion
In conclusion, we have theoretically studied the preparation of spectrally uncorrelated biphotons at MIR wavelengths from doped LN crystals, including MgO doped LN, ZnO doped LN, and In2O3 doped ZnLN with doping ratio from 0 to 7 mol%. The tilt angle, poling period, thermal properties, and HOM interference of the biphotons are calculated under type-II, type-I, and type-0 phase-matching conditions. For 5 mol% MgO doped LN, the three GVM wavelengths are 2474.7 nm, 4016.6 nm, and 3207.6 nm, and the corresponding purities are 0.968, 0.963, and 0.826, respectively. In the calculation of the thermal properties, we found that thermal-related GVM wavelength is not dominated by the doped elements, but by LiNbO3. When the temperature was increased from 20 to 120 , the three GVM wavelengths are increased by about 2.8 nm, -78 nm, and -40 nm, respectively. In the simulation of HOM interference using the 5 mol% MgO doped PPLN, visibility of 96.8% was achieved in a HOM interference between two independent sources, and visibility of 100% was achieved in a HOM interference between the signal and idler from the same SPDC source. The interference patterns oscillate by changing the doping ratio or temperature. The spectrally uncorrelated biphotons can be used to prepare pure single-photon source and entangled photon source at MIR wavelengths.
Acknowledgments
This work is partially supported by the National Key RD Program of China (Grant No. 2018YFA0307400), the National Natural Science Foundations of China (Grant Nos. 91836102, 11704290, 12074299, 61775025, 61405030), and the Program of State Key Laboratory of Quantum Optics and Quantum Optics Devices (No: KF201813). We thank Profs. Zhi-Yuan Zhou, Yan-Xiao Gong, and Ping Xu for helpful discussions.
Appendix : The effective nonlinear coefficient
The effective nonlinear coefficient for collinear phase-matching in uniaxial crystals can be deduced as follow Smith (2016).
For phase-matching condition,
| (15) |
For phase-matching condition,
| (16) |
where , , , , and is the walk-off angle. is the polar angle, is the azimuth angle, and Z is the optical axis, as defined in Fig. 9(a). For PPLN under or phase-matching conditions, , , and , as shown in Fig. 9(b, c). Therefore,
| (17) |
and
| (18) |
The second-order nonlinear coefficient matrix for LN is Smith :
| (19) |
So,
| (20) |
and
| (21) |
Therefore, the configuration of does not exist for PPLN.

References
- Tournie and Cerutti (2019) Eric Tournie and Laurent Cerutti, eds., Mid-infrared optoelectronics materials, devices, and applications (Woodhead Publishing, 2019).
- Ebrahim-Zadeh and Sorokina (2008) Majid Ebrahim-Zadeh and Irina T. Sorokina, eds., Mid-Infrared Coherent Sources and Applications (Springer Science & Business Media, 2008).
- El Shamy et al. (2020) Raghi S. El Shamy, Diaa Khalil, and Mohamed A. Swillam, “Mid infrared optical gas sensor using plasmonic Mach-Zehnder interferometer,” Sci. Rep. 10, 1–9 (2020).
- Chen et al. (2020) Ke Chen, Shuai Liu, Bo Zhang, Zhenfeng Gong, Yewei Chen, Ming Zhang, Hong Deng, Min Guo, Fengxiang Ma, and Feng Zhu, “Highly sensitive photoacoustic multi-gas analyzer combined with mid-infrared broadband source and near-infrared laser,” Opt. Lasers Eng. 124, 105844 (2020).
- Bellei et al. (2016) Francesco Bellei, Alyssa P. Cartwright, Adam N. McCaughan, Andrew E. Dane, Faraz Najafi, Qingyuan Zhao, and Karl K. Berggren, “Free-space-coupled superconducting nanowire single-photon detectors for infrared optical communications,” Opt. Express 24, 3248–3257 (2016).
- Tittl et al. (2015) Andreas Tittl, Ann-Katrin U Michel, Martin Schäferling, Xinghui Yin, Behrad Gholipour, Long Cui, Matthias Wuttig, Thomas Taubner, Frank Neubrech, and Harald Giessen, “A switchable mid-infrared plasmonic perfect absorber with multispectral thermal imaging capability,” Adv. Mater. 27, 4597–4603 (2015).
- Mancinelli et al. (2017) M. Mancinelli, A. Trenti, S. Piccione, G. Fontana, J. S. Dam, P. Tidemand-Lichtenberg, C. Pedersen, and L. Pavesi, “Mid-infrared coincidence measurements on twin photons at room temperature,” Nat. Commun. 8, 15184 (2017).
- Soref (2015) Richard Soref, “Enabling 2 m communications,” Nat. Photon. 9, 358–359 (2015).
- Lee et al. (2016) Kwang Jo Lee, Sunmi Lee, and Heedeuk Shin, “Extended phase-matching properties of periodically poled potassium niobate crystals for mid-infrared polarization-entangled photon-pair generation,” Appl. Opt. 55, 9791–9796 (2016).
- McCracken et al. (2018) Richard A. McCracken, Francesco Graffitti, and Alessandro Fedrizzi, “Numerical investigation of mid-infrared single-photon generation,” J. Opt. Soc. Am. B 35, C38–C48 (2018).
- (11) Lawrence M. Rosenfeld, Dominic A. Sulway, Gary F. Sinclair, Vikas Anant, Mark G. Thompson, John G. Rarity, and Joshua W. Silverstone, “Mid-infrared quantum optics in silicon,” arXiv: 1906.10158 .
- Kundys et al. (2020) Dmytro Kundys, Francesco Graffitti, Richard A. McCracken, Alessandro Fedrizzi, and Bohdan Kundys, “Numerical study of reconfigurable Mid-IR single photon sources based on functional ferroelectrics,” Adv. Quantum Technol. , 1900092 (2020).
- Prabhakar et al. (2020) Shashi Prabhakar, Taylor Shields, Adetunmise C. Dada, Mehdi Ebrahim, Gregor G. Taylor, Dmitry Morozov, Kleanthis Erotokritou, Shigehito Miki, Masahiro Yabuno, Hirotaka Terai, Corin Gawith, Michael Kues, Lucia Caspani, Robert H. Hadfield, and Matteo Clerici, “Two-photon quantum interference and entanglement at 2.1 m,” Sci. Adv. 6, eaay5195 (2020).
- Mosley et al. (2008a) Peter J. Mosley, Jeff S. Lundeen, Brian J. Smith, Piotr Wasylczyk, Alfred B. U’Ren, Christine Silberhorn, and Ian A. Walmsley, “Heralded generation of ultrafast single photons in pure quantum states,” Phys. Rev. Lett. 100, 133601 (2008a).
- Grice et al. (2001) W. P. Grice, A. B. U’Ren, and I. A. Walmsley, “Eliminating frequency and space-time correlations in multiphoton states,” Phys. Rev. A 64, 063815 (2001).
- U’Ren et al. (2006) Alfred B. U’Ren, Christine Silberhorn, Reinhard Erdmann, Konrad Banaszek, Warren P. Grice, Ian A. Walmsley, and Michael G. Raymer, “Generation of pure-state single-photon wavepackets by conditional preparation based on spontaneous parametric downconversion,” arXiv: quant-ph/0611019 (2006).
- Graffitti et al. (2018) Francesco Graffitti, Jeremy Kelly-Massicotte, Alessandro Fedrizzi, and Agata M. Branczyk, “Design considerations for high-purity heralded single-photon sources,” Phys. Rev. A 98, 053811 (2018).
- Laudenbach et al. (2016) Fabian Laudenbach, Hannes Hubel, Michael Hentschel, Philip Walther, and Andreas Poppe, “Modelling parametric down-conversion yielding spectrally pure photon pairs,” Opt. Express 24, 2712–2727 (2016).
- Walmsley and Raymer (2005) Ian A. Walmsley and Michael G. Raymer, “Toward quantum-information processing with photons,” Science 307, 1733 (2005).
- Broome et al. (2013) Matthew A. Broome, Alessandro Fedrizzi, Saleh Rahimi-Keshari, Justin Dove, Scott Aaronson, Timothy C. Ralph, and Andrew G. White, “Photonic boson sampling in a tunable circuit,” Science 339, 794 (2013).
- Valivarthi et al. (2016) Raju Valivarthi, Marcel.li Grimau Puigibert, Qiang Zhou, Gabriel H. Aguilar, Varun B. Verma, Francesco Marsili, Matthew D. Shaw, Sae Woo Nam, Daniel Oblak, and Wolfgang Tittel, “Quantum teleportation across a metropolitan fibre network,” Nat. Photon. 10, 676 (2016).
- Valivarthi et al. (2017) Raju Valivarthi, Qiang Zhou, Caleb John, Francesco Marsili, Varun B Verma, Matthew D Shaw, Sae Woo Nam, Daniel Oblak, and Wolfgang Tittel, “A cost-effective measurement-device-independent quantum key distribution system for quantum networks,” Quantum Sci. Technol. 2, 04LT01 (2017).
- Nagata et al. (2007) Tomohisa Nagata, Ryo Okamoto, Jeremy L. O’Brien, Keiji Sasaki, and Shigeki Takeuchi, “Beating the standard quantum limit with four-entangled photons,” Science 316, 726–729 (2007).
- Yabuno et al. (2012) Masahiro Yabuno, Ryosuke Shimizu, Yasuyoshi Mitsumori, Hideo Kosaka, and Keiichi Edamatsu, “Four-photon quantum interferometry at a telecom wavelength,” Phys. Rev. A 86, 010302 (2012).
- Nikogosyan (2005) David N Nikogosyan, Nonlinear optical crystals: a complete survey (Springer Science & Business Media, 2005).
- Liu et al. (2017) Shi-Long Liu, Shi-Kai Liu, Yin-Hai Li, Shuai Shi, Zhi-Yuan Zhou, and Bao-Sen Shi, “Coherent frequency bridge between visible and telecommunications band for vortex light,” Opt. Express 25, 24290–24298 (2017).
- Yang et al. (2020) Chen Yang, Shi-Long Liu, Zhi-Yuan Zhou, Yan Li, Yin-Hai Li, Shi-Kai Liu, Zhao-Huai Xu, Guang-Can Guo, and Bao-Sen Shi, “Extra-cavity-enhanced difference-frequency generation at 1.63 m,” J. Opt. Soc. Am. B 37, 1367–1371 (2020).
- Wang et al. (2020) TianXin Wang, PengCheng Chen, Chuan Xu, Yong Zhang, DunZhao Wei, XiaoPeng Hu, Gang Zhao, Min Xiao, and ShiNing Zhu, “Periodically poled LiNbO3 crystals from 1D and 2D to 3D,” Sci. China Technol. Sci. , s11431–019–1503–0 (2020).
- Jin et al. (2018) Rui-Bo Jin, Takuma Saito, and Ryosuke Shimizu, “Time-frequency duality of biphotons for quantum optical synthesis,” Phys. Rev. Applied 10, 034011 (2018).
- Kong et al. (2020) Yongfa Kong, Fang Bo, Weiwei Wang, Dahuai Zheng, Hongde Liu, Guoquan Zhang, Romano Rupp, and Jingjun Xu, “Recent progress in lithium niobate: Optical damage, defect simulation, and on-chip devices,” Adv. Mater. 32, 1806452 (2020).
- Abdi et al. (1999) F. Abdi, M. Aillerie, M. Fontana, P. Bourson, T. Volk, B. Maximov, S. Sulyanov, N. Rubinina, and M. Wohlecke, “Influence of Zn doping on electrooptical properties and structure parameters of lithium niobate crystals,” Appl. Phys. B 68, 795–799 (1999).
- Zhang et al. (1998) Guoquan Zhang, Guangyin Zhang, Simin Liu, Jingjun Xu, Qian Sun, and Xinzheng Zhang, “The threshold effect of incident light intensity for the photorefractive light-induced scattering in LiNbO3:Fe,M (M=Mg2+, Zn2+, In3+) crystals,” J. Appl. Phys. 83, 4392–4396 (1998).
- Palatnikov et al. (2006) M.N. Palatnikov, I.V. Biryukova, N.V. Sidorov, A.V. Denisov, V.T. Kalinnikov, P.G.R. Smith, and V.Ya. Shur, “Growth and concentration dependencies of rare-earth doped lithium niobate single crystals,” J. Cryst. Growth 291, 390–397 (2006).
- Dutta et al. (2020) Subhojit Dutta, Elizabeth A. Goldschmidt, Sabyasachi Barik, Uday Saha, and Edo Waks, “Integrated photonic platform for rare-earth ions in thin film lithium niobate,” Nano Lett. 20, 741–747 (2020).
- Mosley et al. (2008b) P J Mosley, J S Lundeen, B J Smith, and I A Walmsley, “Conditional preparation of single photons using parametric downconversion: a recipe for purity,” New J. Phys. 10, 093011 (2008b).
- Jin et al. (2013a) Rui-Bo Jin, Ryosuke Shimizu, Kentaro Wakui, Hugo Benichi, and Masahide Sasaki, “Widely tunable single photon source with high purity at telecom wavelength,” Opt. Express 21, 10659–10666 (2013a).
- Edamatsu et al. (2011) Keiichi Edamatsu, Ryosuke Shimizu, Wakana Ueno, Rui-Bo Jin, Fumihiro Kaneda, Masahiro Yabuno, Hirofumi Suzuki, Shigehiro Nagano, Atsushi Syouji, and Koji Suizu, “Photon pair sources with controlled frequency correlation,” Prog. Inform. 8, 19–26 (2011).
- Jin et al. (2019) Rui-Bo Jin, Neng Cai, Ying Huang, Xiang-Ying Hao, Shun Wang, Fang Li, Hai-Zhi Song, Qiang Zhou, and Ryosuke Shimizu, “Theoretical investigation of a spectrally pure-state generation from isomorphs of KDP crystal at near-infrared and telecom wavelengths,” Phys. Rev. Appl. 11, 034067 (2019).
- Quesada and Brańczyk (2018) Nicolas Quesada and Agata M. Brańczyk, “Gaussian functions are optimal for waveguided nonlinear-quantum-optical processes,” Phys. Rev. A 98, 043813 (2018).
- Jin et al. (2020) Rui-Bo Jin, Wu-Hao Cai, Chunling Ding, Feng Mei, Guang-Wei Deng, Ryosuke Shimizu, and Qiang Zhou, “Spectrally uncorrelated biphotons generated from ”the family of BBO crystal”,” Quantum Engineering 2, e38 (2020).
- Cai et al. (2020) Wu-Hao Cai, Bei Wei, Shun Wang, and Rui-Bo Jin, “Counter-propagating spectrally uncorrelated biphotons at 1550 nm generated from periodically poled TiOO4 (=K, Rb, Cs; =P, As),” J. Opt. Soc. Am. B 37, 3048–3054 (2020).
- Duan et al. (2020) Jia-Chen Duan, Ji-Ning Zhang, Yin-Jun Zhu, Chang-Wei Sun, Yi-Chen Liu, Ping Xu, Zhenda Xie, Yan-Xiao Gong, and Shi-Ning Zhu, “Generation of narrowband counterpropagating polarization-entangled photon pairs based on thin-film lithium niobate on insulator,” J. Opt. Soc. Am. B 37, 2139–2145 (2020).
- Schlarb and Betzler (1994) U. Schlarb and K. Betzler, “Influence of the defect structure on the refractive indices of undoped and Mg-doped lithium niobate,” Phys. Rev. B 50, 751–757 (1994).
- Schlarb et al. (1995) U. Schlarb, M. W hlecke, B. Gather, A. Reichert, K. Betzler, T. Volk, and N. Rubinina, “Refractive indices of Zn-doped lithium niobate,” Opt. Mater. 4, 791–795 (1995).
- Schlarb et al. (1996) U. Schlarb, B. Matzas, A. Reichert, K. Betzler, M. W hlecke, B. Gather, and T. Volk, “Refractive indices of Zn/In-co-doped lithium niobate,” Ferroelectrics 185, 269–272 (1996).
- Brecht et al. (2015) B. Brecht, Dileep V. Reddy, C. Silberhorn, and M. G. Raymer, “Photon temporal modes: A complete framework for quantum information science,” Phys. Rev. X 5, 041017 (2015).
- Ansari et al. (2018) Vahid Ansari, John M. Donohue, Benjamin Brecht, and Christine Silberhorn, “Tailoring nonlinear processes for quantum optics with pulsed temporal-mode encodings,” Optica 5, 534–550 (2018).
- Hong et al. (1987) C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between two photons by interference,” Phys. Rev. Lett. 59, 2044–2046 (1987).
- Brańczyk (2017) Agata M. Brańczyk, “Hong-Ou-Mandel Interference,” arXiv: 1711.00080 (2017).
- Jin et al. (2013b) Rui-Bo Jin, Kentaro Wakui, Ryosuke Shimizu, Hugo Benichi, Shigehito Miki, Taro Yamashita, Hirotaka Terai, Zhen Wang, Mikio Fujiwara, and Masahide Sasaki, “Nonclassical interference between independent intrinsically pure single photons at telecommunication wavelength,” Phys. Rev. A 87, 063801 (2013b).
- Ou (2007) Zhe-Yu Jeff Ou, Multi-photon quantum interference (Springer, 2007).
- Jin et al. (2015) Rui-Bo Jin, Thomas Gerrits, Mikio Fujiwara, Ryota Wakabayashi, Taro Yamashita, Shigehito Miki, Hirotaka Terai, Ryosuke Shimizu, Masahiro Takeoka, and Masahide Sasaki, “Spectrally resolved Hong-Ou-Mandel interference between independent photon sources,” Opt. Express 23, 28836–28848 (2015).
- Grice (1997) I. A. Grice, W. P. & Walmsley, “Spectral information and distinguishability in type-ii down-conversion with a broadband pump,” Phys. Rev. A 56, 1627–1634 (1997).
- Hobden and Warner (1966) M. V. Hobden and J. Warner, “The temperature dependence of the refractive indices of pure lithium niobate,” Phys. Lett 22, 243–244 (1966).
- Zelmon et al. (1997) David E. Zelmon, David L. Small, and Dieter Jundt, “Infrared corrected Sellmeier coefficients for congruently grown lithium niobate and 5 mol.% magnesium oxide-doped lithium niobate,” J. Opt. Soc. Am. B 14, 3319–3322 (1997).
- Kitaeva et al. (1998) G. K. Kitaeva, I.I. Naumova, A.A. Mikhailovsky, P.S. Losevsky, and A.N. Penin, “Visible and infrared dispersion of the refractive indices in periodically poled and single domain Nd:Mg:LiNbO3 crystals,” Appl. Phys. B 66, 201–205 (1998).
- Zhang et al. (2009) De-Long Zhang, Qing-Zhong Yang, Ping-Rang Hua, Hong-Li Liu, Yu-Ming Cui, Liang Sun, Yu-Heng Xu, and Edwin Yue-Bun Pun, “Sellmeier equation for doubly Er/Mg-doped congruent LiNbO3 crystals,” J. Opt. Soc. Am. B 26, 620–626 (2009).
- Yongmao et al. (1992) Chang Yongmao, Wen Jinke, Wang Huafu, and Li Bing, “Refractive index measurement and second harmonic generation in a series of LiNbO3: Mg (5 mol%) crystals,” Chin. Phys. Lett. 9, 427 (1992).
- Cheng et al. (2019) Xiang Cheng, Murat Can Sarihan, Kai-Chi Chang, Yoo Seung Lee, Fabian Laudenbach, Han Ye, Zhongyuan Yu, and Chee Wei Wong, “Design of spontaneous parametric down-conversion in integrated hybrid SixNy-PPLN waveguides,” Opt. Express 27, 30773–30787 (2019).
- Sun et al. (2019) Chang-Wei Sun, Su-Heng Wu, Jia-Chen Duan, Jian-Wei Zhou, Jun-Lei Xia, Ping Xu, Zhenda Xie, Yan-Xiao Gong, and Shi-Ning Zhu, “Compact polarization-entangled photon-pair source based on a dual-periodically-poled Ti:LiNbO3 waveguide,” Opt. Lett. 44, 5598–5601 (2019).
- Niu et al. (2020) Yunfei Niu, Chen Lin, Xiaoyue Liu, Yan Chen, Xiaopeng Hu, Yong Zhang, Xinlun Cai, Yan-Xiao Gong, Zhenda Xie, and Shining Zhu, “Optimizing the efficiency of a periodically poled LNOI waveguide using in situ monitoring of the ferroelectric domains,” Appl. Phys. Lett. 116, 101104 (2020).
- Ge et al. (2018) Licheng Ge, Yuping Chen, Haowei Jiang, Guangzhen Li, Bing Zhu, Yi’an Liu, and Xianfeng Chen, “Broadband quasi-phase matching in a MgO:PPLN thin film,” Photon. Res. 6, 954–958 (2018).
- Brańczyk et al. (2011) Agata M. Brańczyk, Alessandro Fedrizzi, Thomas M. Stace, Tim C. Ralph, and Andrew G. White, “Engineered optical nonlinearity for quantum light sources,” Opt. Express 19, 55–65 (2011).
- Cui et al. (2019) Chaohan Cui, Reeshad Arian, Saikat Guha, N. Peyghambarian, Quntao Zhuang, and Zheshen Zhang, “Wave-function engineering for spectrally uncorrelated biphotons in the telecommunication band based on a machine-learning framework,” Phys. Rev. Appl. 12, 034059 (2019).
- Smith (2016) Arlee Smith, Crystal nonlinear optics with SNLO examples (AS-Photonics, 2016).
- (66) A. Smith, “Snlo,” http://www.as-photonics.com/snlo.