Microscopic theory of magnetoresistance in ferromagnetic materials

Introduction–Magnetoresistance (MR), one of the most fundamental but enigmatic phenomena of condensed matter physics since discovered in 1856 by Kelvin [1], is highly significant and technologically crucial for modern microelectronics industry [2]. Fascinating effects include anisotropic [3, 4, 5, 6, 7, 8], Hanle [9, 10], giant [11, 12], and tunnel MR [13, 14, 15] that give valuable insights into the magnetic properties of various materials and offer tremendous potential for applications in spintronics technology [16]. The origin of this century-old effect is known as the spin-exchange coupling (SEC) between local moments and itinerant electrons in magnetic materials [17, 18, 19, 20, 21, 22, 23, 24, 25], while microscopic mechanisms have not been fully understood due to its intrinsic complexity as a many-body and open-quantum problem.

The conventional microscopic theories of MR in ferromagnets primarily focused on the plasma frequency and momentum relaxation time of itinerant electrons [26]. For example, the anisotropic MR, i.e., the change of resistance with the orientation of the magnetization relative to the electric current direction [27, 28, 29, 30, 31, 32, 33, 34], originates from i) the anisotropic plasma frequency due to the interplay of magnetization and spin-orbit coupling (SOC) [35, 36, 37, 38] and ii) anisotropic momentum relaxation time arising from either the magnetization-dependent scattering rate of itinerant electrons [27, 28, 29, 30, 31, 32] or the magnon population of the local moments [20, 21, 22, 23] (i.e., magnon MR [39, 40]). Additionally, the Hanle spin precession of the spin accumulation results in Hanle MR [9, 10]. Even these theories have established the foundations for understanding Hanle MR and anisotropic MR, they can not quantitatively, or even qualitatively ¹¹1For example, the previous theory of Hanle MR excludes temperature- and magnetic field-dependent spin-exchange field (2), thus incapable of adequately including temperature and magnetic field dependencies of MR in ferromagnetic materials. The previous theory of anisotropic MR is mainly based on purely phenomenological formula, that is, $\Delta\rho_{0}$ and $\Delta\rho_{1}$ in Eq. (7) are phenomenological parameters independent of temperature and magnetic field., analyze the diverse MR effects observed in experiments especially involving complicated dependencies on the strength of the magnetic field ($\boldsymbol{B}$) and temperature ($T$) [3, 4, 5, 6, 42, 43, 40, 44, 45, 46]. Here, we unveil that previous theories have overlooked a crucial aspect - the strong $B$ and $T$ dependencies of the itinerant electrons’ spin precession and relaxation [47, 48, 49] which are ubiquitous in magnetic materials and thus must play a crucial role in MR.

In this Letter, we develop a comprehensive microscopic theory of ferromagnetic materials, based on the theory of open-quantum system, that explicitly accounts for the $B$ and $T$ dependencies of the spin precession and relaxation processes. By solving the anisotropic spin diffusion equation, we derive a universal cosine-square formula of MR that elucidates the microscopic mechanisms of the various MR effects from the magnon-induced spin flip, anisotropic spin relaxation, and Hanle spin precession of itinerant electrons. Furthermore, our analysis unveils intriguing behaviors of MR that allow electrical detection of the strength of microscopic SEC.

Model and theory–The MR effect, at its core, deals with the interplay between local moments and itinerant electrons. We consider a ferromagnetic material described by the total Hamiltonian $H=H_{e}+H_{m}+V_{em}$. The itinerant electrons’ Hamiltonian is given by $H_{e}=p_{n}^{2}/2m+\hbar\omega_{B}{\bf m}\cdot\boldsymbol{\mathbf{\sigma}}_{n}-(\hbar/4m^{2}c^{2})\boldsymbol{\sigma}_{n}\cdot[\boldsymbol{p}_{n}\times\boldsymbol{\nabla}V_{\text{so}}(\boldsymbol{r}_{n})]$ with $\omega_{B}=\textsl{g}\mu_{B}B/\hbar$ and $\mathbf{m}=\boldsymbol{B}/B$, where $\textsl{g}\simeq 2$ is the $g$-factor, $\mu_{B}$ is the Bohr magneton, $\hbar$ is the reduced Planck constant, $\boldsymbol{\sigma}_{n}=(\sigma_{n}^{x},\sigma_{n}^{y},\sigma_{n}^{z})$ is the vector of Pauli matrices representing the $n$th itinerant electron with position $\boldsymbol{r}_{n}$ and momentum $\boldsymbol{p}_{n}$, and $V_{\text{so}}(\boldsymbol{r}_{n})$ includes both intrinsic and extrinsic spin–orbit potential [50]. Hereafter, repeated indices are summed over. We also include a term describing the coupling of the local moments between themselves and the external magnetic field $H_{m}=\textsl{g}\mu_{B}\mathbf{S}_{j}\cdot\boldsymbol{B}-J_{ij}\mathbf{S}_{i}\cdot\mathbf{S}_{j}$, where $J_{ij}>0$ is the coupling constant of the Heisenberg ferromagnet. Finally, $V_{em}$ describes the effect of the local moments with scattering potential [17, 18, 19, 20, 21, 22, 23, 24, 25]

$$V_{em}=-\mathcal{J}_{sd}\boldsymbol{\sigma}_{n}\cdot\mathbf{S}_{j}\delta(\boldsymbol{r}_{n}-\boldsymbol{R_{j}}),$$

(1)

where $\mathbf{S}_{j}$ is the spin of the $j$th local moment with position $\boldsymbol{R_{j}}$ and positive (negative) $\mathcal{J}_{sd}$ corresponds to ferromagnetic (antiferromagnetic) SEC.

There exist two effects caused by the SEC (1). First, the SEC shifts the Hanle spin precession frequency $\omega_{L}=\omega_{B}-\textsl{g}\mu_{B}\mathcal{B}_{sd}$ by spin-exchange field

$$\mathcal{B}_{sd}=n_{\mathrm{S}}\mathcal{J}_{sd}\langle S_{\|}\rangle/(\hbar\textsl{g}\mu_{B}),$$

(2)

where $n_{\mathrm{S}}$ is the density of local moments and $S_{\|}$ is the spin component in the direction of the magnetization, which is assumed to be collinear to $\boldsymbol{B}$. Second, SEC causes anisotropic spin relaxation [47]. The longitudinal (transverse) spin relaxation times $\tau_{\|}$ ($\tau_{\bot}$) can be expressed by the spin expectation value $\langle S_{\parallel}\rangle$ and spin-spin correlation function $\langle S^{2}_{\|}\rangle$ of local moments (see derivations and approximations, established on the theory of open-quantum system [51], in Supplementary Materials (SM) [52])

$\displaystyle\frac{1}{\tau_{\|}}$

$\displaystyle=\frac{1}{\tau_{0}}+\frac{\pi}{\hbar}n_{\text{S}}\nu_{F}\mathcal{J}^{2}_{sd}\beta\epsilon_{L}n_{B}(\epsilon_{L})[S(S+1)-\langle S^{2}_{\|}\rangle-\langle S_{\|}\rangle],$

(3)

$\displaystyle\frac{1}{\tau_{\perp}}$

$\displaystyle=\frac{1}{2\tau_{0}}+\frac{1}{2\tau_{\|}}+\frac{\pi}{\hbar}n_{\text{S}}\nu_{F}\mathcal{J}^{2}_{sd}\langle S^{2}_{\|}\rangle.$

(4)

Here, $\nu_{F}$ is the density of state for each spin at Fermi energy, which is assumed to be the same for spin-up and spin-down species. The spin-relaxation time $\tau_{0}$ arises from such as intrinsic or extrinsic SOC, and the spin-flip from static disorders, which are assumed to be isotropic and independent of $B$ and $T$. The second term of Eq. (3) describes the spin-flip rate associated with magnon emission and absorption, while the third term of Eq. (4) represents the spin dephasing rate arising from scattering processes during which the electron spin, being in a superposition of spin-up and spin-down, acquires a precession phase about the $\boldsymbol{m}$-direction. $n_{B}(\epsilon_{L})=1/(e^{\beta\epsilon_{L}}-1)$ is the Bose-Einstein distribution function at temperature $\beta=1/(k_{B}T)$ and Weiss Larmor frequency $\epsilon_{L}=\hbar\omega_{B}-\langle S_{\|}\rangle\sum_{i}J_{ij}$, where $k_{B}$ is the Boltzmann constant. The spin-spin correlation function can be expressed by $\langle S^{2}_{\parallel}\rangle=S(S+1)+\coth(\beta\epsilon_{L}/2)\left\langle S_{\parallel}\right\rangle$ [47].

To qualitatively discuss the spin-exchange field (2) and spin relaxation time (3) and (4), we consider two regimes. i) $\beta\epsilon_{L}\gg 1$, i.e., the strongly magnetized regime with large $B$ and low $T$, the spins of local moments are fixed and the flip of itinerant electrons’ spins is prohibited. Thus, the spin-exchange field (2) is strongest, i.e., $\mathcal{B}_{sd}=-n_{\mathrm{S}}\mathcal{J}_{sd}S/(\hbar\textsl{g}\mu_{B})$, while the spin relaxation time (3) and (4) becomes anisotropic, i.e., $\tau^{-1}_{\|}=\tau^{-1}_{0}$ and $\tau^{-1}_{\perp}=\tau^{-1}_{0}+\Omega_{0}$ with $\Omega_{0}=\frac{\pi}{\hbar}n_{\text{S}}\nu_{F}(\mathcal{J}_{sd}S)^{2}$, as a result of the vanishing spin-flip rate and the maximum spin dephasing rate. ii) In the opposite limit ($\beta\epsilon_{L}\ll 1$) with small $B$ and high $T$, where the microscopic ferromagnetic order is destroyed, the spin-exchange field (2) vanishes because $\langle S_{\|}\rangle=0$, while the spin relaxation time (3) and (4) become isotropic, i.e., $\tau^{-1}_{\|}=\tau^{-1}_{\perp}=\tau^{-1}_{0}+\Omega_{1}$, where $\Omega_{1}=\frac{2\pi}{3\hbar}\nu_{F}n_{\text{S}}\mathcal{J}^{2}_{sd}S(S+1)$. Consequently, the spin relaxation time and spin-exchange field induced by the SEC strongly rely on $B$ and $T$, and below we will see they are crucial for the $B$- and $T$-dependent MR.

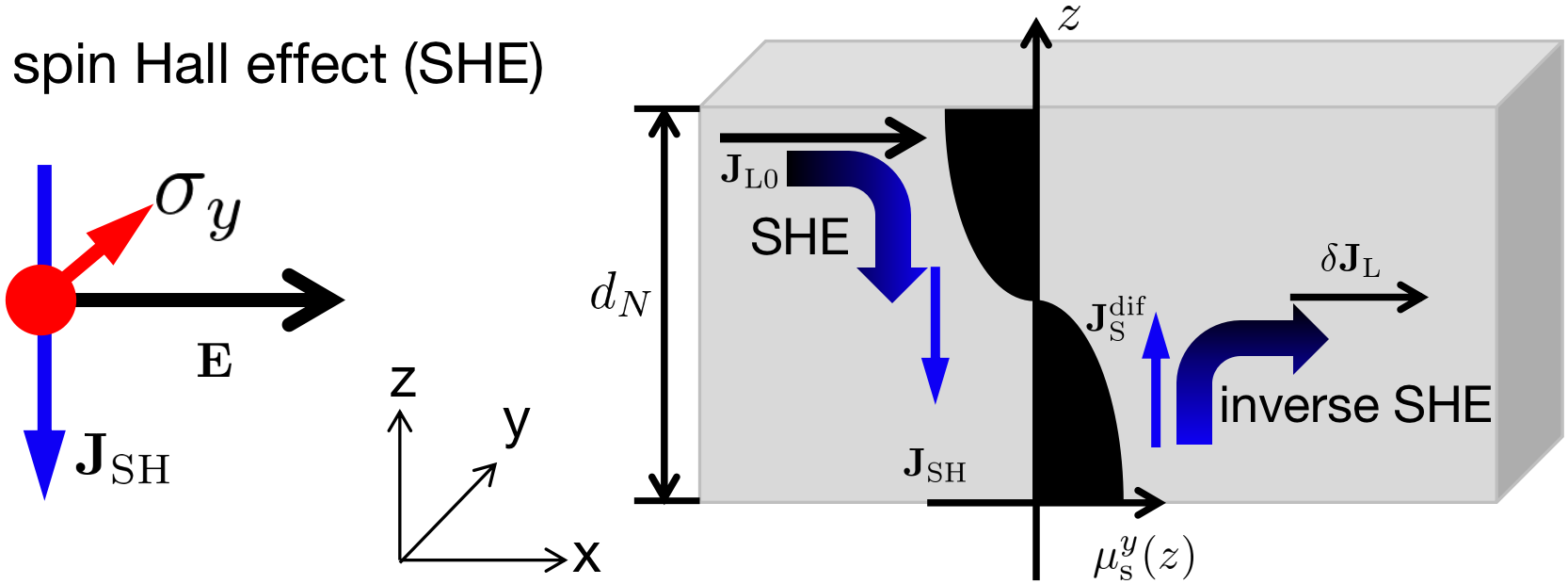
Besides the SEC (1), another dominant ingredient of MR is the SOC [27]. The MR stems from the combination of the spin Hall effect (SHE) and its inverse effect that arise from the SOC [53, 54], as depicted in Fig. 1. In the first step charge current $\boldsymbol{J}_{\text{L0}}=\sigma_{\text{D}}\boldsymbol{E}$ is converted to a drift spin current $\boldsymbol{J}_{\text{SH}}=\theta_{\text{SH}}(\hat{y}\times\boldsymbol{J}_{\text{L0}})$ via the SHE, as shown by the left-curved arrow, Here, $\theta_{\text{SH}}$ represents the charge-spin conversion ratio of the SHE, $\sigma_{\text{D}}$ is the Drude conductivity, and $\boldsymbol{E}$ is an electric field in $x$-axis direction. The drift spin current polarized in $y$-axis direction and flowing in $z$-axis direction leads to considerable spin accumulation $\mu_{\mathrm{s}}^{y}(z)$ that accounts for the diffusive spin current, $J^{\text{dif}}_{\text{S}}=-\frac{\sigma_{\text{D}}}{2e}\partial_{z}\mu_{\mathrm{s}}^{y}(z)$. The boundary conditions require that the total spin current is continuous at the top ($z=d_{N}$) and bottom ($z=0$) interfaces [55, 10]

$\displaystyle\left.J_{\mathrm{s}}^{a}\right|_{z=0,d_{N}}=-\frac{\sigma_{\text{D}}}{2e}\left.\partial_{z}\mu_{\mathrm{s}}^{a}\right|_{z=0,d_{N}}+\delta_{ay}\theta_{\mathrm{SH}}\sigma_{\text{D}}E=0,$

(5)

with $a=\{x,y,z\}$ where $d_{N}$ is the thickness of the ferromagnetic material. In the second step, the diffusive spin current is converted back to charge current by the inverse SHE (right-curved arrow in Fig. 1). We study a ferromagnetic material that is assumed to be homogeneous in the $\hat{x}-\hat{y}$ plane. The resulted spin accumulation $\mu_{s}^{a}$ depends only on $z$ and satisfies the diffusion equation with anisotropic spin relaxation time (see SM [52])

$$\partial_{z}^{2}\mu_{\mathrm{s}}^{a}=\ell_{\mathrm{\bot}}^{-2}\delta_{ab}\mu_{\mathrm{s}}^{b}+\left(\ell_{\mathrm{\parallel}}^{-2}-\ell_{\mathrm{\bot}}^{-2}\right)m_{a}m_{b}\mu_{\mathrm{s}}^{b}-\ell_{\mathrm{L}}^{-2}\epsilon_{abc}m_{c}\mu_{\mathrm{s}}^{c},$$

(6)

where $a,b,c=\{x,y,z\}$. The Hanle spin precession length is given by $\ell_{\mathrm{L}}=\sqrt{\mathcal{D}/\omega_{L}}$, while the longitudinal and transverse spin diffusion lengths are expressed as $\ell_{\mathrm{\bot}}=\sqrt{\mathcal{D}\tau_{\mathrm{\bot}}}$ and $\ell_{\mathrm{\parallel}}=\sqrt{\mathcal{D}\tau_{\mathrm{\parallel}}}$, respectively, where $\mathcal{D}$ is diffusion coefficient. Overall, both SEC and SOC are crucial for the MR and participate in diffusion equation (6) and boundary condition (5), respectively.

Provided by boundary conditions (5), the diffusion equation (6) can be analytically solved and we obtain the widespread phenomenological formula of the longitudinal resistivity (see derivations in SM [52])

$$\rho_{\mathrm{L}}\simeq\rho_{\mathrm{L0}}+2\theta_{\mathrm{SH}}^{2}-\theta_{\mathrm{SH}}^{2}\Delta\rho_{0}+\theta_{\mathrm{SH}}^{2}\Delta\rho_{1}\left(1-\hat{m}_{y}^{2}\right),$$

(7)

with

$$\frac{\Delta\rho_{0}}{\rho_{\mathrm{L0}}}=\frac{2\ell_{\|}}{d_{N}}\tanh\left(\frac{d_{N}}{2\ell_{\|}}\right),$$

(8)

$$\frac{\Delta\rho_{1}}{\rho_{\mathrm{L0}}}=\frac{2\ell_{\|}}{d_{N}}\tanh\left(\frac{d_{N}}{2\ell_{\|}}\right)-\mathrm{Re}\left[\frac{2\Lambda}{d_{N}}\tanh\left(\frac{d_{N}}{2\Lambda}\right)\right],$$

(9)

where $\rho_{\mathrm{L0}}=1/\sigma_{\text{D}}$ and $\Lambda^{-2}=\ell_{\mathrm{\bot}}^{-2}+i\ell_{\mathrm{L}}^{-2}$. Equations (7-9), as the central result, not only microscopically explain the universal cosine-square law of anisotropic MR with the magnetization direction ($\hat{m}_{y}\equiv\sin\alpha$) but also quantitatively describe $B$- and $T$-dependent MR. Importantly, both $T$ and $B$ dependencies of $\Delta\rho_{0}$ and $\Delta\rho_{1}$, i.e., Eqs. (8) and (9), are reflected in Hanle spin precession length $\ell_{\mathrm{L}}$, spin diffusion lengths $\ell_{\mathrm{\bot}}$ and $\ell_{\mathrm{\parallel}}$ through the spin-exchange field (2), spin relaxation time (3) and (4), respectively. The dependence of resistance on $T$ arises from $\langle S_{\|}\rangle$ and $\langle S_{\|}^{2}\rangle$, while that of $B$ has an extra channel - the magnetic-field spin precession frequency $\omega_{B}(\propto B)$.

Then we investigate the microscopic mechanisms of various MR effects using our formulas (7-9). Note that the SEC in magnetic materials is ubiquitous and profoundly affects the MR effects. At $\mathcal{J}_{sd}=0$, the spin diffusion lengths become isotropic (i.e., $\ell_{\|,\perp}=\ell_{0}=\sqrt{\mathcal{D}\tau_{0}}$) and we recover the previous theory of spin precession MR (i.e., Hanle MR [10]) where $\Delta\rho_{1}\propto B^{2}$ for small $B$. Next, we focus on the case of $\mathcal{J}_{sd}\neq 0$. i) The SEC shifts the Hanle spin precession frequency $\omega_{L}=g\mu_{B}(B-\mathcal{B}_{sd})$, introduces a finite value of $\Delta\rho_{1}\propto(B-\mathcal{B}_{sd})^{2}$ even when the anisotropic spin relaxation is artificially removed by setting $\ell_{\|}=\ell_{\perp}$, and contributes to a shifted spin precession MR. Thus, our theory, different from the previous spin precession MR independent of $T$, effectively includes $T$ and $B$ dependencies of MR through the spin-exchange field (2). ii) The SEC causes anisotropic spin diffusion lengths ($\ell_{\|}\neq\ell_{\perp}$), produces a finite value of $\Delta\rho_{1}=\frac{2\ell_{\|}}{d_{N}}\tanh\left(\frac{d_{N}}{2\ell_{\|}}\right)-\frac{2\ell_{\perp}}{d_{N}}\tanh\left(\frac{d_{N}}{2\ell_{\perp}}\right)$ when artificially setting $\omega_{L}=0$, and accounts for anisotropic spin relaxation MR. Thus, our microscopic theory, exceeding the previous phenomenological theory of anisotropic MR, adequately captures the $T$ and $B$ dependencies of $\Delta\rho_{1}$ through the spin relaxation time (3) and (4). iii) The $B$ modulation of $\Delta\rho_{0}$, i.e., Eq. (8), depends only on the longitudinal spin relaxation time (3) originating entirely from spin-flip processes and this MR is unambiguously associated with magnon emission and absorption, thus referring to isotropic magnon MR. Overall, we demonstrate the isotropic magnon, anisotropic spin relaxation and spin precession MR originating from the magnon-induced spin flip, anisotropic spin relaxation, and Hanle spin precession of itinerant electrons, respectively.

To quantitatively analyze the $B$- and $T$-dependent MR effect in ferromagnetic materials, our theory is numerically explored by considering a typical example - the Pt film decorated with magnetic permalloy (Py). Here, the SOC in Pt is characterized by a spin Hall angle $\theta_{\mathrm{SH}}\simeq 0.1$ [56] and spin diffusion length $\ell_{0}=3.0n$m comparable to the thickness of Pt film, $d_{N}=5$ nm. The local moments (Py) have spin $S=2$ and density $n_{\mathrm{S}}a^{3}_{\text{Pt}}=0.1$ where $a_{\text{Pt}}$ is the lattice constant of Pt and $n_{\mathrm{S}}$ should be high enough to generate ferromagnetic order of local moments. Moreover, our SEC $n_{\text{S}}\mathcal{J}_{sd}$ is set to be the order of meV ²²2The SEC between Co adatoms on Cu(100) has been predicted to realize a ferromagnetic interaction of about $n_{\text{S}}\mathcal{J}_{sd}\simeq 350$ meV and an antiferromagnetic one about $n_{\text{S}}\mathcal{J}_{sd}\simeq-17$ meV [60, 58], which have been validated by probing the Kondo resonance in experiments of P. Wahl $et.al$ [58]. Though there is no experimental data of spin-exchange coupling in Pt film decorated with Py, we believe $n_{\text{S}}\mathcal{J}_{sd}\sim$ meV should be an experimentally feasible parameter.. Below, we discuss isotropic magnon, anisotropic spin precession and spin relaxation MR together with diverse MR behaviors according to our universal formulas (7-9).

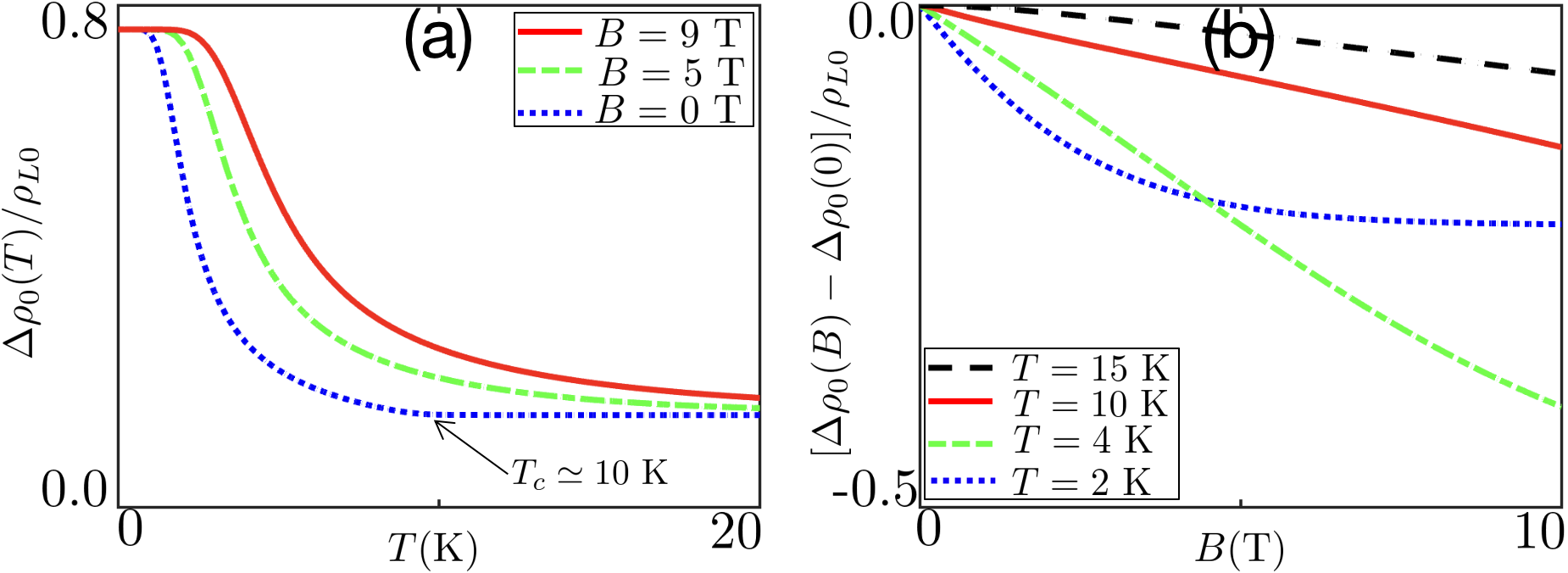
Magnon MR-Our magnon MR, independent of the magnetization direction, is quantified by $\Delta\rho_{0}$, i.e., Eq. (8). With increasing $\ell_{\|}/d_{N}$, $\Delta\rho_{0}$ initially exhibits a linear increase following the expression $\Delta\rho_{0}=2\ell_{\|}/d_{N}$, and gradually approaches a saturation value of 1, in accordance with the asymptotic formula $\Delta\rho_{0}=1-d^{2}_{N}/(12\ell^{2}_{\|})$ in the end. Figures 2(a) and 2(b) plot the $T$ and $B$ dependencies of $\Delta\rho_{0}$, respectively. Note that $\ell_{\|}$ varies from $\sqrt{\mathcal{D}/(\tau^{-1}_{0}+\Omega_{1})}$ to $\ell_{0}$ when cooling $T>T_{c}$ to $T\ll T_{c}$ at $B=0$ [blue curve in Fig. 2(a)], where $T_{c}$ is the critical temperature of the ferromagnetic material. We obtain considerable modulation of magnon MR with $T$, i.e., $|\Delta\rho_{0}(T)-\Delta\rho_{0}(0)|\sim\rho_{\text{L0}}$ [Fig. 2(a)]. To increase the $B$ tunability of $\Delta\rho_{0}$ via the longitudinal spin relaxation time (3), we consider small critical temperature ($T_{c}=10$ K) and large SEC ($n_{\text{S}}\mathcal{J}_{sd}=8$ meV). The latter leads to a large value of $\Omega_{1}$ and a small value of $\sqrt{\mathcal{D}/(\tau^{-1}_{0}+\Omega_{1})}/d_{N}\simeq 0.07$. Then, we obtain sizable $B$ modulation of magnon MR, i.e., $[\Delta\rho_{0}(B)-\Delta\rho_{0}(0)]\sim\rho_{\text{L0}}$, which always shows negative MR [Fig. 2(b)] because increasing $B$ prevents the magnon-induced spin flip and increases $\ell_{\|}$. The predicted characteristics are consistent with magnon MR experiments [40] that, however, depends on the orientation of the magnetization relative to the magnetic field [23, 22].

Anisotropic MR-Anisotropic spin relaxation MR ($\ell_{\|}\neq\ell_{\perp}$) always appears together with the shifted spin precession MR ($\mathcal{B}_{sd}\neq 0$) even when $B\rightarrow 0$, and thus cannot always be easily separated in experiments. Both enter through $B$ dependence of $\Delta\rho_{1}$ and share the same dependence on the magnetization direction, which adds to the uncertainties of interpreting the experimental data. The $T$ dependence of $\Delta\rho_{1}$, i.e., Eq. (9), is plotted in Fig. 3(a). The shape of the curve reveals two contributions, including a spin-exchange field and anisotropic spin relaxation. The former is reflected in sharp vanishing at critical temperature (blue curve), while the latter is plotted in the inset of Fig. 3(a) by artificially setting $\mathcal{B}_{sd}=0$. Anisotropic spin relaxation and spin precession MR demonstrate themselves by the cosine-square characteristics of $\rho_{L}$ concerning the magnetization direction $\alpha$ [blue and green curves of Fig. 3(b)]. At a high temperature ($T\geq T_{c}$), no anisotropic MR is observed at $B\rightarrow 0$ [red line of Fig. 3(b)]. The predicted behaviors are in agreement with anisotropic MR experiments [43].

Diverse behaviors of MR-Next, we show intriguing MR for the magnetic field in $x$-axis direction ($B_{x}$). Figure 4(a) plots a transition from positive to negative MR at small $B$ for antiferromagnetic SEC when the system is cooled from a high $(T=200K)$ to low temperatures $(T=10K)$. This interesting transition can be explained as follows. The SEC (1) induces a spin-exchange field (2), which is linearly proportional to the SEC $\mathcal{J}_{sd}$ and the magnetization $\langle S_{\parallel}\rangle$, i.e., $\mathcal{B}_{sd}\propto\mathcal{J}_{sd}\langle S_{\|}\rangle$. Hence, the ferromagnetic (antiferromagnetic) SEC generates a blue (red) shift of the Hanle spin precession frequency $\omega_{L}=\textsl{g}\mu_{B}(B_{x}-\mathcal{B}_{sd})/\hbar$ with $\mathcal{B}_{sd}<0$ ($\mathcal{B}_{sd}>0$). For high enough temperature (red curve), $\mathcal{B}_{sd}$ vanishes because $\langle S_{\parallel}\rangle\simeq 0$, and we recover the previous Hanle MR that exhibits quadratic behavior concerning small $B_{x}$, i.e., $\rho_{\text{L}}\propto\omega^{2}_{L}\propto B_{x}^{2}$ [10]. Thus, we always get positive MR for ferromagnetic and antiferromagnetic SEC. At a low enough temperature (black curve), i.e., strongly magnetized regime, the spin-exchange field (2), spin relaxation time (3) and (4) acquire their saturated values and become independent of the magnetic field. Then, the magnetic field dependence of resistance purely originates from the magnetic-field spin precession frequency, leading to the shifted spin precession MR $\rho_{\text{L}}\propto\omega^{2}_{L}\propto(B_{x}-\mathcal{B}_{sd})^{2}$ with $\mathcal{B}_{sd}=-n_{\mathrm{S}}\mathcal{J}_{sd}S/(\hbar g\mu_{B})$. The ferromagnetic (antiferromagnetic) SEC leads to positive (negative) MR with $\mathcal{B}_{sd}<0$ $(\mathcal{B}_{sd}>0)$, as indicated by the red and blue curves in Fig. 4(b). Thus, we find a transition from positive to negative MR for antiferromagnetic SEC by cooling the system to low temperatures.

Notably, the minimum of the shifted spin precession MR is where the applied magnetic field offsets the spin-exchange field, i.e., $B_{x}=\mathcal{B}_{sd}$. At saturated temperature ($T=10$K), the motion of the minimum for different $\mathcal{J}_{sd}$ is plotted in Fig. 4(b). We observe the spin-exchange field (2), $\mathcal{B}_{sd}\propto|\mathcal{J}_{sd}|$, is rightly shifted by the stronger antiferromagnetic SEC. This result, in return, can be used to electrically detect the strength of the microscopic SEC, which was previously only detected by the Kondo resonance of scanning tunneling spectroscopy [58].

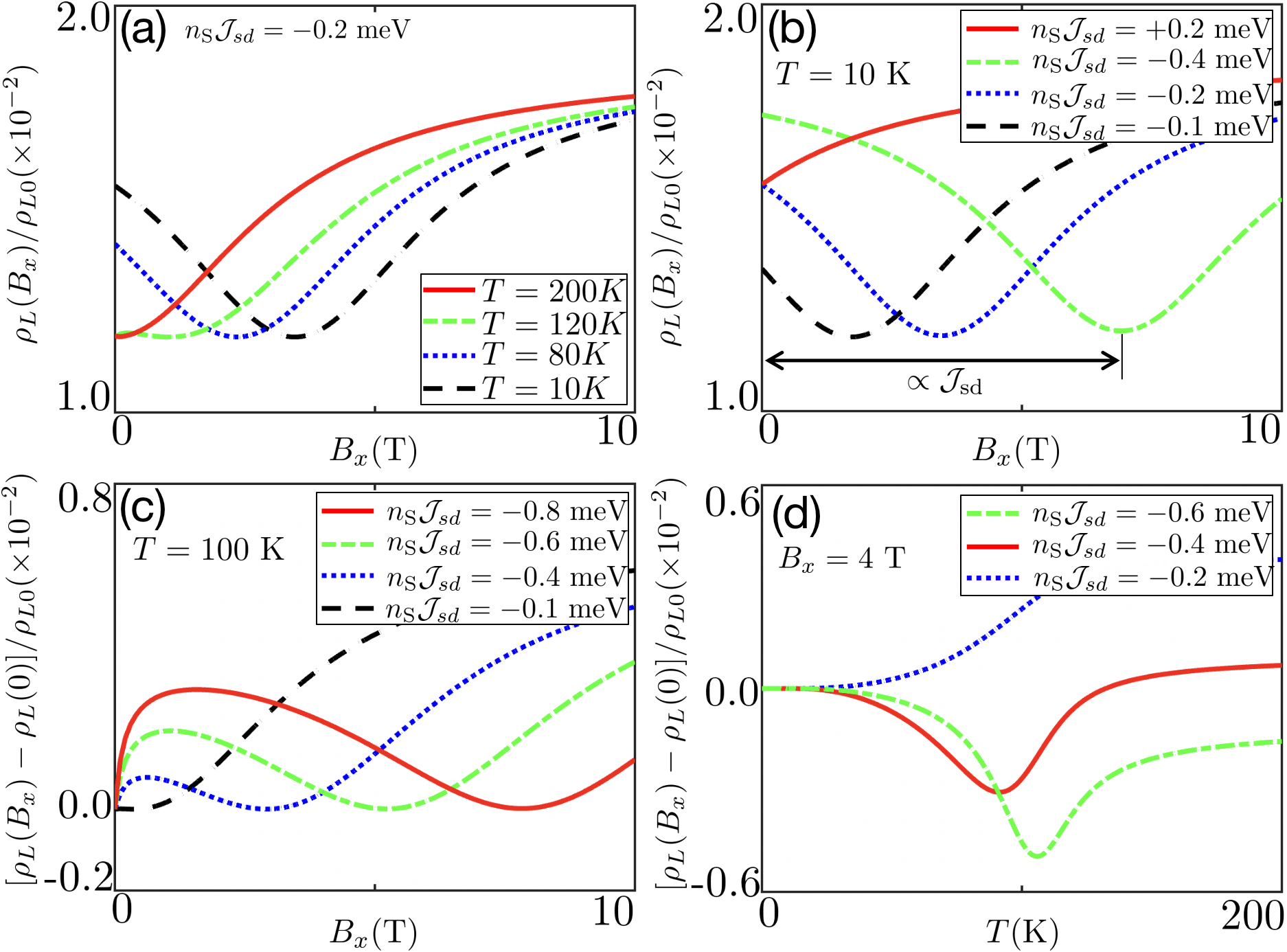
Besides, higher temperature ($T\lesssim T_{c}$) can convert negative MR into a positive one for large antiferromagnetic SEC [Fig. 4(c)]. Because the positive MR produced by the anisotropic spin relaxation MR ($\ell_{\|}\neq\ell_{\perp}$) becomes larger for stronger antiferromagnetic SEC at critical temperature. Thus, the longitudinal resistivity quickly ascends first due to anisotropic MR, descends later, and increases again because of the shifted Hanle MR. Note that the spin-exchange field also relies on $T$. We find a minimum in resistivity with $T$ for sizable antiferromagnetic SEC like the Kondo effect [59], as shown in Fig. 4(d).

Summary-Based on the theory of open-quantum system, we develop a comprehensive microscopic theory to illustrate the diverse MR effects from the magnon-induced spin flip, anisotropic spin relaxation time, and Hanle spin precession of itinerant electrons. Our theory provides insights of experimental observations involving $B$- and $T$-dependent MR, paving the way for further progress in the understanding and practical applications of magnetic materials. Besides, we reveal fruitful behaviors due to the interplay of magnon, spin relaxation and precession MR, allowing electrical detection of the strenghth of the microscopic SEC. Moreover, our method can be generalized to more different magnetic materials (e.g. ferrimagnetic/antiferromagnetic metals/semiconductors).