MetaKRec: Collaborative Meta-Knowledge Enhanced Recommender System

For a knowledge graph enhanced recommender system, we have a set of users $\mathcal{U}=\{u_{1},u_{2},...,u_{\left|\mathcal{U}\right|}\}$, a set of items $\mathcal{I}=\{i_{1},i_{2},...,i_{\left|\mathcal{I}\right|}\}$, and a set of entities $\mathcal{E}=\{e_{1},e_{2},...,e_{\left|\mathcal{E}\right|}\}$. Historical user-item interactions are represented as a user-item bipartite graph $\mathcal{G}_{rec}=\{(u,y_{ui},i)|u\in\mathcal{U},i\in\mathcal{I}\}$, where $y_{ui}=1$ if $u$ has purchased $i$, otherwise $y_{ui}=0$. Besides $\mathcal{G}_{rec}$, we also have a knowledge graph $\mathcal{G}_{kg}$ as side information for items. The knowledge graph is typically formed by entities $\mathcal{E}$ and the relationships $\mathcal{R}$ among them. $\mathcal{G}_{kg}$ is represented by subject-property-object triple facts [14]: $\{(h,r,t)|h,t\in\mathcal{E},r\in\mathcal{R}\}$, where each triple represents the relation between $h$ and $t$ is $r$.

Collaborative Knowledge Graph $\mathcal{G}$ [7] is built by unifying $\mathcal{G}_{rec}$ and $\mathcal{G}_{kg}$. Firstly, we set the item-entity alignment function $f(i)=e$ that maps item $i$ as entity $e$ in the knowledge graph. Then user-item interaction $(u,y_{ui},i)\in\mathcal{G}_{rec}$ is transformed into two triples $(u,\text{Interact},f(i))$ and $(f(i),\text{Interacted by},u)$. Based on the previous alignment, the collaborative knowledge graph is represented by $\mathcal{G}=\{(h,r,t)|h,t\in\mathcal{U}\cup\mathcal{I}\cup\mathcal{E},r\in\mathcal{R}\cup\{\text{Interact},\text{Interacted by}\}\}$. Then the task is formulated to predict the adoption probability $\hat{y}_{ui}$ given $\mathcal{G}$ that contains both historical interactions and the knowledge graph.

Graph neural network (GNN) is a deep learning method applied to graph-structured data. It has been tested to be effective in a wide range of graph-related tasks such as protein function prediction [15], group identification [16] as well as recommender system [17, 18, 19]. GNN is based on the homophily assumption [20] on graphs. It indicates nodes connected in a graph are similar to each other. GNN models homophily by directly aggregating embedding from neighbors to the center neighbor, which is formulated as:

$\displaystyle\mathbf{e}_{u}^{(l+1)}=\mathbf{e}_{u}^{(l)}\oplus\text{AGG}^{(l+1)}(\{\mathbf{e}_{i}^{(l)}\mid i\in\mathcal{N}_{u}\}),$

(1)

where $\mathbf{e}_{u}^{(l)}$ is node $u$’s embedding in $l$-th layer, $\mathcal{N}_{u}$ is $u$’s neighbors, $\mbox{AGG}^{(l)}(\cdot)$ aggregates neighbors’ embedding into a single vector in layer $l$, and $\oplus$ is the function to combine neighborhood representation and the center node’s embedding. Different selection of $\mbox{AGG}^{(l)}(\cdot)$ and $\oplus$ leads to different kinds of GNN layers, such as GCN [21], GAT [22], and GIN [23].

Directly enhancing the recommender system by the original collaborative knowledge graph $\mathcal{G}$ has two drawbacks. 1) The edges between items and entities are still sparse. Message-passing on the sparse graph is neither efficient nor effective. 2) The learning of entity embedding burdens the training procedure. To tackle the two drawbacks, we propose to construct Collaborative Meta-KG (CMKG) $\mathcal{G}_{cmkg}$ from the original collaborative knowledge graph $\mathcal{G}$, which is defined as:

$\mathcal{G}_{cmkg}$ is constructed from $\mathcal{G}$. Based on explicit meta-knowledge, we encode the knowledge graph as multiple $\mathcal{G}_{cmkg}$. In this way, we drop the entities in KG and encode the KG information as edges directly between items in $\mathcal{G}_{cmkg}$. This leads to denser interactions and enables a direct message-passing between items. As shown in Fig. 3, we generate $3$ $\mathcal{G}_{cmkg}$ from the knowledge graph:

• •

  $\mathcal{G}_{cmkg}^{kg1}$: Two items are similar when connected to the same entity. E.g., we transform $(i_{3}\stackrel{{\scriptstyle R_{1}}}{{--}}e_{3}\stackrel{{\scriptstyle R_{2}}}{{--}}i_{4})$ relation in $\mathcal{G}$ to a direct edge $(i_{3}--i_{4})$ in $\mathcal{G}_{cmkg}^{kg1}$.

• •

  $\mathcal{G}_{cmkg}^{kg2}$: Two items are more similar if they are connected to the same entity under the same relation. E.g., we transform $(i_{1}\stackrel{{\scriptstyle R_{1}}}{{--}}e_{1}\stackrel{{\scriptstyle R_{1}}}{{--}}i_{4})$ relation in $\mathcal{G}$ to a direct edge $(i_{1}--i_{4})$ in $\mathcal{G}_{cmkg}^{kg2}$.

• •

  $\mathcal{G}_{cmkg}^{kg3}$: Items are similar if they share similar semantic meanings in the knowledge graph. To this end, we obtain the entities embedding by training a TransE [24] model on the knowledge graph. Then we build edges between two items if the cosine similarity of their TransE embedding is larger than a threshold $t$. E.g., we build an edge between $i_{2}$ and $i_{3}$ because their cosine similarity on TransE embedding is larger than a threshold $t$.

We can also generate $\mathcal{G}_{cmkg}$ from the user-item interactions. MetaKRec generates $2$ $\mathcal{G}_{cmkg}$ based on co-purchase behavior:

• •

  $\mathcal{G}_{cmkg}^{uk1}$: Items are similar if they share similar common users. We compute the Jaccard similarity between item pairs based on interacted users. Item’s user neighborhood is more similar with a higher Jaccard similarity. E.g., we construct an edge between $i_{1}--i_{2}$ in $\mathcal{G}_{cmkg}^{uk1}$ because their Jaccard similarity is larger than $t$.

• •

  $\mathcal{G}_{cmkg}^{uk2}$: Based on Jaccard similarity, we construct the edge between one item and its Top K most similar items. E.g., we construct $i_{3}--i_{4}$ in $\mathcal{G}_{cmkg}^{uk2}$ because $i_{4}$ is in $i_{3}$’s Top K similar items.

All $\mathcal{G}_{cmkg}$ share the historical user-item interactions and differ from the edges between items. Different $\mathcal{G}_{cmkg}$ utilizes different information sources and Meta Knowledge. $\mathcal{G}_{cmkg}^{kg1}$, $\mathcal{G}_{cmkg}^{kg2}$, $\mathcal{G}_{cmkg}^{kg3}$ are built based on knowledge graph. $\mathcal{G}_{cmkg}^{uk1}$ and $\mathcal{G}_{cmkg}^{uk2}$ are built based on user-item interaction graph. The $\mathcal{G}_{cmkg}$ can be built based on different kinds of Meta Knowledge. In MetaKRec , we illustrate the building method in $5$ differently. It is flexible enough to contain more information by transforming the Meta Knowledge into item similarities.

Light graph convolution [25] (LGC) has been shown effective on the user-item bipartite graph. The direct embedding passing between users and items explicitly aggregates the collaborative filtering signal. MetaKRec applies LGC on each generated $\mathcal{G}_{cmkg}$ in Section III-A.

The embedding layer is built before the convolution to represent the users and items. The embedding layer is a look-up table that maps user/item ID to a dense vector:

$$\mathbf{E}=\left(\mathbf{e}_{1},\mathbf{e}_{2},\ldots,\mathbf{e}_{|\mathcal{U}|+|\mathcal{I}|}\right),\\$$

(2)

where $\mathbf{e}\in\mathbb{R}^{d}$ is the $d$-dimensional vector to represent a user/item. The embedding indexed from the loop-up table is before the graph convolution. Then they are fed into the light graph convolution to aggregate neighbor’s information:

$$\mathbf{e}_{n}=\sum_{v\in\mathcal{N}_{n}}\frac{1}{\sqrt{|\mathcal{N}_{n}|}\sqrt{|\mathcal{N}_{v}|}}\mathbf{e}_{v},\\$$

(3)

where $n,v$ can represent both user and item in $\mathcal{G}_{cmkg}$, $\mathcal{N}_{n}$ is the neighbor set of node $n$. The LGC can be stacked in several layers, and we omit the notation for layers for simplicity. We perform the convolution separately for each $\mathcal{G}_{cmkg}$. After the convolution, we have $[\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg1}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg2}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg3}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{uk1}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{uk2}}]$ for node $n$.

Each $\mathcal{G}_{cmkg}$ is one channel for model to encode KG information. Different channels encode node embedding from different $\mathcal{G}_{cmkg}$, and contain different information. The channel attention module is a readout function to aggregate the embedding learned on different $\mathcal{G}_{cmkg}$:

	$\displaystyle\mathbf{e_{n}}$	$\displaystyle=\text{Readout}([\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg1}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg2}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{kg3}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{uk1}},\mathbf{e}_{n}^{\mathcal{G}_{cmkg}^{uk2}}])$		(4)
		$\displaystyle=\sum_{g}a^{g}\mathbf{e}^{\mathcal{G}_{cmkg}^{g}},$		(5)

where $a^{g}$ is the attention weight learned for $\mathcal{G}_{cmkg}^{g}$, and is calculated by:

$$a^{g}=\frac{\text{exp}(\langle\mathbf{W}_{\text{Att}},\mathbf{e}^{\mathcal{G}_{cmkg}^{g}}\rangle)}{\sum_{g^{\prime}}\text{exp}(\langle\mathbf{W}_{\text{Att}},\mathbf{e}^{\mathcal{G}_{cmkg}^{g^{\prime}}}\rangle)}$$

(6)

where $\mathbf{W}_{\text{Att}}\in\mathbb{R}^{d}$ is the parameter to compute attention weight. The channel attention module learns different weights for different channels to optimize the loss function. It can effectively combine information extracted from different $\mathcal{G}_{cmkg}$.

The aggregated embedding for $u$ and $i$ contain information from different $\mathcal{G}_{cmkg}$, and we compute the dot product as the probability that $u$ will purchase $i$:

$$\hat{y}_{u,i}=\mathbf{e}_{u}\cdot\mathbf{e}_{i}.$$

(7)

We randomly sample one negative item over the whole item set for each positive interaction and compute the Bayesian Personalized Ranking (BPR) loss [26] for optimization:

$$\mathcal{L}=-\sum_{(u,i)\in\mathcal{G}_{rec},j\in\mathcal{I}\setminus\mathcal{N}_{u}}\log\sigma(\hat{y}_{u,i}-\hat{y}_{u,j})+\lambda||\Theta||^{2}_{2},$$

(8)

where $j$ is the randomly sampled negative item, $\lambda$ is the regularization hyper-parameter, and $\Theta$ contains all the parameters.

We compare the parameter size of MetaKRec with KG-enhanced recommendation models. The comparison is shown in Table I. $\mathcal{U},\mathcal{I},\mathcal{E},\mathcal{R}$ represent the user, item, entity and relation set, respectively. $\mathcal{P}$ is the intent set in KGIN. $l$ is the number of layers and $d$ is the embedding size. MetaKRec has the fewest parameters, and it only needs the user and item embedding table. All the other KG-enhanced methods need much more parameters to represent the entities. MetaKRec abandons the redundant design of entity embedding and enables direct aggregation between items. As shown in Table III, MetaKRec achieves the best performance with the fewest parameters. It testifies the MetaKRec is effective and efficient.

The overall comparison of the $4$ datasets is shown in Table III. We can have the following observations:

• •

  MetaKRec consistently outperforms the runner-up on all datasets. The improvement is over $5\%$ on all Music and Yelp datasets metrics. The huge improvement validates the effectiveness of our model.

• •

  MetaKRec always beats LightGCN by a large margin. As MetaKRec and LightGCN use the same Light Graph Convolution layer, the improvement is largely brought by the KG information. It shows MetaKRec greatly enhances the recommender system by KG side information.

• •

  KG-enhanced recommender systems (KGAT, KGIN) do not necessarily perform better than models that utilize only user-item bipartite graphs (SGConv, LightGCN). It indicates the collaborative filtering signal on the bipartite graph is most important to achieve accurate recommendations while the knowledge graph is sided information.

• •

  Among all the KG enhanced methods, MetaKRec always achieves the best performance. It reveals that collaborative meta-kg graphs can effectively transform the knowledge graph as side information to enhance the recommender system.

We then test the model’s performance on different Collaborative Meta-KGs. Experiment results on $4$ datasets are illustrated in Tables IV, V, VI, VII respectively. From the $4$ tables, we can have the following observations. 1) The combined model that utilizes all the Collaborative Meta-KGs always achieves the best performance. The improvement on the Amazon dataset is over $20\%$ compared with the runner-up. It shows different Collaborative Meta-KGs acquire different information and can complement each other to achieve a better performance in a joint effort. 2) The performance of each Collaborative Meta-KG does not deteriorate much compared with the joint model. It reveals the collaborative filtering signal between user-item interactions is the most important during building an effective recommender system. The knowledge graph can be utilized as side information to enhance the recommendation performance.

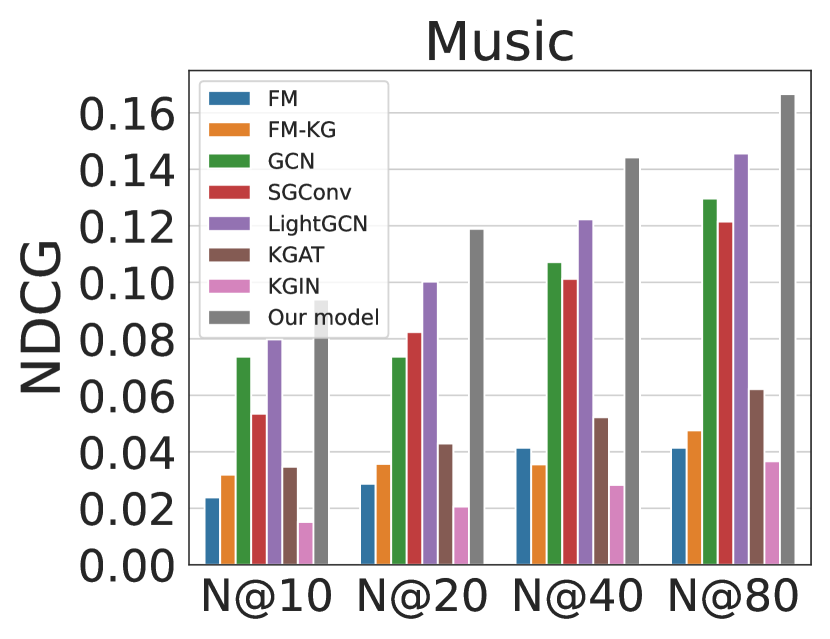
Cold-start is a severe problem in recommender systems. Without enough user-item interactions, it is difficult to obtain an informative representation. This experiment evaluates the model’s performance under the cold-start setting, where we randomly keep only $1$ user interaction for each item in the training set. Here we select Recall and NDCG @ $\{10,20,40,80\}$ as evaluation metrics.

Experiment results on Recall are shown in Fig. 4, and results on NDCG are shown in Fig. 5. From the results, we can observe that MetaKRec achieves the best performance on both Recall and NDCG over all datasets. Compared with the runner-up, the improvement of MetaKRec on Yelp dataset is over $30\%$. On Amazon and Music datasets, MetaKRec surpasses the second best over $15\%$. The lowest improvement on Book dataset is more than $10\%$. The huge improvement on all datasets validates MetaKRec can effectively utilize knowledge graph as side information to cope with the cold-start recommendation problem.

We can also observe that the performance of KGAT and KGIN are even worse than the simple GCN model under the cold-start setting. It shows knowledge graph can not always provide informative information for cold-start items. The complex design of KGAT and KGIN do not contribute to better performance. With fewer parameters, MetaKRec achieves very huge improvement over other KG-enhanced models.

In this experiment, we explore the influence of different experiment settings on MetaKRec . Two influential hyper-parameters are studied: 1) The number of graph convolution layers, and 2) Channel combination methods.

Meta Path/Graph is a kind of powerful learning method on graph data, and it has attracted much research attention in recent years [32, 33]. To evaluate the relevance of different-typed objects, Shi et al. [34] proposed HeteSim to measure the relevance of any object pair under an arbitrary meta path. Meta path-based methods are widely used on graph embedding. Meta-path2vec [35] designed a meta-path-based random walk and utilized skip-gram to perform graph embedding. Sun et al. [36] proposed meta-graph-based network embedding models, which simultaneously considered the hidden relations of all meta information of a meta-graph. Qiu et al. [37] provided the theoretical connections between skip-gram-based network embedding algorithms and the theory of graph Laplacian and presented the NetMF method as well as its approximation algorithm for computing network embedding. Fan et al. [38] proposed a HIN embedding model metagraph2vec to learn the low-dimensional representations for the nodes in HIN, where both the HIN structures and semantics are maximally preserved for malware detection. Fan et al. [39] also introduced an attributed heterogeneous information network (AHIN) to model the rich semantics and complex relations among multi-typed entities and designed different metagraphs to formulate the relatedness between buyers and products. The HeCo proposed by Wang et al. [40] employed network schema and meta-path views to collaboratively supervise each other, moreover, a view mask mechanism was designed to further enhance the contrastive performance.

Unlike previous works, we design meta graphs, particularly for knowledge graph enhanced recommendation. We propose Collaborative Meta Knowledge Graph that explicitly utilizes information from both knowledge graph and user-item interactions. The construction method is also not limited to paths or graph structures, which is flexible enough to encode different kinds of prior knowledge.

KG contains rich entity and relationship information, which can be used as auxiliary information to supplement the relationship between users and items, thus making the recommender system more effective, accurate, and explainable [41]. KG enhanced recommender system also receives much research attention [42, 43, 44]. KTUP [2] and CFKG [1] jointly learn recommendation and knowledge graph completion tasks by the shared embedding table. KGCN [27] is the pioneering work to take the advantage of GNN over knowledge graph to obtain an informative item embedding table. KGNN-LS [45] learns the influence of the knowledge graph on users and transforms KG into a user-specific weighted graph before GNN aggregation. Wang et al. [7] creatively propose the KGAT method, using two designs of recursive embedding propagation and attention-based aggregation to fully use the high-order information in KG to achieve the purpose of enhanced recommendation. Then they propose the KGIN [8] method, which provides a new aggregation scheme to extract useful information about user intent and encode them into user and item representations. ATBRG [46] generates subgraphs for specific user-item pairs and uses a the relation-aware extractor layer to extract informative relations for aggregation. DSKReG [47] samples on useful relations over knowledge graph by gumble softmax, and reconstructs a preference aware aggregation graph before GNN.

All previous researches rely on models to learn informative information from the complex knowledge graph with multiple kinds of relations. Unlike them, MetaKRec utilizes prior meta knowledge over knowledge graphs to construct different meta graphs to enhance recommendation. The reliable human-defined meta-knowledge decreases the noise and enables a simple model to achieve the best performance.