MeMaHand: Exploiting Mesh-Mano Interaction
for Single Image Two-Hand Reconstruction
Abstract
Existing methods proposed for hand reconstruction tasks usually parameterize a generic 3D hand model or predict hand mesh positions directly. The parametric representations consisting of hand shapes and rotational poses are more stable, while the non-parametric methods can predict more accurate mesh positions. In this paper, we propose to reconstruct meshes and estimate MANO parameters of two hands from a single RGB image simultaneously to utilize the merits of two kinds of hand representations. To fulfill this target, we propose novel Mesh-Mano interaction blocks (MMIBs), which take mesh vertices positions and MANO parameters as two kinds of query tokens. MMIB consists of one graph residual block to aggregate local information and two transformer encoders to model long-range dependencies. The transformer encoders are equipped with different asymmetric attention masks to model the intra-hand and inter-hand attention, respectively. Moreover, we introduce the mesh alignment refinement module to further enhance the mesh-image alignment. Extensive experiments on the InterHand2.6M benchmark demonstrate promising results over the state-of-the-art hand reconstruction methods.

1 Introduction
Vision-based 3D hand analysis plays an important role in many applications such as virtual reality (VR) and augmented reality (AR). Two-hand reconstruction from a single RGB image is more challenging due to complex mutual interactions and occlusions. Besides, the skin appearance similarity makes it difficult for the network to align image features to the corresponding hand.
Previous hand reconstruction works can be divided into two categories, parametric methods [3, 33, 34, 7] and non-parametric methods [4, 11, 21, 5, 6, 19, 20]. Parametric methods typically learn to regress pose and shape parameters of MANO model [24], where pose represents joint rotations in axis-angle representation and shape represents the coefficients of shape PCA bases. The MANO prior can yield plausible hand shapes from a single monocular image. However, they can not produce fine-grained hand meshes due to their limited capacity.
With the rapid progress of graph convolutional network (GCN) and transformer techniques [11, 19, 20, 17], it is observed that direct mesh reconstruction can achieve state-of-the-art performance towards the Euclidean distances between the ground truth vertices and the predicted vertices. Nonetheless, the non-parametric methods are less robust in handling challenging viewpoints or severe occlusions.
In this paper, we introduce a novel single-image two-hand reconstruction method designed to predict mesh vertices positions and estimate MANO parameters simultaneously to utilize the merits of two kinds of hand representations. The proposed Mesh-Mano interaction Hand reconstruction architecture (MeMaHand) consists of three modules: 1) the image encoder-decoder module, 2) the mesh-mano interaction module, 3) and the mesh alignment refinement module. To extract contextually meaningful image features, we pre-train a classical image encoder-decoder network on auxiliary tasks including hand segmentation, hand 2D joints and dense mapping encodings. The low-resolution features encode more global knowledge, while the high-resolution features contain more local details. Secondly, the mesh-mano interaction module stacks three mesh-mano interaction blocks (MMIBs) to transform the mesh vertices and MANO parameters queries initialized by the global image feature vector. We observe that the hand prior embedded in the MANO parameters is valuable for predicting stable hand meshes in challenging situations such as severe occlusions. MMIB consists of one graph residual block to aggregate local information and two transformer encoders to model long-range dependencies. The transformer encoders are equipped with different asymmetric attention masks to model the intra-hand and inter-hand attention, respectively. Each MMIB is followed by an upsampling operation to upsample the mesh vertices tokens in a coarse-to-fine manner. Finally, the mesh alignment refinement module utilizes one MMIB to predict offsets for mesh vertices and MANO parameters to enhance mesh-image alignment. To improve the reliability of image evidence, we project mesh vertices predicted by the Mesh-Mano interaction module onto the 2D image plane. The explicit mesh-aligned image features are concatenated to the transformer input tokens.

The whole network, including the pre-trained image feature encoder-decoder, is jointly optimized such that the image features better adapt to our hand mesh reconstruction task. Benefiting from the mesh-mano interaction mechanism and mesh alignment refinement stage, extensive experiments demonstrate that our method outperforms existing both parametric and non-parametric methods on InterHand2.6M [23] dataset. In summary, the contributions of our approach are as follows:
-
•
We propose MeMaHand to integrate the merits of parametric and non-parametric hand representation. The mesh vertices and MANO parameters are mutually reinforced to achieve better performance in mesh recovery and parameter regression.
-
•
A mesh-image alignment feedback loop is utilized to improve the reliability of image evidence. Therefore, more accurate predictions are obtained by rectifying the mesh-image misalignment.
-
•
Our method achieves superior performance on the InterHand2.6M dataset, compared with both non-parametric and parametric methods.
2 Related Works
Parametric Hand Reconstruction. Parametric approaches [1, 2, 12, 13, 33, 24, 3, 34, 7] use a parametric hand model such as MANO [24] and focus on regressing the pose and shape parameters from a single image. The rich embedded prior information (e.g. the geometric dynamic constraints of joint rotations) can assist deep model learning when 3D annotations are insufficient. Weak 2D joints supervision [3] and motion caption data [34] are utilized to train convolutional neural networks (CNN) to predict MANO parameters. The reliance on 3D manual annotations is further totally alleviated by S2HAND [7]. However, the reconstructed mesh can not fully express the local details of variable 3D hand shapes due to the limited capacity of the MANO model.
Non-parametric Hand Reconstruction. Non-parametric methods aim to reconstruct the hand mesh directly [11, 21, 5, 6, 27, 19, 17, 18, 20, 22, 8, 30]. To explicitly encode mesh topology, graph convolutional network (GCN) is adopted for aggregating adjacent vertices features. Hierarchical architectures [11, 17] are designed for mesh generation from coarse to fine. To model long-range dependencies, multi-layer transformer encoders are introduced such that the global interactions can be modeled without being limited by any mesh topology [19, 20]. Most recently, IntagHand [17] achieves the state-of-the-art performance on InterHand2.6M dataset [23]. However, we observe that IntagHand is less robust in handling challenging viewpoints or severe occlusions. The reconstructed mesh may be corrupted into unnatural shapes.
Interacting Two-Hand Reconstruction. Although single-hand methods can extend to two-hand reconstruction, the correlation between the left and right hands is not considered. Besides, the performance deteriorates for the close-interacting hands. Depth cameras [16] are sensitive to tracking accuracy and multi-view images [28, 25] are expensive to acquire. Based on a large-scale interacting hand dataset named InterHand2.6M [23], deep learning based single image methods either estimate hand joint positions [23, 15], or employ a 2.5D heatmap to predict the MANO parameters [31], or directly reconstruct meshes [17]. In summary, existing methods only employ a single specific hand representation. In contrast, our method not only combines the merits of MANO representations and mesh representations but also proposes a dedicated transformer encoder with asymmetric attention masks to make them collaborate seamlessly. Besides, the joint rotation and precise mesh vertices positions can be used for different applications, such as driving CG characters or virtual try-on.
3 Methodology
The overall architecture of MeMaHand is depicted in Fig. 2. Given a single image , the proposed method can predict the mesh vertices positions , MANO pose parameter and shape parameter of two hands simultaneously in one forward pass. In this section, we first describe the overall architecture of MeMaHand in Sec. 3.1. Then, we illustrate the mesh-mano interaction module and mesh-alignment refinement module in Sec. 3.2 and Sec. 3.3, respectively. Finally, we introduce the model objectives used to train our network in Sec. 3.4.
3.1 System Overview
To extract contextually meaningful image features, we pre-train a classical image encoder-decoder module on auxiliary tasks including hand segmentation, hand 2D joints, and dense mapping encodings. The 2D image conditions are generated from the reconstructed mesh of ground-truth MANO parameters. ResNet50 [14] is leveraged as the backbone. Global average pooling feature and multi-scaled image feature are extracted from the image encoder (E) and decoder (D).
Afterward, we propose Mesh-Mano Interaction Module to predict mesh vertices positions and MANO parameters of both left (L) and right (R) hands. We use the global feature to initialize the vertex and MANO queries. The grid-sampled image features are tokenized as well following the practice of Mesh Graphformer [20].
The mesh alignment refinement module further improves the predictions generated by the mesh-mano interaction module. The explicit mesh-aligned image features extracted from the multi-scale feature maps are more informative than grid-sampled image features, which helps rectify the predictions. Details will be elaborated in Sec. 3.3.
3.2 Mesh-Mano Interaction Module
The mesh-mano interaction module reconstructs hand mesh in a coarse-to-fine manner with three Mesh-Mano Interaction Blocks (MMIBs). We leverage the graph coarsening method [17] to build three-level sub meshes with vertex number . Each MMIB is followed by an upsample operation that reverses the topological relationship between adjacent sub-meshes. The full mesh vertices positions () are obtained with a simple from the final output vertex token.

Fig. 3 shows the detailed structure of MMIB. At level , the input tokens of MMIB include two kinds of queries: vertex queries and MANO parameter queries , where indicates left () or right () hand, and represents the feature dimensions. Therefore, the total sequence length is .
Graph Residual Block. The design of the graph residual block is similar to [11, 17]. The Chebyshev spectral graph CNN [9] is adopted to transform the vertex token to intermediate graph features,
| (1) |
where the operation denotes the graph convolution. More details can be found in [9]. For simplicity, we use to represent the concatenation of updated left-hand and right-hand vertex tokens.
Intra-hand Transformer Encoder. While graph CNN is useful for extracting local information, it is less efficient at capturing long-range dependencies. We use transformer encoders to model dependencies not only between long-range vertices but also between mesh vertices and MANO parameters. The spatial image features at resolution are also tokenized as by grid sampling following the practice of Mesh Graphformer [20]. Therefore, the input tokens of intra-hand transformer encoder () consist of graph features (), MANO queries () and grid image feature (). Based on the observation that the mesh vertices regression can lead to more precise mesh reconstruction and the MANO parameters are more stable, we propose an asymmetric attention mask excluding the mano-to-mesh attention such that the MANO parameter tokens will not directly affect the mesh vertex tokens. The mesh-to-mano attention remains. Therefore, the mesh vertex tokens are implicitly regularized by the MANO parameters loss. focuses on modeling the intra-hand dependencies. The inter-hand attention is also excluded. The resulting asymmetric attention mask is shown in Fig. 3. Finally, the intra-hand transformer encoder is formulated as:
| (2) |
where denotes the concatenation operation. For simplicity, represents the concatenation of updated mesh vertex and MANO parameter tokens.
Inter-hand Transformer Encoder. In contrast to , the inter-hand transformer encoder () focuses on modeling the inter-hand correlations. Fig. 3 presents the resulting asymmetric attention mask . The image feature tokens are not used in . Finally, the inter-hand transformer encoder is formulated as:
| (3) |
where can be further split into updated vertex tokens and MANO parameter tokens .
Our proposed MMIB predicts the mesh vertices positions and MANO parameters simultaneously in a unified architecture. Intra-hand and inter-hand mesh-mano dependencies are modeled by two cascaded transformer encoders with different attention masks. After three MMIBs, a simple is applied to obtain the mesh vertices positions and MANO parameters from output tokens,
| (4) | ||||
| (5) |
where indicates the left or right hand. To tackle the noticeable misalignment between the estimated meshes and image evidence, we propose a mesh alignment refinement module to rectify the results.
3.3 Mesh Alignment Refinement Module
To further improve mesh-image alignment, we propose a novel mesh-alignment refinement module inspired by PyMAF [32]. Specifically, we project the mesh vertices predicted by the mesh-mano interaction module onto the multi-scale image features explicitly. Three-scale mesh-aligned image features are concatenated together for each corresponding vertex token. A simple multi-layer perceptron (MLP) is adopted to reduce the dimensions, resulting in a fused image feature .
We utilize one MMIB to refine the mesh vertex and MANO parameter tokens . To effectively utilize the mesh-aligned image evidence, we made some modifications to the tokens. Specifically, we concatenate the image feature to vertex token along the channel dimension. For MANO parameter tokens, we perform a global average pooling operation to obtain global feature vector before concatenation. The rectified tokens are formulated as,
| (6) |
One simple layer is applied to obtain the mesh vertices positions offsets and MANO parameter offsets for rectification,
| (7) | ||||
| (8) | ||||
| (9) |
where and are the final results. Note that we can stack several MMIBs to predict the offsets iteratively. In our experiments, one single MMIB is enough to achieve satisfactory results. PyMAF [32] fuses the mesh-align features into one global feature, which ignores the inherent spatial relationship of mesh vertices. In contrast, our MMIB adopts GCN to model the spatial relation between adjacent mesh vertices. The transformer encoder is responsible for modeling the long-range dependencies.


3.4 Model Objectives
Our method predicts mesh vertices positions and MANO parameters simultaneously. The learning objectives can be divided into three categories: mesh vertex loss, MANO parameter loss and mesh-mano consistency loss.
Mesh Vertex Loss: The widely-used L1 loss is adopted to supervise the vertex positions and the 2D projections:
| (10) |
where represents the ground-truth vertex positions and denotes the projection function. Given vertex positions, the joint positions can be regressed by multiplying the predefined regression matrix . Joint losses are formulated as:
| (11) |
The face normal loss is introduced to regularize the surface normal consistency:
| (12) |
where represents the th edge of face at hand and is the normal vector of this face from the ground truth mesh. The edge length consistency loss is to enforce the edge length consistency:
| (13) |
where represents the th edge of hand and denotes the total edge number, respectively.
MANO Parameter Loss: Given the ground truth MANO parameters, L1 loss is used to regress parameters,
| (14) |
In addition, we reconstruct hand mesh based on the MANO model. The reconstructed mesh should be close to the ground-truth mesh,
| (15) |
Mesh-Mano Consistency Loss. The predicted mesh and the reconstructed mesh from MANO parameters should be consistent with each other:
| (16) |
In summary, the overall training loss is:
| (17) |
where , , , , , and . The whole network including the pre-trained image feature encoder-decoder is jointly optimized such that the image features better adapt to our hand mesh reconstruction task.
4 Experiment
4.1 Datasets and Implementation
Training Dataset. Interhand2.6M [23] is a large-scale hand dataset with ground truth mesh annotations including both single-hand and interacting two-hand images. We pick out the interacting hand (IH) data for training and testing. For a fair comparison, we follow the preprocessing steps of [17] which produces 366K training and 261K testing samples.
Implementation Details. The image encoder uses ResNet50 [14] as the backbone. The decoder contains four simple deconvolutional layers. We first pretrain our image encoder-decoder module on auxiliary tasks. Then, the whole network is jointly optimized with Adam optimizer at a learning rate . Data augmentation includes random rotation, random translation, and random scaling. The batch size is set to 32. It takes around 48 hours to train MeMaHand with 4 Tesla V100 GPUs.
Metrics. Mean Per Joint Position Error (MPJPE) and Mean Per Vertex Position Error (MPVPE) in millimeters are adopted to evaluate the mesh reconstruction accuracy. Additionally, we report the percentage of correct keypoints (PCK) curve and Area Under the Curve (AUC) across the thresholds between 0 and 50 millimeters. To evaluate the mesh-image alignment accuracy, the reconstructed mesh vertices are projected onto the 2D image plane. The mesh-image alignment accuracy is measured by PROJ2D, which calculates the distance in image pixels between the projected ground truth vertices and the predicted vertices.


| Method | MPJPE | MPVPE | AUC | PROJ2D |
|---|---|---|---|---|
| zimmermann et al. [35] | 36.36 | - | - | - |
| Spurr et al. [26] | 15.40 | - | - | - |
| InterNet[23] | 16.00 | - | 0.711 | - |
| Digit[10] | 14.27 | - | - | - |
| Intaghand[17] | 8.79 | 9.03 | 0.806 | 6.47 |
| Ours | 8.65 | 8.89 | 0.832 | 6.22 |
4.2 Comparison with State-of-the-art Methods
We compare our model with state-of-the-art non-parametric methods including InterNet [23] and Intaghand[17] and parametric methods including [3], MinimalHand [34] and InterShape[31]. The officially released weights are used to obtain the results. The model parameters and inference time of our method and other SOTA methods are reported in Tab. 1. The inference of our model can be completed in , comparable to other SOTAs but with better mesh reconstruction results. Besides, the mesh vertex positions as well as the MANO parameters are predicted simultaneously in one single forward pass.
Comparison with Non-parametric Methods. Non-parametric methods directly generate mesh vertice positions, which can express the local details of variable 3D hand shapes. The quantitative results of non-parametric methods are shown in Tab. 2. It can be seen that our method achieves the best performance on all evaluation metrics. Fig. 6(a) presents the PCK curve, which further demonstrates the superiority of our method at all threshold levels.
Fig. 4 presents the qualitative comparison with SOTA non-parametric method IntagHand [17]. Our method performs better on close interacting two-hand reconstruction (first row). Besides, we observe that IntagHand produces collapsed meshes in hard cases such as severe occlusions and challenging viewpoints (second row). In contrast, our method is more robust to such situations. We attribute this success to the integration of MANO representations, which predicts stable hand meshes. More results with alternative views are shown in Figure 5.
| Method | MPJPE | MPVPE | AUC | PROJ2D |
|---|---|---|---|---|
| Boukhayma et al. [3] | 16.93 | 17.98 | 0.672 | - |
| MinimalHand[34] | 23.48 | 23.89 | 0.543 | - |
| InterShape [31] | 13.48 | 13.95 | 0.735 | 9.95 |
| Ours | 10.85 | 10.92 | 0.790 | 6.90 |
Comparison with Parametric Methods. For a fair comparison, the reconstructed hand meshes from our predicted MANO parameters are utilized for evaluation. The quantitative comparisons are listed in Tab. 3. The PCK curve is shown in Fig. 6(a). The MANO parameter estimation of our method outperforms other SOTA parametric methods. Thanks to the mesh-mano interaction block, the MANO token is conditioned on the mesh vertex tokens where spatial relations are retained. Such dependencies are more informative than one-dimensional global feature utilized in competing methods [3, 34, 31].
From Tab. 2 and Tab. 3, we can find the parametric method InterShape [31] has higher statistical errors on joint and vertex positions compared with the non-parametric method IntagHand [17] due to the limited capacity of the parametric model. However, from the second row of Fig. 4, we can see InterShape produces reasonable hand shapes in these challenging cases. By combining the merits of parametric and non-parametric hand representations, our method achieves the best performance both quantitatively and qualitatively.

4.3 Extension to Images in the Wild
We further present the hand reconstruction results on images in the wild. As shown in Fig. 7, our method performs well on real-life images taken from the RGB2Hands dataset [29], which demonstrates the generalization ability of our approach. Recall that our method is designed to predict accurate mesh vertices positions and MANO parameters simultaneously in one forward pass. The MANO pose parameter represents the joint rotations in axis-angle representation, which is useful for animating 3D hands in computer graphics. Accurate hand mesh vertices positions and MANO parameters for hands in the wild can facilitate different human-computer-interaction (HCI) applications.
4.4 Ablation Study
To evaluate the effectiveness of the proposed modules in our framework, we conduct an ablation study on several variants of our method. The quantitative results of all variants are presented in Table 4.
Effectiveness of MANO token. Variant A (w/o MANO token) represents removing the MANO tokens. The transformer encoder only models the dependencies between the mesh vertex tokens and image features. Fig. 8 show the qualitative comparison. Without hand prior information, the reconstructed mesh may be corrupted when parts of the hands are occluded. In contrast, our full model can generate reasonable meshes in these challenging situations.
| MPJPE | MPVPE | AUC | PROJ2D | |
|---|---|---|---|---|
| A: w/o MANO token | 8.87 | 9.09 | 0.818 | 6.85 |
| B: w/o Mesh-Align | 8.79 | 9.01 | 0.826 | 6.64 |
| C: Mesh-Align scale-16 | 8.73 | 8.97 | 0.829 | 6.38 |
| D: Mesh-Align scale-64 | 8.77 | 8.99 | 0.826 | 6.58 |
| E: Regress MANO from | 8.83 | 9.04 | 0.828 | 6.86 |
| F: w/o asymmetric attention | 9.17 | 9.37 | 0.822 | 6.67 |
| G: w/o auxiliary tasks | 9.11 | 9.28 | 0.823 | 6.78 |
| Full Model | 8.65 | 8.89 | 0.832 | 6.22 |

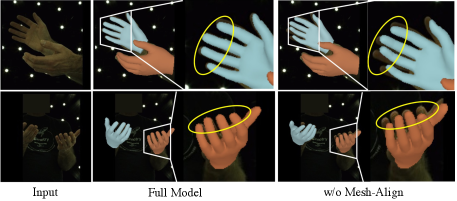
Effectiveness of Mesh Alignment Refinement. Variant B (w/o Mesh-Align) represents removing the mesh alignment refinement module. The predictions generated by the Mesh-Mano interaction module are taken as the final outputs. Variant C and D denote extracting the single-scale image features at resolution 16 and 64, respectively. The performances degrade without using mesh align refinement or using single-scale image features. As shown in Fig. 9, our full model produces better-aligned results.
Effectiveness of MMIB. Parametric and non-parametric representations are widely used for many years. However, combining them is not trivial. In variant E (Regress MANO from ), MMIB is responsible for updating vertex tokens. The MANO parameters are regressed from the global average pooling features with simple fully connected layers rather than through MMIB. The performance gain of variant E is limited as shown in Tab. 4. On the other hand, we propose an asymmetric attention mask to exclude the mano-to-mesh attention. To verify the choice, variant F (w/o asymmetric attention mask) denotes removing the asymmetric attention mechanism. The performance degrades compared with our full model.
Effectiveness of Pretraining on Auxiliary Tasks. Variant G represents the backbone is pre-trained on ImageNet. Our full model performs better since pre-training on auxiliary tasks are essential to extract semantically-meaningful image features. The auxiliary 2D image conditions are generated from the ground-truth mesh of Interhand2.6M training split. We did not use extra datasets.

5 Conclusion
In this paper, we propose a novel approach MeMaHand for two-hand mesh reconstruction from a single image. The mesh-mano interaction module combines the merits of non-parametric and parametric representations. Then, the mesh alignment refinement module further rectifies the results with an explicit mesh alignment feedback loop. Extensive experiments on the InterHand2.6M benchmark demonstrate that our proposed MeMaHand is superior to both existing parametric and non-parametric methods.
Limitations. Although our method generates promising results, it still fails in cases of severe occlusions. Fig. 10 shows some failure cases, where inter-penetration occurs. Taking the physical plausibility into consideration will be our future work.
References
- [1] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Pushing the envelope for rgb-based dense 3d hand pose estimation via neural rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1067–1076, 2019.
- [2] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Weakly-supervised domain adaptation via gan and mesh model for estimating 3d hand poses interacting objects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 6121–6131, 2020.
- [3] Adnane Boukhayma, Rodrigo de Bem, and Philip HS Torr. 3d hand shape and pose from images in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10843–10852, 2019.
- [4] Yujun Cai, Liuhao Ge, Jianfei Cai, and Junsong Yuan. Weakly-supervised 3d hand pose estimation from monocular rgb images. In Proceedings of the European Conference on Computer Vision (ECCV), pages 666–682, 2018.
- [5] Ping Chen, Yujin Chen, Dong Yang, Fangyin Wu, Qin Li, Qingpei Xia, and Yong Tan. I2uv-handnet: Image-to-uv prediction network for accurate and high-fidelity 3d hand mesh modeling. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 12929–12938, 2021.
- [6] Xingyu Chen, Yufeng Liu, Chongyang Ma, Jianlong Chang, Huayan Wang, Tian Chen, Xiaoyan Guo, Pengfei Wan, and Wen Zheng. Camera-space hand mesh recovery via semantic aggregation and adaptive 2d-1d registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13274–13283, 2021.
- [7] Yujin Chen, Zhigang Tu, Di Kang, Linchao Bao, Ying Zhang, Xuefei Zhe, Ruizhi Chen, and Junsong Yuan. Model-based 3d hand reconstruction via self-supervised learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10451–10460, 2021.
- [8] Hongsuk Choi, Gyeongsik Moon, and Kyoung Mu Lee. Pose2mesh: Graph convolutional network for 3d human pose and mesh recovery from a 2d human pose. In European Conference on Computer Vision, pages 769–787. Springer, 2020.
- [9] Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. Advances in neural information processing systems, 29, 2016.
- [10] Zicong Fan, Adrian Spurr, Muhammed Kocabas, Siyu Tang, Michael J Black, and Otmar Hilliges. Learning to disambiguate strongly interacting hands via probabilistic per-pixel part segmentation. In 2021 International Conference on 3D Vision (3DV), pages 1–10. IEEE, 2021.
- [11] Liuhao Ge, Zhou Ren, Yuncheng Li, Zehao Xue, Yingying Wang, Jianfei Cai, and Junsong Yuan. 3d hand shape and pose estimation from a single rgb image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10833–10842, 2019.
- [12] Yana Hasson, Bugra Tekin, Federica Bogo, Ivan Laptev, Marc Pollefeys, and Cordelia Schmid. Leveraging photometric consistency over time for sparsely supervised hand-object reconstruction. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 571–580, 2020.
- [13] Yana Hasson, Gul Varol, Dimitrios Tzionas, Igor Kalevatykh, Michael J Black, Ivan Laptev, and Cordelia Schmid. Learning joint reconstruction of hands and manipulated objects. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 11807–11816, 2019.
- [14] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
- [15] Dong Uk Kim, Kwang In Kim, and Seungryul Baek. End-to-end detection and pose estimation of two interacting hands. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 11189–11198, 2021.
- [16] Nikolaos Kyriazis and Antonis Argyros. Scalable 3d tracking of multiple interacting objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3430–3437, 2014.
- [17] Mengcheng Li, Liang An, Hongwen Zhang, Lianpeng Wu, Feng Chen, Tao Yu, and Yebin Liu. Interacting attention graph for single image two-hand reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2761–2770, 2022.
- [18] Guan Ming Lim, Prayook Jatesiktat, and Wei Tech Ang. Mobilehand: Real-time 3d hand shape and pose estimation from color image. In International Conference on Neural Information Processing, pages 450–459. Springer, 2020.
- [19] Kevin Lin, Lijuan Wang, and Zicheng Liu. End-to-end human pose and mesh reconstruction with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1954–1963, 2021.
- [20] Kevin Lin, Lijuan Wang, and Zicheng Liu. Mesh graphormer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 12939–12948, 2021.
- [21] Gyeongsik Moon and Kyoung Mu Lee. I2l-meshnet: Image-to-lixel prediction network for accurate 3d human pose and mesh estimation from a single rgb image. In European Conference on Computer Vision, pages 752–768. Springer, 2020.
- [22] Gyeongsik Moon and Kyoung Mu Lee. I2l-meshnet: Image-to-lixel prediction network for accurate 3d human pose and mesh estimation from a single rgb image. In European Conference on Computer Vision (ECCV), 2020.
- [23] Gyeongsik Moon, Shoou-I Yu, He Wen, Takaaki Shiratori, and Kyoung Mu Lee. Interhand2. 6m: A dataset and baseline for 3d interacting hand pose estimation from a single rgb image. In European Conference on Computer Vision, pages 548–564. Springer, 2020.
- [24] Javier Romero, Dimitrios Tzionas, and Michael J Black. Embodied hands: Modeling and capturing hands and bodies together. ACM Trans. Graph., 36(6), nov 2017.
- [25] Breannan Smith, Chenglei Wu, He Wen, Patrick Peluse, Yaser Sheikh, Jessica K Hodgins, and Takaaki Shiratori. Constraining dense hand surface tracking with elasticity. ACM Transactions on Graphics (TOG), 39(6):1–14, 2020.
- [26] Adrian Spurr, Jie Song, Seonwook Park, and Otmar Hilliges. Cross-modal deep variational hand pose estimation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 89–98, 2018.
- [27] Xiao Tang, Tianyu Wang, and Chi-Wing Fu. Towards accurate alignment in real-time 3d hand-mesh reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 11698–11707, October 2021.
- [28] Dimitrios Tzionas, Luca Ballan, Abhilash Srikantha, Pablo Aponte, Marc Pollefeys, and Juergen Gall. Capturing hands in action using discriminative salient points and physics simulation. International Journal of Computer Vision, 118(2):172–193, 2016.
- [29] Jiayi Wang, Franziska Mueller, Florian Bernard, Suzanne Sorli, Oleksandr Sotnychenko, Neng Qian, Miguel A Otaduy, Dan Casas, and Christian Theobalt. Rgb2hands: real-time tracking of 3d hand interactions from monocular rgb video. ACM Transactions on Graphics (ToG), 39(6):1–16, 2020.
- [30] Nanyang Wang, Yinda Zhang, Zhuwen Li, Yanwei Fu, Wei Liu, and Yu-Gang Jiang. Pixel2mesh: Generating 3d mesh models from single rgb images. In Proceedings of the European conference on computer vision (ECCV), pages 52–67, 2018.
- [31] Baowen Zhang, Yangang Wang, Xiaoming Deng, Yinda Zhang, Ping Tan, Cuixia Ma, and Hongan Wang. Interacting two-hand 3d pose and shape reconstruction from single color image. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 11354–11363, 2021.
- [32] Hongwen Zhang, Yating Tian, Xinchi Zhou, Wanli Ouyang, Yebin Liu, Limin Wang, and Zhenan Sun. Pymaf: 3d human pose and shape regression with pyramidal mesh alignment feedback loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 11446–11456, 2021.
- [33] Xiong Zhang, Qiang Li, Hong Mo, Wenbo Zhang, and Wen Zheng. End-to-end hand mesh recovery from a monocular rgb image. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 2354–2364, 2019.
- [34] Yuxiao Zhou, Marc Habermann, Weipeng Xu, Ikhsanul Habibie, Christian Theobalt, and Feng Xu. Monocular real-time hand shape and motion capture using multi-modal data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 5346–5355, 2020.
- [35] Christian Zimmermann and Thomas Brox. Learning to estimate 3d hand pose from single rgb images. In Proceedings of the IEEE international conference on computer vision, pages 4903–4911, 2017.