Present address: ]Department of Physics, Syracuse University, Syracuse, NY

Introduction —  The mechanical stability of cells and tissues is largely governed by interconnected biopolymer networks such as actin and collagen. In the linear regime, the rigidity of networks of stiff fibers such as collagen is strongly dependent on the average connectivity or coordination $z$ Wyart et al. (2008); Broedersz et al. (2011); Das et al. (2012). While these structures undergo a mechanical phase transition from a floppy to a rigid state at the critical or isostatic connectivity $z_{c}$ Maxwell (1870), this threshold lies well above the physiological connectivity of fibrous networks in 3D Lindström et al. (2010, 2013); Jansen et al. (2018). Such subisostatic fiber networks, however, undergo a strain-controlled phase transition from floppy to rigid states when subject to a finite deformation Sheinman et al. (2012); Sharma et al. (2016a). This transition is critical and occurs at a threshold shear strain that depends on the network’s connectivity and geometry Feng et al. (2016); Sharma et al. (2016b); Licup et al. (2016). More recent work has shown that the mechanical stability of these networks can be understood in terms of emerging states of self-stress Vermeulen et al. (2017); Mao and Lubensky (2018); Rens and Lerner (2019); Damavandi et al. (2022a, b). Near the critical strain, the shear modulus exhibits a power law behavior with a non-mean-field exponent.

Here, we study the mechanics of subisostatic fiber networks under a finite isotropic extension. Using a 2D triangular lattice-based model, we calculate the nonlinear bulk modulus $B$ with varying bending stiffness of fibers. In the absence of bending interactions between fiber crosslinks, the bulk modulus remains zero until a critical extensional strain $\varepsilon_{c}$ at which $B$ jumps to a finite value (Fig. 1). The onset of a finite bulk modulus coincides with a network-spanning tensional pattern of bonds, as shown in Fig. 1. Near the critical extensional strain, we obtain various critical exponents and verify collapse of our modulus data using a Widom-like scaling function with two branches for strains above and below the threshold value. Moreover, we confirm a hyperscaling relation analogous to what has been previously derived for fiber networks under a simple shear strain Shivers et al. (2019a).

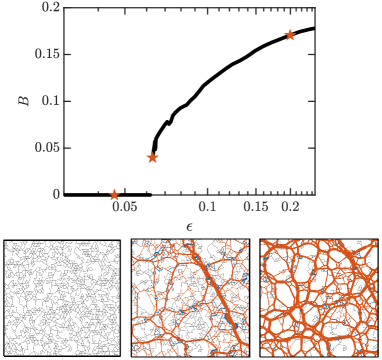
Model —  In order to study the mechanics of fiber networks under bulk extension, we begin with a triangular lattice in 2D. For every node or crosslink in a triangular structure, we have three well-defined crossing fibers. Thus, a full triangular network has a connectivity of 6. To avoid the trivial effect of a system-spanning fiber, we initially cut a random bond from each fiber Das et al. (2007); Broedersz et al. (2011). Consequently in order to mimic realistic subisostatic biopolymer networks, we reduce this connectivity to $z=3.3<z_{c}=2d$ by randomly removing bonds from the initial full lattice. We note that the crosslinks in our model are permanent and freely hinging. Network’s elastic energy include both stretching and bending terms

$$\mathcal{H}=\frac{\mu}{2}\sum_{\langle ij\rangle}\frac{(l_{ij}-l_{ij,0})^{2}}{l_{ij,0}}+\frac{\kappa}{2}\sum_{\langle ijk\rangle}{\frac{(\theta_{ijk}-\theta_{ijk,0})^{2}}{l_{ijk,0}}},$$

(1)

where $l_{ij,0}$ and $l_{ij}$ are the initial (relaxed) and current bond length between nodes $i$ and $j$, $\theta_{ijk,0}$ and $\theta_{ijk}$ are the initial and current angle between neighboring bonds $ij$ and $jk$, respectively, and $l_{ijk,0}=(l_{ij,0}+l_{jk,0})/2$. Here, $\mu$ is the stretching modulus and $\kappa$ is the bending rigidity of the fibers. The first summation is over all connected nodes and the second is over all nearest-neighbor bonds on the same fiber, i.e., collinear adjacent bonds in the initial configuration. We set $\mu=1$ in our simulations and vary the dimensionless bending stiffness $\tilde{\kappa}=\kappa/\mu\ell_{0}^{2}$, where $\ell_{0}=1$ is the average bond length in the undeformed lattice Licup et al. (2015).

Here, we study the nonlinear bulk modulus of diluted triangular networks under the following bulk deformation tensor

$$\Lambda_{B}(\varepsilon)=\begin{bmatrix}1+\varepsilon&0\\ 0&1+\varepsilon\end{bmatrix},$$

(2)

where $\varepsilon$ is the extensional strain. By applying a bulk strain $\varepsilon$, the network’s volume changes as $V=V_{0}(1+\varepsilon)^{2}$. We deform the network in a step-wise manner in a periodic box and minimize the elastic energy in Eq. (1) using FIRE Bitzek et al. (2006) at each strain point to obtain the minimum energy configuration. The stress components are calculated by

$$\sigma_{\alpha\beta}=\frac{1}{2V}\sum_{ij}f_{ij,\alpha}r_{ij,\beta}$$

(3)

where $V$ is the volume (area) of system, $f_{ij,\alpha}$ is the $\alpha$ component of the force exerted on node $i$ by node $j$, and $r_{ij,\beta}$ is the $\beta$ component of the displacement vector connecting nodes $i$ and $j$. The summation is taken over all nodes in the network. We find the nonlinear bulk modulus $B$ as

$$B=-V\frac{\partial P}{\partial V}=V\frac{\partial\sigma_{\perp}}{\partial V}=\frac{1}{2}(1+\varepsilon)\frac{\partial\sigma_{\perp}}{\partial\varepsilon},$$

(4)

where the pressure of the system is $P=-\sigma_{\perp}=-\frac{1}{d}(\sum_{i}\sigma_{ii})$ in $d$ dimensions. The volume of the system is not preserved under an applied isotropic extension, i.e., $V=V_{0}(1+\varepsilon)^{d}$ where $V_{0}$ is the initial volume. Here, we define the nonlinear bulk modulus in the deformed state of the network, which is different from a prior definition of this parameter Sheinman et al. (2012) that is defined in the undeformed volume. We note that we find the critical extensional strain $\varepsilon_{c}$ for every individual random sample using a bisection method. Unless otherwise stated, the results are averaged over 40 random samples. The error bars are the standard deviation for all samples.

Results —  Similar to the behavior observed under an applied shear strain Sharma et al. (2016a); Shivers et al. (2019a), we find that subisostatic central-force networks undergo a floppy to a rigid state at a critical extensional strain $\varepsilon_{c}$ that depends on the connectivity and geometry of the system. At $\varepsilon_{c}$, the nonlinear bulk modulus exhibits a discontinuity $B_{c}$ in agreement with findings of Refs. Merkel et al. (2019); Lee and Merkel (2022), analogous to the behavior of the nonlinear shear modulus at the critical shear strain $\gamma_{c}$ Vermeulen et al. (2017); Merkel et al. (2019); Rens (2019); Arzash et al. (2020).

As shown in Fig. 2c, the bulk modulus discontinuity at $\varepsilon_{c}$ appears to be larger than the shear modulus discontinuity at $\gamma_{c}$, both with a decreasing trend as we increase the system size. In the thermodynamic limit, we observe both finite $B_{c}$ and $K_{c}$. The jump in nonlinear bulk modulus at $\varepsilon_{c}$ is reminiscent of the behavior of linear bulk modulus of particulate systems at jamming Goodrich et al. (2012, 2014) and generic Penrose tilings Stenull and Lubensky (2014). However, for the present strain-controlled transition, this discontinuity is not a reflection of a first-order transition. Rather, since strain is a control variable analogous to temperature, this discontinuity is more analogous to a discontinuity of the heat capacity in a thermal transition at a critical point Shivers et al. (2019a).

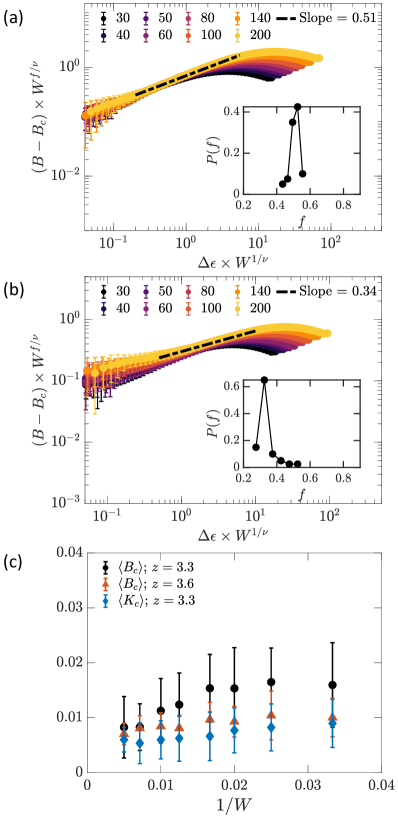
Near $\varepsilon_{c}$, we expect the following finite-size scaling relation to capture the behavior of $B$ in subisostatic central-force networks Arzash et al. (2020)

$$B-B_{c}=W^{-f/\nu}\mathcal{F}(\Delta\varepsilon W^{1/\nu}),$$

(5)

where $\Delta\varepsilon=\varepsilon-\varepsilon_{c}$, $f$ is the bulk modulus scaling exponent in the regime $\varepsilon>\varepsilon_{c}$, $\nu$ is the correlation length exponent, and $\mathcal{F}(x)$ is a scaling function that is expected to increase as $x^{f}$ for large arguments, in order to obtain a well-defined thermodynamic limit. Although we use the same notation for the scaling exponents as for networks under shear, we note that the corresponding exponents may have different values. Figure 2b shows the finite-size scaling behavior of $B$ in diluted triangular networks. In the critical region, we obtain $f=0.34\pm 0.05$ that is significantly smaller than the corresponding exponent $f=0.79\pm 0.07$ for the shear modulus. By increasing the connectivity of the network to $z=3.6$, we find that $f$ increases to $0.51\pm 0.03$ (Fig. 2a). We note that the dependence of critical exponents on $z$ for this transition has also been observed under a shear deformation Sharma et al. (2016a); Arzash et al. (2021). By plotting the bulk modulus discontinuity at $\varepsilon_{c}$, we also find a decrease in $B_{c}$ with increasing system size (Fig. 2c)), although with an apparent finite value in the thermodynamic limit.

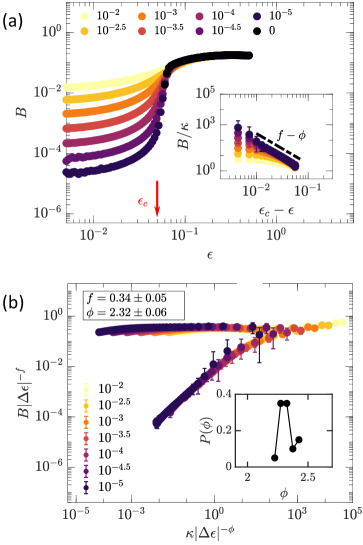
By introducing bending interactions, the subisostatic networks become stabilized in the small strain regime $\varepsilon<\varepsilon_{c}$ with a bulk modulus proportional to the bending stiffness $B\sim\kappa$. This also has the effect of moving the system away from the critical singularity and suppressing the discontinuity in $B$. The nonlinear bulk modulus follows a Widom-like scaling relation given by

$$B\approx\left|\varepsilon-\varepsilon_{c}\right|^{f}\mathcal{G}_{\pm}\left({\kappa}/{\left|\varepsilon-\varepsilon_{c}\right|^{\phi}}\right)$$

(6)

for $\kappa>0$, in which the branches of the scaling function $\mathcal{G}_{\pm}$ account for the bulk strain regimes above and below $\varepsilon_{c}$. Above the critical strain, $\mathcal{G}_{+}(x)$ is approximately constant for $x\ll 1$, while below the critical strain, we expect $\mathcal{G}_{-}(x)\sim x$ for $x\ll 1$, so that $B\sim\kappa|\varepsilon-\varepsilon_{c}|^{f-\phi}$. Near $\varepsilon_{c}$, however, continuity of $B$ requires $\mathcal{G}_{\pm}(x)\sim x^{f/\phi}$ for $x\gg 1$. Figure 3a shows $B$ versus $\varepsilon$ for triangular networks at $z=3.3$ with varying bending stiffness. In the subcritical region, we find $\phi=2.32\pm 0.06$. The data collapse of $B$ corresponding to Eq. (6) is shown in Fig. 3b. For networks with $z=3.6$, we obtain a Widom-like collapse of the modulus (not shown) similar to Fig. 6b using $\phi=2.33\pm 0.1$.

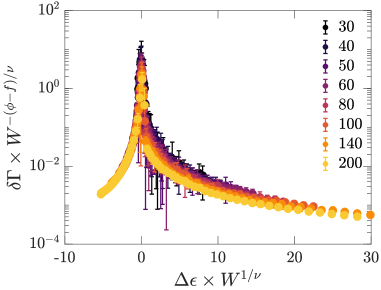
The scaling theory in Ref. Shivers et al. (2019a) can be generalized to athermal networks under an applied bulk strain $\varepsilon$. By following a similar renormalization procedure with $t=\varepsilon-\varepsilon_{c}$ and $B\sim\frac{\partial^{2}}{\partial t^{2}}h(t,\kappa)$, we derive the scaling relations in Ref. Shivers et al. (2019a) with $f$ and $\phi$ corresponding to the scaling exponents under an applied bulk strain. In order to test the hyperscaling relation $f=d\nu-2$, we measure the nonaffine fluctuations $\delta\Gamma$ under extensional strains as

$$\delta\Gamma=\frac{1}{Nl_{c}^{2}\delta\varepsilon^{2}}\sum_{i}{\lVert\delta\mathbf{u}_{i}^{\mathrm{NA}}\rVert^{2}}$$

(7)

in which $N$ is the number of nodes, $l_{c}$ is the average bond length, and $\delta\mathbf{u}_{i}^{\mathrm{NA}}=\delta\mathbf{u}_{i}-\delta\mathbf{u}_{i}^{\mathrm{A}}$ is the nonaffine component of the displacement of node $i$ due to the incremental strain $\delta\varepsilon$. Figure 4 shows the finite-size scaling collapse of $\delta\Gamma$ using the obtained exponents $f$ and $\phi$. The correlation length exponent $\nu$ here assumes the hyperscaling relation $\nu=(f+2)/2\simeq 1.17$. The data collapse confirms that our scaling theory works under an applied volumetric strain.

Discussion —  In this work, we study the behavior of nonlinear bulk modulus $B$ of subisostatic fiber networks using a diluted triangular model. Similar to previous studies of fiber networks under shear Sharma et al. (2016a); Shivers et al. (2019a), we observe that subisostatic networks with central force interactions undergo a critical transition from a floppy to a rigid state as we increase the isotropic extensional strain. By approaching the critical extensional strain from above, we find a power law scaling behavior of $B$ with a non-mean-field exponent that is much smaller than the observed shear modulus exponent for the same model Arzash et al. (2020). By introducing finite bending rigidity $\kappa$, these networks become stable in the linear regime with $B\sim\kappa$. The stabilizing effect of $\kappa$ is evident in a collapse of our modulus data using a Widom-like function with two branches (Fig. 3). By studying the nonaffine strain fluctuations, we confirm that the recent scaling theory that was derived for fiber networks under shear also holds for a bulk deformation, although with different exponents. Our results are in agreement with the observed floppy-to-rigid transition in prior work on bulk modulus of fiber networks Sheinman et al. (2012). Here, however, we focus on the critical aspects of this transition. Furthermore, based on prior studies on various fiber models in 2D and 3D Licup et al. (2016); Rens et al. (2016); Shivers et al. (2019b); Arzash et al. (2019, 2021), we expect to observe an analogous behavior in a different 2D or 3D system under a bulk strain.