Measuring the Virial Factor in SDSS DR7 AGNs with Redshifted H$\beta$ and H$\alpha$ Broad Emission Lines

Black hole mass, $M_{\bullet}$, is an important fundamental parameter of black hole. Reliable measurement of $M_{\bullet}$ always is a key issue of black hole related researches. For active galactic nuclei (AGNs), the reverberation mapping (RM) method or the relevant secondary methods based on single-epoch spectra were widely used to measure $M_{\bullet}$ by a virial mass $M_{\rm{RM}}=fv^{2}_{\rm{FWHM}}r_{\rm{BLR}}/G$ when clouds in broad-line region (BLR) are in virialized motion, where $f$ is the virial factor, $v_{\rm{FWHM}}$ is full width at half maximum of broad emission line, $r_{\rm{BLR}}$ is radius of BLR, and $G$ is the gravitational constant (e.g., Peterson et al., 2004). However, $f$ is very uncertain due to the unclear kinematics and geometry of BLR (e.g., Peterson et al., 2004; Woo et al., 2015). $f$ is commonly considered to be the main source of uncertainty in $M_{\rm{RM}}$. The reverberation-based masses are themselves uncertain typically by a factor of $\sim$ 2.9 (Onken et al., 2004), and the absolute uncertainties in $M_{\rm{RM}}$ given by the secondary methods are typically around a factor of 4 (Vestergaard & Peterson, 2006). If $v_{\rm{FWHM}}$ is replaced with the line width $\sigma_{\rm{line}}$, the second moment of emission line, $f$ becomes $f_{\sigma}$. Based on the photoionization assumption (e.g., Blandford & McKee, 1982; Peterson, 1993), $r_{\rm{BLR}}=\tau_{\rm{ob}}c/(1+z)$, where $c$ is the speed of light, $z$ is the cosmological redshift of source, and $\tau_{\rm{ob}}$ is the observed time lag of the broad-line variations relative to the continuum ones. For non–RM AGNs studied by the secondary methods, $r_{\rm{BLR}}$ can be estimated with the empirical $r_{\rm{BLR}}$–$L_{\rm{5100}}$ relation for H$\beta$ emission line of the RM AGNs, where $L_{\rm{5100}}$ is AGN continuum luminosity at rest-frame wavelength 5100 Å (e.g., Kaspi et al., 2000; Bentz et al., 2013; Du et al., 2018b; Du & Wang, 2019; Yu et al., 2020).

RM surveys had been carried out (e.g., King et al., 2015; Shen et al., 2015a, b, 2016; Grier et al., 2017; Hoormann et al., 2019; Shen et al., 2019). Non-survey RM observation researches had been made for more than 100 AGNs over the last several decades (e.g., Kaspi & Netzer, 1999; Kaspi et al., 2000; Peterson et al., 2005; Bentz et al., 2006; Kaspi et al., 2007; Bentz et al., 2010; Denney et al., 2010; Barth et al., 2011; Haas et al., 2011; Pozo Nuñez et al., 2012; Du et al., 2014; Pei et al., 2014; Wang et al., 2014; Barth et al., 2015; Du et al., 2015; Hu et al., 2015; Bentz et al., 2016; Du et al., 2016; Lu et al., 2016; Pei et al., 2017; Du et al., 2018a, b; Xiao et al., 2018a, b; Zhang et al., 2019; Hu et al., 2020; Bentz et al., 2021; Feng et al., 2021a, b; Hu et al., 2021; Li et al., 2021; Lu et al., 2021; Bentz et al., 2022; Li et al., 2022; Bentz et al., 2023). The single-epoch spectra had been widely used to estimate $M_{\rm{RM}}$ in studies of high-$z$ quasars (e.g., Willott et al., 2010; Wu et al., 2015; Wang et al., 2019; Eilers et al., 2023), and on statistics of AGNs, such as the Sloan Digital Sky Survey (SDSS) quasars (e.g., Hu et al., 2008; Liu et al., 2019). Based on the $M_{\bullet}-\sigma_{\ast}$ relation for the low-$z$ inactive and quiescent galaxies with $\sigma_{\ast}$ to be stellar velocity dispersion of galaxy bulge (e.g., Tremaine et al., 2002; Onken et al., 2004; Piotrovich et al., 2015; Woo et al., 2015), these derived averages of $\langle f\rangle\approx 1$ and/or $\langle f_{\rm{\sigma}}\rangle\approx 5$ were usually used to estimate $M_{\rm{RM}}$ by the RM and/or single-epoch spectra of AGNs. Therefore, measuring $f$ and/or $f_{\rm{\sigma}}$ independently by a new method for individual AGNs is necessary and important to understand the physics of BLR, and the issues related to masses of supermassive black holes (SMBHs), e.g., the formation and growth of SMBHs at $z\gtrsim 6$ (e.g., Wu et al., 2015; Fan et al., 2023), coevolution (or not) of SMBHs and host galaxies (e.g., Tremaine et al., 2002; Kormendy & Ho, 2003; Woo et al., 2013; Caglar et al., 2020), etc.

Some efforts have been made on an object by object basis for small samples of AGNs using high-fidelity RM techniques (e.g., Pancoast et al., 2014a, b) or by using spectral fitting methods (Mejía-Restrepo et al., 2018, and references therein). Liu et al. (2017) proposed a new method to measure $f$ based on the widths and shifts of redward shifted broad emission lines for the RM AGNs. Based on SDSS DR 5 quasars with redward shifted H$\beta$ and Fe ii broad emission lines, Liu et al. (2022) made further efforts of researching $f$ and $f_{\rm{\sigma}}$. Fe iii$\lambda\lambda$ 2039–2113 UV line blend comes from an inner region of BLR (Mediavilla et al., 2018; Mediavilla & Jiménez-Vicente, 2021), and for 10 lensed quasars of higher Eddington ratio, the redward shifted Fe iii blend was used to estimate $f$ with $\langle f\rangle=14.3$ much larger than $\langle f\rangle\approx 1$ (Mediavilla et al., 2020). However, the origins of broad emission lines and BLR are yet unclear for AGNs (e.g., Wang et al., 2017). Thus, it is unclear of the origin of redward shifts of broad emission lines. The redward shifts of broad emission lines are commonly believed to be from inflow (e.g., Hu et al., 2008). Inflow can generate the redward shifts of broad absorption lines, but the broad absorption and emission lines may be from different gas regions due to their distinct velocities (Zhou et al., 2019).

RM observations of Mrk 817 suggest that the redward shifts of broad emission lines do not originate from inflow because of their redward asymmetric velocity-resolved lag maps (Lu et al., 2021), which are not consistent with the blueward asymmetric maps expected from inflow. Redward shifts of broad emission lines in the RM observations of Mrk 110 follow the gravitational redshift prediction (Kollatschny, 2003). The gravitational interpretation of redward shift of the Fe iii blend is preferred than alternative explanations, such as inflow, that will need additional physics to explain the observed correlation between the width and redward shift of the blend (Mediavilla et al., 2018). A sign of the gravitational redshift $z_{\rm{g}}$ was found in a statistical sense for broad H$\beta$ in the single-epoch spectra of SDSS DR 7 quasars (Tremaine et al., 2014). Based on the widths and asymmetries of H$\alpha$ and H$\beta$ broad emission line profiles in a sample of type-1 AGNs taken from SDSS DR 16, Rakić (2022) showed that the BLR gas seems to be virialized. The velocity-resolved lag maps of H$\beta$ broad emission line for Mrk 50 and SBS 1518+593 show characteristic of Keplerian disk or virialized motion (Barth et al., 2011; Du et al., 2018a). Thus, it is likely that the redward shifts of broad emission lines originate from the gravity of the central black hole.

Radiation pressure from accretion disk has significant influences on the stability and dynamics of clouds in BLR (e.g., Marconi et al., 2008; Netzer & Marziani, 2010; Krause et al., 2011, 2012; Naddaf et al., 2021). The dynamics of clouds can determine the three-dimensional geometry of BLR (Naddaf et al., 2021). However, radiation pressure was not considered in estimating $M_{\rm{RM}}$, and the virial factor had been believed to be only from the geometric effect of BLR. Lu et al. (2016) found that the BLR of NGC 5548 could be jointly controlled by the radiation pressure force from accretion disk and the gravity of the central black hole. Krause et al. (2011) found that stable orbits of clouds in BLR exist for very sub-Keplerian rotation, for which the radiation pressure force contributes substantially to the force budget. Thus, the radiation pressure force may result in significant influence on the virial factor. Based on redward-shifted H$\beta$ and Fe ii broad emission lines for a sample of 1973 $z<0.8$ SDSS DR5 quasars, Liu et al. (2022) found a positive correlation of the virial factor with the dimensionless accretion rate or the Eddington ratio. They suggested that the radiation pressure force is a significant contributor to the virial factor, and that the redward shift of H$\beta$ broad emission line is mainly from the gravity of the black hole. In this work, more than 8000 SDSS DR7 AGNs with redward-shifted H$\beta$ and H$\alpha$ broad emission lines, out of Table 2 in Liu et al. (2019), will be adopted to investigate the virial factor, relations of the virial factor with other physical quantities, the origin of the redward shifts of the broad Balmer emission lines, and the implications of the $f$ correction.

The structure is as follows. Section 2 presents method. Section 3 describes sample selection. Section 4 presents analysis and results. Section 5 is potential influence on quasars at $z\gtrsim 6$. Section 6 is potential influence on $M_{\bullet}-\sigma_{\ast}$ map of AGNs. Section 7 presents discussion, and Section 8 is conclusion. Throughout this paper, we assume a standard cosmology with $H_{0}=70\rm{\/\ km\/\ s^{-1}\/\ Mpc^{-1}}$, $\Omega_{\rm{M}}$ = 0.3, and $\Omega_{\rm{\Lambda}}$= 0.7 (Spergel et al., 2007).

A BLR cloud is subject to gravity of black hole, $F_{\rm{g}}$, and radiation pressure force, $F_{\rm{r}}$, due to central continuum radiation. The total mechanical energy and angular momentum are conserved for the BLR clouds because $F_{\rm{g}}$ and $F_{\rm{r}}$ are central forces. Under various assumptions, $F_{\rm{r}}$ can be calculated for more than hundreds of thousands of lines, with detailed photoionization, radiative transfer, and energy balance calculations (e.g., Dannen et al., 2019). In principle, $M_{\bullet}$ could be estimated by the BLR cloud motions when the numerical calculation methods give $F_{\rm{r}}$. However, the various assumptions may significantly influence the reliability of $F_{\rm{r}}$. Especially, many unknown physical parameters are likely various for different AGNs. Thus, a new method was proposed to measure $f$ and then $M_{\rm{RM}}$, avoiding to use the averages of the virial factor or the numerical calculation of $F_{\rm{r}}$ (Liu et al., 2017, 2022).

The virial factor formula in Liu et al. (2022) was derived from the Schwarzschild metric for clouds in the virialized motion

where the gravitational and transverse Doppler shifts are taken into account. If $v_{\rm{FWHM}}$ is replaced with $\sigma_{\rm{line}}$, $f$ becomes $f_{\sigma}$. As $z_{\rm{g}}\ll 1$ or $r_{\rm{g}}/r_{\rm{BLR}}\ll 1$ for broad emission lines (the gravitational radius $r_{\rm{g}}=GM_{\bullet}/c^{2}$), we have

Mediavilla & Jiménez-Vicente (2021) pinpointed that the observed redward shift of the Fe iii$\lambda\lambda$ 2039–2113 emission line blend in quasars originates from the gravity of black hole, while these Fe iii$\lambda\lambda$ 2039–2113 emission lines are broad emission lines. Furthermore, their redward shifts and line widths follow the gravitational redshift prediction (see Figure 4 in Mediavilla et al., 2018). So, the broad emission line position and width should be not only determined by the kinematics of BLR, but also determined by the gravity of black hole. The virialized assumption in measuring $M_{\rm{RM}}$ will ensure that the line position should be governed by the gravity of black hole for the redward shifted broad emission lines in AGNs (this will be tested in the next section). The same method as in Liu et al. (2017, 2022) was used to estimate the virial factor in Mediavilla et al. (2018) (see their Equation 5). Thus, the method in this work, evolved from Liu et al. (2017), is reliable, and the assumption of the gravitational redshift is reasonable.

The Schwarzschild metric is valid at the optical BLR scales, and Equation (1) is valid for a disklike BLR (see Liu et al., 2022). The disklike BLR is preferred by some RM observations of AGNs, e.g., NGC 3516 (e.g., Denney et al., 2010; Feng et al., 2021a), and the VLTI instrument GRAVITY observations of quasar 3C 273 (Sturm et al., 2018). For rapidly rotating BLR clouds, the relativistic beaming effect can give rise to a profile asymmetry with an enhanced blue side in broad emission lines, i.e., blueshifts of broad emission lines (Mediavilla & Insertis, 1989). Thus, the relativistic beaming effect should be neglected for the redward shifted broad emission lines, which should be dominated by the gravitational redshift and transverse Doppler effects. The reliability of the redward shift method was confirmed by the consistent masses estimated from Equations (4) and (7) based on 4 broad emission lines for Mrk 110 (see Figure 2 of Liu et al., 2017). Hereafter, $M_{\rm{RM}}$ denotes $M_{\bullet}$ measured with the RM method and/or the relevant secondary methods, $f_{\rm{g}}$ denotes $\langle f\rangle=1$ for $v_{\rm{FWHM}}$ or $\langle f_{\rm{\sigma}}\rangle=5.5$ for $\sigma_{\rm{line}}$, $M_{\rm{RM}}\equiv M_{\rm{RM}}(f_{\rm{g}}=1)$, the Eddington luminosity $L_{\rm{Edd}}\equiv L_{\rm{Edd}}(f_{\rm{g}}=1)$, the Eddington ratio $L_{\rm{bol}}/L_{\rm{Edd}}\equiv L_{\rm{bol}}/L_{\rm{Edd}}(f_{\rm{g}}=1)$, and $r_{\rm{g}}\equiv r_{\rm{g}}(f_{\rm{g}}=1)$.

Liu et al. (2019) reported a comprehensive and uniform sample of 14584 broad-line AGNs with $z<0.35$ from the SDSS DR7. The stellar continuum was properly removed for each spectrum with significant host absorption line features, and careful analyses of emission line spectra, particularly in the H$\alpha$ and H$\beta$ wavebands, were carried out. The line widths and line centroid wavelengths of the H$\alpha$, H$\beta$, and [O iii] spectra are given in Table 2 of Liu et al. (2019). The redward shifts of broad emission lines H$\beta$ and H$\alpha$ are defined as

where ${\lambda_{\rm{b}}}$ is the centroid wavelength of broad emission line corrected by the cosmological redshift $z_{\rm{SDSS}}$ given by the SDSS site (Liu et al., 2019), ${\lambda_{\rm{n}}}$ is the centroid wavelength of narrow emission line corrected by $z_{\rm{SDSS}}$, and $\lambda_{\rm{0}}$ is the vacuum wavelength of spectrum line ($\lambda_{\rm{0}}=4862.68$ $\rm{\AA}$ for H$\beta$, $\lambda_{\rm{0}}=6564.61$ $\rm{\AA}$ for H$\alpha$, and $\lambda_{\rm{0}}=5008.24$ $\rm{\AA}$ for [O iii]$\lambda 5007$)¹¹1https://classic.sdss.org/dr6/algorithms/linestable.html.

Because of the absence of the uncertainty of ${\lambda_{\rm{n}}}$ for H$\beta$ in Table 2 of Liu et al. (2019), and in order to unify standard of estimating $z_{\rm{g}}$ for the broad H$\beta$ and H$\alpha$, the [O iii]$\lambda 5007$ line is used in Equation (3). First, one of choice criteria is AGN’s flag = 0, which means no emission line with multiple peaks (Liu et al., 2019), because that the multiple peaks of emisson lines may be from dual AGNs (e.g., Wang et al., 2009). Second, AGNs are selected on the basis of $z_{\rm{g}}>0$ and $z_{\rm{g}}-\sigma(z_{\rm{g}})>0$ for the broad H$\beta$ and H$\alpha$, where $\sigma(z_{\rm{g}})$ is the uncertainty of $z_{\rm{g}}$. Third, AGNs are selected on the basis of $v_{\rm{FWHM}}>0$ and $v_{\rm{FWHM}}-\sigma(v_{\rm{FWHM}})>0$ for the broad H$\beta$ and H$\alpha$, where $\sigma(v_{\rm{FWHM}})$ is the uncertainty of $v_{\rm{FWHM}}$. The selection conditions of $z_{\rm{g}}>0$ and $z_{\rm{g}}-\sigma(z_{\rm{g}})>0$ make sure that the shifts of broad emission lines are redward within $1\sigma$ uncertainties. Because the empirical $r_{\rm{BLR}}$–$L_{\rm{5100}}$ relation is established for broad emission line H$\beta$, the relevant researches on the virial factor are made with the broad H$\beta$ and H$\alpha$ in this work. 9185 AGNs are selected out of the 14584 AGNs as Sample 1 only for the broad H$\beta$. 9271 AGNs are selected out of the 14584 AGNs as Sample 2 only for the broad H$\alpha$. The cross-identified AGNs in Samples 1 and 2 are used as Sample 3 that contains 8169 AGNs with $z_{\rm{g}}$ of the broad H$\beta$ and H$\alpha$.

Some physical quantities are taken or estimated from Table 2 in Liu et al. (2019), including $v_{\rm{FWHM}}$(H$\beta$), $v_{\rm{FWHM}}$(H$\alpha$), $z_{\rm{g}}$(H$\beta$), $z_{\rm{g}}$(H$\alpha$), $L_{\rm{5100}}$, $M_{\rm{RM}}$, $L_{\rm{bol}}/L_{\rm{Edd}}$, and the dimensionless accretion rate $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$. The bolometric luminosity $L_{\rm{bol}}$ was estimated in Liu et al. (2019) using $L_{\rm{bol}}=9.8L_{\rm{5100}}$ (McLure & Dunlop, 2004). The details of samples are listed in Tables 1–3. The virial factors, $f$(H$\beta$) and $f$(H$\alpha$), are estimated by Equation (1) for the broad H$\beta$ and H$\alpha$ (see Tables 1–3). $\mathscr{\dot{M}}_{f_{\rm{g}}=1}=L_{\rm{bol}}/L_{\rm{Edd}}/\eta$, where $\eta$ is the efficiency of converting rest-mass energy to radiation. Hereafter, in addition to special statement, we adopt $\eta=0.038$ (Du et al., 2015).

For our selected AGNs, $L_{\rm{5100}}$ spans four orders of magnitude, $M_{\rm{RM}}$ spans more than four orders of magnitude, and $L_{\rm{bol}}/L_{\rm{Edd}}$ spans more than three orders of magnitude. These parameters cover at least one order of magnitude wider than those in Liu et al. (2022). The measured values of $f$ span more than three orders of magnitude, which cover at least one order of magnitude wider than those in Liu et al. (2022). These much wider parameters can ensure that this work is feasible.

In order to study the correlation between $f$, $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$, $L_{\rm{5100}}$, and $v_{\rm{FWHM}}$, as well as $z_{\rm{g}}$ and $r_{\rm{BLR}}/r_{\rm{g}}$, we will perform the Spearman’s rank test and/or the Pearson’s correlation analysis. The bisector linear regression (Isobe et al., 1990) is performed to obtain the slope and intercept coefficients of $y=a+bx$ in fitting our samples, if needed for some quantities. The partial correlation analysis is used to further verify the presence of correlation between $f$ and $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$. All correlation analyses are calculated in log-space. The SPEAR (Press et al., 1992) is used to calculate the Spearman’s rank correlation coefficient $r_{\rm{s}}$ and the $p$-value $P_{\rm{s}}$ of the hypothesis test. The PEARSN (Press et al., 1992) is used to give the Pearson’s correlation coefficient $r$ and the $p$-value $P$ of the hypothesis test.

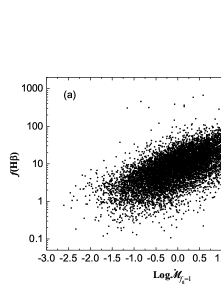
The Spearman’s rank correlation test is run for Samples 1–3, and the analysis results are listed in Table 4. There are positive correlations between the virial factor and $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ or $L_{\rm{bol}}/L_{\rm{Edd}}$ for Samples 1–3 (see Figure 1 and Table 4). The results from the Pearson’s correlation analysis are listed in Table 5. The bisector regression fit can give $a$ and $b$, as well as their uncertainties $\Delta a$ and $\Delta b$, but it does not take into account the obervational errors of data (Isobe et al., 1990). So, based on Monte Carlo simulated data sets from the obervational values and errors, we calculate the best parameters using the bisector regression, and repeat this procedure $10^{4}$ times to generate the distributions of $a_{\rm{MC}}$, $b_{\rm{MC}}$, $\Delta a_{\rm{MC}}$, and $\Delta b_{\rm{MC}}$. The means of the $a_{\rm{MC}}$ and $b_{\rm{MC}}$ distributions are taken to be the final best parameters of $a$ and $b$, respectively. The corresponding uncertainties are given by the combinations of the means of the $\Delta a_{\rm{MC}}$ and $\Delta b_{\rm{MC}}$ distributions with the standard deviations of the $a_{\rm{MC}}$ and $b_{\rm{MC}}$ distributions, respectively. The bisector regression is run for $\log f=a+b\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$, and the fitting results are

where the $p$-values of the hypothesis test are $<10^{-40}$, and in the fittings, the uncertainty of $\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ is taken to be 0.4 determined by the uncertainty of 0.4 dex usually used in $M_{\rm{RM}}$. Equations (4$a$)–(4$d$) correspond to the best fits to data sets ($f$,$\mathscr{\dot{M}}_{f_{\rm{g}}=1}$) for H$\beta$ in Sample 1, H$\alpha$ in Sample 2, H$\beta$ in Sample 3, and H$\alpha$ in Sample 3, respectively. It is clear that $f\propto\mathscr{\dot{M}}_{f_{\rm{g}}=1}^{0.8-0.9}$, and then $f\propto(L_{\rm{bol}}/L_{\rm{Edd}})^{0.8-0.9}$.

Since $f$ may be affected by $F_{\rm{r}}$, it is possible that $f$ is correlated with $L_{\rm{5100}}$. In fact, there are weak correlations between $f$ and $L_{\rm{5100}}$ (see Tables 4–5). Also, the dependence of $f$ and $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ on $v_{\rm{FWHM}}$ may result in a false correlation. Thus, the partial correlation analysis is needed to test the $\log f$–$\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ correlation when excluding the influence of $v_{\rm{FWHM}}$ and/or $L_{\rm{5100}}$. Based on the Pearson’s correlation coefficients in Table 5, the 1st order partial correlation analysis gives a confidence level of $>$ 99.99% for the $\log f$–$\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ correlation when excluding the dependence on $L_{\rm{5100}}$ or $v_{\rm{FWHM}}$ (see Table 6). The 2nd order partial correlation analysis gives a confidence level of $>$ 99.99% for the $\log f$–$\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ correlation when excluding the dependence on $v_{\rm{FWHM}}$ and $L_{\rm{5100}}$, except for the broad H$\alpha$ in Sample 3 at a confidence level of 99.84% (see Table 6). Thus, the positive correlation exists between $f$ and $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$. This positive correlation is qualitatively consistent with the logical expectation when the overall effect of $F_{\rm{r}}$ on the BLR clouds is taken into account to estimate $M_{\rm{RM}}$. In addition, $f>f_{\rm{g}}=1$ for H$\beta$ and H$\alpha$ in most of AGNs (see Figure 1): $>$ 96.5% for H$\beta$ in Sample 1, $>$ 97.2% for H$\alpha$ in Sample 2, and $>$ 97.7% for H$\beta$ and $>$ 97.4% for H$\alpha$ in Sample 3.

In order to test the gravitational origin of the redward shift of broad emission line, we compare $z_{\rm{g}}$ to $r_{\rm{BLR}}/r_{\rm{g}}$, the dimensionless radius of BLR in units of $r_{\rm{g}}$. The Spearman’s rank correlation test shows negative correlation between $z_{\rm{g}}$ and $r_{\rm{BLR}}/r_{\rm{g}}$ (see Table 4). This negative correlation is qualitatively consistent with the expectation that $z_{\rm{g}}$ is mainly from the gravity of the central black hole, because that $M_{\rm{RM}}$ can not be corrected individually for each AGN due to the absence of the individual virial factor that is independent of $z_{\rm{g}}$. So, we can make the overall correction of $M_{\rm{RM}}$ to be $M_{\rm{RM}}/\langle f\rangle$, where $\langle f\rangle$ is the average of $f$ in Samples 1–3 (see Figure 2). This overall correction is equivalent to the parallel shift of the data point in Figure 2. The negative correlation expectation is basically consistent with the trend between $z_{\rm{g}}$ and $r_{\rm{BLR}}/r_{\rm{g}}/\langle f\rangle$ in Figure 2. This indicates that $z_{\rm{g}}$ is dominated by the gravity of the central black hole. In addition, $r_{\rm{g}}/r_{\rm{BLR}}\lesssim 0.01\ll 1$ and $\langle f\rangle r_{\rm{g}}/r_{\rm{BLR}}<0.1$ for AGNs in Tables 1–3. $\langle f\rangle r_{\rm{g}}/r_{\rm{BLR}}\lesssim 0.01$ for $>$ 96% AGNs in Sample 1, $>$ 97% AGNs in Sample 2, and for $>$ 96% AGNs in Sample 3. Thus, the Schwarzschild metric is valid and matches the weak-field limit at the optical BLR scales of AGNs in our samples, which are conditions on the validity of Equation (1) (see Liu et al., 2022).

Since $f>1$ for most of SDSS AGNs in Samples 1–3, the $f$ correction might result in substantial influence on $M_{\rm{RM}}$ and $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$. We choose 8169 AGNs in Sample 3 to illustrate this influence. On average, the corrected $M_{\rm{RM}}$ becomes larger by one order of magnitude than $M_{\rm{RM}}$, and the corrected $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ decreases by about 10 times (see Figure 3). The substantial increase of $M_{\rm{RM}}$ will significantly impact the black hole mass function of these SDSS AGNs, e.g., leading to more AGNs with higher masses. The substantial decrease of $\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ loosens the requirement for accretion rate of accretion disk, and might make the distinction between high- and low-accreting sources less obvious. If $L_{\rm{bol}}/L_{\rm{Edd}}\geq 0.1$, i.e., $\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}\geq 0.42$, for high-accreting sources, the percent of AGNs with $\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}\geq 0.42$ is 31.4%, but the percent of AGNs with $\log(\mathscr{\dot{M}}_{f_{\rm{g}}=1}/f)\geq 0.42$ is only 0.3% (see Figure 3). The percent of high-accreting sources is decreased by about 100 times due to the $f$ correction. In a sense, the $f$ correction blurs the distinction between high- and low-accreting sources.

The virial factor of H$\beta$ is consistent with that of H$\alpha$ for 8169 AGNs in Sample 3 (see Figure 4). The H$\alpha$ lags are consistent with or (slightly) larger than the H$\beta$ lags for RM AGNs (e.g., Kaspi et al., 2000; Bentz et al., 2010; Grier et al., 2017). Because the H$\alpha$ optical depth is larger than the H$\beta$ optical depth, the optical depth effects may result in the larger H$\alpha$ lags that cause the H$\alpha$ emission line to seemingly appear at the larger distances than H$\beta$ (see Bentz et al., 2010), even though the H$\beta$ and H$\alpha$ broad emission lines are from the same region. Thus, it seems that $r_{\rm{BLR}}$(H$\beta$) $\approx r_{\rm{BLR}}$(H$\alpha$). For broad emission lines with different $r_{\rm{BLR}}$, there will be $f\propto r_{\rm{BLR}}^{\alpha}$ ($\alpha>0$) as $F_{\rm{r}}$ is considered and the BLR clouds are in the virialized motion for a given AGN (Liu et al., 2017). The H$\beta$ and H$\alpha$ BLRs have similar virialized kinematics for type-1 AGNs in SDSS DR 16 (Rakić, 2022). If $r_{\rm{BLR}}$(H$\beta$) $\approx r_{\rm{BLR}}$(H$\alpha$) and $f\propto r_{\rm{BLR}}^{\alpha}$, it will be expected that $f$(H$\beta$) is on the whole consistent with $f$(H$\alpha$) for AGNs in Sample 3, as shown in Figure 4.

Quasars at $z\gtrsim 6$ can probe the formation and growth of SMBHs in the Universe within the first billion years after the Big Bang. The quasars, with $M_{\rm{RM}}\gtrsim 10^{9}M_{\odot}$ at $z\gtrsim 7$ and with $M_{\rm{RM}}\gtrsim 10^{10}M_{\odot}$ at $z\gtrsim 6$, make the formation and growth of SMBHs ever more challenging (e.g., Wu et al., 2015; Fan et al., 2023). These SMBHs will need a combination of massive early black hole seeds with highly efficient and sustained accretion (e.g., Fan et al., 2023). However, the single-epoch spectrum method had been widely used to estimate $M_{\rm{RM}}$ of the high-$z$ quasars (e.g., Willott et al., 2010; Wu et al., 2015; Wang et al., 2019; Eilers et al., 2023), and this may result in underestimation of $M_{\rm{RM}}$, overestimation of $L_{\rm{bol}}/L_{\rm{Edd}}$, and significant influence on the formation and growth of SMBHs in the early Universe. Based on Equation (4), We will use $\log f=0.8+0.8\log\mathscr{\dot{M}}_{f_{\rm{g}}=1}$ to estimate $f$ and study its influence for quasars at $z\gtrsim 6$.

There are 113 quasars at $6\lesssim z\lesssim 8$ with reliable Mg ii-based black hole mass estimates (Fan et al., 2023). These 113 quasars have $\langle f\rangle=78$ ($f=$ 12–189), $\langle\log(M_{\rm{RM}}/M_{\odot})\rangle=9.0$, $\langle\log(fM_{\rm{RM}}/M_{\odot})\rangle=10.9$, and $\langle L_{\rm{bol}}/L_{\rm{Edd}}/f\rangle=0.01$ (see Table 7). The $f$ correction makes $M_{\rm{RM}}$ increase by one–two orders of magnitude. Also, substantially reduced $L_{\rm{bol}}/L_{\rm{Edd}}/f=$ 0.007–0.014 will make these 113 quasars accreting at well below the Eddington limit, although likely in the radiatively efficient regime via a geometrically thin, optically thick accretion disk (Shakura & Sunyaev, 1973). Based on Equation (7) in Fan et al. (2023), $M_{\bullet}(t)\propto\exp(t)$, the growth times of SMBHs in these quasars will increase by a factor of 2.5–5.2 due to the $f$ correction. Thus, the black hole seeds don’t seem to have enough time to grow up for SMBHs in quasars at $z\gtrsim 6$, and this gives more strong constraints on the formation and growth of the black hole seeds. Thus, the $f$ correction will make it more difficult to explain the formation and growth of SMBHs at $z\gtrsim 6$, e.g., larger masses of SMBHs need more massive early black hole seeds and/or longer growth times. Bogdán et al. (2023) found evidence for heavy-seed origin of early SMBHs from a $z\approx$10 X-ray quasar. Our results of corrected masses support heavy-seed origin scenarios of early SMBHs.

The highest redshift quasar J031343.84-180636.40, at $z=7.6423$, has $\log(M_{\rm{RM}}/M_{\odot})=9.2$, $\log(fM_{\rm{RM}}/M_{\odot})=11.0$, and $L_{\rm{bol}}/L_{\rm{Edd}}/f=0.01$. Quasar J0100+2802, the most luminous quasar known at $z>6$, has $\log(M_{\rm{RM}}/M_{\odot})\sim 10$, and $L_{\rm{bol}}/L_{\rm{Edd}}\sim 0.8$ (Wu et al., 2015). So, J0100+2802 has $\log(fM_{\rm{RM}}/M_{\odot})\sim 12$, and $L_{\rm{bol}}/L_{\rm{Edd}}/f\sim 0.01$. Quasar J140821.67+025733.2, at $z=2.055$, has a black hole mass of $10^{11.3}M_{\odot}$ with the uncertainty of 0.4 dex (Kozłowski, 2017). It seems reasonable that J0100+2802 has $\log(fM_{\rm{RM}}/M_{\odot})\sim 12$ with the uncertainty of 0.4. Recently, Kokorev et al. (2023) found an AGN at $z=8.50$ with an H$\beta$-based mass of $\log(M_{\rm{RM}}/M_{\odot})=8.2$, and $L_{\rm{bol}}/L_{\rm{Edd}}\sim 0.33$. We have $\log(fM_{\rm{RM}}/M_{\odot})\sim 9.7$, and $L_{\rm{bol}}/L_{\rm{Edd}}/f\sim 0.01$ for this AGN. In addition, Samples 1–3 each have $\langle L_{\rm{bol}}/L_{\rm{Edd}}/f\rangle=0.01$. It is interesting that $\langle L_{\rm{bol}}/L_{\rm{Edd}}/f\rangle=0.01$ exists for quasars/AGNs at $z<0.35$ and $z\gtrsim 6$, and perhaps it is a coincidence.