Measurement of the $e^{+}e^{-}\to\pi^{+}\pi^{-}\pi^{0}$ cross section from 0.7 GeV to 3.0 GeV
via initial-state radiation

The Standard Model (SM) of particle physics has so far successfully withstood most of the challenges it has been confronted with. However, there are still deficiencies in the SM, and the search for physics beyond the SM (‘New Physics’) is a major effort nowadays. A hint for New Physics might come from the anomalous magnetic moment of the muon, $a_{\mu}\equiv\frac{1}{2}(g_{\mu}-2)$. A discrepancy of $(27.06\pm 7.26)\times 10^{-10}$, corresponding to 3.7 standard deviations, between the direct measurement c_bnl and the SM prediction c_thomas_2018 has been found. New experiments are expected to reach a precision of 0.14 ppm at Fermilab c_g-2 and at J-PARC c_jparc . At the same time, the theoretical accuracy is completely limited by the hadronic contributions to $a_{\mu}$. The largest of these contributions is due to the hadronic Vacuum Polarization (hVP).

Although perturbative Quantum Chromodynamics (QCD) theory fails in the energy regime relevant for the calculation of $a_{\mu}$, it is possible to relate the leading order hVP contribution $a_{\mu}^{\rm hVP}$ to hadronic production rates in $e^{+}e^{-}$ annihilations via the dispersion relation

where $\alpha$ is the fine-structure constant, $m_{\mu}$ is the muon mass, $s$ is the center-of-mass energy squared, $R_{\rm had}(s)$ represents the cross section ratio of $e^{+}e^{-}\to{\rm hadrons}$ to $e^{+}e^{-}\to\mu^{+}\mu^{-}$, and $K(s)$ is a kernel function c_3pi_Ks , which is monotonously decreasing with increasing $s$. The energy dependence of both the hadronic cross section and the kernel function imply that $a_{\mu}^{\rm hVP}$ is more sensitive to the $e^{+}e^{-}\to{\rm hadrons}$ cross section in the low energy region.

In order to improve the SM prediction for $a_{\mu}$, precision measurements of hadronic cross sections at $e^{+}e^{-}$ colliders are needed as input to the dispersive calculations. This can be accomplished by a direct, precise measurement of the cross section of $e^{+}e^{-}\to\pi^{+}\pi^{-}\pi^{0}$ in the energy region from $0.7$ to $3.0\,\mathrm{GeV}$, and this is the main topic for the analysis presented in this report. In addition to the evaluation of the hadronic contributions to $a_{\mu}$, the data allow also the study of the decays of the light vector mesons, $\rho$, $\omega$, $\phi$, and excited states.

The hadronic cross section in $e^{+}e^{-}$ annihilations at $\sqrt{s}<1.05\,\mathrm{GeV}$ can be well described by the Vector Meson Dominance (VMD) model. The ground state vector mesons $\rho$, $\omega$, and $\phi$ are well understood, and their properties, such as the mass, width, and main decay modes, are precisely measured c_pdg2014 . However, the conventional VMD model, taking only into account the ground states, is not sufficient to describe $e^{+}e^{-}$ data above $\phi$ mass region. Contributions from radial excitations of possible vector mesons with quantum numbers $I^{G}(J^{PC})=1^{+}(1^{--})$, $0^{-}(1^{--})$ and masses around $\sqrt{s}=1.3\,\mathrm{GeV}$ and $1.6\,\mathrm{GeV}$ need to be taken into account.

At low energies, the $\pi^{+}\pi^{-}\pi^{0}$ spectrum is dominated by the $\omega$ and $\phi$ mesons. The mass region below 1.4 $\,\mathrm{GeV}$ has been studied by SND c_3pi_snd and CMD-2 c_3pi_cmd2 with high statistics. At individual scan points their results show some deviations, however. Above the peak of the $\phi$ resonance, the BABAR experiment has measured the $e^{+}e^{-}\to\pi^{+}\pi^{-}\pi^{0}$ c_g3pi_babar cross section up to $\sqrt{s}=3.0\,\mathrm{GeV}$, exploiting the Initial State Radiation (ISR) method. The result agrees with the SND measurement c_3pi_snd for $\sqrt{s}<1.4\,\mathrm{GeV}$ and significantly exceeds the cross section measured by DM2 c_3pi_dm2 in the region $1.4<\sqrt{s}<2.2\,\mathrm{GeV}$.

The emission of ISR photons with energies $E_{\gamma}$ allows the production of the hadronic states at an “effective” center-of-mass energy $\sqrt{s^{\prime}}$, well below the actual $\sqrt{s}$ of the $e^{+}e^{-}$ collision. Excluding next-to-leading order and final state radiation effects, the actual and the effective center-of-mass energies are related according to $s^{\prime}=s-2\sqrt{s}E_{\gamma}$. The large data samples acquired at recent $e^{+}e^{-}$ colliders permit measuring the hadronic cross section in a wide range by exploiting the ISR technique, which is complementary to studies at energy scan experiments. The ISR method, originally used both at the KLOE c_kloe experiment at DA$\Phi$NE and at the BABAR  c_babar experiment at the PEP-II B-factory, has been applied to measure numerous channels of the cross section $e^{+}e^{-}\to{\rm hadrons}$. This allows for a consistent measurement of the full energy range with the same accelerator and detector conditions. Different reconstruction techniques are applied according to the angular distribution of the ISR photons. Only a small fraction of the photons is emitted with large polar angles and can be reconstructed in the detector. The exclusive reconstruction of such events is referred to as “tagged ISR method” and makes measuring the cross section down to the hadronic mass threshold possible. A tagged ISR measurement of the channel $e^{+}e^{-}\to\pi^{+}\pi^{-}$ has been performed by BESIII recently c_kloss . Most of the ISR photons are emitted along the beam direction, which is beyond the acceptance of currently existing detection systems at $e^{+}e^{-}$ machines. However, it is still possible to reconstruct these events based on energy and momentum conservation, which is referred to as “untagged ISR method”. In this work, candidate events are selected both according to the tagged and untagged ISR selections.

The BESIII detector is a magnetic spectrometer Ablikim:2009aa located at the Beijing Electron Positron Collider (BEPCII) Yu:IPAC2016-TUYA01 . The cylindrical core of the BESIII detector consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identifier modules interleaved with steel. The acceptance of charged particles and photons is 93% over the $4\pi$ solid angle. The charged-particle momentum resolution at $1~{}{\rm GeV}/c$ is $0.5\%$, and the $dE/dx$ resolution is $6\%$ for the electrons from Bhabha scattering. The EMC measures photon energies with a resolution of $2.5\%$ ($5\%$) at $1$ GeV in the barrel (end cap) region. The time resolution of the TOF barrel part is 68 ps, while that of the end cap part is 110 ps.

Two $e^{+}e^{-}$ collision data samples were collected with the BESIII detector at $\sqrt{s}=3.773\,\mathrm{GeV}$ in 2010 and 2011 and they are referred to as “Data I” and “Data II”. The corresponding integrated luminosities are determined to be $927.67\pm 0.10\pm 9.28\,\mathrm{pb}^{-1}$ and $1989.27\pm 0.15\pm 19.89\,\mathrm{pb}^{-1}$, respectively, by using large-angle Bhabha scattering events  c_lum .

The geometry and response of the BESIII detector are modeled in a geant4-based c_geant4 Monte Carlo (MC) simulation software. It is used to produce signal and background MC samples for the determination of the mass resolution and detection efficiency, as well as for the study of background contributions. The signal MC of $e^{+}e^{-}\to\gamma_{\rm ISR}\pi^{+}\pi^{-}\pi^{0}$ is modeled in VMD and generated with the phokhara c_phokhara event generator. The contribution from the $J/\psi$ resonance is not included in this generator. Thus, a MC sample of $e^{+}e^{-}\to\gamma_{\rm ISR}J/\psi\to\gamma_{\rm ISR}\pi^{+}\pi^{-}\pi^{0}$ is generated with the kkmc c_kkmc and EvtGen c_evtgen event generators to study the $J/\psi$ signal, where the $\rho\pi$ model c_besevtgen is used for the decay of $J/\psi\to\pi^{+}\pi^{-}\pi^{0}$.

The dominating background processes $e^{+}e^{-}\to\pi^{+}\pi^{-}\pi^{0}\pi^{0}$ and $e^{+}e^{-}\to\gamma_{\rm ISR}\pi^{+}\pi^{-}\pi^{0}\pi^{0}$ are generated exclusively with phokhara c_phokhara . Further, generic MC samples including $e^{+}e^{-}\to q\bar{q}$, $e^{+}e^{-}\to\gamma_{\rm ISR}J/\psi$, $e^{+}e^{-}\to\gamma_{\rm ISR}\psi^{\prime}$, $\psi(3770)\to D\bar{D}$, and $e^{+}e^{-}\to\tau^{+}\tau^{-}$ are generated with kkmc and EvtGen. The subsequent decays of the resonances are processed according to the branching fractions provided by the Particle Data Group (PDG) c_pdg2014 . Remaining unmeasured decay modes from charmonium states are generated with lundcharm c_lundc . The beam energy spread is considered in all MC simulations. Final-State Radiation (FSR) effects are simulated with photos c_photos .

Event candidates of the final state of interest, denoted hereafter as ISR 3$\pi$, contain two charged tracks and three photons. For the event selection, exactly two charged tracks are required to pass the $e^{+}e^{-}$ interaction point within $1\,\mathrm{cm}$ in the transverse and within $10\,\mathrm{cm}$ in the longitudinal direction relative to the beam axis. Each track is required to be reconstructed within $|\cos\theta|<0.93$, where $\theta$ is the polar angle with respect to the $e^{+}$ beam direction. The two tracks in an event candidate must be oppositely charged. Each track is assumed to be a pion. In order to reduce background contributions from Bhabha scattering, both of the tracks are required to satisfy $E/p<0.8$, where $E$ is the energy deposited in the EMC and $p$ is the magnitude of the momentum measured in the MDC.

Photon candidates are selected from showers in the EMC that are not associated with charged tracks. Good photon candidates reconstructed from the barrel part of the EMC must have a polar angle within $|\cos\theta|<0.8$ and a minimum deposited energy of $25\,\mathrm{MeV}$. To be reconstructed from the end cap, the photon candidates must have a polar angle within $0.86<|\cos\theta|<0.92$ and a minimum energy deposit of $50\,\mathrm{MeV}$. Timing information in the EMC is used to suppress electronic noise and energy deposits unrelated to the event. At least two photons matching these criteria are required for an analysis using the untagged ISR method, and at least three are required for the tagged ISR method. From all possible combinations of two photons, those which fulfill $\chi^{2}_{1C}<10$ in a fit of the photon candidates constrained to the nominal $\pi^{0}$ mass ($1C$) are accepted as $\pi^{0}$ candidates.

The criteria of the event selection are optimized for the three-pion invariant mass region $1.05\leq M_{\pi^{+}\pi^{-}\pi^{0}}\leq 2.00\,\mathrm{GeV}/c^{2}$, where the discrepancy between BABAR and DM2 is most prominent. The optimization is performed with a figure of merit defined as $\frac{S}{\sqrt{S+B}}$, where $S$ refers to the number of signal events, and $B$ refers to the number of events from all background contributions. The signal and background MC samples are normalized to the data by the integrated luminosity.

A kinematic fit is performed to reject background contributions and to improve the mass resolution. The four-momenta of the charged tracks and the photons are constrained to the initial $e^{+}e^{-}$ four-momenta. The two photons, which are assigned to the $\pi^{0}$ candidate, are constrained to the nominal $\pi^{0}$ mass. If there are additional photons or $\pi^{0}$ candidates in a single event, the combination with the minimum $\chi^{2}$ from the kinematic fit is selected. For the tagged ISR method, the constraints add up to $5C$ (four-momenta and $\pi^{0}$ mass), and $\chi^{2}_{5C}<60$ is required. In the untagged ISR method, the radiative photon is considered as an unmeasured massless particle in the kinematic fit. Due to the missing momentum information the number of constraints is reduced to a $2C$ (missing photon mass and $\pi^{0}$ mass) kinematic fit, where $\chi^{2}_{2C}<25$ must be satisfied.

Further reduction of background in the tagged ISR method is achieved by considering the invariant mass distribution of the ISR photon and any other good photon in the event $M_{\gamma_{\rm ISR}\gamma}$. Asymmetric $\pi^{0}$ decays can lead to misidentified ISR photons; these wrongly assigned ISR photons result in a peak in the $M_{\gamma_{\rm ISR}\gamma}$ distribution and are removed by a $\pi^{0}$ veto, requiring $M_{\gamma_{\rm ISR}\gamma}>0.17\,\mathrm{GeV}/c^{2}$. In the untagged ISR method, additional background events are suppressed efficiently with a strict requirement on the scattering angle of the ISR photon determined by the kinematic fit, $i.e$ $|\cos\theta_{\gamma_{\rm ISR}}|>0.9984$.

Due to the less constrained kinematic fit in the untagged ISR method, a non-negligible contribution of beam-induced background is found. An additional requirement is therefore applied to the untagged ISR method, where the two charged tracks are fitted to a common vertex. The vertex must have a distance to the nominal interaction point of less than $2.5\,\textrm{cm}$ in the plane perpendicular to the beams. Background contributions attributed to interactions of the beam halo with the beam pipe are efficiently removed. This additional vertex requirement is not requested in the tagged ISR method because such background is rejected with the four-momentum constraint.

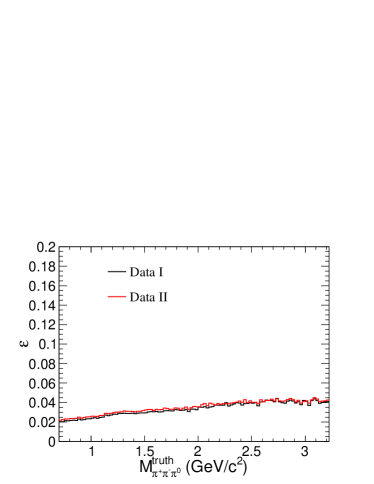
The mass-dependent efficiency is obtained from MC simulations. It varies from 2% to 4% for the tagged ISR method in the mass region $0.7\leq M_{\pi^{+}\pi^{-}\pi^{0}}\leq 3\,\mathrm{GeV}/c^{2}$, and from 0.3% to 15% for the untagged ISR method for masses between $1.05\,\mathrm{GeV}/c^{2}$ and $3\,\mathrm{GeV}/c^{2}$, as shown in the top row of Fig. 1. The distributions are quite similar for the two data sets.

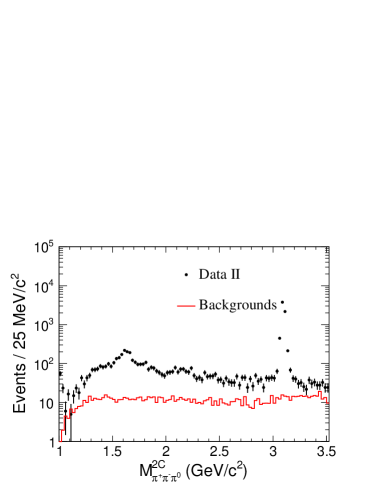
The background contamination of the selected events differs significantly between the tagged and the untagged ISR methods. The $3\pi$ mass spectrum obtained from the tagged analysis has a relatively small background contamination at masses below $1.05\,\mathrm{GeV}/c^{2}$. At larger masses, the spectrum is dominated by background. The untagged method, in comparison, suffers from very low efficiency in the low mass region, but it provides much higher efficiency with much less background contamination in the high mass region. This can be seen from the red lines in Fig. 1(c), 1(d) and lines in Fig. 1(a), 1(b) which show the background levels and the efficiencies for the tagged and untagged methods, respectively.

Using the $\pi^{0}$ side bands is an efficient way to estimate the events with wrongly reconstructed $\pi^{0}$ candidates. The $\pi^{0}$ candidate is constrained to the nominal $\pi^{0}$ mass for the signal mass region, and to $0.10\,\mathrm{GeV}/c^{2}$ and $0.17\,\mathrm{GeV}/c^{2}$ for the side bands. The $\chi^{2}_{1C}$ from the $\pi^{0}$ mass constraint is required to be $\chi^{2}_{1C}<10$ for both signal and side bands regions. Contributions from wrongly reconstructed $\pi^{0}$ in the signal region are subtracted using the averaged number of events in the side bands.

As mentioned earlier, the dominant backgrounds are due to $e^{+}e^{-}\to\pi^{+}\pi^{-}\pi^{0}\pi^{0}$ and $e^{+}e^{-}\to\gamma_{\rm ISR}\pi^{+}\pi^{-}\pi^{0}\pi^{0}$ (referred to as $4\pi$ and ISR 4$\pi$ hereafter). The 4$\pi$ events with a lost soft photon mainly contaminate the tagged ISR method, while the ISR 4$\pi$ events are the dominant background for the untagged ISR method. Other backgrounds contribute to less than 1.3% and are estimated using the generic MC samples. The dominant backgrounds are estimated using a data-driven approach.

First, a clean 4$\pi$ (ISR 4$\pi$) sample is selected from data. The same selections of track and photon candidates as described in Sec. III are used, and at least four (five) good photons are required for the 4$\pi$ (ISR $4\pi$) sample. At least two $\pi^{0}$ candidates are selected from four good photons by a kinematic fit with $\chi^{2}_{1C}<10$ ($\pi^{0}$ mass constraint). If there are more than two good $\pi^{0}$ candidates, the combination with the $\pi^{+}\pi^{-}$ candidates, which yields the minimum $\chi^{2}_{6C(3C)}$ (see below) is selected. The 4$\pi$ events are selected by constraining the two charged pions and two good $\pi^{0}$ candidates to a $6C$ (four-momenta conservation plus two $\pi^{0}$ mass constraints) kinematic fit. A requirement of $\chi^{2}_{6C}<50$ is imposed to reject background contributions to the 4$\pi$ sample. In order to select ISR $4\pi$ events, the two charged pions, four photons from two $\pi^{0}$ candidates, and one missing ISR photon are subjected to a $3C$ kinematic fit. The number of constraints is reduced by the unknown four-momentum of the ISR photon. The $\chi^{2}_{3C}$ value of the fit is required to be less than 20. The direction of the ISR photon predicted by the kinematic fit is required to satisfy $|\cos\theta|>0.999$. The reconstructed $4\pi$ mass is required to be less than $3.65\,\mathrm{GeV}/c^{2}$ to reduce contribution of 4$\pi$ events in the ISR 4$\pi$ sample.

Then, a sample of MC simulated $4\pi$ (ISR $4\pi$) events is produced with the phokhara c_phokhara generator. It is used to determine the efficiency ratio of the ISR $3\pi$ selection and the $4\pi$ (ISR $4\pi$) selection. Events of the ISR 4$\pi$ sample with a generated invariant $4\pi$ mass, $M_{4\pi}^{\rm truth}$, larger than $3.7\,\mathrm{GeV}/c^{2}$ are classified as the 4$\pi$ sample, since they behave quite similar due to the soft ISR photon.

Finally, the efficiency ratio is used to scale the $4\pi$ (ISR $4\pi$) sample selected from data to obtain the background contamination from $4\pi$ (ISR $4\pi$) as a function of the 3$\pi$ invariant mass.

The background-subtracted 3$\pi$ mass spectrum needs to be unfolded to account for effects of FSR and detector response before the cross section can be determined. The simplified Iterative Dynamic Stable method (IDS) c_ids is used to perform the unfolding. It requires the transfer matrix $A_{ij}$ as input, which correlates the number of actually produced events in bin $j$ to the number of reconstructed events in bin $i$.

Different bin sizes are used in the mass spectra to account for both the mass resolution and the different widths of the resonances: $2.5\,\mathrm{MeV}/c^{2}$ in the energy region below $1.05\,\mathrm{GeV}/c^{2}$ (low energy region), and $25\,\mathrm{MeV}/c^{2}$ in the energy region above (high energy region). According to MC studies, the resolution varies from $5.2\,\mathrm{MeV}/c^{2}$ to $6.3\,\mathrm{MeV}/c^{2}$ in the low energy region. At high energies it increases to a range from $6.3\,\mathrm{MeV}/c^{2}$ to $8.8\,\mathrm{MeV}/c^{2}$ for the tagged and from $5.9\,\mathrm{MeV}/c^{2}$ to $11.0\,\mathrm{MeV}/c^{2}$ for the untagged ISR method. The unfolding is performed separately for each energy region. The $\omega$ and $\phi$ resonances in the low energy region are narrow. To ensure a reliable unfolding result, it is important to consider the differences in the detector resolution between MC and data. In the high energy region, where both the widths of the resonances ($\omega(1420)$ and $\omega(1650)$) and the bin sizes are much larger than the detector resolution, the differences of the latter between MC and data is negligible to the unfolded spectra.

To study differences between MC and data, the signals of $\omega$ and $\phi$ in data are fitted using the shape of the 3$\pi$ MC mass distribution to describe the signal. The MC spectrum is convolved with a Gaussian function where the parameters reflect possible mass shifts and differences in the detector resolution between simulation and data. Combined results from the fits to $\omega$ and $\phi$ indicate a shift of the masses by $-0.53\pm 0.25\,\mathrm{MeV}/c^{2}$, and a broadening of the mass resolution by $2.26\pm 0.51\,\mathrm{MeV}/c^{2}$ for Data I, while a slightly larger mass shift of $-1.25\pm 0.01\,\mathrm{MeV}/c^{2}$ and a negligible modification of the resolution are found for Data II. These numbers are used to correct the transfer matrix extracted from simulation, and the errors are considered as systematic uncertainty.

The stability of the IDS method is provided by using regularization functions c_ids , which avoid unfolding large fluctuations in data, e.g. due to subtraction of a large background contribution. The parameters of the regularization functions need to be optimized for a specific unfolding task. The optimization is done by first constructing a toy MC distribution from which a ‘reconstructed toy’ is obtained with the transfer matrix from MC. This toy is made to keep the ‘reconstructed toy’ as close to the real data as possible. The errors for the ‘reconstructed toy’ are taken directly from real data and statistically fluctuated, including the uncertainty from background subtraction. Lastly, the ‘reconstructed toy’ is unfolded to compare with the toy, and the difference is measured by a $\chi^{2}$. A scan for the parameters of the regularization functions is performed to find the optimized one with minimum $\chi^{2}$.

The IDS procedure is applied to the 3$\pi$ mass spectrum obtained after the event selection, the background subtraction, and after applying corrections for data/MC efficiency differences (see Sec. VI below). It provides the distributions unfolded from detector resolutions, distortions, and FSR effects as a function of $\sqrt{s^{\prime}}$, and a covariance matrix of the statistical uncertainties and their bin-to-bin correlations. The $3\pi$ mass spectra after unfolding in different mass regions are shown in Sec. VII.

The contributions of the tracking efficiency, the photon efficiency, the event selections, and the background subtraction to the systematic uncertainties are studied.

The parameters of the vector resonances $\omega,\phi,\omega(1420)$, and $\omega(1650)$ are determined with a combined fit to the $3\pi$ mass spectrum from both the tagged and untagged ISR method in both data sets. The relation

is fitted to the unfolded mass spectrum between 0.7 to $1.8\,\mathrm{GeV}/c^{2}$, where $\varepsilon$ is the detection efficiency, $dL/d\sqrt{s^{\prime}}$ is the effective luminosity, and $\sigma$ is the Born cross section for $e^{+}e^{-}\to 3\pi$. The effective luminosity, defined as $2\cdot\sqrt{s^{\prime}}/s\cdot F(s,\sqrt{s^{\prime}})\cdot L_{ee}$, relies on the total integrated luminosity $L_{ee}$ and the calculated radiator function $F(s,\sqrt{s^{\prime}})$ c_kuraev . The latter describes the probability to radiate an ISR photon so that the production of hadronic final states with a mass of $\sqrt{s^{\prime}}$ is possible. According to the VMD model, $\sigma({\sqrt{s^{\prime}}})$ can be written as the sum of four resonances:

where $m_{V}$ and $\Gamma_{V}$ are the mass and width of the vector meson $V,\phi_{V}$ is the corresponding phase, ${\cal B}(V\to e^{+}e^{-})$ and ${\cal B}(V\to 3\pi)$ are the branching fractions of $V$ decaying into $e^{+}e^{-}$ and $\pi^{+}\pi^{-}\pi^{0}$, respectively, and $\Gamma_{V}(m)=\sum_{i}\Gamma_{i}(m)$ is the total width. Here, $\Gamma_{i}(m)$ is the partial width of the resonance decay into the final state $i$. The mass-dependent widths of $\omega$ and $\phi$ are calculated taking into account all significant decay modes. The decay $V\to 3\pi$ is assumed to proceed via the $\rho\pi$ intermediate state, and $F_{\rho\pi}(m)$ is the 3$\pi$ phase space volume calculated under this hypothesis. Details about the formulas can be found in Ref. c_snd25 . A combined binned $\chi^{2}$ fit is performed. The results are illustrated in Fig. 3. The mass of $\omega$ and $\phi$, the mass and width of $\omega(1420)$ and $\omega(1650)$, and the branching fractions are free parameters. The relative phase between $\omega$ and $\phi$ is taken from Ref. c_snd25 , $\phi_{\phi}=(163\pm 7)^{\circ}$, while the phases of $\omega$, $\omega(1420)$, and $\omega(1650)$ are fixed at $0^{\circ}$, $180^{\circ}$, and $0^{\circ}$, respectively c_phase30 . The widths of $\omega$ and $\phi$ are fixed to the PDG c_pdg2014 values.

Table 2 summarizes the results of the fit.