Measurement of branching fractions of decays to , and
Abstract
Based on 4.5 fb-1 data taken at seven center-of-mass energies ranging from 4.600 to 4.699 GeV with the BESIII detector at the BEPCII collider, we measure the branching fractions of relative to . Combining with the world average branching fraction of , their branching fractions are measured to be for , for , for and for (non-). In all the above results, the first uncertainties are statistical, the second are systematic and the third are from external input of the branching fraction of . Since no signal for is observed, the upper limit of its branching fraction is determined to be 0.13% at the 90 confidence level.
Keywords:
experiments, , -exchange, -emission1 INTRODUCTION
Weak decays of charmed baryons provide useful information for understanding the interplay of weak and strong interactions, complementary to the information obtained from charmed mesons Klein:1989tj ; Asner:2008nq . The lightest charmed baryon is the cornerstone of all charmed baryon spectroscopy, and the measurement of the properties of the provides essential inputs for studying other heavy-quark baryons, such as the singly- and doubly-charmed baryons Yu:2017zst and -baryons Rosner:2012gj . Contrary to the significant progress made in the studies of the heavy meson decay, advancement in the arena of heavy baryons, on both theoretical and experimental sides, has been very slow Cheng:2015iom . Since 2014, much progress has been made by BESIII, Belle and LHCb experiments in studying decays. This includes measurements of absolute branching fractions (BFs) and observation of new decay modes BESIII:lmdenv ; BESIII:hadron ; BESIII:phh ; BESIII:lmdmunv ; BESIII:sigmapipi ; BESIII:nkspi ; BESIII:LmdX ; BESIII:eX ; BESIII:xik ; BESIII:Lmdpieta ; BESIII:KsX ; BESIII:pkseta ; BESIII:npi ; Belle:pkpi ; Belle:pkpi_dcs ; Belle:sigmapipi ; Belle:ppi0peta ; Belle:pomega ; Li:2021iwf , measurements of weak decay asymmetries of decays BESIII:2019odb ; Belle:2022uod , determination of spin BESIII:2020kap , lifetime Belle-II:2022ggx ; LHCb:2019ldj and search for the rare decays LHCb:pomega . All of this supplies rich data for improving theoretical models Cheng:2021qpd . The external -emission process is factorizable, but internal -emission and -exchange processes are not, and non-factorizable contributions have sizeable theoretical uncertainties. The -exchange process is particularly relevant for charmed baryons, where it is not suppressed by helicity and color as in the meson case. Therefore, more precise measurements of the -exchange decays of the play an important role in the identification of the non-factorizable contribution in different theoretical calculations Cheng:2021qpd ; Belle:2001hyr . The two decay modes and are expected to proceed entirely through non-factorizable -exchange diagrams Cheng:1993gf , as shown in Figures 1 and 1.




Complementary studies of charmed baryons, such as the problem of the lifetime Guberina:2002fz , are considered in the framework of Heavy-Quark Expansion Khoze:1983yp , which can be expressed in terms of measurable inclusive quantities of the other two charmed baryons belonging to the same SU(3) flavor multiplet in a model-independent way. In such a treatment, the inclusive decay rates of singly Cabibbo-suppressed decay modes play a prominent role. Two such modes, and , are expected to proceed entirely through internal and external -emission diagrams as shown in Figures 1 and 1, respectively. Measurements of the singly Cabibbo-suppressed decay rates can improve our understanding of the lifetime hierarchy LHCb:2018nfa ; LHCb:2021vll ; Cheng:2021vca . The BFs of both and are predicted to be Cen:2019ims , and is predicted to be Hsiao:2019yur .
The ratios of the BFs (RBFs) of and relative to were measured by CLEO to be and respectively CLEO:1993fhs . In 2002, Belle reported the RBFs of , and relative to , which are , and , respectively Belle:2001hyr .
In this work, we present the measurements of the RBFs of the signal decays , , , (non-) and , relative to the reference decay , by analyzing 4.5 fb-1 data taken at the center-of-mass energies , 4.612, 4.628, 4.641, 4.661, 4.682 and 4.699 GeV BESIII:2022ulv with the BESIII detector at the BEPCII collider. Throughout this paper, charge-conjugate modes are implicitly assumed. In Sect. 2, the BESIII detector and the data samples used in this analysis are described. The event selection is introduced in Sect. 3 and the determination of the BF is presented in Sect. 4. The systematic uncertainties are discussed in Sect. 5. Finally, Sect. 6 summarizes the results.
| (MeV) | (pb-1) | |
|---|---|---|
| 4.600 | 4599.530.070.74 | 586.900.103.90 |
| 4.612 | 4611.860.120.30 | 103.650.050.55 |
| 4.628 | 4628.000.060.32 | 521.530.112.76 |
| 4.641 | 4640.910.060.38 | 551.650.122.92 |
| 4.661 | 4661.240.060.29 | 529.430.122.81 |
| 4.682 | 4681.920.080.29 | 1667.390.218.84 |
| 4.699 | 4698.820.100.36 | 535.540.122.84 |
2 BESIII DETECTOR AND MONTE CARLO SIMULATION
The BESIII detector Ablikim:2009aa records symmetric collisions provided by the BEPCII storage ring Yu:IPAC2016-TUYA01 , which operates with a peak luminosity of cm-2s-1 in the center-of-mass energy range from 2.0 to 4.95 GeV. BESIII has collected large data samples in this energy region Ablikim:2019hff . The cylindrical core of the BESIII detector covers 93% of the full solid angle and consists of a helium-based multilayer drift chamber (MDC), a time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identification modules interleaved with the steel.
The charged-particle momentum resolution at is , and the resolution is for electrons from Bhabha scattering. The EMC measures photon energies with a resolution of () at GeV in the barrel (end cap) region. The time resolution in the TOF barrel region is 68 ps, while that in the end cap region is 110 ps. The end cap TOF system was upgraded in 2015 using multi-gap resistive plate chamber technology, providing a time resolution of 60 ps etof ; etof2 ; etof3 . About 87% of the data used were collected after this upgrade.
Simulated data samples produced with the geant4-based geant4 MC package BOOST bes:boost , which includes the geometric and material description of the BESIII detector geo2 ; detvis and the detector responses, are used to determine detection efficiencies and to estimate backgrounds. The simulation models the beam energy spread and initial state radiation (ISR) in the annihilations with the generator kkmc ref:kkmc ; ref:kkmc2 . The inclusive MC sample includes the production of open charm processes, the ISR production of vector charmonium(-like) states, and the continuum processes. All particle decays are generated with evtgen ref:evtgen using BFs either taken from the Particle Data Group (PDG) pdg:2020 , when available, or otherwise estimated with lundcharm ref:lundcharm ; ref:lundcharm2 . Final state radiation (FSR) from charged final state particles is incorporated using the photos package photos . For the MC production of the events, the cross section line-shape from BESIII measurements is taken into account. The signal decay processes include an incoherent sum of intermediate state resonances, while for the reference mode , a partial-wave analysis is performed to obtain the amplitude model.
3 EVENT SELECTION AND DATA ANALYSIS
In this work, both the signal and reference decays are fully reconstructed. Charged tracks detected in the MDC are required to be within a polar angle () range of , where is defined with respect to the axis, which is the symmetry axis of the MDC. The distance of closest approach to the interaction point (IP) must be less than 10 cm along the axis and less than 1 cm in the transverse plane.
Particle identification (PID) for charged tracks combines measurements of the energy deposited in the MDC (d/d) and the flight time in the TOF to form likelihoods for each hadron hypothesis. Tracks are identified as protons when the proton hypothesis has the greatest likelihood ( and ), while charged kaons and pions are identified by comparing the likelihoods for the kaon and pion hypotheses, and , respectively.
Photon candidates are reconstructed using showers in the EMC. The deposited energy of each shower must be more than 25 MeV in the barrel region () and more than 50 MeV in the end cap region (). To exclude showers that originate from charged tracks, the angle subtended by the EMC shower and the position of the closest charged track at the EMC must be greater than 10 degrees as measured from the IP. To suppress electronic noise and showers unrelated to the event, the difference between the EMC time and the event start time is required to be within [0, 700] ns.
All combinations are considered as candidates, and the reconstructed mass is required to fall in the range of GeV/ GeV/. A kinematic fit is performed to constrain the invariant mass to the known mass pdg:2020 , and candidates with the fit quality are retained.
The candidates are reconstructed from the combinations of with an invariant mass in the range of GeV/ GeV/. This requirement corresponds to approximately (standard deviations) around the known mass pdg:2020 . To reject the possible backgrounds for and modes including in the final states, is required to be outside the range (1.11, 1.12) GeV/. In addition, to remove the decays in the mode , events with in the range (0.48, 0.52) GeV/ are vetoed.
To improve the signal purity, the energy difference for candidates are required to satisfy a mode-dependent requirement shown in Table 2. These ranges are obtained by optimizing signal yield significance with the inclusive MC sample. Here is the total reconstructed energy of the candidate and is the beam energy. Only one candidate with the minimal is accepted. The signal is identified using the beam constrained mass , where is the measured momentum in the center-of-mass system of the collision. After the event selection, there is no obvious peaking background in the distribution for each tag mode, as shown in Figure 2.




| Decay mode | Requirement (GeV) |
|---|---|
4 DETERMINATION OF THE BRANCHING FRACTIONS
The RBF between the signal and reference modes is calculated with
| (1) |
where and are the detection efficiencies, and are the signal yields of the signal mode and the reference mode , respectively. The is the product of the BFs of the intermediate states (, , and for ), and the charge-conjugate channel is included in the simulation. The observables in Equation (1) are determined as follows.
-
•
Reference mode
To obtain the yield of the reference mode, an unbinned maximum likelihood (UML) fit is performed on the distribution separately at each energy point for data. In each fit, the signal shape is described by the MC simulated shape convolved with a Gaussian function with floating mean and width, in order to take into account the resolution difference between data and MC simulation. The distribution of the combinatorial backgrounds is modeled with an ARGUS function ARGUS:1990hfq
(2) where the parameter is free in the fit. The fitted yields of the reference mode at different energy points are given in Table 3. In addition, the detection efficiencies are estimated according to MC simulations, as listed in Table 4. The total fit to data summing over all the energy points is shown in Figure 3.
Table 3: Signal yields in data for various decay modes, where the uncertainties are statistical only. has no significant signal observed. Decay mode 4.600 GeV 4.612 GeV 4.628 GeV 4.641 GeV 4.661 GeV 4.682 GeV 4.699 GeV 112347 20021 100346 102648 102548 313285 94247 14.11.5 2.30.2 11.71.3 13.01.4 12.11.4 43.04.5 14.11.4 14.32.8 2.40.5 12.72.5 13.22.7 14.22.7 47.28.9 14.92.9 (non-) 9.21.7 1.60.3 8.11.5 8.61.6 9.01.6 29.04.0 9.11.6 30.53.6 5.80.7 29.33.5 29.63.5 26.13.4 80.39.5 22.32.6 Table 4: Detection efficiencies (in unit of %) for various decay modes, where the uncertainties are statistical only. The efficiencies do not include the BF of the sequential decay of , or . Decay mode 4.600 GeV 4.612 GeV 4.628 GeV 4.641 GeV 4.661 GeV 4.682 GeV 4.699 GeV 26.120.05 25.210.05 24.900.05 24.960.05 24.780.05 24.440.05 24.230.05 4.220.02 3.920.02 3.980.02 4.110.02 4.300.02 4.530.02 5.190.02 3.660.02 3.380.02 3.460.02 3.550.02 3.750.02 4.020.02 4.190.02 (non-) 4.810.02 4.500.02 4.530.02 4.700.02 4.880.02 5.070.02 6.240.02 16.300.04 15.780.04 15.200.04 15.060.04 14.560.04 14.750.04 14.200.04 5.160.02 4.720.02 4.550.02 4.590.02 4.730.02 4.720.02 4.740.02 


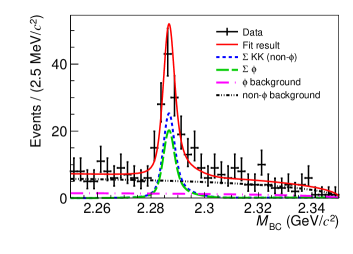

Figure 3: Fit results for different decay modes. The plots show the distributions of (a), (b) and (e) processes. Other plots (c) and (d) show the distributions of and , respectively, for the projections of the 2-D fit used to separate the and (non-) processes. The points with error bars are combined from data at all energy points, the red curves are the overall fit result, the blue and green dashed curves are the signal shapes, the black and pink dashed curves are the background shapes. -
•
Signal mode
The simultaneous UML fit is performed using seven energy point data samples for signal mode, to obtain a more precise result. For this purpose, a common RBF is fitted at various energy points, where the signal yields can be derived from Equation 1 with the input yields of the reference mode in Table 3 and the detection efficiencies in Table 4. The uncertainties of the input values are taken into account in systematic uncertainties, as listed in Table 5. In the fit, the signal shape is extracted from the corresponding signal MC sample and convolved with a Gaussian function with floating mean and width. The background shape is described by an ARGUS function in Equation 2. The summed fit to data from all of the energy points is shown in Figure 3. The RBF results obtained from the fit are given in Table 1, and the signal yields at different energy points are calculated, as listed in Table 3.
-
•
Signal mode
To separate the contribution for mode, a two-dimensional simultaneous UML fit is performed on the vs the distributions, in which common RBF values are estimated. Four components (, (non-), background and non- background) are considered in this fit, as shown in Figures 3 and 3. All the signal shapes are extracted from MC samples and convolved with a Gaussian resolution function with floating mean and width. In the distribution, the combinatorial background is described using the ARGUS function. In the distribution, we use a second-order Chebyshev function to describe the background of the non- process and use the line-shape distribution extracted from the signal MC sample to describe the background.
-
•
Signal mode
The simultaneous UML fit is also performed for , as shown in Figure 3. Since there is no significant signal observed, the upper limit on the BF of this decay is estimated with a likelihood scan method which takes into account the systematic uncertainties as follows
(3) Here, is the likelihood expression of BF, is the statistical likelihood given by the data without considering the systematic uncertainties when taking the nominal BF obtained, is the relative deviation of the estimated BF from the nominal value and is the total systematic uncertainty given in Table 5. The likelihood curve calculated according to Equation 3 is shown in Figure 4. The upper limit on the BF of mode at the 90% confidence level (CL) is estimated to be 0.11% by integrating the likelihood curve in the physical region and considering the BF of the reference mode and systematic uncertainties.

Figure 4: The normalized likelihood value versus the BF of after incorporating the systematic uncertainty. The black points are the initial curve, the red curve is the result with the systematic uncertainty, and the blue arrow points to the upper limit on the BF at the 90 CL.
5 SYSTEMATIC UNCERTAINTY
The sources of systematic uncertainties in the RBF measurements are summarized in Table 5. The systematic uncertainties of MC statistics is for each channel and can be neglected. The systematic uncertainties in reconstruction in both signal and reference modes are canceled in the RBF calculation. The systematic uncertainties of tracking efficiency for charged tracks are also canceled. For each signal decay, the square root of the quadratic sum of all the uncertainties is taken as the total systematic uncertainty.
| Source | |||||
|---|---|---|---|---|---|
| PID | 2.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| PID | 2.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| reconstruction | - | - | 1.0 | - | - |
| requirement | 1.4 | 3.0 | 3.5 | 1.4 | 1.4 |
| fit | 3.3 | 3.0 | 5.9 | 6.1 | 3.0 |
| Signal model | 1.8 | 2.9 | - | 1.0 | 0.7 |
| Reference mode | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 |
| 0.6 | 0.6 | 0.6 | 1.2 | 0.6 | |
| Total | 5.3 | 5.7 | 7.4 | 7.3 | 4.8 |
-
•
PID and reconstruction efficiencies. The uncertainties associated with PID efficiencies are estimated to be 1.0% for each charged track by studying the control samples of , and based on data taken at energies above GeV. However, the PID uncertainty for the common to signal and reference modes cancels, as does that for any common . The uncertainty of reconstruction efficiency is assigned to be 1.0% per by studying the control sample of process.
-
•
requirement. The resolution difference between data and MC simulation need to be considered. Thus a Gaussian function is used to smear MC sample and obtain a new efficiency. The changes in the efficiencies are assigned as the corresponding uncertainties of . The resolution difference is extract by using signal MC shape smeared with the Gaussian function to fit the distribution in data.
-
•
fit. The uncertainty in the fit is mainly due to free parameters of the Gaussian and ARGUS functions and the background description. The relevant systematic uncertainty is estimated with an alternative signal shape without smearing the Gaussian resolution function and an alternative background shape which varies the high-end cutoff of the ARGUS function by GeV/. The largest result change is assigned as the systematic uncertainty. For process, due to that a two-dimensional maximum likelihood fit is performed on the and distribution, the uncertainty of fit is also considered by studying the difference of signal shape convolved with or without a Gaussian resolution function. In addition, the shape of the backgrounds from inclusive decays can not be different from the ARGUS function. To account for this discrepancy, an additional component of the decay backgrounds, which is extracted from the inclusive MC samples, is included in the fit. The resultant changes on the RBF are taken as the systematic uncertainties. For process, an alternative fit to data with larger than 2.27 GeV is implemented and the relative changes on the fitting results are taken into account as systematic uncertainties. All the above items are summed over in quadrature.
-
•
Signal model. The influence of the assumed signal model on the BF measurement comes from the estimation of the signal efficiency. Decay processes with intermediate resonances listed in the PDG pdg:2020 are included in the signal simulation. Examples include and () processes for and () for . In the nominal analysis, the BFs that are used in the generator are taken from the PDG pdg:2020 . Their effects on the new BF measurements are estimated by varying the input BF of the intermediate decay by in the generator. The relative efficiency deviation is taken as the uncertainty.
-
•
Reference mode. For the reference mode , the TF-PWA PWA is used to perform the simple Partial Wave Analysis and consider the possible intermediate resonance states, In the estimation of systematic uncertainty, we remove the low significance state. The difference of efficiency (1.1%) is taken as the systematic uncertainty. For the statistical uncertainties of the fitted yields in the reference mode, a relative uncertainty (1.6%) is transferred into the systematic uncertainty of the RBF. In total, a quadrature sum of the systematic uncertainty (1.9%) is assigned.
-
•
BFs of the intermediate states. The BFs of , and are used as inputs in the baseline analysis, and their uncertainties pdg:2020 are propagated as the systematic uncertainty.
6 SUMMARY
Based on 4.5 fb-1 data taken at to 4.699 GeV with the BESIII detector at the BEPCII collider, the non-factorizable -exchange-only processes, , (non-) and the non-factorizable -emission processes and have been studied. The BF of relative to is measured for the first time. The precisions of BFs for other channels relative to are improved. Combining with the world average pdg:2020 , the BFs of the aforementioned decays are obtained. Table 6 shows the comparison of our results with the PDG values pdg:2020 and the Belle results Belle:2001hyr . The uncertainties of the BFs of and are comparable to those in references Belle:2001hyr ; pdg:2020 . For , the precision of the BF is improved by a factor of two. The theoretical predictions of the BFs of , and in reference Cen:2019ims ; Hsiao:2019yur differ from our results by about and our results will be helpful to correct the theoretical model. The combined results are essential to understand the non-factorizable -exchange and -emission contributions to the decays of .
| Decay mode | RBF (This work) | RBF (Belle) | BF (This work) | BF (PDG) |
|---|---|---|---|---|
| - | 0.11 | - | ||
| (non-) | - | - |
Acknowledgements.
The BESIII collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support. This work is supported in part by National Key Research and Development Program of China under Contracts Nos. 2020YFA0406400, 2020YFA0406300; Joint Large-Scale Scientific Facility Funds of the National Natural Science Foundation of China (NSFC) and Chinese Academy of Sciences (CAS) under Contracts Nos. U1932101, U1732263, U1832207; NSFC under Contracts Nos. 11625523, 11635010, 11675275, 11735014, 11822506, 11835012, 11935015, 11935016, 11935018, 11961141012, 11975021, 12022510, 12035009, 12035013, 12061131003, 12175321, 12221005; State Key Laboratory of Nuclear Physics and Technology, PKU under Grant No. NPT2020KFY04; the CAS Center for Excellence in Particle Physics (CCEPP); the CAS Large-Scale Scientific Facility Program; CAS Key Research Program of Frontier Sciences under Contract No. QYZDJ-SSW-SLH040; 100 Talents Program of CAS; Fundamental Research Funds for the Central Universities; INPAC and Shanghai Key Laboratory for Particle Physics and Cosmology; ERC under Contract No. 758462; European Union Horizon 2020 research and innovation programme under Contract No. Marie Sklodowska-Curie grant agreement No 894790; German Research Foundation DFG under Contracts Nos. 443159800, Collaborative Research Center CRC 1044, FOR 2359, FOR 2359, GRK 214; Istituto Nazionale di Fisica Nucleare, Italy; Ministry of Development of Turkey under Contract No. DPT2006K-120470; National Science and Technology fund; Olle Engkvist Foundation under Contract No. 200-0605; STFC (United Kingdom); The Knut and Alice Wallenberg Foundation (Sweden) under Contract No. 2016.0157; The Royal Society, UK under Contracts Nos. DH140054, DH160214; The Swedish Research Council; U. S. Department of Energy under Contracts Nos. DE-FG02-05ER41374, DE-SC-0012069.References
- (1) S. R. Klein, Int. J. Mod. Phys. A 5, 1457 (1990).
- (2) D. M. Asner et al., Int. J. Mod. Phys. A 24, S1 (2009).
- (3) F. S. Yu, H. Y. Jiang, R. H. Li, C. D. Lü, W. Wang and Z. X. Zhao, Chin. Phys. C 42, 051001 (2018).
- (4) J. L. Rosner, Phys. Rev. D 86, 014017 (2012).
- (5) H. Y. Cheng, Front. Phys. (Beijing) 10, 101406 (2015).
- (6) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 115, 221805 (2015).
- (7) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 116, 052001 (2016).
- (8) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 117, 232002 (2016).
- (9) M. Ablikim et al. (BESIII Collaboration), Phys. Lett. B 767, 42 (2017).
- (10) M. Ablikim et al. (BESIII Collaboration), Phys. Lett. B 772, 388 (2017).
- (11) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 118, 112001 (2017).
- (12) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 121, 062003 (2018).
- (13) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 121, 251801 (2018).
- (14) M. Ablikim et al. (BESIII Collaboration), Phys. Lett. B 783, 200 (2018).
- (15) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. D 99, 032010 (2019).
- (16) M. Ablikim et al. (BESIII Collaboration), Eur. Phys. J. C 80, 935 (2020).
- (17) M. Ablikim et al. (BESIII Collaboration), Phys. Lett. B 817, 136327 (2021).
- (18) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. Lett. 128, 142001 (2022).
- (19) A. Zupanc et al. (Belle Collaboration), Phys. Rev. Lett. 113, 042002 (2014).
- (20) S. B. Yang et al. (Belle Collaboration), Phys. Rev. Lett. 117, 011801 (2016).
- (21) M. Berger et al. (Belle Collaboration), Phys. Rev. D 98, 112006 (2018).
- (22) S. X. Li et al. (Belle Collaboration), Phys. Rev. D 103, 072004 (2021).
- (23) S. X. Li et al. (Belle Collaboration), Phys. Rev. D 104, 072008 (2021).
- (24) H. B. Li and X. R. Lyu, Natl. Sci. Rev. 8, nwab181 (2021).
- (25) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. D 100, 072004 (2019).
- (26) L. K. Li et al. (Belle Collaboration), Sci. Bull. 68, 583 (2023)
- (27) M. Ablikim et al. (BESIII Collaboration), Phys. Rev. D 103, L091101 (2021).
- (28) R. Aaij et al. (LHCb Collaboration), Phys. Rev. D 100, 032001 (2019).
- (29) F. Abudinén et al. (Belle-II Collaboration), Phys. Rev. Lett. 130, 071802 (2023)
- (30) R. Aaij et al. (LHCb Collaboration), Phys. Rev. D 97, 091101 (2018).
- (31) H. Y. Cheng, Chin. J. Phys. 78, 324 (2022).
- (32) K. Abe et al. (Belle Collaboration), Phys. Lett. B 524, 33 (2002).
- (33) H. Y. Cheng and B. Tseng, Phys. Rev. D 48, 4188 (1993).
- (34) B. Guberina and H. Stefancic, Phys. Rev. D 65, 114004 (2002).
- (35) V. A. Khoze and M. A. Shifman, Sov. Phys. Usp. 26, 387 (1983).
- (36) R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 121, 092003 (2018).
- (37) R. Aaij et al. (LHCb Collaboration), Sci. Bull. 67, 479 (2022).
- (38) H. Y. Cheng, Sci. Bull. 67, 445 (2022).
- (39) J. Y. Cen, C. Q. Geng, C. W. Liu and T. H. Tsai, Eur. Phys. J. C 79, no.11, 946 (2019).
- (40) Y. K. Hsiao, Y. Yao and H. J. Zhao, Phys. Lett. B 792, 35-39 (2019).
- (41) P. Avery et al. (CLEO Collaboration), Phys. Rev. Lett. 71, 2391 (1993).
- (42) M. Ablikim et al. (BESIII Collaboration), Chin. Phys. C 46, 113003 (2022).
- (43) M. Ablikim et al. (BESIII Collaboration), Nucl. Instrum. Meth. A 614, 345 (2010).
- (44) C. H. Yu et al., Proceedings of IPAC2016, Busan, Korea, (2016).
- (45) M. Ablikim et al. (BESIII Collaboration), Chin. Phys. C 44, 040001 (2020).
- (46) X. Li et al., Radiat. Detect. Technol. Methods 1, 13 (2017).
- (47) Y. X. Guo et al., Radiat. Detect. Technol. Methods 1, 15 (2017).
- (48) P. Cao et al., Nucl. Instrum. Meth. A 953, 163053 (2020).
- (49) S. Agostinelli et al. (GEANT4 Collaboration), Nucl. Instrum. Meth. A 506, 250 (2003).
- (50) Z. Y. Deng et al., Chin. Phys. C 30, 371 (2006).
- (51) Z. Y. You, Y. T. Liang and Y. J. Mao, Chin. Phys. C 32, 572 (2008).
- (52) K. X. Huang, et al., Nucl. Sci. Tech. 33, 142 (2022).
- (53) S. Jadach, B. F. L. Ward and Z. Was, Phys. Rev. D 63, 113009 (2001).
- (54) S. Jadach, B. F. L. Ward and Z. Was, Comput. Phys. Commun. 130, 260 (2000).
- (55) D. J. Lange, Nucl. Instrum. Meth. A 462, 152 (2001).
- (56) R. L. Workman et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022, 083C01 (2022).
- (57) J. C. Chen et al., Phys. Rev. D 62, 034003 (2000).
- (58) R. L. Yang, R. G. Ping and H. Chen, Chin. Phys. Lett. 31, 061301 (2014).
- (59) E. Richter-Was, Phys. Lett. B 303, 163 (1993).
- (60) H. Albrecht et al. (ARGUS Collaboration), Phys. Lett. B 241, 278 (1990).
- (61) Y. Jiang et al., frameworkTF-PWApackage, GitHublink:https://github.com/jiangyi15/tf-pwa (2020).
M. Ablikim1, M. N. Achasov13,b, P. Adlarson73, R. Aliberti34, A. Amoroso72A,72C, M. R. An38, Q. An69,56, Y. Bai55, O. Bakina35, I. Balossino29A, Y. Ban45,g, V. Batozskaya1,43, K. Begzsuren31, N. Berger34, M. Berlowski43, M. Bertani28A, D. Bettoni29A, F. Bianchi72A,72C, E. Bianco72A,72C, J. Bloms66, A. Bortone72A,72C, I. Boyko35, R. A. Briere5, A. Brueggemann66, H. Cai74, X. Cai1,56, A. Calcaterra28A, G. F. Cao1,61, N. Cao1,61, S. A. Cetin60A, J. F. Chang1,56, T. T. Chang75, W. L. Chang1,61, G. R. Che42, G. Chelkov35,a, C. Chen42, Chao Chen53, G. Chen1, H. S. Chen1,61, M. L. Chen1,56,61, S. J. Chen41, S. M. Chen59, T. Chen1,61, X. R. Chen30,61, X. T. Chen1,61, Y. B. Chen1,56, Y. Q. Chen33, Z. J. Chen25,h, W. S. Cheng72C, S. K. Choi10A, X. Chu42, G. Cibinetto29A, S. C. Coen4, F. Cossio72C, J. J. Cui48, H. L. Dai1,56, J. P. Dai77, A. Dbeyssi19, R. E. de Boer4, D. Dedovich35, Z. Y. Deng1, A. Denig34, I. Denysenko35, M. Destefanis72A,72C, F. De Mori72A,72C, B. Ding64,1, Y. Ding39, Y. Ding33, J. Dong1,56, L. Y. Dong1,61, M. Y. Dong1,56,61, X. Dong74, S. X. Du79, Z. H. Duan41, P. Egorov35,a, Y. L. Fan74, J. Fang1,56, S. S. Fang1,61, W. X. Fang1, Y. Fang1, R. Farinelli29A, L. Fava72B,72C, F. Feldbauer4, G. Felici28A, C. Q. Feng69,56, J. H. Feng57, K Fischer67, M. Fritsch4, C. Fritzsch66, C. D. Fu1, Y. W. Fu1, H. Gao61, Y. N. Gao45,g, Yang Gao69,56, S. Garbolino72C, I. Garzia29A,29B, P. T. Ge74, Z. W. Ge41, C. Geng57, E. M. Gersabeck65, A Gilman67, K. Goetzen14, L. Gong39, W. X. Gong1,56, W. Gradl34, S. Gramigna29A,29B, M. Greco72A,72C, M. H. Gu1,56, Y. T. Gu16, C. Y Guan1,61, Z. L. Guan22, A. Q. Guo30,61, L. B. Guo40, R. P. Guo47, Y. P. Guo12,f, A. Guskov35,a, X. T. H.1,61, W. Y. Han38, X. Q. Hao20, F. A. Harris63, K. K. He53, K. L. He1,61, F. H. Heinsius4, C. H. Heinz34, Y. K. Heng1,56,61, C. Herold58, T. Holtmann4, P. C. Hong12,f, G. Y. Hou1,61, Y. R. Hou61, Z. L. Hou1, H. M. Hu1,61, J. F. Hu54,i, T. Hu1,56,61, Y. Hu1, G. S. Huang69,56, K. X. Huang57, L. Q. Huang30,61, X. T. Huang48, Y. P. Huang1, T. Hussain71, N Hüsken27,34, W. Imoehl27, M. Irshad69,56, J. Jackson27, S. Jaeger4, S. Janchiv31, J. H. Jeong10A, Q. Ji1, Q. P. Ji20, X. B. Ji1,61, X. L. Ji1,56, Y. Y. Ji48, Z. K. Jia69,56, P. C. Jiang45,g, S. S. Jiang38, T. J. Jiang17, X. S. Jiang1,56,61, Y. Jiang61, J. B. Jiao48, Z. Jiao23, S. Jin41, Y. Jin64, M. Q. Jing1,61, T. Johansson73, X. K.1, S. Kabana32, N. Kalantar-Nayestanaki62, X. L. Kang9, X. S. Kang39, R. Kappert62, M. Kavatsyuk62, B. C. Ke79, A. Khoukaz66, R. Kiuchi1, R. Kliemt14, L. Koch36, O. B. Kolcu60A, B. Kopf4, M. Kuessner4, A. Kupsc43,73, W. Kühn36, J. J. Lane65, J. S. Lange36, P. Larin19, A. Lavania26, L. Lavezzi72A,72C, T. T. Lei69,k, Z. H. Lei69,56, H. Leithoff34, M. Lellmann34, T. Lenz34, C. Li42, C. Li46, C. H. Li38, Cheng Li69,56, D. M. Li79, F. Li1,56, G. Li1, H. Li69,56, H. B. Li1,61, H. J. Li20, H. N. Li54,i, Hui Li42, J. R. Li59, J. S. Li57, J. W. Li48, Ke Li1, L. J Li1,61, L. K. Li1, Lei Li3, M. H. Li42, P. R. Li37,j,k, S. X. Li12, T. Li48, W. D. Li1,61, W. G. Li1, X. H. Li69,56, X. L. Li48, Xiaoyu Li1,61, Y. G. Li45,g, Z. J. Li57, Z. X. Li16, Z. Y. Li57, C. Liang41, H. Liang33, H. Liang69,56, H. Liang1,61, Y. F. Liang52, Y. T. Liang30,61, G. R. Liao15, L. Z. Liao48, J. Libby26, A. Limphirat58, D. X. Lin30,61, T. Lin1, B. J. Liu1, B. X. Liu74, C. Liu33, C. X. Liu1, D. Liu19,69, F. H. Liu51, Fang Liu1, Feng Liu6, G. M. Liu54,i, H. Liu37,j,k, H. B. Liu16, H. M. Liu1,61, Huanhuan Liu1, Huihui Liu21, J. B. Liu69,56, J. L. Liu70, J. Y. Liu1,61, K. Liu1, K. Y. Liu39, Ke Liu22, L. Liu69,56, L. C. Liu42, Lu Liu42, M. H. Liu12,f, P. L. Liu1, Q. Liu61, S. B. Liu69,56, T. Liu12,f, W. K. Liu42, W. M. Liu69,56, X. Liu37,j,k, Y. Liu37,j,k, Y. B. Liu42, Z. A. Liu1,56,61, Z. Q. Liu48, X. C. Lou1,56,61, F. X. Lu57, H. J. Lu23, J. G. Lu1,56, X. L. Lu1, Y. Lu7, Y. P. Lu1,56, Z. H. Lu1,61, C. L. Luo40, M. X. Luo78, T. Luo12,f, X. L. Luo1,56, X. R. Lyu61, Y. F. Lyu42, F. C. Ma39, H. L. Ma1, J. L. Ma1,61, L. L. Ma48, M. M. Ma1,61, Q. M. Ma1, R. Q. Ma1,61, R. T. Ma61, X. Y. Ma1,56, Y. Ma45,g, F. E. Maas19, M. Maggiora72A,72C, S. Maldaner4, S. Malde67, A. Mangoni28B, Y. J. Mao45,g, Z. P. Mao1, S. Marcello72A,72C, Z. X. Meng64, J. G. Messchendorp14,62, G. Mezzadri29A, H. Miao1,61, T. J. Min41, R. E. Mitchell27, X. H. Mo1,56,61, N. Yu. Muchnoi13,b, Y. Nefedov35, F. Nerling19,d, I. B. Nikolaev13,b, Z. Ning1,56, S. Nisar11,l, Y. Niu 48, S. L. Olsen61, Q. Ouyang1,56,61, S. Pacetti28B,28C, X. Pan53, Y. Pan55, A. Pathak33, P. Patteri28A, Y. P. Pei69,56, M. Pelizaeus4, H. P. Peng69,56, K. Peters14,d, J. L. Ping40, R. G. Ping1,61, S. Plura34, S. Pogodin35, V. Prasad32, F. Z. Qi1, H. Qi69,56, H. R. Qi59, M. Qi41, T. Y. Qi12,f, S. Qian1,56, W. B. Qian61, C. F. Qiao61, J. J. Qin70, L. Q. Qin15, X. P. Qin12,f, X. S. Qin48, Z. H. Qin1,56, J. F. Qiu1, S. Q. Qu59, C. F. Redmer34, K. J. Ren38, A. Rivetti72C, V. Rodin62, M. Rolo72C, G. Rong1,61, Ch. Rosner19, S. N. Ruan42, N. Salone43, A. Sarantsev35,c, Y. Schelhaas34, K. Schoenning73, M. Scodeggio29A,29B, K. Y. Shan12,f, W. Shan24, X. Y. Shan69,56, J. F. Shangguan53, L. G. Shao1,61, M. Shao69,56, C. P. Shen12,f, H. F. Shen1,61, W. H. Shen61, X. Y. Shen1,61, B. A. Shi61, H. C. Shi69,56, J. L. Shi12, J. Y. Shi1, Q. Q. Shi53, R. S. Shi1,61, X. Shi1,56, J. J. Song20, T. Z. Song57, W. M. Song33,1, Y. J. Song12, Y. X. Song45,g, S. Sosio72A,72C, S. Spataro72A,72C, F. Stieler34, Y. J. Su61, G. B. Sun74, G. X. Sun1, H. Sun61, H. K. Sun1, J. F. Sun20, K. Sun59, L. Sun74, S. S. Sun1,61, T. Sun1,61, W. Y. Sun33, Y. Sun9, Y. J. Sun69,56, Y. Z. Sun1, Z. T. Sun48, Y. X. Tan69,56, C. J. Tang52, G. Y. Tang1, J. Tang57, Y. A. Tang74, L. Y Tao70, Q. T. Tao25,h, M. Tat67, J. X. Teng69,56, V. Thoren73, W. H. Tian50, W. H. Tian57, Y. Tian30,61, Z. F. Tian74, I. Uman60B, B. Wang1, B. L. Wang61, Bo Wang69,56, C. W. Wang41, D. Y. Wang45,g, F. Wang70, H. J. Wang37,j,k, H. P. Wang1,61, K. Wang1,56, L. L. Wang1, M. Wang48, Meng Wang1,61, S. Wang12,f, T. Wang12,f, T. J. Wang42, W. Wang70, W. Wang57, W. H. Wang74, W. P. Wang69,56, X. Wang45,g, X. F. Wang37,j,k, X. J. Wang38, X. L. Wang12,f, Y. Wang59, Y. D. Wang44, Y. F. Wang1,56,61, Y. H. Wang46, Y. N. Wang44, Y. Q. Wang1, Yaqian Wang18,1, Yi Wang59, Z. Wang1,56, Z. L. Wang70, Z. Y. Wang1,61, Ziyi Wang61, D. Wei68, D. H. Wei15, F. Weidner66, S. P. Wen1, C. W. Wenzel4, U. Wiedner4, G. Wilkinson67, M. Wolke73, L. Wollenberg4, C. Wu38, J. F. Wu1,61, L. H. Wu1, L. J. Wu1,61, X. Wu12,f, X. H. Wu33, Y. Wu69, Y. J Wu30, Z. Wu1,56, L. Xia69,56, X. M. Xian38, T. Xiang45,g, D. Xiao37,j,k, G. Y. Xiao41, H. Xiao12,f, S. Y. Xiao1, Y. L. Xiao12,f, Z. J. Xiao40, C. Xie41, X. H. Xie45,g, Y. Xie48, Y. G. Xie1,56, Y. H. Xie6, Z. P. Xie69,56, T. Y. Xing1,61, C. F. Xu1,61, C. J. Xu57, G. F. Xu1, H. Y. Xu64, Q. J. Xu17, W. L. Xu64, X. P. Xu53, Y. C. Xu76, Z. P. Xu41, F. Yan12,f, L. Yan12,f, W. B. Yan69,56, W. C. Yan79, X. Q Yan1, H. J. Yang49,e, H. L. Yang33, H. X. Yang1, Tao Yang1, Y. Yang12,f, Y. F. Yang42, Y. X. Yang1,61, Yifan Yang1,61, M. Ye1,56, M. H. Ye8, J. H. Yin1, Z. Y. You57, B. X. Yu1,56,61, C. X. Yu42, G. Yu1,61, T. Yu70, X. D. Yu45,g, C. Z. Yuan1,61, L. Yuan2, S. C. Yuan1, X. Q. Yuan1, Y. Yuan1,61, Z. Y. Yuan57, C. X. Yue38, A. A. Zafar71, F. R. Zeng48, X. Zeng12,f, Y. Zeng25,h, Y. J. Zeng1,61, X. Y. Zhai33, Y. H. Zhan57, A. Q. Zhang1,61, B. L. Zhang1,61, B. X. Zhang1, D. H. Zhang42, G. Y. Zhang20, H. Zhang69, H. H. Zhang57, H. H. Zhang33, H. Q. Zhang1,56,61, H. Y. Zhang1,56, J. J. Zhang50, J. L. Zhang75, J. Q. Zhang40, J. W. Zhang1,56,61, J. X. Zhang37,j,k, J. Y. Zhang1, J. Z. Zhang1,61, Jianyu Zhang61, Jiawei Zhang1,61, L. M. Zhang59, L. Q. Zhang57, Lei Zhang41, P. Zhang1, Q. Y. Zhang38,79, Shuihan Zhang1,61, Shulei Zhang25,h, X. D. Zhang44, X. M. Zhang1, X. Y. Zhang48, X. Y. Zhang53, Y. Zhang67, Y. T. Zhang79, Y. H. Zhang1,56, Yan Zhang69,56, Yao Zhang1, Z. H. Zhang1, Z. L. Zhang33, Z. Y. Zhang42, Z. Y. Zhang74, G. Zhao1, J. Zhao38, J. Y. Zhao1,61, J. Z. Zhao1,56, Lei Zhao69,56, Ling Zhao1, M. G. Zhao42, S. J. Zhao79, Y. B. Zhao1,56, Y. X. Zhao30,61, Z. G. Zhao69,56, A. Zhemchugov35,a, B. Zheng70, J. P. Zheng1,56, W. J. Zheng1,61, Y. H. Zheng61, B. Zhong40, X. Zhong57, H. Zhou48, L. P. Zhou1,61, X. Zhou74, X. K. Zhou6, X. R. Zhou69,56, X. Y. Zhou38, Y. Z. Zhou12,f, J. Zhu42, K. Zhu1, K. J. Zhu1,56,61, L. Zhu33, L. X. Zhu61, S. H. Zhu68, S. Q. Zhu41, T. J. Zhu12,f, W. J. Zhu12,f, Y. C. Zhu69,56, Z. A. Zhu1,61, J. H. Zou1, J. Zu69,56
(BESIII Collaboration)
1 Institute of High Energy Physics, Beijing 100049, People’s Republic of China
2 Beihang University, Beijing 100191, People’s Republic of China
3 Beijing Institute of Petrochemical Technology, Beijing 102617, People’s Republic of China
4 Bochum Ruhr-University, D-44780 Bochum, Germany
5 Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, USA
6 Central China Normal University, Wuhan 430079, People’s Republic of China
7 Central South University, Changsha 410083, People’s Republic of China
8 China Center of Advanced Science and Technology, Beijing 100190, People’s Republic of China
9 China University of Geosciences, Wuhan 430074, People’s Republic of China
10 Chung-Ang University, Seoul, 06974, Republic of Korea
11 COMSATS University Islamabad, Lahore Campus, Defence Road, Off Raiwind Road, 54000 Lahore, Pakistan
12 Fudan University, Shanghai 200433, People’s Republic of China
13 G.I. Budker Institute of Nuclear Physics SB RAS (BINP), Novosibirsk 630090, Russia
14 GSI Helmholtzcentre for Heavy Ion Research GmbH, D-64291 Darmstadt, Germany
15 Guangxi Normal University, Guilin 541004, People’s Republic of China
16 Guangxi University, Nanning 530004, People’s Republic of China
17 Hangzhou Normal University, Hangzhou 310036, People’s Republic of China
18 Hebei University, Baoding 071002, People’s Republic of China
19 Helmholtz Institute Mainz, Staudinger Weg 18, D-55099 Mainz, Germany
20 Henan Normal University, Xinxiang 453007, People’s Republic of China
21 Henan University of Science and Technology, Luoyang 471003, People’s Republic of China
22 Henan University of Technology, Zhengzhou 450001, People’s Republic of China
23 Huangshan College, Huangshan 245000, People’s Republic of China
24 Hunan Normal University, Changsha 410081, People’s Republic of China
25 Hunan University, Changsha 410082, People’s Republic of China
26 Indian Institute of Technology Madras, Chennai 600036, India
27 Indiana University, Bloomington, Indiana 47405, USA
28 INFN Laboratori Nazionali di Frascati , (A)INFN Laboratori Nazionali di Frascati, I-00044, Frascati, Italy; (B)INFN Sezione di Perugia, I-06100, Perugia, Italy; (C)University of Perugia, I-06100, Perugia, Italy
29 INFN Sezione di Ferrara, (A)INFN Sezione di Ferrara, I-44122, Ferrara, Italy; (B)University of Ferrara, I-44122, Ferrara, Italy
30 Institute of Modern Physics, Lanzhou 730000, People’s Republic of China
31 Institute of Physics and Technology, Peace Avenue 54B, Ulaanbaatar 13330, Mongolia
32 Instituto de Alta Investigación, Universidad de Tarapacá, Casilla 7D, Arica, Chile
33 Jilin University, Changchun 130012, People’s Republic of China
34 Johannes Gutenberg University of Mainz, Johann-Joachim-Becher-Weg 45, D-55099 Mainz, Germany
35 Joint Institute for Nuclear Research, 141980 Dubna, Moscow region, Russia
36 Justus-Liebig-Universitaet Giessen, II. Physikalisches Institut, Heinrich-Buff-Ring 16, D-35392 Giessen, Germany
37 Lanzhou University, Lanzhou 730000, People’s Republic of China
38 Liaoning Normal University, Dalian 116029, People’s Republic of China
39 Liaoning University, Shenyang 110036, People’s Republic of China
40 Nanjing Normal University, Nanjing 210023, People’s Republic of China
41 Nanjing University, Nanjing 210093, People’s Republic of China
42 Nankai University, Tianjin 300071, People’s Republic of China
43 National Centre for Nuclear Research, Warsaw 02-093, Poland
44 North China Electric Power University, Beijing 102206, People’s Republic of China
45 Peking University, Beijing 100871, People’s Republic of China
46 Qufu Normal University, Qufu 273165, People’s Republic of China
47 Shandong Normal University, Jinan 250014, People’s Republic of China
48 Shandong University, Jinan 250100, People’s Republic of China
49 Shanghai Jiao Tong University, Shanghai 200240, People’s Republic of China
50 Shanxi Normal University, Linfen 041004, People’s Republic of China
51 Shanxi University, Taiyuan 030006, People’s Republic of China
52 Sichuan University, Chengdu 610064, People’s Republic of China
53 Soochow University, Suzhou 215006, People’s Republic of China
54 South China Normal University, Guangzhou 510006, People’s Republic of China
55 Southeast University, Nanjing 211100, People’s Republic of China
56 State Key Laboratory of Particle Detection and Electronics, Beijing 100049, Hefei 230026, People’s Republic of China
57 Sun Yat-Sen University, Guangzhou 510275, People’s Republic of China
58 Suranaree University of Technology, University Avenue 111, Nakhon Ratchasima 30000, Thailand
59 Tsinghua University, Beijing 100084, People’s Republic of China
60 Turkish Accelerator Center Particle Factory Group, (A)Istinye University, 34010, Istanbul, Turkey; (B)Near East University, Nicosia, North Cyprus, 99138, Mersin 10, Turkey
61 University of Chinese Academy of Sciences, Beijing 100049, People’s Republic of China
62 University of Groningen, NL-9747 AA Groningen, The Netherlands
63 University of Hawaii, Honolulu, Hawaii 96822, USA
64 University of Jinan, Jinan 250022, People’s Republic of China
65 University of Manchester, Oxford Road, Manchester, M13 9PL, United Kingdom
66 University of Muenster, Wilhelm-Klemm-Strasse 9, 48149 Muenster, Germany
67 University of Oxford, Keble Road, Oxford OX13RH, United Kingdom
68 University of Science and Technology Liaoning, Anshan 114051, People’s Republic of China
69 University of Science and Technology of China, Hefei 230026, People’s Republic of China
70 University of South China, Hengyang 421001, People’s Republic of China
71 University of the Punjab, Lahore-54590, Pakistan
72 University of Turin and INFN, (A)University of Turin, I-10125, Turin, Italy; (B)University of Eastern Piedmont, I-15121, Alessandria, Italy; (C)INFN, I-10125, Turin, Italy
73 Uppsala University, Box 516, SE-75120 Uppsala, Sweden
74 Wuhan University, Wuhan 430072, People’s Republic of China
75 Xinyang Normal University, Xinyang 464000, People’s Republic of China
76 Yantai University, Yantai 264005, People’s Republic of China
77 Yunnan University, Kunming 650500, People’s Republic of China
78 Zhejiang University, Hangzhou 310027, People’s Republic of China
79 Zhengzhou University, Zhengzhou 450001, People’s Republic of China
a Also at the Moscow Institute of Physics and Technology, Moscow 141700, Russia
b Also at the Novosibirsk State University, Novosibirsk, 630090, Russia
c Also at the NRC "Kurchatov Institute", PNPI, 188300, Gatchina, Russia
d Also at Goethe University Frankfurt, 60323 Frankfurt am Main, Germany
e Also at Key Laboratory for Particle Physics, Astrophysics and Cosmology, Ministry of Education; Shanghai Key Laboratory for Particle Physics and Cosmology; Institute of Nuclear and Particle Physics, Shanghai 200240, People’s Republic of China
f Also at Key Laboratory of Nuclear Physics and Ion-beam Application (MOE) and Institute of Modern Physics, Fudan University, Shanghai 200443, People’s Republic of China
g Also at State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871, People’s Republic of China
h Also at School of Physics and Electronics, Hunan University, Changsha 410082, China
i Also at Guangdong Provincial Key Laboratory of Nuclear Science, Institute of Quantum Matter, South China Normal University, Guangzhou 510006, China
j Also at Frontiers Science Center for Rare Isotopes, Lanzhou University, Lanzhou 730000, People’s Republic of China
k Also at Lanzhou Center for Theoretical Physics, Lanzhou University, Lanzhou 730000, People’s Republic of China
l Also at the Department of Mathematical Sciences, IBA, Karachi 75270, Pakistan