[1]\fnmAlexey \surBarsukov
[2]\fnmBodhayan \surRoy
1]\orgdivDepartment of Algebra, \orgnameCharles University, Czechia
2]\orgdivDepartment of Mathematics, \orgnameIndian Institute of Technology Kharagpur, India
Maximum Cut on Interval Graphs of Interval Count Two is NP-complete
Abstract
An interval graph has interval count if it has an interval model, where among every intervals there are two that have the same length. Maximum Cut on interval graphs has been found to be NP-complete recently by Adhikary et al. [1] while deciding its complexity on unit interval graphs (graphs with interval count one) remains a longstanding open problem. More recently, de Figueiredo et al. [2] have made an advancement by showing that the problem remains NP-complete on interval graphs of interval count four. In this paper, we show that Maximum Cut is NP-complete even on interval graphs of interval count two.
keywords:
maximum cut, interval graph, computational complexitypacs:
[MSC Classification]35A01, 65L10, 65L12, 65L20, 65L70
1 Introduction
For a given input graph , the Maximum Cut problem finds a partition of in two sets such that the number of edges between them is maximal.
Maximum Cut is a fundamental and well-known NP-complete problem [3]. The weighted version of the problem is one of Karp’s original 21 NP-complete problems [4]. There are many results describing the complexity of Maximum Cut, where the input of the problem is restricted on some particular classes of graphs. The problem remains NP-complete for many graph classes, such like cubic graphs [5], split graphs [6], co-bipartite graphs [6], unit disk graphs [7], total graphs [8], and interval graphs [1]. On the positive side, polynomial time algorithms are known for planar graphs [9], line graphs [8], graphs not contractible to [10] and graphs with bounded treewidth [6].
There are two papers that have mainly motivated our research. First, a recent proof of NP-completeness of Maximum Cut on interval graphs provided by Adhikary et al. in [1]. Second, a more recent result of de Figueiredo et al. in [2], where they extend the result of the first paper by proving that Maximum Cut is NP-complete on graphs of interval count four. Using the technique of the above work, de Figueiredo et al. prove the NP-completeness of Maximum Cut on permutation graphs as well, which too was open for a long time [11]. The bounding of the number of interval lengths brings us closer to the final goal: to characterize Maximum Cut for unit interval graphs as they are exactly interval graphs of interval count one. There were attempts to provide a polynomial-time algorithm for unit interval graphs [12, 13], but they both were later shown to be incorrect [14, 15]. In this paper, we extend the result of de Figueiredo et al. [2] by proving Theorem 1 which brings us as close as possible to Maximum Cut on unit interval graphs.
Theorem 1.
Maximum Cut on interval graphs of interval count two is NP-complete.
2 Preliminaries
For in , an interval between and , denoted , is the set of all such that . The left and right endpoints of are denoted by and . The length of an interval equals . A set of intervals is called an interval model of a graph if there is a one-to-one mapping such that, for any pair of vertices of , is in if and only if the intervals and have a non-empty intersection. A graph is called interval if it has an interval model. A graph has interval count if there exists a set of size and an interval model of such that, for all in , we have .
A cut of a graph is a partition of its vertices in two classes: . For a cut , a cut edge is an edge that is incident to a vertex in and to a vertex in . The cut value is the number of cut edges of the graph. For a subset of vertices of a graph, the cut value contributed by is the number of cut edges that have at least one of their ends in . Recall that the Maximum Cut problem asks for a cut of the maximal value. Notice that, for interval graphs, Maximum Cut is equivalent to the problem of finding a coloring of an interval model in two colors, say (Red) and (Blue), where the number of differently colored pairs with non-empty intersection is maximal. If an interval has a color , then we use the notation . If is a set of intervals that all have the same color , then we use the notation .
We use intervals of two different lengths: short and long. We assume that, if an interval is short, then , otherwise, for some that will be made precise later.
A block is a set of short intervals such that, for any two intervals , we have and . For a block , denote and for an interval . The size of a block is the number of intervals in it. For example, a block of size is an interval model of the complete graph on vertices.
A union of blocks is a 3-block if
-
•
and and and
-
•
and .
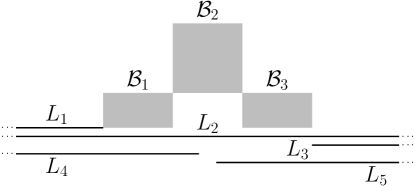
In this article, 3-blocks are displayed as three rectangles, see Figure 1. An interval terminates at a block if and starts from if . For a long interval , we say that it covers if . For example, on Figure 1, terminates at , covers all the blocks, starts from , covers and terminates at , and starts from and covers .
Consider any family of blocks of intervals of the same length such that, for in , we have . A coloring is a mapping . A coloring is alternating if, for , we have . A coloring is almost alternating except for if it becomes alternating after removal of at most intervals from the block .
3 Background
We first revisit the reduction of Adhikary et al. in [1]. They reduced Maximum Cut on cubic graphs to Maximum Cut on interval graphs. Recall that a graph is cubic if the degree of every vertex is equal to 3. In their paper, each vertex and edge of the original cubic graph was represented by a set of intervals, called vertex and edge gadgets respectively. The interval model consisted of first all the vertex gadgets, and then all the edge gadgets arranged from left to right. If an edge was incident to a vertex, then the corresponding vertex and edge gadgets were “linked” by a pair of very long intervals starting from the vertex gadgets and terminating at the edge gadget. They were called link intervals. The number of intervals in any gadget was much greater than the total number of link intervals in the graph. It was shown that, in any Maximum Cut partition of this interval graph, each vertex gadget or edge gadget could have only two possible partitions. For a vertex gadget, these two partitions were made to correspond to its membership in one of the partition sets for a maximum cut of the original cubic graph. If two adjacent vertices of the cubic graph belonged to different sets, then the corresponding edge gadget would make more cut edges with link intervals than if these vertex gadgets were in the same set. Thus, a cut of maximum size of the given cubic graph always corresponded to a cut of maximum size of the constructed interval graph and vice versa. As Maximum Cut on cubic graphs is NP-complete, this reduction implies that it is also NP-complete on interval graphs.
In the reduction above, the gadgets contained intervals of two different lengths. However, the length of each link interval depended on the relative positions of its vertex and edge gadgets. So the total number of different lengths of link intervals was linearly dependent on the size of the cubic graph. So, this interval graph seemed to be far away from unit interval graphs, for which the problem was still open. De Figueiredo et al. in [2] made a very important advancement in this regard. They showed that Maximum Cut was NP-complete even when the total number of lengths used for the intervals was only 4, i.e., when the interval count of the graph was 4. In their paper, the vertex and edge gadgets were basically the same as that of Adhikary et al. in [1]. However, an extra gadget, resembling the vertex and edge gadgets, was used as a “join gadget” between link intervals. Instead of having a link interval running through the entire length between its corresponding vertex and edge gadgets, they used a chain of link intervals joined to each other with the use of join gadgets.
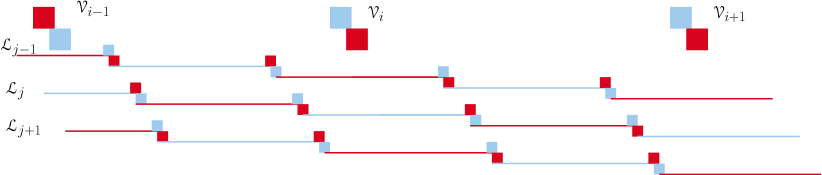
A link chain is a sequence of link intervals with a join gadget between every two consecutive link intervals, where one link interval terminates at the gadget and the other one starts from it. The link intervals of all other link chains that intersect this join gadget, cover it. The join gadgets ensure that, in a maximum cut partition, the link intervals of every link chain are colored with Red and Blue alternately. Thus, link intervals of arbitrary lengths in the original reduction can be replaced by link intervals of a single size. However, one problem remained. Between consecutive vertex or edge gadgets, the link chains had their join gadgets in a fixed order. For example, consider vertex gadgets , and , and link chains , and (fig. 2). If in the gap between and , the join gadget of occurred first, followed by a join gadget each of and respectively, then they would occur in the same order in the gap between and . This would pose a problem if the structure of the graph required and to have a partial intersection with the same edge gadget. In such a case, a second type of link interval with a different length would be used to end link chain early and enable it to partially intersect the same edge gadget along with . Thus, their reduction needed intervals of two lengths for the vertex, edge and join gadgets, and another two lengths as the link intervals, totaling to an interval count of four.
4 Overview of the reduction
We reduce the interval count down to 2 due to our modifications of gadgets and link chains. Instead of using separate lengths of short and long intervals in previous works, the gadgets are now mainly constructed from 3-blocks. The link chains do not use long intervals of two separate lengths anymore. The issue of non-consecutive link chains partially intersecting the same edge gadget is resolved by using a switch gadget that switches the relative positions of join gadgets of link chains.
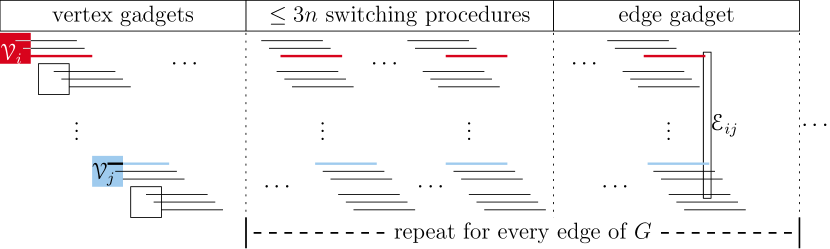
The Maximum Cut problem is NP-complete on cubic graphs [5]. In this article, we provide a polynomial time reduction from Maximum Cut on cubic graphs to Maximum Cut on interval graphs of interval count two. For every cubic graph (of size ), we construct a graph of interval count 2 such that any Maximum Cut partition of corresponds to some Maximum Cut partition of and vice versa. Its top level composition is displayed on Figure 3. On the left, there are vertex gadgets . For each vertex gadget there are three link chains constructed by alternating long intervals and join gadgets. For every edge of there is an edge gadget such that two link chains starting from and respectively both terminate at .
Before reach the edge gadget, we must ensure that there is no other link chain between them. The reason is that, in our construction, neither can intersect another gadget nor a long interval not from can start from or terminate at . Suppose, for example, that . If we straightforwardly connect link chains to , then, as is positioned “between” and , this edge gadget will intersect join gadgets of link chains that start from . To solve this issue, we repetitively apply the switching procedure that switches two consecutive link chains and, therefore, reduces the number of join gadgets between the ones of . After these two chains terminate at , we proceed similarly for every other edge of .
Example 2.
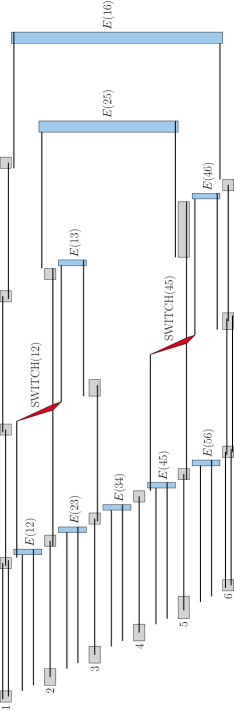
Let be the cubic graph on 6 vertices displayed on Figure 4.

The corresponding interval graph of interval count 2 is displayed on Figure 5. On the left, it has 6 “vertex gadgets” that correspond to the vertices of . For each vertex gadget, there are precisely three chains of long intervals that start from it, each chain represents an edge incident to the corresponding vertex.
At first, we add the “edge gadgets” . The remaining edges are: . Notice that, for any of these edges, it is impossible to connect the corresponding long interval chains with an edge gadget without intersection of two gadgets. Therefore, we add two “switch gadgets” SWITCH(12) and SWITCH(45), and plug into them the corresponding long interval chains in order to switch their relative positions. After that, we add the edge gadgets and . Finally, we deal with the edge and then with .
5 Gadgets
Before we formally describe the reduction graph of interval count two, we present all the gadgets that are used in its construction. Assuming that the size of the cubic graph is , we introduce two parameters that denote the gadget sizes. Let be in and let be in . Next to the definition of each gadget, we add a figure, where this gadget is displayed. On each of the figures, this gadget is colored in Red and Blue. After we construct the whole graph of interval count two, we will argue that, for every Maximum Cut partition of , the coloring of each of its gadgets is similar to one displayed on the corresponding figure.
Vertex gadget
The vertex gadget consists of three 3-blocks and two short intervals: . The blocks of each 3-block have sizes respectively. The 3-blocks are connected by short intervals , they are called short link intervals. That is, we have and and and . For every vertex gadget, there are three long intervals that start from and form the corresponding link chains. A vertex gadget and the three long intervals are displayed on Figure 6.

Edge gadget
An edge gadget consists of two 3-blocks connected by a short link interval. That is, such that and . The blocks of each 3-block have sizes respectively. There are two long intervals of the corresponding link chains terminating at such that and . An edge gadget together with and is displayed on Figure 7. Under a Maximum Cut partition of , for edge gadgets, the colors of and may be arbitrary. So, Figure 7 displays all the cases modulo switching the colors.

Join gadget
Similarly to vertex gadgets, a join gadget consists of 3-blocks of size connected by short link intervals. It can have at most ten 3-blocks, see Figure 8. Every join gadget has at most 3 long intervals terminating at it and the same number of long intervals starting from it. The main purpose of a join gadget is to connect a vertex gadget to edge gadgets by link chains of long intervals. The distance between blocks may be modified in order to readjust the relative distances between long intervals terminating at the gadget, see Figure 8.

Switch gadget
A switch gadget is the only gadget that is not constructed exclusively from 3-blocks. It has 2 parts. The first part consists of 9 bottom blocks and 4 top blocks . At the bottom, , and, for , we have . At the top, for , we have , where is such that . There are two long intervals and such that and . There are two long intervals and such that and . The long intervals are in the same link chain , the long intervals are in the same link chain distinct from . The main property of the first part is that, for any Maximum Cut partition, and . The second part of the switch gadget is a 3-block such that terminates at , covers the 3-block , and a new long interval starts from . Both parts are displayed on Figure 9. The idea about this gadget is that it “switches” the link chains containing and containing , and preserves their colors at the same time: is to the left from but is to the right from , and .
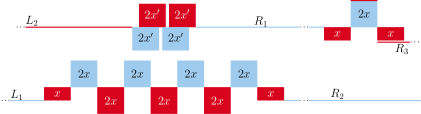
The following lemma ensures that the coloring of the first part on Figure 9 is Maximum Cut.
Lemma 3.
Consider a graph with an interval model as on Figure 9. Then, in any Maximum Cut partition of this graph, (i) for each of the two levels, block colorings are alternating, and (ii) , and .
Proof.
At first, let us compute the size of the cut for any partition, where the colors of the blocks on the top and on the bottom alternate. We do not consider the four long intervals at the moment. The value is the same for any of the four such partitions:
Suppose now that is not maximal. Then we will introduce the following parameters for each block.
-
•
Denote by the numbers of Blue intervals in and .
-
•
Similarly, denote the numbers of Red intervals in and .
-
•
Denote by the numbers of Blue intervals in and in .
-
•
Similarly, denote by the numbers of Red intervals in and in .
We are going to compute the Maximum Cut for the general case and to compare it to in order to find out when it can be the maximal. We are going to split the computation into several parts.
-
•
The part counts the cut-edges inside each of the blocks.
-
•
The and parts count the cut-edges between different blocks that are both on the same level. There are two levels: the top and the bottom .
-
•
The part counts the cut-edges between the two levels.
Now we compute the parts one by one.
Denote by the set of pairs . That is,
Then
Our goal is to prove that is less or equal to 0 and the equality is reached only when the colors alternate. Think of as of a polynomial in and of degree 2:
Clearly, . Compute the terms , , and :
We have extracted the negative squares of from and in order to combine them together with the negative squares of the part of provided by . The other summands of and are almost always negative, except for the minimal and maximal values of . These cases happen exactly when a block is either all Red or all Blue. Then
Clearly, . We are going to find all the cases when . Notice that, for any , there is a summand and a corresponding one for . Thus, we need to consider only the cases when , and . Suppose that ; then and thus , for any , as . So , and thus . Similarly, , and so . Using other clauses of the expression, we conclude that , , and also we have . This means that the colorings of the blocks alternate.
Now we need to prove that . For the contrary, suppose that . Then the cut between the blocks and the long intervals will be at most the sum:
is provided by , is provided by , is provided by , is provided by , and provided by one of . On the other hand, if , then together and provide , for each of two possible colorings of the bottom blocks, and and provide , in total it is . This case is reachable, because we can choose the leftmost bottom block to have a color opposite to . As is not fixed, we can choose the right one that will add as well. So we have to satisfy the inequality
We assumed that so the inequality holds and thus the second case is optimal. We should note that, in the second case, and have the same color because . We have shown that and are colored similarly and that and are colored differently. ∎
6 Construction of the graph
Let be a cubic graph of size . Let the long interval length be while the short interval length is 1. All the intervals of belong to . This ray is split into zones and buffers in the following order:
Each zone (or buffer) is a disjoint union of fragments of the same length, where the distance between two neighbor fragments of the same zone is the same and depends on the long interval length .
-
•
Here, are the zones that correspond to vertices of . For a vertex , is the following disjoint union of fragments of the same size:
This zone usually contains the vertex and the join gadgets corresponding to . The size of its fragments is 32. The distance between the left endpoints of two neighbor fragments is called the phase.
-
•
Buffer zones. For two vertices (and also ), we introduce a buffer zone between . It is denoted by ( is denoted similarly) and is defined as follows:
We need buffer zones in order to do the switching. Every fragment of a buffer zone has size 21.
We need to write instead of because a long interval must start from the rightmost block of some 3-block and must terminate at the leftmost block of another 3-block. So, the length of long intervals must be lesser than the length of the phase by 3.
For , add a vertex gadget into the leftmost fragment of . For each there are 3 long intervals starting from it; they terminate at a join gadget that has 3 new long intervals starting from it, and so on. This produces 3 link chains of long intervals. Each such chain eventually terminates at a corresponding edge gadget.
For every edge , where , we choose a link chain starting from and repeatedly apply the switch procedure (introduced formally in the next paragraph) to this chain until it is in . Once it happens, this chain of and one of the chains of terminate at the same edge gadget . No long interval starts from . Then we choose another edge of and repeat this operation until all edges of are treated. If a chain does not participate in some switch procedure, then, during this procedure, the long intervals of this chain are joined by join gadgets that look the same as vertex gadgets. The composition of is displayed on Figure 3 on fig. 3.
Switch Procedure
Consider some adjacent vertices of the cubic graph , they correspond to two vertex gadgets and to an edge gadget in the interval model of . Suppose that there is another vertex gadget between and . Then, there is a join gadget that corresponds to between any pair of join gadgets of . We require that a gadget can be intersected only by long intervals, in particular, we forbid any gadget to intersect , so we have to switch some link chain starting from with all three link chains that start from , and similarly for any other vertex gadget between and .
We solve it by the switch procedure which is displayed on Figure 10. The line is split into zones and buffers between zones.
For , corresponds to the vertex gadget , it contains and most of the join gadgets of the link chains starting from . Every fragment of is placed between the fragments of and . contains switch gadgets that are used to let a chain starting from pass all three chains starting from , this is exactly what is shown on Figure 10. By repeatedly iterating the switching, we pass all the vertex gadgets between and and eventually connect the corresponding link chains to a common edge gadget . In order to justify the correctness of Figure 10, we describe the precise positions of each gadget and long interval below.

Consider two vertices . is colored in Blue, is colored in gray, – in Red, the black color corresponds to the rest – the union of all other zones and buffers. Suppose that is adjacent to some , for . Then, for some chain of long intervals that starts from the vertex gadget of , we need to put it to the right of , that is to switch it with the long interval chains starting from . On Figure 10, it is equivalent to move one Blue interval to the black segment by passing the orange segment beforehand. We suppose that the long intervals starting from are Blue and those starting from are Red, and so are all other long intervals that are connected to these gadgets by a chain of join gadgets. Say that a gadget is in the fragment of some zone if its leftmost and rightmost points are in and . We are going to show that no gadgets intersect each other by considering each of nine buffer zones on Figure 10.
-
1.
The first buffer does not contain any gadgets.
-
2.
The second buffer intersects two join gadgets. The Blue one is in of and in of . Its long intervals terminate at of and start from of and from of . The Red one is in of and in of . Its long intervals terminate at of and start from of and from of .
-
3.
The third buffer contains the first switch gadget in . Its long intervals terminate at and start from of . It also contains the Red join gadget in of and in of . Its long intervals terminate at of and start from of and from of .
-
4.
The fourth buffer contains the second switch gadget in . Its long intervals terminate at and start from . It also contains the second part of the first switch gadget in . Its long intervals terminate at and start from . It also contains a Red join gadget in of and in of . Its long intervals terminate at and start from of .
-
5.
The fifth buffer contains the second part of the second switch gadget in . Its long intervals terminate at and start from . It also contains the third switch gadget in . Its long intervals terminate at and start from . It also contains a Red join gadget in . Its long intervals terminate at and start from .
-
6.
The sixth buffer contains a Blue join gadget in . Its long intervals terminate at and start from . It also contains the second part of the third switch gadget in . Its long intervals terminate at and start from . It also contains a Red join gadget in . Its long intervals terminate at and start from .
-
7.
The seventh buffer intersects a Blue join gadget that is in of , in of and in of . Its long intervals terminate at of and start from of . It also contains a Red join gadget in . Its long intervals terminate at and start from .
-
8.
The eighth buffer intersects a Red join gadget. It is in of and in of . Its long intervals terminate at of and start from of .
-
9.
The ninth buffer is empty.
7 Gadget partitions
In this section, we describe and prove how exactly each gadget of can be colored under a Maximum Cut partition of . Sometimes, for a property to hold, it is required that satisfies certain numerical constraints. We now list these constraints, and, later, when we provide an explicit construction of , we make sure that all of them are satisfied. Suppose that the cubic graph has vertices. Then, assume the following.
-
1.
Every block of is covered by at most long intervals.
-
2.
Every long interval of covers at most blocks.
For each gadget of , we assume that it is covered by at most long intervals.
Lemma 4.
Let be a 3-block in of size . Then, for any Maximum Cut partition of , , and all except for at most intervals of have the opposite color.
Proof.
Within the graph , there are five ways how a long interval can intersect a 3-block. All these five ways are displayed on Figure 1 on fig. 1. Let be the corresponding sets of long intervals that intersect a given 3-block within the graph . That is,
-
•
denotes all the long intervals that terminate at ;
-
•
denotes all the long intervals that cover , , and ;
-
•
denotes all the long intervals that start from ;
-
•
denotes all the long intervals that terminate at ;
-
•
denotes all the long intervals that start from .
We consider some Maximum Cut partition of . For in , let and be the numbers of Red and Blue intervals in . W.l.o.g., assume that most of the intervals of get the color Red, that is, . Also let , and be the number of intervals of respectively that are colored Blue. Hence , and are the numbers of intervals of respectively , and that are colored Red. We want to show that one of the two following conditions must hold:
-
•
either and , or
-
•
and .
Let us first calculate the cut value contributed by the 3-block. It consists of the three following parts.
-
1.
The number of cut edges formed between the blocks and the long intervals is .
-
2.
The number of cut edges formed by the short intervals of the same block among themselves is .
-
3.
The number of cut edges formed by the short intervals of the different blocks is .
Denote the value by . Denote by the cut value contributed by the 3-block , which is the sum of the three aforementioned numbers:
Now let us modify the cut by making and . This means that we have . So the cut value, denoted by , contributed by the 3-block in this case is:
If we instead have and (i.e., ), then the cut value, denoted by , contributed by the 3-block would be:
W.l.o.g., assume that . This implies that , which means that .
Notice that equals
Notice that if , then . Similarly, if , then . Since we assumed that either or , it implies that . So we have . But since and each , we conclude that . This contradicts the maximality of . Therefore, we conclude that and .
Now we show that . For the contrary, suppose that . Then, . In this case, the value is :
Since and each , we have that , which contradicts the first cut being maximal. So we conclude that .
W.l.o.g., assume that . We want to show that . As , the cut value contributed by the 3-block is now
Notice that . Thus, only if . As , we are done. The case when is treated similarly.
∎
Lemma 5.
Let be an edge gadget of together with two long intervals terminating at and . Suppose that is covered by at most long intervals. Then, (i) the colorings of 3-blocks are almost alternating except for at most intervals of the central blocks, and (ii) if , then the Maximum Cut value provided by is greater than the Maximum Cut value in the case , by at least .
Proof.
Suppose that is covered by long intervals. By Lemma 4, the Maximum Cut of and , is either alternating or almost alternating except for intervals of or , where is the difference between the numbers of Red and Blue long covering intervals.
Suppose that ; then . The color of must be Blue except for at most intervals. For there are two cases.
-
1.
The color of is Red except for at most intervals, and . Then, for any , the cut size is at most .
-
2.
The color of is Blue except for at most intervals, and . Then . Then the cut size is at most .
Suppose that and . Then is partitioned as . is also partitioned as . Then the cut size would be at least .
The difference between the value provided by when and the value in the case when they are equal is at least , which is at least . ∎
Lemma 6.
Suppose that the first part of a switch gadget is covered by long intervals. Then, in any its Maximum Cut partition, the coloring of is alternating and the coloring of is alternating except for at most intervals within or .
Proof.
Let the number of Red and Blue long intervals covering the switch gadget be and respectively, and denote the quantity by . Suppose that . Let , for , be the same as in Lemma 3. Compute the size of the cut:
Consider only those summands that participate in the size of the cut when the coloring of the blocks alternates, i.e., when, for all , :
If we choose , then the distance between some variable (except for ) and the closest end of its domain cannot be greater than . For example, suppose that . Then , and so
So, in this case it will not be a maximum cut.
Suppose that , then either when , or when . But then one of the clauses will be greater than , hence, greater than . Similarly, . Consider the variables . Choose between and such that is greater than , as , it is easy to choose a convenient value for . For such , we will have .
Denote and . Then . Then we can choose only those that satisfy
as, otherwise, it will not be a maximal cut. Denote , we know that . Then the expression can be written in the following form:
Take . Then
The same is true for . We now can imply that , otherwise the cut is not maximal. This is an important result because we can show now that all the blocks except for are monochromatic. Take any , then suppose that for some variable except for , say for example: . Then . So the cut will not be maximal in this case. Same is true for any variable other than . So we can conclude that , and .
Suppose w.l.o.g. that all the variables except for are equal to . Then equals
One can see now that the cut will be optimal if for . For the case when the optimal cut will be when and . Recall that . As , we have . ∎
Reduction
At first, we return to the conditions about that we stated at the beginning of Section 5 and that we assumed to hold.
-
1.
Every block of is covered by at most long intervals.
-
2.
Every long interval of covers at most blocks.
We need to verify that the graph that we have just constructed indeed satisfies them. In total, there are long intervals starting from vertex gadgets, so every block is intersected by at most long intervals. Every long interval covers zones and buffers, each zone contains a join gadget that has at most ten 3-blocks, each buffer contains at most one switch gadget that has 16 blocks. Thus, those 3 conditions are satisfied for .
Let us say that a partition of in 2 classes is good if the following conditions are satisfied.
-
1.
For any gadget, its coloring is alternating or almost alternating except for of a 3-block or one of of a switch gadget that contain at most intervals of the other color.
-
2.
For any short or long interval that starts from or terminates at a block of size , or , we have .
Lemma 7.
Any Maximum Cut partition of is good.
Proof.
The condition (1) is provided by Lemmas 6 and 4. Let be the leftmost interval that does not satisfy (2), suppose that it starts from a block of size at least and . is a part of some link chain that connects a vertex gadget to an edge gadget . Invert and modify the colors of all gadgets and short link and long intervals of this chain that are between and so that all intervals of this chain satisfy (2). The gain after this operation is at least because . Denote by the number of short link and long intervals in the chain, it is at most . The loss is at most the sum of the following values:
-
•
, if both intervals terminating at now have the same color;
-
•
– the cut between the gadgets of covered by the intervals of the chain, where is an upper bound for the number of long intervals covering a gadget and is an upper bound on blocks that a long interval intersects;
-
•
– the cut between the long intervals of intersected by the intervals of the chain;
-
•
– the cut between the gadgets of the chain and the long intervals of covering them (the number of gadgets in the chain also equals ).
As , and , the loss is in . We are free to choose to be large enough for the gain to be strictly greater than the maximal possible loss. Thus, for such value of , the second condition also holds. ∎
A good partition corresponds to some partition of : assign to a vertex the same color that is assigned to the long intervals starting from the vertex gadget . For such and , we will write . Clearly, the other direction is also true: for every there exists a good partition such that . Recall that each gadget is covered by at most long intervals, there are long interval chains, and each long interval covers at most gadgets. The following Lemma 8 implies that Maximum Cut on cubic graphs reduces to Maximum Cut on interval graphs of interval count 2. It is well-known that a Maximum Cut problem is in NP, so, as the size of is polynomial in , it implies Theorem 1.
Lemma 8.
Let be a Maximum Cut partition of , and be a partition of such that . Then is a Maximum Cut partition of .
Proof.
Suppose that is not a Maximum Cut partition, that is, there is another which is maximal. Let be a good partition that satisfies .
For simplicity, we denote by the set of intervals that belong to edge gadgets, and denotes the set of intervals that belong to chains or to other gadgets. Clearly, .
The difference between the cut values of and , for edges induced by , is at most because there are edge gadgets, and each of them changes the cut by at most . The difference between the cut values, for edges induced by , is at most
which belongs to . Finally, as has a strictly greater cut value than , we know that the number of cut edges between and for is greater than the corresponding number for by at least . By Lemma 5 and because an edge gadget is covered by at most long intervals, each of them adds at most to the cut, and there are edge gadgets. As we choose to be in , the cut value of is greater than the cut value of , it is a contradiction. ∎
8 Conclusion
In this article, we have shown that Maximum Cut remains NP-complete for interval graphs of interval count two. The future work in this direction is to understand the complexity of Maximum Cut on unit interval graphs. Apart from that, our result raises the following question.
Question 1.
Let be a fixed set of size . What is the complexity of Maximum Cut on interval graphs that have a model, where the length of each interval is in ?
In the current paper, the length of long intervals depends on the number of vertices of the cubic graph , therefore, it may be arbitrarily large. This question asks, whether the problem remains NP-complete if there is an additional restriction on how much different are the lengths of short and long intervals. If the length of short intervals is 1, and the length of long intervals is , then, by making the value of smaller, the graph class becomes more similar to unit interval graphs that correspond to the case when .
Acknowledgements
The authors are thankful to Kaustav Bose for correcting Lemma 4.
Declaration
Alexey Barsukov is funded by the European Union (ERC, POCOCOP, 101071674). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.
Bodhayan Roy is funded by SERB MATRICS, Grant Number MTR/2021/000474.
References
- \bibcommenthead
- [1] Adhikary, R., Bose, K., Mukherjee, S. & Roy, B. Complexity of maximum cut on interval graphs. Discrete & Computational Geometry 70, 307–322 (2023). URL https://doi.org/10.1007/s00454-022-00472-y.
- [2] de Figueiredo, C. M. H., de Melo, A. A., Oliveira, F. S. & Silva, A. Maximum cut on interval graphs of interval count four is np-complete. Discrete & Computational Geometry (2023). URL https://doi.org/10.1007/s00454-023-00508-x.
- [3] Garey, M. R. & Johnson, D. S. Computers and Intractability: A Guide to the Theory of NP-Completeness (W. H. Freeman & Co., USA, 1979).
- [4] Karp, R. M. Reducibility among Combinatorial Problems, 85–103 (Springer US, Boston, MA, 1972). URL https://doi.org/10.1007/978-1-4684-2001-2_9.
- [5] Berman, P. & Karpinski, M. Wiedermann, J., van Emde Boas, P. & Nielsen, M. (eds) On some tighter inapproximability results (extended abstract). (eds Wiedermann, J., van Emde Boas, P. & Nielsen, M.) Automata, Languages and Programming, 200–209 (Springer Berlin Heidelberg, Berlin, Heidelberg, 1999).
- [6] Bodlaender, H. L. & Jansen, K. On the complexity of the maximum cut problem. Nordic J. of Computing 7, 14–31 (2000).
- [7] Díaz, J. & Kamiński, M. Max-cut and max-bisection are np-hard on unit disk graphs. Theoretical Computer Science 377, 271–276 (2007). URL https://www.sciencedirect.com/science/article/pii/S0304397507000801.
- [8] Guruswami, V. Maximum cut on line and total graphs. Discrete Applied Mathematics 92, 217–221 (1999). URL https://www.sciencedirect.com/science/article/pii/S0166218X99000566.
- [9] Hadlock, F. Finding a maximum cut of a planar graph in polynomial time. SIAM Journal on Computing 4, 221–225 (1975). URL https://doi.org/10.1137/0204019.
- [10] Barahona, F. The max-cut problem on graphs not contractible to k5. Oper. Res. Lett. 2, 107–111 (1983). URL https://doi.org/10.1016/0167-6377(83)90016-0.
- [11] de Figueiredo, C. M. H., de Melo, A. A., Oliveira, F. S. & Silva, A. Maxcut on permutation graphs is np-complete. Journal of Graph Theory 104, 5–16 (2023). URL https://onlinelibrary.wiley.com/doi/abs/10.1002/jgt.22948.
- [12] Bodlaender, H. L., Kloks, T. & Niedermeier, R. Simple max-cut for unit interval graphs and graphs with few p4s. Electronic Notes in Discrete Mathematics 3, 19–26 (1999). URL https://www.sciencedirect.com/science/article/pii/S1571065305800149. 6th Twente Workshop on Graphs and Combinatorial Optimization.
- [13] Boyacı, A., Ekim, T. & Shalom, M. A polynomial-time algorithm for the maximum cardinality cut problem in proper interval graphs. Information Processing Letters 121, 29–33 (2017). URL https://www.sciencedirect.com/science/article/pii/S0020019017300133.
- [14] Bodlaender, H. L., de Figueiredo, C. M. H., Gutierrez, M., Kloks, T. & Niedermeier, R. Ribeiro, C. C. & Martins, S. L. (eds) Simple max-cut for split-indifference graphs and graphs with few p4’s. (eds Ribeiro, C. C. & Martins, S. L.) Experimental and Efficient Algorithms, 87–99 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2004).
- [15] Kratochvíl, J., Masařík, T. & Novotná, J. $${mathcal {u}}$$-bubble model for mixed unit interval graphs and its applications: The maxcut problem revisited. Algorithmica 83, 3649–3680 (2021). URL https://doi.org/10.1007/s00453-021-00837-4.