Massive relativistic compact stars from SU(3) symmetric quark models
Abstract
We construct a set of hyperonic equations of state (EoS) by assuming SU(3) symmetry within the baryon octet and by using a covariant density functional (CDF) theory approach. The low-density regions of our EoS are constrained by terrestrial experiments, while the high-density regime is modeled by systematically varying the nuclear matter skewness coefficient and the symmetry energy slope . The sensitivity of the EoS predictions is explored in terms of parameter of the SU(3) symmetric model that modifies the meson-hyperon coupling constants away from their SU(6) symmetric values. Our results show that model EoS based on our approach can support static Tolman-Oppenheimer-Volkof (TOV) masses in the range - in the large- and small- regime, however, such stars contain only a trace amount of hyperons compared to SU(6) models. We also construct uniformly rotating Keplerian configurations for our model EoS for which the masses of stellar sequences may reach up to . These results are used to explore the systematic dependence of the ratio of maximum masses of rotating and static stars, the lower bound on the rotational frequency of the models that will allow secondary masses in the gravitational waves events to be compact stars with and the strangeness fraction on the model parameters. We conclude that very massive stellar models can be, in principle, constructed within the SU(3) symmetric model, however, they are nucleonic-like as their strangeness fraction drops below 3%.
keywords:
Equation of state , Hyperonic stars, Rapid rotation , Gravitational wave events1 Introduction
Compact stars (CSs) provide unique laboratories to probe dense matter under extreme conditions which cannot be reproduced on Earth. The composition of the deep interiors of CS is not known. It represents the main uncertainty for the determination of the static and dynamic properties of CS. Various high-density compositions have been studied assuming different degrees of freedom, for example, compositions featuring purely nucleonic, heavy baryon-admixed, and/or deconfined quarks matter, for reviews see Refs. [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. In particular, hyperons have been studied as an option as their nucleation may become energetically favorable above a threshold, which is distinct for each hyperon and is controlled by the conditions of -equilibrium and charge neutrality among the baryons and leptons, see Fig. 5 of Ref. [18]. Hyperonization of dense matter then reduces the pressure of dense matter which has a significant impact on the maximum CS mass, for reviews see Refs. [14, 15, 16, 17].
Currently, the most rigorous constraints on the high-density behavior of the equation of state (EoS) come from the observations of a few massive pulsars with masses [19, 20, 21, 22, 23]. These observations set a lower bound on the maximum mass of CS predicted by any model of dense matter. The long-awaited detection of gravitational waves (GWs) from a binary neutron star merger, the GW170817 event placed significant constraints on the tidal deformability of canonical-mass stars and thus provided additional constraints on the EoS of dense matter at intermediate densities [24, 25, 26]. The multi-messenger analyses of GW170817 event suggest that the maximum mass of static CS may not exceed [27, 28, 29, 30, 31]. The X-ray pulse profile modeling of pulsars with data from the NICER observatories recently led to measurements of CS radii. The estimates for one of the most massive known pulsar, PSR J0740+6620 [32, 33], open prospects of constraining the properties of the EoS, in particular, the composition of matter at high densities. PSR J0740+6620 has a mass of about and is thus about 50% more massive than PSR J0030+0451 [34, 35], yet current measurements do not indicate a significant difference in their sizes. This may indicate that the turning point, i.e., the maximum, of the mass-radius relation occurs above the mass of PSR J0740+6620 [36, 37]. Previous models of hyperonic stars were mainly constrained by the masses of massive pulsars [38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 18, 51, 52, 53, 54].
Observational identification of neutron stars (black holes) as members of binary systems requires the knowledge of the upper (lower) limit on the gravitational mass of a neutron star (black hole). The GW190814 event [55], caused by the merger of two stellar objects with an extremely asymmetric mass ratio, contained a primary black hole with a mass of . The secondary’s mass was in the range of . The latter value of mass is within the hypothesized “mass-gap” between neutron stars and black holes, , where no compact object had ever been observed before. Whether the light companion is the most massive neutron star or the lightest black hole discovered so far is unclear yet [56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]. Recently, the event GW200210 [73] was reported in which the components have masses of and . In Refs. [57, 58] we suggested that the secondary component of GW190814 is more likely a black hole rather than a CS, by considering hyperonic EoS models where hyperonic couplings to vector mesons were based on the SU(6) quark model, while those to scalar mesons were fitted to the depth of their potential at nuclear saturation density.
The main motivation of this work is to extend the previous studies [57, 58] of massive hyperonic CS from SU(6) symmetry based vector meson couplings to those that arise within the more general SU(3) symmetry [74] which was implemented in the context of CSs within Hartree [75] and Hartree-Fock [18] based CDF models. This provides a more complete exploration of the parameter space that admits the existence of massive hyperonic stars. Indeed, the SU(6) model combines the flavor SU(3) and spin SU(2) symmetries, which is a special case of the more general SU(3) model [74]. Previously, several authors explored the effect of breaking of SU(6) symmetry down to SU(3) for selected nucleonic EoS in the vector-meson sector [41, 18], scalar-meson sector [42] and both [46]. In the scalar-meson sector the SU(3) relations do not hold after fixing the -hyperon depth [50, 57] and the hyperonic couplings are fixed by the values of hyperonic potential depths. Therefore, the SU(3) relations are useful for the vector-meson sector only. These works demonstrated that within the SU(3) symmetric models for the vector-meson sector it is possible to construct massive hyperonic CSs with maximum masses as high as 2.2-. They used models with fixed properties of nucleonic component within the relativistic mean field models, which preclude by construction a study of the dependence of the results on continuous variations of nuclear matter characteristics such as symmetry energy, its slope as well as the skewness.
This paper is organized as follows. In Sec. 2 we briefly outline the key features of the CDF model for hyperonic matter. Section 3 discusses the bulk properties of hyperonic stars predicted by our CDF approach for a broad range of variations of the parameters. We discuss the implications of these models for the interpretation of GWs produced in binary stellar collisions involving massive secondaries whose masses lies in the “mass-gap”. Finally, a summary of our results is provided in Sec. 4.
2 CDF model for hypernuclear matter
We use in this work the standard CDF theory with density-dependent meson-baryon couplings for a many-body nuclear system whose interaction Lagrangian is given by [76, 77, 18, 78]
| (1) |
where stands for the Dirac spinors. The index labels the baryonic octet with the member masses denoted by . The explicit form of the free Lagrangian can be found in Ref. [76, 77, 18]. The octet of baryons interacts via exchanges of , and mesons, which comprise the minimal set necessary for a quantitative description of nuclear phenomena [79, 80]. We consider further two hidden-strangeness mesons, and , which describe interactions between hyperons [75, 47, 18, 81]. The mesons couple to baryons with coupling constants , which are functions of the baryonic density, , where with being the nuclear saturation density. For the explicit form of the functions see Refs. [77, 18]. The interaction Lagrangian (2) is fixed by first assigning the baryons and mesons their masses in the vacuum. Next, one fixes the three coupling constants () in the nucleonic sector and the four parameters that enter the functions . Then ground state properties of infinite nuclear matter and finite nuclei can be computed uniquely in terms of the above seven adjustable parameters. Note that the constraint conditions on the function reduce the eight parameters for and -mesons to three [77, 18]. In addition, there is one parameter for the -meson. There are in total four parameters that enter the functions .
The EoS of isospin asymmetric nuclear matter can be expanded around nuclear saturation and the isospin symmetric limit in power series [82, 78]
| (2) |
where and . The coefficients of the density-expansion in the first line of Eq. (2) are the characteristic coefficients of nuclear matter in the isoscalar channel, specifically, the saturation energy , incompressibility , and skewness . The coefficients associated with the expansion away from the symmetric limit in the second line are the characteristic parameters in the isovector channel, i.e., the symmetry energy and its slope parameter . The quantities which arise at a higher order of the expansion, specifically and , are only weakly constrained by the conventional fitting protocol used in constructing the density functionals, i.e., the procedure which involves usually fits to nuclear masses and radii. However, the value of controls the high-density behavior of the nucleonic energy density, while the value of determines the intermediate-density behavior of the nucleonic energy density according to Eq. (2).
It is interesting to examine the potentials of the baryons in pure neutron matter, given by
| (3) |
where the meson fields are replaced by their respective expectation values in the Hartree mean-field approximation [76, 77, 42, 18], and denotes the rearrangement term that comes from the density-dependence of the meson-baryon coupling constants [76, 77, 42, 18].
In the SU(3) model three parameters are describing the deviation from SU(6) flavor-spin symmetry. Considering the vector meson sector, the parameter is the weight factor for the contributions of the symmetric and antisymmetric couplings. Its SU(6) value is . Another parameter is the mixing angle which relates the physical mesons to their pure octet and singlet counterparts. And, finally, the third parameter is the ratio of the meson octet and singlet couplings [83, 84, 41, 18].
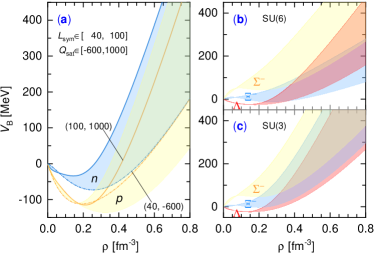
The roles played by the parameters and for the single-particle potentials of baryons are shown in Fig. 1, panel (a), where the nucleonic potentials are shown for models with MeV and MeV, and in panels (b) and (c) where the hyperonic potentials are shown for the cases of SU(6) and extreme SU(3) with .
Given the five macroscopic coefficients in Eq. (2) together with the preassigned values of and Dirac mass [18], we could determine uniquely the seven adjustable parameters of the Lagrangian (2). In Ref. [78] it has been suggested that one can generate a set of nucleonic CDF models by varying only one coefficient in Eq. (2) while keeping the others fixed. Having this in mind, we map the nucleonic EoS given by the Lagrangian (2) for each set of parameters and . For our analysis below we adopt the lower-order coefficients in Eq. (2), i.e., , MeV, and MeV, as those inferred from the DDME2 parametrization [77, 78], which was adjusted to the properties of finite nuclei.
The determination of the meson-hyperon couplings represents a long-standing theoretical challenge due to the lack of sufficiently abundant and accurate experimental data. In the present work, we restrict our attention only to the three lightest quark flavors and adopt the flavor SU(3) symmetric model [74, 75, 18]. To explore the parameter space associate with the SU(3) model we proceed by assuming an ideal mixing value of [85]. This fixation of the mixing angle , which describes the mixing between the singlet and the octet members of a physical isoscalar vector mesons, is motivated by the fact that the mixing between nonstrange and strange quark wave functions in the and -mesons is ideal, i.e., the mixing angle assumes the ideal mixing value quoted above. In addition, from the quadratic mass formula for mesons, one obtains [85], a value that is a very close to the ideal mixing angle . Thus, it is reasonable to keep the condition of “ideal mixing” for the isoscalar vector mesons. The dependence on the remaining parameters, and , can be explored by fixing one of them and varying the other. This has been done previously in Ref. [18] (see their Figs. 11 and 12) showing that reducing the value of either or from their SU(6) values at fixed value of the other parameter yields qualitatively similar modifications of the EoS and the particle fractions. We thus choose to vary only one of them, i.e., , while keeping fixed at its SU(6) value.
Then we are left with a single free parameter to quantify the effects of the SU(3) symmetric model. In this case, the hyperonic coupling constants are defined as [41, 18]
| (4a) | ||||
| (4b) | ||||
| (4c) | ||||
| (4d) | ||||
where in each equation the last relation shows the asymptotes neglecting terms . These asymptotic values can be compared with the SU(6) values of the coupling constants,
| (5a) | ||||
| (5b) | ||||
It is seen that the limit of the SU(3) model implies a much stronger repulsive interaction among hyperons due to -exchange.
In the SU(6) symmetric model, the -meson has a vanishing - coupling, whereas it does couple to the nucleon in SU(3) symmetric model in terms of
| (6) |
where the last relation is the asymptote as above.
To ensure this new coupling scheme does not spoil the fits to the purely nuclear data, we make the replacement [18]
| (7) |
where the denotes the coupling for the case of . For such a scheme, it has been shown in Ref. [18] that the EoS of purely nucleonic matter is (almost) independent of the appearance of -meson. For the isovector meson , one has [41, 18]
| (8) |
The isoscalar-scalar meson-hyperon couplings are then determined by fitting them to certain preselected properties of hypernuclear systems. We fix the coupling constants using the following hyperon potentials in symmetric nucleonic matter at saturation density, , extracted from hypernuclear phenomena [86, 87]:
| (9) |
Finally, we use the estimate , which is extracted from the bond energy [88], to fix the coupling constant . The couplings of the remaining hyperons and to the -meson are determined by the relation . In this manner, we assume that the hyperon potentials scale with density as the nucleonic potential, therefore their high-density behavior is inferred from that of the nucleons. In Fig. 1 (b) we show the potentials of hyperons in pure neutron matter for two limiting cases, and 0. The former corresponds to the SU(6) model while the latter is the extreme case of the SU(3) model. It is seen that the hyperon potential depths (9), indeed, determine only the EoS region around the saturation density. In contrast, the meson coupling constants (4) affect largely the high-density regime of the EoS and consequently the degree of stiffness of the EoS, which is closely linked to the inner core composition of CSs.
For any set of coupling constants the EoS of the core of a CS is determined by applying the conditions of weak equilibrium and change neutrality. This EoS is then matched (interpolated) smoothly to the EoS of the crustal matter given by Refs. [89, 90] at the core-crust transition density . The details of core-crust matching procedure and the model of the crust EoS affect to some extent the value of the radius and, therefore, the tidal deformability for light CSs [91, 92], but the uncertainties are negligible for massive stars of interest herein.
3 Gross properties of hyperonic stars
In this section, we will explore the gross parameters of hyperonic stars for a selected set of parameters that control the stiffness of the EoS. In the nucleonic sector we vary the characteristics of nuclear matter and . In the hyperonic sector, we vary the parameter associated with the breaking of the SU(3) symmetry. Our choice of parameters that describe the EoS of hypernuclear matter is as follows:
-
1.
(I) Soft EoS in the nucleonic sector with MeV, which is close to the lower values of the 90% confidence ranges of the PREX-2 neutron skin measurement [93, 94, 95]. Our EoS predicts for mass star a radius and tidal deformability in the ranges of km and when the remaining parameters and are varied. These values are within the range derived for the multimessenger GW170817 event [25, 26].
-
2.
(II) Stiff EoS in the nucleonic sector with MeV, which is close to the central value of the PREX-2 analysis [94]. In this case, we find that the radius and deformability are larger, their values for a mass star being in the range of km and . These values are in agreement with the mass and radius inferences from the NICER experiment for PSR J0030+0451 [34, 35], but are outside of the range deduced from the GW170817 event [25, 26]. Exceptions to this are models with MeV.

Figure 2 shows a collection of EoS that cover the relevant range of parameters both for the nucleonic and hyperonic sectors. The model EoS is distinguished by (a) the values of and 100 MeV which control the intermediate-density stiffness in the nucleonic sector; (b) the values of which control the high-density stiffness of the nucleonic sector and are drawn from the interval MeV with a step size of 100 MeV; (c) the values of the -parameter which takes on two values: for the SU(6) model and , which is an extreme case of the SU(3) model. As can be seen, the intermediate-density soft models show a delay in the appearance of hyperons as the density is increased. As a consequence, the EoS is stiffer at high densities once the hyperons are admixed with the nucleonic matter. Note the different ordering of the thresholds of the appearance of hyperons in the SU(3) and SU(6) models. In the SU(6) case, hyperons appear first and are followed by , then hyperons as the density is increased. In the SU(3) model, ’s are followed by the hyperons and the onset of is shifted to densities that are not relevant for stable CSs. Note that here and below we will keep occasionally the EoS models with maximum masses below the mass limit to account for the possibility of two families of CSs, in which case stars with masses of and higher are strange stars [96].
3.1 Static sequences of hyperonic stars

We start by considering sequences of static (non-rotating) stars which are described by the Tolman-Oppenheimer-Volkoff (TOV) equation for a given input EoS. Figure 3 shows the maximum mass , its strangeness fraction ( with being the total strangeness(baryon) numbers in a star [51]), and the mass of the star at which the hyperon first appears, as functions of the and parameters for the two classes of models with and 100 MeV, as described above. The parameter ranges are and , where the upper value of corresponds to its SU(6) value.
According to the results shown in Fig. 3 the following conclusions can be drawn:
(i) The upper left corner of the parameter space (low and ) is inconsistent with the mass measurement of PSR J0740+6620 [21, 22], i.e., the consistency of the SU(6) symmetric model requires large values of . Moving away from SU(6) symmetry stiffens the EoS and consequently relaxes the large requirement. For example, in the extreme limit where the mass constraint above is met for any value of . Models with smaller values of (c.f. panels a and d) predict (counterintuitively) a wider range of parameters that produce massive enough stars, because smaller implies softer nucleonic EoS at the intermediate densities and, therefore, delayed onset of hyperons. The strangeness fraction of maximum-mass configurations is anti-correlated with the maximum masses of stars, since the more massive the star the smaller the fraction of hyperons and the strangeness fraction . Thus, going away from the SU(6) symmetry limit suppresses the emergence of hyperons in massive stars by large factors of -4. The most massive models then have a negligible hyperonic content and are close in their properties to their purely nucleonic stars. According to the lower panels of Fig. 3, the masses of stars in which the threshold for the appearance of hyperons is reached shifts to higher values as one moves away from SU(6) value and increases the value of . This is a direct consequence of the stiffening of the EoS in the nucleonic sector by larger values of and in the hyperonic sector by smaller values of .
(ii) A combination of numerical simulations with simple but reasonable assumptions lead to the conclusion that the GW170817 event resulted in a rapidly rotating neutron star which collapsed to a black hole, a scenario that allowed scientists to deduce an approximate upper limit for the TOV stellar mass in the range of [29, 28, 30, 31]. The upper limit of this value range is obtained if finite temperature EoS effects are included in the analysis [31]. According to Fig. 3, the stars in the high- and low- domain have masses that violate this upper limit. These are also the stars with strongly reduced hyperon fractions of - since the onset of hyperons occurs only in the most massive () stars.
(iii) Finally, note that this high- and low- domain features stars with masses . Thus the stars from this domain would be compatible with the mass of the secondary in the GW190814 event [55] and its interpretation as a low-spin star with a trace of hyperons (-). Inverting the argument and assuming that GW190814 event contained a massive CS one can put limits on the values of parameters of the CDF, specifically in our case we require MeV and . We recall that the latter constraint implies and , see Eq. (4). We stress again that for these models hyperon populations is very small since . We also note that the requirement MeV is consistent with the recent nuclear CDFs [97, 98] that were calibrated by finite nuclei.

We plot in Fig. 4 the mass and radius of the maximum-mass configuration as functions of strangeness fraction in the core for a collection of our EoS. As seen in Fig. 4, for fixed values of the mass depends linearly on . In the case where is fixed, the relation has a polynomial form. The same scalings also apply to the radius (see also the discussion of the last relation in Ref. [41]). However, the mass or the radius as a function of the parameters and are randomly distributed and cannot be easily fitted. Some of the models shown in Fig. 4 have maximum masses below the mass band of PSR J0740+6620 [21] and therefore are ruled out. This conclusion works only within the single CS family scenario and can be circumvented in a scenario where there is a separate family of strange stars [96]. In this scenario very compact hyperonic stars with masses far below are possible.
3.2 Keplerian sequences of hyperonic stars

Next we consider uniformly rotating stellar models assuming stationary, ideal fluid equilibria described by general relativity [99, 100, 101, 102]. Let us first focus on the Keplerian limit of equilibria rotating at the maximal value of the rotation frequency. Because these configurations have the maximal value of the centrifugal force they carry the maximum mass allowed by uniform rotation. The rotating equilibria were computed with the public domain RNS code [103].
The maximum mass of the Keplerian sequence and the corresponding strangeness fraction are shown in Fig. 5 for varying values of the parameters and for two classes of models distinguished by the value of . The maximum mass is shifted to higher values compared to its non-rotating limit by about 20%, as expected [99, 100, 104]. In the large-positive- and small- domain the masses increase up to values of around , which are within the “mass-gap” between the measured masses of CSs and black holes. If the secondary in the GW190814 event was a rapidly spinning CS, then the tension between such an interpretation and the underlying EoS models is resolved. Turning to the strangeness fraction of these massive objects, we note that for stars with it is in the range -, whereas for the stars with we find , i.e., the hyperons have essentially disappeared. We conclude that achieving large masses in the range -3.0 requires a significant suppression of the hyperon population which can occur for the SU(3) model in the limit . It follows from the discussion above that only nucleonic stars (ignoring, for all practical purposes, the vanishing small amount of hyperons) with a rather stiff EoS (large-positive- values) can achieve large enough masses which enter the “mass-gap” region.

Figure 6 shows the mass ratio as a function of . For many EoS models, this quantity is a constant. However, it is evident from the figure that the mass ratio increases with the increase of . Furthermore, the smaller the value of , i.e., the softer the intermediate density EoS, the larger the value of . Our values of can be compared with those obtained from the fits to a large collection of nucleonic EoS [105], which gives . The ratios obtained from models with MeV and are slightly shifted upward with respect to the fit obtained from nucleonic models, while obtained from models with MeV and are shifted downward.
If we consider only the scenario of one family of CSs and require , a constant value for of (at 90% CI) is obtained. If we further assume that the secondary object in the GW190814 event was a rapidly spinning star rotating at its Kepler frequency with a mass in the range (at 90% CI) [55], then by using the values of shown in Fig. 6 we can evaluate the possible values of as: (at 90% CI).
3.3 GW sources with interpreted as fast rotating compact stars

So far we have generated massive hyperonic stars, both static and fast spinning, with masses that cover well the range of inferred secondary masses in GW190814 and GW200210 events [55, 73] for which it was deduced that and with 76% probability [73]. At this point, let us evaluate in addition the minimal frequencies and that are necessary to rotationally support stars with masses of 2.5 and , for any given EoS. These mass-values constitute the lower limit of the 90% CI interval for the mass of the secondary in GW190814 and the central value of the secondary in GW200210, respectively.
Figure 7 (a) shows these frequencies calculated for our EoS models which predict stars with masses of 2.5 or either in the static limit () or under rotation. The values of and corresponding to the circles (and pentagrams) can be read-off from Fig. 5. The corresponding dimensionless spin parameters ( with being the angular momentum of the pulsar) and strangeness fractions for the same models are shown in Figs. 7 (b) and (c). Note that any particular model is uniquely identified by their static maximum masses shown by the horizontal axis. For the sake of comparison, we show in Fig. 7 (a) the frequency 716 Hz [106] of PSR J1748-2446ad, which has the highest rotation frequency of all known pulsars. In addition, we show the rather speculative case of a possibly ultra-fast rotating object with a frequency of 1250 Hz, suggested by the observation of narrow pulses in the fast radio burst FRB 181112 [107].
The EoS models identified by their value suggest the following comments on the possible origin of very massive CS: (i) For , the secondary objects in the GW190814 event would need to be rotating at a frequency Hz, which is close to the Keplerian limit. (ii) For , the secondary’s rotational frequency needs to be about 1000 Hz, which is below the Keplerian limit and is by 25% larger than that of PSR J1748-2446ad. (iii) Finally, if , the secondary of GW190814 is either a static or a slowly spinning CS, with a frequency that is far below the Keplerian one and that of PSR J1748-2446ad.
Less can be said about the nature of the GW200210’s secondary, due to the large uncertainty in its mass. Nevertheless, the comments made above about GW190814’s secondary apply to the GW200210’s secondary too, provided its mass is . Taking the larger mean value as a working hypothesis, one deduces that which would require spin frequencies Hz for the secondary to be a CS. Qualitatively we may conclude that the above models require stiff nucleonic EoS with MeV and maximally broken SU(6) symmetry, see Figs. 3 (a) and (d). As seen from Fig. 7 (b), the dimensionless spin parameters has values for our models. The maximum value , which correspond to the Keplerian limit, is essentially independent of the EoS models and is consistent with that obtained in Refs. [100, 102, 108]. Finally, as seen from Fig. 7 (c), the CS models that can account for very large masses contain a marginal of hyperons. For example, we find that the strangeness fraction is for a star and for a star. These values imply that massive stars are almost purely nucleonic.
4 Summary and conclusions
In this work, we constructed EoS models within CDF theory with degrees of freedom that include the full baryon octet. The meson-hyperon coupling constants are chosen to break the SU(6) spin-flavor symmetry down to SU(3). The hyperon potentials were further fitted to the most reliable values of their potentials at nuclear saturation density extracted from hypernuclear data. Because of the more general SU(3) symmetry, the hyperonic couplings depend on additional parameters, among which the -parameter (defined above) is most suitable for exploring the impact of symmetry breaking. The density-dependences of the nucleonic and hyperonic couplings is modeled using the same parameters. The nucleonic sector of the CDF was modeled phenomenologically at high density by varying the slope coefficient and skewness coefficient , while maintaining the low-density features predicted by the DDME2 parametrization.
With this input, we investigated the mass and radius of non-rotating as well as rapidly rotating stellar configurations. Our EoS models can accommodate static CSs as massive as - in the large- and small- domain. However, the hyperon content in this regime drops to several percent and, therefore, cannot significantly influence the properties of CS. Thus, one may conclude that the highly massive stellar models obtained with the SU(3) symmetric models for the EoS are essentially nucleonic stars. The global parameters of these stars are consistent with the parameters of stars based on purely nucleonic EoS models [58, 60, 61, 62, 63, 64, 65] (we exclude here the models calling for quark deconfinement [66, 67, 68, 69, 70, 71, 13, 72]). This also confirms that genuinely hyperonic stars with a significant hyperonic fraction of 10-20% are confined to lower masses [57, 58, 66, 53, 54].
We further constructed the rotating counterparts of our static stellar models, including stars rotating at the Keplerian limit, in which case the maximum mass of the nearly nucleonic models can reach values up to . Our modeling allows us to estimate the ratio of the Keplerian to static maximum mass, , and to show that it is constant only for stars with . We find a linear dependence of on . Note that sub-two-solar-mass stars are not excluded if there are two families of CS in which the massive stars are strange.
We have also determined the minimum frequencies required to explain the secondary stellar objects in the gravitational events GW190814 and GW200210. We found that the most extreme models from the large- and small- domain produce masses in the required range. This domain is minimal for non-rotating stars and increases as rotation is allowed. It is maximal for the Keplerian case which allows for very fast rotation at frequencies Hz. We stress again that even though our CDF study includes the full baryon octet, the highly massive CS models turn out to contain only a very small amount of hyperons (strangeness fractions of typical ). These stars can therefore be considered as nucleonic stars.
Acknowledgements
The research of H.F. and J.L. is supported by the National Natural Science Foundation of China (Grant No. 12105232), the Venture & Innovation Support Program for Chongqing Overseas Returnees (Grant No. CX2021007), and by the “Fundamental Research Funds for the Central Universities” (Grant No. SWU-020021). The research of A.S. is funded by Deutsche Forschungsgemeinschaft Grant No. SE 1836/5-2 and the Polish NCN Grant No. 2020/37/B/ST9/01937 at Wrocław University. F.W. acknowledges support by the U.S. National Science Foundation under Grant PHY-2012152.
References
- [1] F. Weber, Strange quark matter and compact stars, Prog. Part. Nucl. Phys. 54 (2005) 193–288. arXiv:astro-ph/0407155, doi:10.1016/j.ppnp.2004.07.001.
- [2] A. Sedrakian, The physics of dense hadronic matter and compact stars, Prog. Part. Nucl. Phys. 58 (2007) 168–246. arXiv:nucl-th/0601086, doi:10.1016/j.ppnp.2006.02.002.
- [3] J. M. Lattimer, M. Prakash, The Equation of State of Hot, Dense Matter and Neutron Stars, Phys. Rept. 621 (2016) 127–164. arXiv:1512.07820, doi:10.1016/j.physrep.2015.12.005.
- [4] A. L. Watts, et al., Colloquium: Measuring the neutron star equation of state using x-ray timing, Rev. Mod. Phys. 88 (2016) 021001. arXiv:1602.01081, doi:10.1103/RevModPhys.88.021001.
- [5] M. Oertel, M. Hempel, T. Klähn, S. Typel, Equations of state for supernovae and compact stars, Rev. Mod. Phys. 89 (2017) 015007. arXiv:1610.03361, doi:10.1103/RevModPhys.89.015007.
- [6] D. Chatterjee, I. Vidaña, Do hyperons exist in the interior of neutron stars?, Eur. Phys. J. A 52 (2016) 29. arXiv:1510.06306, doi:10.1140/epja/i2016-16029-x.
- [7] K. Yagi, N. Yunes, Approximate Universal Relations for Neutron Stars and Quark Stars, Phys. Rept. 681 (2017) 1–72. arXiv:1608.02582, doi:10.1016/j.physrep.2017.03.002.
- [8] G. Baym, et al., From hadrons to quarks in neutron stars: a review, Rept. Prog. Phys. 81 (2018) 056902. arXiv:1707.04966, doi:10.1088/1361-6633/aaae14.
- [9] A. Sedrakian, J. W. Clark, Superfluidity in nuclear systems and neutron stars, Eur. Phys. J. A 55 (2019) 167. arXiv:1802.00017, doi:10.1140/epja/i2019-12863-6.
- [10] L. Baiotti, Gravitational waves from neutron star mergers and their relation to the nuclear equation of state, Prog. Part. Nucl. Phys. 109 (2019) 103714. arXiv:1907.08534, doi:10.1016/j.ppnp.2019.103714.
- [11] J. J. Li, A. Sedrakian, Implications from GW170817 for -isobar Admixed Hypernuclear Compact Stars, Astrophys. J. Lett. 874 (2019) L22. arXiv:1904.02006, doi:10.3847/2041-8213/ab1090.
- [12] F. J. Llanes-Estrada, E. Lope-Oter, Hadron matter in neutron stars in view of gravitational wave observations, Prog. Part. Nucl. Phys. 109 (2019) 103715. arXiv:1907.12760, doi:10.1016/j.ppnp.2019.103715.
- [13] G. Malfatti, M. G. Orsaria, I. F. Ranea-Sandoval, G. A. Contrera, F. Weber, Delta baryons and diquark formation in the cores of neutron stars, Phys. Rev. D 102 (2020) 063008. arXiv:2008.06459, doi:10.1103/PhysRevD.102.063008.
- [14] L. Tolos, L. Fabbietti, Strangeness in Nuclei and Neutron Stars, Prog. Part. Nucl. Phys. 112 (2020) 103770. arXiv:2002.09223, doi:10.1016/j.ppnp.2020.103770.
- [15] A. Sedrakian, J.-J. Li, F. Weber, Hyperonization in compact stars (2021). arXiv:2105.14050.
- [16] I. Vidaña, Hyperons in Finite and Infinite Nuclear Systems, Universe 7 (2021) 376. doi:10.3390/universe7100376.
- [17] G. F. Burgio, H. J. Schulze, I. Vidana, J. B. Wei, Neutron stars and the nuclear equation of state, Prog. Part. Nucl. Phys. 120 (2021) 103879. arXiv:2105.03747, doi:10.1016/j.ppnp.2021.103879.
- [18] J. J. Li, W. H. Long, A. Sedrakian, Hypernuclear stars from relativistic Hartree-Fock density functional theory, Eur. Phys. J. A 54 (2018) 133. arXiv:1801.07084, doi:10.1140/epja/i2018-12566-6.
- [19] P. Demorest, T. Pennucci, S. Ransom, M. Roberts, J. Hessels, Shapiro Delay Measurement of A Two Solar Mass Neutron Star, Nature 467 (2010) 1081–1083. arXiv:1010.5788, doi:10.1038/nature09466.
- [20] J. Antoniadis, et al., A Massive Pulsar in a Compact Relativistic Binary, Science 340 (2013) 6131. arXiv:1304.6875, doi:10.1126/science.1233232.
- [21] H. T. Cromartie, et al., Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar, Nature Astron. 4 (2019) 72–76. arXiv:1904.06759, doi:10.1038/s41550-019-0880-2.
- [22] E. Fonseca, et al., Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620, Astrophys. J. Lett. 915 (2021) L12. arXiv:2104.00880, doi:10.3847/2041-8213/ac03b8.
- [23] R. W. Romani, D. Kandel, A. V. Filippenko, T. G. Brink, W. Zheng, PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star, Astrophys. J. Lett. 934 (2022) L17. arXiv:2207.05124, doi:10.3847/2041-8213/ac8007.
- [24] B. P. Abbott, et al., GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral, Phys. Rev. Lett. 119 (2017) 161101. arXiv:1710.05832, doi:10.1103/PhysRevLett.119.161101.
- [25] B. P. Abbott, et al., GW170817: Measurements of neutron star radii and equation of state, Phys. Rev. Lett. 121 (2018) 161101. arXiv:1805.11581, doi:10.1103/PhysRevLett.121.161101.
- [26] B. P. Abbott, et al., Properties of the binary neutron star merger GW170817, Phys. Rev. X 9 (2019) 011001. arXiv:1805.11579, doi:10.1103/PhysRevX.9.011001.
- [27] B. Margalit, B. D. Metzger, Constraining the Maximum Mass of Neutron Stars From Multi-Messenger Observations of GW170817, Astrophys. J. Lett. 850 (2017) L19. arXiv:1710.05938, doi:10.3847/2041-8213/aa991c.
- [28] M. Shibata, et al., Modeling GW170817 based on numerical relativity and its implications, Phys. Rev. D 96 (2017) 123012. arXiv:1710.07579, doi:10.1103/PhysRevD.96.123012.
- [29] M. Ruiz, S. L. Shapiro, A. Tsokaros, GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass, Phys. Rev. D 97 (2018) 021501. arXiv:1711.00473, doi:10.1103/PhysRevD.97.021501.
- [30] L. Rezzolla, E. R. Most, L. R. Weih, Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars, Astrophys. J. Lett. 852 (2018) L25. arXiv:1711.00314, doi:10.3847/2041-8213/aaa401.
- [31] S. Khadkikar, A. R. Raduta, M. Oertel, A. Sedrakian, Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state, Phys. Rev. C 103 (2021) 055811. arXiv:2102.00988, doi:10.1103/PhysRevC.103.055811.
- [32] T. E. Riley, et al., A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy, Astrophys. J. Lett. 918 (2021) L27. arXiv:2105.06980, doi:10.3847/2041-8213/ac0a81.
- [33] M. C. Miller, et al., The Radius of PSR J0740+6620 from NICER and XMM-Newton Data, Astrophys. J. Lett. 918 (2021) L28. arXiv:2105.06979, doi:10.3847/2041-8213/ac089b.
- [34] M. C. Miller, et al., PSR J0030+0451 Mass and Radius from Data and Implications for the Properties of Neutron Star Matter, Astrophys. J. Lett. 887 (2019) L24. arXiv:1912.05705, doi:10.3847/2041-8213/ab50c5.
- [35] T. E. Riley, et al., A View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation, Astrophys. J. Lett. 887 (2019) L21. arXiv:1912.05702, doi:10.3847/2041-8213/ab481c.
- [36] I. Legred, K. Chatziioannou, R. Essick, S. Han, P. Landry, Impact of the PSR J0740+6620 radius constraint on the properties of high-density matter, Phys. Rev. D 104 (2021) 063003. arXiv:2106.05313, doi:10.1103/PhysRevD.104.063003.
- [37] S. Huth, et al., Constraining Neutron-Star Matter with Microscopic and Macroscopic Collisions, Nature 606 (2022) 276–280. arXiv:2107.06229, doi:10.1038/s41586-022-04750-w.
- [38] I. Bednarek, P. Haensel, J. L. Zdunik, M. Bejger, R. Manka, Hyperons in neutron-star cores and two-solar-mass pulsar, Astron. Astrophys. 543 (2012) A157. arXiv:1111.6942, doi:10.1051/0004-6361/201118560.
- [39] E. Massot, J. Margueron, G. Chanfray, On the maximum mass of hyperonic neutron stars, Eur. Phys. Lett. 97 (2012) 39002. arXiv:1201.2772, doi:10.1209/0295-5075/97/39002.
- [40] S. Weissenborn, D. Chatterjee, J. Schaffner-Bielich, Hyperons and massive neutron stars: the role of hyperon potentials, Nucl. Phys. A 881 (2012) 62–77. arXiv:1111.6049, doi:10.1016/j.nuclphysa.2012.02.012.
- [41] S. Weissenborn, D. Chatterjee, J. Schaffner-Bielich, Hyperons and massive neutron stars: vector repulsion and SU(3) symmetry, Phys. Rev. C 85 (2012) 065802. arXiv:1112.0234, doi:10.1103/PhysRevC.85.065802.
- [42] G. Colucci, A. Sedrakian, Equation of state of hypernuclear matter: impact of hyperon–scalar-meson couplings, Phys. Rev. C 87 (2013) 055806. arXiv:1302.6925, doi:10.1103/PhysRevC.87.055806.
- [43] C. Providência, et al., Imprint of the symmetry energy on the inner crust and strangeness content of neutron stars, Eur. Phys. J. A 50 (2014) 44. arXiv:1307.1436, doi:10.1140/epja/i2014-14044-7.
- [44] E. N. E. van Dalen, G. Colucci, A. Sedrakian, Constraining hypernuclear density functional with -hypernuclei and compact stars, Phys. Lett. B 734 (2014) 383–387. arXiv:1406.0744, doi:10.1016/j.physletb.2014.06.002.
- [45] R. O. Gomes, V. Dexheimer, S. Schramm, C. A. Z. Vasconcellos, Many-body forces in the equation of state of hyperonic matter, Astrophys. J. 808 (2015) 8. arXiv:1411.4875, doi:10.1088/0004-637X/808/1/8.
- [46] L. L. Lopes, D. P. Menezes, Hypernuclear matter in a complete SU(3) symmetry group, Phys. Rev. C 89 (2014) 025805. arXiv:1309.4173, doi:10.1103/PhysRevC.89.025805.
- [47] M. Oertel, C. Providência, F. Gulminelli, A. R. Raduta, Hyperons in neutron star matter within relativistic mean-field models, J. Phys. G 42 (2015) 075202. arXiv:1412.4545, doi:10.1088/0954-3899/42/7/075202.
- [48] K. A. Maslov, E. E. Kolomeitsev, D. N. Voskresensky, Solution of the hyperon puzzle within a relativistic mean-field model, Phys. Lett. B 748 (2015) 369–375. arXiv:1504.02915, doi:10.1016/j.physletb.2015.07.032.
- [49] L. Tolos, M. Centelles, A. Ramos, Equation of State for Nucleonic and Hyperonic Neutron Stars with Mass and Radius Constraints, Astrophys. J. 834 (2017) 3. arXiv:1610.00919, doi:10.3847/1538-4357/834/1/3.
- [50] M. Fortin, S. S. Avancini, C. Providência, I. Vidaña, Hypernuclei and massive neutron stars, Phys. Rev. C 95 (2017) 065803. arXiv:1701.06373, doi:10.1103/PhysRevC.95.065803.
- [51] M. Fortin, A. R. Raduta, S. Avancini, C. Providência, Relativistic hypernuclear compact stars with calibrated equations of state, Phys. Rev. D 101 (2020) 034017. arXiv:2001.08036, doi:10.1103/PhysRevD.101.034017.
- [52] J. R. Stone, P. A. M. Guichon, A. W. Thomas, Nuclear Symmetry Energy and Hyperonic Stars in the QMC Model, Front. Astron. Space Sci. 9 (2022) 903007. doi:10.3389/fspas.2022.903007.
- [53] Z.-H. Tu, S.-G. Zhou, Effects of the -Meson on the Properties of Hyperon Stars in the Density-dependent Relativistic Mean Field Model, Astrophys. J. 925 (2022) 16. arXiv:2109.07678, doi:10.3847/1538-4357/ac3996.
- [54] X. Sun, Z. Miao, B. Sun, A. Li, Astrophysical implications on hyperon couplings and hyperon star properties with relativistic equations of states (2022). arXiv:2205.10631.
- [55] R. Abbott, et al., GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object, Astrophys. J. Lett. 896 (2020) L44. arXiv:2006.12611, doi:10.3847/2041-8213/ab960f.
- [56] E. R. Most, L. J. Papenfort, L. R. Weih, L. Rezzolla, A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star, Mon. Not. Roy. Astron. Soc. 499 (2020) L82–L86. arXiv:2006.14601, doi:10.1093/mnrasl/slaa168.
- [57] A. Sedrakian, F. Weber, J. J. Li, Confronting GW190814 with hyperonization in dense matter and hypernuclear compact stars, Phys. Rev. D 102 (2020) 041301. arXiv:2007.09683, doi:10.1103/PhysRevD.102.041301.
- [58] J. J. Li, A. Sedrakian, F. Weber, Rapidly rotating -resonance-admixed hypernuclear compact stars, Phys. Lett. B 810 (2020) 135812. arXiv:2010.02901, doi:10.1016/j.physletb.2020.135812.
- [59] A. Nathanail, E. R. Most, L. Rezzolla, GW170817 and GW190814: tension on the maximum mass, Astrophys. J. Lett. 908 (2021) L28. arXiv:2101.01735, doi:10.3847/2041-8213/abdfc6.
- [60] F. J. Fattoyev, C. J. Horowitz, J. Piekarewicz, B. Reed, GW190814: Impact of a 2.6 solar mass neutron star on the nucleonic equations of state, Phys. Rev. C 102 (2020) 065805. arXiv:2007.03799, doi:10.1103/PhysRevC.102.065805.
- [61] N.-B. Zhang, B.-A. Li, GW190814’s Secondary Component with Mass 2.50–2.67 M⊙ as a Superfast Pulsar, Astrophys. J. 902 (2020) 38. arXiv:2007.02513, doi:10.3847/1538-4357/abb470.
- [62] A. Tsokaros, M. Ruiz, S. L. Shapiro, GW190814: Spin and equation of state of a neutron star companion, Astrophys. J. 905 (2020) 48. arXiv:2007.05526, doi:10.3847/1538-4357/abc421.
- [63] K. Huang, J. Hu, Y. Zhang, H. Shen, The possibility of the secondary object in GW190814 as a neutron star, Astrophys. J. 904 (2020) 39. arXiv:2008.04491, doi:10.3847/1538-4357/abbb37.
- [64] B. Biswas, R. Nandi, P. Char, S. Bose, N. Stergioulas, GW190814: on the properties of the secondary component of the binary, Mon. Not. Roy. Astron. Soc. 505 (2021) 1600–1606. arXiv:2010.02090, doi:10.1093/mnras/stab1383.
- [65] I. Tews, et al., On the Nature of GW190814 and Its Impact on the Understanding of Supranuclear Matter, Astrophys. J. Lett. 908 (2021) L1. arXiv:2007.06057, doi:10.3847/2041-8213/abdaae.
- [66] V. Dexheimer, R. O. Gomes, T. Klähn, S. Han, M. Salinas, GW190814 as a massive rapidly rotating neutron star with exotic degrees of freedom, Phys. Rev. C 103 (2021) 025808. arXiv:2007.08493, doi:10.1103/PhysRevC.103.025808.
- [67] H. Tan, J. Noronha-Hostler, N. Yunes, Neutron Star Equation of State in Light of GW190814, Phys. Rev. Lett. 125 (2020) 261104. arXiv:2006.16296, doi:10.1103/PhysRevLett.125.261104.
- [68] I. Bombaci, A. Drago, D. Logoteta, G. Pagliara, I. Vidaña, Was GW190814 a Black Hole–Strange Quark Star System?, Phys. Rev. Lett. 126 (2021) 162702. arXiv:2010.01509, doi:10.1103/PhysRevLett.126.162702.
- [69] Z. Roupas, G. Panotopoulos, I. Lopes, QCD color superconductivity in compact stars: color-flavor locked quark star candidate for the gravitational-wave signal GW190814, Phys. Rev. D 103 (2021) 083015. arXiv:2010.11020, doi:10.1103/PhysRevD.103.083015.
- [70] J.-E. Christian, J. Schaffner-Bielich, Supermassive neutron stars rule out twin stars, Phys. Rev. D 103 (2021) 063042. arXiv:2011.01001, doi:10.1103/PhysRevD.103.063042.
- [71] T. Demircik, C. Ecker, M. Järvinen, Rapidly Spinning Compact Stars with Deconfinement Phase Transition, Astrophys. J. Lett. 907 (2021) L37. arXiv:2009.10731, doi:10.3847/2041-8213/abd853.
- [72] M. Ju, J. Hu, H. Shen, Hadron-quark Pasta Phase in Massive Neutron Stars, Astrophys. J. 923 (2021) 250. arXiv:2111.08909, doi:10.3847/1538-4357/ac30dd.
- [73] R. Abbott, et al., GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run (2021). arXiv:2111.03606.
- [74] J. J. de Swart, The octet model and its Clebsch-Gordan coefficients, Rev. Mod. Phys. 35 (1963) 916–939. doi:10.1103/RevModPhys.35.916.
- [75] J. Schaffner, et al., Multiply strange nuclear systems, Annals Phys. 235 (1994) 35–76. doi:10.1006/aphy.1994.1090.
- [76] S. Typel, H. H. Wolter, Relativistic mean field calculations with density dependent meson nucleon coupling, Nucl. Phys. A 656 (1999) 331–364. doi:10.1016/S0375-9474(99)00310-3.
- [77] G. A. Lalazissis, T. Niksic, D. Vretenar, P. Ring, New relativistic mean-field interaction with density-dependent meson-nucleon couplings, Phys. Rev. C 71 (2005) 024312. doi:10.1103/PhysRevC.71.024312.
- [78] J. J. Li, A. Sedrakian, Constraining compact star properties with nuclear saturation parameters, Phys. Rev. C 100 (2019) 015809. arXiv:1903.06057, doi:10.1103/PhysRevC.100.015809.
- [79] B. D. Serot, J. D. Walecka, Recent progress in quantum hadrodynamics, Int. J. Mod. Phys. E 6 (1997) 515–631. arXiv:nucl-th/9701058, doi:10.1142/S0218301397000299.
- [80] D. Vretenar, A. V. Afanasjev, G. A. Lalazissis, P. Ring, Relativistic Hartree Bogoliubov theory: static and dynamic aspects of exotic nuclear structure, Phys. Rept. 409 (2005) 101–259. doi:10.1016/j.physrep.2004.10.001.
- [81] A. R. Raduta, A. Sedrakian, F. Weber, Cooling of hypernuclear compact stars, Mon. Not. Roy. Astron. Soc. 475 (2018) 4347–4356. arXiv:1712.00584, doi:10.1093/mnras/stx3318.
- [82] J. Margueron, R. Hoffmann Casali, F. Gulminelli, Equation of state for dense nucleonic matter from metamodeling. II. Predictions for neutron star properties, Phys. Rev. C 97 (2018) 025806. arXiv:1708.06895, doi:10.1103/PhysRevC.97.025806.
- [83] C. B. Dover, A. Gal, Hyperon Nucleus Potentials, Prog. Part. Nucl. Phys. 12 (1985) 171–239. doi:10.1016/0146-6410(84)90004-8.
- [84] T. A. Rijken, V. G. J. Stoks, Y. Yamamoto, Soft core hyperon - nucleon potentials, Phys. Rev. C 59 (1999) 21–40. arXiv:nucl-th/9807082, doi:10.1103/PhysRevC.59.21.
- [85] P. A. Zyla, et al., Review of Particle Physics, Prog. Theor. Exp. Phys. 2020 (2020) 083C01. doi:10.1093/ptep/ptaa104.
- [86] A. Feliciello, T. Nagae, Experimental review of hypernuclear physics: recent achievements and future perspectives, Rept. Prog. Phys. 78 (2015) 096301. doi:10.1088/0034-4885/78/9/096301.
- [87] A. Gal, E. V. Hungerford, D. J. Millener, Strangeness in nuclear physics, Rev. Mod. Phys. 88 (2016) 035004. arXiv:1605.00557, doi:10.1103/RevModPhys.88.035004.
- [88] J. K. Ahn, et al., Double- hypernuclei observed in a hybrid emulsion experiment, Phys. Rev. C 88 (2013) 014003. doi:10.1103/PhysRevC.88.014003.
- [89] G. Baym, C. Pethick, P. Sutherland, The ground state of matter at high densities: Equation of state and stellar models, Astrophys. J. 170 (1971) 299–317. doi:10.1086/151216.
- [90] G. Baym, H. A. Bethe, C. Pethick, Neutron star matter, Nucl. Phys. A 175 (1971) 225–271. doi:10.1016/0375-9474(71)90281-8.
- [91] M. Fortin, C. Providencia, A. R. Raduta, F. Gulminelli, J. L. Zdunik, P. Haensel, M. Bejger, Neutron star radii and crusts: uncertainties and unified equations of state, Phys. Rev. C 94 (2016) 035804. arXiv:1604.01944, doi:10.1103/PhysRevC.94.035804.
- [92] J. Piekarewicz, F. J. Fattoyev, Impact of the neutron star crust on the tidal polarizability, Phys. Rev. C 99 (2019) 045802. arXiv:1812.09974, doi:10.1103/PhysRevC.99.045802.
- [93] D. Adhikari, et al., Accurate determination of the neutron skin thickness of through parity-violation in electron scattering, Phys. Rev. Lett. 126 (2021) 172502. arXiv:2102.10767, doi:10.1103/PhysRevLett.126.172502.
- [94] B. T. Reed, F. J. Fattoyev, C. J. Horowitz, J. Piekarewicz, Implications of PREX-2 on the Equation of State of Neutron-Rich Matter, Phys. Rev. Lett. 126 (2021) 172503. arXiv:2101.03193, doi:10.1103/PhysRevLett.126.172503.
- [95] P.-G. Reinhard, X. Roca-Maza, W. Nazarewicz, Information Content of the Parity-Violating Asymmetry in 208Pb, Phys. Rev. Lett. 127 (2021) 232501. arXiv:2105.15050, doi:10.1103/PhysRevLett.127.232501.
- [96] A. Drago, A. Lavagno, G. Pagliara, Can very compact and very massive neutron stars both exist?, Phys. Rev. D 89 (2014) 043014. arXiv:1309.7263, doi:10.1103/PhysRevD.89.043014.
- [97] A. Taninah, S. E. Agbemava, A. V. Afanasjev, P. Ring, Parametric correlations in energy density functionals, Phys. Lett. B 800 (2020) 135065. arXiv:1910.13007, doi:10.1016/j.physletb.2019.135065.
- [98] B. Wei, et al., Novel relativistic mean field Lagrangian guided by pseudo-spin symmetry restoration, Chin. Phys. C 44 (2020) 074107. doi:10.1088/1674-1137/44/7/074107.
- [99] F. Weber, N. Glendenning, Applicability of the improved hartle method for the construction of general relativistic rotating neutron star models, Astrophys. J. 390 (1991) 541. doi:10.1086/171304.
- [100] G. B. Cook, S. L. Shapiro, S. A. Teukolsky, Rapidly Rotating Neutron Stars in General Relativity: Realistic Equations of State, Astrophys. J. 424 (1994) 823. doi:10.1086/173934.
- [101] N. Stergioulas, J. L. Friedman, Comparing Models of Rapidly Rotating Relativistic Stars Constructed by two Numerical Methods, Astrophys. J. 444 (1995) 306. arXiv:astro-ph/9411032, doi:10.1086/175605.
- [102] P. Haensel, M. Salgado, S. Bonazzola, Equation of state of dense matter and maximum rotation frequency of neutron stars, Astro. Astrophys. 296 (1995) 745.
- [103] www.gravity.phys.uwm.edu/rns/.
- [104] V. Paschalidis, N. Stergioulas, Rotating stars in relativity, Living Reviews in Relativity 20 (2017) 1–169.
- [105] C. Breu, L. Rezzolla, Maximum mass, moment of inertia and compactness of relativistic stars, Mon. Not. Roy. Astron. Soc. 459 (2016) 646–656. arXiv:1601.06083, doi:10.1093/mnras/stw575.
- [106] J. W. T. Hessels, et al., A radio pulsar spinning at 716 Hz, Science 311 (2006) 1901–1904. arXiv:astro-ph/0601337, doi:10.1126/science.1123430.
- [107] S. Yamasaki, T. Totani, K. Kiuchi, FRB 181112 as a Rapidly-Rotating Massive Neutron Star just after a Binary Neutron Star Merger?: Implications for Future Constraints on Neutron Star Equations of State (2020). arXiv:2010.07796.
- [108] K.-W. Lo, L.-M. Lin, The Spin Parameter of Uniformly Rotating Compact Stars, Astrophys. J. 728 (2011) 12. arXiv:1011.3563, doi:10.1088/0004-637X/728/1/12.