Mapping the distribution of the magnetic field strength along the NGC 315 jet
Abstract
We study magnetic field strengths along the jet in NGC 315. First, we estimated the angular velocity of rotation in the jet magnetosphere by comparing the measured velocity profile of NGC 315 with the magneto-hydrodynamic jet model of proposed by Tomimatsu and Takahashi. Similar to the case of M87, we find that the model can reproduce the logarithmic feature of the velocity profile and suggest a slowly rotating black hole magnetosphere for NGC 315. By substituting the estimated into the jet power predicted by the Blandford-Znajek mechanism, we estimate the magnetic field strength near the event horizon of the central black hole as . We then estimate magnetic-field strengths along the jet by comparing the spectral index distribution obtained from VLBI observations with a synchrotron-emitting jet model. Then we constrain the magnetic field strength at a de-projected distance from the black hole to be in the range for , where represents the gravitational radius. By combining the obtained field strengths at the event horizon and the downstream section of the jet, we find that the accretion flow at the jet base is consistent with a magnetically arrested disk (MAD). We discuss a comparison of the jet power and the magnetic flux anchored to the event horizon in NGC 315 and M87.
1 Introduction
Magnetic fields are believed to play an essential role in launching relativistic jets in active galactic nuclei (AGN) (e.g., Begelman et al., 1984; Blandford et al., 2019, and references therein). The current leading scenario for jet launching mechanism is a magnetically driven jet ultimately powered by the rotational energy of the central black hole proposed by (Blandford & Znajek, 1977, hereafter BZ77). Therefore, testing BZ77 is crucial to understanding the mechanism of jet formation. One of the most important tasks for testing BZ77 is to reveal the strength of the magnetic field from the scale of the event horizon to the downstream of the jet and its radial distribution along the jet. The nearby massive elliptical galaxy M87 provides an ideal laboratory for investigating properties of magnetic fields in great detail. The first imaging of M87’s black hole shadow by Event Horizon Telescope (EHT) at 230 GHz has provided a giant leap in our understanding of black holes (Event Horizon Telescope Collaboration, 2019a, b, c, d, e, f). The EHT further detected the linearly polarized emission with the spiraling structure, suggesting a signature of poloidal magnetic fields threading the accretion flow (Event Horizon Telescope Collaboration et al., 2021a, b). The measurement of the jet velocity profile of the M87 jet based on high-cadence KaVA array observations at 22 GHz and 43 GHz were performed by Park et al. (2019). The measured velocity field showed a clear discrepancy with the velocity field predicted by general relativistic magnetohydrodynamics (GRMHD) simulations performed where the jet propagates long distances on the order of (McKinney, 2006; Chatterjee et al., 2019) where is the gravitational radius of the central black hole and is the mass of the central supermassive black hole.
It posed the challenge of explaining the observed jet velocity profile with GRMHD simulations. To mitigate the discrepancy between the observation and theoretical models in the jet velocity field, slowly rotating black hole magnetosphere (i.e., the small angular velocity of the magnetic field ) has been proposed where the smaller makes a light-cylinder radius larger, and it consequently pushes out a location of a starting point of the jet acceleration (Kino et al., 2022). 111 Some may consider entrainment as a physical process to explain the slower velocity within . It could be possible to decelerate the flow with intense entrainment with surrounding ambient material after the jet’s bulk acceleration reaches its maximum velocity at a distance of about from the central engine, as suggested in GRMHD simulations (e.g., Chatterjee et al., 2019, Fig. 13). The thermal energy generated during the interaction between the jet and surrounding medium may help re-accelerate the jet. However, the numerical simulation by Ricci et al. (2023), which investigated thermal acceleration, did not show sufficient deceleration, resulting in a significant overestimation the jet velocity within . Moreover, such significant deceleration and re-acceleration do not produce a smooth velocity profile but rather a beat-like profile, which is not suggested in the velocity profile of NGC 315. For these reasons, explaining the velocity profile through the entrainment phenomenon appears challenging. By using the estimated , one can make the order estimation of the magnetic field strength on the event horizon scale () in M87 by assuming Blandford–Znajek process is in action.
However, our current understanding of the profile of the magnetic field strengths along jets in AGN is limited only for M87 (Ro et al., 2023, and the references therein), because of the limitations of the number of samples. For this, it generally requires both of (1) largeness of angular size of a central black hole, and (2) measurement of a jet’s velocity profile with enough range of distance in order to know jet’s acceleration feature. Jet acceleration features from non-relativistic to relativistic speed in jet collimation regions have been measured only in M87 (Kovalev et al., 2007; Ly et al., 2007; Acciari et al., 2009; Asada et al., 2014; Hada et al., 2016, 2017; Mertens et al., 2016; Walker et al., 2018; Kim et al., 2018; Park et al., 2019), Cygnus A (Krichbaum et al., 1998; Bach et al., 2003; Boccardi et al., 2016), 1H 0323+342 (Hada et al., 2018), and NGC 315 (Park et al., 2021; Ricci et al., 2022). Unfortunately, low-luminosity AGNs having a large angular-size black hole at their center (e.g., Ramakrishnan et al., 2023, and references therein) do not always have a clear jet feature and rather limited numbers of samples.
The nearby giant elliptical radio galaxy NGC 315 located at the redshift of (Trager et al., 2000) is the suitable target for investigating the jet acceleration mechanism, because the proximity of distance and the large mass of the black hole enables us to resolve the innermost part of the jet base. The mass of the central black hole in NGC 315 has been estimated based on gas kinematics (Noel-Storr et al., 2007), the black-hole mass and stellar-velocity dispersion relation ( relation) (e.g., Woo & Urry, 2002; Beifiori et al., 2009; Inayoshi et al., 2020), and CO observations with the Atacama Large Millimater/submillimeter Array (ALMA) (Boizelle et al., 2021), which lies in the range . Thanks to its proximity and largeness of the central black hole, one can explore the innermost part of the NGC 315 and the measured velocity field of the NGC 315 jet clearly show the acceleration feature from non-relativistic speed to the relativistic one thanks to its proximity and largeness of the central black hole (Park et al., 2021; Ricci et al., 2022). NGC 315 is also known one of the GeV -ray emitters. Palomar spectroscopic survey of nearby galactic nuclei make it suitable to the study of nearby AGN, especially low luminosity AGN (Ho et al., 1995, 1997; Ho, 2008). Of the 197 low luminosity AGN in the Palomar sample, only four sources were detected in -rays (de Menezes et al., 2020). These four sources correspond to misaligned Fanaroff Riley I (FR I) type radio galaxies, accompanying kpc-scale radio jets. Two of them are NGC 315 and M87 and they have similar and SED. Towards understanding the jet launching mechanism, it is of great importance to investigate and compare the properties of magnetic fields in these jets.
In § 2, we briefly overview the models to be utilized in the present work. In § 3, we apply these models to the NGC 315 jet and describe the obtained results. In § 4, we will compare the obtained physical properties of NGC 315 and M87. In § 5, we summarize our findings. In this work, we assume the standard -CDM cosmology with the parameter values of , and (see Planck Collaboration et al., 2020). Hereafter, we use the median value for the black hole mass. This corresponds to a linear scale of or equivalently at a distance of Mpc. The Schwarzschild radius is given by .
2 Models
2.1 Dynamics: MHD jet model
In this work, we utilize the MHD jet model proposed by Tomimatsu & Takahashi (2003) (hereafter TT03) in the framework of special relativity. In the black hole magnetosphere, due to the balance between the gravitational force of the black hole and magneto-centrifugal force, a stagnation (a.k.a separation) surface is generated that separates the inflow and outflow regions (e.g., Takahashi et al., 1990; McKinney, 2006; Pu et al., 2015; Pu & Takahashi, 2020). Comparing semi-analytical approaches and GRMHD simulation approaches, the semi-analytical approaches have the following advantages. The large spatial extent of the acceleration region has posed a challenge for such calculations by GRMHD simulations and they tend to be eventually limited by computational costs and numerical dissipation (e.g., McKinney, 2006; Komissarov et al., 2007, for details), while semi-analytic approaches are free from these concerns. When discussing properties of axisymmetric and steady MHD flows in general, the magnetic field geometry should be consistent with Grad-Shafranov equation (e.g., Nitta et al., 1991), and the flow should be trans-fast-magnetosonic (Takahashi et al., 1990; Takahashi, 2002). However, it is technically difficult to obtain a solution satisfying both of these conditions (e.g., Beskin, 2010, for review). TT03 model is the only semi-analytic solution to satisfy both of these conditions. Given that a radial profile of the poloidal component of the jet’s four-velocity () is sensitive to the magnetic field geometry, we utilize TT03 model in this work. TT03 model is applicable to the region outside the light cylinder (). In general, the jet is accelerated outside the light cylinder. 222 Flow properties inside the light cylinder have been recently investigated by several authors (e.g., Takahashi et al., 2021; Camilloni et al., 2022; Beskin et al., 2023). Beskin et al. (2023) suggests that a dense cylindrical core appears over long enough distances near the axis with its radius comparable to . Camilloni et al. (2022) showed that in the force-free magnetosphere in Kerr geometry, there is a logarithmic term in the angular velocity.
The outer boundary wall condition would be given by a parabolic streamline along the poloidal magnetic field lines. Since multiple normalizations are conducted, it would be helpful to explicitly write down the boundary condition here. The outer boundary wall shape is denoted as (, ) in the cylindrical coordinate and it satisfies the following relation:
| (1) |
where the is the half-opening angle of the jet at the inlet boundary and the magnetic flux function on the boundary wall satisfies . Note that the case of corresponds to a conical boundary wall shape. In this work, we will give the value of with reference to the overall results of the detailed VLBI observations in §4.
On the contrary to the case of varying , does not alter the profile of itself. As already shown, is governed by the light cylinder radius and it is given by . Slower rotation of leads to more distant starting point of the jet acceleration from the central black hole.
In this work, a location of intersection between the boundary-wall ( surface) and the light-cylinder is important. Hereafter, we denote the location as (, ). By inserting at Eq. (1), the location of , from which the jet acceleration starts (see Figure 1 in Kino et al., 2022), is obtained as follows:
| (2) |
We note that the geometrical factor also affects the location of .
2.2 Nonthermal synchrotron emission model
Following Ro et al. (2023), we introduce a spectral index model along the jet. The essence of the model can be explained as follows. A change of a spectral index along the jet reflects a change in the nonthermal electrons’ energy distribution function (eDF hereafter) along the jet. Spectral indices of nonthermal electrons () and nonthermal synchrotron emission () are connected as where the sign of the spectral index as is defined and presents synchrotron flux per unit frequency. Time evolution of eDF is described by the continuity equation including nonthermal electron injection and energy losses. (1) In the case of a constant and continuous injection of non-thermal electrons, the synchrotron spectrum has a break, and the spectral index steepens by before and after the break. (2) For instantaneous injection, the cutoff energy decreases with time. Above the cutoff energy, the synchrotron spectrum decreases exponentially. Neither (1) nor (2) alone can explain the properties of the observed spectral index of the M87 jet. To overcome this problem, Ro et al. (2023) proposed a model where the injection-rate function of nonthermal electrons has -dependence written as
| (3) |
where and are a normalization factor and a spectral index of injected nonthermal electrons, respectively. The index describes -dependence of (see details Ro et al., 2023). By matching an observed synchrotron spectral index and a model-predicted one, one can constrain on strengths of magnetic fields along the jet () and the nonthermal electron injection function. The model generally describes that the stronger magnetic field strength realizes the closer distance for the steeping of the spectral index due to synchrotron cooling in the jet. A smaller leads to a larger injection of the nonthermal electrons, which compensates for the reduction of the number of electrons due to the cooling at a certain distance along the jet. It realizes a suppression of the steepening of the spectral index (i.e., larger ).
3 Observational properties of NGC 315
3.1 The jet collimation profile
The jet collimation profile of NGC 315 has been explored in previous works (Park et al., 2021; Boccardi et al., 2021). Transverse intensity profile along the jet axis is obtained by the multi-frequency observations and the jet width at each distance is obtained. The obtained jet width profile defined as in the previous section shows the parabollic shape characterized by
| (4) |
measured by (Park et al., 2021). In this work, we do not treat the rapidly expanding jet region (so-called geometrical flaring region; Canvin et al. 2005) at , because it is beyond the application of the TT03 model. Hereafter, we focus on the inner parabolic region of acceleration and collimation zone of the NGC 315 jet with the index during the application of TT03 model to NGC 315.
3.2 The jet base opening angle ()
Following the previous work of (Ricci et al., 2022, in Figure 4) where the intrinsic half-opening angle has been measured, hereafter the full-opening angle is set as
| (5) |
This value falls in the typical range of for various radio galaxies (e.g., Pushkarev et al., 2017). This value of NGC 315 satisfies guarantees that .
3.2.1 The poloidal velocity of the jet ()
The poloidal component of the jet velocity (four-velocity) of NGC 315 was derived from the observed jet-to-counterjet intensity ratio where , , and are the jet velocity (three-velocity), the jet bulk Lorentz factor, and the angle between the jet axis and our line of sight, respectively (Park et al., 2021). Here it is assumed that the jet and the counterjet are intrinsically the same and the toroidal component of the jet velocity is negligible. Solving the degeneracy between and was carefully done by comparing the observed and with the jet kinematics obtained by the monitoring observations with KaVA array and the derived the angle is (Park et al., 2021), which is consistent with the independent estimation of the viewing angle on kilo-parsec scale jet Laing & Bridle (2014). Therefore, in the present work, we use the data obtained in (Park et al., 2021). Note that Ricci et al. (2022) also suggested a similar trend for the jet velocity profile of NGC 315. As was pointed out in Park et al. (2021), the measured of NGC 315 shows "the slow acceleration" as was firstly seen in the M87 jet (Park et al., 2019). Park et al. (2021) suggests that possible ingredients to make it happen may be a variety of magnetization degree at the jet base, and/or interaction between the jet and ambient medium is suggested. Recently Kino et al. (2022) proposed a new scenario where a slower angular velocity of the black hole magnetosphere can mitigate the slow acceleration problem. The maximum Lorentz factor of NGC 315 reaches about
| (6) |
at . The measured of NGC 315 shows the rapid deceleration at the outer region of probably suggests the significant interaction between the jet and surrounding matter that causes the observed deceleration FR I jets may decelerate by entrainment of the surrounding matter (e.g., Baan, 1980; Bicknell, 1984; De Young, 1993; Kawakatu et al., 2009) or by injection of mass lost by stars within the jet volume (e.g., Komissarov, 1994; Perucho et al., 2014). Whichever case realizes, the region is beyond the application of the TT03 model and thus we do not treat this decelerating region in this work.
3.3 The jet power ()
It is generally difficult to constrain on the total power of AGN jets, because of the existence of invisible components such as low-energy electrons/positrons and protons (e.g., Kino et al., 2012; Sikora et al., 2020, and references therein). Following the work of Ricci et al. (2022), we set the allowed range of the total power of the jet () as follows:
| (7) |
The lower limit is estimated from the Bondi accretion rate (Nemmen & Tchekhovskoy, 2015), while the upper limit is derived from the empirical relationship between the radio core luminosity and using the empirical relationship between core luminosity and jet power (e.g., Heinz et al., 2007).
3.4 Mass accretion rate ()
A mass accretion rate () can be estimated in several ways. Firstly, can be estimated based on a bolometric luminosity () by using the relation of where is the conversion efficiency of the mass accretion energy to . The bolometric luminosity in NGC 315 can be derived from the [O III] 5007 emission line together with the relation . The can be obtained also from a direct integration of the nucleus’s SED. Both of them indicate the consistent value of (Gu et al., 2007; Ricci et al., 2022) which derives when assuming (Ricci et al., 2022). Secondly, may be estimated when HI broad absorption line is detected (van Gorkom et al., 1989) that can be related to the fueling gas that is falling into the nucleus. Morganti et al. (2009) estimated in NGC 315 and it is suggested as using the assumed infalling velocity of . Other independent work of SED model fitting for the central region of NGC 315 also suggest a comparable value of (Kimura & Toma, 2020). Therefore, the allowed range of in this work is set as
| (8) |
in the following discussion.
In addition, Morganti et al. (2009) estimated by using the empirical relationship between and Bondi accretion power (e.g., Allen et al., 2006; Balmaverde et al., 2008). Although the estimated maximum mass accretion rate seems extremely large, we will investigate this case as well as an additional one.
4 Estimation of magnetic field strengths
Here we show the estimated strengths of the magnetic fields along the NGC 315 jet by applying the above-explained models.
4.1 Constraining
Figure 1 presents the best-fit profile of the model-predicted overlaid to the VLBI-measured . As seen here, the jet flow is described as multiple streamlines of the plasma flow along the magnetic surfaces with their curvature is calculated in TT03 model. As emphasized in (Kino et al., 2022), the key feature is the location of the starting point of the jet acceleration. The allowed range of the angular velocity is
| (9) |
Errors bars for the innermost measurement of , introduce uncertainties for the determination of the starting point of the jet acceleration 333 It is noteworthy that a recent work of Ricci et al. (2023) shows that if thermal energy in the jet is comparable to or exceeds magnetic energy, thermal acceleration becomes significant at parsec scales. If this is the case, then the discrepancy between the observed velocity field and the model-predicted one would get even larger..
In order to take into account such uncertainties, here we have conducted two cases of the fittings. Case 1 fits the higher value of the data point that realizes a smaller width of , while Case 2 fits the lower value of the data point that realizes a larger width of . The resultant small difference in the starting point of the jet acceleration is seen in Figure 1. For both cases, we fit the observation data point with the fastest speed at . Since the jet is only logarithmically accelerated, Case 2 requires a larger than Case 1.
The dashed vertical lines show the distance of the jet collimation break. The observation data show the jet deceleration at a distance further away than the jet collimation break (i.e., ). At the jet deceleration region, TT03 model is not applicable. In addition, it would be worth noting the Bondi radius within which the gravitational influence of the central black hole dominates, where , and are the sound speed and the temperature of the surrounding hot atmosphere (e.g., Russell et al., 2015). For NGC 315, the temperature of the hot atmosphere within 1 arcsec has which leads , which is significantly larger than .
Next, we estimate magnetic field strength on the horizon scale () by assuming BZ process is in action at the jet base of NGC 315. The BZ power and the ratio of the angular velocity of the magnetic field line and the event horizon can be given by
| (10) |
and
| (11) |
where (e.g., Beskin & Kuznetsova, 2000; Takahashi et al., 2021) and is the outer horizon radius of the black hole and is the dimensionless spin parameter. For simplicity, for is shown here. Here we normalized with a typical value suggested at the jet base (e.g., Beskin & Kuznetsova, 2000; Tchekhovskoy et al., 2011). From Eqs. (10) and (11), it can be readily seen that and are the two parameters that govern the value of .
Note that there is uncertainty in the value of due to . At a glance, it seems natural to substitute with the 4-6 degrees measured at the jet downstream. However, this value leads to , causing a problem of unphysically large BH being required through Eq. (10). This may be probably due to the rapid change in the magnetic field shape near the horizon scale, deviating significantly from the smooth parabolic shape (assumed in TT03). Indeed, GRMHD simulations for MAD state have shown a tendency for the magnetic field to abruptly change to a larger opening angle near the BH, penetrating the horizon (e.g., Tchekhovskoy et al., 2011). Therefore, integrating only within the narrow range of degrees on the event horizon significantly underestimate the magnetic flux threading the event horizon. To compromise this problem, we set as approximately 1 radian in light of GRMHD simulations. In the case of M87, actual 86 GHz VLBI image shows of order of 1 radian half opening angle (Hada et al., 2018; Kim et al., 2018). Hence, the choice of did not matter (Kino et al., 2022). On the contrary, the jet base of NGC 315 has not yet been spatially resolved to that depth. Hence, we assume radian.
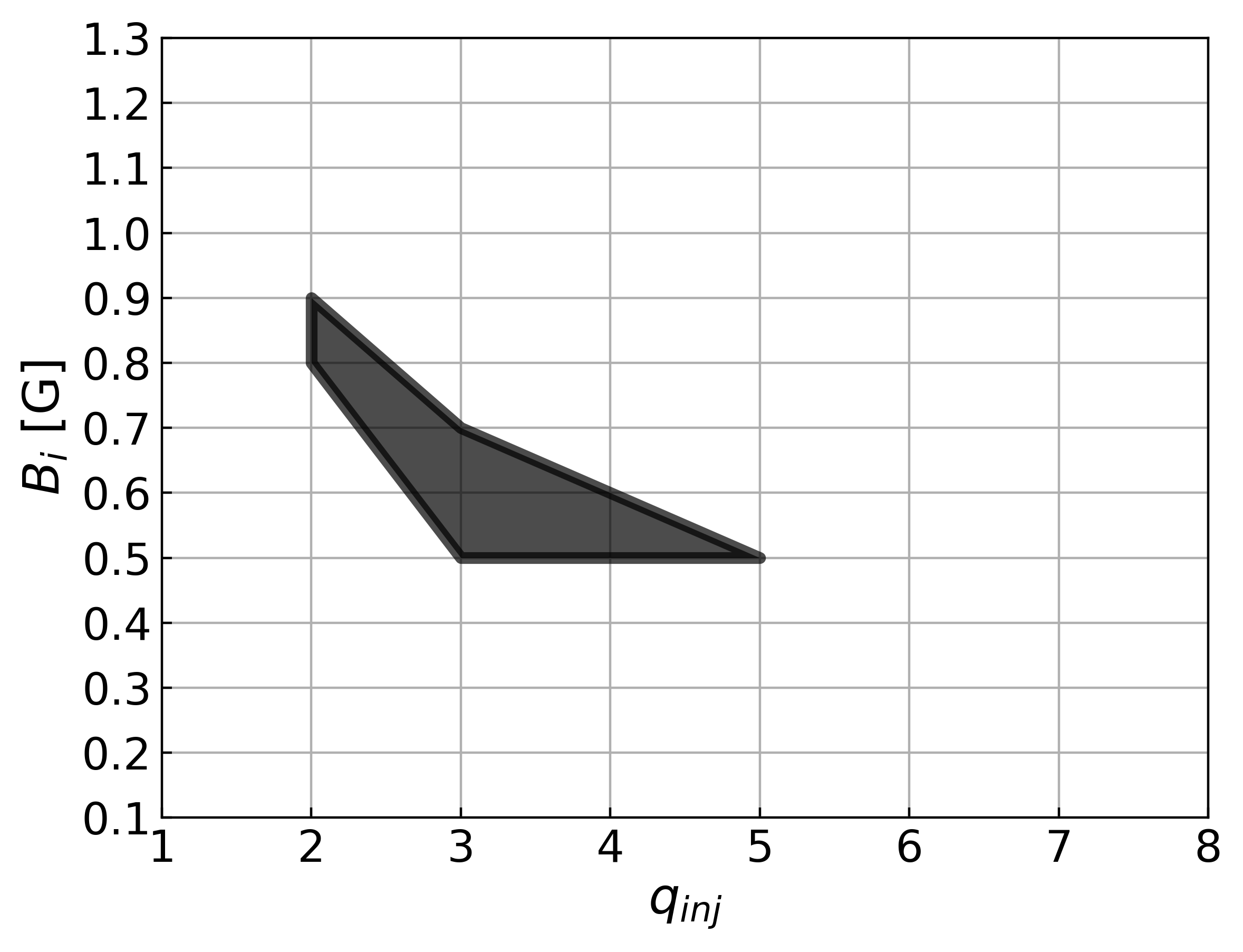
Following the recent GRMHD simulations of highly magnetized jets (e.g., Porth et al., 2019; Ripperda et al., 2019), we set the value of the magnetic field threading angle as radian and it leads to . Here, we assume the allowed range of the black hole spin as (e.g., Zamaninasab et al., 2014; Nakamura et al., 2018) since too small spin is not able to explain the required jet power. By combining the estimated and assumed together with the assumption of BZ-driven jet i.e., , we obtain the allowed range of and the corresponding as follows:
| (12) |
Figure 2 presents the estimated range of . The lower end of is comparable to that estimated in the previous work Ricci et al. (2022). We stress that one of the uniqueness of our analysis is the estimation of based on the observed jet velocity profile.
4.2 Constraining at the jet downstream
Following the method proposed by Ro et al. (2023), here we will constrain the physical quantities of the NGC 315 jet from the observed spectral index distribution. We use the data obtained on January 05th, 2020 (project code: BP243; Park et al., 2021) to investigate the spectral index distribution of the NGC 315. In particular, we use the higher frequency pair (15 GHz and 22 GHz) in these multi-frequency observations, since this is less effective by the synchrotron self-absorption. The information of data is summarized in Table 1 of Park et al. (2021). To avoid artificial spectral steepening, we used the visibility data with a common -range of 8 to 445 , where is the wavelength of the corresponding radio wave. We convolved the two images into a circular beam with a radius of 0.9 mas. We also correct the core shift between two frequencies. According to Park et al. (2021), the position difference between the 15 GHz core and the 22 GHz core is mas in right ascension and mas in declination.
Figure 3 shows a spectral index map of NGC 315 between 15 GHz and 22 GHz. We obtain spectral index values up to 10 mas from the radio core. It also shows that the core has a relatively flat spectrum while the jet has a steep spectrum, which has already been reported in previous studies (Park et al., 2021; Ricci et al., 2022). Using this spectral index map, we constructed the spectral index distribution of the jet by taking the weighted average of the spectral indices in the direction perpendicular to the jet as it moves down the jet pixel by pixel. When calculating the weighted mean, we used pixel values located within one beam size from the jet axis (0.9 mas). The error is estimated by multiplying the formal error of the weighted mean by , where is the number of the pixel, to compensate for the biases due to correlations between pixel values.
Figure 4 summarizes the results of the spectral index analysis for the NGC 315 jet. In the left panel, the gray solid line shows the radial distributions of the spectral index between 15 GHz and 22 GHz () as a function of de-projected distance from the SMBH in units of . The spectral distribution out to 8 mas (corresponding to 49,000 in the de-projected distance) from the central black hole is obtained. A steepening of the spectral index is seen until 2.5 mas, after which it is constant. This behaviour is qualitatively same to the one observed in the M87 jet (Ro et al., 2023). By applying the spectral index distribution model described in § 2.2, here we constrain and . Using , the -profile of the magnetic field strengths over the region 0.75 – 8 mas (corresponding to 5,200 – 49,000 in the de-projected distance) is given by
| (13) |
where the relations of , , and are used (Zamaninasab et al., 2014; Park et al., 2021). To compare the model and the observations, the allowed region is defined based on the observational spectral index distributions with three parameters: (1) The spectral index at , (2) the location of the end of the steepening region (), and (3) the spectral index range after the steepening region (). These parameters for the NGC 315 jet are . mas, . We then create many modeled spectral index distributions for different values of the parameters and . The field strength was set from 0.1 G to 1.3 G in 0.1 G increment, and the injection index is set as . In all cases, we assumed a constant slope of the nonthermal electron injection function as (i.e., , horizontal dashed line in Figure 4, left). We limited the parameters by excluding models that exist outside the allowed range. Thus, applying the synchrotron-emitting jet model of Ro et al. (2023) to the VLBI observation data, we finally obtain the allowed range as together with (Figure 4, right).
We also applied our model to the spectral index distribution between 22 GHz and 43 GHz in the literature (; Figure 2 of Ricci et al., 2022). From this, we examine the spectrum of the region between 0.22 and 2.2 mas (1,600 – 13,500 in de-projected distance) from the black hole. However, shows a fast steepening at 0.4 mas, and the amount of steepening is larger than , suggesting so-called fast-cooling regime for nonthermal electrons (Sari et al., 1998). Therefore, the spectral index between 22 GHz and 43 GHz gives the lower limit of with G at .
4.3 Magnetic field strengths along the jet
In Figure 5, we show the estimated and along the NGC 315 jet. In the subsection 4.1, we have derived based on the constraints from and the estimated values and it resides in the range and this is plotted at . In the subsection 4.2, we have also constrained the field strength at the jet downstream region based on the radial distribution of the spectral index between 15 and 22 GHz, and the black area is the corresponding allowed range of in the range of . The gray-shaded region is the extrapolation of the filled-black region. The lower limit of (blue-colored) is also appended, which is estimated from the radial distribution of the spectral index between 22 and 43 GHz. In addition, other independent estimations of the magnetic field strengths are also plotted. Kimura & Toma (2020) explored multi-wavelength emission spectrum from NGC 315 and suggested that the observed -ray from NGC 315 is well explained by the hadronic emission from MAD. 444 Igumenshchev et al. (2003) found that, given the right initial conditions in MHD simulations, magnetic fields can become dynamically important in BH accretion flows, to the extent that they impede the inward motion of gas and create a ‘magnetically arrested disc’ and this is named as MAD (Narayan et al., 2003), see also Bisnovatyi-Kogan & Ruzmaikin (1974). Hot accretion flows in the MAD regime can launch powerful jets.
To understand physical properties of the accretion flow and the jet base, we make an order estimation of the magnetic field strengths in a MAD regime as a reference value by using the literature value of for NGC 315. In light of Narayan et al. (2003), the magnetic field supports the plasma against the gravitational pull by the black hole. The strength of the magnetic field that satisfies the force balance between the gravitational pull and the magnetic support can be given by where , , and are the radial velocity of the accreting matter, the height of the accretion disk, and the radial distance in the accretion disk, respectively (Ricci et al., 2022, and references therein). The estimated value (the green-shaded region in Figure 5) indicates the baseline that the SANE region will realize if the estimated value is below that value. Here we assume a scale height of the accretion disk and a medium value of which is between the value assumed in Narayan et al. (2003) (i.e., ) and the value assumed in Ricci et al. (2022) (i.e, ). Unfortunately, the uncertainty of is so large that the divided region is fairly thick. Therefore, the values of and does not affect significantly. As shown in Fig. 5, we find that the extrapolated region (gray-colored) is consistent with MAD regime. The estimated in sub-section 4.1 also suggests that the accretion flow of NGC 315 is in a MAD regime. This claim agrees with the previous study of Ricci et al. (2022). In addition, the magnetic field strengths estimated in Kimura & Toma (2020) also reside in the MAD regime.
5 Discussion
5.1 A note on a small
Previous works develop an analogy of direct current (DC) circuit analysis for power flow through the black hole magnetosphere, known as the membrane paradigm of black holes (Thorne et al., 1986, and references therein). In this context, we consider a meaning of a small indicated in this work. A plasma-filled (i.e., non-vacuum) black-hole magnetosphere resembles a DC circuit. The magnetized rotating black hole acts as a battery driving the current (). Strong magnetic field lines threading the event horizon function like current-carrying wires, allowing charged particles to slide along them. These magnetic wires connect the event horizon to a distant, weakly-magnetized load region, where the current returns to the black hole battery. This DC circuit analysis between a certain two magnetic-field surfaces can give the relation among, , , the resistance across the event horizon (),and the load region () as follows:
| (14) |
where , and , are the voltage drop at the event horizon and that of the load region, respectively (see Section IV in the textbook of Thorne et al., 1986). If assuming the power into the load region is maximized, the analogy of a laboratory DC circuit suggests the impedance matching of (MacDonald & Thorne, 1982), leading to . GRMHD simulations have also suggested that the ratio fits in the similar range of (e.g., McKinney & Narayan, 2007; Penna et al., 2013). Therefore, indicated in this work may correspond to an impedance mismatching. In a DC circuit, an impedance mismatching causes energy transmission losses. Therefore, to compensate for this lost energy, a relatively large in is needed in this work to meet the required for NGC 315. Although detailed physical processes in the load regions in astropysical AGN jet system are unclear, it seems likely that the electric fields of the load region will accelerate charged particles to high energies (Thorne et al., 1986).
5.2 Magnetic flux threading the event horizon of in NGC 315
Magnetic flux threading the event horizon () is one of the key parameters that characterizes the jet launching (e.g., Zamaninasab et al., 2014). Although the dimensionless magnetic flux threading one hemisphere of the event horizon ( where is the magnetic flux threading the black hole) is actively discussed in GRMHD simulations (e.g., Tchekhovskoy et al., 2011; Narayan et al., 2022), the strength of is highly uncertain in actual jet objects. Therefore, it is worthwhile to estimate a typical in order to compare GRMHD simulations and observations. Using the estimated , we can make the order estimation of (in Gaussian-cgs units) for NGC315 as follows:
| (15) |
or equivalently
| (16) |
Since it is generally difficult to estimate , Zamaninasab et al. (2014) suggested an alternative way where assuming poloidal magnetic flux threading parsec-scale jets is comparable to . Using the relation of , they indicated that the jet-launching regions of AGN jets are threaded by dynamically important fields, which obstruct gas infall, compress the accretion disk vertically, slow down the disk rotation by carrying away its angular momentum in an outflow and determine the direction of jets. Our estimated value for NGC 315 shown in Eq. (16) agrees with the result of (Zamaninasab et al., 2014).
In addition, it is also worth checking the value of the efficiency with which the black hole generates the jet power () as the ratio of to the inflow rate at which rest mass energy flows into the black hole (Tchekhovskoy et al., 2011). Together with the assumption of , the value for NGC 315 is estimated as
| (17) |
The estimation of implies that the NGC 315 jet carries away more energy than the entire rest mass energy of the accreted gas, suggesting the need of extracting the rotational energy of the black hole. The estimated order of in Eq. (17) can be comparable to the maximal value of seen in GRMHD simulations (e.g., Tchekhovskoy et al., 2011; Narayan et al., 2022).
5.3 Comparison with NGC 315 and M87
5.3.1 Relation of and
In light of recent GRMHD numerical simulations, as the value of increases, the accretion flow mode switches from SANE to MAD. Based on this knowledge, an ansatz emerges that in actual jet objects, the larger the value, the more powerful the jets may be produced. However, the estimation and discussion of (or ) value in actual jet objects have hardly been conducted. In order to address this ansatz, it would be worth comparing the range of estimated values and for NGC 315 and M87 even although there are only two sources treated here. Zamaninasab et al. (2014) showed a positive correlation between and the square of the luminosity of the accretion disk. This also appears to support the positive correlation between and jet power, since it is widely known that has a positive correlation with the luminosity of the accretion disk (e.g., Rawlings & Saunders, 1991; Ghisellini et al., 2014).
In Figure 6, we investigate the relationship between and for NGC 315 and M87. According to Event Horizon Telescope Collaboration et al. (2021b), the range is classified as MAD, while the range below is classified as SANE. The range in between is defined as semi-MAD in this work. Although the estimation of the value depends on the adopted , the estimated suggests that NGC 315 generally aligns with a MAD regime unless an extremely high mass accretion rate, , is realized. However, discussing a correlation between and using Figure 6 is challenging due to significant uncertainties in caused by and . In particular, introduces a large uncertainty in . Nonetheless, it is important to explore the relation between and in terms of exploring BZ77. To further test BZ77, it is essential to narrow the allowed range of . In the case of M87, polarimetric observation by the EHT significantly narrowed the allowed region of (Event Horizon Telescope Collaboration et al., 2021b). Following this, we expect that future higher sensitivity and higher resolution VLBI observations, such as the next generation EHT (ngEHT) and the Black Hole Explorer (BHEX) (e.g., Kurczynski et al., 2022; Johnson et al., 2023; Doeleman et al., 2023), will similarly narrow down the in NGC315. From a theoretical standpoint, existing GRMHD numerical experiments have not sufficiently explored the parameter range where . Investigating a correlation between and accross a wide range will be an important next step in understanding the jet launching mechanism.
5.3.2 Implication: What determines the location of the ?
Although there are mounting observational measurements of for various AGN jets (e.g., Asada & Nakamura, 2012; Hada et al., 2013; Tseng et al., 2016; Nakahara et al., 2018; Algaba et al., 2019; Nakahara et al., 2020; Kovalev et al., 2020; Boccardi et al., 2021; Yi et al., 2024), what determines the location of the is still an open issue. There are two possible scenarios. One scenario suggests that the location of the is associated with differences in the central engine and/or jet’s intrinsic magnetic fields (Potter & Cotter, 2015; Nokhrina et al., 2019; Kovalev et al., 2020; Nokhrina et al., 2020), while the other scenario proposes that the surrounding matter around the jet determines of the location of the (e.g., Park et al., 2021; Okino et al., 2022; Rohoza et al., 2024). NGC 315 seems to be decelerated down to a non-relativistic speed at which is much closer than (Park et al., 2021). For M87, the jet apparent speeds become smaller beyond (Park et al., 2019) and it can be understood as the M87 jet is decelerated at . Both NGC 315 and M87 could be understood in terms of the locations of being determined by the different locations of the surrounding material. However, it is difficult to determine which of the two possible scenarios is realized because the strength of the central engine is not clearly constrained and compared. To address this, we attempt to investigate the relationship between and . However, it cannot be conclusive with the current best data due to the large uncertainty in (see Sub-section 5.3.1). But if a positive correlation between and could be found in the future, then that would support the idea that surrounding matter around the jet play a more dominant role for determination of the location of the . Further investigation is eagerly anticipated.
6 Summary
In the present work, we investigate magnetic field strengths along the jet in NGC 315, building upon the earlier work by Kino et al. (2022). Before summarizing the results, we briefly address two frequently asked questions and provide their answers.
-
•
Some may consider entrainment as a physical process to explain the slower velocity within . It could be possible to decelerate the flow with intense entrainment with surrounding ambient material after the jet’s bulk acceleration reaches its maximum velocity at a distance of about from the central engine, as suggested in GRMHD simulations (e.g., Chatterjee et al., 2019, Fig. 13). The thermal energy generated during the interaction between the jet and surrounding medium may help re-accelerate the jet. However, the numerical simulation by Ricci et al. (2023), which investigated thermal acceleration, did not show sufficient deceleration, resulting in a significant overestimation the jet velocity within . Moreover, such significant deceleration and re-acceleration do not produce a smooth velocity profile but rather a beat-like profile, which is not suggested in the velocity profile of NGC 315. For these reasons, explaining the velocity profile through the entrainment phenomenon appears challenging.
-
•
Assuming maximal power transfer to the load region, akin to a laboratory DC circuit, suggests impedance matching: (MacDonald & Thorne, 1982), implying . As discussed in Section 5.1, GRMHD simulations also indicate typically falls in the range of (e.g., McKinney & Narayan, 2007; Penna et al., 2013). Thus, suggested in this study may be understood as impedance mismatching. In a DC circuit, such mismatching results in energy transmission losses. To compensate, this study requires a relatively large magnetic field in to achieve the necessary jet power for NGC 315.
Below, we summarize our findings in the present work.
-
•
First, we estimated the angular velocity of rotation in the jet magnetosphere by comparing the measured velocity profile of NGC 315 with the MHD jet model of TT03, following the recent work of Kino et al. (2022) on M87. Then, we find that the model can reproduce the logarithmic feature of the velocity profile with , suggesting slowly rotating black hole magnetosphere for NGC 315. By substituting this into the jet power predicted by the Blandford-Znajek mechanism, we estimate the magnetic field strength near the event horizon as .
-
•
We then estimate the magnetic-field strengths along the jet by comparing the spectral index distribution obtained from VLBI observations with a synchrotron-emitting jet model based on the recent work of Ro et al. (2023). Then we constrain the magnetic field strength at the de-projected distance of to be in the range . By combining the obtained field strengths at the event horizon and the downstream section of the jet, we find that the accretion flow at the jet base is consistent with a MAD.
-
•
Using the estimated in this work, the dimensionless magnetic field flux threading the event horizon is estimated. It can be well above , suggesting MAD regime is realized in NGC 315. In addition, the efficiency of the jet power production () for NGC 315 can be comparable with the maximal value of seen in GRMHD simulations (e.g., Tchekhovskoy et al., 2011; Narayan et al., 2022).
-
•
The comparison of and between NGC 315 and M87 has been made. However, it is difficult to clarify a relation between and because of uncertainties in . This causes a large uncertainty in . To improve our understanding of BZ77, we expect that future higher sensitivity and higher resolution VLBI observations, such as ngEHT and BHEX (e.g., Kurczynski et al., 2022; Johnson et al., 2023; Doeleman et al., 2023), would narrow down the , thereby providing a better constraint on in NGC 315.
Acknowledgment
We thank the referee for his or her constructive comments and careful reading of the manuscript, which helped improve its overall clarity. This work was partially supported by the MEXT/JSPS KAKENHI (JP17K05439, JP21H01137, JP21H04488, JP22H00157, JP23H00117, and JP23K03448). This research was also supported by MEXT as “Program for Promoting Researches on the Supercomputer Fugaku” (Toward a unified view of the universe: from large scale structures to planets, JPMXP1020200109) and JICFuS.
References
- Acciari et al. (2009) Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, Science, 325, 444, doi: 10.1126/science.1175406
- Algaba et al. (2019) Algaba, J. C., Rani, B., Lee, S. S., et al. 2019, ApJ, 886, 85, doi: 10.3847/1538-4357/ab4b45
- Allen et al. (2006) Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21, doi: 10.1111/j.1365-2966.2006.10778.x
- Asada & Nakamura (2012) Asada, K., & Nakamura, M. 2012, ApJ, 745, L28, doi: 10.1088/2041-8205/745/2/L28
- Asada et al. (2014) Asada, K., Nakamura, M., Doi, A., Nagai, H., & Inoue, M. 2014, ApJ, 781, L2, doi: 10.1088/2041-8205/781/1/L2
- Baan (1980) Baan, W. A. 1980, ApJ, 239, 433, doi: 10.1086/158127
- Bach et al. (2003) Bach, U., Kadler, M., Krichbaum, T. P., et al. 2003, in Proceedings of the Second ENIGMA Meeting, ed. C. M. Raiteri & M. Villata, 216–223
- Balmaverde et al. (2008) Balmaverde, B., Baldi, R. D., & Capetti, A. 2008, A&A, 486, 119, doi: 10.1051/0004-6361:200809810
- Begelman et al. (1984) Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Reviews of Modern Physics, 56, 255, doi: 10.1103/RevModPhys.56.255
- Beifiori et al. (2009) Beifiori, A., Sarzi, M., Corsini, E. M., et al. 2009, ApJ, 692, 856, doi: 10.1088/0004-637X/692/1/856
- Beskin (2010) Beskin, V. S. 2010, MHD Flows in Compact Astrophysical Objects, doi: 10.1007/978-3-642-01290-7
- Beskin et al. (2023) Beskin, V. S., Kniazev, F. A., & Chatterjee, K. 2023, MNRAS, 524, 4012, doi: 10.1093/mnras/stad2064
- Beskin & Kuznetsova (2000) Beskin, V. S., & Kuznetsova, I. V. 2000, Nuovo Cimento B Serie, 115, 795. https://arxiv.org/abs/astro-ph/0004021
- Bicknell (1984) Bicknell, G. V. 1984, ApJ, 286, 68, doi: 10.1086/162577
- Bisnovatyi-Kogan & Ruzmaikin (1974) Bisnovatyi-Kogan, G. S., & Ruzmaikin, A. A. 1974, Ap&SS, 28, 45, doi: 10.1007/BF00642237
- Blandford et al. (2019) Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467, doi: 10.1146/annurev-astro-081817-051948
- Blandford & Znajek (1977) Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433, doi: 10.1093/mnras/179.3.433
- Boccardi et al. (2016) Boccardi, B., Krichbaum, T. P., Bach, U., et al. 2016, A&A, 585, A33, doi: 10.1051/0004-6361/201526985
- Boccardi et al. (2021) Boccardi, B., Perucho, M., Casadio, C., et al. 2021, A&A, 647, A67, doi: 10.1051/0004-6361/202039612
- Boizelle et al. (2021) Boizelle, B. D., Walsh, J. L., Barth, A. J., et al. 2021, ApJ, 908, 19, doi: 10.3847/1538-4357/abd24d
- Camilloni et al. (2022) Camilloni, F., Dias, O. J. C., Grignani, G., et al. 2022, J. Cosmology Astropart. Phys, 2022, 032, doi: 10.1088/1475-7516/2022/07/032
- Chatterjee et al. (2019) Chatterjee, K., Liska, M., Tchekhovskoy, A., & Markoff, S. B. 2019, MNRAS, 490, 2200, doi: 10.1093/mnras/stz2626
- de Menezes et al. (2020) de Menezes, R., Nemmen, R., Finke, J. D., Almeida, I., & Rani, B. 2020, MNRAS, 492, 4120, doi: 10.1093/mnras/staa083
- De Young (1993) De Young, D. S. 1993, ApJ, 405, L13, doi: 10.1086/186754
- Doeleman et al. (2023) Doeleman, S. S., Barrett, J., Blackburn, L., et al. 2023, Galaxies, 11, 107, doi: 10.3390/galaxies11050107
- Event Horizon Telescope Collaboration (2019a) Event Horizon Telescope Collaboration. 2019a, ApJ, 875, L1, doi: 10.3847/2041-8213/ab0ec7
- Event Horizon Telescope Collaboration (2019b) —. 2019b, ApJ, 875, L2, doi: 10.3847/2041-8213/ab0c96
- Event Horizon Telescope Collaboration (2019c) —. 2019c, ApJ, 875, L3, doi: 10.3847/2041-8213/ab0c57
- Event Horizon Telescope Collaboration (2019d) —. 2019d, ApJ, 875, L4, doi: 10.3847/2041-8213/ab0e85
- Event Horizon Telescope Collaboration (2019e) —. 2019e, ApJ, 875, L5, doi: 10.3847/2041-8213/ab0f43
- Event Horizon Telescope Collaboration (2019f) —. 2019f, ApJ, 875, L6, doi: 10.3847/2041-8213/ab1141
- Event Horizon Telescope Collaboration et al. (2021a) Event Horizon Telescope Collaboration, Akiyama, K., Algaba, J. C., et al. 2021a, ApJ, 910, L12, doi: 10.3847/2041-8213/abe71d
- Event Horizon Telescope Collaboration et al. (2021b) —. 2021b, ApJ, 910, L13, doi: 10.3847/2041-8213/abe4de
- Ghisellini et al. (2014) Ghisellini, G., Tavecchio, F., Maraschi, L., Celotti, A., & Sbarrato, T. 2014, Nature, 515, 376, doi: 10.1038/nature13856
- Gu et al. (2007) Gu, Q. S., Huang, J. S., Wilson, G., & Fazio, G. G. 2007, ApJ, 671, L105, doi: 10.1086/525018
- Hada et al. (2013) Hada, K., Kino, M., Doi, A., et al. 2013, ApJ, 775, 70, doi: 10.1088/0004-637X/775/1/70
- Hada et al. (2016) —. 2016, ApJ, 817, 131, doi: 10.3847/0004-637X/817/2/131
- Hada et al. (2017) Hada, K., Park, J. H., Kino, M., et al. 2017, PASJ, 69, 71, doi: 10.1093/pasj/psx054
- Hada et al. (2018) Hada, K., Doi, A., Wajima, K., et al. 2018, ApJ, 860, 141, doi: 10.3847/1538-4357/aac49f
- Heinz et al. (2007) Heinz, S., Merloni, A., & Schwab, J. 2007, ApJ, 658, L9, doi: 10.1086/513507
- Ho (2008) Ho, L. C. 2008, ARA&A, 46, 475, doi: 10.1146/annurev.astro.45.051806.110546
- Ho et al. (1995) Ho, L. C., Filippenko, A. V., & Sargent, W. L. 1995, ApJS, 98, 477, doi: 10.1086/192170
- Ho et al. (1997) Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJS, 112, 315, doi: 10.1086/313041
- Igumenshchev et al. (2003) Igumenshchev, I. V., Narayan, R., & Abramowicz, M. A. 2003, ApJ, 592, 1042, doi: 10.1086/375769
- Inayoshi et al. (2020) Inayoshi, K., Ichikawa, K., & Ho, L. C. 2020, ApJ, 894, 141, doi: 10.3847/1538-4357/ab8569
- Johnson et al. (2023) Johnson, M. D., Akiyama, K., Blackburn, L., et al. 2023, Galaxies, 11, 61, doi: 10.3390/galaxies11030061
- Kawakatu et al. (2009) Kawakatu, N., Kino, M., & Nagai, H. 2009, ApJ, 697, L173, doi: 10.1088/0004-637X/697/2/L173
- Kim et al. (2018) Kim, J. Y., Krichbaum, T. P., Lu, R. S., et al. 2018, A&A, 616, A188, doi: 10.1051/0004-6361/201832921
- Kimura & Toma (2020) Kimura, S. S., & Toma, K. 2020, ApJ, 905, 178, doi: 10.3847/1538-4357/abc343
- Kino et al. (2012) Kino, M., Kawakatu, N., & Takahara, F. 2012, ApJ, 751, 101, doi: 10.1088/0004-637X/751/2/101
- Kino et al. (2022) Kino, M., Takahashi, M., Kawashima, T., et al. 2022, ApJ, 939, 83, doi: 10.3847/1538-4357/ac8c2f
- Komissarov (1994) Komissarov, S. S. 1994, MNRAS, 269, 394, doi: 10.1093/mnras/269.2.394
- Komissarov et al. (2007) Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51, doi: 10.1111/j.1365-2966.2007.12050.x
- Kovalev et al. (2007) Kovalev, Y. Y., Lister, M. L., Homan, D. C., & Kellermann, K. I. 2007, ApJ, 668, L27, doi: 10.1086/522603
- Kovalev et al. (2020) Kovalev, Y. Y., Pushkarev, A. B., Nokhrina, E. E., et al. 2020, MNRAS, 495, 3576, doi: 10.1093/mnras/staa1121
- Krichbaum et al. (1998) Krichbaum, T. P., Alef, W., Witzel, A., et al. 1998, A&A, 329, 873
- Kurczynski et al. (2022) Kurczynski, P., Johnson, M. D., Doeleman, S. S., et al. 2022, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 12180, Space Telescopes and Instrumentation 2022: Optical, Infrared, and Millimeter Wave, ed. L. E. Coyle, S. Matsuura, & M. D. Perrin, 121800M
- Laing & Bridle (2014) Laing, R. A., & Bridle, A. H. 2014, MNRAS, 437, 3405, doi: 10.1093/mnras/stt2138
- Ly et al. (2007) Ly, C., Walker, R. C., & Junor, W. 2007, ApJ, 660, 200, doi: 10.1086/512846
- MacDonald & Thorne (1982) MacDonald, D., & Thorne, K. S. 1982, MNRAS, 198, 345, doi: 10.1093/mnras/198.2.345
- McKinney (2006) McKinney, J. C. 2006, MNRAS, 368, 1561, doi: 10.1111/j.1365-2966.2006.10256.x
- McKinney & Narayan (2007) McKinney, J. C., & Narayan, R. 2007, MNRAS, 375, 513, doi: 10.1111/j.1365-2966.2006.11301.x
- Mertens et al. (2016) Mertens, F., Lobanov, A. P., Walker, R. C., & Hardee, P. E. 2016, A&A, 595, A54, doi: 10.1051/0004-6361/201628829
- Morganti et al. (2009) Morganti, R., Peck, A. B., Oosterloo, T. A., et al. 2009, A&A, 505, 559, doi: 10.1051/0004-6361/200912605
- Nakahara et al. (2018) Nakahara, S., Doi, A., Murata, Y., et al. 2018, ApJ, 854, 148, doi: 10.3847/1538-4357/aaa45e
- Nakahara et al. (2020) —. 2020, AJ, 159, 14, doi: 10.3847/1538-3881/ab465b
- Nakamura et al. (2018) Nakamura, M., Asada, K., Hada, K., et al. 2018, ApJ, 868, 146, doi: 10.3847/1538-4357/aaeb2d
- Narayan et al. (2022) Narayan, R., Chael, A., Chatterjee, K., Ricarte, A., & Curd, B. 2022, MNRAS, 511, 3795, doi: 10.1093/mnras/stac285
- Narayan et al. (2003) Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69, doi: 10.1093/pasj/55.6.L69
- Nemmen & Tchekhovskoy (2015) Nemmen, R. S., & Tchekhovskoy, A. 2015, MNRAS, 449, 316, doi: 10.1093/mnras/stv260
- Nitta et al. (1991) Nitta, S.-Y., Takahashi, M., & Tomimatsu, A. 1991, Phys. Rev. D, 44, 2295, doi: 10.1103/PhysRevD.44.2295
- Noel-Storr et al. (2007) Noel-Storr, J., Baum, S. A., & O’Dea, C. P. 2007, ApJ, 663, 71, doi: 10.1086/518359
- Nokhrina et al. (2019) Nokhrina, E. E., Gurvits, L. I., Beskin, V. S., et al. 2019, MNRAS, 489, 1197, doi: 10.1093/mnras/stz2116
- Nokhrina et al. (2020) Nokhrina, E. E., Kovalev, Y. Y., & Pushkarev, A. B. 2020, MNRAS, 498, 2532, doi: 10.1093/mnras/staa2458
- Okino et al. (2022) Okino, H., Akiyama, K., Asada, K., et al. 2022, ApJ, 940, 65, doi: 10.3847/1538-4357/ac97e5
- Owen et al. (2000) Owen, F. N., Eilek, J. A., & Kassim, N. E. 2000, ApJ, 543, 611, doi: 10.1086/317151
- Park et al. (2021) Park, J., Hada, K., Nakamura, M., et al. 2021, ApJ, 909, 76, doi: 10.3847/1538-4357/abd6ee
- Park et al. (2019) Park, J., Hada, K., Kino, M., et al. 2019, ApJ, 887, 147, doi: 10.3847/1538-4357/ab5584
- Penna et al. (2013) Penna, R. F., Narayan, R., & Sądowski, A. 2013, MNRAS, 436, 3741, doi: 10.1093/mnras/stt1860
- Perucho et al. (2014) Perucho, M., Martí, J. M., Laing, R. A., & Hardee, P. E. 2014, MNRAS, 441, 1488, doi: 10.1093/mnras/stu676
- Planck Collaboration et al. (2020) Planck Collaboration, Aghanim, N., Akrami, Y., et al. 2020, A&A, 641, A6, doi: 10.1051/0004-6361/201833910
- Porth et al. (2019) Porth, O., Chatterjee, K., Narayan, R., et al. 2019, ApJS, 243, 26, doi: 10.3847/1538-4365/ab29fd
- Potter & Cotter (2015) Potter, W. J., & Cotter, G. 2015, MNRAS, 453, 4070, doi: 10.1093/mnras/stv1657
- Pu et al. (2015) Pu, H.-Y., Nakamura, M., Hirotani, K., et al. 2015, ApJ, 801, 56, doi: 10.1088/0004-637X/801/1/56
- Pu & Takahashi (2020) Pu, H.-Y., & Takahashi, M. 2020, ApJ, 892, 37, doi: 10.3847/1538-4357/ab77ab
- Pushkarev et al. (2017) Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2017, MNRAS, 468, 4992, doi: 10.1093/mnras/stx854
- Rafferty et al. (2006) Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216, doi: 10.1086/507672
- Ramakrishnan et al. (2023) Ramakrishnan, V., Nagar, N., Arratia, V., et al. 2023, Galaxies, 11, 15, doi: 10.3390/galaxies11010015
- Rawlings & Saunders (1991) Rawlings, S., & Saunders, R. 1991, Nature, 349, 138, doi: 10.1038/349138a0
- Ricci et al. (2023) Ricci, L., Perucho, M., López-Miralles, J., Martí, J. M., & Boccardi, B. 2023, arXiv e-prints, arXiv:2312.06410, doi: 10.48550/arXiv.2312.06410
- Ricci et al. (2022) Ricci, L., Boccardi, B., Nokhrina, E., et al. 2022, A&A, 664, A166, doi: 10.1051/0004-6361/202243958
- Ripperda et al. (2019) Ripperda, B., Bacchini, F., Porth, O., et al. 2019, ApJS, 244, 10, doi: 10.3847/1538-4365/ab3922
- Ro et al. (2023) Ro, H., Kino, M., Sohn, B. W., et al. 2023, A&A, 673, A159, doi: 10.1051/0004-6361/202142988
- Rohoza et al. (2024) Rohoza, V., Lalakos, A., Paik, M., et al. 2024, ApJ, 963, L29, doi: 10.3847/2041-8213/ad24fc
- Russell et al. (2015) Russell, H. R., Fabian, A. C., McNamara, B. R., & Broderick, A. E. 2015, MNRAS, 451, 588, doi: 10.1093/mnras/stv954
- Sari et al. (1998) Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17, doi: 10.1086/311269
- Satyapal et al. (2005) Satyapal, S., Dudik, R. P., O’Halloran, B., & Gliozzi, M. 2005, ApJ, 633, 86, doi: 10.1086/449304
- Sikora et al. (2020) Sikora, M., Nalewajko, K., & Madejski, G. M. 2020, MNRAS, 499, 3749, doi: 10.1093/mnras/staa3128
- Stawarz et al. (2006) Stawarz, Ł., Aharonian, F., Kataoka, J., et al. 2006, MNRAS, 370, 981, doi: 10.1111/j.1365-2966.2006.10525.x
- Takahashi (2002) Takahashi, M. 2002, ApJ, 570, 264, doi: 10.1086/339497
- Takahashi et al. (2021) Takahashi, M., Kino, M., & Pu, H.-Y. 2021, Phys. Rev. D, 104, 103004, doi: 10.1103/PhysRevD.104.103004
- Takahashi et al. (1990) Takahashi, M., Nitta, S., Tatematsu, Y., & Tomimatsu, A. 1990, ApJ, 363, 206, doi: 10.1086/169331
- Tchekhovskoy et al. (2011) Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79, doi: 10.1111/j.1745-3933.2011.01147.x
- Thorne et al. (1986) Thorne, K. S., Price, R. H., & MacDonald, D. A. 1986, Black holes: The membrane paradigm
- Tomimatsu & Takahashi (2003) Tomimatsu, A., & Takahashi, M. 2003, ApJ, 592, 321, doi: 10.1086/375579
- Trager et al. (2000) Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 120, 165, doi: 10.1086/301442
- Tseng et al. (2016) Tseng, C.-Y., Asada, K., Nakamura, M., et al. 2016, ApJ, 833, 288, doi: 10.3847/1538-4357/833/2/288
- van Gorkom et al. (1989) van Gorkom, J. H., Knapp, G. R., Ekers, R. D., et al. 1989, AJ, 97, 708, doi: 10.1086/115016
- Walker et al. (2018) Walker, R. C., Hardee, P. E., Davies, F. B., Ly, C., & Junor, W. 2018, ApJ, 855, 128, doi: 10.3847/1538-4357/aaafcc
- Woo & Urry (2002) Woo, J.-H., & Urry, C. M. 2002, ApJ, 581, L5, doi: 10.1086/345944
- Yi et al. (2024) Yi, K., Park, J., Nakamura, M., Hada, K., & Trippe, S. 2024, arXiv e-prints, arXiv:2405.03365, doi: 10.48550/arXiv.2405.03365
- Zamaninasab et al. (2014) Zamaninasab, M., Clausen-Brown, E., Savolainen, T., & Tchekhovskoy, A. 2014, Nature, 510, 126, doi: 10.1038/nature13399