Manifold Regularized Dynamic Network Pruning
Abstract
Neural network pruning is an essential approach for reducing the computational complexity of deep models so that they can be well deployed on resource-limited devices. Compared with conventional methods, the recently developed dynamic pruning methods determine redundant filters variant to each input instance which achieves higher acceleration. Most of the existing methods discover effective sub-networks for each instance independently and do not utilize the relationship between different inputs. To maximally excavate redundancy in the given network architecture, this paper proposes a new paradigm that dynamically removes redundant filters by embedding the manifold information of all instances into the space of pruned networks (dubbed as ManiDP). We first investigate the recognition complexity and feature similarity between images in the training set. Then, the manifold relationship between instances and the pruned sub-networks will be aligned in the training procedure. The effectiveness of the proposed method is verified on several benchmarks, which shows better performance in terms of both accuracy and computational cost compared to the state-of-the-art methods. For example, our method can reduce 55.3% FLOPs of ResNet-34 with only 0.57% top-1 accuracy degradation on ImageNet.
1 Introduction
Deep convolutional neural networks (CNNs) have achieved state-of-the-art performance on a large variety of computer vision tasks, \eg, image classification [15, 48, 23, 59], objection detection [10, 44, 11], and video analysis [7, 12, 21]. Besides the model performance, recent researches pay more attention on the model efficiency, especially the computational complexity [56, 47, 46]. Since there are considerable real-world applications required to be deployed on resource constrained hardwares, \eg, mobile phones and wearable devices, techniques that effectively reduce the cost of modern deep networks are required [31, 13, 58, 60].
To this end, a number of model compression algorithms have been developed without affecting network performance. For instance, quantization [53, 14, 43, 57] uses less bits to represent network weights and knowledge distillation [19, 54, 4, 40, 55] is to train a compact network based on the knowledge of a teacher network. Low-rank approximation [35, 24, 29] tries to decompose the original filters to smaller ones while pruning method directly discards the redundant neurons to get a sparser network. Among them, channel pruning (or filter pruning) [18, 49, 36, 33] is regarded as a kind of structured pruning method, which directly discards redundant filters to obtain a compact network with lower computational cost. Since the pruned network can be well employed on mainstream hardwares to obtain considerable speed-up, channel pruning is widely used in industrial products.
The conventional channel pruning methods obtain a static network applied to all input samples, which do not excavate redundancy maximally, as the diverse demands for network parameters and capacity from different instances are neglected. In fact, the importance of filters is highly input-dependent. A few methods proposed recently prune channels according to individual instances dynamically and achieve better performance. For example, Gao et al. [9] introduce small auxiliary modules to predict the saliencies of channels with given input data, and prune unimportant filters at run-time. Instance-wise sparsity is adopted in [32] to induce different sub-networks for different samples. However, the existing methods prune channels for individual instances independently, which neglects the relationship between different instances. A sparsity constraint with same intensity is usually used for different input instances, regardless of the diversity of instance complexity. Besides, the similarity between instances is also valuable information deserving to explore.

In this paper, we explore a new paradigm for dynamic pruning to maximally excavate network redundancy corresponding to arbitrary instance. The manifold information of all samples in the given dataset is exploited in the training process and corresponding sub-networks are derived to preserve the relationship between different instances (Figure 1). Specifically, we first propose to identify the complexity of each instances in the training set and adaptively adjust the penalty weight on channel sparsity. Then, we further preserve the similarity between samples in the pruned results, \ie, the sub-network for each input sample. In practice, the features with abundant semantic information obtained by the network are used for calculating the similarity. By exploiting the proposed approach, we can allocate the overall resources more reasonably, and then obtain pruned networks with higher performance and lower costs. Experiments are throughly conducted on a series of benchmarks for demonstrating the effectiveness of the new method. Compared with the state-of-the-art pruning algorithms, we obtain higher performance in terms of both network accuracy and speed-up ratios.
2 Related Work
Channel Pruning is a kind of coarse-grain structural pruning method that discards the whole redundant filters to obtain a compact network, which can achieve practical acceleration without specific hardware [52, 50, 30, 33, 3]. It contains the conventional static pruning methods and recent dynamic algorithms, and we briefly review them as follows.
Static Pruning. A compact network shared by different instances is desired in static pruning. Wen et al. [52] impose structural sparsity on the weights of convolutional filters to discover and prune redundant channels. Liu et al. [33] associates a scaling factor to each channel and the sparsity regularization is imposed on the factors. Recently, more methods are proposed which achieve state-of-the-art performance on several benchmarks. For example, Molchanov et al. [37] uses Taylor expansion to estimate the contribution of a filter to the final output and discard filters with small scores, while Liebenwein et al. [27] construct an importance distribution that reflects the filter importance. To reduce the disturbance of irrelevant factors, Tang et al. [49] set up a scientific control during pruning filters, which can discover compact networks with high performance. These methods prune same filters for different input instances and obtain a ’static’ network with limited representation capability, whose performance degrades obviously when a large pruning rate is required.
Dynamic Pruning. Beyond the static pruning methods, an alternative way is to determine the importance of filters according to input data, and skip unnecessary calculation in the test phase [42]. Dong et al. [6] use low-cost collaborative layers to induce sparsity on the original convolutional kernels at the running time. Hua et al. [20] generate decision maps by partial input channels to identify the unimportant regions in feature maps. However, the skipped ineffective regions in [20] are irregular and practical acceleration depends on special hardware such as FPGAs and ASICs. Gao et al. [9] introduces squeeze-excitation modules to predict the saliency of channels and skip those with less contribution to the classification results. Complementary to them, this paper focuses on effectively training the dynamic network to allocate a proper sub-network for each instance, which is vital to achieve a satisfactory trade-off between accuracy and computational cost.
3 Preliminaries
In this section, we introduce the formulations of channel pruning for deep neural networks and the dynamic pruning problem.
Denote the dataset with samples as , and are the corresponding labels. For a CNN model with layers, denotes weight parameters of the convolution filters in the -th layer. is the output feature map of the -th layer with channels, which can be calculated with convolution filters and the features in the previous layer, \ie, , where denotes the convolutional operation and is the activation function.
Channel pruning discovers and eliminates redundant channels in a given neural network to reduce the overall computational complexity while retaining a comparable performance [52, 33, 37, 27]. Basically, the conventional channel pruning can be formulated as
| (1) |
where denotes all the weight parameters of the network, and is the task-dependent loss function (\eg, the cross-entropy loss for classification task). is the -norm that induces channel-wise sparsity on convolution filters, \ie, , where straightens the tensor to vector form and is the -norm111Note that the methods using scaling factors can also be regarded as this form as the factors can be absorbed to convolution kernels [33]. The trade-off coefficient balances the two losses, and a larger induces sparser convolution kernel and then obtain a more compact network.
Dynamic pruning is developed for further excavating the correction between input instances and pruned channels [9, 42, 20]. Wherein, the importance of output channels depends on the inputs, and different sub-networks will be generated for each individual instance for flexibly discovering the network redundancy. To this end, a control module is introduced to process the input feature and predict the channel saliency in the -th layer for input .222In the following, we denote channel saliency as for brevity. In practice, a smaller element in implies that the corresponding channel is less important. The controller is usually implemented by utilizing a squeeze-excitation module as suggested in [9]. Then, redundant channels are determined through a gate operation, \ie, , where the element is set to 0 when is less than the threshold and keeps unchanged otherwise. By exploiting the mask in the previous layer, the feature can be efficiently calculated as:
| (2) |
where denotes that each channel of feature is multiplied by the corresponding element in mask . Since is usually very sparse and the calculation of redundant channels are skipped, the computational complexity of Eq. (2) will be significantly lower than that of the original convolution layer.
To retain the desirable performance, the dynamic network is also trained with both the cross-entropy loss and the sparsity regularization, \ie,
| (3) |
where is the -norm penalty on the channel saliency . Obviously, a larger coefficient also produces sparer saliency and thus yields more compact networks with lower computational cost. Compared to the static pruning method (Eq. (1)) that uses a same compact network to handle all the input data, the dynamic one (Eq. (3)) aims to prune channels for different instances accordingly.
4 Manifold Regularized Dynamic Pruning
The main purpose of dynamic pruning is to fully excavate the network redundancy for each instance. However, the manifold information, \ie, the relationship between samples in the entire dataset has rarely been studied. The manifold hypothesis states that the high-dimensional data can be embedded into low-dimensional manifold, and samples locate closely in the manifold space own analogous properties. The mapping function from input samples to their corresponding sub-networks should be smooth over the manifold space, and then the relationship between samples need to be preserved in sub-networks. This manifold information can effectively regularize the solution space of instance-network pairs to help allocate a proper sub-network for each instance. In the following, we explore the manifold information from two complementary perspectives, \ie, complexity and similarity.
4.1 Instance Complexity
For a given task, the difficulty of accurately predicting example labels can be various, which thus implies the necessity of investigating models with different capacities for different inputs. Intuitively, a more complex sample with vague semantic information (\eg, images with insignificant objects, mussy background, \etc) may need a more complex network with a strong representation ability to extract the effective information, while a much simpler network lower computational cost could be enough to make the correct prediction for a simpler instance. Actually, this intuition reflects the relationship between instances on a 1-dimensional complexity space, where the different instances are sorted according to their difficulties for the given task. To exploit this property, we firstly measure the complexity of instances and sub-networks, respectively, and then develop an adaptive objective function to align the complexity relationship between instances and that between sub-networks.
Considering that input instances are expected to have correct predictions made by the networks, the task-specific loss (cross-entropy loss) of the networks is adopted to measure the complexity of current input . A larger cross-entropy loss implies that the current instance has not been fitted well, which is more complex and needs a network with stronger representation capability for extracting the information. For a sub-network, the sparsity of channel saliency determines the number of effective filters in it, and a sparser induce a more compact network with lower complexity. Hence, we use the sparsity of channel saliencies as the measurement of network complexity.
Recall that in Eq. (3), the weight coefficient is vital to determine the strength of sparsity penalty on channel saliencies. However, a same weight coefficient is assigned to all different instances without discrimination. In fact, a simple instance whose cross-entropy loss can be minimized easily may desire a compact sub-network for computational efficiency. On the other hand, those examples that have not been well fitted by the current network yet would need more network capacity to pursue the prediction accuracy, instead of pushing the sparsity further. Thus, the weight of sparsity penalty that controls the network complexity should increase when the cross-entropy loss decreases and vice versa. In an extreme case, no sparsity constraint should be given to the corresponding sub-networks for those under-fitted examples. Specifically, a set of binary learnable variables are used to indicate whether the sub-network for input instance should be thinned out. Thus the optimization objective can be formulated as:
| (4) | ||||
where is a hyper-parameter shared by all instances to balance the classification accuracy and network sparsity. is the -norm that induces sparsity on channel saliencies and is the set of network parameters. is a pre-defined threshold for instance complexity and the samples with cross-entropy losses larger than are considered as over complex. Eq. (4) is optimized in a min-max paradigm, \ie, the minimization is applied on parameter to train the network, while the maximization on variables indicates whether the corresponding sub-networks should be made sparse. In practice, has a closed-form solution. Note that always holds, and the optimal solution of only depends on the relative magnitude of cross-entropy loss and the complexity threshold , \ie,
| (5) |
Eq (5) indicates that no sparsity is imposed on the corresponding sub-network () if the cross-entropy loss of instance exceeds . In practice, the network is trained in mini-batch, and we empirically use the average cross-entropy loss over the whole dataset in the previous epoch as the threshold . For brevity, the coefficient for the sparsity loss is denoted as , \ie,
| (6) |
The value of is always in range [0, ] and it has a larger value for simpler instances. Then, the max-min optimization problem (Eq. (4)) can be simplified as:
| (7) |
In the training process mentioned above, a negative feedback mechanism [1, 2] naturally exists to dynamically control the instance complexity and network complexity. As shown in Figure 2, when an instance is sent to the network and produces a large cross-entropy loss , it is considered as a complex instance and the penalty weight is reduced to induce a complex sub-network. On account of the powerful representation capability of the complex network, the cross-entropy loss of the same instance can be easily minimized, and reduce the relative complexity of the instance. If the dynamic network takes a simple instance as input, the dynamic process is just the opposite. This negative feedback mechanism stabilizes the training process, and finally sub-networks with appropriate model capability for making correct prediction are allocated to the input instances.

4.2 Instance Similarity
Besides mapping instances to the complexity space, the similarity between samples is also an effective clue to customize the networks for different instances. Inspired by the manifold regularization [51, 61], we expect that the instance similarity can be well preserved by their corresponding sub-networks, \ie, if two instances are similar, the allocated sub-networks for them tend to own similar property as well.
The intermediate features produced by a deep neural network can be treated as an effective representation of input sample . Compared to the original data, ground-truth information is embedded to the intermediate features during training, and hence the intermediate features are more suitable to measure the similarity between different samples. The sub-network for instance can be described by the channel saliencies, which determine the architecture of the network. Note that both the channel saliencies and intermediate features are corresponding to each layer, and thus we can calculate the similarity matrix of channel saliencies and similarity matrix of features layer-by-layer, where the element () in the matrix reflect the similarity between saliencies (features) derived from different sample and . Suppose that the classical cosine similarity [38] is adopted, is calculated as:
| (8) |
where denotes -norm. For intermediate feature in the -the layer, it is first flattened to a vector using the average pooling operation , and then the similarity matrix is:
| (9) |
Given the similarity matrices and mentioned above, a loss function is developed to impose consistency constraint on them, \ie,
| (10) |
where and denote the input data and network parameters, respectively, and measures the difference between the two similarity matrices. Here we adopt a simple way that compares the corresponding elements of the two matrices, \ie, , where denotes Frobenius norm. In the practical implementation of network training, the similarity matrices are calculated over input data in each mini-batch for efficiency.
Combining the adaptive sparsity loss (Eq. (7)), the final objective function for training the dynamic network is:
| (11) | ||||
where is a weight coefficient for the consistency loss . In Eq. (11), the manifold information is simultaneously excavated from two complementary perspectives, \ie, complexity and similarity. The former imposes the consistency between instances complexity and sub-networks complexity, while the latter induces instances with similar features to select similar sub-networks. Though different perspectives are emphasized, both loss functions describe intrinsic relationships between instances and networks, and can be simultaneously optimized to get an optimal solution.
Based on the channel saliencies of each layer, the dynamic pruning is applied to the given network for different input data separately. Given different input examples , the average channel saliencies over different instance are first calculated as , where is the number of channels in the -th layer. Then the elements in is sorted so that and the threshold is set as , where is the pre-defined pruning rate and denotes round-off. At inference, only channels with saliencies larger than the threshold need to be calculated and the redundant features are skipped, which reduces the computation and memory cost. Based on the threshold derived from the average saliencies , the actual pruning rate are different for each instances, since the channel saliency depends on the input and variant numbers of elements are larger than the threshold . A series of sub-networks with various computational cost are obtained, which are intuitively visualized in Figure 8 of Section 5.3.
| Model | Method | Dynamic | Top-1 Error (%) | Top-5 Error (%) | Top-1 Gap (%) | Top-5 Gap (%) | FLOPs (%) |
|---|---|---|---|---|---|---|---|
| ResNet-18 | Baseline | - | 30.24 | 10.92 | 0.0 | 0.0 | 0.0 |
| MIL [6] | ✗ | 33.67 | 13.06 | 3.43 | 2.14 | 33.3 | |
| SFP [16] | ✗ | 32.90 | 12.22 | 2.66 | 1.30 | 41.8 | |
| FPGM [17] | ✗ | 31.59 | 11.52 | 1.35 | 0.60 | 41.8 | |
| PFP [27] | ✗ | 34.35 | 13.25 | 4.11 | 2.33 | 43.1 | |
| DSA [39] | ✗ | 31.39 | 11.65 | 1.15 | 0.73 | 40.0 | |
| LCCN [6] | ✓ | 33.67 | 13.06 | 3.43 | 2.14 | 34.6 | |
| CGNet [20] | ✓ | 31.70 | - | 1.46 | - | 50.7 | |
| FBS [9] | ✓ | 31.83 | 11.78 | 1.59 | 0.86 | 49.5 | |
| ManiDP-A | ✓ | 31.12 | 11.24 | 0.88 | 0.32 | 51.0 | |
| ManiDP-B | ✓ | 31.65 | 11.71 | 1.41 | 0.79 | 55.1 | |
| ResNet-34 | Baseline | - | 26.69 | 8.58 | 0.0 | 0.0 | 0.0 |
| SFP [16] | ✗ | 28.17 | 9.67 | 1.48 | 1.09 | 41.1 | |
| FPGM [17] | ✗ | 27.46 | 8.87 | 0.07 | 0.29 | 41.1 | |
| Taylor [37] | ✗ | 27.17 | - | 0.48 | - | 24.2 | |
| DMC [8] | ✗ | 27.43 | 8.89 | 0.74 | 0.31 | 43.4 | |
| LCCN [6] | ✓ | 27.01 | 8.81 | 0.32 | 0.23 | 24.8 | |
| CGNet [20] | ✓ | 28.70 | - | 2.01 | - | 50.4 | |
| FBS [9] | ✓ | 28.34 | 9.87 | 1.85 | 1.29 | 51.2 | |
| ManiDP-A | ✓ | 26.70 | 8.58 | 0.01 | 0.0 | 46.8 | |
| ManiDP-B | ✓ | 27.26 | 8.96 | 0.57 | 0.38 | 55.3 |
| Model | Method | Dynamic | Top-1 Error (%) | Top-5 Error (%) | Top-1 Gap (%) | Top-5 Gap (%) | FLOPs (%) |
|---|---|---|---|---|---|---|---|
| MobileNetV2 | Baseline | - | 28.20 | 9.57 | 0.0 | 0.0 | 0.0 |
| ThiNet [36] | ✗ | 36.25 | 14.59 | 8.05 | 5.02 | 44.7 | |
| DCP [62] | ✗ | 35.78 | - | 7.58 | - | 44.7 | |
| MetaP [34] | ✗ | 28.80 | - | 0.60 | - | 27.7 | |
| DMC [8] | ✗ | 31.63 | 11.54 | 3.43 | 1.97 | 46.0 | |
| FBS [9] | ✓ | 29.07 | 9.91 | 0.87 | 0.34 | 33.6 | |
| ManiDP-A | ✓ | 28.58 | 9.72 | 0.38 | 0.15 | 37.2 | |
| ManiDP-B | ✓ | 30.38 | 10.55 | 2.18 | 0.98 | 51.2 |
5 Experiments
In this section, the proposed dynamic pruning method based manifold regularization (ManiDP) is empirically investigated on image classification datasets CIFAR-10 [22] and ImageNet (LSVRC-2012) [5]. CIFAR-10 contains 60k 3232 colored images from 10 categories, where 50k images are used as the training set and 10k for testing. The large-scale ImageNet (LSVRC-2012) dataset composes of 1.28M training images and 50k validation images, which are collected from 1k categories. Prevalent ResNet [15] models with different depths and light-weight MobilenetV2 [45] are used to verify the effectiveness of the proposed method.
Implementation Details. For a fair comparison, the pruning rates for all layers in the network are the same following [9]. In the training phase, we increase the pruning rate from 0 to an appointed value to gradually make the pre-trained networks sparse. The coefficient regulating the weights of sparsity loss is set to 0.005 for CIFAR-10 and 0.03 for ImageNet, empirically. The coefficient for the similarity loss is set to 10 for both two datasets. All the networks are trained using the stochastic gradient descent(SGD) with momentum 0.9. For CIFAR-10, the initial learning rate, batch-size and training epochs are set to 0.2, 128 and 300, respectively, while they are 0.25, 1024 and 120 for ImageNet. Standard data augmentation strategies containing random crop and horizontal flipping are used. For CIFAR-10, the images are padded to size 4040 and then cropped to size 3232. For ImageNet, images with resolution are sent to the networks. All the experiments are conducted with PyTorch [41] on NVIDIA V100 GPUs.
5.1 Comparison on ImageNet
The proposed method is compared with state-of-the-art network pruning algorithms on the large-scale ImageNet dataset. The pruning results of ResNet and MobileNetV2 are shown in Table 1 and Table 2, respectively, where the top-1/top-5 errors of the pruned networks and the reduction ratios of FLOPs are reported. For dynamic pruning methods, the average FLOPs of the sub-networks over the whole test dataset are calculated as computational cost.
For ResNet in Table 1, ‘ManiDP-A’ and ‘ManiDP-B’ denote two pruned networks with different pruning rates, respectively. The competing methods include both SOTA static channel pruning method developed recently ([16, 17, 39, 25, 26]) and the pioneering dynamic methods ([9, 6, 20]), indicated by ✗ and ✓ in the table. Our method can reduce substantial computational cost for a given network with negligible performance degradation. For example, the proposed ‘ManiDP-A’ can reduce 46.8% FLOPs ResNet-34 with only 0.01% performance degradation. Compared with the SOTA pruning algorithms, our method obtains pruned networks with less computational cost but lower test errors. The static methods are obviously inferior to ours, \eg, the SOTA method DSA [39] only reduces 40.0% FLOPs and obtain a pruned network with 31.39% top-1 error (ResNet-18), while the proposed ‘ManiDP-A’ can achieve lower test error (31.12%) with more FLOPs reduced (51.0%). Our method also shows superiority to the existing dynamic pruning methods, \eg, FBS [9] achieves 31.83% top-1 error with 49.5% FLOPs pruned, which is worse than our method. We can infer that the proposed ManiDP method can excavate the redundancy of networks adequately to get compact but powerful networks with high performance.
| Model | Method | Theoretical | Realistic |
| Acl. (%) | Acl. (%) | ||
| ResNet-18 | ManiDP-A | 51.0 | 35.4 |
| ManiDP-B | 55.6 | 40.5 | |
| ResNet-34 | ManiDP-A | 46.8 | 32.0 |
| ManiDP-B | 55.3 | 37.4 | |
| MobileNetV2 | ManiDP-A | 37.2 | 30.4 |
| ManiDP-B | 51.2 | 38.5 |
To validate the effectiveness of the proposed ManiDP method on light-weight networks, we further compare it with SOTA methods on the efficient MobileNetV2 [45] designed for resource-limited devices, and the results are shown in Table 2. Our method also achieves a better trade-off between network accuracy and computational cost than the existing methods. For examples, the proposed ‘ManiDP-A’ reduces 37.2% FLOPs of MobileNetV2 with only 0.38% accuracy loss, while the pruned network obtained by the competing method FBS [9] sacrifices 0.87% accuracy for pruning 33.6% FLOPs. The results show that even light-weight networks are over parameterized when exploring redundancy for each instances separately, which can be further accelerated by the proposed method and deployed on edge devices.
The realistic accelerations of the pruned Networks on ImageNet are shown in Table 3, which is calculated by counting the average inference time for handling each image on CPUs. The realistic acceleration is slightly less than the theoretical acceleration calculated by FLOPs, which is due to practical factors such as I/O operations (\eg, accessing weights of networks), BLAS libraries and buffer switch, whose impact can be further reduced by practical engineering optimization.
| Depth | Method | Dynamic | Error (%) | FLOPs (%) |
|---|---|---|---|---|
| 20 | Baseline | - | 7.78 | 0.0 |
| SFP[16] | ✗ | 9.17 | 42.2 | |
| FPGM [17] | ✗ | 9.56 | 54.0 | |
| DSA [39] | ✗ | 8.62 | 50.3 | |
| Hinge [25] | ✗ | 8.16 | 45.5 | |
| DHP [26] | ✗ | 8.46 | 51.8 | |
| FBS [9] | ✓ | 9.03 | 53.1 | |
| ManiDP | ✓ | 7.95 | 54.2 | |
| 32 | Baseline | - | 7.34 | 0.0 |
| MIL[6] | ✗ | 9.26 | 31.2 | |
| SFP [16] | ✗ | 7.92 | 41.5 | |
| FPGM [17] | ✗ | 8.07 | 53.2 | |
| FBS [9] | ✓ | 8.02 | 55.7 | |
| ManiDP | ✓ | 7.85 | 63.2 | |
| 56 | Baseline | - | 6.30 | 0.0 |
| SFP [16] | ✗ | 7.74 | 52.6 | |
| FPGM [17] | ✗ | 6.51 | 52.6 | |
| HRank [28] | ✗ | 6.83 | 50.0 | |
| DSA [39] | ✗ | 7.09 | 52.2 | |
| Hinge [25] | ✗ | 6.31 | 50.0 | |
| DHP [26] | ✗ | 6.42 | 50.9 | |
| FBS [9] | ✓ | 6.48 | 53.6 | |
| ManiDP | ✓ | 6.36 | 62.4 |
| Model | Complexity | Similarity | Error / Gap (%) |
|---|---|---|---|
| ✗ | ✗ | 6.88 / 0.58 | |
| ResNet-56 | ✓ | ✗ | 6.61 / 0.31 |
| (CIFAR-10) | ✗ | ✓ | 6.53 / 0.23 |
| ✓ | ✓ | 6.36 / 0.06 | |
| ✗ | ✗ | 28.12 / 1.43 | |
| ResNet-34 | ✓ | ✗ | 27.67 / 0.98 |
| (ImageNet) | ✗ | ✓ | 27.63 / 0.94 |
| ✓ | ✓ | 27.29 / 0.57 |
5.2 Comparison on CIFAR-10
On the benchmark CIFAR-10 dataset, the comparison between the proposed ManiDP and SOTA channel pruning methods are shown in Table 4. Compared with SOTA methods, a significantly higher FLOPs reduction is achieved by our method with less degradation of performance. For example, using our method, more than 60% FLOPs of the ResNet-56 model are reduced while the test error can still achieve 6.36% using ManiDP. Compared to the static methods (\eg, HRank [28] with 6.83% error and 50.0% FLOPs reduction) and dynamic method (\eg, FBS [9] with 6.48% error and 53.6% FLOPs reduction), our method shows notable superiority.
5.3 Ablation Studies
Effectiveness of Manifold Information. To maximally excavate network redundancy corresponding to each instance, the manifold information between instances is explored from two perspectives, \ie, complexity and similarity. The impacts of whether exploiting complexity or similarity relationship is empirically investigated in Table 5, indicated by ✓ and ✗. The classification error and the performance gap compared to the base models are reported. Without utilizing the complexity relationship means fixing the trade-off coefficient between lasso loss and cross-entropy loss, which obviously increases the error incurred by pruning (\eg, 1.43% \vs0.94% on ImageNet). The unsatisfactory performance is due to the improper alignment, \ie, cumbersome sub-networks may be assigned to simple examples, while complex instances are handled by tiny sub-networks with limited representation capability. For the similarity relationship, deactivating it (setting coefficient for similarity loss to zero) incurs larger performance degradation (\eg, 1.43% \vs0.98%), which validates the effectiveness of exploring the similarity between features of instances and the corrsponding sub-networks. Thus, exploiting both the two perspectives of manifold information is necessary to achieve negligible performance degradation (\ie, only 0.57% error increase on ImageNet).

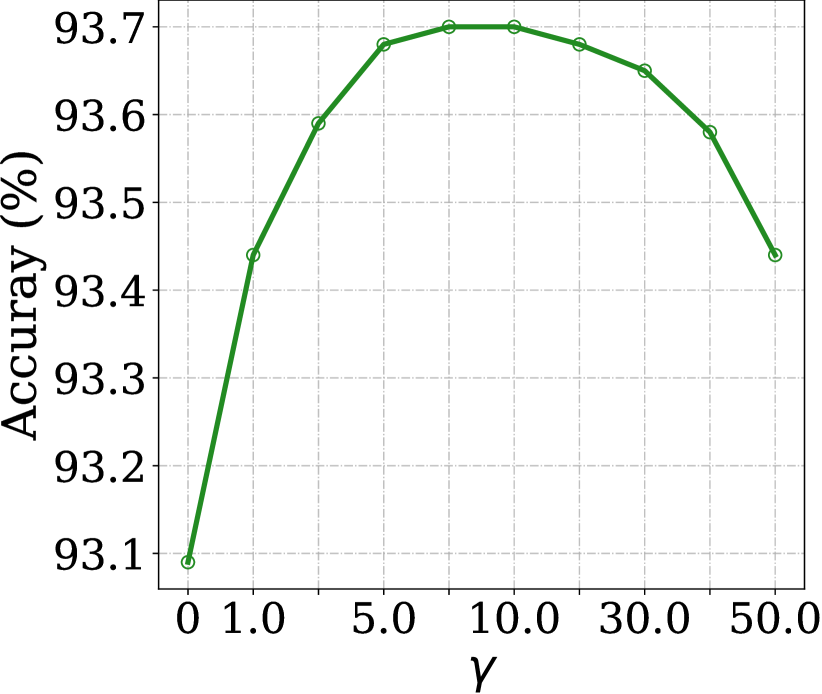
Weight coefficients and . The weights of sparsity loss and similarity loss are controlled by coefficients (Eq. (4)) and (Eq. 11), whose impact on the final test accuracies is shown in Figure 3. A larger induces more sparsity on channel saliencies, which will have less impact on the network outputs when discarding channels with small saliencies. On the other hand, the sparsity will affect the representation ability of networks and incur accuracy drop (Figure 3 (a)). Analogous phenomenon exists when varying coefficient for similarity loss. The test accuracy of the pruned network is improved when increasing unless it is set to an extremely large value, as the similarity between different instances is excavated more adequately. Note that our method is robust to both hyper-parameters and works well in a wide range (\eg, range [0.001,0.01] for and values around 10.0 for ), empirically.
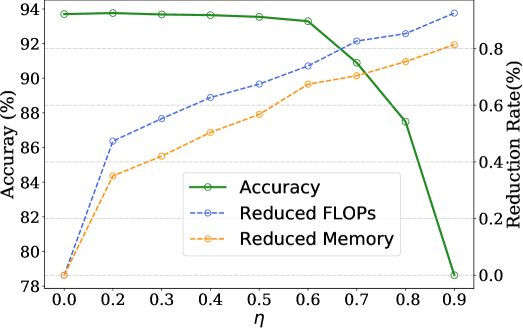
Memory/FLOPs and accuracies \wrtPruning Rate. The impact of different pruning rate is shown in Figure 4. When a single instance is sent to the network, the memory cost for accessing network weights can be reduced as ineffective weights do not participate the inference process. With a large reduction of computational cost and memory, the pruned network can still achieve a high performance. For example, when setting the pruning rare to 0.6% with 73.87% FlOPs and 67.42% memory reduction, the pruned ResNet-56 can still achieve an accuracy of 93.29% (only 0.41% accuracy drop compared to the original network).
Visualization. Different sub-networks with various computational costs (\ie, FLOPs) are generated for each instance by pruning different channels. Using ResNet-34 as the backbone, the FLOPs distribution of different sub-networks over the validation set of ImageNet are shown in Figure 8, where -axis denotes FLOPs and the -axis is the number of sub-networks. The FLOPs of sub-networks varies in a certain range \wrtthe complexity of instances. Most of the sub-networks own medium sizes and a small quantity of sub-networks activate more/less channels to handle harder/simpler instances. Some representative images handled by the corresponding sub-networks are also shown in the figure. Intuitively, a simple example (\eg, ‘bird’ and ‘dog’ in the red frames) that can be correctly predicted by a compact network usually contains clear targets, while images with obscure semantic information (\eg, too large ‘orange’ and too small ‘flower’ in the blue frames) require larger networks with more powerful representation ability. More visualization results are shown in the supplementary material.

6 Conclusion
This paper proposes a manifold regularized dynamic pruning method (ManiDP) to maximally excavate the redundancy of neural networks. We explore the manifold information in the sample space to discover the relationship between different instances from two perspectives, \ie, complexity and similarity, and then the relationship is preserved in the corresponding sub-networks. An adaptive penalty weight for network sparsity is developed to align the instance complexity and network complexity, while the similarity relationship is preserved by matching the similarity matrices. Extensive experiments are conducted on several benchmarks to verify the effectiveness of our method. Compared with the state-of-the-art methods, the pruned networks obtained by the proposed ManiDP can achieve better performance with less computational cost. For example, our method can reduce 55.3% FLOPs of ResNet-34 with only 0.57% top-1 accuracy degradation on ImageNet.
Acknowledgment. This work is supported by National Natural Science Foundation of China under Grant No. 61876007, and Australian Research Council under Project DE180101438 and DP210101859.
References
- [1] Oreste Acuto, Vincenzo Di Bartolo, and Frédérique Michel. Tailoring t-cell receptor signals by proximal negative feedback mechanisms. Nature Reviews Immunology, 8(9):699–712, 2008.
- [2] Eulalia Belloc and Raúl Méndez. A deadenylation negative feedback mechanism governs meiotic metaphase arrest. Nature, 452(7190):1017–1021, 2008.
- [3] Hanting Chen, Yunhe Wang, Han Shu, Yehui Tang, Chunjing Xu, Boxin Shi, Chao Xu, Qi Tian, and Chang Xu. Frequency domain compact 3d convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1641–1650, 2020.
- [4] Hanting Chen, Yunhe Wang, Chang Xu, Chao Xu, and Dacheng Tao. Learning student networks via feature embedding. IEEE Transactions on Neural Networks and Learning Systems, 2020.
- [5] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255. Ieee, 2009.
- [6] Xuanyi Dong, Junshi Huang, Yi Yang, and Shuicheng Yan. More is less: A more complicated network with less inference complexity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5840–5848, 2017.
- [7] Christoph Feichtenhofer, Axel Pinz, and Richard P Wildes. Spatiotemporal multiplier networks for video action recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4768–4777, 2017.
- [8] Shangqian Gao, Feihu Huang, Jian Pei, and Heng Huang. Discrete model compression with resource constraint for deep neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1899–1908, 2020.
- [9] Xitong Gao, Yiren Zhao, Lukasz Dudziak, Robert Mullins, and Cheng-zhong Xu. Dynamic channel pruning: Feature boosting and suppression. In International Conference on Learning Representations, 2018.
- [10] Ross Girshick. Fast r-cnn. In Proceedings of the IEEE international conference on computer vision, pages 1440–1448, 2015.
- [11] Jianyuan Guo, Kai Han, Yunhe Wang, Chao Zhang, Zhaohui Yang, Han Wu, Xinghao Chen, and Chang Xu. Hit-detector: Hierarchical trinity architecture search for object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11405–11414, 2020.
- [12] Jianyuan Guo, Yuhui Yuan, Lang Huang, Chao Zhang, Jin-Ge Yao, and Kai Han. Beyond human parts: Dual part-aligned representations for person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 3642–3651, 2019.
- [13] Kai Han, Yunhe Wang, Qi Tian, Jianyuan Guo, Chunjing Xu, and Chang Xu. Ghostnet: More features from cheap operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1580–1589, 2020.
- [14] Kai Han, Yunhe Wang, Yixing Xu, Chunjing Xu, Enhua Wu, and Chang Xu. Training binary neural networks through learning with noisy supervision. In International Conference on Machine Learning, pages 4017–4026. PMLR, 2020.
- [15] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- [16] Yang He, Guoliang Kang, Xuanyi Dong, Yanwei Fu, and Yi Yang. Soft filter pruning for accelerating deep convolutional neural networks. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pages 2234–2240, 2018.
- [17] Yang He, Ping Liu, Ziwei Wang, Zhilan Hu, and Yi Yang. Filter pruning via geometric median for deep convolutional neural networks acceleration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4340–4349, 2019.
- [18] Yihui He, Xiangyu Zhang, and Jian Sun. Channel pruning for accelerating very deep neural networks. In Proceedings of the IEEE International Conference on Computer Vision, pages 1389–1397, 2017.
- [19] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2015.
- [20] Weizhe Hua, Yuan Zhou, Christopher M De Sa, Zhiru Zhang, and G Edward Suh. Channel gating neural networks. In Advances in Neural Information Processing Systems, pages 1886–1896, 2019.
- [21] Lai Jiang, Mai Xu, Tie Liu, Minglang Qiao, and Zulin Wang. Deepvs: A deep learning based video saliency prediction approach. In Proceedings of the european conference on computer vision (eccv), pages 602–617, 2018.
- [22] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- [23] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. Communications of the ACM, 60(6):84–90, 2017.
- [24] Vadim Lebedev, Yaroslav Ganin, Maksim Rakhuba, Ivan Oseledets, and Victor Lempitsky. Speeding-up convolutional neural networks using fine-tuned cp-decomposition. arXiv preprint arXiv:1412.6553, 2014.
- [25] Yawei Li, Shuhang Gu, Christoph Mayer, Luc Van Gool, and Radu Timofte. Group sparsity: The hinge between filter pruning and decomposition for network compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8018–8027, 2020.
- [26] Yawei Li, Shuhang Gu, Kai Zhang, Luc Van Gool, and Radu Timofte. Dhp: Differentiable meta pruning via hypernetworks. 2020.
- [27] Lucas Liebenwein, Cenk Baykal, Harry Lang, Dan Feldman, and Daniela Rus. Provable filter pruning for efficient neural networks. In International Conference on Learning Representations, 2020.
- [28] Mingbao Lin, Rongrong Ji, Yan Wang, Yichen Zhang, Baochang Zhang, Yonghong Tian, and Ling Shao. Hrank: Filter pruning using high-rank feature map. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1529–1538, 2020.
- [29] Shaohui Lin, Rongrong Ji, Chao Chen, Dacheng Tao, and Jiebo Luo. Holistic cnn compression via low-rank decomposition with knowledge transfer. IEEE transactions on pattern analysis and machine intelligence, 41(12):2889–2905, 2018.
- [30] Shaohui Lin, Rongrong Ji, Yuchao Li, Yongjian Wu, Feiyue Huang, and Baochang Zhang. Accelerating convolutional networks via global & dynamic filter pruning. In IJCAI, pages 2425–2432, 2018.
- [31] Shaohui Lin, Rongrong Ji, Chenqian Yan, Baochang Zhang, Liujuan Cao, Qixiang Ye, Feiyue Huang, and David Doermann. Towards optimal structured cnn pruning via generative adversarial learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2790–2799, 2019.
- [32] Chuanjian Liu, Yunhe Wang, Kai Han, Chunjing Xu, and Chang Xu. Learning instance-wise sparsity for accelerating deep models. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pages 3001–3007, 7 2019.
- [33] Zhuang Liu, Jianguo Li, Zhiqiang Shen, Gao Huang, Shoumeng Yan, and Changshui Zhang. Learning efficient convolutional networks through network slimming. In Proceedings of the IEEE International Conference on Computer Vision, pages 2736–2744, 2017.
- [34] Zechun Liu, Haoyuan Mu, Xiangyu Zhang, Zichao Guo, Xin Yang, Kwang-Ting Cheng, and Jian Sun. Metapruning: Meta learning for automatic neural network channel pruning. In Proceedings of the IEEE International Conference on Computer Vision, pages 3296–3305, 2019.
- [35] Yongxi Lu, Abhishek Kumar, Shuangfei Zhai, Yu Cheng, Tara Javidi, and Rogerio Feris. Fully-adaptive feature sharing in multi-task networks with applications in person attribute classification. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 5334–5343, 2017.
- [36] Jian-Hao Luo, Hao Zhang, Hong-Yu Zhou, Chen-Wei Xie, Jianxin Wu, and Weiyao Lin. Thinet: pruning cnn filters for a thinner net. IEEE transactions on pattern analysis and machine intelligence, 41(10):2525–2538, 2018.
- [37] Pavlo Molchanov, Arun Mallya, Stephen Tyree, Iuri Frosio, and Jan Kautz. Importance estimation for neural network pruning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 11264–11272, 2019.
- [38] Hieu V Nguyen and Li Bai. Cosine similarity metric learning for face verification. In Asian conference on computer vision, pages 709–720. Springer, 2010.
- [39] Xuefei Ning, Tianchen Zhao, Wenshuo Li, Peng Lei, Yu Wang, and Huazhong Yang. Dsa: More efficient budgeted pruning via differentiable sparsity allocation. In Proceedings of the European conference on computer vision, 2020.
- [40] Wonpyo Park, Dongju Kim, Yan Lu, and Minsu Cho. Relational knowledge distillation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3967–3976, 2019.
- [41] Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. Automatic differentiation in pytorch. 2017.
- [42] Yongming Rao, Jiwen Lu, Ji Lin, and Jie Zhou. Runtime network routing for efficient image classification. IEEE transactions on pattern analysis and machine intelligence, 41(10):2291–2304, 2018.
- [43] Mohammad Rastegari, Vicente Ordonez, Joseph Redmon, and Ali Farhadi. Xnor-net: Imagenet classification using binary convolutional neural networks. In European conference on computer vision, pages 525–542. Springer, 2016.
- [44] Joseph Redmon, Santosh Divvala, Ross Girshick, and Ali Farhadi. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 779–788, 2016.
- [45] Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, and Liang-Chieh Chen. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4510–4520, 2018.
- [46] Pravendra Singh, Vinay Kumar Verma, Piyush Rai, and Vinay Namboodiri. Leveraging filter correlations for deep model compression. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pages 835–844, 2020.
- [47] Xiu Su, Shan You, Tao Huang, Fei Wang, Chen Qian, Changshui Zhang, and Chang Xu. Locally free weight sharing for network width search. arXiv preprint arXiv:2102.05258, 2021.
- [48] Yehui Tang, Yunhe Wang, Yixing Xu, Hanting Chen, Boxin Shi, Chao Xu, Chunjing Xu, Qi Tian, and Chang Xu. A semi-supervised assessor of neural architectures. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1810–1819, 2020.
- [49] Yehui Tang, Yunhe Wang, Yixing Xu, Dacheng Tao, Chunjing Xu, Chao Xu, and Chang Xu. Scop: Scientific control for reliable neural network pruning. arXiv preprint arXiv:2010.10732, 2020.
- [50] Yehui Tang, Shan You, Chang Xu, Jin Han, Chen Qian, Boxin Shi, Chao Xu, and Changshui Zhang. Reborn filters: Pruning convolutional neural networks with limited data. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 5972–5980, 2020.
- [51] Jing Wang, Zhenyue Zhang, and Hongyuan Zha. Adaptive manifold learning. Advances in neural information processing systems, 17:1473–1480, 2004.
- [52] Wei Wen, Chunpeng Wu, Yandan Wang, Yiran Chen, and Hai Li. Learning structured sparsity in deep neural networks. In Advances in neural information processing systems, pages 2074–2082, 2016.
- [53] Jiaxiang Wu, Cong Leng, Yuhang Wang, Qinghao Hu, and Jian Cheng. Quantized convolutional neural networks for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4820–4828, 2016.
- [54] Yixing Xu, Yunhe Wang, Hanting Chen, Kai Han, Chunjing Xu, Dacheng Tao, and Chang Xu. Positive-unlabeled compression on the cloud. arXiv preprint arXiv:1909.09757, 2019.
- [55] Yixing Xu, Chang Xu, Xinghao Chen, Wei Zhang, Chunjing Xu, and Yunhe Wang. Kernel based progressive distillation for adder neural networks. arXiv preprint arXiv:2009.13044, 2020.
- [56] Zhaohui Yang, Yunhe Wang, Xinghao Chen, Boxin Shi, Chao Xu, Chunjing Xu, Qi Tian, and Chang Xu. Cars: Continuous evolution for efficient neural architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1829–1838, 2020.
- [57] Zhaohui Yang, Yunhe Wang, Kai Han, Chunjing Xu, Chao Xu, Dacheng Tao, and Chang Xu. Searching for low-bit weights in quantized neural networks. arXiv preprint arXiv:2009.08695, 2020.
- [58] Haoran You, Xiaohan Chen, Yongan Zhang, Chaojian Li, Sicheng Li, Zihao Liu, Zhangyang Wang, and Yingyan Lin. Shiftaddnet: A hardware-inspired deep network. arXiv preprint arXiv:2010.12785, 2020.
- [59] Shan You, Tao Huang, Mingmin Yang, Fei Wang, Chen Qian, and Changshui Zhang. Greedynas: Towards fast one-shot nas with greedy supernet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1999–2008, 2020.
- [60] Shan You, Chang Xu, Chao Xu, and Dacheng Tao. Learning from multiple teacher networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 1285–1294, 2017.
- [61] Bo Zhu, Jeremiah Z Liu, Stephen F Cauley, Bruce R Rosen, and Matthew S Rosen. Image reconstruction by domain-transform manifold learning. Nature, 555(7697):487–492, 2018.
- [62] Zhuangwei Zhuang, Mingkui Tan, Bohan Zhuang, Jing Liu, Yong Guo, Qingyao Wu, Junzhou Huang, and Jinhui Zhu. Discrimination-aware channel pruning for deep neural networks. In Advances in Neural Information Processing Systems, pages 875–886, 2018.

7 Supplementary Material
7.1 Coefficient for different instances
In the training procedure, the coefficient (Eq. (6) of the main paper) controls the weight of sparsity loss according to the complexity of each instance. Recall that , where is a fixed hyper-parameter for all instances. Using ResNet-56 as the backbone, the variable parts for complex/simple examples in CIFAR-10 are shown in Figure 6. keeps small for complex examples (\eg, the vague ‘ship’ in (a)) and then less channels of the pre-defined networks are pruned for keeping their representation capabilities. When sending simple examples (\eg, clear ‘airplane’ in (b)) to the dynamic network, keeps large in most of the epochs, and thus the corresponding sub-network becomes sparser continuously as the numbers of iteration increases. Note that changes dynamically in the training process. For example, the sparsity weight automatically decreases in the last few epochs as the corresponding sub-network is compact enough and should pay more attention to accuracy (Figure 6 (b)), which ensures that the models can fit input instances well.

7.2 Similarity Matrices
The similarity matrices for intermediate features and for channel saliencies are shown in Figure 7, where different colors denote the degree of similarity (\ie, a yellower point means higher degree of similarity between two instances). The ResNet-56 model trained with/without the similarity loss (Eq. (10) in the main paper) is used to generate features and channel saliencies for calculating the similarity between instances randomly sampled from CIFAR-10. When training dynamic network without similarity loss , the similarity calculated by features and that by channel saliencies are very different (Figure 7 (a), (b)). When using similarity loss (Figure 7 (c), (d)), the similarity matrices and are more analogous as the similarity loss penalizes the inconsistency between similarity matrices to align the similarity relationship in the two spaces.
7.3 Visualization of instances with different complexity
We sample representative images with different complexity from ImageNet and intuitively show them in Figure 8. From top to bottom, the computational costs of sub-networks used to predict labels continue to increase. Intuitively, simple instances that can be accurately predicted by compacted networks usually contain clear targets, while the semantic information in complex images are vague and thus requires larger networks with powerful representation capability.
