Magnetocaloric effect and its electric-field regulation in CrI₃/metal heterostructure

Weiwei He State Key Laboratory of Mechanics and Control for Aerospace Structures & Key Lab for Intelligent Nano Materials and Devices of Ministry of Education & Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 210016, China Ziming Tang State Key Laboratory of Mechanics and Control for Aerospace Structures & Key Lab for Intelligent Nano Materials and Devices of Ministry of Education & Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 210016, China Qihua Gong State Key Laboratory of Mechanics and Control for Aerospace Structures & Key Lab for Intelligent Nano Materials and Devices of Ministry of Education & Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 210016, China [email protected] Min Yi State Key Laboratory of Mechanics and Control for Aerospace Structures & Key Lab for Intelligent Nano Materials and Devices of Ministry of Education & Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 210016, China [email protected] Wanlin Guo State Key Laboratory of Mechanics and Control for Aerospace Structures & Key Lab for Intelligent Nano Materials and Devices of Ministry of Education & Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 210016, China

Abstract

The extraordinary properties of a heterostructure by stacking atom-thick van der Waals (vdW) magnets have been extensively studied. However, the magnetocaloric effect (MCE) of heterostructures that are based on monolayer magnets remains to be explored. Herein, we deliberate MCE of vdW heterostructure composed of a monolayer CrI₃ and metal atomic layers (Ag, Hf, Au, and Pb). It is revealed that heterostructure engineering by introducing metal substrate can improve MCE of CrI₃, particularly boosting relative cooling power to 471.72 µJ m^-2 and adiabatic temperature change to 2.1 K at 5 T for CrI₃/Hf. This improved MCE is ascribed to the enhancement of magnetic moment and intralayer exchange coupling in CrI₃ due to the CrI₃/metal heterointerface induced charge transfer. Electric field is further found to tune MCE of CrI₃ in heterostructures and could shift the peak temperature by around 10 K in CrI₃/Hf, thus manipulating the working temperature window of MCE. The discovered electric-field and substrate regulated MCE in CrI₃/metal heterostructure opens new avenues for low-dimensional magnetic refrigeration.

\altaffiliation

Authors contributed equally. \altaffiliationAuthors contributed equally. \alsoaffiliationMIIT Key Laboratory of Aerospace Information Materials and Physics & College of Physics, Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing 211106, China \abbreviationsIR,NMR,UV

Keywords: Magnetocaloric effect, Heterostructure, Monolayer magnets, Metal substrate, Electric field

1 1. INTRODUCTION

Magnetic cooling based on magnetocaloric effect (MCE) has emerged as a promising alternative to gaseous cooling with its ever-increasing energy consumption and greenhouse gas emissions ^{1, 2, 3, 4}. As the inherited characteristics of magnetic materials, MCE is closely related to the magnetic properties and magnetization behavior under a magnetic field. The unpaired spins in magnetic materials are aligned when a magnetic field is applied, leading to a decrease in magnetic entropy and subsequent release of heat into the surroundings. Using MCE, it is possible to achieve target temperatures ranging from ultra-low to room temperature ^{5, 6}. Up to date, the majority of literature on MCE has focused on bulk magnetocaloric materials ^{7, 8, 9, 10} or thin films with nanometers to micrometers thickness ^{11, 12, 13}, restricting the application of magnetic refrigeration in compact and miniaturized nanodevices.

In recent years, two-dimensional (2D) van der Waals (vdW) magnets with a wide variety of unconventional properties, which differ from their bulk counterparts ^{14, 15, 16, 17, 18, 19}, have drawn immense interest in fundamental research and device applications ^{20, 21, 22, 23, 24}. Layered vdW magnets are bonded to each other through weak vdW forces, allowing the easy separation of monolayers. For instance, in the monolayer CrI₃ that is fabricated by micromechanical exfoliation of bulk CrI₃ crystals, the magnetic anisotropy cancels out the thermal fluctuations at finite temperatures and the long-range magnetic order remains ¹⁴. Therefore, the spontaneous magnetization in 2D magnets offers new perspectives for exploring MCE down to the monolayer limit.

The application and characterization of monolayer CrI₃ usually requires that it be stacked on top of a substrate rather than isolated ^{25, 26, 27}. Thus, vdW magnetic heterostructures with intrinsic magnetism and excellent stacking capability have attracted extensive research ^{28, 29, 30, 31, 32, 33}. Diverse combination of heterostructures formed by CrI₃ is an effective approach toward achieving novel properties, such as thermal spin-filtering effect ³⁴, quantum anomalous Hall effect ^{35, 36}, half-metallicity ^{37, 38, 39} , and enhanced magnetic properties ^{40, 41, 42}. The effect of various substrates on CrI₃ in terms of MCE, however, remains to be elucidated, which has stimulated our great interests in MCE of CrI₃ in hererostructures.

In the present work, we investigate MCE of CrI₃/metal heterostructure and its electric-field ( $E$ ) control. Four types of metals, i.e., Ag, Hf, Au, and Pb, are chosen to construct the heterostructures with monolayer CrI₃. First-principles calculations indicate that metal substrates significantly enhance the magnetic moment and nearest-neighbor exchange interaction of CrI₃, while they have different roles in magnetocrystalline energy (MAE). Atomistic spin simulations show that Curie temperature ( $T_{\text{C}}$ ) and saturation magnetization of CrI₃ in heterostructures are boosted compared with the free-standing one. In addition, magnetocaloric thermodynamics confirms that heterostructure engineering improves MCE of monolayer CrI₃, which is further enhanced in CrI₃/Hf by applying a negative $E$ . Our work not only demystifies tunable MCE in 2D magnets via substrates and $E$ , but also opens new vistas for low-dimensional magnetically cooling devices.

2 2. RESULTS AND DISCUSSION

2.1 2.1 Magnetic properties and its electric-field tunability

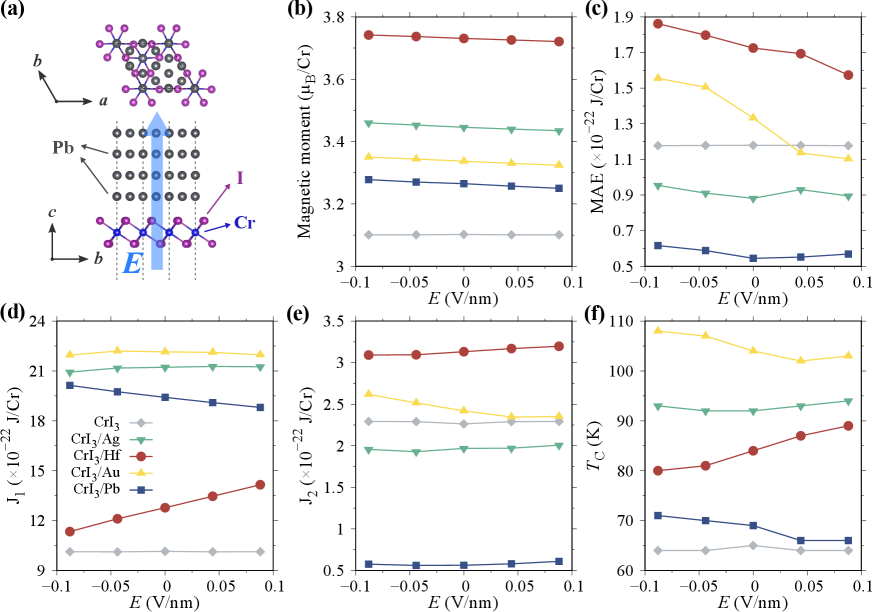
Refer to caption — Figure 1: The atomic structure and magnetic properties of CrI₃ as a function of $E$ in CrI₃/metal vdW heterostructures. (a) Top and side views of CrI₃/Pb(111) heterostructure. Dark grey, purple, and purplish-blue balls represent Pb, I, and Cr atoms, respectively. (b) Magnetic moment per Cr atom, (c) MAE, (d) and (e) magnetic exchange interaction parameters $J_{i}$ , and (f) $T_{\text{C}}$ of CrI₃ in monolayer and CrI₃/metal heterostructures as a function of $E$ .

Due to the interfacial interaction, 2D vdW magnets can change their magnetic properties upon contact with other materials. Based on thermodynamic stability assessment, Yang et al. investigated the magnetic properties of CrI₃ with 3 $d$ transition-metal atoms (from Sc to Zn) absorbed on its surface ⁴³. In our work, four types of metal are selected (e.g., Ag, Hf, Au, Pb) to construct heterostructures with a favorable lattice match. Fig. 1(a) shows the atomic stacking in CrI₃/Pb heterostructure. The other three types of CrI₃/metal (Ag, Au, and Hf) heterostructure are presented in Fig. S1 (Supporting Information). It is noteworthy that CrI₃ in heterostructures has fixed lattice parameters of monolayer CrI₃, allowing the metals to be compressed or stretched within an acceptable strain range around $\pm$ 5%. As illustrated in Fig. 1(a), we are able to investigate $E$ controlled magnetic properties of CrI₃/metal heterostructures with the help of dipole layer method.

Magnetic properties of CrI₃ are affected by metal substrate and $E$ . As shown in Fig. 1(b)-(f), the impact of different metal substrates on CrI₃ are dissimilar. The magnetic moment, $J_{1}$ , and $T_{\text{C}}$ of CrI₃ absorbed upon four kinds of metal layers are increased when compared to those of monolayer CrI₃. In contrast, MAE of CrI₃ is weakened by Ag and Pb substrates, while Au and Hf substrates improve it. The change of $J_{2}$ shows a similar trend. Taking CrI₃/Hf heterostructure as an example, a detail analysis of the influence of metal substrate on the magnetic moment and MAE of CrI₃ is presented. As can be seen from Fig. S2, the introduction of Hf intrigues the redistribution of electrons from spin-down channel to spin-up channel on the CrI₃ side, thereby increasing the magnetic moment of Cr in Fig. 1(b). Considering that I atom (5 $p$ -element) has a much stronger spin-orbit coupling (SOC) effect than Cr (3 $d$ -element) ⁴⁴, $p$ -orbital resolved MAE of I is analyzed in Fig. S3. The enhancement of matrix element differences ( $p_{x}$ , $p_{y}$ ) compensates for the decrease of ( $p_{x}$ , $p_{z}$ ), eventually improving MAE of CrI₃/Hf in Fig. 1(c).

Magnetic performance of CrI₃/metal heterostructures under $E$ exhibit more diverse variations. Fig. 1(b) shows the effect of $E$ on the magnetic moment of Cr . It can be seen that compared to monolayer CrI₃, heterostructures not only achieve an increase in magnetic moment of Cr by promoting spin polarization through charge transfer, but also introduce the strong magneto-electric response that is neglectable in monolayer CrI₃. Under a positive $E$ , the magnetic moment of Cr slightly decreases when the strength of $E$ increases. This could be explained by the charge redistribution that leads to a decrease of net charge in the spin-up channel ^{41, 45}. Fig. S2 further shows the charge difference in CrI₃/Hf heterostructure under different $E$ . MAE of CrI₃ in CrI₃/Hf diminishes with the increasing $E$ , as shown in Fig. 1(c). Similar to the CrI₃/metal heterostructure without $E$ , the synergistic effect of matrix element differences ( $p_{x}$ , $p_{y}$ ) and ( $p_{x}$ , $p_{z}$ ) promotes the response of MAE to $E$ (Fig. S3). Fig. 1(d) and 1(e) reveal the trends of ferromagnetic exchange interaction parameters $J_{1}$ and $J_{2}$ as a function of $E$ . From our calculations, it is evident that when $E$ is increased, $J_{1}$ and $J_{2}$ of CrI₃ in CrI₃/Hf are enhanced, while $J_{1}$ of CrI₃/Pb and $J_{2}$ of CrI₃/Au are decreased. To explain the modulation of $J_{i}$ by $E$ and metal substrate, the energy differences between ferromagnetic (FM) and antiferromagnetic (AFM) states are presented in Fig. S4. Similar trends are also found in Fig. 1(f) : $T_{\text{C}}$ of CrI₃ in CrI₃/Hf increases by about 10 K as $E$ is raised, whereas $T_{\text{C}}$ of CrI₃ adsorbed on Pb and Au decreases by 5 K.

2.2 2.2 Demagnetization behavior of CrI₃ in heterostructures

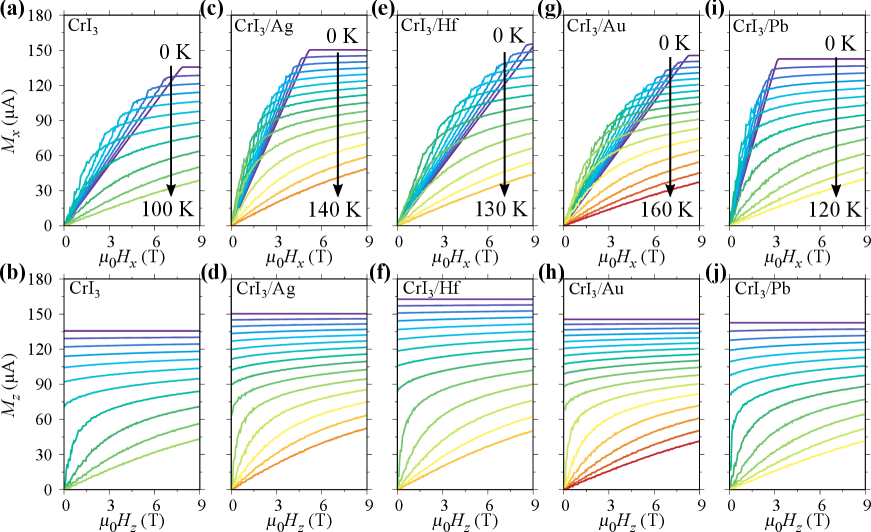
In our previous work ⁴⁶, we found that MCE indeed remains in various 2D magnets and can be remarkably tuned by strain. As a starting point for assessing MCE of CrI₃ in heterostructures, we first examine the demagnetization behavior of CrI₃ at different temperatures. Fig. 2 gives the isothermal magnetization curves in monolayer CrI₃ and heterostructures under in-plane and out-of-plane $H$ . The magnetization vector of Cr atoms turns to the direction of applied field as $H$ increases, and gradually becomes saturated under a high field. Moreover, saturation magnetization decreases with increasing temperature. Meanwhile, saturation magnetization of CrI₃ at 0 K should be proportional to the magnetic moment of Cr atom. Thus, CrI₃/Hf heterostructure at the same temperature is expected to have the highest saturation magnetization according to Fig. 1(b).

Figure 2 also confirms the anisotropy of demagnetization behavior. The out-of-plane magnetic fields saturate magnetization curves much more easily than in-plane ones, owing to the out-of-plane MAE in Fig. 1(c). This anisotropic phenomenon has been explained at length in bulk CrI₃ ^{47, 48}, and conclusions are also applicable to monolayers. When compared to monolayer CrI₃, the magnetization curves of CrI₃ in CrI₃/Ag and CrI₃/Pb heterostructures tend to saturation at lower fields (Fig. 2(c) and(i)), while those of CrI₃ in CrI₃/Hf and CrI₃/Au heterostructures remain unsaturated under $H$ up to 8 T (Fig. 2(e) and(d)). This is related to different effects of metal substrate on MAE of CrI₃, which is similar to the trend in Fig. 1(c). In addition, magnetization curves in different heterostructures are distinguished at the same temperature. Compared with the magnetization curve of monolayer CrI₃ at 100 K, CrI₃ in CrI₃/Au shows the same magnetization degree until 160 K. Magnetization curves of CrI₃ in CrI₃/Hf at different $E$ are supplemented in Fig. S5. The saturation magnetization at 0 K and the anisotropy under different $E$ only change slightly under $E$ modulation.

2.3 2.3 Magnetocaloric effect and its electric-field tunability

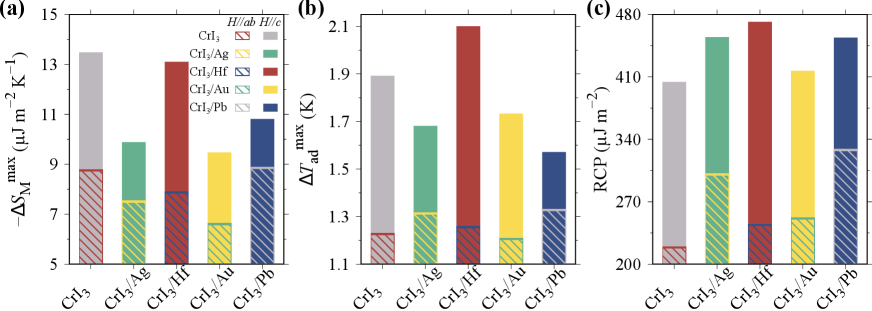
To explore the influence of metal substrates on MCE, maximum magnetic entropy change ( $-\Delta S_{\text{M}}^{\text{max}}$ ), maximum adiabatic temperature change ( $\Delta T_{\text{ad}}^{\text{max}}$ ), and relative cooling power (RCP) with a magnetic field of 5 T applied in different directions are shown in Fig. 3. $-\Delta S_{\text{M}}^{\text{max}}$ , $\Delta T_{\text{ad}}^{\text{max}}$ , and RCP of monolayer CrI₃ in our work are calculated to be 13.48 µJ m^-2 K, 1.89 K, and 404.35 µJ m^-2, respectively. The estimated results of monolayer CrI₃ are in good agreement with the experimental work of bulk counterpart ⁴⁷, whose $-\Delta S_{\text{M}}^{\text{max}}$ and $\Delta T_{\text{ad}}^{\text{max}}$ are measured as around 3.8 J kg^-1 K and 1.55 K under an out-of-plane magnetic field of 5 T. It also can be seen in Fig. 3 that metal substrates do improve MCE of CrI₃, particularly in terms of increasing RCP. CrI₃ in all heterostructures achieves a higher RCP compared with monolayer CrI₃, as shown in Fig. 3(c). Among them, RCP of CrI₃ in CrI₃/Hf heterostructure is as high as 471.72 µJ m^-2 at 5 T, suggesting there is more heat transferred between hot and cold reservoirs during a magnetic refrigeration cycle. In heterostructures, however, $-\Delta S_{\text{M}}^{\text{max}}$ of CrI₃ absorbed on four types of metal substrates does not surpass that of monolayer CrI₃ (Fig. 3(a)), mainly owing to the improved $T_{\text{C}}$ of CrI₃. More specifically, according to Eq 2, materials with superior $-\Delta S_{\text{M}}^{\text{max}}$ possess a comparatively larger magnetization and a relatively low $T_{\text{C}}$ . The small increase in the magnetization cannot counteract the substantial improvement in $T_{\text{C}}$ of CrI₃ in heterostructures, thus leading to a decrease in $-\Delta S_{\text{M}}^{\text{max}}$ . In contrast to $-\Delta S_{\text{M}}^{\text{max}}$ , $\Delta T_{\text{ad}}^{\text{max}}$ reflects the enhancement of MCE by metal substrates. On account of the significantly improved magnetic moment and moderate $T_{\text{C}}$ , Hf substrate can increase $\Delta T_{\text{ad}}^{\text{max}}$ of CrI₃ by 10.7% (up to 2.1 K) under an out-of-plane magnetic field, as shown in Fig. 3(b). The correlation between MCE and the applied field directions is also present in Fig. 3. It is clear that the difference between in-plane and out-of-plane MCE in CrI₃/Hf heterostructure is larger than that in monolayer CrI₃, while it is smaller in CrI₃/Ag and CrI₃/Pb heterostructures. The effect of substrates on anisotropic MCE in CrI₃ is also essentially attributed to the effect of substrates on MAE (Fig. 1(c)).

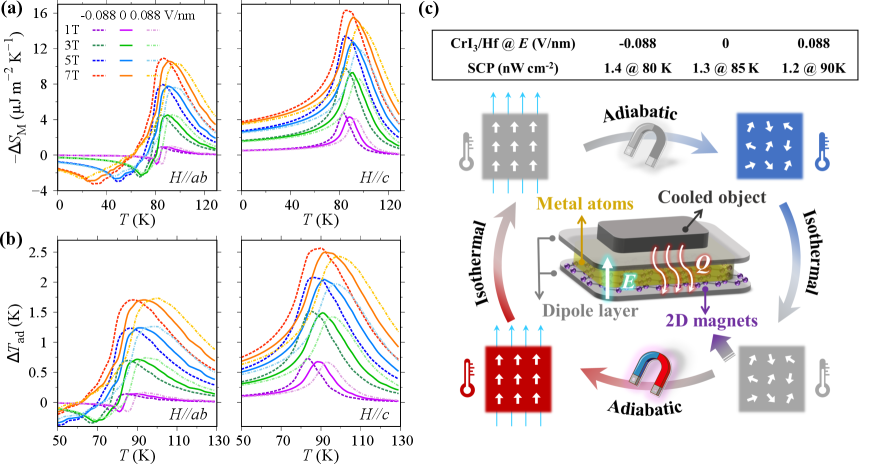
Figure 4(a) and (b) present the $E$ -tunable MCE of CrI₃ in CrI₃/Hf heterostructure under the in-plane and out-of-plane $H$ . Our calculation results show that, the magnetocaloric performance of CrI₃ in CrI₃/Hf heterostructure is further enhanced at a negative $E$ , while the isothermal magnetic entropy change ( $-\Delta S_{\text{M}}$ ) decreased slightly at a positive $E$ (Fig. 4(a)). This can be understood from Eq.2, which indicates that the partial derivative of magnetization with respect to temperature determines the entropy change. As shown in Fig. S5, a negative $E$ induces the magnetization of CrI₃ in CrI₃/Hf to be more sensitive to temperature changes than a positive $E$ , resulting in higher $-\Delta S_{\text{M}}^{\text{max}}$ under the same $H$ . A similar explanation can be used for $\Delta T_{\text{ad}}^{\text{max}}$ in Fig. 4(b). In addition, there is a consistent trend between the shift of peak temperature position in MCE curves and the adjustment of $T_{\text{C}}$ regulated by $E$ , as shown in Fig. 4(a) and (b). By applying $E$ to CrI₃/Hf heterostructure, the peak temperature of $-\Delta S_{\text{M}}$ and adiabatic temperature change ( $\Delta T_{\text{ad}}$ ) curves is shift up to 10 K, thereby extending the working temperature window of MCE for CrI₃/metal heterostructures. $-\Delta S_{\text{M}}$ and $\Delta T_{\text{ad}}$ curves of CrI₃ in other heterostructures are given in Fig. S6 and Fig. S7, and these curves are almost unaffected by $E$ modulation.

Schematic illustration of magnetic Carnot refrigeration cycle using CrI₃/metal heterostructure under $E$ is shown in Fig. 4(c). We propose an ideal assumption that when the cooled object touches a heterostructure under an applied periodic magnetic field, heat can be completely transferred outward from the cooled object. With an operating frequency of 1 Hz, the ideal specific cooling power (SCP) of CrI₃/Hf heterostructure around 85 K is close to 1.3 nW cm² at 5 T. Compared to monolayer CrI₃ ⁴⁶, CrI₃/Hf heterostructure has an operating temperature increase of roughly 20 K owing to the metal substrate, and the operating temperature could be further shift up to 10 K by applying $E$ .

3 3. CONCLUSIONS

In summary, MCE of monolayer CrI₃ absorbed on various metal substrates and its $E$ modulation is comprehensively investigated using first-principles calculations, atomistic spin simulations, and magnetocaloric thermodynamics. Magnetic properties of CrI₃ are affected by metal substrates and exhibit more diverse variations under $E$ , mainly owing to the charge transfer at the interface. Ag, Hf, Au, and Pb substrate are demonstrated to improve the magnetocaloric performance of CrI₃, particularly with RCP and $\Delta T_{\text{ad}}$ of CrI₃ in CrI₃/Hf are increased to 471.72 µJ m^-2 and 2.1 K at 5 T, respectively. Ag and Pb are found to weaken the MCE anisotropy, while Hf enhances it. Moreover, CrI₃ in CrI₃/Hf with a negative $E$ exhibits better magnetocaloric performance than that with a positive one. Through $E$ modulation, the peak temperature of $-\Delta S_{\text{M}}$ and $\Delta T_{\text{ad}}$ curves in CrI₃/Hf can be shift up to 10 K, allowing for widely tunable working temperature window of MCE. Our results on MCE of heterostructure formed by monolayer magnets and its $E$ regulation provide an important basis for designing and building authentic low-dimensional magnetic refrigeration devices.

4 4. METHODOLOGY

The first-principles calculations within density functional theory are carried out to calculate the magnetic properties of monolayer CrI₃ absorbed on four types of metal substrates (Ag, Hf, Au, and Pb) by using Vienna Ab initio Simulation Package (VASP) ^{49, 50}. The exchange-correlation functional is treated with the the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) form ⁵¹. The CrI₃/metal heterostructures are constructed by stacking four metallic layers onto a monolayer CrI₃ sheet. To avoid the interaction between neighboring slabs, the vacuum space along the $z$ -axis is set to 35 Å ⁵². A cutoff energy of 500 eV is utilized. The convergence criteria for energy and force in structure relaxation are 10^-5 eV and 0.01 eV/Å, respectively. The energy convergence is 10^-6 eV in self-consistent electronic calculations. The $5\times 5\times 1$ , $11\times 11\times 1$ , and $11\times 11\times 1$ Monkhorst–Pack $k$ -mesh in the CrI₃/Pb heterostructure ( $3\times 3\times 1$ , $5\times 5\times 1$ , and $5\times 5\times 1$ in other heterostructures that contain more atoms) are adopted in the ionic optimization, electronic optimization, and MAE calculation, respectively ⁵³. The MAE is obtained by calculating the energy differences between the spin quantization axes whose directions are aligned with different crystallographic axes. In order to calculate the MAE, SOC is considered⁵⁴. The magnetic exchange parameters are determined by substituting the magnetic configuration energies into the classic spin Hamiltonian ⁵⁵

\displaystyle H

\displaystyle=E_{0}-\frac{1}{2}J_{1}\sum_{N}\mathbf{s}_{i}\cdot\mathbf{s}_{j}-\frac{1}{2}J_{2}\sum_{NN}\mathbf{s}_{i}\cdot\mathbf{s}_{j},

(1)

where $E_{0}$ is the energy without spin contribution, $\mathbf{s}_{i}$ represents the unit vector of the atomistic spin direction at atom $i$ . $J_{1}$ and $J_{2}$ denote the nearest-neighbour (NN) and next-NN exchange interaction parameters, respectively.

After obtaining the magnetic exchange parameters from first-principles calculations, $T_{\text{C}}$ and temperature-dependent magnetization can be determined by the atomic spin model that has been numerically implemented in VAMPIRE ^{56, 57, 58}. The demagnetization field caused by the atomistic spins themselves is also considered. The figures of merit for MCE are generally described by $\Delta S_{\text{M}}$ and $\Delta T_{\text{ad}}$ upon a variation of magnetic field ( $H$ ). Based on the classical thermodynamics and the Maxwell relation, $\Delta S_{\text{M}}$ is given by ^{59, 60}

\Delta S_{\text{M}}=\int_{0}^{H}\left(\frac{\partial S}{\partial H}\right)_{T}\text{d}H=\mu_{0}\int_{0}^{H}\left(\frac{\partial M}{\partial T}\right)_{H}\text{d}H,

(2)

where $S$ and $M$ refer to entropy and magnetization, respectively. $\mu_{0}$ is vacuum permeability. Normally, MCE is characterized by $-\Delta S_{\text{M}}$ , given that the degree of disorder in the magnetic moment decreases with increasing $H$ . $\Delta T_{\text{ad}}$ can be similarly calculated as

	$\displaystyle\Delta T_{\text{ad}}$	$\displaystyle=-\mu_{0}\int_{0}^{H}\frac{T}{\rho c_{\text{p}}}\left(\frac{\partial S}{\partial H}\right)_{T}\text{d}H$		(3)
		$\displaystyle=-\mu_{0}\int_{0}^{H}\frac{T}{\rho c_{\text{p}}}\left(\frac{\partial M}{\partial T}\right)_{H}\text{d}H,$		(3)

where $\rho$ and $c_{\text{p}}$ are density and specific heat capacity of monolayer CrI₃, respectively. RCP as another descriptor for MCE is used to characterize the heat transfer across reservoirs and reveal the potential MCE in magnets, which is calculated as

\text{RCP}=\left|\Delta S_{\text{M}}^{\text{max}}\right|\times\delta T_{\text{FWHM}},

(4)

where the $\delta T_{\text{FWHM}}$ means the full width at half maximum of the $-\Delta S_{\text{M}}$ vs $T$ curve.

Supporting Information

Top and side views of CrI₃/metal vdW heterostructures; Spin-dependent plane integrated charge density difference along $c/z$ direction; The $p$ -orbital resolved MAE of I atom in CrI₃; Energy difference between FM and AFM configurations of CrI₃ in CrI₃/metal vdW heterostructures; Isothermal demagnetization curves of CrI₃ in CrI₃/Hf heterostructure under different $E$ ; Electric-field-tunable $-\Delta S_{\text{M}}$ vs $T$ curves for CrI₃/metal heterostructures; Electric-field-tunable $\Delta T_{\text{ad}}$ vs $T$ curves for CrI₃/metal heterostructures.

Acknowledgment

The authors acknowledge the support from the National Natural Science Foundation of China (12272173, 11902150), the National Overseas Thousand Youth Talents Program, the Research Fund of State Key Laboratory of Mechanics and Control of Mechanical Structures (MCMS-I-0419G01 and MCMS-I-0421K01), a project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions, and the Interdisciplinary Innovation Fund for Doctoral Students of Nanjing University of Aeronautics and Astronautics (KXKCXJJ202306). This work is partially supported by High Performance Computing Platform of Nanjing University of Aeronautics and Astronautics. Simulations were also performed on Hefei advanced computing center.

References

Gutfleisch et al. 2011 Gutfleisch, O.; Willard, M. A.; Brück, E.; Chen, C. H.; Sankar, S. G.; Liu, J. P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Advanced Materials 2011, 23, 821–842
Gottschall et al. 2019 Gottschall, T.; Skokov, K. P.; Fries, M.; Taubel, A.; Radulov, I.; Scheibel, F.; Benke, D.; Riegg, S.; Gutfleisch, O. Making a cool choice: The materials library of magnetic refrigeration. Advanced Energy Materials 2019, 9, 1901322
Kitanovski and Kitanovski 2020 Kitanovski, A.; Kitanovski, A. Energy applications of magnetocaloric materials. Advanced Energy Materials 2020, 10, 1903741
Hou et al. 2022 Hou, H.; Qian, S.; Takeuchi, I. Materials, physics and systems for multicaloric cooling. Nature Reviews Materials 2022, 7, 633–652
Hashimoto et al. 1981 Hashimoto, T.; Numasawa, T.; Shino, M.; Okada, T. Magnetic refrigeration in the temperature range from 10 K to room temperature: The ferromagnetic refrigerants. Cryogenics 1981, 21, 647–653
Zarkevich and Zverev 2020 Zarkevich, N. A.; Zverev, V. I. Viable materials with a giant magnetocaloric effect. Crystals 2020, 10, 815
Pecharsky and Gschneidner 1997 Pecharsky, V. K.; Gschneidner, K. A. Giant Magnetocaloric Effect in $\text{Gd}_{\text{5}}(\text{Si}_{\text{2}}\text{Ge}_{\text{2}})$ . Physical Review Letters 1997, 78, 4494
Luo et al. 2006 Luo, Q.; Zhao, D. Q.; Pan, M. X.; Wang, W. H. Magnetocaloric effect in Gd-based bulk metallic glasses. Applied Physics Letters 2006, 89, 081914
Zhang et al. 2010 Zhang, X. X.; Tejada, J.; Xin, Y.; Sun, G. F.; Wong, K. W.; Bohigas, X. Magnetocaloric effect in $\text{La}_{\text{0.67}}\text{Ca}_{\text{0.33}}\text{MnO}_{\text{$\delta$}}$ and $\text{La}_{\text{0.60}}\text{Y}_{\text{0.07}}\text{Ca}_{\text{0.33}}\text{MnO}_{\text{$\delta$}}$ bulk materials. Applied Physics Letters 2010, 69, 3596
Franco et al. 2018 Franco, V.; Blázquez, J.; Ipus, J.; Law, J.; Moreno-Ramírez, L.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Progress in Materials Science 2018, 93, 112–232
Moya et al. 2012 Moya, X.; Hueso, L. E.; Maccherozzi, F.; Tovstolytkin, A. I.; Podyalovskii, D. I.; Ducati, C.; Phillips, L. C.; Ghidini, M.; Hovorka, O.; Berger, A.; Vickers, M. E.; Defay, E.; Dhesi, S. S.; Mathur, N. D. Giant and reversible extrinsic magnetocaloric effects in $\text{La}_{\text{0.7}}\text{Ca}_{\text{0.3}}\text{MnO}_{\text{3}}$ films due to strain. Nature Materials 2012, 12, 52–58
Yüzüak et al. 2013 Yüzüak, E.; Dincer, I.; Elerman, Y.; Auge, A.; Teichert, N.; Hütten, A. Inverse magnetocaloric effect of epitaxial Ni-Mn-Sn thin films. Applied Physics Letters 2013, 103, 222403
Khovaylo et al. 2014 Khovaylo, V. V.; Rodionova, V. V.; Shevyrtalov, S. N.; Novosad, V. Magnetocaloric effect in “reduced” dimensions: Thin films, ribbons, and microwires of Heusler alloys and related compounds. Physica Status Solidi B 2014, 251, 2104–2113
Huang et al. 2017 Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D. R.; Cheng, R.; Seyler, K. L.; Zhong, D.; Schmidgall, E.; McGuire, M. A.; Cobden, D. H., et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273
Gong et al. 2017 Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y., et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269
Bonilla et al. 2018 Bonilla, M.; Kolekar, S.; Ma, Y.; Diaz, H. C.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H. R.; Phan, M. H.; Batzill, M. Strong roomerature ferromagnetism in $\text{VSe}_{\text{2}}$ monolayers on van der Waals substrates. Nature Nanotechnology 2018, 13, 289–293
Deng et al. 2018 Deng, Y.; Yu, Y.; Song, Y.; Zhang, J.; Wang, N. Z.; Sun, Z.; Yi, Y.; Wu, Y. Z.; Wu, S.; Zhu, J.; Wang, J.; Chen, X. H.; Zhang, Y. Gate-tunable room-temperature ferromagnetism in two-dimensional $\text{Fe}_{\text{3}}\text{GeTe}_{\text{2}}$ . Nature 2018, 563, 94–99
Yin et al. 2021 Yin, Y.; Yi, M.; Guo, W. High and anomalous thermal conductivity in monolayer $\text{MSi}_{\text{2}}\text{Z}_{\text{4}}$ semiconductors. ACS Applied Materials & Interfaces 2021, 13, 45907–45915
Yin et al. 2022 Yin, Y.; Gong, Q.; Yi, M.; Guo, W. Emerging versatile two-dimensional $\text{MoSi}_{\text{2}}\text{N}_{\text{4}}$ family. Advanced Functional Materials 2022, 2214050
Li et al. 2019 Li, H.; Ruan, S.; Zeng, Y. J. Intrinsic van der Waals magnetic materials from bulk to the 2D limit: New frontiers of spintronics. Advanced Materials 2019, 31, 1900065
Hou et al. 2019 Hou, X.; Chen, H.; Zhang, Z.; Wang, S.; Zhou, P. 2D atomic crystals: A promising solution for next-generation data storage. Advanced Electronic Materials 2019, 5, 1800944
Wang et al. 2020 Wang, H.; Qi, J.; Qian, X. Electrically tunable high Curie temperature two-dimensional ferromagnetism in van der Waals layered crystals. Applied Physics Letters 2020, 117, 083102
Xue et al. 2022 Xue, M.; He, W.; Gong, Q.; Yi, M.; Guo, W. Nonlinear elasticity and strain-tunable magnetocalorics of antiferromagnetic monolayer $\text{MnPS}_{\text{3}}$ . Extreme Mechanics Letters 2022, 57, 101900
Tang et al. 2023 Tang, Z. M.; Gong, Q.; Yi, M.-Y. Spin-selective contact type and strong Fermi level pinning at $\text{CrI}_{\text{3}}$ /metal interface. Materials Today Nano 2023, 22, 100309
Li et al. 2019 Li, T.; Jiang, S.; Sivadas, N.; Wang, Z.; Xu, Y.; Weber, D.; Goldberger, J. E.; Watanabe, K.; Taniguchi, T.; Fennie, C. J.; Fai Mak, K.; Shan, J. Pressure-controlled interlayer magnetism in atomically thin $\text{CrI}_{\text{3}}$ . Nature Materials 2019, 18, 1303–1308
Ubrig et al. 2019 Ubrig, N.; Wang, Z.; Teyssier, J.; Taniguchi, T.; Watanabe, K.; Giannini, E.; Morpurgo, A. F.; Gibertini, M. Low-temperature monoclinic layer stacking in atomically thin $\text{CrI}_{\text{3}}$ crystals. 2D Materials 2019, 7, 015007
Guo et al. 2021 Guo, X. et al. Structural monoclinicity and its coupling to layered magnetism in few-layer $\text{CrI}_{\text{3}}$ . ACS Nano 2021, 15, 10444–10450
Zhang et al. 2018 Zhang, J.; Zhao, B.; Zhou, T.; Xue, Y.; Ma, C.; Yang, Z. Strong magnetization and Chern insulators in compressed graphene/ $\text{CrI}_{\text{3}}$ van der Waals heterostructures. Physical Review B 2018, 97, 085401
Song et al. 2018 Song, T.; Cai, X.; Tu, M. W. Y.; Zhang, X.; Huang, B.; Wilson, N. P.; Seyler, K. L.; Zhu, L.; Taniguchi, T.; Watanabe, K.; McGuire, M. A.; Cobden, D. H.; Xiao, D.; Yao, W.; Xu, X. Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science 2018, 360, 1214–1218
Gibertini et al. 2019 Gibertini, M.; Koperski, M.; Morpurgo, A. F.; Novoselov, K. S. Magnetic 2D materials and heterostructures. Nature Nanotechnology 2019, 14, 408–419
Li et al. 2020 Li, H.; Xu, Y. K.; Cheng, Z. P.; He, B. G.; Zhang, W. B. Spin-dependent Schottky barriers and vacancy-induced spin-selective ohmic contacts in magnetic vdW heterostructures. Physical Chemistry Chemical Physics 2020, 22, 9460–9466
Gong et al. 2020 Gong, Q.; Yi, M.; Xu, B. X. Electric field induced magnetization reversal in magnet/insulator nanoheterostructure. International Journal of Smart and Nano Materials 2020, 11, 298–309
Yao et al. 2021 Yao, Y.; Zhan, X.; Sendeku, M. G.; Yu, P.; Dajan, F. T.; Li, N.; Wang, J.; Zhu, C.; Wang, F.; Wang, Z.; He, J. Recent progress on emergent two-dimensional magnets and heterostructures. Nanotechnology 2021, 32, 472001
Tan et al. 2021 Tan, X.; Ding, L.; Du, G. F.; Fu, H. H. Spin caloritronics in two-dimensional $\text{CrI}_{\text{3}}$ / $\text{NiCl}_{\text{2}}$ van der Waals heterostructures. Physical Review B 2021, 103, 115415
Petrov et al. 2019 Petrov, E. K.; Silkin, I. V.; Menshchikova, T. V.; Chulkov, E. V. Cr-containing ferromagnetic film–topological insulator heterostructures as promising materials for the quantum anomalous hall effect. JETP Letters 2019, 109, 121–125
Gao et al. 2022 Gao, Y.; Li, H.; Zhu, W. Prediction of quantum anomalous Hall effect in $\text{CrI}_{\text{3}}$ / $\text{ScCl}_{\text{2}}$ bilayer heterostructure. Chinese Physics B 2022, 31, 107304
Zhao et al. 2019 Zhao, Y.; Zhang, J. J.; Yuan, S.; Chen, Z. Nonvolatile electrical control and heterointerface-induced half-metallicity of 2D ferromagnets. Advanced Functional Materials 2019, 29, 1901420
Chakraborty and Ravikumar 2021 Chakraborty, S.; Ravikumar, A. Substrate induced electronic phase transitions of $\text{CrI}_{\text{3}}$ based van der Waals heterostructures. Scientific Reports 2021, 11, 198
Wang et al. 2021 Wang, G.; Qin, W.; Wang, S.; Teketel, B. S.; Yu, W.; Luo, T.; Xu, B.; Lin, B. $\text{CrI}_{\text{3}}$ / $\text{Y}_{\text{2}}\text{CH}_{\text{2}}$ :Heterointerface-induced stable half-metallicity of two-dimensional $\text{CrI}_{\text{3}}$ monolayer ferromagnets. ACS Applied Materials and Interfaces 2021, 13, 16694–16703
Chen et al. 2019 Chen, S.; Huang, C.; Sun, H.; Ding, J.; Jena, P.; Kan, E. Boosting the Curie temperature of two-dimensional semiconducting $\text{CrI}_{\text{3}}$ monolayer through van der Waals heterostructures. The Journal of Physical Chemistry C 2019, 123, 17987–17993
Hu et al. 2021 Hu, J. K.; Tan, J. X.; Wu, D.; Zhang, Z. H.; Fan, Z. Q. Exploring magnetic stability and valley splitting on $\text{CrI}_{\text{3}}$ /SiC van der Waals heterostructure. Applied Surface Science 2021, 560, 149858
Yu et al. 2022 Yu, W.; Luo, W.; Zhang, X.; Wu, Y.; Jia, X.; Yang, X.; Cai, X.; Song, A.; Zhang, Z.; Zhang, W. B. Strain and electric field dependent spin polarization in two-dimensional arsenene/ $\text{CrI}_{\text{3}}$ heterostructure. Journal of Alloys and Compounds 2022, 912, 165093
Yang et al. 2021 Yang, Q.; Hu, X.; Shen, X.; Krasheninnikov, A. V.; Chen, Z.; Sun, L. Enhancing ferromagnetism and tuning electronic properties of $\text{CrI}_{\text{3}}$ monolayers by adsorption of transition-metal atoms. ACS Applied Materials & Interfaces 2021, 13, 21593–21601
Jiang et al. 2018 Jiang, P.; Li, L.; Liao, Z.; Zhao, Y. X.; Zhong, Z. Spin direction-controlled electronic band structure in two-dimensional ferromagnetic $\text{CrI}_{\text{3}}$ . Nano Letters 2018, 18, 3844–3849
Liu et al. 2018 Liu, J.; Shi, M.; Lu, J.; Anantram, M. P. Analysis of electrical-field-dependent Dzyaloshinskii-Moriya interaction and magnetocrystalline anisotropy in a two-dimensional ferromagnetic monolayer. Physical Review B 2018, 97, 8–10
He et al. 2023 He, W.; Yin, Y.; Gong, Q.; Evans, R. F.; Gutfleisch, O.; Xu, B.; Yi, M.; Guo, W. Giant magnetocaloric effect in magnets down to the monolayer limit. arXiv preprint 2023,
Liu and Petrovic 2018 Liu, Y.; Petrovic, C. Anisotropic magnetocaloric effect in single crystals of $\text{CrI}_{\text{3}}$ . Physical Review B 2018, 97, 174418
Tran et al. 2022 Tran, H. B.; Momida, H.; ichiro Matsushita, Y.; Shirai, K.; Oguchi, T. Insight into anisotropic magnetocaloric effect of $\text{CrI}_{\text{3}}$ . Acta Materialia 2022, 231, 117851
Kresse and Furthmüller 1996 Kresse, G.; Furthmüller, J. Efficient iterative schemes for $ab~{}initio$ total-energy calculations using a plane-wave basis set. Physical Review B 1996, 54, 11169–11186
Kresse and Joubert 1999 Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B 1999, 59, 1758–1775
Perdew et al. 1996 Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Physical Review Letters 1996, 77, 3865–3868
Neugebauer and Scheffler 1992 Neugebauer, J.; Scheffler, M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Physical Review B 1992, 46, 16067–16080
Monkhorst and Pack 1976 Monkhorst, H. J.; Pack, J. D. Special points for Brillouin-zone integrations. Physical Review B 1976, 13, 5188–5192
Vaz et al. 2008 Vaz, C. A. F.; Bland, J. A. C.; Lauhoff, G. Magnetism in ultrathin film structures. Reports on Progress in Physics 2008, 71, 056501
Skubic et al. 2008 Skubic, B.; Hellsvik, J.; Nordström, L.; Eriksson, O. A method for atomistic spin dynamics simulations: Implementation and examples. Journal of Physics: Condensed Matter 2008, 20, 315203
Evans et al. 2014 Evans, R. F.; Fan, W. J.; Chureemart, P.; Ostler, T. A.; Ellis, M. O.; Chantrell, R. W. Atomistic spin model simulations of magnetic nanomaterials. Journal of Physics: Condensed Matter 2014, 26, 103202
Gong et al. 2019 Gong, Q.; Yi, M.; Evans, R. F.; Xu, B. X.; Gutfleisch, O. Calculating temperature-dependent properties of $\text{Nd}_{\text{2}}\text{Fe}_{\text{14}}\text{B}$ permanent magnets by atomistic spin model simulations. Physical Review B 2019, 99, 214409
Gong et al. 2019 Gong, Q.; Yi, M.; Xu, B. X. Multiscale simulations toward calculating coercivity of Nd-Fe-B permanent magnets at high temperatures. Physical Review Materials 2019, 3, 84406
Pecharsky and Gschneidner 1999 Pecharsky, V. K.; Gschneidner, K. A. Magnetocaloric effect from indirect measurements: Magnetization and heat capacity. Journal of Applied Physics 1999, 86, 565–575
Gschneidner and Pecharsky 2000 Gschneidner, K. A.; Pecharsky, V. K. Magnetocaloric materials. Annual Review of Materials Science 2000, 30, 387–429

\includepdfmerge

SI.pdf,1-9

Magnetocaloric effect and its electric-field regulation in CrI3/metal heterostructure