Magnetization dependent tunneling conductance of ferromagnetic barriers

Recent experiments on van der Waals antiferrmagnets such as CrI₃, CrCl₃ and MnPS₃ have shown that using atomically thin layers as tunnel barriers and measuring the temperature ($T$) and magnetic field ($H$) dependence of the conductance allows their magnetic phase diagram to be mapped. In contrast, barriers made of CrBr₃ –the sole van der Waals ferromagnet investigated in this way– were found to exhibit small and featureless magnetoconductance, seemingly carrying little information about magnetism. Here we show that –despite these early results– the conductance of CrBr₃ tunnel barriers does provide detailed information about the magnetic state of atomically thin CrBr₃ crystals for $T$ both above and below the Curie temperature ($T_{C}=32$ K). Our analysis establishes that the tunneling conductance depends on $H$ and $T$ exclusively through the magnetization $M(H,T)$, over the entire temperature range investigated (2-50 K). The phenomenon is reproduced in detail by the spin-dependent Fowler-Nordheim model for tunneling, and is a direct manifestation of the spin splitting of the CrBr₃ conduction band. These findings demonstrate that the investigation of magnetism by tunneling conductance measurements is not limited to antiferromagnets, but can also be applied to ferromagnetic materials.

Probing magnetism in atomically thin van der Waals crystals is challenging because most experimental methods commonly employed to study bulk compounds are not sufficiently sensitive to detect any magnetic signal from such a small amount of materialBurch2018 ; Gong2019 ; Marco2019 ; Mak2019 ; avsar2020 ; Huang2020 . Recently, it has been shown that magnetic phase boundaries –and even the complete magnetic phase diagram– of insulating atomically thin magnets can be detected by using them as tunnel barriers, and measuring their temperature-dependent magnetoconductanceSong2018Science ; Klein2018Science ; Wang2018 ; wang2019NN ; cai2019NL ; klein2019NP ; Kim2019PNAS ; Kim2019NL ; Long2020NL . The sensitivity of the tunneling magnetoconductance to magnetism originates from the dependence of the tunneling probability on the magnetic statemoodera2007review . As $H$ and $T$ are varied across a magnetic transition, the alignment of the spins in the barrier changes sharply, and so does the tunneling probability of electrons with different spin orientations. The net result is an equally sharp change in the measured conductance that can be traced to identify the phase boundary.

These conclusions have been drawn from experiments on different antiferromagnetic insulators (CrI₃Song2018Science ; Klein2018Science ; Wang2018 , CrCl₃wang2019NN ; cai2019NL ; klein2019NP ; Kim2019PNAS and MnPS₃Long2020NL ), and it is not at all clear that the technique can be equally effective to probe ferromagnetic insulators, since in that case no magnetic phase boundaries are present below the Curie temperature. Indeed, tunneling conductance measurements on ferromagnetic CrBr₃ barriers have shown only an extremely small and featureless low-temperature tunneling magnetoconductanceGhazaryan2018 ; Kim2019PNAS ; Kim2019NL , and no pronounced effect was observed, which could be related to magnetism without microscopic modeling. In contrast to this early results, here we show directly from experimental data that the temperature and magnetic field dependence of the tunneling conductance of ferromagnetic CrBr₃ barriers is entirely determined by the magnetization of the material, and can be used to extract detailed, quantitative information both above and below the Curie temperature.

CrBr₃ is a van der Waals layered material that –irrespective of thickness (i.e., from bulk down to monolayer)– exhibits a transition to a ferromagnetic state with an easy axis perpendicular to the layersTsubokawa1960 ; Jennings1965PR ; Ho1969 ; Neutron1971 ; Kim2019NE ; Chen2019Science ; zhang2019NL ; Jin2020NM ; Sun2021 (see Fig. 1a, Supplementary Note 1 and Supplementary Fig. 1). Bulk magnetization measurements in Fig. 1b show that the Curie temperature of our crystals is $T_{C}\simeq 32$ K, with a saturation magnetization corresponding to a magnetic moment of $3\mu_{B}$ per chromium atom, in line with previous reportsTsubokawa1960 ; Jennings1965PR ; Ho1969 ; Neutron1971 . Single crystals are exfoliated into thin layers and used to nano-fabricate hBN-encapsulated graphite/CrBr₃/graphite tunnel junctions inside a glove box (see inset of Fig. 1c for a scheme, Supplementary Fig. 2 for an optical image of the device, and Methods for detailed information about device assembly). Fig. 1c presents the current-voltage ($I$-$V$) characteristics for two representative devices with different thickness $d$ (corresponding to $N=7$ and 8 layers), showing typical tunneling transport at low temperatures and the scaling behavior predicted by the Fowler-Nordheim tunneling formula (i.e., $\log(I/V^{2})\propto d/V$)FN1928 ; FN1969 . As shown in Fig. 1d, application of an external magnetic field up to 3 T at $T=2$ K causes only minor (<6%) and featureless variations in the conductance $G=I/V$. This is consistent with previous reportsKim2019PNAS ; Kim2019NL and expected for a ferromagnetic semiconductor, in which –at low temperature– the spins are spontaneously fully polarized already in the absence of an applied magnetic field.

Despite the negligible low-temperature magnetoconductance, Fig. 1e shows that the conductance measured at zero applied magnetic field $G(H=0,T)$ increases by a factor of three as $T$ is lowered from the Curie temperature $T_{C}=32$ K down to 2 K. As the conductance is virtually temperature independent above $T_{C}$ (for $32<T<50$ K), we infer directly from the experimental data that the conductance increase is due to CrBr₃ entering the ferromagnetic state. This observation implies that magnetism does influence the electrical conductance of the tunnel barriers and that the effect is sizable: a threefold increase in conductance is comparable to the magnetoresistance of most common magnetic tunnel junctions (i.e., tunneling spin valve devicesvzutic2004 ) and of CrCl₃ antiferromagnetic tunnel barrierscai2019NL ; klein2019NP ; wang2019NN ; Kim2019PNAS ; Kim2019NL .

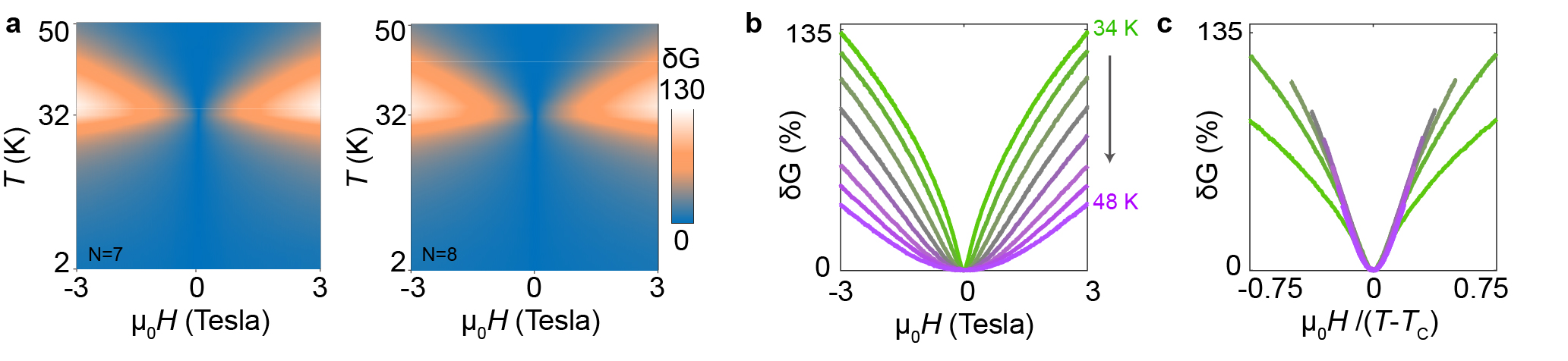
This observation motivates us to look more in detail at the temperature-dependent magnetoconductance of CrBr₃ barriers, $\delta G(H,T)\equiv[G(H,T)-G(0,T)]/G(0,T)$. The full dependence of $\delta G(H,T)$ on $T$ and $H$ is shown in Fig. 2a for both the 7- and 8-layer CrBr₃ devices, with the two of them exhibiting identical behavior. In both devices, $\delta G(H,T)$ is positive and peaks at $T=T_{C}$ irrespective of the applied magnetic field $H$. The positive magnetoconductance can be understood, since at high $T$ the application of a magnetic field does lead to a better alignment of the spins in CrBr₃. Similarly to what happens in CrI₃ and CrCl₃ tunnel barriers, a better spin alignment enhances the tunneling probability, causing the conductance to increase. We note that when $T$ approaches $T_{C}$ from above –coming from the paramagnetic state of CrBr₃– the magnetic field required to increase the conductance systematically decreases, indicating that the spin susceptibility $\chi$ is enhanced. This trend is reminiscent of the behavior expected from the critical fluctuations in the neighborhood of the ferromagnetic transitionblundell2003magnetism .

The idea that the magnetoconductance for $T>T_{C}$ probes the fluctuations of the spins in the critical regime of the paramagnetic state can be tested quantitatively if we recall that in a mean-field description of this regime, the linear spin polarizability $\chi\propto 1/(T-T_{C})$ as $T$ approaches $T_{C}$blundell2003magnetism . We can then check whether the conductance depends on the magnetic field induced spin polarization, or equivalently on the magnetization (whose mean-field expression is given by the Curie-Weiss law, $M\propto\mu_{0}H/(T-T_{C})$), by simply plotting $\delta G(H,T)$ as a function of $\mu_{0}H/(T-T_{C})$ for any $T>T_{C}$ (see Fig. 2b). For sufficiently small $\mu_{0}H/(T-T_{C})$ all curves indeed collapse on top of each other (Fig. 2c), irrespective of the temperature at which they are measured, confirming that in the linear regime the field-induced increase of the conductance is determined by the net spin polarization (i.e., by the field-induced magnetization).

The relation between magnetoconductance and magnetization can be tested beyond the linear regime, by using the magnetization $M(H,T)$ measured on bulk crystals (Fig. 3b) to re-plot the magnetoconductance of our tunnel barriers $\delta G(H,T)$ (Fig. 3a) as a function of $M$. The result is shown in Fig. 3c, with curves of different colors representing magnetoconductance measurements done at different temperatures. When plotted as a function of $M$ all curves collapse on top of each other throughout the entire range of $H$ and $T>T_{C}$ investigated. We can therefore conclude directly from the data that the magnetoconductance $\delta G$ depends on $H$ and $T$ only through the magnetization $M(H,T)$ even well outside the linear regime. That is: for $T>T_{C}$, $\delta G(H,T)=\delta G(M(H,T))$ .

To extend our analysis from the paramagnetic state to $T<T_{C}$, when the CrBr₃ barriers are ferromagnetic, we look at the temperature dependence of the conductance measured at zero applied field. To this end, we consider the quantity $\Delta G(H,T)\equiv[G(0,T)-G(0,T_{C})]/G(0,T_{C})$, i.e., the relative increase in conductance observed as $T$ is lowered below the Curie temperature. If the conductance is a function of magnetization, this function should be the same underlying the behavior of $\delta G(H,T)$ for $T>T_{C}$, because the temperature dependence of $G(0,T)$ originates exclusively from the temperature dependence of the spontaneous magnetization $M(H=0,T)$, which in the ferromagnetic state increases from zero at $T=T_{C}$, to its saturation value for $T\ll T_{C}$. Consistently with this idea, the data in Fig. 1e shows an increase in conductance upon lowering $T$. However, to establish whether the functional dependence of the magnetoconductance on magnetization below $T_{C}$ is the same as the one found for $T>T_{C}$ a more quantitative analysis is needed.

For such an analysis we cannot rely on the magnetization measured on bulk crystals, because in the ferromagnetic state the magnetization of bulk samples at $H=0$ is entirely determined by the formation of magnetic domainsblundell2003magnetism ; kuhlow1975 , whereas exfoliated atomically thin crystals of the size used in our devices have been found to behave as single domainsKim2019NE ; Jin2020NM ; Sun2021 . Indeed, magnetization measurements on CrBr₃ bulk crystals for $T<T_{C}$ exhibit virtually no remnant magnetization nor any hysteresis upon cycling the applied magnetic field (see Supplementary Fig. 1), whereas Hall magnetometry of atomically thin, exfoliated CrBr₃ crystals exhibit finite remnant magnetization and a clear hysteresisKim2019NE . That is why in what follows we use the temperature-dependent, zero-field magnetization obtained in Hall magnetometry experiments that –as discussed in Ref. Kim2019NE, – is very well reproduced by the temperature dependence calculated using the XXZ model with anisotropic exchange interaction, shown in Fig. 3e.

We use the spontaneous magnetization curve shown in Fig. 3e to re-plot the quantity $\Delta G(H,T)$ shown in Fig. 3d, as a function of $M$. The result is represented by the open circles in Fig. 3c. The data fall on top of the $\delta G(M)$ curve found in our analysis of transport in the paramagnetic state of CrBr₃, for $T>T_{C}$. The excellent agreement demonstrates that the conductance of CrBr₃ tunnel barriers depends on temperature and magnetic field only through its magnetization over the full experimental range investigated, and that the dependence is described by the same function from well above $T_{C}$ to the lowest temperature reached in our measurements (2 K). This conclusion is extremely robust, because it is drawn directly from the analysis of the experimental data, without any theoretical assumption (the 8-layer device exhibits an identical behavior, as discussed in Supplementary Note 3 and shown in Supplementary Fig. 5).

These experimental results have a straightforward interpretation within the context of Fowler-Nordheim (FN) tunneling transport commonly used to interpret the conductance of van der Waals magnetic barriers. In FN tunnelling, the applied bias tilts the conduction band across the CrBr₃ layer, effectively reducing the thickness of the tunnel barrier, so that eventually the tunneling probability for electrons becomes sizable and a finite current is observedFN1928 ; FN1969 . The $I-V$ characteristics in the FN tunneling regime satisfy the relation:

where $m^{*}$ is the effective mass describing the motion of electrons in CrBr₃ in the direction perpendicular to the planes, $\phi_{B}$ is the barrier height determined by the distance between the Fermi level in the contacts and the conduction band edge in CrBr₃, $h$ is Planck’s constant and $e$ the (modulus of the) electron charge. For a ferromagnet, an analogous relation is expected to hold separately for electrons with spin up and spin down, which experience different barrier heights $\phi_{\uparrow}$ and $\phi_{\downarrow}$, due to the spin-splitting of the conduction band present for $T<T_{C}$ (see Fig. 4a). The total conductance is then given by the sum of the contributions given by electrons with spin up and spin down :

where $A$ is a constant determined by the barrier dimensions.

We use this expression to analyze the experimental data by assuming that the spin splitting of the conduction band in the ferromagnetic state is linearly proportional to the magnetization, resulting in barrier heights for spin up and down given by $\phi_{\uparrow,\downarrow}=\phi_{B0}\pm\gamma M$. We calculate the magnetoconductance $[G(M)-G(M=0)]/G(M=0)$ using the value of $\sqrt{2m^{*}}\phi_{B0}$ extracted from the measured $I-V$ curves, and treating $\gamma$ as the sole fitting parameter. The result of this procedure –represented by the black curve in Fig. 3c– reproduces the experimental data perfectly. Interestingly, a conceptually similar approach has been followed in earlier beautiful work on the tunneling conductance of EuO barriers in the ferromagnetic stateMoodera2008PRL . That work, however, focused exclusively on the case of $T<T_{C}$ and zero applied magnetic field, by analyzing the temperature dependence of the conductance in terms of the measured temperature dependence of the magnetization. Our results show that the approach has a much broader validity: it can be applied both below and above $T_{C}$, it remains valid in the presence of a magnetic field, and –as CrBr₃ and EuO are very different materials– it describes very different classes of ferromagnetic insulators. If used in conjunction with a model predicting the magnetic field and temperature dependence of the magnetization, this approach allows the full magnetoconductance to be calculated. This is illustrated by the color plot in Fig. 4d that –despite having being obtained with the simplest possible Weiss model of Ising ferromagnetism– reproduces all the qualitative features observed in the experiments (compare Fig. 4d with Fig. 2a), and even exhibits a nearly quantitative agreement. Alternatively, it is also possible to extract the temperature and magnetic field dependence of the magnetization from the measured magnetoconductance, as discussed in Supplementary Note 2 and shown in Supplementary Fig. 4.

The excellent agreement between the calculated and the measured magnetoconductance (see Fig. 3c) suggests the possibility to extract the spin splitting energy quantitatively, from the value of the fitting parameter $\gamma$. This is however not straightforward, because Eq. (2) depends on the product $\sqrt{m^{*}}(\phi_{0})^{3/2}$, and the effective mass $m^{*}$ is not known. Fig. 4b shows the spin splitting energy as a function of magnetization obtained by taking the value of $\gamma$ used to fit the $\delta G=\delta G(M)$ curves in Fig. 3c, and assuming the effective mass $m^{*}$ to be either the free electron mass $m_{0}$ or 10 $m_{0}$, a very large value chosen to mimic the flatness of the CrBr₃ bands in the direction perpendicular to the layerswang2011Calculation ; soriano2020review . We find that at saturation the energy splitting separating the spin-up and the spin-down bands is approximately 110 meV if $m^{*}=m_{0}$ and 50 meV if $m^{*}=10m_{0}$, indicating that for realistic values of the effective mass the spin-splitting energy is between 50 and 110 meV. We emphasize, however, that care is certainly needed in interpreting the meaning of this quantity microscopically, because –as applied to CrBr₃ barriers– the Fowler-Nordheim model is a phenomenological approach that does not take into account the complexity of the microscopic electronic structure of the material. In particular, it does not take into account that the conduction band consists of two distinct, nearly degenerate electronic bands originating from the $e_{1g}$ and $t_{2g}$ orbitals of the Cr atoms.

Irrespective of these details, the key result presented here is that the measured tunneling magnetoconductance of CrBr₃ is entirely determined by its magnetization, which is why magnetoconductance measurements can be used to investigate the magnetic properties of the material. We envision, for instance, that magnetoconductance measurements will allow detailed investigations of the critical behavior of the magnetic susceptibility in the paramagnetic state for $T$ very close to $T_{C}$ and provide a new, experimentally simple way to determine critical exponents. This is possible because the required data analysis only relies on the fact that at small $M$ the magnetoconductance is a quadratic function of the magnetization (see Supplementary Note 2 and Supplementary Fig. 3). Another interesting possibility is to analyze magnetoconductance measurements over a broad range of temperatures and magnetic fields, to discriminate between microscopic theoretical models that predict a different functional dependence for $M(H,T)$ (see Supplementary Note 2 and Supplementary Fig. 4). These are just two examples that illustrate the most important aspect of our results, namely that measurements of the tunneling conductance are not limited to the investigation of antiferromagnetic barriers, but can also provide detailed information about the magnetic properties of ferromagnetic insulators.