Magnetically Tuned Continuous Transition from Weak to Strong Coupling in Terahertz Magnon Polaritons
Abstract
Depending on the relative rates of coupling and dissipation, a light–matter coupled system is either in the weak- or strong-coupling regime. Here, we present a unique system where the coupling rate continuously increases with an externally applied magnetic field while the dissipation rate remains constant, allowing us to monitor a weak-to-strong coupling transition as a function of magnetic field. We observed a Rabi splitting of a terahertz magnon mode in yttrium orthoferrite above a threshold magnetic field of 14 T. Based on a microscopic theoretical model, we show that with increasing magnetic field the magnons transition into magnon polaritons through an exceptional point, which will open up new opportunities for in situ control of non-Hermitian systems.
Understanding and harnessing the interplay of driving and dissipation in open quantum systems is an important contemporary problem in technology and science. Many quantum technologies, including quantum computation, sensing, and transduction, are enabled by coherent light–matter coupling, but the coherence can be easily washed out when the matter interacts with dissipative environments. On the other hand, dissipation can be engineered for dissipative quantum error correction schemes as well as for stabilizing qubits against decoherence [1, 2, 3, 4]. Further, driven-dissipative many-body systems can exhibit exotic nonequilibrium phenomena and phases [5, 6, 7].
In a strongly coupled light–matter system, the coupling rate exceeds the rates of dissipation for light () and matter (), satisfying , where is called the cooperativity [8, 9, 10]. Typically, the matter is placed in a small-mode-volume photonic cavity to enhance . Such cavity-quantum-electrodynamic systems have recently attracted much theoretical attention as controllable open quantum systems, in which the physics of exceptional points, non-hermitian Hamiltonians, and parity-time symmetry can be explored [11, 12, 13, 14, 15, 16, 17]. In particular, exceptional points, which are spectral singularities where the eigenvalues and eigenvectors coalesce [18], are expected to be useful for manipulating light via nontrivial topological effects [19, 20, 21].
Experimentally, several physical platforms have shown a transition from the weak-coupling regime () to the strong-coupling regime (), including intersubband polaritons in quantum wells through gating [22] or ultrafast optical excitation [23], microcavity exciton polaritons in aligned carbon nanotubes through polarization rotation [24], a metal–semiconductor hybrid resonator through spacer thickness variation [25], and magnon-polaritons in yttrium iron garnet through position tuning inside a microwave cavity [26, 27]. However, continuous facile tuning of , , or by an external field in a single sample has not been achieved.
Here, we demonstrate in situ tuning of by an external magnetic field () for propagating bulk magnon-polaritons in the antiferromagnetic state of yttrium orthoferrite (YFeO3). We used single-shot terahertz (THz) time-domain spectroscopy [28, 29] in high magnetic fields up to T and observed a field-induced peak splitting of a THz magnon mode in YFeO3. The magnon peak in transmission spectra remains a single peak until a critical field (14 T) is reached, where it splits into two, and the two-peak spectrum persists up to 30 T. Our microscopic model quantitatively explains the experimental data. The model shows that the coupling rate continuously increases with increasing , and exact driving-dissipation compensation () occurs at the critical field, which is the exceptional point in this system. The magnitude of splitting also increased with increasing sample thickness, in proportion to the square root of the thickness.
The YFeO3 samples we studied were -cut single crystals grown in an optical floating zone furnace. The thickness of the main sample studied was mm. We performed THz magnetospectroscopy measurements on these samples using the Rice Advanced Magnet with Broadband Optics (RAMBO) [30], which combines single-shot THz detection and pulsed high magnetic fields up to 30 T [28]; see Fig. 1(a). Bursts of THz radiation were generated through optical rectification by passing the output beam of an amplified Ti:Sapphire laser ( kHz, fs, nm, mJ, Clark-MXR, Inc., CPA-2001) through a LiNbO3 crystal. We recorded the time-domain waveform of the THz pulses that transmitted through the sample by electro-optic sampling in ZnTe in a single-shot manner using a reflective echelon [28, 29].
YFeO3 is a canted antiferromagnet and hosts two magnon modes – the quasiferromagnetic (qFM) mode and the quasiantiferromagnetic (qAFM) mode. The spin motion of the qFM mode is depicted in Fig. 1(b), where and represent Fe3+ spins in the two Fe sublattices, and is the net magnetization as a result of canting. In the present work, we were primarily interested in the coupling between the magnetic field component of the incident THz radiation, , and the qFM mode. Figure 1(c) schematically shows the experimental configuration we employed. The two spins lie in the – plane, which are shown by blue solid arrows. The Cartesian coordinates , , and are parallel to the crystal , , and axes, respectively. The electric field component of the incident THz radiation, , was along the -axis, and the magnetic field component, , was along the -axis, respectively. In this geometry, only the qFM mode can be excited through the Zeeman torque [31]. The external millisecond-long pulsed magnetic field generated by the RAMBO system was applied parallel to the -axis; it was essentially constant for the duration of the picosecond-long THz pulse, and therefore, it can be safely considered to be a DC magnetic field, , shown by a black arrow.

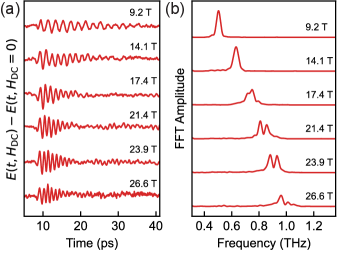
Figure 2(a) shows a series of time-domain traces of THz electric fields transmitted through the sample at various selected DC magnetic fields from 9.2 T to 26.6 T. For each magnetic field, we subtracted the THz electric-field waveform at zero magnetic field, , from the THz electric-field waveform recorded at the magnetic field, . This differentiation procedure allows us to focus on the magnetic-field-induced changes in the material’s THz response. At low magnetic fields ( T), we observe long-lived coherent oscillations, with monotonically decaying amplitude, due to the qFM magnon mode excited by the incident THz pulse, as expected for this configuration [32]. Above 14 T, however, the data start showing beating behavior, indicating the existence of two oscillation modes with different but similar frequencies. The corresponding Fourier transforms of the data into the frequency domain corroborate this description, as shown in Fig. 2(b). At 9.2 T and 14.1 T, there is a single peak observed, whose center frequency increases with the magnetic field. Above 14 T, the peak splits into two, and the splitting magnitude increases with increasing magnetic field.
To understand our experimental data quantitatively, we developed a microscopic theoretical model. Complete derivations are reported in Supplementary Information. First, we derive the relative permeability in the -cut crystal configuration, following the Herrmann model [31]. We consider two sublattices with spins and , as depicted in Figs. 1(b) and 1(c). The free energy of this system is given by
| (1) | ||||
which contains the isotropic exchange interaction (the first term with coefficient ), the Dzyaloshinskii-Moriya interaction (the second term with coefficient ), the anisotropy energies (the third and fourth terms with coefficients and , respectively), and the Zeeman interaction with the external DC magnetic field (the last term); is the vacuum permeability.
The equation of motion for the th component of the spins can be written as
| (2) |
where are the normalized spins with , is the gyromagnetic ratio, and is the dimensionless Gilbert damping coefficient. By solving Eq. (2) with the free energy given by Eq. (1), we can obtain the resonance frequency, , and the magnetic susceptibility tensor for the qFM and qAFM modes without any fitting parameters. Because THz magnetic field is along the -axis, we here focus on the element of the magnetic susceptibility tensor is shown in Eq. (3),
| (3) | ||||
where is the matter decay rate, which includes Gilbert damping and interactions. All necessary physical quantities are taken from the literature (see Supplementary Information).
Next, we calculated THz transmittance spectra by the scattering matrix method using the relative permeability obtained from the microscopic model (see Supplementary Information) and deduced the resonance frequencies. Figure 3(a) summarizes the frequencies () of the peaks normalized by the center magnon frequency () determined both from the experiment and calculation. The numerical data is presented as a color map, while open circles indicate the experimental data. Dashed lines are square-root fits. Figure 3(b) shows theoretical traces at T and T obtained from the color map in Fig. 3(a). Theory and experimental data are in good agreement. As the applied magnetic field increases, the splitting between the two peaks increases. The transition from weak coupling to strong coupling occurs through the exceptional point (a spectral singularity where the eigenvalues and eigenvectors coalesce [18]). This dependence of the splitting on the magnetic field can be explained by the magnetic field dependence of the oscillator strength, . For the case of scalar susceptibility and zero damping it can be shown (see Supplementary Information) that the frequency splitting, , depends on the oscillator strength, as:
| (4) |
We see that the oscillator strength and magnon frequency contribute to the frequency splitting of the magnon-polariton. Equation (3) shows that depends on the average of the components of the two spins , which increases continuously with increasing magnetic field applied along the -axis. Thus, the frequency splitting increase with magnetic field.
With further theoretical analysis, we can obtain the light matter coupling strength, , as a function of the magnetic field, which is plotted in Fig. 3(c), where the dashed line indicates the light and matter losses, . The existence of an exceptional point can be naturally explained as the competition between the matter dissipation rate () and light effective loss rate (), which are independent of the magnetic field, and the light-matter coupling strength (), which increases with the field. At low magnetic fields, the dissipation wins, while at high magnetic fields, the coupling wins. Thus, in this system, the external magnetic field induces an in situ continuous transition between the weak-coupling regime (at low fields) and the strong-coupling regime (at high fields). At the exceptional point (14 T), the loss and the coupling strength are equal. Therefore, the effective loss rate of light can be calculated THz with THz. Such relatively high effective loss rate (escape rate) of light reflects the absence of the cavity structure.

Finally, we also found that the magnitude of splitting also increases with the sample thickness, ; see Fig. 3(d). A similar splitting of THz magnon polaritons has been previously observed as a function of temperature at zero magnetic field [33, 34], but only qualitative explanations were given. Here, we demonstrated that the splitting shows a dependence at a fixed magnetic field, as shown in Fig. 3(d). The dashed line, which is proportional to , was obtained from calculations using our microscopic model (see Supplementary Information), as detailed below, and agrees well with the experimental data. The coupling strength, , is known to be proportional to the density of two-level objects, , i.e., [35, 36, 8]. Usually, such a dependence is discussed in the context of light-matter coupling in a cavity [37, 38], where the volume is kept constant, and the density dependence is replaced with the dependence on the number of spins, [39, 35, 24, 40]. In our case, this cannot be true, as the density of spins is constant as a function of thickness. However, the splitting as a function of thickness also follows the square square-root dependence, , as summarized in Fig. 3(d). Such behavior instead can be understood as arising from the boundary conditions of Maxwell equations for the THz wave propagation, similar to exciton-polaritons in a finite system [41].
In conclusion, we investigated YFeO3 crystals with different thicknesses using single-shot THz time-domain spectroscopy in high magnetic fields up to 30 T. We observed that above about 14 T the quasiferromagnetic magnon mode splits into two peaks and the frequency splitting keeps increasing with increasing magnetic field. This behavior can be explained by the formation of bulk magnon polaritons. Our theoretical model based on the microscopic permeability tensor and scattering matrix method agrees well with the experimental data. From the model, it follows that the frequency splitting dependence on magnetic fields arises from the dependence of the oscillator strength on the magnetic field. Furthermore, we show that the coupling strength can be continuously tuned by the applied magnetic field. Thus, our results demonstrate that the strong photon–magnon coupling can be controlled by the magnetic field. This adds bulk THz magnon polaritons in antiferromagnets to other systems supporting exceptional points, which are promising for further exploration of non-Hermitian physics and advanced sensing.
Acknowledgments. J.K. acknowledges support from the U.S. Army Research Office (grant W911NF2110157). This research was partially supported by the National Science Foundation through the Center for Dynamics and Control of Materials: an NSF MRSEC under Cooperative Agreement No. DMR-1720595. M.B. acknowledges support from the JST PRESTO program (grant JPMJPR1767). J.T. and I.K. acknowledge the support from the Japan Society for the Promotion of Science (JSPS) (KAKENHI No. 20H05662). S.C., W.R. and G.M. are grateful for financial support from the National Natural Science Foundation of China (NSFC, No.12074242), and the Science and Technology Commission of Shanghai Municipality (No.21JC1402600).
References
- Verstraete et al. [2009] F. Verstraete, M. M. Wolf, and J. Ignacio Cirac, Quantum computation and quantum-state engineering driven by dissipation, Nat. Phys. 5, 633 (2009).
- Schmidt et al. [2011] R. Schmidt, A. Negretti, J. Ankerhold, T. Calarco, and J. T. Stockburger, Optimal control of open quantum systems: Cooperative effects of driving and dissipation, Phys. Rev. Lett. 107, 130404 (2011).
- Reiter et al. [2017] F. Reiter, A. S. Sørensen, P. Zoller, and C. A. Muschik, Dissipative quantum error correction and application to quantum sensing with trapped ions, Nat. Commun. 8, 1822 (2017).
- Touzard et al. [2018] S. Touzard, A. Grimm, Z. Leghtas, S. O. Mundhada, P. Reinhold, C. Axline, M. Reagor, K. Chou, J. Blumoff, K. M. Sliwa, S. Shankar, L. Frunzio, R. J. Schoelkopf, M. Mirrahimi, and M. H. Devoret, Coherent oscillations inside a quantum manifold stabilized by dissipation, Phys. Rev. X 8, 021005 (2018).
- Hartmann et al. [2006] M. J. Hartmann, F. G. S. L. Brandão, and M. B. Plenio, Strongly interacting polaritons in coupled arrays of cavities, Nat. Phys. 2, 849 (2006).
- Foss-Feig et al. [2017] M. Foss-Feig, J. T. Young, V. V. Albert, A. V. Gorshkov, and M. F. Maghrebi, Solvable family of driven-dissipative many-body systems, Phys. Rev. Lett. 119, 190402 (2017).
- Ma et al. [2019] R. Ma, B. Saxberg, C. Owens, N. Leung, Y. Lu, J. Simon, and D. I. Schuster, A dissipatively stabilized Mott insulator of photons, Nature 566, 51 (2019).
- Peraca et al. [2020] N. M. Peraca, A. Baydin, W. Gao, M. Bamba, and J. Kono, Ultrastrong light–matter coupling in semiconductors, in Semiconductors and Semimetals, Vol. 105 (Elsevier, 2020) pp. 89–151.
- Forn-Díaz et al. [2019] P. Forn-Díaz, L. Lamata, E. Rico, J. Kono, and E. Solano, Ultrastrong coupling regimes of light-matter interaction, Rev. Mod. Phys. 91, 025005 (2019).
- Kockum et al. [2019] A. F. Kockum, A. Miranowicz, S. De Liberato, S. Savasta, and F. Nori, Ultrastrong coupling between light and matter, Nat. Rev. Phys. 1, 19 (2019).
- Quijandría et al. [2018] F. Quijandría, U. Naether, S. K. Özdemir, F. Nori, and D. Zueco, PT -symmetric circuit QED, Phys. Rev. A 97, 053846 (2018).
- Lu et al. [2021] Y.-W. Lu, J.-F. Liu, R. Liu, R. Su, and X.-H. Wang, Quantum exceptional chamber induced by large nondipole effect of a quantum dot coupled to a nano-plasmonic resonator, Nanophotonics 10, 2431 (2021).
- Minganti et al. [2019] F. Minganti, A. Miranowicz, R. W. Chhajlany, and F. Nori, Quantum exceptional points of non-Hermitian Hamiltonians and Liouvillians: The effects of quantum jumps, Phys. Rev. A 100, 062131 (2019).
- Huber et al. [2020] J. Huber, P. Kirton, S. Rotter, and P. Rabl, Emergence of PT-symmetry breaking in open quantum systems, SciPost Phys. 9, 052 (2020).
- Arkhipov et al. [2021] I. I. Arkhipov, F. Minganti, A. Miranowicz, and F. Nori, Generating high-order quantum exceptional points in synthetic dimensions, Phys. Rev. A 104, 012205 (2021).
- Purkayastha et al. [2020] A. Purkayastha, M. Kulkarni, and Y. N. Joglekar, Emergent PT symmetry in a double-quantum-dot circuit QED setup, Phys. Rev. Research 2, 043075 (2020).
- Xie et al. [2021] D. Xie, C. Xu, and A. M. Wang, Parameter estimation and quantum entanglement in PT symmetrical cavity magnonics system, Results in Physics 26, 104430 (2021).
- Heiss [2012] W. D. Heiss, The physics of exceptional points, J. Phys. A: Math. Theor. 45, 444016 (2012).
- Miri and Alù [2019] M.-A. Miri and A. Alù, Exceptional points in optics and photonics, Science 363, eaar7709 (2019).
- Özdemir et al. [2019] Ş. K. Özdemir, S. Rotter, F. Nori, and L. Yang, Parity–time symmetry and exceptional points in photonics, Nat. Mater. 18, 783 (2019).
- Ashida et al. [2020] Y. Ashida, Z. Gong, and M. Ueda, Non-Hermitian physics, Advances in Physics 69, 249 (2020).
- Anappara et al. [2005] A. A. Anappara, A. Tredicucci, G. Biasiol, and L. Sorba, Electrical control of polariton coupling in intersubband microcavities, Appl. Phys. Lett. 87, 051105 (2005).
- Günter et al. [2009] G. Günter, A. A. Anappara, J. Hees, A. Sell, G. Biasiol, L. Sorba, S. De Liberato, C. Ciuti, A. Tredicucci, A. Leitenstorfer, and R. Huber, Sub-cycle switch-on of ultrastrong light–matter interaction, Nature 458, 178 (2009).
- Gao et al. [2018] W. Gao, X. Li, M. Bamba, and J. Kono, Continuous transition between weak and ultrastrong coupling through exceptional points in carbon nanotube microcavity exciton–polaritons, Nat. Photon. 12, 362 (2018).
- Doiron and Naik [2019] C. F. Doiron and G. V. Naik, Non-Hermitian Selective Thermal Emitters using Metal–Semiconductor Hybrid Resonators, Adv. Mater. 31, 1904154 (2019).
- Zhang et al. [2017] D. Zhang, X.-Q. Luo, Y.-P. Wang, T.-F. Li, and J. Q. You, Observation of the exceptional point in cavity magnon-polaritons, Nat Commun 8, 1368 (2017).
- Zhang et al. [2019] X. Zhang, K. Ding, X. Zhou, J. Xu, and D. Jin, Experimental observation of an exceptional surface in synthetic dimensions with magnon polaritons, Phys. Rev. Lett. 123, 237202 (2019).
- Noe II et al. [2016] G. T. Noe II, I. Katayama, F. Katsutani, J. J. Allred, J. A. Horowitz, D. M. Sullivan, Q. Zhang, F. Sekiguchi, G. L. Woods, M. C. Hoffmann, H. Nojiri, J. Takeda, and J. Kono, Single-shot terahertz time-domain spectroscopy in pulsed high magnetic fields, Opt. Exp. 24, 30328 (2016).
- Baydin et al. [2021] A. Baydin, T. Makihara, N. M. Peraca, and J. Kono, Time-domain terahertz spectroscopy in high magnetic fields, Front. Optoelectron. 14, 110 (2021).
- Tay et al. [2022] F. Tay, A. Baydin, F. Katsutani, and J. Kono, Magneto-optical Spectroscopy with RAMBO: A Table-Top 30 T Magnet, arXiv:2202.09732 (2022).
- Herrmann [1963] G. Herrmann, Resonance and high frequency susceptibility in canted antiferromagnetic substances, J. Phys. Chem. Solids 24, 597 (1963).
- Makihara et al. [2021] T. Makihara, K. Hayashida, G. T. Noe II, X. Li, N. Marquez Peraca, X. Ma, Z. Jin, W. Ren, G. Ma, I. Katayama, J. Takeda, H. Nojiri, D. Turchinovich, S. Cao, M. Bamba, and J. Kono, Ultrastrong magnon–magnon coupling dominated by antiresonant interactions, Nat. Commun. 12, 3115 (2021).
- Grishunin et al. [2018] K. Grishunin, T. Huisman, G. Li, E. Mishina, T. Rasing, A. V. Kimel, K. Zhang, Z. Jin, S. Cao, W. Ren, G.-H. Ma, and R. V. Mikhaylovskiy, Terahertz Magnon-Polaritons in TmFeO3, ACS Photonics 5, 1375 (2018).
- Shi et al. [2020] L. Y. Shi, D. Wu, Z. X. Wang, T. Lin, C. M. Hu, and N. L. Wang, Revealing strong magnon-photon coupling in a polar antiferromagnet Fe2Mo3O8 by time domain terahertz spectroscopy, arXiv:2004.05823 (2020).
- Li et al. [2018] X. Li, M. Bamba, N. Yuan, Q. Zhang, Y. Zhao, M. Xiang, K. Xu, Z. Jin, W. Ren, G. Ma, S. Cao, D. Turchinovich, and J. Kono, Observation of Dicke cooperativity in magnetic interactions, Science 361, 794 (2018).
- Zhang et al. [2016] Q. Zhang, M. Lou, X. Li, J. L. Reno, W. Pan, J. D. Watson, M. J. Manfra, and J. Kono, Collective non-perturbative coupling of 2D electrons with high-quality-factor terahertz cavity photons, Nat. Phys. 12, 1005 (2016).
- Huebl et al. [2013] H. Huebl, C. W. Zollitsch, J. Lotze, F. Hocke, M. Greifenstein, A. Marx, R. Gross, and S. T. B. Goennenwein, High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids, Phys. Rev. Lett. 111, 127003 (2013).
- Yuan and Wang [2017] H. Y. Yuan and X. R. Wang, Magnon-photon coupling in antiferromagnets, Appl. Phys. Lett. 110, 082403 (2017).
- Dicke [1954] R. H. Dicke, Coherence in spontaneous radiation processes, Phys. Rev. 93, 99 (1954).
- Yahiaoui et al. [2021] R. Yahiaoui, Z. A. Chase, C. Kyaw, F. Tay, A. Baydin, G. T. Noe II, J. Song, J. Kono, A. Agrawal, M. Bamba, and T. A. Searles, Tunable plasmonic ultrastrong coupling: Emulating Dicke physics at room temperature, arXiv:2108.02494 (2021).
- Bamba and Ishihara [2009] M. Bamba and H. Ishihara, Crossover of exciton-photon coupled modes in a finite system, Phys. Rev. B 80, 125319 (2009).