Magnetically supramassive neutron stars

Determining the chemical makeup that defines the equation of state (EOS) of neutron star matter constitutes one of the key open problems in high-energy astrophysics. Matching data from electromagnetic, and more recently gravitational-wave (GW), observations of extreme phenomena, such as short gamma-ray bursts (SGRBs), with theoretical predictions from general-relativistic magnetohydrodynamics (GRMHD) offers an invaluable tool in this respect. As evidenced by the joint GW-GRB event GW170817 detected by Fermi and the advanced Laser Interferometer GW Observatory (aLIGO) Abbott et al. (2017, 2018), neutron star mergers can be production sites for SGRBs, the prompt-emission and afterglow light-curves of which reveal unique information about the nature of the remnant Rowlinson et al. (2013); Ravi and Lasky (2014); Lasky and Glampedakis (2016); Suvorov and Kokkotas (2021).

If the merging stars are not too massive, a third, more extreme neutron star may emerge from the crash site rather than a black hole. It is generally posited that this star can have one of three fates depending on its mass, $M$, in relation to the maximum mass (for a given EOS) resulting from the integration of the Tolman-Oppenheimer-Volkoff (TOV) stellar structure equations, $M_{\text{{\tiny TOV}}}$: (i) Long-term stability, where the star survives indefinitely, for $M\leq M_{\text{{\tiny TOV}}}$; (ii) medium-term metastability for $M_{\text{{\tiny TOV}}}<M\lesssim 1.2M_{\text{{\tiny TOV}}}$, where uniform rotation stabilises the remnant (often termed ‘supramassive’; Stergioulas (2003)), or (iii) short-term metastability for $1.2M_{\text{{\tiny TOV}}}\lesssim M\lesssim 1.6M_{\text{{\tiny TOV}}}$, where differential rotation stabilises the remnant (‘hypermassive’; Weih et al. (2018)). In this Letter we suggest that the remnant neutron star has a fourth option, namely, long-term metastability, where the collapse is eventually instigated by core magnetic field decay. Such neutron stars could be fittingly called ‘magnetically supramassive’.

In particular, the magnetar subclass of neutron stars may contain extremely strong magnetic fields within their stellar cores, which could potentially help stabilise them against gravitational collapse Cardall et al. (2001); Stergioulas (2003); Dexheimer et al. (2017). Violent dynamo activity at birth Thompson and Duncan (1996), possibly in combination with the Kelvin-Helmholtz Ciolfi (2020) and magneto-rotational Reboul-Salze et al. (2021) instabilities, may thus facilitate the growth of magnetic pressures within the remnant to the point that the birth mass may non-negligibly exceed $M_{\text{{\tiny TOV}}}$, even without rapid rotation. Following a swift $(\gtrsim$ seconds) spin-down phase, the star would then survive on a magnetic-diffusion timescale on the order of $\sim 1-10$ years, depending on the core temperature, internal field strength, birth mass, and EOS Goldreich and Reisenegger (1992); Ho et al. (2012). Here we provide some analytic estimates for mass limits and collapse times of magnetically supramassive stars based on magneto-thermal arguments, finally offering some discussion on observational signatures of such objects, most notably from SGRBs.

In much the same way that rotational kinetic energy can help stave off gravitational collapse, so too can magnetic energy. The Lorentz force associated with the magnetic field contributes an effectively anisotropic stratification which, for poloidal fields, drives the star towards an oblate shape and can work together with the hydrostatic pressure to resist gravity Cardall et al. (2001); Dexheimer et al. (2017). Microphysical effects, such as Landau quantization and the spin polarization of neutrons within the stellar core, also start to influence the bulk properties of the star for ultra-strong magnetic fields Sedrakian et al. (2017). Overall, there is a secondary stiffening effect on the EOS for super-Schwinger fields Broderick et al. (2000), and even more massive stars can be produced. A rigorous calculation of the maximum mass sustained by a neutron star under the influence of rotation and/or a strong magnetic field requires the numerical integration of the GRMHD structure equations for a given realistic EOS. Fortunately, for the purposes of this work, this complication can be avoided and we can instead rely on a far simpler analytical approach based on energy arguments.

Consider first the classic, rotationally supramassive case. The maximum mass of a static configuration is $M_{\text{{\tiny TOV}}}$, though rotation contributes to the available energy pool and pushes this limit higher. Assuming a uniformly rotating star, the sum of the gravitational and rotational kinetic energies are $U_{\text{grav}}+U_{\text{rot}}=-3GM^{2}/5\lambda R+\tfrac{1}{2}I_{0}\Omega^{2}$, for moment of inertia $I_{0}\approx\tfrac{2}{5}MR^{2}$ and rotational velocity $\Omega$, where we have introduced the phenomenological parameter $\lambda$ to account for EOS and GR effects (for a uniform Newtonian model, $\lambda=1$). The maximum mass of the rotating configuration, $M_{\text{rot}}$, can then be estimated by considering a star rotating at the mass-shedding (Kepler) limit, $\Omega_{\rm K}\approx\sqrt{GM_{\text{{\tiny TOV}}}/R^{3}}$, and equating the sum of the kinetic and potential energies of this more massive star with the maximum binding energy available to a static star. Solving $-3GM_{\text{{\tiny TOV}}}^{2}/5\lambda R=-3GM_{\text{rot}}^{2}/5\lambda R+\tfrac{1}{2}I_{0}\Omega_{\rm K}^{2}$, we find $M_{\text{rot}}=M_{\text{{\tiny TOV}}}\sqrt{1+\tfrac{\lambda}{3}}$, which is in remarkably good agreement with the numerical simulations for $\lambda\lesssim 2$ Stergioulas (2003); Weih et al. (2018).

The above procedure can be similarly carried out with the magnetic energy, $U_{\text{mag}}=\tfrac{1}{6}B^{2}R^{3}$, in place of the rotational energy. Note, however, that $B$ here is not the surface field strength but rather a volume-averaged internal field strength, the magnitude of which may be dominated by the outer-core toroidal field or inner-core poloidal field. As such, even if a relatively conservative surface field is realised, $B_{\text{surf}}\lesssim 10^{16}\text{ G}$, the value of $B$ here could potentially approach the Virial limit, $B_{\rm max}\sim 10^{18}\lambda^{-1/2}(M/M_{\odot})(R/10\text{km})^{-2}$ G, depending on the field topology. We emphasise however that it is unclear whether fields of this strength are ever reached in Nature; even in merger simulations with large $(\sim 10^{15}$ G) seed fields, magnetic energies tend to saturate at a few times $10^{51}$ erg Ciolfi (2020); Shibata et al. (2021), implying an upper limit $B_{\text{max}}\sim 6\times 10^{16}(U_{\text{mag}}/2\times 10^{51}\text{ erg})^{1/2}(R/15\text{km})^{-3/2}$ G.

However, intense and largely unresolvable magnetic substructures are prevalent in many studies, and it is conceivable that greater amplifications could be attained if finer spatial grids, necessary to fully resolve the Kelvin-Helmholtz and/or magneto-rotational instabilities, are employed (see Ref. Ciolfi (2020) for a thorough discussion). On the observational side, there is reasonable evidence that at least some of the X-ray afterglows seen to follow many SGRBs are powered by spindown energy injections from a newborn magnetar (Ravi and Lasky, 2014; Lasky and Glampedakis, 2016; Suvorov and Kokkotas, 2021). In many cases, fittings within this paradigm favour polar fields $B_{p}$, again likely lower than the internal field strength, that are a few by $10^{16}\text{ G}$; in some rare instances though, most notably GRB 100625A, best-fit values of $B_{p}\gtrsim 10^{17}~{}\text{G}$ have been reported (Rowlinson et al., 2013). These estimates however assume perfectly efficient emissions, and therefore represent upper limits.

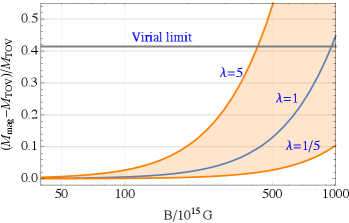
Either way, for the maximum magnetic mass we estimate

$$\frac{M_{\rm mag}}{M_{\text{{\tiny TOV}}}}=\left(1+\frac{5\lambda}{18}\frac{B^{2}R^{4}}{GM_{\text{{\tiny TOV}}}^{2}}\right)^{1/2}.$$

(1)

This result is again in reasonable agreement with the numerical calculations. For instance, for a $n=1$ polytropic EOS, Ref. Cardall et al. (2001) found that the (baryonic) mass increases from $2.19M_{\odot}$ to $2.28M_{\odot}$ (i.e., a $4\%$ increase) for a GR stellar model with radius $R=13.8$ km and magnetic dipole moment $\mu\approx BR^{3}/(2\sqrt{g_{rr}})=2\times 10^{35}\text{ G cm}^{3}$ (for Schwarzschild factor $g_{rr}$). This result, and others for the same EOS, matches well with the simple formula (1) for $\lambda\lesssim 3$. For the APR EOS Akmal et al. (1998) (which passes constraints coming from GW170817 Abbott et al. (2018)), we find instead $\lambda\sim 1$, unless $B\gtrsim 10^{18}$ G in which case the aforementioned stiffening results in a better-fit value $\lambda\gtrsim 2$ Cardall et al. (2001). Similar results are found using simulation data from other works for various EOS, such as Ref. Dexheimer et al. (2017). We therefore consider the range $0.2\leq\lambda\leq 5$ for demonstration purposes; Figure 1 illustrates the formula (1) in this respect.

A magnetic field residing in the interior of a neutron star can dissipate via the main mechanisms of Ohmic decay, likely accelerated by Hall drift, and ambipolar diffusion Goldreich and Reisenegger (1992). For the magnetic field-temperature parameter space relevant to the core of a newborn neutron star, the field decay is dominated by ambipolar diffusion. This mechanism involves the drift of the charged particles (protons and electrons) relative to the neutron fluid. The magnetic field, anchored to the charged fluids, follows this motion and the induction-generated electric field leads to magnetic flux transport and field line straightening. The drift culminates in the release of magnetic energy while heating up the star Goldreich and Reisenegger (1992); Ho et al. (2012).

The characteristic decay time for the magnetic field reads $\tau_{\rm amb}=L/w_{\rm amb}$, where $L$ denotes a typical distance over which the magnetic field varies and $w_{\rm amb}$ is the typical velocity lag between the charged and uncharged fluids. This lag is determined by the balance between the Lorentz force and the inter-particle collisional forces. Typically $\tau_{\rm amb}$ is broken up into solenoidal and irrotational components associated with the Helmholtz-Hodge decomposition of $\mathbf{w}_{\rm amb}$, though such a distinction is not necessary for our simple demonstration. The MHD equations associated with the system imply that Goldreich and Reisenegger (1992)

$$\tau_{\rm amb}\approx 25\,L_{5}^{2}\,B_{17}^{-2}\,T_{9}^{2}\,\left(\rho/\rho_{\text{nuc}}\right)^{2/3}\text{ yr},$$

(2)

where $L_{5}=L/10^{5}\,\mbox{cm}$, $B_{17}=B/10^{17}\,\mbox{G}$, and $T_{9}=T/10^{9}\,\mbox{K}$. (Note, however, that since $|\textbf{B}|/|\nabla\textbf{B}|\propto\ell^{-1}$ for a pure $\ell$-pole, $L$ may be lower in the early stages as the field unknots from a highly-tangled configuration, as would be expected in a newborn magnetar Thompson and Duncan (1996); Reboul-Salze et al. (2021), thereby accelerating the decay.)

A rigorous treatment of the ambipolar diffusion-driven decay of the magnetic field involves the numerical evolution of the system’s coupled GRMHD-thermal equations. However, and in spite of recent progress Passamonti et al. (2017), such calculation has not been completed yet. For the approximate analysis of this paper it is sufficient to work with the phenomenological evolution law Ho et al. (2012)

$$B(t)=B_{0}\left(1+\frac{t}{\tau_{\rm amb}}\right)^{-1}.$$

(3)

The ambipolar timescale, $\tau_{\rm amb}$, can be treated as a constant with fixed values of $B$ and $T$ during the magnetic field evolution or it can be promoted to a ‘dynamical’ parameter with a time-varying temperature $T(t)$. At densities $\rho\approx\rho_{\rm nuc}$, the stellar core is expected to cool via neutrino emission produced by the modified Urca reactions; the associated temperature law is given by Shapiro and Teukolsky (1983)

$$\frac{T_{\rm mU}(t)}{10^{9}\mbox{K}}=\left[\frac{t(\mbox{yr})}{(\rho/\rho_{\rm nuc})^{1/3}}+\left(\frac{10^{9}\,\mbox{K}}{T_{0}}\right)^{6}\right]^{-1/6},$$

(4)

where $T_{0}\sim 10^{11}\,\mbox{K}$ is a typical post-merger core temperature (see e.g. Foucart et al. (2016)). Examples of magnetic field evolution, as described by (3), are shown in Fig. 2; these include a case of static $\tau_{\rm amb}$ with $B=B_{0}=3\times 10^{17}\,\mbox{G}$ and $T_{9}=1$ as well as two cases of dynamical $\tau_{\rm amb}$ with $T=T_{\rm mU}(t)$ and $B=(B_{0},B_{0}/2)$ (i.e., this last case considers a four-fold increase in $\tau_{\rm amb}$). In all cases the $B(t)$ curve remains almost flat before its rapid decay at $t\gtrsim\tau_{\rm amb}$.

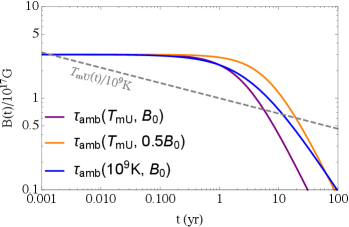
A reduction of $B$ by a sizable factor should cause the neutron star’s prompt collapse. The precise collapse timescale $t_{\rm col}$ is defined as the point where the birth mass, $M_{\rm min}$, comes to exceed the maximum sustainable by the combined (decaying) magnetic and (stable) hydrostatic pressures, i.e. when $M_{\rm mag}(t_{\rm col})=M_{\rm min}$. Examples of $t_{\rm col}(B_{0})$ are shown in Fig. 3 for $M_{\rm min}=1.03M_{\text{{\tiny TOV}}}$ and different choices of $\lambda$ and temperature evolution $T$ (i.e. static or dynamical $\tau_{\rm amb}$). The curves show marginal variation with $B_{0}$, which can be taken as evidence of a balance between a faster evolution/larger mass gap for higher $B_{0}$ and a slower evolution/smaller mass gap for lower $B_{0}$. According to these results, a magnetically supramassive star is unlikely to last more than a decade or so after its birth.

Owing to their extreme field strengths, magnetically supramassive stars should be especially active during their relatively short lifetimes. SGRBs with extended afterglow, which are thought to be (at least partially) powered by spindown energy injections from a newborn magnetar Rowlinson et al. (2013); Lasky and Glampedakis (2016), are a promising candidate regarding observational signatures. If indeed a magnetically supramassive star was born following a merger, the afterglow ‘plateau’ – an often-observed phase of roughly constant X-ray flux Ciolfi (2020) – should be short-lived because of intense spin-down, though the luminosity will be exceptionally high since $B$ is large. Importantly however, if the flux is abruptly truncated, this would indicate a cessation of the magnetar’s contribution and a rotationally-supramassive (or accretion-induced) collapse (Ravi and Lasky, 2014). In the magnetically-supramassive case, the magnetar engine will also eventually shut off, but the collapse should occur sufficiently late such that the drop is undetectable. Generally speaking, after an electromagnetic spin-down timescale, $\tau_{\text{em}}\sim 50\left(B_{p}/10^{16}\text{ G}\right)^{-2}\left(\nu/\text{kHz}\right)^{-2}$ s for spin frequency $\nu$, has elapsed, the X-ray luminosity, which traces the spin-down luminosity up to some efficiency factor, would be expected to decay quadratically until becoming invisible due to measurement noise. Prototypical examples in this class are GRBs 080702A, 100117A, and 100625A, the latter of which seemingly displayed an especially short-lived ($\gtrsim 10$ s) plateau followed by a power-law decay, and may have given birth to a magnetar with $B_{p}\gtrsim 10^{17}$ G Rowlinson et al. (2013); Suvorov and Kokkotas (2021).

Magnetically supramassive stars would be expected to collapse $\gtrsim$ years after birth. Once an event horizon inevitably comes to cloak the star, field lines will snap, inducing magnetic shocks that can accelerate electrons to relativistic velocities, producing radiation in the $\gtrsim$ GHz band. This mechanism, though considered only in the context of rotationally supramassive stars, was put forth as a progenitor for extragalactic fast radio bursts (FRBs) Falcke and Rezzolla (2014). We note that the emitted power in a curvature-radiation scenario scales as $B^{2}\nu^{2}$, and can accommodate the observed FRB energetics even for slow stars (i.e., at times $t\gg\tau_{\text{em}}$) if $B$ is large enough. Something of a ‘smoking gun’ for magnetically supramassive systems may then be a short-lived, bright plateau followed by a power-law decay (without an abrupt cutoff after $\sim 10^{2}$ s) after an SGRB, with a (non-repeating) FRB occurring $\gtrsim$ years later once collapse sets in. Such a scenario would be difficult to explain with a traditionally supramassive magnetar (since collapse would set in on the much-shorter spindown timescale Ravi and Lasky (2014)) or a black hole (since fallback accretion would have long since concluded Ciolfi (2020)).

Late-time X-ray flares are also observed in some afterglow light-curves, sometimes up to $\gtrsim 10^{6}$ seconds post prompt emission Bernardini et al. (2011). Even at times $t\ll\tau_{\rm amb}$, a non-negligible amount of energy may be liberated by ambipolar diffusion if $B$ is extremely large and thus, much like in the case of anomalous X-ray pulsars and soft-gamma repeaters Thompson and Duncan (1996), magnetic dissipation could be responsible for the triggering of these flares.

Besides their electromagnetic signature, neutron stars with $B_{17}\gtrsim 1$ magnetic fields are expected to sustain huge ellipticities (‘mountains’) $\epsilon$, thus becoming copious sources of GWs with characteristic amplitude $h\approx 4\times 10^{-24}(10\,\mbox{Mpc}/D)(\epsilon/10^{-2})(\nu/\text{kHz})^{2}$ before they have substantially spun down Lasky and Glampedakis (2016). Strains of this order may be detectable by aLIGO or next generation detectors, offering another route for observational constraints. The quasi-normal mode spectrum of an ultra-magnetised star would also be significantly shifted relative to that of an otherwise equal but unmagnetised star Lander et al. (2010), and thus the ringdown profile could be used as an indicator of whether the system is likely to be magnetically supramassive or not. It is also worth noting that to produce a supramassive remnant marginally heavier than $M_{\text{{\tiny TOV}}}$ in a coalescence, it is likely that the pre-merging stars would have to be relatively light, $M\lesssim 1.3M_{\odot}$, which has implications for GW emission and evolutionary modelling Foucart et al. (2016).

We conclude with a few remarks about future avenues on the modelling of magnetically supramassive stars. Based on our earlier discussion, these should include more rigorous, coupled magneto-thermal evolutions that include realistic EOS and superfluidity along the lines of Refs. Ho et al. (2012); Beloborodov and Li (2016) and the careful delimitation of the dUrca reactions’ parameter space. In parallel, future GRMHD simulations of coalescing neutron stars with their ever increasing resolution should be able to provide an improved understanding of the possibility of forming such objects.