Magnetic, transport and topological properties of Co-based shandite thin films
Abstract
The kagome ferromagnet, Co-based shandite Co3Sn2S2, shows a large anomalous Hall effect (AHE) associated with the Weyl nodes. A thin film with a Co kagome monolayer was predicted to exhibit the quantum AHE, which awaits the experimental realisation. However, it is challenging to precisely predict how the Weyl nodes reside in thin films where the lattice and electronic structures are in general different from the bulk. Here we report comprehensive ab initio results for thin films of Co3Sn2S2 with one, two and three Co layers with Sn or S surface terminations. We find that all the Sn-end films stabilise a ferromagnetic state similar to the bulk, and retain the large AHE down to the monolayer limit where the AHE is quantised, while the magnetic and topological properties drastically change with the number of Co layers in the S-end films. Our results would stimulate further experimental exploration of thin Weyl materials.
Introduction
After the prediction of the Berezinskii-Kosterlitz-Thouless transition and Haldane’s seminal work for a spontaneous quantum anomalous Hall effect (AHE) in two spatial dimensions, it has been widely recognised that condensed matters can be characterised using the concept of topology Nobel . The Weyl semimetals are a representative in three dimensions that have attracted much attention because of the variety of interesting physical properties arising from their unique topology AMV . The energy spectrum of the Weyl semimetals possesses Weyl nodes, which can be regarded as “monopoles” with chirality or in momentum space. The Weyl nodes always appear in pairs with positive and negative chirality NN , and this feature generates the Fermi arc on the surface through the bulk-edge correspondence Murakami , as indeed observed by the angle-resolved photoemission spectroscopy Xu ; Souma . The peculiar topology of the Weyl semimetals is also detected in quantum transport phenomena, such as the large AHE Murakami ; Burkov ; Suzuki , the anomalous Nernst effect (ANE) Sakai and the negative magnetoresistance associated with the chiral anomaly due to the monopoles Burkov ; XHuang ; Zhang .
A prescription for the Weyl semimetals is to lift the degeneracy in the Dirac nodes by breaking symmetry. The Weyl semimetals with broken spatial inversion symmetry have been confirmed in several materials, e.g., transition metal pnictides Xu ; Souma ; WFFBD and dichalcogenides Soluyanov ; Feng , whereas those with broken time-reversal symmetry have been rather scarce, with only a few theoretical proposals WTVS ; XWWDF ; KF and experiments under the magnetic field Suzuki ; Sakai . Recently, however, a kagome ferromagnet Co-based shandite, Co3Sn2S2, has been discovered to possess the Weyl nodes by spontaneous breaking of time-reversal symmetry, in the vicinity of meV from the Fermi level QXu ; Wang ; Liu . Indeed, theoretical and experimental studies revealed that the giant AHE and ANE observed in this compound are of the intrinsic contribution from the Weyl nodes QXu ; Wang ; Liu ; Guin ; Yang ; Minami ; Yanagi .
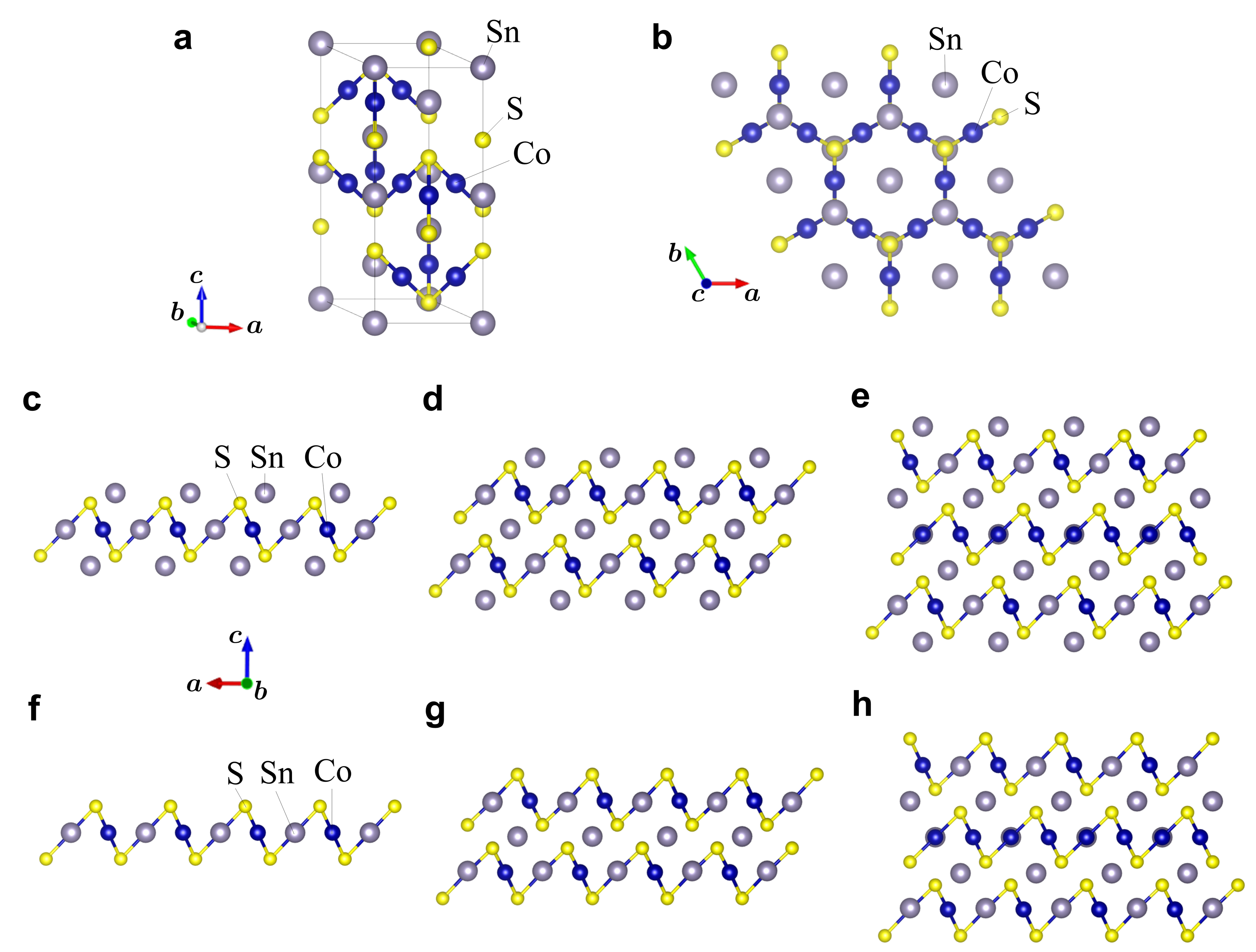
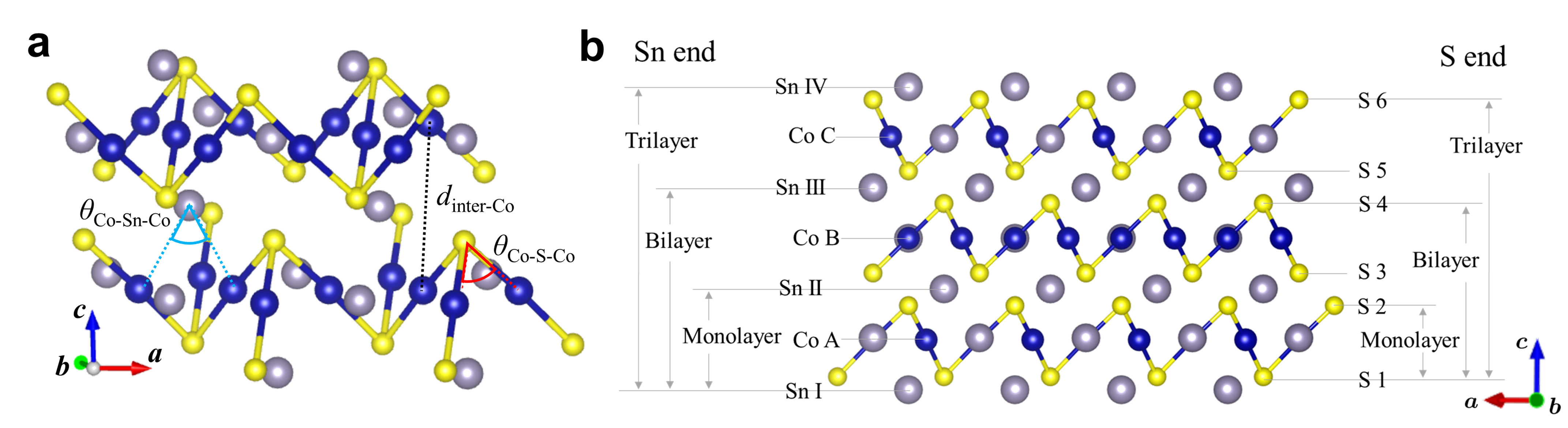
Co3Sn2S2 has a quasi-two-dimensional lattice structure with Co kagome layers, as shown in Fig. 1a, b. Recently, two types of Co kagome monolayers with different surface terminations, Co3Sn3S2 and Co3SnS2, were investigated theoretically Muechler . As a remnant of the Weyl nodes in the bulk, both monolayers are predicted to show a large AHE; especially in Co3Sn3S2 with Sn-end surfaces, the Weyl gap opens at the Fermi level, which leads to the quantum AHE. Stimulated by this theoretical prediction, experimental attempts to fabricate monolayer systems have been carried out, and the magnetism, transport phenomena and surface states have been discussed for atomically thin films of Co3Sn2S2 Fujiwara ; Shiogai ; Ikeda1 ; Ikeda2 . In the theoretical study, however, the lattice parameters were fixed at the bulk values for both monolayers, despite the fact that the lattice structures are expected to be relaxed in a different manner depending on the surface termination, sensitively affecting the magnetism and band topology of the atomically thin films GG ; BHuang . More importantly, since the Weyl points are the topological singularities predicted for the three-dimensional bulk systems, it remains elusive how they appear while changing the film thickness.
In this study, we perform comprehensive ab initio calculations of the band topology and transport properties for thin films of Co3Sn2S2, with special attention to the optimal lattice structures and stable magnetic states. We study monolayers, bilayers and trilayers of Co kagome planes with two different surface terminations by Sn and S atoms (Fig. 1c–h). From the obtained magnetic and electronic states, we compute the anomalous Hall conductivity and the anomalous Nernst conductivity. Through the systematic study in comparison with the bulk, we discuss the evolution of the topological properties with the number of kagome layers from one, two, three to infinity.
Results and discussions
Lattice structures and magnetic states. First, we optimise the lattice structures of each system (see Methods). The optimised structures are summarised in Table 1 (see also Supplementary Note 1). All the thin films maintain nearly the symmetry. Compared to the bulk, the in-plane lattice constants change by less than % for the Sn-end systems, while substantial decreases are observed for the S-end systems, maximally about % for the monolayer case. Such lattice deformation was not taken into account in the previous study for the monolayers Muechler . We note that the distance between the Co layers for bilayers and trilayers does not change so much from the bulk value, while it is slightly larger for the Sn-end systems than the S-end ones. We also estimate the differences in the formation energies between Sn-end and S-end thin films in each layer number (see Methods). The estimates suggest that the Sn-end monolayer, bilayer and trilayer are more stable than the S-end counterparts by , and eV per formula unit, respectively.
| System | Lattice constant | Co layer distance | Magnetic state | Co moment () | |
| Sn-end | monolayer | 5.325 | - | FM | 0.415 |
| bilayer | 5.355 | 4.434 | FM | 0.372 | |
| trilayer | 5.370 | 4.436 | FM | 0.365 (top, bottom) | |
| 0.362 (middle) | |||||
| S-end | monolayer | 5.194 | - | FM | 1.01 |
| bilayer | 5.276 | 4.410 | interlayer AFM | 0.339 | |
| trilayer | 5.310 | 4.412 | interlayer ferri | 0.207 (top, bottom) | |
| 0.080 (middle) | |||||
| bulk | 5.358 | 4.403 | FM | 0.350 | |
| 13.123 | |||||
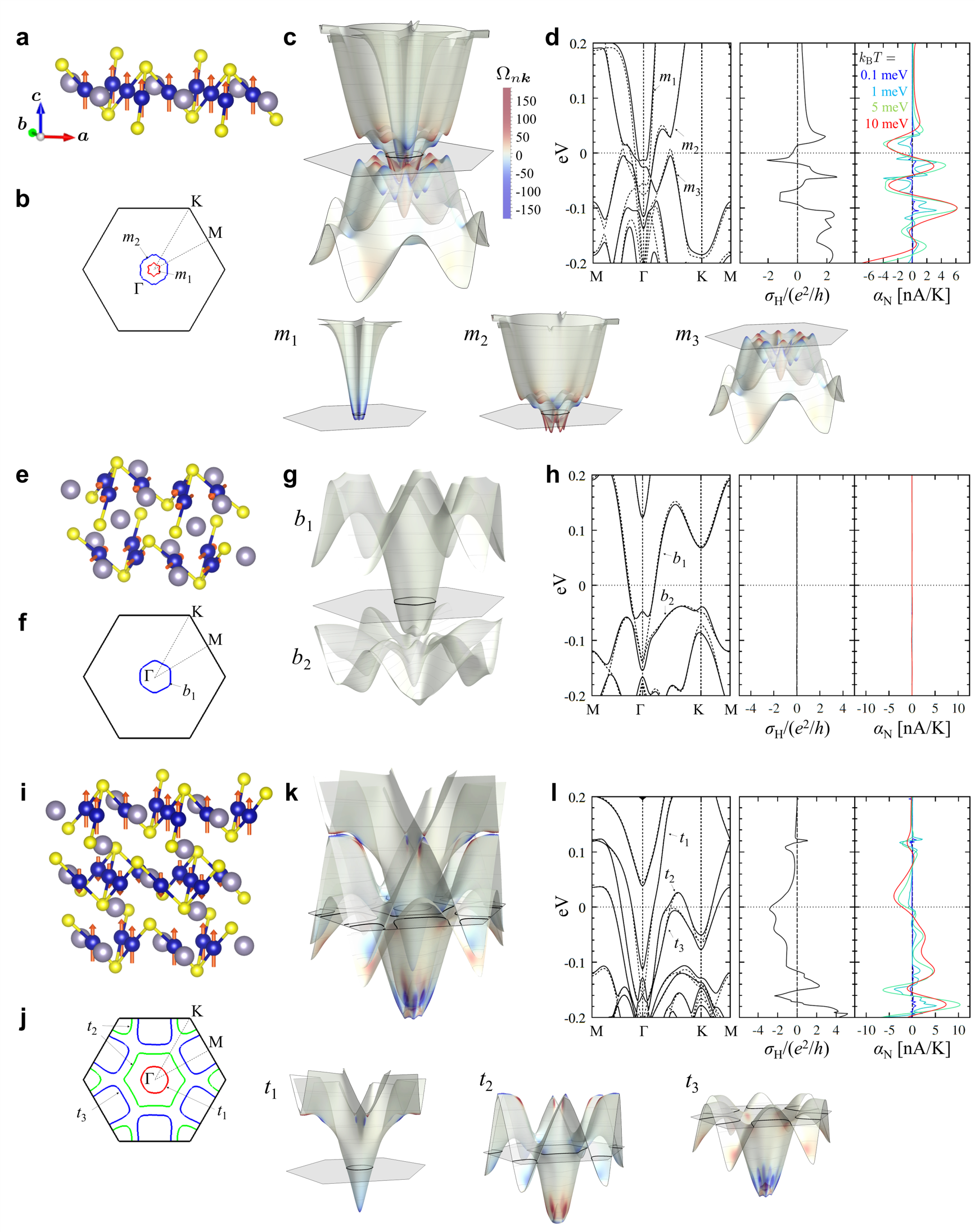
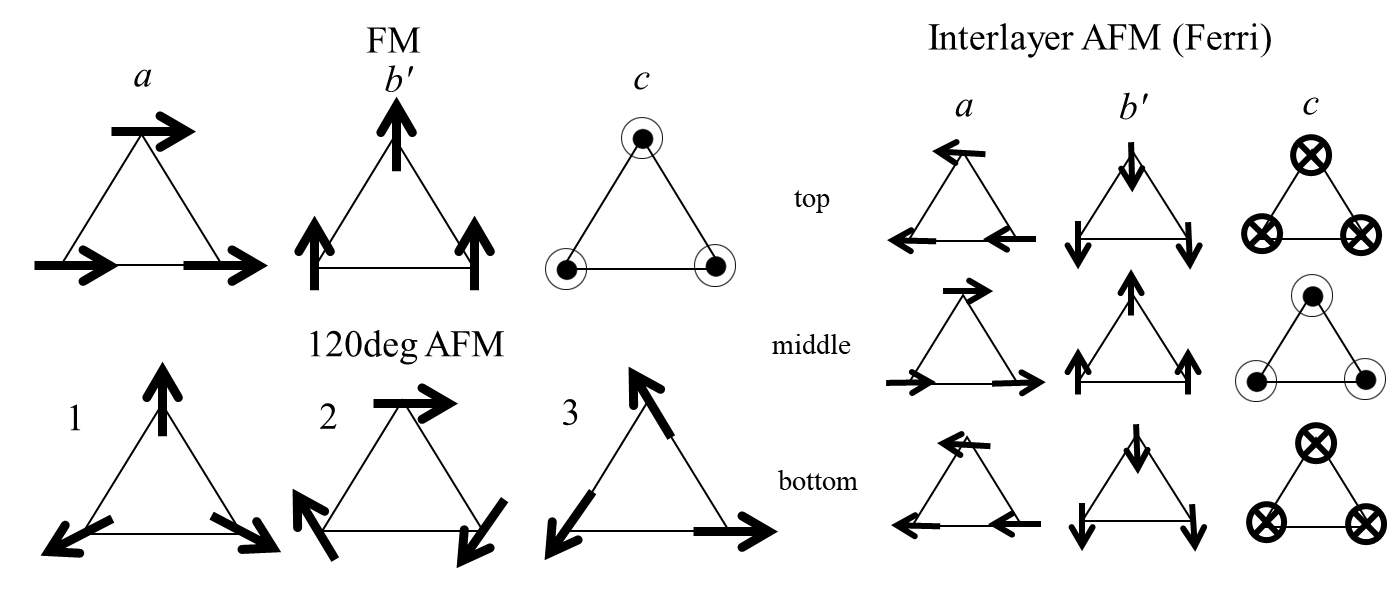
Next, for the optimised structures, we compare the ab initio energy for various magnetic states (see Supplementary Note 2). The lowest-energy states and the magnitudes of Co moments are summarised in Table 1 (see Methods); see also Fig. 2a, e, i, m and Fig. 3a, e, i. For the bulk, a ferromagnetic state is obtained with Co moment of along the out-of-plane direction, where is the Bohr magneton; the total magnetic moment per unit cell is because of small but nonzero antiparallel magnetic moments at Sn and S atoms. The result agrees well with the previous studies Liu ; Wang ; Yanagi . For the Sn-end thin films, similar out-of-plane ferromagnetic states are obtained for all the monolayer, bilayer and trilayer systems. The Co moment changes with the number of Co layers: for monolayer, for bilayer, and (top and bottom layers) and (middle layer) for trilayer; the value is monotonically reduced to the bulk one as the number of Co layers increases. We note that the net moment per primitive unit cell is , and for monolayer, bilayer and trilayer, respectively, indicating that the value per Co layer is the same as in the bulk. In contrast, for the S-end thin films, we obtain different magnetic states depending on the layer number: an out-of-plane ferromagnetic state for monolayer, an intralayer in-plane ferromagnetic and interlayer antiferromagnetic state for bilayer, and an intralayer out-of-plane ferromagnetic and interlayer ferrimagnetic state for trilayer, as shown in Fig. 3a, e, i, whose net magnetic moments per unit cell are , and , respectively. The Co moment is also largely different from the Sn-end cases: for monolayer, for bilayer, and (top and bottom layers) and (middle layer) for trilayer. The contrasting behaviours between the Sn- and S-end series are summarised in Fig. 4a.
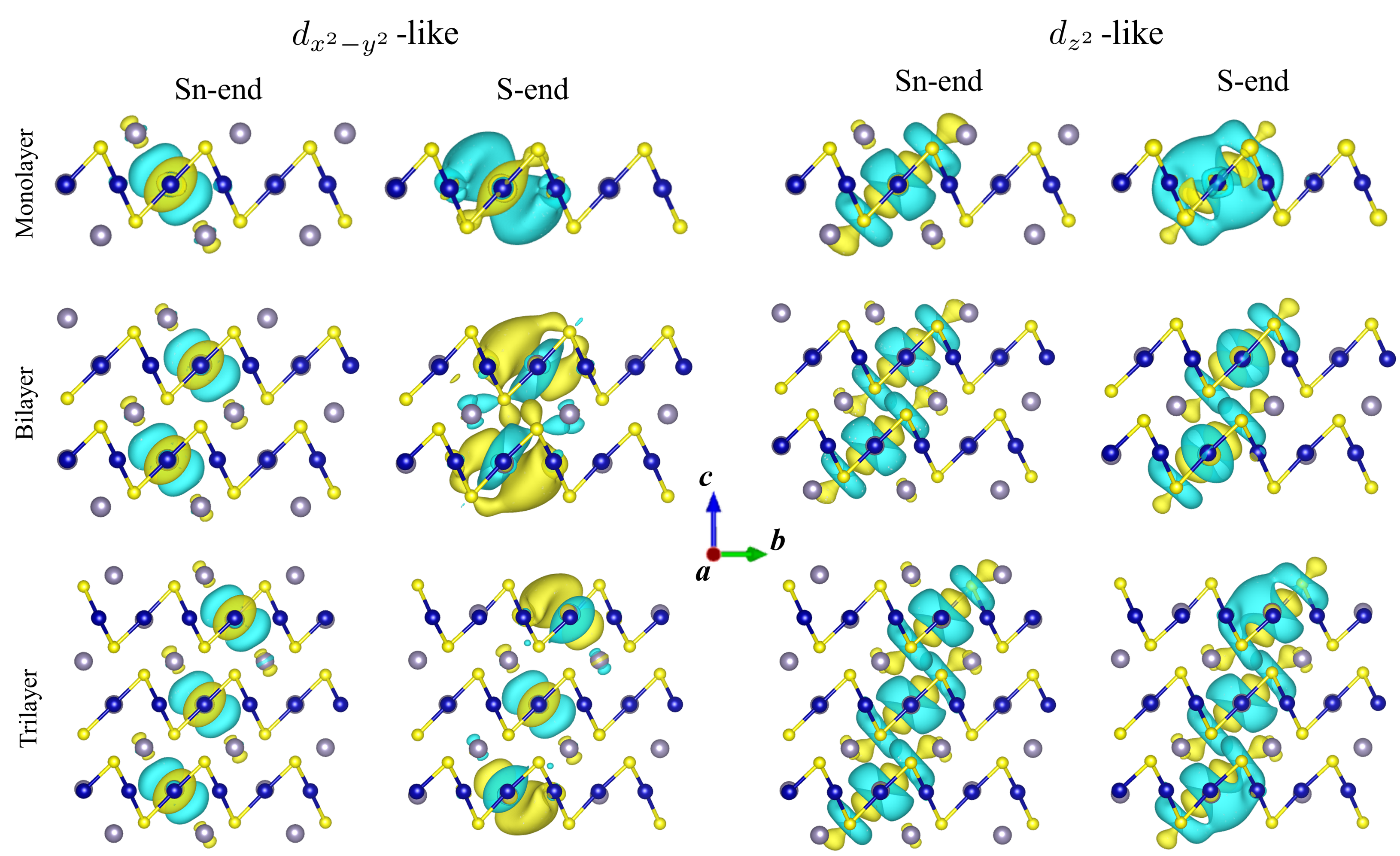
Our results indicate that the ferromagnetic order within each Co kagome layer is stable, regardless of the number of Co layers and the surface termination. In addition, the magnetic order has out-of-plane anisotropy, except for the S-end bilayer system. These suggest that the out-of-plane ferromagnetic state of the Co layer, which is a building block for the bulk system, is robust in most cases of thin films. Meanwhile, our results reveal that the surface termination matters to the interlayer magnetism as well as the magnetic anisotropy. Analysing the maximally-localised Wannier functions, we indeed find that the spatial extensions of the Co orbitals are substantially different for different surface terminations, which would be relevant to the interlayer magnetic interactions (see Supplementary Note 3).
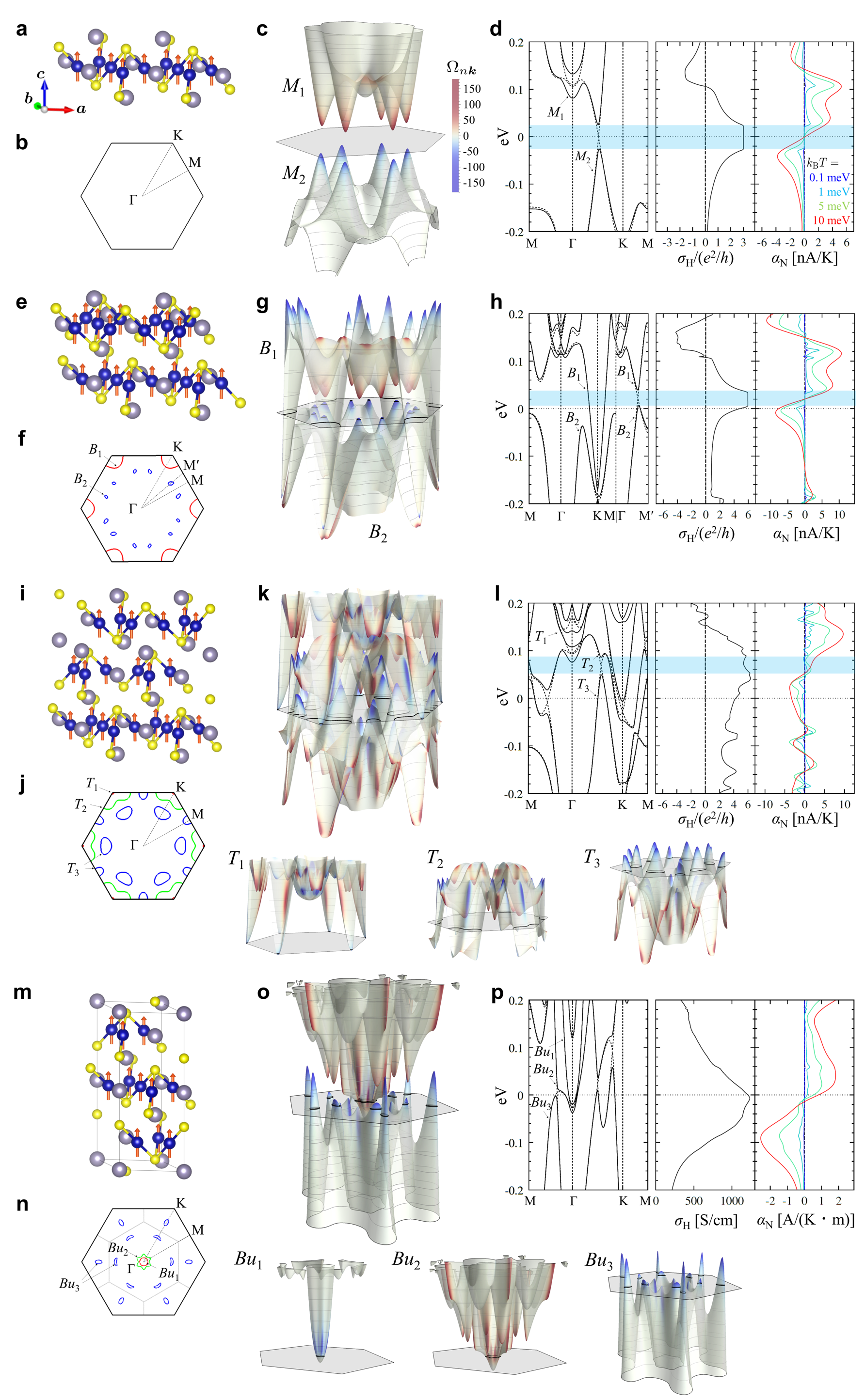
Electronic structures and band topology. The differences in the lattice structures and the stable magnetic states result in qualitatively different electronic states between the Sn- and S-end series. We show the Fermi surfaces in Fig. 2b, f, j, n and Fig. 3b, f, j and the band structures near the Fermi level in Fig. 2c, g, k, o and Fig. 3c, g, k. In the band structures, we also plot the Berry curvature for each band by colour which is computed for the tight-binding models constructed by the Wannier functions obtained from the ab initio calculations; we calculate the Chern number of each band as well (see Methods).
Let us first discuss the Sn-end films in Fig. 2. In the case of the monolayer, the band structure has a gap of meV at the Fermi level between the bands and , and there is no Fermi surface. The bands and have the Chern number and , respectively. The gap is opened by the spin-orbit coupling at the Weyl nodes on the - line in momentum space, resulting in the large values of the Berry curvatures near the band top and bottom. Thus, the system is an insulator with the Weyl gap, as pointed out in the previous study without structural optimisation Muechler . This is reasonable, given the little changes in the lattice structure as well as the magnetism after the optimisation in our calculations. In the bilayer, however, the system becomes metallic with the electron Fermi surfaces around the point in the band and the pairs of the hole pockets on both sides of each - line in the band . The Chern numbers of the bands and are and , respectively. By closely looking at the band structure, we can identify the Weyl gap of meV between and slightly above the Fermi level, which appears to correspond to that in the monolayer case but split into two, leading to the hole pocket pair; see also the band structure in Fig. 2h. In the trilayer system, the band structure becomes more complicated, but still retains the characteristic features in the monolayer and bilayer: One of the Weyl gaps opens between the bands and on the -K line above the Fermi level, while the other two are along the -M line, as shown in the band structure in Fig. 2l. The Chern numbers of the bands , and are , and , respectively. These overall systematic changes of the electronic states appear to smoothly connect to the bulk. In fact, as shown in Fig. 2n, o, the cut of the bulk band structure shows similar distribution of the Weyl gap and the Berry curvature to the above Sn-end films. In particular, the large Berry curvature in the Sn-end films can be regarded as a remnant of the intersections of the nodal gap in the bulk system QXu ; Minami . Thus, in the Sn-end series, where the out-of-plane ferromagnetic state persists, the electronic structure and the topological properties change systematically as the number of Co layers increases.
Next, we discuss the S-end cases. In the monolayer, the system is metallic with two electron pockets around the point as shown in Fig. 3b, in contrast to the Sn-end case. The result is also different from the previous study without structural optimisation Muechler . The difference is ascribed to the substantial shrinkage of the lattice constants shown in Table 1. We find considerable values of the Berry curvature in the bands close to the Fermi level, which affect the transport properties as discussed later. In the case of the bilayer, the system is also metallic with one electron pocket around the point; all the bands are doubly degenerate due to the interlayer antiferromagnetic ordering, cancelling out the Berry curvature. In the trilayer, there are three bands forming two electron pockets around the point, one electron pocket around the K point, and one hole pocket around the M point. In each band, the Berry curvature takes nonzero values, similar to the monolayer case. In addition, we find two small Weyl gaps between the bands and along the - line and another one between and along - line close to the Fermi level. Although this apparently resembles the case of Sn-end trilayer and bulk systems, these bands show qualitatively different Berry curvatures due to the different magnetic state. Thus, in stark contrast to the Sn-end cases, the S-end series shows no systematic change not only in the magnetic orders but also in the electronic structure and the band topology.
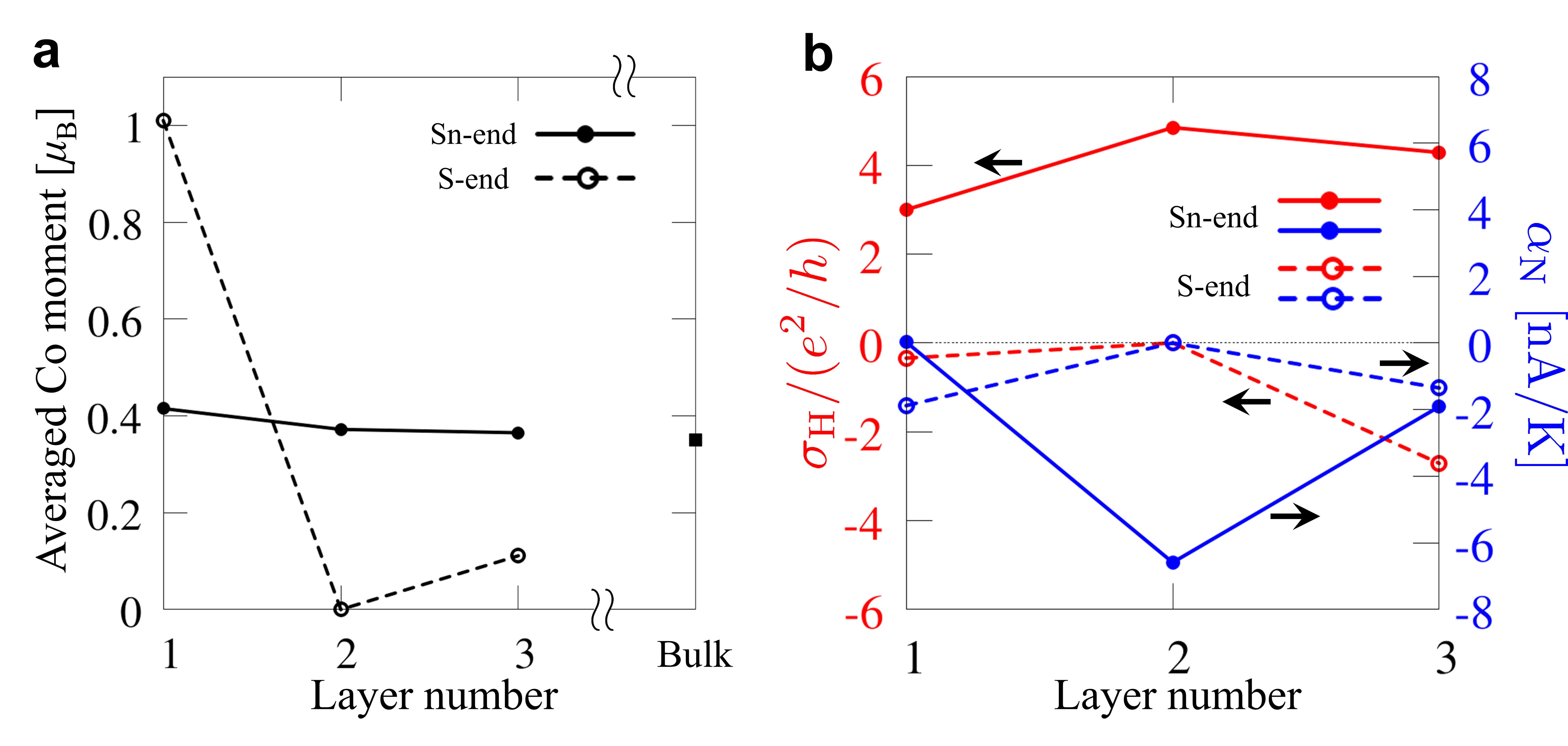
Transport properties. Now we turn to the transport properties. First of all, in the bulk case, our results on the anomalous Hall conductivity and the anomalous Nernst conductivity well reproduce the previous ones Liu ; Wang ; Yanagi , as shown in Fig. 2p. Then, in the Sn-end series, the monolayer shows a quantised AHE with , where and are the elementary charge and the Planck constant, respectively, corresponding to the Weyl gap in the blue-shaded energy window in Fig. 2d including the Fermi level. The result coincides with the previous one without structural optimisation Muechler . In the bilayer, we find that exhibits a plateau at slightly above the Fermi level in the blue-shaded region, which corresponds to the Weyl gap between the bands and , as shown in Fig. 2h. The plateau with almost twice of the monolayer case is due to the systematic change of the band structure from monolayer to bilayer mentioned above. Note that the contribution from the band crossing the Fermi level is negligible. Such a plateau is absent in the trilayer case, but a large value of is still observed in the energy window corresponding to the gap between the bands and , as shown in Fig. 2l. Thus, in the Sn-end series, we obtain systematic evolution of the AHE, from the quantum AHE in the monolayer to the large AHE in the bulk limit, reflecting the band structure with the Weyl gap. We note that is always positive in the Sn-end series. The results are summarised in Fig. 4b.
In contrast, does not show systematic changes in the S-end cases, as shown in Fig. 3d, h and l: , and for the monolayer, bilayer and trilayer, respectively. The absence of the AHE in the bilayer case is due to the cancellation of the Berry curvature by the band degeneracy discussed above, and the negative values of for the monolayer and trilayer originate from the different band topology from the Sn-end series. Note that in the monolayer case, is largely different from that of the previous study Muechler because of the structural optimisation.
We also compute the anomalous Nernst conductivity for both series of the films. According to the generalised Mott formula XYFN ; Yanagi , is related with the energy derivative of . This holds for our results, as plotted in Fig. 2d, h, l, p and Fig. 3d, h, l. In the Sn-end series, is almost zero at the Fermi level for the monolayer because of the quantisation of , while it takes a negative value for the bilayer and trilayer cases corresponding to the positive derivative of . Interestingly, takes a large negative value for the bilayer since the Fermi level is on the verge of the plateau-like feature of where increases rapidly. Since is positive in the bulk, our results suggest a sign change while increasing the number of Co layers, in contrast to . Meanwhile, in the S-end cases, vanishes for the bilayer, while it takes small negative values for the monolayer and trilayer. The layer number dependences for both cases are summarised in Fig. 4b.
Coulomb interactions. Let us comment on the effect of Coulomb interactions. We tested the GGA+ calculation for the S-end monolayer and bilayer systems. The results indicate that the S-end monolayer maintains the metallic state with modifications of the band structure, while the S-end bilayer shows a transition to the FM state around eV (see Supplementary Note 4). However, in the bulk Co shandite, the results using the GGA+ method are inconsistent with experimental findings YXu , suggesting that this method is not be suitable for this compound. Instead, a renormalisation of the band structure obtained by the GGA method explains well the ARPES measurements DFLiu and optical responses YXu ; Okamura . Given the smooth connection to the bulk in the Sn-end systems, we expect that this holds also for the thin films studied here and our GGA results would be useful for comparison with experiments. Further investigation on the effect of Coulomb interactions is left to future research.
Conclusions
Our systematic ab initio study for the thin films of Co-based shandite revealed that the number of Co kagome layers and the surface termination are both relevant to the lattice structure, the magnetic state, the electronic band structure and its topology, and transport properties. We found that the Sn-end series shows similar behaviours to the bulk, and retains the large AHE down to the monolayer limit where the quantum AHE is realised, reflecting the systematic change of the gapped Weyl nodes in the band structure. In contrast, the S-end series exhibits nonmonotonic behaviours with respect to the layer number, owing to the dominantly antiferromagnetic interlayer coupling. Our results would stimulate further experimental studies of the thin films of Co-based shandite to realise the quantum AHE in the monolayer form. The important implication of our results is that the measurements of the AHE and ANE as well as the magnetism will distinguish the film thickness and the surface termination, both of which are usually hard to directly identify in experiments. In particular, the sign of , which is positive in the Sn-end films while negative in the S-end films, can be relevant measurement. Furthermore, the different sign of from the bulk will also be useful to measure the film thickness. Furthermore, our prediction of the systematic evolution of the topological band structure would stimulate optical measurements, which have been useful to detect the chirality and gap structure of the Weyl nodes away from the Fermi level Ma ; YXu ; Okamura .
Methods
DFT calculation. The OpenMX code OpenMX ; Ozaki was used for structural optimisation and electronic structure calculations based on the density functional theory (DFT). The exchange-correlation functional was considered within the generalised gradient approximation (GGA) proposed by Perdew-Burke-Ernzerhof (PBE) PBE and the norm-conserving pseudopotentials were used. The Kohn-Sham wave functions were expressed by superpositions of pseudo-atomic orbitals as a basis set, which are chosen as Co6.0S-s3p2d1, Sn7.0-s3p2d2 and S6.0-s2p2d1 for bulk and monolayers, and Co6.0S-s3p3d3, Sn7.0-s4p3d1 and S6.0-s2p2d1 for bilayers and trilayers; see Ref. OpenMX for the details. For the calculations of thin films, we prepared the slabs with the bulk in-plane lattice parameter ( Li ) and inserted the vacuum space along the axis which is larger than . The quasi-Newton method was used for the relaxation of the atomic positions and the lattice vectors until the residual force becomes lesser than per atom. The structural optimisation was performed by nonrelativistic calculations for the ferromagnetic state, except for the S-end bilayer and trilayer systems, where we took interlayer antiferromagnetic and ferrimagnetic states, respectively. Then, the electronic structure calculations were performed by the fully relativistic calculations TH , which incorporate the effect of spin-orbit coupling, for various magnetic states (ferromagnetic, collinear antiferromagnetic and 120-degree noncollinear antiferromagnetic for the intraplane, and ferromagnetic and antiferromagnetic for the interplane), and employ the lowest-energy solution. We set the cutoff energy for the FFT grid to 1800 Ry, and sampled the Brillouin zone with and -points for the thin films and the bulk, respectively. We confirmed that the lowest-energy magnetic states do not change in the calculations with and -points. We estimated the difference in the formation energy Freysoldt ; SZTZ between Sn-end and S-end thin films. The formation energy for each surface termination is given as , where is total DFT energy, is the layer number and denotes Sn-end and S-end films, respectively. The difference in the formation energy of the -layer films is calculated as We here set the relative chemical potential as zero for each element; comprehensive studies considering various chemical potentials should be done more systematically elsewhere SZTZ . The local magnetic moments are calculated from the Mulliken population analysis.
Band topology and transport properties. The Bloch functions obtained by the DFT calculations were projected to the Wannier functions within the maximal localisation procedure MV ; SMV using the OpenMX code WOT . We employed Co , Sn and , and S orbitals. The target Bloch states were chosen by setting the outer energy window properly for each system; we confirmed that the tight-binding models constructed from the Wannier functions well reproduced the original DFT band structure within the inner energy window which was also properly chosen for each case. Using the obtained tight-binding models, the anomalous Hall conductivity and the anomalous Nernst conductivity were calculated based on the Kubo formula:
| (1) | ||||
| (2) |
respectively, where is the Boltzmann constant, is Dirac’s constant, is a -dimensional volume of the system, and are the Fermi distribution function and the entropy density, respectively; the summations are taken for the wave number within the first Brillouin zone and for the band index . In Eqs. (1) and (2), is the Berry curvature calculated by
| (3) |
with the current operator
| (4) |
where and are the band indices, , is the tight-binding Hamiltonian obtained from the maximally-localised Wannier functions, and and are the eigenvalue and the eigenvector of , respectively. In addition, we calculate the Chern number for the each band by FHS
| (5) |
where is calculated at each plaquette on the equally-spaced -grid in the first Brillouin zone. The number of the -mesh in the first Brillouin zone was taken as for monolayers and bilayers, for the S-end trilayer, for the Sn-end trilayer and for the bulk. As for , the temperatures are set as 0.1, 1, 5 and 10 meV, which are chosen to be lower than the Curie temperature 130 K of the thin films with the thickness 1.3 nm (roughly correspond to the trilayer) Ikeda1 .
Acknowledgements
The authors thank M. H. N. Assadi, K. Fujiwara, K. Nomura, S. Okumura, A. Ozawa and A. Tsukazaki for fruitful discussions. The parts of the calculation have been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo. This work is supported by JST CREST (Grant No. JPMJCR18T2) and JSPS KAKENHI (Grant No. JP21K13875 and JP22K03509).
References
- (1) Gibney, E. & Castelvecchi, D. Physics of 2D exotic matter wins Nobel, Nature 538, 18 (2016).
- (2) Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys. 90, 015001 (2018).
- (3) Nielsen, H. B. & Ninomiya, M. The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal, Phys. Lett. B 130, 389 (1983).
- (4) Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase, New J. Phys. 9, 356 (2007).
- (5) Xu, S.-Y. et al. Discovery of a Weyl Fermion Semimetal and Topological Fermi Arcs, Science 349, 613 (2015).
- (6) Souma, S. et al. Direct observation of nonequivalent Fermi-arc states of opposite surfaces in the noncentrosymmetric Weyl semimetal NbP, Phys. Rev. B 93, 161112(R) (2016).
- (7) Burkov, A. A. Chiral anomaly and transport in Weyl metals, J. Phys.: Condens. Matter 27, 113201 (2015).
- (8) Suzuki, T. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet, Nat. Phys. 12, 1119 (2016).
- (9) Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal, Nat. Phys. 14, 1119 (2018).
- (10) Huang, X. et al. Phys. Rev. X 5, 031023 (2015).
- (11) Zhang, C.-L. et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal, Nat. Commun. 7, 10735 (2016).
- (12) Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides, Phys. Rev. X 5, 011029 (2015).
- (13) Soluyanov, A. A. et al. Type-II Weyl semimetals, Nature 527, 495 (2015).
- (14) Feng, B. et al. Spin texture in type-II Weyl semimetals WTe2, Phys. Rev. B 96, 195134 (2016).
- (15) Wan, X. G., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates, Phys. Rev. B 83, 205101 (2011).
- (16) Xu, G., Weng, H. M., Wang, Z. J., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4. Phys. Rev. Lett. 107, 186806 (2011).
- (17) Kübler, J. & Felser, C. Weyl points in the ferromagnetic Heusler compound Co2MnAl, Europhys. Lett. 114, 47005 (2016).
- (18) Xu, Q. et al. Topological surface Fermi arcs in the magnetic Weyl semimetal Co3Sn2S2, Phys. Rev. B 97, 235416 (2018).
- (19) Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions, Nat. Commun. 9, 3681 (2018).
- (20) Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal, Nat. Phys. 14, 1125 (2018).
- (21) Guin, S. N. et al. Zero-Field Nernst Effect in a Ferromagnetic Kagome-Lattice Weyl-Semimetal Co3Sn2S2, Adv. Mater. 31, 1806622 (2019).
- (22) Yang, H. et al. Giant anomalous Nernst effect in the magnetic Weyl semimetal Co3Sn2S2, Phys. Rev. Mater. 4, 024202 (2020).
- (23) Minami, S. et al. Enhancement of the transverse thermoelectric conductivity originating from stationary points in nodal lines, Phys. Rev. B 102, 205128 (2020).
- (24) Yanagi, Y. et al. First-principles investigation of magnetic and transport properties in hole-doped shandite compounds Co3InxSn2-xS2, Phys. Rev. B 103, 205112 (2021).
- (25) Muechler, L. et al. Emerging chiral edge states from the confinement of a magnetic Weyl semimetal in Co3Sn2S2, Phys. Rev. B 101, 115106 (2020).
- (26) Fujiwara, K. et al. Ferromagnetic Co3Sn2S2 thin films fabricated by co-sputtering, Jpn. J. Appl. Phys. 58, 050912 (2019).
- (27) Shiogai, J. et al. Robust perpendicular magnetic anisotropy of Co3Sn2S2 phase in sulfur deficient sputtered thin film, Phys. Rev. Mater. 5, 024403 (2021).
- (28) Ikeda, J. et al. Critical thickness for the emergence of Weyl features in Co3Sn2S2 thin films, Commun. Mater. 2, 18 (2021).
- (29) Ikeda, J. et al. Two-dimensionality of metallic surface conduction in Co3Sn2S2 thin films, Commun. Phys. 4, 117 (2021).
- (30) Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures, Nature 499, 419 (2013).
- (31) Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature 546, 270 (2017).
- (32) Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-Phase Effect in Anomalous Thermoelectric Transport, Phys. Rev. Lett. 97, 026603 (2006).
- (33) Xu, Y. et al. Electronic correlations and flattened band in magnetic Weyl semimetal candidate Co3Sn2S2, Nat. Commun. 11, 3985 (2020).
- (34) Liu, D. F. et al. Magnetic Weyl semimetal in a kagomé crystal. Science 365, 1282 (2019).
- (35) Okamura, Y. et al. Giant magneto-optical responses in magnetic Weyl semimetal Co3Sn2S2, Nat. Commun. 11, 4619 (2020).
- (36) Ma, Q. et al. Direct optical detection of Weyl fermion chirality in a topological semimetal, Nat. Phys. 13, 842 (2017).
- (37) http://www.openmx-square.org.
- (38) Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures Phys. Rev. B.67, 155108, (2003).
- (39) Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996).
- (40) Li, G. et al. Surface states in bulk single crystal of topological semimetal Co3Sn2S2 toward water oxidation, Sci. Adv. 5, eaaw9867 (2019).
- (41) Theurich, G. & Hill, N. A. Self-consistent treatment of spin-orbit coupling in solids using relativistic fully separable ab initio pseudopotentials, Phys. Rev. B 64, 073106 (2001).
- (42) Freysoldt, C. et al. First-principles calculations for point defects in solids, Rev. Mod. Phys. 86, 253 (2014).
- (43) Sin, C.-K., Zhang, J., Tse, K. & Zhu, J. A brief review of formation energies calculation of surfaces and edges in semiconductors, J. Semicond. 41, 061101(2020).
- (44) Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands, Phys. Rev. B 56, 12847 (1997).
- (45) Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands, Phys. Rev. B 65, 035109 (2001).
- (46) Weng, H., Ozaki, T. & Terakura, K. Revisiting magnetic coupling in transition-metal-benzene complexes with maximally localized Wannier functions, Phys. Rev. B 79, 235118 (2009).
- (47) Fukui, T., Hatsugai, Y. & Suzuki, H. Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances, J. Phys. Soc. Jpn. 74, 1674 (2005).
- (48) Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, J. Appl. Cryst. 44, 1272 (2011).
Supplementary Information for “One, two, three, infinity: topological properties of thin films of Co-based shandite”
Supplementary Note 1: Details of the optimized lattice structures
We present additional information of the optimised lattice structures in Supplementary Table 1: the averaged angles for neighbouring Co-Sn-Co and Co-S-Co bonds, and , respectively, and the averaged bond lengths of the nearest-neighbour Co ions in different layers, . In most cases, the bond angles and lengths do not change so much from the bulk values, except for at the surfaces.
| System | (degree) | (degree) | ||
|---|---|---|---|---|
| Sn-end | monolayer | 58.8 (A-I, A-II) | 73.6 (A-1, A-2) | - |
| bilayer | 60.4 (A-I, B-IV) | 73.1 (A-1, B-4) | 4.69 | |
| 58.9 (A-II, B-II) | 77.5 (A-2, B-3) | |||
| trilayer | 60.6 (A-II, C-IV) | 73.3 (A-1, C-6) | 4.67 | |
| 59.0 (A-II, C-III) | 77.6 (A-2, C-5) | |||
| 59.6 (B-II, B-III) | 76.4 (B-3, B-4) | |||
| S-end | monolayer | - | 72.0 (A-1, A-2) | - |
| bilayer | 58.1 (A-II, B-II) | 71.9 (A-1, B-4) | 4.65 | |
| trilayer | 76.9 (A-2, B-3) | 4.66 | ||
| 58.5 (A-II, C-III) | 71.3 (A-1, C-6) | |||
| 78.7 (A-2, C-5) | ||||
| 58.5 (B-II, B-III) | ||||
| 75.4 (B-3, B-4) | ||||
| bulk | 60.0 | 76.1 | 4.64 | |
Supplementary Note 2: Energy comparison for various magnetic states
We show in Supplementary Table 2 the energy for different magnetic states obtained by the fully relativistic ab initio calculations for the optimised lattice structures. As listed in Supplementary Figure 2, we took the initial states as ferromagnetic (FM) states, 120 degree noncollinear antiferromagnetic (120AFM) states, and intralayer FM and interlayer collinear antiferromagnetic (IAFM) states [interlayer collinear ferrimagnetic (IFRM) state for trilayer]. For the FM states, we considered three types whose magnetic moments are along the out-of-plane () and two in-plane ( and ) directions; for the 120AFM states, we considered three types with different chirality and helicity; for the IAFM states, we considered three types similar to the FM cases. For the Sn-end systems, the FM states with the out-of-plane magnetic moments are the most stable, similar to the bulk, with the energy differences from the in-plane FM states being about 12 meV. In contrast, for the S-end systems, the stable magnetic states and the directions of the magnetic moments depend on the layer number as described in the main text. The energy differences between the most stable states and the other competing states are less than meV, which are smaller than the Sn-end cases. This implies that the magnetic anisotropy is smaller for the S-end films than the Sn-end ones.
| System | PM | FM | 120AFM | IAFM/IFRM | |||||
| Sn-end | monolayer | 122 | 0.993 | 1.01 | 0 | 85.7 | - | - | - |
| bilayer | 162 | 1.57 | 1.60 | 0 | 128 | 30.1 | 30.1 | 29.3 | |
| trilayer | 219 | 2.28 | 2.28 | 0 | 195 | 71.4 | 71.4 | 70.4 | |
| S-end | monolayer | 393 | 0.033 | 0.034 | 0 | 162 | - | - | - |
| bilayer | 79.7 | 28.6 | 28.5 | 29.5 | - | 0.009 | 0 | 0.532 | |
| trilayer | 34.7 | 22.9 | 23.1 | 22.8 | - | 0.030 | 0.046 | 0 | |
| bulk | 58.1 | 0.619 | 0.623 | 0 | - | - | - | - | |
Supplementary Note 3: Maximally-localized Wannier functions for orbitals
We display the maximally-localised Wannier functions with Co and orbital characters in Supplementary Figure 3, which are mostly different between the Sn- and S-end films among the orbitals. The results are obtained for the paramagnetic state by the relativistic calculations. In all cases, the Wannier functions in the S-end systems, especially of the Co ions near the surfaces, have wider spatial extensions to the interlayer directions. This difference leads to different overlaps of the wave functions between the Sn- and S-end systems, possibly being relevant to the difference in the interlayer magnetic interactions.
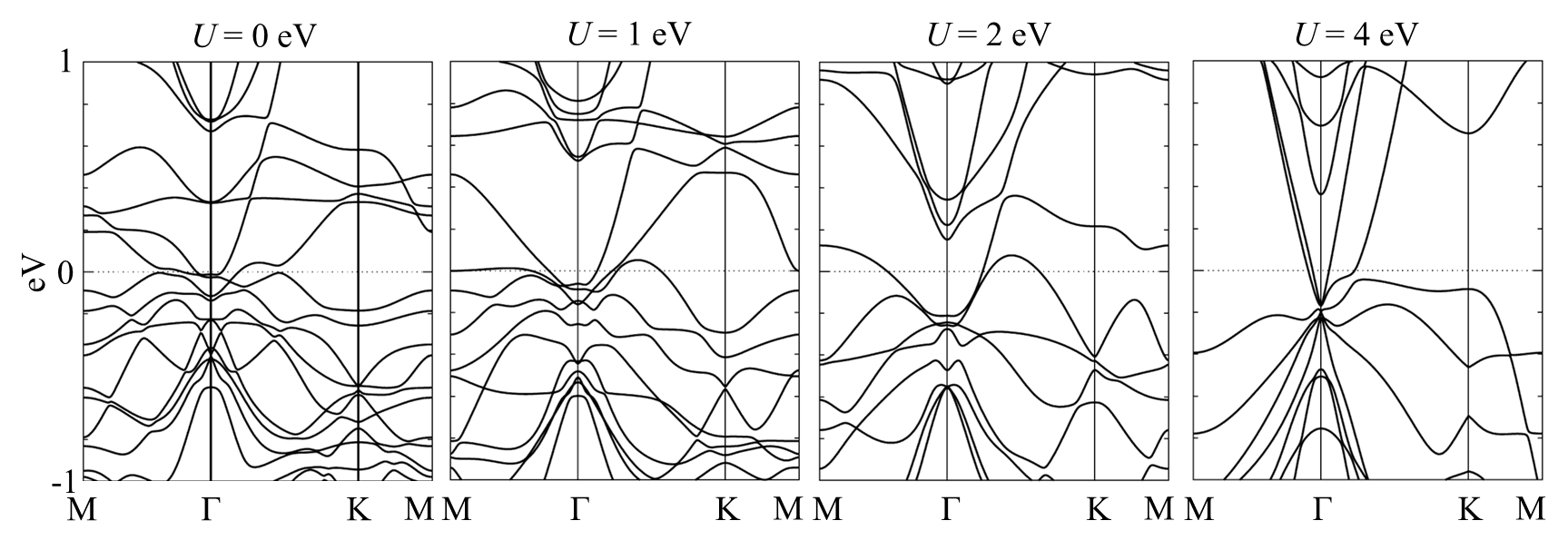
Supplementary Note 4: GGA+ calculation
Supplementary Figure 4 shows the results of the GGA+ calculations for the S-end monolayer under different on the Co electrons within the fully relativistic framework. We find that the band gap is not opened up at least to eV, indicating that the S-end monolayer remains metallic even when including the Coulomb interactions at the level of GGA+. However, the transport properties will be altered because of the large modification of the band structure. We also performed GGA+ calculations for the S-end bilayer, and find that the system turns into a FM state for eV, where the double band degeneracy is lifted and the anomalous Hall and Nernst effects are expected to occur.