Magnetic phase diagram and possible Kitaev-like behavior of honeycomb-lattice antimonate Na3Co2SbO6
Abstract
Recent theoretical studies have suggested that Kitaev physics and such effects as formation of a mysterious spin-liquid state can be expected not only in -RuCl3 and iridates, but also in conventional transition metal compounds. Using DC and AC magnetometry, thermodynamic and 23Na nuclear magnetic resonance measurements (NMR) we studied such a candidate material Na3Co2SbO6. A full phase diagram of Na3Co2SbO6 in a wide range of magnetic fields and temperatures is presented. The results demonstrate transformation of the antiferromagnetic structure under the external magnetic field, gradual development of the saturation phase, as well as evidence of gapped behavior in certain parts of the phase diagram.
I Introduction
Since proposal of the Kitaev model realization in honeycomb -RuCl3 and iridates, a lot of efforts had been concentrated on study of these systems [1] The quest for the spin liquid due to the anisotropic (Kitaev) exchange interaction had been continued by considering more conventional materials [2; 3; 4]. It has been known for a long time that low-energy excitations in Co2+ can be modeled by the pseudospin j [5; 6]. Indeed, in the octahedral surrounding, states can be described by the effective orbital moment , which together with spin leads to the total moment j. Of course, both and states contribute to the exchange coupling, but in a common edge geometry (nearly 90° metal-ligand-metal bonds), the antiferromagnetic (AFM) exchange can be largely compensated by the ferromagnetic (FM) terms [7], so that strongly anisotropic Ising-like exchange can dominate. This suggestion resulted in a flurry of both theoretical and experimental interest to Co2+ compounds with a honeycomb layered geometry as a new playground for the Kitaev physics.
However, already first ab initio and model calculations have shown that the situation is more complicated in these systems [8; 9; 10]. In fact, a direct exchange between orbitals for the nearest neighbors leads to a substantial isotropic exchange, which in case of BaCo2(AsO4)2 turned out to be an order of magnitude larger than the Kitaev term [9]. Moreover, together with this, the large exchange coupling between 3rd neighbors strongly questions possibility of Kitaev model realization in Co2+ compounds. This explains why most of them orders at very low temperature [11; 12]. Nevertheless, an external magnetic field was suggested to stabilize an emergent state in such materials as BaCo2(AsO4)2 [13] and Na2Co2TeO6 [11]. The nature of this field-induced state is debated now, but it appears to be related to the Kitaev physics.
In the present paper, we study honeycomb antimonate Na3Co2SbO6, that was recently proposed as a compound which is proximate to a Kitaev spin-liquid phase [7]. The crystal structure of this material is very similar to Na2Co2TeO6 and differs mainly in the way how Co planes are stacked: in Na2Co2TeO6 the stacking is staggered, while in Na3Co2SbO6 Co-honeycombs are placed directly on top of each other [14]. Single-crystal neutron diffraction shows that at temperature 5 K Na3Co2SbO6 orders magnetically with antiferromagnetic zigzag structure [15] (note that depending on quality of samples varies from 4.4 to 8.3 K [16; 14; 15]). Effective magnetic moment of 5.2-5.5[14; 16; 15] strongly suggests a large orbital contribution. Rich variety of field-induced phases was observed by DC magnetometry in this material [17]. Results of recent inelastic neutron scattering measurements are summarized in Tab. 1. They suggest a significant [18] or even dominating[19; 20] Kitaev term in this material, while theoretical calculations in contrast expect large isotropic exchanges for both first and third nearest neighbors (and small Kitaev term) [10].
| Ref. [19] | -2.1 | 0.8 | -9.0 | 0.3 | -0.8 |
| Ref. [20] | -2.1 | 1.2 | -4.0 | -0.7 | 0.6 |
| Ref. [20] | -4.7 | 1.0 | 3.6 | 1.3 | -1.4 |
| Ref. [18] | -1.4 | 0.6 | -10 | -0.3 | -0.6 |
| Ref. [18] | -5.0 | 0.6 | 2 | -4 | 0.3 |
Despite the fact that in recent years a number of experimental studies of this system have appeared, the manifestation of Kitaev physics has not been definitely confirmed or refuted here. There are several main reasons for this situation: the results were obtained in narrow individual regions of the phase diagram, and the data are strongly sample dependent. Moreover, the mutual orientation of the lattice and the external field is very important for the Kitaev behavior, but sufficiently large single crystals are still not available for comprehensive studies in a wide range of fields and temperatures. As was observed in and compounds, the Kitaev behavior is most pronounced in a rather narrow region of the phase diagram, where the AFM order is already suppressed by the field, and saturation has not yet been reached. In many cobalt compounds, the suppression of the AFM order occurs in relatively large fields 8T, which complicates most of experiments, although studies by local methods (see, for example [21] for Na2Co2TeO6) of the correlated dynamic region above the ordering can be the argument in a favor of possible Kitaev behavior. In Na3Co2SbO6,̃ the suppression of the zig-zag AFM order occurs at lower fields, which gives prospects for experimental studies of the spin-liquid behavior. In order to mark a possible spin-liquid region, we carried out a step-by-step study of magnetic behavior of this material in a wide range of fields and temperatures, covering all the supposed regions of the phase diagram. Having a powder sample, we cannot definitely confirm the Kitaev behavior, but by applying the formalism used for “classical” Kitaev compounds, one can identify borders of the regions where such a description is possible and estimate the corresponding parameters. Therefore, these results can pave the way for further more detailed studies on single crystals, which can give unambiguously correct quantitative results.
Thus, in the present paper, using AC and DC magnetometry, heat capacity and NMR measurements, we establish a phase diagram of Na3Co2SbO6 and investigate physical properties of this system. It is shown that magnetic moments are confined to the honeycomb plane and order below = 7.6 K, while a magnetic field suppresses this ordering already at T. Analysis of the experimental data suggests that the spin gap develops above this field.
The paper is organized as follows. Experimental details are summarized in Sec. II. Main results of 23Na NMR, thermodynamic and magnetometry experiments are presented in Sec. III. The results are discussed and the H-T diagram is given in Sec. IV. The conclusions are summarized in Sec. V. Some additional experimental data are presented in Sec. VII.
II Experimental details

| Radiation | , Å | , Å | , Å | , ∘ |
|---|---|---|---|---|
| Neutron [16] | 5.35648(10) | 9.28723(19) | 5.65100(7) | 108.358(1) |
| Synchrotron [22] | 5.3649(6) | 9.2782(3) | 5.6533(5) | 108.490(8) |
| Co Kα1 | 5.3640(1) | 9.2774(2) | 5.6545(1) | 108.491(2) |
The polycrystalline Na3Co2SbO6 sample was prepared by a conventional two-step solid-state synthesis. First, stoichiometric amounts of Sb2O3 (99.6%, Alfa Aesar), Co3O4 (99.9%, Sigma Aldrich) and 5% excess of Na2CO3 (99.9%, Merck) were ground together and annealed at 800°C in air for 15 h. After cooling down to room temperature, the mixture was ground again, pressed into a pellet and annealed in air at 980°C for 40 h followed by quenching in air. After synthesis, the sample was stored in an Ar-filled glove-box with the H2O/O2 contents less than 0.1 ppm. The phase purity of the sample was verified by powder X-ray diffraction, using STOE STADI P diffractometer with a Co-Kα1 radiation, = 1.7889 Å, in a transmission mode. Rietveld analysis using the Fullprof software [23] (see Fig. 1) confirmed the structural model based on the neutron diffraction data [16].
Part of the experimental data was obtained for the sample studied earlier [22]. Excellent agreement of the lattice parameters (Table 2), together with some thermodynamic and magnetic characteristics, proves that both samples are essentially identical. For NMR and magnetometry experiments, the powder sample was placed in a sealed quartz container in an argon atmosphere after preparation.
Heat capacity measurements were carried out by a relaxation method using a Quantum Design PPMS system. The plate-shaped sample was obtained by cold pressing of the polycrystalline powder. Data were collected at zero magnetic field and under an applied field up to 9 T in the temperature range 2–30 K. The AC magnetic susceptibility data were collected at the magnetic field = 0.0001 T in the temperature range between 2–45 K while varying the frequency between 0.5–10 kHz. The static magnetic measurements were performed by means of a Quantum Design SQUID –magnetometer. The temperature dependence of magnetic susceptibility was measured at various magnetic fields 0 T 7 T in the temperature range 1.8–300 K. Nuclear magnetic resonance (NMR) measurements were performed with a Tecmag Redstone pulsed spectrometer at fixed Larmor frequencies at several external field ranges. The spectra were collected by step-by-step sweeping the field and integrating the echo signal obtained by the standard Hahn echo pulse sequence at each field step. The longitudinal relaxation rate of 23Na nuclei was measured at the maximum of the spectrum magnitude with saturation recovery and stimulated echo pulse protocols. The evolution of the magnetization after the pulse sequence is described by the equation for spin 3/2 [24]. Due to the partial overlap of the main line and quadrupole satellites in the inhomogeneously broadened powder spectra, the stretch factor was applied:
| (1) |
where is a delay between the pulses and T1 is a spin-lattice relaxation time.
III Experimental results and discussion
III.1 Specific heat

The specific heat data at various external magnetic fields are presented in Fig. 2. As it was found earlier [22] the temperature dependence in zero magnetic field demonstrates a distinct -type anomaly, associated with an onset of the magnetic order at K. Under magnetic field ( 1 T) the singularity at somewhat broadens and shifts to lower temperatures (inset in Fig. 2a). Higher fields lead to progressive weakening and eventual fading of the anomaly, which finally transforms to a broad hump; its position shifts to higher temperatures with the field (Fig. 2b).
In order to analyze the nature of the magnetic phase transition in Na3Co2SbO6 at various external fields and evaluate corresponding contribution to the specific heat we used data for its non-magnetic isostructural analogue Li3Zn2SbO6. The correction to this contribution for Na3Co2SbO6 has been made taking into account the difference between the molar masses for each type of atom in the compound (Na-Li and Co-Zn). [25] The magnetic contribution to the specific heat was determined by subtracting the lattice contribution using the data for Li3Zn2SbO6 (Fig. 2b). Analysis of the low-temperature part of was performed in the terms of the spin-wave (SW) theory [26]
| (2) |
where is low-temperature specific heat due to spin-wave excitations, stands for the dimensionality of the magnetic lattice and is defined as the exponent in the dispersion relation . The analysis has shown that below the Cm(T) dependence follows satisfactorily – law at low fields 1 T (see inset in Fig. 3b). This result implies a presence of antiferromagnetic magnons consistent with 3D antiferromagnetic ordering at the low temperatures in this field range. The same procedure for fields 1 T 2 T reveals = 2, indicating the predominance of 2D AFM exchanges in the studied compound. It is noteworthy that 1 T corresponds to the metamagnetic transition observed in [22; 16]. In the vicinity of quantum critical point, temperature dependence of magnetic specific heat obeys power law [27]. It is worth mentioning that the low-temperature magnetic specific heat in Na3Co2SbO6 for fields T and higher can be described by the same model with the spin gap as was used for -RuCl3 [27]
| (3) |
In order to estimate the energy gap, was fitted by (2), the results are shown by dashed curves on Fig. 2b.
III.2 Static magnetization
In accordance with previously reported data [22], the static susceptibility of Na3Co2SbO6 (Fig. 3) demonstrates an antiferromagnetic behavior with low-field Weiss temperature K. For low external fields 1.5 T, magnetic susceptibility passes through a maximum with decrease in temperature and then drops. From the maximum , one can find the Néel temperature = 7.6 K at 0.05 T and it decreases with increase in magnetic field. The fit of field dependence of TN (Fig. 3 insert) by expression with z = 0.25 0.013 yields the field of the suppression of 3D AFM order T. The critical exponent z is consistent with the magnetization and neutron scattering data for -RuCl3 [28]. At the same time, the NMR data (see below) indicate some features typical for the AFM transition even above 1.3 T. Apparently, the strong anisotropy of the magnetic properties entails a difference in the field of AFM order suppression for different orientations of the powder crystallites. The M/H(T) data for some directions of single crystals [17; 15] show that the magnitude of the peak at a field parallel to the honeycomb plane is much larger than at perpendicular direction. Therefore, the Néel temperature in the powder sample is determined mainly by crystallites of this orientation. In addition, there is a strong anisotropy even in the plane [17]. Thus, below we will assume that the AFM order exists in the fields below 2 T. The data obtained at T indicate the saturation developed in the studied sample.

III.3 Nuclear magnetic resonance
To study the local properties of the magnetic spin system, we performed NMR measurements on the powder sample of Na3Co2SbO6 on the 23Na nuclei which have a spin , the gyromagnetic ratio = 11.2685 MHz/T, and the quadruple moment Q = 0.104 10-28 m2. The measurements were carried out at several frequencies 10.7, 13.512, 22.52, 30.33, 45.04 and 86.714 MHz in the corresponding field ranges since the effect of an external field on local magnetic characteristics is of particular interest. Temperature transformation of NMR spectra in some of field ranges is presented in Fig. 4.
At temperatures of the order of 100 K and above, a classical powder spectrum with quadrupole shoulders can be recorded. As the temperature decreases, the line broadens and shifts towards lower fields. The low temperature spectrum at has a flat top but does not have a stepwise rectangular shape that is typical for antiferromagnets [29]. This can be understood assuming the fact that the total width of the spectrum at low T is comparable to the quadrupole splitting and the overlap of the main line and quadrupole satellites smears the shape of the spectrum resulting in a bell-like profile. The same reason makes the modelling of the line powder profile technically impossible and one cannot resolve the positions of the spectral contributions from the parallel and perpendicular orientations of the crystallites.

The dynamics of the electron spin system determines the process of nuclear spin-lattice relaxation (see Fig. 5, left panels). The relaxation rate at external fields exhibits a sharp peak at K indicating the magnetic phase transition TN. The temperature of this peak decreases with increasing field, similarly to the Néel temperature determined from the static magnetic susceptibility data. Relaxation in the nearest upper vicinity of TN can be described in terms of the critical exponent
| (4) |
where [30]. The obtained critical parameters are p = 0.328 0.013, K for 1.2 T and p = 0.319 0.031, K for 2 T. Such a small value of p is typical for XY-triangular and honeycomb lattices [31; 32] and can be estimated as close to the calculated p = 0.32 obtained assuming 0.5 [33] and z = 0.64 [34]. It confirms the results of paragraph III.1: in-plane 2D spin correlations at 1 T play a key role in the magnetism of Na3Co2SbO6 including onset of a three-dimensional AFM order.
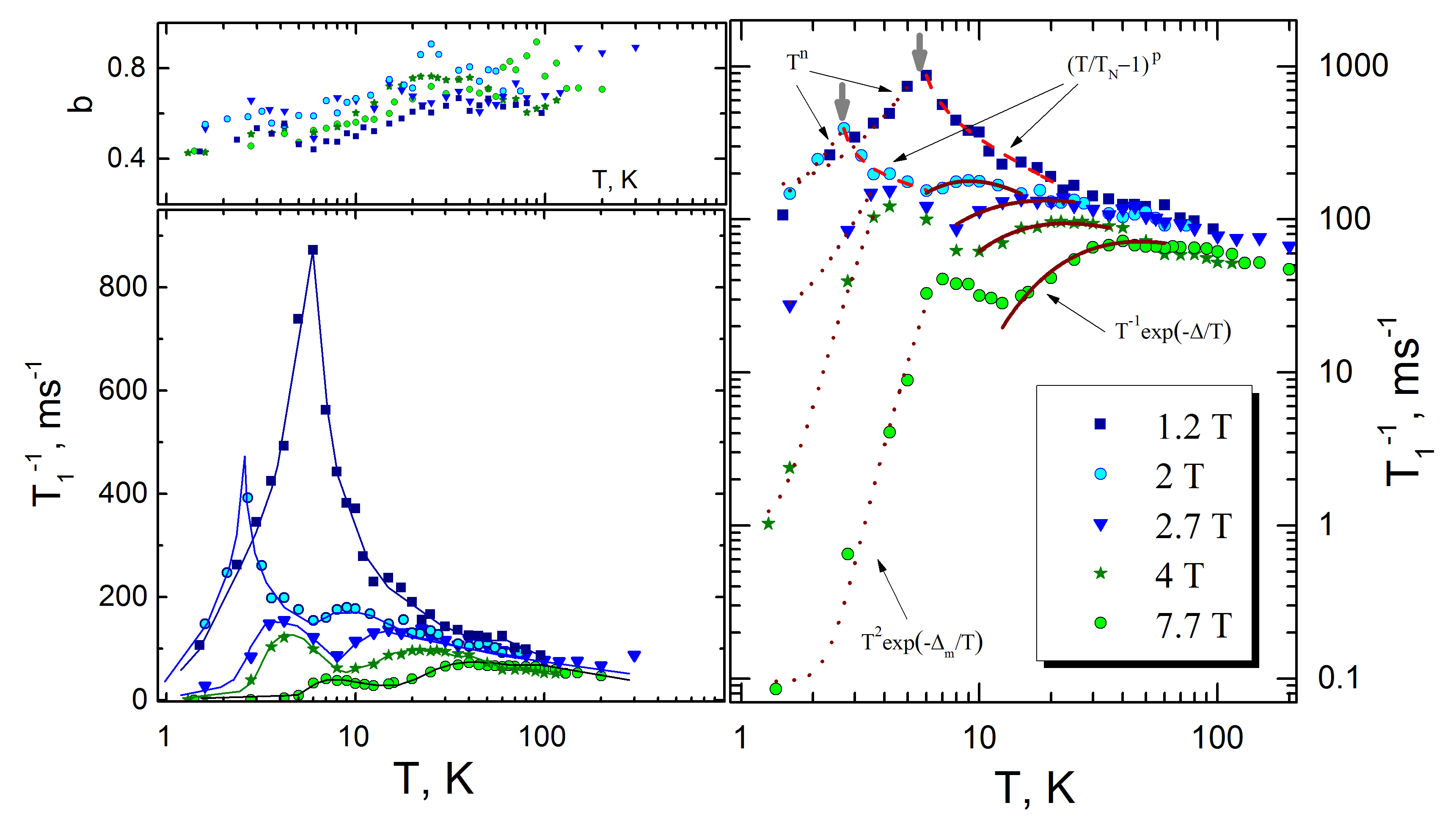
With a further increase of the field, a less pronounced but clearly observed maximum appears on the temperature dependence of the relaxation rate. Its position shifts to the higher with the field and corresponds to the plateau-like behavior of temperature dependence of static susceptibility taken in the same fields. While the electron spin fluctuations slow down with temperature, the nuclear spin-lattice relaxation depends on correlation time as [35]
| (5) |
where is the correlation time and is the Larmor frequency. Below the maximum of this dependence, . This allows attributing this maximum to the establishment of a quasi-static saturated phase induced by the external field. To characterize the spin dynamics at low temperatures, we tried to estimate the magnon gap using a formula for a gapped three-magnon process [36]
| (6) |
where . At , such an estimation gives a gap of the order of 4 – 16 K, which grows with the field (see Fig. 6). At the same time, fitting of the (T) curve below 2.5 T, i.e., in the AFM state, results in an extremely low value of the gap, and the data can be described by a power law typical for three-magnon scattering in the antiferromagnets at temperatures above the energy gap in the spin wave spectrum. This is consistent with the small anisotropy gap value 2 K determined from the field of metamagnetic transition [22; 16]. It should be noted that the number of experimental points does not allow making a reliable quantitative analysis; therefore, the presented conclusions should be only considered as an estimation.
Above or the assumed saturation temperature , the temperature dependence of the relaxation rate in the high fields contains a wide hump. It is noteworthy that this hump firstly appears at 2 T, which is somewhat lower than . This feature can be interpreted as the so-called “low-dimensional maximum”, which characterizes the slowdown of 2D spin correlations in two-dimensional compounds. Given the possible Kitaev-Heisenberg physics in the compound under study, it is tempting to apply as a working hypothesis the approach developed to describe the Kitaev behavior of nuclear spin-lattice relaxation for -RuCl3 [37; 38]. This theoretical model [39] correlates the boundaries of this hump with the magnitude of the Kitaev exchange and propose the extended exponential function
| (7) |
We evaluate the spin gap assuming (see Fig. 5, right panel) as K at 2 T and K at 7.7 T which is comparable to the values obtained for -RuCl3. Certainly given a relatively small change of in the considered temperature range the so obtained values of the gap should be considered as estimates. Nevertheless they appeared consistent with the gap values obtained from the specific heat (see the discussion below).
IV Discussion
In the T-H diagram, one can distinguish an AFM ordered phase at T. Some traces of AFM order are observed up to 2 T due to different crystalline orientation in the powder sample. The AFM correlations (see Section VII) are developed in a broad temperature range above marked by blue color in Fig. 6.

.
Above = 2T, a wide correlated region with a spin-liquid gaped behavior is appeared (marked by blue color in Fig. 6). Experimentally this region is characterized by a wide hump registered by methods with very different time scales, i.e. on the temperature dependence of the specific heat, AC susceptibility, and nuclear relaxation. Such a feature is typical for low-dimensional systems. It is often associated with development of 2D short-range magnetic correlations. However, increasing the hump maximum temperature with field in Na3Co2SbO6 definitely exclude the AFM origin of these correlations.
Since Na3Co2SbO6 is considered as a possible Kitaev material one can try to use a formalism developed for other Kitaev systems to describe the experimental results in this H-T region (see [39; 38; 37; 27]). This approach allows to testify to the gap character of spin excitations. Remarkably that the gap values obtained by static (specific heat, green open symbols in Fig. 6 ) and dynamic (NMR, blue squares in Fig. 6) techniques are close to each other. The field behavior of the gap is almost linear. In Kitaev model [40], the Majorana fermion gap is proportional to , but presence of non-Kitaev interactions results in the field-induced gap for any field orientation and make it linearly dependent on the field [41]. The gap value is comparable to the energy of the spin wave spectrum peak around - meV observed by inelastic neutron scattering experiments and described in frameworks of Kitaev–Heisenberg model [20]. Alternative scenario of this gap development due to ferro-magnons seems to be doubtful taking into account the AC susceptibility data (see Section VII.3).
The ferromagnetic excitations can be indeed observed in fields above 2.8 T, but at significantly lower temperatures. Here both local (NMR line shift) and bulk static susceptibility indicate the development of saturation. The characteristic growth in the relaxation rate is observed (blue circles on Fig. 6) , which is not so sharp as the Néel peak at low fields. Taking the dependence below this maximum, one can estimate the magnon gap . The slope of the dependence is about 2.19 K/T (blue triangles on Fig. 6). This slope is consistent with the Zeeman energy of a single spin flip, i.e., a one-magnon excitation, which, with the g factor g = 3.3 [22] , would be 2.21 K/T. Indeed, for the XXZ model, typical for Kitaev physics, it was shown [42] that the one-magnon excitations has the lowest energy in such dynamics near saturation, if the ratio of the single-ion anisotropy to -component of the exchange tensor is higher than 1.33. NMR, as a local method, is sensitive to the excitations mostly on long wave vectors. Therefore, using the results of DFT calculations of the single-ion anisotropy and exchange components in Na3Co2SbO6 [15], one can expect the observation of a one-magnon process for the saturation region.
It should be noted that at fields T we observed a combination of both AFM and spin-liquid features. It can be easy explained taking into account the strong anisotropy of Kitaev-Heisenberg systems behavior (see for example [43]). The AFM phase field boundary is strongly depended on the crystalline particle orientation in Na3Co2SbO6. The data of magnetometry and magnetic neutron diffraction presented in the work [17] suggest that the traces of the AFM phase observed at are associated with powder particles with the a axis parallel to the field. Moreover, studies of a powder sample obviously contain a certain error in determining the magnitude and field dependence of the Kitaev gap in the spectrum of spin excitations. Therefore, here we test applicability of the Kitaev-Heisenberg description for Na3Co2SbO6, whereas the exact values of spin-gap can be obtained in further measurements on single crystals.
V Conclusions
In conclusion, we performed bulk (heat capacity, DC and AC susceptibility) and local (NMR) probe measurements of the powder sample of honeycomb system Na3Co2SbO6 in a wide range of temperatures and magnetic fields. These experiments reveal regions with a static spontaneous and field-induced magnetic order, a wide temperature range of spin correlations of various nature as well as a region of fields, where a gap in spin excitation spectrum develops. The parameters of spin excitations in different regions of the phase diagram were estimated, including the magnitude and temperature dependence of the field-induced energy gap, which determines the specific temperature dependence of bulk and local characteristics well above the saturation region. Our measurements give some evidence of possible formation of a spin-liquid-like phase and realizing the Kitaev-Heisenberg scenario in Na3Co2SbO6 under external magnetic field. In this context, it would be enlightening to investigate similarly a high-quality single-crystal sample in order to clarify the details of the model parameters.
VI Acknowledgments
The authors are grateful to Dr. P. Maksimov, Dr. S. Winter, Dr. H.-J. Grafe, Prof. B. Büchner, and Dr. V. Kataev for useful discussions. A.V. acknowledges support by the Megagrant program of Russian Government through the project 075-15-2021-604. The work of D.M. was made in 2021. S.V.S. thanks Russian Science Foundation for support of theoretical analyses (RSF 20-62-46047). E.V. would like to thank financial support from the government assignment for FRC Kazan scientific Center of RAS.
VII Appendix
VII.1 23Na NMR line shift and hyperfine constant
The shift of the NMR line can be defined as = ((100%, where is the field of the spectral magnitude maximum and = . Its temperature-dependent part corresponds to the local static susceptibility and in paramagnetic state it is proportional to the bulk susceptibility = , where A is the hyperfine tensor. The hyperfine interaction constants taken from the linear part of the ( dependencies (see Fig. 7) in each external field are found to be almost equal and the average value is determined as 0.250.014 kOe/. This value is comparable to that observed in Na2Co2TeO6 [44] and is significantly smaller than for copper [45] and nickel [32] honeycomb compounds. The difference in the electronic configurations and orbital occupancy for cobalt ions seems to be responsible for the smaller orbital overlap and the transfer of spin density to sodium ions. As a result, despite the larger bulk susceptibility in cobalt compounds compared to nickel or copper ones (see also [46] for tellurates), the increase in the local hyperfine field on sodium nuclei is insignificant. This leads to a remarkably larger decoupling of the honeycomb planes and to a more pronounced two-dimensionality of the strongest exchanges in the cobalt compound as a result.

VII.2 local susceptibility
The NMR is well known probe of local fields, susceptibility and correlations and we use it to establish the field and temperature limits of correlated regions. The line shift is proportional to the local field which is static on the NMR timescale . In most cases when the fluctuations of electron spins are much faster than inversed NMR frequency, time averaging can be done at zero frequency, i.e. . In specific situations, for example in some low-dimensional systems, where the correlation time is comparable to the NMR time scale in the extended temperature range, the result of time averaging differs from that at zero frequency and NMR shift deviates from bulk static susceptibility.
Slight deviation of dependence from linear at fields indicates the slowdown of cobalt spin fluctuations at low temperatures. Development of antiferromagnetic correlations with big correlation time suppressing the local field at the sodium positions located between the cobalt planes. At the local static susceptibility does not deviate from the bulk one anymore.

The spin-lattice relaxation can be considered as a direct probe of the local dynamic susceptibility of the electron spin subsystem [47]
| (8) |
where is the q-dependent hyperfine constant, q is the wave vector and is the Larmor frequency. In the paramagnetic regime is proportional to the static bulk susceptibility. The sharp deviation of the local dynamic susceptibility from the static bulk one occurs below 10 K in the entire range of fields (see Fig. 7), marking the critical slowing down of the electron spin fluctuations in the vicinity of the transition to the static state. In fields above , the local dynamic susceptibility deviates from the static one already at 20 - 50 K, marking the development of dynamic correlations at a relatively low-frequency part of the spin fluctuation spectra.
VII.3 Bulk dynamic susceptibility
The AC susceptibility at zero external field exhibits a sharp peak at the Néel temperature. Above , the critical low-temperature anomaly is absent, but a wide hump is observed, which shifts to higher temperatures with increasing field. At any fields, the curves obtained at different frequencies do not exhibit any frequency dependence (see Fig. 8). This rules out that the hump is associated with any kind of conventional glassy transition. The hump is not accompanied by an anomaly of and therefore one cannot attribute it to the crossover to the field-induced ferromagnetic order, since at ferro- or ferrimagnetic transition or crossover the imaginary component is present [48]. On the other hand, this broad maximum shifts to higher temperatures with the applied DC field and it does not allow us to attribute it to the development of two-dimensional antiferromagnetic correlations in cobalt planes. It is remarkable that a pronounced anomaly in this temperature range is absent in the temperature dependence of both the bulk and the local static susceptibility, but it is observed in the dynamic susceptibility in both the kHz and MHz (NMR relaxation) ranges indicating the dynamic nature of the emerging magnetic state. It should be noted that the temperature of the AC susceptibility hump maximum corresponds in order of magnitude to the values of the Kitaev-Heisenberg gap obtained from nuclear relaxation analysis.
References
- Takagi et al. [2019] H. Takagi, T. Takayama, G. Jackeli, G. Khaliullin, and S. E. Nagler, Nature Reviews Physics 1, 264–280 (2019), URL https://doi.org/10.1038/s42254-019-0038-2.
- Liu and Khaliullin [2018] H. Liu and G. Khaliullin, Phys. Rev. B 97, 014407 (2018), URL https://link.aps.org/doi/10.1103/PhysRevB.97.014407.
- Sano et al. [2018] R. Sano, Y. Kato, and Y. Motome, Phys. Rev. B 97, 014408 (2018).
- Motome et al. [2020] Y. Motome, R. Sano, S. Jang, Y. Sugita, and Y. Kato, J. Phys. Cond. Matt. 32, 404001 (2020), ISSN 23318422.
- Abragam and Bleaney [1970] A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions (Clarendon Press, Oxford, 1970).
- Khomskii and Streltsov [2021] D. I. Khomskii and S. V. Streltsov, Chem. Rev. 121, 2992 (2021).
- Liu et al. [2020] H. Liu, J. Chaloupka, and G. Khaliullin, Phys. Rev. Lett. 125, 047201 (2020), URL https://link.aps.org/doi/10.1103/PhysRevLett.125.047201.
- Das et al. [2021] S. Das, S. Voleti, T. Saha-Dasgupta, and A. Paramekanti, Phys. Rev. B 104, 134425 (2021), URL https://link.aps.org/doi/10.1103/PhysRevB.104.134425.
- Maksimov et al. [2022] P. A. Maksimov, A. V. Ushakov, Z. V. Pchelkina, Y. Li, S. M. Winter, and S. V. Streltsov, Physical Review B 106, 165131 (2022), URL https://arxiv.org/abs/2204.09695.
- Winter [2022] S. M. Winter, Journal of Physics: Materials 5, 045003 (2022), URL https://arxiv.org/abs/2204.09856.
- Lin et al. [2021] G. Lin, J. Jeong, C. Kim, Y. Wang, Q. Huang, T. Masuda, S. Asai, S. Itoh, G. Günther, M. Russina, et al., Nature Communication 12, 5559 (2021), URL https://doi.org/10.1038/s41467-021-25567-7.
- Zvereva et al. [2016] E. A. Zvereva, M. I. Stratan, A. V. Ushakov, V. B. Nalbandyan, I. L. Shukaev, A. V. Silhanek, M. Abdel-Hafiez, S. V. Streltsov, and A. N. Vasiliev, Dalton Trans. 45, 7373 (2016), URL http://dx.doi.org/10.1039/C6DT00516K.
- Zhong et al. [2020] R. Zhong, T. Gao, N. P. Ong, and R. J. Cava, Science Advances 6, eaay6953 (2020), URL https://www.science.org/doi/abs/10.1126/sciadv.aay6953.
- Viciu et al. [2007] L. Viciu, Q. Huang, E. Morosan, H. W. Zandbergen, N. I. Greenbaum, T. M. Mcqueen, and R. Cava, Journal of Solid State Chemistry 180, 1060 (2007).
- Yan et al. [2019] J.-Q. Yan, S. Okamoto, Y. Wu, Q. Zheng, H. D. Zhou, H. B. Cao, and M. A. McGuire, Phys. Rev. Materials 3, 074405 (2019), URL https://link.aps.org/doi/10.1103/PhysRevMaterials.3.074405.
- Wong et al. [2016] C. Wong, M. Avdeev, and C. D. Ling, Journal of Solid State Chemistry 243, 18 (2016), ISSN 0022-4596, URL https://www.sciencedirect.com/science/article/pii/S0022459616302997.
- Li et al. [2022] X. Li, Y. Gu, Y. Chen, V. O. Garlea, K. Iida, K. Kamazawa, Y. Li, G. Deng, Q. Xiao, X. Zheng, et al., Giant magnetic in-plane anisotropy and competing instabilities in Na3Co2SbO6 (2022), eprint 2204.04593.
- Sanders et al. [2022] A. L. Sanders, R. A. Mole, J. Liu, A. J. Brown, D. Yu, C. D. Ling, and S. Rachel, Physical Review B 106, 014413 (2022), URL http://arxiv.org/abs/2112.12254.
- Songvilay et al. [2020] M. Songvilay, J. Robert, S. Petit, J. Rodriguez-Rivera, W. Ratcliff, F. Damay, V. Balédent, M. Jiménez-Ruiz, P. Lejay, E. Pachoud, et al., Physical Review B 102, 224429 (2020).
- Kim et al. [2021] C. Kim, J. Jeong, G. Lin, P. Park, T. Masuda, S. Asai, S. Itoh, H.-S. Kim, H. Zhou, J. Ma, et al., Journal of Physics: Condensed Matter 34, 045802 (2021), URL https://doi.org/10.1088/1361-648x/ac2644.
- [21] J. Kikuchi, T. Kamoda, N. Mera, Y. Takahashi, K. Okumura, and Y. Yasui, arXiv.2206.05409 (????).
- Stratan et al. [2019] M. I. Stratan, I. L. Shukaev, T. M. Vasilchikova, A. N. Vasiliev, A. N. Korshunov, A. I. Kurbakov, V. B. Nalbandyan, and E. A. Zvereva, New J. Chem. 43, 13545 (2019), URL http://dx.doi.org/10.1039/C9NJ03627J.
- Roisnel and Rodríquez-Carvajal [2001] T. Roisnel and J. Rodríquez-Carvajal, in European Powder Diffraction EPDIC 7 (Trans Tech Publications Ltd, 2001), vol. 378 of Materials Science Forum, pp. 118–123.
- Narath [1967] A. Narath, Phys. Rev. 162, 320 (1967), URL https://link.aps.org/doi/10.1103/PhysRev.162.320.
- Tari [2003] A. Tari, The Specific Heat of Matter at Low Temperature (Imperial College Press, London, 2003).
- de Jongh and Miedema [1974] L. de Jongh and A. Miedema, Advances in Physics 23, 1 (1974), URL https://doi.org/10.1080/00018739700101558.
- Wolter et al. [2017] A. U. B. Wolter, L. T. Corredor, L. Janssen, K. Nenkov, S. Schönecker, S.-H. Do, K.-Y. Choi, R. Albrecht, J. Hunger, T. Doert, et al., Phys. Rev. B 96, 041405 (2017), URL https://link.aps.org/doi/10.1103/PhysRevB.96.041405.
- Sears et al. [2017] J. A. Sears, Y. Zhao, Z. Xu, J. W. Lynn, and Y.-J. Kim, Phys. Rev. B 95, 180411 (2017), URL https://link.aps.org/doi/10.1103/PhysRevB.95.180411.
- Yamada and Sakata [1986] Y. Yamada and A. Sakata, Journal of the Physical Society of Japan 55, 1751 (1986), eprint https://doi.org/10.1143/JPSJ.55.1751, URL https://doi.org/10.1143/JPSJ.55.1751.
- Borsa et al. [1992] F. Borsa, M. Corti, T. Goto, A. Rigamonti, D. C. Johnston, and F. C. Chou, Phys. Rev. B 45, 5756 (1992), URL https://link.aps.org/doi/10.1103/PhysRevB.45.5756.
- Kurbakov et al. [2022] A. I. Kurbakov, A. E. Susloparova, V. Y. Pomjakushin, Y. Skourski, E. L. Vavilova, T. M. Vasilchikova, G. V. Raganyan, and A. N. Vasiliev, Phys. Rev. B 105, 064416 (2022), URL https://link.aps.org/doi/10.1103/PhysRevB.105.064416.
- Itoh [2015] Y. Itoh, Journal of the Physical Society of Japan 84, 064714 (2015), URL https://doi.org/10.7566/JPSJ.84.064714.
- Plumer and Mailhot [1994] M. L. Plumer and A. Mailhot, Phys. Rev. B 50, 16113 (1994), URL https://link.aps.org/doi/10.1103/PhysRevB.50.16113.
- Zhang and Yang [1994] G. M. Zhang and C. Z. Yang, Phys. Rev. B 50, 12546 (1994), URL https://link.aps.org/doi/10.1103/PhysRevB.50.12546.
- Slichter [1989] C. Slichter, Principles of Magnetic Resonance (Springer, New York, 1989).
- Narath and Fromhold [1966] A. Narath and A. T. Fromhold, Phys. Rev. Lett. 17, 354 (1966), URL https://link.aps.org/doi/10.1103/PhysRevLett.17.354.
- Janša et al. [2018] N. Janša, A. Zorko, M. Gomilšek, M. Pregelj, K. W. Krämer, D. Biner, A. Biffin, C. Rüegg, and M. Klanjšek, Nature Physics 14, 786–790 (2018), URL https://www.nature.com/articles/s41567-018-0129-5.
- Nagai et al. [2020] Y. Nagai, T. Jinno, J. Yoshitake, J. Nasu, Y. Motome, M. Itoh, and Y. Shimizu, Phys. Rev. B 101, 020414 (2020), URL https://link.aps.org/doi/10.1103/PhysRevB.101.020414.
- Yoshitake et al. [2016] J. Yoshitake, J. Nasu, and Y. Motome, Phys. Rev. Lett. 117, 157203 (2016), URL https://link.aps.org/doi/10.1103/PhysRevLett.117.157203.
- Kitaev [2006] A. Kitaev, Annals of Physics 321, 2 (2006), ISSN 00034916, URL http://linkinghub.elsevier.com/retrieve/pii/S0003491605002381.
- Song et al. [2016] X.-Y. Song, Y.-Z. You, and L. Balents, Phys. Rev. Lett. 117, 037209 (2016), URL https://link.aps.org/doi/10.1103/PhysRevLett.117.037209.
- Wu et al. [2022] N. Wu, H. Katsura, S.-W. Li, X. Cai, and X.-W. Guan, Phys. Rev. B 105, 064419 (2022), URL https://link.aps.org/doi/10.1103/PhysRevB.105.064419.
- Li et al. [2021] H. Li, H.-K. Zhang, J. Wang, H.-Q. Wu, Y. Gao, D.-W. Qu, Z.-X. Liu, S.-S. Gong, and W. Li, Nature Communications 12, 4007 (2021).
- Lee et al. [2021] C. H. Lee, S. Lee, Y. S. Choi, Z. H. Jang, R. Kalaivanan, R. Sankar, and K.-Y. Choi, Phys. Rev. B 103, 214447 (2021), URL https://link.aps.org/doi/10.1103/PhysRevB.103.214447.
- Kuo et al. [2012] C. Kuo, T. Jian, and C. Lue, Journal of Alloys and Compounds 531, 1 (2012), ISSN 0925-8388, URL https://www.sciencedirect.com/science/article/pii/S0925838812004100.
- Berthelot et al. [2012] R. Berthelot, W. Schmidt, A. Sleight, and M. Subramanian, Journal of Solid State Chemistry 196, 225 (2012), ISSN 0022-4596, URL https://www.sciencedirect.com/science/article/pii/S0022459612003970.
- Moriya [1963] T. Moriya, Journal of the Physical Society of Japan 18, 516 (1963), eprint https://doi.org/10.1143/JPSJ.18.516, URL https://doi.org/10.1143/JPSJ.18.516.
- Bałanda [2013] M. Bałanda, ACTA PHYSICA POLONICA A 124, 964 (2013), URL 10.12693/APhysPolA.124.964.