Magnetic parity violation and Parity-time-reversal-symmetric magnets
Abstract
Parity-time-reversal symmetry ( symmetry), a symmetry for the combined operations of space inversion () and time reversal (), is a fundamental concept of physics and characterizes the functionality of materials as well as and symmetries. In particular, the -symmetric systems can be found in the centrosymmetric crystals undergoing the parity-violating magnetic order which we call the odd-parity magnetic multipole order. While this spontaneous order leaves symmetry intact, the simultaneous violation of and symmetries gives rise to various emergent responses that are qualitatively different from those allowed by the nonmagnetic -symmetry breaking or by the ferromagnetic order. In this review, we introduce candidates hosting the intriguing spontaneous order and overview the characteristic physical responses. Various off-diagonal and/or nonreciprocal responses are identified, which are closely related to the unusual electronic structures such as hidden spin-momentum locking and asymmetric band dispersion.
I Introduction
Over the past few decades, the exploration of physical responses arising from symmetry breaking has been extensively conducted in various research fields. One notable example is the response induced by the parity-symmetry (-symmetry) breaking. Materials lacking space inversion centers, such as ferroelectric materials and zinc-blende type semiconductors, are attracting a lot of interest in light of the interconversion between different degrees of freedom and the nonlinear effects applied to frequency conversion. The physical properties often involve the bulk electronic structure and are of paramount interest in condensed matter physics.
A lot of studies have been devoted to nonmagnetic systems in terms of the violation, and previous studies have explored a wide range of materials such as nonmagnetic semiconductors with significant spin-orbit coupling by spectroscopic and transport measurements Ishizaka et al. (2011); Murakawa et al. (2013); Krempaský et al. (2016). We also find works on the -violating effect in magnetic materials named magnetic parity violation, that is, the violation of and time-reversal () symmetries. The magnetic parity violation occurs trivially due to the noncentrosymmetric crystal structure and external magnetic field by which the and symmetries are respectively broken. On the other hand, the simultaneous violation of the two symmetries can happen in a series of antiferromagnets. The antiferromagnetic materials, called magnetoelectric systems, have been of much interest in the field of multiferroic science because the magnetic-electric interconversion originates from the magnetic parity violation Fiebig (2005); Spaldin et al. (2008). Owing to the controllability ensured by the magnetic-electric coupling, the antiferromagnetic state can be nicely computed by external fields Van Aken et al. (2007); Zimmermann et al. (2014). Since the antiferromagnetic domains can be monitored via electric and optical signals Kosub et al. (2015, 2017); Kocsis et al. (2018), there may exist applications such as memory devices invulnerable to magnetic noises.
Much attention has been drawn to the magnetoelectric material which is mostly insulating to keep the electric polarization. Few studies, however, have been performed on the interplay between the magnetic parity violation and itinerant properties such as electric conductivity. Recent rapid developments paved the way for spintronic physics based on the antiferromagnets, so-called antiferromagnetic spintronics Jungwirth et al. (2016); Baltz et al. (2018). The promising candidates for the growing field include not only magnetoelectric insulators but also various kinds of antiferromagnetic metals such as those offering the anomalous Hall effect Šmejkal et al. (2022) and those switchable by the electric current Wadley et al. (2016). The large variety of candidates stems from the fact that the symmetry breaking by the antiferromagnetic order varies depending on the structural degree of freedom coupled to the magnetic order. Furthermore, since the energy scale relevant to the antiferromagnetic order may be much higher than that of the ferromagnets, the antiferromagnetic spintronics possesses advantageous properties (e.g., large transition temperature and faster magnetic dynamics) when compared to the ferromagnetic spintronics. These growing interests motivate us to take a deeper look into the role of the magnetic parity violation in metals. To this end, we overview the physics originating from the magnetic parity violation mainly in terms of itinerant properties.
The organization is the following. Firstly, we present a brief symmetry analysis of the magnetic parity violation with a comparative study with that of the electric parity violation, the -symmetry violation preserving the symmetry (Sec. II). Many candidate materials manifesting the magnetic parity violation show a special property in their crystal structure, namely locally noncentrosymmetric crystal symmetry. The characteristics arising from the structure are seemingly inaccessible without microscopic measurements (Sec. II.2), whereas it is unveiled in a macroscopic manner because of the antiferroic ordering (Sec. II.3). Such an intimate coupling between the structural degree of freedom and antiferroic ordering cultivates the basic understanding of the itinerant property of magnetically-parity-violating materials. In Sec. III, we present some representative examples of the emergent responses induced by the magnetic parity violation. Similarly to discussions in Sec. II.3, there are contrasting roles of the magnetic and electric parity violations in a broad range of physical responses such as electric-elastic coupling (Sec. III.2) and nonreciprocal transport and optical responses (Sec. III.3). Based on the arguments presented in these sections, one can figure out that the symmetry (symmetry of the combined operation of and ) holds an essential role in disentangling the emergent responses induced by the parity violation. Moreover, we overview recent studies working on the control of the magnetic parity violation in Sec. IV. In light of the field of antiferromagnetic spintronics, a lot of efforts have been made to control and utilize the parity-violating magnets. Similarly to a series of antiferromagnets, the magnetic parity violation may exist in superconductors. We introduce candidate superconductors hosting the magnetic parity violation and the physical property resulting from the interplay between superconductivity and magnetic parity violation (Sec. V). Finally, we summarize the review and give some outlooks in Sec. VI.
II Magnetic Parity Violation and Space-Time Symmetry
The parity violation can be classified by whether it is accompanied by the -symmetry breaking. We call the parity violations magnetic parity violation and electric parity violation, when the symmetry breaking accompanies violation or not, respectively. The electric parity violation may be typical and is found in mundane acentric crystals and those undergoing structural transitions such as the ferroelectric order. The magnetic parity violation trivially occurs by applying the external magnetic field to systems manifesting the electric parity violation. On the other hand, the magnetic parity violation can occur not to be admixed with the electric parity violation. In this section, we explain the symmetry of each parity violation and discuss candidates for magnetically-parity-violating materials (Sec. II.1). The candidate materials consist of a class of antiferromagnets called -symmetric magnets. A lot of -symmetric magnets show a common feature in their crystal structure, that is, locally-noncentrosymmetric structure. We briefly discuss the structural feature and associated physical properties such as hidden magnetic degrees of freedom (Sec. II.2).
II.1 Parity-time-reversal symmetry and parity violations
Two types of parity violation are clearly distinguished by the space-time symmetry. One may take account of - and -parities to characterize the space-time symmetry. We, however, stress that the combination of and operations plays a fundamental role as well as and symmetries. To this end, we raise examples of symmetry breaking arising from the antiferromagnetic order.

The antiferromagnetic order is defined by the antiferroic alignment of magnetic moments in crystals. Owing to the -odd nature of magnetic moments, the antiferromagnetic order is accompanied by the -symmetry violation. The symmetry related to the operation, however, may be retained; e.g., for the antiferromagnetic order in the square lattice, there exists symmetry coupled to the lattice translation [Fig. 1(a)]. The preserved symmetry is equivalent to the symmetry in terms of the bulk physical properties because the microscopic lattice translation does not lead to any symmetry constraint. Such an effective symmetry makes it difficult to detect the antiferromagnetic state without microscopic spectroscopy such as neutron diffraction.
The antiferromagnetic order gives rise to various symmetry breaking due to the crystal structure in contrast to the case of checkerboard antiferromagnetic order depicted in Fig. 1(a). Here, we consider the zigzag chain to corroborate the space-time symmetry arising from the magnetic parity violation. The zigzag chain is comprised of two sites (A and B sites) inside the unit cell Yanase (2014) [Fig. 1(b)]. The system holds the symmetry due to interchanging the sublattices, while each site is not an inversion center. Let us introduce the antiferromagnetic order with the zero propagation vector () [Fig. 1(c)]. The ordered state is described by using the magnetic moments localized at sites as
| (1) |
Intriguingly, the antiferromagnetic order breaks both of the and symmetries in the macroscopic scale. It is readily checked by applying the operations to the magnetic configuration given in Eq. (1). The operation interchanging the two sites does not flip the localized magnetic moments due to the axial symmetry of magnetic moments. Then, the magnetic moments at each site are transformed as
| (2) |
Similarly, the operation reverses the magnetic moments with keeping structural degrees of freedom invariant as
| (3) |
As a result, the antiferromagnetic state shows the odd parity under the and operation, which is a magnetic parity violation. The symmetry breaking is not compensated by any symmetry operation such as a lattice translation in sharp contrast to the antiferromagnetic order shown in Fig. 1(a).
One can notice the symmetry unique to the antiferromagnetic zigzag chain by considering Eqs. (2) and (3). The antiferromagnetic state returns to the original configuration under the combined operation as
| (4) |
which indicates the symmetry. In the light of the -even nature, the parity-violating magnets may be called -symmetric magnets. The -symmetric magnets are comprised of intriguing materials such as magnetoelectric materials Fiebig (2005) and electrically-switchable antiferromagnets Wadley et al. (2016).
The intact symmetry is a fundamental property distinguishing the -symmetric magnets from systems showing the electric parity violation. For an example of electric parity violation, the macroscopic electric polarization is flipped under the operation while it is invariant under the operation (-odd, -even). The electric polarization is therefore absent in the -symmetric systems. As a result, parity-violating systems are divided into three classes; the -symmetric case with only the electric parity violation, -symmetric case with only the magnetic parity violation, and the otherwise manifesting both electric and magnetic parity violations. The third class contains an important series of the multiferroic magnets such as MnO3 (: rare-earth element) Kimura et al. (2003); Tokura et al. (2014), which is not in the scope of this review. As a result, we have obtained the classification of parity violations based on the parity under , , and operations.
Adding the case of the ferromagnets, we tabulate the space-time symmetry of ordered states in Fig. 2. Owing to different space-time symmetry, the order is not admixed with each other unless the preserved symmetry is lost.

Keys to the magnetic parity violation are antiferromagnetism and the crystal structure showing the local parity violation at atomic sites as depicted in Fig. 1(b). The -symmetric magnets can be found in a broad range of materials as tabulated in Refs. Schmid (1973); Siratori et al. (1992); Gallego et al. (2016); Watanabe and Yanase (2018a). The structural feature, called locally-noncentrosymmetric property, is ascribed to various structural degrees of freedom other than atomic sites; layers, clusters of atoms, chains, and so on (see Sec. II.2). Furthermore, the magnetic parity violation can be realized without the locally-noncentrosymmetric structure by unconventional order such as the loop-current order Zhao et al. (2015); Seyler et al. (2020); Murayama et al. (2021); Watanabe and Yanase (2021b) and exotic superconductivity Wang and Fu (2017); Kanasugi and Yanase (2022); Kitamura et al. (2023). Interestingly, the magnetic parity violation can be implemented by micro-fabrications as demonstrated in Refs. Lehmann et al. (2019, 2020).
II.2 Hidden Magnetic Degrees of Freedom in Crystals
The locally-noncentrosymmetric property can be found in various sectors in crystal structure Fischer et al. (2023). The series of locally-noncentrosymmetric crystals consists of the subsector degree of freedom such as atomic site, cluster, chain, and so on (Fig. 3). We here introduce a key ingredient to understand the itinerant property unique to locally-noncentrosymmetric crystals, that is hidden magnetic degrees of freedom such as spin and Berry curvature.

Firstly, we explain spin-charge coupling hidden by the inversion partners in crystals. The concept has been introduced to predict the -symmetric counterpart of Chern insulator proposed in Ref. Haldane (1988), that is quantum spin Hall insulator Kane and Mele (2005); Fu et al. (2007). Independently, the concept has been proposed in the contexts of superconductivity Yanase (2010); Fischer et al. (2011), spintronic applications Železný et al. (2014), and the first-principles study of spin-momentum coupling Zhang et al. (2014). A prototypical example is the bilayer two-dimensional electron gas which may be found in double quantum wells and layered materials such as the cuprate Liu et al. (2013) [Fig. 3(c)]. Although the inversion center is present between the layers, the symmetry does not hold if each layer is taken to be the origin. The locally-noncentrosymmetric symmetry indicates that each layer is under unidirectional potential arising from the other layer. Owing to the global parity, the polarity of the unidirectional field should be opposite between the two layers.
The structural property is built into the peculiar spin-orbit interaction as follows. The two-dimensional electron gas manifests the so-called Rashba spin-orbit coupling in the presence of the polar field as written by the one-body Hamiltonian
| (5) |
where the polar field is along the direction, and the electron’s momentum and spin . The Rashba spin-orbit coupling gives rise to the vortex-like spin configuration in the momentum space as confirmed in spin-resolved spectroscopy of bulk materials such as BiTeI Ishizaka et al. (2011); Landolt et al. (2012). In the case of the bilayer system, the Rashba spin-orbit coupling has the opposite signs as
| (6) |
for the upper layer and
| (7) |
for the lower layer. It indicates that spins are closely coupled to the layer degree of freedom as well as the momentum and that the spin-momentum locking is completely compensated.
To elucidate the electronic structure, let us write down a Hamiltonian of the bilayer system in the field-quantization representation as
| (8) |
The creation (annihilation) operators () are for the upper () and lower () layers and implicitly include the spin degree of freedom written by the Pauli matrices . A constituent Hamiltonian reads as
| (9) |
for the diagonal components and the tunneling parameter for the off-diagonal components. When the constant tunneling parameter varies, the energy spectrum of Hamiltonian Eq. (8) changes as schematically depicted in Fig. 4(a,b,c). It is noteworthy that in the case of no tunneling () one can observe the energy spectrum similar to that with the Rashba spin-orbit coupling nevertheless each spectrum shows double degeneracy due to the symmetry [Fig. 4(a)]. This is because the opposite spin-momentum coupling in two layers leads to the vanishing spin polarization at each momentum as
| (10) |
where is the eigenstate for energy of Eq. (8) denoted by the momentum , level index , and Kramers degree of freedom . On the other hand, there exists the spin-momentum locking in a staggered manner as given by
| (11) |
The obtained subsector-dependent spin-momentum coupling is called hidden spin polarization Zhang et al. (2014). If the hopping surpasses the spin-orbit coupling quantified by [Fig. 4 (b,c)], the entanglement of wavefunction localized at each layer weakens the hidden spin-polarization Maruyama et al. (2012).

The concept of hidden spin polarization is generalized to other locally-noncentrosymmetric crystals Kane and Mele (2005); Fu et al. (2007); Yanase (2014); Železný et al. (2014). For instance, given that local inversion asymmetry comes from the sublattice degree of freedom as in the zigzag chain and the honeycomb net [Fig. 3(b)], the hidden spin polarization is given by the sublattice-dependent spin-orbit coupling
| (12) |
The basis for Pauli matrices is spanned by the two sublattice degrees of freedom, and thus indicates that the antisymmetric spin-orbit coupling () appears in a staggered manner for electrons localized at each sublattice. The expression for the vector is determined by the local site symmetry of the sublattice Fischer et al. (2023); Guan et al. (2022) such as
| (13) |
with the coupling constant given for the next-nearest neighbor hopping path of the zigzag chain [Fig. 3(a)], and
| (14) |
for that of the honeycomb lattice Kane and Mele (2005); Hayami et al. (2014b) [Fig. 3(b)]. The coupling is similarly obtained in more complex cases such as locally-noncentrosymmetric crystals consisting of sublattice like Cr2O3 Sumita et al. (2017); Daido et al. (2019); Hayami et al. (2014b); Niu et al. (2017).
After the discovery of the hidden spin polarization, many studies have been devoted to utilizing and maximizing this peculiar charge-spin coupling mostly for the case of local asymmetry of atomic sites. For instance, since the hidden spin-orbit coupling gives a significant modification of the spin susceptibility, the superconducting state acquires more robustness to the paramagnetic pair breaking Maruyama et al. (2012) as reviewed in Refs. Sigrist et al. (2014); Fischer et al. (2023). In addition to the enriched property of nonmagnetic superconductors, the hidden spin-momentum coupling leads to various physical phenomena if coupled to the antiferroic order (see the following sections).
The hidden spin-charge coupling has been quantitatively evaluated for various materials. The model studies clarified important ingredients for the large sublattice-dependent spin-orbit coupling, that is the atomic spin-orbit coupling and odd-parity hopping allowed by the local parity violation Fischer et al. (2011); Yanase (2014); Hayami et al. (2014b, a). It follows that the hidden spin polarization is significant for the bands consisting of orbitals at heavy atoms Liu et al. (2013); Yao et al. (2017); Goh et al. (2012). On one hand, as implied in Fig. 4(a-c), the inter-sublattice hopping may smear out the hidden spin-charge coupling. In this regard, large hidden spin polarization may occur due to negligible inter-sublattice hopping that can be realized in the layered materials such as 2H-stacking transition metal dichalcogenides (e.g., WSe2) Gong et al. (2013); Riley et al. (2014); Jones et al. (2014); Gehlmann et al. (2016); Bertoni et al. (2016); Razzoli et al. (2017); Devarakonda et al. (2020); Tu et al. (2020) and layered superconductor Liu et al. (2013, 2015); Nakamura and Yanase (2017); Wu et al. (2017); Gotlieb et al. (2018). The layered materials are promising platforms for manipulating the spin-orbit coupling due to the high controllability offered by gating fields and the epitaxial-growth method. Gong et al. (2013); Goh et al. (2012); Shimozawa et al. (2016). Interestingly, nonsymmorphic space group symmetry may realize the segregation between sublattice degrees of freedom in the high-symmetry subspace of the Brillouin zone Young and Kane (2015) and therefore leads to enhanced hidden spin polarization. The hidden spin polarization protected by the nonsymmorphic symmetry has been pointed out by theories Yanase (2016); Sławińska et al. (2016); Yuan et al. (2019) and demonstrated in experiments Santos-Cottin et al. (2016); Zhang et al. (2021). In the two-sublattice Hamiltonian Eq. (8), the inter-sublattice decoupling is represented by vanishing hopping at high-symmetry momentum. Such decoupling can also be protected by symmorphic symmetries, depending on the symmetry of the local orbitals Akashi et al. (2017); Nakamura and Yanase (2017).
Since the electronic bands of layered materials are described in a spin- and layer-resolved manner, the spin-resolved ARPES study may allow us to measure the hidden spin polarization if there is no complete compensation in the spin polarization between the photoelectrons emitted by the scattering at each layer Zhang et al. (2014); Riley et al. (2014). For example, the intimate coupling between the spin, valley, and layer degrees of freedom in van der Waals materials has been reported by Ref. Razzoli et al. (2017) (Fig. 5). Such an interplay between various degrees of freedom has been investigated by photoluminescence measurements as well Wu et al. (2013); Zhu et al. (2014); Jones et al. (2014).

In the preceding discussions, we considered the electrical activity of spins hidden by the locally noncentrosymmetric structure. It is noteworthy that other -odd quantities are coupled to the momentum in a similar manner to spins Lin et al. (2020). For instance, the celebrated Kane-Mele model shows the hidden Berry curvature offering the quantum spin Hall effect Kane and Mele (2005). The hidden magnetic properties have been explored in terms of the orbital magnetic moment and Berry curvature Go et al. (2018); Cho et al. (2018); Beaulieu et al. (2020).
II.3 Multipolar degree of freedom of visible antiferromagnets
The locally-noncentrosymmetric symmetry can be incorporated into the model studies by using the hidden spin-orbit coupling introduced in Sec. II.2. This peculiar spin-charge coupling seemingly may not dramatically affect the physical property due to the fact that the symmetry-breaking effect is compensated between subsectors. On the other hand, once the antiferroic ordering such as anti-ferroelectricity and antiferromagnetism occurs, staggered order parameters may give rise to macroscopic symmetry breaking. As a result, the emergent responses arise from the coupling between the hidden spin-charge coupling and ‘antiferroic’ order. It is convenient for clarifying the macroscopic physical properties to introduce the multipolar degrees of freedom Watanabe and Yanase (2018a); Hayami et al. (2018); Winkler and Zülicke (2023); Watanabe and Yanase (2017).

Let us again consider the antiferromagnetic state of the zigzag chain where magnetic moments are ordered along the direction as an example. Note that the Néel vector is taken to be along the axis different from that depicted in Fig. 1(c). As implied by the form of spin-orbit coupling in Eq. (13), each sublattice is under the polar field along the direction in a staggered manner. By taking the cross product of the local polar fields and magnetic moments , the products are the same between the sublattices A and B
| (15) |
which are termed with an atomic toroidal moment [Fig. 6(a)]. Thus, the antiferromagnetic state is translated into the ferroic arrangement of atomic toroidal moments, which is in agreement with the zero propagation vector indicating the uniformly manifesting physical quantity. As depicted in Fig. 6(b,c), the atomic toroidal moments uniformly align along the direction, and its direction is opposite between the two antiferromagnetic states. Given that the toroidal moment is the polar vector with the -odd and -even parities, one can see that the obtained ferro-toroidal state shows the magnetic parity violation. Similarly, if the zigzag chain undergoes a antiferroic ordering of nonmagnetic even-parity objects such as commensurate charge density wave and orbital order, the order results in the ferroic alignment of odd-parity and -preserving quantities such as electric polarization. It indicates that the ordered state shows the electric parity violation Hitomi and Yanase (2014, 2016).
These examples imply that the antiferroic order in the locally noncentrosymmetric crystals is a promising playground for the spontaneous parity violation in solids and that the ordered state may be classified in terms of the electric or magnetic anisotropy showing the -odd parity, that is the odd-parity electric or magnetic multipolar field Kusunose (2008); Kuramoto et al. (2009). Similar arguments are obtained for the even-parity magnetic multipolar order without uniform magnetization such as collinear magnetic order in a rutile-type magnet, MnF2, and noncollinear magnetic order in Mn3X ( Ga, Ge, Sn, Ir, and Pt) Nakatsuji et al. (2015); Nayak et al. (2016); Šmejkal et al. (2020). In those cases, the seemingly antiferroic order is characterized by and classified into an even-parity multipolar phase, whereas the local parity violation is not required because the ferroic even-parity multipolar order does not break the symmetry. It is noteworthy that the importance of the magnetic octupole moment has been confirmed in Mn3Sn and Mn3Ge Suzuki et al. (2017); Nomoto and Arita (2020); Kimata et al. (2021); Higo et al. (2022); Go et al. (2022); Yoon et al. (2023).
Physical consequences of the odd-parity multipolar order can be derived by group-theoretical tools once the symmetry of the phase is identified. Let us raise some examples of odd-parity multipoles and associated physical properties from the viewpoint of the representation analysis below. Notably, the odd-parity multipolar symmetry can emerge not only due to the antiferroic order in the locally-noncentrosymmetric systems but also by other exotic quantum phases such as the loop-current order Zhao et al. (2015); Murayama et al. (2021). We emphasize that the classification result obtained by group theory can be applied to any system showing electric and magnetic parity violations.
The uniformly emerging order parameter characterizing the (second-order) phase transition is classified by irreducible representations of a given crystallographic point group. For instance, when the ordered phase belongs to the representation of the tetragonal point group (), odd-parity multipole moments appear in the ferroic manner. When the -type phase transition is attributed to multipolar degrees of freedom, candidates for the order parameter are the electric octupole moment
| (16) |
for the electric parity violation and the magnetic quadrupole moment
| (17) |
for the magnetic parity violation Watanabe and Yanase (2017). These multipole moments indicate the lowest order of electric or magnetic anisotropy in real space. Since these multipole moments show the opposite parity under the or operation, the corresponding irreducible representation should be labeled by the -parity such as for and for ; i.e., the odd-parity irreducible representation is -even and -odd for , or -odd and -even for (subscript ‘u’ denotes the odd parity). 111 We implicitly assume that the para phase is -symmetric and -symmetric to characterize the multipolar order by the definite parity of each operation. Generalized representation analysis is similarly obtained by making use of the magnetic point group Erb and Hlinka (2020).
As in the classification of order parameters in terms of the real-space basis [Eqs. (16) and (17)], the relevant basis functions in the momentum space () are identified in the group-theoretical manner Sigrist and Ueda (1991). Referring to the classification presented in Refs. Watanabe and Yanase (2017, 2018a); Hayami et al. (2018), we can construct a basis function formed by the momentum and magnetic moment as
| (18) |
for the representaion and
| (19) |
for the representation. One may notice that the momentum-space basis for the electric parity violation of Eq. (18) is obtained by replacing with in the real-space basis for the magnetic parity violation [Eq. (17)] and vice versa. The cross-correlation is a consequence of the intact symmetry, that is or symmetry.

The correspondence between the real- and momentum-space basis functions conveniently gives clues to understanding the itinerant property of the parity-violating materials such as changes in the electronic structure and emergent responses. Leaving discussions of the physical responses to the following sections, let us consider the band structure undergoing the -type odd-parity multipolar order for an example. In case of the electric parity violation, the odd-parity electric multipolar anisotropy of Eq. (16) corresponds to spontaneous emergence of the spin-momentum locking of Eq. (18) whose form is similar to that of the Rashba spin-orbit coupling of Eq. (5). Contrastingly, in the case of the magnetic parity violation, the magnetic multipolar anisotropy of Eq. (17) gives rise to the spin-independent modulation of electronic bands of Eq. (19). The asymmetric energy spectrum has been observed in experiments of a -symmetric magnet Fedchenko et al. (2022); Lytvynenko et al. (2023). These characteristic changes in the band structure are strictly forbidden if the or symmetry is present; the asymmetric modulation such as Eq. (19) is forbidden due to the symmetry, while the spin-momentum locking as in Eq. (18) is absent in total if the symmetry is retained. The modified band structures arising from electric and magnetic parity violation are summarized in Fig. 7.
The microscopic grounds for the multipole moments in solids remain to be completed, though the macroscopic aspects have been addressed from the viewpoint of point group symmetry. The origin of the multipole moments may be attributed to the atomic orbitals well-localized at rare-earth atoms in some f-electron systems Kuramoto et al. (2009). The quantitative estimates of the multipole moments have been explored by first-principles calculations Cricchio et al. (2010); Bultmark et al. (2009); Suzuki et al. (2018); e.g., the close relationship between the magneto-electric coupling and the odd-parity magnetic multipole moments has been pointed out Spaldin et al. (2013); Thöle et al. (2016, 2020).
Furthermore, recent theoretical studies revisited the connection between the observable physical property and multipolar degrees of freedom in the context of generalized free energy. For instance, the thermodynamic magnetic quadrupole moments are defined to be conjugate to the gradient of magnetic fields, and they are directly related to the magnetoelectric property Gao et al. (2018); Shitade et al. (2018); Bhowal and Spaldin (2022). It is noteworthy that the thermodynamic multipole moments contribute to other cross-correlated responses such as the nonlinear thermoelectric response Gao and Xiao (2018), temperature-gradient-induced magnetization (gravito-magnetoelectric effect) Shitade et al. (2019); Shinada and Peters (2023), and spin accumulations Shitade and Tatara (2022). In the same spirit, the electric quadrupole moments are defined and estimated in the language of thermodynamics and quantum geometry Daido et al. (2020); Kitamura et al. (2021). It is desirable to perform further explorations for higher-order multipolar degrees of freedom in solids Tahir and Chen (2023).
Finally, we comment on material realizations of the -symmetric (odd-parity magnetic multipolar) magnets. Although the uniform odd-parity magnetic multipolar fields show up in the presence of special crystal and antiferromagnetic structures, one can notice that they exist in a broad range of materials as we tabulate candidates in Appendix A. Historically, enormous efforts have been made to explore materials undergoing the -symmetric magnetic order, with special attention to the oxides motivated by the interests in the magnetoelectric coupling in magnetic insulators such as Cr2O3 and LiCoPO4 Fiebig (2005). On the other hand, as mentioned in the introductory part, recent studies shed light on magnetic metals as well with the developments in the field of antiferromagnetic spintronics Jungwirth et al. (2016); Baltz et al. (2018). The candidates cover a diverse class of materials such as ferro-pnictide (e.g., BaMn2As2, EuMnBi2, CuMnAs, YbMnBi2) Borisenko et al. (2019); Wadley et al. (2015); Sakai (2022); Tanida et al. (2022) and rare-earth-based magnetic conductors Saito et al. (2018); Arakawa et al. (2023); Ota et al. (2022). It is expected that the magnetic parity violation may show intriguing interplays with the physical properties unique to the metals like topological electrons nearby the Fermi energy Tang et al. (2016); Šmejkal et al. (2018), giant magnetoresistance Aoyama et al. (2022); Sun et al. (2021); Ogasawara et al. (2021), and what is discussed in the following sections (e.g., magnetopiezoelectric effect and nonreciprocal electrical transport induced by the magnetic parity violation).
III Emergent Responses of -symmetric magnets
III.1 Electric-Magnetic Classification of Response Function
The contrasting space-time symmetry of the odd-parity electric/magnetic multipolar materials is reflected in the response as well as the electronic structure described in Sec. II.3. In this section, taking the linear response function, we introduce the -odd/-even classification of physical responses and argue that the and symmetries play complementary roles.
The response formula is generally given by
| (20) |
where the physical quantity responds to the external field conjugate to a physical quantity by the perturbed Hamiltonian . Based on the Kubo formula, we derive the ac response function in the Lehmann representation
| (21) |
with the summation over the many-body eigenstates for the unperturbed Hamiltonian. We introduced the eigenenergy , Boltzmann factor (: partition function), and infinitesimal positive parameter . Physical quantities are given by the matrix element for the eigenstates . The response function is classified by the parity under a symmetry operation such as , , and operations. In the case of magnetization response to the electric field [] known as the magnetoelectric effect, the response function has odd- (), odd- (), and even-parity () under the , , and operations, respectively. Note that the parity satisfies the relation .
The response function is further divided into the symmetric and antisymmetric parts under the permutation of and as
| (22) |
The components are respectively given by
| (23) |
and
| (24) |
We may gain an intuitive understanding of the symmetric and antisymmetric terms by considering the dc limit (). By replacing with the phenomenological scattering effect , each contribution is given as
| (25) |
The antisymmetric contribution explicitly depends on the sign of and is proportional to for the equi-energy transitions (). As a result, the response is in an intimate relation with the dissipative phenomenon accompanied by energy absorption. On the other hand, the symmetric term does depend on and remains finite even in the limit of . This property indicates that the symmetric term is generically irrelevant to the scattering process and may occur without dissipation. In the light of these contrasting aspects with respect to dissipation, the antisymmetric and symmetric terms are also called dissipative and dissipation-less responses, respectively Freimuth et al. (2014); Železný et al. (2017a); Watanabe and Yanase (2017).
Following the symmetry arguments in Ref. Watanabe et al. (2024), we finally obtain the -parity decomposition of the antisymmetric and symmetric responses in Eqs. (23) and (24). We here introduce the -even and -odd contributions which appear with and without -symmetry, respectively. As displayed in Table 1, the symmetric and antisymmetric parts of a given response function are classified by the -parity ; for a response with , only the symmetric part is allowed in the -symmetric system, while the antisymmetric contribution is admixed by the -symmetry breaking. On the other hand, for the case of , the response in the -symmetric system is solely attributed to the antisymmetric part, but it contains both antisymmetric and symmetric contributions when the symmetry is lost. For instance, the dc electric conductivity tensor () formally shows the odd-parity under the operation, and thus . Therefore, only the antisymmetric part is finite in the -symmetric system, consistent with the fact that the allowed longitudinal response is dissipative as formulated in the Boltzmann’s semiclassical theory of transport phenomena. The symmetric part is relevant to the -symmetry breaking. This argument agrees with the fact that the electric conductivity tensor hosts the symmetric part such as the Hall conductivity which can generically be free from dissipation. 222The symmetric and antisymmetric terms of the electric conductivity do not indicate the tensor symmetry of ; for instance, the antisymmetric term we introduced is not the Hall response () but the dissipative and longitudinal conductivity (). This is because we relate the electric conductivity with the inverse response written by ( is the electric polarization, is the vector potential). The antisymmetric term therefore satisfies . The well-known Onsager relation is reproduced by using the relations and . Similarly, one can derive the symmetric-antisymmetric decomposition by using the linear response formula in the canonical-correlation representation, by which the Onsager reciprocity is obtained more explicitly Watanabe et al. (2024).
Similarly, the response function with is decomposed into the -even and -odd contributions. An example is the nonmagnetic and magnetic spin Hall effects which are of high interest in recent studies on spintronic effects. The spin-polarized current response to the electric fields is given by the formula
| (26) |
where denotes the current with the spin polarization along the direction. Specifically, the spin Hall conductivity is defined by the off-diagonal elements . The -even component can make contributions through the symmetric part of the tensor [Eq. (24)], consistent with the dissipationless nature of the spin-Hall effect, as demonstrated in intensive studies of the spin Hall effect of nonmagnetic semiconductors Sinova et al. (2015). On the other hand, the -symmetry violation gives rise to the antisymmetric counterpart [Eq. (23)] of spin Hall response called magnetic spin Hall effect Kimata et al. (2019). Since its dissipative aspect is closely linked with the metallic conductivity, the magnetic spin Hall effect is characteristic of magnetic (-odd) metals Železný et al. (2017b); Mook et al. (2020).
| Symmetric | Antisymmetric | |
|---|---|---|
| even | odd | |
| odd | even |
It is noteworthy that either -even or -odd contribution may appear without being concomitant with the other due to the additional symmetry constraint. For example, the magnetoelectric effect is -odd () and can occur in parity-violating materials. The electric parity violation allows the system to have the antisymmetric part of because of the preserved symmetry. This response is accompanied by dissipation and is called the inverse magnetogalvanic effect (Edelstein effect). On the other hand, those with the pure magnetic parity violation manifest only the symmetric counterpart not being admixed with the antisymmetric contribution, because the magnetoelectric effect is incompatible with the space-time symmetry of magnetic parity violation due to the -odd nature. Consequently, the - and -symmetries play complementary roles in -odd physical responses due to the -symmetry constraint. The symmetry argument is applicable to the nonlinear responses as well as the linear response, as we see later in Sec. III.3.
III.2 Magnetic Counterpart of Piezoelectric Effect
The piezoelectric effect is the interconversion between the stress and electric polarization allowed in noncentrosymmetric materials. The effect has been widely used for applications such as the transducer. The response formula reads as
| (27) |
with electric polarization , stress , and strain . Typically, the piezoelectric-active materials are limited to insulators such as ferroelectric ceramics to hold electric polarization. By taking and in Eq. (20), the time-reversal parity indicates that the -even part is the symmetric part (see Table 1) and may be attributed to the equilibrium property in the DC limit, being consistent with the piezoelectric effect. On the other hand, the -parity classification in Table 1 also makes us aware of the possibility of the -odd and antisymmetric contribution to the electric-elastic coupling. Notably, owing to the -odd property of the response (), the -odd contribution is allowed without being admixed with the conventional piezoelectric effect in the -symmetric systems.
Let us take the response function given by and and corroborate the DC limit. Owing to the -symmetry constraint, the surviving term is purely the antisymmetric part as
| (28) |
We introduced the phenomenological scattering effect parametrized by similarly to Eq. (25). In the clean limit (), the response is dominated by the equi-energy transition process () giving rise to the response as much as .
In the independent particle approximation, the formula in the clean limit is recast as Watanabe and Yanase (2017)
| (29) |
where is the elementary charge of electrons and the summation is over the momentum () and the band indices (). We introduced the velocity operator for electrons and the Fermi-Dirac distribution function . The strain and velocity operators are evaluated by the Bloch states having the eigenvalue for the Hamiltonian. The Fermi-surface factor indicates that metallic conductivity is required for this piezoelectric-like response in sharp contrast to the conventional piezoelectric response allowed even in insulators.
This unconventional type of “piezoelectricity” is termed as magnetopiezoelectric effect and was predicted by theories with a semiclassical theory including the quantum-geometrical effect Varjas et al. (2016) and with full-quantum treatment based on the linear response theory Watanabe and Yanase (2017). When the stimulus is replaced with the electric current , the response formula is rewritten by
| (30) |
where the response function is obtained as by using the formula for longitudinal conductivity . The obtained magnetopiezoelectric response function is not sensitive to the phenomenological scattering parameter. This is because the Drude-type conductivity leads to the scattering-rate dependence of with Eq. (28). As a result, the response function does depend on the generic material properties as in the case of inverse magneto-galvanic effect Levitov et al. (1985); Edelstein (1990). It indicates the fact that the electric current plays an essential role in this magnetic counterpart of the piezoelectric response rather than the electric field. It follows that the magnetopiezoelectric response occurs under the electric current flow and is inevitably accompanied by the Joule heating. The energy loss may be unfavorable for future applications based on the magnetic metals. The undesirable heating effect may be alleviated by utilizing the superconducting property (see Sec. V). The metallic property could also be an advantage of the magnetopiezoelectric effect for applications as we discuss at the end of this subsection. We summarize the contrasting properties of the known piezoelectric effect and the magnetopiezoelectric effect in Table 2. For the switchability of the -symmetric magnetic order and the magnetopiezoelectric effect, one can refer to the discussions in Sec. IV.
| Piezoelectric effect () | Magnetopiezoelectric effect () | |
| parity | Even | Odd |
| Stimulus | Electric field | Electric current |
| System | Insulator & Metal | Metal |
| Relaxation time dependence | ||
| Joule heating | No | Yes |
| Switching | w/ or w/o | w/ or w/o |
The magnetopiezoelectric effect can also be observed in nonmagnetic materials with the electric parity violation by applying the external magnetic field. In this case, not only the symmetry but also the symmetry is broken, and the elastic-electric coupling is obtained as the combination of the conventional piezoelectric response and the magnetopiezoelectric response. The admixture may prevent us from specifying the magnetopiezoelectric response Varjas et al. (2016). On the other hand, there is no such concern in the case of the -symmetric magnets because the symmetry exactly forbids the conventional piezoelectric response.
In the following, we explain the microscopic grounds for the magnetopiezoelectric effect by taking a -symmetric magnetic metal, hole-doped BaMn2Pn2 (Pn=As, Sb, Bi) Watanabe and Yanase (2017). BaMn2As2, for instance, undergoes the G-type antiferromagnetic order at high Néel temperature which breaks the symmetry. The violation originates from the coupling between the antiferromagnetic order and the locally noncentrosymmetric environment of Mn sites [Fig. 8(a)]. Considering the site symmetry at Mn atoms, one can derive the antisymmetric spin-orbit coupling as
| (31) |
where denote the coupling constants of the sublattice-dependent anti-symmetric spin-orbit coupling. The locally noncentrosymmetric Mn atoms show hidden spin polarization described by Eq. (12) with Eq. (31), and it couples to the antiferromagnetic order.
The ordered state manifests the magnetic parity violation. Specifically, the magnetic point group symmetry is
| (32) |
consisting of the unitary symmetry with the point group and of the anti-unitary symmetry including the symmetry (). Although the parent compound BaMn2As2 shows insulating behavior with a small gap (meV), the metallic conductivity is acquired by doping hole carriers or by applying high pressure. Thus, the material is a promising candidate for -symmetric magnetic metals by which we can demonstrate the interplay between the metallic conductivity and magnetic parity violation.
By imposing the unitary symmetry in Eq. (32), the allowed components of the response tensor Eq. (28) are
| (33) |
We again stress that the preserved symmetry forbids the conventional (inverse) piezoelectric effect of Eq. (27). Taking the independent-particle approximation, the microscopic origin can be inferred from the formula Eq. (29). To grasp the intuitive picture of the magnetopiezoelectric effect in BaMn2As2, let us focus on the electronic structure unique to it. The metallic conductivity is ascribed to the hole pocket placed at point, which is expected to realize the interplay between the magnetic parity violation and itinerant property. According to the magnetic point group symmetry of Eq. (32), the active odd-parity magnetic multipoles are such as the magnetic quadrupole [Eq. (17)] and magnetic hexadecapole moment Watanabe and Yanase (2018a). The group-theoretical argument introduced in Sec. II.3 allows us to identify the anti-symmetric modulation in the electronic structure given by the tetrahedral modulation of the energy spectrum [Eq. (19)].
The obtained asymmetric electronic band structure plays an essential role in the magnetopiezoelectric effect. When applying the electric field to metals, the Fermi surface is shifted along the applied direction as obtained in the semiclassical theory of transport as
| (34) |
The field-induced shift () is coupled to the asymmetry in the band dispersion () and may induce additional anisotropy in the Fermi surface. In the case of BaMn2As2, the coupling between the tetrahedral modulation and the field-induced shift along the -axis results in the nematic anisotropy in the - plane. The resultant nematic anisotropy is absent in equilibrium according to the magnetic symmetry of Eq. (32).
By Letting be -type nematic anisotropy in the Fermi surface, the response formula reads as
| (35) |
where the electric-elastic coupling is defined with the electronic strain . The strain is induced by the dissipative electrical stimulus leading to the shift in Eq. (34). Then, the response formula may be better to be rewritten by using the electric current as
| (36) |
agreeing with Eq. (30). The current-induced electronic strain may subsequently induce the lattice strain through the electron-phonon coupling.

The theoretical prediction of magnetopiezoelectric responses has been confirmed by a series of experiments Shiomi et al. (2019b, a, 2020). The experiments with the -symmetric magnets such as EuMnBi2 and CaMn2Bi2 are consistent with theories. It has been verified that the elastic response is proportional to the applied current density and follows the aforementioned symmetry analysis Shiomi et al. (2020) (Fig. 8). While extensive research has been devoted to maximizing the magnitude of the conventional piezoelectric effect, the magnetopiezoelectric effect has not been fully explored for its material dependence and potential applications. For instance, the magnetopiezoelectric effect varies by the magnetic order and may apply to future elastic devices due to its compatibility with the functionality unique to metals (e.g., giant magnetoresistance Aoyama et al. (2022); Huynh et al. (2019); Ogasawara et al. (2021); Sun et al. (2021)) and nontrivial temperature dependence coming from that of magnetic moments. Notably, the switchable property of -symmetric magnetic order (see Sec. IV) may be favorable for that purpose. More explorations by experiments and quantitative estimates by the first-principles calculations are highly desirable.
III.3 Nonreciprocal Property of Electronic Transport and Optical Response
The -parity classification introduced in Sec. III.1 is generalized to the nonlinear responses, while the parameter dependence of each contribution gets more complicated than the linear response functions. For an example of the nonlinear response, let us consider the electric current response to double electric fields
| (37) |
The generated current is not flipped under the reversal of the electric field. Thus, the response can be termed as the nonreciprocal current generation and is characteristic of parity-violating materials Tokura and Nagaosa (2018). The formula covers various phenomena attracting a lot of interest for a long time such as the nonreciprocal conductivity (), second-harmonic generation (), photocurrent generation (), and parametric generation (). In the following, we mainly discuss the nonreciprocal conductivity and photocurrent generation from the viewpoint of the symmetry. 333 The photocurrent may respond to the irradiating light in materials without the parity violation such as due to the drag effect Plank et al. (2016). In this review, we consider only the nonreciprocal photocurrent response arising from the parity violation.
III.3.1 Nonreciprocal conductivity
A typical example of the DC nonreciprocal current generation is the diode effect of the p-n semiconductor junction where the parity violation comes from the artificial and mesoscale electric field in the depletion layer. Bulk materials similarly show unidirectional behaviors in their conductivity because of the microscopic symmetry breaking. The (bulk) nonreciprocal conductivity is further divided into that with the external magnetic field and that without it, called field-induced and field-free nonreciprocal conductivity, respectively.
Firstly, we briefly overview each type of nonreciprocal conductivity realized in materials manifesting the electric parity violation. There exist extensive works on the field-induced nonreciprocal conductivity realized by the electric parity violation and external magnetic field. For the longitudinal component () in Eq. (37), the response is quantified by the nonlinear resistivity
| (38) |
up to the correction linear in the electric current. The linear resistance usually surpasses the nonreciprocal correction, and thus the nonreciprocal correction is approximately obtained as
| (39) |
Then, the nonreciprocal conductivity quantifies the nonreciprocal electric transport. Under a weak magnetic field, the nonreciprocal resistivity is approximately written as
| (40) |
where a field-induced contribution is determined by the effect of electric parity violation such as the strength of antisymmetric spin-orbit coupling of Eq. (5). Although the nonreciprocal correction is typically smaller than the linear response, it can be identified by using the AC measurement with small but finite frequency Ideue et al. (2017).
From the viewpoint of symmetry, the field-induced nonreciprocal longitudinal transport can be classified into two classes; one comes from the magnetoelectric anisotropy and the other from the trigonal anisotropy Szaller et al. (2013). In the case of the magnetoelectric anisotropy, the unidirectionality is parallel to the -odd polar vector resulting from the coupling of electric parity violation and external magnetic fields. In the seminal work of Ref. Rikken et al. (2001), the -odd polar vector, given by , is built onto the two-dimensional electron gas in a semiconductor device with the perpendicular external electric and magnetic fields. The -odd polar vector similarly appears under the magnetic field along the whirling spiral in a chiral system Krstić et al. (2002); Rikken and Wyder (2005); Yokouchi et al. (2017); Aoki et al. (2019); Akaike et al. (2021); Jiang et al. (2020), namely magnetochiral anisotropy, since the chirality couples axial vectors to polar vectors with their -parity kept. On the other hand, the trigonal anisotropy does not require the polar asymmetry of systems as demonstrated in MoS2 under the out-of-plane magnetic field Wakatsuki et al. (2017).
The nonreciprocal conductivity manifests enhancement by the strong spin-orbit coupling and sizable -breaking effect. In spin-orbit-coupled materials such as a topological insulator Yasuda et al. (2016, 2017), Weyl semimetal Morimoto and Nagaosa (2016a); Wang et al. (2022), and polar semiconductor consisting of heavy elements Ideue et al. (2017); Li et al. (2021). Similarly, the field-induced nonreciprocal conductivity significantly increases by large spin splitting via the coupling to the ferromagnetic order Železný et al. (2021); Yoshimi et al. (2022).
The field-free nonreciprocal conductivity of nonmagnetic systems is also of much interest, though the studies have been devoted to the transverse response, that is, nonlinear Hall effect (). Notably, the nonlinear Hall response occurs without being admixed with the linear-response signal since the preserved symmetry forbids the linear Hall response. The known mechanism for the nonlinear Hall response stems from the intrinsic or extrinsic origin. The intrinsic mechanism originates from, so-called, the Berry curvature dipole Deyo et al. (2009); Moore and Orenstein (2010); Sodemann and Fu (2015), where the Hall effect occurs due to the imbalance in the Berry curvature at stimulated by the electric current. The extrinsic effect denotes the mechanism essentially beyond the independent-particle approximation such as the electron-disorder scattering and electron-electron interaction. In the case of the disorder effect, the skew and side-jump scatterings contribute to the nonreciprocal conductivity Du et al. (2019); Xiao et al. (2019); Nandy and Sodemann (2019); Isobe et al. (2020); Du et al. (2021b) similarly to the anomalous Hall and spin Hall responses Nagaosa et al. (2010); Sinova et al. (2015). The intrinsic and extrinsic contributions can be comparable to each other Du et al. (2021a); e.g., a spin-orbit-coupled semiconductor WTe2 shows the large nonlinear Hall effect which may be from the comparable contributions from the intrinsic and extrinsic effects Ma et al. (2019); Kang et al. (2019). Note that one can exclude the Berry curvature dipole effect by taking the highly-symmetric noncentrosymmetric materials with nongyrotropic point group symmetry since gyrotropic symmetry is required for the Berry curvature dipole Toshio et al. (2020); Isobe et al. (2020); He et al. (2021); Dzsaber et al. (2021).
Next, let us consider the nonreciprocal conductivity of the -symmetric magnets, that is the response purely induced by the magnetic parity violation. The nonreciprocal conductivity of the -symmetric materials received delayed attention despite intensive interest in that of the -symmetric materials, possibly because parity-violation-induced phenomena have been rarely explored in the antiferromagnetic conductors. Circumventing this situation, recent experimental work has identified nonreciprocal transport of the -symmetric magnets Godinho et al. (2018); Ota et al. (2022); Gao et al. (2023); Wang et al. (2023). The nonreciprocal transport of -symmetric magnets is expected to be huge due to the remarkable parity violation. The energy scale of the parity violation can be as much as the Hund’s coupling, which is much larger than the external Zeeman field. It is worth mentioning that the nonreciprocal nature is in intimate relation with the domain state of -symmetric magnetic order and that it can be applied to the antiferromagnetic spintronics (see also Sec. IV).
Let us look into theoretical backgrounds for the nonreciprocal transport mainly with respect to the band-electron system. A basic understanding of the phenomena is obtained by examining the intrinsic mechanism identified by a simple theoretical set-up where the perturbation calculation is performed under the independent-particle approximation. The scattering effect is phenomenologically taken into account by the relaxation-time approximation in the semiclassical transport theory Ideue et al. (2017) and by introducing the damping term into the von-Neumann equation of the quantum transport theory Ventura et al. (2017); Matsyshyn and Sodemann (2019). Including the mechanisms originating from the electric and magnetic parity violations, there exist three intrinsic effects in the clean limit; the nonlinear Drude, Berry curvature dipole, and intrinsic Hall effects. The formula for each mechanism is given as
| (41) | ||||
| (42) |
for the nonlinear Drude effect Ideue et al. (2017),
| (43) | ||||
| (44) | ||||
| (45) |
for the Berry-curvature-dipole effect Deyo et al. (2009); Sodemann and Fu (2015), and
| (46) |
for the intrinsic Hall effect Gao et al. (2014); Watanabe and Yanase (2020); Watanabe (2021). All the formulas comprise the Fermi-surface effect , and hence the above intrinsic mechanisms are allowed in conductors and prohibited in insulators. The derivations have been presented in the density-matrix formalism Matsyshyn and Sodemann (2019); Watanabe and Yanase (2020); Yatsushiro et al. (2022); Kaplan et al. (2024) and diagrammatic approach João and Viana Parente Lopes (2020); Michishita and Nagaosa (2022); Oiwa and Kusunose (2022).
Since the intraband matrix element of the velocity operator is given as in the band-electron system, only the band energy is relevant to the nonlinear Drude effect. This is in agreement with the fact that the nonlinear Drude term can be captured by Boltzmann’s transport theory. On the other hand, the multiband property plays an essential role in the latter two effects as they include the Berry curvature
| (47) |
and the band-resolved quantum metric Gao et al. (2020)
| (48) |
with the Berry connection ( is the periodic part of the Bloch state). We have also introduced the Berry curvature dipole
| (49) |
indicating the dipolar distribution of the Berry curvature along the Fermi surface. The multiband nature is captured by the full-quantum theory and by the semiclassical transport theory taking account of the quantum-geometric corrections; e.g., following the semiclassical transport theory, the Berry curvature dipole effect comes from the anomalous-velocity correction () Xiao et al. (2010). Although the intrinsic Hall effect originates from the anomalous velocity as well, the Berry curvature comes from the -induced virtual transition, namely positional-shift effect Gao et al. (2014).
The Berry curvature dipole effect depends on the scattering rate as . The sensitivity to scatterings is intuitively figured out by the imbalance of Berry curvature dipole driven by the electric current Toshio et al. (2020). Similarly to the current-induced correction to the distribution function in Eq. (34), the compensation between opposite Berry curvature at is removed under the ohmic electric current. The resultant total Berry curvature is finite in the steady state and allows for the deflection of electrons. The obtained Hall response originating from the current-induced Berry curvature is consistent with the symmetry of the nonlinear Hall effect. On the other hand, the intrinsic Hall effect does not show prominent dependence on the scattering rate as much as , because of the uncompensated Berry curvature as well as the positional shift stem from the interband mixing.
The mechanism of nonreciprocal transport is classified by the preserved anti-unitary symmetry ( and symmetries) as summarized in Table 3 based on its dependence on the phenomenological relaxation time defined by . As in the case of linear response function (see Sec. III.1), the anti-unitary symmetry determines the dependence; i.e., for the -symmetric case and for the -symmetric case. When the system manifests both electric and magnetic parity violations (without or symmetry), all of the effects contribute Shao et al. (2020). Note that the nonlinear Drude effect gives rise to the longitudinal nonreciprocity by taking an appropriate geometry of measurement, while the Berry curvature and intrinsic Hall effects lead to only the Hall response. As a result of the adopted approximations, the -symmetric magnetic metals offer both longitudinal and transverse nonreciprocal conductivity, while the -symmetric conductors do show only the Hall response if without the electron correlation effect or more rigorous treatment of disorder scattering Morimoto and Nagaosa (2018); Du et al. (2019); Isobe et al. (2020).
| Nonlinear Drude | Berry curvature dipole | Intrinsic Hall | |
|---|---|---|---|
| N/A | |||
| N/A |
The -symmetric magnetic metals show the nonlinear Drude and intrinsic Hall effects which may dominate the nonreciprocal conductivity with the scarce and moderate disorder concentration, respectively. When the Fermi energy is placed in the vicinity of the Dirac dispersion, the quantum-geometrical effect is so significant as to overwhelm the nonlinear Drude effect Wang et al. (2021); Liu et al. (2021) as implied in even-layer MnBi2Te4 Gao et al. (2023); Wang et al. (2023). For an example of the nonreciprocal conductivity of -symmetric magnets, Ref. Watanabe and Yanase (2020) reported that the nonlinear Drude effect of the carrier-doped BaMn2As2 is estimated to be
| (50) |
with the small density of electron in the clean limit (). The result shows that the nonreciprocal conductivity is informative for investigating the -symmetric magnetic order. Firstly, the response is related to the magnitude and sign of the hidden spin-momentum coupling constant in Eq. (31) which may be hard to directly measure since it is originally hidden by the sublattice degree of freedom. Secondly, the response directly indicates the AFM-domain state by (: sign of Néel vector) and will be a promising tool for the electronics based on -symmetric magnets.
The nonreciprocal conductivity shows the richer property when one goes beyond the independent-particle approximation such as by taking account of the electron-correlation and disorder-scattering effects Morimoto and Nagaosa (2018); Isobe et al. (2020); Michishita and Nagaosa (2022); Kofuji et al. (2021); Kappl et al. (2023). For instance, the scattering event occurs in the presence of impurities Du et al. (2019); Xiao et al. (2019); Nandy and Sodemann (2019); Ma et al. (2023a), spin degree of freedom Yasuda et al. (2017); Ishizuka and Nagaosa (2020), and magnetic-multipolar object Isobe and Nagaosa (2022); Liu et al. (2022). Recent studies further clarified that superconductivity leads to the giant nonreciprocal conductivity by the superconducting fluctuation and the vortex motion. Although we do not discuss it in detail, interested readers can refer to Refs. Tokura and Nagaosa (2018); Nagaosa and Yanase (2024).
The disorder effect is particularly of importance for the conduction phenomena as intensively investigated in the studies of the anomalous Hall effect Nagaosa et al. (2010), where the so-called skew-scattering effect due to disorders can surpass the intrinsic mechanism determined by the Berry curvature Onoda et al. (2008). For the nonreciprocal transport, the field-free nonlinear Hall effect may be attributed to comparable contributions of the intrinsic mechanism [Eq. (45)] and of the skew scattering effect Kang et al. (2019). It is therefore important to take a brief look at the disorder effect on the nonreciprocal conductivity.
The disorder effect beyond the relaxation-time approximation has been corroborated in recent theories. The known mechanisms such as the side-jump and skew-scattering effects can be incorporated by the semiclassical theory and by a full quantum-mechanical theory Du et al. (2021a). Following a semiclassical formulation with the Boltzmann kinetic equation, disorder scattering affects the collision integral and correction to the energy spectrum. In the clean limit, the extrinsic mechanism (skew-scattering term and side-jump term ) contributes to the nonreciprocal conductivity with the relaxation time dependence
| (51) |
where and denote the characteristic time for relaxation due to the symmetric and antisymmetric scattering, respectively Du et al. (2019); Isobe et al. (2020). Specifically, the antisymmetric scattering event is given by the difference in the scattering rates between and , the latter of which can be substituted by the scattering process in the presence of the symmetry.
We illustrate the origin of the asymmetric scattering rate in the light of wave-packet dynamics Isobe et al. (2020). In the presence of the electric parity violation, the wave-packet comprised of the Bloch states manifests spinning behavior due to the orbital angular momentum Chang and Niu (1996); Xiao et al. (2010), which is highly related to the Berry curvature Sinitsyn (2008). Let us consider that the spinning wave packet with the momentum gets deflected into the orbit with by the impurity scattering like the Magnus effect [Fig. 9(a)]. If the incident momentum flipped, the wave packet with the momentum shows self-rotation in the opposite way as ensured by the symmetry as and thereby shows nonreciprocal scattering [Fig. 9(a,b)].
The -symmetric magnets do not allow for such a nonreciprocal-deflection process because of the zero Berry curvature at every momentum []. The absence of extrinsic contributions follows from the fact that the scattering matrix is reciprocal in the presence of the symmetry unless the spin-flip process is taken into account. As a result, the nonreciprocal conductivity of the -symmetric magnets is free from the extrinsic mechanism of Eq. (51) in contrast to that of the nonmagnetic materials. Note that the argument can be applied to systems with the effective symmetry; e.g., the isotropic two-dimensional Dirac electron retains the antiunitary symmetry , the combination of operation and out-of-plane two-fold rotation. The symmetry satisfying makes the scattering process reciprocal in the two-dimensional plane. It implies that an ideal Dirac electron on the topological-insulator surface shows the nonreciprocal conductivity tolerant of the disorder scattering.
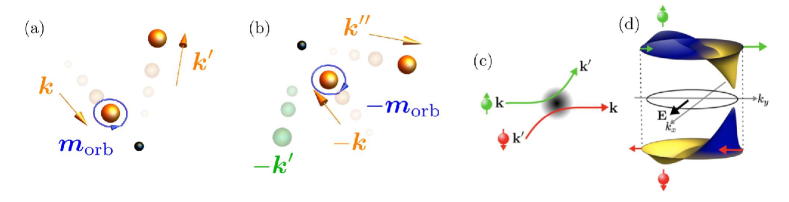
Equation (51) claims that extrinsic effects are comparable to or dominating the intrinsic effects when they are not forbidden by the symmetry, since the leading contribution in the clean limit is the skew-scattering mechanism in the order of . The contributions in Eq. (51) comes from scattering events without spin flip, whereas the spin-flip process gives rise to another extrinsic mechanism characteristic of -symmetric magnets Ma et al. (2023a) [Fig. 9(c)]. For instance, there exists anomalous skew-scattering effect , which depends on the relaxation time as
| (52) |
being comparable to the nonlinear Drude effect of Eq. (42) with a moderate antisymmetric scattering rate . The nonvanishing skew-scattering effect is closely related to the hidden Berry curvature of -symmetric magnets. For the -symmetric magnets comprised of A/B sublattice, the strong exchange splitting may result in electric transport carried by spin-up electrons on the sublattice A and the spin-down electrons on the sublattice B. The two kinds of carriers are connected by the symmetry and undergo the opposite Berry curvature even at the same momentum , by which the total Berry curvature is completely compensated at each momentum. The hidden Berry curvature gives rise to the sublattice-dependent anomalous velocity under the electric field as
| (53) |
where for the sublattice A (B) [Fig. 9(d)]. The staggered anomalous velocity may offer a nonvanishing nonlinear Hall response, since electrons at each site may experience different spin-dependent antisymmetric scattering events which are correlated with the sublattice [Fig. 9(c)]. The emergence of the hidden Berry curvature stems from the -symmetric magnetic order by which the spin degeneracy is lifted at each sublattice in a staggered manner. If disorder concentration is not negligible, another mechanism for the nonreciprocal conductivity also plays an important role. For instance, the side-jump effect similarly gives contributions differently from Eq. (51) Ma et al. (2023a); Atencia et al. (2023) and may be dominant in the presence of moderate disorder scattering.
Finally, the space-time classification of Table 3 remains meaningful even when taking into account the extrinsic mechanism Watanabe and Yanase (2020); Ma et al. (2023a); in other words, the (conventional) skew-scattering and side-jump effects of Eq. (51) vanishes by the symmetry, while the anomalous skew-scattering effect survives in the -symmetric system due to its -odd and -even nature. The classification is similarly extended to cover the self-energy effect as corroborated in the Green’s-function fashion Michishita and Nagaosa (2022).
III.3.2 Photocurrent generation
The photocurrent generation (photogalvanic effect, photovoltaic effect) is a response extensively applied to our daily lives such as solar panels and photodetector. The response can occur due to microscopic parity violation as the nonreciprocal conductivity does, while it has been implemented by mesoscale parity violation such as the internal electric fields of the semiconductor-based p-n junction and ferroelectric materials Fridkin and Popov (1978); Sturman (1992). The mechanism derived from microscopic symmetry breaking is called bulk photocurrent generation. In contrast to typical photo-electric rectifiers, bulk photocurrent generation is allowed not only in polar materials but also in noncentrosymmetric but nonpolar materials including well-known zinc-blende-type semiconductors such as GaAs. The bulk photocurrent response has been attracting enormous interest from theoretical and experimental investigators due to an active discussion of applications to conversion efficiency Nagaosa and Morimoto (2017); Spanier et al. (2016); Liu et al. (2020); Pusch et al. (2023).
The (bulk) photocurrent responses have been microscopically investigated in studies of the band-electron systems Sturman (1992); von Baltz and Kraut (1981); Kristoffel (1985); Sipe and Shkrebtii (2000). For instance, it was shown that the electric parity violation gives rise to various mechanisms for the photocurrent response. The mechanism is in close relation to the quantum geometry of electronic structure similar to the mechanism of nonreciprocal conductivity (see Sec. III.3.1) Moore and Orenstein (2010); de Juan et al. (2020). In the light of topological material science, a lot of theoretical and experimental works have been devoted to the photocurrent responses in topological materials Ma et al. (2021); Orenstein et al. (2021); Ma et al. (2023b); Morimoto et al. (2023). For example, the significant photocurrent generation is attributed to the electron-hole creations around Weyl nodes of TaAs Ma et al. (2017) and RhSi Rees et al. (2020); de Juan et al. (2017). These results indicate that the photocurrent response is a possible probe of the quantum geometry in solids in addition to its potential for energy harvesting devices and other engineering applications. Furthermore, the photocurrent measurement being sensitive to the symmetry of materials has been applied to various quantum materials to examine exotic quantum phases such as those of cuprate superconductor and excitonic insulators Xu et al. (2020); Lim et al. (2020). Diagnosis based on the photocurrent response may be advantageous compared to the widely-used other nonlinear optical probe such as second-harmonic generation where the interference with the reference signals should be prepared Ma et al. (2023b).
Recent works have further addressed the microscopic mechanism of the photocurrent responses induced by the magnetic parity violation after the symmetry analysis Men’shenin and Turov (2000). We first introduce the photocurrent mechanism induced by the electric and magnetic parity violations in the context of the band-electron picture. Similarly to the nonreciprocal transport response, the electric and magnetic parity violations play contrasting roles in the photocurrent generation. Then, several remarks will be made about modifications coming from the disorder scattering and electron correlation.
The mechanism of photocurrent generation has been thoroughly investigated in the framework of the independent-particle approximation. Such intrinsic mechanism stems from the carrier dynamics such as due to the Fermi-surface (FS) and particle-hole creation (PH) effects, which give the photocurrent conductivity
| (54) |
where the frequency dependence of in Eq. (37) is implicit. Assuming the absence of scatterers, the known Fermi-surface effects are given by
| (55) |
that is nonlinear Drude, Berry curvature dipole, intrinsic Fermi-surface effects, respectively Holder et al. (2020); Moore and Orenstein (2010); de Juan et al. (2020). The mechanism based on particle-hole excitations gives contributions that are similarly decomposed into
| (56) |
called electric-injection, magnetic-injection, shift, and gyration-current mechanisms Sipe and Shkrebtii (2000); Zhang et al. (2019c); von Baltz and Kraut (1981); Watanabe and Yanase (2021a); Ahn et al. (2020); Okumura et al. (2021). These contributions to the photocurrent conductivity are classified in terms of their definite parity under the and operations as tabulated in Fig. 10. In contrast to the DC response in Sec. III.3.1, the space-time classification of photocurrent response is related to the degrees of freedom of irradiating light such as frequency () and polarization state (linearly-polarized light and circularly-polarized light). 444 More accurately, the photocurrent responds to linearly polarized, circularly polarized, and unpolarized light. The mechanism for the unpolarized-light-induced photocurrent response is the same as that for the linearly-polarized light, while it contributes even under the circularly-polarized light since the unpolarized-light contribution originates from . Then, the circular contribution is obtained by taking the difference in the responses to the light with opposite circular polarizations.

Let us write down the explicit formulas for each contribution. The Fermi-surface effects are formulated as
| (57) | ||||
| (58) | ||||
| (59) |
all of which consist of the Fermi-surface effect and vanish without any gapless quasiparticle excitations. In particular, the nonlinear Drude and Berry curvature dipole effects resemble the contributions to the nonreciprocal conductivity of Eqs. (42), (45) and are therefore allowed in the presence of the magnetic and electric parity violations, respectively (see also Table 3). Under the nearly-static electric field, the formulas for dc and ac nonreciprocal current generation are given in a unified manner by properly taking into account the scattering effect Du et al. (2019).
The intrinsic Fermi-surface effect is further divided into
| (60) |
that include the Berry curvature and quantum metric as
| (61) | ||||
| (62) |
where is the band-resolved Berry curvature which leads to the Berry curvature by summing over one of the band indices as . Since the band-resolved Berry curvature determines the helicity-dependent dipole excitations at under the circularly-polarized light. This term is finite in the system with the electric parity violation because the opposite sign in Fermi-surface deviations at multiplied with the staggered Berry curvature gives nonvanishing contribution. Thus, it is called the electric intrinsic Fermi-surface (e-iFS) effect. Contrastingly, the band-resolved quantum metric related to the linearly-polarized-light excitation does show the same sign between of Eq. (62) leading to the perfect compensation.
One can see the opposite situation in the case of the -symmetric system. The electric intrinsic Fermi-surface effect is forbidden since the retained symmetry leads to the zero Berry curvature. Instead, Eq. (62) including the band-resolved quantum metric offers finite photocurrent response, since the asymmetric electronic band structure of the -symmetric system [Fig. 7(d)] allows for the uncompensated contribution. Thus, Eq. (62) is the magnetic counterpart of Eq. (61), named the magnetic intrinsic Fermi-surface (m-iFS) effect. As a result, the quantum-geometrical factors lead to the contrasting mechanism for photocurrent generation originating from the characteristic electronic structure purely showing the electric or magnetic parity violation.
The photocurrent conductivity arising from the mechanism based on particle-hole excitations is written by
| (63) | |||
| (64) | |||
| (65) | |||
| (66) |
All the formulas include the factor representing the particle-hole excitations
| (67) |
Note that the diverging behavior due to in Eqs. (63) and (64) is bounded by scattering effects de Juan et al. (2017). denotes the derivative covariant under the gauge transformation by which different energy eigenstates are not admixed with each other. For instance, in the case of the U(1) gauge associated with the non-degenerate energy spectrum, the covariant derivative is defined by
| (68) |
where the additional terms including the intraband Berry connection make gauge covariant as
| (69) |
under the gauge transformation .
Recalling that the absorptive part (‘antisymmetric’ in Table 1) in the resonant optical conductivity is
| (70) |
the photocurrent response described by can be explained by two steps; irradiating light excites particle-hole pairs similarly to the linear optical response, and the created particle and hole are rectified along opposite directions by ‘director’ determined by the microscopic parity-violating property. For instance, the director is the group-velocity difference in bands for the injection current mechanism.
The shift- and gyration-current mechanisms similarly consist of the director. When we do not consider the degeneracy of band energy at each momentum for simplicity, the two formulas are recast as
| (71) | |||
| (72) |
where we consider for the shift current and for the gyration current without loss of generality because the photocurrents of each effect respond to the linearly-polarized and circularly-polarized lights, respectively. For the gyration-current mechanism, the circularly polarized light is incident along the direction by which the photo-electric field is in the plane. The directors are given by the linear shift vector
| (73) |
for the shift current mechanism von Baltz and Kraut (1981) and the circular shift vector
| (74) |
for the gyration current mechanism Watanabe and Yanase (2021a) with the circular Berry connections . Since the intraband Berry connection roughly represents the position of the wave packet with , the shift vectors of Eqs. (73) (74) correspond to the wave-packet positional shift along the direction during the dipole transition Morimoto and Nagaosa (2016b); Fregoso et al. (2017) [Fig. 11(a)]. As a result, the directors of the shift- and gyration-current mechanisms are interpreted based on the real-space picture, while those of the injection current mechanism are based on the momentum-space picture.
As in the case of the intrinsic Fermi-surface effects, Eqs. (63) and (64) are respectively allowed by the electric and magnetic parity violations due to the relevant quantum-geometrical quantities. The -even but -odd nature of the linear shift vector indicates that the shift current effect is unique to the -symmetric materials, while the case is opposite for the gyration current characteristic of the -symmetric materials. Note that the shift and gyration current effects can also be explained by the quantum-geometrical quantities defined in the two-band model, that is, the Christoffel symbols which can be halved into the - and -symmetric parts Ahn et al. (2020). Notably, the photocurrent response is similarly induced by the orbital order. For instance, photocurrent generation due to the orbital-current order has been predicted Watanabe and Yanase (2021b); Artamonov et al. (1992) and expected to give implications for the wide range of exotic quantum phases Murayama et al. (2021).
So far, we have explained the photocurrent mechanism derived within the independent particle approximation. It may be desirable to develop more elaborate treatments for quantitative estimations; e.g., disorder-scattering and electron-correlation effects. For instance, the photocurrent performance of the electric and magnetic injection effects suffer from hard degradation because the response decreases in inversely proportional to the increasing scattering rate of Eqs. (63) and (64).
The disorder scattering modifies the shift mechanism written by Eqs. (71) and (72). However, although the scattering may smear out the resonant condition represented by in Eq. (67), the shift mechanism is expected to show strong tolerance for the disorder effects. Supporting this argument, in Ref. Hatada et al. (2020), the robustness against the disorder concentration has been successfully observed in doped polar semiconductors, in which the shift-current response undergoes negligible degradation despite the high doping level as much as that allowing for sizable electric conductivity. Theoretical studies of the shift-current mechanism are in agreement with the experimental results as the response does not significantly change unless the disorders smear out the multiband property relevant to optical excitations Morimoto and Nagaosa (2016b); Ishizuka and Nagaosa (2021) [Fig. 11(b)].
The gyration current similarly leads to disorder-tolerant photocurrent response to the circularly-polarized light because of its similarity to the shift current [Eq. (72) and Fig. 11(a)]. Although there exists no experimental demonstration of the disorder-concentration dependence of the gyration current, it may be feasible by the systematic study of doped magnetic semiconductors such as Mn-based -symmetric magnets (BaMn2Pn2, SrMn2Pn2, and so on) Watanabe and Yanase (2018a). It is noteworthy that the ultrafast spectroscopy is informative in identifying the shift mechanism of the gyration-current response as evidenced in Ref. Sotome et al. (2019b, a) reporting that the photocurrent generation is distinguished from the polarization current Bass et al. (1962) by its temporal form [Fig. 11(c)].

Lastly, let us comment on the disorder effect on the Fermi-surface effects [Eq. (55)] which is non-negligible, particularly in the case the low-frequency light irradiation such as terahertz light. The significant contributions have been observed by detailed studies of frequency dependence of the photocurrent generation Olbrich et al. (2014); Hild et al. (2023) where extrinsic scattering effects play a key role, while the resonant contributions are dominant in the frequency range of visible light Plank et al. (2018); Matsubara et al. (2022). The extrinsic mechanism for the photocurrent generation has been formulated in the framework of the semiclassical theory. The formulas give unified descriptions for the nonreciprocal conductivity and photocurrent generation. Let us exemplify it by considering the Berry curvature dipole effect given by
| (75) |
in which converges to Eq. (45) in the dc limit (), and reproduces Eq. (58) in the optical limit Sodemann and Fu (2015); Du et al. (2019). Because the extrinsic mechanism can contribute to the photocurrent generation Belinicher et al. (1982); Du et al. (2019); Isobe et al. (2020); Ma et al. (2023a), the skew scattering and side jump effects should be taken into account when we discuss the low-frequency photocurrent response.
The semiclassical treatments may be reasonable for the nonlinear Drude effect [Eq. (57)] and the Berry-curvature-dipole effect of Eq. (75), whereas one has to carefully consider disorder effects on the intrinsic Fermi-surface effects [Eq. (59)]. Previous theoretical studies have corroborated the possibility of observing the photocurrent response to the light in the in-gap frequency regime, which is related to the intrinsic Fermi-surface effects Belinicher et al. (1986). More rigorous considerations of electric-field correction to the Hamiltonian, namely optical Stark effect, have recently concluded that the in-gap photocurrent is absent in a steady state, while there exists transient photocurrent Taguchi et al. (2016); Onishi et al. (2022); Pershoguba and Yakovenko (2022). The absence of such off-resonant photocurrent generation may be circumvented by including the coupling to the phonon Golub and Glazov (2022) and by taking into account the correction to the distribution function Shi et al. (2023); Matsyshyn et al. (2023); Shi et al. (2024).
IV Availability of -symmetric Magnets and Physical Properties
IV.1 Switching the compensated magnets
In general, the antiferromagnetic state is hard to observe because of the zero magnetization, as is evident from the fact that the antiferromagnetism was microscopically identified centuries after the discovery of ferromagnet Shull and Samuel Smart (1949). The difficulty in manipulation is partly because there is no universal macroscopic field coupled to the antiferromagnetic state in contrast to known controllable order parameters of ferromagnetic and ferroelectric states. It is, however, not the case for a series of antiferromagnetic where magnetic anisotropy and crystal structure play a key role.
For instance, if the antiferromagnetic order shows the multi-axial magnetic symmetry, the stimuli for the switching ferromagnetic order may control the antiferromagnetic order as well Jungwirth et al. (2016). Let us consider the biaxial antiferromagnets where the Néel vector orientation favors either of the or direction. The Néel vector directed along the axis can be switched into the -axis by the external magnetic field along the axis since it is energetically favorable for the staggered magnetic moments to be perpendicular to the magnetic fields as in the case of the spin-flop transition. This spin-flop-like mechanism has been applied to the biaxial antiferromagnet IrMn Marti et al. (2014). Similar manipulation of antiferromagnetic order is feasible by making use of the external fields having the same symmetry as the magnetic field such as spin-polarized electric current and pure spin current Gomonay and Loktev (2010); Moriyama et al. (2018); Reichlová et al. (2015). The written antiferromagnetic state can be detected in the anisotropic magnetoresistance by which the - or -collinear antiferromagnetic states manifest different electric resistivity typically as much as a few percent Shick et al. (2010). The difference in the magnetoresistance may be improved significantly with a tunneling junction Park et al. (2011).
The spin-flop-like switching of antiferromagnetic order can be applied to various materials showing multi-axial magnetoanisotropy such as Fe2O3 and NiO, but it does not allow us to distinguish the direction of the Néel vector, and . Similarly, the anisotropic magnetoresistance depends on the antiferromagnetic order in the even-order of its order parameter as .
Being in high contrast to partially switchable antiferromagnetic materials, another series of magnets have properties favorable for spintronic applications. The key is the sublattice degree of freedom with which the antiferromagnetic order can be characterized by the ferroic ordering of even- and odd-parity magnetic multipole moments as discussed in Sec. II.3. For the case of even-parity magnetic multipole order, one may identify high controllability of antiferromagnetic order by using the external magnetic field, piezomagnetic property, and electric current Šmejkal et al. (2022). We do not present detailed discussions of antiferromagnets characterized by the even-parity multipolar order by leaving them to other literature such as Ref. Han et al. (2023); Nakatsuji and Arita (2022). In the following, we review the availability of the odd-parity magnetic multipolar class including -symmetric magnets.
The scheme of switching -symmetric magnets differs between the insulators and metals in which we can make use of the magnetoelectric effect and antiferromagnetic Edelstein effect, respectively. For the former case, the antiferromagnetic domain state may be distinguished by the magnetoelectric free energy
| (76) |
where the coefficient depends on the polarization state of the -symmetric magnets as it changes the sign () when the magnetic moments are flipped. By applying both the magnetic and electric fields to be aligned with the symmetry of the allowed magnetoelectric components in , the antiferromagnetic state can be manipulated in the deterministic manner distinguishing the sign of the Néel vector. The scheme is applied to the magnetoelectric annealing Borisov et al. (2005) and has served the successful observation of switching of the antiferromagnetic order Van Aken et al. (2007). Note that the magnetoelectric energy is typically small and hence manipulation requires the system with good insulating properties to apply the large electric bias.
The different mechanism is available for the switching of the -symmetric magnetic metals. Although the good metallic properties may be unfavorable in the context of magnetoelectric switching, we can utilize the hidden spin polarization coupled to the electrons’ momentum instead. The locally-noncentrosymmetric crystal, a key to -symmetric magnetic order, manifests the locking between spin, sublattice, and momentum even in the paramagnetic state as introduced in Sec. II.2. This intriguing locking gives rise to the transport phenomenon written by
| (77) |
with the spin magnetization response to the electric current at the -th sublattice Yanase (2014); Železný et al. (2014). Owing to the locally-noncentrosymmetric symmetry, the response function obeys the relation where the sites are interchanged under the operation. As a result, the response denotes the correlation between the electric current and antiferromagnetic spin polarization, because the induced spin polarization is compensated in total (). By analogy with the Edelstein effect (magnetization response to electric current, inverse magnetogalvanic effect) Levitov et al. (1985); Edelstein (1990), it is called antiferromagnetic Edelstein effect Watanabe and Yanase (2017).

The microscopic grounds for the antiferromagnetic Edelstein effect have been established similarly to the (ferromagnetic) Edelstein effect. Let us illustrate the mechanism in the framework of the semiclassical theory Železný et al. (2014). Note that we here assume the paramagnetic state of a locally-noncentrosymmetric crystal since the mechanism does not require the antiferromagnetic order. As in Eq. (34), the electric current induces the Fermi-surface shift in metals as
| (78) |
in which denotes the phenomenological relaxation time and is the longitudinal conductivity. In agreement with the form of current-induced response in Eq. (77), the relaxation-time dependence is canceled out as by taking the current as the external stimulus. Owing to the staggered deviation at [] in the paramagnetic state, the local magnetization is not compensated after the summation over the momentum [Fig. 12(c)] as
| (79) |
different from that in equilibrium where the hidden spin polarization at each crystal momentum vanishes in total due to the degeneracy between the opposite momentums ( for every sublattice) [Fig. 12(b)]. Notably, the antiferroic magnetization occurs only in the presence of the metallic conductivity as is inferred by the Fermi-surface term , being contrasting to the magnetoelectric effect.
We note that the structure of hidden spin polarization is determined by the local site symmetry of sites Železný et al. (2017a). When the locally-noncentrosymmetric crystal structure consists of the two sublattices, the symmetry of in Eq. (77) is identified by the sublattice-dependent antisymmetric spin-orbit coupling of Eq. (12) such as for the bilayer system [Eq. (9)] and for the zigzag chain [Eq. (13)]. In the terminology of crystallography, the antiferromagnetic Edelstein effect occurs due to the gyrotropic site symmetry of each sublattice since the gyrotropy ensures the linear coupling between the momentum and spin polarization . Vanishing antiferromagnetic Edelstein effect () of the honeycomb net follows from the non-gyrotropic site symmetry offering the hidden spin polarization given by Eq. (14).
To obtain a significant response, it is desirable to maximize the hidden spin polarization on the Fermi surface. For instance, special crystal symmetry such as the nonsymmorphic symmetry suppresses the inter-sublattice hopping which smears out the sublattice-dependent spin-momentum locking (see also Sec. II.2). On the other hand, small inter-sublattice hopping may contribute to enhancing the hidden spin polarization with the fine-tuning of material parameters. For the Hamiltonian for the bilayer system [Eq. (8)], the hidden spin polarization is sizable but undergoes the partial compensation between contributions from the inner and outer Fermi surfaces in the absence of the tunneling hopping (). As depicted in the left panel of Fig. 12(d), the energy spectrum is singly occupied only in a narrow chemical-potential range. Such a favorable parameter range can be broadened by including moderate tunneling hopping. As in the plot with of Fig. 12(d), one can obtain the single Fermi surface with a non-negligible hidden spin polarization over a wider range of chemical potential. Note that the hidden spin polarization gets weak if is much larger than the spin-orbit coupling (right panel of Fig. 12(d)). It has been shown in Ref. Yanase (2014) that the antiferromagnetic Edelstein effect is significant when the chemical potential is placed in the range where the single Fermi surface appears. The spin-current generation stemming from the antiferromagnetic Edelstein effect similarly undergoes enhancement Suzuki et al. (2023).
When the induced antiferroic magnetization has the same symmetry as that of the equilibrium spin configuration, it can directly act on the -symmetric magnetic order as the so-called Néel spin-orbit torque Železný et al. (2014). As the symmetry of the response is determined by the locally-noncentrosymmetric crystal structure, the induced spin torque is field-like; the favorable antiferroic spin polarization depends not on the antiferromagnetic state but on the direction of applied current Manchon et al. (2019). The field-like nature allows for deterministic current-induced switching without any auxiliary fields.
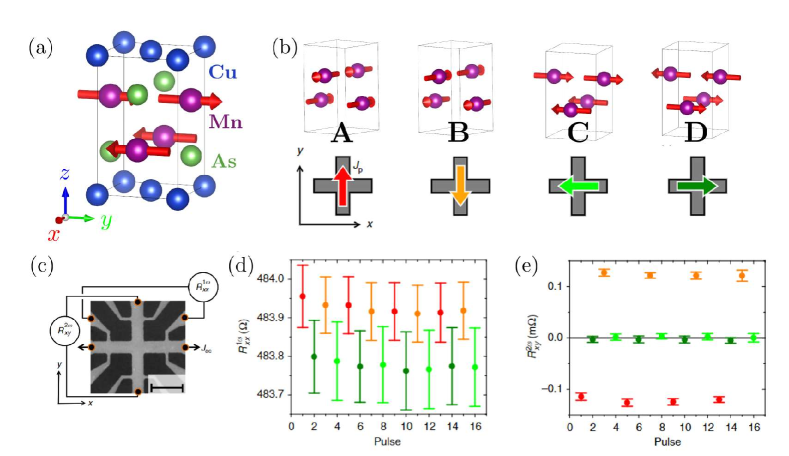
Following the theoretical predictions, the switching of antiferromagnetic states has been experimentally demonstrated by -symmetric magnetic metals such as CuMnAs Wadley et al. (2016); Olejník et al. (2017); Wadley et al. (2018) [Fig. 13(a)] and Mn2Au Bodnar et al. (2018). The domain state written by the large pulsive electric current has been monitored by the anisotropic magnetoresistance related to the biaxial magnetoanisotropy. Both of CuMnAs and Mn2Au show the biaxial in-plane magnetoanisotropy by which the Néel vector is favorably directed along the and axes. It follows that there are four possible domain states written by the Néel vector as [Fig. 13(b)]. These magnetic materials show the locally polar symmetry as in the case of the bilayer system [Eq. (9)] Barthem et al. (2013); Wadley et al. (2015), and the large electric current drives the Néel vector to be perpendicular to the applied direction as the current leads to .
The domain state of biaxial antiferromagnets can be detected if there is appreciable anisotropic magnetoresistance in antiferromagnetic metals whose electronic structure may undergo significant modification by the magnetic order Elmers et al. (2020). The signal is quantified by the Néel-vector dependent part of the electric resistance . In the case of CuMnAs, one can find the difference in as
| (80) |
by which the antiferromagnetic state is monitored [Fig. 13(d)]. The order-induced anisotropy in the electronic property has been similarly probed via optical measurements Saidl et al. (2017); Grzybowski et al. (2017); Wadley et al. (2018); Sapozhnik et al. (2018); Grigorev et al. (2021).
The readout based on anisotropic magnetoresistance may not be direct evidence for the perfect switching because the anisotropic magnetoresistance does not distinguish all the possible domain states completely; i.e., the magnetoresistance is equivalent between the domain states interchanged by the operation, for example, . In addition, one may take account of thermal effects implying that observed signals are possibly attributed to the nonequilibrium state not to the domain state in equilibrium Zhang et al. (2019b); Chiang et al. (2019); Cheng et al. (2020); Churikova et al. (2020); Surýnek et al. (2020). In contrast to the readout by the anisotropic magnetoresistance, the polarity can be identified by the nonreciprocal conductivity which is sensitive to the magnetic parity violation (see also Sec. III.3.1). The observed change in the odd-parity nonreciprocal response indicates the perfect switching of the -symmetric magnetic order Godinho et al. (2018) [Fig. 13(e)], where the domain states with the opposite Néel vectors have been separately detected by the nonlinear Hall conductivity with the antisymmetry
| (81) |
Here, the Néel-vector dependence of the nonreciprocal conductivity is explicitly denoted as in Eq. (80). Note that while . Similarly, the -symmetric magnetic state can be distinguished unambiguously by odd-parity physical phenomena introduced in preceding sections such as the magnetopiezoelectric effect, photocurrent response, and so on Song et al. (2021); Zhang et al. (2019c).
The scheme for perfect switching based on the antiferromagnetic Edelstein effect has been proposed in several candidate materials and has been subsequently generalized to identify the switchability of -symmetric magnets in a group-theoretical framework Watanabe and Yanase (2018b). Among a lot of candidate materials for -symmetric magnetic states, a class of the magnetic states, that is the magnetic toroidal state (Fig. 6), enables the current-induced manipulation. Similarly to the nonmagnetic and noncentrosymmetric materials possessing the electric parity violation, -symmetric magnets are classified into the polar and nonpolar classes concerning the unitary symmetry including no operation. For instance, the -symmetric magnetic states of CuMnAs and Mn2Au show the polar symmetry in the unitary part of their magnetic point group (), while that of BaMn2As2 is noncentrosymmetric but nonpolar () [Eq. (32)]. As a result, the former can be manipulated by the electric current, whereas the latter cannot be done. Note that the criterion based on the toroidal degree of freedom applies to general cases including -violating and noncentrosymmetric magnets. The presence of the magnetic toroidal moment ensures the feasibility of current-induced switching (see also Appendix A). This criterion is also generalized to cover the switchability of nonpolar magnets with the help of strain Watanabe and Yanase (2018b) such as demonstrated in ferromagnetic semiconductor Chernyshov et al. (2009).
IV.2 Control of electronic property with -symmetric magnetic order
The proof-of-concept experiment of electrical control of antiferromagnets paved the way for intensive investigations of its reading-writing scheme. It is anticipated that one can realize unprecedented designing of physical properties if the -symmetric magnetic order is under our control. For instance, since the topologically-nontrivial electrons are hosted on the antiferromagnetic conductors Tang et al. (2016), strong modulation of the electronic bands may be feasible through current-aided manipulation Šmejkal et al. (2017) and by the spin-flop transition Masuda et al. (2016).
Furthermore, owing to the -symmetric but -violating symmetry, the symmetry and its characteristic responses can be tuned in a nontrivial manner. As tabulated in Fig. 2, the symmetry forbids uniform electric and magnetic polarizations and thereby keeps the spin degeneracy intact at each crystal momentum. Since the degenerate states show the intimate coupling between the spin and sublattice degree of freedom, the spin-momentum-sublattice locking can exert unique transport phenomena like the layer Hall effect Gao et al. (2021) where the anomalous Hall response occurs in the staggered way between the twined layers. The degeneracy is easily lifted by the external fields violating the symmetry such as the external magnetic and electric fields. The available elimination of -ensured degeneracy implies that one can manipulate the physical phenomena arising from the ferroelectric and ferromagnetic order. For instance, it has been shown that the electric-field effect gives rise to the uniform Berry curvature and associated magnetooptical and magnetogalvanic effects in layered materials such as CrI3 Jiang et al. (2018b, a); Huang et al. (2018) and even-layer MnBi2Te4 Du et al. (2020).
Similarly, the external magnetic field leads to the physical phenomena originating from the -symmetry violation. For instance, induced small canting of antiferromagnetic moments leads to sizable anomalous Hall response which is called chiral Hall effect Lux et al. (2020). This sizable response is in contrast to the typical case of canted antiferromagnets where the anomalous Hall response may not be significant when the induced magnetization is small. Intriguingly, the spin-momentum texture experiences the magnetic-field-induced correction that is entirely different from the typical case. To corroborate the induced spin-momentum structure, let us consider the bilayer system undergoing the layer-dependent spin polarization. The obtained -symmetric antiferromagnetic state can be found in layered magnetic materials. When the magnetic field is in the out-of-plane direction, the combination of the -symmetric magnetic order and external field results in lifting the spin-layer-coupled degeneracy at every crystal momentum and thereby in the Rashba-type spin-momentum locking.

The resultant Rashba spin-orbit coupling stems from the purely magnetic modification of electronic structure and does not require the noncentrosymmetric crystal structure, being in sharp contrast to the known cases of spin-momentum locking such as those found in nonmagnetic polar crystals. Thus, such magnetically-induced antisymmetric spin-orbit coupling is dubbed with magnetic antisymmetric spin-orbit coupling (magnetic ASOC) Watanabe and Yanase (2020). Let us exemplify the magnetic ASOC by taking the model Hamiltonian for the bilayer system [Eq. (8)]. We further add the antiferromagnetic molecular field and Zeeman field written by
| (82) |
with . Note that and are Pauli matrices for the spin and layer degrees of freedom, respectively. In the case of zero tunneling hopping (), the momentum-resolved spin polarization quantifying the magnetic ASOC is analytically obtained as
| (83) |
for the lower-energy eigenstates of the upper () and lower () layers. The hidden Rashba spin-orbit coupling is given with the vector . The two lower energy spectrums are originally degenerate due to the symmetry, and their energies are slightly separated by the Zeeman field as much as . The resultant difference in Fermi-surface volumes and Fermi wavelengths () between the layers gives rise to the uncompensated Rashba-like spin-momentum texture (Fig. 14).
Furthermore, the magnetic ASOC may take a form different from that of the hidden ASOC determined by the crystal structure in the nonmagnetic phase. For instance, under the in-plane magnetic field such as , the induced magnetic ASOC has the form of being irrelevant to the existing Rashba spin-orbit coupling hidden by the layer degree of freedom. The interlayer tunneling hopping plays an essential role in producing this type of magnetic ASOC. This is in sharp contrast to the fact that the large inter-subsector hopping weakens the hidden spin polarization governed by the paramagnetic Hamiltonian.
The magnetic ASOC may offer tunable spin-momentum locking, while the conventional ASOC is usually determined by the noncentrosymmetric crystal structure whose parity violation is hard to control externally. Considering vast -symmetric magnetic materials Watanabe and Yanase (2018a), we can find various types of magnetic ASOC different from the Rashba ASOC, such as the Dresselhaus-type Watanabe and Yanase (2020) and the chiral ones. The concept of the magnetic ASOC can be comprehensively generalized to magnetically-induced electric parity violations. Then, combining the -symmetric magnet with the external magnetic field, one can obtain the various physical phenomena unique to the nonmagnetic and noncentrosymmetric crystals; e.g., piezoelectricity, nonlinear Hall effect arising from the Berry curvature dipole Watanabe and Yanase (2020), photogalvanic effects for charge and spin current Merte et al. (2023), and so on. The emergence of the Berry curvature dipole is identified by the discussions parallel to those of the magnetic ASOC because the spin and momentum-space Berry curvature have the same space-time symmetry (-even and -odd). The magnetically-tunable responses discussed above can be systematically identified with the help of magnetic symmetry analysis Erb and Hlinka (2020); Watanabe and Yanase (2020); Yatsushiro et al. (2022) and are expected to be a key to rich spintronic phenomena based on antiferromagnetic materials.
V Parity-violating Superconducting Responses
In the preceding sections, we overviewed the physical phenomena induced by the magnetic parity violation. Various emergent responses and itinerant properties originate from the electronic structure unique to the parity violation. Similarly, such intriguing electronic structures have a significant influence on the quantum phases emerging in metals such as superconductivity. Noncentrosymmetric superconductors, superconductors with the lack of the symmetry, have been intensively studied in light of the strong spin-orbit coupling as found in heavy fermion and van der Waals materials Bauer and (eds.); Ideue and Iwasa (2021). Those studies mainly worked on modifications of the basic superconducting properties such as critical magnetic fields and pairing states. This section is devoted to discussions of physical phenomena unique to the parity violation in superconductors.
Let us consider candidates for the noncentrosymmetric superconductors other than known materials crystalizing in the noncentrosymmetric structure. The parity violation can be invoked in the following three ways; (1) parity-violating order concurrently existing with the superconductivity, (2) the supercurrent injection, and (3) multiple superconducting transitions where the parity is different between those superconducting pairing potentials Watanabe et al. (2022b).
Firstly, the parity violation due to the spontaneous order is ascribed to the nonmagnetic and magnetic origins. Specifically, for the former the ferroelectric- or piezoelectric-like order has been identified to coexist with the superconductivity in doped SrTiO3 Rischau et al. (2017) and heavy-fermion systems Hu et al. (2017), while for the latter the odd-parity magnetic multipolar order may be involved in the superconductivity of a locally-noncentrosymmetric superconductor CeRh2As2 Kibune et al. (2022); Kitagawa et al. (2022). The order-induced modifications of the electronic structures may assist the emergence of exotic superconductivity such as the finite-momentum pairing state in the presence of the magnetic parity violation Sumita and Yanase (2016); Sumita et al. (2017). Although similar interplay between the superconductivity and magnetic parity violation can be realized in the noncentrosymmetric superconductors under the external magnetic field Bauer and (eds.); Smidman et al. (2017); Kaur et al. (2005); Wakatsuki et al. (2017); Dimitrova and Feigel’man (2003), the odd-parity magnetic order may offer more significant modification of the electronic property with the energy scale of the Hund’s coupling, which can be much larger than the Zeeman coupling, and cause a prominent parity-violating effect on the superconductivity.
Secondly, the parity violation can be built into the superconductor by the supercurrent injection. The superfluidity allows the current to flow without the Joule heating and thereby realizes the parity-violating phase even in prototypical -wave superconductors. Owing to its space-time symmetry, the biased electric current gives rise to the magnetic parity violation. The resulting finite-momentum superconductivity has been verified in experiments detecting the optical signals unique to the parity violation Yang et al. (2019); Nakamura et al. (2020); Vaswani et al. (2020).
Lastly, the superconductivity itself can break the symmetry. Since the parity is definite in the conventional pairing states such as the even-parity -wave and odd-parity for -wave superconductivity in centrosymmetric materials, the parity violation does not happen at the single superconducting transition. Note that the operation is effectively retained in the odd-parity superconducting states because the symmetry is preserved in the form of its combination with the U(1) gauge transformation. This is a significant difference from the odd-parity multipolar order. On the other hand, spontaneous symmetry breaking occurs if the system exhibits multiple superconducting transitions. Evidencing such possibility, Ginzburg-Landau analysis of the multiple superconducting transitions showed that the -wave pairing state, an exotic pairing state showing the purely magnetic parity violation, is stable when both of - and -wave superconductivity emerge Wang and Fu (2017). Interestingly, the multiband nature in the normal phase allows for richer properties of magnetically parity-violating superconductivity in the Bogoliubov-quasiparticle spectrum Kanasugi and Yanase (2022); Kitamura et al. (2023). Following the parallel discussion of the electrically-switchable -symmetric magnets, one can identify the possibility of supercurrent-induced switching of the magnetically parity-violating superconductivity, such as between the -wave states. When the superconducting order parameters have the same symmetry as the magnetic toroidal order, it is called anapole superconductivity Kanasugi and Yanase (2022) and allows supercurrent-induced switching. The spontaneously parity-violating superconductivity demands the stringent condition of sizable fluctuations leading to the multiple Cooper instability and thus material realization requires further studies, while such fluctuations have been implied in a heavy-fermion superconductor Ishizuka and Yanase (2021); Aoki et al. (2022).
The superconductivity-induced symmetry breaking is similarly found in the chiral superconductivity manifesting the -symmetry breaking. The chiral superconductivity, however, differs from the parity-violating superconductivity as it can occur in the single transition labeled by a multi-dimensional irreducible representation Sigrist and Ueda (1991); Sigrist (2005).
Considering the playgrounds for the parity-violating superconductivity, one may be interested in their characteristic physical responses. Recently, active experimental and theoretical research has identified various nonreciprocal responses related to superconductivity. For instance, tremendous interest has been drawn by the recent discoveries of the nonreciprocal charge transport of superconductors such as nonreciprocal conductivity, superconducting diode effect, and nonreciprocal Josephson effect Ideue and Iwasa (2021); Nadeem et al. (2023); Nagaosa and Yanase (2024). Furthermore, the superconducting property shows up in various responses including cross-correlated and optical responses as follows.
Here, we review the cross-correlated responses in superconductors. Let us consider the free energy in the superconducting state dependent on external fields (magnetic field , stress , and vector potential )
| (84) |
Importantly, the vector potential characterizes the supercurrent injection through the London equation. Taking the derivative with respect to each field, we obtain the conjugate quantities as
| (85) |
that is, magnetization, strain, and supercurrent. The free energy is transformed as
| (86) |
under the operation and
| (87) |
under the operation. Then, corrections to the free energy arising from the parity violation is given by
| (88) |
up to the bilinear form. The coefficient is -even but -odd, while the parity of is opposite for each operation. It follows that the cross-correlation () is unique to the superconductors with the electric (magnetic) parity violation. One can obtain the cross-correlated response from the former coupling as
| (89) |
that is the superconducting Edelstein effect Edelstein (1995) being in stark contrast to the normal Edelstein (inverse magnetogalvanic) effect in which the ohmic current leads to the magnetization Levitov et al. (1985); Edelstein (1990) 555 Note that the inverse response written by does not occur in the DC regime due to the Bloch’s no-go theorem Ohashi and Momoi (1996).. Notably, the magnetization response of Eq. (89) can be significant due to nontrivial contribution from the topological edge states of nodal superconductors Ikeda and Yanase (2020).
For the latter coupling in Eq. (88), one can identify the strain response to the supercurrent
| (90) |
called superconducting piezoelectric effect Chazono et al. (2022, 2023). As in the case of the magnetization-supercurrent correlation, the superconducting piezoelectric effect is clearly distinguished from the conventional (inverse) piezoelectric and magnetopiezoelectric effects in terms of the fields stimulating the strain, since the latter two effects are involved in the electric field and ohmic current, respectively. One can refer to Eqs. (27) and (30) for comparison. Unlike them, superconducting Edelstein and superconducting piezoelectric effects are the responses to the supercurrent.
We summarize the cross-correlated responses in Fig. 15. To be of interest, it has been shown that the superconducting piezoelectric effect displays an abrupt change during the crossover between the two superconducting phases in the Rashba superconductor Chazono et al. (2022), that is, helical and Fulde-Ferrell states Dimitrova and Feigel’man (2003); Kaur et al. (2005). This implies that the cross-correlated response plays a key to identifying the exotic phase induced by the coupling between superconductivity and magnetic parity violation. Notably, the supercurrent injection in bulk can be replaced with the biased Josephson junction Kapustin and Radzihovsky (2022) because the vector potential plays a role equivalent to the gradient of the superconducting phase due to the minimal coupling. For instance, the giant superconducting Edelstein effect is possibly realized in the biased Josephson junction, which could be essential for superconductor-based spintronics. Although the research of superconducting nonreciprocal responses has advanced significantly as reviewed below and elsewhere Nagaosa and Yanase (2024); Nadeem et al. (2023), cross-correlated responses in superconductors have not been explored experimentally, pointing to the next issue in superconducting science.

Next, we discuss the nonreciprocal responses in superconductors. The free energy can be expanded to nonlinear order with respect to the external fields as well. Considering only the effects of vector-potentials, we obtain the correction up to the cubic components as
| (91) |
The quadratic correction results in the well-known Meissner response, while the cubic coefficient gives -odd, -odd, and -even corrections. Then, one arrives at the nonreciprocal response induced by the magnetic parity violation
| (92) |
This formula represents the nonreciprocal Meissner effect, by which the supercurrent response differs depending on the direction of the supercurrent shielding the external magnetic field Watanabe et al. (2022a). The nonreciprocal response is determined by the nonreciprocal correction to the superfluid weight , namely, nonreciprocal superfluid weight. Its relevance to the superfluid weight follows from the relation
| (93) |
The nonreciprocal superfluid weight plays a key role in various nonreciprocal responses of superconductors, not only the nonreciprocal Meissner effect [Eq. (92)], but also the nonreciprocal conductivity Hoshino et al. (2018) and the nonreciprocal optical responses Watanabe et al. (2022b).
For the nonreciprocal current generation of Eq. (37), let us again consider the photocurrent response as in Sec. III.3.2. The perturbative calculations are straightforwardly performed if one works on the molecular-field (BCS) approximation for the superconductivity Xu et al. (2019); Watanabe et al. (2022b) where the electronic excitation is attributed to the Bogoliubov quasiparticles. The nonreciprocal optics of superconductors have unique features that are not found in the normal conducting phase. One is the optical excitation associated with the van Hove singularity in the Bogoliubov spectrum, which gives the peak of the DOS at the gap edge, and another is the anomalous nonreciprocal optical responses.
To introduce these features, we consider the expression for the photocurrent conductivity in the clean limit. The formula consists of two contributions
| (94) |
The first and second terms are conventional and anomalous contributions, respectively. The conventional contribution () is given by the expressions similar to those in the normal state [Eq. (54)]; e.g., it originates from the Fermi-surface excitation and the resonantly-created Bogoliubov quasiparticles Xu et al. (2019); Watanabe et al. (2022b). The Fermi-surface contribution may be significant in nodal-gap superconductors such as those manifesting the Bogoliubov Fermi surface Agterberg et al. (2017), although it disappears in the full gap superconductors at zero temperatures. Note that the Berry connection contributing to various nonreciprocal optical responses is defined in the parameter space described by the vector potential, not by the momentum. This is because the electrons and holes are treated on equal footing in the framework of the Bogoliubov-de Gennes Hamiltonian and thereby the minimal coupling does not imply the equivalence between the derivatives with respect to the vector potential () and to the crystal momentum ().
Let us consider the resonant optical response of superconductors included in the conventional contribution . An intriguing property of the resonant superconducting optical responses is the optical excitation available after the formation of the superconducting gap. When the system undergoes the superconducting transition, the superconducting gap gives rise to the van Hove singularity, which is related to the characteristic behaviors of physical properties. In terms of the optical response, the energy spectrum of Bogoliubov quasiparticles indicates the optical excitation bridging the van Hove singularities as (: pair potential) in addition to the high-frequency optical path [Fig. 16(b)]. We note that the path gives the optical response similar to that given by the path in the normal state [Fig. 16(a)] if the frequency of light is much higher than the superconducting gap energy. Thus, the optical path is unique to the superconducting state, however, it was considered to make no contribution to the optical response due to the selection rule related to the symmetry Schrieffer (1964).
The absence of optical excitations relevant to the optical path has been recently revisited in the context of the superconducting fitness Ahn and Nagaosa (2021) quantifying the multiband nature of the pair potential Fischer (2013); Ramires and Sigrist (2016). The newly-contributing optical path does not work in prototypical superconductors such as the conventional -wave superconductors, whereas it is not the case if one takes into account the strong-coupling effect, multi-band nature in the normal state, and supercurrent flow Bickers et al. (1990); Ahn and Nagaosa (2021); Jujo (2022). Consistent with this argument, the peak structure stemming from the van Hove singularity has been identified in the optical spectrum for the linear Ahn and Nagaosa (2021) and second-order optical responses Tanaka et al. (2023).

In contrast to the conventional contributions discussed above, the anomalous contribution to the photocurrent conductivity Eq. (94) is characteristic of the parity-violating superconductors and has no counterpart in the normal phase. The formula is explicitly given by the two terms both of which are written by the total derivative with respect to the vector potential as
| (95) |
with the paramagnetic current operator and indices () for the energy eigenstates. We note that the gapful superconductivity is assumed in Eq. (95). It should be noticed that the chain rule between and holds in the normal state, and thereby the anomalous contribution vanishes due to the periodicity in the momentum space Michishita and Peters (2021). The nonreciprocal superfluid weight covers various superconducting properties such as the Meissner and photocurrent responses, similarly to the (linear) superfluid weight Ferrell and Glover (1958).
The anomalous contribution is comprised of the nonreciprocal superfluid density and the second term of Eq. (95). The latter part is proportional to the vector-potential derivative of the reactive part in the linear optical conductivity
| (96) |
Given this expression, the second term in Eq. (95) is called the conductivity derivative. By taking the DC limit, the conductivity derivative becomes the derivative of the Berry curvature as
| (97) | ||||
| (98) |
Note that the derivative of the Berry curvature is totally different from the Berry curvature dipole defined in Eq. (45) where the derivative acts only on the Berry curvature. Being concerned with the anomalous photocurrent response at the frequency below the superconducting gap, we can attribute the response to the derivative of the superfluid weight and the total Berry curvature . These terms give rise to the photocurrent responses to the linearly and circularly polarized light, respectively.
An intriguing property of the anomalous contribution is the diverging behavior in the low-frequency limit; i.e., the nonreciprocal superfluid weight leads to the diverging photocurrent conductivity with the frequency of irradiating light , and the derivative of the Berry curvature does . The diverging behavior does not result from the assumption of the clean limit in Eq. (94), while scattering effects restrict the normal contributions to a finite value in the DC limit Du et al. (2019); Michishita and Peters (2021). The robustness of the low-frequency divergence has been confirmed in the numerical studies by varying the scattering rate Watanabe et al. (2022b). The low-frequency divergence and disorder-tolerant nature may be advantageous for applications to optoelectronic devices based on superconductors.
Furthermore, the two anomalous contributions show the contrasting space-time symmetry and are therefore conveniently classified by the electric and magnetic parity violations. The nonreciprocal superfluid weight is -odd and -even as mentioned around Eq. (91), while the derivative of the Berry curvature has the same space-time symmetry as the Berry curvature dipole, that is -even and -odd. It implies that the anomalous nonreciprocal optical response is a convenient tool for identifying the symmetry of parity violation. Under the irradiation of the low-frequency light, the -symmetric superconductors show significant photocurrent response to the linearly-polarized light and the -symmetric superconductors do that to the circularly-polarized light.
The anomalous mechanism works not only in the photocurrent response but also in other nonreciprocal optical responses in superconductors. In the DC limit, the anomalous terms are determined by several indicators irrespective of the frequency in the response function Watanabe et al. (2022b). For the gapful superconductors, the formula is given by
| (99) |
to which the nonreciprocity in the superfluid weight and the Berry curvature universally contribute. Thus, the low-frequency divergence is similarly predicted in various responses including the second-harmonic generation (). It may be relevant to recent experiments where the supercurrent-induced parity breaking leads to the second-harmonic generation Nakamura et al. (2020).
Finally, it should be noted that the nonreciprocal and superconducting optical responses may be informative for quantifying the parity mixing in the superconducting pairing. The superconducting gap symmetry does not show the definite parity under the violation in noncentrosymmetric systems, and the resultant parity mixing is expected to give rise to intriguing superconducting properties Bauer and (eds.). It has been a longstanding issue whether such parity mixing can be evaluated in the experiments. In this regard, the nonreciprocal optical response was found to be enhanced in the presence of moderate parity mixing Watanabe et al. (2022b); Tanaka et al. (2023), similar to the nonreciprocal paraconductivity Wakatsuki and Nagaosa (2018). The quantitative estimates of the parity mixing can be obtained by future optical measurements of tunable materials, such as Li2(Pt3-xPdx)B Badica et al. (2005) where the parity mixing presumably changes by chemical substitution.
VI Summary and Outlook
The role of magnetic parity violation in solid state electron systems has been reviewed with the comparison to that of the electric parity violation, a known type of parity violation found in the materials crystalizing in a noncentrosymmetric structure. Since the magnetic parity violation is accompanied by the time-reversal-symmetry breaking, it may be considered less fundamental than the electric parity violation. The preserved space-time symmetry, however, allows us to make clear distinctions between physical phenomena induced by either the electric or magnetic parity violation; i.e., the -symmetric system manifests the physical properties arising from the electric parity violation, while the -symmetric system shows phenomena unique to the magnetic parity violation.
The physical responses originating purely from the magnetic parity violation have been intensively discussed in the field of multiferroics in terms of the magnetoelectric phenomena. In addition, recent studies have been devoted to the investigation of magnetically parity-violating physical phenomena, which have advanced the earlier studies of the electric parity violation, such as for the photocurrent response. The identified responses are complementary to those induced by the electric parity violation. The complementary roles of magnetic and electric parity violation have been highlighted and grasped by their contrasting electronic structures.
The magnetic parity violation may lead to nontrivial physical phenomena due to its combination with other quantum nature of materials, for example, giant optoelectronic responses enhanced by the quantum-geometrical effect of topological electrons, nonreciprocity in the electromagnetic responses in superconductors, and so on. Despite the rapid growth in theoretical understandings of magnetic parity violation and the ubiquity of -symmetric magnetic materials Watanabe and Yanase (2018a) (see also Appendix A), the material realization and experimental observations of emergent responses remain elusive. Promising materials include those having the Dirac electrons such as quasi-two-dimensional Mn compounds (e.g., even-layer MnBi2Te4 and EuMnBi2) Zhang et al. (2019a); Sakai (2022) and massless Dirac systems (e.g., CuMnAs) Tang et al. (2016); Šmejkal et al. (2017); Linn et al. (2023).
The material realization may be feasible in playgrounds other than the bulk materials. The magnetic parity violation has been realized by metamaterials where the magnetic islands are arrayed Lehmann et al. (2019) and the ferromagnetic thin films are patterned Matsubara et al. (2022); Hild et al. (2023). The high tunability of physical responses is advantageous, and it has been demonstrated, for example, for the photocurrent generation in the magnetic metamaterials Matsubara et al. (2022). Furthermore, the magnetic parity violation may be found in the fictitious fields of the topological solitons. Recent studies clarified that the emergent magneto-multipolar fields of the magnetic hopfion give rise to various spin-charge-coupled phenomena Pershoguba et al. (2021); Liu et al. (2022).
The systematics based on the preserved space-time symmetry is expected to be applied to a broad range of physical responses other than those explained in this review. For instance, the -even/-odd decomposition is similarly found in various physical phenomena such as second-harmonic generation Bhalla et al. (2022), parametric conversion Wang et al. (2010); Werake and Zhao (2010) and photo-induced and current-induced spin current responses Young et al. (2013); Hamamoto et al. (2017); Kim et al. (2017); Xu et al. (2021); Xiao et al. (2021); Matsubara et al. (2022); Hayami et al. (2022); Adamantopoulos et al. (2022); Merte et al. (2023). The mechanism for each response has been mainly investigated in the framework of band electrons’ Hamiltonian, whereas further precise treatments including disorders and interactions may allow for quantitative estimates and imply the potential of the responses in probing the quantum nature of matter. For instance, parity-violating responses may show enhancement due to the electron correlation effect Peters and Yanase (2018) and collective modes such as phonons Okamura et al. (2022), spin fluctuation Yokouchi et al. (2017); Morimoto and Nagaosa (2019); Ishizuka and Nagaosa (2020); Iguchi et al. (2024), plasmon Sano et al. (2021); Toshio and Kawakami (2022), and exciton Morimoto and Nagaosa (2020); Sotome et al. (2021); Kaneko et al. (2021).
Acknowledgement
H.W. expresses a lot of thanks to Naoto Nagaosa, Riki Toshio, and Yoshihiro Michishita for valuable discussions and comments. The authors thank Inti Sodemann Villadiego for his fruitful comments. This review partly features our works done with collaborators. We here express our courtesy to them, particularly to Akito Daido, Atsuo Shitade, Hinako Murayama, Hiroto Tanaka, Junta Iguchi. Kohei Shinohara, Kousuke Ishida, Liu Yizhou, Masakazu Matsubara, Michiya Chazono, Yugo Onishi, Yuki Shiomi. The authors were supported by Grant-in-Aid for Scientific Research on Innovative Areas “J-Physics” (Grant No. JP15H05884), SPIPITS 2020 of Kyoto University, and JSPS KAKENHI (Grants No. JP15K05164, No. JP15H05745, No. JP16H00991, No. JP18H01178, No. JP18H04225, No. JP18H05227, No. JP18J23115, No. JP20H05159, No. JP21K18145, No. JP21J00453, No. JP22H04933, No. JP22H01181, No. JP23K17353, No. JP23K13058, No. JP24H00007).
We made use of the useful software vesta for visualization of crystal and magnetic structures Momma and Izumi (2011).
Appendix A Table of magnetic multipolar magnets
Many magnetic materials are characterized by the zero propagation vector of order parameter, by which the unit cell does not change at the magnetic phase transition. Zero propagation vector implies that the seemingly antiferroic magnetic order does induce uniform fields through the coupling to the crystal sublattice degree of freedom. From the viewpoint of symmetry, such a uniform field is classified into the even-parity and odd-parity magnetic multipolar fields in terms of parity under the space-inversion () operation.
Let us consider the point group symmetry of those magnetic multipolar materials. The even-parity magnetic multipolar order breaks the symmetry as well as the symmetry while preserving the symmetry. On the contrary, the odd-parity magnetic multipolar order, though it similarly breaks the symmetry, is -even and -odd. Then, when we assume the centrosymmetric symmetry of the paramagnetic state, the point group of the magnetic state is comprised of the space-inversion operation () but lacks parity-time-reversal operation () in the case of even-parity magnetic multipolar systems, while it is comprised of but lacks for the odd-parity magnetic multipolar systems. Owing to the preserved or symmetry, either even-parity or odd-parity magnetic multipolar field is allowed.
Letting be the magnetic point group, the coset decomposition is obtained as
| (100) |
for the even-parity magnetic multipolar systems and
| (101) |
for the odd-parity magnetic multipolar systems. The subgroup of is convenient to identify the emergent responses induced by each magnetic multipolar field; e.g. a response unique to the odd-parity magnetic multipolar systems is subject to symmetry constraints of and thereby may be zero even when it is not forbidden by the symmetry.
In Tables LABEL:Table-even_parity_multipolar, LABEL:Table-odd_parity_multipolar, we tabulate the pairs of and with some characteristics and candidate materials. Notably, since we consider the -symmetric or -symmetric magnetic point groups, the even- and odd-parity magnetic multipolar fields show up without being admixed with each other. The even-parity magnetic multipolar symmetry is characterized by whether the magnetic dipolar field (M) and piezomagnetic effect (PM) are allowed. For instance, if the magnetic dipole field is active (M: ), the magnetic materials denoted by the symmetry show the anomalous Hall effect.
Similarly, the odd-parity magnetic multipolar symmetry is characterized by the magnetic toroidal moment (T), magnetic quadrupole moment (MQ), and magnetopiezoelectric effect (MPE). If ‘T: ’, the -symmetric magnetic order may be switchable with the electric current Watanabe and Yanase (2018b) (see also Sec. IV). Magnetic materials with ‘MQ: ’ allow for various odd-parity responses formulated by the rank-2 and -symmetric axial tensor such as the magnetoelectric effect, photocurrent response under the circularly-polarized lights (see Sec. III.3.2), and so on. Magnetic materials with ‘MPE: ’ similarly host odd-parity responses described by the -symmetric tensor sharing the same symmetry as that of the magnetopiezoelectric effect [e.g, nonreciprocal electric conductivity (Sec. III.3.1) and photocurrent response under the linearly-polarized and unpolarized lights (Sec. III.3.2)]. Note that ‘T’ is always active if ‘MQ’ is active because the magnetic quadrupole moments include the magnetic toroidal moment.
| MPG | M | PM | Candidate materials | ||
|---|---|---|---|---|---|
| N/A | |||||
| Cd2Os2O7 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x17.png)
|
||||
| NiS2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x18.png)
|
||||
| N/A | |||||
| Mn5Ge3 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x19.png)
|
||||
| CrNb4S8 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x20.png)
|
||||
| N/A | |||||
| N/A | |||||
| CoF3 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x21.png)
|
||||
| Mn3Ir |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x22.png)
|
||||
| Mn3NiN |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x23.png)
|
||||
| KMnF3 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x24.png)
|
||||
| Nd2NiO4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x25.png)
|
||||
| MnF2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x26.png)
|
||||
| MnV2O4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x27.png)
|
||||
| MnTe |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x28.png)
|
||||
| Mn3Sn |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x29.png)
|
||||
| MnCO3 |
|
||||
| KMnF4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x31.png)
|
||||
| RbMnF4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x32.png)
|
||||
| MPG | T | MQ | MPE | Candidate materials | ||
|---|---|---|---|---|---|---|
| N/A | ||||||
| N/A | ||||||
| N/A | ||||||
| N/A | ||||||
| N/A | ||||||
| N/A | ||||||
| U14Au51 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x33.png)
|
|||||
| PbMn2Ni6Te3O18 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x34.png)
|
|||||
| Cr2O3 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x35.png)
|
|||||
| Ca2YZr2Fe3O12 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x36.png)
|
|||||
| MnGeO3 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x37.png)
|
|||||
| GdB4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x38.png)
|
|||||
| Co3Al2Si3O12 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x39.png)
|
|||||
| BaMn2As2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x40.png)
|
|||||
| TlFe1.6Se2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x41.png)
|
|||||
| KOsO4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x42.png)
|
|||||
| LiMnPO4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x43.png)
|
|||||
| CuMnAs |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x44.png)
|
|||||
| Na2RuO4 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x45.png)
|
|||||
| SrMn2As2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x46.png)
|
|||||
| YbMn2Sb2 |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/385fa40a-e724-48c5-b251-c7a51987a0ea/x47.png)
|
|||||
References
- Adamantopoulos et al. (2022) Adamantopoulos, T, M Merte, D Go, F Freimuth, S Blügel, and Y Mokrousov (2022), “Laser-induced charge and spin photocurrents at the BiAg2 surface: A first-principles benchmark,” Physical Review Research 4 (4), 043046.
- Agterberg et al. (2017) Agterberg, D F, P M R Brydon, and C Timm (2017), “Bogoliubov fermi surfaces in superconductors with broken time-reversal symmetry,” Physical Review Letters 118 (12), 127001.
- Ahn et al. (2020) Ahn, Junyeong, Guang-Yu Guo, and Naoto Nagaosa (2020), “Low-Frequency divergence and quantum geometry of the bulk photovoltaic effect in topological semimetals,” Physical Review X 10 (4), 041041.
- Ahn and Nagaosa (2021) Ahn, Junyeong, and Naoto Nagaosa (2021), “Theory of optical responses in clean multi-band superconductors,” Nature Communications 12 (1), 1617.
- Akaike et al. (2021) Akaike, M, Y Nii, H Masuda, and Y Onose (2021), “Nonreciprocal electronic transport in PdCrO2: Implication of spatial inversion symmetry breaking,” Physical Review B 103 (18), 184428.
- Akashi et al. (2017) Akashi, Ryosuke, Yo Iida, Kohei Yamamoto, and Kanako Yoshizawa (2017), “Interference of the bloch phase in layered materials with stacking shifts,” Physical Review B 95 (24), 245401.
- Aoki et al. (2022) Aoki, D, J-P Brison, J Flouquet, K Ishida, G Knebel, Y Tokunaga, and Y Yanase (2022), “Unconventional superconductivity in UTe2,” Journal of physics. Condensed matter: an Institute of Physics journal 34 (24), 243002.
- Aoki et al. (2019) Aoki, Ryuya, Yusuke Kousaka, and Yoshihiko Togawa (2019), “Anomalous nonreciprocal electrical transport on chiral magnetic order,” Physical Review Letters 122 (5), 057206.
- Aoyama et al. (2022) Aoyama, Takuya, Masahiro Kudo, Kaoru Igarashi, Kazutoshi Emi, Shojiro Kimura, Yoshinori Imai, and Kenya Ohgushi (2022), “Enhanced anisotropic magnetoresistance in the odd-parity multipole-ordered conductor Ba1-xKxMn2As2,” Physical Review B 105 (22), 224422.
- Arakawa et al. (2023) Arakawa, Keito, Takeshi Hayashida, Kenta Kimura, Ryusuke Misawa, Takayuki Nagai, Tatsuya Miyamoto, Hiroshi Okamoto, Fumitoshi Iga, and Tsuyoshi Kimura (2023), “Detecting magnetoelectric effect in a metallic antiferromagnet via nonreciprocal rotation of reflected light,” Physical Review Letters 131 (23), 236702.
- Artamonov et al. (1992) Artamonov, Yu A, A A Gorbatsevich, and Yu V Kopaev (1992), “Photovoltaic effect in an orbital antiferromagnet,” Soviet Physics, Journal of Experimental and Theoretical Physics 74, 296, [ibid., Zh. Éksp. Teor. Fiz. 101 (2), 557 (1992)].
- Atencia et al. (2023) Atencia, Rhonald Burgos, Di Xiao, and Dimitrie Culcer (2023), “Disorder in the nonlinear anomalous hall effect of -symmetric dirac fermions,” Physical Review B 108, L201115.
- Badica et al. (2005) Badica, Petre, Takaaki Kondo, and Kazumasa Togano (2005), “Superconductivity in a new pseudo-binary Li2B(Pd1-xPtx)3 () boride system,” Journal of the Physical Society of Japan 74 (3), 1014–1019.
- von Baltz and Kraut (1981) von Baltz, Ralph, and Wolfgang Kraut (1981), “Theory of the bulk photovoltaic effect in pure crystals,” Physical Review B 23 (10), 5590–5596.
- Baltz et al. (2018) Baltz, V, A Manchon, M Tsoi, T Moriyama, T Ono, and Y Tserkovnyak (2018), “Antiferromagnetic spintronics,” Reviews of Modern Physics 90 (1), 328.
- Barthem et al. (2013) Barthem, V M T S, C V Colin, H Mayaffre, M-H Julien, and D Givord (2013), “Revealing the properties of Mn2Au for antiferromagnetic spintronics,” Nature Communications 4 (1), 2892.
- Bass et al. (1962) Bass, M, P A Franken, J F Ward, and G Weinreich (1962), “Optical Rectification,” Physical Review Letters 9 (11), 446–448.
- Bauer and (eds.) Bauer, E, and M. Sigrist (eds.) (2012), Non-Centrosymmetric Superconductors: Introduction and Overview, Vol. 847 (Springer, Berlin).
- Beaulieu et al. (2020) Beaulieu, S, J Schusser, S Dong, M Schüler, T Pincelli, M Dendzik, J Maklar, A Neef, H Ebert, K Hricovini, M Wolf, J Braun, L Rettig, J Minár, and R Ernstorfer (2020), “Revealing hidden orbital pseudospin texture with Time-Reversal dichroism in photoelectron angular distributions,” Physical Review Letters 125 (21), 216404.
- Belinicher et al. (1986) Belinicher, V I, E L Ivchenko, and G E Pikus (1986), “Transient photocurrent in gyrotropic crystals,” Soviet Physics Semiconductors-Ussr 20 (5), 558–561, [ibid., Fiz. Tekh. Poluprovodn. 20, 886 (1986)].
- Belinicher et al. (1982) Belinicher, V I, E L Ivchenko, and B I Sturman (1982), “Kinetic theory of the displacement photovoltaic effect in piezoelectrics,” Soviet Physics, Journal of Experimental and Theoretical Physics 56 (2), 359–366, [ibid., Zh. Eksp. Teor. Fiz. 83 649 (1982)].
- Bertoni et al. (2016) Bertoni, R, C W Nicholson, L Waldecker, H Hübener, C Monney, U De Giovannini, M Puppin, M Hoesch, E Springate, R T Chapman, C Cacho, M Wolf, A Rubio, and R Ernstorfer (2016), “Generation and evolution of spin-, valley-, and Layer-Polarized excited carriers in Inversion-Symmetric WSe2,” Physical Review Letters 117 (27), 277201.
- Bhalla et al. (2022) Bhalla, Pankaj, Kamal Das, Dimitrie Culcer, and Amit Agarwal (2022), “Resonant Second-Harmonic generation as a probe of quantum geometry,” Physical Review Letters 129 (22), 227401.
- Bhowal and Spaldin (2022) Bhowal, Sayantika, and Nicola A Spaldin (2022), “Magnetoelectric classification of skyrmions,” Physical Review Letters 128 (22), 227204.
- Bickers et al. (1990) Bickers, N E, D J Scalapino, R T Collins, and Z Schlesinger (1990), “Infrared conductivity in superconductors with a finite mean free path,” Physical Review B 42 (1), 67–75.
- Bodnar et al. (2018) Bodnar, S Yu, L Šmejkal, I Turek, T Jungwirth, O Gomonay, J Sinova, A A Sapozhnik, H-J Elmers, M Kläui, and M Jourdan (2018), “Writing and reading antiferromagnetic Mn2Au by néel spin-orbit torques and large anisotropic magnetoresistance,” Nature Communications 9 (1), 231.
- Borisenko et al. (2019) Borisenko, Sergey, Daniil Evtushinsky, Quinn Gibson, Alexander Yaresko, Klaus Koepernik, Timur Kim, Mazhar Ali, Jeroen van den Brink, Moritz Hoesch, Alexander Fedorov, Erik Haubold, Yevhen Kushnirenko, Ivan Soldatov, Rudolf Schäfer, and Robert J Cava (2019), “Time-reversal symmetry breaking type-II weyl state in YbMnBi2,” Nature Communications 10 (1), 3424.
- Borisov et al. (2005) Borisov, Pavel, Andreas Hochstrat, Xi Chen, Wolfgang Kleemann, and Christian Binek (2005), “Magnetoelectric switching of exchange bias,” Physical Review Letters 94 (11), 117203.
- Bultmark et al. (2009) Bultmark, Fredrik, Francesco Cricchio, Oscar Grånäs, and Lars Nordström (2009), “Multipole decomposition of energy and its application to actinide compounds,” Physical Review B 80, 035121.
- Chang and Niu (1996) Chang, Ming-Che, and Qian Niu (1996), “Berry phase, hyperorbits, and the Hofstadter spectrum: Semiclassical dynamics in magnetic Bloch bands,” Physical Review B 53 (11), 7010.
- Chazono et al. (2023) Chazono, Michiya, Shota Kanasugi, Taisei Kitamura, and Youichi Yanase (2023), “Piezoelectric effect and diode effect in anapole and monopole superconductors,” Physical Review B 107 (21), 214512.
- Chazono et al. (2022) Chazono, Michiya, Hikaru Watanabe, and Youichi Yanase (2022), “Superconducting piezoelectric effect,” Physical Review B 105 (2), 024509.
- Cheng et al. (2020) Cheng, Yang, Sisheng Yu, Menglin Zhu, Jinwoo Hwang, and Fengyuan Yang (2020), “Electrical switching of tristate antiferromagnetic néel order in -Fe2O3 epitaxial films,” Physical Review Letters 124 (2), 027202.
- Chernyshov et al. (2009) Chernyshov, Alexandr, Mason Overby, Xinyu Liu, Jacek K Furdyna, Yuli Lyanda-Geller, and Leonid P Rokhinson (2009), “Evidence for reversible control of magnetization in a ferromagnetic material by means of spin–orbit magnetic field,” Nature Physics 5 (9), 656–659.
- Chiang et al. (2019) Chiang, C C, S Y Huang, D Qu, P H Wu, and C L Chien (2019), “Absence of evidence of electrical switching of the antiferromagnetic néel vector,” Physical Review Letters 123 (22), 227203.
- Cho et al. (2018) Cho, Soohyun, Jin-Hong Park, Jisook Hong, Jongkeun Jung, Beom Seo Kim, Garam Han, Wonshik Kyung, Yeongkwan Kim, S-K Mo, J D Denlinger, Ji Hoon Shim, Jung Hoon Han, Changyoung Kim, and Seung Ryong Park (2018), “Experimental observation of hidden berry curvature in inversion-symmetric bulk -wse2,” Physical Review Letters 121 (18), 186401.
- Churikova et al. (2020) Churikova, A, D Bono, B Neltner, A Wittmann, L Scipioni, A Shepard, T Newhouse-Illige, J Greer, and G S D Beach (2020), “Non-magnetic origin of spin hall magnetoresistance-like signals in pt films and epitaxial NiO/pt bilayers,” Applied physics letters 116 (2), 022410.
- Cricchio et al. (2010) Cricchio, Francesco, Oscar Grånäs, and Lars Nordström (2010), “Low spin moment due to hidden multipole order from spin-orbital ordering in lafeaso,” Physical Review B 81, 140403.
- Daido et al. (2020) Daido, Akito, Atsuo Shitade, and Youichi Yanase (2020), “Thermodynamic approach to electric quadrupole moments,” Physical Review B 102, 235149.
- Daido et al. (2019) Daido, Akito, Tsuneya Yoshida, and Youichi Yanase (2019), “ topological superconductivity in UCoGe,” Physical Review Letters 122 (22), 227001.
- Devarakonda et al. (2020) Devarakonda, A, H Inoue, S Fang, C Ozsoy-Keskinbora, T Suzuki, M Kriener, L Fu, E Kaxiras, D C Bell, and J G Checkelsky (2020), “Clean 2D superconductivity in a bulk van der waals superlattice,” Science 370 (6513), 231–236.
- Deyo et al. (2009) Deyo, E, L E Golub, E L Ivchenko, and B Spivak (2009), “Semiclassical theory of the photogalvanic effect in non-centrosymmetric systems,” arXiv:0904.1917 [cond-mat.mes-hall] .
- Dimitrova and Feigel’man (2003) Dimitrova, O V, and M V Feigel’man (2003), “Phase diagram of a surface superconductor in parallel magnetic field,” Journal of Experimental and Theoretical Physics Letters 78 (10), 637–641.
- Du et al. (2020) Du, Shiqiao, Peizhe Tang, Jiaheng Li, Zuzhang Lin, Yong Xu, Wenhui Duan, and Angel Rubio (2020), “Berry curvature engineering by gating two-dimensional antiferromagnets,” Physical Review Research 2 (2), 022025.
- Du et al. (2021a) Du, Z Z, Hai-Zhou Lu, and X C Xie (2021a), “Nonlinear hall effects,” Nature Reviews Physics 3 (11), 744–752.
- Du et al. (2019) Du, Z Z, C M Wang, Shuai Li, Hai-Zhou Lu, and X C Xie (2019), “Disorder-induced nonlinear hall effect with time-reversal symmetry,” Nature Communications 10 (1), 3047.
- Du et al. (2021b) Du, Z Z, C M Wang, Hai-Peng Sun, Hai-Zhou Lu, and X C Xie (2021b), “Quantum theory of the nonlinear hall effect,” Nature Communications 12 (1), 5038.
- Dzsaber et al. (2021) Dzsaber, Sami, Xinlin Yan, Mathieu Taupin, Gaku Eguchi, Andrey Prokofiev, Toni Shiroka, Peter Blaha, Oleg Rubel, Sarah E Grefe, Hsin-Hua Lai, Qimiao Si, and Silke Paschen (2021), “Giant spontaneous hall effect in a nonmagnetic Weyl-Kondo semimetal,” Proceedings of the National Academy of Sciences of the United States of America 118 (8).
- Edelstein (1990) Edelstein, V M (1990), “Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems,” Solid State Commun. 73 (3), 233–235.
- Edelstein (1995) Edelstein, V M (1995), “Magnetoelectric effect in polar superconductors,” Physical Review Letters 75 (10), 2004–2007.
- Elmers et al. (2020) Elmers, H J, S V Chernov, S W D’Souza, S P Bommanaboyena, S Yu Bodnar, K Medjanik, S Babenkov, O Fedchenko, D Vasilyev, S Y Agustsson, C Schlueter, A Gloskovskii, Yu Matveyev, V N Strocov, Y Skourski, L Šmejkal, J Sinova, J Minár, M Kläui, G Schönhense, and M Jourdan (2020), “Néel vector induced manipulation of valence states in the collinear antiferromagnet Mn2Au,” ACS nano 14 (12), 17554–17564.
- Erb and Hlinka (2020) Erb, K C, and J Hlinka (2020), “Vector and bidirector representations of magnetic point groups,” Phase transitions 93 (1), 1–42.
- Fedchenko et al. (2022) Fedchenko, O, L Šmejkal, M Kallmayer, Ya Lytvynenko, K Medjanik, S Babenkov, D Vasilyev, M Kläui, J Demsar, G Schönhense, M Jourdan, J Sinova, and H J Elmers (2022), “Direct observation of antiferromagnetic parity violation in the electronic structure of Mn2Au,” Journal of physics. Condensed matter: an Institute of Physics journal 34 (42), 425501.
- Ferrell and Glover (1958) Ferrell, Richard A, and Rolfe E Glover (1958), “Conductivity of superconducting films: A sum rule,” Physical Review 109 (4), 1398–1399.
- Fiebig (2005) Fiebig, Manfred (2005), “Revival of the magnetoelectric effect,” Journal of Physics D: Applied Physics 38 (8), R123.
- Fischer (2013) Fischer, Mark H (2013), “Gap symmetry and stability analysis in the multi-orbital fe-based superconductors,” New journal of physics 15 (7), 073006.
- Fischer et al. (2011) Fischer, Mark H, Florian Loder, and Manfred Sigrist (2011), “Superconductivity and local noncentrosymmetricity in crystal lattices,” Physical Review B 84 (18), 184533.
- Fischer et al. (2023) Fischer, Mark H, Manfred Sigrist, Daniel F Agterberg, and Youichi Yanase (2023), “Superconductivity and local inversion-symmetry breaking,” Annual Review of Condensed Matter Physics 14 (1), 153–172.
- Fregoso et al. (2017) Fregoso, Benjamin M, Takahiro Morimoto, and Joel E Moore (2017), “Quantitative relationship between polarization differences and the zone-averaged shift photocurrent,” Physical Review B 96 (7), 075421.
- Freimuth et al. (2014) Freimuth, Frank, Stefan Blügel, and Yuriy Mokrousov (2014), “Spin-orbit torques in Co/Pt(111) and Mn/W(001) magnetic bilayers from first principles,” Physical Review B 90 (17), 174423.
- Fridkin and Popov (1978) Fridkin, Vladimir M, and B N Popov (1978), “Anomalous photovoltaic effect in ferroelectrics,” Soviet Physics Uspekhi 21 (12), 981.
- Fu et al. (2007) Fu, Liang, C L Kane, and E J Mele (2007), “Topological insulators in three dimensions,” Physical Eeview Letters 98 (10), 106803.
- Gallego et al. (2016) Gallego, S V, J M Perez-Mato, L Elcoro, E S Tasci, R M Hanson, K Momma, M I Aroyo, and G Madariaga (2016), “MAGNDATA: towards a database of magnetic structures. I. the commensurate case,” Journal of Applied Crystallography 49 (5), 1750–1776.
- Gao et al. (2021) Gao, Anyuan, Yu-Fei Liu, Chaowei Hu, Jian-Xiang Qiu, Christian Tzschaschel, Barun Ghosh, Sheng-Chin Ho, Damien Bérubé, Rui Chen, Haipeng Sun, Zhaowei Zhang, Xin-Yue Zhang, Yu-Xuan Wang, Naizhou Wang, Zumeng Huang, Claudia Felser, Amit Agarwal, Thomas Ding, Hung-Ju Tien, Austin Akey, Jules Gardener, Bahadur Singh, Kenji Watanabe, Takashi Taniguchi, Kenneth S Burch, David C Bell, Brian B Zhou, Weibo Gao, Hai-Zhou Lu, Arun Bansil, Hsin Lin, Tay-Rong Chang, Liang Fu, Qiong Ma, Ni Ni, and Su-Yang Xu (2021), “Layer hall effect in a 2D topological axion antiferromagnet,” Nature 595 (7868), 521–525.
- Gao et al. (2023) Gao, Anyuan, Yu-Fei Liu, Jian-Xiang Qiu, Barun Ghosh, Thaís Trevisan, V, Yugo Onishi, Chaowei Hu, Tiema Qian, Hung-Ju Tien, Shao-Wen Chen, Mengqi Huang, Damien Bérubé, Houchen Li, Christian Tzschaschel, Thao Dinh, Zhe Sun, Sheng-Chin Ho, Shang-Wei Lien, Bahadur Singh, Kenji Watanabe, Takashi Taniguchi, David C Bell, Hsin Lin, Tay-Rong Chang, Chunhui Rita Du, Arun Bansil, Liang Fu, Ni Ni, Peter P Orth, Qiong Ma, and Su-Yang Xu (2023), “Quantum metric nonlinear hall effect in a topological antiferromagnetic heterostructure,” Science 381 (6654), 181–186.
- Gao et al. (2018) Gao, Yang, David Vanderbilt, and Di Xiao (2018), “Microscopic theory of spin toroidization in periodic crystals,” Physical Review B 97, 134423.
- Gao and Xiao (2018) Gao, Yang, and Di Xiao (2018), “Orbital magnetic quadrupole moment and nonlinear anomalous thermoelectric transport,” Physical Review B 98 (6), 060402.
- Gao et al. (2014) Gao, Yang, Shengyuan A Yang, and Qian Niu (2014), “Field induced positional shift of bloch electrons and its dynamical implications,” Physical Review Letters 112 (16), 166601.
- Gao et al. (2020) Gao, Yang, Yinhan Zhang, and Di Xiao (2020), “Tunable layer circular photogalvanic effect in twisted bilayers,” Physical Review Letters 124 (7), 077401.
- Gehlmann et al. (2016) Gehlmann, Mathias, Irene Aguilera, Gustav Bihlmayer, Ewa Młyńczak, Markus Eschbach, Sven Döring, Pika Gospodarič, Stefan Cramm, Beata Kardynał, Lukasz Plucinski, Stefan Blügel, and Claus M Schneider (2016), “Quasi 2D electronic states with high spin-polarization in centrosymmetric MoS2 bulk crystals,” Scientific Reports 6, 26197.
- Go et al. (2018) Go, Dongwook, Daegeun Jo, Changyoung Kim, and Hyun-Woo Lee (2018), “Intrinsic spin and orbital hall effects from orbital texture,” Physical Review Letters 121 (8), 086602.
- Go et al. (2022) Go, Dongwook, Moritz Sallermann, Fabian R Lux, Stefan Blügel, Olena Gomonay, and Yuriy Mokrousov (2022), “Noncollinear Spin Current for Switching of Chiral Magnetic Textures,” Physical review letters 129 (9), 097204.
- Godinho et al. (2018) Godinho, J, H Reichlová, D Kriegner, V Novák, K Olejník, Z Kašpar, Z Šobáň, P Wadley, R P Campion, R M Otxoa, P E Roy, J Železný, T Jungwirth, and J Wunderlich (2018), “Electrically induced and detected néel vector reversal in a collinear antiferromagnet,” Nature Communications 9 (1), 4686.
- Goh et al. (2012) Goh, S K, Y Mizukami, H Shishido, D Watanabe, S Yasumoto, M Shimozawa, M Yamashita, T Terashima, Y Yanase, T Shibauchi, A I Buzdin, and Y Matsuda (2012), “Anomalous upper critical field in CeCoIn5/YbCoIn5 superlattices with a rashba-type heavy fermion interface,” Physical Review Letters 109 (15), 157006.
- Golub and Glazov (2022) Golub, L E, and M M Glazov (2022), “Raman photogalvanic effect: Photocurrent at inelastic light scattering,” Physical Review B 106 (20), 205205.
- Gomonay and Loktev (2010) Gomonay, Helen V, and Vadim M Loktev (2010), “Spin transfer and current-induced switching in antiferromagnets,” Physical Review B 81 (14), 144427.
- Gong et al. (2013) Gong, Zhirui, Gui-Bin Liu, Hongyi Yu, Di Xiao, Xiaodong Cui, Xiaodong Xu, and Wang Yao (2013), “Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers,” Nature Communications 4 (1), 2053.
- Gotlieb et al. (2018) Gotlieb, Kenneth, Chiu-Yun Lin, Maksym Serbyn, Wentao Zhang, Christopher L Smallwood, Christopher Jozwiak, Hiroshi Eisaki, Zahid Hussain, Ashvin Vishwanath, and Alessandra Lanzara (2018), “Revealing hidden spin-momentum locking in a high-temperature cuprate superconductor,” Science 362 (6420), 1271–1275.
- Grigorev et al. (2021) Grigorev, Vladimir, Mariia Filianina, Stanislav Yu Bodnar, Sergei Sobolev, Nilabha Bhattacharjee, Satya Bommanaboyena, Yaryna Lytvynenko, Yurii Skourski, Dirk Fuchs, Mathias Kläui, Martin Jourdan, and Jure Demsar (2021), “Optical readout of the néel vector in the metallic antiferromagnet Mn2Au,” Physical Review Applied 16 (1), 014037.
- Grzybowski et al. (2017) Grzybowski, M J, P Wadley, K W Edmonds, R Beardsley, V Hills, R P Campion, B L Gallagher, J S Chauhan, V Novak, T Jungwirth, F Maccherozzi, and S S Dhesi (2017), “Imaging current-induced switching of antiferromagnetic domains in CuMnAs,” Physical Review Letters 118 (5), 057701.
- Guan et al. (2022) Guan, Shan, Jia-Xin Xiong, Zhi Wang, and Jun-Wei Luo (2022), “Progress of hidden spin polarization in inversion-symmetric crystals,” Science China Physics, Mechanics, and Astronomy 65 (3), 237301.
- Haldane (1988) Haldane, F D (1988), “Model for a quantum hall effect without landau levels: Condensed-matter realization of the “parity anomaly”,” Physical Review Letters 61 (18), 2015–2018.
- Hamamoto et al. (2017) Hamamoto, Keita, Motohiko Ezawa, Kun Woo Kim, Takahiro Morimoto, and Naoto Nagaosa (2017), “Nonlinear spin current generation in noncentrosymmetric spin-orbit coupled systems,” Physical Review B 95 (22), 224430.
- Han et al. (2023) Han, Jiahao, Ran Cheng, Luqiao Liu, Hideo Ohno, and Shunsuke Fukami (2023), “Coherent antiferromagnetic spintronics,” Nature Materials 22 (6), 684–695.
- Hatada et al. (2020) Hatada, Hiroki, Masao Nakamura, Masato Sotome, Yoshio Kaneko, Naoki Ogawa, Takahiro Morimoto, Yoshinori Tokura, and Masashi Kawasaki (2020), “Defect tolerant zero-bias topological photocurrent in a ferroelectric semiconductor,” Proceedings of the National Academy of Sciences of the United States of America 117 (34), 20411–20415.
- Hayami et al. (2014a) Hayami, Satoru, Hiroaki Kusunose, and Yukitoshi Motome (2014a), “Spontaneous parity breaking in spin-orbital coupled systems,” Physical Review B 90 (8), 081115.
- Hayami et al. (2014b) Hayami, Satoru, Hiroaki Kusunose, and Yukitoshi Motome (2014b), “Toroidal order in metals without local inversion symmetry,” Physical Review B 90 (2), 024432.
- Hayami et al. (2022) Hayami, Satoru, Megumi Yatsushiro, and Hiroaki Kusunose (2022), “Nonlinear spin hall effect in -symmetric collinear magnets,” Physical Review B 106 (2), 024405.
- Hayami et al. (2018) Hayami, Satoru, Megumi Yatsushiro, Yuki Yanagi, and Hiroaki Kusunose (2018), “Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors,” Physical Review B 98 (16), 165110.
- He et al. (2021) He, Pan, Hiroki Isobe, Dapeng Zhu, Chuang-Han Hsu, Liang Fu, and Hyunsoo Yang (2021), “Quantum frequency doubling in the topological insulator Bi2Se3,” Nature Communications 12 (1), 698.
- Higo et al. (2022) Higo, Tomoya, Kouta Kondou, Takuya Nomoto, Masanobu Shiga, Shoya Sakamoto, Xianzhe Chen, Daisuke Nishio-Hamane, Ryotaro Arita, Yoshichika Otani, Shinji Miwa, and Satoru Nakatsuji (2022), “Perpendicular full switching of chiral antiferromagnetic order by current,” Nature 607 (7919), 474–479.
- Hild et al. (2023) Hild, M, L E Golub, A Fuhrmann, M Otteneder, M Kronseder, M Matsubara, T Kobayashi, D Oshima, A Honda, T Kato, J Wunderlich, C Back, and S D Ganichev (2023), “Terahertz spin ratchet effect in magnetic metamaterials,” Physical Review B 107 (15), 155419.
- Hitomi and Yanase (2014) Hitomi, Takanori, and Youichi Yanase (2014), “Electric octupole order in bilayer ruthenate Sr3Ru2O7,” Journal of the Physical Society of Japan 83 (11), 114704.
- Hitomi and Yanase (2016) Hitomi, Takanori, and Youichi Yanase (2016), “Electric octupole order in bilayer rashba system,” Journal of the Physical Society of Japan 85 (12), 124702.
- Holder et al. (2020) Holder, Tobias, Daniel Kaplan, and Binghai Yan (2020), “Consequences of time-reversal-symmetry breaking in the light-matter interaction: Berry curvature, quantum metric, and diabatic motion,” Physical Review Research 2 (3), 033100.
- Hoshino et al. (2018) Hoshino, Shintaro, Ryohei Wakatsuki, Keita Hamamoto, and Naoto Nagaosa (2018), “Nonreciprocal charge transport in two-dimensional noncentrosymmetric superconductors,” Physical Review B 98 (5), 054510.
- Hu et al. (2017) Hu, Y J, Y W Cheung, W C Yu, Masaki Imai, Hibiki Kanagawa, Joichi Murakawa, Kazuyoshi Yoshimura, and Swee K Goh (2017), “Soft phonon modes in the vicinity of the structural quantum critical point,” Physical Review B 95 (15), 155142.
- Huang et al. (2018) Huang, Bevin, Genevieve Clark, Dahlia R Klein, David MacNeill, Efrén Navarro-Moratalla, Kyle L Seyler, Nathan Wilson, Michael A McGuire, David H Cobden, Di Xiao, Wang Yao, Pablo Jarillo-Herrero, and Xiaodong Xu (2018), “Electrical control of 2D magnetism in bilayer CrI3,” Nature Nanotechnology 13 (7), 544–548.
- Huynh et al. (2019) Huynh, Kim-Khuong, Takuma Ogasawara, Keita Kitahara, Yoichi Tanabe, Stephane Yu Matsushita, Time Tahara, Takanori Kida, Masayuki Hagiwara, Denis Arčon, and Katsumi Tanigaki (2019), “Negative and positive magnetoresistance in the itinerant antiferromagnet BaMn2Pn2 ( Pn = p,as,sb, and bi),” Physical Review B 99 (19), 195111.
- Ideue et al. (2017) Ideue, T, K Hamamoto, S Koshikawa, M Ezawa, S Shimizu, Y Kaneko, Y Tokura, N Nagaosa, and Y Iwasa (2017), “Bulk rectification effect in a polar semiconductor,” Nature Physics 13 (6), 578–583.
- Ideue and Iwasa (2021) Ideue, Toshiya, and Yoshihiro Iwasa (2021), “Symmetry breaking and nonlinear electric transport in van der waals nanostructures,” Annual Review of Condensed Matter Physics 12 (1), 201–223.
- Iguchi et al. (2024) Iguchi, Junta, Hikaru Watanabe, Yuta Murakami, Takuya Nomoto, and Ryotaro Arita (2024), “Bulk photovoltaic effect in antiferromagnet: Role of collective spin dynamics,” Physical Review B 109, 064407.
- Ikeda and Yanase (2020) Ikeda, Yuhei, and Youichi Yanase (2020), “Giant surface edelstein effect in -wave superconductors,” Physical Review B 102 (21), 214510.
- Ishizaka et al. (2011) Ishizaka, K, M S Bahramy, H Murakawa, M Sakano, T Shimojima, T Sonobe, K Koizumi, S Shin, H Miyahara, A Kimura, K Miyamoto, T Okuda, H Namatame, M Taniguchi, R Arita, N Nagaosa, K Kobayashi, Y Murakami, R Kumai, Y Kaneko, Y Onose, and Y Tokura (2011), “Giant rashba-type spin splitting in bulk BiTeI,” Nature Materials 10 (7), 521–526.
- Ishizuka and Nagaosa (2020) Ishizuka, Hiroaki, and Naoto Nagaosa (2020), “Anomalous electrical magnetochiral effect by chiral spin-cluster scattering,” Nature Communications 11 (1), 2986.
- Ishizuka and Nagaosa (2021) Ishizuka, Hiroaki, and Naoto Nagaosa (2021), “Theory of bulk photovoltaic effect in anderson insulator,” Proceedings of the National Academy of Sciences of the United States of America 118 (10).
- Ishizuka and Yanase (2021) Ishizuka, Jun, and Youichi Yanase (2021), “Periodic anderson model for magnetism and superconductivity in UTe2,” Physical Review B 103 (9), 094504.
- Isobe and Nagaosa (2022) Isobe, Hiroki, and Naoto Nagaosa (2022), “Toroidal scattering and nonreciprocal transport by magnetic impurities,” Journal of the Physical Society of Japan 91 (11), 115001.
- Isobe et al. (2020) Isobe, Hiroki, Su-Yang Xu, and Liang Fu (2020), “High-frequency rectification via chiral bloch electrons,” Science Advances 6 (13), eaay2497.
- Jiang et al. (2020) Jiang, N, Y Nii, H Arisawa, E Saitoh, and Y Onose (2020), “Electric current control of spin helicity in an itinerant helimagnet,” Nature Communications 11 (1), 1601.
- Jiang et al. (2018a) Jiang, Shengwei, Lizhong Li, Zefang Wang, Kin Fai Mak, and Jie Shan (2018a), “Controlling magnetism in 2D CrI3 by electrostatic doping,” Nature Nanotechnology 13 (7), 549–553.
- Jiang et al. (2018b) Jiang, Shengwei, Jie Shan, and Kin Fai Mak (2018b), “Electric-field switching of two-dimensional van der waals magnets,” Nature Materials 17 (5), 406–410.
- João and Viana Parente Lopes (2020) João, S M, and J M Viana Parente Lopes (2020), “Basis-independent spectral methods for non-linear optical response in arbitrary tight-binding models,” Journal of physics. Condensed matter: an Institute of Physics journal 32 (12), 125901.
- Jones et al. (2014) Jones, Aaron M, Hongyi Yu, Jason S Ross, Philip Klement, Nirmal J Ghimire, Jiaqiang Yan, David G Mandrus, Wang Yao, and Xiaodong Xu (2014), “Spin–layer locking effects in optical orientation of exciton spin in bilayer WSe2,” Nature physics 10 (2), 130–134.
- de Juan et al. (2020) de Juan, F, Y Zhang, T Morimoto, Y Sun, J E Moore, and A G Grushin (2020), “Difference frequency generation in topological semimetals,” Physical Review Research 2 (1), 012017.
- de Juan et al. (2017) de Juan, Fernando, Adolfo G Grushin, Takahiro Morimoto, and Joel E Moore (2017), “Quantized circular photogalvanic effect in weyl semimetals,” Nature Communications 8 (1), 15995.
- Jujo (2022) Jujo, Takanobu (2022), “Surface resistance and amplitude mode under uniform and static external field in conventional superconductors,” Journal of the Physical Society of Japan 91 (7), 074711.
- Jungwirth et al. (2016) Jungwirth, T, X Marti, P Wadley, and J Wunderlich (2016), “Antiferromagnetic spintronics,” Nature Nanotechnology 11 (3), 231–241.
- Kanasugi and Yanase (2022) Kanasugi, Shota, and Youichi Yanase (2022), “Anapole superconductivity from -symmetric mixed-parity interband pairing,” Communications Physics 5 (1), 1–10.
- Kane and Mele (2005) Kane, C L, and E J Mele (2005), “Quantum spin hall effect in graphene,” Physical Review Letters 95 (22), 226801.
- Kaneko et al. (2021) Kaneko, Tatsuya, Zhiyuan Sun, Yuta Murakami, Denis Golež, and Andrew J Millis (2021), “Bulk photovoltaic effect driven by collective excitations in a correlated insulator,” Physical Review Letters 127 (12), 127402.
- Kang et al. (2019) Kang, Kaifei, Tingxin Li, Egon Sohn, Jie Shan, and Kin Fai Mak (2019), “Nonlinear anomalous hall effect in few-layer WTe2,” Nature Materials 18 (4), 324–328.
- Kaplan et al. (2024) Kaplan, Daniel, Tobias Holder, and Binghai Yan (2024), “Unification of nonlinear anomalous Hall effect and nonreciprocal magnetoresistance in metals by the quantum geometry,” Physical Review Letters 132 (2), 026301.
- Kappl et al. (2023) Kappl, Patrick, Friedrich Krien, Clemens Watzenböck, and Karsten Held (2023), “Nonlinear responses and three-particle correlators in correlated electron systems exemplified by the anderson impurity model,” Physical Review B 107 (20), 205108.
- Kapustin and Radzihovsky (2022) Kapustin, Anton, and Leo Radzihovsky (2022), “Piezosuperconductivity: Novel effects in noncentrosymmetric superconductors,” Physical Review B 105 (13), 134514.
- Kaur et al. (2005) Kaur, R P, D F Agterberg, and M Sigrist (2005), “Helical vortex phase in the noncentrosymmetric CePt3Si,” Physical Review Letters 94 (13), 137002.
- Kibune et al. (2022) Kibune, Mayu, Shunsaku Kitagawa, Katsuki Kinjo, Shiki Ogata, Masahiro Manago, Takanori Taniguchi, Kenji Ishida, Manuel Brando, Elena Hassinger, Helge Rosner, Christoph Geibel, and Seunghyun Khim (2022), “Observation of antiferromagnetic order as odd-parity multipoles inside the superconducting phase in CeRh2As2,” Physical Review Letters 128 (5), 057002.
- Kim et al. (2017) Kim, Kun Woo, Takahiro Morimoto, and Naoto Nagaosa (2017), “Shift charge and spin photocurrents in dirac surface states of topological insulator,” Physical Eeview B 95 (3), 035134.
- Kimata et al. (2019) Kimata, Motoi, Hua Chen, Kouta Kondou, Satoshi Sugimoto, Prasanta K Muduli, Muhammad Ikhlas, Yasutomo Omori, Takahiro Tomita, Allan H MacDonald, Satoru Nakatsuji, and Yoshichika Otani (2019), “Magnetic and magnetic inverse spin hall effects in a non-collinear antiferromagnet,” Nature 565 (7741), 627–630.
- Kimata et al. (2021) Kimata, Motoi, Norimasa Sasabe, Kensuke Kurita, Yuichi Yamasaki, Chihiro Tabata, Yuichi Yokoyama, Yoshinori Kotani, Muhammad Ikhlas, Takahiro Tomita, Kenta Amemiya, Hiroyuki Nojiri, Satoru Nakatsuji, Takashi Koretsune, Hironori Nakao, Taka-Hisa Arima, and Tetsuya Nakamura (2021), “X-ray study of ferroic octupole order producing anomalous hall effect,” Nature Communications 12 (1), 5582.
- Kimura et al. (2003) Kimura, T, T Goto, H Shintani, K Ishizaka, T Arima, and Y Tokura (2003), “Magnetic control of ferroelectric polarization,” Nature 426 (6962), 55–58.
- Kitagawa et al. (2022) Kitagawa, Shunsaku, Mayu Kibune, Katsuki Kinjo, Masahiro Manago, Takanori Taniguchi, Kenji Ishida, Manuel Brando, Elena Hassinger, Christoph Geibel, and Seunghyun Khim (2022), “Two-dimensional XY-type magnetic properties of locally noncentrosymmetric superconductor CeRh2As2,” Journal of the Physical Society of Japan 91 (4).
- Kitamura et al. (2021) Kitamura, Taisei, Jun Ishizuka, Akito Daido, and Youichi Yanase (2021), “Thermodynamic electric quadrupole moments of nematic phases from first-principles calculations,” Physical Review B 103, 245114.
- Kitamura et al. (2023) Kitamura, Taisei, Shota Kanasugi, Michiya Chazono, and Youichi Yanase (2023), “Quantum geometry induced anapole superconductivity,” Physical Review B 107 (21), 214513.
- Kocsis et al. (2018) Kocsis, Vilmos, Karlo Penc, Toomas Rõõm, Urmas Nagel, Jakub Vít, Judit Romhányi, Yusuke Tokunaga, Yasujiro Taguchi, Yoshinori Tokura, István Kézsmárki, and Sándor Bordács (2018), “Identification of antiferromagnetic domains via the optical magnetoelectric effect,” Physical Review Letters 121 (5), 057601.
- Kofuji et al. (2021) Kofuji, Akira, Yoshihiro Michishita, and Robert Peters (2021), “Effects of strong correlations on the nonlinear response in Weyl-Kondo semimetals,” Physical Review B 104 (8), 085151.
- Kosub et al. (2017) Kosub, Tobias, Martin Kopte, Ruben Hühne, Patrick Appel, Brendan Shields, Patrick Maletinsky, René Hübner, Maciej Oskar Liedke, Jürgen Fassbender, Oliver G Schmidt, and Denys Makarov (2017), “Purely antiferromagnetic magnetoelectric random access memory,” Nature Communications 8, 13985.
- Kosub et al. (2015) Kosub, Tobias, Martin Kopte, Florin Radu, Oliver G Schmidt, and Denys Makarov (2015), “All-electric access to the magnetic-field-invariant magnetization of antiferromagnets,” Physical Review Letters 115 (9), 097201.
- Krempaský et al. (2016) Krempaský, J, S Muff, F Bisti, M Fanciulli, H Volfová, A P Weber, N Pilet, P Warnicke, H Ebert, J Braun, F Bertran, V V Volobuev, J Minár, G Springholz, J H Dil, and V N Strocov (2016), “Entanglement and manipulation of the magnetic and spin-orbit order in multiferroic rashba semiconductors,” Nature Communications 7 (1), 1–7.
- Kristoffel (1985) Kristoffel, N (1985), “On the possibility of anomalous bulk photovoltaic effect and of induced absorption in the nominal transparency region of a noncentrosymmetric crystal in a magnetic field,” Physica status solidi. B, Basic research 127 (1), 413–418.
- Krstić et al. (2002) Krstić, V, S Roth, M Burghard, K Kern, and G L J A Rikken (2002), “Magneto-chiral anisotropy in charge transport through single-walled carbon nanotubes,” The Journal of Chemical Physics 117 (24), 11315–11319.
- Kuramoto et al. (2009) Kuramoto, Yoshio, Hiroaki Kusunose, and Annamária Kiss (2009), “Multipole orders and fluctuations in strongly correlated electron systems,” Journal of the Physical Society of Japan 78 (7), 072001.
- Kusunose (2008) Kusunose, Hiroaki (2008), “Description of multipole in f-electron systems,” Journal of the Physical Society of Japan 77 (6), 064710.
- Landolt et al. (2012) Landolt, Gabriel, Sergey V Eremeev, Yury M Koroteev, Bartosz Slomski, Stefan Muff, Titus Neupert, Masaki Kobayashi, Vladimir N Strocov, Thorsten Schmitt, Ziya S Aliev, Mahammad B Babanly, Imamaddin R Amiraslanov, Evgueni V Chulkov, Jürg Osterwalder, and J Hugo Dil (2012), “Disentanglement of surface and bulk rashba spin splittings in noncentrosymmetric BiTeI,” Physical Review Letters 109 (11), 116403.
- Lehmann et al. (2020) Lehmann, Jannis, Amadé Bortis, Peter M Derlet, Claire Donnelly, Naëmi Leo, Laura J Heyderman, and Manfred Fiebig (2020), “Relation between microscopic interactions and macroscopic properties in ferroics,” Nature Nanotechnology 15 (11), 896–900.
- Lehmann et al. (2019) Lehmann, Jannis, Claire Donnelly, Peter M Derlet, Laura J Heyderman, and Manfred Fiebig (2019), “Poling of an artificial magneto-toroidal crystal,” Nature Nanotechnology 14 (2), 141–144.
- Levitov et al. (1985) Levitov, L S, Yu V Nazarov, and G M Eliashberg (1985), “Magnetoelectric effects in conductors with mirror isomer symmetry,” Soviet Physics, Journal of Experimental and Theoretical Physics 61 (1), 133, ibid., Zh. Exp. Teor. Fiz. 88, 229 (1985).
- Li et al. (2021) Li, Yan, Yang Li, Peng Li, Bin Fang, Xu Yang, Yan Wen, Dong-Xing Zheng, Chen-Hui Zhang, Xin He, Aurélien Manchon, Zhao-Hua Cheng, and Xi-Xiang Zhang (2021), “Nonreciprocal charge transport up to room temperature in bulk rashba semiconductor -GeTe,” Nature Communications 12 (1), 540.
- Lim et al. (2020) Lim, Sejoon, Chandra M Varma, Hiroshi Eisaki, and Aharon Kapitulnik (2020), “Observation of broken inversion and chiral symmetries in the pseudogap phase in single and double layer bismuth-based cuprates,” .
- Lin et al. (2020) Lin, Zuzhang, Chong Wang, Yong Xu, and Wenhui Duan (2020), “Hidden physical effects in noncentrosymmetric crystals,” Physical Review B 102 (16), 165143.
- Linn et al. (2023) Linn, A Garrison, Peipei Hao, Kyle N Gordon, Dushyant Narayan, Bryan S Berggren, Nathaniel Speiser, Sonka Reimers, Richard P Campion, Vít Novák, Sarnjeet S Dhesi, Timur K Kim, Cephise Cacho, Libor Šmejkal, Tomáš Jungwirth, Jonathan D Denlinger, Peter Wadley, and Daniel S Dessau (2023), “Experimental electronic structure of the electrically switchable antiferromagnet CuMnAs,” npj Quantum Materials 8 (1), 1–8.
- Liu et al. (2021) Liu, Huiying, Jianzhou Zhao, Yue-Xin Huang, Weikang Wu, Xian-Lei Sheng, Cong Xiao, and Shengyuan A Yang (2021), “Intrinsic second-order anomalous hall effect and its application in compensated antiferromagnets,” Physical Review Letters 127 (27), 277202.
- Liu et al. (2020) Liu, Jing, Fengnian Xia, Di Xiao, F Javier García de Abajo, and Dong Sun (2020), “Semimetals for high-performance photodetection,” Nature Materials 19 (8), 830–837.
- Liu et al. (2013) Liu, Qihang, Yuzheng Guo, and Arthur J Freeman (2013), “Tunable rashba effect in two-dimensional LaOBiS2 films: ultrathin candidates for spin field effect transistors,” Nano Letters 13 (11), 5264–5270.
- Liu et al. (2015) Liu, Qihang, Xiuwen Zhang, Hosub Jin, Kanber Lam, Jino Im, Arthur J Freeman, and Alex Zunger (2015), “Search and design of nonmagnetic centrosymmetric layered crystals with large local spin polarization,” Physical Review B 91 (23), 235204.
- Liu et al. (2022) Liu, Yizhou, Hikaru Watanabe, and Naoto Nagaosa (2022), “Emergent magnetomultipoles and nonlinear responses of a magnetic hopfion,” Physical Review Letters 129 (26), 267201.
- Lux et al. (2020) Lux, Fabian R, Frank Freimuth, Stefan Blügel, and Yuriy Mokrousov (2020), “Chiral hall effect in noncollinear magnets from a cyclic cohomology approach,” Physical Review Letters 124 (9), 096602.
- Lytvynenko et al. (2023) Lytvynenko, Y, O Fedchenko, S V Chernov, S Babenkov, D Vasilyev, O Tkach, A Gloskovskii, T R F Peixoto, C Schlueter, V Grigorev, M Filianina, S Sobolev, A Kleibert, M Kläui, J Demsar, G Schönhense, M Jourdan, and H J Elmers (2023), “Control of the asymmetric band structure in Mn2Au by a ferromagnetic driver layer,” Physical Review B 108 (10), 104413.
- Ma et al. (2023a) Ma, Da, Arpit Arora, Giovanni Vignale, and Justin C W Song (2023a), “Anomalous skew-scattering nonlinear hall effect and chiral photocurrents in -symmetric antiferromagnets,” Physical Review Letters 131 (7), 076601.
- Ma et al. (2021) Ma, Qiong, Adolfo G Grushin, and Kenneth S Burch (2021), “Topology and geometry under the nonlinear electromagnetic spotlight,” Nature Materials 20 (12), 1601–1614.
- Ma et al. (2023b) Ma, Qiong, Roshan Krishna Kumar, Su-Yang Xu, Frank H L Koppens, and Justin C W Song (2023b), “Photocurrent as a multiphysics diagnostic of quantum materials,” Nature Reviews Physics 5 (3), 170–184.
- Ma et al. (2017) Ma, Qiong, Su-Yang Xu, Ching-Kit Chan, Cheng-Long Zhang, Guoqing Chang, Yuxuan Lin, Weiwei Xie, Tomás Palacios, Hsin Lin, Shuang Jia, Patrick A Lee, Pablo Jarillo-Herrero, and Nuh Gedik (2017), “Direct optical detection of weyl fermion chirality in a topological semimetal,” Nature Physics 13 (9), 842–847.
- Ma et al. (2019) Ma, Qiong, Su-Yang Xu, Huitao Shen, David MacNeill, Valla Fatemi, Tay-Rong Chang, Andrés M Mier Valdivia, Sanfeng Wu, Zongzheng Du, Chuang-Han Hsu, Shiang Fang, Quinn D Gibson, Kenji Watanabe, Takashi Taniguchi, Robert J Cava, Efthimios Kaxiras, Hai-Zhou Lu, Hsin Lin, Liang Fu, Nuh Gedik, and Pablo Jarillo-Herrero (2019), “Observation of the nonlinear hall effect under time-reversal-symmetric conditions,” Nature 565 (7739), 337–342.
- Manchon et al. (2019) Manchon, A, J Železný, I M Miron, T Jungwirth, J Sinova, A Thiaville, K Garello, and P Gambardella (2019), “Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems,” Reviews of Modern Physics 91 (3), 035004.
- Marti et al. (2014) Marti, X, I Fina, C Frontera, Jian Liu, P Wadley, Q He, R J Paull, J D Clarkson, J Kudrnovský, I Turek, J Kuneš, D Yi, J-H Chu, C T Nelson, L You, E Arenholz, S Salahuddin, J Fontcuberta, T Jungwirth, and R Ramesh (2014), “Room-temperature antiferromagnetic memory resistor,” Nature Materials 13 (4), 367–374.
- Maruyama et al. (2012) Maruyama, Daisuke, Manfred Sigrist, and Youichi Yanase (2012), “Locally non-centrosymmetric superconductivity in multilayer systems,” Journal of the Physical Society of Japan 81 (3), 034702.
- Masuda et al. (2016) Masuda, Hidetoshi, Hideaki Sakai, Masashi Tokunaga, Yuichi Yamasaki, Atsushi Miyake, Junichi Shiogai, Shintaro Nakamura, Satoshi Awaji, Atsushi Tsukazaki, Hironori Nakao, Youichi Murakami, Taka-Hisa Arima, Yoshinori Tokura, and Shintaro Ishiwata (2016), “Quantum hall effect in a bulk antiferromagnet EuMnBi2 with magnetically confined two-dimensional dirac fermions,” Science advances 2 (1), e1501117.
- Matsubara et al. (2022) Matsubara, Masakazu, Takatsugu Kobayashi, Hikaru Watanabe, Youichi Yanase, Satoshi Iwata, and Takeshi Kato (2022), “Polarization-controlled tunable directional spin-driven photocurrents in a magnetic metamaterial with threefold rotational symmetry,” Nature Communications 13 (1), 6708.
- Matsyshyn and Sodemann (2019) Matsyshyn, O, and I Sodemann (2019), “Nonlinear hall acceleration and the quantum rectification sum rule,” Physical Review Letters 123 (24), 246602.
- Matsyshyn et al. (2023) Matsyshyn, Oles, Justin C W Song, Inti Sodemann Villadiego, and Li-Kun Shi (2023), “Fermi-Dirac staircase occupation of floquet bands and current rectification inside the optical gap of metals: An exact approach,” Physical Review B 107 (19), 195135.
- Men’shenin and Turov (2000) Men’shenin, V V, and E A Turov (2000), “The antiferromagnetic photovoltaic effect,” JETP letters 72 (1), 14–17, ibid., Pis’ma v Zhurnal Éksperimentalnol̆i Teoreticheskol̆ Fiziki 72, 23-27 (2000).
- Merte et al. (2023) Merte, M, F Freimuth, D Go, T Adamantopoulos, F R Lux, L Plucinski, O Gomonay, S Blügel, and Y Mokrousov (2023), “Photocurrents, inverse Faraday effect, and photospin Hall effect in Mn2Au,” APL materials 11 (7), 071106.
- Michishita and Nagaosa (2022) Michishita, Yoshihiro, and Naoto Nagaosa (2022), “Dissipation and geometry in nonlinear quantum transports of multiband electronic systems,” Physical Review B 106 (12), 125114.
- Michishita and Peters (2021) Michishita, Yoshihiro, and Robert Peters (2021), “Effects of renormalization and non-hermiticity on nonlinear responses in strongly correlated electron systems,” Physical Review B 103 (19), 195133.
- Momma and Izumi (2011) Momma, Koichi, and Fujio Izumi (2011), “VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data,” Journal of applied crystallography 44 (6), 1272–1276.
- Mook et al. (2020) Mook, Alexander, Robin R Neumann, Annika Johansson, Jürgen Henk, and Ingrid Mertig (2020), “Origin of the magnetic spin Hall effect: Spin current vorticity in the Fermi sea,” Physical Review Research 2 (2), 023065.
- Moore and Orenstein (2010) Moore, J E, and J Orenstein (2010), “Confinement-induced berry phase and helicity-dependent photocurrents,” Physical Review Letters 105 (2), 026805.
- Morimoto et al. (2023) Morimoto, Takahiro, Sota Kitamura, and Naoto Nagaosa (2023), “Geometric aspects of nonlinear and nonequilibrium phenomena,” Journal of the Physical Society of Japan 92 (7), 072001.
- Morimoto and Nagaosa (2016a) Morimoto, Takahiro, and Naoto Nagaosa (2016a), “Chiral Anomaly and Giant Magnetochiral Anisotropy in Noncentrosymmetric Weyl Semimetals,” Physical review letters 117 (14), 146603.
- Morimoto and Nagaosa (2016b) Morimoto, Takahiro, and Naoto Nagaosa (2016b), “Topological nature of nonlinear optical effects in solids,” Science Advances 2 (5), e1501524.
- Morimoto and Nagaosa (2018) Morimoto, Takahiro, and Naoto Nagaosa (2018), “Nonreciprocal current from electron interactions in noncentrosymmetric crystals: roles of time reversal symmetry and dissipation,” Scientific Reports 8 (1), 2973.
- Morimoto and Nagaosa (2019) Morimoto, Takahiro, and Naoto Nagaosa (2019), “Shift current from electromagnon excitations in multiferroics,” Physical Review B 100 (23), 235138.
- Morimoto and Nagaosa (2020) Morimoto, Takahiro, and Naoto Nagaosa (2020), “Photocurrent of exciton polaritons,” Physical Rview B 102 (23), 235139.
- Moriyama et al. (2018) Moriyama, Takahiro, Kent Oda, Takuo Ohkochi, Motoi Kimata, and Teruo Ono (2018), “Spin torque control of antiferromagnetic moments in NiO,” Scientific Reports 8 (1), 14167.
- Murakawa et al. (2013) Murakawa, H, M S Bahramy, M Tokunaga, Y Kohama, C Bell, Y Kaneko, N Nagaosa, H Y Hwang, and Y Tokura (2013), “Detection of Berry’s phase in a Bulk Rashba semiconductor,” Science 342 (6165), 1490–1493.
- Murayama et al. (2021) Murayama, H, K Ishida, R Kurihara, T Ono, Y Sato, Y Kasahara, H Watanabe, Y Yanase, G Cao, Y Mizukami, T Shibauchi, Y Matsuda, and S Kasahara (2021), “Bond directional anapole order in a Spin-Orbit coupled mott insulator Sr2Ir1-xRhxO4,” Physical Review X 11 (1), 011021.
- Nadeem et al. (2023) Nadeem, Muhammad, Michael S Fuhrer, and Xiaolin Wang (2023), “The superconducting diode effect,” Nature Reviews Physics 5 (10), 558–577.
- Nagaosa and Morimoto (2017) Nagaosa, Naoto, and Takahiro Morimoto (2017), “Concept of quantum geometry in optoelectronic processes in solids: Application to solar cells,” Advanced materials) 29 (25).
- Nagaosa et al. (2010) Nagaosa, Naoto, Jairo Sinova, Shigeki Onoda, A H MacDonald, and N P Ong (2010), “Anomalous hall effect,” Reviews of Modern Physics 82 (2), 1539–1592.
- Nagaosa and Yanase (2024) Nagaosa, Naoto, and Youichi Yanase (2024), “Nonreciprocal transport and optical phenomena in quantum materials,” Annual Review of Condensed Matter Physics 15 (1).
- Nakamura et al. (2020) Nakamura, Sachiko, Kota Katsumi, Hirotaka Terai, and Ryo Shimano (2020), “Nonreciprocal terahertz second-harmonic generation in superconducting NbN under supercurrent injection,” Physical Review Letters 125 (9), 097004.
- Nakamura and Yanase (2017) Nakamura, Yasuharu, and Youichi Yanase (2017), “Odd-parity superconductivity in bilayer transition metal dichalcogenides,” Physical Review B 96 (5), 054501.
- Nakatsuji and Arita (2022) Nakatsuji, Satoru, and Ryotaro Arita (2022), “Topological magnets: Functions based on berry phase and multipoles,” Annual Review of Condensed Matter Physics 13 (1), 119–142.
- Nakatsuji et al. (2015) Nakatsuji, Satoru, Naoki Kiyohara, and Tomoya Higo (2015), “Large anomalous hall effect in a non-collinear antiferromagnet at room temperature,” Nature 527 (7577), 212–215.
- Nandy and Sodemann (2019) Nandy, S, and Inti Sodemann (2019), “Symmetry and quantum kinetics of the nonlinear hall effect,” Physical Review B 100 (19), 195117.
- Nayak et al. (2016) Nayak, Ajaya K, Julia Erika Fischer, Yan Sun, Binghai Yan, Julie Karel, Alexander C Komarek, Chandra Shekhar, Nitesh Kumar, Walter Schnelle, Jürgen Kübler, Claudia Felser, and Stuart S P Parkin (2016), “Large anomalous hall effect driven by a nonvanishing berry curvature in the noncolinear antiferromagnet Mn3Ge,” Science Advances 2 (4), e1501870.
- Niu et al. (2017) Niu, Q, W. C. Yu, K. Y. Yip, Z. L. Lim, H. Kotegawa, E. Matsuoka, H. Sugawara, H. Tou, Y. Yanase, and Swee K. Goh (2017), “Quasilinear quantum magnetoresistance in pressure-induced nonsymmorphic superconductor chromium arsenide,” Nature Communications 8 (1), 15358.
- Nomoto and Arita (2020) Nomoto, Takuya, and Ryotaro Arita (2020), “Cluster multipole dynamics in noncollinear antiferromagnets,” Physical Review Research 2 (1), 012045.
- Ogasawara et al. (2021) Ogasawara, Takuma, Kim-Khuong Huynh, Time Tahara, Takanori Kida, Masayuki Hagiwara, Denis Arčon, Motoi Kimata, Stephane Yu Matsushita, Kazumasa Nagata, and Katsumi Tanigaki (2021), “Large negative magnetoresistance in the antiferromagnet BaMn2Bi2,” Physical Review B 103 (12), 125108.
- Ohashi and Momoi (1996) Ohashi, Yoji, and Tsutomu Momoi (1996), “On the bloch theorem concerning spontaneous electric current,” Journal of the Physical Society of Japan 65 (10), 3254–3259.
- Oiwa and Kusunose (2022) Oiwa, Rikuto, and Hiroaki Kusunose (2022), “Systematic analysis method for nonlinear response tensors,” Journal of the Physical Society of Japan 91 (1), 014701.
- Okamura et al. (2022) Okamura, Yoshihiro, Takahiro Morimoto, Naoki Ogawa, Yoshio Kaneko, Guang-Yu Guo, Masao Nakamura, Masashi Kawasaki, Naoto Nagaosa, Yoshinori Tokura, and Youtarou Takahashi (2022), “Photovoltaic effect by soft phonon excitation,” Proceedings of the National Academy of Sciences of the United States of America 119 (14), e2122313119.
- Okumura et al. (2021) Okumura, Shun, Takahiro Morimoto, Yasuyuki Kato, and Yukitoshi Motome (2021), “Quadratic optical responses in a chiral magnet,” Physical Review B 104 (18), L180407.
- Olbrich et al. (2014) Olbrich, P, L E Golub, T Herrmann, S N Danilov, H Plank, V V Bel’kov, G Mussler, Ch Weyrich, C M Schneider, J Kampmeier, D Grützmacher, L Plucinski, M Eschbach, and S D Ganichev (2014), “Room-temperature high-frequency transport of dirac fermions in epitaxially grown Sb2Te3- and Bi2Te3-based topological insulators,” Physical Review Letters 113 (9), 096601.
- Olejník et al. (2017) Olejník, K, V Schuler, X Marti, V Novák, Z Kašpar, P Wadley, R P Campion, K W Edmonds, B L Gallagher, J Garces, M Baumgartner, P Gambardella, and T Jungwirth (2017), “Antiferromagnetic CuMnAs multi-level memory cell with microelectronic compatibility,” Nature Communications 8 (1), 15434.
- Onishi et al. (2022) Onishi, Yugo, Hikaru Watanabe, Takahiro Morimoto, and Naoto Nagaosa (2022), “Effects of relaxation on the photovoltaic effect and possibility for photocurrent within the transparent region,” Physical Review B 106 (23), 235110.
- Onoda et al. (2008) Onoda, Shigeki, Naoyuki Sugimoto, and Naoto Nagaosa (2008), “Quantum transport theory of anomalous electric, thermoelectric, and thermal hall effects in ferromagnets,” Physical Review B 77 (16), 165103.
- Orenstein et al. (2021) Orenstein, J, J E Moore, T Morimoto, D H Torchinsky, J W Harter, and D Hsieh (2021), “Topology and symmetry of quantum materials via nonlinear optical responses,” Annual Review of Condensed Matter Physics 12 (1), 247–272.
- Ota et al. (2022) Ota, K, M Shimozawa, T Muroya, T Miyamoto, S Hosoi, A Nakamura, Y Homma, F Honda, D Aoki, and K Izawa (2022), “Zero-field current-induced hall effect in ferrotoroidic metal,” arXiv:2205.05555 [cond-mat.str-el] .
- Park et al. (2011) Park, B G, J Wunderlich, X Martí, V Holý, Y Kurosaki, M Yamada, H Yamamoto, A Nishide, J Hayakawa, H Takahashi, A B Shick, and T Jungwirth (2011), “A spin-valve-like magnetoresistance of an antiferromagnet-based tunnel junction,” Nature Materials 10 (5), 347–351.
- Pershoguba et al. (2021) Pershoguba, Sergey S, Domenico Andreoli, and Jiadong Zang (2021), “Electronic scattering off a magnetic hopfion,” Physical Review B 104 (7), 075102.
- Pershoguba and Yakovenko (2022) Pershoguba, Sergey S, and Victor M Yakovenko (2022), “Direct current in a stirred optical lattice,” Annals of Physics 447, 169075.
- Peters and Yanase (2018) Peters, Robert, and Youichi Yanase (2018), “Strong enhancement of the edelstein effect in -electron systems,” Physical Review B 97 (11), 115128.
- Plank et al. (2016) Plank, H, L. E. Golub, S. Bauer, V. V. Bel’kov, T. Herrmann, P. Olbrich, M. Eschbach, L. Plucinski, C. M. Schneider, J. Kampmeier, M. Lanius, G. Mussler, D. Grützmacher, and S. D. Ganichev (2016), “Photon drag effect in three-dimensional topological insulators,” Physical Review B 93, 125434.
- Plank et al. (2018) Plank, H, J Pernul, S Gebert, S N Danilov, J König-Otto, S Winnerl, M Lanius, J Kampmeier, G Mussler, I Aguilera, D Grützmacher, and S D Ganichev (2018), “Infrared/terahertz spectra of the photogalvanic effect in (bi,sb)te based three-dimensional topological insulators,” Physical Review Materials 2 (2), 024202.
- Pusch et al. (2023) Pusch, Andreas, Udo Römer, Dimitrie Culcer, and Nicholas J Ekins-Daukes (2023), “Energy conversion efficiency of the bulk photovoltaic effect,” PRX Energy 2 (1), 013006.
- Ramires and Sigrist (2016) Ramires, Aline, and Manfred Sigrist (2016), “Identifying detrimental effects for multiorbital superconductivity: Application to sr2ruo4,” Physical Review B 94 (10), 104501.
- Razzoli et al. (2017) Razzoli, E, T Jaouen, M-L Mottas, B Hildebrand, G Monney, A Pisoni, S Muff, M Fanciulli, N C Plumb, V A Rogalev, V N Strocov, J Mesot, M Shi, J H Dil, H Beck, and P Aebi (2017), “Selective probing of hidden spin-polarized states in inversion-symmetric bulk MoS2,” Physical Review Letters 118 (8), 086402.
- Rees et al. (2020) Rees, Dylan, Kaustuv Manna, Baozhu Lu, Takahiro Morimoto, Horst Borrmann, Claudia Felser, J E Moore, Darius H Torchinsky, and J Orenstein (2020), “Helicity-dependent photocurrents in the chiral weyl semimetal RhSi,” Science Advances 6 (29), eaba0509.
- Reichlová et al. (2015) Reichlová, H, D Kriegner, V Holý, K Olejník, V Novák, M Yamada, K Miura, S Ogawa, H Takahashi, T Jungwirth, and J Wunderlich (2015), “Current-induced torques in structures with ultrathin IrMn antiferromagnets,” Physical Review B 92 (16), 165424.
- Rikken et al. (2001) Rikken, G L, J Fölling, and P Wyder (2001), “Electrical magnetochiral anisotropy,” Physical Review Letters 87 (23), 236602.
- Rikken and Wyder (2005) Rikken, G L J A, and P Wyder (2005), “Magnetoelectric anisotropy in diffusive transport,” Physical Review Letters 94 (1), 016601.
- Riley et al. (2014) Riley, J M, F Mazzola, M Dendzik, M Michiardi, T Takayama, L Bawden, C Granerød, M Leandersson, T Balasubramanian, M Hoesch, T K Kim, H Takagi, W Meevasana, Ph Hofmann, M S Bahramy, J W Wells, and P D C King (2014), “Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor,” Nature Physics 10 (11), 835–839.
- Rischau et al. (2017) Rischau, Carl Willem, Xiao Lin, Christoph P Grams, Dennis Finck, Steffen Harms, Johannes Engelmayer, Thomas Lorenz, Yann Gallais, Benoît Fauqué, Joachim Hemberger, and Kamran Behnia (2017), “A ferroelectric quantum phase transition inside the superconducting dome of Sr1-xCaxTiO3-δ,” Nature Physics 13 (7), 643–648.
- Saidl et al. (2017) Saidl, V, P Němec, P Wadley, V Hills, R P Campion, V Novák, K W Edmonds, F Maccherozzi, S S Dhesi, B L Gallagher, F Trojánek, J Kuneš, J Železný, P Malý, and T Jungwirth (2017), “Optical determination of the néel vector in a CuMnAs thin-film antiferromagnet,” Nature Photonics 11 (2), 91–96.
- Saito et al. (2018) Saito, Hiraku, Kenta Uenishi, Naoyuki Miura, Chihiro Tabata, Hiroyuki Hidaka, Tatsuya Yanagisawa, and Hiroshi Amitsuka (2018), “Evidence of a new Current-Induced magnetoelectric effect in a toroidal magnetic ordered state of UNi4B,” Journal of the Physical Society of Japan 87 (3), 033702.
- Sakai (2022) Sakai, Hideaki (2022), “High-field studies on layered magnetic and polar dirac metals: Novel quantum transport phenomena coupled with spin-valley degrees of freedom,” Journal of the Physical Society of Japan 91 (10).
- Sano et al. (2021) Sano, Ryotaro, Riki Toshio, and Norio Kawakami (2021), “Nonreciprocal electron hydrodynamics under magnetic fields: Applications to nonreciprocal surface magnetoplasmons,” Physical Review B 104 (24), L241106.
- Santos-Cottin et al. (2016) Santos-Cottin, David, Michele Casula, Gabriel Lantz, Yannick Klein, Luca Petaccia, Patrick Le Fèvre, François Bertran, Evangelos Papalazarou, Marino Marsi, and Andrea Gauzzi (2016), “Rashba coupling amplification by a staggered crystal field,” Nature Communications 7, 11258.
- Sapozhnik et al. (2018) Sapozhnik, A A, M Filianina, S Yu Bodnar, A Lamirand, M-A Mawass, Y Skourski, H-J Elmers, H Zabel, M Kläui, and M Jourdan (2018), “Direct imaging of antiferromagnetic domains in mn 2 au manipulated by high magnetic fields,” Physical Review B 97 (13), 134429.
- Schmid (1973) Schmid, Hans (1973), “On a magnetoelectric classification of materials,” Int. J. Magn 4 (337-361), 2.
- Schrieffer (1964) Schrieffer, J Robert (1964), Theory of superconductivity (Westview Press).
- Seyler et al. (2020) Seyler, K L, A de la Torre, Z Porter, E Zoghlin, R Polski, M Nguyen, S Nadj-Perge, S D Wilson, and D Hsieh (2020), “Spin-orbit-enhanced magnetic surface second-harmonic generation in Sr2IrO4,” Physical Review B 102 (20), 201113.
- Shao et al. (2020) Shao, Ding-Fu, Shu-Hui Zhang, Gautam Gurung, Wen Yang, and Evgeny Y. Tsymbal (2020), “Nonlinear anomalous hall effect for néel vector detection,” Physical Review Letters 124, 067203.
- Shi et al. (2023) Shi, Li-Kun, Oles Matsyshyn, Justin C W Song, and Inti Sodemann Villadiego (2023), “Berry-dipole photovoltaic demon and the thermodynamics of photocurrent generation within the optical gap of metals,” Physical Review B 107 (12), 125151.
- Shi et al. (2024) Shi, Li-Kun, Oles Matsyshyn, Justin C W Song, and Inti Sodemann Villadiego (2024), “Floquet Fermi liquid,” Physical Review Letters 132 (14), 146402.
- Shick et al. (2010) Shick, A B, S Khmelevskyi, O N Mryasov, J Wunderlich, and T Jungwirth (2010), “Spin-orbit coupling induced anisotropy effects in bimetallic antiferromagnets: A route towards antiferromagnetic spintronics,” Physical Review B 81 (21), 212409.
- Shimozawa et al. (2016) Shimozawa, Masaaki, Swee K Goh, Takasada Shibauchi, and Yuji Matsuda (2016), “From kondo lattices to kondo superlattices,” Reports on Progress in Physics 79 (7), 074503.
- Shinada and Peters (2023) Shinada, Koki, and Robert Peters (2023), “Orbital gravitomagnetoelectric response and orbital magnetic quadrupole moment correction,” Physical Review B 107, 214109.
- Shiomi et al. (2019a) Shiomi, Y, Y Koike, N Abe, H Watanabe, and T Arima (2019a), “Enhanced magnetopiezoelectric effect at the néel temperature in camn2bi2,” Physical Review B 100 (5), 054424.
- Shiomi et al. (2019b) Shiomi, Y, H Watanabe, H Masuda, H Takahashi, Y Yanase, and S Ishiwata (2019b), “Observation of a magnetopiezoelectric effect in the antiferromagnetic metal EuMnBi2,” Physical Review Letters 122 (12), 127207.
- Shiomi et al. (2020) Shiomi, Yuki, Hidetoshi Masuda, Hidefumi Takahashi, and Shintaro Lshiwata (2020), “Large magneto-piezoelectric effect in EuMnBi2 single crystal at low temperatures,” Scientific Reports 10 (1), 7574.
- Shitade et al. (2019) Shitade, Atsuo, Akito Daido, and Youichi Yanase (2019), “Theory of spin magnetic quadrupole moment and temperature-gradient-induced magnetization,” Physical Review B 99 (2), 024404.
- Shitade and Tatara (2022) Shitade, Atsuo, and Gen Tatara (2022), “Spin accumulation without spin current,” Physical Review B 105 (20), L201202.
- Shitade et al. (2018) Shitade, Atsuo, Hikaru Watanabe, and Youichi Yanase (2018), “Theory of orbital magnetic quadrupole moment and magnetoelectric susceptibility,” Physical Review B 98 (2), 020407.
- Shull and Samuel Smart (1949) Shull, C G, and J Samuel Smart (1949), “Detection of antiferromagnetism by neutron diffraction,” Physical Review 76 (8), 1256.
- Sigrist (2005) Sigrist, Manfred (2005), “Review on the Chiral -Wave Phase of Sr2RuO4,” Progress of Theoretical Physics Supplement 160, 1–14.
- Sigrist et al. (2014) Sigrist, Manfred, Daniel F Agterberg, Mark H Fischer, Jun Goryo, Florian Loder, Sung-Hyon Rhim, Daisuke Maruyama, Youichi Yanase, Tomohiro Yoshida, and Suk Joo Youn (2014), “Superconductors with staggered non-centrosymmetricity,” Journal of the Physical Society of Japan 83 (6), 061014.
- Sigrist and Ueda (1991) Sigrist, Manfred, and Kazuo Ueda (1991), “Phenomenological theory of unconventional superconductivity,” Reviews of Modern Physics 63 (2), 239–311.
- Sinitsyn (2008) Sinitsyn, N A (2008), “Semiclassical theories of the anomalous Hall effect,” Journal of Physics: Condensed Matter 20 (2), 023201.
- Sinova et al. (2015) Sinova, Jairo, Sergio O Valenzuela, J Wunderlich, C H Back, and T Jungwirth (2015), “Spin hall effects,” Reviews of Modern Physics 87 (4), 1213–1260.
- Sipe and Shkrebtii (2000) Sipe, J E, and A I Shkrebtii (2000), “Second-order optical response in semiconductors,” Physical Review B 61 (8), 5337–5352.
- Siratori et al. (1992) Siratori, K, K Kohn, and E Kita (1992), “Magnetoelectric effect in magnetic materials,” Acta Physica Polonica A 81 (4-5), 431–466.
- Šmejkal et al. (2018) Šmejkal, Libor, Yuriy Mokrousov, Binghai Yan, and Allan H MacDonald (2018), “Topological antiferromagnetic spintronics,” Nature Physics 14 (3), 242–251.
- Smidman et al. (2017) Smidman, M, M B Salamon, H Q Yuan, and D F Agterberg (2017), “Superconductivity and spin-orbit coupling in non-centrosymmetric materials: a review,” Reports on Progress in Physics 80 (3), 036501.
- Sodemann and Fu (2015) Sodemann, Inti, and Liang Fu (2015), “Quantum nonlinear hall effect induced by berry curvature dipole in Time-Reversal invariant materials,” Physical Review Letters 115 (21), 216806.
- Song et al. (2021) Song, Tiancheng, Eric Anderson, Matisse Wei-Yuan Tu, Kyle Seyler, Takashi Taniguchi, Kenji Watanabe, Michael A McGuire, Xiaosong Li, Ting Cao, Di Xiao, Wang Yao, and Xiaodong Xu (2021), “Spin photovoltaic effect in magnetic van der waals heterostructures,” Science Advances 7 (36), eabg8094.
- Sotome et al. (2019a) Sotome, M, M Nakamura, J Fujioka, M Ogino, Y Kaneko, T Morimoto, Y Zhang, M Kawasaki, N Nagaosa, Y Tokura, and N Ogawa (2019a), “Spectral dynamics of shift current in ferroelectric semiconductor SbSI,” Proceedings of the National Academy of Sciences of the United States of America 116 (6), 1929–1933.
- Sotome et al. (2019b) Sotome, M, M Nakamura, J Fujioka, M Ogino, Y Kaneko, T Morimoto, Y Zhang, M Kawasaki, N Nagaosa, Y Tokura, and N Ogawa (2019b), “Ultrafast spectroscopy of shift-current in ferroelectric semiconductor Sn2P2S6,” Applied Physics Letters 114 (15), 151101.
- Sotome et al. (2021) Sotome, M, M Nakamura, T Morimoto, Y Zhang, G-Y Guo, M Kawasaki, N Nagaosa, Y Tokura, and N Ogawa (2021), “Terahertz emission spectroscopy of ultrafast exciton shift current in the noncentrosymmetric semiconductor CdS,” Physical Review B 103 (24), L241111.
- Spaldin et al. (2013) Spaldin, Nicola A, Michael Fechner, Eric Bousquet, Alexander Balatsky, and Lars Nordström (2013), “Monopole-based formalism for the diagonal magnetoelectric response,” Physical Review B 88 (9), 094429.
- Spaldin et al. (2008) Spaldin, Nicola A, Manfred Fiebig, and Maxim Mostovoy (2008), “The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect,” Journal of Physics: Condensed Matter 20 (43), 434203.
- Spanier et al. (2016) Spanier, Jonathan E, Vladimir M Fridkin, Andrew M Rappe, Andrew R Akbashev, Alessia Polemi, Yubo Qi, Zongquan Gu, Steve M Young, Christopher J Hawley, Dominic Imbrenda, Geoffrey Xiao, Andrew L Bennett-Jackson, and Craig L Johnson (2016), “Power conversion efficiency exceeding the Shockley–Queisser limit in a ferroelectric insulator,” Nature Photonics 10 (9), 611–616.
- Sturman (1992) Sturman, Paul J (1992), Photovoltaic and photo-refractive effects in noncentrosymmetric materials, 1st ed., Ferroelectricity and Related Phenomena (Taylor & Francis, London, England).
- Sumita et al. (2017) Sumita, Shuntaro, Takuya Nomoto, and Youichi Yanase (2017), “Multipole superconductivity in nonsymmorphic Sr2IrO4,” Physical Review Letters 119 (2), 027001.
- Sumita and Yanase (2016) Sumita, Shuntaro, and Youichi Yanase (2016), “Superconductivity in magnetic multipole states,” Physical Review B 93 (22), 224507.
- Sun et al. (2021) Sun, Z L, A F Wang, H M Mu, H H Wang, Z F Wang, T Wu, Z Y Wang, X Y Zhou, and X H Chen (2021), “Field-induced metal-to-insulator transition and colossal anisotropic magnetoresistance in a nearly dirac material EuMnSb2,” npj Quantum Materials 6 (1), 1–8.
- Surýnek et al. (2020) Surýnek, M, V Saidl, Z Kašpar, V Novák, R P Campion, P Wadley, and P Němec (2020), “Investigation of magnetic anisotropy and heat dissipation in thin films of compensated antiferromagnet CuMnAs by pump–probe experiment,” Journal of Applied Physics 127 (23), 233904.
- Suzuki et al. (2017) Suzuki, M-T, T Koretsune, M Ochi, and R Arita (2017), “Cluster multipole theory for anomalous Hall effect in antiferromagnets,” Physical Review B 95 (9), 094406.
- Suzuki et al. (2018) Suzuki, Michi-To, Hiroaki Ikeda, and Peter M Oppeneer (2018), “First-principles theory of magnetic multipoles in condensed matter systems,” Journal of the Physical Society of Japan 87 (4), 041008.
- Suzuki et al. (2023) Suzuki, Yuta, Yuma Kitagawa, Shin-Ichiro Tezuka, and Hiroshi Akera (2023), “Spin-current generation from local spin polarization induced by current through local inversion asymmetry: Double quantum well structure,” Physical Review B 107 (11), 115306.
- Szaller et al. (2013) Szaller, Dávid, Sándor Bordács, and István Kézsmárki (2013), “Symmetry conditions for nonreciprocal light propagation in magnetic crystals,” Physical Review B 87 (1), 014421.
- Sławińska et al. (2016) Sławińska, Jagoda, Awadhesh Narayan, and Silvia Picozzi (2016), “Hidden spin polarization in nonmagnetic centrosymmetric BaNiS2 crystal: Signatures from first principles,” Physical Review B 94 (24), 241114.
- Taguchi et al. (2016) Taguchi, Katsuhisa, Tatsushi Imaeda, Masatoshi Sato, and Yukio Tanaka (2016), “Photovoltaic chiral magnetic effect in weyl semimetals,” Physical Review B 93 (20), 201202.
- Tahir and Chen (2023) Tahir, Muhammad, and Hua Chen (2023), “Transport of Spin Magnetic Multipole Moments Carried by Bloch Quasiparticles,” Physical Review Letters 131 (10), 106701.
- Tanaka et al. (2023) Tanaka, Hiroto, Hikaru Watanabe, and Youichi Yanase (2023), “Nonlinear optical responses in noncentrosymmetric superconductors,” Physical Review B 107 (2), 024513.
- Tang et al. (2016) Tang, Peizhe, Quan Zhou, Gang Xu, and Shou-Cheng Zhang (2016), “Dirac fermions in an antiferromagnetic semimetal,” Nature Physics 12 (12), 1100–1104.
- Tanida et al. (2022) Tanida, Hiroshi, Hiroto Matsuoka, Keisuke Mitsumoto, Yuji Muro, Tadashi Fukuhara, and Hisatomo Harima (2022), “Nonsymmorphic antiferromagnet LaMnSi: Single-crystal studies,” Journal of the Physical Society of Japan 91 (1), 013704.
- Thöle et al. (2016) Thöle, Florian, Michael Fechner, and Nicola A Spaldin (2016), “First-principles calculation of the bulk magnetoelectric monopole density: Berry phase and wannier function approaches,” Physical Review B 93 (19), 195167.
- Thöle et al. (2020) Thöle, Florian, Andriani Keliri, and Nicola A Spaldin (2020), “Concepts from the linear magnetoelectric effect that might be useful for antiferromagnetic spintronics,” Journal of Applied Physics 127 (21), 213905.
- Tokura and Nagaosa (2018) Tokura, Yoshinori, and Naoto Nagaosa (2018), “Nonreciprocal responses from non-centrosymmetric quantum materials,” Nature Communications 9 (1), 3740.
- Tokura et al. (2014) Tokura, Yoshinori, Shinichiro Seki, and Naoto Nagaosa (2014), “Multiferroics of spin origin,” Reports on Progress in Physics 77 (7), 076501.
- Toshio and Kawakami (2022) Toshio, Riki, and Norio Kawakami (2022), “Plasmonic quantum nonlinear hall effect in noncentrosymmetric two-dimensional materials,” Physical Review B 106 (20), L201301.
- Toshio et al. (2020) Toshio, Riki, Kazuaki Takasan, and Norio Kawakami (2020), “Anomalous hydrodynamic transport in interacting noncentrosymmetric metals,” Physical Review Research 2 (3), 032021.
- Tu et al. (2020) Tu, J, X B Chen, X Z Ruan, Y F Zhao, H F Xu, Z D Chen, X Q Zhang, X W Zhang, J Wu, L He, Y Zhang, R Zhang, and Y B Xu (2020), “Direct observation of hidden spin polarization in -MoTe2,” Physical Review B 101 (3), 035102.
- Van Aken et al. (2007) Van Aken, Bas B, Jean-Pierre Rivera, Hans Schmid, and Manfred Fiebig (2007), “Observation of ferrotoroidic domains,” Nature 449 (7163), 702–705.
- Varjas et al. (2016) Varjas, Dániel, Adolfo G Grushin, Roni Ilan, and Joel E Moore (2016), “Dynamical piezoelectric and magnetopiezoelectric effects in polar metals from berry phases and orbital moments,” Physical Review Letters 117 (25), 257601.
- Vaswani et al. (2020) Vaswani, C, M Mootz, C Sundahl, D H Mudiyanselage, J H Kang, X Yang, D Cheng, C Huang, R H J Kim, Z Liu, L Luo, I E Perakis, C B Eom, and J Wang (2020), “Terahertz second-harmonic generation from lightwave acceleration of symmetry-breaking nonlinear supercurrents,” Physical Review Letters 124 (20), 207003.
- Ventura et al. (2017) Ventura, G B, D J Passos, J M B Lopes dos Santos, J M Viana Parente Lopes, and N M R Peres (2017), “Gauge covariances and nonlinear optical responses,” Physical Review B 96 (3), 035431.
- Wadley et al. (2015) Wadley, P, V Hills, M R Shahedkhah, K W Edmonds, R P Campion, V Novák, B Ouladdiaf, D Khalyavin, S Langridge, V Saidl, P Nemec, A W Rushforth, B L Gallagher, S S Dhesi, F Maccherozzi, J Železný, and T Jungwirth (2015), “Antiferromagnetic structure in tetragonal CuMnAs thin films,” Scientific Reports 5 (1), 17079.
- Wadley et al. (2016) Wadley, P, B Howells, J Železný, C Andrews, V Hills, R P Campion, V Novák, K Olejník, F Maccherozzi, S S Dhesi, S Y Martin, T Wagner, J Wunderlich, F Freimuth, Y Mokrousov, J Kuneš, J S Chauhan, M J Grzybowski, A W Rushforth, K W Edmonds, B L Gallagher, and T Jungwirth (2016), “Electrical switching of an antiferromagnet,” Science 351 (6273), 587–590.
- Wadley et al. (2018) Wadley, Peter, Sonka Reimers, Michal J Grzybowski, Carl Andrews, Mu Wang, Jasbinder S Chauhan, Bryan L Gallagher, Richard P Campion, Kevin W Edmonds, Sarnjeet S Dhesi, Francesco Maccherozzi, Vit Novak, Joerg Wunderlich, and Tomas Jungwirth (2018), “Current polarity-dependent manipulation of antiferromagnetic domains,” Nature Nanotechnology 13 (5), 362–365.
- Wakatsuki and Nagaosa (2018) Wakatsuki, Ryohei, and Naoto Nagaosa (2018), “Nonreciprocal Current in Noncentrosymmetric Rashba Superconductors,” Physical Review Letters 121 (2), 026601.
- Wakatsuki et al. (2017) Wakatsuki, Ryohei, Yu Saito, Shintaro Hoshino, Yuki M Itahashi, Toshiya Ideue, Motohiko Ezawa, Yoshihiro Iwasa, and Naoto Nagaosa (2017), “Nonreciprocal charge transport in noncentrosymmetric superconductors,” Science Advances 3 (4), e1602390.
- Wang et al. (2021) Wang, Chong, Yang Gao, and Di Xiao (2021), “Intrinsic nonlinear hall effect in antiferromagnetic tetragonal CuMnAs,” Physical Review Letters 127 (27), 277201.
- Wang et al. (2010) Wang, Jing, Bang-Fen Zhu, and Ren-Bao Liu (2010), “Second-order nonlinear optical effects of spin currents,” Physical Review Letters 104 (25), 256601.
- Wang et al. (2023) Wang, Naizhou, Daniel Kaplan, Zhaowei Zhang, Tobias Holder, Ning Cao, Aifeng Wang, Xiaoyuan Zhou, Feifei Zhou, Zhengzhi Jiang, Chusheng Zhang, Shihao Ru, Hongbing Cai, Kenji Watanabe, Takashi Taniguchi, Binghai Yan, and Weibo Gao (2023), “Quantum-metric-induced nonlinear transport in a topological antiferromagnet,” Nature 621 (7979), 487–492.
- Wang et al. (2022) Wang, Yongjian, Henry F Legg, Thomas Bömerich, Jinhong Park, Sebastian Biesenkamp, A A Taskin, Markus Braden, Achim Rosch, and Yoichi Ando (2022), “Gigantic Magnetochiral Anisotropy in the Topological Semimetal ZrTe5,” Physical Review Letters 128 (17), 176602.
- Wang and Fu (2017) Wang, Yuxuan, and Liang Fu (2017), “Topological phase transitions in multicomponent superconductors,” Physical Review Letters 119 (18), 187003.
- Watanabe (2021) Watanabe, Hikaru (2021), Theoretical Study of Nonlinear Current Generation in Parity-time Inversion Symmetric Magnets, Ph.D. thesis (Kyoto University).
- Watanabe et al. (2022a) Watanabe, Hikaru, Akito Daido, and Youichi Yanase (2022a), “Nonreciprocal meissner response in parity-mixed superconductors,” Physical Review B 105 (10), L100504.
- Watanabe et al. (2022b) Watanabe, Hikaru, Akito Daido, and Youichi Yanase (2022b), “Nonreciprocal optical response in parity-breaking superconductors,” Physical Review B 105 (2), 024308.
- Watanabe et al. (2024) Watanabe, Hikaru, Kohei Shinohara, Takuya Nomoto, Atsushi Togo, and Ryotaro Arita (2024), “Symmetry analysis with spin crystallographic groups: Disentangling effects free of spin-orbit coupling in emergent electromagnetism,” Physical Review B 109 (9), 094438.
- Watanabe and Yanase (2017) Watanabe, Hikaru, and Youichi Yanase (2017), “Magnetic hexadecapole order and magnetopiezoelectric metal state in Ba1-xKxMn2As2,” Physical Review B 96 (6), 064432, ; material properties are detailed in references therein.
- Watanabe and Yanase (2018a) Watanabe, Hikaru, and Youichi Yanase (2018a), “Group-theoretical classification of multipole order: Emergent responses and candidate materials,” Physical Review B 98 (24), 245129.
- Watanabe and Yanase (2018b) Watanabe, Hikaru, and Youichi Yanase (2018b), “Symmetry analysis of current-induced switching of antiferromagnets,” Physical Review B 98 (22), 220412.
- Watanabe and Yanase (2020) Watanabe, Hikaru, and Youichi Yanase (2020), “Nonlinear electric transport in odd-parity magnetic multipole systems: Application to mn-based compounds,” Physical Review Research 2 (4), 043081.
- Watanabe and Yanase (2021a) Watanabe, Hikaru, and Youichi Yanase (2021a), “Chiral photocurrent in parity-violating magnet and enhanced response in topological antiferromagnet,” Physical Review X 11 (1), 011001.
- Watanabe and Yanase (2021b) Watanabe, Hikaru, and Youichi Yanase (2021b), “Photocurrent response in parity-time symmetric current-ordered states,” Physical Review B 104 (2), 024416.
- Werake and Zhao (2010) Werake, Lalani K, and Hui Zhao (2010), “Observation of second-harmonic generation induced by pure spin currents,” Nature Physics 6 (11), 875–878.
- Winkler and Zülicke (2023) Winkler, R, and U Zülicke (2023), “Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond,” Physical Review B 107 (15), 155201.
- Wu et al. (2013) Wu, Sanfeng, Jason S Ross, Gui-Bin Liu, Grant Aivazian, Aaron Jones, Zaiyao Fei, Wenguang Zhu, Di Xiao, Wang Yao, David Cobden, and Xiaodong Xu (2013), “Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2,” Nature Physics 9 (3), 149–153.
- Wu et al. (2017) Wu, Shi-Long, Kazuki Sumida, Koji Miyamoto, Kazuaki Taguchi, Tomoki Yoshikawa, Akio Kimura, Yoshifumi Ueda, Masashi Arita, Masanori Nagao, Satoshi Watauchi, Isao Tanaka, and Taichi Okuda (2017), “Direct evidence of hidden local spin polarization in a centrosymmetric superconductor LaO0.55F0.45BiS2,” Nature Communications 8 (1), 1919.
- Xiao et al. (2019) Xiao, Cong, Z Z Du, and Qian Niu (2019), “Theory of nonlinear hall effects: Modified semiclassics from quantum kinetics,” Physical Review B 100 (16), 165422.
- Xiao et al. (2010) Xiao, Di, Ming-Che Chang, and Qian Niu (2010), “Berry phase effects on electronic properties,” Reviews of Modern Physics 82 (3), 1959–2007.
- Xiao et al. (2021) Xiao, Rui-Chun, Ding-Fu Shao, Yu-Hang Li, and Hua Jiang (2021), “Spin photogalvanic effect in two-dimensional collinear antiferromagnets,” npj Quantum Materials 6 (1).
- Xu et al. (2021) Xu, Haowei, Hua Wang, Jian Zhou, and Ju Li (2021), “Pure spin photocurrent in non-centrosymmetric crystals: bulk spin photovoltaic effect,” Nature Communications 12 (1), 4330.
- Xu et al. (2020) Xu, Su-Yang, Qiong Ma, Yang Gao, Anshul Kogar, Alfred Zong, Andrés M Mier Valdivia, Thao H Dinh, Shin-Ming Huang, Bahadur Singh, Chuang-Han Hsu, Tay-Rong Chang, Jacob P C Ruff, Kenji Watanabe, Takashi Taniguchi, Hsin Lin, Goran Karapetrov, Di Xiao, Pablo Jarillo-Herrero, and Nuh Gedik (2020), “Spontaneous gyrotropic electronic order in a transition-metal dichalcogenide,” Nature 578 (7796), 545–549.
- Xu et al. (2019) Xu, Tianrui, Takahiro Morimoto, and Joel E Moore (2019), “Nonlinear optical effects in inversion-symmetry-breaking superconductors,” Physical Review B 100 (22), 220501.
- Yanase (2010) Yanase, Youichi (2010), “Random Spin–Orbit coupling in spin triplet superconductors: Stacking faults in Sr2RuO4 and CePt3Si,” Journal of the Physical Society of Japan 79 (8), 084701.
- Yanase (2014) Yanase, Youichi (2014), “Magneto-Electric effect in Three-Dimensional coupled zigzag chains,” Journal of the Physical Society of Japan 83 (1), 014703.
- Yanase (2016) Yanase, Youichi (2016), “Nonsymmorphic weyl superconductivity in based on representation,” Physical Review B 94, 174502.
- Yang et al. (2019) Yang, X, C Vaswani, C Sundahl, M Mootz, L Luo, J H Kang, I E Perakis, C B Eom, and J Wang (2019), “Lightwave-driven gapless superconductivity and forbidden quantum beats by terahertz symmetry breaking,” Nature Photonics 13 (10), 707–713.
- Yao et al. (2017) Yao, Wei, Eryin Wang, Huaqing Huang, Ke Deng, Mingzhe Yan, Kenan Zhang, Koji Miyamoto, Taichi Okuda, Linfei Li, Yeliang Wang, Hongjun Gao, Chaoxing Liu, Wenhui Duan, and Shuyun Zhou (2017), “Direct observation of spin-layer locking by local rashba effect in monolayer semiconducting PtSe2 film,” Nature Communications 8, 14216.
- Yasuda et al. (2017) Yasuda, K, A Tsukazaki, R Yoshimi, K Kondou, K S Takahashi, Y Otani, M Kawasaki, and Y Tokura (2017), “Current-nonlinear hall effect and spin-orbit torque magnetization switching in a magnetic topological insulator,” Physical Review Letters 119 (13), 137204.
- Yasuda et al. (2016) Yasuda, K, A Tsukazaki, R Yoshimi, K S Takahashi, M Kawasaki, and Y Tokura (2016), “Large unidirectional magnetoresistance in a magnetic topological insulator,” Physical Review Letters 117 (12), 127202.
- Yatsushiro et al. (2022) Yatsushiro, Megumi, Rikuto Oiwa, Hiroaki Kusunose, and Satoru Hayami (2022), “Analysis of model-parameter dependences on the second-order nonlinear conductivity in -symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains,” Physical Review B 105 (15), 155157.
- Yokouchi et al. (2017) Yokouchi, T, N Kanazawa, A Kikkawa, D Morikawa, K Shibata, T Arima, Y Taguchi, F Kagawa, and Y Tokura (2017), “Electrical magnetochiral effect induced by chiral spin fluctuations,” Nature Communications 8 (1), 866.
- Yoon et al. (2023) Yoon, Ju-Young, Pengxiang Zhang, Chung-Tao Chou, Yutaro Takeuchi, Tomohiro Uchimura, Justin T Hou, Jiahao Han, Shun Kanai, Hideo Ohno, Shunsuke Fukami, and Luqiao Liu (2023), “Handedness anomaly in a non-collinear antiferromagnet under spin-orbit torque,” Nature Materials 22, 1106–1113.
- Yoshimi et al. (2022) Yoshimi, Ryutaro, Minoru Kawamura, Kenji Yasuda, Atsushi Tsukazaki, Kei S Takahashi, Masashi Kawasaki, and Yoshinori Tokura (2022), “Nonreciprocal electrical transport in the multiferroic semiconductor (Ge,Mn)Te,” Physical Review B 106 (11), 115202.
- Young and Kane (2015) Young, Steve M, and Charles L Kane (2015), “Dirac semimetals in two dimensions,” Physical Review Letters 115 (12), 126803.
- Young et al. (2013) Young, Steve M, Fan Zheng, and Andrew M Rappe (2013), “Prediction of a linear spin bulk photovoltaic effect in antiferromagnets,” Physical Review Letters 110 (5), 057201.
- Yuan et al. (2019) Yuan, Linding, Qihang Liu, Xiuwen Zhang, Jun-Wei Luo, Shu-Shen Li, and Alex Zunger (2019), “Uncovering and tailoring hidden rashba spin-orbit splitting in centrosymmetric crystals,” Nature Communications 10 (1), 906.
- Železný et al. (2021) Železný, J, Z Fang, K Olejník, J Patchett, F Gerhard, C Gould, L W Molenkamp, C Gomez-Olivella, J Zemen, T Tichý, T Jungwirth, and C Ciccarelli (2021), “Unidirectional magnetoresistance and spin-orbit torque in NiMnSb,” Physical Review B 104 (5), 054429.
- Železný et al. (2017a) Železný, J, H Gao, Aurélien Manchon, Frank Freimuth, Yuriy Mokrousov, J Zemen, J Mašek, Jairo Sinova, and T Jungwirth (2017a), “Spin-orbit torques in locally and globally noncentrosymmetric crystals: Antiferromagnets and ferromagnets,” Physical Review B 95 (1), 014403.
- Železný et al. (2017b) Železný, Jakub, Yang Zhang, Claudia Felser, and Binghai Yan (2017b), “Spin-Polarized current in noncollinear antiferromagnets,” Physical Review Letters 119 (18), 187204.
- Zhang et al. (2019a) Zhang, Dongqin, Minji Shi, Tongshuai Zhu, Dingyu Xing, Haijun Zhang, and Jing Wang (2019a), “Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect,” Physical Review Letters 122 (20), 206401.
- Zhang et al. (2021) Zhang, Ke, Shixuan Zhao, Zhanyang Hao, Shiv Kumar, Eike F Schwier, Yingjie Zhang, Hongyi Sun, Yuan Wang, Yujie Hao, Xiaoming Ma, Cai Liu, Le Wang, Xiaoxiao Wang, Koji Miyamoto, Taichi Okuda, Chang Liu, Jiawei Mei, Kenya Shimada, Chaoyu Chen, and Qihang Liu (2021), “Observation of Spin-Momentum-Layer locking in a centrosymmetric crystal,” Physical Review Letters 127 (12), 126402.
- Zhang et al. (2019b) Zhang, Pengxiang, Joseph Finley, Taqiyyah Safi, and Luqiao Liu (2019b), “Quantitative study on current-induced effect in an antiferromagnet insulator/pt bilayer film,” Physical Review Letters 123 (24), 247206.
- Zhang et al. (2014) Zhang, Xiuwen, Qihang Liu, Jun-Wei Luo, Arthur J Freeman, and Alex Zunger (2014), “Hidden spin polarization in inversion-symmetric bulk crystals,” Nature Physics 10 (5), 387–393.
- Zhang et al. (2019c) Zhang, Yang, Tobias Holder, Hiroaki Ishizuka, Fernando de Juan, Naoto Nagaosa, Claudia Felser, and Binghai Yan (2019c), “Switchable magnetic bulk photovoltaic effect in the two-dimensional magnet CrI3,” Nature Communications 10 (1), 3783.
- Zhao et al. (2015) Zhao, L, D H Torchinsky, H Chu, V Ivanov, R Lifshitz, R Flint, T Qi, G Cao, and D Hsieh (2015), “Evidence of an odd-parity hidden order in a spin-orbit coupled correlated iridate,” Nature Physics 12 (1), 32–36.
- Zhu et al. (2014) Zhu, Bairen, Hualing Zeng, Junfeng Dai, Zhirui Gong, and Xiaodong Cui (2014), “Anomalously robust valley polarization and valley coherence in bilayer WS2,” Proceedings of the National Academy of Sciences of the United States of America 111 (32), 11606–11611.
- Zimmermann et al. (2014) Zimmermann, Anne S, Dennis Meier, and Manfred Fiebig (2014), “Ferroic nature of magnetic toroidal order,” Nature Communications 5, 4796.
- Šmejkal et al. (2017) Šmejkal, L, J Železný, J Sinova, and T Jungwirth (2017), “Electric control of dirac quasiparticles by spin-orbit torque in an antiferromagnet,” Physical Review Letters 118 (10), 106402.
- Šmejkal et al. (2020) Šmejkal, Libor, Rafael González-Hernández, T Jungwirth, and J Sinova (2020), “Crystal time-reversal symmetry breaking and spontaneous hall effect in collinear antiferromagnets,” Science Advances 6 (23), eaaz8809.
- Šmejkal et al. (2022) Šmejkal, Libor, Allan H MacDonald, Jairo Sinova, Satoru Nakatsuji, and Tomas Jungwirth (2022), “Anomalous hall antiferromagnets,” Nature Reviews Materials 7 (6), 482–496.
- Železný et al. (2014) Železný, J, H Gao, K Výborný, J Zemen, J Mašek, Aurélien Manchon, J Wunderlich, Jairo Sinova, and T Jungwirth (2014), “Relativistic néel-order fields induced by electrical current in antiferromagnets,” Physical Review Letters 113 (15), 157201.