Magnetic field-induced deformation of the spin-density wave microphases in Ca3Co2O6
Abstract
The frustrated triangular Ising magnet Ca3Co2O6 has long been known for an intriguing combination of extremely slow spin dynamics and peculiar magnetic orders, such as the evenly-spaced non-equilibrium metamagnetic magnetization steps and the long-wavelength spin density wave (SDW) order, the latter of which is essentially an emergent crystal of solitons. Recently, an elaborate field-cooling protocol to bypass the low-field SDW phase was proposed to overcome the extraordinarily long timescale of spin relaxation that impeded previous experimental studies in equilibrium, which may point to a deep connection between the low-temperature slow relaxation and the cooling process passing through the low-field SDW phase. As the first step to elucidate the conjectured connection, we investigate the magnetic field-induced deformation of the SDW state and incommensurate-commensurate transitions, thereby mapping out the equilibrium in-field phase diagram for a realistic three-dimensional lattice spin model by using Monte Carlo simulations. We also discuss Ginzburg-Landau theory that includes several Umklapp terms as well as an effective sine-Gordon model, which can qualitatively explain the observed magnetic field-induced deformation of the SDW microphases.
I Introduction
Frustrated magnets can have a manifold of nearly degenerate low-energy states from which interesting phenomena may emerge, such as exotic magnetic and nonmagnetic orders, topological order, liquid-like or even glassy behavior, and so on, varying from one material to another.Lacroix2011 Even a classical system can host unconventional quasiparticles, such as skyrmions,Bogdanov2020 solitons, and monopoles in spin ice,Bramwell01; Paulsen2014; Bramwell20 and they may crystallize into novel spin textures like skyrmion crystals Okubo2012; Leonov2015 or soliton crystals.Bak82; Selke88 Such emergent crystalline states can often be sensitive to external perturbations, which makes them attractive as potential devices in some cases.Fert2017 They can also provide a platform to study far-from-equilibrium dynamics due to metastable states.Kudasov06; Paulsen2014
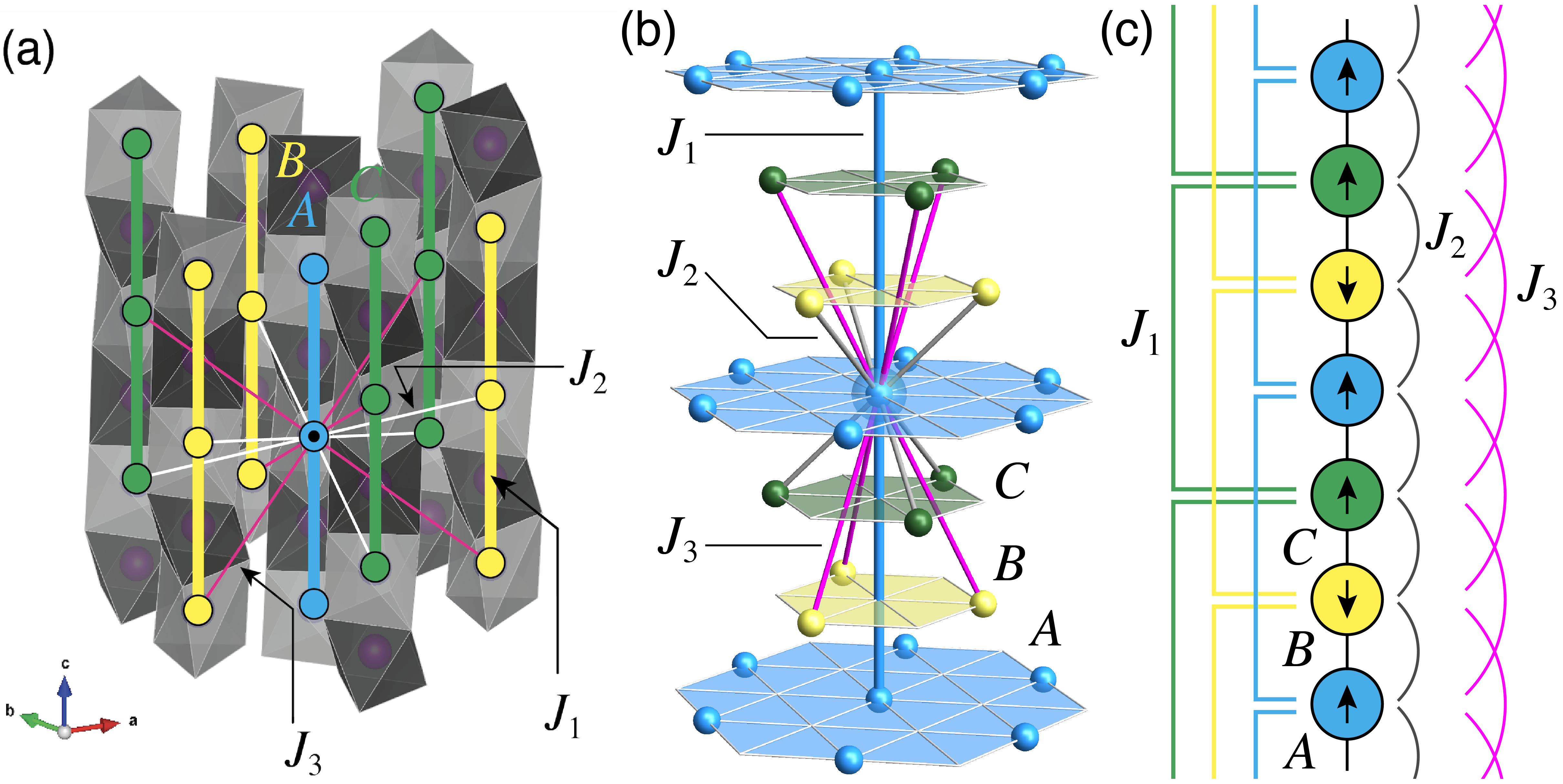
Since the late 90’s,Fjellvag96; Aasland97; Kageyama97; Kageyama97b the frustrated triangular Ising magnet Ca3Co2O6 (CCO) has long been known for an intriguing combination of extremely slow spin dynamics and peculiar magnetic phases, such as metamagnetic magnetization steps and an incommensurate spin-density wave (SDW) state,Agrestini08a; Mazzoli09; Agrestini08b; Moyoshi11; Fleck10; Paddison14; Motoya18 the latter of which can be seen as a soliton crystal.Kamiya12 In CCO, trigonal prismatic Co3+ sites form ferromagnetic Ising chains running along the axis, while arranged in a triangular lattice in the plane coupled by weak antiferromagnetic interactions (Fig. 1).Leedahl19 Below spin-freezing temperature , CCO exhibits striking evenly-spaced metamagnetic magnetization steps,Kageyama97 whose origin has been a subject of long-time debates.Kageyama97; Kageyama97b; Maignan00; Hardy04b; Maignan04; Moyoshi11; Kim18 Interestingly, while the step heights are sensitive to protocol details such as sweep rate of the external magnetic field, the transition magnetic fields (1.2 T, 2.4 T, and 3.6 T, with additional steps at higher fields) are rather robust.Hardy04b Although some theory invoked an analogy with quantum tunneling in molecular magnets,Maignan04 an alternative scenario is that peculiar frustration in CCO causes a non-equilibrium phenomenon.Kudasov06 In the so-called “rigid chain” model,Yao06a; Yao06b; Kudasov08; Qin09; Soto09; Zukovic12 each ferromagnetic chain is replaced by an effective Ising spin on a two-dimensional antiferromagnetic triangular lattice. Based on this mapping, it was argued that the metamagnetic transition steps in CCO may arise from the same kind of degenerate manifold as in the two-dimensional triangular lattice Ising model.Kudasov06
However, the origin of the slow dynamics can be more intricate than suggested by the rigid chain picture. More recently, resonant x-ray Agrestini08a; Mazzoli09 and neutron spectroscopies Agrestini08b; Moyoshi11; Fleck10; Paddison14; Motoya18 revealed the SDW order below 25 K, which has a three-sublattice structure and a very long modulation wavelength ( magnetic sites) along the axis. It was found that increases as temperature is lowered and the corresponding relaxation time grows substantially. Eventually, the system starts to deviate from equilibrium below 13 K,Moyoshi11 which is much higher than for the appearance of the metamagnetic magnetization steps. Since the spin chains are not ferromagnetically ordered in the SDW state, the interpretation of the rigid chain picture is, if not questionable, more subtle than originally proposed.
Indeed, the SDW phase may hold the key to understanding the peculiar slow dynamics at low temperatures. It was recently demonstrated that the slow spin dynamics can be bypassed by an elaborate field-cooling protocol, where every in-field measurement is performed after a separate cooling in the target magnetic field.Nekrashevic21 Remarkably, the protocol allowed for reaching the 1/3 magnetization plateau down to without being suffered from metastable states, which was in good agreement with MC simulations in equilibrium. Since the SDW order is believed to disappear and replaced by a ferrimagnetic state at high magnetic fields, the new experiment may suggest that the spin relaxation at low temperatures may be influenced by the extent to which the system has been through the low-field SDW phase during the cooling. In fact, it is known that the SDW order is accompanied by short-range order indicative of spin disordering,Agrestini11 which could be due to the combination of the -dependent ordering wavevector and the slowness in the relaxation to follow the variation. Moyoshi11
As mentioned above, the observed SDW state is essentially a soliton crystal as in the axial next-nearest-neighbor Ising (ANNNI) model,Kamiya12 a prototypical model for spontaneous superstructures due to competition between nearest and next nearest neighbor Ising interactions in one direction of a square or cubic lattice.Bak82; Selke88 The -dependent change of Moyoshi11 corresponds to different magnetic microphases,Kamiya12 similar to other self-organizing modulated phases in physical and chemical systems.Seul1995 Thus, CCO may provide a rare intersection where the ANNNI model phenomenology Bak82; Selke88 meets out-of-equilibrium physics in a solid state system with only short-range interactions. To elucidate this conjecture in CCO and similar materials such as Ca3Co2-xMnxO6,Zapf18; Kim18 Sr2Ca2CoMn2O9,Hardy18 and Ca3CoRhO6,Niitaka01 it is a matter of paramount importance to investigate the magnetic field-induced deformation of the SDW state and incommensurate-commensurate (IC-C) transitions under the condition much closer to equilibrium than ever reached before. The goal of this work to present an equilibrium in-field phase diagram for a realistic three-dimensional (3D) lattice spin model for CCO, thereby providing a theoretical guide for experiments. We address both model-specific and universal physics by combining mean-field theory (Sec. III), MC simulations (Sec. IV), and Ginzburg-Landau (GL) theory (Sec. V).
II Model
In CCO, spins have large easy-axis anisotropy,Kageyama97 which permits a description by an effective classical Ising model,
| (1) |
where , with , , and being the -factor, the Bohr magneton, and a magnetic field, respectively, and denotes neighboring sites connected by , . is the intrachain ferromagnetic interaction and () is the antiferromagnetic interchain interaction shifted by 1/3 (2/3) lattice parameters along the axis (Fig. 1). An ab initio study suggested Fresard04 and K and K was reported by an NMR experiment, which further suggested K and K to explain the SDW ordering wavevector.Allodi14 Below, for simplicity, we assume and denote the ratio by ; in relation with CCO, .
III Mean field theory
In CCO, and compete with after a few steps along a spiral path due to the vertical shifts of the interchain interactions.Chapon09 This spiral structure is the key to realize the same kind of geometrical frustration as in the ANNNI model Bak82; Selke88 despite the apparent structural differences. We first briefly discuss a heuristic mean-field theory in zero field by assuming a ferromagnetic order in each plane, which are separated by 1/3 lattice parameters from each other along the axis (Fig. 1).Kamiya12 The mean field equation for the magnetization of layer is
| (2) |
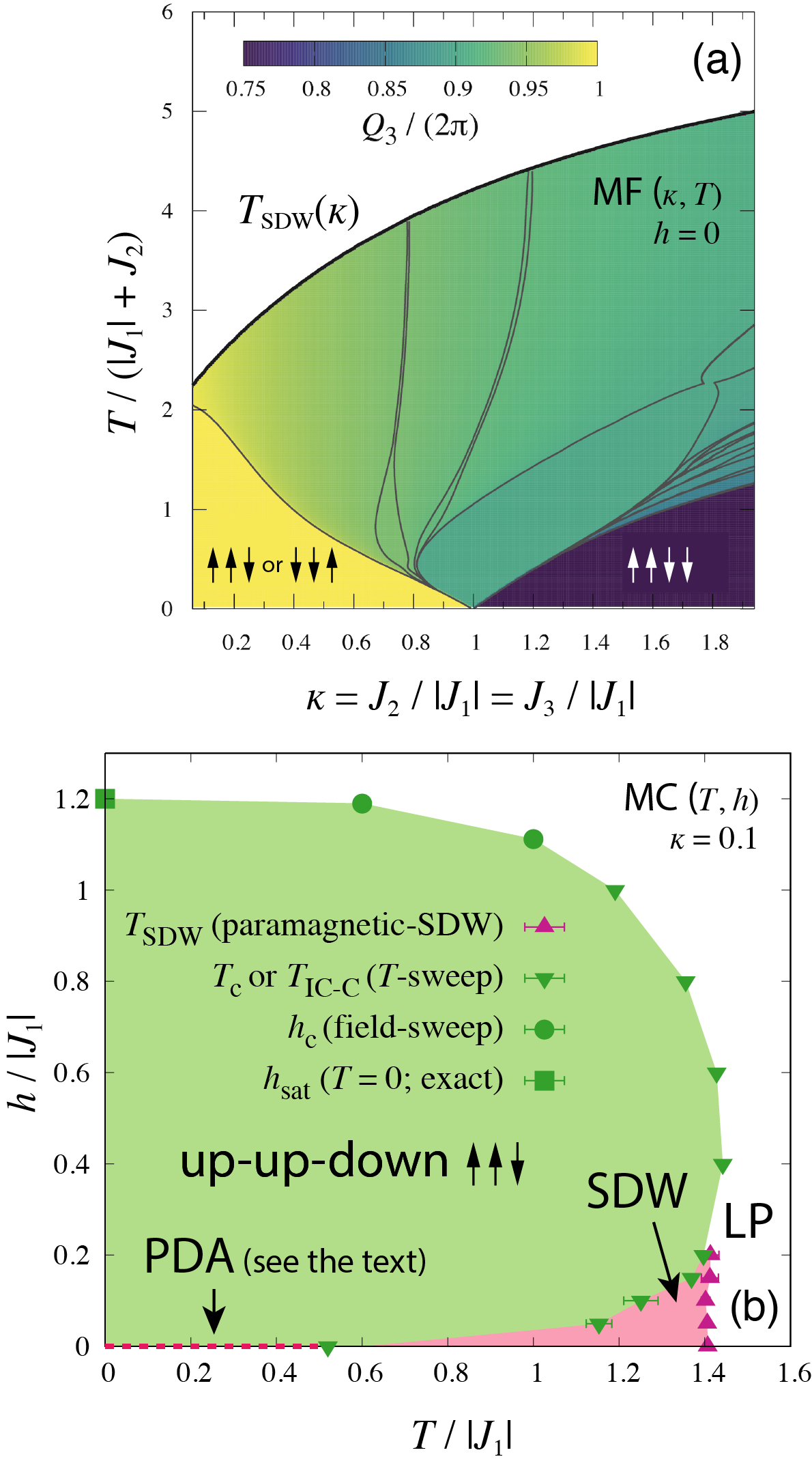
where . In this quasi-one-dimensional description, , , and serve as the effective third, first, and second neighbor interactions, respectively, realizing a very similar situation as in the prototypical ANNNI model [Fig. 1(c)]. The reason for assuming an in-plane ferromagnetic order, even though the interchain interactions and are much smaller than the intrachain interaction , is that the energy scale associated with the competition between SDW states with different wavelengths along the axis can be even smaller, as will be discussed by using a sine-Gordon model. In Fig. 2(a), we show the mean field phase diagram, by extending the previous work.Kamiya12 Below the SDW transition temperature , the ordering wavevector varies quasi-continuously. Eventually, there is a lock-in IC-C transition at , below which the magnetic unit cell of the mean field solution is or for and for in the effective one-dimensional description in Fig. 1(c). We find that quasi-continuous changes of dominate the overall phase diagram, corresponding to numerous microphases of soliton lattice states, especially for relatively small .Kamiya12 Meanwhile, distinct discontinuous changes of are also seen in the region with relatively large , where a few relatively extended commensurate states are found. However, the latter case has little significance in relation with CCO, where has been suggested to be very small.
IV Monte Carlo simulation
IV.1 Set up
Next, to demonstrate the ANNNI-like physics in an unbiased way, we present the results of our MC simulations. We consider a lattice of size with periodic boundary conditions, where the total number of spins is . We combine single-spin updates, intra-chain cluster updates Kamiya12, and replica exchanges Hukushima96 included every 10 MC steps. Several hundreds of replicas are needed for largest lattices to maintain a reasonable exchange acceptance rate to guarantee efficient sampling at low temperatures (e.g., 400 replicas for for ). By fixing and in most cases shown below, we performed simulations for –. Here, although is larger than estimated for CCO, no qualitatively different physics for smaller is suggested in our mean field phase diagram, as long as the SDW order is concerned [Fig. 2(a)].
The aspect ratio is chosen to simulate long-wavelength SDW states with as little finite-size tension as possible while not making the system excessively anisotropic to address thermodynamic behaviors in 3D. As discussed by using a GL theory, the ordering wavevector at is expected to be the minima of the Fourier transform of the exchange interactions, which we find with for and for . Because is very close to the three-sublattice commensurate wavevector , even a single periodicity of the spin modulation requires a large number of unit cells along the axis. (Here, is equivalent to in our notation, but is not.) The minimum size thus required for is , which can be a bit problematic. For , we find , which is also quite anisotropic but within the acceptable range. The aspect ratio is determined on this basis.
IV.2 Modified Binder parameter method
To determine the transition point of a second-order phase transition into a commensurate ordering, say with a wavevector , a standard method is to analyze the order parameter and the corresponding Binder parameter .LandauBinder However, the possible -dependent variation as well as incommensurability of the ordering wavevector poses a challenge in numerical studies of the ANNNI model and its variants,Gendiar2005; KaiZhang2010; KaiZhang2011 demanding a modified approach. In such a model, a finite-size system with periodic boundary conditions is expected to develop a spin correlation whose dominant wavevector is necessarily commensurate but near the true ordering wavevector in thermodynamic limit. Such an effective ordering wavevector, , can be detected as a peak in the finite-size spin structure factor and we expect . Indeed, the observed behavior of shows relatively small variance with respect to , supporting this expectation (Fig. 3). Based on the estimate of , we evaluate and , thereby
| (3) |
which is a Binder parameter defined at . As in the usual usage of the Binder parameter,LandauBinder we look into the crossing point of for different system sizes to evaluate .
Unlike the conventional approach, however, the wavevector associated with the Binder parameter for one system size can be different from one for another size. Furthermore, it can also be -dependent. To analyze the effect of a small deviation of the wavevector from the true (incommensurate) ordering wavevector , we review the standard scaling theory for correlation functions.Cardy The two-point SDW correlation function , where is the coarse-grained SDW order parameter with the momentum , is expected to have the following transformation under the scaling by a factor ,
| (4) |
where , is the scaling dimension of the order parameter, and is the critical exponent of correlation length . It follows that the correlation function has the universal finite-size scaling form of
| (5) |
from which we find
| (6) |
A similar argument can also be made for the four-point correlation function , leading to
| (7) |
Thus, near the critical point , we find that the Binder parameter associated with the effective ordering wavevector behaves as
| (8) |
whereas (corresponding to the Gaussian distribution for a one-component complex order parameter) and in the high- and low- limits, respectively. Here, , , , and are finite-size scaling functions.
It is reasonable to assume that these scaling functions are sufficiently isotropic with respect to small , with an appropriate rescaling along the principle axes if needed.Cardy In fact, reflection symmetry along the -axis concerning the sign of is enough for the following discussion. As a wavevector best approximating the true ordering wavevector for a given system size , we expect . Since, as usually the case, the universal scaling functions can be expected as a sufficiently slowly-varying function near the critical point , the right hand side of Eq. (8) is almost a size-independent constant. Therefore, the Binder parameter at the size-dependent effective ordering wavevectors to exhibit a crossing behavior at around , as the temperature is lowered from the paramagnetic phase.
In the meantime, to determine for the lock-in IC-C transition into a commensurate phase in low fields, or for a direct transition into the same phase in high fields, we use the ordinary the Binder parameter at the corresponding commensurate wavevector .
IV.3 Ordering wavevector and the phase diagram
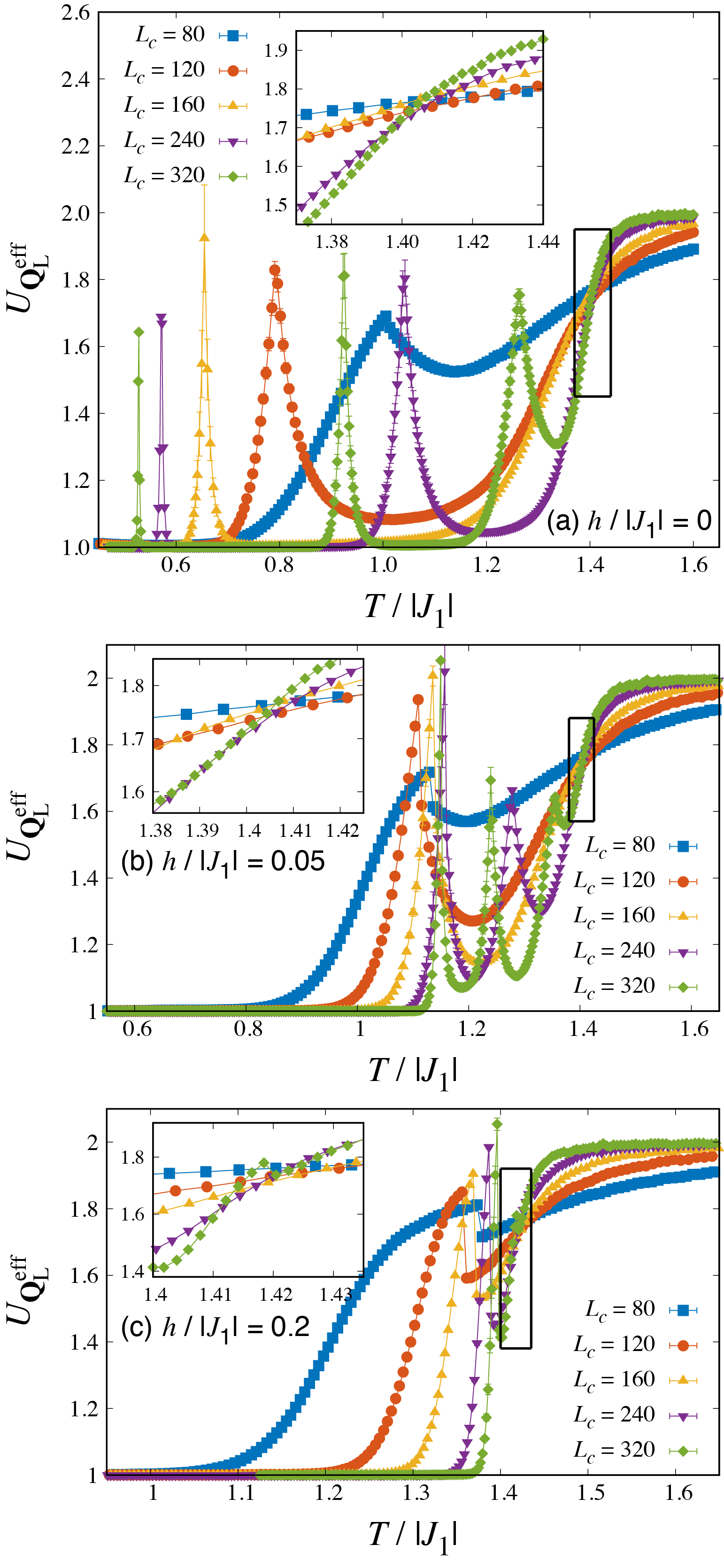
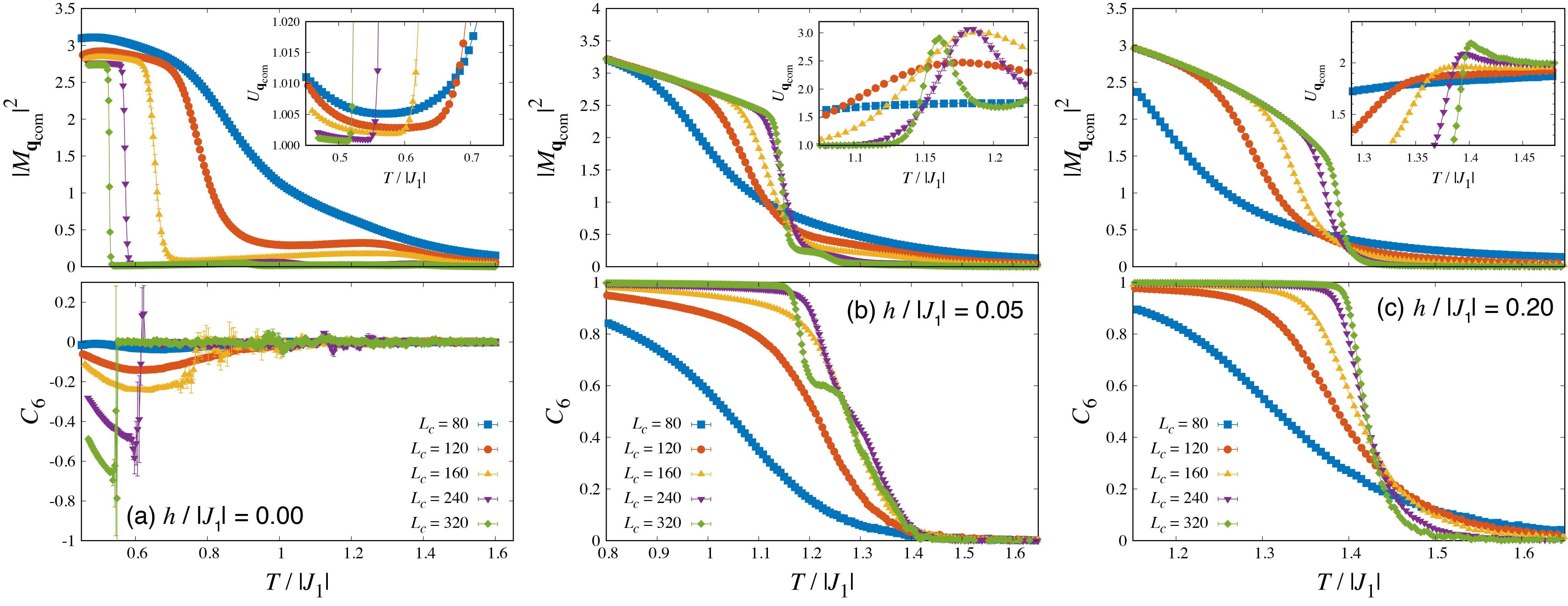
Below, we discuss the details of the phase diagram for [Fig. 2(b)], obtained at , focusing on the behavior of the ordering wavevector (Fig. 3). At low fields, we observe that the ordering wavevector at slightly, but clearly, deviates from . Below , slowly drifts towards as further lowering . Roughly speaking, the ordering wavevector changes more rapidly as the magnetic field is increased. The observed step-like behavior of is simply due to the finite-size discretization of the wavevector (e.g., for ), which also causes spurious peaks in at wildly size-dependent temperatures (Fig. 3). Considering the wide range of the system sizes we investigated, the most natural interpretation is that the change of the wavevector in thermodynamic limit, , is (quasi-)continuous towards . When changes from one value to another as a function of in a finite-size system, a disordering effect appears at large distance due to the mismatch between an ideal wavevector and the system size. The mismatch-induced disordering effect causes a spurious spiky peak in (Fig. 4) and interfere with high-precision determination of as the behavior of near the crossing point is affected and becomes less systematic. Therefore, we treat the first crossing points of for simply on an equal footing, which nonetheless allows us to determine the transition point of the SDW ordering to the satisfactory precision, e.g., for , respectively (Fig. 4). The estimated roughly coincides with the highest- peak in the specific heat (see Fig. 3).
At low temperatures, the ordering wavevector is pinned at , corresponding to a three-sublattice ordered phase. At low fields, the low- phase appears through a lock-in IC-C transition, where the translational symmetry along the axis, which is broken in the SDW state, is restored. By analyzing the behavior of , we find that increases rapidly with (see Fig. 2), e.g., for , respectively. Since is nearly constant in , the SDW phase shrinks rather rapidly with increasing , and above a magnetic field-induced multicritical point , where is the saturation field, no incommensurate phase exists. The estimated IC-C transition temperatures coincide with the temperatures at which the finite-size ordering wavevector reaches at each field, as expected. Also, increases rapidly around the estimated temperatures and becomes almost size-independent at lower temperatures (Fig. 5). While the IC-C transitions studied in the present MC work exhibit typical features of a first-order transition, such as the correction in the finite-size transition temperature varying as , they may be a spurious behavior caused by discrete wavevectors in finite size systems, as also found in specific heat as the spurious spiky peaks.
For , the two main candidates for the three-sublattice order are the ferrimagnetic (FIM) state and the partially-disordered antiferromagnetic (PDA) state, similar to the case in triangular lattice antiferromagnetic Ising models.Blankschtein84; Coppersmith85; Isakov03; Heinonen89; Bunker93; Isakov03; Lin14 In the FIM state, each spin chain has a ferromagnetic order and different spin chains takes the three-sublattice structure. In the PDA phase, the spin chains in the first and the second sublattices have a ferromagnetic order with spin- and , respectively, with the spin chains in the third sublattice disordered. A convenient indicator for a finite-size calculation is
| (9) |
which takes () for the FIM (PDA) state.Isakov03 For , we confirm the PDA state below (Fig. 5), though the result should be distinguished from the previous claim of the same state in CCO below 25 K.Kageyama97 We find no evidence of an additional order-order transition at low as reported in CCO,Agrestini11 at least for . For , we find the FIM state at low down to , implying that the observed PDA state is extremely fragile against the magnetic field. The FIM phase yields the 1/3 magnetization plateau. Nekrashevic21 At high fields, we find a direct transition into the FIM phase without the intervening SDW phase. We find that the transition is of the first order, which is consistent with the symmetry breaking in , as in the three-state Potts model.Blote1979; Janke97
V Ginzburg-Landau theory
Finally, for a more universal description of the commensurate and incommensurate phases in CCO and similar materials, we consider a GL theory. As will be shown below, the theory is essentially in the same form as that for the ANNNI model.Aharony1981; Bak80 Interestingly, however, the GL theory for ANNNI-like models in magnetic fields Yokoi81 has yet been thoroughly discussed in the literature, despite its experimental relevance.
We use a complex order parameter , , which can be formally introduced by using the Hubbard-Stratonovich transformation. describes the local three-sublattice order in a coarse-grained way, which can be either the FIM order or the PDA order depending on the phase factor. For , we find the following GL Hamiltonian,
| (10) |
where , , , and are GL coefficients and . A crucial point of the present theory is that the wavevector of the local order described by is slightly shifted from the minima of the Fourier transform of the exchange interactions, as briefly mentioned before. For this reason, includes the vector potential-like (but constant) contribution in the gradient term. also includes the six-order term () as the leading Umklapp term, the order of which is determined by the size of the magnetic sublattice of the commensurate order and time reversal symmetry; a factor of three comes from and time reversal symmetry requires another factor of two.
As is clear from the origin, the gradient term acts as adding a momentum to , in favor of the three-sublattice long-wavelength SDW state . Although the SDW state thus appears to benefit from the exchange energy, the sinusoidal modulation made of localized Ising-like moments also requires entropy contribution to the free energy. In contrast, because of the shift of from the minima of , the commensurate three-sublattice ordered state, , may appear not to acquire the full energy gain of the exchange interaction. However, the state is quite compatible with the Ising anisotropy. In the GL theory (10), the Umklapp term plays the role of the entropy contribution related with the Ising anisotropy. While the commensurate state may be favored by the Umklapp term by adjusting its constant phase factor, the incommensurate SDW states generally gain no corresponding contribution because of the phase cancellation in the integral over the space. In fact, we could rederive the GL theory in terms of instead of , and the result is an ordinary -theory for the one-component complex order parameter without Umklapp terms if is incommensurate. Hence, the key role in the GL theory (10) is played by the competition between the gradient and the Umklapp terms favoring incommensuration and commensuration, respectively. Thus, although somewhat different in appearance, the Hamiltonian of this system (1) realizes essentially the same kind of situation as the classic ANNNI model.Bak80
At , critical fluctuations renders nonzero with the additional momentum , resulting in the SDW state with the ordering wavevector . In other words, we expect a condensation of the softest mode rather than . Since the Umklapp term has no effect for the incommensurate SDW states, the transition, which breaks translation symmetry along the axis, will be in the 3D XY universality class (emergent U(1) symmetry). The observed main peak of the specific heat, which exhibits a sign of smearing [Fig. 3(a)], is consistent with the negative exponent for the XY universality class.Campostrini2001
For , the competition between the gradient term and the Umklapp term sets in, which affects the phase factor of , thereby . To see this, we may write and apply a mean-field decoupling for the massive amplitude fluctuation (“Higgs”) mode and the phase mode .Bak80 The result is the following sine-Gordon model for ,
| (11) |
The gradient term tends to drift the phase, which can lead to a plethora of soliton lattices through the competition against the cosine term,Bak80; Chaikin-Lubensky1995 in good agreement with our mean field and MC studies. In the meantime, because the order parameter amplitude increases as is lowered below , the strength of the cosine term is enhanced. Consequently, the model at low is expected to undergo a lock-in transition eventually. For (), the phase is locked-in at [] with an integer , corresponding to the FIM ( or ) state and the PDA state,Blankschtein84; Coppersmith85; Isakov03; Heinonen89; Bunker93; Lin14 respectively. Although our mean field calculation implies while our unbiased MC simulation suggests in zero field, the subtle discrepancy does not require a serious attention as is generated through fluctuations.
For , the uniform component is allowed by symmetry and may be induced by the magnetic field. Consequently, in addition to , a lower-order Umklapp term appears in the GL Hamiltonian. We find
| (12) |
as the leading-order contribution with the new coupling constant . The total effective GL Hamiltonian for is
| (13) |
where is the noninteracting part for with and being the gapped spin wave parameters near . By a similar mean field decoupling as in the case, we find a new term in the sine-Gordon model,
| (14) |
The field-induced Umklapp term has the following consequences. Firstly, because of the reduced symmetry in the space, only a subset of the FIM states is favored by among the three-sublattice ordered states. Depending on the sign of , the favored states are or , each of which is three-fold degenerate, though is naturally anticipated for . Secondly, as the prefactor is , as opposed to in zero field, the strength of the field-induced Umklapp term is expected to grow faster for . Moreover, since the prefactor is , we expect that this trend is further enhanced for larger . Therefore, the region of the incommensurate SDW microphases is expected to become narrower for larger , in excellent agreement with our MC results (Fig. 2). Thirdly, considering that our MC simulation shows the PDA state at below , the zero- and the field-induced Umklapp terms (, respectively) must compete against each other in the present system. The competition opens a possibility of a kind of mixed phase below , though our MC results shows no evidence down to an extremely low field, . Finally, near , the present GL theory suggests the condensation of the softest mode rather than , as in the case of zero magnetic field. Hence, we expect the emergent U(1) symmetry at also for , because Umklapp terms disappear from the GL theory in terms of the incommensurate critical mode . The theory thus predicts for any magnetic field, which is indeed consistent with our MC results at low magnetic fields. However, the simulation closer to the magnetic field-induced multicritical point might point to a deviation from this behavior, suggesting that approaches towards for the larger systems we investigated [Fig. 3(c)]. This observation may be an indication that the multicritical point is a Lifshitz point induced by a magnetic field.
VI Summary and outlook
To summarize, we presented the magnetic phase diagram in equilibrium of the 3D spin model for the frustrated quasi-one-dimensional triangular Ising antiferromagnet Ca3Co2O6. We identified the region of incommensurate SDW microphases in a magnetic field (Fig. 2). We found the deformation of SDW microphases as a function of , characterized by the temperature dependence of the ordering wavevector , occurring much more rapidly in a magnetic field than in zero field (Fig. 3). The deformation eventually leads to the IC-C transition into the PDA (FIM) state for (). Between the PDA and the FIM phases, there may be a mixed phase in an extremely low-field regime, though not confirmed in this work. The GL theory we derived includes different symmetry-allowed Umklapp terms for and . The GL theory allowed for further deriving an effective sine-Gordon model that provides a qualitative explanation of the observed magnetic field-induced deformation of the SDW microphases. Moreover, these effective theories demonstrate that the present system can be seen as an incarnation of the classic ANNNI model,Bak80 despite different appearance of the lattice structure and the complicated network of the exchange interactions.
Finally, we discuss the relation between the theoretical phase diagram in this work and the previous experiments. As mentioned in Introduction, the material is known for the intriguing combination of the slow relaxation phenomena and the long-wavelength SDW order. As the recent field-cooling study suggested,Nekrashevic21 the slow relaxation at low temperature may be greatly influenced by the cooling process passing through the low-field SDW phase at intermediate temperature. To verify the conjectured relation experimentally, the challenge is that experiments under equilibrium conditions are known to be notoriously difficult for Ca3Co2O6. For example, a resonant X-ray experiments reported a field-induced IC-C transition at 5 K,Mazzoli09 which is unfortunately most likely non-equilibrium because the temperature is too low. However, at intermediate temperatures above , there are some experiments that seem to capture the desired physics of the field-induced deformation of the SDW phase and the IC-C transition. For example, a SR measurements at 20 K reported a magnetic field-induced phase transition at around 0.4 T.Takeshita2007 Although the original interpretation of the result suggested a PDA-FIM transition, the obtained phase boundary is very similar to the SDW-FIM transition line shown in the present work. Since the SDW phase was not confirmed back then, it is quite possible that the anomaly in the SR experiment is the sign of the IC-C transition induced by the magnetic field. We also note that a similar phase diagram was obtained also by weak anomaly in the magnetic entropy change.Lampen14 We thus believe that further experiments studying the field-induced IC-C transition in Ca3Co2O6, such as neutron scattering and other spectroscopies focusing on the low-field regime, will be very promising, especially when combined with the recently proposed field-cooling protocol.Nekrashevic21 Such experiments may provide further insights in the peculiar slow dynamics and out-of-equilibrium behaviors in Ca3Co2O6 and related materials.
Acknowledgements.
The author is grateful to valuable discussions with Vivien Zapf, Xiaxin Ding, Ivan Nekrashevich, and Cristian Batista. The author acknowledges the support by the NSFC (Nos. 11950410507, 12074246, and U2032213) and MOST (No. 2016YFA0300501) research programs.References
- Lacroix et al. (2011) C. Lacroix, P. Mendels, and F. Mila, eds., Introduction to Frustrated Magnetism: Materials, Experiments, Theory (Springer-Verlag, Heidelberg, 2011).
- Bogdanov and Panagopoulos (2020) A. N. Bogdanov and C. Panagopoulos, Nat. Rev. Phys. 2, 492 (2020).
- Bramwell and Gingras (2001) S. T. Bramwell and M. J. P. Gingras, Science 294, 1495 (2001).
- Paulsen et al. (2014) C. Paulsen, M. J. Jackson, E. Lhotel, B. Canals, D. Prabhakaran, K. Matsuhira, S. R. Giblin, and S. T. Bramwell, Nat. Phys. 10, 135 (2014).
- Bramwell and Harris (2020) S. T. Bramwell and M. J. Harris, J. Phys. Condens. Matter. 32, 374010 (2020).
- Okubo et al. (2012) T. Okubo, S. Chung, and H. Kawamura, Phys. Rev. Lett. 108, 017206 (2012).
- Leonov and Mostovoy (2015) A. O. Leonov and M. Mostovoy, Nat. Commun. 6, 8275 (2015).
- Bak (1982) P. Bak, Rep. Prog. Phys. 45, 587 (1982).
- Selke (1988) W. Selke, Phys. Rep. 170, 213 (1988).
- Fert et al. (2017) A. Fert, N. Reyren, and V. Cros, Nat. Rev. Mater. 2 (2017), 10.1038/natrevmats.2017.31.
- Kudasov (2006) Y. B. Kudasov, Phys. Rev. Lett. 96, 027212 (2006).
- Fjellvåg et al. (1996) H. Fjellvåg, E. Gulbrandsen, S. Aasland, A. Olsen, and B. C. Hauback, J. Solid State Chem. 124, 190 (1996).
- Aasland et al. (1997) S. Aasland, H. Fjellvåg, and B. Hauback, Solid State Commun. 101, 187 (1997).
- Kageyama et al. (1997a) H. Kageyama, K. Yoshimura, K. Kosuge, H. Mitamura, and T. Goto, J. Phys. Soc. Jpn. 66, 1607 (1997a).
- Kageyama et al. (1997b) H. Kageyama, K. Yoshimura, K. Kosuge, M. Azuma, M. Takano, H. Mitamura, and T. Goto, J. Phys. Soc. Jpn. 66, 3996 (1997b).
- Agrestini et al. (2008a) S. Agrestini, L. C. Chapon, A. Daoud-Aladine, J. Schefer, A. Gukasov, C. Mazzoli, M. R. Lees, and O. A. Petrenko, Phys. Rev. Lett. 101, 097207 (2008a).
- Mazzoli et al. (2009) C. Mazzoli, A. Bombardi, S. Agrestini, and M. R. Lees, Physica B 404, 3042 (2009).
- Agrestini et al. (2008b) S. Agrestini, C. Mazzoli, A. Bombardi, and M. R. Lees, Phys. Rev. B 77, 140403(R) (2008b).
- Moyoshi and Motoya (2011) T. Moyoshi and K. Motoya, J. Phys. Soc. Jpn. 80, 034701 (2011).
- Fleck et al. (2010) C. L. Fleck, M. R. Lees, S. Agrestini, G. J. McIntyre, and O. A. Petrenko, Europhys. Lett. 90, 67006 (2010).
- Paddison et al. (2014) J. A. M. Paddison, S. Agrestini, M. R. Lees, C. L. Fleck, P. P. Deen, A. L. Goodwin, J. R. Stewart, and O. A. Petrenko, Phys. Rev. B 90, 014411 (2014).
- Motoya et al. (2018) K. Motoya, T. Kihara, H. Nojiri, Y. Uwatoko, M. Matsuda, and T. Hong, J. Phys. Soc. Jpn. 87, 114703 (2018).
- Kamiya and Batista (2012) Y. Kamiya and C. D. Batista, Phys. Rev. Lett. 109, 067204 (2012).
- Leedahl et al. (2019) B. Leedahl, M. Sundermann, A. Amorese, A. Severing, H. Gretarsson, L. Zhang, A. C. Komarek, A. Maignan, M. W. Haverkort, and L. H. Tjeng, Nat Commun 10, 5447 (2019).
- Maignan et al. (2000) A. Maignan, C. Michel, A. C. Masset, C. Martin, and B. Raveau, Euro. Phys. J. B 15, 657 (2000).
- Hardy et al. (2004) V. Hardy, M. R. Lees, O. A. Petrenko, D. M. Paul, D. Flahaut, S. Hébert, and A. Maignan, Phys. Rev. B 70, 064424 (2004).
- Maignan et al. (2004) A. Maignan, V. Hardy, S. Hébert, M. Drillon, M. R. Lees, O. Petrenko, D. M. K. Paul, and D. Khomskii, J. Mater. Chem. 14, 1231 (2004).
- Kim et al. (2018a) J. W. Kim, E. D. Mun, X. Ding, A. Hansen, M. Jaime, N. Harrison, H. T. Yi, Y. Chai, Y. Sun, S. W. Cheong, and V. S. Zapf, Phys. Rev. B 98, 024407 (2018a).
- Yao et al. (2006a) X. Y. Yao, S. Dong, and J. M. Liu, Phys. Rev. B 73, 212415 (2006a).
- Yao et al. (2006b) X. Yao, S. Dong, H. Yu, and J. Liu, Phys. Rev. B 74, 134421 (2006b).
- Kudasov et al. (2008) Y. B. Kudasov, A. S. Korshunov, V. N. Pavlov, and D. A. Maslov, Phys. Rev. B 78, 132407 (2008).
- Qin et al. (2009) M. H. Qin, K. F. Wang, and J. M. Liu, Phys. Rev. B 79, 172405 (2009).
- Soto et al. (2009) R. Soto, G. Martínez, M. N. Baibich, J. M. Florez, and P. Vargas, Phys. Rev. B 79, 184422 (2009).
- ŽukoviÄ et al. (2012) M. ŽukoviÄ, L. MižiÅ¡in, and A. Bobák, Phys. Lett. A 376, 1731 (2012).
- Nekrashevich et al. (2021) I. Nekrashevich, X. Ding, F. Balakirev, H. T. Yi, S.-W. Cheong, L. Civale, Y. Kamiya, and V. S. Zapf, in preparation (2021).
- Agrestini et al. (2011) S. Agrestini, C. L. Fleck, L. C. Chapon, C. Mazzoli, A. Bombardi, M. R. Lees, and O. A. Petrenko, Phys. Rev. Lett. 106, 197204 (2011).
- Seul and Andelman (1995) M. Seul and D. Andelman, Science 267, 476 (1995).
- Kim et al. (2018b) J. W. Kim, E. D. Mun, X. Ding, A. Hansen, M. Jaime, N. Harrison, H. T. Yi, Y. Chai, Y. Sun, S. W. Cheong, and V. S. Zapf, Phys. Rev. B 98, 024407 (2018b).
- Hardy et al. (2018) V. Hardy, V. Caignaert, O. Pérez, L. Hervé, N. Sakly, B. Raveau, M. M. Seikh, and F. Damay, Phys. Rev. B 98, 144414 (2018).
- Niitaka et al. (2001) S. Niitaka, K. Yoshimura, K. Kosuge, M. Nishi, and K. Kakurai, Phys. Rev. Lett. 87, 177202 (2001).
- Frésard et al. (2004) R. Frésard, C. Laschinger, T. Kopp, and V. Eyert, Phys. Rev. B 69, 140405(R) (2004).
- Allodi et al. (2014) G. Allodi, P. Santini, S. Carretta, S. Agrestini, C. Mazzoli, A. Bombardi, M. R. Lees, and R. De Renzi, Phys. Rev. B 89, 104401 (2014).
- Chapon (2009) L. C. Chapon, Phys. Rev. B 80, 172405 (2009).
- Hukushima and Nemoto (1996) K. Hukushima and K. Nemoto, J. Phys. Soc. Jpn. 65, 1604 (1996).
- Landau and Binder (2021) D. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, 5th ed. (Cambridge University Press, 2021).
- Gendiar and Nishino (2005) A. Gendiar and T. Nishino, Phys. Rev. B 71, 024404 (2005).
- Zhang and Charbonneau (2010) K. Zhang and P. Charbonneau, Phys. Rev. Lett. 104, 195703 (2010).
- Zhang and Charbonneau (2011) K. Zhang and P. Charbonneau, Phys. Rev. B 83, 214303 (2011).
- Cardy (1996) J. Cardy, Scaling and Renormalization in Statistical Physics (Cambridge University Press, 1996).
- Blankschtein et al. (1984) D. Blankschtein, M. Ma, A. N. Berker, G. S. Grest, and C. M. Soukoulis, Phys. Rev. B 29, 5250 (1984).
- Coppersmith (1985) S. N. Coppersmith, Phys. Rev. B 32, 1584 (1985).
- Isakov and Moessner (2003) S. V. Isakov and R. Moessner, Phys. Rev. B 68, 104409 (2003).
- Heinonen and Petschek (1989) O. Heinonen and R. G. Petschek, Phys. Rev. B 40, 9052 (1989).
- Bunker et al. (1993) A. Bunker, B. D. Gaulin, and C. Kallin, Phys. Rev. B 48, 15861 (1993).
- Lin et al. (2014) S.-Z. Lin, Y. Kamiya, G.-W. Chern, and C. D. Batista, Phys. Rev. Lett. 112, 155702 (2014).
- Blöte and Swendsen (1979) H. W. J. Blöte and R. H. Swendsen, Phys. Rev. Lett. 43, 799 (1979).
- Janke and Villanova (1997) W. Janke and R. Villanova, Nucl. Phys. B 489, 679 (1997).
- Aharony and Bak (1981) A. Aharony and P. Bak, Phys. Rev. B 23, 4770 (1981).
- Bak and von Boehm (1980) P. Bak and J. von Boehm, Phys. Rev. B 21, 5297 (1980).
- Yokoi et al. (1981) C. S. O. Yokoi, M. D. Coutinho-Filho, and S. R. Salinas, Phys. Rev. B 24, 4047 (1981).
- Campostrini et al. (2001) M. Campostrini, M. Hasenbusch, A. Pelissetto, P. Rossi, and E. Vicari, Phys. Rev. B 63, 214503 (2001).
- Chaikin and Lubensky (1995) P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter Physics (Cambridge University Press, 1995).
- Takeshita et al. (2007) S. Takeshita, T. Goko, J. Arai, and K. Nishiyama, J. Phys. Chem. Solids 68, 2174 (2007).
- Lampen et al. (2014) P. Lampen, N. S. Bingham, M. H. Phan, H. Srikanth, H. T. Yi, and S. W. Cheong, Phys. Rev. B 89, 144414 (2014).