Magnetic-field-controlled spin fluctuations and quantum criticality in Sr3Ru2O7
Abstract
When the transition temperature of a continuous phase transition is tuned to absolute zero, new ordered phases and physical behaviour emerge in the vicinity of the resulting quantum critical point. Sr3Ru2O7 can be tuned through quantum criticality with magnetic field at low temperature. Near its critical field it displays the hallmark -linear resistivity and a electronic heat capacity behaviour of strange metals. However, these behaviours have not been related to any critical fluctuations. Here we use inelastic neutron scattering to reveal the presence of collective spin fluctuations whose relaxation time and strength show a nearly singular variation with magnetic field as is approached. The large increase in the electronic heat capacity and entropy near can be understood quantitatively in terms of the scattering of conduction electrons by these spin-fluctuations. On entering the spin-density-wave ordered phase present near , the fluctuations become stronger suggesting that the order is stabilised through an “order-by-disorder” mechanism.
The nature of the quantum criticality in Sr3Ru2O7 has been debated for twenty years, since the discovery of its anomalous field-dependent electronic properties [1, 2, 3, 4]. Early proposals suggested that critical fluctuations were associated with metamagnetism [1] or fluctuations in the Fermi surface [2]. However, the discovery of spin density wave (SDW) order in Sr3Ru2O7 [5] brought these proposals into question.
The application of a large magnetic field to metals that have antiferromagnetic or spin-density wave order typically destabilises this order because the magnetic moments tend to align with the field. However certain metals, including Sr3Ru2O7 [5] and URu2Si2 [6], have recently been discovered to exhibit magnetic order that is favoured by the magnetic field over a small range of field values. In the case of Sr3Ru2O7, this tuning effect of the field is believed to arise because of a field-induced Lifshitz transition in the Fermi surface [7] which changes the nesting and the wavevector-dependent susceptibility . Spin orbit coupling is also important as shown by the strong dependence of the SDW order on the magnetic field direction [5].
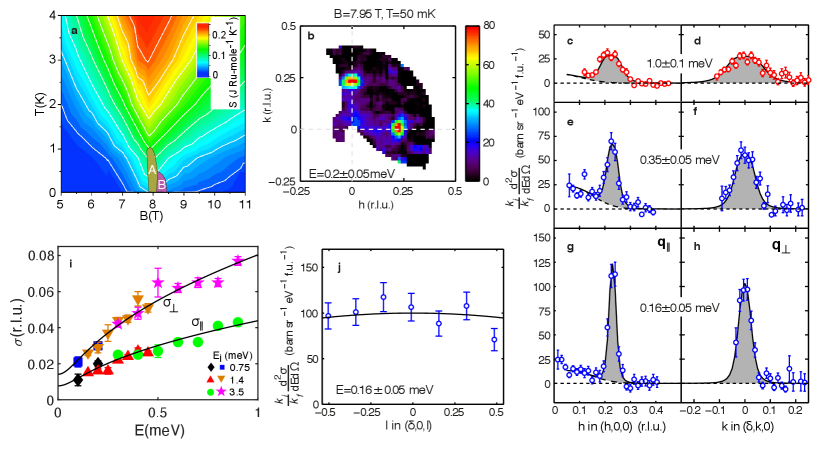
When a magnetic field is applied along the -axis, that is perpendicular to the RuO2 planes, two SDW phases (A and B) are observed [5] for 1 K and T. The phase diagram is shown in Fig. 1a. Transport and thermodynamic measurements [1, 8, 9] indicate a large region of temperature-induced fluctuations surrounding the SDW ordered phases. There is a quantum critical fan centred on T as shown in the field and temperature dependent entropy [8, 9] plotted in Fig. 1a. Note the ridge at characteristic of quantum criticality. As , the low-temperature coefficient of specific heat [3] diverges as and the exponent [1] of the resistivity in falls to . At a low temperature divergence is observed until it is cut off at the SDW ordering temperature [10].
In this work we investigate the very low-energy collective magnetic excitations to determine how they relate to the strange metal and quantum critical behaviour. We find that they are dominated by an overdamped transverse mode with in-plane fluctuations whose characteristic relaxation rate evolves in a nearly singular way. We use a phenomenological spin fluctuation model to relate this behaviour to the low-temperature thermal properties.
Results
We study the very-low energy collective spin fluctuations of Sr3Ru2O7 near the SDW ordering wavevector using inelastic neutron scattering (INS). Measurements are made over the energy range 0–1 meV as a function of . We used the LET time-of-flight spectrometer at the ISIS neutron spallation source (see Methods). Fig. 1b shows a Q-map of the magnetic scattering at meV for T and mK. Strong inelastic scattering can be seen near the SDW ordering wavevectors [5] and with . Higher-energy ( meV) excitations with similar wavevectors have been previously observed in Sr3Ru2O7 at K [12, 13]. Fig. 1c-h show cuts through for various energies. It can be seen that the magnetic excitations broaden with energy. We can define the energy-dependent peak widths (half-width at half maximum) for cuts parallel and perpendicular to as and respectively. These are determined from data such as that in Fig. 1c-h and shown in Fig. 1i. Fig. 1j shows a cut along through , the almost constant intensity indicates a lack of -dependence of the response and is consistent with the moments in the RuO2 bilayers fluctuating independently [12] as previously observed at and higher energies. In our analysis we treat the system as being 2D and ignore the dependence of the excitations.
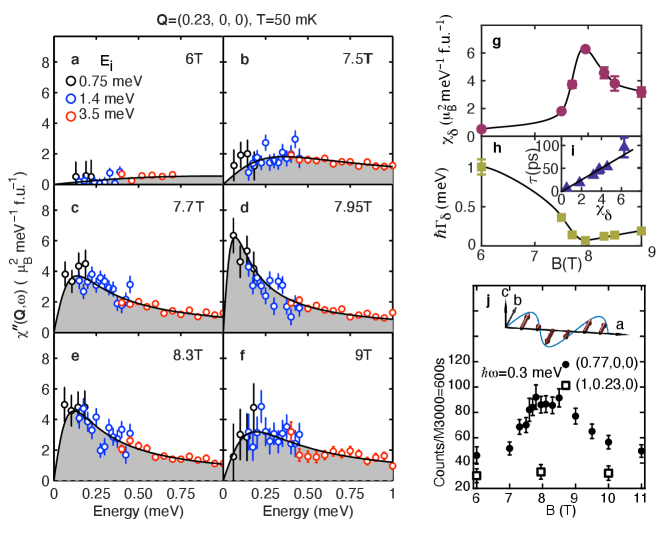
Data such as that in Fig. 1b-h can be converted to the magnetic response function (see Methods). Fig. 2a-f shows the energy-dependence of at for increasing through . Our data is consistent with an overdamped (relaxational) magnetic response at all fields investigated which can be described by a Lorentzian energy dependence. We observe a dramatic reduction in the energy scale of the magnetic response and an increase in its amplitude as the applied field approaches . This is direct evidence that the scattering we observe is associated with the quantum critical point at .
The observed response is characteristic of nearly antiferromagnetic metals (See Methods). It can be well described using a 2D phenomenological model used by Moriya [14, 15] and Millis-Monien-Pines (MMP) [16], for convenience we call this the MMP form:
| (1) |
The MMP form has been widely used to describe cuprate superconductors [16]. In the present case of incommensurate spin density fluctuations we have and , rather than and in the cuprates. The components of the reduced wavevector parallel and perpendicular to are and respectively. The corresponding correlation lengths are and respectively. Near , Eqn. 1 yields excitations described by an overdamped harmonic oscillator with a relaxation rate given by
| (2) |
The solid lines in Fig. 1c-h are fits to the -dependence predicted by Eqn. 1 for each energy transfer with the corresponding extracted widths, and , plotted in 1i. The solid lines in 1i show the predictions the MMP form (Eqn. 1) with the fitted parameters in Table. 1. In addition, the -dependence of at is well described by the overdamped response (Eq. 1) at T and other fields as shown in Fig. 2a-f. Thus the MMP form provides an excellent description of our data.
The lowest energy and strongest fluctuations occur at . These are parameterised by the relaxation rate and susceptibility . The field dependence of these parameters is shown in Fig. 2g,h. We see a dramatic softening (Fig. 2h) and an increase in strength (Fig. 2g) of the fluctuations on approaching . At T, the fluctuating moment associated with the low-energy (1 meV) excitations is Ru-1 which is larger than the ordered moment =0.1 Ru-1 [5].
We can also measure at other reciprocal space positions to probe the polarisation of the excitations. Fig. 2j shows data collected using the IN14 spectrometer at the Institut Laue-Langevin for meV and fields through . At the position we see that the field-dependent intensity mirrors the behaviour at in Fig. 2g, with a peak in SDW phases near . In contrast, no such peak is observed at implying that the spin fluctuation mode (SFM) is only seen when the propagation vector (reduced to the first Brillouin zone) is parallel to . Using the standard theory for magnetic INS (See Methods for details.) we can infer that the spin fluctuations associated with the soft mode propagating along the -axis are polarised along the -axis (see Fig. 2j). The polarisation is perpendicular to the -axis and the propagation vector, and in the same direction as the ordered moment of the SDW [5]. Thus the soft excitation near is found to be a transverse spin fluctuation mode polarised within the RuO2 planes.
Discussion
We have identified an overdamped collective transverse spin-fluctuation mode which is uniquely controlled by magnetic field and becomes soft near . In this section, we discuss the origin of the mode and its relationship to the SDW order and strange metal properties of Sr3Ru2O7. The characteristic wavevectors of emerging magnetic order and low-energy magnetic excitations of quantum materials can often be understood in terms of nesting features of the underlying Fermi surface. In the case of Sr3Ru2O7, density functional theory (DFT) calculations [7] have shown that exchange splitting induced by a large magnetic field causes a topological Lifshitz transition (LT) in the Fermi surface (FS) which creates new pockets of the -band. The four -pockets are centred on the point of the BZ and derive from a FS reconstruction due to the RuO6 octahedra rotations present in the Sr3Ru2O7 structure [11]. The presence of the -pockets allows nesting for a certain range of fields with wavevectors similar to those of the SDW order and the soft-magnetic excitations reported here. We believe the SFM is a paramagnon-like excitation [19] characteristic of metals close to magnetic order. Such modes are understood in terms of the Hubbard model where single-particle spin-flip excitations involving electronic states near the Fermi energy are enhanced by the electron interactions on the Ru site.
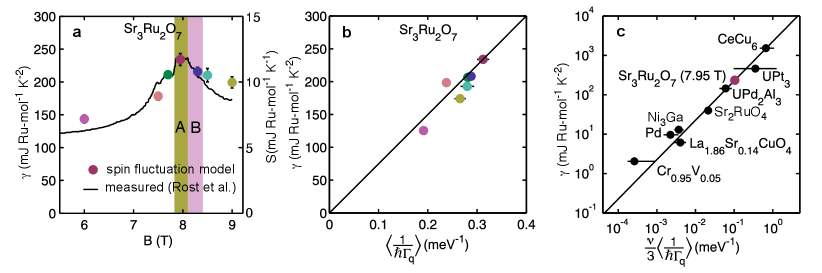
Our results show that the SFM becomes stronger in the SDW ordered state (see Fig. 2). Thus the SDW state in Sr3Ru2O7 forms together with a background of strong quantum and thermal magnetic fluctuations. An interesting feature of Sr3Ru2O7 is that at finite constant the entropy of the SDW phases is larger than in the surrounding regions at lower and higher fields (see Fig. 3a) [3]. This may be understood in terms of the data in Fig. 2. If is large then the fluctuation-dissipation theorem implies that strong spin fluctuations are present. The increase in observed for fields near (see Fig. 2) means that, at the small but finite temperature investigated ( mK), thermal fluctuations would be induced increasing the entropy of the system as observed experimentally (this is estimated explicitly below). Our data supports the notion that the SDW state in Sr3Ru2O7 is stabilised by fluctuations i.e. the free energy is lowered by the system sampling more configurations. The presence of fluctuations can be inferred from the variation of entropy with field and our scattering measurements. This “order-by-disorder” mechanism whereby fluctuations stabilise an ordered phase has been discussed by Onsager, Villain and others [20] in a wide variety of systems ranging from colloidal suspensions to insulating magnets.
The quantum critical and strange metal behaviour of Sr3Ru2O7 have been revealed by -dependent transport and thermal measurements [1, 3, 10, 9]. Clearly it is important to establish how this behaviour relates to the spin fluctuations reported here. The strong spin fluctuations we observe near could provide scattering [21] resulting in strange metal -linear behaviour transport if they have the appropriate -dependence. This will be studied in future work. The signature of quantum criticality in the thermal properties of Sr3Ru2O7 is illustrated in Fig. 1a and Fig. 3a. At finite temperature, there is a divergence in field of the specific heat approaching the SDW phases. We can use our data to make a quantitative estimate of the electronic specific heat and establish whether the signatures seen in thermal measurements are due to spin fluctuations.
The low temperature thermal properties of metals near magnetic instabilities have been discussed in terms of spin fluctuation (paramagnon) theory originally developed in the 1960s [19, 22] and “self-consistent renormalization” (SCR) or self-consistent one-loop approximation introduced in the 1970s [23, 24, 25, 26, 27, 28]. These models address the enhancement of the low-temperature specific heat in metals that arises from the scattering of electrons by spin fluctuations. The spin fluctuations concerned are strongly damped and can drastically alter the thermodynamic properties of the metals. Edwards and Lonzarich [26], and Moriya and collaborators [27, 28] have obtained (See Methods for details) an approximate expression for the contribution of spin fluctuations to in the limit. This is
| (3) |
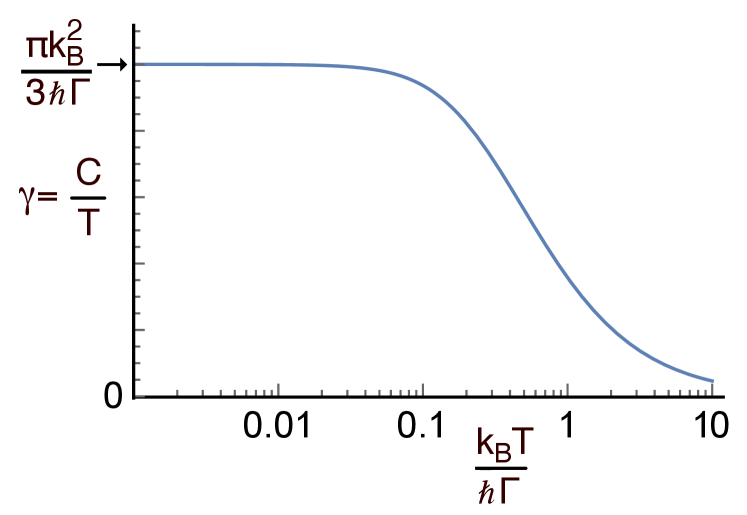
where is the number of polarisations of the spin fluctuations that contribute to the specific heat, is the spin-fluctuation relaxation rate, and denotes an average over the Brillouin zone (BZ). Fig. 4 shows the heat capacity expected for a single mode with temperature independent . Eq. 3 may be checked experimentally by measuring throughout the Brillouin zone using inelastic neutron scattering. Fig. 3c shows a comparison of the measured and heat capacity for a variety of correlated metals(see Methods for details) demonstrating this method broadly works [17, 18]. We have assumed that for all the systems except Sr3Ru2O7.
To estimate the low- specific heat of Sr3Ru2O7 using Eq. 3 we set since only a single transverse spin fluctuation mode is observed (Fig. 2j). The magnetic response is parameterised using Eq. 1 with the parameters in Table. 1 for 7.95 T. Our estimate (see Methods) yields J K-2 Ru-mol-1 which agrees with the measured value [10] J K-2 Ru-mol-1.
For T we made INS measurements over a wide range of wavevectors and energies to demonstrate that Eq. 1 provides a good description of the magnetic response. At other fields, data was only collected near the incommensurate position where the spin fluctuations are strongest and have the lowest energy scale. This allows the field dependence of and , but not , to be determined (see Fig. 2g-h). Near a critical point, we expect and to be controlled by the correlation length . In mean-field theory (see Millis-Monien-Pines[16] and Moriya and Ueda [15]), we expect and . This is consistent with the data plotted in Fig. 2i where it is shown that . Thus, if we assume
| (4) |
and use the values of and determined at T (Table. 1) we have a field-dependent model for the magnetic response . This may be used to compute and hence the field-dependence of the heat capacity. The result of this procedure is shown by the points in Fig. 3a. The heat capacity calculated from our spin fluctuation model shows a remarkable agreement with experimental measurements (solid line). The model reproduces the increase in and entropy on approaching the SDW phases and also the increase of these quantities on entering the SDW phases.
| ( meV-1f.u.-1) | 12.5(3) |
|---|---|
| (r.l.u) | 0.230(2) |
| (r.l.u.) | 0.0116(5) |
| (r.l.u.) | 0.022(1) |
| (meV ) | 0.07(1) |
| (r.l.u2) | 145(22) |
| ( r.l.u2 ) | 522(86) |
We show how the collective spin fluctuations in the correlated electron metal Sr2Ru3O7 evolve in a near singular way, as a magnetic field sweeps the system through a quantum critical point at very low temperature. These fluctuations may stabilise the SDW order observed in this system. We demonstrate how a simple phenomenological model describing the scattering of electrons by the collective spin fluctuations can compute the low temperature heat capacity and entropy of Sr2Ru3O7. Hence the novel thermal and transport properties of Sr2Ru3O7 [1, 2, 3, 4] can be understood in terms of the spin fluctuations reported here and the SDW order [5]. The model appears to have more general applicability to other materials with damped magnetic excitations. For example, it might be used to test whether the doping-dependent peak in the heat capacity in cuprate superconductors [29] can be understood through magnetic excitations.
I Methods
Sample growth and characterisation. Our sample was an array of 9 single crystals sample with total mass of 6.6 g and was grown using an image furnace [30]. The samples were co-aligned on thin aluminium plates with the [001] direction out of plane (parallel to applied field) and the sample had a total mosaic of 1.5∘. Susceptibility, transport and neutron diffraction measurements on samples used in the present experiment showed that they were of comparable purity to previous studies [2, 4, 3]. In particular, they exhibit the hallmarks of the quantum critical phases shown in Figure 1.
Neutron scattering measurements. Experiments were performed at the LET spectrometer at the ISIS spallation source and the IN14 spectrometer at the ILL at temperatures down to mK and fields up to T. For LET we used incident energies =0.75, 1.4 and 3.5 meV. INS can be used to probe the imaginary part of the generalised susceptibility , a measure of the strength of magnetic excitations at a particular . The magnetic scattering cross section is given by [31]
| (5) |
where barn sr-1, is the Landé factor, and are the incident and final neutron wave vectors, is the magnetic form factor for the Ru atom and . Our data were placed on an absolute scale by comparing the scattering signal with that from a V standard. Our quoted susceptibilities are and the factor is used to determine the polarization of the excitations.
Spin fluctuation heat capacity model. Spin fluctuation theory in the “self-consistent renormalization” (SCR) or self-consistent one-loop approximation [23, 24, 25, 26, 27, 28] can be used to estimate the low-temperature free energy can be expressed [22, 25] as
| (6) |
where is the free energy of a harmonic oscillator with frequency and is the relaxation rate of a spontaneous spin fluctuation of wavevector and polarization . Eq. 6 may be used to obtain an approximate expression [28] for the linear coefficient of specific heat ,
| (7) | ||||
| (8) |
This is the sum of the specific heat of harmonic oscillators with the frequency distribution of the spin-fluctuation spectrum, where
| (9) |
To illustrate the result, we evaluate Eq. 8 numerically for a single mode with temperature independent and . The result is shown in Fig. 4.
A renormalization group (RG) analysis by Millis [32] obtained the quantum critical behaviour for various magnetic models. In the case of the 2D antiferromagnet, which is of interest here, both SCR [27, 28] and RG [32] theory yield a logarithmic contribution to at low temperatures.
Edwards and Lonzarich [26], and Moriya and collaborators [27, 28] have obtained an approximate expression (Eq. 3) for in the limit based on Eqns. 6-9.
Application of the spin-fluctuation theory of the specific heat to Sr3Ru2O7
We estimate the low- specific heat of Sr3Ru2O7 using Eq. 3 treating the spin fluctuations as being 2D and assuming the only a single transverse spin fluctuation mode contributes to the specific heat i.e. . The magnetic response is parameterised using Eq. 1 with the parameters in Table 1 for 7.95 T and mK. In order to estimate the heat capacity using Eq. 3, we average over the BZ. Fluctuations corresponding to the four wavevectors are believed to pervade the whole sample so no domain averaging is required. The average is dominated by the regions near the four wavevectors, where there is little overlap of the different terms in the sum of Eq. 1. Thus can be computed by averaging using Eq. 2. We find, for T, meV-1. Hence J K-2 Ru-mol-1.
II Data availability
All relevant data are available from the corresponding authors upon reasonable request.
III Acknowledgements
We acknowledge informative discussions with P. Coleman, A. Chubukov, R. Evans, A. Green, G. G. Lonzarich, M. Zhu and A. P. MacKenzie. Our work was supported by the UK EPSRC (Grant Nos. EP/J015423/1 and EP/R011141/1).
IV Author contributions
C.L. and R.S.P. prepared the samples. C.L., S.M.H., S.R., T.P.C., M.L., R.B., T.G., A.H., A.W., E.M.F. made neutron scattering measurements. C.L. and S.M.H. analyzed the data and wrote the initial manuscript. All authors contributed to the discussion and provided feedback on the manuscript.
V Competing interests
The authors declare no competing interests.
References
- Grigera et al. [2001] S. A. Grigera, R. S. Perry, A. J. Schofield, M. Chiao, S. R. Julian, G. G. Lonzarich, S. I. Ikeda, Y. Maeno, A. J. Millis, and A. P. Mackenzie, Magnetic field-tuned quantum criticality in the metallic ruthenate Sr3Ru2O7, Science 294, 329 (2001).
- Grigera et al. [2004] S. A. Grigera, P. Gegenwart, R. A. Borzi, F. Weickert, A. J. Schofield, R. S. Perry, T. Tayama, T. Sakakibara, Y. Maeno, A. G. Green, and A. P. Mackenzie, Disorder-sensitive phase formation linked to metamagnetic quantum criticality, Science 306, 1154 (2004).
- Rost et al. [2009] A. W. Rost, R. S. Perry, J. F. Mercure, A. P. Mackenzie, and S. A. Grigera, Entropy landscape of phase formation associated with quantum criticality in Sr3Ru2O7, Science 325, 1360 (2009).
- Borzi et al. [2007] R. A. Borzi, S. A. Grigera, J. Farrell, R. S. Perry, S. J. S. Lister, S. L. Lee, D. A. Tennant, Y. Maeno, and A. P. Mackenzie, Formation of a nematic fluid at high fields in Sr3Ru2O7, Science 315, 214 (2007).
- Lester et al. [2015] C. Lester, S. Ramos, R. S. Perry, T. P. Croft, R. I. Bewley, T. Guidi, P. Manuel, D. D. Khalyavin, E. M. Forgan, and S. M. Hayden, Field-tunable spin-density-wave phases in Sr3Ru2O7, Nat. Mat. 14, 373 (2015).
- Knafo et al. [2016] W. Knafo, F. Duc, F. Bourdarot, K. Kuwahara, H. Nojiri, D. Aoki, J. Billette, P. Frings, X. Tonon, E. Lelièvre-Berna, J. Flouquet, and L. P. Regnault, Field-induced spin-density wave beyond hidden order in URu2Si2, Nat. Comm. 7, 13075 (2016).
- Efremov et al. [2019] D. V. Efremov, A. Shtyk, A. W. Rost, C. Chamon, A. P. Mackenzie, and J. J. Betouras, Multicritical Fermi surface topological transitions, Phys. Rev. Lett. 123, 207202 (2019).
- Tokiwa et al. [2016] Y. Tokiwa, M. Mchalwat, R. S. Perry, and P. Gegenwart, Multiple metamagnetic quantum criticality in , Phys. Rev. Lett. 116, 226402 (2016).
- Sun et al. [2018] D. Sun, A. W. Rost, R. S. Perry, A. P. Mackenzie, and M. Brando, Low temperature thermodynamic investigation of the phase diagram of Sr3Ru2O7, Phys. Rev. B 97, 115101 (2018).
- Rost et al. [2011] A. W. Rost, S. A. Grigera, J. A. N. Bruin, R. S. Perry, D. Tian, S. Raghu, S. A. Kivelson, and A. P. Mackenzie, Thermodynamics of phase formation in the quantum critical metal Sr3Ru2O7, Proc. Nat. Acad. Sci. 108, 16549 (2011).
- Shaked et al. [2000] H. Shaked, J. Jorgensen, O. Chmaissem, S. Ikeda, and Y. Maeno, Neutron diffraction study of the structural distortions in Sr3Ru2O7, J. Solid State Chem. 154, 361 (2000).
- Capogna et al. [2003] L. Capogna, E. M. Forgan, S. M. Hayden, A. Wildes, J. A. Duffy, A. P. Mackenzie, R. S. Perry, S. Ikeda, Y. Maeno, and S. P. Brown, Observation of two-dimensional spin fluctuations in the bilayer ruthenate Sr3Ru2O7 by inelastic neutron scattering, Phys. Rev. B 67, 012504 (2003).
- Ramos et al. [2008] S. Ramos, E. M. Forgan, C. Bowell, S. M. Hayden, A. J. Schofield, A. Wildes, E. A. Yelland, S. P. Brown, M. Laver, R. S. Perry, and Y. Maeno, Spin dynamics in Sr3Ru2O7 near the metamagnetic transition by inelastic neutron scattering, Physica B 403, 1270 (2008).
- Moriya [1970] T. Moriya, Spin fluctuations in nearly antiferromagnetic metals, Phys. Rev. Lett. 24, 1433 (1970).
- Moriya and Ueda [2000] T. Moriya and K. Ueda, Spin fluctuations and high temperature superconductivity, Adv. Phys. 49, 555 (2000).
- Millis et al. [1990] A. J. Millis, H. Monien, and D. Pines, Phenomenological model of nuclear relaxation in the normal state of YBa2Cu3O7, Phys. Rev. B 42, 167 (1990).
- Hayden et al. [2000] S. M. Hayden, R. Doubble, G. Aeppli, T. G. Perring, and E. Fawcett, Strongly enhanced magnetic excitations near the quantum critical point of Cr1-xVx and why strong exchange enhancement need not imply heavy fermion behavior, Phys. Rev. Lett. 84, 999 (2000).
- Steffens et al. [2019] P. Steffens, Y. Sidis, J. Kulda, Z. Q. Mao, Y. Maeno, I. I. Mazin, and M. Braden, Spin fluctuations in from polarized neutron scattering: Implications for superconductivity, Phys. Rev. Lett. 122, 047004 (2019).
- Doniach and Engelsberg [1966] S. Doniach and S. Engelsberg, Low-temperature properties of nearly ferromagnetic Fermi liquids, Phys. Rev. Lett. 17, 750 (1966).
- Green et al. [2018] A. G. Green, G. Conduit, and F. Krüger, Quantum order-by-disorder in strongly correlated metals, Ann. Rev. Condens. Mat. Phys. 9, 59 (2018).
- Mousatov et al. [2020] C. H. Mousatov, E. Berg, and S. A. Hartnoll, Theory of the strange metal Sr3Ru2O7, Proc. Nat. Acad. Sci. 117, 2852 (2020).
- Brinkman and Engelsberg [1968] W. F. Brinkman and S. Engelsberg, Spin-fluctuation contributions to the specific heat, Phys. Rev. 169, 417 (1968).
- Murata and Doniach [1972] K. K. Murata and S. Doniach, Theory of magnetic fluctuations in itinerant ferromagnets, Phys. Rev. Lett. 29, 285 (1972).
- Moriya [1985] T. Moriya, Spin Fluctuations in Itinerant Electron Magnetism (Springer, Berlin, 1985).
- Lonzarich [1986] G. Lonzarich, The magnetic equation of state and heat capacity in weak itinerant ferromagnets, J. Mag. Mag. Mat. 54-57, 612 (1986).
- Edwards and Lonzarich [1992] D. M. Edwards and G. G. Lonzarich, The entropy of fluctuating moments at low temperatures, Phil. Mag. B 65, 1185 (1992).
- Moriya and Takimoto [1995] T. Moriya and T. Takimoto, Anomalous properties around magnetic instability in heavy electron systems, J. Phys. Soc Jap. 64, 960 (1995).
- Ishigaki and Moriya [1999] A. Ishigaki and T. Moriya, On the spin fluctuation-enhanced specific heat around the magnetic instabilities, J. Phys. Soc Jap. 68, 3673 (1999).
- Michon et al. [2019] B. Michon, C. Girod, S. Badoux, J. Kačmarčík, Q. Ma, M. Dragomir, H. A. Dabkowska, B. D. Gaulin, J.-S. Zhou, S. Pyon, T. Takayama, H. Takagi, S. Verret, N. Doiron-Leyraud, C. Marcenat, L. Taillefer, and T. Klein, Thermodynamic signatures of quantum criticality in cuprate superconductors, Nature 567, 218 (2019).
- Perry and Maeno [2004] R. Perry and Y. Maeno, Systematic approach to the growth of high-quality single crystals of Sr3Ru2O7, J. Cryst. Growth 271, 134 (2004).
- Boothroyd [2020] A. T. Boothroyd, Principles of Neutron Scattering from Condensed Matter (Oxford University Press, Oxford, 2020).
- Millis [1993] A. J. Millis, Effect of a nonzero temperature on quantum critical points in itinerant fermion systems, Phys. Rev. B 48, 7183 (1993).