\catchline

Magic square and Dirac flavor neutrino mass matrix

Yuta Hyodo Course of Physics, Graduate School of Science, Tokai University,
4-1-1 Kitakaname, Hiratsuka, Kanagawa 259-1292, Japan
[email protected] Teruyuki Kitabayashi Department of Physics, Tokai University,
4-1-1 Kitakaname, Hiratsuka, Kanagawa 259-1292, Japan
[email protected]

(Day Month Year; Day Month Year)

Abstract

{history}

\ccode

PACS numbers:14.60.Pq

1 Introduction

Understanding the nature of the flavor structure of elementary particles is one of the long-term problems in particle physics and cosmology [1, 2]. Many texture ansatz to solve the flavor puzzle are proposed, such as tri-bi maximal texture [3, 4, 5], texture zeros [6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41], $\mu-\tau$ symmetric texture [42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62] and textures under $A_{n}$ as well as $S_{n}$ symmetries [63].

So-called magic texture is one of the textures of the flavor neutrino mass matrix for Majorana type neutrinos [64, 65]. The magic texture is parametrized as

\displaystyle M=\left(\begin{matrix}a&b&c\\ b&d&a+c-d\\ c&a+c-d&b-c+d\end{matrix}\right).

(1)

The applications of the magic texture have been studied for texture zeros of flavor neutrino mass matrix [66], with two simple extensions [67] and for baryon asymmetry of the Universe [68].

The name “magic” is inspired by the nature of the magic square [69]. A magic square of order $n$ is a $n\times n$ square grid filled with distinct natural numbers . Each cell contains a number in the range $1,2,\cdots,n^{2}$ . The sum of the numbers in each row, each column and diagonal is equal. For example, a magic square of order 3 is schematically shown as

	$\displaystyle\begin{array}[]{\|c\|c\|c\|}\hline\cr\ 2&\ 7&\ 6\\ \hline\cr 9&5&1\\ \hline\cr 4&3&8\\ \hline\cr\end{array}\begin{array}[]{c}\leftarrow 15\\ \leftarrow 15\\ \leftarrow 15\\ \end{array}$		(8)
	$\displaystyle\begin{array}[]{ccccccc}&\nearrow&~{}\uparrow&~{}\uparrow&~{}\uparrow&\nwarrow&\\ 15&&~{}15&~{}15&~{}15&&15\\ \end{array}$		(11)

where the sum (which is called magic constant or magic sum) is fifteen. The magic texture in Eq.(1) has a part of the nature of magic square, e.g., the sum of the elements in each row and each column is equal to $a+b+c$ .

In this paper, we estimate the compatibility of the magic square with the Dirac, instead of the Majorana, flavor neutrino mass matrix by numerical calculations. We show that some parts of the nature of the magic square are appeared approximately in the Dirac flavor neutrino mass matrix. Moreover, as the main conclusion of this paper, we demonstrate that the magic squares prefer the normal mass ordering rather than the inverted mass ordering for the Dirac neutrinos.

This paper is organized as follows. In Section.2, ten types of magic square for the Dirac neutrinos are defined. In Section.3, the magic nature of the Dirac flavor neutrino mass matrix is estimated. Section 4 is devoted to a summary.

2 Classification

For a matrix

	$\displaystyle\qquad\quad\left(\begin{matrix}a&~{}b&~{}c\\ d&~{}e&~{}f\\ g&~{}h&~{}i\end{matrix}\right)\begin{array}[]{c}\leftarrow S_{1}\\ \leftarrow S_{2}\\ \leftarrow S_{3}\\ \end{array}$		(15)
	$\displaystyle\begin{array}[]{ccccccc}&\nearrow&\uparrow&\uparrow&\uparrow&\nwarrow&\\ ~{}~{}T^{\prime}&&S_{4}&S_{5}&S_{6}&&T\\ \end{array}$		(18)

we define the following eight sums

	$\displaystyle S_{1}=a+b+c,\quad S_{2}=d+e+f,\quad S_{3}=g+h+i,$
	$\displaystyle S_{4}=a+d+g,\quad S_{5}=b+e+h,\quad S_{6}=c+f+i,$
	$\displaystyle T=a+e+i,\quad T^{\prime}=c+e+g,$		(19)

and the following ten types of magic square for the Dirac neutrinos in the from of the $3\times 3$ matrix.

Type-I: The exact magic square (we call it type-I magic square) should satisfy the following requirement

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime}.

(20)

In this case, the standard deviation should vanish:

\displaystyle sd_{\rm I}=\sqrt{\frac{\sum_{i=1}^{6}(S_{i}-\bar{S})^{2}+(T-\bar{S})^{2}+(T^{\prime}-\bar{S})^{2}}{8}},

(21)

where

\displaystyle\bar{S}=(S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6}+T+T^{\prime})/8,

(22)

is the average of the sums $S_{1},S_{2},\cdots,S_{6},T$ and $T^{\prime}$ . For example, in the case of order 3 magic square

\displaystyle\left(\begin{array}[]{ccc}2&7&6\\ 9&5&1\\ 4&3&8\\ \end{array}\right),

(26)

the sums

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime}=15,

(27)

and the average $\bar{S}=15$ are obtained and the standard deviation becomes $sd_{\rm I}=0$ . Moreover, we obtain the vanishing standard deviation for the following decimal magic square:

\displaystyle\left(\begin{array}[]{ccc}0.2&0.7&0.6\\ 0.9&0.5&0.1\\ 0.4&0.3&0.8\\ \end{array}\right).

(31)

Indeed, the sums of this decimal magic square

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime}=1.5,

(32)

and the average $\bar{S}=1.5$ are obtained and the standard deviation becomes $sd_{\rm I}=0$ .

The standard deviation $sd_{\rm I}$ is a good number to show that whether a matrix has the nature of the exact type-I magic square or not; however, the standard deviation is not good number for our purpose in this paper. For example, the matrix

\displaystyle\left(\begin{array}[]{ccc}2+1&7&6\\ 9&5&1\\ 4&3&8\\ \end{array}\right),

(36)

and

\displaystyle\left(\begin{array}[]{ccc}0.2+0.1&0.7&0.6\\ 0.9&0.5&0.1\\ 0.4&0.3&0.8\\ \end{array}\right),

(40)

have a small perturbation for the type-I magic square in the (1,1) element. Because the requirement of the type-I magic square is only the relation of $S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime}$ , these two matrices are same level of type-I magic square; however, the standard deviations of the matrices in Eq.(36) and Eq.(40) are $0.484$ and $0.0484$ , respectively.

We define the magic index for the type-I magic square as follows

\displaystyle s_{\rm I}=\sqrt{\frac{\sum_{i=1}^{6}(\frac{S_{i}}{\bar{S}}-1)^{2}+(\frac{T}{\bar{S}}-1)^{2}+(\frac{T^{\prime}}{\bar{S}}-1)^{2}}{8}}.

(41)

The magic index $s_{\rm I}$ of the matrices in Eq.(36) and Eq.(40) are same as $0.0315$ .

The small magic index of a matrix means the matrix is much compatible with the magic square.

Type-II: If we relax the requirement of the exact magic square in Eq.(20), we can define the quasi-magic squares. Omitting the trace $T$ in the exact magic requirement in Eq.(20), we have a new requirement

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T^{\prime},

(42)

for a matrix. We call a matrix with the requirement of Eq.(42) the type-II magic square. For the type-II magic square, we define the following magic index

\displaystyle s_{\rm II}=\sqrt{\frac{\sum_{i=1}^{6}(\frac{S_{i}}{\bar{S}}-1)^{2}+(\frac{T^{\prime}}{\bar{S}}-1)^{2}}{7}},

(43)

where

\displaystyle\bar{S}=(S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6}+T^{\prime})/7.

(44)

Type-III: Omitting the sum $T^{\prime}$ in the exact magic constraint in Eq.(20), we have other new requirement

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T,

(45)

for a matrix. We call a matrix with the requirement of Eq.(45) the type-III magic square and we define the following type-III magic index

\displaystyle s_{\rm III}=\sqrt{\frac{\sum_{i=1}^{6}(\frac{S_{i}}{\bar{S}}-1)^{2}+(\frac{T}{\bar{S}}-1)^{2}}{7}},

(46)

where

\displaystyle\bar{S}=(S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6}+T)/7.

(47)

Type-IV: We define the type-IV magic square by omitting the sum $T^{\prime}$ and trace $T$ in the exact magic requirement in Eq.(20). In this case, the requirement becomes

\displaystyle S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=S_{6},

(48)

and we define the following type-IV magic index

\displaystyle s_{\rm IV}=\sqrt{\frac{\sum_{i=1}^{6}(\frac{S_{i}}{\bar{S}}-1)^{2}}{6}},

(49)

where

\displaystyle\bar{S}=(S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6})/6.

(50)

We note that the type-I,-II,-III and -IV magic squares for the Dirac neutrinos are naive extensions of the magic texture of the Majorana neutrino mass matrix in Eq.(1). Especially, the type-IV magic square is the most straight extension of the magic texture for Majorana neutrinos in Eq.(1).

Type-V, -VI, -VII, -VIII, -XI and -X: We add more scenarios by omitting the one of the sum in { $S_{1}$ , $S_{2}$ , $\cdots$ , $S_{6}$ }. Namely, we define the type-V magic square with the following requirement (by omitting $S_{1}$ )

\displaystyle S_{2}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime},

(51)

and the type-V magic index

\displaystyle s_{\rm V}=\sqrt{\frac{\sum_{i=2}^{6}(\frac{S_{i}}{\bar{S}}-1)^{2}+(\frac{T}{\bar{S}}-1)^{2}+(\frac{T^{\prime}}{\bar{S}}-1)^{2}}{7}},

(52)

where

\displaystyle\bar{S}=(S_{2}+S_{3}+S_{4}+S_{5}+S_{6}+T+T^{\prime})/7.

(53)

Similarly, we define more five types of magic square with the following requirements

•

$S_{1}=S_{3}=S_{4}=S_{5}=S_{6}=T=T^{\prime}$ : type-VI (by omitting $S_{2}$ )
•

$S_{1}=S_{2}=S_{4}=S_{5}=S_{6}=T=T^{\prime}$ : type-VII (by omitting $S_{3}$ )
•

$S_{1}=S_{2}=S_{3}=S_{5}=S_{6}=T=T^{\prime}$ : type-VII (by omitting $S_{4}$ )
•

$S_{1}=S_{2}=S_{3}=S_{4}=S_{6}=T=T^{\prime}$ : type-IX (by omitting $S_{5}$ )
•

$S_{1}=S_{2}=S_{3}=S_{4}=S_{5}=T=T^{\prime}$ : type-X (by omitting $S_{6}$ )

The magic indices $s_{\rm VI}$ , $s_{\rm VII}$ , $\cdots$ $s_{\rm X}$ are defined by the same way for $s_{\rm V}$ in Eq.(52).

3 Magic square and Dirac neutrino mass matrix

In this section, first, we show the brief review of the Dirac neutrino mass matrix and the experimental data of the neutrinos. Then, we estimate the compatibility of the magic square with the Dirac flavor neutrino mass matrix by numerical calculations.

3.1 Neutrino mass matrix

The minimal flavor neutrino mass matrix for Dirac neutrinos is obtained by [70]

\displaystyle M=\left(\begin{array}[]{ccc}M_{ee}&M_{e\mu}&M_{e\tau}\\ M_{\mu e}&M_{\mu\mu}&M_{\mu\tau}\\ M_{\tau e}&M_{\tau\mu}&M_{\tau\tau}\\ \end{array}\right)=\left(\begin{array}[]{ccc}U_{e1}m_{1}&U_{e2}m_{2}&U_{e3}m_{3}\\ U_{\mu 1}m_{1}&U_{\mu 2}m_{2}&U_{\mu 3}m_{3}\\ U_{\tau 1}m_{1}&U_{\tau 2}m_{2}&U_{\tau 3}m_{3}\\ \end{array}\right),

(60)

where $m_{1},m_{2}$ and $m_{3}$ denote the neutrino mass eigenstates and

$\displaystyle U_{e1}$	$\displaystyle=$	$\displaystyle c_{12}c_{13},\quad U_{e2}=s_{12}c_{13},\quad U_{e3}=s_{13}e^{-i\delta},$	(61)
$\displaystyle U_{\mu 1}$	$\displaystyle=$	$\displaystyle-s_{12}c_{23}-c_{12}s_{23}s_{13}e^{i\delta},$
$\displaystyle U_{\mu 2}$	$\displaystyle=$	$\displaystyle c_{12}c_{23}-s_{12}s_{23}s_{13}e^{i\delta},\quad U_{\mu 3}=s_{23}c_{13},$
$\displaystyle U_{\tau 1}$	$\displaystyle=$	$\displaystyle s_{12}s_{23}-c_{12}c_{23}s_{13}e^{i\delta},$
$\displaystyle U_{\tau 2}$	$\displaystyle=$	$\displaystyle-c_{12}s_{23}-s_{12}c_{23}s_{13}e^{i\delta},\quad U_{\tau 3}=c_{23}c_{13},$

denote the elements of the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix [71, 72, 73, 74]. We used the abbreviations $c_{ij}=\cos\theta_{ij}$ and $s_{ij}=\sin\theta_{ij}$ ( $i,j$ =1,2,3). The Dirac CP phase is denoted by $\delta$ . In this paper, we assume that the mass matrix of the charged leptons is diagonal and real.

A global analysis of current data shows the following the best-fit values of the squared mass differences $\Delta m_{ij}^{2}=m_{i}^{2}-m_{j}^{2}$ and the mixing angles for the so-called normal mass ordering (NO), $m_{1}<m_{2}<m_{3}$ , of the neutrinos [75]:

$\displaystyle\frac{\Delta m^{2}_{21}}{10^{-5}{\rm eV}^{2}}$	$\displaystyle=$	$\displaystyle 7.39^{+0.21}_{-0.20}\quad(6.79\rightarrow 8.01),$
$\displaystyle\frac{\Delta m^{2}_{31}}{10^{-3}{\rm eV}^{2}}$	$\displaystyle=$	$\displaystyle 2.528^{+0.029}_{-0.031}\quad(2.436\rightarrow 2.618),$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle=$	$\displaystyle 33.82^{+0.78}_{-0.76}\quad(31.61\rightarrow 36.27),$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle=$	$\displaystyle 48.6^{+1.0}_{-1.4}\quad(41.1\rightarrow 51.3),$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle=$	$\displaystyle 8.60^{+0.13}_{-0.13}\quad(8.22\rightarrow 8.98),$
$\displaystyle\delta/^{\circ}$	$\displaystyle=$	$\displaystyle 221^{+39}_{-28}\quad(144\rightarrow 357),$	(62)

where the $\pm$ denotes the $1\sigma$ region and the parentheses denote the $3\sigma$ region. On the other hands, for the so-called inverted mass ordering, $m_{3}<m_{1}\lesssim m_{2}$ , we have

$\displaystyle\frac{\Delta m^{2}_{21}}{10^{-5}{\rm eV}^{2}}$	$\displaystyle=$	$\displaystyle 7.39^{+0.21}_{-0.20}\quad(6.79\rightarrow 8.01),$
$\displaystyle\frac{\Delta m^{2}_{32}}{10^{-3}{\rm eV}^{2}}$	$\displaystyle=$	$\displaystyle-2.510^{+0.030}_{-0.031}\quad(-2.601\rightarrow-2.416),$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle=$	$\displaystyle 33.82^{+0.78}_{-0.75}\quad(31.61\rightarrow 36.27),$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle=$	$\displaystyle 48.4^{+1.0}_{-1.2}\quad(41.4\rightarrow 51.3),$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle=$	$\displaystyle 8.64^{+0.12}_{-0.13}\quad(8.26\rightarrow 9.02),$
$\displaystyle\delta/^{\circ}$	$\displaystyle=$	$\displaystyle 282^{+23}_{-25}\quad(205\rightarrow 348).$	(63)

Moreover, the following constraints

\displaystyle\sum m_{i}<0.12-0.69~{}{\rm eV},

(64)

from the cosmological observation of the cosmic microwave background radiation [76, 39, 77, 78, 79] as well as

\displaystyle|M_{ee}|<0.066-0.155~{}{\rm eV},

(65)

from the neutrino less double beta decay experiments [80, 39] are obtained.

3.2 Numerical analysis

3.2.1 Setup

To estimate the compatibility of the magic square with the Dirac flavor neutrino mass matrix by numerical calculations, we employ the following real matrix

\displaystyle\left(\begin{matrix}a&b&c\\ d&e&f\\ g&h&i\end{matrix}\right)=\left(\begin{array}[]{ccc}|M_{ee}|&|M_{e\mu}|&|M_{e\tau}|\\ |M_{\mu e}|&|M_{\mu\mu}|&|M_{\mu\tau}|\\ |M_{\tau e}|&|M_{\tau\mu}|&|M_{\tau\tau}|\\ \end{array}\right),

(69)

instead of the complex Dirac mass matrix in Eq.(60).

In our numerical calculation, we require that the square mass differences $\Delta m^{2}_{ij}$ , mixing angles $\theta_{ij}$ and the Dirac CP violating phase $\delta$ are varied within the $3\sigma$ experimental ranges and the lightest neutrino mass is varied within $0.001-0.1$ eV. We also require that the constraints $|M_{ee}|<0.155$ eV and $\sum m_{i}<0.241$ eV (TT, TE, EE+LowE+lensing [76, 40]) are satisfied.

In the following subsubsections, we show the result from the numerical calculations for the ten types of magic squares. Because the type-I,-II,-III and -IV magic squares are naive extensions of the magic texture of the Majorana neutrino mass matrix in Eq.(1), we separate our discussion into some parts. First, we will see the results for the type-I,-II,-III and -IV magic squares. Next, the results for type-V,-VI, $\cdots$ -X magic squares are presented. Moreover, we have a discussion with the results of the recently reported T2K and NOvA tension.

3.2.2 Type-I,-II,-III and -IV

\tbl

Minimum and maximum values of magic index for the type-I,-II,-III and -IV magic squares. type magic index NO IO I $s_{\rm I}^{\rm min}$ 0.132 0.136 $s_{\rm I}^{\rm max}$ 0.783 0.462 II $s_{\rm II}^{\rm min}$ 0.102 0.107 $s_{\rm II}^{\rm max}$ 0.874 0.504 III $s_{\rm III}^{\rm min}$ 0.0729 0.0956 $s_{\rm III}^{\rm max}$ 0.739 0.476 IV $s_{\rm IV}^{\rm min}$ 0.0593 0.0888 $s_{\rm IV}^{\rm max}$ 0.832 0.525

We show the results from the numerical calculations for the type-I,-II,-III and -IV magic squares in Tables 3.2.2 - 3.2.2 as well as Figures 1 and 2.

Table 3.2.2 shows that the minimum and maximum values of the magic indices of type-I, -II, -III and type-IV magic squares for the Dirac flavor neutrino mass matrix. We recall that the small magic index of a matrix means the matrix is much compatible with the magic square. We note the following three points:

•

The top row in the Table 3.2.2 shows that the minimum of the type-I magic index are $s_{1}^{\rm min}=0.132$ and $s_{1}^{\rm min}=0.136$ for NO and IO, respectively. Thus, the exact magic square (type-I magic square) is hardly realized for the Dirac flavor neutrino mass matrix.
•

The smallest minimum magic index for NO(IO) is obtained in the case of type-IV as $0.0593$ ( $0.0888$ ). Thus, if we relax the requirement of the magic squares from exact magic square (type-I) to relatively rough magic square (type-IV), some parts of the nature of the magic square are appeared for the Dirac flavor neutrino mass matrix.
•

The magic squares prefer the normal mass ordering rather than the inverted mass ordering.

\tbl

The sums $S_{1},S_{2},\cdots,S_{6},T,T^{\prime}$ of the type-I, -II, -III and type-IV magic squares for the Dirac flavor neutrino mass matrix in the unit of ${\rm eV}$ . The upper (lower) half of the table shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . NO type $s$ $S_{1}$ $S_{2}$ $S_{3}$ $S_{4}$ $S_{5}$ $S_{6}$ $T^{\prime}$ $T$ I $s_{\rm I}^{\rm min}$ 0.117 0.133 0.139 0.120 0.130 0.138 0.0971 0.158 $s_{\rm I}^{\rm max}$ 0.0128 0.0387 0.0433 0.00166 0.0144 0.0788 0.0126 0.0436 II $s_{\rm II}^{\rm min}$ 0.117 0.135 0.137 0.122 0.129 0.139 0.100 - $s_{\rm II}^{\rm max}$ 0.0129 0.0383 0.0432 0.00168 0.0145 0.0782 0.0123 - III $s_{\rm III}^{\rm min}$ 0.118 0.137 0.136 0.123 0.129 0.139 - 0.149 $s_{\rm III}^{\rm max}$ 0.0129 0.0387 0.0432 0.00163 0.0144 0.0788 - 0.0434 IV $s_{\rm IV}^{\rm min}$ 0.118 0.137 0.136 0.123 0.129 0.139 - - $s_{\rm IV}^{\rm max}$ 0.0127 0.0389 0.0432 0.00166 0.0144 0.0788 - - IO type $s$ $S_{1}$ $S_{2}$ $S_{3}$ $S_{4}$ $S_{5}$ $S_{6}$ $T^{\prime}$ $T$ I $s_{\rm I}^{\rm min}$ 0.129 0.126 0.138 0.137 0.148 0.107 0.105 0.160 $s_{\rm I}^{\rm max}$ 0.0677 0.0451 0.0529 0.0798 0.0843 0.00156 0.0406 0.0619 II $s_{\rm II}^{\rm min}$ 0.128 0.132 0.133 0.138 0.147 0.109 0.107 - $s_{\rm II}^{\rm max}$ 0.0694 0.0462 0.0543 0.0820 0.0864 0.00155 0.0414 - III $s_{\rm III}^{\rm min}$ 0.128 0.131 0.134 0.140 0.146 0.108 - 0.150 $s_{\rm III}^{\rm max}$ 0.0683 0.0429 0.0559 0.0782 0.0873 0.00158 - 0.0723 IV $s_{\rm IV}^{\rm min}$ 0.127 0.133 0.132 0.137 0.147 0.109 - - $s_{\rm IV}^{\rm max}$ 0.0677 0.0430 0.0552 0.0777 0.0865 0.00163 - -

Table 3.2.2 shows the sums $S_{1},S_{2},\cdots,S_{6},T,T^{\prime}$ of the type-I, -II, -III and type-IV magic squares for the Dirac flavor neutrino mass matrix in the unit of ${\rm eV}$ . The upper (lower) half of the Table 3.2.2 shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . We note the following point:

•

The sum of the diagonal elements $T^{\prime}$ or $T$ tends to differ from other sums in the type-I and type-II. This character of $T^{\prime}$ or $T$ yields the large magic index (deviation from the magic square).

\tbl

The neutrino parameters $m_{i},\theta_{ij},\delta$ of the type-I, -II, -III and type-IV magic squares for the Dirac flavor neutrino mass matrix. The upper (lower) half of the table shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ NO type $s$ $m_{1}{\rm[eV]}$ $m_{2}{\rm[eV]}$ $m_{3}{\rm[eV]}$ $\theta_{12}/^{\circ}$ $\theta_{23}/^{\circ}$ $\theta_{13}/^{\circ}$ $\delta/^{\circ}$ I $s_{\rm I}^{\rm min}$ 0.0745 0.0750 0.0897 36.12 51.19 8.851 183.9 $s_{\rm I}^{\rm max}$ 0.00104 0.00834 0.0511 33.14 41.39 8.400 345.7 II $s_{\rm II}^{\rm min}$ 0.0746 0.0750 0.0894 35.56 41.17 8.964 181.4 $s_{\rm II}^{\rm max}$ 0.00105 0.00838 0.0507 34.92 41.12 8.270 345.9 III $s_{\rm III}^{\rm min}$ 0.0748 0.0754 0.0899 36.20 51.10 8.866 340.2 $s_{\rm III}^{\rm max}$ 0.00101 0.00832 0.0511 35.43 41.48 8.277 336.7 IV $s_{\rm IV}^{\rm min}$ 0.0751 0.0756 0.0899 35.88 51.17 8.980 354.5 $s_{\rm IV}^{\rm max}$ 0.00104 0.00832 0.0512 32.88 41.51 8.294 325.1 IO type $s$ $m_{1}{\rm[eV]}$ $m_{2}{\rm[eV]}$ $m_{3}{\rm[eV]}$ $\theta_{12}/^{\circ}$ $\theta_{23}/^{\circ}$ $\theta_{13}/^{\circ}$ $\delta/^{\circ}$ I $s_{\rm I}^{\rm min}$ 0.0852 0.0856 0.0691 36.21 51.20 8.982 205.1 $s_{\rm I}^{\rm max}$ 0.0487 0.0494 0.00101 35.50 51.08 8.619 343.9 II $s_{\rm II}^{\rm min}$ 0.0852 0.0856 0.0701 33.23 41.41 8.881 205.3 $s_{\rm II}^{\rm max}$ 0.0500 0.0506 0.00101 35.66 51.10 8.822 347.4 III $s_{\rm III}^{\rm min}$ 0.0851 0.0855 0.0699 35.74 50.98 8.947 343.5 $s_{\rm III}^{\rm max}$ 0.0498 0.0506 0.00102 31.62 51.16 8.594 210.3 IV $s_{\rm IV}^{\rm min}$ 0.0852 0.0857 0.0701 32.25 48.50 8.906 329.1 $s_{\rm IV}^{\rm max}$ 0.0494 0.0500 0.00106 32.14 50.68 8.959 208.5

Table 3.2.2 shows the neutrino parameters $m_{i},\theta_{ij},\delta$ of the type-I, -II, -III and type-IV magic squares for the Dirac flavor neutrino mass matrix. As same as Table 3.2.2, the upper (lower) half of the Table 3.2.2 shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . The following ranges of the neutrino parameters are roughly favored for the magic squares:

$\displaystyle m_{i}/{\rm eV}$	$\displaystyle\sim$	$\displaystyle 0.07-0.09,$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 36,$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 51,{\rm(for~{}type-I,-III,-IV)},\quad\sim 41,{\rm(for~{}type-II)},$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 8.9$
$\displaystyle\delta/^{\circ}$	$\displaystyle\sim$	$\displaystyle 181-184,{\rm(for~{}type-I,-II)},\quad\sim 340,{\rm(for~{}type-III,IV)},$	(70)

for NO and

$\displaystyle m_{i}/{\rm eV}$	$\displaystyle\sim$	$\displaystyle 0.07-0.09,$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 33-36,$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 51,{\rm(for~{}type-I,-III,-IV)},\quad\sim 41,{\rm(for~{}type-II)},$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 8.9$
$\displaystyle\delta/^{\circ}$	$\displaystyle\sim$	$\displaystyle 205,{\rm(for~{}type-I,-II)},\quad\sim 329-344,{\rm(for~{}type-III,IV)},$	(71)

for IO.

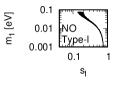
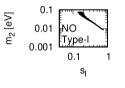
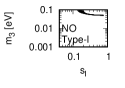
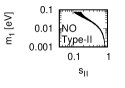
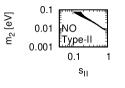
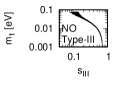
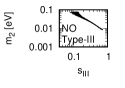
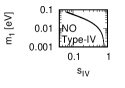
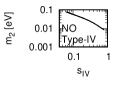
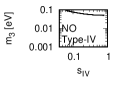
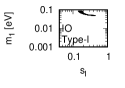
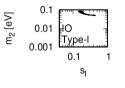
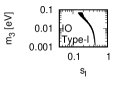
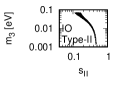
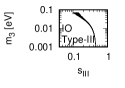
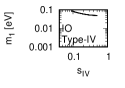
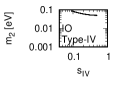
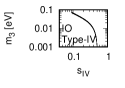
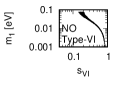
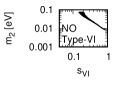
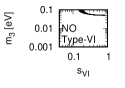
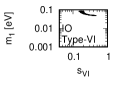
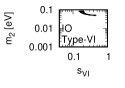
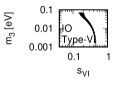
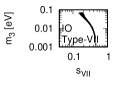
Figure 1 and Figure 2 show that the dependence of the neutrino parameters $m_{i},\theta_{ij},\delta$ on the magic index $s$ in the case of NO and IO, respectively. We note the following four points:

•

The large neutrino masses yield small magic indices (the large masses are favorable for magic squares).
•

The minimum of $s_{\rm I}$ , $s_{\rm II}$ and $s_{\rm III}$ for type-I, -II and -III are obtained with large $\theta_{12}$ , $\theta_{23}$ and $\theta_{13}$ .
•

The minimum of $s_{\rm I}$ and $s_{\rm II}$ for type-I and type-II are obtained with small $\delta$ .
•

The minimum of $s_{\rm III}$ for type-III is obtained with large $\delta$ .

for both NO and IO.

We would like to emphasis again the following remarkable result of our numerical calculations:

•

All types of the magic squares prefer the normal mass ordering rather than the inverted mass ordering for the type-V,-VI, $\cdots$ , -X magic squares (see Table 3.2.2).

Although the neutrino mass ordering (either NO or IO) is not determined experimentaly, a global analysis shows that the preference for the normal mass ordering is mostly due to neutrino oscillation measurements [81, 39, 82]. The theoretical origin of the mass ordering of neutrinos is still big problem. There is a possibility that the origin of the normal mass ordering is the magic nature of the neutrinos. This conclusion becomes more rigid in the next subsubsection.

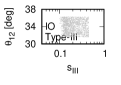
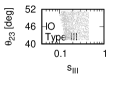
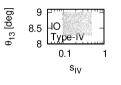
Refer to caption — Figure 1: Dependence of the neutrino parameters $m_{i},\theta_{ij},\delta$ on the magic index $s$ in the case of NO for the type-I,-II,-III and -IV magic squares.

3.2.3 Type-V,-VI, $\cdots$ , -X

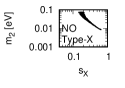
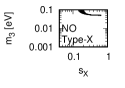
We show the results from the numerical calculations for the type-V,-VI, $\cdots$ , -X magic squares in Tables 3.2.3 - 3.2.3 as well as Figures 3 and 6.

Table 3.2.3 shows that the minimum and maximum values of the magic indices of type-V,-VI, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix. Again, we recall that the small magic index of a matrix means the matrix is much compatible with the magic square. We note the following two points:

•

The smallest minimum magic index for NO is obtained in the case of type-V as $0.133$ and for IO is obtained in the case of type-X as $0.120$ . These minimum magic indices are lager than the type-IV magic indices $0.0593$ (NO) and $0.0888$ (IO) in Table 3.2.2. Thus, the most compatible type of magic square for Dirac neutrinos is the type-IV which is the most straight extension of the Majorana magic mass matrix texture.
•

The magic squares prefer the normal mass ordering rather than the inverted mass ordering except with type-IX and type-X. According to the results shown in Tables 3.2.2 and 3.2.3, we conclude that the possibility that the origin of the normal mass ordering is the magic nature of the neutrinos becomes more rigid.

\tbl

Minimum and maximum values of magic index for the type-V,-VI, $\cdots$ , -X magic squares. type magic index NO IO V $s_{\rm V}^{\rm min}$ 0.133 0.144 $s_{\rm V}^{\rm max}$ 0.742 0.492 VI $s_{\rm VI}^{\rm min}$ 0.140 0.143 $s_{\rm VI}^{\rm max}$ 0.873 0.480 VII $s_{\rm VII}^{\rm min}$ 0.138 0.144 $s_{\rm VII}^{\rm max}$ 0.864 0.483 VIII $s_{\rm VIII}^{\rm min}$ 0.137 0.145 $s_{\rm VIII}^{\rm max}$ 0.655 0.482 IX $s_{\rm IX}^{\rm min}$ 0.142 0.137 $s_{\rm IX}^{\rm max}$ 0.752 0.468 X $s_{\rm X}^{\rm min}$ 0.139 0.120 $s_{\rm X}^{\rm max}$ 0.674 0.250

Table 3.2.3 shows the sums $S_{1},S_{2},\cdots,S_{6},T,T^{\prime}$ of the type-V,-VI, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix in the unit of ${\rm eV}$ . The upper (lower) half of the Table 3.2.3 shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . We note the following point:

•

The magnitudes of the each entries in Table 3.2.3 for the type-V,-VI, $\cdots$ , -X magic squares are almost same with the magnitudes of the each entries in Table 3.2.2 for the type-I,-II, $\cdots$ , -IV magic squares.

\tbl

The sums $S_{1},S_{2},\cdots,S_{6},T,T^{\prime}$ of the type-V,-VI, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix in the unit of ${\rm eV}$ . The upper (lower) half of the table shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . NO type $s$ $S_{1}$ $S_{2}$ $S_{3}$ $S_{4}$ $S_{5}$ $S_{6}$ $T^{\prime}$ $T$ V $s_{\rm V}^{\rm min}$ - 0.133 0.138 0.120 0.130 0.139 0.0970 0.158 $s_{\rm V}^{\rm max}$ - 0.0437 0.0379 0.001657 0.0147 0.0783 0.0118 0.0364 VI $s_{\rm VI}^{\rm min}$ 0.117 - 0.139 0.120 0.130 0.138 0.0975 0.159 $s_{\rm VI}^{\rm max}$ 0.0127 - 0.0382 0.00172 0.0143 0.0781 0.0116 0.0369 VII $s_{\rm VII}^{\rm min}$ 0.118 0.133 - 0.121 0.131 0.139 0.0980 0.159 $s_{\rm VII}^{\rm max}$ 0.0129 0.0431 - 0.00163 0.0142 0.0787 0.0119 0.0371 VIII $s_{\rm VIII}^{\rm min}$ 0.117 0.133 0.139 - 0.130 0.139 0.0973 0.159 $s_{\rm VIII}^{\rm max}$ 0.0129 0.0431 0.0374 - 0.0143 0.0775 0.0116 0.0358 IX $s_{\rm IX}^{\rm min}$ 0.115 0.131 0.137 0.118 - 0.137 0.0954 0.156 $s_{\rm IX}^{\rm max}$ 0.0131 0.0435 0.0378 0.00165 - 0.0781 0.0118 0.0363 X $s_{\rm X}^{\rm min}$ 0.0117 0.133 0.138 0.119 0.123 - 0.0972 0.159 $s_{\rm X}^{\rm max}$ 0.0126 0.0387 0.0429 0.00163 0.0146 - 0.0125 0.0431 IO type $s$ $S_{1}$ $S_{2}$ $S_{3}$ $S_{4}$ $S_{5}$ $S_{6}$ $T^{\prime}$ $T$ V $s_{\rm V}^{\rm min}$ - 0.126 0.136 0.137 0.147 0.106 0.103 0.159 $s_{\rm V}^{\rm max}$ - 0.0453 0.0530 0.0799 0.0847 0.00156 0.0407 0.0627 VI $s_{\rm VI}^{\rm min}$ 0.128 - 0.137 0.137 0.147 0.106 0.104 0.159 $s_{\rm VI}^{\rm max}$ 0.0677 - 0.0449 0.0779 0.0865 0.00159 0.0421 0.0713 VII $s_{\rm VII}^{\rm min}$ 0.129 0.127 - 0.138 0.148 0.108 0.105 0.161 $s_{\rm VII}^{\rm max}$ 0.0684 0.0456 - 0.0806 0.0854 0.00168 0.0409 0.0631 VIII $s_{\rm VIII}^{\rm min}$ 0.128 0.126 0.137 - 0.147 0.107 0.103 0.159 $s_{\rm VIII}^{\rm max}$ 0.0668 0.0528 0.0440 - 0.0853 0.00166 0.0420 0.0709 IX $s_{\rm IX}^{\rm min}$ 0.128 0.126 0.137 0.137 - 0.107 0.104 0.160 $s_{\rm IX}^{\rm max}$ 00.0678 0.0449 0.0532 0.0801 - 0.00154 0.0408 0.0612 X $s_{\rm X}^{\rm min}$ 0.121 0.119 0.129 0.130 0.140 - 0.0989 0.151 $s_{\rm X}^{\rm max}$ 0.0681 0.0458 0.0531 0.0802 0.0850 - 0.0407 0.0629

\tbl

The neutrino parameters $m_{i},\theta_{ij},\delta$ of the type-V,-VI, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix. The upper (lower) half of the table shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ NO type $s$ $m_{1}{\rm[eV]}$ $m_{2}{\rm[eV]}$ $m_{3}{\rm[eV]}$ $\theta_{12}/^{\circ}$ $\theta_{23}/^{\circ}$ $\theta_{13}/^{\circ}$ $\delta/^{\circ}$ V $s_{\rm V}^{\rm min}$ 0.0743 0.0748 0.0898 36.25 51.24 8.914 170.7 $s_{\rm V}^{\rm max}$ 0.00102 0.00858 0.0509 34.18 51.19 8.377 330.6 VI $s_{\rm VI}^{\rm min}$ 0.0746 0.0752 0.0895 35.97 51.23 8.972 180.6 $s_{\rm VI}^{\rm max}$ 0.00107 0.00834 0.0508 33.10 50.47 8.277 340.5 VII $s_{\rm VII}^{\rm min}$ 0.0750 0.0755 0.0899 36.08 51.17 8.970 172.8 $s_{\rm VII}^{\rm max}$ 0.00101 0.00830 0.0510 33.27 50.16 8.576 350.4 VIII $s_{\rm VIII}^{\rm min}$ 0.0748 0.0753 0.0897 36.20 50.77 8.872 164.8 $s_{\rm VIII}^{\rm max}$ 0.00102 0.0839 0.0504 34.27 51.25 8.457 351.8 IX $s_{\rm IX}^{\rm min}$ 0.0734 0.0739 0.0889 36.23 51.12 8.711 183.0 $s_{\rm IX}^{\rm max}$ 0.00101 0.00859 0.0508 34.63 51.10 8.438 335.8 X $s_{\rm X}^{\rm min}$ 0.0743 0.0748 0.0889 36.05 51.05 8.959 182.9 $s_{\rm X}^{\rm max}$ 0.00104 0.00844 0.0506 31.78 41.71 8.361 356.4 IO type $s$ $m_{1}{\rm[eV]}$ $m_{2}{\rm[eV]}$ $m_{3}{\rm[eV]}$ $\theta_{12}/^{\circ}$ $\theta_{23}/^{\circ}$ $\theta_{13}/^{\circ}$ $\delta/^{\circ}$ V $s_{\rm V}^{\rm min}$ 0.0843 0.0847 0.0689 36.07 50.78 8.825 208.8 $s_{\rm V}^{\rm max}$ 0.0489 0.0496 0.00101 34.82 51.06 8.795 341.3 VI $s_{\rm VI}^{\rm min}$ 0.0847 0.0851 0.0689 36.10 51.06 8,865 205.5 $s_{\rm VI}^{\rm max}$ 0.0494 0.0501 0.00103 31.80 41.88 8.847 343.6 VII $s_{\rm VII}^{\rm min}$ 0.0853 0.0857 0.0696 35.97 50.76 9.009 206.9 $s_{\rm VII}^{\rm max}$ 0.0493 0.05000 0.00109 34.86 51.29 8.918 342.4 VIII $s_{\rm VIII}^{\rm min}$ 0.0846 0.0851 0.0689 35.92 50.93 9.015 217.0 $s_{\rm VIII}^{\rm max}$ 0.0487 0.0494 0.00107 31.68 41.45 8.480 340.9 IX $s_{\rm IX}^{\rm min}$ 0.0848 0.0853 0.0694 35.91 51.11 8.835 206.7 $s_{\rm IX}^{\rm max}$ 0.0486 0.0494 0.00100 36.14 51.18 8.435 347.2 X $s_{\rm X}^{\rm min}$ 0.0805 0.0810 0.0643 36.19 50.89 8.895 207.8 $s_{\rm X}^{\rm max}$ 0.0491 0.0498 0.00120 35.04 50.84 8.858 346.7

Table 3.2.3 shows the neutrino parameters $m_{i},\theta_{ij},\delta$ of the type-V,-VI, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix. As same as Table 3.2.3, the upper (lower) half of the Table 3.2.3 shows the sums in the case of NO (IO). For each type of magic squares, the upper (lower) row shows the sums for $s_{\rm min}$ ( $s_{\rm max})$ . The following ranges of the neutrino parameters are roughly favored for the magic squares:

$\displaystyle m_{i}/{\rm eV}$	$\displaystyle\sim$	$\displaystyle 0.07-0.09,$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 36,$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 51,$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 8.9,$
$\displaystyle\delta/^{\circ}$	$\displaystyle\sim$	$\displaystyle 165-180,$	(72)

for NO and

$\displaystyle m_{i}/{\rm eV}$	$\displaystyle\sim$	$\displaystyle 0.07-0.085,$
$\displaystyle\theta_{12}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 36,$
$\displaystyle\theta_{23}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 51,$
$\displaystyle\theta_{13}/^{\circ}$	$\displaystyle\sim$	$\displaystyle 8.8-9.0$
$\displaystyle\delta/^{\circ}$	$\displaystyle\sim$	$\displaystyle 205-217,$	(73)

for IO. In comparison with the type-I, -II $\cdots$ -IV magic squares, the variance of each neutrino parameters is small in the case of type-V,-VI, $\cdots$ , -X magic squares.

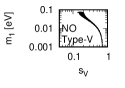
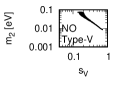
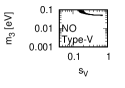
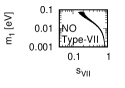
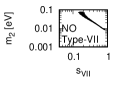
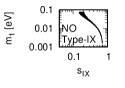
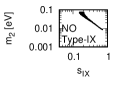
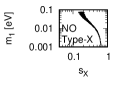
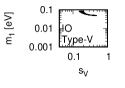
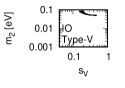
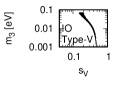
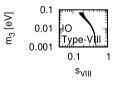
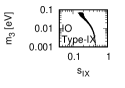
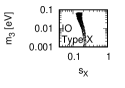
Figure 3 and Figure 4 show that the dependence of the neutrino parameters $m_{i},\theta_{ij},\delta$ on the magic index $s$ in the case of NO. Figure 5 and Figure 6 show the same as Figure 3 and Figure 4 but in the case of IO. We note the following two points:

•

The large neutrino masses yield small magic indices (the large masses are favorable for magic squares).
•

The minimum of magic index $s_{i}$ $(i={\rm V,VI,\cdots,X})$ is obtained with large $\theta_{12}$ , $\theta_{23}$ and $\theta_{13}$ as well as with small $\delta$ .

for both NO and IO.

3.2.4 T2K and NOvA tension

Recently, T2K and NOvA reported a tension in the measurement of $\delta$ and $\sin^{2}\theta_{23}$ for the normal mass ordering of neutrinos [83, 84]. Both experiments favor the upper octant of $\theta_{23}$ ; however, the T2K data shows $\delta>\pi$ against the NOvA result $\delta<\pi$ . Now, we have a discussion with the results of the latest T2K and NOvA experiments.

Table 3.2.4 shows the mixing angle $\theta_{23}$ and the Dirac CP phase $\delta$ for minimum magic index of the type-I, -II, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix with NO. The symbol “O” (“ $\times$ ”) means the corresponding case is favorable (unfavorable) with recent T2K or NOvA data.

Since the most compatible type of magic square is the type-IV (which has the smallest minimum magic index $s_{\rm IV}^{\rm min}=0.0593$ ), it seems that the T2K result is more favorable than the NOvA result in the context of the magic square.

\tbl

The mixing angle $\theta_{23}$ and the Dirac CP phase $\delta$ for minimum magic index of the type-I, -II, $\cdots$ , -X magic squares for the Dirac flavor neutrino mass matrix with NO. The symbol “O” (“ $\times$ ”) means the corresponding case is favorable (unfavorable) with recent T2K or NOvA data. I II III IV V VI VII VIII IX X $s_{i}^{\rm min}$ 0.132 0.102 0.0729 0.0593 0.133 0.140 0.138 0.137 0.142 0.139 $\theta_{23}/^{\circ}$ 51.19 41.17 51.10 51.17 51.24 51.23 51.17 50.77 51.12 51.05 $\delta/^{\circ}$ 183.9 181.4 340.2 354.5 170.7 180.6 172.8 164.8 183.0 182.9 T2K O $\times$ O O $\times$ O $\times$ $\times$ O O NOvA $\times$ $\times$ $\times$ $\boldmath{\times}$ O $\times$ O O $\times$ $\times$

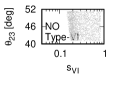
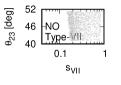
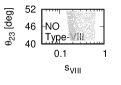
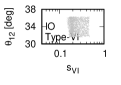
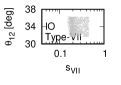
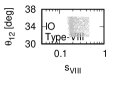
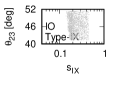
4 Summary

The magic texture is one of the successful textures of the flavor neutrino mass matrix for the Majorana type neutrinos. The name “magic” is inspired by the nature of the magic square. In this paper, we have estimated the compatibility of the magic square with the Dirac, instead of the Majorana, flavor neutrino mass matrix by numerical calculations. We have shown that some parts of the nature of the magic square are appeared approximately in the Dirac flavor neutrino mass matrix and the magic squares prefer the normal mass ordering rather than the inverted mass ordering for the Dirac neutrinos. Moreover, we have mentioned about the recently reported a tension between T2K and NOvA experiments. It turned our that the T2K result is more favorable than the NOvA result in the context of the magic square.

Finally, we would like to comment about Eq.(69). In this paper, we have estimated the compatibility of the magic square with the real matrix in Eq.(69) instead of the complex Dirac mass matrix in Eq.(60). This approach may be enough as a first step of the study about the relation between the magic square and the Dirac flavor neutrino mass matrix; however, if we estimate the compatibility of the magic square with the complex Dirac mass matrix in Eq.(60) by an appropriate method, the results may be modified. A detailed analysis of this topic will be found in our future study.

References

[1] S. F. King, J. Phys. G 42, 123001 (2015).
[2] F. Feruglio and A. Romanino, “Neutrino Flavour Symmetries”, arXiv:1912.06028 (Dec 2019).
[3] P. F. Harrison, D. H. Perkins, and W. G. Scott, Phys. Lett. B 530, 167 (2002).
[4] Z. -z. Xing, Phys. Lett. B 533, 85 (2002).
[5] P. F. Harrison and W. G. Scott, Phys. Lett. B 535, 163 (2002).
[6] M. S. Berger and K. Siyeon, Phys. Rev. D 64, 053006 (2001).
[7] P. H. Frampton, S. L. Glashow, and D. Marfatia, Phys. Lett. B 536, 79 (2002).
[8] Z. -z. Xing, Phys. Lett. B 530, 159 (2002).
[9] Z. -z. Xing, Phys. Lett. B 539, 85 (2002).
[10] A. Kageyama, S. Kaneko, N. Shimoyana, and M. Tanimoto, Phys. Lett. B 538, 96 (2002).
[11] Z. -z. Xing, Phys. Rev. D 69, 013006 (2004).
[12] W. Grimus, A. S. Joshipura, L. Lavoura, and M. Tanimoto, Eur. Phys. J. C 36, 227 (2004).
[13] C. I. Low, Phys. Rev. D 70, 073013 (2004).
[14] C. I. Low, Phys. Rev. D 71, 073007 (2005).
[15] W. Grimus and L. Lavoura, J. Phys. G 31, 693 (2005).
[16] S. Dev, S. Kumar, S. Verma, and S. Gupta, Phys. Rev. D 76, 013002 (2007).
[17] Z. -z. Xing and S. Zhou, Phys. Lett. B 679, 249 (2009).
[18] H. Fritzsch, Z. -z. Xing, and S. Zhou, J. High Energy Phys. 09, 083 (2011).
[19] S. Kumar, Phys. Rev. D 84, 077301 (2011).
[20] S. Dev, S. Gupta, and R. R. Gautam, Phys. Lett. B 701, 605 (2011).
[21] T. Araki, J. Heeck, and J. Kubo, J. High Energy Phys. 07, 083 (2012).
[22] P. Ludle, S. Morisi, and E. Peinado, Nucl. Phys. B 857, 411 (2012).
[23] E. Lashin and N. Chamoun, Phys. Rev. D 85, 113011 (2012).
[24] K. Deepthi, S. Gollu, and R. Mohanta, Eur. Phys. J. C 72, 1888 (2012).
[25] D. Meloni and G. Blankenburg, Nucl. Phys. B 867, 749 (2013).
[26] D. Meloni, A. Meroni, and E. Peinado, Phys. Rev. D 89, 053009 (2014).
[27] S. Dev, R. R. Gautam, L. Singh, and M. Gupta, Phys. Rev. D 90, 013021 (2014).
[28] R. G. Felipe and H. Serodio, Nucl. Phys. B 886, 75 (2014).
[29] P. O. Ludl and W. Grimus, J. High Energy Phys. 07, 090 (2014).
[30] L. M. Cebola, D. E. Costa, and R. G. Felipe, Phys. Rev. D 92, 025005 (2015).
[31] R. R. Gautam, M. Singh, and M. Gupta, Phys. Rev. D 92, 013006 (2015).
[32] S. Dev, L. Singh, and D. Raj, Eur. Phys. J. C 75, 394 (2015).
[33] T. Kitabayashi and M. Yasuè, Phys. Rev. D 93, 053012 (2016).
[34] S. Zhou, Chin. Phys. C 40, 033102 (2016).
[35] M. Singh, G. Ahuja and M. Gupta, Prog. Theor. Exp. Phys. 2016, 123B08 (2016).
[36] K. Bora, D. Borah and D. Dutta, Phys. Rev. D 96, 075006 (2017).
[37] D. M. Barreiros, R. G. Felipe and F. R. Joaquim, Phys. Rev. D 97, 115016 (2018).
[38] D. M. Barreiros, R. G. Felipe and F. R. Joaquim, J. High Energy Phys. 01, 223 (2019).
[39] F. Capozzi, E. D. Valentino and E. Lisi, A. Marrone, A. Melchiorri and A. Palazzo, Phys. Rev. D 101, 116013 (2020).
[40] M. Singh, EPL 2020, 11002 (2020).
[41] D. M. Barreiros, F. R. Joaquim and T. T. Yanagida, arXiv:2003.06332.
[42] T. Fukuyama and H. Nishiura, (1997), arXiv:hep-ph/9702253.
[43] C. S. Lam, Phys. Lett. B 507, 214 (2001).
[44] E. Ma and M. Raidal, Phys. Rev. Lett. 87, 011802 (2001); Erratum Phys. Rev. Lett. 87, 159901 (2001).
[45] K. R. S. Balaji, W. Grimus, and T. Schwetz, Phys. Lett. B 508, 301 (2001).
[46] Y. Koide, H. Nishiura, K. Matsuda, T. Kikuchi, and T. Fukuyama, Phys. Rev. D 66, 093006 (2002).
[47] T. Kitabayashi and M. Yasue, Phys. Rev. D 67, 015006 (2003).
[48] Y. Koide, Phys. Rev. D 69, 093001 (2004).
[49] I. Aizawa, M. Ishiguro, T. Kitabayashi, and M. Yasue, Phys. Rev. D 70, 015011 (2004).
[50] A. Ghosal, Mod. Phys. Lett. A 19, 2579 (2004).
[51] R. N. Mohapatra and W. Rodejohann, Phys. Rev. D 72, 053001 (2005).
[52] Y. Koide, Phys. Lett. B 607, 123 (2005).
[53] T. Kitabayashi and M. Yasue, Phys. Lett. B 621, 133 (2005).
[54] N. Haba and W. Rodejohann, Phys. Rev. D 74, 017701 (2006).
[55] Z.-z. Xing, H. Zhang, and S. Zhou,Phys. Lett. B 641, 189 (2006).
[56] Y. H. Ahn, S. K. Kang, C. S. Kim, and J. Lee, Phys. Rev. D 73, 093005 (2006).
[57] A. S. Joshipura, Eur. Phys. J. C 53, 77 (2008).
[58] J. C. Gomez-Izquierdo and A. Perez-Lorenzana, Phys. Rev. D 82, 033008 (2010).
[59] H.-J. He and F.-R. Yin, Phys. Rev. D 84, 033009 (2011).
[60] H.-J. He and X.-J. Xu, Phys. Rev. D 86, 111301 (2012).
[61] J. C. Gomez-Izquierdo, Eur. Phys. J. C 77, 551 (2017).
[62] T. Fukuyama, Prog. Theor. Exp. Phys. 2017, 033B11 (2017).
[63] G. Altarelli and F. Feruglio, Rev. Mod. Phys. 82, 2701 (2010).
[64] P. F. Harrison and W. G. Scott, Phys. Lett. B 594, 324 (2004).
[65] C. S. Lam, Phys. Lett. B 640, 260 (2006).
[66] R. R. Gautam and S. Kumar, Phys. Rev. D 94, 036004 (2016).
[67] K. S. Channey and S. Kumar, J. Phys. G: Nucl. Part. Phys. 46, 015001 (2019).
[68] S. Verma and M. Kashav, arXiv:1910.04467v2 (Jan. 2020).
[69] A. Levitin, and M. Levitin, “Algorithmic Puzzles”, Oxford University Press, NewYork (2011).
[70] C. Hagedron and W. Rodejohann, J. High Energy Phys. 07, 034 (2005).
[71] B. Pontecorvo, Sov. Phys. JETP 6 (1957) 429.
[72] B. Pontecorvo, Sov. Phys. JETP 7 (1958) 172;
[73] Z. Maki, M. Nakagawa and S. Sakata, Prog. Theor. Phys. 28, 870 (1962).
[74] M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98, 030001 (2018).
[75] I. Esteban, M. C. Gonzalez-Garcia, A. H-Cabezudo, M. Maltoni, and T. Schwetz, J. High Energy Phys. 01, 106 (2019). See also, NuFIT webpage, http://www.nu-fit.org.
[76] N. Aghanim, et al. (Planck Collaboration), “Planck 2018 results. VI. Cosmological parameters”, arXiv:1807.06209v2 (Sep 2019).
[77] E. Giusarma, M. Gerbino, O. Mena, S. Vagnozzi, S. Ho and K. Freese, Phys. Rev. D 94, 083522 (2016).
[78] S. Vagnozzi, E. Giusarma, O. Mena, K. Freese, M. Gerbino, S. Ho and M. Lattanzi, Phys. Rev. D 96, 123503 (2017).
[79] E. Giusarma, S. Vagnozzi, S. Ho, S. Ferraro, K. Freese, R. K.-Rubio and K.-B. Luk, Phys. Rev. D 98, 123536 (2018).
[80] M. Agostini, et al., (GERDA Collaboration), Science 365, 1445 (2019).
[81] P. F. de Salas, D. V. Forero, C. A. Ternes, Tórtola and J.W.F. Valle, Phys. Lett. B 782, 633 (2018).
[82] M. G. Aartsen, et al., (IceCube-Gen2 Collaboration) and T. J. C. Bezerra, et al., (JUNO Collaboration), Phys. Rev. D 101, 032006 (2020).
[83] A. Himmel, (NOvA Collaboration), “New Oscillation Results from the NOvA Experiment”, Neutrino 2020, Fermilab (Jul. 2020). https://conferences.fnal.gov/nu2020/
[84] P.Dunne, (T2K Collaboration), “Latest Neutrino Oscillation Results from T2K”, Neutrino 2020, Fermilab (Jul. 2020). https://conferences.fnal.gov/nu2020/

Magic square and Dirac flavor neutrino mass matrix

Abstract

1 Introduction

2 Classification

3 Magic square and Dirac neutrino mass matrix

3.1 Neutrino mass matrix

3.2 Numerical analysis

3.2.1 Setup

3.2.2 Type-I,-II,-III and -IV

3.2.3 Type-V,-VI, ⋯\cdots, -X

3.2.4 T2K and NOvA tension

4 Summary

References

3.2.3 Type-V,-VI, $\cdots$ , -X