Machine learning topological invariants of non-Hermitian systems
Abstract
The study of topological properties by machine learning approaches has attracted considerable interest recently. Here we propose machine learning the topological invariants that are unique in non-Hermitian systems. Specifically, we train neural networks to predict the winding of eigenvalues of four prototypical non-Hermitian Hamiltonians on the complex energy plane with nearly accuracy. Our demonstrations in the non-Hermitian Hatano-Nelson model, Su-Schrieffer-Heeger model and generalized Aubry-André-Harper model in one dimension, and two-dimensional Dirac fermion model with non-Hermitian terms show the capability of the neural networks in exploring topological invariants and the associated topological phase transitions and topological phase diagrams in non-Hermitian systems. Moreover, the neural networks trained by a small data set in the phase diagram can successfully predict topological invariants in untouched phase regions. Thus, our work paves the way to revealing non-Hermitian topology with the machine learning toolbox.
I Introduction
Machine learning, which lies at the core of the artificial intelligence and data science, has recently achieved huge success from industrial applications (especially in computer vision and the natural language process) to fundamental researches in physics, cheminformatics and biology Jordan and Mitchell (2015); LeCun et al. (2015); Goodfellow et al. (2016); Carleo et al. (2019). In physics, machine learning has shown its availability in experimental data analysis Biswas et al. (2013); Rem et al. (2019); Kasieczka et al. (2019) and classification of phases of matter Wang (2016); Carrasquilla and Melko (2017); Zhang and Kim (2017); Deng et al. (2017); Huembeli et al. (2019); Dong et al. (2019); Van Nieuwenburg et al. (2017); Carvalho et al. (2018); Zhang et al. (2018a); Sun et al. (2018); Huembeli et al. (2018); Tsai et al. (2020); Ming et al. (2019); Rodriguez-Nieva and Scheurer (2019); Holanda and Griffith (2020); Ohtsuki and Mano (2020). Among these applications, one of the most interesting problems is to extract the global properties of topological phases of matter from local inputs, such as the topological invariants that intrinsically nonlocal. Recent works have shown that artificial neural networks can be trained to predict the topological invariants of band insulators with a high accuracy Zhang et al. (2018a); Sun et al. (2018). The advantage of this approach is that the neural network can capture global topology directly from local raw data inputs. Other theoretical proposals for identifying topological phases by using supervised or unsupervised learning have been suggested Carvalho et al. (2018); Huembeli et al. (2018); Rodriguez-Nieva and Scheurer (2019); Holanda and Griffith (2020); Ohtsuki and Mano (2020); Zhang et al. (2020a); Long et al. (2020); Scheurer and Slager (2020); Balabanov and Granath (2020, 2021). Notably, the convolutional neural network (CNN) trained from raw experimental data has been demonstrated to identify topological phases Rem et al. (2019); Lian et al. (2019).
On the other hand, growing efforts have been invested in uncovering exotic topological states and phenomena in non-Hermitian systems in recent years Diehl et al. (2008); Malzard et al. (2015); Lee (2016); Yao and Wang (2018); Yao et al. (2018); Song et al. (2019); Kunst et al. (2018); Takata and Notomi (2018); Wang et al. (2019); Zeng et al. (2017); Lang et al. (2018); Hamazaki et al. (2019); Jin and Song (2019); Kawabata et al. (2019a); Liu et al. (2019); Lee et al. (2019); Yamamoto et al. (2019); Hatano and Nelson (1996, 1997); Gong et al. (2018); Ghatak and Das (2019); Leykam et al. (2017); Shen et al. (2018); Zhang et al. (2018b, 2020b, 2020c); Luo and Zhang ; Jiang et al. (2019); Longhi (2019); Liu et al. (2020a); Wu and An (2020); Zeng et al. (2020); Zeng and Xu (2020); Tang et al. (2020); Liu et al. (2020b); Zhang et al. (2020d); Xu and Chen (2020); Liu et al. (2020c); Xi et al. ; Lee et al. (2020); Yoshida et al. (2019). The non-Hermiticity may come from gain and loss effects Zeng et al. (2017); Lang et al. (2018); Takata and Notomi (2018); Wang et al. (2019); Hamazaki et al. (2019), non-reciprocal hoppings Hatano and Nelson (1996, 1997), or dissipations in open systems Diehl et al. (2008); Malzard et al. (2015). Non-Hermiticity-induced topological phases are also investigated in disordered Zhang et al. (2020c); Luo and Zhang ; Jiang et al. (2019); Longhi (2019); Liu et al. (2020a); Wu and An (2020); Zeng et al. (2020); Zeng and Xu (2020); Tang et al. (2020); Liu et al. (2020b) and interacting systems Zhang et al. (2020d); Xu and Chen (2020); Liu et al. (2020c); Xi et al. ; Lee et al. (2020); Yoshida et al. (2019). In non-Hermitian topological systems, there are not only topological properties defined by the eigenstates (such as topological Bloch bands), but also topological invariants solely lying on the eigenenergies. For instance, complex energy landscapes and exceptional points give rise to different topological invariants, which include the winding number (vorticity) defined solely in the complex energy plane Gong et al. (2018); Ghatak and Das (2019); Leykam et al. (2017); Shen et al. (2018). This winding number and several closely related winding numbers in the presence of symmetries can lead to a richer topological classification than that of their Hermitian counterparts. In addition, it was revealed Borgnia et al. (2020); Okuma et al. (2020); Zhang et al. (2020e) that the nonzero winding number in the complex energy plane is the topological origin of the so-called non-Hermitian skin effect Lee (2016); Yao and Wang (2018); Yao et al. (2018); Song et al. (2019); Kunst et al. (2018). Considering that the topological invariants in Hermitian systems have been studied recently based on the machine learning approach Carvalho et al. (2018); Zhang et al. (2018a); Sun et al. (2018); Huembeli et al. (2018); Rodriguez-Nieva and Scheurer (2019); Holanda and Griffith (2020); Ohtsuki and Mano (2020); Zhang et al. (2020a); Long et al. (2020); Scheurer and Slager (2020), the flexibility of machine learning such a different kind of winding number in non-Hermitian systems is urgent and meaningful research.
In this work, we adapt machine learning with neural networks to predict non-Hermitian topological invariants and classify the topological phases in several prototypical non-Hermitian models in one and two dimensions. We first take the Hatano-Nelson model Hatano and Nelson (1996, 1997) as a feasibility verification of machine learning in identifying non-Hermitian topological phases. We show that the trained CNN can predict the winding numbers of eigenenergies with a high accuracy even for those phases that are not included in the training, whereas the fully connected neural network (FCNN) can only predict those in the trained phases. We interpolate the intermediate value of the CNN and find a strong relationship with the winding angle of the eigenenergies in the complex plane. We then use the CNN to study topological phase transitions in a non-Hermitian Su-Schrieffer-Heeger (SSH) model Su et al. (1979) with non-reciprocal hopping. We find that the CNN can precisely detect the transition points near the phase boundaries even though trained only by the data in the deep phase region. By using the CNN, we further obtain the topological phase diagram of a non-Hermitian generalized Aubry-André-Harper (AAH) model Harper (1955); Aubry and Andre (1980); Liu et al. (2015) with non-reciprocal hopping and a complex quasiperiodic potential. The winding numbers evaluated from the CNN show an accuracy of more than 99% with theoretical values in the whole parameter space, even though the complex on-site potential is absent in the training process. Finally, we extend our scenario to a two-dimensional non-Hermitian Dirac fermion model Shen et al. (2018) and show the feasibility of neural networks in revealing the winding numbers associated with exceptional points. Our work may provide an efficient and general approach to reveal non-Hermitian topology based on the machine learning toolbox.
The rest of this paper is organized as follows. We first study the winding number of the Hatano-Nelson model as a feasibility verification of our machine learning method in Sec. II. Different performances of the CNN and the FCNN are also discussed. Section III is devoted to revealing the topological phase transition in the non-Hermitian SSH model by the CNN. In Sec. IV, we show that the CNN can precisely predict the topological phase diagram of the non-Hermitian generalized AAH model. In Sec. V, we extend our scenario to reveal the winding numbers associated with exceptional points in a two-dimensional non-Hermitian Dirac fermion model. A further discussion and short summary are finally presented in Sec. VI.
II Learning topological invariants in Hatano-Nelson model
Let us begin with the Hatano-Nelson model, which is a prototypical single-band non-Hermitian model and takes the following Hamiltonian in a one-dimensional lattice of length Hatano and Nelson (1996, 1997):
| (1) |
Here denotes the amplitudes of non-reciprocal hopping, is the creation (annihilation) operator at the -th lattice site, denotes the hopping length between two sites, and is the on-site energy in the lattice. The original Hatano-Nelson model takes the disorder potential with random and the nearest-neighbor hopping with , as shown in Fig. 1(a). Here we consider the clean case by setting and take as a parameter in learning the topological phase transition with neural networks. Under the periodic boundary condition, the corresponding eigenenergies in this case are given by
| (2) |
where is the Hamiltonian in momentum space with the quasimomentum .

Following Ref. Gong et al. (2018), we can define the winding number in the complex energy place as a topological invariant in the Hatano-Nelson model,
| (5) |
where denotes the principal value of the argument belonging to . For a discretized with finite lattice site , the complex-energy winding number reduces to
| (6) |
where . Note that for Hermitian systems (), one has due to the real energy spectrum with . According to this definition, a nontrivial winding number gives the number of times the complex eigenenergy encircles the base point , which is unique to non-Hermitian systems. The complex eigenenergy windings for two typical cases with are shown in Fig. 1(b). To examine whether the neural networks have the ability to learn the winding number in a general formalism, we enable the parameter to control the number of times the complex eigenenergy encircles the origin of the complex plane. When the loop winds around the origin times during the variation of from to , the winding number is , where indicates counterclockwise and clockwise windings, respectively.

We now build a supervised task for learning the winding number given by Eq. (6) based on neural networks. First, we need labeled data sets for the training and evaluation. Since the winding number is intrinsically nonlocal and characterized by a complex energy spectrum, we feed neural networks with the normalized spectrum-dependent configurations at points discretized uniformly from to , where and . Therefore, the input data are an -dimensional matrix of the form
with a period of : . In the following, we set , which is large enough to take discrete energy spectra as the input data of neural networks. Labels are computed according to Eq. (6) for the corresponding configurations.
The machine learning workflow is schematically shown in Fig. 2. For the Hatano-Nelson model with different , the output of the neural network is a real number , and the predicted winding number is interpreted as the integer that is closest to . We first train the neural networks with both complex spectrum configurations and their corresponding true winding numbers. After the training, we feed only the complex-spectrum-dependent configurations to the neural networks and compare their predictions with the true winding numbers, from which we determine the percentage of the correct predictions as the accuracy. In this case, we consider two typical classes of neural networks: the CNN and FCNN, respectively. The neural networks are similar to those in Ref. Zhang et al. (2018a) for calculating the winding number of the Bloch vectors in Hermitian topological bands.
The CNN in our training has two convolution layers with 32 kernels of size and 1 kernel of size , followed by a fully connected layer of two neurons before the output layer. The total number of trainable parameters is 262. The FCNN has two hidden layers with 32 and 2 neurons, respectively. The total number of trainable parameters is 2213. The architecture of two classes of neural networks is shown in Fig. 2. All hidden layers have rectified linear units as activation functions and the output layer has linear activation function . The objective function to be optimized is defined by
| (7) |
where and are, respectively, the winding number of the th complex eigenenergies predicted by the neural networks and the true winding number, and is the total number of the training data set. We take training configurations, which consist of a ratio of of them having winding numbers , respectively. The test set consists of some configurations with winding numbers that are not included in the training set and that are not seen by neural networks during the training. The number of configurations for each kind of winding number is . The training details are given in the Appendix A.

After training, we test with other configurations and the predicted winding numbers are shown in Fig. 3 (a). Note that the networks tend to produce close to integers and thus we take each final winding number as the integer closest to . As shown in Fig. 3 (b), we plot the probability distribution of predicted from the CNN on different test data sets. The test results of two neural networks are presented in Table. 1, which shows a very high accuracy (more than ) of the CNN and FCNN on the test data set with the winding numbers . We can find that the CNN performs generally better than the FCNN. Surprisingly, the CNN works well even in the cases of , which consist of configurations with larger winding numbers not seen by neural networks during the training. On the contrary, the FCNN cannot predict the true winding numbers even though it has more trainable parameters. These results indicate that the convolutional layer respects the translation symmetry of complex spectrum in the momentum space explicitly and convolutional layers can take local winding angle explicitly through the kernels.
To further see the advantage of the CNN, we open up the black box of neural networks and find the relationship between intermediate activation values and physical quantities, i.e. the winding angle . Based on the convolutional layers, we consider that the activation value after two convolutions should have a linear dependence on to some extent and the following fully-connected layers use a simple linear regression. We plot versus , with and being the -th component of intermediate values after two convolution layers. As shown in Fig. 3 (c), the intermediate output is approximately linear with within certain regions. A linear combination of these intermediate values with correct coefficients in the following fully connected layers can then easily lead to the true winding number. In this way, the CNN realizes a calculation workflow that is equivalent to the wingding angle in Eq. (6).
| CNN Accuracy | 99.8 % | 99.4 % | 98.0% | ||
| FCNN Accuracy | 99.2% | 99.0% | 98.5% |
III Learning topological transition in non-Hermitian SSH model
Based on the accurate winding number calculated by the CNN, we further use a similar CNN to study topological phase transitions in the non-Hermitian SSH model, as shown in Fig. 4 (a). The considered model with nonreciprocal intra-cell hopping in the one-dimensional dimerized lattice of unit cells can be described by the following Hamiltonian:
| (8) |
Here and (, ) denote the creation (annihilation) operators on the -th and sublattices, is the uniform intra-cell hopping amplitude, is the non-Hermitian parameter, and is the inter-cell hopping amplitude. When , this model reduces to the Hermitian SSH model. Under the periodic boundary condition, the corresponding Hamiltonian in the momentum space is given by
| (9) |
The two energy bands are then given by
| (10) |
Following Ref. Leykam et al. (2017); Shen et al. (2018); Gong et al. (2018); Ghatak and Das (2019); Kawabata et al. (2019b) and considering the sublattice symmetry, one can define an inter-band winding number
| (11) |
For discretized with finite , it reduces to
| (12) |
with in this model. Notably, is half the total windings of and around the origin of the complex plane as is increased from to . The inter-band winding number is quantized as because the windings of and are always integers due to periodicity Shen et al. (2018). We consider , , and in our study.

For this model, we set the configuration of input data as . To learn the topological phase transition in this model, we treat it as a classification task assisted by neural networks. The output of the neural network is the probabilities of different winding numbers. We define as the output probabilities of winding numbers , respectively. The predicted winding number is interpreted as , which has the highest probability. The architecture of the CNN is shown in Fig. 2, with some training details given in the Appendix A. For our task, the objective function to be optimized is defined by
| (13) |
where is the label of the th configuration, and the set represents the winding number predicted by the neural networks. The expression means that it will take the value 1 when the condition is satisfied and the value 0 in the opposite case. In this model, and represent the winding numbers correspondingly.
To see whether the CNN is a good tool to study topological phase transitions in this model, we define a Euclidean distance between the configuration and the phase boundaries in the parameter space of the Hamiltonian:
| (14) |
where (straight lines in the parameter space about and ) is the equation of phase boundaries with being the parameters of the equation. In addition, we define a distance threshold . In the following, we choose as a demonstration and the situation of is discussed later. The training data set consists of configurations satisfying that are sampled from different phases with different winding numbers.
We test the CNN with two test data sets: (I) configurations satisfying and (II) 300 configurations distributed uniformly in . The data sets distribution and some training details are given in the Appendix A. After the training, both test data sets, I and II, are evaluated by the CNN. We use the same training and test workflow for . Figure 4 (b) shows the accuracy of the test data sets versus the distance threshold . We find that the CNN achieves a high accuracy in different , meaning that the CNN can detect the phase transitions precisely in these regions. Moreover, we locate the phase transition points from the crossing points of prediction probabilities; the phase transitions determined by this method are relatively accurate, as shown in Fig. 4 (c). In the deep phase, the probability for the true winding number stays at nearly . On the other hand, the probability for increases linearly at the phase transitions. In a word, the CNN is a great supplementary tool to study the phase transitions when only phase properties in some confident regions (e.g., the deep phase) are provided.

IV Learning topological phase diagram in non-Hermitian AAH model
To show that our results can be generalized to other non-Hermitian topological models, we consider a generalized AAH model in a one-dimensional quasicrystal as shown in Fig. 5 (a), with two kinds of non-Hermiticities arising from the nonreciprocal hopping Jiang et al. (2019) and complex on-site potential phase Longhi (2019). The Hamiltonian of such a non-Hermitian AAH model is given by Tang et al. (2021)
| (15) |
where the non-reciprocal hopping terms and the on-site potential are parameterized as
| (16) | ||||
Here denotes the right-hopping (left-hopping) amplitude between the -th and the -th site with parameters and being real, denotes the complex quasiperiodic potential with and an irrational number, and the parameters and tune the non-reciprocity and complex phase, respectively. For finite quasiperiodic systems, one can take the lattice site number as a rational number and with being the -th Fibonacci number since . In the following, we set and .
The winding numbers discussed previously cannot be directly used here due to the periodicity breaking. In this case, one can consider a ring chain with an effective magnetic flux penetrating through the center, such that the Hamiltonian matrix can be rewritten as
| (17) |
One can define the winding number with respect to and the energy base Gong et al. (2018); Jiang et al. (2019):
| (18) |
Here counts the number of times the complex spectral trajectory encircles the energy base ( does not belong to the energy spectrum) when the flux varies from to . For discretized with , the winding number can be rewritten as
| (19) |
where .
Below we show that the generalization ability enables the CNN to precisely obtain topological phase diagrams of this non-Hermitian generalized AAH model, even though we only use nonreciprocal-hopping configurations in the training. To do this, we treat the problem as a classification task and set the configuration in this case as with . The architecture of the CNN is similar to that of the non-Hermitian SSH model, but the output layer now becomes two neurons for two kinds of winding numbers. We define as the output probabilities of the winding numbers , respectively. The objective function in this case is given by [similarly to that in Eq. (13)]
| (20) |
where (with ) represent , respectively.
To test the generality of the neural network, we train the neural network with configurations corresponding to Hamiltonians with , and test it by using configurations corresponding to Hamiltonians with both nonreciprocal hopping amplitudes () and complex potentials (). The training data set includes configurations with and the interval ; each one consists of configurations corresponding Hamiltonians sampled from the two-dimensional parameter space spanned by . The test data set includes 110 pairs of parameters, which consist of from to with the interval and from to with the interval . We sample configurations corresponding to Hamiltonians from the region for each pair of parameters.
After the training, we find that the CNN performs well even without knowledge of the complex on-site potential () during the training process. Figure 5(b) shows the test accuracy table with respect to the two non-Hermiticity parameters and , with the accuracy more than in the whole parameter region. Moreover, we present the topological phase diagrams with respect to and predicted by the CNN, as shown in Fig. 5(c). It is clear that the CNN performs excellently in the deep phase with only a little struggle near the topological phase transitions. We attribute the high accuracy in this learning task to two factors. First, the normalizing data enable both the training and the test data distribution in the complex unit, which is important for the generality of the neural network. Second, the topological transitions in this model are consistent with the real-complex transitions in the energy spectrum Tang et al. (2021), which reduces the complexity of the problem when input data are dependent on a complex spectrum.
V Generalization to two-dimensional model
Previously, we have used neural networks to investigate the topological properties of several non-Hermitian models in one dimension. In this section, we extend our scenario to reveal the winding numbers associated with exceptional points in the two-dimensional non-Hermitian Dirac fermion model proposed in Ref. Shen et al. (2018). The Dirac Hamiltonian with non-Hermitian terms in two-dimensional momentum space is given by Shen et al. (2018)
| (21) |
where are the Pauli matrices, denote the non-Hermitian modulation parameters, and and denotes the real and imaginary parts of the Dirac mass, respectively. The corresponding energy dispersion is obtained as
| (22) |
where , and . The inter-band winding number is defined for the energies and in the complex energy plane Shen et al. (2018):
| (23) |
where is a closed loop in the two-dimensional momentum space. A nonzero winding number implies a band degeneracy in the region enclosed by . For a pair of separable bands, the winding number can be nonzero only for non-contractible loops in the momentum space. Here we choose loop as a unit circle that encircles an exceptional point (a band degeneracy in non-Hermitian band structures) when the Hamiltonian has exceptional points; otherwise we randomly choose a closed loop. The exact topological phase diagram Shen et al. (2018) in the parameter space spanned by () is shown in Fig. 6(a). The winding number is 0 in the regime , and the corresponding Hamiltonian has a pair of separable bands without band degeneracies. In the regime , the two bands cross at two isolated exceptional points in the two-dimensional momentum space Shen et al. (2018)
| (24) |
where . For the regime , the inter-band winding numbers circling an exceptional point are half-integers and have opposite signs for . Thus, the winding number associated with the exceptional points characterizes topological phase transitions in this model. Note that here we consider the loop clockwise circling the exceptional point for the two energy bands in the complex plane, as displayed in Fig. 6(b).

In the training, we discretize the loop to equally distributed points and set the configuration of input data as with . The corresponding winding numbers are used as the data labels. We use a workflow similar to that described in Sec. III and a CNN with the same structure as described in Sec. IV to study topological phase transitions characterized by in this two-dimensional non-Hermitian model. The training data set consists of configurations satisfying , sampled from different phases with different winding numbers. We test the CNN with two test data sets: (I) configurations satisfying and (II) 600 configurations distributed uniformly in . The CNN evaluates both the test data sets, I and II, after the training. In Fig. 6(c), we plot the accuracy versus the distance threshold , where the CNN is able to detect the winding number precisely for different thresholds . Furthermore, the topological phase transitions can be revealed by the crossing points of the prediction probabilities as shown in Fig. 6(d). These results demonstrate the feasibility of neural networks in learning the topological invariants in two-dimensional non-Hermitian models.
VI Conclusions
In summary, we have demonstrated that artificial neural networks can be used to predict the topological invariants and the associated topological phase transitions and topological phase diagrams in four different non-Hermitian models with a high accuracy. The eigenenergy winding numbers in the Hatano-Nelson model are presented as a demonstration of our machine learning method. The CNN trained by the data set within the deep phases has been shown to correctly detect the phase transition near each boundary of the non-Hermitian SSH model. We have also investigated the non-Hermitian generalized AAH model with non-reciprocal hopping and a complex quasiperiodic potential. It is found that the topological phase diagram in the non-Hermiticity parameter space predicted by the CNN has a high accuracy with the theoretical counterpart. Furthermore, we have generalized our scenario to reveal the winding numbers associated with exceptional points in the two-dimensional non-Hermitian Dirac fermion model. Our results have shown the generality of the machine learning method in classifying topological phases in prototypical non-Hermitian models.
Finally, we make some remarks on future studies on machine learning non-Hermitian topology. Some exotic features of non-Hermitian topological systems are sensitive to the boundary condition, such as the non-Hermitian skin effect under open boundary conditions Lee (2016); Yao and Wang (2018); Yao et al. (2018); Song et al. (2019); Kunst et al. (2018), which is closely related to the winding number of complex eigenenergies Zhang et al. (2020e); Yang et al. (2020); Okuma et al. (2020). The energy spectrum under periodic boundary conditions may deviate drastically from that under open boundary conditions. Further studies on the non-Hermitian skin effects and the classification of non-Hermitian topological phases under open boundary conditions based on machine learning algorithms will be conducted. In addition, machine learning non-Hermitian topological invariants defined by the eigenstates would be an interesting further study.
Note added. Recently, we noticed two related works on machine learning non-Hermitian topological states Narayan and Narayan (2021); Yu and Deng (2020), which focused on the winding number of the Hamiltonian vectors and the cluster of non-Hermitian topological phases in an unsupervised fashion, respectively.

Appendix A Training details
We first describe some training details for the Hatano-Nelson model. We use the deep learning framework PyTorch Paszke et al. (2019) to construct and train the neural network. Weights are randomly initialized to a normal distribution with the Xavier algorithm Glorot and Bengio (2010) and the biases are initialized to 0. We use the Adam optimizerKingma and Ba (2014) to minimize the output of the neural network with the true value . We set the initial learning rate at 0.001 and use the ReduceLROnPlateau algorithm Paszke et al. (2019) to lower by 10 times when the improvement of the validation loss stops for 20 epochs. All hyper-parameters are set to default, unless mentioned otherwise. In order to prevent neural overfitting, regularization with strength and early stop Yao et al. (2007) are used during the training. We use mini-batch training with the batch size 64 and a validation set to confirm that there is no overfitting during training. We take configurations, which consist of samples with winding numbers . The typical loss during a training instance of the CNN and FCNN is shown in Fig. 7 (a), from which one can see that there is no sign of overfitting.
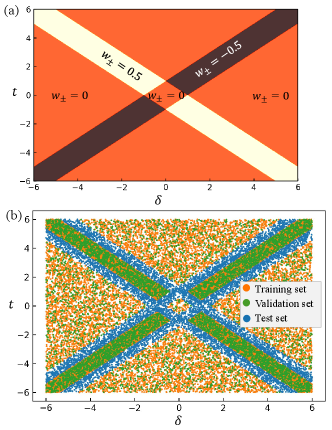
We now provide some training details for the non-Hermitian SSH model. In this case, the CNN has two convolution layers with 32 kernels of size and 1 kernel of size , followed by a fully connected layer of 16 neurons before the output layer. In this model, the output layer consists of three neurons for three different inter-band winding numbers. All the hidden layers have ReLU as activation functions and the output layer has the softmax function . The exact topological phase diagram in the parameter space spanned by and is shown in Fig. 8 (a). The training data set satisfying with here and the test data set satisfying are randomly sampled from the parameter space. The data set distribution is shown in Fig. 8 (b). The numbers of configurations in the training data set, validation data set, and test data set are about , , and , respectively. Typical loss during training instances of the CNN for different training data sets is plotted in Fig. 7 (b), which clearly shows that the neural networks converge quickly without overfitting.
Finally, we present briefly some details for the non-Hermitian generalized AAH model. In this case, the validation set consists of configurations corresponding to non-reciprocal-hopping Hamiltonians (with ) that are not included in the training data set. The typical loss is shown in Fig. 7 (c), with the networks converging quickly without overfitting.
Acknowledgements.
We thank Dan-Bo Zhang for helpful discussions. This work was supported by the National Natural Science Foundation of China (Grants No. U1830111, No. U1801661, and No. 12047522), the Key-Area Research and Development Program of Guangdong Province (Grant No. 2019B030330001), and the Science and Technology Program of Guangzhou (Grants No. 201804020055 and No. 2019050001).References
- Jordan and Mitchell (2015) M. I. Jordan and T. M. Mitchell, Science 349, 255 (2015).
- LeCun et al. (2015) Y. LeCun, Y. Bengio, and G. Hinton, Nature 521, 436 (2015).
- Goodfellow et al. (2016) I. J. Goodfellow, Y. Bengio, and A. Courville, Deep Learning (MIT Press, Cambridge, MA, USA, 2016) http://www.deeplearningbook.org.
- Carleo et al. (2019) G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto, and L. Zdeborová, Rev. Mod. Phys. 91, 045002 (2019).
- Biswas et al. (2013) R. Biswas, L. Blackburn, J. Cao, R. Essick, K. A. Hodge, E. Katsavounidis, K. Kim, Y.-M. Kim, E.-O. Le Bigot, C.-H. Lee, J. J. Oh, S. H. Oh, E. J. Son, Y. Tao, R. Vaulin, and X. Wang, Phys. Rev. D 88, 062003 (2013).
- Rem et al. (2019) B. S. Rem, N. Käming, M. Tarnowski, L. Asteria, N. Fläschner, C. Becker, K. Sengstock, and C. Weitenberg, Nat. Phys. 15, 917 (2019).
- Kasieczka et al. (2019) G. Kasieczka, T. Plehn, A. Butter, K. Cranmer, D. Debnath, B. M. Dillon, M. Fairbairn, D. A. Faroughy, W. Fedorko, C. Gay, L. Gouskos, J. F. Kamenik, P. Komiske, S. Leiss, A. Lister, S. Macaluso, E. Metodiev, L. Moore, B. Nachman, K. Nordström, J. Pearkes, H. Qu, Y. Rath, M. Rieger, D. Shih, J. Thompson, and S. Varma, SciPost Physics 7, 14 (2019).
- Wang (2016) L. Wang, Phys. Rev. B 94, 195105 (2016).
- Carrasquilla and Melko (2017) J. Carrasquilla and R. G. Melko, Nat. Phys. 13, 431 (2017).
- Zhang and Kim (2017) Y. Zhang and E.-A. Kim, Phys. Rev. Lett. 118, 216401 (2017).
- Deng et al. (2017) D.-L. Deng, X. Li, and S. Das Sarma, Phys. Rev. B 96, 195145 (2017).
- Huembeli et al. (2019) P. Huembeli, A. Dauphin, P. Wittek, and C. Gogolin, Phys. Rev. B 99, 104106 (2019).
- Dong et al. (2019) X.-Y. Dong, F. Pollmann, and X.-F. Zhang, Phys. Rev. B 99, 121104 (2019).
- Van Nieuwenburg et al. (2017) E. P. Van Nieuwenburg, Y.-H. Liu, and S. D. Huber, Nat. Phys. 13, 435 (2017).
- Carvalho et al. (2018) D. Carvalho, N. A. García-Martínez, J. L. Lado, and J. Fernández-Rossier, Phys. Rev. B 97, 115453 (2018).
- Zhang et al. (2018a) P. Zhang, H. Shen, and H. Zhai, Phys. Rev. Lett. 120, 066401 (2018a).
- Sun et al. (2018) N. Sun, J. Yi, P. Zhang, H. Shen, and H. Zhai, Phys. Rev. B 98, 085402 (2018).
- Huembeli et al. (2018) P. Huembeli, A. Dauphin, and P. Wittek, Phys. Rev. B 97, 134109 (2018).
- Tsai et al. (2020) Y.-H. Tsai, M.-Z. Yu, Y.-H. Hsu, and M.-C. Chung, Phys. Rev. B 102, 054512 (2020).
- Ming et al. (2019) Y. Ming, C.-T. Lin, S. D. Bartlett, and W.-W. Zhang, npj Comput. Mater. 5, 1 (2019).
- Rodriguez-Nieva and Scheurer (2019) J. F. Rodriguez-Nieva and M. S. Scheurer, Nat. Phys. 15, 790 (2019).
- Holanda and Griffith (2020) N. L. Holanda and M. A. R. Griffith, Phys. Rev. B 102, 054107 (2020).
- Ohtsuki and Mano (2020) T. Ohtsuki and T. Mano, J. Phys. Soc. Jpn. 89, 022001 (2020).
- Zhang et al. (2020a) Y. Zhang, P. Ginsparg, and E.-A. Kim, Phys. Rev. Research 2, 023283 (2020a).
- Long et al. (2020) Y. Long, J. Ren, and H. Chen, Phys. Rev. Lett. 124, 185501 (2020).
- Scheurer and Slager (2020) M. S. Scheurer and R.-J. Slager, Phys. Rev. Lett. 124, 226401 (2020).
- Balabanov and Granath (2020) O. Balabanov and M. Granath, Phys. Rev. Research 2, 013354 (2020).
- Balabanov and Granath (2021) O. Balabanov and M. Granath, Machine Learning: Science and Technology 2, 025008 (2021).
- Lian et al. (2019) W. Lian, S.-T. Wang, S. Lu, Y. Huang, F. Wang, X. Yuan, W. Zhang, X. Ouyang, X. Wang, X. Huang, L. He, X. Chang, D.-L. Deng, and L. Duan, Phys. Rev. Lett. 122, 210503 (2019).
- Diehl et al. (2008) S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. Büchler, and P. Zoller, Nat. Phys. 4, 878 (2008).
- Malzard et al. (2015) S. Malzard, C. Poli, and H. Schomerus, Phys. Rev. Lett. 115, 200402 (2015).
- Lee (2016) T. E. Lee, Phys. Rev. Lett. 116, 133903 (2016).
- Yao and Wang (2018) S. Yao and Z. Wang, Phys. Rev. Lett. 121, 086803 (2018).
- Yao et al. (2018) S. Yao, F. Song, and Z. Wang, Phys. Rev. Lett. 121, 136802 (2018).
- Song et al. (2019) F. Song, S. Yao, and Z. Wang, Phys. Rev. Lett. 123, 246801 (2019).
- Kunst et al. (2018) F. K. Kunst, E. Edvardsson, J. C. Budich, and E. J. Bergholtz, Phys. Rev. Lett. 121, 026808 (2018).
- Takata and Notomi (2018) K. Takata and M. Notomi, Phys. Rev. Lett. 121, 213902 (2018).
- Wang et al. (2019) H. Wang, J. Ruan, and H. Zhang, Phys. Rev. B 99, 075130 (2019).
- Zeng et al. (2017) Q.-B. Zeng, S. Chen, and R. Lü, Phys. Rev. A 95, 062118 (2017).
- Lang et al. (2018) L.-J. Lang, Y. Wang, H. Wang, and Y. D. Chong, Phys. Rev. B 98, 094307 (2018).
- Hamazaki et al. (2019) R. Hamazaki, K. Kawabata, and M. Ueda, Phys. Rev. Lett. 123, 090603 (2019).
- Jin and Song (2019) L. Jin and Z. Song, Phys. Rev. B 99, 081103 (2019).
- Kawabata et al. (2019a) K. Kawabata, S. Higashikawa, Z. Gong, Y. Ashida, and M. Ueda, Nat. Commun. 10, 1 (2019a).
- Liu et al. (2019) T. Liu, Y.-R. Zhang, Q. Ai, Z. Gong, K. Kawabata, M. Ueda, and F. Nori, Phys. Rev. Lett. 122, 076801 (2019).
- Lee et al. (2019) C. H. Lee, L. Li, and J. Gong, Phys. Rev. Lett. 123, 016805 (2019).
- Yamamoto et al. (2019) K. Yamamoto, M. Nakagawa, K. Adachi, K. Takasan, M. Ueda, and N. Kawakami, Phys. Rev. Lett. 123, 123601 (2019).
- Hatano and Nelson (1996) N. Hatano and D. R. Nelson, Phys. Rev. Lett. 77, 570 (1996).
- Hatano and Nelson (1997) N. Hatano and D. R. Nelson, Phys. Rev. B 56, 8651 (1997).
- Gong et al. (2018) Z. Gong, Y. Ashida, K. Kawabata, K. Takasan, S. Higashikawa, and M. Ueda, Phys. Rev. X 8, 031079 (2018).
- Ghatak and Das (2019) A. Ghatak and T. Das, J. Phys.: Condens. Matter 31, 263001 (2019).
- Leykam et al. (2017) D. Leykam, K. Y. Bliokh, C. Huang, Y. D. Chong, and F. Nori, Phys. Rev. Lett. 118, 040401 (2017).
- Shen et al. (2018) H. Shen, B. Zhen, and L. Fu, Phys. Rev. Lett. 120, 146402 (2018).
- Zhang et al. (2018b) D.-W. Zhang, Y.-Q. Zhu, Y. X. Zhao, H. Yan, and S.-L. Zhu, Advances in Physics 67, 253 (2018b).
- Zhang et al. (2020b) G.-Q. Zhang, D.-W. Zhang, Z. Li, Z. D. Wang, and S.-L. Zhu, Phys. Rev. B 102, 054204 (2020b).
- Zhang et al. (2020c) D.-W. Zhang, L.-Z. Tang, L.-J. Lang, H. Yan, and S.-L. Zhu, Sci. China Phys. Mech. Astron. 63, 1 (2020c).
- (56) X.-W. Luo and C. Zhang, arXiv:1912.10652v1 .
- Jiang et al. (2019) H. Jiang, L.-J. Lang, C. Yang, S.-L. Zhu, and S. Chen, Phys. Rev. B 100, 054301 (2019).
- Longhi (2019) S. Longhi, Phys. Rev. Lett. 122, 237601 (2019).
- Liu et al. (2020a) T. Liu, H. Guo, Y. Pu, and S. Longhi, Phys. Rev. B 102, 024205 (2020a).
- Wu and An (2020) H. Wu and J.-H. An, Phys. Rev. B 102, 041119 (2020).
- Zeng et al. (2020) Q.-B. Zeng, Y.-B. Yang, and Y. Xu, Phys. Rev. B 101, 020201 (2020).
- Zeng and Xu (2020) Q.-B. Zeng and Y. Xu, Phys. Rev. Research 2, 033052 (2020).
- Tang et al. (2020) L.-Z. Tang, L.-F. Zhang, G.-Q. Zhang, and D.-W. Zhang, Phys. Rev. A 101, 063612 (2020).
- Liu et al. (2020b) H. Liu, Z. Su, Z.-Q. Zhang, and H. Jiang, Chinese Physics B 29, 050502 (2020b).
- Zhang et al. (2020d) D.-W. Zhang, Y.-L. Chen, G.-Q. Zhang, L.-J. Lang, Z. Li, and S.-L. Zhu, Phys. Rev. B 101, 235150 (2020d).
- Xu and Chen (2020) Z. Xu and S. Chen, Phys. Rev. B 102, 035153 (2020).
- Liu et al. (2020c) T. Liu, J. J. He, T. Yoshida, Z.-L. Xiang, and F. Nori, Phys. Rev. B 102, 235151 (2020c).
- (68) W. Xi, Z.-H. Zhang, Z.-C. Gu, and W.-Q. Chen, arXiv:1911.01590v4 .
- Lee et al. (2020) E. Lee, H. Lee, and B.-J. Yang, Phys. Rev. B 101, 121109 (2020).
- Yoshida et al. (2019) T. Yoshida, K. Kudo, and Y. Hatsugai, Sci. Rep. 9, 16895 (2019).
- Borgnia et al. (2020) D. S. Borgnia, A. J. Kruchkov, and R.-J. Slager, Phys. Rev. Lett. 124, 056802 (2020).
- Okuma et al. (2020) N. Okuma, K. Kawabata, K. Shiozaki, and M. Sato, Phys. Rev. Lett. 124, 086801 (2020).
- Zhang et al. (2020e) K. Zhang, Z. Yang, and C. Fang, Phys. Rev. Lett. 125, 126402 (2020e).
- Su et al. (1979) W. P. Su, J. R. Schrieffer, and A. J. Heeger, Phys. Rev. Lett. 42, 1698 (1979).
- Harper (1955) P. G. Harper, Proc. Phys. Soc. Sect. A 68, 874 (1955).
- Aubry and Andre (1980) S. Aubry and G. Andre, Ann. Israel Phys. Soc. 3, 133 (1980).
- Liu et al. (2015) F. Liu, S. Ghosh, and Y. D. Chong, Phys. Rev. B 91, 014108 (2015).
- Kawabata et al. (2019b) K. Kawabata, K. Shiozaki, M. Ueda, and M. Sato, Phys. Rev. X 9, 041015 (2019b).
- Tang et al. (2021) L.-Z. Tang, G.-Q. Zhang, L.-F. Zhang, and D.-W. Zhang, arXiv: 2101.05505 (2021).
- Yang et al. (2020) Z. Yang, K. Zhang, C. Fang, and J. Hu, Phys. Rev. Lett. 125, 226402 (2020).
- Narayan and Narayan (2021) B. Narayan and A. Narayan, Phys. Rev. B 103, 035413 (2021).
- Yu and Deng (2020) L.-W. Yu and D.-L. Deng, arXiv: 2010.14516 (2020).
- Paszke et al. (2019) A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, and S. Chintala, in Advances in Neural Information Processing Systems 32 (Curran Associates, Inc., 2019) pp. 8026–8037.
- Glorot and Bengio (2010) X. Glorot and Y. Bengio, in Proceedings of Machine Learning Research, Vol. 9, edited by Y. W. Teh and M. Titterington (JMLR Workshop and Conference Proceedings, Chia Laguna Resort, Sardinia, Italy, 2010) pp. 249–256.
- Kingma and Ba (2014) D. P. Kingma and J. Ba, arXiv:1412.6980 (2014).
- Yao et al. (2007) Y. Yao, L. Rosasco, and A. Caponnetto, Constructive Approximation 26, 289 (2007).