Machine Learning meets Quantum Foundations: A Brief Survey
Abstract
The goal of machine learning is to facilitate a computer to execute a specific task without explicit instruction by an external party. Quantum foundations seeks to explain the conceptual and mathematical edifice of quantum theory. Recently, ideas from machine learning have successfully been applied to different problems in quantum foundations. Here, we compile the representative works done so far at the interface of machine learning and quantum foundations. We conclude the survey with potential future directions.
I Introduction
The rise of machine learning in recent times has remarkably transformed science and society. The goal of machine learning is to get computers to act without being explicitly programmed shalev2014understanding ; goodfellow2016deep . Some of the typical applications of machine learning are self-driving cars, efficient web search, improved speech recognition, enhanced understanding of the human genome and online fraud detection. This viral spread in interest has exploded to various areas of science and engineering, in part due to the hope that artificial intelligence may supplement human intelligence to understand some of the deep problems in science.
The techniques from machine-learning have been used for automated theorem proving, drug discovery and predicting the 3-D structure of proteins based on its genetic sequence alquraishi2019alphafold ; bridge2014machine ; lavecchia2015machine . In physics, techniques from machine learning have been applied for many important avenues arsenault2015machine ; zhang2017quantum ; carrasquilla2017machine ; van2017learning ; deng2017machine ; wang2016discovering ; broecker2017machine ; ch2017machine ; zhang2017machine ; wetzel2017unsupervised ; hu2017discovering ; yoshioka2018learning ; torlai2016learning ; huang2019near ; aoki2016restricted ; you2018machine ; pasquato2016detecting ; hezaveh2017fast ; biswas2013application ; abbott2016observation ; kalinin2015big ; schoenholz2016structural ; liu2017self ; huang2017accelerated ; torlai2018neural ; chen2018equivalence ; huang2017neural ; schindler2017probing ; haug2019engineering ; cai2018approximating ; broecker2017quantum ; nomura2017restricted ; biamonte2017quantum ; haug2020classifying including the study of black hole detection abbott2016observation , topological codes torlai2017neural , phase transition hu2017discovering , glassy dynamicsschoenholz2016structural , gravitational lenseshezaveh2017fast , Monte Carlo simulation huang2017accelerated ; liu2017self , wave analysis biswas2013application , quantum state preparation bukov2018reinforcement1 ; bukov2018reinforcement2 , anti-de Sitter/conformal field theory (AdS/CFT) correspondence hashimoto2018deep and characterizing the landscape of string theories carifio2017machine . Vice versa, the methods from physics have also transformed the field of machine learning both at the foundational and practical front lin2017does ; cichocki2014tensor . For a comprehensive review on machine learning for physics, refer to Carleo et al carleo2019machine and references therein. For a thorough review on machine learning and artificial intelligence in the quantum domain, refer to Dunjko et al dunjko2016quantum or Benedetti et al benedetti2019parameterized .
Philosophies in science can, in general, be delineated from the study of the science itself. Yet, in physics, the study of quantum foundations has essentially sprouted an enormously successful area called quantum information science. Quantum foundations tells us about the mathematical as well as conceptual understanding of quantum theory. Ironically, this area has potentially provided the seeds for future computation and communication, without at the moment reaching a consensus among all the physicists regarding what quantum theory tells us about the nature of reality hardy2010physics .
In recent years, techniques from machine learning have been used to solve some of the analytically/numerically complex problems in quantum foundations. In particular, the methods from reinforcement learning and supervised learning have been used for determination of the maximum quantum violation of various Bell inequalities, the classification of experimental statistics in local/nonlocal sets, training AI for playing Bell nonlocal games, using hidden neurons as hidden variables for completion of quantum theory, and machine learning-assisted state classification krivachy2019neural ; canabarro2019machine ; bharti2019teach ; deng2018machine .
Machine learning also attempts to mimic human reasoning leading to the almost remote possibility of machine-assisted scientific discovery iten2020discovering . Can machine learning do the same with the foundations of quantum theory? At a deeper level, machine learning or artificial intelligence, presumably with some form of quantum computation, may capture somehow the essence of Bell nonlocality and contextuality. Of course, such speculation belies the fact that human abstraction and reasoning could be far more complicated than the capabilities of machines.
In this brief survey, we compile some of the representative works done so far at the interface of quantum foundations and machine learning. The survey includes eight sections excluding the introduction (section I). In section II, we discuss the basics of machine learning. Section III contains a brief introduction to quantum foundations. In sections IV to VII, we discuss various applications of machine learning in quantum foundations. There is a rich catalogue of works, which we could not incorporate in detail in sections IV to VII, but we find them worth mentioning. We include such works briefly in section VIII. Finally, we conclude in section IX with open questions and some speculations.
II Machine Learning
Machine learning is a branch of artificial intelligence which involves learning from data goodfellow2016deep ; shalev2014understanding . The purpose of machine learning is to facilitate a computer to achieve a specific task without explicit instruction by an external party. According to Mitchel (1997) mitchell1997machine “A computer program is said to learn from experience with respect to some class of tasks and performance measure , if the performance at tasks in , as measured by , improves with .” Note that the meaning of the word “task” doesn’t involve the process of learning. For instance, if we are programming a robot to play Go, playing Go is the task. Some of the examples of machine learning tasks are following.
-
•
Classification: In classification tasks, the computer program is trained to learn the appropriate function Given an input, the learned program determines which of the categories the input belongs to via . Deciding if a given picture depicts a cat or a dog is a canonical example of a classification task.
-
•
Regression: In regression tasks, the computer program is trained to predict a numerical value for a given input. The aim is to learn the appropriate function A typical example of regression is predicting the price of a house given its size, location and other relevant features.
-
•
Anomaly detection: In anomaly detection (also known as outlier detection) tasks, the goal is to identify rare items, events or objects that are significantly different from the majority of the data. A representative example of anomaly detection is credit card fraud detection where the credit card company can detect misuse of the customer’s card by modelling his/her purchasing habits.
-
•
Denoising: Given a noisy example , the goal of denoising is to predict the conditional probability distribution over noise-free data .
The measure of the success of a machine learning algorithm depends on the task . For example, in the case of classification, can be measured via the accuracy of the model, i.e. fraction of examples for which the model produces the correct output. An equivalent description can be in terms of error rate, i.e. fraction of examples for which the model produces the incorrect output. The goal of machine learning algorithms is to work well on previously unseen data. To get an estimate of model performance , it is customary to estimate on a separate dataset called test set which the machine has not seen during the training. The data employed for training is known as the training set.
Depending on the kind of experience, , the machine is permitted to have during the learning process, the machine learning algorithms can be categorized into supervised learning, unsupervised learning, and reinforcement learning.
-
1.
Supervised learning: The goal is to learn a function , that returns the label given the corresponding unlabeled data . A prominent example would be images of cats and dogs, with the goal to recognize the correct animal. The machine is trained with labeled example data, such that it learns to correctly identify datasets it has not seen before. Given a finite set of training samples from the join distribution , the task of supervised learning is to infer the probability of a specific label given example data i.e., . The function that assigns labels can be inferred from the aforementioned conditional probability distribution.
-
2.
Unsupervised learning: For this type of machine learning, data is given without any label. The goal is to recognize possible underlying structures in the data. The task of the unsupervised machine learning algorithms is to learn the probability distribution or some interesting properties of the distribution, when given access to several examples . It is worth stating that the distinction between supervised and unsupervised learning can be blurry. For example, given a vector the joint probability distribution can be factorized (using the chain rule of probability) as
(1) The above factorization (1) enables us to transform a unsupervised learning task of learning into supervised learning tasks. Furthermore, given the supervised learning problem of learning the conditional distribution one can convert it into the unsupervised learning problem of learning the joint distribution and then infer via
(2) This last argument suggests that supervised and unsupervised learning are not entirely distinct. Yet, this distinction between supervised versus unsupervised is sometimes useful for the classification of algorithms.
-
3.
Reinforcement learning: Here, neither data nor labels are available. The machine has to generate the data itself and improve this data generation process through optimization of a given reward function. This method is somewhat akin to a human child playing games: The child interacts with the environment, and initially performs random actions. By external reinforcement (e.g. praise or scolding by parents), the child learns to improve itself. Reinforcement learning has shown immense success recently. Through reinforcement learning, machines have mastered games that were initially thought to be too complicated for computers to master. This was for example demonstrated by Deepind’s AlphaZero which has defeated the best human player in the board game Go silver2017mastering .
One of the central challenges in machine learning is to devise algorithms that perform well on previously unseen data. The learning ability of a machine to achieve a high performance on previously unseen data is called generalization. The input data to the machine is a set of variables, called features. A specific instance of data is called feature vector. The error measure on the feature vectors used for training is called training error. In contrast, the error measure on the test dataset, which the machine has not seen during the training, is called generalization error or test error. Given an estimate of training error, how can we estimate test error? The field of statistical learning theory aptly answers this question. The training and test data are generated according to a probability distribution over some datasets. Such a distribution is called data-generating distribution. It is conventional to make independent and identically distributed (IID) assumption, i.e. each example of the dataset is independent of another and, the training and test set are identically distributed. Under such assumptions, the performance of the machine learning algorithm depends on its ability to reduce the training error as well as the gap between training and test error. If a machine-learning algorithm fails to get sufficiently low training error; the phenomenon is called under-fitting. On the other hand, if the training error is low, but the test error is large, the phenomenon is called over-fitting. The capacity of a machine learning model to fit a wide variety of functions is called model capacity. A machine learning algorithm with low model capacity is likely to underfit, whereas a too high model capacity often leads to over-fitting the data. One of the ways to alter the model capacity of a machine learning algorithm is by constraining the class of functions that the algorithm is allowed to choose. For example, to fit a curve to a dataset, one often chooses a set of polynomials as fitting functions (see Fig.1). If the degree of the polynomials is too low, the fit may not be able to reproduce the data sufficiently (under-fitting, orange curve). However, if the degree of the polynomials is too high, the fit will reproduce the training dataset too well, such that noise and the finite sample size is captured in the model (over-fitting, green curve).

II.1 Artificial Neural Networks
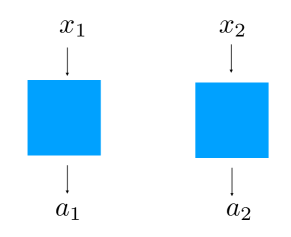
Most of the recent advances in machine learning were facilitated by using artificial neurons. The basic structure is a single artificial neuron (AN), which is a real-valued function of the form,
| (3) |
In equation 3, the function is usually known as activation function. Some of the well-known activation functions are
-
1.
Threshold function: if and otherwise,
-
2.
Sigmoid function: and
-
3.
Rectified Linear (ReLu) function: max
The vector in equation 3 is known as weight vector.
Many of those artificial neurons can be combined together via communication links to perform complex computation. This can be achieved by feeding the output of neurons (weighted by the weights ) as an input to another neuron, where the activation function is applied again. Such a graph structure with the set of nodes as artificial neurons and edges in as connections, is known as an artificial neural network or neural network in short. The first layer, where the data is fed in, is called input layer. The layers of neurons in-between are the hidden layers, which are defining feature of deep learning. The last layer is called output layer. A neural network with more than one hidden layer is called deep neural network. Machine learning involving deep neural networks is called Deep learning. A feedforward neural network is a directed acyclic graph, which means that the output of the neurons is fed only into forward direction (see Fig.2). Apart from the feedforward neural network, some of the popular neural network architectures are convolutional neural networks (CNN), recurrent neural networks (RNN), generative adversarial network (GAN), Boltzmann machine and restricted Boltzmann machines (RBM). We provide a brief summary of RBM here. For a detailed understanding of various other neural networks, refer to goodfellow2016deep .

An RBM is a bipartite graph with two kinds of binary-valued neuron units, namely visible and hidden (see Fig.3) The weight matrix encodes the weight corresponding to the connection between visible unit and hidden unit hinton2012practical . Let the bias weight (offset weight) for the visible unit be and hidden unit be .
For a given configuration of visible and hidden neurons , one can define an energy function inspired from statistical models for spin systems as
| (4) |
The probability of a configuration is given by Boltzmann distribution,
| (5) |
where is a normalization factor, commonly known as partition function. As there are no intra-layer connections, one can sample from this distribution easily. Given a set of visible units , the probability of a specific hidden unit being is
| (6) |
where is the sigmoid activation function as introduced earlier. A similar relation holds for the reverse direction, e.g. given a set of hidden units, what is the probability of the visible unit.

With these concepts, complicated probability distributions over some variable can be encoded and trained within the RBM. Given a set of training vectors , the goal is find the weights of the RBM that fit the training set best
| (7) |
RBMs have been shown to be a good Ansatz to represent many-body wavefunctions, which are difficult to handle with other methods due to the exponential scaling of the dimension of the Hilbert space. This method has been successfully applied to quantum many-body physics and quantum foundations problems deng2018machine ; carleo2017solving .
In context beyond physics, machine learning with deep neural networks has accomplished many significant milestones, such as mastering various games, image recognition, self-driving cars, and so forth. Its impact on the physical sciences is just about to start carleo2019machine ; deng2018machine .
II.2 Relation with Artificial Intelligence
The term “artificial intelligence” was first coined in the famous 1956 Dartmouth conference mccarthy2006proposal . Though the term was invented in 1956, the operational idea can be traced back to Alan Turing’s influential “Computing Machinery and Intelligence” paper in 1950, where Turing asks if a machine can think turing2009computing . The idea of designing machines that can think dates back to ancient Greece. Mythical characters such as Pygmalion, Hephaestus and Daedalus can be interpreted as some of the legendary inventors and Galatea, Pandora and Hephaestus can be thought of as examples of artificial life goodfellow2016deep . The field of artificial intelligence is difficult to define, as can be seen by four different and popular candidate definitions russell2002artificial . The definitions start with “AI is the discipline that aims at building …”
-
1.
(Reasoning-based and human-based): agents that can reason like humans.
-
2.
(Reasoning-based and ideal rationality): agents that think rationally.
-
3.
(behavior-based and human-based): agents that behave like humans.
-
4.
(behavior-based and ideal rationality): agents that behave rationally.
Apart from its foundational impact in attempting to understand “intelligence,” AI has reaped practical impacts such as automated routine labour and automated medical diagnosis, to name a few among many. The real challenge of AI is to execute tasks which are easy for people to perform, but hard to express formally. An approach to solve this problem is by allowing machines to learn from experience, i.e. via machine learning. From a foundational point of judgment, the study of machine learning is vital as it helps us understand the meaning of “intelligence”. It is worthwhile mentioning that deep learning is a subset of machine learning which can be thought of as a subset of AI (see Fig.9).

III Quantum Foundations
The mathematical edifice of quantum theory has intrigued and puzzled physicists, as well as philosophers, for many years. Quantum foundations seeks to understand and develop the mathematical as well as conceptual understanding of quantum theory. The study concerns the search for non-classical effects such as Bell nonlocality, contextuality and different interpretations of quantum theory. This study also involves the investigation of physical principles that can put the theory into an axiomatic framework, together with an exploration of possible extensions of quantum theory. In this survey, we will focus on non-classical features such as Entanglement, Bell nonlocality, contextuality and quantum steering in some detail.
An interpretation of quantum theory can be viewed as a map from the elements of the mathematical structure of quantum theory to elements of reality. Most of the interpretations of quantum theory seek to explain the famous measurement problem. Some of the brilliant interpretations are the Copenhagen interpretation, quantum Bayesianism fuchs2011quantum , the many-world formalism everett1957relative ; dewitt2015many and the consistent history interpretation omnes1992consistent . The axiomatic reconstruction of quantum theory is generally categorized into two parts: the generalized probabilistic theory (GPT) approach barrett2007information and the black-box approach acin2017black . The physical principles underlying the framework for axiomatizing quantum theory are non-trivial communication complexity van2013implausible ; brassard2006limit , information causality pawlowski2009information , macroscopic locality navascues2010glance , negating the advantage for nonlocal computation linden2007quantum , consistent exclusivity yan2013quantum and local orthogonality fritz2013local . The extensions of the quantum theory include collapse models mcqueen2015four , quantum measure theory sorkin1994quantum and acausal quantum processes oreshkov2012quantum .
III.1 Entanglement
Quantum interaction inevitably leads to quantum entanglement. The individual states of two classical systems after an interaction are independent of each other. Yet, this is not the case for two quantum systems raimond2001manipulating ; horodecki2009quantum . Quantum states can be pure or mixed. For a bipartite pure quantum state is entangled if it cannot be written as a product state, i.e. for some and . A mixed bipartite state is however expressed in terms of a density matrix, . Like for pure state, a density matrix is entangled if it cannot be expressed in the form . An partite state is called separable if it can be represented as a convex combination of product states i.e.
| (8) |
where and A quantum state is called separable if it is not entangled.
Computationally it is not easy to check if a mixed state, especially in higher dimensions and for more parties, is separable or entangled. Numerous measures of quantum entanglement for both pure and mixed states are proposed horodecki2009quantum : for bipartite systems where the dimension of is 2, a good measure is concurrence wootters2001entanglement . Other measures for quantifying entanglement are entanglement of formation, robustness of entanglement, Schmidt rank, squashed entanglement and so forth horodecki2009quantum . It turns out that for any entangled state , there exists a Hermitian matrix such that and for all separable states , horodecki1996necessary ; terhal2002detecting ; krammer2009multipartite ; ekert2002direct .
Quantum entanglement was mooted a long time ago by Erwin Schrödinger, but it took another thirty years or so for John Bell to show that quantum theory imposes strong constraints on statistical correlations in experiments. Yet, correlations are not tantamount to causation and one wonders if machine learning could do better pearle2000causality . In the sixties and seventies, this Gedanken experiment was given further impetus with some ingenious experimental designs freedman1972experimental ; kocher1967polarization ; aspect1981experiences ; aspect1982experimental . The advent of quantum information in the nineties gave a further push: quantum entanglement became a useful resource for many quantum applications, ranging from teleportation bennett1993teleporting , communication ekert1991quantum , purification bennett1996purification , dense coding bennett1992communication and computation deutsch1985quantum ; feynman2018feynman . Interestingly, quantum entanglement is a fascinating area that emerges almost serendipitously from the foundation of quantum mechanics into real practical applications in the laboratories.
III.2 Bell Nonlocality
According to John Bell Bell64 , any theory based on the collective premises of locality and realism must be at variance with experiments conducted by spatially separated parties involving shared entanglement, if the underlying measurement events are space-like separated. The phenomenon, as discussed before, is known as Bell nonlocality brunner2014bell . Apart from its significance in understanding foundations of quantum theory, Bell nonlocality is a valuable resource for many emerging device-independent quantum technologies like quantum key distribution (QKD), distributed computing, randomness certification and self-testing ekert1991quantum ; pironio2010random ; Yao_self . The experiments which can potentially manifest Bell nonlocality are known as Bell experiments. A Bell experiment involves spatially separated parties . Each party receives an input and gives an output For various input-output combinations one gets the statistics of the following form:
| (9) |
We will refer to as behavior. A Bell experiment involving space-like separated parties, each party having access to inputs and each input corresponding to outputs is referred to as scenario. The famous Clauser-Horn-Shimony-Holt (CHSH) experiment is a scenario CHSH , and it is the simplest scenario in which Bell nonlocality can be demonstrated (see Fig. 5).
A behavior admits local hidden variable description if and only if
| (10) |

This is known as local behavior. The set of local behaviors forms a convex polytope, and the facets of this polytope are Bell inequalities (see Fig. 6). In quantum theory, Born rule governs probability according to
| (11) |
where are positive-operator valued measures (POVMs) and is a shared density matrix. If a behavior satisfying Eq.11 falls outside , it then violates at least one Bell inequality, and such behavior is said to manifest Bell nonlocality. The condition that parties do not communicate during the course of the Bell experiment is known as no-signalling condition. Intuitively speaking, it means that the choice of input of one party can not be used for signalling among parties. Mathematically it means,
| (12) |
The set of behaviours which satisfy the no signalling condition are known as no-signalling behaviours. We will denote the aforementioned set by . The no-signalling set also forms a polytope. Furthermore, (see Fig. 6). The no-signalling behaviours which do not lie in are also known as post-quantum behaviours. In the (2,2,2) scenario i.e. CHSH Scenario, there is a unique Bell inequality, namely CHSH inequality, upto relabelling of inputs and outputs. The CHSH inequality is given by
| (13) |
where All local hidden variable theories satisfy CHSH inequality. In quantum theory, suitably chosen measurement settings and state can lead to violation of CHSH inequality and thus the CHSH inequality can be used to witness Bell nonlocal nature of quantum theory. Quantum behaviours achieve upto known as the Tsirelson bound. The upper bound for no-signalling behaviours (no-signalling bound) on the CHSH inequality is .
III.3 Contextuality
An intuitive feature of classical models is non-contextuality which means that any measurement has a value independent of other compatible measurements it is performed together with. A set of compatible measurements is called context. It was shown by Simon Kochen and Ernst Specker (as well as John Bell) kochen1967problem that non-contextuality conflicts with quantum theory.
The contextual nature of quantum theory can be established via simple constructive proofs. In Fig. 7 (A), one considers an array of operators on a two-qubit system in any quantum state. There are nine operators, and each of them has eigenvalue . The three operators in each row or column commute and so it is easy to check that each operator is the product of the other two operators on a particular row or column, with a single exception, the third operator in the third column equals the minus of the product of the other two. Suppose there exist pre-assigned values ( or ) for the outcomes of the nine operators, then we can replace the none operators by the pre-assigned values. However, there is no consistent way to assign such values to the nine operators so that the product of the numbers in every row or column (except for the operators along the bold line) yield 1 (the product yields -1). Notice that each operator (node) appears in exactly two lines or context. Kochen and Specker provided the first proof of quantum contextuality with a complicated construct involving 117 operators on a 3-dimensional space kochen1967problem . Another example is the pentagram mermin1993hidden in Fig. 7.

Bell nonlocality is regarded as a particular case of contextuality where the space-like separation of parties involved creates ”context” CSW ; amaral2018graph . The study of contextuality has led not only to insights into the foundations of quantum mechanics, but it also offers practical implications as well Cabello_QKD ; bharti2019non ; raussendorf2013contextuality ; bharti2019robust ; mansfield2018quantum ; saha2019state ; bharti2019local ; delfosse2015wigner ; singh2017quantum ; pashayan2015estimating ; bharti2018simple ; bermejo2017contextuality ; catani2018state ; arora2019revisiting ; Howard2014 . There are several frameworks for contextuality including sheaf-theoretic framework abramsky2011sheaf , graph and hypergraph framework CSW ; acin2015combinatorial , contextuality-by-default framework dzhafarov2017contextuality ; dzhafarov2019joint ; kujala2019measures and operational framework spekkens2005contextuality . A scenario exhibits contextuality if it does not admit the non-contextual hidden variable (NCHV) model KS67 .
III.4 Quantum Steering
Correlations produced by steering lie between the Bell nonlocal correlations and those generated from entangled states quintino2015inequivalence ; wiseman2007steering . A state that manifests Bell nonlocality for some suitably chosen measurement settings also exhibits steering schrodinger1935discussion . Furthermore, a state which exhibits steering must be entangled. A state demonstrates steering if it does not admit “local hidden state (LHS)” model wiseman2007steering . We discuss this formally here.
Alice and Bob share some unknown quantum state Alice can perform a set of POVM measurements The probability of her getting outcome after choosing measurement is given by
| (14) |
where is Bob’s residual state upon normalization. A set of operators acting on Bob’s space is called an assemblage if
| (15) |
and
| (16) |
Condition 15 is the analogue of the no-signalling condition. An assemblage is said to admit LHS model if there exists some hidden variable and some quantum state acting on Bob’s space such that
| (17) |
A bipartite state is said to be steerable from Alice to Bob if there exist measurements for Alice such that the corresponding assemblage does not satisfy equation 17. Determining whether an assemblage admits LHS model is a semidefinite program (SDP). The concept of steering is asymmetric by definition, i.e. even if Alice could steer Bob’s state, Bob may not be able to steer Alice’s state.
IV Neural network as Oracle for Bell Nonlocality
The characterization of the local set for the convex scenario via Bell inequalities becomes intractable as the complexity of the underlying scenario grows (in terms of the number of parties, measurement settings and outcomes). For networks where several independent sources are shared among many parties, the situation gets increasingly worse. The local set is remarkably non-convex, and hence proper analytical and numerical characterization, in general, is lacking. Applying machine learning technique to tackle these issues were studied by Canabarro et al. canabarro2019machine and Krivachy et al. krivachy2019neural . In the work by Canabarro et al., the detection and characterization of nonlocality is done through an ensemble of multilayer perceptrons blended with genetic algorithms (see IV.1).
IV.1 Machine Learning Nonlocal Correlations
Given a behavior, deciding whether it is classical or non-classical is an extremely challenging task since the underlying scenario grows in complexity very quickly. Canabarro et al. canabarro2019machine use supervised machine learning with an ensemble of neural networks to tackle the approximate version of the problem (i.e. with a small margin of error) via regression. The authors ask “How far is a given correlation from the local set.” The input feature vector to the neural network is a random correlation vector. For a given behavior, the output (label) is the distance of the feature vector from the classical, i.e. local set. The nonlocality quantifier of a behavior is the minimum trace distance, denoted by brito2018quantifying . For the two-party scenario, the nonlocality quantifier is given by
| (18) |
where is the local set and is the input size for the parties. The training points are generated by sampling the set of non-signalling behaviors randomly and then calculating its distance from the local set via equation 18. Given a behavior , the distance predicted by the neural network is never equal to the actual distance, i.e. there is always a small error 0). Let us represent the learned hypothesis as The performance metric of the learned hypothesis is given by
| (19) |
In experiments such as entanglement swapping, which comprises three separated parties sharing two independent sources of quantum states, the local set admits the following form and the set is non-convex,
| (20) |
Here, non-convexity emerges from the independence of the sources i.e.

In this case, the Bell inequalities are no longer linear. Characterizing the set of classical as well as quantum behaviors gets complicated for such scenarios tavakoli2014nonlocal ; branciard2010characterizing .
Canabarro et al. train the model for convex as well as non-convex scenarios. They also train the model to learn post-quantum correlations. The techniques studied in the paper are valuable for understanding Bell nonlocality for large quantum networks, for example those in quantum internet.
IV.2 Oracle for Networks
Given an observed probability distribution corresponding to scenarios where several independent sources are distributed over a network, deciding whether it is classical or non-classical is an important question, both from practical as well as foundational viewpoint. The boundary separating the classical and non-classical correlations is extremely non-convex and thus a rigorous analysis is exceptionally challenging.
In reference krivachy2019neural , the authors encode the causal structure into the topology of a neural network and numerically determine if the target distribution is “learnable”. A behavior belongs to the local set if it is learnable. The authors harness the fact that the information flow in feedforward neural networks and causal structures are both determined by a directed acyclic graph. The topology of the neural network is chosen such that it respects the causality structure. The local set corresponding to even elementary causal networks such as triangle network is profoundly non-convex, and thus analytical characterization of the same is a notoriously tricky task. Using the neural network as an oracle, Krivachy et al. krivachy2019neural convert the membership in a local set problem to a learnability problem. For a neural network with adequate model capacity, a target distribution can be approximated if it is local. The authors examine the triangle network with quaternary outcomes as a proof-of-principle example. In such a scenario, there are three independent sources, say and . Each of the three parties receives input from two of the three sources and process the inputs to provide outputs via fixed response functions. The outputs for Alice, Bob and Charlie will be indicated by The scenario as discussed here can be characterized by the probability distribution over the random variables and . If the network is classical, then the distribution can be represented by a directed acyclic graph known as a Bayesian network (BN).
Assuming the distribution over the random variables and to be classical, it is assumed without loss of generality that the sources send a random variable drawn uniformly from the interval to A classical distribution for such a case admits the following form:
| (21) |
The neural network is constructed such that it can approximate the distribution of type Eq.21. The inputs to the neural network are and drawn uniformly at random and the outputs are the conditional probabilities i.e. and .

The cost function is chosen to be any measure of the distance between the target distribution and the network’s output . The authors employ the techniques to a few other cases, such as the elegant distribution and a distribution proposed by Renou et al. renou2019genuine . The application of the technique to the elegant distribution suggests that the distribution is indeed nonlocal as conjectured in gisin2019entanglement . Furthermore, the distribution proposed by Renou et al. appears to have nonlocal features for some parameter regime. For the sake of completeness, now we discuss the elegant distribution and the distribution proposed by Renou et al.
Elegant distribution – The distribution is generated by three parties performing entangled measurements on entangles systems. The three parties share singlets i.e. Every party performs entangled measurements on their two qubits. The eigenstates of the entangled measurements are given by
| (22) |
where are vectors symmetrically distributed on the Bloch sphere i.e. point to the vertices of a tetrahedron, for
Renou et al. distribution – The distribution is generated by three parties sharing the entangled state and performing the same measurement on each of their two qubits. The measurements are characterized by a single parameter with eigenstates and .
V Machine Learning for optimizing Settings for Bell Nonlocality
Bell inequalities have become a standard tool to reveal the non-local structure of quantum mechanics. However, finding the best strategies to violate a given Bell inequality can be a difficult task, especially for many-body settings or even non-convex scenarios. Especially the latter setting is challenging, as standard optimisation tools are unable to be applied to this case. To violate a given Bell inequality, two inter-dependent tasks have to be addressed: Which measurements have to be performed to reveal the non-locality? And which quantum states show the maximal violation? Recently, Dong-Ling Deng has approached the latter task for convex settings with many-body Bell inequalities using restricted Boltzmann machines deng2018machine . Bharti et al. bharti2019teach have approached both tasks in conjunction for both convex and non-convex inequalities.
V.1 Detecting Bell nonlocality with many-body states
Several methods from machine learning have been adopted to tackle intricate quantum many-body problems carleo2017solving ; saito2018machine ; deng2018machine ; gao2017efficient . Dong-Ling Deng deng2018machine employs machine learning techniques to detect quantum nonlocality in many-body systems using the restricted Boltzmann machine (RBM) architecture. The key idea can be split into two parts:
-
•
After choosing appropriate measurement settings, Bell inequalities for convex scenarios can be expressed as an operator. This operator can be thought of as an Hamiltonian. The eigenstate with the maximal eigenvalue is the state that gives the maximum violation for the underlying Bell inequality. This state can be found by calculating the ground state of the negative of the Hamiltonian.
-
•
Finding the ground state of a quantum Hamiltonian is QMA-hard and thus in general difficult. However, using heuristic techniques involving the RBM architecture, the problem is recast into the task of finding the approximate answer in some cases.
Techniques like density matrix renormalization group (DMRG) schollwock2005density , projected entangled pair states (PEPS) verstraete2008matrix and multiscale entanglement renormalization ansatz (MERA) vidal2008class are traditionally used to find (or approximate) ground states of many-body Hamiltonians. But these techniques only work reliably for optimization problems involving low-entanglement states. Moreover, DMRG works well only for systems with short-range interactions in the one-dimensional case. As evident from references carleo2017solving , RBM can represent quantum many-body problems beyond 1-D and low-entanglement.
V.2 Playing Bell Nonlocal Games
Prediction of winning strategies for (classical) games and decision-making processes with reinforcement learning (RL) has made significant progress in game theory in recent years. Motivated partly by these results, the authors in Bharti et al. bharti2019teach have looked at a game-theoretic formulation of Bell inequalities (known as Bell games) and applied machine learning techniques to it. To violate a Bell inequality, both the quantum state as well as the measurements performed on the quantum states have to be chosen in a specific manner. The authors transform this problem into a decision making process. This is achieved by choosing the parameters in a Bell game in a sequential manner, e.g. the angles of the measurement operators, the angles parameterizing the quantum states, or both. Using RL, these sequential actions are optimized for the best configuration corresponding to the optimal/near-optimal quantum violation (see Fig.10). The authors train the RL agent with a cost function that encourages high quantum violations via proximal policy optimization - a state-of-the-art RL algorithm that combines two neural networks. The approach succeeds for well known convex Bell inequalities, but it can also solve Bell inequalities corresponding to non-convex optimization problems, such as in larger quantum networks. So far, the field has struggled solving these inequalities; thus, this approach offers a novel possibility towards finding optimal (or near-optimal) configurations.

Furthermore, the authors present an approach to find settings corresponding to maximum quantum violation of Bell inequalities on near-term quantum computers. The quantum state is parameterized by a circuit consisting of single-qubit rotations and CNOT gates acting on neighbouring qubits arranged in a linear fashion. Both the gates and the measurement angles are optimized using a variational hybrid classic-quantum algorithm, where the classical optimization is performed by RL. The RL agent learns by first randomly trying various measurement angles and quantum states. Over the course of the training, the agent improves itself by learning from experience, and is capable of reaching the maximal quantum violation.
VI Machine Learning-Assisted State Classification
A crucial problem in quantum information is identifying the degree of entanglement within a given quantum state. For Hilbert space dimensions up to , one can use Peres-Horodecki criterion, also known as positive partial transpose criterion (PPT) to distinguish entangled and separable states. However, there is no generic observable or entanglement witness as it is in fact a NP-hard problem horodecki2009quantum . Thus, one must rely on heuristic approaches. This poses a fundamental question: Given partial or full information about the state, are there ways to classify whether it is entangled or not? Machine learning has offered a way to find answers to this question.
VI.1 Classification with Bell Inequalities
In reference ma2018transforming , the authors blend Bell inequalities with a feed-forward neural network to use them as state classifiers. The goal is to classify states as entangled or separable. If a state violates a Bell inequality, it must be entangled. However, Bell inequalities cannot be used as a reliable tool for entanglement classification i.e. even if a state is entangled, it might not violate an entanglement witness based on the Bell inequality. For example, the density matrix violates the CHSH inequality only for , but is entangled for werner1989quantum . Moreover, given a Bell inequality, the measurement settings that witness entanglement of a quantum state (if possible) depend on the quantum state. Prompted by these issues, the authors ask if they can transform Bell inequalities into a reliable separable-entangled states classifier. The coefficients of the terms in the CHSH inequalities are The local hidden variable bound on the inequality is (see equation 13). Assuming fixed measurement settings corresponding to CHSH inequality, the authors examine whether it is possible to get better performance in terms of entanglement classification compared with the values . The main challenge to answer such a question in a supervised learning setting is to get labelled data that is verified to be either separable or entangled.
To train the neural network, the correlation vector corresponding to the appropriate Bell inequality was chosen as input with the state being entangled or separable as corresponding output. The correlation vector contains the expectation of the product of Alice’s and Bob’s measurement operators. The performance of the network improved as the model capacity was increased, which hints that the hypothesis which separates entangled states from separable ones must be sufficiently “complex.” The authors also trained a neural network to distinguish bi-separable and bound-entangled states.
VI.2 Classification by Representing Quantum States with Restricted Boltzmann Machines
Harney et al. harney2019entanglement use reinforcement learning with RBMs to detect entangled states. RBMs have demonstrated being capable of learning complex quantum states. The authors modify RBMs such that they can only represent separable states. This is achieved by separating the RBM into partitions that are only connected within themselves, but not with the other partitions. Each partition represents a (possibly) entangled subsystems, that however is not entangled with the other partitions. This choice enforces a specific -separable Ansatz of the wavefunction. This RBM is trained to represent a target state. If the training converges, it must be representable by the Ansatz and thus be -separable. However, if the training does not converge, the Ansatz is insufficient and the target state is either of a different -separable form or fully entangled.
VI.3 Classification with Tomographic Data
Can tools from machine learning help to distinguish entangled and separable states given the full quantum state (e.g. obtained by quantum tomography) as an input? Two recent studies address this question.
In Lu et al. lu2018separability , the authors detect entanglement by employing classic (i.e. non-deep learning) supervised learning. To simplify data generation of entangled and separable states, the authors approximate the set of separable states by a convex hull (CHA). States that lie outside the convex hull are assumed to be most likely entangled. For the decision process, the authors use ensemble training via bootstrap aggregating (bagging). Here, various supervised learning methods are trained on the data, and they form a committee together that decides whether a given state is entangled or not. The algorithm is trained with the quantum state and information encoding the position relative to the convex hull as inputs. The authors show that accuracy improves if bootstrapping of machine learning methods is combined with CHA.
In a different approach Goes et al. goes2020automated , the authors present an automated machine learning approach to classify random states of two qutrits as separable (SEP), entangled with positive partial transpose (PPTES) or entangled with negative partial transpose (NPT). For training, the authors elaborate a way to find enough samples to train on. The procedure is as follows: A random quantum state is sampled, then using the General Robustness of Entanglement (GR) and PPT criterion, it is classified to either SEP, PPTES or NPT. The GR measures the closeness to the set of separable states. The authors compare various supervised learning methods to distinguish the states. The input features fed into the machine are the components of the quantum state vector and higher-order combinations thereof, whereas the labels are the type of entanglement. Besides, they also train to estimate the GR with regression techniques and use it to validate the classifiers.
VII Neural Networks as “Hidden" Variable Models for Quantum Systems
Understanding why deep neural networks work so well is an active area of research. The presence of the word “hidden” for hidden variables in quantum foundations and hidden neurons in deep learning neurons may not be that accidental. Using conditional Restricted Boltzmann machines (a variant of Restricted Boltzmann machines), Steven Weinstein provides a completion of quantum theory in reference weinstein2018neural . The completion, however, doesn’t contradict Bell’s theorem as the assumption of “statistical independence” is not respected. The statistical independence assumption demands that the complete description of the system before measurement must be independent of the final measurement settings. The phenomena where apparent nonlocality is observed by violating statistical independence assumption is known as “nonlocality without nonlocality” weinstein2009nonlocality .
In a Bell-experiment corresponding to CHSH scenario, the detector settings and , and the corresponding measurement outcomes and for a single experimental trial can be represented as a four-dimensional vector Such a vector can be encoded in a binary vector where Here, has been mapped to The four-dimensional binary vector represents the value taken by four visible units of an RBM. The dependencies between the visible units is encoded using sufficient number of hidden units With four hidden neurons, the authors could reproduce the statistics predicted by EPR experiment with high accuracy. For example, say the vector occurs in of the trials, then after training the machine would associate Quantum mechanics gives us only the conditional probabilities and thus learning joint probability using RBM is resource-wasteful. The authors harness this observation by encoding the conditional statistics only in a conditional RBM (cRBM).
The difference between a cRBM and RBM is that the units corresponding to the conditioning variables (detector settings here) are not dynamical variables. There are no probabilities assigned to conditioning variables, and thus the only probabilities generated by cRBM are conditional probabilities. This provides a more compact representation compared to an RBM.
VIII A Few More Applications
Work on quantum foundations has led to the birth of quantum computing and quantum information. Recently, the amalgamation of quantum theory and machine learning has led to a new area of research, namely quantum machine learning schuld2018supervised . For further reading on quantum machine learning, refer to schuld2015introduction and references therein. Further, for recent trends and exploratory works in quantum machine learning, we refer the reader to dunjko2020non and references therein.
Techniques from machine learning have been used to discover new quantum experiments melnikov2018active ; krenn2016automated . In reference krenn2016automated , Krenn et. al. provide a computer program which helps designing novel quantum experiments. The program was called Melvin. Melvin provided solutions which were quite counter-intuitive and different than something a human scientist ordinarily would come up with. Melvin’s solutions have led to many novel results gu2018gouy ; wang2017generation ; babazadeh2017high ; schlederer2016cyclic ; erhard2018experimental ; malik2016multi . The ideas from Melvin have further provided machine generated proofs of Kochen-Specker theorem pavivcic2019automated .
IX Conclusion and Future Work
In this survey, we discussed the various applications of machine learning for problems in the foundations of quantum theory such as determination of the quantum bound for Bell inequalities, the classification of different behaviors in local/nonlocal sets, using hidden neurons as hidden variables for completion of quantum theory, training AI for playing Bell nonlocal games, ML-assisted state classification, and so forth. Now we discuss a few open questions at the interface. Some of these open questions have been mentioned in references canabarro2019machine ; krivachy2019neural ; bharti2019teach ; deng2018machine
Witnessing Bell nonlocality in many-body systems is an active area of research tura2014detecting ; deng2018machine . However, designing experimental-friendly many-body Bell inequalities is a difficult task. It would be interesting if machine learning could help design optimal Bell inequalities for scenarios involving many-body systems. In reference deng2018machine , the author used RBM based representation coupled with reinforcement learning to find near-optimal quantum values for various Bell inequalities corresponding to various convex Bell scenarios. It is well known that optimization becomes comparatively easier once the representation gets compact. It would be interesting if one can use other neural networks based representations such as convolutional neural networks for finding optimal (or near-optimal) quantum values.
As mentioned in reference canabarro2019machine , it is an excellent idea to deploy techniques like anomaly detection for the detection of non-classical behaviors. This can be done by subjecting the machine to training with local behaviors only.
In many of the applications, e.g. classification of entangled states, the computer gives a guess, but we are not sure about the correctness. This is never said and cannot be overlooked, as it is a limitation of these applications. The intriguing question is to understand how the output of the computer can be employed to provide a certification of the result, for instance, an entanglement witness. One could use ideas from probabilistic machine learning in such cases ghahramani2015probabilistic . The probabilistic framework, which explains how to represent and handle uncertainty about models and predictions, plays a fundamental role in scientific data analysis. Harnessing the tools from probabilistic machine learning such as Bayesian optimization and automatic model discovery could be conducive in understanding how to utilize machine output to provide a certification of the result.
In reference bharti2019teach , the authors used reinforcement learning to train AI to play Bell nonlocal games and obtain optimal (or near-optimal) performance. The agent is offered a reward at the end of each epoch which is equal to the expectation value of the Bell operator corresponding to the state and measurement settings chosen by the agent. Such a reward scheme is sparse and hence it might not be scalable. It would be interesting to come up with better reward schemes. Furthermore, in this approach only a single agent tries to learn the optimization landscape and discovers near-optimal (or optimal) measurement settings and state. It would be exciting to extend the approach to multi-agent setting where every space-like separated party is considered a separate agent. It is worth mentioning that distributing the actions and observations of a single agent into a list of agents reduces the dimensionality of agent inputs and outputs. Furthermore, it also dramatically improves the amount of training data produced per step of the environment. Agents learn better if they tend to interact as compared to the case of solitary learning.
Bell inequalities separate the set of local behaviours from the set of non-local behaviours. The analogous boundary separating quantum from the post-quantum set is known as quantum Bell inequality masanes2005extremal ; thinh2019computing . Finding quantum Bell inequalities is an interesting and challenging problem. However, one can aim to obtain the approximate expression by supervised learning with the quantum Bell inequalities being the boundary separating the quantum set from the post-quantum set. Moreover, it is interesting to see if it is possible to guess physical principles by merely opening the neural-network black box.
Driven by the success of machine learning in Bell nonlocality, it is genuine to ask if the methods could be useful to solve problems in quantum steering and contextuality. Recently, ideas from the exclusivity graph approach to contextuality were used to investigate problems involving causal inference poderini2019exclusivity . Ideas from quantum foundations could further assist in developing a deeper understanding of machine learning or in general artificial intelligence.
In artificial intelligence, one of the tests to distinguish between humans and machines is the famous “Turing Test (TT)” due to Alan Turing russell2002artificial ; saygin2000turing . The purpose of TT is to determine if a computer is linguistically distinguishable from a human. In TT, a human and a machine are sealed in different rooms. A human jury who does not know which room contains a human and which room not, asks questions to them, by email, for example. Based on the returned outcome, if the judge cannot do better than fifty-fifty, then the machine in question is said to have passed TT. The task of distinguishing the humans from machine based on the statistics of the answers (say output given questions (say input is a statistical distinguishability test assuming the rooms plus its inhabitants as black boxes. In the black-box approach to quantum theory, experiments are regarded as a black box where the experimentalist introduces a measurement (input) and obtains the outcome of the measurement (output). One of the central goals of this approach is to deduce statements regarding the contents of the black box based on input-output statistics acin2017black . It would be nice to see if techniques from the black-box approach to quantum theory could be connected to TT.
Acknowledgements.
We wish to acknowledge the support of the Ministry of Education and the National Research Foundation, Singapore. We thank Valerio Scarani for valuable discussions.Data Availability
Data sharing is not applicable to this survey as no new data were created or analyzed in this study.
References
- (1) Shai Shalev-Shwartz and Shai Ben-David. Understanding machine learning: From theory to algorithms. Cambridge university press, 2014.
- (2) Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.
- (3) Mohammed AlQuraishi. Alphafold at casp13. Bioinformatics, 35(22):4862–4865, 2019.
- (4) James P Bridge, Sean B Holden, and Lawrence C Paulson. Machine learning for first-order theorem proving. Journal of automated reasoning, 53(2):141–172, 2014.
- (5) Antonio Lavecchia. Machine-learning approaches in drug discovery: methods and applications. Drug discovery today, 20(3):318–331, 2015.
- (6) Louis-François Arsenault, O Anatole von Lilienfeld, and Andrew J Millis. Machine learning for many-body physics: efficient solution of dynamical mean-field theory. arXiv preprint arXiv:1506.08858, 2015.
- (7) Yi Zhang and Eun-Ah Kim. Quantum loop topography for machine learning. Physical review letters, 118(21):216401, 2017.
- (8) Juan Carrasquilla and Roger G Melko. Machine learning phases of matter. Nature Physics, 13(5):431–434, 2017.
- (9) Evert PL Van Nieuwenburg, Ye-Hua Liu, and Sebastian D Huber. Learning phase transitions by confusion. Nature Physics, 13(5):435–439, 2017.
- (10) Dong-Ling Deng, Xiaopeng Li, and S Das Sarma. Machine learning topological states. Physical Review B, 96(19):195145, 2017.
- (11) Lei Wang. Discovering phase transitions with unsupervised learning. Physical Review B, 94(19):195105, 2016.
- (12) Peter Broecker, Juan Carrasquilla, Roger G Melko, and Simon Trebst. Machine learning quantum phases of matter beyond the fermion sign problem. Scientific reports, 7(1):1–10, 2017.
- (13) Kelvin Chng, Juan Carrasquilla, Roger G Melko, and Ehsan Khatami. Machine learning phases of strongly correlated fermions. Physical Review X, 7(3):031038, 2017.
- (14) Yi Zhang, Roger G Melko, and Eun-Ah Kim. Machine learning z 2 quantum spin liquids with quasiparticle statistics. Physical Review B, 96(24):245119, 2017.
- (15) Sebastian J Wetzel. Unsupervised learning of phase transitions: From principal component analysis to variational autoencoders. Physical Review E, 96(2):022140, 2017.
- (16) Wenjian Hu, Rajiv RP Singh, and Richard T Scalettar. Discovering phases, phase transitions, and crossovers through unsupervised machine learning: A critical examination. Physical Review E, 95(6):062122, 2017.
- (17) Nobuyuki Yoshioka, Yutaka Akagi, and Hosho Katsura. Learning disordered topological phases by statistical recovery of symmetry. Physical Review B, 97(20):205110, 2018.
- (18) Giacomo Torlai and Roger G Melko. Learning thermodynamics with boltzmann machines. Physical Review B, 94(16):165134, 2016.
- (19) Hsin-Yuan Huang, Kishor Bharti, and Patrick Rebentrost. Near-term quantum algorithms for linear systems of equations. arXiv preprint arXiv:1909.07344, 2019.
- (20) Ken-Ichi Aoki and Tamao Kobayashi. Restricted boltzmann machines for the long range ising models. Modern Physics Letters B, 30(34):1650401, 2016.
- (21) Yi-Zhuang You, Zhao Yang, and Xiao-Liang Qi. Machine learning spatial geometry from entanglement features. Physical Review B, 97(4):045153, 2018.
- (22) Mario Pasquato. Detecting intermediate mass black holes in globular clusters with machine learning. arXiv preprint arXiv:1606.08548, 2016.
- (23) Yashar D Hezaveh, Laurence Perreault Levasseur, and Philip J Marshall. Fast automated analysis of strong gravitational lenses with convolutional neural networks. Nature, 548(7669):555–557, 2017.
- (24) Rahul Biswas, Lindy Blackburn, Junwei Cao, Reed Essick, Kari Alison Hodge, Erotokritos Katsavounidis, Kyungmin Kim, Young-Min Kim, Eric-Olivier Le Bigot, Chang-Hwan Lee, et al. Application of machine learning algorithms to the study of noise artifacts in gravitational-wave data. Physical Review D, 88(6):062003, 2013.
- (25) Benjamin P Abbott, Richard Abbott, TD Abbott, MR Abernathy, Fausto Acernese, Kendall Ackley, Carl Adams, Thomas Adams, Paolo Addesso, RX Adhikari, et al. Observation of gravitational waves from a binary black hole merger. Physical review letters, 116(6):061102, 2016.
- (26) Sergei V Kalinin, Bobby G Sumpter, and Richard K Archibald. Big–deep–smart data in imaging for guiding materials design. Nature materials, 14(10):973–980, 2015.
- (27) Samuel S Schoenholz, Ekin D Cubuk, Daniel M Sussman, Efthimios Kaxiras, and Andrea J Liu. A structural approach to relaxation in glassy liquids. Nature Physics, 12(5):469–471, 2016.
- (28) Junwei Liu, Yang Qi, Zi Yang Meng, and Liang Fu. Self-learning monte carlo method. Physical Review B, 95(4):041101, 2017.
- (29) Li Huang and Lei Wang. Accelerated monte carlo simulations with restricted boltzmann machines. Physical Review B, 95(3):035105, 2017.
- (30) Giacomo Torlai, Guglielmo Mazzola, Juan Carrasquilla, Matthias Troyer, Roger Melko, and Giuseppe Carleo. Neural-network quantum state tomography. Nature Physics, 14(5):447–450, 2018.
- (31) Jing Chen, Song Cheng, Haidong Xie, Lei Wang, and Tao Xiang. Equivalence of restricted boltzmann machines and tensor network states. Physical Review B, 97(8):085104, 2018.
- (32) Yichen Huang and Joel E Moore. Neural network representation of tensor network and chiral states. arXiv preprint arXiv:1701.06246, 2017.
- (33) Frank Schindler, Nicolas Regnault, and Titus Neupert. Probing many-body localization with neural networks. Physical Review B, 95(24):245134, 2017.
- (34) Tobias Haug, Rainer Dumke, Leong-Chuan Kwek, Christian Miniatura, and Luigi Amico. Engineering quantum current states with machine learning. arXiv:1911.09578, 2019.
- (35) Zi Cai and Jinguo Liu. Approximating quantum many-body wave functions using artificial neural networks. Physical Review B, 97(3):035116, 2018.
- (36) Peter Broecker, Fakher F Assaad, and Simon Trebst. Quantum phase recognition via unsupervised machine learning. arXiv preprint arXiv:1707.00663, 2017.
- (37) Yusuke Nomura, Andrew S Darmawan, Youhei Yamaji, and Masatoshi Imada. Restricted boltzmann machine learning for solving strongly correlated quantum systems. Physical Review B, 96(20):205152, 2017.
- (38) Jacob Biamonte, Peter Wittek, Nicola Pancotti, Patrick Rebentrost, Nathan Wiebe, and Seth Lloyd. Quantum machine learning. Nature, 549(7671):195–202, 2017.
- (39) Tobias Haug, Wai-Keong Mok, Jia-Bin You, Wenzu Zhang, Ching Eng Png, and Leong-Chuan Kwek. Classifying global state preparation via deep reinforcement learning. arXiv:2005.12759, 2020.
- (40) Giacomo Torlai and Roger G Melko. Neural decoder for topological codes. Physical review letters, 119(3):030501, 2017.
- (41) Marin Bukov. Reinforcement learning for autonomous preparation of floquet-engineered states: Inverting the quantum kapitza oscillator. Physical Review B, 98(22):224305, 2018.
- (42) Marin Bukov, Alexandre GR Day, Dries Sels, Phillip Weinberg, Anatoli Polkovnikov, and Pankaj Mehta. Reinforcement learning in different phases of quantum control. Physical Review X, 8(3):031086, 2018.
- (43) Koji Hashimoto, Sotaro Sugishita, Akinori Tanaka, and Akio Tomiya. Deep learning and the ads/cft correspondence. Physical Review D, 98(4):046019, 2018.
- (44) Jonathan Carifio, James Halverson, Dmitri Krioukov, and Brent D Nelson. Machine learning in the string landscape. Journal of High Energy Physics, 2017(9):157, 2017.
- (45) Henry W Lin, Max Tegmark, and David Rolnick. Why does deep and cheap learning work so well? Journal of Statistical Physics, 168(6):1223–1247, 2017.
- (46) Andrzej Cichocki. Tensor networks for big data analytics and large-scale optimization problems. arXiv preprint arXiv:1407.3124, 2014.
- (47) Giuseppe Carleo, Ignacio Cirac, Kyle Cranmer, Laurent Daudet, Maria Schuld, Naftali Tishby, Leslie Vogt-Maranto, and Lenka Zdeborová. Machine learning and the physical sciences. Review of Modern Physics, 91(4):045002, 2019.
- (48) Vedran Dunjko, Jacob M Taylor, and Hans J Briegel. Quantum-enhanced machine learning. Physical review letters, 117(13):130501, 2016.
- (49) Marcello Benedetti, Erika Lloyd, Stefan Sack, and Mattia Fiorentini. Parameterized quantum circuits as machine learning models. Quantum Science and Technology, 4(4):043001, 2019.
- (50) Lucien Hardy and Robert Spekkens. Why physics needs quantum foundations. arXiv preprint arXiv:1003.5008, 2010.
- (51) Tamás Kriváchy, Yu Cai, Daniel Cavalcanti, Arash Tavakoli, Nicolas Gisin, and Nicolas Brunner. A neural network oracle for quantum nonlocality problems in networks. arXiv preprint arXiv:1907.10552, 2019.
- (52) Askery Canabarro, Samuraí Brito, and Rafael Chaves. Machine learning nonlocal correlations. Physical review letters, 122(20):200401, 2019.
- (53) Kishor Bharti, Tobias Haug, Vlatko Vedral, and Leong-Chuan Kwek. How to teach ai to play bell non-local games: Reinforcement learning. arXiv preprint arXiv:1912.10783, 2019.
- (54) Dong-Ling Deng. Machine learning detection of bell nonlocality in quantum many-body systems. Physical review letters, 120(24):240402, 2018.
- (55) Raban Iten, Tony Metger, Henrik Wilming, Lídia Del Rio, and Renato Renner. Discovering physical concepts with neural networks. Physical Review Letters, 124(1):010508, 2020.
- (56) Tom M Mitchell et al. Machine learning. 1997. Burr Ridge, IL: McGraw Hill, 45(37):870–877, 1997.
- (57) David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, et al. Mastering the game of go without human knowledge. Nature, 550(7676):354, 2017.
- (58) Geoffrey E Hinton. A practical guide to training restricted boltzmann machines. In Neural networks: Tricks of the trade, pages 599–619. Springer, 2012.
- (59) Giuseppe Carleo and Matthias Troyer. Solving the quantum many-body problem with artificial neural networks. Science, 355(6325):602–606, 2017.
- (60) John McCarthy, Marvin L Minsky, Nathaniel Rochester, and Claude E Shannon. A proposal for the dartmouth summer research project on artificial intelligence, august 31, 1955. AI magazine, 27(4):12–12, 2006.
- (61) Alan M Turing. Computing machinery and intelligence. In Parsing the Turing Test, pages 23–65. Springer, 2009.
- (62) Stuart Russell and Peter Norvig. Artificial intelligence: a modern approach. 2002.
- (63) Christopher A Fuchs and Rüdiger Schack. A quantum-bayesian route to quantum-state space. Foundations of Physics, 41(3):345–356, 2011.
- (64) Hugh Everett III. " relative state" formulation of quantum mechanics. Reviews of modern physics, 29(3):454, 1957.
- (65) Bryce Seligman DeWitt and Neill Graham. The many worlds interpretation of quantum mechanics. Princeton University Press, 2015.
- (66) Roland Omnes. Consistent interpretations of quantum mechanics. Reviews of Modern Physics, 64(2):339, 1992.
- (67) Jonathan Barrett. Information processing in generalized probabilistic theories. Physical Review A, 75(3):032304, 2007.
- (68) Antonio Acín and Miguel Navascués. Black box quantum mechanics. In Quantum [Un] Speakables II, pages 307–319. Springer, 2017.
- (69) Wim Van Dam. Implausible consequences of superstrong nonlocality. Natural Computing, 12(1):9–12, 2013.
- (70) Gilles Brassard, Harry Buhrman, Noah Linden, André Allan Méthot, Alain Tapp, and Falk Unger. Limit on nonlocality in any world in which communication complexity is not trivial. Physical Review Letters, 96(25):250401, 2006.
- (71) Marcin Pawłowski, Tomasz Paterek, Dagomir Kaszlikowski, Valerio Scarani, Andreas Winter, and Marek Żukowski. Information causality as a physical principle. Nature, 461(7267):1101–1104, 2009.
- (72) Miguel Navascués and Harald Wunderlich. A glance beyond the quantum model. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 466(2115):881–890, 2010.
- (73) Noah Linden, Sandu Popescu, Anthony J Short, and Andreas Winter. Quantum nonlocality and beyond: limits from nonlocal computation. Physical review letters, 99(18):180502, 2007.
- (74) Bin Yan. Quantum correlations are tightly bound by the exclusivity principle. Physical review letters, 110(26):260406, 2013.
- (75) Tobias Fritz, Ana Belén Sainz, Remigiusz Augusiak, J Bohr Brask, Rafael Chaves, Anthony Leverrier, and Antonio Acín. Local orthogonality as a multipartite principle for quantum correlations. Nature communications, 4(1):1–7, 2013.
- (76) Kelvin J McQueen. Four tails problems for dynamical collapse theories. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 49:10–18, 2015.
- (77) Rafael D Sorkin. Quantum mechanics as quantum measure theory. Modern Physics Letters A, 9(33):3119–3127, 1994.
- (78) Ognyan Oreshkov, Fabio Costa, and Časlav Brukner. Quantum correlations with no causal order. Nature communications, 3(1):1–8, 2012.
- (79) Jean-Michel Raimond, M Brune, and Serge Haroche. Manipulating quantum entanglement with atoms and photons in a cavity. Reviews of Modern Physics, 73(3):565, 2001.
- (80) Ryszard Horodecki, Paweł Horodecki, Michał Horodecki, and Karol Horodecki. Quantum entanglement. Reviews of modern physics, 81(2):865, 2009.
- (81) William K Wootters. Entanglement of formation and concurrence. Quantum Information & Computation, 1(1):27–44, 2001.
- (82) Michal Horodecki, Pawel Horodecki, and Ryszard Horodecki. On the necessary and sufficient conditions for separability of mixed quantum states. Phys. Lett. A, 223(quant-ph/9605038):1, 1996.
- (83) Barbara M Terhal. Detecting quantum entanglement. Theoretical computer science, 287(1):313–335, 2002.
- (84) Philipp Krammer, Hermann Kampermann, Dagmar Bruß, Reinhold A Bertlmann, Leong Chuang Kwek, and Chiara Macchiavello. Multipartite entanglement detection via structure factors. Physical review letters, 103(10):100502, 2009.
- (85) Artur K Ekert, Carolina Moura Alves, Daniel KL Oi, Michał Horodecki, Paweł Horodecki, and Leong Chuan Kwek. Direct estimations of linear and nonlinear functionals of a quantum state. Physical review letters, 88(21):217901, 2002.
- (86) Judea Pearle. Causality. Cambridge: Cambridge University Press, 2000.
- (87) Stuart J Freedman and John F Clauser. Experimental test of local hidden-variable theories. Physical Review Letters, 28(14):938, 1972.
- (88) Carl A Kocher and Eugene D Commins. Polarization correlation of photons emitted in an atomic cascade. Physical Review Letters, 18(15):575, 1967.
- (89) Alain Aspect. Expériences basées sur les inégalités de bell. Le Journal de Physique Colloques, 42(C2):C2–63, 1981.
- (90) Alain Aspect, Jean Dalibard, and Gérard Roger. Experimental test of bell’s inequalities using time-varying analyzers. Physical review letters, 49(25):1804, 1982.
- (91) Charles H Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, and William K Wootters. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Physical review letters, 70(13):1895, 1993.
- (92) Artur K Ekert. Quantum cryptography based on bell’s theorem. Physical Review Letters, 67(6):661, 1991.
- (93) Charles H Bennett, Gilles Brassard, Sandu Popescu, Benjamin Schumacher, John A Smolin, and William K Wootters. Purification of noisy entanglement and faithful teleportation via noisy channels. Physical review letters, 76(5):722, 1996.
- (94) Charles H Bennett and Stephen J Wiesner. Communication via one-and two-particle operators on einstein-podolsky-rosen states. Physical review letters, 69(20):2881, 1992.
- (95) David Deutsch. Quantum theory, the church–turing principle and the universal quantum computer. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 400(1818):97–117, 1985.
- (96) Richard P Feynman. Feynman lectures on computation. CRC Press, 2018.
- (97) J. S. Bell. On the einstein podolsky rosen paradox. Physics (Long Island City, N.Y.), 1:195–200, Nov 1964.
- (98) Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. Bell nonlocality. Reviews of Modern Physics, 86(2):419, 2014.
- (99) Stefano Pironio, Antonio Acín, Serge Massar, A Boyer de La Giroday, Dzmitry N Matsukevich, Peter Maunz, Steven Olmschenk, David Hayes, Le Luo, T Andrew Manning, et al. Random numbers certified by bell’s theorem. Nature, 464(7291):1021, 2010.
- (100) Dominic Mayers and Andrew Yao. Self testing quantum apparatus. Quantum Info. Comput., 4(4):273–286, July 2004.
- (101) John F. Clauser, Michael A. Horne, Abner Shimony, and Richard A. Holt. Proposed experiment to test local hidden-variable theories. Physical Review Letters, 23:880–884, Oct 1969.
- (102) SIMON KOCHEN and EP SPECKER. The problem of hidden variables in quantum mechanics. Journal of Mathematics and Mechanics, 17(1):59–87, 1967.
- (103) N David Mermin. Hidden variables and the two theorems of john bell. Reviews of Modern Physics, 65(3):803, 1993.
- (104) Adán Cabello, Simone Severini, and Andreas Winter. Graph-theoretic approach to quantum correlations. Phys. Rev. Lett., 112(4):040401, 2014.
- (105) Barbara Amaral and Marcelo Terra Cunha. On Graph Approaches to Contextuality and their Role in Quantum Theory. Springer, Cham, Switzerland, 2018.
- (106) Adán Cabello, Vincenzo D’Ambrosio, Eleonora Nagali, and Fabio Sciarrino. Hybrid ququart-encoded quantum cryptography protected by kochen-specker contextuality. Physical Review A, 84:030302, Sep 2011.
- (107) Kishor Bharti, Maharshi Ray, and Leong-Chuan Kwek. Non-classical correlations in n-cycle setting. Entropy, 21(2):134, 2019.
- (108) Robert Raussendorf. Contextuality in measurement-based quantum computation. Physical Review A, 88(2):022322, 2013.
- (109) Kishor Bharti, Maharshi Ray, Antonios Varvitsiotis, Naqueeb Ahmad Warsi, Adán Cabello, and Leong-Chuan Kwek. Robust self-testing of quantum systems via noncontextuality inequalities. Physical review letters, 122(25):250403, 2019.
- (110) Shane Mansfield and Elham Kashefi. Quantum advantage from sequential-transformation contextuality. Physical review letters, 121(23):230401, 2018.
- (111) Debashis Saha, Paweł Horodecki, and Marcin Pawłowski. State independent contextuality advances one-way communication. New Journal of Physics, 21(9):093057, 2019.
- (112) Kishor Bharti, Maharshi Ray, Antonios Varvitsiotis, Adán Cabello, and Leong-Chuan Kwek. Local certification of programmable quantum devices of arbitrary high dimensionality. arXiv preprint arXiv:1911.09448, 2019.
- (113) Nicolas Delfosse, Philippe Allard Guerin, Jacob Bian, and Robert Raussendorf. Wigner function negativity and contextuality in quantum computation on rebits. Physical Review X, 5(2):021003, 2015.
- (114) Jaskaran Singh, Kishor Bharti, et al. Quantum key distribution protocol based on contextuality monogamy. Physical Review A, 95(6):062333, 2017.
- (115) Hakop Pashayan, Joel J Wallman, and Stephen D Bartlett. Estimating outcome probabilities of quantum circuits using quasiprobabilities. Physical review letters, 115(7):070501, 2015.
- (116) Kishor Bharti, Atul Singh Arora, Leong Chuan Kwek, and Jérémie Roland. A simple proof of uniqueness of the kcbs inequality. arXiv preprint arXiv:1811.05294, 2018.
- (117) Juan Bermejo-Vega, Nicolas Delfosse, Dan E Browne, Cihan Okay, and Robert Raussendorf. Contextuality as a resource for models of quantum computation with qubits. Physical review letters, 119(12):120505, 2017.
- (118) Lorenzo Catani and Dan E Browne. State-injection schemes of quantum computation in spekkens’ toy theory. Physical Review A, 98(5):052108, 2018.
- (119) Atul Singh Arora, Kishor Bharti, et al. Revisiting the admissibility of non-contextual hidden variable models in quantum mechanics. Physics Letters A, 383(9):833–837, 2019.
- (120) Mark Howard, Joel Wallman, Victor Veitch, and Joseph Emerson. Contextuality supplies the ’magic’ for quantum computation. Nature, 510:351 EP –, Jun 2014.
- (121) Samson Abramsky and Adam Brandenburger. The sheaf-theoretic structure of non-locality and contextuality. New Journal of Physics, 13(11):113036, 2011.
- (122) Antonio Acín, Tobias Fritz, Anthony Leverrier, and Ana Belén Sainz. A combinatorial approach to nonlocality and contextuality. Communications in Mathematical Physics, 334(2):533–628, 2015.
- (123) Ehtibar N Dzhafarov, Víctor H Cervantes, and Janne V Kujala. Contextuality in canonical systems of random variables. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375(2106):20160389, 2017.
- (124) Ehtibar N Dzhafarov. On joint distributions, counterfactual values and hidden variables in understanding contextuality. Philosophical Transactions of the Royal Society A, 377(2157):20190144, 2019.
- (125) Janne V Kujala and Ehtibar N Dzhafarov. Measures of contextuality and non-contextuality. Philosophical Transactions of the Royal Society A, 377(2157):20190149, 2019.
- (126) Robert W Spekkens. Contextuality for preparations, transformations, and unsharp measurements. Physical Review A, 71(5):052108, 2005.
- (127) S. Kochen and E. P. Specker. The problem of hidden variales in quantum mechanics. J. Math. Mech., 17:59–87, 1967.
- (128) Marco Túlio Quintino, Tamás Vértesi, Daniel Cavalcanti, Remigiusz Augusiak, Maciej Demianowicz, Antonio Acín, and Nicolas Brunner. Inequivalence of entanglement, steering, and bell nonlocality for general measurements. Physical Review A, 92(3):032107, 2015.
- (129) Howard M Wiseman, Steve James Jones, and Andrew C Doherty. Steering, entanglement, nonlocality, and the einstein-podolsky-rosen paradox. Physical review letters, 98(14):140402, 2007.
- (130) Erwin Schrödinger. Discussion of probability relations between separated systems. In Mathematical Proceedings of the Cambridge Philosophical Society, volume 31, pages 555–563. Cambridge University Press, 1935.
- (131) Samuraí Gomes de Aguiar Brito, B Amaral, and R Chaves. Quantifying bell nonlocality with the trace distance. Physical Review A, 97(2):022111, 2018.
- (132) Armin Tavakoli, Paul Skrzypczyk, Daniel Cavalcanti, and Antonio Acín. Nonlocal correlations in the star-network configuration. Physical Review A, 90(6):062109, 2014.
- (133) Cyril Branciard, Nicolas Gisin, and Stefano Pironio. Characterizing the nonlocal correlations created via entanglement swapping. Physical review letters, 104(17):170401, 2010.
- (134) Marc-Olivier Renou, Elisa Bäumer, Sadra Boreiri, Nicolas Brunner, Nicolas Gisin, and Salman Beigi. Genuine quantum nonlocality in the triangle network. Physical review letters, 123(14):140401, 2019.
- (135) Nicolas Gisin. Entanglement 25 years after quantum teleportation: testing joint measurements in quantum networks. Entropy, 21(3):325, 2019.
- (136) Hiroki Saito and Masaya Kato. Machine learning technique to find quantum many-body ground states of bosons on a lattice. Journal of the Physical Society of Japan, 87(1):014001, 2018.
- (137) Xun Gao and Lu-Ming Duan. Efficient representation of quantum many-body states with deep neural networks. Nature communications, 8(1):1–6, 2017.
- (138) Ulrich Schollwöck. The density-matrix renormalization group. Reviews of modern physics, 77(1):259, 2005.
- (139) Frank Verstraete, Valentin Murg, and J Ignacio Cirac. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Advances in Physics, 57(2):143–224, 2008.
- (140) Guifré Vidal. Class of quantum many-body states that can be efficiently simulated. Physical review letters, 101(11):110501, 2008.
- (141) Yue-Chi Ma and Man-Hong Yung. Transforming bell’s inequalities into state classifiers with machine learning. npj Quantum Information, 4(1):1–10, 2018.
- (142) Reinhard F Werner. Quantum states with einstein-podolsky-rosen correlations admitting a hidden-variable model. Physical Review A, 40(8):4277, 1989.
- (143) Cillian Harney, Stefano Pirandola, Alessandro Ferraro, and Mauro Paternostro. Entanglement classification via neural network quantum states. arXiv preprint arXiv:1912.13207, 2019.
- (144) Sirui Lu, Shilin Huang, Keren Li, Jun Li, Jianxin Chen, Dawei Lu, Zhengfeng Ji, Yi Shen, Duanlu Zhou, and Bei Zeng. Separability-entanglement classifier via machine learning. Phys. Rev. A, 98(1):012315, 2018.
- (145) Caio BD Goes, Askery Canabarro, Eduardo I Duzzioni, and Thiago O Maciel. Automated machine learning can classify bound entangled states with tomograms. arXiv preprint arXiv:2001.08118, 2020.
- (146) Steven Weinstein. Neural networks as" hidden" variable models for quantum systems. arXiv preprint arXiv:1807.03910, 2018.
- (147) Steven Weinstein. Nonlocality without nonlocality. Foundations of Physics, 39(8):921–936, 2009.
- (148) Maria Schuld and Francesco Petruccione. Supervised learning with quantum computers, volume 17. Springer, 2018.
- (149) Maria Schuld, Ilya Sinayskiy, and Francesco Petruccione. An introduction to quantum machine learning. Contemporary Physics, 56(2):172–185, 2015.
- (150) Vedran Dunjko and Peter Wittek. A non-review of quantum machine learning: trends and explorations. Quantum Views, 4:32, 2020.
- (151) Alexey A Melnikov, Hendrik Poulsen Nautrup, Mario Krenn, Vedran Dunjko, Markus Tiersch, Anton Zeilinger, and Hans J Briegel. Active learning machine learns to create new quantum experiments. Proceedings of the National Academy of Sciences, 115(6):1221–1226, 2018.
- (152) Mario Krenn, Mehul Malik, Robert Fickler, Radek Lapkiewicz, and Anton Zeilinger. Automated search for new quantum experiments. Physical review letters, 116(9):090405, 2016.
- (153) Xuemei Gu, Mario Krenn, Manuel Erhard, and Anton Zeilinger. Gouy phase radial mode sorter for light: Concepts and experiments. Physical review letters, 120(10):103601, 2018.
- (154) Feiran Wang, Manuel Erhard, Amin Babazadeh, Mehul Malik, Mario Krenn, and Anton Zeilinger. Generation of the complete four-dimensional bell basis. Optica, 4(12):1462–1467, 2017.
- (155) Amin Babazadeh, Manuel Erhard, Feiran Wang, Mehul Malik, Rahman Nouroozi, Mario Krenn, and Anton Zeilinger. High-dimensional single-photon quantum gates: concepts and experiments. Physical review letters, 119(18):180510, 2017.
- (156) Florian Schlederer, Mario Krenn, Robert Fickler, Mehul Malik, and Anton Zeilinger. Cyclic transformation of orbital angular momentum modes. New Journal of Physics, 18(4):043019, 2016.
- (157) Manuel Erhard, Mehul Malik, Mario Krenn, and Anton Zeilinger. Experimental greenberger–horne–zeilinger entanglement beyond qubits. Nature Photonics, 12(12):759–764, 2018.
- (158) Mehul Malik, Manuel Erhard, Marcus Huber, Mario Krenn, Robert Fickler, and Anton Zeilinger. Multi-photon entanglement in high dimensions. Nature Photonics, 10(4):248, 2016.
- (159) Mladen Pavičić, Mordecai Waegell, Norman D Megill, and PK Aravind. Automated generation of kochen-specker sets. Scientific reports, 9(1):1–11, 2019.
- (160) Jordi Tura, Remigiusz Augusiak, Ana Belén Sainz, Tamas Vértesi, Maciej Lewenstein, and Antonio Acín. Detecting nonlocality in many-body quantum states. Science, 344(6189):1256–1258, 2014.
- (161) Zoubin Ghahramani. Probabilistic machine learning and artificial intelligence. Nature, 521(7553):452–459, 2015.
- (162) Ll Masanes. Extremal quantum correlations for n parties with two dichotomic observables per site. arXiv preprint quant-ph/0512100, 2005.
- (163) Le Phuc Thinh. Computing quantum bell inequalities. arXiv preprint arXiv:1909.05472, 2019.
- (164) Davide Poderini, Rafael Chaves, Iris Agresti, Gonzalo Carvacho, and Fabio Sciarrino. Exclusivity graph approach to instrumental inequalities. arXiv preprint arXiv:1909.09120, 2019.
- (165) Ayse Pinar Saygin, Ilyas Cicekli, and Varol Akman. Turing test: 50 years later. Minds and machines, 10(4):463–518, 2000.