[1,2,3]\fnmKazuhiro \surHada
[1]\orgdivGraduate School of Science, \orgnameNagoya City University, \orgaddress\streetYamanohata 1, Mizuho-cho, Mizuho-ku, \cityNagoya, \postcode467-8501, \stateAichi, \countryJapan
[2]\orgdivMizusawa VLBI Observatory, \orgnameNational Astronomical Observatory of Japan, \orgaddress\street2-12 Hoshigaoka-cho, Mizusawa, \cityOshu, \postcode023-0861, \stateIwate, \countryJapan
3]\orgdivAstronomical Science Program, \orgnameThe Graduate University for Advanced Studies (SOKENDAI), \orgaddress\street2-21 Osawa, \cityMitaka, \postcode181-8588, \stateTokyo, \countryJapan
4]\orgdivInstitute of Astronomy and Astrophysics, \orgnameAcademia Sinica, \orgaddress\street11F of Astronomy-Mathematics Building, AS/NTU No. 1, Sec. 4, Roosevelt Road, \cityTaipei, \postcode10617, \stateTaiwan
5]\orgdivDepartment of General Science and Education, \orgnameNational Institute of Technology, Hachinohe College, \orgaddress\street16-1 Uwanotai, Tamonoki, \cityHachinohe, \postcode039-1192, \stateAomori, \countryJapan
6]\orgnameKogakuin University of Technology & Engineering, Academic Support Center, \orgaddress\street2665-1 Nakano-machi, \cityHachioji, \postcode192-0015, \stateTokyo, \countryJapan
7]\orgnameNational Astronomical Observatory of Japan, \orgaddress\street2-21 Osawa, \cityMitaka, \postcode181-8588, \stateTokyo, \countryJapan
M 87: a cosmic laboratory for deciphering black hole accretion and jet formation
Abstract
Over the past decades, there has been significant progress in our understanding of accreting supermassive black holes (SMBHs) that drive active galactic nuclei (AGNs), both from observational and theoretical perspectives. As an iconic target for this area of study, the nearby giant elliptical galaxy M 87 has received special attention thanks to its proximity, large mass of the central black hole and bright emission across the entire electromagnetic spectrum from radio to very-high-energy -rays. In particular, recent global millimeter-very-long-baseline-interferometer observations towards this nucleus have provided the first-ever opportunity to image the event-horizon-scale structure of an AGN, opening a new era of black hole astrophysics. On large scales, M 87 exhibits a spectacular jet propagating far beyond the host galaxy, maintaining its narrowly collimated shape over seven orders of magnitude in distance. Elucidating the generation and propagation, as well as the internal structure, of powerful relativistic jets remains a longstanding challenge in radio-loud AGNs. M 87 offers a privileged opportunity to examine such a jet with unprecedented detail.
In this review, we provide a comprehensive overview of the observational knowledge accumulated about the M 87 black hole across various wavelengths. We cover both accretion and ejection processes at spatial scales ranging from outside the Bondi radius down to the event horizon. By compiling these observations and relevant theoretical studies, we aim to highlight our current understanding of accretion and jet physics for this specific object.
keywords:
Galaxies: active, Galaxies: jets, black hole physics| Quantities | |
|---|---|
| Distance to a given source | |
| Solar mass | |
| Black hole mass | |
| Dimensionless spin parameter | |
| Black hole angular momentum | |
| Gravitational radius | |
| Radius of the event horizon | |
| Radius of the ergosphere | |
| Schwarzschild radius | |
| Transition radius from an ADAF to a standard accretion disk | |
| Angular frequency of the event horizon | |
| Angular frequency of magnetic field line | |
| Bondi accretion radius | |
| Core radius of ambient gas | |
| Adiabatic sound speed | |
| (ion) | Ion temperature |
| (electron) | Electron temperature |
| Mass accretion rate | |
| Bondi accretion rate | |
| Electron number density | |
| Mass density | |
| Eddington mass accretion rate | |
| Mass accretion rate normalized by | |
| Critical value (upper limit) of | |
| Viscosity parameter in an accretion flow | |
| Accretion efficiency | |
| Magnetic flux threading the event horizon | |
| Dimensionless magnetic flux threading the event horizon | |
| Total power of the jet | |
| Radiation power of the jet | |
| Proton power of the jet | |
| Electron-positron pair power of the jet | |
| Poynting power of the jet | |
| Power supplied by Blandford & Znajek process | |
| Jet opening angle | |
| Jet viewing angle | |
| Lorentz factor | |
| Jet speed divided by the speed of light | |
| Magnetization parameter | |
| Doppler factor of the emission region | |
| Turnover frequency caused by SSA | |
| Nonthermal electron-positron energy density | |
| Energy density of magnetic field | |
| Optical depth for synchrotron self-absorption | |
| Acronyms for objects, physical quantities and states | |
| ACZ | Acceleration and collimation zone |
| ADAF | Advection-dominated accretion flow |
| ADIOS | Adiabatic inflow-outflow solution |
| AGN | Active galactic nucleus |
| BLO | BL Lac object |
| BZ | Blandford & Znajek |
| CD | Current-driven |
| HD | Hydrodynamics |
| EVPA | Electric vector polarization angle |
| FR | Fanaroff-Riley |
| FR-I | Fanaroff-Riley Class I |
| FR-II | Fanaroff-Riley Class II |
| FSRQ | Flat-spectrum radio quasar |
| GR | General relativity |
| GRRT | General relativistic radiative transfer |
| GRMHD | General relativistic magnetohydrodynamics |
| IGM | Intergalactic medium |
| ISCO | Innermost stable circular orbit |
| ISM | Interstellar medium |
| JCB | Jet collimation break |
| KH | Kelvin-Helmholtz |
| MAD | Magnetically-arrested disk |
| MFPA | Magnetic field position angle |
| MHD | Magnetohydrodynamics |
| MWL | Multi-wavelength |
| NLSy1 | Narrow-line Seyfert 1 |
| RIAF | Radiatively inefficient accretion flow |
| RM | Rotation measure |
| RQ | Radio-quiet |
| RL | Radio-loud |
| SANE | Standard accretion and normal evolution |
| SED | Spectral energy distribution |
| SMBH | Supermassive black hole |
| SSA | Synchrotron self-absorption |
| UV | Ultraviolet |
| VHE | Very-high-energy |
| Acronyms for observing facilities, telescopes and instruments | |
| ALMA | Atacama Large Millimeter/submillimeter Array |
| BHEX | Black Hole Explorer |
| CFHT | Canada-France-Hawaii Telescope |
| EAVN | East Asian VLBI Network |
| EHT | Event Horizon Telescope |
| EVN | European VLBI Network |
| eXTP | enhanced X-ray Timing and Polarization Mission |
| GLT | Greenland Telescope |
| GMVA | Global Millimeter VLBI Array |
| HAWC | High-Altitude Water Cherenkov Observatory |
| HST | Hubble Space Telescope |
| HEGRA | High-Energy-Gamma-Ray Astronomy |
| H.E.S.S | High Energy Stereoscopic System |
| LOFAR | Low Frequency Array |
| ngEHT | next-generation Event Horizon Telescope |
| ngVLA | next-generation Very Large Array |
| MAGIC | Major Atmospheric Gamma-ray Imaging Cherenkov Telescope |
| SKA | Square Kilometer Array |
| SMA | Submillimeter Array |
| STIS | Space Telescope Imaging Spectrograph |
| VLA | Very Large Array |
| VLBA | Very Long Baseline Array |
| VLBI | Very long baesline interferometry |
| VERA | VLBI Exploration of Radio Astrometry |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VLT | Very Large Telescope |
| VSOP | VLBI Space Observatory Programee |
1 Introduction
1.1 General context
A fraction of galaxies emit an immense amount of energy from the compact central regions, often surpassing the combined brightness of their entire host galaxies. These are known as active galactic nuclei (AGNs), and it is widely accepted that they are powered by the accretion of material onto supermassive black holes (SMBHs) at their cores (Lynden-Bell 1969; Rees 1984). The quest to understand the nature of AGNs and SMBHs has persisted since their initial discovery and remains a paramount focus of the current astrophysics. Furthermore, there is growing evidence that the energetic activities of AGN profoundly influence the formation and cosmological evolution of galaxies and galaxy clusters, as represented by the empirical correlation between the stellar velocity dispersion of galaxy bulges and the mass of central SMBHs (Magorrian et al 1998; Kormendy and Ho 2013). This feedback mechanism may manifest through the intense radiation emitted by luminous accretion disks or the mechanical energy of powerful jets/outflows emanating from the nuclei.
AGNs display diverse observational properties, with various types and subclasses distinguished based on different features. While some of this diversity can be attributed to an orientation effect, where the central engine remains essentially identical, intrinsic differences in the central object also contribute to the range of AGN activity. Most notably, AGNs are divided into two distinct classes based on the ratio of radio to optical luminosity (i.e., radio loudness): radio-quiet (RQ) AGNs and radio-loud (RL) AGNs (Antonucci 1993; Urry and Padovani 1995). The former constitutes the predominant population of AGNs, with their spectral energy distributions (SED) primarily dominated by thermal emission from accretion disks observed across optical, ultraviolet, and X-ray wavelengths. In contrast, the latter class represents only 10–15% of AGNs (Kellermann et al 1989), but is characterized by powerful jets consisting of relativistically beamed outflows composed of highly magnetized plasma. The relativistic jets make the appearance of AGNs more spectacular. When viewed from large orientation angles, radio jets extend from kiloparsec (kpc) to Megaparsec (Mpc) scales, displaying a two-sided morphology centered on the nucleus. Such misaligned RLAGNs are referred to as radio galaxies. Conversely, when the jets are viewed from small angles, the apparent structure of the source becomes compact but shows intense nonthermal radiation and variability from radio to -rays due to a strong Doppler-boosting effect. This type of jetted AGNs is known as blazars. Both radio galaxies and blazars are further classified into subclasses based on the observed jet powers, radio morphology and the characteristics of the observed SED and emission lines (Urry and Padovani 1995).
Despite the wealth of observational features seen across the entire electromagnetic spectrum, our understanding on the physical processes governing the accretion and ejection associated with SMBHs is still incomplete: How exactly is matter transferred from galactic scales to event horizon scales? What control the power of relativistic jets? What causes the intrinsic diversity of AGNs? One obvious challenge is that AGN and its environment are highly complex and a variety of complicated physical processes are at work. Besides, the relevant physical scales associated with the BH accretion/ejection are tiny, typically within parsec (pc) scales or much less, making them difficult to spatially resolve with most current astronomical facilities. Hence, the key to advancing our understanding lies in identifying a nearby target that enable detailed spatial resolution and investigation of the SMBH vicinity, coupled with the availability of high-resolution observational facilities.
1.2 M 87
In this review we specifically focus on M 87 (NGC 4486), a nearby giant elliptical galaxy in the center of the Virgo cluster located at a distance of Mpc (Blakeslee et al 2009; Bird et al 2010; Cantiello et al 2018). This object was originally discovered and cataloged by Charles Messier in 1781. In 1918, Heber Curtis at Lick Observatory detected ‘a curious straight ray …apparently connected with the nucleus by a thin line of matter’ in their optical image of this galaxy (Curtis 1918). Although the exact physical origin of this feature was not known at that time, this was later recognized as the first discovery of an astrophysical jet. About 40 years later, Walter Baade discovered that the light from the ‘jet’ was strongly polarized, first indicative of nonthermal synchrotron origin of the jet emission (Baade 1956). M 87 has also been known as one of the brightest radio sources on the sky (as Virgo A or 3C 274) since the early days of radio astronomy (e.g., Bolton et al 1949). The large-scale radio structure associated with the galaxy extends as large as 80 kpc (Mills 1952; Baade and Minkowski 1954; Owen et al 2000), and Fanaroff and Riley classified this source as ‘Class I’ based on its radio morphology and relatively low radio luminosity (Fanaroff and Riley 1974)111Based on more than 50 samples of radio galaxies, Fanaroff and Riley (1974) classified radio galaxies into Class I and Class II, which are currently known as FR-I and FR-II, respectively. FR-I radio galaxies often have symmetric radio jets whose intensity falls away from the nucleus, while FR-II radio galaxies typically exhibit more highly collimated jets leading to bright hot spots far from the nucleus. Fanaroff and Riley (1974) also found that FR-I/FR-II sources have lower/higher luminosities, with a division around at 178 MHz. These facts have led to the suggestion that FR-I sources host relatively weakly accreting AGNs, while FR-II sources contain more powerful AGNs.. After 1980s the advent of the Very Large Array (VLA) revealed the kpc-to-subkpc-scale radio structures in great detail (along with a well-collimated one-sided jet) thanks to its high-dynamic-range imaging capability at subarcsecond-scale angular resolution (e.g., Biretta et al 1983; Owen et al 1989). In 1990s, high-resolution optical spectroscopic observations with the Hubble Space Telescope (HST) revealed a rotating ionized gas disk in the central pc-scale nuclear regions of the galaxy (Harms et al 1994; Ford et al 1994; Macchetto et al 1997), which provided the first strong hint for the presence of a central black hole with exceeding a billion solar masses in the center of this galaxy (see Sect. 3 for details).
Since its discovery, M 87 has been a privileged target for studying the physics of accretion and jet formation associated with an SMBH. Compared to distant quasars, M 87 is much closer to us. Combined with a large mass of the central SMBH, this makes the apparent diameter of the SMBH second largest on the sky after the Galactic Center Sgr A*, which allows us to resolve the source structure into smaller gravitational scales at a given angular resolution. On the other hand, unlike Sgr A*, M 87 exhibits a powerful relativistic jet, which is the most outstanding feature characterizing RLAGNs. Moreover, M 87 is sufficiently bright across the entire electromagnetic spectrum not only in radio/optical but also in X-rays and -rays, making this source an excellent target to study broadband multi-wavelength (MWL) properties associated with AGN activities (Fig. 1).

(a full image credit is described at the bottom of the figure).
In particular, rapid and remarkable advances have recently been made by high-resolution very-long-baseline-interferometry (VLBI) observations at radio wavelengths. The most groundbreaking example is the detection of the black hole shadow with the Event Horizon Telescope (EHT; Event Horizon Telescope Collaboration et al 2019a, b, c, d, e, f), a global VLBI network operated at 1.3 millimeters (mm). This provided the first visual evidence for the existence of SMBH as the central engine of AGN (see Sect. 3). Global VLBI observations at mm wavelengths (including 3 mm) are also capable of probing the inner part of accretion flows for M 87 (see Sect. 4). At even longer wavelengths, VLBI observations are generally more sensitive to the larger-scale emission, enabling us to image the collimation and acceleration regions of relativistic jets extending from near-horizon scales to galactic/kpc scales (see Sect. 5).
In summary, M 87 provides a rare opportunity to address various key questions relevant to (RL)AGNs as well as the physical connection among the SMBH, accretion flows and relativistic jets, especially under the low accretion/Eddington regime (see Sect. 4), across all electromagnetic wavelengths and spatial scales. In fact, despite being a single object, M 87 has been studied for many decades in the astrophysical community, with international workshops focused on this object (e.g., Blandford 1999). Attention to this object has been growing even more rapidly in the last few years. Fig. 2 displays annual trends in article publication related to M 87. While the number of annual publications has steadily increased from 1970s to 2010s, one can see a dramatic rise in publications since 2019/2020, very likely motivated by the first EHT imaging results. Therefore, now it would be a good time to review the current observational understanding of this active galaxy.

1.3 Structure of this review
In this review, we provide a comprehensive overview of the current observational understanding of the active galaxy M 87, covering a broad range of spatial scales from event horizon scales to kpc scales. The review is structured as follows. In Sect. 2, we first summarize the key parameters characterizing AGN/SMBH intrinsic activity. In Sect. 3, 4 and 5, we highlight various observational progress on M 87, dividing the topics into three key components: the central SMBH, the accretion flows onto SMBH, and the relativistic jet, respectively. In Sect. 6, we summarize our current understanding of this source and highlight some future prospects. Finally, we conclude the review in Sect. 7. Readers may also refer to Boccardi et al (2017) for a focused review on millimeter-VLBI observations of AGNs, and to Blandford et al (2019) for an extensive review covering both observational and theoretical efforts on studies of AGN jets in general.
2 Key parameters for characterizing AGNs
Galaxies are fundamental building blocks in the universe, and humans live in the Milky Way galaxy. Almost every galaxy is now believed to host an SMBH at its center. One of the most remarkable predictions of Einstein’s theory of general relativity (GR) is the existence of BHs. In fact, recent EHT and mm-wave VLBI images of M 87 resolved the BH shadow for the first time (Sect. 3), and the accretion flows with the emerging jet (Sect. 4 and 5). These three key ingredients have constituted our solid hypothesis for the AGN paradigm over the past decades. However, we still do not fully understand even the basic property of the galactic nucleus in the Milky Way galaxy. Looking beyond our own system, is the AGN paradigm really true for galactic centers other than M 87? If so, what are the fundamental parameters governing the strength and diversity of AGNs? Thanks to the ultra-high-resolution radio imaging down to 20 microarcseconds (as) scales, we are now reaching the vicinity of SMBH in both our galactic center SgrA∗ and M 87, which finally allows us to directly test what we have hypothesized over the past decades. Here we summarize some key parameters in the study of SMBHs/AGNs. Extensive studies utilizing a suite of cutting-edge observational instruments allow us to quantitatively investigate these parameters in the pursuit of understanding the accretion/ejection physics.
2.1 Black hole mass ()
SMBHs are found in most, if not all, galactic nuclei with a mass range of , from to (Kormendy and Ho 2013). RLAGNs exist in a variety of host galaxies, from disk-dominated spirals to giant ellipticals, with a similar range as described above (Ho 2002). It seems that there is no clear difference in the BH mass range () between RLAGNs and RQAGNs (Woo and Urry 2002), implying that may not be a dominant factor in characterizing AGN activity at radio bands.
Blazars, the other population of RLAGNs, fall into two sub-classes i) flat-spectrum radio quasars (FSRQs; objects with emission-line dominated spectra) and ii) BL Lac objects (BLOs; nearly line-less objects), with generally higher SED peaks (for both synchrotron and inverse Compton radiation) in FSRQs than in BLOs. The of blazars spans from to (Wu et al 2002; Shaw et al 2012; Xiao et al 2022) with a possible localization for BLOs at and for FSRQs at (Ghisellini et al 2010; Chen et al 2015).
The majority of RLAGNs (‘jetted’) have been believed to be hosted by elliptical galaxies with high BH masses (Fabian and Canizares 1988), while late-type galaxies, such as spirals with lower BH masses , were traditionally considered as RQAGNs (‘non-jetted’) (Laor 2000). This conventional hypothesis, however, has been updated during the last two decades by discovering radio-loud narrow-line Seyfert 1 galaxies (RLNLSy1s) with (e.g., Komossa et al 2006; Yuan et al 2008; Mathur et al 2012). Furthermore, the detection of -ray emitting RLNLSy1 objects (Abdo et al 2009) has opened a new era for understanding the jetted RLAGNs hosted in diverse types of galaxies, including spirals, with a wide range of .
There are various independent methods proposed to calculate : the traditional virial BH mass, the stellar velocity dispersion or the bulge luminosity, and the variation time scale. The of M 87 has been estimated with several methods as introduced in Sect. 3.

2.2 Black hole spin ()
BHs can rotate like other stars. Their rotation speeds could be close to the speed of light, causing a dramatic change in the metric and in the way matter moves (the mass accretion and the energy extraction). The properties of a BH are uniquely characterized by its mass, angular momentum, and electrical charge, based on the no-hair theorem of GR. In reality, a charged BH may be hard to exist due to its neutralization by discharge to its surroundings (difficult to maintain particle creation and/or accretion of matter onto the hole). Therefore, astrophysical BHs can be determined solely by the mass and angular momentum (henceforth referred to as spin).
An uncharged, rotating (spinning) BH is described by the Kerr metric (Kerr 1963) with the BH mass and angular momentum . A dimensionless angular momentum (spin) parameter () that measures a fraction of the angular momentum relative to its maximum value is defined as follows:
| (1) |
where and are the gravitational constant and the speed of light, respectively. Here, we introduce the ‘gravitational radius’ as the standard definition. The BH can be rotating in a prograde () or retrograde () manner in that system.
We also do want to locate the event horizon (), the boundary of the BH. In the Schwarzschild metric (a static metric for the spacetime around a non-rotating BH with , where the spatial coordinates are now spherical-polar, Schwarzschild 1916), we have (: Schwarzschild radius). But for the Kerr metric, the radius of the BH event horizon is described as , where with maximally spinning cases in both prograde and retrograde fashions. Note that the horizon is still spherical even for a spinning BH. Another important radius appears in the Kerr metric, , which is larger than for all and (azimuthal and polar angles, respectively), except at the poles where the two are equal. Note that at the equator, always , for any BH spin.
The region , called the ‘ergosphere’, is peculiar: everything must rotate in the same direction as the BH, just as everything must fall toward the BH within the horizon. The BH rotation causes the inertial frames to be dragged at an angular frequency , where
| (2) |
is the angular frequency of the event horizon Misner et al (1973). This implies that the rotation rate does not vanish beyond the ergosphere, but rapidly drops off outward. Thus, the frame dragging is almost concentrated near or within this region.
In the vicinity of a spinning BH, magnetic field lines advected with the accreting matter, can also rotate. When the field lines thread the event horizon, significant amounts of energy and angular momentum are extracted from the rapidly spinning BH along all field lines (see Fig. 3). Each field line is wound in such a way that the toroidal (azimuthal) field component is generated. An angular frequency of the field line will take an intermediate value between and outside the ergosphere. In general, BHs are not considered to be a perfect conductor so that the field lines threading the event horizon can slip with respect to the horizon: . Typically, is considered Blandford and Znajek (1977); MacDonald and Thorne (1982), but it depends on the geometry of the BH magnetosphere and/or the spin parameter Komissarov (2001); Penna et al (2013); Penna (2015).
2.3 Mass accretion rate ()
The mass accretion rate , i.e. the rate at which the mass of the accreting compact object increases with time, is a fundamental parameter, and we evaluate it in units of in the astrophysical context. On galactic scales, the hot X-ray emitting intergalactic medium (IGM) through quasi-spherical accretion (Bondi 1952) is widely used to estimate the amount of the accretion power by the SMBH. The Bondi accretion radius where the gravitational potential of the SMBH dominates over the thermal energy of the IGM gas, is given by
| (3) |
where and are the adiabatic sound speed of the gas at the accretion radius (Allen et al 2006) and the Boltzmann constant, respectively. Typical values of the IGM temperature and are adopted. Correspondingly, the Bondi accretion rate is given by
| (4) |
for an adiabatic index and the mass density with the electron number density (Russell et al 2013).
Suppose that the BH accretion starts around the sphere of influence (), where the BH’s gravity becomes dominant relative to that of the host galaxy, at an accretion rate similar to the Bondi rate (where is the accretion efficiency). For the Bondi accretion of M 87, readers can refer to Sect. 4.1. In the radiatively inefficient regime, we assume a typical value of the viscosity parameter in the hot, advection-dominated accretion flows (ADAF: , Narayan and Yi 1995; Mahadevan 1997) and we can refer to the solution of a ‘giant’ ADAF which provides (Narayan and Fabian 2011). A flatter radial mass density profile (than the ADAF solution) suggests a reduction in the mass accretion rate towards the BH: (while in ADAF). It would be worth considering that the hot gas is convectively unstable (Abramowicz et al 2002), moderately magnetized, and/or the outflow (wind) co-exists (Blandford and Begelman 1999), as examined by both hydro and magnetohydrodynamic (MHD) simulations (e.g., Yuan and Narayan 2014, references therein).
An extensive numerical survey of slowly rotating magnetized BH accretion through the Bondi radius provides a power-law slope of Pang et al (2011). Indeed, inside the Bondi radius, a self-consistent profile of the electron number density is obtained in X-ray observations toward M 87 (see Sect. 4). Three-dimensional general relativistic magnetohydrodynamics (GRMHD) simulations provide at (Sądowski et al 2013; Yuan et al 2015). Considering theoretical/numerical and direct observational results, a substantial reduction of the mass accretion rate compared with the Bondi rate would be expected towards the inner scales.
In the radiatively inefficient accretion flows (RIAFs), the mass accretion rate relative to the Eddingtion rate, is well below the unity, where
| (5) |
with the standard radiative efficiency . There is a critical value (upper limit) for existing an ADAF (Narayan and Yi 1995). Given that the Bondi accretion rate is well below the Eddington rate (see Sect. 4.1), the BH accretion in M 87 is certainly in the RIAF regime, where the disk is optically thin and hot, and thus becomes geometrically thick (the ion is heated up to the virial temperature , while the electron temperature is much cooler : Nakamura et al 1997; Quataert and Gruzinov 1999).
In the quiescent state (QS) far below the critical mass accretion rate (say ), an ADAF-type accretion flow occupies all the way down to the innermost stable circular orbit (ISCO) around the BH. However, there is a state transition from an ADAF to a radiatively efficient (luminous), geometrically thin, standard accretion disk (Shakura and Sunyaev 1973; Novikov and Thorne 1973). A large transition radius is expected in the QS such as M 87 and Sgr A∗ (Narayan and McClintock 2008). In the low state (LS) where is higher than that in QS (i.e., ), the radiative efficiency becomes larger, and the transition radius gets smaller. In the intermediate state (IS), where , the radiative efficiency is as high as and the transition radius approaches the ISCO. Finally, the state transition is completed in the high state (HS), where , and the accretion flow changes completely to a thin disk down to the ISCO. This system is in the thermal state so that its spectrum is well-described by a multi-color disk model (see also Esin et al 1997; Narayan and McClintock 2008; Ho 2009, for more details).
Among the jetted RLAGNs, low power radio galaxies such as FR-I sources (e.g., M 87) can fall into the QS. High power radio galaxies such as FR-II sources (e.g., Cygnus A) can be in the LS. Ghisellini et al (2010) studied all blazars of known redshift detected by the Fermi satellite and provided a possible ‘split’ between BLOs and FSRQs in the accretion mode, which occurs at (see also Xu et al 2009; Chen et al 2015). Based on these observational facts, we can categorize BLOs in the LS and the IS, while FSRQs in the HS. Furthermore, some Fermi FSRQs may be in the very high state (VHS) where . This is the so-called the ‘super-Eddington’ accretion regime in the optically thick RIAF or slim disk (Begelman and Meier 1982; Abramowicz et al 1988). Also, NLSy1s are considered to be in the VHS (Collin and Kawaguchi 2004); transient and highly variable NLSy1s may indicate that such high-amplitude variability is linked with a transition between a standard disk and a slim disk as a result of the thermal instability, with (Kawaguchi 2003).
2.4 Magnetic flux threading a black hole ()
The magnetic field that an isolated BH can possess is weak: if there is a strong magnetic field, the mass accretion is prevented by its magnetic pressure and torque. Blandford and Znajek (1977) estimated the critical field strength for a maximally spinning BH as . On the other hand, the field strength brought in by accreting matter can be much stronger. Thus, an intrinsic magnetic field of the BH can be considered as astrophysically unimportant.
GRMHD simulations reveal that the poloidal magnetic flux in the accretion flow is advected inward until the ram pressure of accreting material (, shown as in Fig. 3) is balanced with the magnetic pressure (, where is the strength of magnetic field lines, shown as in Fig. 3). The accumulated poloidal magnetic flux onto the event horizon threading (one hemisphere of) the BH () is a key parameter that essentially characterizes the accretion flow properties. This is given in the following form (Tchekhovskoy et al 2011; Yuan and Narayan 2014):
| (6) |
When
the dimensionless parameter
(in Gaussian units),
a strong magnetic field pushes aside the accretion flow and tends to produce outflows. This is known as the Magnetically Arrested Disk (MAD) state
(Igumenshchev et al 2003; Narayan et al 2003; Tchekhovskoy et al 2011).
On the other hand,
the case
corresponds to the Standard Accretion and Normal Evolution (SANE) state, where weak and turbulent magnetic fields dominate the accretion flow (Narayan et al 2012).
2.5 Jet power ()
The jet launching mechanism in AGNs is a longstanding challenge in astrophysics. Electromagnetic radiation emitted from AGN jets spanning from radio to very-high-energy (VHE) rays have improved our understanding of AGN jets. The total power of the jet () is the sum of the several components as described by
| (7) |
where , , , and , are the radiation power, the proton power, the electron-positron pair power, and the Poynting power of the jet, respectively. (e.g., Sikora et al 2020).
If the Blandford and Znajek (BZ) process (Blandford and Znajek 1977), where the electromagnetic energy extraction from a rotating BH is operated as a jet launching mechanism, holds at the jet base and BZ power () can be given by
| (8) |
where , is the geometrical factor, and is assumed (see Tchekhovskoy et al 2010, 2011, for details).
Observed AGN luminosities form two separated sequences on the radio-loudness–Eddington-ratio plane, suggesting larger BH spins for radio-loud sources (Sikora et al 2007). Zamaninasab et al (2014) suggest dynamically important magnetic fields near accreting BH based on the estimation of . They seem to support the idea of the BZ process at work and thus, most of theoretical studies assume that magnetic fields play a key role in jet formation. However, it is not obvious whether observed electromagnetic signals indeed suggest that the magnetic field plays a major role in the dynamics or not. This assertion should be verified through comprehensive observations, and M 87 can provide us an excellent platform to explore this (see Sect. 5.10).
The is directly obtained from observational data and they are mostly dominated by the power of synchrotron emission () and inverse-Compton emission () (Kataoka and Stawarz 2005). Based on the works of (Sikora et al 2007; Ghisellini et al 2014) the observed bolometric luminosity is known to be in a wide range of . On the other hand, constraining the plasma composition and estimating , and in AGN jets remains challenging and is still a subject of debate since the observed emissions predominantly originated from only nonthermal pair (Wardle et al 1998; Sikora and Madejski 2000; Kataoka et al 2008; Kino et al 2012; Kawakatu et al 2016; Sikora et al 2020).
Although the estimation of contains a certain degree of ambiguity due to the reason mentioned above, the jet power of FSRQs can maximally reach up to , while that of radio galaxies can reach as low as (see for example Rawlings and Saunders 1991; Daly 2019; Chen et al 2023b, and references therein).
3 Central supermassive black hole
3.1 BH mass
The mass of the central SMBH () of M 87 has been estimated using three different approaches: stellar dynamics modeling (e.g., Gebhardt et al 2011), gas dynamical modeling (e.g., Harms et al 1994; Macchetto et al 1997; Walsh et al 2013), and BH shadow measurements (Event Horizon Telescope Collaboration et al 2019a, f; Event Horizon Telescope Collaboration et al 2024).
Stellar dynamical measurements involve assessing the central rise in stellar velocity dispersion towards the center of the galaxy. This method began with the assumption of a simple Gaussian distribution of stellar dynamics, then it has evolved to estimate the mass-to-distance ratio, , with high accuracy through the development of sophisticated modeling techniques utilizing the full line-of-sight stellar velocity distributions achieved with high angular resolution spectroscopic observations. As a byproduct, it provides the mass-to-light ratio, , of the stellar populations at its center, which can be used to validate measurements by comparing them with independent estimates derived from population synthesis. Utilizing these approaches, of M 87 was estimated to be for an assumed distance of 17.9 Mpc (corresponding to for 16.8 Mpc) (Gebhardt et al 2011). Recently, new estimates on have been proposed by adopting new triaxial orbit models, resulting in a relatively smaller mass of ( (Liepold et al 2023). On the other hand, a larger mass of has been suggested by new measurements using the Canada–France–Hawaii Telescope (CFHT) and the Very Large Telescope (VLT) adaptive optics observations (Simon et al 2024). However they also estimated a smaller mass of depending on the adopted stellar density profile (Simon et al 2024).
Gas dynamical estimates rely on modeling the dynamics of the H and [N II] emission lines from the central gas disk. In early 1990s, Harms et al (1994) detected a spatially resolved ionized gas disk with the HST. They identified an asymmetry in the velocity field and estimated . Following this, Macchetto et al (1997) revealed the rotation curve of the ionized gas disk surrounding the nucleus. The velocities measured from the emission lines were consistent with the hypothesis that the ionized gas disk undergoes Keplerian rotation, leading to . Later, Walsh et al (2013) further refined the analysis and derived based on comprehensive gas-dynamical modeling with new HST data acquired with the Space Telescope Imaging Spectrograph (STIS). Historically, these estimates using gas dynamics have shown excellent agreement with each other, whereas there has been a factor of 2 discrepancy with the derived from the stellar dynamics.
While the above two methods are based on the orbital motion of gas or stars relatively far from the central BH, it is also possible to estimate by directly measuring the size of the BH shadow using ultra-high-angular-resolution VLBI observations at millimeter wavelengths. According to GR, the apparent size of the BH shadow is expected to be approximately 5 times the Schwarzschild radius (e.g., Event Horizon Telescope Collaboration et al 2019f). The first observational hint for such a gravitationally-lensed shadow feature was obtained for Sgr A* and M 87, with proto-EHT experiments at 1.3 mm using three stations in the United States (Doeleman et al 2008, 2012). The first-ever BH shadow image of M 87 obtained with EHT discovered an asymmetric ring-like structure with a diameter of 42 3 as (Event Horizon Telescope Collaboration et al 2019a, d, Fig. 4 left).
Comparing the observed M 87 EHT images with a large GRMHD simulation library, they concluded that the observed ring-like structure is in good agreement with the shadow of a spinning Kerr BH (Event Horizon Telescope Collaboration et al 2019e). By calibrating the observed ring diameter with the predicted ring diameter based on the simulations, they derived the gravitational radius and estimated to be assuming a distance of 16.8 Mpc (Event Horizon Telescope Collaboration et al 2019f). The first EHT results based on the 2017 observations have been confirmed with another independent EHT dataset taken in 2018 (Event Horizon Telescope Collaboration et al 2024, Fig. 4 right), providing strong supporting evidence that the ring seen in the EHT images represents the BH shadow predicted by GR.
The estimated from the EHT data is in good agreement with that derived from the stellar dynamics, while it deviates from the ones estimated from the gas dynamics with a confidence level of 99 (Event Horizon Telescope Collaboration et al 2019f). This discrepancy may be attributed to the inclusion of internal gas motions within the disk, along with adopting slight changes in the inclination angle of the disk (Jeter et al 2019; Jeter and Broderick 2021). Therefore a further study is warranted, particularly using future high-resolution optical instruments.

3.2 BH spin
The spin of a BH is a fundamental parameter and crucial for describing its nature. In astrophysical contexts, the BH spin emerges as a compelling explanation for the extraordinary power exhibited by jets. Take, for example, the case of M 87, where the estimated mass accretion rate onto the SMBH ranges from 10-3 to 10-4 . This translates to a mass accretion power of 1043-44 erg s-1 (as discussed in Sect. 4.3). However, the expected kinematic power of the jets falls in the range of 1043-45 erg s-1 (as outlined in Sect. 5.11). Hence, it requires an energy conversion efficiency of , implying that the simple mass accretion power alone may be insufficient to explain the jet power. It is postulated that the subtraction of the rotating energy of the BH can compensate for this difference.
The direct imaging of SMBH shadow provides another important clue regarding the nature of BH beyond its mass. The observed brightness asymmetry of the 1.3 mm ring is likely caused by the effect of Doppler beaming associated with the frame dragging effect of a spinning Kerr BH. Since the observed ring appears brighter in the southern part of the emission, it suggests that the BH spin vector is oriented away from Earth if the BH spin axis aligns with the large-scale jet (Event Horizon Telescope Collaboration et al 2019f). The bright spot observed in 2018 shifted by 30 degrees relative to that observed in 2017, and the asymmetry observed in 2018 is more consistent with the orientation of the large-scale jet (Event Horizon Telescope Collaboration et al 2024). These observed features indicate the presence of a spinning BH at the center of M 87, although the value of the spin has not yet been tightly constrained in these observations. Further strong evidence of the spinning black hole will be provided by precise measurement of the photon ring with next generation VLBI observations (see Sect. 6.2), and the next step is to determine the direction of the spin relative to the rotation of the accreting matter (prograde/retrograde).
4 Accretion flows
4.1 Onset of BH accretion: the Bondi scales
As described in Sect. 2.3, the nature of accretion flows onto SMBH can be probed by observing the X-ray hot gas atmosphere. The density and temperature profiles of the X-ray hot gas in M 87 on kpc scales were extensively investigated using Chandra X-ray data (Di Matteo et al 2003; Russell et al 2018). Di Matteo et al (2003) inferred the decrease in the gas temperature from 10 kpc down to the central 1 kpc. Within this distance range, they observed the density profile to flatten inside the central 2 kpc, while it follows beyond 2 kpc up to 10 kpc (see Fig. 5). With these observed profiles, they calculated the Bondi radius to be 150 pc for a BH mass of and estimated the Bondi accretion rate to be . The temperature and density profiles were further refined by Russell et al (2018) through a stacking analysis of twelve 5-ks Chandra data. By adopting the refined temperature and density profile together with a newly estimated of 6.5 109 (Event Horizon Telescope Collaboration et al 2019a, f), we estimate the Bondi radius and Bondi accretion rate to be
| (9) |
and
| (10) |


Hence, the comparison with introduced in Eq.(5) ( for and ) indicates that the accretion onto the M 87 nucleus is significantly sub-Eddington, as also inferred from the underluminous core X-ray luminosity ( erg s-1; Di Matteo et al 2003). It is notable that Russell et al (2018) found no evidence of gas temperature increase within a radius of 0.25 kpc, as expected in the classical Bondi-type accretion flows, while a further increase in density profile was observed within 0.3 kpc. This led them to suggest that the classical Bondi accretion flow may not be accurately achieved, and that a substantial decrease in the mass accretion rate onto the central SMBH within .
In addition to probing the hot plasma through X-ray observations, efforts have been made to unveil the cold accretion flow at similar or slightly smaller scales using radio interferometry data. Tan et al (2008) utilized the Submillimeter Array (SMA) at 230 GHz to detect CO (J = 2–1) line emission, aiming to identify the presence of cold molecular gas in a thin disk around the M 87 BH. Although they detected 230 GHz continuum emission from the nucleus and several knots at arcsecond scals, they estimated a conservative upper limit on the mass of molecular gas to be 8 106 within 100 pc of the central BH. Subsequently, Simionescu et al (2018) detected extended CO (2–1) line emission approximately 40 arcseconds away, corresponding to 3.4 kpc in the southeast direction from the nucleus, using the Atacama Large Millimeter/submillimeter Array (ALMA). They derived the corresponding molecular gas mass to be (4.7 0.4) 105 . Following this, Li (2022) conducted a systematic survey utilizing ALMA archival data. However, they did not find conclusive evidence of CO line emission in the vicinity of the M 87 nucleus.
4.2 Inside the Bondi radius
It is difficult for the current X-ray instruments to spatially resolve the scales well below . To explore the nature of accretion flows within scales, a powerful approach would be the measurement of polarization and Faraday rotation measure (RM) at mm/submm wavelengths since the bulk of mm/submm synchrotron emission from ADAF/RIAF-type accretion flows is likely originated in the close vicinity of the central SMBH (e.g., Yuan and Narayan 2014). This approach was originally developed for the nearest SMBH Sgr A*, which exhibits highly linear polarization with significant RM (e.g., Aitken et al 2000; Bower et al 2003; Marrone et al 2006, 2007). By attributing the observed RM to the magnetized plasma associated with the accretion flow, the accretion rate of Sgr A∗ at small radii was constrained to be depending on the adopted accretion models (Marrone et al 2006, 2007).
Following the success in constraining the of Sgr A*, Kuo et al (2014) applied a similar method to M 87 using 1.3 mm polarimetric data taken by the SMA. They obtained an upper limit of (the magnitude of RM) to be . Adopting a simple analytic model of the accretion flow similar to the case of Sgr A*, the onto the M 87 SMBH was constrained to be . This indicates a substantial decrease in compared to the Bondi accretion rate. This is in good agreement with expectations from the RIAF models, ruling out the classcial ADAF.
Large RM values towards the M 87 nucleus were later confirmed by Goddi et al (2021) using multi-epoch ALMA data at 3 and 1.3 mm. Thanks to the improved sensitivity of ALMA, they further detected significant time variation of RM both in magnitude and sign. This suggests a more complicated origin of the Faraday rotation rather than a simple accretion flow, making a more accurate estimate of rather challenging.
To look into the structure inside more directly, high-resolution VLBI observations are required. Using the Very Long Baseline Array (VLBA) at cm wavelengths, there were several attempts to explore the pc-scale polarimetric and RM properties of M 87 (e.g., Junor et al 2001; Zavala and Taylor 2002; Park et al 2019b, see also Sect. 5.5). Most notably, Park et al (2019b) revealed a spatially-resolved RM profile inside and found that decreases with distance from 10 mas to 350 mas (corresponding to deprojected distances 5000–200000 ) away from the nucleus. They indicated that the observed radial slope of RM at these scales is reproduced by a gas density profile of for the Faraday screen. Such a density profile is expected for RIAF-type hot accretion flows with substantial winds or mass loss (ADiabatic Inflow-Outflow Solutions (ADIOS); Blandford and Begelman 1999), which is consistent with the significant reduction of near SMBH inferred from the mm/submm interferometric RM studies.
We note that optical observations also provide additional constraints. Besides constraining the SMBH mass, the HST data that detected the nuclear gas disk can be used to further infer the accretion rate associated with the gas disk. As described in Sect. 3.1, the mass estimated from the gas dynamics differs from those from the stellar dynamics and the EHT. The discrepancy could stem from inappropriate assumptions about the dynamics of the gas disk, as discussed in detail by Kormendy and Ho (2013). Jeter et al (2019) refined the gas-dynamical model by adopting a sub-Keplerian disk velocity together with a different viewing angle and demonstrated that the refined model can explain the larger BH mass. By using the refined model with conservative estimates of the cold gas at 100 pc scale by Tan et al (2008), they estimated the mass accretion rate associated with the gas disk to be .
4.3 The event horizon scales
The accretion flow structure near event-horizon scales has become accessible through direct imaging with mm-VLBI. As described in Sect. 3, the EHT observations at 1.3 mm unveiled a ring-like structure in the core of M 87 (Event Horizon Telescope Collaboration et al 2019a, d, f). By comparing the EHT images with an extensive library of GRMHD and GR radiative transfer (GRRT) simulated images, the observed ring-like structure was found to be in good agreement with the emission associated with the accretion flow (Event Horizon Telescope Collaboration et al 2019e). Further constraints on the properties of the 1.3 mm ring-like structure were obtained based on the subsequent analysis of linear-polarization data (Event Horizon Telescope Collaboration et al 2021a, b). It was reported that the observed electric vector polarization angle (EVPA) distributions predominantly describe a nearly azimuthal pattern, suggesting that the poloidal magnetic field component is more dominant than the toroidal one at these scales. An extensive comparison of the EHT polarization images with a large GRMHD simulation library indicated that MAD is the favored state of the accretion flow, rather than SANE ones, suggesting the presence of dynamically important magnetic fields near SMBH. The recent further detection of circular-polarization signals in the EHT 2017 data additionally reinforces the MAD scenario (Event Horizon Telescope Collaboration 2023). Based on the GRMHD models that are in good agreement with the observations, the mass accretion rate at the EHT scales was estimated to be (Event Horizon Telescope Collaboration et al 2021b). Analysis of the EHT total-intensity and polarization images also provided horizon-scale estimates on other physical quantities such as electron density (), electron temperature (), and magnetic field strength ( G).

Following the EHT imaging of the BH shadow at 1.3 mm, recent Global Millimeter VLBI Array (GMVA) observations connected to ALMA and the Greenland Telescope (GLT) have revealed another ring-like image in the M 87 nucleus at a wavelength of 3.5 mm (Lu et al 2023, see also Fig. 6). The diameter of the 3.5 mm ring is approximately 8.4 times the Schwarzschild radius, which is 50% larger than the diameter of the 1.3 mm ring. Additionally, the inner edge diameter of the 3.5 mm ring is also larger than the diameter of the EHT ring. The larger and thicker ring size at 3.5 mm is likely caused by the opacity effect of synchrotron emission at a lower frequency. A comparison of the GMVA image with GRMHD simulations in Lu et al (2023) provides a strong indication that the observed ring-like structure at 3.5 mm is dominated by the accretion flow.
4.4 Evolution of from Bondi to event horizon scales
As a summary of this section, in Fig. 7 we show a plot compiling various estimates of in the literature, measured at various scales. Although the statistics are still very limited, a collection of these estimates reveals a substantial decrease in mass supply towards the innermost regions with respect to the Bondi accretion rate. This is clear evidence that the classical ADAF is no longer valid as the model for the M 87 accretion flows, while the suggested radial evolution of is consistent with with ADIOS-like solutions.

5 Relativistic jets
5.1 Jet collimation
5.1.1 Classical view
Narrowly collimated AGN jets extend well beyond their host galaxies on kpc scales. They sometimes propagate up to tens of kpc to Mpc scales, forming giant radio lobes as the end-point of jets where a huge amount of the energy, originally generated in the vicinity of SMBH, is deposited into the ISM or IGM (Blandford 1990). How can such a collimation of the highly relativistic plasma beam be sustained over many orders of magnitude in gravitational distance? On kpc scales, a number of AGN jets have been imaged with various instruments, commonly exhibiting conical structures with constant jet opening angles a few degrees. For example, the conical structure of the M 87 jet at 1 arcsec was confirmed in 1970s–1980s with a photometric analysis (de Vaucouleurs and Nieto 1979) and VLA imaging (Owen et al 1980; Reid et al 1982).
On pc scales, according to the classical standard picture of AGN jets, the compact radio core (also referred to as the ‘VLBI core’) seen at the apparent jet origin in a VLBI map has been widely believed as the throat of a diverging conical jet (Blandford and Königl 1979) (see also Sect. 5.3). Alternatively, Daly and Marscher (1988) proposed that the VLBI core represents the first ‘re-collimation Mach disk–oblique shock’ system, which is supposed to be located far from the BH (). Thus, the jet acceleration and collimation zone (ACZ) was supposed to exist in the upstream region of the mm-wave radio core, or may not exist (Marscher and Gear 1985).
5.1.2 Jet collimation break
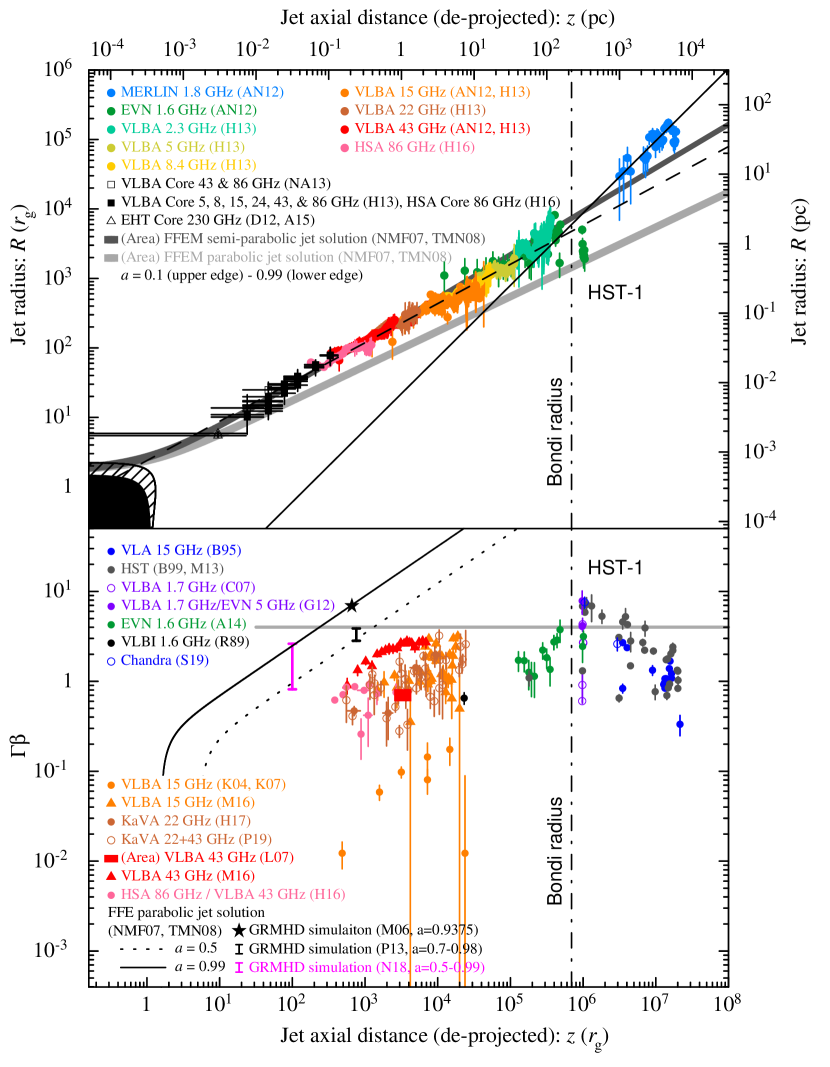
Based on early studies of the kpc-scale jet morphology (e.g., Reid et al 1982) and the theory of MHD jets (Blandford and Payne 1982; Li et al 1992), the conical structure of the M 87 jet would suggest that the collimation of the jet (Junor et al 1999), as well as the jet bulk acceleration, seemed to terminate on pc scales. However, there was no plausible/coherent picture of the ACZ on AGN jets until mid 2010s (see also Sect. 5.2.1). The upper panel of Fig. 8 overviews the global geometry of the M 87 jet obtained by compiling the literature (see the caption for references, Nakamura et al 2018).
Multi-frequency VLBI observations by Asada and Nakamura (2012) revealed that the global structure of the jet sheath is characterized by a semi-parabolic stream at (dashed line in Fig. 8 upper panel), while it changes into a conical stream (solid line in Fig. 8 upper panel) beyond the Bondi radius. This provides the first observational evidence of the jet collimation break (JCB) in AGN jets as a possible consequence of the gravitational interaction between the SMBH and host galaxy: the ACZ may be self-regulated under these co-evolving system. After the discovery of JCB in the M 87 jet, subsequent investigations on many other jet sources also found similar jet geometrical transitions (e.g., Tseng et al 2016; Nakahara et al 2018, 2019, 2020; Hada et al 2018; Park et al 2021b; Boccardi et al 2021; Kovalev et al 2020; Okino et al 2022).
Near the jet base of M 87, a parabola-like profile further continues down to a few tens of from the BH (Nakamura and Asada 2013; Hada et al 2013, 2016; Kim et al 2018a), while the recent GMVA+ALMA+GLT 86 GHz image has detected a wider emission width than expected from the parabola closer to the BH (Lu et al 2023). This additional emission could be assocaited with the winds from RIAF supporting the initial jet collimation phase.
5.1.3 Testing magnetically organized ACZ
For comparison with the observed data, the upper panel of Fig. 8 additionally overlays the outermost streamlines (anchored to the event horizon with the maximum colatitude angle of ) of the semi-analytical, force-free electrodynamic jet model (Narayan et al 2007; Tchekhovskoy et al 2008) with different BH spin parameters (). The observed jet profile match well with the theoretical expectations of a semi-parabolic stream, although they deviate beyond the Bondi scale.
Also, high-resolution GRMHD simulations (Nakamura et al 2018) exhibit a large Lorentz factor () sheath as a consequence of the so-called ‘magnetic nozzle’ effect (Camenzind 1987; Komissarov et al 2007; Tchekhovskoy et al 2009) along the funnel edge in the form of a parabola. This could be a theoretical analog to the ‘limb-brightened’ structure seen in the M 87 jet. A detailed analytical study, using a steady-state axisymmetric force-free jet model, reproduces symmetrically limb-brightened radio images when the jet’s magnetic field lines pass through a fast-spinning BH, while this is not the case for the magnetic field lines passing through a slowly-spinning BH or a Keplerian accretion disk (Takahashi et al 2018). Thus, the quasi-symmetric limb-brightend jet feature seen in M 87 would imply a spinning BH-driven jet.
5.2 Jet dynamics
5.2.1 Radial evolution
Compared to the well-established jet collimation profile, the dynamics of the M 87 jet remain largely controversial. The bottom panel of Fig. 8 summarizes the observed velocity distributions (converted to four-velocity ) as a fuction of jet axial distance. On kpc scales, the proper motion of the jet is relatively well characterized (Biretta et al 1999; Meyer et al 2013; Snios et al 2019, see also Sect. 5.8), showing an overall superluminal motion that decelerates from 6 (corresponding to 7–9) at a deprojected distance of 200 pc (HST-1; Sect. 5.7) to 0.5 at distances greater than 1000 pc. However, on pc-to-subpc scales, early VLBI monitoring programs conducted at monthly or yearly intervals often reported very slow speeds (Reid et al 1989; Dodson et al 2006; Kovalev et al 2007; Ly et al 2007). These low speeds are inconsistent with the observed large jet-to-counterjet brightness ratio, implying that the sparse monitoring intervals are insufficient to accurately measure the inner jet motion.
A transition from subluminal to superluminal motion at intermediate scales between the jet base and HST-1 was initially reported by Asada et al (2014) with the European VLBI Network (EVN) observations at 1.6 GHz. Subsequently, multiple groups conducted more frequent monitoring programs of the M 87 inner jet using VLBA or East Asian VLBI Network (EAVN) at 22/43 GHz (Walker et al 2016; Mertens et al 2016; Hada et al 2017; Walker et al 2018; Park et al 2019a). These studies consistently detected fast motions (up to 2–3 ) within a few 100 from the jet base, accounting for the large jet-to-counterjet ratio. They also found a trend of gradual acceleration with distance, culminating in maximum speed at HST-1. The observed acceleration regions appear to be coincident with those where the jet shape is parabolic, indicating a close connection between collimation and acceleration over a wide range of distances from the BH.
Nevertheless, these studies also claimed the presence of multiple velocity components even at the same radial distances from the BH (seen as large data scatters on pc scales in the bottom panel of Fig. 8), implying that the true jet velocity fields are likely more complex. This may suggest that one speed is associated with a bulk flow while another traces a pattern or instability filament (Mertens et al 2016). Alternatively, the jet may contain velocity stratification where different jet speeds represent different layers within the jet (Park et al 2019a). Further accumulation of velocity measurements is needed to distinguish between these scenarios.
5.2.2 Transverse evolution
It has been relatively less known that the inner jet of M 87 exhibits morphological evolution perpendicular to the jet axis. This phenomenon was initially reported by Walker et al (2016) and Walker et al (2018), who compiled a set of VLBA 43 GHz images spanning 17 years and observed a quasi-sinusoidal oscillation of the pc-scale jet with a period of approximately 8–10 years. Similar year-scale oscillations of the M 87 pc-scale jet were also reported at 15 GHz (Britzen et al 2017). More recently, Cui et al (2023) have provided a significant update on the analysis of the jet transverse motion by compiling a large dataset of EAVN/VLBA 43/22 GHz data spanning 22 years from 2000 to 2022. They identified two cycles of oscillation in the jet position angle, implying a periodicity with a period of 11 years.
The origin of the observed long-term oscillation is subject to debate. Walker et al (2018) interpreted the variation as a Kelvin-Helmholtz (KH) instability mode developed at the boundary between the jet and the external medium. Alternatively, Cui et al (2023) proposed that the observed periodic oscillation could be explained if the jet base is precessing, likely via a Lense-Thirring effect caused by a tilted accretion disk with respect to the SMBH spin.
Besides the year-scale variations, Ro et al (2023b) recently reported that the M 87 jet exhibits transverse fluctuations on much shorter timescales (roughly one year or less). Although the exact origin of this type of oscillation remains unclear, it could be associated with the propagation of jet HD/MHD instability or perturbed mass accretion occurring in the magnetically-arrested disk.

5.3 Radio core
While the EHT 230 GHz observations resolved the shadow of SMBH at the jet base, it is worth noting the nature of the ‘radio core’ seen at the lower radio frequencies. The radio core, a bright compact feature at the apparent origin of an AGN jet seen in a VLBI image, is most likely either a synchrotron-self-absorbed opaque surface of the jet base at a given frequency (e.g., Konigl 1981; Lobanov 1998) or a standing shock feature (e.g., Daly and Marscher 1988; Marscher et al 2008). In the case of M 87, multi-frequency VLBA astrometric observations measured a core-shift between 2 and 88 GHz with a frequency dependence of (Hada et al 2011; Jiang et al 2021), in agreement with the M 87 radio core at these frequencies being a photosphere of the jet base within a few tens from the central BH. On the other hand, as introduced in Section 4, the recent GMVA+ALMA+GLT 86 GHz observations have spatially resolved the radio core into a ring-like structure, with emission likely dominated by the inner part of accretion flows (Lu et al 2023). Thus at 3 mm, the emission from both the accretion flows and the jet base could be blended when the radio core is imaged with a lower angular resolution.
At cm wavelengths. a handful of ultra-high-resolution space-VLBI observations resolved the radio core region into highly complex morphology (Dodson et al 2006; Asada et al 2016; Kim et al 2023). Especially at lower frequencies (1.6/5 GHz), space-VLBI images revealed diffuse substructures surrounding the compact core perpendicular to the jet axis (Dodson et al 2006; Asada et al 2016). The nature of this low-level emission has not yet been explored in detail, but it may hint at the presence of transverse stratification in the base of jet/outflows.
5.4 Counter jet
The jet of M 87 is predominantly one-sided on both kpc and pc scales, indicating its strong Doppler-boosted nature. This suggests that the viewing angle of the jet is relatively small or/and the jet speed is highly relativistic at these scales. On parsec scales, hints of the counter jet were observed in some early VLBI images (e.g., Reid et al 1989; Junor and Biretta 1995), but it did not receive much attention until Ly et al (2004) claimed the first detection of a faint counter jet at the eastern side of the radio core, although the possibility of a calibration artifact was not entirely ruled out.
The (sub)pc-scale counter jet of M 87 is now routinely observed in high-quality VLBI images at various frequencies (Fig.10), and careful imaging tests by multiple teams demonstrate that this feature is very likely real (e.g., Kovalev et al 2007; Ly et al 2007; Kim et al 2018b; Walker et al 2018; Nikonov et al 2023). Interestingly, Kovalev et al (2007) and Walker et al (2018) reported that the counter jet was also edge-brightened similar to the main jet, and a similar structure was also identified in more recent study by Nikonov et al (2023) (Fig. 10). The counter jet appears to extend 3 mas from the core at 15 GHz, but looks even more extend if we take a look at the high-sensitivity VLBI image at 8 GHz presented in Nikonov et al (2023). The kinematics of the counter jet are much less constrained than that of the main jet, but independent measurements by different groups (Kovalev et al 2007; Ly et al 2007; Hada et al 2016; Mertens et al 2016) consistently reported substantially slow apparent speeds (0.01–0.17 ).
The jet-to-counter-jet brightness ratio depends on various factors such as observing frequency, core distance, possible variability, and whether the ratio is calculated using integrated fluxes or peak intensity. However, a typical range would be of the order of 10 at 1 mas from the core. Combining this with proper motion measurement of the jet and counter jet, a conservative estimate of the jet viewing angle results in 13–40∘. A tighter constraint of 14–20∘ is obtained by considering more detailed jet velocity field (Mertens et al 2016), consistent with the angle suggested from the HST-1 superluminal motion (Sect. 5.7).

5.5 Polarization
Since the first identification of polarized emission from M 87 by Baade (1956), the polarimetric properties of this jet have been extensively investigated across various scales and wavelengths. Polarimetry serves as a powerful tool for probing the structure of magnetic field, the internal jet structure as well as interactions between the jet and its surrounding environment.
On kpc scales, the polarization of the M 87 jet has been studied in great detail since 1980s using VLA in cm radio bands (e.g., Owen et al 1989, 1990) and later also using HST in optical bands and ALMA in mm bands (e.g., Capetti et al 1997; Perlman et al 1999; Avachat et al 2016; Goddi et al 2021). Polarized emission is detected throughout jet regions on kpc scales, with enhanced signals predominantly associated with the bright knot regions. While the observed magnetic field position angles (MFPAs; formally rotated from the measured EVPAs) on kpc scales are largely parallel to the jet axis in both radio/optical bands, only the optical MFPA vectors tend to become perpendicular to the jet at the upsteam end of some bright knots, suggesting a multi-layered structure in the jet (Perlman et al 1999). More recently, analyzing a wideband (4–18 GHz) Jansky VLA full-polarimetric data, Pasetto et al (2021) revealed extremely detailed radio polarization and Faraday RM distributions that support the presence of a helical magnetic field on kpc scales. See also Sect. 5.8 for a review on the kpc-scale jet.
In contrast to the rich polarization structures seen at kpc and horizon scales (see Sect. 4.3), still much less is known about the polarimetric properties on intermediate (0.1–100 pc) scales, as the pc-scale jet of M 87 is largely unpolarized at radio wavelengths. Pioneering studies were conducted by Junor et al (2001) and Zavala and Taylor (2002) using VLBA at cm wavelengths (5–15 GHz), where they detected patchy polarization features in the jet portion around 20 mas from the core with considerably large RM magnitudes (thousands to rad m-2). Weak patchy polarization features were also detected closer to the core at 86 GHz (Hada et al 2016). A significant advance was made by Park et al (2019b), where they revealed more detailed RM distributions along the pc-scale jet by revisiting multi-frequency polarimetric VLBA data at 2–8 GHz. They found that the RM magnitude gradually decreases with distance from one parsec scales to just before HST-1. The observed slope of RM distributions was reproduced with the scenario that the Faraday screen is the winds from the hot accretion flows, which may be relevant to the observed collimation and acceleration of the M87 jet on the same scales. More recently, Nikonov et al (2023) have reported the presence of an RM gradient also in the direction perpendicular to the jet based on their high-sensitivity VLBI images at 8 and 15 GHz.
Between the horizon scales and parsec scales, the polarization structure of the radio core at subpc scales remains controversial. Walker et al (2018) and Kravchenko et al (2020) reported complex EVPA patterns that appeared to be wrapped around the 43 GHz core. However, a later analysis by Park et al (2021a) with an improved calibration method did not find such a complex feature but detected a simple compact polarization component with its peak coinciding with the total intensity peak. To obtain a definitive answer and bridge the magnetic field structure between horizon and parsec scales, higher sensitivity VLBI observations at 43/86 GHz combined with a refined polarization calibration technique would be required.

5.6 Spine-sheath structure
As mentioned in Sect. 5.1, the pc-scale jet of M 87 is widely known to show a limb-brightened structure with a parabolic shape. However, when imaged at a higher resolution or/and sensitivity, another streamline appears to emerge in the middle of the jet (Fig. 11). Such a ‘spine’ component was clearly detected in high-quality VLBI images at cm wavelengths (Asada et al 2016; Hada 2017; Tazaki et al 2023; Nikonov et al 2023) and also in stacked VLBI images at 43/86 GHz (Walker et al 2018; Kim et al 2018b). The central spine emission appears to be substantially narrower than the whole jet width. Recently, a new GMVA 3 mm M87 image connected to ALMA and GLT has clearly detected a triple-ridge jet structure even closer to the core (Lu et al 2023). These images obtained at various scales/frequencies indicate that such a ‘spine-sheath’ structure of this jet is maintained over a wide range of distances from the BH vicinity to further out.
The nature of the observed triple-ridge profile remains a matter of debate, with some potential scenarios proposed to explain the origin. One possibility is that the central ridge is actually part of the outer sheath associated with the same layer as the northern/southern limbs, while the true spine emission near the jet axis is less dominant due to either a low emissivity or deboosting (Mertens et al 2016; Walker et al 2018). solely reproduced by a BH-powered jet (Asada et al 2016; Orihara2019), with different streamlines or beaming factors. Another possibility is that the central ridge is associated with the true spine within the jet interior, which may be anchored in the central rotating BH (Asada et al 2016; Sob’yanin 2017; Ogihara et al 2019).
5.7 HST-1
At a deprojected distance of 200 pc from the nucleus, the M 87 jet harbors a notable feature known as ‘HST-1’. This feature was initially discovered with HST by Biretta et al (1999), and has been attracting special attention from the high-energy astrophysical community for several reasons.
First, HST-1 contains highly superluminal components of (4–6) that are observed across radio, optical and X-ray bands (e.g., Biretta et al 1999; Cheung et al 2007; Giroletti et al 2012; Snios et al 2019). The observed apparent speeds appear to be the highest in the entire velocity field of the M87 jet (Meyer et al 2013; Asada et al 2014, see also Fig. 8 bottom). This suggests that HST-1 represents a maximally Doppler-boosted region in the M 87 jet, and also tightly constrain the jet viewing angle to be . Second, as elaborated further in Sect. 5.9, HST-1 experienced a notable MWL outburst around 2005 (Harris et al 2006), followed by the ejection of superluminal components (Cheung et al 2007, Fig. 12 top). Third, HST-1 is located in the transition region of the jet geometry, where the jet shape changes from parabolic to conical. Additionally, there is a contraction of the jet cross section at HST-1 itself (Asada and Nakamura 2012), accompanied by highly enhanced polarization and RM (Park et al 2019b). The combination of these observational characteristics has led to an intriguing hypothesis that HST-1 represents a recollimation shock region at the end of ACZ in the M 87 jet, releasing significant energy in the form of high-energy flares. HST-1 could therefore be a possible counterpart of the unresolved core of distant blazars.

When viewed at the highest resolution, HST-1 exhibits intricate internal structure and time evolution (e.g., Chang et al 2010). It consists of multiple substructures with different velocities and trajectories. Long-term VLBI monitoring observations of HST-1 detected repeated ejection of new superluminal components from the upstream edge of the HST-1 complex (‘HST-1d’; Cheung et al 2007; Giroletti et al 2012; Hada et al 2014a, see also an updated plot in Fig. 12), suggesting that the upstream edge is where particles passing through are reenergized. After the ejection, while all the components are ejected from a similar location, their subsequent trajectories are quite different from one another, with most components following curved paths. This implies that the actual trajectories of these components are three-dimensional. The presence of helical motion in HST-1 is suggested by Chen et al (2011), where they detected a progressive rotation of HST-1’s EVPA using VLA data around the 2005 event. Unfortunately, the brightness of HST-1 has been continuously decreasing since the 2005 event across all wavelengths, rendering it very faint and challenging to observe as of 2024. Reenergization of HST-1 is eagarly awaited.
5.8 Kpc-scale jet
5.8.1 Spatially decomposed ideal laboratory
The M 87 jet on kpc scales has been well studied across a wide range of wavelengths from radio to X-rays over four decades. A conical shape with an opening angle of (de Vaucouleurs and Nieto 1979; Owen et al 1980, 1989; Reid et al 1982) starts from the innermost bright knot G, lying about 1 arcsec from the nucleus in VLA observations (Owen et al 1989). This region was later resolved by the HST into a structured complex known as HST-1 as introduced in the previous section. The structure of the jet downstream of HST-1 (1–18 arcsec or 0.1–1.5 kpc in projected distance) can be characterized by trailing clumps or knots of bright gas (HST-1 to C: Fig. 13) with an apparent deceleration to subluminal speed (around 6 to 0.5 Biretta et al 1995, 1999) and filamentary structures (‘wiggles/kinks’ Owen et al 1989; Sparks et al 1996).

The high overpressure in the synchrotron gas and the highly polarized (in both the knot: 40–60 % and interknot: 20–40 %) helical filaments (Owen et al 1989; Perlman et al 1999) indicate the existence of underlying ordered magnetic fields with a three-dimensional helix seen in projection; magnetic fields, therefore, appear to play a role in determining the M 87 jet structure even on large scales. While the projected MFPA vectors in the kpc-scale jet typically lie along the jet, the vectors at the brightest edges of the knots HST-1, D (especially in the optical band), A, and C becomes perpendicular to the jet, indicating the presence of longitudinal compression by a shock front and/or a tightly wound magnetic helix (Owen et al 1989; Perlman et al 1999). Detailed broadband (from radio through optical to X-ray) spectral shape of the knots (HST-1 to C) in the M 87 jet favors the scenario in which synchrotron emission dominates the radiation and in-situ particle acceleration (by the first-order Fermi process) almost certainly occurs in the large scale M 87 jet (both within knots and outside them; Perlman and Wilson 2005).
Under the assumption of the minimum energy condition, the knots themselves appear to be significantly overpressured (Owen et al 1989) with respect to the ambient thermal gas (Young et al 2002), but the interknot regions do not (Sparks et al 1996). In order to maintain a conical streamline of the adiabatic jet within a uniform ambient gas (an isothermal King profile with a core radius arcsec), the fields may have to be much stronger and more highly ordered than a weak and tangled field at the equipartition level ( a few of 100 G). Magnetic fields, therefore, appear to play a crucial role in determining the structure of the M 87 jet even on larger scales beyond 100 pc.
5.8.2 Origin of the comprehensive structure
A MWL study of the M 87 jet during 2002–2009 examined by Avachat et al (2016) reveals some differences in polarimetric and spectral features compared to the earlier result (Perlman et al 1999); a number of regions in the jet have a helical morphology as inferred from the the MFPA distributions. The presence of a systematic helical magnetic field in the particle-dominated jet, presumably maintained by KH instabilities (Lobanov et al 2003; Hardee and Eilek 2011), has recently been reported by utilizing Jansky VLA broadband full-polarization radio data (Fig. 13, Pasetto et al 2021); a clear ‘double-helix’ morphology of the jet together with systematic transverse RM gradients is resolved in the scales of 0.3–1 kpc in projection.
As shown in Fig. 13, the trails of the bright emission structure (‘knots’) are prominent. The innermost region of this trend, the HST-1 complex, appears to be an ignition point. Knots are interpreted as internal shocks in a collimated plasma beam (Rees 1978). Of particular interest is the brightest emission structure A–B–C. Knots A and C have certain similarities (Owen et al 1989; Perlman et al 1999); (1) bright transverse linear features (normal to the jet axis) indicative of a shock front (Biretta et al 1983), and (2) the dominance of transverse magnetic field suggesting ordered helical magnetic components. Visible side-to-side oscillation is also observed between these knots and MFPA vectors appear to follow the fluctuating jet axis in this part (including knot B).
A sudden enhancement of emission at knot A, at the upstream edge of that knot, indicates a reverse shock and a rapid drop in emission at the downstream edge of knot C, suggesting that it is the corresponding forward shock (Harris and Krawczynski 2006). Particle acceleration is associated with both the forward and reverse modes. Sudden changes in MFPA vector orientation strongly imply the existence of MHD fast/slow-mode waves; the transverse component of the magnetic field increases across a fast-mode front, while decreases across a slow-mode front. The brightest emission structures A-B-C could be quad-relativistic MHD shocks (forward fast/slow and reverse slow/fast), preceding knots from the HST-1 complex; as is shown in Fig. 12, an ejection of the paired super/sub-luminmal components (comp 1/1b in Fig. 12) from HST-1d, the upsream of the HST-1 complex, is reproduced in relativistic MHD simulations (Nakamura et al 2010).

Similar patterns of trailing bright knots, together with the systematic orientation of the projected MFPA vectors, may also be accompanied by such ‘zigzag’ patterns of the transverse velocity field (a flattened view of a helical motion) in HST observations (Meyer et al 2013; Nakamura and Meier 2014, Fig. 14). Such a helical distortion could be seen as a consequence of growing kink mode () of the current-driven (CD) instability, triggered by the slow mode MHD shocks (e.g., Nakamura and Meier 2004). Readers may refer to some recent results of highly magnetized (the initial magnetization ), relativistic MHD jet simulations (Barniol Duran et al 2017); the kink instability is triggered when the jet passes through the recollimation region (Bromberg and Tchekhovskoy 2016). Supposing that this can apply to the M 87 jet, the HST-1 complex is responsible for the recurrent ejection of super/sub-luminal components and the resultant ‘kinked segment’ (unwinding of the magnetic coils) advect with the bulk flow (e.g., knots D, E, F, and A-B-C: Biretta et al 1999; Meyer et al 2013).
We find an older, but suggestive simulation result of a highly magnetized, overpressured jet sheath against the uniform ISM environment (Clarke et al 1986), which may be applicable to a conical expansion in the M 87 jet. In a system like M 87, no cocoon surrounds the ‘naked’ jet and the post-shocked jet material is confined by the Lorentz force to form a ‘nose cone’ that leads the Mack disk (Burns et al 1991). In general, the surface-driven KH instability may be visible to the jet exterior, but it may be in conflict with the naked jet structure in M87. The growth of helical KH mode is suppressed even in a weakly magnetized jet with the axial magnetic field (Mizuno et al 2007).
To address this issue (whether KH or CD instability dominates in organizing the kpc-scale jet in M 87), we should consider the fraction of the dominant energy flux in jets. In magnetically driven jets, one of the standard models, the dominant Poynting flux near the BH (see also Sect. 2.5) is converted into kinetic energy flux downstream, allowing the jet to achieve relativistic speeds. A transition from magnetically dominated to kinetically dominated states in jets would of course be expected further downstream (e.g. pc to kpc scales). The efficiency of this conversion (from Poynting to kinetic energy flux) depends on non-uniform lateral collimation or divergence of the poloidal magnetic filed lines inside the jet (magnetic nozzle effect; see also Sect. 5.1.3). As a consequence, a magnetically dominated jet may exist even on kpc scales (particularly in low-power FR-I sources like M 87) even after the jet structural transition (from parabolic to conical; e.g., Barniol Duran et al 2017). Further observational investigation would be encouraged.
5.9 Broadband/MWL properties of (sub)pc-scale jet
5.9.1 Discovery of fast variability of VHE -ray emission
Until mid-2000, the only extragalactic objects known to emit TeV -ray radiation were blazars. An early observational study with High Energy Gamma Ray Astronomy (HEGRA) collaboration reported weak evidence for TeV -ray emission from M 87 in the data during 1998 and 1999 (Aharonian et al 2003). The first clear detection of fast variations of TeV -ray flux in M 87 was reported in 2005 by Aharonian et al (2006) using High Energy Stereoscopic System (H.E.S.S.). Similar phenomena were later confirmed by Very Energetic Radiation Imaging Telescope Array System (VERITAS) and Major Atmospheric Gamma-ray Imaging Cherenkov Telescope (MAGIC) (Acciari et al 2008; Albert et al 2008). The variation time scales of days indicate that the characteristic size of the TeV -ray emission region is given by , where is the Doppler factor of the emission region (Aharonian et al 2006). While a majority of AGNs detected in VHE -rays are strongly beamed blazars, M 87 is weakly or at most moderately beaming. Hence, the compactness of likely indicates that TeV -rays are produced in the vicinity of the BH. The discovery of TeV -ray emission stimulated subsequent efforts of coordinated MWL observations of this source.
5.9.2 The giant X-ray flare at HST-1 peaked in 2005
During an intensive Chandra X-ray monitoring program of this source starting from early 2000s, a giant X-ray flare was detected from HST-1, whose X-ray flux peaked in 2005 (Harris et al 2003, 2006). The X-ray intensity of HST-1 increased by more than a factor of 50 from 2000 to 2005. Year-scale light curves of HST-1 in optical and UV bands also showed the rise and decay synchronous with the X-ray flare (Perlman et al 2011; Madrid 2009). Using the observed decay time scale for the X-ray flare, the magnetic field strength at HST-1 can be estimated as , where a synchrotron cooling is considered (Harris et al 2009). Indeed, superluminal motions at HST-1 were clearly detected from the VLBI monitoring observations of the HST-1 components (Cheung et al 2007; Giroletti et al 2012). While the light curves of HST-1 in X-ray, UV, optical and VLA 2 cm bands reached a maximum in 2005, the light curves of the nucleus in these bands showed no obvious correlation with the TeV flare in 2005. Therefore, the TeV emission in 2005 was suggested to originate in HST-1 and led to the hypothesis that HST-1 represents a blazar-like feature in distant jet sources (Harris et al 2008).
5.9.3 Location of VHE flares: nucleus vs HST-1
M 87 has been established as a VHE -ray emitter after the 2005 TeV event (Aharonian et al 2006). Since then, exploring the origin of VHE -ray emitting region and its emission mechanism has been one of the major topics in the study of M 87. In Abramowski et al (2012), long-term MWL light curves during 2001–2011 are summarized, where enhanced VHE activities were detected in 2005, 2008, and 2010 by H.E.S.S., MAGIC and VERITAS. This shed a new light on the location of the VHE -ray emitting region in M 87.
In this context, near-in-time high-resolution VLBI monitoring observations coordinated with the -ray facilities have played a key role in localizing the site of high-energy events. To summarize, the VLBI data suggest that the -ray events that have occurred since 2008 have always originated from the nucleus.
-
•
The H.E.S.S. Collaboration reported a higher -ray flux in 2005 than in the adjacent years (Aharonian et al 2006). Owing to the observed rapid variability, they argued that the likely origin of the TeV emission was the nucleus (i.e. close to the SMBH). On the other hand, Cheung et al (2007) argued that the TeV emission originates from HST-1 that contains superluminal components rather than from the nucleus.
-
•
The MWL observing campaign in 2008 revealed a period of strong VHE -ray flares accompanied by a significant increase in the radio flux from the VLBA 43 GHz core. This implies that VHE-emitting particles are produced in the vicinity of the central BH (Acciari et al 2009, and references therein). As the flare progressed, the brightened region extended about 0.77 mas from the core, resulting in the emergence of new components at an apparent speed of 1.1 .
-
•
During the VHE event in 2010 April, VLBA observations (as well as Chandra) confirmed a quiescent state of HST-1. On the other hand, the VLBA radio core at 22/43 GHz near in time to the VHE peak showed a slightly (10%) higher flux level than that of before/after the event (Hada et al 2012). The size of the 43 GHz core was estimated to be 17 , which was comparable to the suggested size of the VHE emitting region. These results tend to favor the scenario that the VHE -ray flare in 2010 April is associated with the radio core.
-
•
During 2012 February–March, an elevated level of the M 87 VHE -ray flux was reported (Beilicke and VERITAS Collaboration 2012)222 Note, however, that a recent report by MAGIC Collaboration et al (2020) indicates that the differential flux between 2012 and 2015 is at a similar level to that during the low-emission states reported by MAGIC between 2005 and 2007.. A densely-sampled radio monitoring program with the VLBI Exploration for Radio Astrometry (VERA) at 22/43 GHz detected a significant flux increase from the radio core coincident with the VHE activity (Hada et al 2014b). Meanwhile, EVN observations confirmed a quiescent state of HST-1 in terms of its flux density and mas-scale structure. The VLBI results, combined with a coincident proto-EHT 230 GHz data (Akiyama et al 2015), suggested that the active event in 2012 originates in the jet base within 56 near the BH.
| Time | Radio/VLBI | X-ray | VHE | References |
|---|---|---|---|---|
| 2005 | HST-1 | HST-1 | flare | b,c |
| 2008 Feb | nucleus | nucleus | flare | d |
| 2010 Apr | nucleus | quiet | flare | e |
| 2012 Mar | nucleus | quiet | elevated fluxa | a,f,g,h |
| 2017 Apr | quiet | quiet | quiet | i |
| 2018 Apr | quiet | nucleus | flare | j |
(a): A recent report indicates a quiescent state (MAGIC Collaboration et al 2020); (b) Cheung et al (2007); (c) Harris et al (2009); (d) Acciari et al (2009); (e) Abramowski et al (2012); (f) Beilicke and VERITAS Collaboration (2012); (g) Hada et al (2014b); (h)Akiyama et al (2015); (i) EHT MWL Science Working Group et al (2021) and references therein; (j) EHT MWL Science Working Group et al (2024) and references therein.
5.9.4 MWL campaign observations in EHT era
Given that the structure of jets varies both temporally and spatially, it is essential for MWL instruments to measure radiation fluxes from the same celestial direction as simultaneously as possible.
In the 2017 M 87 MWL observations where EHT joined for the first time (EHT MWL Science Working Group et al 2021), there were two advancements compared to the prior MWL campaigns: first, quasi-simultaneous observations across various MWL instruments were well organized, minimizing any uncertainty caused by non-simultaneous dataset. The 2017 M 87 MWL observing campaign provides the most complete quasi-simultaneous broadband SED of an AGN to date. Second, the size of the compact (radio) emitting region was tightly constrained thanks to the high-resolution EHT imaging. These advantages have allowed us to examine the MWL properties of this active nucleus more accurately. As a first step, EHT MWL Science Working Group et al (2021) modeled the observed SED using simple single zone models with the purpose of highlighting some baseline properties of the peak emission regions (Fig.15). The key insights obtained from their SED modeling can be summarized as follows:
-
•
When the observed SED is modeled together with the size and mm flux constraints from EHT, the predicted VHE -ray flux from such a compact region significantly underestimates the observed VHE -ray flux. This suggests that the observed VHE -ray radiation is primarily generated in locations different from the EHT region, and challenges the conventional picture that the bulk of observed MWL radiation from radio to -rays originates in a single region.
-
•
The synchrotron self-absorption (SSA) turnover frequency of the radio spectrum results in approximately equal to the observing frequency of EHT i.e., 230 GHz. Previous SED modeling studies of M 87 estimated the magnetic field strength of the emission region to be a few milli Gauss (Abdo et al 2009; MAGIC Collaboration et al 2020). However, the results from EHT MWL Science Working Group et al (2021) showed a significantly larger value, approximately Gauss, differing by three orders of magnitude. The difference can be attributed to the difference in the value of . Prior to the EHT era, the best-fit in SED models tended to be lower than 230 GHz since VLBI observations at lower frequencies were still not able to resolve the spatial scales expected from the models. This inevitably led to milli-Gauss order magnetic field strengths.

.
There are a few more recent publications based on TeV -ray data obtained after 2021 (Ureña Mena et al 2022; H.E.S.S. Collaboration et al 2024; Molero et al 2023). Also, a second EHT-MWL joint campaign was performed in 2018, where M 87 showed a flaring activity in TeV bands in contrast to the case in 2017 (EHT MWL Science Working Group et al 2024). These accumulated EHT and MWL data will further refine the localization of VHE -ray emitting region in this source.
The exact physical origin of the M 87 VHE -ray emission remains a topic of debate. Various potential mechanisms are proposed in the literature, including: (i) originating from magnetospheric vacuum gaps (e.g., Neronov and Aharonian 2007; Levinson and Rieger 2011; Katsoulakos and Rieger 2018; Kisaka et al 2022), (ii) arising from magnetic reconnection processes (e.g., Ripperda et al 2022; Hakobyan et al 2023), and (iii) stemming from hadronic processes (e.g., Reimer et al 2004; Barkov et al 2012; Kimura and Toma 2020). Further dedicated joint observational efforts between the EHT and VHE observatories will elucidate the physical mechanisms underlying the origin of VHE -ray emission.
5.10 Magnetic field strengths
In this section, we review the estimations of some key quantities relevant to the strength of magnetic field based on actual observational data of M 87.
5.10.1 Radial profile of magnetic field strength
First, here we overview how the strength of magnetic field () spatially evolves in the M 87 jet. For M 87, were estimated at various locations through modelings of diverse observational features such as: spectra of SSA radio core (e.g., Reynolds et al 1996; Kino et al 2014); radio spectra of optically-thin jet (Ro et al 2023b); brightness temperature of the radio core (Kim et al 2018b); EHT images (Event Horizon Telescope Collaboration et al 2019e, 2021b); radio-to--ray broadband SED (e.g., Georganopoulos et al 2005; Abdo et al 2009; Prieto et al 2016); core-shift (e.g., Zamaninasab et al 2014; Jiang et al 2021); variability in radio/X-ray light curves (Harris et al 2003, 2009; Acciari et al 2009; Hada et al 2012).

Ro et al (2023a) compiled these past measurements as a function of radial distance from the jet base (Fig. 16). Although individual measurements have rather large uncertainties (as large as a factor of 10), a collection of independent estimates infer 1–100 G levels within a hundred gravitational radii (Kino et al 2015; Hada et al 2016; Event Horizon Telescope Collaboration et al 2021b; EHT MWL Science Working Group et al 2021). When assuming at the jet base of M 87, the magnetic field strength at the event horizon may exceed G (Blandford et al 2019; Kino et al 2022) (see also Sects. 5.10.3 and 5.11), 333 Kino et al (2022) proposed a slower angular frequency than that typically suggested to explain the observed jet velocity profile shown in Fig. 8. This slower necessitates a larger at the horizon. although its exact requirement depends on somewhat ambiguous value of (see Sect. 5.11). On the other hand, drops to sub-mG levels at a distance of HST-1 (Harris et al 2003, 2009; Giroletti et al 2012). It is still uncertain how evolves between BH to HST-1, but a recent spectral analysis of a pc-scale jet has deduced and its radial slope at intermediate scales (Ro et al 2023b), starting to reveal the global evolution of in the jet ACZ.
5.10.2 at the jet base
Next, we discuss another important quantity, , the ratio of the energy density of magnetic field () to that of nonthermal electron-positron energy density () in the jet. This ratio at the jet base can be constrained by observed electromagnetic signals, indicating the dynamical significance of the magnetic field in jet launching. Firstly, we summarize findings from the previous studies based on one-zone models focusing on the opaque SSA sphere. It has long been known that once the angular size and the synchrotron flux from the surface are obtained, one can uniquely determine inside the surface (e.g., Kellermann and Pauliny-Toth 1969; Blandford and Rees 1978). However, spatially resolving jet bases has been challenging due to limited telescope resolution. Recent improvements in VLBI observations now enables the application of this method at the base of the M87 jet, suggesting (Kino et al 2015).
Broadband SED fitting of the MWL emission is another well-known method to investigate . With the capability to observe AGN jets in the high-energy domain, one can detect not only synchrotron radiation but also inverse Compton scattering components (e.g., Gaidos et al 1996; Chadwick et al 1999; Hartman et al 1999; Abdo et al 2010; Rieger and Aharonian 2012; Abdo et al 2013) (see Sect. 5.9). This allows us to differentiate between and , making it possible to determine both of them without degeneracy. From a one-zone fitting to the radio-to--ray broadband SED, it is suggested that in the compact emission region of M 87 the jet (Abdo et al 2009; MAGIC Collaboration et al 2020).
Hence, the estimated values showed contrasting results even among simple uniform one-zone models. However, the situation is improving. As explained in Sect. 5.9, the MWL analysis including EHT data seems to gradually mitigate the contradiction (EHT MWL Science Working Group et al 2021). In the compact region near the BH observed by EHT, tends to decrease and become the order of unity, approaching the situation presumed in GRMHD simulations (Fig. 15). On the other hand, the VHE -ray emission region is suggested to be , located at a different place away from the BH vicinity.
5.10.3 at the event horizon
As summarized in Sects. 5.10.1 and 5.10.2, various observational data colleted over the years for M 87 support the idea of the jet being magnetically driven. Therefore, we now estimate the value of , the magnetic flux threading the event horizon of the central BH. Using Eq. (6) together with the values of (Sect. 4) and (Sect. 3) obtained for M 87, the magnetic flux threading the event horizon can be estimated as follows:
| (11) |
where is assumed in line with recent GRMHD simulations. This seems to agree with the sequence of magnetic flux estimated at the downstream of jets (Zamaninasab et al 2014), Using the relation , where is the strength of the magnetic field at the event horizon, the magnetic field strength can be estimated as follows:
| (12) |
which can be comparable to the estimates of mentioned in Sect. 5.10.1. Together with the above estimated and Eq. (8), BZ power of M 87 can be estimated as
| (13) |
where is given by Eq. (2) and here we set and (e.g., Tchekhovskoy et al 2010). In this way, can establish a connection between the event horizon and the downstream region of the jet. The estimated shown in Eq. (5.10.3) can be comparable to from observations (see Sect. 5.11), suggesting a capablility to supply the jet power.
5.11 Estimation of
As reviewed in Sect. 2.5, it is difficult to put a limit on the total amount of nonthermal electrons (and positrons) because information can only be obtained directly from the jet’s electromagnetic observations for a portion of nonthermal electrons (and positrons). Therefore, there have been no significant recent progress in the estimation of for M87, and we will rely on the estimates made in relatively past studies. In the following, we proceed with the review in order of increasing spatial scale.
On several 10 kpc scales, is estimated from the energy required to inflate the observed X-ray cavity and radio lobe structures. The previous works suggest (Owen et al 2000; Young et al 2002; Allen et al 2006; Rafferty et al 2006). The spherical shock model provides an estimate of the mean power of the shock outburst as averaged over the past year on kpc scale (Forman et al 2005). An application of synchrotron aging model against the Low-Frequency Array (LOFAR) observation of the radio lobe suggests an age of 40 Myr, which leads to (de Gasperin et al 2012).
At a distance of about 1 kpc from the central BH, Knot A is known to be a bright optical feature in the jet downstream side. Bicknell and Begelman (1996) made an estimation of using the Knot A. Interpreting knot A as an oblique shock within the jet results in a jet power estimate of . The estimated is consistent with the above-mentioned jet power required to feed the radio lobe. In addition, the search for a steady and extended -ray signal around M 87 can constrain the upper limit of cosmic-ray energy density, as discussed in a recent study by the H.E.S.S. collaboration, which addressed the upper limit of (H.E.S.S. Collaboration et al 2023).
By identifying HST-1 as a recollimation shock, Stawarz et al (2006) estimated by the pressure balance between the ambient matter and HST-1. They derive a jet power of the order of . The estimated is again consistent with the above-mentioned jet power required to feed the radio lobe.
In addition, it is worth noting that Broderick et al (2015) pointed out that the above-mentioned implies a certain minimum and if the central compact object in M 87 were not a BH but had a surface, the emission from the accreting matter onto the surface would exceed the observed fluxes in near-infrared and optical bands, suggesting the presence of an event horizon.
6 Where do we stand?
Through Sect. 3, 4 and 5, we have reviewed various observational results and progress on the central SMBH, accretion flows and relativistic jets of M 87. By putting together the accumulated knowledge, here we summarize our current understanding of this active galaxy. We also provide notes on future outlooks, highlighting some remaining questions to be explored in future studies.
6.1 Key parameters
In Table 3 we summarize estimated values of various parameters and observational quantities for M 87, including those introduced in Sect. 2. The table reflects our current level of understanding about this source. One can see that some of the key quantities are already determined with sufficient accuracy, while some other parameters remain highly uncertain. It is also worth noting that, for some important physical quantities (e.g., the accretion rate, jet shape, jet velocity, magnetic field strength), we are starting to see their spatial evolution over many orders of magnitude in radial distance () or jet axial distance (), owing to the accumulation of observational data at different scales and the progress of multi-scale studies over the past years. Therefore, we are now beginning to connect the physics between horizon scales and galactic scales, which is essential for a comprehensive understanding of this active galaxy as a whole system.
| Parameters/quantities | Reference values | Related sections/figures |
| Key parameters introduced in Sect. 2 | ||
| Sect. 3.1 | ||
| likely | Sect. 3.2, 5.1.3, 5.2.2, 5.6 | |
| (near horizon) | Sect. 4.3 | |
| (at Bondi radius) | 0.2 | Sect. 4.1 |
| Sect. 5.10 | ||
| Sect. 5.11 | ||
| Other observational parameters/quantities | ||
| Source distance | 16.8 Mpc | Sect. 1.2, 3.1 |
| Bondi radius | 220 pc () | Sect. 4.1 |
| X-ray core luminosity | erg s-1 | Sect. 4.1 |
| Core ring diameter (1.3 mm) | 42 as | Sect. 3.1, 4.3 |
| Core ring diameter (3.5 mm) | 64 as | Sect. 4.3 |
| Jet viewing angle | 14–20∘ | Sect. 5.2.1, 5.4, 5.7 |
| Jet position angle | 284–292∘ (nominal 288∘) | Sect. 5.2.2, 5.8 |
| Jet radius () | Sect. 5.1, Fig. 8 | |
| Jet radius () | Sect. 5.1, Fig. 8 | |
| Core-shift (1-88 GHz) | Sect. 5.3 | |
| Maximum apparent jet speed | 6 | Sect. 5.2.1, 5.7, 5.8.1 |
| Maximum | a few | Sect. 4.2, 5.5 |
| Radial () / jet-axial () evolution* | ||
| Sect. 4, Fig. 7 | ||
| Sect. 4.2, 5.5 | ||
| Sect. 4.2 | ||
| Sect. 5.2.1, 5.8.1, Fig. 8 | ||
| Sect. 5.10, Fig. 16 | ||
*: Here we do not put reference values since these quantities significantly evolve with distance. Instead, the readers may refer to related sections/figures and references therein for details.
6.2 What’s left, and what are the next steps?
More than a quarter of a century has passed since the first dedicated workshop on the radio galaxy M 87 in Tegernsee, Germany in 1997. During the conference, some important questions were left unanswered (Blandford 1999): ‘Why is M 87 so dim?’; ’Does the Jet Power Come from the Disk or the Hole?’; ’How is the Jet Collimated and of What Is It Made?’; ’What’s Going on in Knot A?’. We believe that these fundamental quests have been extensively studied both observationally and theoretically since then. In addition, the second M 87 workshop444https://events.asiaa.sinica.edu.tw/workshop/20160523/ in Taipei, Taiwan, in 2016 drove momentum for the imaging of a BH shadow, along with preparations for the 100th anniversary of the discovery of astrophysical jets. Now, we know answers to the questions above and we know that there are SMBHs at the center of galaxies. This is, however, still a good time to be studying M 87, as Roger Blandford mentioned before.
Below we describe some of the selected remaining challenges or topics that should be explored in future studies of M 87.
-
•
BH spin: As summarized in Table 3, a growing number of studies suggest that the M 87 SMBH is likely spinning, whereas the exact value of the spin remains highly uncertain. Constraining the spin parameter is crucial for testing the spacetime properties near the SMBH and for testing the jet launching mechanism via BZ processes. To directly constrain the spin, one of the most promising ways would be to accurately measure the shape of a photon ring, where the ring shape is expected to deviate from a pure circular shape as the spin increases (up to 5%) (Takahashi 2004; Johannsen and Psaltis 2010). The ring-like structure observed by the ground-based EHT baselines at 1.3 mm is likely still dominated by the emission from the gas surrounding the BH, while the emission from a lensed photon ring becomes significant only at baselines longer than 20 G (Johnson et al 2020). To detect signals from such an uncontaminated photon ring, future higher-resolution mm/submm VLBI projects, such as the next-generation EHT (ngEHT555https://www.ngeht.org/), Black Hole Explorer (BHEX666https://www.blackholeexplorer.org/) with a space satellite and/or VLBI at even higher frequencies (e.g., GLT; Chen et al 2023a) will be promising.
-
•
BH-jet connection: While the EHT 2017/2018 data clearly detected the BH shadow, they failed to recover the surrounding jet emission mainly due to the limited baseline coverage of the array, leaving the exact connection between the shadow and jet launching still unresolved. Future EHT, ngEHT and/or BHEX observations at 230/345 GHz with significantly enhanced array capabilities hold promise for detecting both the shadow and the jet-base emission in the same image (e.g., Event Horizon Telescope Collaboration 2024), which is also crucial for constraining the BH spin as well as the jet-launching mechanism. This exploration will be further reinforced by complementing multi-frequency high-resolution images at 86 GHz and 43 GHz, through which one can trace a full evolution of initial jet formation from 1 to 1000 .
-
•
Dynamical/Time-domain view: Thanks to the accumulation of multi-epoch, multi-wavelength, and multi-scale observational data, now we know that the structure of M 87 is variable at all spatial scales (from horizon to kpc) and time scales (from day to years). However, none of these observed variable features remain fully understood due to the complex nature of the underlying physics and the general lack of time-domain observational data. Time-domain/dynamical information provides much richer insights into the accretion and jet physics as well as the mechanisms of high-energy emission and particle acceleration processes. Continued multi-epoch, multi-instrument, multi-wavelength observations are highly encouraged to improve our knowledge of the time-domain properties of this object.
-
•
Mass transport processes: Dating back to the mid-1990s, ADAF (Narayan and Yi 1995) was proposed to account for SgrA* and the subsequent development of RIAF with substantial mass loss including the convection (Abramowicz et al 2002) and winds (Blandford and Begelman 1999) has advanced our understanding of the mass transport towards sub-Eddington BHs including M 87. A substantial decrease in may be the norm, but we may not have a problem with this fact even if when considering jet production (Ghisellini et al 2005). When an accreting BH is in the MAD state (Narayan et al 2003), the spinning BH is able to power the jet (Blandford and Znajek 1977). However, the angular distribution of the accretion flow and winds remains unclear, so the net amount of mass transport onto the BH has not yet been confirmed at a quantitative level. The issue of mass and energy transport should be examined in multiple dimensions(Yuan and Narayan 2014; Yuan et al 2022). The fate of winds with significant mass loading is of particular interest, and further investigations with Faraday RM measurement are encouraged.
-
•
Jet structure: As reviewed in Sect. 5, a growing number of pc-scale VLBI images suggest that the transverse structure of the M 87 jet is likely more complicated than previously thought, as represented by the spine-sheath-like morphology. Additionally, these relativistic flows are likely surrounded by (invisible) non-relativistic outflows/winds. On kpc scales, high-quality VLA images confirm the double-helix morphology of the large-scale jet (a similar helical structure has recently been suggested also in the pc-scale jet; Nikonov et al 2023). Revealing the detailed internal structure of the M 87 jet is essential to better understand the formation, propagation and interaction with the external medium. To facilitate this study, further improvement in both angular resolution and image dynamic range for the extended jet is required. Future deep interferometric imaging observations with the next-generation VLA (ngVLA777https://ngvla.nrao.edu/) and the Square Kilometer Array (SKA888https://www.skao.int/) operated at cm wavelengths will enable us to conduct this kind of study.
-
•
Magnetic fields: Clarifying the geometry of magnetic field is crucial for understanding jet formation. On near-horizon scales, Chael et al (2023) pointed out that the sign of arg() correlates with Poynting flux direction, and the EHT’s measurement of arg()999The arg() is the second azimuthal Fourier mode of linear polarization in a near-horizon images (Palumbo et al 2020). implies electromagnetic energy outflow. Chael et al (2023) found that (i) arg() strongly depends on the BH spin, and (ii) arg() shows a radial dependence, evolving rapidly near the inner shadow as fields are wound up. Thus whether this energy outflow is spin-powered or not remains inconclusive. To test whether the BZ mechanism really is at work or not in the M 87 jet, measuring arg() closer to the event horizon is imperative. Higher-dynamic range or/and higher resolution polarization images with ngEHT/BHEX will be essential to clarify the radial dependence of arg(). On a parsec scale view of the M 87 jet, the linearly polarized emissions are weak and still detected only part of the jet (e.g., Zavala and Taylor 2002; Park et al 2019a). To explore the overall radial evolution of the magnetic field geometry and understand how it evolves from the BH to larger scales, future high-sensitivity VLBI and multi-wavelength polarimetric observations are highly anticipated.
-
•
Particle acceleration and high-energy emission: The origin of energetic particles emitting VHE -rays is of great interest, as described in Sect. 5.9. During the 2018 EHT campaign, flaring episodes constrained the size of the VHE -ray emitting region in SED modeling. However, a one-zone model cannot fully explain the SED, requiring an additional component. Two processes likely produce the energetic particles emitting VHE -rays: magnetic reconnection and shock acceleration. More sensitive VHE instruments such as the Cherenkov Telescope Array (Acharya et al 2013; Cherenkov Telescope Array Consortium et al 2019), may help identify the VHE -ray emitting region due to their better short-timescale sensitivity and spectral resolution. Investigating EVPA time evolution of the high-energy emission may also help distinguish these scenarios. Magnetic reconnection flares may cause drastic changes of EVPA, while shock-induced flares may not. Future X-ray polarization mission eXTP (Zhang et al 2019) could help distinguish these scenarios.
6.3 Broader context: comparison with other sources
The extensive M 87 studies over the past decades have dramatically improved our understanding of various key properties of AGNs/SMBHs. Nevertheless, M 87 occupies only part of the whole AGN parameter space. To explore the diverse properties of AGNs and how M 87 fits into the context of a ‘unified picture’ of AGNs, comparison with other sources is essential.
First, the Galactic Center SgrA* is one of the most frequently compared objects with M 87 since they are the only two sources where the SMBH shadow is spatially resolved (Event Horizon Telescope Collaboration et al 2022a, b, c, d, e, f). Unlike M 87, SgrA* does not have a clear jet. This sharp contrast offers a unique opportunity to tackle the question, directly at the horizon scales, of why some SMBHs exhibit powerful jets while others do not. Interestingly, the EHT results of SgrA* favor the MAD state and high spin models, which might be expected to generate a jet efficiently like M 87. Other primary differences are that SgrA* has a much lower and than M 87 both in absolute terms and when scaled by mass, which may also limit the jet power.
Second, while our understanding of weakly accreting SMBHs has greatly improved thanks to the intensive studies on M 87 (and SgrA*), the physics of accretion/ejection for other types of RLAGNs, especially those with highly accreting SMBHs, remains far less understood. Such sources may produce even more powerful jets, but they are typically much more distant than M 87. Recent ultra-high-resolution mm-VLBI and space-VLBI observations have started to resolve the inner jet regions within 100-1000 for an increasing number of RLAGN samples (Kim et al 2020; Janssen et al 2021; Issaoun et al 2022; Jorstad et al 2023; Fuentes et al 2023; Paraschos et al 2024), covering a variety of jet viewing angles, accretion rates, jet powers and nuclear environments. By comparing the observed jet properties of these sources with those of M 87 at matched gravitational scales, we will be able to better answer the diversity and universality of RLAGN physics across diverse accretion rates. For instance, an ongoing debate is what physics ultimately controls the extension of jet ACZ. As reviewed in Sect. 5, the jet profile of M 87 is constrained very well and many other AGN jets appear to exhibit similar parabolic-to-conical transitions regardless of AGN types, suggesting that such a jet transition is universal. However, while the M 87 jet breaks at the Bondi radius, a majority of other jets seem to break at distances different from their Bondi scales (e.g., Kovalev et al 2020; Boccardi et al 2021; Okino et al 2022). Thus, it is worth continuing to explore how magnetically-driven jets evolve under the stratified atmosphere governed by SMBHs in future observations. This would require more samples with a broad range of AGN parameter space.
7 Summary
In this review, we provided a comprehensive overview about the recent observational progress of M 87 from galactic scales to event horizon scales, obtained across various wavelengths from radio to TeV -rays. Here we conclude our review by itemizing some key points.
-
•
The mass of M87’s central SMBH has been estimated using various methods, including stellar dynamics, gas dynamics, and BH shadow measurements. The current plausible value would be that were consistently obtained from the stellar dynamics and the BH shadow image.
-
•
The nature of accretion flows from Bondi scales to horizon scales was reviewed. The highly sub-Eddington accretion rate at Bondi scales makes BH accretion of M 87 RIAF-type flows. Putting all estimates at different scales together, substantial decrease in towards smaller radii is indicated. This suggests that only a fraction of accretion energy available at large scales is actually supplied to the central SMBH, and significant mass loss processes are taking place between SMBH and Bondi scales. The observed Faraday RM profiles at parsec scales suggest substantial winds from hot accretion flows, which may be responsible for the reduction of mass supply at small radii.
-
•
We also highlighted the complexity and diversity of phenomena associated with the relativistic jet in M 87. The collimation profile of this jet is now quite well established over 107 orders of magnitude in distance. Although still relatively less defined compared to the jet shape, our observational understanding of the jet dynamics (both along and perpendicular the jet axis) has also been significantly updated in recent years thanks to various intensive VLBI monitoring programs. Furthermore, recent high-dynamic-range radio imaging both at pc and kpc scales has revealed the transverse or internal jet structures (e.g., spine-sheath and helical structures) in great detail, highlighting the complexity of jet physics.
-
•
An increasing number of independent studies observed at different spatial scales and wavelengths consistently suggest that the M 87 central SMBH is spinning. The spinning BH likely plays a key role in generating the observed relativistic jet of M 87, through the Blandford & Znajek processes. Nevertheless, the exact value of the spin remains less constrained and stands as a crucial question to be explored in future studies.
-
•
Polarization structures of M 87 are now revealed in great detail at all scales from horizon to kpc scales, providing additional insights about the physical properties of accretion flows and relativistic jet, as well as the structure of magnetic fields associated with them. The observed polarization characteristics associated with the EHT ring strongly favor MAD states, suggesting the presence of dynamically important magnetic fields near BH, which can be also responsible for producing the observed powerful jet. The organized MWL polarization properties observed in the large-scale jet indicate that magnetic fields continue to play a critical role in determining the structure of the M 87 jet even at kpc scales.
-
•
We also summarized the broadband MWL observing campaigns conducted in the past. With the exception of the 2005 event where HST-1 clearly exhibited MWL ourbursts, most of high-energy (X-ray and -ray) events seem to be associated with the nucleus rather than far from the BH. Nevertheless, the exact location and mechanisms of the -ray emission are still a matter of debate. Continued efforts of coordinated simultaneous MWL observations along with high-resolution radio instruments are highly encouraged.
By combining the numerous pieces of knowledge summarized above, we are beginning to seamlessly trace a progression of key physical processes that characterize an AGN, from accretion onto the SMBH to jet launching and propagation beyond the host galaxy, along with energy dissipation through intense radiation. The study of M 87 has demonstrated that these processes are tightly interrelated across a wide range of physical scales, underlining the importance of multi-scale, multi-faceted approaches to fully disentangle this intricate system.
-
•
Despite the tremendous advances in our knowledge of this object, several outstanding questions remain. Next-generation instruments planned for the next decade will be crucial in addressing these remaining questions. It should also be emphasized that comparing M 87 with other sources at matched gravitational scales is essential for understanding the diverse properties of AGNs.
Acknowledgments We thank the anonymous referee and the journal editors for their valuable comments and suggestions, which significantly improved the manuscript. We thank Juan Carlos Algaba, Alice Pasetto and Hyunwook Ro for producing Fig.1, 13 and 16 for this review, respectively. We thank Alexei Nikonov for providing the data that allowed us to create Fig.10 for this review. We also thank Derek Ward-Thompson, Kazi Rygl, Bong Won Sohn, and Victor Barbosa Martins for their reading and commenting on the manuscript. Part of this work was supported by the MEXT/JSPS KAKENHI (grants 21H04488, 21H01137, 22H00157 and 24K07100), the Mitsubishi Foundation grant (grants 201911019 and 202310034), the National Science and Technology Council grant (NSTC 111-2112-M-001-041, NSTC 111-2124-M-001-005, and NSTC 112-2124-M-001-014) and the Academia Sinica Career Development Award grant AS-CDA 110-M05.
References
- \bibcommenthead
- Abdo et al (2009) Abdo AA, Ackermann M, Ajello M, et al (2009) Fermi Large Area Telescope Gamma-Ray Detection of the Radio Galaxy M87. ApJ 707(1):55–60. 10.1088/0004-637X/707/1/55, https://arxiv.org/abs/arXiv:0910.3565 [astro-ph.HE]
- Abdo et al (2010) Abdo AA, Ackermann M, Ajello M, et al (2010) Fermi Large Area Telescope First Source Catalog. ApJS 188(2):405–436. 10.1088/0067-0049/188/2/405, https://arxiv.org/abs/arXiv:1002.2280 [astro-ph.HE]
- Abdo et al (2013) Abdo AA, Ajello M, Allafort A, et al (2013) The Second Fermi Large Area Telescope Catalog of Gamma-Ray Pulsars. ApJS 208(2):17. 10.1088/0067-0049/208/2/17, https://arxiv.org/abs/arXiv:1305.4385 [astro-ph.HE]
- Abramowicz et al (1988) Abramowicz MA, Czerny B, Lasota JP, et al (1988) Slim Accretion Disks. ApJ 332:646. 10.1086/166683
- Abramowicz et al (2002) Abramowicz MA, Igumenshchev IV, Quataert E, et al (2002) On the Radial Structure of Radiatively Inefficient Accretion Flows with Convection. ApJ 565(2):1101–1106. 10.1086/324717, https://arxiv.org/abs/arXiv:astro-ph/0110371 [astro-ph]
- Abramowski et al (2012) Abramowski A, Acero F, Aharonian F, et al (2012) The 2010 Very High Energy -Ray Flare and 10 Years of Multi-wavelength Observations of M 87. ApJ 746(2):151. 10.1088/0004-637X/746/2/151, https://arxiv.org/abs/arXiv:1111.5341 [astro-ph.CO]
- Acciari et al (2008) Acciari VA, Beilicke M, Blaylock G, et al (2008) Observation of Gamma-Ray Emission from the Galaxy M87 above 250 GeV with VERITAS. ApJ 679(1):397–403. 10.1086/587458, https://arxiv.org/abs/arXiv:0802.1951 [astro-ph]
- Acciari et al (2009) Acciari VA, Aliu E, Arlen T, et al (2009) Radio Imaging of the Very-High-Energy -Ray Emission Region in the Central Engine of a Radio Galaxy. Science 325(5939):444. 10.1126/science.1175406, https://arxiv.org/abs/arXiv:0908.0511 [astro-ph.HE]
- Acharya et al (2013) Acharya BS, Actis M, Aghajani T, et al (2013) Introducing the CTA concept. Astroparticle Physics 43:3–18. 10.1016/j.astropartphys.2013.01.007
- Aharonian et al (2003) Aharonian F, Akhperjanian A, Beilicke M, et al (2003) Is the giant radio galaxy M 87 a TeV gamma-ray emitter? A&A 403:L1–L5. 10.1051/0004-6361:20030372, https://arxiv.org/abs/arXiv:astro-ph/0302155 [astro-ph]
- Aharonian et al (2006) Aharonian F, Akhperjanian AG, Bazer-Bachi AR, et al (2006) Fast Variability of Tera-Electron Volt Rays from the Radio Galaxy M87. Science 314(5804):1424–1427. 10.1126/science.1134408, https://arxiv.org/abs/arXiv:astro-ph/0612016 [astro-ph]
- Aitken et al (2000) Aitken DK, Greaves J, Chrysostomou A, et al (2000) Detection of Polarized Millimeter and Submillimeter Emission from Sagittarius A*. ApJ 534(2):L173–L176. 10.1086/312685
- Akiyama et al (2015) Akiyama K, Lu RS, Fish VL, et al (2015) 230 GHz VLBI Observations of M87: Event-horizon-scale Structure during an Enhanced Very-high-energy -Ray State in 2012. ApJ 807(2):150. 10.1088/0004-637X/807/2/150, https://arxiv.org/abs/arXiv:1505.03545 [astro-ph.HE]
- Albert et al (2008) Albert J, Aliu E, Anderhub H, et al (2008) Very High Energy Gamma-Ray Observations of Strong Flaring Activity in M87 in 2008 February. ApJ 685(1):L23. 10.1086/592348, https://arxiv.org/abs/arXiv:0806.0988 [astro-ph]
- Allen et al (2006) Allen SW, Dunn RJH, Fabian AC, et al (2006) The relation between accretion rate and jet power in X-ray luminous elliptical galaxies. MNRAS 372(1):21–30. 10.1111/j.1365-2966.2006.10778.x, https://arxiv.org/abs/arXiv:astro-ph/0602549 [astro-ph]
- Antonucci (1993) Antonucci R (1993) Unified models for active galactic nuclei and quasars. ARA&A 31:473–521. 10.1146/annurev.aa.31.090193.002353
- Asada and Nakamura (2012) Asada K, Nakamura M (2012) The structure of the m87 jet: A transition from parabolic to conical streamlines. The Astrophysical Journal Letters 745(2):L28
- Asada and Nakamura (2012) Asada K, Nakamura M (2012) The Structure of the M87 Jet: A Transition from Parabolic to Conical Streamlines. ApJ 745(2):L28. 10.1088/2041-8205/745/2/L28, https://arxiv.org/abs/arXiv:1110.1793 [astro-ph.HE]
- Asada et al (2014) Asada K, Nakamura M, Doi A, et al (2014) Discovery of Sub- to Superluminal Motions in the M87 Jet: An Implication of Acceleration from Sub-relativistic to Relativistic Speeds. ApJ 781:L2
- Asada et al (2016) Asada K, Nakamura M, Pu HY (2016) Indication of the Black Hole Powered Jet in M87 by VSOP Observations. ApJ 833:56. 10.3847/1538-4357/833/1/56
- Avachat et al (2016) Avachat SS, Perlman ES, Adams SC, et al (2016) Multi-wavelength Polarimetry and Spectral Study of the M87 Jet During 2002-2008. ApJ 832(1):3. 10.3847/0004-637X/832/1/3, https://arxiv.org/abs/arXiv:1609.03936 [astro-ph.HE]
- Baade (1956) Baade W (1956) Polarization in the Jet of Messier 87. ApJ 123:550–551. 10.1086/146194
- Baade and Minkowski (1954) Baade W, Minkowski R (1954) On the Identification of Radio Sources. ApJ 119:215. 10.1086/145813
- Barkov et al (2012) Barkov MV, Bosch-Ramon V, Aharonian FA (2012) Interpretation of the Flares of M87 at TeV Energies in the Cloud-Jet Interaction Scenario. ApJ 755(2):170. 10.1088/0004-637X/755/2/170, https://arxiv.org/abs/arXiv:1202.5907 [astro-ph.HE]
- Barniol Duran et al (2017) Barniol Duran R, Tchekhovskoy A, Giannios D (2017) Simulations of AGN jets: magnetic kink instability versus conical shocks. MNRAS 469(4):4957–4978. 10.1093/mnras/stx1165, https://arxiv.org/abs/arXiv:1612.06929 [astro-ph.HE]
- Begelman and Meier (1982) Begelman MC, Meier DL (1982) Thick accretion disks - Self-similar, supercritical models. ApJ 253:873–896. 10.1086/159688
- Beilicke and VERITAS Collaboration (2012) Beilicke M, VERITAS Collaboration (2012) VERITAS observations of M87 in 2011/2012. In: Aharonian FA, Hofmann W, Rieger FM (eds) High Energy Gamma-Ray Astronomy: 5th International Meeting on High Energy Gamma-Ray Astronomy, pp 586–589, 10.1063/1.4772328, 1210.7830
- Bicknell and Begelman (1996) Bicknell GV, Begelman MC (1996) Understanding the Kiloparsec-Scale Structure of M87. ApJ 467:597. 10.1086/177636
- Bird et al (2010) Bird S, Harris WE, Blakeslee JP, et al (2010) The inner halo of M 87: a first direct view of the red-giant population. A&A 524:A71. 10.1051/0004-6361/201014876, https://arxiv.org/abs/arXiv:1009.3202 [astro-ph.GA]
- Biretta et al (1983) Biretta JA, Owen FN, Hardee PE (1983) Observations of the M 87 jet at 15 GHz with 0”.12 resolution. ApJ 274:L27–L30. 10.1086/184144
- Biretta et al (1995) Biretta JA, Zhou F, Owen FN (1995) Detection of Proper Motions in the M87 Jet. ApJ 447:582. 10.1086/175901
- Biretta et al (1999) Biretta JA, Sparks WB, Macchetto F (1999) Hubble Space Telescope Observations of Superluminal Motion in the M87 Jet. ApJ 520(2):621–626. 10.1086/307499
- Blakeslee et al (2009) Blakeslee JP, Jordán A, Mei S, et al (2009) The ACS Fornax Cluster Survey. V. Measurement and Recalibration of Surface Brightness Fluctuations and a Precise Value of the Fornax-Virgo Relative Distance. ApJ 694(1):556–572. 10.1088/0004-637X/694/1/556, https://arxiv.org/abs/arXiv:0901.1138 [astro-ph.CO]
- Blandford (1999) Blandford R (1999) Introducing M 87. In: Röser HJ, Meisenheimer K (eds) The Radio Galaxy Messier 87, Lecture Notes in Physics, vol 530. Springer, Berlin, Heidelberg, pp 1–9, 10.1007/BFb0106413
- Blandford et al (2019) Blandford R, Meier D, Readhead A (2019) Relativistic Jets from Active Galactic Nuclei. ARA&A 57:467–509. 10.1146/annurev-astro-081817-051948, https://arxiv.org/abs/arXiv:1812.06025 [astro-ph.HE]
- Blandford (1990) Blandford RD (1990) Physical processes in active galactic nuclei. In: Blandford RD, Netzer H, Woltjer L, et al (eds) Active Galactic Nuclei, pp 161–275
- Blandford and Begelman (1999) Blandford RD, Begelman MC (1999) On the fate of gas accreting at a low rate on to a black hole. MNRAS 303(1):L1–L5. 10.1046/j.1365-8711.1999.02358.x, https://arxiv.org/abs/arXiv:astro-ph/9809083 [astro-ph]
- Blandford and Königl (1979) Blandford RD, Königl A (1979) Relativistic jets as compact radio sources. ApJ 232:34–48. 10.1086/157262
- Blandford and Payne (1982) Blandford RD, Payne DG (1982) Hydromagnetic flows from accretion disks and the production of radio jets. MNRAS 199:883–903. 10.1093/mnras/199.4.883
- Blandford and Rees (1978) Blandford RD, Rees MJ (1978) Extended and compact extragalactic radio sources: interpretation and theory. Phys. Scr 17:265–274. 10.1088/0031-8949/17/3/020
- Blandford and Znajek (1977) Blandford RD, Znajek RL (1977) Electromagnetic extraction of energy from Kerr black holes. MNRAS 179:433–456. 10.1093/mnras/179.3.433
- Boccardi et al (2017) Boccardi B, Krichbaum TP, Ros E, et al (2017) Radio observations of active galactic nuclei with mm-VLBI. A&A Rev. 25(1):4. 10.1007/s00159-017-0105-6, https://arxiv.org/abs/arXiv:1711.07548 [astro-ph.HE]
- Boccardi et al (2021) Boccardi B, Perucho M, Casadio C, et al (2021) Jet collimation in NGC 315 and other nearby AGN. A&A 647:A67. 10.1051/0004-6361/202039612, https://arxiv.org/abs/arXiv:2012.14831 [astro-ph.HE]
- Bolton et al (1949) Bolton JG, Stanley GJ, Slee OB (1949) Positions of Three Discrete Sources of Galactic Radio-Frequency Radiation. Nature 164(4159):101–102. 10.1038/164101b0
- Bondi (1952) Bondi H (1952) On spherically symmetrical accretion. MNRAS 112:195. 10.1093/mnras/112.2.195
- Bower et al (2003) Bower GC, Wright MCH, Falcke H, et al (2003) Interferometric Detection of Linear Polarization from Sagittarius A* at 230 GHz. ApJ 588(1):331–337. 10.1086/373989, https://arxiv.org/abs/arXiv:astro-ph/0302227 [astro-ph]
- Britzen et al (2017) Britzen S, Fendt C, Eckart A, et al (2017) A new view on the M 87 jet origin: Turbulent loading leading to large-scale episodic wiggling. A&A 601:A52. 10.1051/0004-6361/201629469
- Broderick et al (2015) Broderick AE, Narayan R, Kormendy J, et al (2015) The Event Horizon of M87. ApJ 805(2):179. 10.1088/0004-637X/805/2/179, https://arxiv.org/abs/arXiv:1503.03873 [astro-ph.HE]
- Bromberg and Tchekhovskoy (2016) Bromberg O, Tchekhovskoy A (2016) Relativistic MHD simulations of core-collapse GRB jets: 3D instabilities and magnetic dissipation. MNRAS 456(2):1739–1760. 10.1093/mnras/stv2591, https://arxiv.org/abs/arXiv:1508.02721 [astro-ph.HE]
- Burns et al (1991) Burns JO, Norman ML, Clarke DA (1991) Numerical Models of Extragalactic Radio Sources. Science 253(5019):522–530. 10.1126/science.253.5019.522
- Camenzind (1987) Camenzind M (1987) Hydromagnetic flows from rapidly rotating compact objects. II - The relativistic axisymmetric jet equilibrium. A&A 184(1-2):341–360
- Cantiello et al (2018) Cantiello M, Blakeslee JP, Ferrarese L, et al (2018) The Next Generation Virgo Cluster Survey (NGVS). XVIII. Measurement and Calibration of Surface Brightness Fluctuation Distances for Bright Galaxies in Virgo (and Beyond). ApJ 856(2):126. 10.3847/1538-4357/aab043, https://arxiv.org/abs/arXiv:1802.05526 [astro-ph.GA]
- Capetti et al (1997) Capetti A, Macchetto FD, Sparks WB, et al (1997) HST polarization observations of the jet of M87. A&A 317:637–645
- Chadwick et al (1999) Chadwick PM, Lyons K, McComb TJL, et al (1999) Very High Energy Gamma Rays from PKS 2155-304. ApJ 513(1):161–167. 10.1086/306862, https://arxiv.org/abs/arXiv:astro-ph/9810209 [astro-ph]
- Chael et al (2023) Chael A, Lupsasca A, Wong GN, et al (2023) Black Hole Polarimetry I. A Signature of Electromagnetic Energy Extraction. ApJ 958(1):65. 10.3847/1538-4357/acf92d, https://arxiv.org/abs/arXiv:2307.06372 [astro-ph.HE]
- Chang et al (2010) Chang CS, Ros E, Kovalev YY, et al (2010) VLBI detection of the HST-1 feature in the M 87 jet at 2 cm. A&A 515:A38. 10.1051/0004-6361/200913915, https://arxiv.org/abs/arXiv:1002.2588 [astro-ph.CO]
- Chen et al (2023a) Chen MT, Asada K, Matsushita S, et al (2023a) The Greenland Telescope-Construction, Commissioning, and Operations in Pituffik. PASP 135(1051):095001. 10.1088/1538-3873/acf072, https://arxiv.org/abs/arXiv:2307.10468 [astro-ph.IM]
- Chen et al (2023b) Chen Y, Gu Q, Fan J, et al (2023b) Jet power, intrinsic -ray luminosity, and accretion in jetted AGNs. MNRAS 519(4):6199–6209. 10.1093/mnras/stad065
- Chen et al (2011) Chen YJ, Zhao GY, Shen ZQ (2011) The core-like nature of HST-1 in the M87 jet. MNRAS 416(1):L109–L113. 10.1111/j.1745-3933.2011.01110.x, https://arxiv.org/abs/arXiv:1107.0769 [astro-ph.CO]
- Chen et al (2015) Chen YY, Zhang X, Xiong D, et al (2015) Black Hole Mass, Jet Power, and Accretion in AGNs. AJ 150(1):8. 10.1088/0004-6256/150/1/8, https://arxiv.org/abs/arXiv:1504.05413 [astro-ph.HE]
- Cherenkov Telescope Array Consortium et al (2019) Cherenkov Telescope Array Consortium, Acharya BS, Agudo I, et al (2019) Science with the Cherenkov Telescope Array. World Scientific, 10.1142/10986
- Cheung et al (2007) Cheung CC, Harris DE, Stawarz Ł (2007) Superluminal Radio Features in the M87 Jet and the Site of Flaring TeV Gamma-Ray Emission. ApJ 663(2):L65–L68. 10.1086/520510, https://arxiv.org/abs/arXiv:0705.2448 [astro-ph]
- Clarke et al (1986) Clarke DA, Norman ML, Burns JO (1986) Numerical Simulations of a Magnetically Confined Jet. ApJ 311:L63. 10.1086/184799
- Collin and Kawaguchi (2004) Collin S, Kawaguchi T (2004) Super-Eddington accretion rates in Narrow Line Seyfert 1 galaxies. A&A 426:797–808. 10.1051/0004-6361:20040528, https://arxiv.org/abs/arXiv:astro-ph/0407181 [astro-ph]
- Cui et al (2023) Cui Y, Hada K, Kawashima T, et al (2023) Precessing jet nozzle connecting to a spinning black hole in M87. Nature 621(7980):711–715. 10.1038/s41586-023-06479-6, https://arxiv.org/abs/arXiv:2310.09015 [astro-ph.HE]
- Curtis (1918) Curtis HD (1918) The Planetary Nebulae. Publications of Lick Observatory 13:55–74
- Daly (2019) Daly RA (2019) Black Hole Spin and Accretion Disk Magnetic Field Strength Estimates for More Than 750 Active Galactic Nuclei and Multiple Galactic Black Holes. ApJ 886(1):37. 10.3847/1538-4357/ab35e6, https://arxiv.org/abs/arXiv:1905.11319 [astro-ph.HE]
- Daly and Marscher (1988) Daly RA, Marscher AP (1988) The Gasdynamics of Compact Relativistic Jets. ApJ 334:539. 10.1086/166858
- de Gasperin et al (2012) de Gasperin F, Orrú E, Murgia M, et al (2012) M 87 at metre wavelengths: the LOFAR picture. A&A 547:A56. 10.1051/0004-6361/201220209, https://arxiv.org/abs/arXiv:1210.1346 [astro-ph.GA]
- de Vaucouleurs and Nieto (1979) de Vaucouleurs G, Nieto JL (1979) A photometric analysis of the jet in Messier 87. ApJ 231:364–371. 10.1086/157199
- Di Matteo et al (2003) Di Matteo T, Allen SW, Fabian AC, et al (2003) Accretion onto the Supermassive Black Hole in M87. ApJ 582(1):133–140. 10.1086/344504, https://arxiv.org/abs/arXiv:astro-ph/0202238 [astro-ph]
- Dodson et al (2006) Dodson R, Edwards PG, Hirabayashi H (2006) Milliarcsecond-Scale Spectral Properties and Jet Motions in M 87. PASJ 58:243–251. 10.1093/pasj/58.2.243, https://arxiv.org/abs/astro-ph/0511383
- Doeleman et al (2008) Doeleman SS, Weintroub J, Rogers AEE, et al (2008) Event-horizon-scale structure in the supermassive black hole candidate at the Galactic Centre. Nature 455(7209):78–80. 10.1038/nature07245, https://arxiv.org/abs/arXiv:0809.2442 [astro-ph]
- Doeleman et al (2012) Doeleman SS, Fish VL, Schenck DE, et al (2012) Jet-Launching Structure Resolved Near the Supermassive Black Hole in M87. Science 338(6105):355. 10.1126/science.1224768, https://arxiv.org/abs/arXiv:1210.6132 [astro-ph.HE]
- EHT MWL Science Working Group et al (2021) EHT MWL Science Working Group, Algaba JC, Anczarski J, et al (2021) Broadband Multi-wavelength Properties of M87 during the 2017 Event Horizon Telescope Campaign. ApJ 911(1):L11. 10.3847/2041-8213/abef71, https://arxiv.org/abs/arXiv:2104.06855 [astro-ph.HE]
- EHT MWL Science Working Group et al (2024) EHT MWL Science Working Group, The Event Horizon Telescope Collaboration, The Fermi Large Area Telescope Collaboration, et al (2024) Broadband Multi-wavelength Properties of M87 during the 2018 EHT Campaign including a Very High Energy Flaring Episode. arXiv e-prints arXiv:2404.17623. 10.48550/arXiv.2404.17623, https://arxiv.org/abs/arXiv:2404.17623 [astro-ph.HE]
- Esin et al (1997) Esin AA, McClintock JE, Narayan R (1997) Advection-Dominated Accretion and the Spectral States of Black Hole X-Ray Binaries: Application to Nova Muscae 1991. ApJ 489(2):865–889. 10.1086/304829, https://arxiv.org/abs/arXiv:astro-ph/9705237 [astro-ph]
- Event Horizon Telescope Collaboration (2023) Event Horizon Telescope Collaboration (2023) First M87 Event Horizon Telescope Results. IX. Detection of Near-horizon Circular Polarization. arXiv e-prints arXiv:2311.10976. https://arxiv.org/abs/arXiv:2311.10976 [astro-ph.HE]
- Event Horizon Telescope Collaboration (2024) Event Horizon Telescope Collaboration (2024) Mid-Range Science Objectives for the Event Horizon Telescope. arXiv e-prints arXiv:2410.02986. 10.48550/arXiv.2410.02986, https://arxiv.org/abs/arXiv:2410.02986 [astro-ph.HE]
- Event Horizon Telescope Collaboration et al (2019a) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019a) First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJ 875(1):L1. 10.3847/2041-8213/ab0ec7
- Event Horizon Telescope Collaboration et al (2019b) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019b) First M87 Event Horizon Telescope Results. II. Array and Instrumentation. ApJ 875(1):L2. 10.3847/2041-8213/ab0c96
- Event Horizon Telescope Collaboration et al (2019c) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019c) First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. ApJ 875(1):L3. 10.3847/2041-8213/ab0c57
- Event Horizon Telescope Collaboration et al (2019d) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019d) First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. ApJ 875(1):L4. 10.3847/2041-8213/ab0e85
- Event Horizon Telescope Collaboration et al (2019e) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019e) First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. ApJ 875(1):L5. 10.3847/2041-8213/ab0f43
- Event Horizon Telescope Collaboration et al (2019f) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2019f) First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. ApJ 875(1):L6. 10.3847/2041-8213/ab1141
- Event Horizon Telescope Collaboration et al (2021a) Event Horizon Telescope Collaboration, Akiyama K, Algaba JC, et al (2021a) First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. ApJ 910(1):L12. 10.3847/2041-8213/abe71d
- Event Horizon Telescope Collaboration et al (2021b) Event Horizon Telescope Collaboration, Akiyama K, Algaba JC, et al (2021b) First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. ApJ 910(1):L13. 10.3847/2041-8213/abe4de
- Event Horizon Telescope Collaboration et al (2022a) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022a) First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. ApJ 930(2):L12. 10.3847/2041-8213/ac6674
- Event Horizon Telescope Collaboration et al (2022b) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022b) First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. ApJ 930(2):L13. 10.3847/2041-8213/ac6675
- Event Horizon Telescope Collaboration et al (2022c) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022c) First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. ApJ 930(2):L14. 10.3847/2041-8213/ac6429
- Event Horizon Telescope Collaboration et al (2022d) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022d) First Sagittarius A* Event Horizon Telescope Results. IV. Variability, Morphology, and Black Hole Mass. ApJ 930(2):L15. 10.3847/2041-8213/ac6736
- Event Horizon Telescope Collaboration et al (2022e) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022e) First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. ApJ 930(2):L16. 10.3847/2041-8213/ac6672
- Event Horizon Telescope Collaboration et al (2022f) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2022f) First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. ApJ 930(2):L17. 10.3847/2041-8213/ac6756
- Event Horizon Telescope Collaboration et al (2024) Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, et al (2024) The persistent shadow of the supermassive black hole of M 87. I. Observations, calibration, imaging, and analysis. A&A 681:A79. 10.1051/0004-6361/202347932
- Fabian and Canizares (1988) Fabian AC, Canizares CR (1988) Do massive black holes reside in elliptical galaxies? Nature 333(6176):829–831. 10.1038/333829a0
- Fanaroff and Riley (1974) Fanaroff BL, Riley JM (1974) The morphology of extragalactic radio sources of high and low luminosity. MNRAS 167:31P–36P. 10.1093/mnras/167.1.31P
- Ford et al (1994) Ford HC, Harms RJ, Tsvetanov ZI, et al (1994) Narrowband HST Images of M87: Evidence for a Disk of Ionized Gas around a Massive Black Hole. ApJ 435:L27. 10.1086/187586
- Forman et al (2005) Forman W, Nulsen P, Heinz S, et al (2005) Reflections of Active Galactic Nucleus Outbursts in the Gaseous Atmosphere of M87. ApJ 635(2):894–906. 10.1086/429746, https://arxiv.org/abs/arXiv:astro-ph/0312576 [astro-ph]
- Fuentes et al (2023) Fuentes A, Gómez JL, Martí JM, et al (2023) Filamentary structures as the origin of blazar jet radio variability. Nature Astronomy 7:1359–1367. 10.1038/s41550-023-02105-7, https://arxiv.org/abs/arXiv:2311.01861 [astro-ph.HE]
- Gaidos et al (1996) Gaidos JA, Akerlof CW, Biller S, et al (1996) Extremely rapid bursts of TeV photons from the active galaxy Markarian 421. Nature 383(6598):319–320. 10.1038/383319a0
- Gebhardt et al (2011) Gebhardt K, Adams J, Richstone D, et al (2011) The Black Hole Mass in M87 from Gemini/NIFS Adaptive Optics Observations. ApJ 729(2):119. 10.1088/0004-637X/729/2/119, https://arxiv.org/abs/arXiv:1101.1954 [astro-ph.CO]
- Georganopoulos et al (2005) Georganopoulos M, Perlman ES, Kazanas D (2005) Is the Core of M87 the Source of Its TeV Emission? Implications for Unified Schemes. ApJ 634(1):L33–L36. 10.1086/498714, https://arxiv.org/abs/arXiv:astro-ph/0510783 [astro-ph]
- Ghisellini et al (2005) Ghisellini G, Tavecchio F, Chiaberge M (2005) Structured jets in TeV BL Lac objects and radiogalaxies. Implications for the observed properties. A&A 432(2):401–410. 10.1051/0004-6361:20041404, https://arxiv.org/abs/arXiv:astro-ph/0406093 [astro-ph]
- Ghisellini et al (2010) Ghisellini G, Tavecchio F, Foschini L, et al (2010) General physical properties of bright Fermi blazars. MNRAS 402(1):497–518. 10.1111/j.1365-2966.2009.15898.x, https://arxiv.org/abs/arXiv:0909.0932 [astro-ph.CO]
- Ghisellini et al (2014) Ghisellini G, Tavecchio F, Maraschi L, et al (2014) The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 515(7527):376–378. 10.1038/nature13856, https://arxiv.org/abs/arXiv:1411.5368 [astro-ph.HE]
- Giroletti et al (2012) Giroletti M, Hada K, Giovannini G, et al (2012) The kinematic of HST-1 in the jet of M 87. A&A 538:L10. 10.1051/0004-6361/201218794, https://arxiv.org/abs/arXiv:1202.0013 [astro-ph.CO]
- Goddi et al (2021) Goddi C, Martí-Vidal I, Messias H, et al (2021) Polarimetric Properties of Event Horizon Telescope Targets from ALMA. ApJ 910(1):L14. 10.3847/2041-8213/abee6a, https://arxiv.org/abs/arXiv:2105.02272 [astro-ph.GA]
- Hada (2017) Hada K (2017) The Structure and Propagation of the Misaligned Jet M87. Galaxies 5(1):2. 10.3390/galaxies5010002
- Hada et al (2011) Hada K, Doi A, Kino M, et al (2011) An origin of the radio jet in M87 at the location of the central black hole. Nature 477(7363):185–187. 10.1038/nature10387
- Hada et al (2012) Hada K, Kino M, Nagai H, et al (2012) VLBI Observations of the Jet in M 87 during the Very High Energy -Ray Flare in 2010 April. ApJ 760(1):52. 10.1088/0004-637X/760/1/52, https://arxiv.org/abs/arXiv:1210.4942 [astro-ph.HE]
- Hada et al (2013) Hada K, Kino M, Doi A, et al (2013) The Innermost Collimation Structure of the M87 Jet Down to ~10 Schwarzschild Radii. ApJ 775(1):70. 10.1088/0004-637X/775/1/70, https://arxiv.org/abs/arXiv:1308.1411 [astro-ph.CO]
- Hada et al (2014a) Hada K, Giroletti M, Giovannini G, et al (2014a) Continuing EVN monitoring of HST-1 in the jet of M87. In: Proceedings of the 12th European VLBI Network Symposium and Users Meeting (EVN 2014). 7-10 October 2014. Cagliari, p 18, 10.22323/1.230.0018, 1504.01808
- Hada et al (2014b) Hada K, Giroletti M, Kino M, et al (2014b) A Strong Radio Brightening at the Jet Base of M 87 during the Elevated Very High Energy Gamma-Ray State in 2012. ApJ 788(2):165. 10.1088/0004-637X/788/2/165, https://arxiv.org/abs/arXiv:1405.1082 [astro-ph.HE]
- Hada et al (2016) Hada K, Kino M, Doi A, et al (2016) High-sensitivity 86 GHz (3.5 mm) VLBI Observations of M87: Deep Imaging of the Jet Base at a Resolution of 10 Schwarzschild Radii. ApJ 817(2):131. 10.3847/0004-637X/817/2/131, https://arxiv.org/abs/arXiv:1512.03783 [astro-ph.HE]
- Hada et al (2017) Hada K, Park JH, Kino M, et al (2017) Pilot KaVA monitoring on the M87 jet: confirming the inner jet structure and superluminal motions at sub-pc scales. PASJ 69:71. https://arxiv.org/abs/1706.02066 [astro-ph.HE]
- Hada et al (2018) Hada K, Doi A, Wajima K, et al (2018) Collimation, Acceleration, and Recollimation Shock in the Jet of Gamma-Ray Emitting Radio-loud Narrow-line Seyfert 1 Galaxy 1H0323+342. ApJ 860(2):141. 10.3847/1538-4357/aac49f, https://arxiv.org/abs/arXiv:1805.08299 [astro-ph.HE]
- Hakobyan et al (2023) Hakobyan H, Ripperda B, Philippov AA (2023) Radiative Reconnection-powered TeV Flares from the Black Hole Magnetosphere in M87. ApJ 943(2):L29. 10.3847/2041-8213/acb264, https://arxiv.org/abs/arXiv:2209.02105 [astro-ph.HE]
- Hardee and Eilek (2011) Hardee PE, Eilek JA (2011) Using Twisted Filaments to Model the Inner Jet in M 87. ApJ 735(1):61. 10.1088/0004-637X/735/1/61, https://arxiv.org/abs/arXiv:1104.4480 [astro-ph.CO]
- Harms et al (1994) Harms RJ, Ford HC, Tsvetanov ZI, et al (1994) HST FOS Spectroscopy of M87: Evidence for a Disk of Ionized Gas around a Massive Black Hole. ApJ 435:L35. 10.1086/187588
- Harris and Krawczynski (2006) Harris DE, Krawczynski H (2006) X-Ray Emission from Extragalactic Jets. ARA&A 44(1):463–506. 10.1146/annurev.astro.44.051905.092446, https://arxiv.org/abs/arXiv:astro-ph/0607228 [astro-ph]
- Harris et al (2003) Harris DE, Biretta JA, Junor W, et al (2003) Flaring X-Ray Emission from HST-1, a Knot in the M87 Jet. ApJ 586(1):L41–L44. 10.1086/374773, https://arxiv.org/abs/arXiv:astro-ph/0302270 [astro-ph]
- Harris et al (2006) Harris DE, Cheung CC, Biretta JA, et al (2006) The Outburst of HST-1 in the M87 Jet. ApJ 640(1):211–218. 10.1086/500081, https://arxiv.org/abs/arXiv:astro-ph/0511755 [astro-ph]
- Harris et al (2008) Harris DE, Cheung CC, Stawarz L, et al (2008) The Continuing Saga of the Explosive Event(s) in the M87 Jet: Is M87 a Blazar? In: Rector TA, De Young DS (eds) Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, p 80, 0707.3124
- Harris et al (2009) Harris DE, Cheung CC, Stawarz Ł, et al (2009) Variability Timescales in the M87 Jet: Signatures of E 2 Losses, Discovery of a Quasi Period in HST-1, and the Site of TeV Flaring. ApJ 699(1):305–314. 10.1088/0004-637X/699/1/305, https://arxiv.org/abs/arXiv:0904.3925 [astro-ph.CO]
- Hartman et al (1999) Hartman RC, Bertsch DL, Bloom SD, et al (1999) The Third EGRET Catalog of High-Energy Gamma-Ray Sources. ApJS 123(1):79–202. 10.1086/313231
- H.E.S.S. Collaboration et al (2023) H.E.S.S. Collaboration, Aharonian F, Ait Benkhali F, et al (2023) Constraining the cosmic-ray pressure in the inner Virgo Cluster using H.E.S.S. observations of M 87. A&A 675:A138. 10.1051/0004-6361/202346056, https://arxiv.org/abs/arXiv:2305.09607 [astro-ph.HE]
- H.E.S.S. Collaboration et al (2024) H.E.S.S. Collaboration, Aharonian F, Ait Benkhali F, et al (2024) Curvature in the very-high energy gamma-ray spectrum of M87. arXiv e-prints arXiv:2402.13330. 10.48550/arXiv.2402.13330, https://arxiv.org/abs/arXiv:2402.13330 [astro-ph.HE]
- Ho (2002) Ho LC (2002) On the Relationship between Radio Emission and Black Hole Mass in Galactic Nuclei. ApJ 564(1):120–132. 10.1086/324399, https://arxiv.org/abs/arXiv:astro-ph/0110440 [astro-ph]
- Ho (2009) Ho LC (2009) Radiatively Inefficient Accretion in Nearby Galaxies. ApJ 699(1):626–637. 10.1088/0004-637X/699/1/626, https://arxiv.org/abs/arXiv:0906.4104 [astro-ph.GA]
- Igumenshchev et al (2003) Igumenshchev IV, Narayan R, Abramowicz MA (2003) Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. ApJ 592(2):1042–1059. 10.1086/375769, https://arxiv.org/abs/arXiv:astro-ph/0301402 [astro-ph]
- Issaoun et al (2022) Issaoun S, Wielgus M, Jorstad S, et al (2022) Resolving the Inner Parsec of the Blazar J1924-2914 with the Event Horizon Telescope. ApJ 934(2):145. 10.3847/1538-4357/ac7a40, https://arxiv.org/abs/arXiv:2208.01662 [astro-ph.HE]
- Janssen et al (2021) Janssen M, Falcke H, Kadler M, et al (2021) Event Horizon Telescope observations of the jet launching and collimation in Centaurus A. Nature Astronomy 5:1017–1028. 10.1038/s41550-021-01417-w, https://arxiv.org/abs/arXiv:2111.03356 [astro-ph.GA]
- Jeter and Broderick (2021) Jeter B, Broderick AE (2021) Reconciling EHT and Gas-dynamics Measurements in M87: Is the Jet Misaligned at Parsec Scales? ApJ 908(2):139. 10.3847/1538-4357/abda3d, https://arxiv.org/abs/arXiv:2010.11303 [astro-ph.GA]
- Jeter et al (2019) Jeter B, Broderick AE, McNamara BR (2019) Impact of Accretion Flow Dynamics on Gas-dynamical Black Hole Mass Estimates. ApJ 882(2):82. 10.3847/1538-4357/ab3221, https://arxiv.org/abs/arXiv:1810.05238 [astro-ph.HE]
- Jiang et al (2021) Jiang W, Shen Z, Martí-Vidal I, et al (2021) Millimeter-VLBI Observations of Low-luminosity Active Galactic Nuclei with Source-frequency Phase Referencing. ApJ 922(1):L16. 10.3847/2041-8213/ac375c, https://arxiv.org/abs/arXiv:2111.08930 [astro-ph.GA]
- Johannsen and Psaltis (2010) Johannsen T, Psaltis D (2010) Testing the No-hair Theorem with Observations in the Electromagnetic Spectrum. II. Black Hole Images. ApJ 718(1):446–454. 10.1088/0004-637X/718/1/446, https://arxiv.org/abs/arXiv:1005.1931 [astro-ph.HE]
- Johnson et al (2020) Johnson MD, Lupsasca A, Strominger A, et al (2020) Universal interferometric signatures of a black hole’s photon ring. Science Advances 6(12):eaaz1310. 10.1126/sciadv.aaz1310, https://arxiv.org/abs/arXiv:1907.04329 [astro-ph.IM]
- Jorstad et al (2023) Jorstad S, Wielgus M, Lico R, et al (2023) The Event Horizon Telescope Image of the Quasar NRAO 530. ApJ 943(2):170. 10.3847/1538-4357/acaea8, https://arxiv.org/abs/arXiv:2302.04622 [astro-ph.HE]
- Junor and Biretta (1995) Junor W, Biretta JA (1995) The Radio Jet in 3C274 at 0.01 PC Resolution. AJ 109:500. 10.1086/117295
- Junor et al (1999) Junor W, Biretta JA, Livio M (1999) Formation of the radio jet in M87 at 100 Schwarzschild radii from the central black hole. Nature 401(6756):891–892. 10.1038/44780
- Junor et al (2001) Junor W, Biretta JA, Wardle JFC (2001) VLBA lambda lambda 6, 4 cm polarimetry of Vir A. In: Schilizzi RT (ed) Galaxies and their Constituents at the Highest Angular Resolutions, p 136
- Kataoka and Stawarz (2005) Kataoka J, Stawarz Ł (2005) X-Ray Emission Properties of Large-Scale Jets, Hot Spots, and Lobes in Active Galactic Nuclei. ApJ 622(2):797–810. 10.1086/428083, https://arxiv.org/abs/arXiv:astro-ph/0411042 [astro-ph]
- Kataoka et al (2008) Kataoka J, Madejski G, Sikora M, et al (2008) Multiwavelength Observations of the Powerful Gamma-Ray Quasar PKS 1510-089: Clues on the Jet Composition. ApJ 672(2):787–799. 10.1086/523093, https://arxiv.org/abs/arXiv:0709.1528 [astro-ph]
- Katsoulakos and Rieger (2018) Katsoulakos G, Rieger FM (2018) Magnetospheric Gamma-Ray Emission in Active Galactic Nuclei. ApJ 852(2):112. 10.3847/1538-4357/aaa003, https://arxiv.org/abs/arXiv:1712.04203 [astro-ph.HE]
- Kawaguchi (2003) Kawaguchi T (2003) Comptonization in Super-Eddington Accretion Flow and Growth Timescale of Supermassive Black Holes. ApJ 593(1):69–84. 10.1086/376404, https://arxiv.org/abs/arXiv:astro-ph/0304373 [astro-ph]
- Kawakatu et al (2016) Kawakatu N, Kino M, Takahara F (2016) Evidence for a significant mixture of electron/positron pairs in FRII jets constrained by cocoon dynamics. MNRAS 457(1):1124–1136. 10.1093/mnras/stw010, https://arxiv.org/abs/arXiv:1601.00771 [astro-ph.HE]
- Kellermann and Pauliny-Toth (1969) Kellermann KI, Pauliny-Toth IIK (1969) The Spectra of Opaque Radio Sources. ApJ 155:L71. 10.1086/180305
- Kellermann et al (1989) Kellermann KI, Sramek R, Schmidt M, et al (1989) VLA Observations of Objects in the Palomar Bright Quasar Survey. AJ 98:1195. 10.1086/115207
- Kerr (1963) Kerr RP (1963) Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 11(5):237–238. 10.1103/PhysRevLett.11.237
- Kim et al (2018a) Kim JY, Krichbaum TP, Lu RS, et al (2018a) The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. A&A 616:A188. 10.1051/0004-6361/201832921, https://arxiv.org/abs/arXiv:1805.02478 [astro-ph.GA]
- Kim et al (2018b) Kim JY, Krichbaum TP, Lu RS, et al (2018b) The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. A&A 616:A188. 10.1051/0004-6361/201832921, https://arxiv.org/abs/arXiv:1805.02478 [astro-ph.GA]
- Kim et al (2020) Kim JY, Krichbaum TP, Broderick AE, et al (2020) Event Horizon Telescope imaging of the archetypal blazar 3C 279 at an extreme 20 microarcsecond resolution. A&A 640:A69. 10.1051/0004-6361/202037493
- Kim et al (2023) Kim JY, Savolainen T, Voitsik P, et al (2023) RadioAstron Space VLBI Imaging of the Jet in M87. I. Detection of High Brightness Temperature at 22 GHz. ApJ 952(1):34. 10.3847/1538-4357/accf17, https://arxiv.org/abs/arXiv:2304.09816 [astro-ph.GA]
- Kimura and Toma (2020) Kimura SS, Toma K (2020) Hadronic High-energy Emission from Magnetically Arrested Disks in Radio Galaxies. ApJ 905(2):178. 10.3847/1538-4357/abc343, https://arxiv.org/abs/arXiv:2003.13173 [astro-ph.HE]
- Kino et al (2012) Kino M, Kawakatu N, Takahara F (2012) Calorimetry of Active Galactic Nucleus Jets: Testing Plasma Composition in Cygnus A. ApJ 751(2):101. 10.1088/0004-637X/751/2/101, https://arxiv.org/abs/arXiv:1204.3363 [astro-ph.HE]
- Kino et al (2014) Kino M, Takahara F, Hada K, et al (2014) Relativistic Electrons and Magnetic Fields of the M87 Jet on the ~10 Schwarzschild Radii Scale. ApJ 786(1):5. 10.1088/0004-637X/786/1/5, https://arxiv.org/abs/arXiv:1403.0650 [astro-ph.HE]
- Kino et al (2015) Kino M, Takahara F, Hada K, et al (2015) Magnetization Degree at the Jet Base of M87 Derived from the Event Horizon Telescope Data: Testing the Magnetically Driven Jet Paradigm. ApJ 803(1):30. 10.1088/0004-637X/803/1/30, https://arxiv.org/abs/arXiv:1502.03900 [astro-ph.HE]
- Kino et al (2022) Kino M, Takahashi M, Kawashima T, et al (2022) Implications from the Velocity Profile of the M87 Jet: A Possibility of a Slowly Rotating Black Hole Magnetosphere. ApJ 939(2):83. 10.3847/1538-4357/ac8c2f, https://arxiv.org/abs/arXiv:2209.07264 [astro-ph.HE]
- Kisaka et al (2022) Kisaka S, Levinson A, Toma K, et al (2022) The Response of Black Hole Spark Gaps to External Changes: A Production Mechanism of Rapid TeV Flares? ApJ 924(1):28. 10.3847/1538-4357/ac35da, https://arxiv.org/abs/arXiv:2108.02971 [astro-ph.HE]
- Komissarov (2001) Komissarov SS (2001) Direct numerical simulations of the Blandford-Znajek effect. MNRAS 326(3):L41–L44. 10.1046/j.1365-8711.2001.04863.x
- Komissarov et al (2007) Komissarov SS, Barkov MV, Vlahakis N, et al (2007) Magnetic acceleration of relativistic active galactic nucleus jets. MNRAS 380(1):51–70. 10.1111/j.1365-2966.2007.12050.x, https://arxiv.org/abs/arXiv:astro-ph/0703146 [astro-ph]
- Komossa et al (2006) Komossa S, Voges W, Xu D, et al (2006) Radio-loud Narrow-Line Type 1 Quasars. AJ 132(2):531–545. 10.1086/505043, https://arxiv.org/abs/arXiv:astro-ph/0603680 [astro-ph]
- Konigl (1981) Konigl A (1981) Relativistic jets as X-ray and gamma-ray sources. ApJ 243:700–709. 10.1086/158638
- Kormendy and Ho (2013) Kormendy J, Ho LC (2013) Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. ARA&A 51(1):511–653. 10.1146/annurev-astro-082708-101811, https://arxiv.org/abs/arXiv:1304.7762 [astro-ph.CO]
- Kovalev et al (2007) Kovalev YY, Lister ML, Homan DC, et al (2007) The Inner Jet of the Radio Galaxy M87. ApJ 668(1):L27–L30. 10.1086/522603, https://arxiv.org/abs/arXiv:0708.2695 [astro-ph]
- Kovalev et al (2020) Kovalev YY, Pushkarev AB, Nokhrina EE, et al (2020) A transition from parabolic to conical shape as a common effect in nearby AGN jets. MNRAS 495(4):3576–3591. 10.1093/mnras/staa1121, https://arxiv.org/abs/arXiv:1907.01485 [astro-ph.GA]
- Kravchenko et al (2020) Kravchenko E, Giroletti M, Hada K, et al (2020) Linear polarization in the nucleus of M87 at 7 mm and 1.3 cm. A&A 637:L6. 10.1051/0004-6361/201937315, https://arxiv.org/abs/arXiv:2006.07059 [astro-ph.GA]
- Kuo et al (2014) Kuo CY, Asada K, Rao R, et al (2014) Measuring Mass Accretion Rate onto the Supermassive Black Hole in M87 Using Faraday Rotation Measure with the Submillimeter Array. ApJ 783(2):L33. 10.1088/2041-8205/783/2/L33, https://arxiv.org/abs/arXiv:1402.5238 [astro-ph.GA]
- Laor (2000) Laor A (2000) On Black Hole Masses and Radio Loudness in Active Galactic Nuclei. ApJ 543(2):L111–L114. 10.1086/317280, https://arxiv.org/abs/arXiv:astro-ph/0009192 [astro-ph]
- Levinson and Rieger (2011) Levinson A, Rieger F (2011) Variable TeV Emission as a Manifestation of Jet Formation in M87? ApJ 730(2):123. 10.1088/0004-637X/730/2/123, https://arxiv.org/abs/arXiv:1011.5319 [astro-ph.HE]
- Li (2022) Li X (2022) Molecular Line Search in Archival ALMA Imaging of M87. Macalester Journal of Physics and Astronomy 10(1):5
- Li et al (1992) Li ZY, Chiueh T, Begelman MC (1992) Electromagnetically Driven Relativistic Jets: A Class of Self-similar Solutions. ApJ 394:459. 10.1086/171597
- Liepold et al (2023) Liepold ER, Ma CP, Walsh JL (2023) Keck Integral-field Spectroscopy of M87 Reveals an Intrinsically Triaxial Galaxy and a Revised Black Hole Mass. ApJ 945(2):L35. 10.3847/2041-8213/acbbcf, https://arxiv.org/abs/arXiv:2302.07884 [astro-ph.GA]
- Lobanov et al (2003) Lobanov A, Hardee P, Eilek J (2003) Internal structure and dynamics of the kiloparsec-scale jet in M87. New A Rev. 47(6-7):629–632. 10.1016/S1387-6473(03)00109-X
- Lobanov (1998) Lobanov AP (1998) Ultracompact jets in active galactic nuclei. A&A 330:79–89. 10.48550/arXiv.astro-ph/9712132, https://arxiv.org/abs/arXiv:astro-ph/9712132 [astro-ph]
- Lu et al (2023) Lu RS, Asada K, Krichbaum TP, et al (2023) A ring-like accretion structure in M87 connecting its black hole and jet. Nature 616(7958):686–690. 10.1038/s41586-023-05843-w, https://arxiv.org/abs/arXiv:2304.13252 [astro-ph.HE]
- Ly et al (2004) Ly C, Walker RC, Wrobel JM (2004) An Attempt to Probe the Radio Jet Collimation Regions in NGC 4278, NGC 4374 (M84), and NGC 6166. AJ 127(1):119–124. 10.1086/379855, https://arxiv.org/abs/arXiv:astro-ph/0309743 [astro-ph]
- Ly et al (2007) Ly C, Walker RC, Junor W (2007) High-Frequency VLBI Imaging of the Jet Base of M87. ApJ 660(1):200–205. 10.1086/512846, https://arxiv.org/abs/arXiv:astro-ph/0701511 [astro-ph]
- Lynden-Bell (1969) Lynden-Bell D (1969) Galactic Nuclei as Collapsed Old Quasars. Nature 223(5207):690–694. 10.1038/223690a0
- Macchetto et al (1997) Macchetto F, Marconi A, Axon DJ, et al (1997) The Supermassive Black Hole of M87 and the Kinematics of Its Associated Gaseous Disk. ApJ 489(2):579–600. 10.1086/304823, https://arxiv.org/abs/arXiv:astro-ph/9706252 [astro-ph]
- MacDonald and Thorne (1982) MacDonald D, Thorne KS (1982) Black-hole electrodynamics - an absolute-space/universal-time formulation. MNRAS 198:345–382. 10.1093/mnras/198.2.345
- Madrid (2009) Madrid JP (2009) Hubble Space Telescope Observations of an Extraordinary Flare in the M87 Jet. AJ 137(4):3864–3868. 10.1088/0004-6256/137/4/3864, https://arxiv.org/abs/arXiv:0904.3546 [astro-ph.CO]
- MAGIC Collaboration et al (2020) MAGIC Collaboration, Acciari VA, Ansoldi S, et al (2020) Monitoring of the radio galaxy M 87 during a low-emission state from 2012 to 2015 with MAGIC. MNRAS 492(4):5354–5365. 10.1093/mnras/staa014, https://arxiv.org/abs/arXiv:2001.01643 [astro-ph.HE]
- Magorrian et al (1998) Magorrian J, Tremaine S, Richstone D, et al (1998) The Demography of Massive Dark Objects in Galaxy Centers. AJ 115(6):2285–2305. 10.1086/300353, https://arxiv.org/abs/arXiv:astro-ph/9708072 [astro-ph]
- Mahadevan (1997) Mahadevan R (1997) Scaling Laws for Advection-dominated Flows: Applications to Low-Luminosity Galactic Nuclei. ApJ 477(2):585–601. 10.1086/303727, https://arxiv.org/abs/arXiv:astro-ph/9609107 [astro-ph]
- Marrone et al (2006) Marrone DP, Moran JM, Zhao JH, et al (2006) Interferometric Measurements of Variable 340 GHz Linear Polarization in Sagittarius A*. ApJ 640(1):308–318. 10.1086/500106, https://arxiv.org/abs/arXiv:astro-ph/0511653 [astro-ph]
- Marrone et al (2007) Marrone DP, Moran JM, Zhao JH, et al (2007) An Unambiguous Detection of Faraday Rotation in Sagittarius A*. ApJ 654(1):L57–L60. 10.1086/510850, https://arxiv.org/abs/arXiv:astro-ph/0611791 [astro-ph]
- Marscher and Gear (1985) Marscher AP, Gear WK (1985) Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. ApJ 298:114–127. 10.1086/163592
- Marscher et al (2008) Marscher AP, Jorstad SG, D’Arcangelo FD, et al (2008) The inner jet of an active galactic nucleus as revealed by a radio-to--ray outburst. Nature 452(7190):966–969. 10.1038/nature06895
- Mathur et al (2012) Mathur S, Fields D, Peterson BM, et al (2012) Supermassive Black Holes, Pseudobulges, and the Narrow-line Seyfert 1 Galaxies. ApJ 754(2):146. 10.1088/0004-637X/754/2/146, https://arxiv.org/abs/arXiv:1102.0537 [astro-ph.CO]
- Mertens et al (2016) Mertens F, Lobanov AP, Walker RC, et al (2016) Kinematics of the jet in M 87 on scales of 100-1000 Schwarzschild radii. A&A 595:A54. 10.1051/0004-6361/201628829, https://arxiv.org/abs/arXiv:1608.05063 [astro-ph.HE]
- Meyer et al (2013) Meyer ET, Sparks WB, Biretta JA, et al (2013) Optical Proper Motion Measurements of the M87 Jet: New Results from the Hubble Space Telescope. ApJ 774(2):L21. 10.1088/2041-8205/774/2/L21, https://arxiv.org/abs/arXiv:1308.4633 [astro-ph.CO]
- Mills (1952) Mills BY (1952) Apparent Angular Sizes of Discrete Radio Sources: Observations at Sydney. Nature 170(4338):1063–1064. 10.1038/1701063a0
- Misner et al (1973) Misner CW, Thorne KS, Wheeler JA (1973) Gravitation
- Mizuno et al (2007) Mizuno Y, Hardee P, Nishikawa KI (2007) Three-dimensional Relativistic Magnetohydrodynamic Simulations of Magnetized Spine-Sheath Relativistic Jets. ApJ 662(2):835–850. 10.1086/518106, https://arxiv.org/abs/arXiv:astro-ph/0703190 [astro-ph]
- Molero et al (2023) Molero M, Batista P, Fortson L, et al (2023) Long-term monitoring of the radio-galaxy M87 in gamma-rays: joint analysis of MAGIC, VERITAS and Fermi-LAT data. arXiv e-prints arXiv:2309.14159. 10.48550/arXiv.2309.14159, https://arxiv.org/abs/arXiv:2309.14159 [astro-ph.HE]
- Nakahara et al (2018) Nakahara S, Doi A, Murata Y, et al (2018) Finding Transitions of Physical Condition in Jets from Observations over the Range of 103-109 Schwarzschild Radii in Radio Galaxy NGC 4261. ApJ 854(2):148. 10.3847/1538-4357/aaa45e
- Nakahara et al (2019) Nakahara S, Doi A, Murata Y, et al (2019) The Cygnus A Jet: Parabolic Streamlines up to Kiloparsec Scales. ApJ 878(1):61. 10.3847/1538-4357/ab1b0e
- Nakahara et al (2020) Nakahara S, Doi A, Murata Y, et al (2020) The Two-sided Jet Structures of NGC 1052 at Scales from 300 to 4 × 107 Schwarzschild Radii. AJ 159(1):14. 10.3847/1538-3881/ab465b, https://arxiv.org/abs/arXiv:1909.12510 [astro-ph.GA]
- Nakamura et al (1997) Nakamura KE, Kusunose M, Matsumoto R, et al (1997) Optically Thin, Advection-Dominated Two-Temperature Disks. PASJ 49:503–512. 10.1093/pasj/49.4.503
- Nakamura and Asada (2013) Nakamura M, Asada K (2013) The Parabolic Jet Structure in M87 as a Magnetohydrodynamic Nozzle. ApJ 775(2):118. 10.1088/0004-637X/775/2/118, https://arxiv.org/abs/arXiv:1308.1436 [astro-ph.HE]
- Nakamura and Meier (2004) Nakamura M, Meier DL (2004) Poynting Flux-dominated Jets in Decreasing-Density Atmospheres. I. The Nonrelativistic Current-driven Kink Instability and the Formation of “Wiggled” Structures. ApJ 617(1):123–154. 10.1086/425337, https://arxiv.org/abs/arXiv:astro-ph/0406405 [astro-ph]
- Nakamura and Meier (2014) Nakamura M, Meier DL (2014) A Magnetohydrodynamic Model of the M87 Jet. II. Self-consistent Quad-shock Jet Model for Optical Relativistic Motions and Particle Acceleration. ApJ 785(2):152. 10.1088/0004-637X/785/2/152, https://arxiv.org/abs/arXiv:1403.3477 [astro-ph.HE]
- Nakamura et al (2010) Nakamura M, Garofalo D, Meier DL (2010) A Magnetohydrodynamic Model of the M87 Jet. I. Superluminal Knot Ejections from HST-1 as Trails of Quad Relativistic MHD Shocks. ApJ 721(2):1783–1789. 10.1088/0004-637X/721/2/1783, https://arxiv.org/abs/arXiv:1008.3512 [astro-ph.HE]
- Nakamura et al (2018) Nakamura M, Asada K, Hada K, et al (2018) Parabolic Jets from the Spinning Black Hole in M87. ApJ 868(2):146. 10.3847/1538-4357/aaeb2d, https://arxiv.org/abs/arXiv:1810.09963 [astro-ph.HE]
- Narayan and Fabian (2011) Narayan R, Fabian AC (2011) Bondi flow from a slowly rotating hot atmosphere. MNRAS 415(4):3721–3730. 10.1111/j.1365-2966.2011.18987.x, https://arxiv.org/abs/arXiv:1105.0594 [astro-ph.CO]
- Narayan and McClintock (2008) Narayan R, McClintock JE (2008) Advection-dominated accretion and the black hole event horizon. New A Rev. 51(10-12):733–751. 10.1016/j.newar.2008.03.002, https://arxiv.org/abs/arXiv:0803.0322 [astro-ph]
- Narayan and Yi (1995) Narayan R, Yi I (1995) Advection-dominated Accretion: Underfed Black Holes and Neutron Stars. ApJ 452:710. 10.1086/176343, https://arxiv.org/abs/arXiv:astro-ph/9411059 [astro-ph]
- Narayan et al (2003) Narayan R, Igumenshchev IV, Abramowicz MA (2003) Magnetically Arrested Disk: an Energetically Efficient Accretion Flow. PASJ 55:L69–L72. 10.1093/pasj/55.6.L69, https://arxiv.org/abs/arXiv:astro-ph/0305029 [astro-ph]
- Narayan et al (2007) Narayan R, McKinney JC, Farmer AJ (2007) Self-similar force-free wind from an accretion disc. MNRAS 375(2):548–566. 10.1111/j.1365-2966.2006.11272.x, https://arxiv.org/abs/arXiv:astro-ph/0610817 [astro-ph]
- Narayan et al (2012) Narayan R, SÄ dowski A, Penna RF, et al (2012) GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: role of outflows. MNRAS 426(4):3241–3259. 10.1111/j.1365-2966.2012.22002.x, https://arxiv.org/abs/arXiv:1206.1213 [astro-ph.HE]
- Neronov and Aharonian (2007) Neronov A, Aharonian FA (2007) Production of TeV Gamma Radiation in the Vicinity of the Supermassive Black Hole in the Giant Radio Galaxy M87. ApJ 671(1):85–96. 10.1086/522199, https://arxiv.org/abs/arXiv:0704.3282 [astro-ph]
- Nikonov et al (2023) Nikonov AS, Kovalev YY, Kravchenko EV, et al (2023) Properties of the jet in M87 revealed by its helical structure imaged with the VLBA at 8 and 15 GHz. MNRAS 526(4):5949–5963. 10.1093/mnras/stad3061, https://arxiv.org/abs/arXiv:2307.11660 [astro-ph.GA]
- Novikov and Thorne (1973) Novikov ID, Thorne KS (1973) Astrophysics of black holes. In: Black Holes (Les Astres Occlus), pp 343–450
- Ogihara et al (2019) Ogihara T, Takahashi K, Toma K (2019) A Mechanism for the Triple-ridge Emission Structure of AGN Jets. ApJ 877(1):19. 10.3847/1538-4357/ab1909, https://arxiv.org/abs/arXiv:1904.07243 [astro-ph.HE]
- Okino et al (2022) Okino H, Akiyama K, Asada K, et al (2022) Collimation of the Relativistic Jet in the Quasar 3C 273. ApJ 940(1):65. 10.3847/1538-4357/ac97e5, https://arxiv.org/abs/arXiv:2112.12233 [astro-ph.HE]
- Owen et al (1980) Owen FN, Hardee PE, Bignell RC (1980) VLA observations of the M87 jet at 6 and 2 centimeters. ApJ 239:L11–L15. 10.1086/183282
- Owen et al (1989) Owen FN, Hardee PE, Cornwell TJ (1989) High-Resolution, High Dynamic Range VLA Images of the M87 Jet at 2 Centimeters. ApJ 340:698. 10.1086/167430
- Owen et al (1990) Owen FN, Eilek JA, Keel WC (1990) Detection of Large Faraday Rotation in the Inner 2 Kiloparsecs of M87. ApJ 362:449. 10.1086/169282
- Owen et al (2000) Owen FN, Eilek JA, Kassim NE (2000) M87 at 90 Centimeters: A Different Picture. ApJ 543(2):611–619. 10.1086/317151, https://arxiv.org/abs/arXiv:astro-ph/0006150 [astro-ph]
- Palumbo et al (2020) Palumbo DCM, Wong GN, Prather BS (2020) Discriminating Accretion States via Rotational Symmetry in Simulated Polarimetric Images of M87. ApJ 894(2):156. 10.3847/1538-4357/ab86ac, https://arxiv.org/abs/arXiv:2004.01751 [astro-ph.HE]
- Pang et al (2011) Pang B, Pen UL, Matzner CD, et al (2011) Numerical parameter survey of non-radiative black hole accretion: flow structure and variability of the rotation measure. MNRAS 415(2):1228–1239. 10.1111/j.1365-2966.2011.18748.x, https://arxiv.org/abs/arXiv:1011.5498 [astro-ph.GA]
- Paraschos et al (2024) Paraschos GF, Kim JY, Wielgus M, et al (2024) Ordered magnetic fields around the 3C 84 central black hole. A&A 682:L3. 10.1051/0004-6361/202348308, https://arxiv.org/abs/arXiv:2402.00927 [astro-ph.HE]
- Park et al (2019a) Park J, Hada K, Kino M, et al (2019a) Kinematics of the M87 Jet in the Collimation Zone: Gradual Acceleration and Velocity Stratification. ApJ 887(2):147. 10.3847/1538-4357/ab5584, https://arxiv.org/abs/arXiv:1911.02279 [astro-ph.HE]
- Park et al (2019b) Park J, Hada K, Kino M, et al (2019b) Faraday Rotation in the Jet of M87 inside the Bondi Radius: Indication of Winds from Hot Accretion Flows Confining the Relativistic Jet. ApJ 871(2):257. 10.3847/1538-4357/aaf9a9, https://arxiv.org/abs/arXiv:1812.08386 [astro-ph.HE]
- Park et al (2021a) Park J, Asada K, Nakamura M, et al (2021a) A Revised View of the Linear Polarization in the Subparsec Core of M87 at 7 mm. ApJ 922(2):180. 10.3847/1538-4357/ac26bf, https://arxiv.org/abs/arXiv:2107.13243 [astro-ph.HE]
- Park et al (2021b) Park J, Hada K, Nakamura M, et al (2021b) Jet Collimation and Acceleration in the Giant Radio Galaxy NGC 315. ApJ 909(1):76. 10.3847/1538-4357/abd6ee, https://arxiv.org/abs/arXiv:2012.14154 [astro-ph.HE]
- Pasetto et al (2021) Pasetto A, Carrasco-González C, Gómez JL, et al (2021) Reading M87’s DNA: A Double Helix Revealing a Large-scale Helical Magnetic Field. ApJ 923(1):L5. 10.3847/2041-8213/ac3a88, https://arxiv.org/abs/arXiv:2112.06971 [astro-ph.GA]
- Penna (2015) Penna RF (2015) Black hole jet power from impedance matching. Phys. Rev. D 92(8):084017. 10.1103/PhysRevD.92.084017, https://arxiv.org/abs/arXiv:1504.00360 [astro-ph.HE]
- Penna et al (2013) Penna RF, Narayan R, Sądowski A (2013) General relativistic magnetohydrodynamic simulations of Blandford-Znajek jets and the membrane paradigm. MNRAS 436(4):3741–3758. 10.1093/mnras/stt1860, https://arxiv.org/abs/arXiv:1307.4752 [astro-ph.HE]
- Perlman and Wilson (2005) Perlman ES, Wilson AS (2005) The X-Ray Emissions from the M87 Jet: Diagnostics and Physical Interpretation. ApJ 627(1):140–155. 10.1086/430340, https://arxiv.org/abs/arXiv:astro-ph/0503024 [astro-ph]
- Perlman et al (1999) Perlman ES, Biretta JA, Zhou F, et al (1999) Optical and Radio Polarimetry of the M87 Jet at 0.2” Resolution. AJ 117(5):2185–2198. 10.1086/300844, https://arxiv.org/abs/arXiv:astro-ph/9901176 [astro-ph]
- Perlman et al (2011) Perlman ES, Adams SC, Cara M, et al (2011) Optical Polarization and Spectral Variability in the M87 Jet. ApJ 743(2):119. 10.1088/0004-637X/743/2/119, https://arxiv.org/abs/arXiv:1109.6252 [astro-ph.HE]
- Prieto et al (2016) Prieto MA, Fernández-Ontiveros JA, Markoff S, et al (2016) The central parsecs of M87: jet emission and an elusive accretion disc. MNRAS 457(4):3801–3816. 10.1093/mnras/stw166, https://arxiv.org/abs/arXiv:1508.02302 [astro-ph.GA]
- Quataert and Gruzinov (1999) Quataert E, Gruzinov A (1999) Turbulence and Particle Heating in Advection-dominated Accretion Flows. ApJ 520(1):248–255. 10.1086/307423, https://arxiv.org/abs/arXiv:astro-ph/9803112 [astro-ph]
- Rafferty et al (2006) Rafferty DA, McNamara BR, Nulsen PEJ, et al (2006) The Feedback-regulated Growth of Black Holes and Bulges through Gas Accretion and Starbursts in Cluster Central Dominant Galaxies. ApJ 652(1):216–231. 10.1086/507672, https://arxiv.org/abs/arXiv:astro-ph/0605323 [astro-ph]
- Rawlings and Saunders (1991) Rawlings S, Saunders R (1991) Evidence for a common central-engine mechanism in all extragalactic radio sources. Nature 349(6305):138–140. 10.1038/349138a0
- Rees (1978) Rees MJ (1978) The M87 jet: internal shocks in a plasma beam? MNRAS 184:61P–65P. 10.1093/mnras/184.1.61P
- Rees (1984) Rees MJ (1984) Black Hole Models for Active Galactic Nuclei. ARA&A 22:471–506. 10.1146/annurev.aa.22.090184.002351
- Reid et al (1982) Reid MJ, Schmitt JHMM, Owen FN, et al (1982) VLBI observations of the nucleus and jet of M 87. ApJ 263:615–623. 10.1086/160533
- Reid et al (1989) Reid MJ, Biretta JA, Junor W, et al (1989) Subluminal Motion and Limb Brightening in the Nuclear Jet of M87. ApJ 336:112. 10.1086/166998
- Reimer et al (2004) Reimer A, Protheroe RJ, Donea AC (2004) M 87 as a misaligned synchrotron-proton blazar. A&A 419:89–98. 10.1051/0004-6361:20034231
- Reynolds et al (1996) Reynolds CS, Fabian AC, Celotti A, et al (1996) The matter content of the jet in M87: evidence for an electron-positron jet. MNRAS 283(3):873–880. 10.1093/mnras/283.3.873, https://arxiv.org/abs/arXiv:astro-ph/9603140 [astro-ph]
- Rieger and Aharonian (2012) Rieger FM, Aharonian F (2012) Probing the Central Black Hole in M87 with Gamma-Rays. Modern Physics Letters A 27(28):1230030. 10.1142/S0217732312300303, https://arxiv.org/abs/arXiv:1208.2702 [astro-ph.HE]
- Ripperda et al (2022) Ripperda B, Liska M, Chatterjee K, et al (2022) Black Hole Flares: Ejection of Accreted Magnetic Flux through 3D Plasmoid-mediated Reconnection. ApJ 924(2):L32. 10.3847/2041-8213/ac46a1, https://arxiv.org/abs/arXiv:2109.15115 [astro-ph.HE]
- Ro et al (2023a) Ro H, Kino M, Sohn BW, et al (2023a) Spectral analysis of a parsec-scale jet in M 87: Observational constraint on the magnetic field strengths in the jet. A&A 673:A159. 10.1051/0004-6361/202142988, https://arxiv.org/abs/arXiv:2303.01014 [astro-ph.HE]
- Ro et al (2023b) Ro H, Yi K, Cui Y, et al (2023b) Transverse Oscillations of the M87 Jet Revealed by KaVA Observations. Galaxies 11(1):33. 10.3390/galaxies11010033, https://arxiv.org/abs/arXiv:2303.01106 [astro-ph.HE]
- Russell et al (2013) Russell HR, McNamara BR, Edge AC, et al (2013) Radiative efficiency, variability and Bondi accretion on to massive black holes: the transition from radio AGN to quasars in brightest cluster galaxies. MNRAS 432(1):530–553. 10.1093/mnras/stt490, https://arxiv.org/abs/arXiv:1211.5604 [astro-ph.CO]
- Russell et al (2018) Russell HR, Fabian AC, McNamara BR, et al (2018) The imprints of AGN feedback within a supermassive black hole’s sphere of influence. MNRAS 477(3):3583–3599. 10.1093/mnras/sty835, https://arxiv.org/abs/arXiv:1803.09769 [astro-ph.GA]
- Schwarzschild (1916) Schwarzschild K (1916) On the Gravitational Field of a Mass Point According to Einstein’s Theory. Abh K Preuss Akad Wiss 1916:189–196
- Shakura and Sunyaev (1973) Shakura NI, Sunyaev RA (1973) Black holes in binary systems. Observational appearance. A&A 24:337–355
- Shaw et al (2012) Shaw MS, Romani RW, Cotter G, et al (2012) Spectroscopy of Broad-line Blazars from 1LAC. ApJ 748(1):49. 10.1088/0004-637X/748/1/49, https://arxiv.org/abs/arXiv:1201.0999 [astro-ph.HE]
- Sikora and Madejski (2000) Sikora M, Madejski G (2000) On Pair Content and Variability of Subparsec Jets in Quasars. ApJ 534(1):109–113. 10.1086/308756, https://arxiv.org/abs/arXiv:astro-ph/9912335 [astro-ph]
- Sikora et al (2007) Sikora M, Stawarz Ł, Lasota JP (2007) Radio Loudness of Active Galactic Nuclei: Observational Facts and Theoretical Implications. ApJ 658(2):815–828. 10.1086/511972, https://arxiv.org/abs/arXiv:astro-ph/0604095 [astro-ph]
- Sikora et al (2020) Sikora M, Nalewajko K, Madejski GM (2020) On the significance of relativistically hot pairs in the jets of FR II radio galaxies. MNRAS 499(3):3749–3754. 10.1093/mnras/staa3128, https://arxiv.org/abs/arXiv:2004.03606 [astro-ph.HE]
- Simionescu et al (2018) Simionescu A, Tremblay G, Werner N, et al (2018) ALMA observation of the disruption of molecular gas in M87. MNRAS 475(3):3004–3009. 10.1093/mnras/sty047, https://arxiv.org/abs/arXiv:1801.01264 [astro-ph.GA]
- Simon et al (2024) Simon DA, Cappellari M, Hartke J (2024) Supermassive black hole mass in the massive elliptical galaxy M87 from integral-field stellar dynamics using OASIS and MUSE with adaptive optics: assessing systematic uncertainties. MNRAS 527(2):2341–2361. 10.1093/mnras/stad3309, https://arxiv.org/abs/arXiv:2303.18229 [astro-ph.GA]
- Sądowski et al (2013) Sądowski A, Narayan R, Penna R, et al (2013) Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. MNRAS 436(4):3856–3874. 10.1093/mnras/stt1881, https://arxiv.org/abs/arXiv:1307.1143 [astro-ph.HE]
- Snios et al (2019) Snios B, Nulsen PEJ, Kraft RP, et al (2019) Detection of Superluminal Motion in the X-Ray Jet of M87. ApJ 879(1):8. 10.3847/1538-4357/ab2119, https://arxiv.org/abs/arXiv:1905.04330 [astro-ph.HE]
- Sob’yanin (2017) Sob’yanin DN (2017) Jet in jet in M87. MNRAS 471(4):4121–4127. 10.1093/mnras/stx1767, https://arxiv.org/abs/arXiv:1708.08270 [astro-ph.HE]
- Sparks et al (1996) Sparks WB, Biretta JA, Macchetto F (1996) The Jet of M87 at Tenth-Arcsecond Resolution: Optical, Ultraviolet, and Radio Observations. ApJ 473:254. 10.1086/178141
- Stawarz et al (2006) Stawarz Ł, Aharonian F, Kataoka J, et al (2006) Dynamics and high-energy emission of the flaring HST-1 knot in the M 87 jet. MNRAS 370(2):981–992. 10.1111/j.1365-2966.2006.10525.x, https://arxiv.org/abs/arXiv:astro-ph/0602220 [astro-ph]
- Takahashi et al (2018) Takahashi K, Toma K, Kino M, et al (2018) Fast-spinning Black Holes Inferred from Symmetrically Limb-brightened Radio Jets. ApJ 868(2):82. 10.3847/1538-4357/aae832, https://arxiv.org/abs/arXiv:1802.00292 [astro-ph.HE]
- Takahashi (2004) Takahashi R (2004) Shapes and Positions of Black Hole Shadows in Accretion Disks and Spin Parameters of Black Holes. ApJ 611(2):996–1004. 10.1086/422403, https://arxiv.org/abs/arXiv:astro-ph/0405099 [astro-ph]
- Tan et al (2008) Tan JC, Beuther H, Walter F, et al (2008) A Search for Molecular Gas in the Nucleus of M87 and Implications for the Fueling of Supermassive Black Holes. ApJ 689(2):775–781. 10.1086/592592, https://arxiv.org/abs/arXiv:astro-ph/0610488 [astro-ph]
- Tazaki et al (2023) Tazaki F, Cui Y, Hada K, et al (2023) Super-Resolved Image of M87 Observed with East Asian VLBI Network. Galaxies 11(2):39. 10.3390/galaxies11020039, https://arxiv.org/abs/arXiv:2303.01048 [astro-ph.HE]
- Tchekhovskoy et al (2008) Tchekhovskoy A, McKinney JC, Narayan R (2008) Simulations of ultrarelativistic magnetodynamic jets from gamma-ray burst engines. MNRAS 388(2):551–572. 10.1111/j.1365-2966.2008.13425.x, https://arxiv.org/abs/arXiv:0803.3807 [astro-ph]
- Tchekhovskoy et al (2009) Tchekhovskoy A, McKinney JC, Narayan R (2009) Efficiency of Magnetic to Kinetic Energy Conversion in a Monopole Magnetosphere. ApJ 699(2):1789–1808. 10.1088/0004-637X/699/2/1789, https://arxiv.org/abs/arXiv:0901.4776 [astro-ph.HE]
- Tchekhovskoy et al (2010) Tchekhovskoy A, Narayan R, McKinney JC (2010) Black Hole Spin and The Radio Loud/Quiet Dichotomy of Active Galactic Nuclei. ApJ 711(1):50–63. 10.1088/0004-637X/711/1/50, https://arxiv.org/abs/arXiv:0911.2228 [astro-ph.HE]
- Tchekhovskoy et al (2011) Tchekhovskoy A, Narayan R, McKinney JC (2011) Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. MNRAS 418(1):L79–L83. 10.1111/j.1745-3933.2011.01147.x, https://arxiv.org/abs/arXiv:1108.0412 [astro-ph.HE]
- Tseng et al (2016) Tseng CY, Asada K, Nakamura M, et al (2016) Structural Transition in the NGC 6251 Jet: an Interplay with the Supermassive Black Hole and Its Host Galaxy. ApJ 833(2):288. 10.3847/1538-4357/833/2/288, https://arxiv.org/abs/arXiv:1610.06351 [astro-ph.HE]
- Ureña Mena et al (2022) Ureña Mena F, Hawc, Abeysekara AU, et al (2022) Modeling the non-flaring VHE emission from M87 as detected by the HAWC gamma ray observatory. In: 37th International Cosmic Ray Conference, p 841, 10.22323/1.395.0841, 2108.01048
- Urry and Padovani (1995) Urry CM, Padovani P (1995) Unified Schemes for Radio-Loud Active Galactic Nuclei. PASP 107:803. 10.1086/133630, https://arxiv.org/abs/arXiv:astro-ph/9506063 [astro-ph]
- Walker et al (2016) Walker RC, Hardee PE, Davies F, et al (2016) Observations of the Structure and Dynamics of the Inner M87 Jet. Galaxies 4(4):46. 10.3390/galaxies4040046, https://arxiv.org/abs/arXiv:1610.08600 [astro-ph.HE]
- Walker et al (2018) Walker RC, Hardee PE, Davies FB, et al (2018) The Structure and Dynamics of the Subparsec Jet in M87 Based on 50 VLBA Observations over 17 Years at 43 GHz. ApJ 855:128. 10.3847/1538-4357/aaafcc, https://arxiv.org/abs/arXiv:1802.06166 [astro-ph.HE]
- Walsh et al (2013) Walsh JL, Barth AJ, Ho LC, et al (2013) The M87 Black Hole Mass from Gas-dynamical Models of Space Telescope Imaging Spectrograph Observations. ApJ 770(2):86. 10.1088/0004-637X/770/2/86, https://arxiv.org/abs/arXiv:1304.7273 [astro-ph.CO]
- Wardle et al (1998) Wardle JFC, Homan DC, Ojha R, et al (1998) Electron-positron jets associated with the quasar 3C279. Nature 395(6701):457–461. 10.1038/26675
- Woo and Urry (2002) Woo JH, Urry CM (2002) The Independence of Active Galactic Nucleus Black Hole Mass and Radio Loudness. ApJ 581(1):L5–L7. 10.1086/345944, https://arxiv.org/abs/arXiv:astro-ph/0211118 [astro-ph]
- Wu et al (2002) Wu XB, Liu FK, Zhang TZ (2002) Supermassive black hole masses of AGNs with elliptical hosts. A&A 389:742–751. 10.1051/0004-6361:20020577, https://arxiv.org/abs/arXiv:astro-ph/0203158 [astro-ph]
- Xiao et al (2022) Xiao H, Ouyang Z, Zhang L, et al (2022) The Relativistic Jet and Central Engine of Fermi Blazars. ApJ 925(1):40. 10.3847/1538-4357/ac36da, https://arxiv.org/abs/arXiv:2111.02082 [astro-ph.HE]
- Xu et al (2009) Xu YD, Cao X, Wu Q (2009) On the BL Lacertae Objects/Radio Quasars and the FR I/II Dichotomy. ApJ 694(2):L107–L110. 10.1088/0004-637X/694/2/L107, https://arxiv.org/abs/arXiv:0902.2426 [astro-ph.GA]
- Young et al (2002) Young AJ, Wilson AS, Mundell CG (2002) Chandra Imaging of the X-Ray Core of the Virgo Cluster. ApJ 579(2):560–570. 10.1086/342918, https://arxiv.org/abs/arXiv:astro-ph/0202504 [astro-ph]
- Yuan and Narayan (2014) Yuan F, Narayan R (2014) Hot Accretion Flows Around Black Holes. ARA&A 52:529–588. 10.1146/annurev-astro-082812-141003, https://arxiv.org/abs/arXiv:1401.0586 [astro-ph.HE]
- Yuan et al (2015) Yuan F, Gan Z, Narayan R, et al (2015) Numerical Simulation of Hot Accretion Flows. III. Revisiting Wind Properties Using the Trajectory Approach. ApJ 804(2):101. 10.1088/0004-637X/804/2/101, https://arxiv.org/abs/arXiv:1501.01197 [astro-ph.HE]
- Yuan et al (2022) Yuan F, Wang H, Yang H (2022) The Accretion Flow in M87 is Really MAD. ApJ 924(2):124. 10.3847/1538-4357/ac4714, https://arxiv.org/abs/arXiv:2201.00512 [astro-ph.HE]
- Yuan et al (2008) Yuan W, Zhou HY, Komossa S, et al (2008) A Population of Radio-Loud Narrow-Line Seyfert 1 Galaxies with Blazar-Like Properties? ApJ 685(2):801–827. 10.1086/591046, https://arxiv.org/abs/arXiv:0806.3755 [astro-ph]
- Zamaninasab et al (2014) Zamaninasab M, Clausen-Brown E, Savolainen T, et al (2014) Dynamically important magnetic fields near accreting supermassive black holes. Nature 510(7503):126–128. 10.1038/nature13399
- Zavala and Taylor (2002) Zavala RT, Taylor GB (2002) Faraday Rotation Measures in the Parsec-Scale Jets of the Radio Galaxies M87, 3C 111, and 3C 120. ApJ 566(1):L9–L12. 10.1086/339441, https://arxiv.org/abs/arXiv:astro-ph/0201458 [astro-ph]
- Zhang et al (2019) Zhang S, Santangelo A, Feroci M, et al (2019) The enhanced X-ray Timing and Polarimetry mission—eXTP. Sci China Phys Mech Astron 62(2):29502. 10.1007/s11433-018-9309-2, https://arxiv.org/abs/arXiv:1812.04020 [astro-ph.IM]