Low-rank Tensor Learning with
Nonconvex Overlapped Nuclear Norm Regularization

\nameQuanming Yao \email[email protected]
\addrDepartment of Electronic Engineering, Tsinghua University \AND\nameYaqing Wang \email[email protected]
\addrBaidu Research \AND\nameBo Han \email[email protected]
\addrDepartment of Computer Science, Hong Kong Baptist University \ANDJames T. Kwok \email[email protected]
\addrDepartment of Computer Science and Engineering, Hong Kong University of Science and Technology Corresponding Author.

Abstract

Nonconvex regularization has been popularly used in low-rank matrix learning. However, extending it for low-rank tensor learning is still computationally expensive. To address this problem, we develop an efficient solver for use with a nonconvex extension of the overlapped nuclear norm regularizer. Based on the proximal average algorithm, the proposed algorithm can avoid expensive tensor folding/unfolding operations. A special “sparse plus low-rank” structure is maintained throughout the iterations, and allows fast computation of the individual proximal steps. Empirical convergence is further improved with the use of adaptive momentum. We provide convergence guarantees to critical points on smooth losses and also on objectives satisfying the Kurdyka-Łojasiewicz condition. While the optimization problem is nonconvex and nonsmooth, we show that its critical points still have good statistical performance on the tensor completion problem. Experiments on various synthetic and real-world data sets show that the proposed algorithm is efficient in both time and space and more accurate than the existing state-of-the-art.

Keywords: Low-rank tensor, Proximal algorithm, Proximal average algorithm, Nonconvex regularization, Overlapped nuclear norm.

1 Introduction

Tensors can be seen as high-order matrices and are widely used for describing multilinear relationships in the data. They have been popularly applied in areas such as computer vision, data mining and machine learning (Kolda and Bader, 2009; Zhao et al., 2016; Song et al., 2017; Papalexakis et al., 2017; Hong et al., 2020; Janzamin et al., 2020). For example, color images (Liu et al., 2013), hyper-spectral images (Signoretto et al., 2011; He et al., 2019), and knowledge graphs (Nickel et al., 2015; Lacroix et al., 2018) can be naturally represented as third-order tensors, while color videos can be seen as 4-order tensors (Candès et al., 2011; Bengua et al., 2017). In YouTube, users can follow each other and belong to the same subscribed channels. By treating channel as the third dimension, the users’ co-subscription network can also be represented as a third-order tensor (Lei et al., 2009).

In many applications, only a few entries in the tensor are observed. For example, each YouTube user usually only interacts with a few other users (Lei et al., 2009; Davis et al., 2011), and in knowledge graphs, we can only have a few labeled edges describing the relations between entities (Nickel et al., 2015; Lacroix et al., 2018). Tensor completion, which aims at filling in this partially observed tensor, has attracted a lot of recent interest (Rendle and Schmidt-Thieme, 2010; Signoretto et al., 2011; Bahadori et al., 2014; Cichocki et al., 2015).

In the related task of matrix completion, the underlying matrix is often assumed to be low-rank (Candès and Recht, 2009), as its rows/columns share similar characteristics. The nuclear norm, which is the tightest convex envelope of the matrix rank (Boyd and Vandenberghe, 2009), is popularly used as its surrogate in low-rank matrix completion (Cai et al., 2010; Mazumder et al., 2010). In tensor completion, the low-rank assumption also captures relatedness in the different tensor dimensions (Tomioka et al., 2010; Acar et al., 2011; Song et al., 2017; Hong et al., 2020). However, tensors are more complicated than matrices. Indeed, even the computation of tensor rank is NP-hard (Hillar and Lim, 2013). In recent years, many convex relaxations based on the matrix nuclear norm have been proposed for tensors. Examples include the tensor trace norm (Cheng et al., 2016), overlapped nuclear norm (Tomioka et al., 2010; Gandy et al., 2011), and latent nuclear norm (Tomioka et al., 2010). Among these convex relaxations, the overlapped nuclear norm is the most popular as it (i) can be evaluated exactly by performing SVD on the unfolded matrices (Cheng et al., 2016), (ii) has better low-rank approximation (Tomioka et al., 2010), and (iii) can lead to exact recovery (Tomioka et al., 2011; Tomioka and Suzuki, 2013; Mu et al., 2014).

The (overlapped) nuclear norm equally penalizes all singular values. Intuitively, larger singular values are more informative and should be less penalized (Mazumder et al., 2010; Lu et al., 2016b; Yao et al., 2019b). To alleviate this problem in low-rank matrix learning, various adaptive nonconvex regularizers have been recently introduced. Examples include the capped- $\ell_{1}$ norm (Zhang, 2010b), log-sum-penalty (LSP) (Candès et al., 2008), truncated nuclear norm (TNN) (Hu et al., 2013), smoothed-capped-absolute-deviation (SCAD) (Fan and Li, 2001) and minimax concave penalty (MCP) (Zhang, 2010a). All these assign smaller penalties to the larger singular values. This leads to better recovery performance in many applications such as image recovery (Lu et al., 2016b; Gu et al., 2017) and collaborative filtering (Yao et al., 2019b), and lower statistical errors of various matrix completion and regression problems (Gui et al., 2016; Mazumder et al., 2020).

Motivated by the success of adaptive nonconvex regularizers in low-rank matrix learning, there are recent works that apply nonconvex regularization in learning low-rank tensors. For example, the TNN regularizer is used with the overlapped nuclear norm regularizer on video processing (Xue et al., 2018) and traffic data processing (Chen et al., 2020). In this paper, we propose a general nonconvex variant of the overlapped nuclear norm regularizer for low-rank tensor completion. Unlike the standard convex tensor completion problem, the resulting optimization problem is nonconvex and more difficult to solve. Previous algorithms in (Xue et al., 2018; Chen et al., 2020) are computationally expensive, and have neither convergence results nor statistical guarantees.

To solve this issue, based on the proximal average algorithm (Bauschke et al., 2008), we develop an efficient solver with much smaller time and space complexities. The keys to its success are on (i) avoiding expensive tensor folding/unfolding, (ii) maintaining a “sparse plus low-rank” structure on the iterates, and (iii) incorporating the adaptive momentum (Li and Lin, 2015; Li et al., 2017; Yao et al., 2017). Convergence guarantees to critical points are provided under the usual smoothness assumption for the loss and further Kurdyka-Łojasiewicz (Attouch et al., 2013) condition on the whole learning objective.

Besides, we study its statistical guarantees, and show that critical points of the proposed objective can have small statistical errors under the restricted strong convexity condition (Agarwal et al., 2010). Informally, for tensor completion with unknown noise, we show that the recovery error can be bounded as $\|\mathscr{X}^{*}-\tilde{\mathscr{X}}\|_{F}\leq\mathcal{O}(\lambda\kappa_{0}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}})$ (see Theorem 16), where $\mathcal{O}$ omits constant terms, $\mathscr{X}^{*}$ (resp. $\tilde{\mathscr{X}}$ ) is the ground-truth (resp. recovered) tensor, $M$ is the tensor order and $k_{i}$ is the rank of unfolding matrix on the $i$ th mode. When Gaussian additive noise is assumed, we show that the recovery error also depends linearly with the noise level $\sigma$ (see Corollary 17) and $\sqrt{\log I^{\pi}/\left\|\bf{\Omega}\right\|_{1}}$ where $I^{\pi}$ is the tensor size and $\left\|\bf{\Omega}\right\|_{1}$ is the number of observed elements (see Corollary 18).

We further extend it for use with Laplacian regularizer as in spatial-temporal analysis and non-smooth losses as in robust tensor completion. Experiments on a variety of synthetic and real-world data sets (including images, videos, hyper-spectral images, social networks, knowledge graphs and spatial-temporal climate observation records) show that the proposed algorithm is more efficient and has much better empirical performance than other low-rank tensor regularization and decomposition methods.

Difference with the Conference Version

A preliminary conference version of this work (Yao et al., 2019a) was published in ICML-2019. The main differences with this conference version are as follows.

1).

Only third-order tensor and square loss are considered in (Yao et al., 2019a), while the proposed algorithm here, which is enabled by Proposition 4, can work on tensors with arbitrary orders. The difficulties of extending to higher order tensors are also discussed after Proposition 4.
2).

Statistical guarantee of the proposed model for the tensor completion problem is added in Section 3.5, which shows that tensors that are not too spiky can be recovered. We also show how the recovery performance can depend on noise level, tensor ranks, and the number of observations.
3).

In Section 4, we enable the proposed method work with robust loss function (which is nonconvex and nonsmooth) and Laplacian regularizer. These enable the proposed algorithm to be applied to a wider range of application scenarios such as knowledge graph completion, spatial-temporal analysis and robust video recovery.
4).

Extensive experiments are added. Specifically, quality of the obtained critical points is studied in Section 5.1.3; application to knowledge graphs in Section 5.3, application to robust video completion in Section 5.4, and application to spatial-temporal data in Section 5.5.

Notation

Vectors are denoted by lowercase boldface, matrices by uppercase boldface, and tensors by Euler.

For a matrix ${\bm{\bm{A}}}\in\mathbb{R}^{m\times n}$ (without loss of generality, we assume that $m\geq n$ ), $\sigma_{i}({\bm{\bm{A}}})$ denotes its $i$ th singular, its nuclear norm is $\|{\bm{\bm{A}}}\|_{*}=\sum_{i}\sigma_{i}$ ; $\|{\bm{\bm{A}}}\|_{\infty}$ returns its maximum singular.

For tensors, we follow the notation in (Kolda and Bader, 2009). For a $M$ -order tensor $\mathscr{X}\in\mathbb{R}^{I^{1}\times\dots\times I^{M}}$ (without loss of generality, we assume $I^{1}\geq\dots\geq I^{M}$ ), its $(i_{1},\dots,i_{M})$ th entry is $\mathscr{X}_{i_{1}\dots i_{M}}$ . One can unfold $\mathscr{X}$ along its $d$ th mode to obtain the matrix ${\bm{\bm{X}}}_{\left\langle d\right\rangle}\in\mathbb{R}^{I^{d}\times(\frac{I^{\pi}}{I^{d}})}$ with $I^{\pi}=\prod_{i=1}^{M}I^{i}$ , whose $(i_{d},j)$ entry is $\mathscr{X}_{i_{1}\dots i_{M}}$ with $j=1+\sum_{l=1,l\neq d}^{M}(i_{l}-1)\prod_{m=1,m\neq d}^{l-1}I^{m}$ . One can also fold a matrix ${\bm{\bm{X}}}$ back to a tensor $\mathscr{X}={\bm{\bm{X}}}^{{\left\langle d\right\rangle}}$ , with $\mathscr{X}_{i_{1}\dots i_{M}}={\bm{\bm{X}}}_{i_{d}j}$ , and $j$ as defined above. A slice in a tensor $\mathscr{X}$ is a matrix $\bm{x}$ obtained by fixing all but two $\mathscr{X}$ ’s indices. The inner product of two $M$ -order tensors $\mathscr{X}$ and $\mathscr{Y}$ is ${\left\langle\mathscr{X},\mathscr{Y}\right\rangle}=\sum_{i_{1}=1}^{I^{1}}...\sum_{i_{M}=1}^{I^{M}}\mathscr{X}_{i_{1}...i_{M}}\mathscr{Y}_{i_{1}...i_{M}}$ , the Frobenius norm is $\|\mathscr{X}\|_{F}=\sqrt{\langle\mathscr{X},\mathscr{X}\rangle}$ , $\|\mathscr{X}\|_{\max}$ returns the value of the element in $\mathscr{X}$ with the maximum absolute value.

For a proper and lower-semi-continuous function $f$ , $\partial f$ denotes its Frechet subdifferential (Attouch et al., 2013).

Finally, $P_{{\bm{\bm{\Omega}}}}\left(\cdot\right)$ is the observer operator, i.e., given a binary tensor ${\bm{\bm{\Omega}}}\in\{0,1\}^{I_{1}\times...\times I_{M}}$ and an arbitrary tensor $\mathscr{X}\in\mathbb{R}^{I_{1}\times...\times I_{M}}$ , $[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}\right)]_{i_{1}...i_{M}}=\mathscr{X}_{i_{1}...i_{M}}$ if ${\bm{\bm{\Omega}}}_{i_{1}...i_{M}}=1$ and $[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}\right)]_{i_{1}...i_{M}}=0$ otherwise.

2 Related Works

2.1 Low-Rank Matrix Learning

Learning of a low-rank matrix ${\bm{\bm{X}}}\in\mathbb{R}^{m\times n}$ can be formulated as the following optimization problem:

\displaystyle\min\nolimits_{{\bm{\bm{X}}}}f({\bm{\bm{X}}})+\lambda r({\bm{\bm{X}}}),

(1)

where $r$ is a low-rank regularizer, $\lambda\geq 0$ is a hyperparameter, and $f$ is a loss function that is $\rho$ -Lipschitz smooth¹¹1In other words, $\|\nabla f({\bm{\bm{X}}})-\nabla f({\bm{\bm{Y}}})\|_{F}\leq\rho\left\|{\bm{\bm{X}}}-{\bm{\bm{Y}}}\right\|_{F}$ for any ${\bm{\bm{X}}},{\bm{\bm{Y}}}$ .. Existing methods for low-rank matrix learning generally fall into three types: (i) nuclear norm minimization; (ii) nonconvex regularization; and (iii) matrix factorization.

2.1.1 Nuclear Norm Minimization

A common choice for $r$ is the nuclear norm regularizer. Using the proximal algorithm (Parikh and Boyd, 2013) on (1), the iterate at iteration $t$ is given by ${\bm{\bm{X}}}_{t+1}=\text{prox}_{\frac{\lambda}{\tau}\|\cdot\|_{*}}(\bm{Z}_{t})$ , where

\bm{Z}_{t}={\bm{\bm{X}}}_{t}-\frac{1}{\tau}\nabla f({\bm{\bm{X}}}_{t}).

(2)

Here, $\tau>\rho$ controls the stepsize ( $1/\tau$ ), and

\displaystyle\text{prox}_{\frac{\lambda}{\tau}\left\|\cdot\right\|_{*}}(\bm{Z})=\arg\min\nolimits_{{\bm{\bm{X}}}}\frac{1}{2}\left\|{\bm{\bm{X}}}-\bm{Z}\right\|_{F}^{2}+\frac{\lambda}{\tau}\left\|{\bm{\bm{X}}}\right\|_{*}

(3)

is the proximal step. The following Lemma shows that $\text{prox}_{\frac{\lambda}{\tau}\left\|\cdot\right\|_{*}}(\bm{Z})$ can be obtained by shrinking the singular values of $\bm{Z}$ , which encourages ${\bm{\bm{X}}}_{t}$ to be low-rank.

Lemma 1

(Cai et al., 2010) $\text{prox}_{\lambda\left\|\cdot\right\|_{*}}(\bm{Z})=\bm{U}(\bm{\Sigma}-\lambda\bm{I})_{+}\bm{V}^{\top}$ , where $\bm{U}\bm{\Sigma}\bm{V}^{\top}$ is the SVD of $\bm{Z}$ , and $\left[({\bm{\bm{X}}})_{+}\right]_{ij}=\max({\bm{\bm{X}}}_{ij},0)$ .

A special class of low-rank matrix learning problems is matrix completion, which attempts to find a low-rank matrix that agrees with the observations in data $\bm{O}$ :

\displaystyle\min\nolimits_{{\bm{\bm{X}}}}\frac{1}{2}\left\|P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}-\bm{O}\right)\right\|_{F}^{2}+\lambda\left\|{\bm{\bm{X}}}\right\|_{*}.

(4)

Here, positions of the observed elements in $\bm{O}$ are indicated by $1$ ’s in the binary matrix ${\bm{\bm{\Omega}}}$ . Setting $f({\bm{\bm{X}}})=\frac{1}{2}\left\|P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}-\bm{O}\right)\right\|_{F}^{2}$ in (1), ${\bm{\bm{Z}}}_{t}$ in (2) becomes:

\displaystyle{\bm{\bm{Z}}}_{t}={\bm{\bm{X}}}_{t}-\frac{1}{\tau}P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}_{t}-{\bm{\bm{O}}}\right).

(5)

Note that ${\bm{\bm{X}}}_{t}$ is low-rank and $\frac{1}{\tau}P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}_{t}-{\bm{\bm{O}}}\right)$ is sparse. ${\bm{\bm{Z}}}_{t}$ thus has a “sparse plus low-rank” structure. This allows the SVD computation in Lemma 1 to be much more efficient (Mazumder et al., 2010). Specifically, on using the power method to compute ${\bm{\bm{Z}}}_{t}$ ’s SVD, most effort is spent on multiplications of the forms ${\bm{\bm{Z}}}_{t}\bm{b}$ and $\bm{a}^{\top}{\bm{\bm{Z}}}_{t}$ (where $\bm{a}\in\mathbb{R}^{n}$ and $\bm{b}\in\mathbb{R}^{m}$ ). Let ${\bm{\bm{X}}}_{t}$ in (5) be low-rank factorized as $\bm{U}_{t}\bm{V}_{t}^{\top}$ , where $\bm{U}_{t}\in\mathbb{R}^{m\times k_{t}}$ and $\bm{V}_{t}\in\mathbb{R}^{n\times k_{t}}$ with rank $k_{t}$ . Computing

\displaystyle{\bm{\bm{Z}}}_{t}\bm{b}=\bm{U}_{t}\left(\bm{V}_{t}^{\top}\bm{b}\right)-\frac{1}{\tau}P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{Y}}}_{t}-\bm{O}\right)\bm{b}

(6)

takes $O((m+n)k_{t}+\|{\bm{\bm{\Omega}}}\|_{1})$ time. Usually, $k_{t}\ll n$ and $\|{\bm{\bm{\Omega}}}\|_{1}\ll mn$ . Thus, this is much faster than directly multiplying ${\bm{\bm{Z}}}_{t}$ and $\bm{b}$ , which takes $O(mn)$ time. The same holds for computing $\bm{a}^{\top}{\bm{\bm{Z}}}_{t}$ . The proximal step in (3) takes a total of $O((m+n)k_{t}k_{t+1}+\|{\bm{\bm{\Omega}}}\|_{1}k_{t+1})$ time, while a direct computation without utilizing the “sparse plus low-rank” structure takes $O(mnk_{t+1})$ time. Besides, as only $P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}_{t}\right)$ and the factorized form of ${\bm{\bm{X}}}_{t}$ need to be kept, the space complexity is reduced from $O(mn)$ to $O((m+n)k_{t}+\|{\bm{\bm{\Omega}}}\|_{1})$ .

2.1.2 Nonconvex Low-Rank Regularizer

Instead of using a convex $r$ in (1), the following nonconvex regularizer has been commonly used (Gui et al., 2016; Lu et al., 2016b; Gu et al., 2017; Yao et al., 2019b):

\displaystyle\phi({\bm{\bm{X}}})=\sum\nolimits_{i=1}^{n}\kappa(\sigma_{i}({\bm{\bm{X}}})),

(7)

where $\kappa$ is nonconvex and possibly nonsmooth. We assume the following on $\kappa$ .

Assumption 1

$\kappa(\alpha)$ is a concave and non-decreasing function on $\alpha\geq 0$ , with $\kappa(0)=0$ and $\lim_{\alpha\rightarrow 0^{+}}\kappa^{\prime}(\alpha)=\kappa_{0}$ for a positive constant $\kappa_{0}$ .

Table 1 shows the $\kappa$ ’s corresponding to the popular nonconvex regularizers of capped- $\ell_{1}$ penalty (Zhang, 2010b), log-sum-penalty (LSP) (Candès et al., 2008), truncated nuclear norm (TNN) (Hu et al., 2013), smoothed-capped-absolute-deviation (SCAD) (Fan and Li, 2001), and minimax concave penalty (MCP) (Zhang, 2010a). These nonconvex regularizers have similar statistical guarantees (Gui et al., 2016), and perform empirically better than the convex nuclear norm regularizer (Lu et al., 2016b; Yao et al., 2019b). The proximal algorithm can also be used, and converges to a critical point (Attouch et al., 2013). Analogous to Lemma 1, the underlying proximal step

\displaystyle\text{prox}_{\frac{\lambda}{\tau}\phi}(\bm{Z})=\arg\min\nolimits_{{\bm{\bm{X}}}}\frac{1}{2}\left\|{\bm{\bm{X}}}-\bm{Z}\right\|_{F}^{2}+\frac{\lambda}{\tau}\phi({\bm{\bm{X}}})

(8)

can be obtained as follows.

Lemma 2

(Lu et al., 2016b) $\text{prox}_{\lambda\phi}(\bm{Z})=\bm{U}\text{\,Diag}\left(y_{1},\dots,y_{n}\right)\bm{V}^{\top}$ , where $\bm{U}\bm{\Sigma}\bm{V}^{\top}$ is the SVD of $\bm{Z}$ , and $y_{i}=\arg\min\nolimits_{y\geq 0}\frac{1}{2}(y-\sigma_{i}(\bm{Z}))^{2}+\lambda\kappa(y)$ .

Table 1: Common examples of

\kappa(\sigma_{i}({\bm{\bm{X}}}))

. Here,

\theta

is a constant. For the capped-

\ell_{1}

, LSP and MCP,

\theta>0

; for SCAD,

\theta>2

; and for TNN,

\theta

is a positive integer.

	$\kappa(\sigma_{i}({\bm{\bm{X}}}))$
nuclear norm (Candès and Recht, 2009)	$\sigma_{i}({\bm{\bm{X}}})$
capped- $\ell_{1}$ (Zhang, 2010b)	$\min(\sigma_{i}({\bm{\bm{X}}}),\theta)$
LSP (Candès et al., 2008)	$\log(\frac{\sigma_{i}({\bm{\bm{X}}})}{\theta}+1)$
TNN (Hu et al., 2013)	$\begin{cases}\sigma_{i}({\bm{\bm{X}}})&\text{if}\;i>\theta\\ 0&\text{otherwise}\end{cases}$
SCAD (Fan and Li, 2001)	$\begin{cases}\sigma_{i}({\bm{\bm{X}}})&\text{if}\;\sigma_{i}({\bm{\bm{X}}})\leq 1\\ \frac{(2\theta\sigma_{i}({\bm{\bm{X}}})-\sigma_{i}({\bm{\bm{X}}})^{2}-1)}{2(\theta-1)}&\text{if}\;1<\sigma_{i}({\bm{\bm{X}}})\leq\theta\\ \frac{(\theta+1)^{2}}{2}&\text{otherwise}\end{cases}$
MCP (Zhang, 2010a)	$\begin{cases}\sigma_{i}({\bm{\bm{X}}})-\frac{\alpha^{2}}{2\theta}&\text{if}\;\sigma_{i}({\bm{\bm{X}}})\leq\theta\\ \frac{\theta^{2}}{2}&\text{otherwise}\end{cases}$

2.1.3 Matrix Factorization

Note that the aforementioned regularizers require access to individual singular values. As computing the singular values of a $m\times n$ matrix (with $m\geq n$ ) via SVD takes $O(mn^{2})$ time, this can be costly for a large matrix. Even when rank- $k$ truncated SVD is used, the computation cost is still $O(mnk)$ . To reduce the computational burden, factored low-rank regularizers are proposed (Srebro et al., 2005; Mazumder et al., 2010). Specifically, equation (1) is rewritten into a factored form as

\min\nolimits_{\bm{W},\bm{H}}f(\bm{W}\bm{H}^{\top})+\lambda\cdot h(\bm{W},\bm{H}),

(9)

where ${\bm{\bm{X}}}$ is factorized as $\bm{W}\bm{H}^{\top}$ with $\bm{W}\in\mathbb{R}^{m\times k}$ and $\bm{H}\in\mathbb{R}^{n\times k}$ , $h$ is a regularizer on ${\bm{\bm{W}}}$ and ${\bm{\bm{H}}}$ , and $\lambda\geq 0$ is a hyperparameter. When $\lambda=0$ , this reduces to matrix factorization (Vandereycken, 2013; Boumal and Absil, 2015; Tu et al., 2016; Wang et al., 2017). After factorization, gradient descent or alternative minimization are usually used for optimization. When certain conditions (such as proper initialization, restricted strong convexity (RSC) (Negahban and Wainwright, 2012), or restricted isometry property (RIP) (Candès and Tao, 2005)) are met, statistical guarantees can be obtained (Zheng and Lafferty, 2015; Tu et al., 2016; Wang et al., 2017).

Note that in Table 1, the nuclear norm is the only regularizer $r({\bm{\bm{X}}})$ that has an equivalent factored form $h(\bm{W},\bm{H})$ . For a matrix ${\bm{\bm{X}}}$ with ground-truth rank no larger than $k$ , it has been shown that the nuclear norm can be rewritten in a factored form as (Srebro et al., 2005)

\displaystyle\left\|{\bm{\bm{X}}}\right\|_{*}=\min\nolimits_{{\bm{\bm{X}}}=\bm{W}\bm{H}^{\top}}\frac{1}{2}\left(\left\|\bm{W}\right\|_{F}^{2}+\left\|\bm{H}\right\|_{F}^{2}\right).

However, the other nonconvex regularizers need to penalize individual singular values, and so cannot be written in factored form.

2.2 Low-Rank Tensor Learning

A $M$ -order tensor $\mathscr{X}$ has rank one if it can be written as the outer product of $M$ vectors, i.e., $\mathscr{X}=\bm{x}^{1}\circ\bm{x}^{2}\circ\dots\circ\bm{x}^{M}$ where $\circ$ denotes the outer product (i.e., $\mathscr{X}_{i_{1},\ldots,i_{M}}=\bm{x}^{1}_{i_{1}}\cdot\bm{x}^{2}_{i_{2}}\cdot\dots\cdot\bm{x}^{M}_{i_{M}}$ ). In general, the rank of a tensor $\mathscr{X}$ is the smallest number of rank-one tensors that generate $\mathscr{X}$ as their sum (Kolda and Bader, 2009).

To impose a low-rank structure on tensors, factorization methods (such as the Tucker / CP (Kolda and Bader, 2009; Hong et al., 2020), tensor-train (Oseledets, 2011) and tensor ring (Zhao et al., 2016) decompositions) have been used for low-rank tensor learning. These methods assume that the tensor can be decomposed into low-rank factor matrices (Kolda and Bader, 2009), which are then learned by alternating least squares or coordinate descent (Acar et al., 2011; Xu et al., 2013; Balazevic et al., 2019). Kressner et al. (2014) proposed to utilize the Riemannian structure on the manifold of tensors with fixed multilinear rank, and then perform nonlinear conjugate gradient descent. It can be speeded up by preconditioning (Kasai and Mishra, 2016). However, these models suffer from the problem of local minimum, and have no theoretical guarantee on the convergence rate. Moreover, its per-iteration cost depends on the product of all the mode ranks, and so can be expensive. Thus, they may lead to worse approximations and inferior performance (Tomioka et al., 2011; Liu et al., 2013; Guo et al., 2017).

Due to the above limitations, the nuclear norm, which has been commonly used in low-rank matrix learning, has been extended to the learning of low-rank tensors (Tomioka et al., 2010; Signoretto et al., 2011; Gu et al., 2014; Yuan and Zhang, 2016; Zhang and Aeron, 2017). The most commonly used low-rank tensor regularizer is the following (convex) overlapped nuclear norm:

Definition 3

(Tomioka et al., 2010) The overlapped nuclear norm of a $M$ -order tensor $\mathscr{X}$ is $\left\|\mathscr{X}\right\|_{\text{overlap}}$ $=$ $\sum_{i=1}^{M}\lambda_{i}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}$ , where $\{\lambda_{i}\geq 0\}$ are hyperparameters.

Note that the nuclear norm is a convex envelop of the matrix rank (Candès and Recht, 2009). Similarly, $\left\|\mathscr{X}\right\|_{\text{overlap}}$ is a convex envelop of the tensor rank (Tomioka et al., 2010, 2011). Empirically, $\left\|\mathscr{X}\right\|_{\text{overlap}}$ has better performance than the other nuclear norm variants in many tensor applications such as image inpainting (Liu et al., 2013) and multi-relational link prediction (Guo et al., 2017). On the theoretical side, let $\mathscr{X}^{*}$ be the ground-truth tensor, and $\mathscr{X}$ be the tensor obtained by solving the overlapped nuclear norm regularized problem. The statistical error between $\mathscr{X}^{*}$ and $\mathscr{X}$ has been established in tensor decomposition (Tomioka et al., 2011) and robust tensor decomposition problems (Gu et al., 2014). Specifically, under the restricted strong convexity (RSC) condition (Negahban and Wainwright, 2012), $\|\mathscr{X}^{*}-\mathscr{X}\|_{F}$ can be bounded by $O(\sigma\sum\nolimits_{i=1}^{M}\sqrt{k_{i}})$ , where $\sigma$ is the noise level and $k_{i}$ is the rank of $\mathscr{X}^{*}_{{\left\langle i\right\rangle}}$ . Furthermore, we can see that when $\sigma=0$ (no noise), exactly recovery can be guaranteed.

2.3 Proximal Average (PA) Algorithm

Let $\mathcal{H}$ be a Hilbert space of $\mathscr{X}$ , which can be a scalar/vector/matrix/tensor variable. Consider the following optimization problem:

\displaystyle\min\nolimits_{\mathscr{X}\in\mathcal{H}}F(\mathscr{X})=f(\mathscr{X})+\sum\nolimits_{i=1}^{K}\lambda_{i}\,g_{i}(\mathscr{X}),

(10)

where $f$ is the loss and each $g_{i}$ is a regularizer with hyper-parameter $\{\lambda_{i}\}$ . Often, $g(\mathscr{X})=\sum_{i=1}^{K}$ $\lambda_{i}$ $g_{i}(\mathscr{X})$ is complicated, and its proximal step does not have a simple solution. Hence, the proximal algorithm cannot be efficiently used. However, it is possible that the proximal step for each individual $g_{i}$ can be easy obtained. For example, let $g_{1}({\bm{\bm{X}}})=\left\|{\bm{\bm{X}}}\right\|_{1}$ and $g_{2}({\bm{\bm{X}}})=\left\|{\bm{\bm{X}}}\right\|_{*}$ . The closed-form solution on the proximal step for $g_{1}$ (resp. $g_{2}$ ) is given by the soft-thresholding operator (Efron et al., 2004) (resp. singular value thresholding operator (Cai et al., 2010)). However, the closed-form solution does not exist for the proximal step with $g_{1}+g_{2}$ .

In this case, the proximal average (PA) algorithm (Bauschke et al., 2008) can be used instead. The PA algorithm generates $\mathscr{X}_{t}$ ’s as

$\displaystyle\mathscr{X}_{t}$	$\displaystyle=\sum\nolimits_{i=1}^{K}\mathscr{Y}_{t}^{i},$	(11)
$\displaystyle\mathscr{Z}_{t}$	$\displaystyle=\mathscr{X}_{t}-\frac{1}{\tau}\nabla f(\mathscr{X}_{t}),$	(12)
$\displaystyle\mathscr{Y}_{t+1}^{i}$	$\displaystyle=\text{prox}_{\frac{\lambda_{i}g_{i}}{\tau}}(\mathscr{Z}_{t}),\quad i=1,\dots,K.$	(13)

As each individual proximal step in (13) is easy, the PA algorithm can be significantly faster than the proximal algorithm (Yu, 2013; Zhong and Kwok, 2014; Yu et al., 2015; Shen et al., 2017). When both $f$ and $g$ are convex, the PA algorithm converges to an optimal solution of (10) with a proper choice of stepsize $\tau$ (Yu, 2013; Shen et al., 2017). Recently, the PA algorithm has also been extended to nonconvex $f$ and $g_{i}$ ’s (Zhong and Kwok, 2014; Yu et al., 2015). Moreover, $\tau$ can be adaptively changed to obtain an empirically faster convergence (Shen et al., 2017).

3 Proposed Algorithm

Analogous to the low-rank matrix completion problem in (1), we consider the following low-rank tensor completion problem with a nonconvex extension of the overlapped nuclear norm:

\displaystyle\min_{\mathscr{X}}\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)+\sum\nolimits_{i=1}^{D}\lambda_{i}\,\phi(\mathscr{X}_{{\left\langle i\right\rangle}}).

(14)

Here, the observed elements are in $\mathscr{O}_{i_{1}...i_{M}}$ , $\mathscr{X}$ is the tensor to be recovered, $\ell(\cdot,\cdot)$ is a smooth loss function, and $\phi$ is a nonconvex regularizer in the form in (7). Unlike the overlapped nuclear norm in Definition 3, here we only sum over $D\leq M$ modes. This is useful when some modes are already small (e.g., the number of bands in color images), and so do not need to be low-rank regularized. When $D=M$ and $\kappa(\alpha)=\alpha$ in (7), problem (14) reduces to (convex) overlapped nuclear norm regularization. When $D=1$ and $\ell$ is the square loss, (14) reduces to the matrix completion problem:

\displaystyle\min\nolimits_{{\bm{\bm{X}}}\in\mathbb{R}^{I^{1}\times(\frac{I^{\pi}}{I^{1}})}}\frac{1}{2}\left\|P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}-\mathscr{O}_{{\left\langle 1\right\rangle}}\right)\right\|_{F}^{2}+\lambda_{1}\phi({\bm{\bm{X}}}),

which can be solved by the proximal algorithm as in (Lu et al., 2016b; Yao et al., 2019b). In the sequel, we only consider $D>1$ .

3.1 Issues with Existing Solvers

First, consider the case where $\kappa$ in (7) is convex. While $D$ may not be equal to $M$ , it can be easily shown that existing optimization solvers in (Tomioka et al., 2010; Boyd et al., 2011; Liu et al., 2013) can still be used. However, when $\kappa$ is nonconvex, the fast low-rank tensor completion (FaLRTC) solver (Liu et al., 2013) cannot be applied, as the dual of (14) cannot be derived. Tomioka et al. (2010) used the alternating direction of multiple multipliers (ADMM) (Boyd et al., 2011) solver for the overlapped nuclear norm. Recently, it is used in (Chen et al., 2020) to solve a special case of (14), in which $\phi$ is the truncated nuclear norm (TNN) regularizer (see Table 1). Specifically, (14) is first reformulated as

\displaystyle\min\nolimits_{\mathscr{X}}\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)+\sum\nolimits_{i=1}^{D}\lambda_{i}\,\phi({\bm{\bm{X}}}_{i})\;\text{s.t.}\;{\bm{\bm{X}}}_{i}=\mathscr{X}_{{\left\langle i\right\rangle}},\;i=1,\dots,D.

Using ADMM, it then generates iterates as

$\displaystyle\mathscr{X}_{t+1}$	$\displaystyle=\arg\min\nolimits_{\mathscr{X}}\!\!\!\!\!\!\sum_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\!\!\!\!\!\!\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)\!+\!\frac{\zeta}{2}\sum\nolimits_{i=1}^{D}\big{\\|}({\bm{\bm{X}}}_{i})_{t}\!-\!\mathscr{X}_{{\left\langle i\right\rangle}}\!+\!\frac{1}{\zeta}(\bm{M}_{i})_{t}\big{\\|}_{F}^{2},$	(15)
$\displaystyle({\bm{\bm{X}}}_{i})_{t+1}$	$\displaystyle=\text{prox}_{\frac{\lambda_{i}}{\zeta}}(({\bm{\bm{X}}}_{i})_{t+1}+\frac{1}{\zeta}(\bm{M}_{i})_{t}),\quad i=1,\dots,D,$	(16)
$\displaystyle(\bm{M}_{i})_{t+1}$	$\displaystyle=(\bm{M}_{i})_{t}+\frac{1}{\zeta}\left(({\bm{\bm{X}}}_{i})_{t+1}-(\mathscr{X}_{{\left\langle i\right\rangle}})_{t+1}\right),\quad i=1,\dots,D,$	(17)

where $\bm{M}_{i}$ ’s are the dual variables, and $\zeta>0$ . The proximal step in (16) can be computed from Lemma 2. Convergence of this ADMM procedure is guaranteed in (Hong et al., 2016; Wang et al., 2019). However, it does not utilize the sparsity induced by ${\bm{\bm{\Omega}}}$ . Moreover, as the tensor $\mathscr{X}$ needs to be folded and unfolded repeatedly, the iterative procedure is expensive, taking $O(I^{\pi})$ space and $O(I^{\pi}\sum_{i=1}^{D}I^{i})$ time per iteration.

On the other hand, the proximal algorithm (Section 2.1) cannot be easily used, as the proximal step for $\sum_{i=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ is not simple in general.

3.2 Structure-aware Proximal Average Iterations

Note that $\phi$ in (7) admits a difference-of-convex decomposition (Hartman, 1959; Le Thi and Tao, 2005), i.e., $\phi$ can be decomposed as $\phi=\phi_{1}-\phi_{2}$ where $\phi_{1}$ and $\phi_{2}$ are convex (Yao et al., 2019b). The proximal average (PA) algorithm (Section 2.3) has been recently extended for nonconvex $f$ and $g_{i}$ ’s, where each $g_{i}$ admits a difference-of-convex decomposition (Zhong and Kwok, 2014). Hence, as (14) is in the form in (10), one can generate the PA iterates as:

$\displaystyle\mathscr{X}_{t}$	$\displaystyle=$	$\displaystyle\sum\nolimits_{i=1}^{D}\mathscr{Y}^{i}_{t},$	(18)
$\displaystyle\mathscr{Z}_{t}$	$\displaystyle=$	$\displaystyle\mathscr{X}_{t}-\frac{1}{\tau}\varpi(\mathscr{X}_{t}),$	(19)
$\displaystyle\mathscr{Y}^{i}_{t+1}$	$\displaystyle=$	$\displaystyle\big{[}\text{prox}_{\frac{\lambda_{i}\phi}{\tau}}([\mathscr{Z}_{t}]_{{\left\langle i\right\rangle}})\big{]}^{{\left\langle i\right\rangle}},\quad i=1,\dots,D.$	(20)

where $\xi(\mathscr{X}_{t})$ is a sparse tensor with

\displaystyle\big{[}\varpi(\mathscr{X}_{t})\big{]}_{i_{1}\dots i_{M}}=\begin{cases}0&(i_{1},\dots,i_{M})\not\in\mathbf{\Omega}\\ \ell^{\prime}\left([\mathscr{X}_{t}]_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)&(i_{1},\dots,i_{M})\in\mathbf{\Omega}\end{cases}.

(21)

In (20), each individual proximal step can be computed using Lemma 2. However, tensor folding and unfolding are still required. A direct application of the PA algorithm is as expensive as using ADMM (see Table 2).

In the following, we show that by utilizing the “sparse plus low-rank” structure, the PA iterations can be computed efficiently without tensor folding/unfolding. In the earlier conference version (Yao et al., 2019a), we only considered the case $M=3$ . Here, we extend this to $M\geq 3$ by noting that the coordinate format of sparse tensors can naturally handle tensors with arbitrary orders (Section 3.2.1) and the proximal step can be performed without tensor folding/unfolding (Section 3.2.2).

3.2.1 Efficient Computations of $\mathscr{X}_{t}$ and $\mathscr{Z}_{t}$ in (18), (19)

First, rewrite (20) as $\mathscr{Y}^{i}_{t+1}=[{\bm{\bm{Y}}}^{i}_{t+1}]^{{\left\langle i\right\rangle}}$ , where ${\bm{\bm{Y}}}^{i}_{t+1}=\text{prox}_{\frac{\lambda_{i}\phi}{\tau}}({\bm{\bm{Z}}}^{i}_{t})$ and ${\bm{\bm{Z}}}^{i}_{t}=\left[\mathscr{Z}_{t}\right]_{{\left\langle i\right\rangle}}$ . Recall that ${\bm{\bm{Y}}}_{t}^{i}$ obtained from the proximal step is low-rank. Let its rank be $k^{i}_{t}$ . Hence, ${\bm{\bm{Y}}}_{t}^{i}$ can be represented as $\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}$ , where $\bm{U}_{t}^{i}\in\mathbb{R}^{I^{i}\times k_{t}^{i}}$ and $\bm{V}_{t}^{i}\in\mathbb{R}^{(\frac{I^{\pi}}{I^{i}})\times k_{t}^{i}}$ . In each PA iteration, we avoid constructing the dense $\mathscr{Y}_{t}^{i}$ by storing the above low-rank factorized form of ${\bm{\bm{Y}}}_{t}^{i}$ instead. Similarly, we also avoid constructing $\mathscr{X}_{t}$ in (18) by storing it implicitly as

\displaystyle\mathscr{X}_{t}=\sum\nolimits_{i=1}^{D}\big{(}\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}\big{)}^{{\left\langle i\right\rangle}}.

(22)

$\mathscr{Z}_{t}$ in (19) can then be rewritten as

\displaystyle\mathscr{Z}_{t}=\sum\nolimits_{i=1}^{D}\left(\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}\right)^{{\left\langle i\right\rangle}}-\frac{1}{\tau}\xi(\mathscr{X}_{t}).

(23)

The sparse tensor $\xi(\mathscr{X}_{t})$ in (21) can be constructed efficiently by using the coordinate format²²2For a sparse $M$ -order tensor, its $p$ th nonzero element is represented in the coordinate format as $(i_{p}^{1},\dots,i_{p}^{M},v_{p})$ , where $i_{p}^{1},\dots,i_{p}^{M}$ are indices on each mode and $v_{p}$ is the value. (Bader and Kolda, 2007). Using (22), each $[\xi(\mathscr{X}_{t})]_{i_{1}\dots i_{M}}$ can be computed by finding the corresponding rows in $\{\bm{U}_{t}^{i},\bm{V}_{t}^{i}\}$ as shown in Algorithm 1. This takes $O(\sum_{i=1}^{D}k_{t}^{i})$ time.

Algorithm 1 Computing the

p

th element

v_{p}

with index

(i_{p}^{1}\dots i_{p}^{M})

\xi(\mathscr{X}_{t})

0: factorizations

\{\bm{U}_{t}^{1}(\bm{V}_{t}^{1})^{\top},\dots,\bm{U}_{t}^{D}(\bm{V}_{t}^{D})^{\top}\}

{\bm{\bm{Y}}}_{t}^{1}

\dots

{\bm{\bm{Y}}}_{t}^{D}

, and observed elements in

P_{{\bm{\bm{\Omega}}}}\left(\mathscr{O}\right)

;

v_{p}\leftarrow 0

;

2: for

d=1,\dots,D

\bm{u}^{\top}\leftarrow

i^{d}_{p}

th row of

\bm{U}_{t}^{d}

;

\bm{v}^{\top}\leftarrow

(\sum_{k\neq d}^{M}i^{k}_{p}I^{\pi}+i^{d}_{p})

th row of

\bm{V}_{t}^{d}

;

v_{p}\leftarrow v_{p}+\bm{u}^{\top}\bm{v}

;

6: end for

v_{p}\leftarrow\ell^{\prime}(v_{p},\mathscr{O}_{i_{p}^{1}\dots i_{p}^{M}})

;

8: return

v_{p}

3.2.2 Efficient Computation of $\mathscr{Y}^{i}_{t+1}$ in (20)

Recall that the proximal step in (20) requires SVD, which involves matrix multiplications in the form $\bm{a}^{\top}(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}$ (where $\bm{a}\in\mathbb{R}^{I^{i}}$ ) and $(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}\bm{b}$ (where $\bm{b}\in\mathbb{R}^{\frac{I^{\pi}}{I^{i}}}$ ). Using the “sparse plus low-rank” structure in (23), these can be computed as

\displaystyle\bm{a}^{\top}(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}=\big{(}\bm{a}^{\top}\bm{U}_{t}^{i}\big{)}(\bm{V}_{t}^{i})^{\top}+\sum\nolimits_{j\neq i}\bm{a}^{\top}\big{[}(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}-\frac{1}{\tau}\bm{a}^{\top}[\xi(\mathscr{X}_{t})]_{{\left\langle i\right\rangle}},

(24)

and

\displaystyle(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}\bm{b}=\bm{U}_{t}^{i}\big{[}(\bm{V}_{t}^{i})^{\top}\bm{b}\big{]}+\sum\nolimits_{j\neq i}\big{[}(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}\bm{b}-\frac{1}{\tau}[\xi(\mathscr{X}_{t})]_{{\left\langle i\right\rangle}}\bm{b}.

(25)

The first terms in (24) and (25) can be easily computed in $O((\frac{I^{\pi}}{I^{i}}+I^{i})k_{t}^{i})$ space and time. The last terms ( $\bm{a}^{\top}\left[\xi(\mathscr{X}_{t})\right]_{{\left\langle i\right\rangle}}$ and $\left[\xi(\mathscr{X}_{t})\right]_{{\left\langle i\right\rangle}}\bm{b}$ ) are sparse, and can be computed in $O(\|{\bm{\bm{\Omega}}}\|_{1})$ space and time by using sparse tensor packages such as the Tensor Toolbox (Bader and Kolda, 2007). However, a direct computation of the $\bm{a}^{\top}[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}$ and $[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}\bm{b}$ terms involves tensor folding/unfolding, and is expensive. By examining how elements are ordered by folding/unfolding, the following shows that these multiplications can indeed be computed efficiently without explicit folding/unfolding.

Proposition 4

Let $\bm{U}\in\mathbb{R}^{I^{j}\times k}$ , $\bm{V}\in\mathbb{R}^{(\frac{I^{\pi}}{I^{j}})\times k}$ , and $\bm{u}_{p}$ (resp. $\bm{v}_{p}$ ) be the $p$ th column of $\bm{U}$ (resp. $\bm{V}$ ). For any $i\neq j$ , $\bm{a}\in\mathbb{R}^{I^{i}}$ and $\bm{b}\in\mathbb{R}^{\frac{I^{\pi}}{I^{i}}}$ , we have

	$\displaystyle\bm{a}^{\top}\big{[}(\bm{U}\bm{V}^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}$	$\displaystyle=\sum\nolimits_{p=1}^{k}\bm{u}_{p}^{\top}\otimes\big{[}\bm{a}^{\top}\text{mat}(\bm{v}_{p};I^{i},\bar{I}^{ij})\big{]},$		(26)
	$\displaystyle\big{[}(\bm{U}\bm{V}^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}\bm{b}$	$\displaystyle=\sum\nolimits_{p=1}^{k}\text{mat}\big{(}\bm{v}_{p};I^{i},\bar{I}^{ij}\big{)}\text{mat}\big{(}\bm{b};\bar{I}^{ij},I^{j}\big{)}\bm{u}_{p},$		(27)

where $\otimes$ is the Kronecker product, $\bar{I}^{ij}=I^{\pi}/(I^{i}I^{j})$ , and $\text{mat}(\bm{x};a,b)$ reshapes a vector $\bm{x}$ of length $ab$ into a matrix of size $a\times b$ .

In the earlier conference version (Yao et al., 2019a), Proposition 3.2 there (not the proposed algorithm) limits the usage to $M=3$ . Without Proposition 4, the algorithm can suffer from expensive computation cost, and thus has no efficiency advantage over the simple use of the PA algorithm. Specifically, when mapping the vector $\bm{v}_{p}$ back to a matrix, we do not need to take a special treatment on the size of matrix. The reason is that, $\bm{v}_{p}$ has $I_{i}I_{j}$ elements and we just need to map it back to a matrix of size $I_{i}\times I_{j}$ . Thus, we do not have parameters for mat operation in the conference version. However, when $M>3$ , $\bm{v}_{p}$ has $I^{\pi}/I^{i}$ elements, we need to check whether ideas used in the conference version can be done in a similar way. As a result, we have two more parameters for the mat operation here, which customize reshaping matrix to a proper size.

Remark 5

For a second-order tensor (i.e., matrix case with $M=2$ ), Proposition 4 becomes

\displaystyle\bm{a}^{\top}\big{[}(\bm{U}\bm{V}^{\top})^{{\left\langle 1\right\rangle}}\big{]}_{{\left\langle 2\right\rangle}}=\sum\nolimits_{p=1}^{k}(\bm{a}^{\top}\bm{v}_{p})\bm{u}_{p}^{\top}\quad\text{and}\quad\big{[}(\bm{U}\bm{V}^{\top})^{{\left\langle 1\right\rangle}}\big{]}_{{\left\langle 2\right\rangle}}\bm{b}=\sum\nolimits_{p=1}^{k}\bm{v}_{p}(\bm{b}^{\top}\bm{u}_{p}).

With the usual square loss (i.e., $\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)$ in (14) equals $\frac{1}{2}\left\|P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}-\mathscr{O}\right)\right\|_{F}^{2}$ ), (25) then reduces to (6) when $D=1$ . When $D=2$ , $\sum\nolimits_{i=1}^{D}\lambda_{i}\,\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ in (14) becomes $\lambda_{1}\phi({\bm{\bm{X}}})+\lambda_{2}\phi({\bm{\bm{X}}}^{\top})=(\lambda_{1}+\lambda_{2})\phi({\bm{\bm{X}}})$ , and is the same as the corresponding regularizer when $D=1$ . Hence, the reduction from (25) to (6) still holds.

3.2.3 Time and Space Complexities

A direct computation of $\bm{a}^{\top}[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}$ takes $O(k_{t}^{i}I^{\pi})$ time and $O(I^{\pi})$ space. By using the computation in Proposition 4, these are reduced to $O((\frac{1}{I^{i}}+\frac{1}{I^{j}})k_{t}^{i}I^{\pi})$ time and $O((\frac{1}{I^{j}}+\frac{1}{I^{i}})k_{t}^{i}I^{\pi})$ space. This is also the case for $[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}\bm{b}$ . Details are in the following.

	operation	time	space
reshaping	$\text{mat}(\bm{v}_{p};I^{j},\bar{I}^{ij})$	$O(\frac{I^{\pi}}{I^{i}})$	$O(\frac{I^{\pi}}{I^{i}})$
multiplication	$\bm{a}^{\top}(\cdot)$	$O(\frac{I^{\pi}}{I^{i}})$	$O(\frac{I^{\pi}}{I^{i}})$
Kronecker product	$\bm{u}_{p}^{\top}\otimes(\cdot)$	$O(\frac{I^{\pi}}{I^{j}})$	$O(\frac{I^{\pi}}{I^{j}})$
summation	$\sum_{p=1}^{k_{t}^{i}}(\cdot)$	$O(\frac{k_{t}^{i}I^{\pi}}{I^{j}})$	$O((\frac{1}{I^{j}}+\frac{1}{I^{i}})k_{t}^{i}I^{\pi})$
total for (26)		$O((\frac{1}{I^{j}}+\frac{k_{t}^{i}}{I^{j}})I^{\pi})$	$O((\frac{1}{I^{j}}+\frac{1}{I^{i}})k_{t}^{i}I^{\pi})$

	operation	time	space
reshaping	$\text{mat}\left(\bm{b};\bar{I}^{ij},I^{i}\right)$	$O(\frac{I^{\pi}}{I^{j}})$	$O(\frac{I^{\pi}}{I^{j}})$
multiplication	$(\cdot)\bm{u}_{p}$	$O(\frac{I^{\pi}}{I^{i}})$	$O(\frac{I^{\pi}}{I^{j}})$
reshaping	$\text{mat}\left(\bm{v}_{p};I^{j},\bar{I}^{ij}\right)$	$O(\frac{I^{\pi}}{I^{i}})$	$O(\frac{I^{\pi}}{I^{i}})$
multiplication	$\text{mat}\left(\bm{v}_{p};I^{j},\bar{I}^{ij}\right)(\cdot)$	$O(\frac{I^{\pi}}{I^{j}})$	$O(\frac{I^{\pi}}{I^{i}})$
summation	$\sum_{p=1}^{k_{t}^{i}}(\cdot)$	$O(k_{t}^{i}I^{i})$	$O(k_{t}^{i}I^{i})$
total for (27)		$O((\frac{1}{I^{j}}+\frac{k_{t}^{i}}{I^{j}})I^{\pi})$	$O((\frac{1}{I^{j}}+\frac{1}{I^{i}})k_{t}^{i}I^{\pi})$

Combining the above, and noting that we have to keep the factorized form $\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}$ of ${\bm{\bm{Y}}}_{t}^{i}$ , computing all the proximal steps in (20) takes

\displaystyle O\big{(}\sum\nolimits_{i=1}^{D}\sum\nolimits_{j\neq i}(\frac{1}{I^{i}}+\frac{1}{I^{j}})k_{t}^{i}I^{\pi}+\|{\bm{\bm{\Omega}}}\|_{1}\big{)}

(28)

space and

\displaystyle O\big{(}\sum\nolimits_{i=1}^{D}\sum\nolimits_{j\neq i}(\frac{1}{I^{i}}+\frac{1}{I^{j}})k_{t}^{i}k_{t+1}^{i}I^{\pi}+\|{\bm{\bm{\Omega}}}\|_{1}(k_{t}^{i}+k_{t+1}^{i})\big{)}

(29)

time. Empirically, as will be seen in the experimental results in Section 5.1.2, $k_{t}^{i}$ , $k_{t+1}^{i}\ll I^{i}$ . Hence, (28) and (29) are much smaller than the complexities with a direct usage of PA and ADMM in Section 3.1 (Table 2).

Table 2: Comparison of the proposed NORT with PA and ADMM for (14) in Section 3.1.

algorithm	complexity		adaptive
algorithm	time per iteration	space	momentum
PA (Zhong and Kwok, 2014)	$O(I^{\pi}\sum_{i=1}^{D}I^{i})$	$O(I^{\pi})$	$\times$
ADMM (Chen et al., 2020)	$O(I^{\pi}\sum_{i=1}^{D}I^{i})$	$O(I^{\pi})$	$\times$
NORT (Algorithm 2)	see (29)	see (28)	$\surd$

3.3 Use of Adaptive Momentum

The PA algorithm uses only first-order information, and can be slow to converge empirically (Parikh and Boyd, 2013). To address this problem, we adopt adaptive momentum, which uses historical iterates to speed up convergence. This has been popularly used in stochastic gradient descent (Duchi et al., 2011; Kingma and Ba, 2014), proximal algorithms (Li and Lin, 2015; Yao et al., 2017; Li et al., 2017), cubic regularization (Wang et al., 2020), and zero-order black-box optimization (Chen et al., 2019). Here, we adopt the adaptive scheme in (Li et al., 2017).

The resultant procedure, which will be called NOnconvex Regularized Tensor (NORT), is shown in Algorithm 2. When the extrapolation step $\bar{\mathscr{X}}_{t}$ achieves a lower function value (step 4), the momentum $\gamma_{t}$ is increased to further exploit the opportunity of acceleration; otherwise, $\gamma_{t}$ is decayed (step 7). When step 5 is performed, $\mathscr{V}_{t}=\mathscr{X}_{t}+\gamma_{t}(\mathscr{X}_{t}-\mathscr{X}_{t-1})$ . $\mathscr{Z}_{t}$ in step 9 becomes

\displaystyle\mathscr{Z}_{t}=(1+\gamma_{t})\sum\nolimits_{i=1}^{D}\big{(}\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}\big{)}^{{\left\langle i\right\rangle}}-\gamma_{t}\sum\nolimits_{i=1}^{D}\big{(}\bm{U}_{t-1}^{i}(\bm{V}_{t-1}^{i})^{\top}\big{)}^{{\left\langle i\right\rangle}}-\frac{1}{\tau}\xi(\mathscr{V}_{t}),

(30)

which still has the “sparse plus low-rank” structure. When step 7 is performed, $\mathscr{V}_{t}=\mathscr{X}_{t}$ , and obviously the resultant $\mathscr{Z}_{t}$ is “sparse plus low-rank”. Thus, the more efficient reformulations in Proposition 4 can be applied in computing the proximal steps at step 11. Note that the rank of ${\bm{\bm{X}}}_{t+1}^{i}$ in step 11 is determined implicitly by the proximal step. As $\mathscr{X}_{t}$ and $\mathscr{Z}_{t}$ are implicitly represented in factorized forms, $\mathscr{V}_{t}$ and $\bar{\mathscr{X}}_{t}$ (in step 3) do not need to be explicitly constructed. As a result, the resultant time and space complexities are the same as those in Section 3.2.3.

Algorithm 2 NOnconvex Regularized Tensor (NORT) Algorithm.

1: Initialize

\tau>\rho+D\kappa_{0}

\gamma_{1},p\in(0,1]

\mathscr{X}_{0}=\mathscr{X}_{1}=0

and

t=1

;

2: while not converged do

\bar{\mathscr{X}}_{t}\leftarrow\mathscr{X}_{t}+\gamma_{t}(\mathscr{X}_{t}-\mathscr{X}_{t-1})

;

4: if

F(\bar{\mathscr{X}}_{t})\leq F(\mathscr{X}_{t})

then

\mathscr{V}_{t}\leftarrow\bar{\mathscr{X}}_{t}

and

\gamma_{t+1}\leftarrow\min(\frac{\gamma_{t}}{p},1)

;

6: else

\mathscr{V}_{t}\leftarrow\mathscr{X}_{t}

and

\gamma_{t+1}\leftarrow p\gamma_{t}

;

8: end if

\mathscr{Z}_{t}\leftarrow\mathscr{V}_{t}-\frac{1}{\tau}\xi(\mathscr{V}_{t})

; // compute

\xi(\mathscr{V}_{t})

using Algorithm 1

10: for

i=1,\dots,D

11:

{\bm{\bm{X}}}^{i}_{t+1}\leftarrow\text{prox}_{\frac{\lambda_{i}\phi}{\tau}}((\mathscr{Z}_{t})_{{\left\langle i\right\rangle}})

; // keep as

\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top}

;

12: end for // implicitly construct

\mathscr{X}_{t+1}\leftarrow\sum_{i=1}^{D}\big{(}\bm{U}_{t+1}^{i}(\bm{V}_{t+1}^{i})^{\top}\big{)}^{{\left\langle i\right\rangle}}

;

13:

t=t+1

14: end while

15: return

\mathscr{X}_{t}

3.4 Convergence Properties

In this section, we analyze the convergence properties of the proposed algorithm. As can be seen from (14), we have $f(\mathscr{X})=\sum\nolimits_{\mathbf{\Omega}_{i_{1}\ldots i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)$ here. Moreover, throughout this section, we assume that the loss $f$ is (Lipschitz-)smooth.

Note that existing proofs for PA algorithm (Yu, 2013; Zhong and Kwok, 2014; Yu et al., 2015) cannot be directly used, as adaptive momentum has not been used with the PA algorithm on nonconvex problems (see Table 2), and also that they do not involve tensor folding/unfolding operations. Our proof strategy will still follow the three main steps in proving convergence of PA:

1.

Show that the proximal average step with $g_{i}$ ’s in (13) corresponds to a regularizer;
2.

Show that this regularizer, when combined with the loss $f$ in (10), serves as a good approximation of the original objective $F$ .
3.

Show that the proposed algorithm finds critical points of this approximate optimization problem.

First, the following Proposition shows that the average step in (18) and proximal steps in (20) together correspond to a new regularizer $\bar{g}_{\tau}$ .

Proposition 6

For any $\tau>0$ , $\sum_{i=1}^{D}[\text{prox}_{\frac{1}{\tau}\lambda_{i}\phi}([\mathscr{Z}]_{{\left\langle i\right\rangle}})]^{{\left\langle i\right\rangle}}=\text{prox}_{\frac{1}{\tau}\bar{g}_{\tau}}(\mathscr{Z})$ , where

\displaystyle\bar{g}_{\tau}(\mathscr{X})=\tau\big{[}\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}:\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}=\mathscr{X}}\sum\nolimits_{d=1}^{D}\big{(}\frac{1}{2}\left\|{\bm{\bm{X}}}_{d}\right\|_{F}^{2}+\frac{\lambda_{d}}{\tau}\phi({\bm{\bm{X}}}_{d})\big{)}-\frac{D}{2}\left\|\mathscr{X}\right\|_{F}^{2}\big{]}.

Analogous to (10), let the objective corresponding to regularizer $\bar{g}_{\tau}$ be

F_{\tau}(\mathscr{X})=f(\mathscr{X})+\bar{g}_{\tau}(\mathscr{X}).

(31)

The following bounds the difference between the optimal values ( $F^{\min}$ and $F_{\tau}^{\min}$ , respectively) of the objectives $F$ in (10) and $F_{\tau}$ . It thus shows that $F_{\tau}$ serves as an approximation to $F$ , which is controlled by $\tau$ .

Proposition 7

$0\leq F^{\min}-F_{\tau}^{\min}\leq\frac{\kappa_{0}^{2}}{2\tau}\sum_{i=1}^{D}\lambda_{i}^{2}$ , where $\kappa_{0}$ is defined in Assumption 1.

Before showing the convergence of the proposed algorithm, the following Proposition first shows the condition of being critical points of $F_{\tau}(\mathscr{X})$ .

Proposition 8

If there exists $\tau>0$ such that $\tilde{\mathscr{X}}=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\nabla f(\tilde{\mathscr{X}})/\tau)$ , then $\tilde{\mathscr{X}}$ is a critical point of $F_{\tau}(\tilde{\mathscr{X}})$ .

Finally, we show how convergence to critical points can be ensured by the proposed algorithm under smooth assumption of loss $f$ (Section 3.4.1) and Kurdyka-Łojasiewicz condition for the approximated objective $F_{\tau}$ (Section 3.4.2).

3.4.1 With Smoothness Assumption on Loss $f$

The following shows that Algorithm 2 converges to a critical point (Theorem 9).

Theorem 9

The sequence $\{\mathscr{X}_{t}\}$ generated from Algorithm 2 has at least one limit point, and all limits points are critical points of $F_{\tau}(\mathscr{X})$ .

Proof [Sketch, details are in Appendix B.5.] The main idea is as follows. First, we show that (i) if step 5 is performed, $F_{\tau}(\mathscr{X}_{t+1})\leq F_{\tau}(\mathscr{X}_{t})-\frac{\eta}{2}\left\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\|_{F}^{2}$ ; (ii) if step 7 is performed, we have $F_{\tau}(\mathscr{X}_{t+1})\leq F_{\tau}(\mathscr{X}_{t})-\frac{\eta}{2}\left\|\mathscr{X}_{t+1}-\mathscr{X}_{t}\right\|_{F}^{2}$ . Combining the above two conditions, we obtain

\displaystyle\frac{2}{\eta}(F_{\tau}(\mathscr{X}_{1})-F_{\tau}(\mathscr{X}_{T+1}))\geq\sum\nolimits_{j\in\chi_{1}(T)}\left\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\|_{F}^{2}+\sum\nolimits_{j\in\chi_{2}(T)}\left\|\mathscr{X}_{t+1}-\mathscr{X}_{t}\right\|_{F}^{2},

where $\chi_{1}(T)$ and $\chi_{2}(T)$ are partitions of $\{1,\dots,T\}$ such that when $j\in\chi_{1}(T)$ step 5 is performed, and when $j\in\chi_{2}(T)$ step 7 is performed. Finally, when $T\rightarrow\infty$ , we discuss three cases: (i) $\chi_{1}(\infty)$ is finite, $\chi_{2}(\infty)$ is infinite; (ii) $\chi_{1}(\infty)$ is infinite, $\chi_{2}(\infty)$ is finite; and (iii) both $\chi_{1}(\infty)$ and $\chi_{2}(\infty)$ are infinite. Let $\tilde{\mathscr{X}}$ be a limit point of $\{\mathscr{X}_{t}\}$ , and $\{\mathscr{X}_{j_{t}}\}$ be a subsequence that converges to $\tilde{\mathscr{X}}$ . In all three cases, we show that

\displaystyle\lim\limits_{j_{t}\rightarrow\infty}\left\|\mathscr{X}_{j_{t}+1}-\mathscr{X}_{j_{t}}\right\|_{F}^{2}=\|\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}}))-\tilde{\mathscr{X}}\|_{F}^{2}=0.

Thus, we must have $\tilde{\mathscr{X}}$ is also a critical point based on Proposition 8. It is easy to see that we have not made any specifications on the limit points. Thus, all limit points are also critical points.

Recall that $\mathscr{X}_{t+1}$ is generated from $\mathscr{V}_{t}$ in steps 9-12 and $\mathscr{X}_{t+1}=\mathscr{V}_{t}$ indicates convergence to a critical point (Proposition 8). Thus, we can measure convergence of Algorithm 2 by $\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}$ . Corollary 10 shows that a rate of $O(1/T)$ can be obtained, which is also the best possible rate for first-order methods on general nonconvex problems (Nesterov, 2013; Ghadimi and Lan, 2016).

Corollary 10

$\min\nolimits_{t=1,\dots,T}\frac{1}{2}\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}^{2}\leq\frac{1}{\eta T}\big{[}F_{\tau}(\mathscr{X}_{1})-F^{\min}_{\tau}\big{]}$ , where $\eta=\tau-\rho-DL$ .

Remark 11

A larger $\tau$ leads to a better approximation to the original problem $F$ (Proposition 7). However, it also make the stepsize $1/\tau$ smaller (step 11 in Algorithm 2) and thus slower convergence (Corollary 10).

3.4.2 With Kurdyka-Łojasiewicz Condition on Approximated Objective $F_{\tau}$

In Section 3.4.1, we showed the convergence results when $f$ is smooth and $g$ is of the form in (7). In this section, we consider using the Kurdyka-Łojasiewicz (KL) condition (Attouch et al., 2013; Bolte et al., 2014) on $F_{\tau}$ , which has been popularly used in nonconvex optimization, particularly in gradient descent (Attouch et al., 2013) and proximal gradient algorithms (Bolte et al., 2014; Li and Lin, 2015; Li et al., 2017). For example, the class of semi-algebraic functions satisfy the KL condition. More examples can be found in (Bolte et al., 2010, 2014).

Definition 12

A function $h$ : $\mathbb{R}^{n}\rightarrow(-\infty,\infty]$ has the uniformized KL property if for every compact set $\mathcal{S}\in\text{dom}(h)$ on which $h$ is a constant, there exist $\epsilon$ , $c>0$ such that for all $\bm{u}\in\mathcal{S}$ and all $\bar{\bm{u}}\in\{\bm{u}:\min\nolimits_{\bm{v}\in\mathcal{S}}\left\|\bm{u}-\bm{v}\right\|_{2}\leq\epsilon\}\cap\{\bm{u}:f(\bar{\bm{u}})<f(\bm{u})<f(\bar{\bm{u}})+c\}$ , one has $\psi^{\prime}\left(f(\bm{u})-f(\bm{\bar{u}})\right)\min\nolimits_{\bm{v}\in\partial f(\bm{u})}\left\|\bm{v}\right\|_{2}>1$ , where $\psi(\alpha)=\frac{C\alpha^{x}}{x}$ for some $C>0$ , $\alpha\in[0,c)$ and $x\in(0,1]$ .

Since the KL property (Attouch et al., 2013; Bolte et al., 2014) does not require $h$ to be smooth or convex, it thus allows convergence analysis under the nonconvex and nonsmooth setting. However, such a property cannot replace the smoothness assumption in Section 3.4.1, as there are example functions which are smooth but fail to meet the KL condition (Section 4.3 of (Bolte et al., 2010)).

The following Theorem extends Algorithm 2 to be used with the uniformized KL property.

Theorem 13

Assume that $F_{\tau}$ in (31) has the uniformized KL property, and let $r_{t}=F_{\tau}(\mathscr{X}_{t})-F_{\tau}^{\min}$ . For a sufficiently large $t_{0}$ ,

a)

If $x$ in Definition 12 equals $1$ , then $r_{t}=0$ for all $t\geq t_{0}$ ;
b)

If $x\in[\frac{1}{2},1)$ , $r_{t}\leq(\frac{d_{1}C^{2}}{1+d_{1}C^{2}})^{t-t_{0}}r_{t_{0}}$ where $d_{1}=2(\tau+\rho)^{2}/\eta$ ;
c)

If $x\in(0,\frac{1}{2})$ , $r_{t}\leq(\frac{C}{(t-t_{0})d_{2}(1-2x)})^{1/(1-2x)}$ where $d_{2}=\min\big{(}\frac{1}{2d_{1}C},\frac{C}{1-2x}(2^{\frac{2x-1}{2x-2}}-1)r_{t_{0}}\big{)}$ .

Proof [Sketch, details are in Appendix B.7.] The proof idea generally follows that for (Bolte et al., 2014) with a special treatment for $\mathscr{V}_{t}$ here. First, we show

\displaystyle\lim\limits_{t\rightarrow\infty}\min\nolimits_{\mathscr{U}_{t}\in\partial F_{\tau}(\mathscr{X}_{t})}\left\|\mathscr{U}_{t}\right\|_{F}\leq\lim\limits_{t\rightarrow\infty}(\tau+\rho)\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}=0.

Next, using the KL condition, we have

\displaystyle 1\leq\psi^{\prime}\left(F_{\tau}(\mathscr{X}_{t+1})-F_{\tau}^{\min}\right)(\tau+\rho)\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}.

Then, let $r_{t}=F_{\tau}(\mathscr{X}_{t})-F_{\tau}^{\min}$ . From its definition, we have

\displaystyle r_{t}-r_{t+1}\geq F_{\tau}(\mathscr{V}_{t})-F_{\tau}(\mathscr{X}_{t+1}).

Combining the above three inequalities, we obtain

\displaystyle 1\leq\frac{2(\tau+\rho)^{2}}{\eta}\left[\psi^{\prime}(r_{t+1})\right]^{2}(r_{t}-r_{t+1}).

Since $\phi(\alpha)=\frac{C\alpha^{x}}{x}$ , then $\phi^{\prime}(\alpha)=C\alpha^{x-1}$ . The above inequality becomes $1\leq d_{1}C^{2}r_{t+1}^{2x-2}(r_{t}-r_{t+1})$ , where $d_{1}=\frac{2(\tau+\rho)^{2}}{\eta}$ . It is shown in (Bolte et al., 2014; Li and Lin, 2015; Li et al., 2017) that for the sequence $\{r_{t}\}$ satisfying the above inequality, we have convergence to zero with the different rates stated in the Theorem.

In Corollary 10 and Theorem 13, the convergence rates do not depend on $p$ , and thus do not demonstrate the effect of momentum. Empirically, the proposed algorithm does have faster convergence when momentum is used, and will be shown in Section 5. This also agrees with previous studies in (Duchi et al., 2011; Kingma and Ba, 2014; Li and Lin, 2015; Li et al., 2017; Yao et al., 2017).

3.5 Statistical Guarantees

Existing statistical analysis on nonconvex regularization has been studied in the context of sparse and low-rank matrix learning. For example, the SCAD (Fan and Li, 2001), MCP (Zhang, 2010a) and capped- $\ell_{1}$ (Zhang, 2010b) penalties have shown to be better than the convex $\ell_{1}$ -regularizer on sparse learning problems; and SCAD, MCP and LSP have shown to be better than the convex nuclear norm in matrix completion (Gui et al., 2016). However, these results cannot be extended to the tensor completion problem here as the nonconvex overlapped nuclear norm regularizer in (10) is not separable. Statistical analysis on tensor completion has been studied with CP and Tucker decompositions (Mu et al., 2014), tensor ring decomposition (Huang et al., 2020), convex overlapped nuclear norm (Tomioka et al., 2011), and tensor nuclear norm (Yuan and Zhang, 2016; Cheng et al., 2016). They show that tensor completion is possible under the incoherence condition when the number of observations is sufficiently large. In comparison, in this section, we will (i) use the restricted strong convexity condition (Agarwal et al., 2010; Negahban et al., 2012)) instead of the incoherence condition, and (ii) study nonconvex overlapped nuclear norm regularization.

3.5.1 Controlling the Spikiness and Rank

In the following, we assume that elements in ${\bm{\bm{\Omega}}}$ are drawn i.i.d. from the uniform distribution. However, when the sample size $\left\|\mathbf{\Omega}\right\|_{1}\ll I^{\pi}$ , tensor completion is not always possible. Take the special case of matrix completion as an example. If $\mathscr{X}$ is an almost-zero matrix with only one element being $1$ , it cannot be recovered unless the nonzero element is observed. However, when $\mathscr{X}$ gets larger, there is a vanishing probability of observing the nonzero element, and so $P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}\right)=\mathbf{0}$ with high probability (Candès and Recht, 2009; Negahban and Wainwright, 2012).

To exclude tensors that are too “spiky” and allow tensor completion, we introduce

\displaystyle m_{\text{spike}}(\mathscr{X})=\sqrt{I^{\pi}}\left\|\mathscr{X}\right\|_{\max}/\left\|\mathscr{X}\right\|_{F},

(32)

which is an extension of the measure $\sqrt{I^{1}I^{2}}\left\|{\bm{\bm{X}}}\right\|_{\max}/\left\|{\bm{\bm{X}}}\right\|_{F}$ in (Negahban and Wainwright, 2012; Gu et al., 2014) for matrices. Note that $m_{\text{spike}}(\mathscr{X})$ is invariant to the scale of $\mathscr{X}$ and $1\leq m_{\text{spike}}(\mathscr{X})\leq\sqrt{I^{\pi}}$ . Moreover, $m_{\text{spike}}(\mathscr{X})=1$ when all elements in $\mathscr{X}$ have the same value (least spiky); and $m_{\text{spike}}(\mathscr{X})=\sqrt{I^{\pi}}$ when $\mathscr{X}$ has only one nonzero element (spikiest). Similarly, to measure how close is $\mathscr{X}$ to low-rank, we use

\displaystyle m_{\text{rank}}(\mathscr{X})=\sum\nolimits_{i=1}^{D}\alpha_{i}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}/\left\|\mathscr{X}\right\|_{F},

(33)

where $\alpha_{i}=\lambda_{i}/\sum_{d=1}^{D}\lambda_{d}$ ’s are pre-defined constants depending on the penalty strength. This is also extended from the measure $\left\|{\bm{\bm{X}}}\right\|_{*}/\left\|{\bm{\bm{X}}}\right\|_{F}$ in (Negahban and Wainwright, 2012; Gu et al., 2014) on matrices. Note that $m_{\text{rank}}(\mathscr{X})$ $\leq$ $\sum_{i=1}^{D}$ $\alpha_{i}$ $\sqrt{\text{rank}(\mathscr{X}_{{\left\langle i\right\rangle}})}$ , with equality holds when all nonzero singular values of $\mathscr{X}_{i}$ ’s are the same. The target tensor $\mathscr{X}$ should thus have small $m_{\text{spike}}(\mathscr{X})$ and $m_{\text{rank}}(\mathscr{X})$ . In (14), assume for simplicity that $D=M$ and $\lambda_{i}=\lambda$ for $i=1,\dots,M$ . We then have the following constrained version of (14):

\displaystyle\min\nolimits_{\mathscr{X}}\frac{1}{2}\left\|P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}-\mathscr{O}\right)\right\|_{F}^{2}+\lambda r(\mathscr{X})\quad\text{s.t.}\quad\left\|\mathscr{X}\right\|_{\max}\leq C,

(34)

where $r(\mathscr{X})=\sum\nolimits_{i=1}^{D}\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ encourages $\mathscr{X}$ to be low-rank (i.e., small $m_{\text{rank}}$ ), and the constraint on $\left\|\mathscr{X}\right\|_{\max}$ avoids $\mathscr{X}$ to be spiky (i.e., small $m_{\text{spike}}$ ).

3.5.2 Restricted Strong Convexity (RSC)

Following (Tomioka et al., 2011; Negahban and Wainwright, 2012; Loh and Wainwright, 2015; Zhu et al., 2018), we introduce the restricted strong convexity (RSC) condition.

Definition 14

(Restricted strong convexity (RSC) condition (Agarwal et al., 2010)) Let $\Delta$ be an arbitrary $M$ -order tensor. It satisfies the RSC condition if there exist constants $\alpha_{1},\alpha_{2}>0$ and $\tau_{1},\tau_{2}\geq 0$ such that

\displaystyle\left\|P_{{\bm{\bm{\Omega}}}}\left(\Delta\right)\right\|_{F}^{2}\geq\begin{cases}\alpha_{1}\left\|\Delta\right\|_{F}^{2}-\tau_{1}\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}\big{(}\sum_{i=1}^{M}\left\|\Delta_{{\left\langle i\right\rangle}}\right\|_{*}\big{)}^{2}&\text{if }\left\|\Delta\right\|_{F}\leq 1\\ \alpha_{2}\left\|\Delta\right\|_{F}^{2}-\tau_{2}\sqrt{\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}}\big{(}\sum_{i=1}^{M}\left\|\Delta_{{\left\langle i\right\rangle}}\right\|_{*}\big{)}&\text{otherwise}\end{cases}.

(35)

Let $d_{i}=\frac{1}{2}(I_{i}+\frac{I^{\pi}}{I_{i}})$ for $i=1,\dots,M$ . Consider the set of tensors parameterized by $n,\gamma\geq 0$ :

\displaystyle\tilde{\mathcal{C}}(n,\gamma)=\left\{\mathscr{X}\in\mathbb{R}^{I_{1}\times\dots\times I_{M}},\mathscr{X}\not=0\;|\;m_{\text{spike}}(\mathscr{X})\cdot m_{\text{rank}}(\mathscr{X})\leq\frac{1}{\gamma L}\min_{i=1,\dots,M}\sqrt{\frac{n}{d_{i}\log d_{i}}}\right\},

where $L$ is a positive constant. The following Lemma shows that the RSC condition holds when the low-rank tensor is not too spiky. If the RSC condition does not hold, the tensor can be too hard to be recovered.

Lemma 15

There exists $c_{0}$ , $c_{1}$ , $c_{2}$ , $c_{3}\geq 0$ such that $\forall\Delta\in\tilde{\mathcal{C}}(\left\|{\bm{\bm{\Omega}}}\right\|_{1},c_{0})$ , where $\left\|{\bm{\bm{\Omega}}}\right\|_{1}>c_{3}\underset{i=1,\dots,M}{\max}(d_{i}\log d_{i})$ , we have

\displaystyle\frac{\left\|P_{{\bm{\bm{\Omega}}}}\left(\Delta\right)\right\|_{F}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\geq\frac{1}{8}\left\|\Delta\right\|_{F}\left\{1-\frac{128L\cdot m_{\text{spike}}(\Delta)}{\sqrt{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\right\},

(36)

with a high probability of at least $1-\max_{i=1,\dots,M}c_{1}\exp(-c_{2}d_{i}\log d_{i})$ .

Another condition commonly used in low-rank matrix/tensor learning is incoherence (Candès and Recht, 2009; Mu et al., 2014; Yuan and Zhang, 2016), which prevents information of the row/column spaces of the matrix/tensor from being too concentrated in a few rows/columns. However, as discussed in (Negahban and Wainwright, 2012), the RSC condition is less restrictive than the incoherence condition, and can better describe “spikiness” (details are in Appendix A). Thus, we adopt the RSC instead of the incoherence condition here.

3.5.3 Main results

Let $\mathscr{X}^{*}\in\mathbb{R}^{I_{1}\times\dots\times I_{M}}$ be the ground-truth tensor, and $\tilde{\mathscr{X}}$ be an estimate of $\mathscr{X}^{*}$ obtained as a critical point of (34). The following bounds the distance between $\mathscr{X}^{*}$ and $\tilde{\mathscr{X}}$ .

Theorem 16

Assume that $\kappa$ is differentiable, and the RSC condition holds with $3\kappa_{0}M/4<\alpha_{1}$ . Assume that there exists positive constant $R>0$ such that $\sum_{i=1}^{M}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}\leq R$ , and $\lambda$ satisfies

\displaystyle\frac{4}{\kappa_{0}}\max\left(\max_{i}\left\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}^{*}-\mathscr{O}\right)\right]_{{\left\langle i\right\rangle}}\right\|_{\infty},\alpha_{2}\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\right)\leq\lambda\leq\frac{\alpha_{2}}{4R\kappa_{0}},

(37)

where $\|{\bm{\bm{\Omega}}}\|_{1}\geq\max\left(\tau_{1}^{2},\tau_{2}^{2}\right)\frac{16R^{2}\log(I^{\pi})}{\alpha_{2}^{2}}$ . Then,

\displaystyle\big{\|}\mathscr{X}^{*}-\tilde{\mathscr{X}}\big{\|}_{F}\leq\frac{\lambda\kappa_{0}c_{v}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}},

(38)

where $a_{v}=\alpha_{1}-\frac{3M\kappa_{0}}{4}$ , $c_{v}=1-\frac{1}{2M}$ , and $k_{i}$ is the rank of $\mathscr{X}^{*}_{{\left\langle i\right\rangle}}$ .

Proof [Sketch, details are in Appendix B.9.2.] The general idea of this proof is inspired from (Loh and Wainwright, 2015).³³3Note, however, that Loh and Wainwright (2015) use different mathematical tools as they consider sparse vectors with separable dimensions, while we consider overlapped tensor regularization with coupled singular values. There are three main steps:

•

Let $\tilde{\mathscr{V}}=\tilde{\mathscr{X}}-\mathscr{X}^{*}$ . We prove by contradiction that $\|\tilde{\mathscr{V}}\|_{F}\leq 1$ . Thus, we only need to consider the first condition in (35).

•

Let $h_{i}(\mathscr{X})\!=\!\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ . From Assumption 1, we have that $h_{i}(\mathscr{X})+\frac{\mu}{2}\left\|\mathscr{X}\right\|_{F}^{2}$ is convex. Using this together with the first condition in (35), we obtain

\displaystyle\left(\alpha_{1}-\frac{\mu M}{2}\right)\|\tilde{\mathscr{V}}\|_{F}^{2}

\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\big{(}h_{i}(\mathscr{X}^{*})-h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\kappa_{0}}{2}\sum\nolimits_{i=1}^{M}\|\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}}\|_{*}.

•

Using the above inequality and properties of $h_{i}$ , we obtain

\displaystyle a_{v}\|\tilde{\mathscr{V}}\|_{F}^{2}\leq\lambda\sum\nolimits_{i=1}^{M}b_{v}h_{i}(\mathscr{X}^{*})-c_{v}h_{i}(\tilde{\mathscr{X}}),

where $a_{v}=\alpha_{1}-\frac{3M}{4}\kappa_{0}$ , $b_{v}=1+\frac{1}{2M}$ and $c_{v}=1-\frac{1}{2M}$ . Finally, using Lemma 30 in Appendix B.9.1 on the above inequality, we have $\|\tilde{\mathscr{V}}\|_{F}\leq\frac{\lambda\kappa_{0}c_{v}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}$ .

Since $\left\|\mathscr{X}\right\|_{\max}\leq C$ in (34), we have $\sum_{i=1}^{M}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}\leq\sum_{i=1}^{M}\sqrt{k_{i}(I_{i}+\frac{I^{\pi}}{I_{i}})}C$ (as $\left\|{\bm{\bm{X}}}\right\|_{*}\leq\sqrt{k}\left\|{\bm{\bm{X}}}\right\|_{F}\leq\sqrt{mnk}\left\|{\bm{\bm{X}}}\right\|_{\max}$ for a rank- $k$ matrix ${\bm{\bm{X}}}\in\mathbb{R}^{m\times n}$ ). Thus, in Theorem 16, we can take $R=\sum_{i=1}^{M}$ $\sqrt{k_{i}(I_{i}+I^{\pi}/I_{i})}C$ , which is finite and cannot be arbitrarily large. While we do not have access to the ground-truth $\mathscr{X}^{*}$ in practice, Theorem 16 shows that the critical point $\tilde{\mathscr{X}}$ can be bounded by a finite distance from $\mathscr{X}^{*}$ , which means that an arbitrary critical point may not be bad. From (38), we can also see that the error $\|\mathscr{X}^{*}-\tilde{\mathscr{X}}\|_{F}$ increases with the tensor order $M$ and rank $k_{i}$ . This is reasonable as tensors with higher orders or larger ranks are usually harder to estimate. Besides, recall that $\kappa_{0}$ in Assumption 1 reflects how nonconvex the function $\kappa(\alpha)$ is; while $\alpha_{1}$ in Definition 14 measures strong convexity. Thus, these two quantities play opposing roles in (38). Specifically, a larger $\alpha_{1}$ leads to a larger $a_{v}$ , and subsequently smaller $\|\mathscr{X}^{*}-\tilde{\mathscr{X}}\|_{F}$ ; whereas a larger $\kappa_{0}$ leads to a larger $\frac{\lambda\kappa_{0}c_{v}}{a_{v}}$ , and subsequently larger $\|\mathscr{X}^{*}-\tilde{\mathscr{X}}\|_{F}$ .

Finally, note that the range for $\lambda$ is (37) can be empty, which means there can be no $\lambda$ to ensure Theorem 16. To understand when this can happen, consider the two extreme cases:

C1.

There is no noise in the observations, i.e., $P_{{\bm{\bm{\Omega}}}}\left(\mathscr{X}^{*}-\mathscr{O}\right)$ $=0$ : In this case, (37) reduces to

\displaystyle\frac{4\alpha_{2}}{\kappa_{0}}\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\leq\lambda\leq\frac{\alpha_{2}}{4R\kappa_{0}}.

Thus, such a $\lambda$ may not exist when the number of observations $\left\|\bm{\Omega}\right\|_{1}$ is too small.

C2.

All elements are observed: we then have $\left\|P_{{\bm{\bm{\Omega}}}}\left(\Delta\right)\right\|_{F}=\left\|\Delta\right\|_{F}$ , and so $\alpha_{1}=\alpha_{2}=1$ and $\tau_{1}=\tau_{2}=0$ in Definition 14. Besides, the noise is not too small, which means $\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\leq\max_{i}\|\left[\mathscr{X}^{*}-\mathscr{O}\right]_{{\left\langle i\right\rangle}}\|_{\infty}$ . Then, (37) reduces to

\displaystyle\frac{4}{\kappa_{0}}\max_{i}\left\|\left[\mathscr{X}^{*}-\mathscr{O}\right]_{{\left\langle i\right\rangle}}\right\|_{\infty}\leq\lambda\leq\frac{1}{4R\kappa_{0}}.

Thus, such a $\lambda$ may not exist when the noise is too high.

Overall, when $\lambda$ does not exist, it is likely that the tensor completion problem is too hard to have good recovery performance.

On the other hand, there are cases that $\lambda$ always exists. For example, when $\mathscr{O}=\mathscr{X}^{*}=0$ , we have $R=0$ . The requirement on $\lambda$ is then $\frac{4\alpha_{2}}{\kappa_{0}}\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\leq\lambda\leq+\infty$ , and such a $\lambda$ always exists.

3.5.4 Dependencies on Noise Level and Number of Observations

In this section, we demonstrate how the noise level affects (38). We assume that the observations are contaminated by additive Gaussian noise, i.e.,

\displaystyle\mathscr{O}_{i_{1}\dots i_{M}}=\begin{cases}\mathscr{X}^{*}_{i_{1}\dots i_{M}}+\xi_{i_{1}\dots i_{M}}&\text{if}\quad{\bm{\bm{\Omega}}}_{i_{1}\dots i_{M}}=1\\ 0&\text{otherwise}\end{cases},

(39)

where $\xi_{i_{1}\dots i_{M}}$ is a random variable following the normal distribution $\mathcal{N}(0,\sigma^{2})$ . The effects of the noise level $\sigma$ and number of observations in ${\bm{\bm{\Omega}}}$ are shown in Corollaries 17 and 18, respectively, which can be derived from Theorem 16.

Corollary 17

Let $\mathscr{E}=\mathscr{O}-\mathscr{X}^{*}$ and $\lambda=b_{1}\max_{i}\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}$ . When $\left\|{\bm{\bm{\Omega}}}\right\|_{1}$ is sufficiently large and $b_{1}\in[\frac{4}{\kappa_{0}},\frac{\alpha_{2}}{4R\kappa_{0}\max_{i}\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}}]$ (to ensure $\lambda$ satisfies (37)), then $\mathbb{E}[\|\mathscr{X}^{*}-\tilde{\mathscr{X}}\|_{F}]\leq\sigma\frac{\kappa_{0}c_{v}\sqrt{I^{\pi}}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}$ .

Corollary 17 shows that the recovery error decreases as the noise level $\sigma$ gets smaller, and we can expect an exact recovery when $\sigma=0$ , which is empirically verified in Section 5.1.4. When $\kappa(\alpha)=\alpha$ , $r(\mathscr{X})$ becomes the convex overlapping nuclear norm. In this case, Theorem 2 in (Tomioka et al., 2011) shows that the recovery error can be bounded as $\big{\|}\mathscr{X}^{*}-\tilde{\mathscr{X}}\big{\|}_{F}\leq O(\sigma\sum\nolimits_{i=1}^{M}\sqrt{k_{i}})$ . Thus, Corollary 17 can be seen as an extension of Theorem 2 in (Tomioka et al., 2011) to the nonconvex case.

Corollary 18

Let $\lambda=b_{3}\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}$ . Suppose that the noise level $\sigma$ is sufficiently small and $b_{3}\in\left[4,\frac{1}{(4R\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}})}\right]$ (to ensure $\lambda$ satisfies (37)). Then, $\big{\|}\mathscr{X}^{*}\!-\!\tilde{\mathscr{X}}\big{\|}_{F}\!\leq\!\frac{b_{3}\kappa_{0}c_{v}}{a_{v}}\sqrt{\frac{\log I^{\pi}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}$ .

Corollary 18 shows that the recovery error decays as $\sqrt{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}$ gets larger. Such a dependency on the number of observed elements is the same as in matrix completion problems with nonconvex regularization (Gui et al., 2016). Corollary 18 can be seen as an extension of Corollary 3.6 in (Gui et al., 2016) to the tensor case.

4 Extensions

In this section, we show how the proposed NORT algorithm in Section 3 can be extended for robust tensor completion (Section 4.1) and tensor completion with graph Laplacian regularization (Section 4.2).

4.1 Robust Tensor Completion

In tensor completion applications such as video recovery and shadow removal, the observed data often have outliers (Candès et al., 2011; Lu et al., 2016a). Instead of using the square loss, more robust losses like the $\ell_{1}$ loss (Candès et al., 2011; Lu et al., 2013; Gu et al., 2014) and capped- $\ell_{1}$ loss (Jiang et al., 2015), are preferred.

In the following, we assume that the loss is of the form $\ell(a)=\kappa_{\ell}(|a|)$ , where $\kappa_{\ell}$ is smooth and satisfies Assumption 1. The optimization problem then becomes

\displaystyle\min\nolimits_{\mathscr{X}}F_{\ell}(\mathscr{X})=\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\kappa_{\ell}\left(|\mathscr{X}_{i_{1}\dots i_{M}}-\mathscr{O}_{i_{1}\dots i_{M}}|\right)+\sum\nolimits_{i=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle i\right\rangle}}).

(40)

Since $\kappa_{\ell}(|a|)$ is non-differentiable at $a=0$ , Algorithm 2 cannot be directly used. Motivated by smoothing the $\ell_{1}$ loss with the Huber loss (Huber, 1964) and the difference-of-convex decomposition of $\kappa_{\ell}$ (Le Thi and Tao, 2005; Yao and Kwok, 2018), we propose to smoothly approximate $\kappa_{\ell}(|a|)$ by

\displaystyle\tilde{\kappa}_{\ell}(|a|;\delta)=\kappa_{0}\cdot\tilde{\ell}(|a|;\delta)+\Big{(}\kappa_{\ell}(|a|)-\kappa_{0}\cdot|a|\Big{)},

(41)

where $\kappa_{0}$ is in Assumption 1, $\delta$ is a smoothing parameter, and $\tilde{\ell}$ is the Huber loss (Huber, 1964):

\displaystyle\tilde{\ell}(a;\delta)=\begin{cases}|a|&|a|\geq\delta\\ \frac{1}{2\delta}a^{2}+\frac{1}{2}\delta&\text{otherwise}\end{cases}.

The following Proposition shows that $\tilde{\kappa}_{\ell}$ is smooth, and a small $\delta$ ensures that it is a close approximation to $\kappa_{\ell}$ .

Proposition 19

$\tilde{\kappa}_{\ell}(|a|;\delta)$ is differentiable and $\lim_{\delta\rightarrow 0}\tilde{\kappa}_{\ell}(|a|;\delta)=\kappa_{\ell}(|a|)$ .

Problem (40) is then transformed to

\displaystyle\min\nolimits_{\mathscr{X}}\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\tilde{\kappa}_{\ell}(|\mathscr{X}_{i_{1}...i_{M}}-\mathscr{O}_{i_{1}...i_{M}}|;\delta)+\sum\nolimits_{i=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle i\right\rangle}}).

(42)

In Algorithm 3, we gradually reduce the smoothing factor in step 3, and use Algorithm 2 to solve the smoothed problem (42) in each iteration.

Algorithm 3 Smoothing NORT for (40).

1: Initialize

\delta_{0}\in(0,1)

and

s=1

;

2: while not converged do

3: transform to problem (42) with

\tilde{\kappa}_{\ell}

using

\delta=(\delta_{0})^{s}

;

4: obtain

\mathscr{X}_{s}

by solving the smoothed objective with Algorithm 2;

s=s+1

;

6: end while

7: return

\mathscr{X}_{s}

Convergence of Algorithm 3 is ensured in Theorem 20. However, the statistical guarantee in Section 3.5 does not hold as the robust loss is not smooth.

Theorem 20

The sequence $\{\mathscr{X}_{s}\}$ generated from Algorithm 3 has at least one limit point, and all limits points are critical points of $F_{\ell\tau}(\mathscr{X})=\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\kappa_{\ell}\left(|\mathscr{X}_{i_{1}\dots i_{M}}-\mathscr{O}_{i_{1}\dots i_{M}}|\right)+\bar{g}_{\tau}(\mathscr{X})$ .

4.2 Tensor Completion with Graph Laplacian Regularization

The graph Laplacian regularizer is often used in tensor completion (Narita et al., 2012; Song et al., 2017). For example, in Section 5.5, we will consider an application in spatial-temporal analysis (Bahadori et al., 2014), namely, climate prediction based on meteorological records. The spatial-temporal data is represented by a 3-order tensor $\mathscr{O}\in\mathbb{R}^{I^{1}\times I^{2}\times I^{3}}$ , where $I^{1}$ is the number of locations, $I^{2}$ is the number of time stamps, and $I^{3}$ is the number of variables corresponding to climate observations (such as temperature and precipitation). Usually, observations are only available at a few stations, and slices in $\mathscr{O}$ corresponding to the unobserved locations are missing. Learning these entries can then be formulated as a tensor completion problem. To allow generalization to the unobserved locations, correlations among locations have to be leveraged. This can be achieved by using the graph Laplacian regularizer (Belkin et al., 2006) on a graph $G$ with nodes being the locations (Bahadori et al., 2014). Let the affinity matrix of $G$ be $\bm{A}\in\mathbb{R}^{m\times m}$ , and the corresponding graph Laplacian matrix be $\bm{G}=\bm{D}-\bm{A}$ , where $D_{ii}=\sum_{j}A_{ij}$ . As the spatial locations are stored along the tensor’s first dimension, the graph Laplacian regularizer is defined as $h(\mathscr{X}_{{\left\langle 1\right\rangle}})=\text{Tr}(\mathscr{X}_{{\left\langle 1\right\rangle}}^{\top}\bm{G}\mathscr{X}_{{\left\langle 1\right\rangle}})$ , which encourages nearby stations to have similar observations. When $\bm{G}=\bm{I}$ , it reduces to the commonly used Frobenius-norm regularizer $\left\|\mathscr{X}\right\|_{F}^{2}$ (Hsieh et al., 2015). With regularizer $h(\mathscr{X}_{{\left\langle 1\right\rangle}})$ , problem (14) is then extended to:

\displaystyle\min\nolimits_{\mathscr{X}}\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)+\sum\nolimits_{i=1}^{D}\lambda_{i}\,\phi(\mathscr{X}_{{\left\langle i\right\rangle}})+\mu\,h(\mathscr{X}_{{\left\langle 1\right\rangle}}),

(43)

where $\mu$ is a hyperparameter.

Using the PA algorithm, it can be easily seen that the updates in (18)-(20) for $\mathscr{X}_{t}$ and $\mathscr{Y}_{t}$ remain the same, but that for $\mathscr{Z}_{t}$ becomes

\mathscr{Z}_{t}=\mathscr{X}_{t}-\frac{1}{\tau}\xi(\mathscr{X}_{t})+\mu\nabla\text{Tr}(\mathscr{X}_{{\left\langle 1\right\rangle}}^{\top}\bm{G}\mathscr{X}_{{\left\langle 1\right\rangle}}).

To maintain efficiency of NORT, the key is to exploit the low-rank structures. Using (22), $\mathscr{Z}_{t}$ can be written as

\displaystyle\mathscr{Z}_{t}

\displaystyle=

\displaystyle\sum\nolimits_{i=1}^{D}(\bm{U}_{t}^{i}(\bm{V}_{t}^{i})^{\top})^{{\left\langle i\right\rangle}}-\frac{1}{\tau}\xi(\mathscr{X}_{t})-\mu[\bm{G}\mathscr{X}_{{\left\langle 1\right\rangle}}]^{{\left\langle 1\right\rangle}}.

(44)

$\bm{G}\mathscr{X}_{{\left\langle 1\right\rangle}}$ can also be rewritten in low-rank form as

\displaystyle\bm{G}\mathscr{X}_{{\left\langle 1\right\rangle}}=(\bm{G}\bm{U}_{t}^{1})(\bm{V}_{t}^{1})^{\top}+\bm{G}\sum\nolimits_{j\neq 1}\big{[}(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle 1\right\rangle}}.

For matrix multiplications of the forms $\bm{a}^{\top}(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}$ and $(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}\bm{b}$ involved in the SVD of the proximal step, we have

\displaystyle\!\!\bm{a}^{\top}(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}\!=\!(\bm{a}^{\top}(\bm{I}\!-\!\mu\bm{G})\bm{U}_{t}^{i})(\bm{V}_{t}^{i})^{\top}\!\!\!+\!\sum\nolimits_{j\neq i}\bm{a}^{\top}(\bm{I}\!-\!\mu\bm{G})\big{[}(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}\!\!-\!\frac{1}{\tau}\bm{a}^{\top}[\xi(\mathscr{X}_{t})]_{{\left\langle i\right\rangle}},\!\!

(45)

and

\displaystyle(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}\bm{b}=(\bm{I}\!-\!\mu\bm{G})\bm{U}_{t}^{i}\big{[}(\bm{V}_{t}^{i})^{\top}\bm{b}\big{]}+(\bm{I}-\mu\bm{G})\sum\nolimits_{j\neq i}\big{[}(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}\big{]}_{{\left\langle i\right\rangle}}\bm{b}-\frac{1}{\tau}[\xi(\mathscr{X}_{t})]_{{\left\langle i\right\rangle}}\bm{b}.

(46)

Thus, one can still leverage the efficient computational procedures in Proposition 4 to compute $\bm{\hat{a}}^{\top}[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}$ , where $\bm{\hat{a}}^{\top}\!\!\!=\!\bm{a}^{\top}\!(\bm{I}\!-\!\mu\bm{G})$ in (45), and $[(\bm{U}_{t}^{j}(\bm{V}_{t}^{j})^{\top})^{{\left\langle j\right\rangle}}]_{{\left\langle i\right\rangle}}\bm{b}$ in (46).

By taking $f(\mathscr{X})=\sum\nolimits_{\mathbf{\Omega}_{i_{1}...i_{M}}=1}\ell\left(\mathscr{X}_{i_{1}\dots i_{M}},\mathscr{O}_{i_{1}\dots i_{M}}\right)+\mu\,h(\mathscr{X}_{{\left\langle 1\right\rangle}})$ , it is easy to see that the statistical analysis in Section 3.4 and convergence analysis in Section 3.5 still hold.

5 Experiments

In this section, experiments are performed on both synthetic (Section 5.1) and real-world data sets (Sections 5.2-5.5), using a PC with Intel-i9 CPU and 32GB memory. To reduce statistical variation, all results are averaged over five repetitions.

5.1 Synthetic Data

We follow the setup in (Song et al., 2017). First, we generate a 3-order tensor (i.e., $M=3$ ) $\bar{\mathscr{O}}=\sum_{i=1}^{r_{g}}s_{i}(\bm{a}_{i}\circ\bm{b}_{i}\circ\bm{c}_{i})$ , where $\bm{a}_{i}\in\mathbb{R}^{I^{1}}$ , $\bm{b}_{i}\in\mathbb{R}^{I^{2}}$ and $\bm{c}_{i}\in\mathbb{R}^{I^{3}}$ , $\circ$ denotes the outer product (i.e., $[\bm{a}\circ\bm{b}\circ\bm{c}]_{ijk}=a_{i}b_{j}c_{k}$ ). $r_{g}$ denotes the ground-truth rank and is set to 5, with all $k_{i}$ ’s equal to $r_{g}=5$ . All elements in $\bm{a}_{i}$ ’s, $\bm{b}_{i}$ ’s, $\bm{c}_{i}$ ’s and $s_{i}$ ’s are sampled independently from the standard normal distribution. Each element of $\bar{\mathscr{O}}$ is then corrupted by noise from $\mathcal{N}(0,0.01^{2})$ to form $\mathscr{O}$ . A total of $\|{\bm{\bm{\Omega}}}\|_{1}=\frac{I^{3}}{r_{g}}\sum_{i=1}^{3}I^{i}\log(I^{\pi})$ random elements are observed from $\mathscr{O}$ . We use $50\%$ of them for training, and the remaining $50\%$ for validation. Testing is evaluated on the unobserved elements in $\mathscr{\bar{O}}$ .

We use the square loss and three nonconvex penalties: capped- $\ell_{1}$ (Zhang, 2010a), LSP (Candès et al., 2008) and TNN (Hu et al., 2013). The following methods are compared:

•

PA-APG (Yu, 2013), which solves the convex overlapped nuclear norm minimization problem;
•

GDPAN (Zhong and Kwok, 2014), which directly applies the PA algorithm to (14) as described in (18)-(20);
•

LRTC (Chen et al., 2020), which uses ADMM (Boyd et al., 2011) on (14) as described in (15)-(17); and
•

The proposed NORT algorithm (Algorithm 2), and its slower variant without adaptive momentum (denoted “sNORT”). Recall from Corollary 10 that $\tau$ has to be larger than $\rho+D\kappa_{0}$ . However, a large $\tau$ leads to slow convergence (Remark 11). Hence, we set $\tau=1.01(\rho+D\kappa_{0})$ . Moreover, as in (Li et al., 2017), we set $\gamma_{1}=0.1$ and $p=0.5$ in Algorithm 2.

All algorithms are implemented in Matlab, with sparse tensor and matrix operations performed via Mex files in C. All hypeprparamters (including the $\lambda_{i}$ ’s in (14) and hyperparameter in the baselines) are tuned by grid search using the validation set. We early stop training if the relative change of objective in consecutive iterations is smaller than $10^{-4}$ or reaching the maximum of $2000$ iterations.

5.1.1 Recovery Performance Comparison

In this experiment, we set $I^{1}=I^{2}=I^{3}=\hat{c}$ , where $\hat{c}=200$ and $400$ . Following (Lu et al., 2016b; Yao et al., 2017, 2019b), performance is evaluated by the (i) root-mean-square-error on the unobserved elements: $\text{RMSE}=\left\|P_{\bar{{\bm{\bm{\Omega}}}}}(\mathscr{X}-\bar{\mathscr{O}})\right\|_{F}/\left\|\bar{{\bm{\bm{\Omega}}}}\right\|_{1}^{0.5}$ , where $\mathscr{X}$ is the low-rank tensor recovered, and $\bar{{\bm{\bm{\Omega}}}}$ contains the unobserved elements in $\bar{\mathscr{O}}$ ; (ii) CPU time; and (iii) space, which is measured as the memory used by MATLAB when running each algorithm.

Results on RMSE and space are shown in Table 3. We can see that the nonconvex regularizers (capped- $\ell_{1}$ , LSP and TNN, with methods GDPAN, LRTC, sNORT and NORT) all yield almost the same RMSE, which is much lower than that of using the convex nuclear norm regularizer in PA-APG. As for the space required, sNORT and NORT take orders of magnitude smaller space than the others. LRTC takes the largest space due to the use of multiple auxiliary and dual variables. Convergence of the optimization objective is shown in Figure 1. As can be seen, NORT is the fastest, followed by sNORT and GDPAN, while LRTC is the slowest. These demonstrate the benefits of avoiding repeated tensor folding/unfolding operations and faster convergence of the proximal average algorithm.

Table 3: Testing RMSE and space required for the synthetic data.

		$\hat{c}=200$ (sparsity: $4.77\%$ )		$\hat{c}=400$ (sparsity: $2.70\%$ )
		RMSE	space (MB)	RMSE	space (MB)
convex	PA-APG	0.0110 $\pm$ 0.0007	600.8 $\pm$ 70.4	0.0098 $\pm$ 0.0001	4804.5 $\pm$ 598.2
	GDPAN	0.0010 $\pm$ 0.0001	423.1 $\pm$ 11.4	0.0006 $\pm$ 0.0001	3243.3 $\pm$ 489.6
nonconvex	LRTC	0.0010 $\pm$ 0.0001	698.9 $\pm$ 21.5	0.0006 $\pm$ 0.0001	5870.6 $\pm$ 514.0
(capped- $\ell_{1}$ )	sNORT	0.0010 $\pm$ 0.0001	10.1 $\pm$ 0.1	0.0006 $\pm$ 0.0001	44.6 $\pm$ 0.3
	NORT	0.0009 $\pm$ 0.0001	14.4 $\pm$ 0.1	0.0006 $\pm$ 0.0001	66.3 $\pm$ 0.6
	GDPAN	0.0010 $\pm$ 0.0001	426.9 $\pm$ 9.7	0.0006 $\pm$ 0.0001	3009.3 $\pm$ 376.2
nonconvex	LRTC	0.0010 $\pm$ 0.0001	714.0 $\pm$ 24.1	0.0006 $\pm$ 0.0001	5867.7 $\pm$ 529.1
(LSP)	sNORT	0.0010 $\pm$ 0.0001	10.8 $\pm$ 0.1	0.0006 $\pm$ 0.0001	44.6 $\pm$ 0.2
	NORT	0.0010 $\pm$ 0.0001	14.0 $\pm$ 0.1	0.0006 $\pm$ 0.0001	62.1 $\pm$ 0.5
	GDPAN	0.0010 $\pm$ 0.0001	427.3 $\pm$ 10.1	0.0006 $\pm$ 0.0001	3009.2 $\pm$ 412.2
nonconvex	LRTC	0.0010 $\pm$ 0.0001	759.0 $\pm$ 24.3	0.0006 $\pm$ 0.0001	5865.5 $\pm$ 519.3
(TNN)	sNORT	0.0010 $\pm$ 0.0001	10.2 $\pm$ 0.1	0.0006 $\pm$ 0.0001	44.7 $\pm$ 0.2
	NORT	0.0010 $\pm$ 0.0001	14.4 $\pm$ 0.2	0.0006 $\pm$ 0.0001	63.1 $\pm$ 0.6

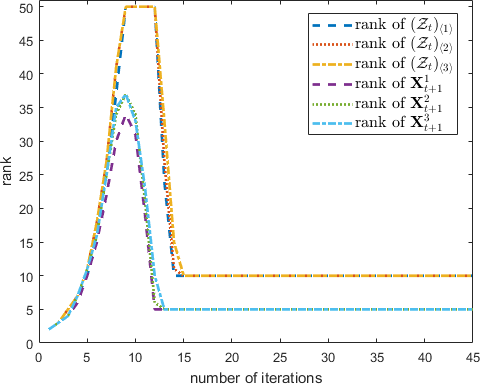
Refer to caption — (a) capped- $\ell_{1}$ .

5.1.2 Ranks during Iteration

Unlike factorization methods which explicitly constrain the iterate’s rank, in NORT (Algorithm 2), this is only implicitly controlled by the nonconvex regularizer. As shown in Table 2, having a large rank during the iteration may affect the efficiency of NORT. Figure 2 shows the ranks of $(\mathscr{Z}_{t})_{{\left\langle i\right\rangle}}$ and ${\bm{\bm{X}}}_{t+1}^{i}$ at step 11 of Algorithm 2. As can be seen, the ranks of the iterates remain small compared with the tensor size ( $\hat{c}=400$ ). Moreover, the ranks of ${\bm{\bm{X}}}_{t+1}^{1}$ , ${\bm{\bm{X}}}_{t+1}^{2}$ , and ${\bm{\bm{X}}}_{t+1}^{3}$ all converge to the true rank (i.e., $5$ ) of the ground-truth tensor.

5.1.3 Quality of Critical Points

In this experiment, we empirically validate the statistical performance of critical points analysed in Theorem 16. Note that $\mathscr{X}_{0}$ and $\mathscr{X}_{1}$ are initialized as the zero tensor in Algorithm 2, and $\mathscr{X}_{t}$ is implicitly stored by a summation of $D$ factorized matrices in (22). We randomly generate $\mathscr{X}_{0}=\mathscr{X}_{1}=\sum\nolimits_{i=1}^{D}\big{(}{\bm{\bm{u}}}^{i}({\bm{\bm{v}}}^{i})^{\top}\big{)}^{{\left\langle i\right\rangle}}$ , where elements in $\bm{u}^{i}$ ’s and $\bm{v}^{i}$ ’s follow $\mathcal{N}(0,1)$ . The statistical error is measured as the RMSE between $\mathscr{X}_{t}$ during iterating of NORT (Algorithm 2) and the underlying ground-truth $\mathscr{X}^{*}$ (i.e., $\|\mathscr{X}_{t}-\mathscr{X}^{*}\|_{F}^{2}$ ), while the optimization error is measured as the RMSE between iterate $\mathscr{X}_{t}$ and the globally optimal solution $\dot{\mathscr{X}}$ of (14) (i.e., $\|\mathscr{X}_{t}-\dot{\mathscr{X}}\|_{F}^{2}$ ). We use the same experimental setup as in Section 5.1.1. As the exact $\dot{\mathscr{X}}$ is not known, it is approximated by the $\tilde{\mathscr{X}}$ which obtains the lowest training objective value over 20 repetitions.

Figure 3 shows the statistical error versus optimization error obtained by NORT with the (smooth) LSP regularizer and (nonsmooth) capped- $\ell_{1}$ regularizer. While both the statistical and optimization errors decrease with more iterations, the statistical error is generally larger than the optimization error since we may not have exact recovery when noise is present. Moreover, the optimization errors for different runs terminate at different values, indicating that NORT indeed converges to different local solutions. However, all these have similar statistical errors, which validates Theorem 16. Finally, while the capped- $\ell_{1}$ regularizer does not satisfy Assumption 1 (which is required by Theorem 16), Figure 3(b) still shows a similar pattern as Figure 3(a). This helps explain the good empirical performance obtained by the capped- $\ell_{1}$ regularizer (Jiang et al., 2015; Lu et al., 2016b; Yao et al., 2019b).

5.1.4 Effects of Noise Level and Number of Observations

In this section, we show the effects of noise level $\sigma$ and number of observed elements $\left\|\mathbf{\Omega}\right\|_{1}$ on the testing RMSE and training time. We use the same experimental setup as in Section 5.1.1. Since PA-APG is much worse (see Table 3) while LRTC and sNORT are slower than NORT (see Figure 1), we only use GDPAN as comparison baseline.

Figure 4(a) shows the testing RMSE with $\sigma$ at different $\left\|\mathbf{\Omega}\right\|_{1}$ ’s (here, we plot $s=\left\|{\bm{\bm{\Omega}}}\right\|_{1}/I^{\pi}$ ). As can be seen, the curves show a linear dependency on $\sigma$ when $\left\|{\bm{\bm{\Omega}}}\right\|_{1}$ is sufficiently large, which agrees with Corollary 17. Figure 4(b) shows the testing RMSE versus $\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}$ at different $\sigma$ ’s. As can be seen, there is a linear dependency when the noise level $\sigma$ is small, which agrees with Corollary 18. Finally, note that NORT and GDPAN obtain very similar testing RMSEs as both solve the same objective (but with different algorithms).

Figure 5 shows the effects of noise level on the convergence of testing RMSE versus (training) CPU time. As can be seen, testing RMSEs generally terminates at a higher level when the noise level gets larger, and NORT is much faster than GDPAN under all noise level.

Figure 6 shows the effects of numbers of observations on the convergence of testing RMSE versus (training) CPU time. First, we can see that NORT is much faster than GDPAN under various numbers of observations. Then, when $s$ gets smaller and the tensor completion problem is more ill-posed, more iterations are needed by both NORT and GDPAN, which makes them take more time to converge.

5.1.5 Effects of Tensor Order and Rank

In this experiment, we use a similar experimental setup as in Section 5.1.1, except that the tensor order $M$ is varied from $2$ to $5$ . As high-order tensors have large memory requirements, while we always set $I^{1}=I^{2}=I^{3}=\hat{c}=400$ , we set $I^{4}=5$ when $M=4$ and $I^{4}=I^{5}=5$ when $M=5$ . Figure 7(a) shows the testing RMSE versus $M$ . As can be seen, the error grows almost linearly, which agrees with Theorem 16. Moreover, note that at $M=5$ , GDPAN runs out of memory because it needs to maintain dense tensors in each iteration.

Figure 7(b) shows the testing RMSE w.r.t. $\sqrt{r_{g}}$ (where $r_{g}$ is the ground-truth tensor rank). As can be seen, the error grows linearly w.r.t. $\sqrt{r_{g}}$ , which again agrees with Theorem 16.

Figure 8(a) shows the convergence of testing RMSE versus (training) CPU time at different tensor orders. As can be seen, while both GDPAN and NORT need more time to converge for higher-order tensors, NORT is consistently faster than GDPAN. Figure 8(b) shows the convergence of testing RMSE at different ground-truth ranks. As can be seen, while NORT is still faster than GDPAN at different ground-truth tensor ranks ( $r_{g}$ ), the relative speedup gets smaller when $r_{g}$ gets larger. This is because NORT needs to construct sparse tensors (e.g., Algorithm 1) before using them for multiplications, and empirically, the handling of sparse tensors requires more time on memory addressing as the rank increases (Bader and Kolda, 2007).

5.2 Tensor Completion Applications

Table 4: Algorithms compared on the real-world data sets.

	algorithm	model	basic solver
convex	ADMM (Tomioka et al., 2010)		ADMM
	FaLRTC (Liu et al., 2013)	overlapped nuclear norm	accelerated proximal algorithm on dual problem
	PA-APG (Yu, 2013)		accelerated PA algorithm
	FFW (Guo et al., 2017)	latent nuclear norm	efficient Frank-Wolfe algorithm
	TR-MM (Nimishakavi et al., 2018)	squared latent nuclear norm	Riemannian optimization on dual problem
	TenNN (Zhang and Aeron, 2017)	tensor-SVD	ADMM
factorization	RP (Kasai and Mishra, 2016)	Turker decomposition	Riemannian preconditioning
	TMac (Xu et al., 2013)	multiple matrices factorization	alternative minimization
	CP-WOPT (Hong et al., 2020)	CP decomposition	nonlinear conjugate gradient
	TMac-TT (Bengua et al., 2017)	tensor-train decomposition	alternative minimization
	TRLRF (Yuan et al., 2019)	tensor-ring decomposition	ADMM
non-convex	GDPAN (Zhong and Kwok, 2014)		nonconvex PA algorithm
	LRTC (Chen et al., 2020)	nonconvex overlapped nuclear norm regularization	ADMM
	NORT (Algorithm 2)		proposed algorithm

In this section, we use the square loss. As different nonconvex regularizers have similar performance, we will only use LSP in the sequel. The proposed NORT algorithm is compared with:⁴⁴4We used our own implementations of LRTC, PA-APG and GDPAN as their codes are not publicly available.

(i)

algorithms for various convex regularizers including: ADMM (Boyd et al., 2011)⁵⁵5https://web.stanford.edu/~boyd/papers/admm/, PA-APG (Yu, 2013), FaLRTC (Liu et al., 2013)⁶⁶6https://github.com/andrewssobral/mctc4bmi/tree/master/algs_tc/LRTC, FFW (Guo et al., 2017)⁷⁷7https://github.com/quanmingyao/FFWTensor, TR-MM (Nimishakavi et al., 2018)⁸⁸8https://github.com/madhavcsa/Low-Rank-Tensor-Completion, and TenNN (Zhang and Aeron, 2017)⁹⁹9http://www.ece.tufts.edu/~shuchin/software.html;
(ii)

factorization-based algorithms including: RP (Kasai and Mishra, 2016)¹⁰¹⁰10https://bamdevmishra.in/codes/tensorcompletion/, TMac (Xu et al., 2013)¹¹¹¹11http://www.math.ucla.edu/~wotaoyin/papers/tmac_tensor_recovery.html, CP-WOPT (Hong et al., 2020)¹²¹²12https://www.sandia.gov/~tgkolda/TensorToolbox/, TMac-TT (Bengua et al., 2017)¹³¹³13https://sites.google.com/site/jbengua/home/projects/efficient-tensor-completion- for-color-image-and-video-recovery-low-rank-tensor-train, and TRLRF (Yuan et al., 2019)¹⁴¹⁴14https://github.com/yuanlonghao/TRLRF;
(iii)

algorithms that can handle nonconvex regularizers including GDPAN (Zhong and Kwok, 2014) and LRTC (Chen et al., 2020).

More details are in Table 4. We do not compare with (i) sNORT, as it has already been shown to be slower than NORT; (ii) iterative hard thresholding (Rauhut et al., 2017), as its code is not publicly available and the more recent TMac-TT solves the same problem; (iii) the method in (Bahadori et al., 2014), as it can only deal with cokriging and forecasting problems.

Unless otherwise specified, performance is evaluated by (i) root-mean-squared-error on the unobserved elements: $\text{RMSE}=\left\|P_{{\bm{\bm{\Omega}}}^{\bot}}(\mathscr{X}-\mathscr{O})\right\|_{F}/\left\|{\bm{\bm{\Omega}}}^{\bot}\right\|_{1}^{0.5}$ , where $\mathscr{X}$ is the low-rank tensor recovered, and ${\bm{\bm{\Omega}}}^{\bot}$ contains the unobserved elements in $\mathscr{O}$ ; and (ii) CPU time.

5.2.1 Color Images

We use the Windows, Tree and Rice images from (Hu et al., 2013), which are resized to $1000\times 1000\times 3$ (Figure 9). Each pixel is normalized to $[0,1]$ . We randomly sample 5% of the pixels for training, which are then corrupted by Gaussian noise $\mathcal{N}(0,0.01^{2})$ ; and another 5% clean pixels are used for validation. The remaining unseen clean pixels are used for testing. Hyperparameters of the various methods are tuned by using the validation set.

Table 5 shows the RMSE results. As can be seen, the best convex methods (PA-APG and FaLRTC) are based on the overlapped nuclear norm. This agrees with our motivation to build a nonconvex regularizer based on the overlapped nuclear norm. GDPAN, LRTC and NORT have similar RMSEs, which are lower than those by convex regularization and the factorization approach. Convergence of the testing RMSE is shown in Figure 10. As can be seen, while ADMM solves the same convex model as PA-APG and FaLRTC, it has slower convergence. FFW, RP and TR-MM are very fast but their testing RMSEs are higher than that of NORT. By utilizing the “sparse plus low-rank” structure and adaptive momentum, NORT is more efficient than GDPAN and LRTC.

Table 5: Testing RMSEs on color images. For all images 5% of the total pixels, which are corrupted by Gaussian noise

\mathcal{N}(0,0.01^{2})

, are used for training.

dataset		Rice	Tree	Windows
convex	ADMM	0.0680 $\pm$ 0.0003	0.0915 $\pm$ 0.0005	0.0709 $\pm$ 0.0004
	PA-APG	0.0583 $\pm$ 0.0016	0.0488 $\pm$ 0.0007	0.0585 $\pm$ 0.0002
	FaLRTC	0.0576 $\pm$ 0.0004	0.0494 $\pm$ 0.0011	0.0567 $\pm$ 0.0005
	FFW	0.0634 $\pm$ 0.0003	0.0599 $\pm$ 0.0005	0.0772 $\pm$ 0.0004
	TR-MM	0.0596 $\pm$ 0.0005	0.0515 $\pm$ 0.0011	0.0634 $\pm$ 0.0002
	TenNN	0.0647 $\pm$ 0.0004	0.0562 $\pm$ 0.0004	0.0586 $\pm$ 0.0003
factorization	RP	0.0541 $\pm$ 0.0011	0.0575 $\pm$ 0.0010	0.0388 $\pm$ 0.0026
	TMac	0.1923 $\pm$ 0.0005	0.1750 $\pm$ 0.0006	0.1313 $\pm$ 0.0005
	CP-WOPT	0.0912 $\pm$ 0.0086	0.0750 $\pm$ 0.0060	0.0964 $\pm$ 0.0102
	TMac-TT	0.0729 $\pm$ 0.0022	0.0665 $\pm$ 0.0147	0.1045 $\pm$ 0.0107
	TRLRF	0.0640 $\pm$ 0.0004	0.0780 $\pm$ 0.0048	0.0588 $\pm$ 0.0035
nonconvex	GDPAN	0.0467 $\pm$ 0.0002	0.0394 $\pm$ 0.0006	0.0306 $\pm$ 0.0007
	LRTC	0.0468 $\pm$ 0.0001	0.0392 $\pm$ 0.0006	0.0304 $\pm$ 0.0008
	NORT	0.0468 $\pm$ 0.0001	0.0386 $\pm$ 0.0009	0.0297 $\pm$ 0.0007

Finally, Table 6 compares NORT with PA-APG and RP, which are the best convex-regularization-based and factorization-based algorithms, respectively, as observed in Table 5. Table 6 shows the testing RMSEs at different noise levels $\sigma$ ’s. As can be seen, the testing RMSEs of all methods increase as $\sigma$ increases. NORT has lower RMSEs at all $\sigma$ settings. This is because natural images may not be exactly low-rank, and adaptive penalization of the singular values can better preserve the spectrum. A similar observation has also been made for nonconvex regularization on images (Yao et al., 2019b; Lu et al., 2016b). However, when the noise level becomes very high ( $\sigma=0.1$ with pixel values in $[0,1]$ ), though NORT is still the best, its testing RMSE is not small.

Table 6: Testing RMSEs on image Tree at different noise levels

\sigma

. The percentage followed by the marker

\uparrow

indicates the relative increase of testing RMSE compared with NORT.

		$\sigma=0.001$	$\sigma=0.01$	$\sigma=0.1$
(convex)	PA-APG	0.0149 (35.8% $\uparrow$ )	0.0488 (24.6% $\uparrow$ )	0.1749 (18.6% $\uparrow$ )
(factorization)	RP	0.0139 (26.0% $\uparrow$ )	0.0575 (15.6% $\uparrow$ )	0.1623 (10.1% $\uparrow$ )
(nonconvex)	NORT	0.0110	0.0386	0.1474

5.2.2 Remote Sensing Data

Experiments are performed on three hyper-spectral images (Figure 11): Cabbage (1312 $\times$ 432 $\times$ 49), Scene (1312 $\times$ 951 $\times$ 49) and Female (592 $\times$ 409 $\times$ 148).¹⁵¹⁵15Cabbage and Scene images are from https://sites.google.com/site/hyperspectralcolorimaging/dataset, while the Female images are downloaded from http://www.imageval.com/scene-database-4-faces-3-meters/. : The third dimension is for the bands of images.

We use the same setup as in Section 5.2.1, and hyperparameters are tuned on the validation set. ADMM, TenNN, GDPAN, LRTC, TMac-TT and TRLRF are slow and so not compared. Results are shown in Table 7. Again, NORT achieves much lower testing RMSE than convex regularization and factorization approach. Figure 12 shows convergence of the testing RMSE. As can be seen, NORT is the fastest.

Table 7: Testing RMSEs on remote sensing data.

		Cabbage	Scene	Female
convex	PA-APG	0.0913 $\pm$ 0.0006	0.1965 $\pm$ 0.0002	0.1157 $\pm$ 0.0003
	FaLRTC	0.0909 $\pm$ 0.0002	0.1920 $\pm$ 0.0001	0.1133 $\pm$ 0.0004
	FFW	0.0962 $\pm$ 0.0004	0.2037 $\pm$ 0.0002	0.2096 $\pm$ 0.0006
	TR-MM	0.0959 $\pm$ 0.0001	0.1965 $\pm$ 0.0002	0.1397 $\pm$ 0.0006
factorization	RP	0.0491 $\pm$ 0.0011	0.1804 $\pm$ 0.0005	0.0647 $\pm$ 0.0003
	TMac	0.4919 $\pm$ 0.0059	0.5970 $\pm$ 0.0029	1.9897 $\pm$ 0.0006
	CP-WOPT	0.1846 $\pm$ 0.0514	0.4811 $\pm$ 0.0082	0.1868 $\pm$ 0.0013
nonconvex	NORT	0.0376 $\pm$ 0.0004	0.1714 $\pm$ 0.0012	0.0592 $\pm$ 0.0002

5.2.3 Social Networks

In this experiment, we consider multi-relational link prediction (Guo et al., 2017) as a tensor completion problem. Experiment is performed on the YouTube data set¹⁶¹⁶16http://leitang.net/data/youtube-data.tar.gz (Lei et al., 2009), which contains 15,088 users and five types of user interactions. Thus, it forms a 15088 $\times$ 15088 $\times$ 5 tensor, with a total of 27,257,790 nonzero elements. Besides the full set, we also experiment with a YouTube subset obtained by randomly selecting 1,000 users (leading to 12,101 observations). We use $50\%$ of the observations for training, another $25\%$ for validation and the rest for testing. Table 8 shows the testing RMSE, and Figure 13 shows the convergence. As can be seen, NORT achieves smaller RMSE and is also much faster.

Table 8: Testing RMSEs on YouTube data sets. FaLRTC, PA-APG, TR-MM and CP-WOPT are slow, and thus not run on the full set.

		subset	full set
convex	FaLRTC	0.657 $\pm$ 0.060	—
	PA-APG	0.651 $\pm$ 0.047	—
	FFW	0.697 $\pm$ 0.054	0.395 $\pm$ 0.001
	TR-MM	0.670 $\pm$ 0.098	—
factorization	RP	0.522 $\pm$ 0.038	0.410 $\pm$ 0.001
	TMac	0.795 $\pm$ 0.033	0.611 $\pm$ 0.007
	CP-WOPT	0.785 $\pm$ 0.040	—
nonconvex	NORT	0.482 $\pm$ 0.030	0.370 $\pm$ 0.001

5.3 Link Prediction in Knowledge Graph

Knowledge Graph (KG) (Nickel et al., 2015; Toutanova et al., 2015) is an active research topic in data mining and machine learning. Let $\mathcal{E}$ be the entity set and $\mathcal{R}$ be the relation set. In a KG, nodes are the entities, while edges are relations representing the triplets $\mathcal{S}=\{(h,r,t)\}$ , where $h\in\mathcal{E}$ is the head entity, $t\in\mathcal{E}$ is the tail entity, and $r\in\mathcal{R}$ is the relation between $h$ and $t$ .

KGs have many downstream applications, such as link prediction and triplet classification. It is common to store KGs as tensors, and solve the KG learning tasks with tensor methods (Lacroix et al., 2018; Balazevic et al., 2019). Take link prediction as an example. The KG can be seen as a 3-order incomplete tensor $\mathscr{O}=\{\pm 1\}\in\mathbb{R}^{I^{1}\times I^{2}\times I^{3}}$ , where $I^{1}=I^{2}=|\mathcal{E}|$ and $I^{3}=|\mathcal{R}|$ . $\mathscr{O}_{i_{1}i_{2}i_{3}}=1$ when entities $i_{1}$ and $i_{2}$ have the relation $i_{3}$ , and $-1$ otherwise. Let ${\bm{\bm{\Omega}}}$ be a mask tensor denoting the observed values in $\mathscr{O}$ , i.e., ${\bm{\bm{\Omega}}}_{i_{1}i_{2}i_{3}}=1$ if $\mathscr{O}_{i_{1}i_{2}i_{3}}$ is observed and $0$ otherwise. The task is to predict elements in $\mathscr{O}$ which are not observed. Since $\mathscr{O}$ is binary, it is common to use the log loss as $\ell(\cdot,\cdot)$ in (14). The objective then becomes:

\displaystyle\min\nolimits_{\mathscr{X}}\sum\nolimits_{(i_{1}i_{2}i_{3})\in{\bm{\bm{\Omega}}}}\log(1+\exp(-\mathscr{X}_{i_{1}i_{2}i_{3}}\mathscr{O}_{i_{1}i_{2}i_{3}}))+\sum\nolimits_{i=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle i\right\rangle}}).

(47)

In step 9 of Algorithm 2, it is easy to see that

\displaystyle[\xi(\mathscr{X}_{t})]_{i_{1}i_{2}i_{3}}=\left\{\begin{array}[]{cc}\frac{-\mathscr{O}_{i_{1}i_{2}i_{3}}\cdot\exp(-\mathscr{X}_{i_{1}i_{2}i_{3}}\mathscr{O}_{i_{1}i_{2}i_{3}})}{1+\exp(-\mathscr{X}_{i_{1}i_{2}i_{3}}\mathscr{O}_{i_{1}i_{2}i_{3}})}&(i_{1}i_{2}i_{3})\in{\bm{\bm{\Omega}}}\\ 0&(i_{1}i_{2}i_{3})\notin{\bm{\bm{\Omega}}}\end{array}\right..

Experiments are performed on two benchmark data sets: WN18RR¹⁷¹⁷17https://github.com/TimDettmers/ConvE (Dettmers et al., 2018) and FB15k-237¹⁸¹⁸18https://www.microsoft.com/en-us/download/details.aspx?id=52312 (Toutanova et al., 2015), which are subsets of WN18 and FB15k (Bordes et al., 2013), respectively. WN18 is a subset of WordNet (Miller, 1995), and FB15k is a subset of the Freebase database (Bollacker et al., 2008). To avoid test leakage, WN18RR and FB15k-237 do not contain near-duplicate and inverse-duplicate relations. Hence, link prediction on WN18RR and FB15k-237 is harder but more recommended than that on WN18 and FB15k (Dettmers et al., 2018). To form the entity set $\mathcal{E}$ , we keep the top 500 (head and tail) entities that appear most frequently in the relations ( $r$ ’s). Relations that do not link to any of these 500 entities are removed, and those remained form the relation set $\mathcal{R}$ . Following the public splits on entities in $\mathcal{E}$ and relations in $\mathcal{R}$ (Han et al., 2018), we split the observed triplets in $\mathcal{S}$ into a training set $\mathcal{S}_{\text{train}}$ , validation set $\mathcal{S}_{\text{val}}$ and testing set $\mathcal{S}_{\text{test}}$ . For each observed triplet $(h,r,t)\in\mathcal{S}_{\text{train}}$ , we sample a negative triplet from $\mathcal{\hat{S}}_{(h,r,t)}=\{(\hat{h},r,t)\notin\mathcal{S}|\hat{h}\in\mathcal{E}\}\cap\{(h,r,\hat{t})\notin\mathcal{S}|\hat{t}\in\mathcal{E}\}$ . We avoid duplicate negative triplets during sampling. We then represent the KG’s by tensors $\mathscr{O}$ ’s of size $500\times 500\times 8$ for WN18RR, and $500\times 500\times 39$ for FB15k-237 with corresponding mask tensors ${\bm{\bm{\Omega}}}$ ’s.

Following (Bordes et al., 2013; Dettmers et al., 2018), performance is evaluated on the testing triplets in $\bar{{\bm{\bm{\Omega}}}}$ by the following metrics: (i) mean reciprocal ranking: $\text{MRR}=1/\|\bar{{\bm{\bm{\Omega}}}}\|_{0}\sum_{(i_{1}i_{2}i_{3})\in\bar{{\bm{\bm{\Omega}}}}}$ $1/\text{rank}_{i_{3}}$ , where $\text{rank}_{i_{3}}$ is the ranking of score $\mathscr{X}_{i_{1}i_{2}i_{3}}$ among $\{\mathscr{X}_{i_{1}i_{2}j}\}$ with $j=1,\dots,|\mathcal{R}|$ in descending order; (ii) Hits $@1=1/\|\bar{{\bm{\bm{\Omega}}}}\|_{0}\sum_{(i_{1}i_{2}i_{3})\in\bar{{\bm{\bm{\Omega}}}}}\mathbb{I}(\text{rank}_{i_{3}}\leq 1)$ , where $\mathbb{I}(c)$ is the indicator function which returns 1 if the constraint $c$ is satisfied and 0 otherwise; and (iii) Hits $@3=1/\|\bar{{\bm{\bm{\Omega}}}}\|_{0}\sum_{(i_{1}i_{2}i_{3})\in\bar{{\bm{\bm{\Omega}}}}}\mathbb{I}(\text{rank}_{i_{3}}\leq 3)$ . For these three metrics, the higher the better.

The aforementioned algorithms are designed for the square loss, but not for the log loss in (47). We adapt the gradient-based algorithms including PA-APG, ADMM and CP-WOPT, as we only need to change the gradient calculation for (47). As a further baseline, we implement the classic Tucker decomposition (Tucker, 1966; Kolda and Bader, 2009) to optimize (47). While RP (Kasai and Mishra, 2016) is the state-of-the-art Tucker-type algorithm, it uses Riemannian preconditioning and cannot be easily modified to handle nonsmooth loss.

Results on WN18RR and FB15k-237 are shown in Tables 9 and 10, respectively. As can be seen, NORT again obtains the best ranking results. Figure 14 shows convergence of MRR with CPU time, and NORT is about two orders of magnitude faster than the other methods.

Table 9: Testing performance on the WN18RR data set.

		MRR	Hits@1	Hits@3
convex	ADMM	0.362 $\pm$ 0.029	0.156 $\pm$ 0.024	0.422 $\pm$ 0.038
convex	PA-APG	0.399 $\pm$ 0.017	0.203 $\pm$ 0.023	0.500 $\pm$ 0.038
factorization	Tucker	0.439 $\pm$ 0.013	0.309 $\pm$ 0.016	0.438 $\pm$ 0.026
factorization	CP-WOPT	0.417 $\pm$ 0.018	0.266 $\pm$ 0.027	0.453 $\pm$ 0.019
nonconvex	NORT	0.523 $\pm$ 0.022	0.375 $\pm$ 0.033	0.578 $\pm$ 0.024

Table 10: Testing performance on the FB15k-237 data set.

		MRR	Hits@1	Hits@3
convex	ADMM	0.466 $\pm$ 0.006	0.411 $\pm$ 0.006	0.452 $\pm$ 0.011
convex	PA-APG	0.514 $\pm$ 0.013	0.463 $\pm$ 0.015	0.590 $\pm$ 0.016
factorization	Tucker	0.471 $\pm$ 0.018	0.355 $\pm$ 0.017	0.465 $\pm$ 0.015
factorization	CP-WOPT	0.420 $\pm$ 0.021	0.373 $\pm$ 0.015	0.488 $\pm$ 0.014
nonconvex	NORT	0.677 $\pm$ 0.007	0.609 $\pm$ 0.007	0.698 $\pm$ 0.011

5.4 Robust Tensor Completion

In this section, we apply the proposed method on robust video tensor completion. Three videos (Eagle¹⁹¹⁹19http://youtu.be/ufnf_q_3Ofg, Friends²⁰²⁰20http://youtu.be/xmLZsEfXEgE and Logo²¹²¹21http://youtu.be/L5HQoFIaT4I) from (Indyk et al., 2019) are used. Example frames are shown in Figure 15. For each video, $200$ consecutive $360\times 640$ frames are downloaded from Youtube, and the pixel values are normalized to $[0,1]$ . Each video can then be represented as a fourth-order tensor $\bar{\mathscr{O}}$ with size $360\times 640\times 3\times 200$ . Each element of $\bar{\mathscr{O}}$ is normalized to $[0,1]$ . This clean tensor $\bar{\mathscr{O}}$ is corrupted by a noise tensor $\mathscr{N}$ to form $\mathscr{O}$ . $\mathscr{N}$ is a sparse random tensor with approximately 1% nonzero elements. Each entry is first drawn uniformly from the interval $[0,1]$ , and then multiplied by $5$ times the maximum value of $\bar{\mathscr{O}}$ . Hyperparameters are chosen based on performance on the first 100 noisy frames. Denoising performance is measured by the RMSE between the clean tensor $\bar{\mathscr{O}}$ and reconstructed tensor $\mathscr{X}$ on the last 100 frames.

For the robust tensor completion, we take RTDGC (Gu et al., 2014) as the baseline, which adopts the $\ell_{1}$ loss and overlapped nuclear norm in (40) (i.e., $\kappa_{\ell}(x)=x$ and $\phi$ is the nuclear norm). As this is non-smooth and non-differentiable, RTDGC uses ADMM (Boyd et al., 2011) for the optimization, which handles the robust loss and low-rank regularizer separately. As discussed in Section 4.1, we use the smoothing NORT (Algorithm 3, with $\delta_{0}=0.9$ ) to optimize (42), the smoothed version of (40). Table 11 shows the RMSE results. As can be seen, NORT obtains better denoising performance than RTDGC. This again validates the efficacy of nonconvex low-rank learning. Figure 16 shows convergence of the testing RMSE. As shown, NORT leads to a lower RMSE and converges much faster as folding/unfolding are avoided.

Table 11: Testing RMSEs on the videos.

		Eagle	Friends	Logo
convex	RTDGC	0.122 $\pm$ 0.007	0.128 $\pm$ 0.005	0.112 $\pm$ 0.008
nonconvex	NORT	0.090 $\pm$ 0.003	0.075 $\pm$ 0.002	0.088 $\pm$ 0.004

5.5 Spatial-temporal Data

In this experiment, we predict climate observations for locations that do not have any records. This is formulated as a regularized tensor completion problem in (43). We use the square loss with a graph Laplacian regularizer constructed as in (43).

We use the CCDS and USHCN data sets from (Bahadori et al., 2014). CCDS²²²²22https://viterbi-web.usc.edu/~liu32/data/NA-1990-2002-Monthly.csv contains monthly observations of 17 variables (such as carbon dioxide and temperature) in 125 stations from January 1990 to December 2001. USHCN²³²³23http://www.ncdc.noaa.gov/oa/climate/research/ushcn contains monthly observations of 4 variables (minimum, maximum, average temperature and total precipitation) in 1218 stations from from January 1919 to November 2019. As discussed in Section 4.2, these records are collectively represented by a 3-order tensor $\mathscr{O}\in\mathbb{R}^{I^{1}\times I^{2}\times I^{3}}$ , where $I^{1}$ is the number of locations, $I^{2}$ is the number of recorded time stamps, and $I^{3}$ is the number of variables corresponding to climate observations. Consequently, CCDS is represented as a $125\times 156\times 17$ tensor and USHCN is represented as a $1218\times 1211\times 4$ tensor. The affinity matrix is denoted $\bm{A}$ , with $\bm{A}_{ij}$ being the similarity $s(i,j)=\exp(-2b_{ij})$ between locations $i$ and $j$ ( $b_{ij}$ is the Haversine distance between $i$ and $j$ ). Following (Bahadori et al., 2014), we normalize the data to zero mean and unit variance, then randomly sample 10% of the locations for training, another 10% for validation, and the rest for testing.

Algorithms FaLRTC, FFW, TR-MM, RP and TMac cannot be directly used for this graph Laplacian regularized tensor completion problem, while PA-APG, ADMM, Tucker and CP-WOPT can be adapted by modifying the gradient calculation. Hence we adapt and implement PA-APG, ADMM, Tucker and CP-WOPT as baselines in this section. In addition, we compare with a greedy algorithm (denoted “Greedy”)²⁴²⁴24This method is denoted “ORTHOGONAL” in (Bahadori et al., 2014) and obtains the best results there. from (Bahadori et al., 2014), which successively adds a rank-1 matrix to approximate the mode- $n$ unfolding with the rank constraint. For the factorization-based algorithms Tucker and CP-WOPT, the graph Laplacian regularizer $h$ takes the corresponding factor matrix rather than $\mathscr{X}_{{\left\langle 1\right\rangle}}$ as the input. Specifically, recall that Tucker factorizes $\mathscr{X}$ into $[\mathscr{G};{\bm{\bm{B}}}^{1},{\bm{\bm{B}}}^{2},{\bm{\bm{B}}}^{3}]$ , where $\mathscr{G}\in\mathbb{R}^{k^{1}\times k^{2}\times k^{3}}$ , ${\bm{\bm{B}}}^{i}\in\mathbb{R}^{I^{i}\times k^{i}}$ , $i=1,2,3$ , and $k^{i}$ ’s are hyperparameters. When $k^{1}=k^{2}=k^{3}$ and $\mathscr{G}$ is superdiagonal, this reduces to the CP-WOPT decomposition. The graph Laplacian regularizer is then constructed as $h({\bm{\bm{B}}}^{1})$ to leverage location proximity. As an additional baseline, we also experiment with a NORT variant that does not use the Laplacian regularizer (denoted “NORT-no-Lap”).

Table 12: Testing RMSEs on CCDS and USHCN data sets.

		CCDS	USHCN
convex	ADMM	0.890 $\pm$ 0.016	0.691 $\pm$ 0.005
convex	PA-APG	0.866 $\pm$ 0.014	0.680 $\pm$ 0.009
factorization	Tucker	0.856 $\pm$ 0.026	0.647 $\pm$ 0.006
factorization	CP-WOPT	0.887 $\pm$ 0.018	0.688 $\pm$ 0.009
rank constraint	Greedy	0.871 $\pm$ 0.008	0.658 $\pm$ 0.012
nonconvex	NORT-no-Lap	0.997 $\pm$ 0.001	1.391 $\pm$ 0.001
nonconvex	NORT	0.793 $\pm$ 0.002	0.583 $\pm$ 0.012

Table 12 shows the RMSE results. Again, NORT obtains the lowest testing RMSEs. Moreover, when the Laplacian regularizer is not used, the testing RMSE is much higher, demonstrating that the missing slices cannot be reliably completed. Figure 17 shows the convergence. As can be seen, NORT is orders of magnitude faster than the other algorithms. The gaps on the performance and speed between NORT and the other baselines are more obvious on the larger USHCN data set. Further, note from Figures 17(a) and 17(b) that though NORT-no-Lap has converged, it cannot decrease the testing RMSE during learning (Figures 17(c) and 17(d)). This validates the efficacy of the graph Laplacian regularizer.

6 Conclusion

In this paper, we propose a low-rank tensor completion model with nonconvex regularization. An efficient nonconvex proximal average algorithm is developed, which maintains the “sparse plus low-rank” structure throughout the iterations and incorporates adaptive momentum. Convergence to critical points is guaranteed, and the obtained critical points can have small statistical errors. The algorithm is also extended for nonsmooth losses and additional regularization, demonstrating broad applicability of the proposed algorithm. Experiments on a variety of synthetic and real data sets are performed. Results show that the proposed algorithm is more efficient and more accurate than existing state-of-the-art.

In the future, we will extend the proposed algorithm to simultaneous completion of multiple tensors, e.g., collaborative tensor completion (Zheng et al., 2013) and coupled tensor completion (Wimalawarne et al., 2018). Besides, it is also interesting to study how the proposed algorithm can be efficiently parallelized on GPUs and distributed computing environments (Phipps and Kolda, 2019).

Acknowledgement

BH was supported by the RGC Early Career Scheme No.22200720 and NSFC Young Scientists Fund No. 62006202.

Appendix

Appendix A Comparison with Incoherence Condition

The matrix incoherence condition (Candès and Recht, 2009; Candès et al., 2011; Negahban and Wainwright, 2012) is in form of the singular value decomposition ${\bm{\bm{X}}}=\bm{U}\bm{\Sigma}\bm{V}^{\top}\in\mathbb{R}^{m\times n}$ , where $\bm{U}\in\mathbb{R}^{m\times r}$ (resp. $\bm{V}\in\mathbb{R}^{n\times r}$ ) contains the left (resp. right) singular vectors and $\bm{\Sigma}\in\mathbb{R}^{r\times r}$ is the diagonal matrix containing singular values. The purpose of this condition is to enforce that the left and right singular vectors should not be aligned with the standard basis (i.e., vector ${\bm{\bm{e}}}_{i}$ ’s with the $i$ th dimension being $1$ and others being $0$ ). Typically, this condition is stated as

\displaystyle\max_{j=1,\dots,m}\left|[\bm{U}\bm{U}^{\top}]_{jj}\right|\leq\mu_{0}\frac{r}{m},\quad\text{and}\quad\max_{j=1,\dots,n}\left|[\bm{V}\bm{V}^{\top}]_{jj}\right|\leq\mu_{0}\frac{r}{n},

(48)

for some constant $\mu_{0}>0$ . Note that (48) does not depend on the singular values of ${\bm{\bm{X}}}$ . However, this condition can be restrictive in realistic settings, where the underlying matrix is contaminated by noise. In this case, the observed matrix can have small singular values. Therefore, we need to impose conditions related to the singular values, and (32) shows such a dependency. An example matrix satisfying the matrix RSC condition but not the incoherence condition is in Section 3.4.2 of (Negahban and Wainwright, 2012). As a result, the RSC condition, which involves singular values, is less restrictive than the incoherence condition, and can better describe “spikiness”.

Appendix B Proofs

B.1 Proposition 4

Proof For simplicity, we consider the case where $\bm{U}\in\mathbb{R}^{I^{j}\times k}$ (resp. $\bm{V}\in\mathbb{R}^{(\frac{I^{\pi}}{I^{j}})\times k}$ ) has only one single column $\bm{u}\in\mathbb{R}^{I^{j}}$ (resp. $\bm{v}\in\mathbb{R}^{\frac{I^{\pi}}{I^{j}}}$ ). We need to fold $\bm{u}\bm{v}^{\top}$ along with the $j$ th mode and then unfold it along its $i$ th mode. Let us consider the structure of $\mathscr{X}=(\bm{u}\bm{v}^{\top})^{{\left\langle j\right\rangle}}$ , we can express it as

\displaystyle\mathscr{X}_{{\left\langle j\right\rangle}}=\big{[}\mathbf{u}\bm{v}_{1}^{\top},...,\mathbf{u}\bm{v}_{\frac{I^{\pi}}{(I^{i}I^{j})}}^{\top}\big{]}\in\mathbb{R}^{I^{j}\times\frac{I^{\pi}}{I^{j}}},

where $\bm{v}=[\bm{v}_{1};\dots;\bm{v}_{\frac{I^{\pi}}{(I^{i}I^{j})}}]$ with each $\bm{v}_{p}\in\mathbb{R}^{I^{i}}$ . When unfolding $\mathscr{X}$ with the $i$ th mode, the unfolding matrix is

\displaystyle\big{[}\bm{v}_{1}\bm{u}^{\top},\dots,\bm{v}_{\frac{I^{\pi}}{(I^{i}I^{j})}}\bm{u}^{\top}\big{]}\in\mathbb{R}^{I^{i}\times\frac{I^{\pi}}{I^{i}}}.

(49)

Thus,

	$\displaystyle\bm{a}^{\top}\big{[}\bm{v}_{1}\bm{u}^{\top},\dots,\bm{v}_{I^{3}}\bm{u}^{\top}\big{]}$	$\displaystyle=$	$\displaystyle\big{[}(\bm{a}^{\top}\bm{v}_{1})\bm{u}^{\top},...,(\bm{a}^{\top}\bm{v}_{I^{3}})\bm{u}^{\top}\big{]},$		(50)
		$\displaystyle=$	$\displaystyle\left(\bm{a}^{\top}\text{mat}\left(\bm{v}_{p};I^{i},\bar{I}^{ij}\right)\right)\otimes\bm{u}^{\top}.$		(50)

Similarly, let $\bm{b}=\big{[}\bm{b}_{1};\dots;\bm{b}_{\frac{I^{\pi}}{I^{i}I^{j}}}\big{]}$ , where each $\bm{b}_{p}\in\mathbb{R}^{I^{j}}$ . From (49), we have

$\displaystyle\big{[}\bm{v}_{1}\bm{u}^{\top},\dots,\bm{v}_{\frac{I^{\pi}}{(I^{i}I^{j})}}\bm{u}^{\top}\big{]}\bm{b}$	$\displaystyle=$	$\displaystyle\sum\nolimits_{j=1}^{\frac{I^{\pi}}{I^{i}I^{j}}}\bm{v}_{i}(\bm{u}^{\top}\bm{b}_{i}),$	(51)
	$\displaystyle=$	$\displaystyle\big{[}\bm{v}_{1};\dots;\bm{v}_{\frac{I^{\pi}}{I^{i}I^{j}}}\big{]}\begin{bmatrix}\bm{u}^{\top}\bm{b}_{1}\\ \vdots\\ \bm{u}^{\top}\bm{b}_{\frac{I^{\pi}}{I^{i}I^{j}}}\end{bmatrix},$
	$\displaystyle=$	$\displaystyle\big{[}\bm{v}_{1};\dots;\bm{v}_{\frac{I^{\pi}}{I^{i}I^{j}}}\big{]}\big{[}\bm{b}_{1};\dots;\bm{b}_{\frac{I^{\pi}}{I^{i}I^{j}}}\big{]}^{\top}\bm{u},$
	$\displaystyle=$	$\displaystyle\text{mat}\left(\bm{v};I^{i},\bar{I}^{ij}\right)\text{mat}\left(\bm{b};\bar{I}^{ij},I^{j}\right)\bm{u}.$

When $\bm{U}$ (resp. $\bm{V}$ ) has $k$ columns, combining with the fact that $\bm{U}\bm{V}^{\top}=\sum_{p=1}^{k}\bm{u}_{p}\bm{v}_{p}^{\top}$ with (50) and (51), we obtain (26) and (27).

B.2 Proposition 6

Proof Define $\bar{\lambda}_{d}=\lambda_{d}/\tau$ , then

	$\displaystyle\sum\nolimits_{d=1}^{D}\min\nolimits_{{\bm{\bm{X}}}_{d}}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}-\mathscr{Z}_{{\left\langle d\right\rangle}}\right\\|_{F}^{2}+\bar{\lambda}_{d}\,\phi({\bm{\bm{X}}}_{d}),$
	$\displaystyle\!\!\!=\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}}\frac{D}{2}\left\\|\mathscr{Z}\right\\|_{F}^{2}-\big{<}\mathscr{Z},\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\big{>}+\frac{D}{2}\sum\nolimits_{d=1}^{D}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}+\sum\nolimits_{d=1}^{D}\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d}),$
	$\displaystyle\!\!\!=\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}}\frac{D}{2}\left\\|\mathscr{Z}\!-\!\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}\!\!\!-\frac{D}{2}\left\\|\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}\!\!\!+\sum\nolimits_{d=1}^{D}\big{[}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}\!+\!\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\big{]}.$		(52)

Next, we introduce an extra parameter as $\mathscr{X}=\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}$ , and express (52) as

	$\displaystyle\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}:\mathscr{X}=\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}}\frac{D}{2}\left\\|\mathscr{Z}-\mathscr{X}\right\\|_{F}^{2}-\frac{D}{2}\left\\|\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}+\sum\nolimits_{d=1}^{D}\left[\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}+\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\right],$
	$\displaystyle=\!\min_{\mathscr{X}}\left\{\frac{D}{2}\left\\|\mathscr{Z}-\mathscr{X}\right\\|_{F}^{2}+\min_{\{{\bm{\bm{X}}}_{d}\}:\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}=\mathscr{X}}\sum\nolimits_{d=1}^{D}\left[\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}\!+\!\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\right]\!-\!\frac{D}{2}\left\\|\mathscr{X}\right\\|_{F}^{2}\right\}.$		(53)

We transform the above equation as

\displaystyle\min\nolimits_{\mathscr{X}}\frac{1}{2}\left\|\mathscr{Z}-\mathscr{X}\right\|_{F}^{2}+\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{X})=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X}),

where $\bar{g}_{\tau}(\mathscr{X})$ is defined as

	$\displaystyle\bar{g}_{\tau}(\mathscr{X})$	$\displaystyle=\tau\left[\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}}\sum\nolimits_{d=1}^{D}\big{(}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}+\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\big{)}-\frac{D}{2}\left\\|\mathscr{X}\right\\|_{F}^{2}\right],$		(54)
		$\displaystyle\text{\;s.t.\;}\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}=\mathscr{X}.$

Thus, there exists $\bar{g}_{\tau}$ such that $\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{Z})=\sum\nolimits_{i=1}^{D}\big{[}\text{prox}_{\bar{\lambda}_{d}\phi}(\left[\mathscr{Z}\right]_{{\left\langle i\right\rangle}})\big{]}^{{\left\langle i\right\rangle}}$ .

B.3 Proposition 7

Let $g(\mathscr{X})=\sum_{d=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle d\right\rangle}})$ . Before proving Proposition 7, we first extend Proposition 2 in (Zhong and Kwok, 2014) in the following auxiliary Lemma.

B.3.1 Auxiliary Lemma

Lemma 21

$0\leq g(\mathscr{X})-\bar{g}_{\tau}(\mathscr{X})\leq\frac{\kappa_{0}^{2}}{2\tau}\sum\nolimits_{d=1}^{D}\lambda_{d}^{2}$ .

Proof From the definition of $\bar{g}_{\tau}$ in (54), if $\mathscr{X}={\bm{\bm{X}}}^{{\left\langle 1\right\rangle}}_{1}=...={\bm{\bm{X}}}^{{\left\langle D\right\rangle}}_{D}$ , we have

	$\displaystyle\bar{g}_{\tau}(\mathscr{X})$	$\displaystyle\leq\tau\big{(}\sum\nolimits_{d=1}^{D}\big{(}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}\!+\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\big{)}\!-\!\frac{D}{2}\left\\|\mathscr{X}\right\\|_{F}^{2}\big{)},$
		$\displaystyle=\sum\nolimits_{d=1}^{D}\lambda_{d}\phi({\bm{\bm{X}}}_{d})=\sum\nolimits_{d=1}^{D}\lambda_{d}\phi(\mathscr{X}_{{\left\langle d\right\rangle}})=g(\mathscr{X}).$

Thus, $g(\mathscr{X})-\bar{g}_{\tau}(\mathscr{X})\geq 0$ . Next, we prove the “ $\leq$ ” part in the Lemma. Note that

	$\displaystyle\sup\nolimits_{{\bm{\bm{X}}}_{d}}\lambda_{d}\phi({\bm{\bm{X}}}_{d})-\tau\min\nolimits_{{\bm{\bm{Y}}}}\big{(}\frac{1}{2}\left\\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}+\bar{\lambda}_{d}\phi({\bm{\bm{Y}}})\big{)},$
	$\displaystyle=\sup\nolimits_{{\bm{\bm{X}}}_{d},{\bm{\bm{Y}}}}\lambda_{d}\phi({\bm{\bm{X}}}_{d})-\frac{\tau}{2}\left\\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}-\lambda_{d}\phi({\bm{\bm{Y}}}).$		(55)

Since $\phi$ is $\kappa_{0}$ -Lipschitz continuous, let $\alpha=\left\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\|_{F}$ , we have

$\displaystyle\mathscr{\eqref{eq:app2}}$	$\displaystyle=\sup\nolimits_{{\bm{\bm{X}}}_{d},{\bm{\bm{Y}}}}\lambda_{d}\left[\phi({\bm{\bm{X}}}_{d})-\phi({\bm{\bm{X}}})\right]-\frac{\tau}{2}\left\\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\\|_{F}^{2},$
	$\displaystyle\leq\sup\nolimits_{{\bm{\bm{X}}}_{d},{\bm{\bm{Y}}}}\lambda_{d}\kappa_{0}\left\\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\\|_{F}-\frac{\tau}{2}\left\\|{\bm{\bm{Y}}}-{\bm{\bm{X}}}_{d}\right\\|_{F}^{2},$
	$\displaystyle=\sup\nolimits_{\alpha}\big{[}\lambda_{d}\kappa_{0}\alpha-\frac{\tau}{2}\alpha^{2}\big{]}=\sup\nolimits_{\alpha}-\frac{1}{2}\big{[}\alpha-\frac{\lambda_{d}\kappa_{0}}{\tau}\big{]}^{2}+\frac{\lambda_{d}^{2}\kappa_{0}^{2}}{2}\leq\frac{\lambda_{d}^{2}\kappa_{0}^{2}}{2\tau}.$	(56)

Next, we have

$\displaystyle g(\mathscr{X})-\bar{g}_{\tau}(\mathscr{X})$	$\displaystyle\leq g(\mathscr{X})-\tau\big{(}\min\nolimits_{\mathscr{Y}}\frac{1}{2}\left\\|\mathscr{X}-\mathscr{Y}\right\\|_{F}^{2}+\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{Y})\big{)},$	(57)
	$\displaystyle=\sum\nolimits_{d=1}^{D}\lambda_{d}\phi(\mathscr{X}_{{\left\langle d\right\rangle}})-\tau\sum\nolimits_{d=1}^{D}\big{(}\min\nolimits_{\{{\bm{\bm{Y}}}_{d}\}}\frac{1}{2}\left\\|\mathscr{X}_{{\left\langle d\right\rangle}}-{\bm{\bm{Y}}}_{d}\right\\|_{F}^{2}+\frac{\lambda_{d}}{\tau}\phi({\bm{\bm{Y}}}_{d})\big{)},$	(58)
	$\displaystyle\leq\sup\nolimits_{\mathscr{X}}\sum\nolimits_{d=1}^{D}\lambda_{d}\phi(\mathscr{X}_{{\left\langle d\right\rangle}})-\tau\sum\nolimits_{d=1}^{D}\big{(}\min\nolimits_{\{{\bm{\bm{Y}}}_{d}\}}\frac{1}{2}\left\\|\mathscr{X}_{{\left\langle d\right\rangle}}-{\bm{\bm{Y}}}_{d}\right\\|_{F}^{2}+\frac{\lambda_{d}}{\tau}\phi({\bm{\bm{Y}}}_{d})\big{)},$
	$\displaystyle\leq\sum\nolimits_{d=1}^{D}\frac{\lambda_{d}^{2}\kappa_{0}^{2}}{2\tau}.$	(59)

Note that (57) comes from the fact that

\displaystyle\min\nolimits_{\mathscr{Y}}\frac{1}{2}\left\|\mathscr{X}-\mathscr{Y}\right\|_{F}^{2}+\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{Y})\leq\frac{1}{2}\left\|\mathscr{X}-\mathscr{X}\right\|_{F}^{2}+\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{X})=\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{X}),

then (58) is from the definition of $\bar{g}_{\tau}$ in Proposition 6, and (59) is from (56).

B.3.2 Proof of Proposition 7

Proof From Lemma 21, we have

\displaystyle\min_{\mathscr{X}}F(\mathscr{X})-\min_{\mathscr{X}}F_{\tau}(\mathscr{X})\geq\min_{\mathscr{X}}F(\mathscr{X})-F_{\tau}(\mathscr{X})=g(\mathscr{X})-\bar{g}_{\tau}(\mathscr{X})\geq 0.

Let $\mathscr{X}_{1}=\arg\min\nolimits_{\mathscr{X}}F(\mathscr{X})$ and $\mathscr{X}_{\tau}=\arg\min\nolimits_{\mathscr{X}}F_{\tau}(\mathscr{X})$ . Then, we have

\displaystyle\min_{\mathscr{X}}F(\mathscr{X})\!-\!\min_{\mathscr{X}}F_{\tau}(\mathscr{X})=\!F(\mathscr{X}_{1})\!-\!F_{\tau}(\mathscr{X}_{\tau})\leq\!F(\mathscr{X}_{\tau})\!-\!F_{\tau}(\mathscr{X}_{\tau})\!=\!g(\mathscr{X}_{\tau})\!-\!\bar{g}_{\tau}(\mathscr{X}_{\tau})\!\leq\!\frac{\kappa_{0}^{2}}{2\tau}\sum\nolimits_{d=1}^{D}\lambda_{d}^{2}.

Thus, $0\leq\min F-\min F_{\tau}\leq\frac{\kappa_{0}^{2}}{2\tau}\sum\nolimits_{d=1}^{D}\lambda_{d}^{2}$ .

B.4 Proposition 8

Proof The proof of this proposition can also be found in (Zhong and Kwok, 2014), we add one here for the completeness. Recall that

\displaystyle\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\nabla f(\tilde{\mathscr{X}})/\tau)=\arg\min_{\mathscr{X}}\frac{1}{2}\left\|\mathscr{X}-\left(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}})\right)\right\|_{F}^{2}+\frac{1}{\tau}\bar{g}_{\tau}(\mathscr{X}).

Let $\mathscr{Z}=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\nabla f(\tilde{\mathscr{X}})/\tau)$ . Thus,

\displaystyle 0\in\mathscr{Z}-\left(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}})\right)+\frac{1}{\tau}\partial\bar{g}_{\tau}(\mathscr{X}).

When $\mathscr{Z}=\tilde{\mathscr{X}}$ , we have $0\in\nabla f(\tilde{\mathscr{X}})+\partial\bar{g}_{\tau}(\mathscr{X})$ . Thus, $\tilde{\mathscr{X}}$ is a critical point of $F_{\tau}$ .

B.5 Theorem 9

First, we introduce the following Lemmas, which are basic properties for the proximal step.

Lemma 22

(Parikh and Boyd, 2013) Let $\tau>\rho+D\kappa_{0}$ and $\eta=\tau-\rho+D\kappa_{0}$ . Then, $F_{\tau}(\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X}))\leq F_{\tau}(\mathscr{X})-\frac{\eta}{2}\big{\|}\mathscr{X}-\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X})\big{\|}_{F}^{2}$ .

Lemma 23

(Parikh and Boyd, 2013) If $\mathscr{X}\!=\!\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X}\!-\!\frac{1}{\tau}\nabla f(\mathscr{X}))$ , then $\mathscr{X}$ is a critical point of $F_{\tau}$ .

Lemma 24

(Hare and Sagastizábal, 2009) The proximal map $\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X})$ is continuous.

Proof (of Theorem 9) Recall that $\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X})=\sum\nolimits_{i=1}^{D}\text{prox}_{\frac{\lambda_{i}\phi}{\tau}}(\mathscr{X}_{{\left\langle i\right\rangle}})$ . From Lemma 22,

•

If step 7 is performed, we have

\displaystyle F_{\tau}(\mathscr{X}_{t+1})\leq F_{\tau}(\mathscr{V}_{t})-\frac{\eta}{2}\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}^{2}\leq F_{\tau}(\mathscr{X}_{t})-\frac{\eta}{2}\left\|\mathscr{X}_{t+1}-\mathscr{X}_{t}\right\|_{F}^{2}.

(60)

•

If step 5 is performed,

	$\displaystyle F_{\tau}(\mathscr{X}_{t+1})\leq F_{\tau}(\mathscr{V}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}^{2}$	$\displaystyle\leq F_{\tau}(\bar{\mathscr{X}}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\\|_{F}^{2},$
		$\displaystyle\leq F_{\tau}(\mathscr{X}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\\|_{F}^{2}.$		(61)

Combining (60) and (61), we have

\displaystyle\frac{2}{\eta}(F_{\tau}(\mathscr{X}_{1})-F_{\tau}(\mathscr{X}_{T+1}))\geq\sum\nolimits_{j\in\chi_{1}(T)}\left\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\|_{F}^{2}+\sum\nolimits_{j\in\chi_{2}(T)}\left\|\mathscr{X}_{t+1}-\mathscr{X}_{t}\right\|_{F}^{2},

(62)

where $\chi_{1}(T)$ and $\chi_{2}(T)$ are a partition of $\{1,...,T\}$ such that when $j\in\chi_{1}(T)$ step 5 is performed, and when $j\in\chi_{2}(T)$ step 7 is performed. As $F_{\tau}$ is bounded from below and $\lim_{\left\|\mathscr{X}\right\|_{F}\rightarrow\infty}F_{\tau}(\mathscr{X})=\infty$ , taking $T=\infty$ in (62), we have

\displaystyle\sum\nolimits_{j\in\chi_{1}(\infty)}\left\|\mathscr{X}_{t+1}-\mathscr{Y}_{t}\right\|_{F}^{2}+\sum\nolimits_{j\in\chi_{2}(\infty)}\left\|\mathscr{X}_{t+1}-\mathscr{X}_{t}\right\|_{F}^{2}=c,

where $c\leq\frac{2}{\eta}\left[F_{\tau}(\mathscr{X}_{1})-F_{\tau}^{\text{min}}\right]$ is a positive constant. Thus, the sequence $\{\mathscr{X}_{t}\}$ is bounded, and it must have limit points. Besides, one of the following three cases must hold.

$\chi_{1}(\infty)$ is finite, $\chi_{2}(\infty)$ is infinite. Let $\tilde{\mathscr{X}}$ be a limit point of $\{\mathscr{X}_{t}\}$ , and $\{\mathscr{X}_{j_{t}}\}$ be a subsequence that converges to $\tilde{\mathscr{X}}$ . In this case, on using Lemma 24, we have

	$\displaystyle\lim\limits_{j_{t}\rightarrow\infty}\left\\|\mathscr{X}_{j_{t}+1}-\mathscr{X}_{j_{t}}\right\\|_{F}^{2}$	$\displaystyle=\lim\limits_{j_{t}\rightarrow\infty}\left\\|\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X}_{j_{t}}-\frac{1}{\tau}\nabla f(\mathscr{X}_{j_{t}}))-\mathscr{X}_{j_{t}}\right\\|_{F}^{2},$
		$\displaystyle=\left\\|\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}}))-\tilde{\mathscr{X}}\right\\|_{F}^{2}=0.$

Thus, $\tilde{\mathscr{X}}=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}}))$ , and $\tilde{\mathscr{X}}$ is a critical point of $F_{\tau}$ from Lemma 23.

$\chi_{1}(\infty)$ is infinite, $\chi_{2}(\infty)$ is finite. Let $\tilde{\mathscr{X}}$ be a limit point of $\{\mathscr{X}_{t}\}$ , and $\{\mathscr{X}_{j_{t}}\}$ be a subsequence that converges to $\tilde{\mathscr{X}}$ . In this case, we have

	$\displaystyle\lim\limits_{j_{t}\rightarrow\infty}\left\\|\mathscr{X}_{j_{t}+1}-\mathscr{Y}_{j_{t}}\right\\|_{F}^{2}$	$\displaystyle=\lim\limits_{j_{t}\rightarrow\infty}\left\\|\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{X}_{j_{t}}-\frac{1}{\tau}\nabla f(\mathscr{X}_{j_{t}}))-\mathscr{Y}_{j_{t}}\right\\|_{F}^{2},$
		$\displaystyle=\left\\|\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\tilde{\mathscr{X}}-\frac{1}{\tau}\nabla f(\tilde{\mathscr{X}}))-\tilde{\mathscr{X}}\right\\|_{F}^{2}=0.$

3.

Both $\chi_{1}(\infty)$ and $\chi_{2}(\infty)$ are infinite. From the above cases, we can see that either $\chi_{1}(\infty)$ or $\chi_{2}(\infty)$ is infinite, and limit points are also the critical points of $F_{\tau}$ .

Thus, all limit points of $\{\mathscr{X}_{t}\}$ are critical points of $F_{\tau}$ .

B.6 Corollary 10

This corollary can be easily derived from the proof of Theorem 9.

Proof Since $\mathscr{X}_{t+1}=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{V}_{t}-\frac{1}{\tau}\nabla f(\mathscr{V}_{t}))$ , conclusion (i) directly follows from Lemma 23. From (62), we have

	$\displaystyle\min\nolimits_{1,\dots,T}\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}^{2}$	$\displaystyle\leq\frac{1}{T}\sum\nolimits_{t=1\dots T}\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}^{2},$
		$\displaystyle\leq\frac{2}{\eta T}(F_{\tau}(\mathscr{X}_{1})-F_{\tau}(\mathscr{X}_{T+1}))\leq\frac{2}{\eta T}(F_{\tau}(\mathscr{X}_{1})-F_{\tau}^{\min}).$

Thus, we obtain Conclusion (ii).

B.7 Theorem 13

We first bound $\partial F_{\tau}$ in Lemma 25, then prove Theorem 13.

Lemma 25

For iterations in Algorithm 2, we have $\min\nolimits_{\mathscr{U}_{t}\in\partial F_{\tau}(\mathscr{X}_{t})}\left\|\mathscr{U}_{t}\right\|_{F}\!\leq\!(\tau+\rho)\left\|\mathscr{X}_{t+1}\!-\!\mathscr{V}_{t}\right\|_{F}$ .

Proof Since $\mathscr{X}_{t+1}$ is generated from the proximal step, i.e., $\mathscr{X}_{t+1}=\text{prox}_{\frac{\bar{g}_{\tau}}{\tau}}(\mathscr{V}_{t}-\frac{1}{\tau}\nabla f(\mathscr{V}))$ , from its optimality condition, we have

\displaystyle\mathscr{X}_{t+1}-\big{(}\mathscr{V}_{t}-\frac{1}{\tau}\nabla f(\mathscr{V}_{t})\big{)}+\frac{1}{\tau}\partial\bar{g}_{\tau}(\mathscr{X}_{t+1})\ni\bm{0}.

Let $\mathscr{U}_{t}=\tau\left[\mathscr{X}_{t+1}-\mathscr{V}_{t}\right]-\left[\nabla f(\mathscr{V}_{t})-\nabla f(\mathscr{X}_{t+1})\right]$ . We have

\displaystyle\partial F_{\tau}(\mathscr{X}_{t+1})=\left[\nabla f(\mathscr{X}_{t+1})+\partial\bar{g}_{\tau}(\mathscr{X}_{t+1})\right]\in\mathscr{U}_{t}.

Thus, $\left\|\mathscr{U}_{t}\right\|_{F}\leq\tau\left\|\mathscr{X}_{t+1}\!-\!\mathscr{V}_{t}\right\|_{F}\!+\!\left\|\nabla f(\mathscr{V}_{t})\!-\!\nabla f(\mathscr{X}_{t+1})\right\|_{F}\leq\left(\tau+\rho\right)\left\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\|_{F}$ .

Proof (of Theorem 13). From Theorem 9, we have $\lim\limits_{T\rightarrow\infty}F_{\tau}(\mathscr{X}_{t})=F_{\tau}^{\min}$ . Then, from Lemma 25, we have

\displaystyle\lim\limits_{t\rightarrow\infty}\min\nolimits_{\mathscr{U}_{t}\in\partial F_{\tau}(\mathscr{X}_{t})}\!\left\|\mathscr{U}_{t}\right\|_{F}\!\leq\!\lim\limits_{t\rightarrow\infty}(\tau\!+\!\rho)\left\|\mathscr{X}_{t+1}\!-\!\mathscr{V}_{t}\right\|_{F}\!=\!0.

Thus, for any $\epsilon$ , $c>0$ and $t>t_{0}$ where $t_{0}$ is a sufficiently large positive integer, we have

\displaystyle\mathscr{X}_{t}\in\left\{\mathscr{X}\,|\min\nolimits_{\mathscr{U}\in\partial F_{\tau}(\mathscr{X})}\left\|\mathscr{U}\right\|_{F}\leq\epsilon,F^{\min}_{\tau}<F_{\tau}(\mathscr{X})<F_{\tau}^{\min}+c\right\}.

Then, the uniformized KL property implies for all $t\geq t_{0}$ ,

	$\displaystyle 1$	$\displaystyle\leq\psi^{\prime}\left(F_{\tau}(\mathscr{X}_{t+1})-F_{\tau}^{\min}\right)\min\nolimits_{\mathscr{U}_{t}\in\partial F_{\tau}(\mathscr{X}_{t})}\left\\|\mathscr{U}_{t}\right\\|_{F},$
		$\displaystyle=\psi^{\prime}\left(F_{\tau}(\mathscr{X}_{t+1})-F_{\tau}^{\min}\right)(\tau+\rho)\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}.$		(63)

Moreover, from Lemma 22, we have

\displaystyle\left\|\mathscr{X}_{t+1}\!-\!\mathscr{V}_{t}\right\|_{F}^{2}\leq\frac{2}{\eta}\left[F_{\tau}(\mathscr{V}_{t})-F_{\tau}(\mathscr{X}_{t+1})\right].

(64)

Let $r_{t}=F_{\tau}(\mathscr{X}_{t})-F_{\tau}^{\min}$ , we have

	$\displaystyle r_{t}-r_{t+1}$	$\displaystyle=F_{\tau}(\mathscr{X}_{t})-F_{\tau}^{\min}-\left[F_{\tau}(\mathscr{X}_{t+1})-F_{\tau}^{\min}\right],$
		$\displaystyle\geq F_{\tau}(\mathscr{V}_{t})-F_{\tau}^{\min}-\left[F_{\tau}(\mathscr{X}_{t+1})-F_{\tau}^{\min}\right]=F_{\tau}(\mathscr{V}_{t})-F_{\tau}(\mathscr{X}_{t+1}).$		(65)

Combine (63), (64) and (65), we have

	$\displaystyle 1$	$\displaystyle\leq\left[\psi^{\prime}(r_{t})\right]^{2}(\tau+\rho)^{2}\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}^{2},$
		$\displaystyle\leq\frac{2(\tau+\rho)^{2}}{\eta}\left[\psi^{\prime}(r_{t})\right]^{2}\left[F_{\tau}(\mathscr{V}_{t})-F_{\tau}(\mathscr{X}_{t+1})\right]\leq\frac{2(\tau+\rho)^{2}}{\eta}\left[\psi^{\prime}(r_{t+1})\right]^{2}(r_{t}-r_{t+1}).$		(66)

Since $\phi(\alpha)=\frac{C}{x}\alpha^{x}$ , then $\phi^{\prime}(\alpha)=C\alpha^{x-1}$ , (66) becomes $1\leq d_{1}C^{2}r_{t+1}^{2x-2}(r_{t}-r_{t+1})$ , where $d_{1}=\frac{2(\tau+\rho)^{2}}{\eta}$ . Finally, it is shown in (Bolte et al., 2014; Li and Lin, 2015; Li et al., 2017) that the sequence $\{r_{t}\}$ satisfying the above inequality, convergence to zero with different rates stated in the Theorem.

B.8 Lemma 15

First, we introduce the following Lemma.

Lemma 26 (Theorem 1 in (Negahban and Wainwright, 2012))

Consider a matrix ${\bm{\bm{X}}}\in\mathbb{R}^{m\times n}$ . Let $d=\frac{1}{2}\left(m+n\right)$ and $m_{\text{rank}}({\bm{\bm{X}}})=\frac{\left\|{\bm{\bm{X}}}\right\|_{*}}{\left\|{\bm{\bm{X}}}\right\|_{F}}$ . Define a constraint set $\mathcal{C}$ (with parameters $c_{0},n$ ) as

\displaystyle\mathcal{C}(n,c_{0})=\left\{{\bm{\bm{X}}}\in\mathbb{R}^{m\times n},{\bm{\bm{X}}}\not=0\;|\;m_{\text{spike}}({\bm{\bm{X}}})\cdot m_{\text{rank}}({\bm{\bm{X}}})\leq\frac{1}{c_{0}L}\sqrt{\frac{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}{d\log d}}\right\},

where $L$ is a constant. There are constants $(c_{0},c_{1},c_{2},c_{3})$ such that when $\left\|{\bm{\bm{\Omega}}}\right\|_{1}>c_{3}\max(d\log d)$ , we have

\displaystyle\frac{\left\|P_{{\bm{\bm{\Omega}}}}\left({\bm{\bm{X}}}\right)\right\|_{F}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\geq\frac{1}{8}\left\|{\bm{\bm{X}}}\right\|_{F}\left\{1-\frac{128L\cdot m_{\text{spike}}({\bm{\bm{X}}})}{\sqrt{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\right\},\quad\forall{\bm{\bm{X}}}\in\mathcal{C}(\left\|{\bm{\bm{\Omega}}}\right\|_{1},c_{0}),

with a high probability greater at least of $1-c_{1}\exp(-c_{2}d\log d)$ .

Proof (of Lemma 15) For a $M$ th-order tensor $\Delta$ , using Lemma 26 on each unfolded matrix $\Delta_{{\left\langle i\right\rangle}}$ ( $i=1,\dots,M$ ), we have

\displaystyle\frac{\left\|P_{{\bm{\bm{\Omega}}}}\left(\Delta_{{\left\langle i\right\rangle}}\right)\right\|_{F}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\geq\frac{1}{8}\left\|\Delta\right\|_{F}\left\{1-\frac{128L\cdot m_{\text{spike}}(\Delta_{{\left\langle i\right\rangle}})}{\sqrt{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\right\},

(67)

for all $\Delta_{{\left\langle i\right\rangle}}\in\mathcal{C}^{i}(\left\|{\bm{\bm{\Omega}}}\right\|_{1},c_{0})$ . Note that the L.H.S. of (67) is the same for all $i=1,...,M$ . Thus, to ensure (67) holds for all $\Delta_{{\left\langle i\right\rangle}}$ , we need to take the intersection of all $\Delta_{{\left\langle i\right\rangle}}$ , which leads to

\displaystyle\left\{\mathscr{X}\in\mathbb{R}^{I_{1}\times...\times I_{M}},\mathscr{X}\not=0\;|\;m_{\text{spike}}(\mathscr{X})\cdot m_{\text{rank}}(\mathscr{X}_{{\left\langle i\right\rangle}})\leq\frac{1}{c_{0}L}\sqrt{\frac{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}{d_{i}\log d_{i}}}\right\}.

(68)

Recall that $m_{\text{rank}}(\mathscr{X})=\frac{1}{M}\sum\nolimits_{i=1}^{M}m_{\text{rank}}(\mathscr{X}_{{\left\langle i\right\rangle}})$ as defined in (33). Thus, $\tilde{\mathcal{C}}(n,c_{0})$ is a subset of (68). As a result, (36) holds.

B.9 Theorem 16

Here, we first introduce some auxiliary lemmas in Appendix B.9.1, which will be used to prove Theorem 16 in Appendix B.9.2.

B.9.1 Auxiliary Lemmas

Lemma 27 (Lemma 4 in (Loh and Wainwright, 2015))

For $\kappa$ in Assumption 1, we have

(i).

The function $\alpha\rightarrow\frac{\kappa(\alpha)}{\alpha}$ is nonincreasing on $\alpha>0$ ;
(ii).

The derivative of $\kappa$ is upper bounded by $\kappa_{0}$ ;
(iii).

The function $\alpha\rightarrow\kappa(\alpha)+\frac{\alpha^{2}c}{2}$ is convex only when $c\geq\kappa_{0}$ ;
(iv).

$\lambda|\alpha|\leq\lambda\kappa(|\alpha|)+\frac{\alpha^{2}\kappa_{0}}{2}$ .

Lemma 28

$\left\langle\mathscr{X},\mathscr{Y}\right\rangle\leq\min\nolimits_{i=1,...,K}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{\infty}\left\|\mathscr{Y}_{{\left\langle i\right\rangle}}\right\|_{*}$ .

Proof First, we have $\left\langle\mathscr{X},\mathscr{Y}\right\rangle=\left\langle\mathscr{X}_{{\left\langle i\right\rangle}},\mathscr{Y}_{{\left\langle i\right\rangle}}\right\rangle$ for all $i\in\{1,\dots,M\}$ . Then, since $\left\|\cdot\right\|_{\infty}$ and $\left\|\cdot\right\|_{*}$ are dual norm with each other, $\left\langle\mathscr{X}_{{\left\langle i\right\rangle}},\mathscr{Y}_{{\left\langle i\right\rangle}}\right\rangle\leq\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{\infty}\left\|\mathscr{Y}_{{\left\langle i\right\rangle}}\right\|_{*}$ . Thus, we have $\left\langle\mathscr{X},\mathscr{Y}\right\rangle\leq\min\nolimits_{i=1,...,K}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{\infty}\left\|\mathscr{Y}_{{\left\langle i\right\rangle}}\right\|_{*}$ .

Lemma 29

For all $i\!\in\!\{1,...m\}$ , we have $\left\|\mathscr{X}\right\|_{F}\!\leq\!\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}$ and $\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}\!\leq\!\sqrt{\min(I^{i},\frac{I^{\pi}}{I^{i}})}\left\|\mathscr{X}\right\|_{F}$ .

Proof Note that $\left\|\mathscr{X}\right\|_{F}=\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{F}$ and $\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{F}\leq\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}$ , thus $\left\|\mathscr{X}\right\|_{F}\leq\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}$ . Then, since $\left\|{\bm{\bm{X}}}\right\|_{*}\leq\sqrt{\min(p,q)}\left\|{\bm{\bm{X}}}\right\|_{F}$ for a matrix ${\bm{\bm{X}}}$ of size $p\times q$ , we have $\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{*}\leq\sqrt{\min(I^{i},I^{\pi}/I^{i})}\left\|\mathscr{X}_{{\left\langle i\right\rangle}}\right\|_{F}$ $=\sqrt{\min(I^{i},I^{\pi}/I^{i})}\left\|\mathscr{X}\right\|_{F}$ .

Lemma 30

Define $h_{i}(\mathscr{X})=\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ . Let $\varPhi_{k}(\bm{A})$ produce the best rank $k$ approximation to matrix $\bm{A}$ and $\varPsi_{k}(\bm{A})=\bm{A}-\varPhi_{k}(\bm{A})$ . Suppose $\varepsilon_{i}>0$ for $i\in\{1,...,M\}$ are constants such that $\varepsilon_{i}h_{i}(\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))-h_{i}(\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))\geq 0$ . Then,

\displaystyle\varepsilon_{i}h_{i}(\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))-h_{i}(\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))\leq\kappa_{0}(\varepsilon_{i}\left\|\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\|_{*}-\left\|\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\|_{*}).

(69)

Moreover, if $\mathscr{X}^{*}_{{\left\langle i\right\rangle}}$ is of rank $k_{i}$ , for any tensor $\mathscr{X}$ satisfying $\varepsilon_{i}h_{i}(\mathscr{X}^{*}_{{\left\langle i\right\rangle}})-h_{i}(\mathscr{X}_{{\left\langle i\right\rangle}})\geq 0$ and $\varepsilon_{i}>1$ , we have

\displaystyle\varepsilon_{i}h_{i}(\mathscr{X}^{*}_{{\left\langle i\right\rangle}})\!-\!h_{i}(\mathscr{X}_{{\left\langle i\right\rangle}})\leq\kappa_{0}(\varepsilon_{i}\left\|\varPhi_{k_{i}}(\mathscr{V}_{{\left\langle i\right\rangle}})\right\|_{*}\!-\!\left\|\varPsi_{k_{i}}(\mathscr{V}_{{\left\langle i\right\rangle}})\right\|_{*}),

(70)

where $\mathscr{V}=\mathscr{X}^{*}-\mathscr{X}$ .

Proof We first prove (69). Let $h(\alpha)=\frac{\alpha}{\kappa(\alpha)}$ on $\alpha>0$ . From Lemma 27, we know $h(\alpha)$ is a non-decreasing function. Therefore,

	$\displaystyle\left\\|\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{*}$	$\displaystyle=\sum\nolimits_{j=k_{i}+1}\kappa\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)h\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right),$
		$\displaystyle\leq h\left(\sigma_{1}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)\sum\nolimits_{j=k_{i}+1}\kappa\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)=h\left(\sigma_{1}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)\cdot h_{i}\left(\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right).$		(71)

Again, using non-decreasing property of $h$ , we have

	$\displaystyle h_{i}\left(\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right)h\left(\sigma_{k_{i}+1}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)$	$\displaystyle=h\left(\sigma_{k_{i}+1}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)\sum\nolimits_{j=1}^{k_{i}}\kappa\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right),$
		$\displaystyle\leq\sum\nolimits_{j=1}^{k_{i}}\kappa\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)h\left(\sigma_{j}\left(\mathscr{A}_{{\left\langle i\right\rangle}}\right)\right)=\left\\|\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{*}.$		(72)

Note that $h(\alpha)\geq 1/\kappa_{0}$ from Lemma 27, and combining (71) and (72), we have

	$\displaystyle 0\leq\varepsilon_{i}\cdot h_{i}(\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))-h_{i}(\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}}))$	$\displaystyle\leq\big{(}\varepsilon_{i}\left\\|\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{}-\left\\|\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{}\big{)}/h\left(\sigma_{1}(\mathscr{A}_{{\left\langle i\right\rangle}})\right)$
		$\displaystyle\leq\kappa_{0}\big{(}\varepsilon_{i}\left\\|\varPhi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{}-\left\\|\varPsi_{k_{i}}(\mathscr{A}_{{\left\langle i\right\rangle}})\right\\|_{}\big{)}.$

Thus, (69) is obtained. Next, we prove (70). The triangle inequality and subadditivity of $h_{i}$ (see Lemma 5 in (Loh and Wainwright, 2015)) imply that

	$\displaystyle 0\leq\varepsilon_{i}\cdot h_{i}(\mathscr{X}^{*}_{{\left\langle i\right\rangle}})-h_{i}(\mathscr{X}_{{\left\langle i\right\rangle}})$	$\displaystyle=\varepsilon_{i}\cdot h_{i}(\varPhi_{m_{i}}(\mathscr{X}^{*}_{{\left\langle i\right\rangle}}))-h_{i}(\varPhi_{m_{i}}(\mathscr{X}_{{\left\langle i\right\rangle}}))-h_{i}(\varPsi_{m_{i}}(\mathscr{X}_{{\left\langle i\right\rangle}})),$
		$\displaystyle\leq\varepsilon_{i}\cdot h_{i}\left(\varPhi_{m_{i}}\left(\mathscr{V}_{{\left\langle i\right\rangle}}\right)\right)-h_{i}\left(\varPsi_{m_{i}}\left(\mathscr{V}_{{\left\langle i\right\rangle}}\right)\right),$
		$\displaystyle\leq\kappa_{0}\big{(}\varepsilon_{i}\left\\|\varPhi_{k_{i}}(\mathscr{V}_{{\left\langle i\right\rangle}})\right\\|_{}-\left\\|\varPsi_{k_{i}}(\mathscr{V}_{{\left\langle i\right\rangle}})\right\\|_{}\big{)}.$

Thus, (70) is obtained.

Lemma 31

$\left\|\partial\phi({\bm{\bm{X}}})\right\|_{\infty}\leq\kappa_{0}$ where $\phi$ is defined in (7).

Proof Let ${\bm{\bm{X}}}$ be of size $m\times n$ with $m\leq n$ , and SVD of ${\bm{\bm{X}}}$ be $\bm{U}\bm{\Sigma}\bm{V}^{\top}$ where $\bm{\Sigma}=\text{\,Diag}\left(\sigma_{1},\dots,\sigma_{m}\right)$ . From Theorem 3.7 in (Lewis and Sendov, 2005), we have

\displaystyle\partial\phi({\bm{\bm{X}}})=\bm{U}\text{\,Diag}\left(\kappa^{\prime}(\sigma_{1}),...,\kappa^{\prime}(\sigma_{m})\right)\bm{V}^{\top}.

From Lemma 27, we have $\kappa^{\prime}(\sigma_{1})\leq\kappa^{\prime}(\sigma_{2})\leq...\leq\kappa_{0}$ . Since $\left\|{\bm{\bm{X}}}\right\|_{\infty}$ returns the maximum singular value of ${\bm{\bm{X}}}$ , we have $\left\|\partial\phi({\bm{\bm{X}}})\right\|_{\infty}\leq\kappa^{\prime}(\sigma_{m})\leq\kappa_{0}$ .

Lemma 32

$\phi({\bm{\bm{X}}})+\frac{\kappa_{0}}{2}\left\|{\bm{\bm{X}}}\right\|_{F}^{2}$ is convex.

Proof Using the definition of $\phi$ in (7) and the fact $\left\|{\bm{\bm{X}}}\right\|_{F}^{2}=\sum_{i}\sigma_{i}({\bm{\bm{X}}})$ , we have

\displaystyle\gamma({\bm{\bm{X}}})=\phi({\bm{\bm{X}}})+\kappa_{0}/2\left\|{\bm{\bm{X}}}\right\|_{F}^{2}=\sum\nolimits_{i}\psi(\sigma_{i}({\bm{\bm{X}}})),

where $\psi(\alpha)=\kappa(\alpha)+\kappa_{0}\alpha^{2}/2$ . Since $\psi(\alpha)$ is convex (Lemma 27), $\gamma({\bm{\bm{X}}})$ is convex (using Proposition 6.1 in (Lewis and Sendov, 2005)).

B.9.2 Proof of Theorem 16

Proof Part 1). Let $\tilde{\mathscr{V}}=\tilde{\mathscr{X}}-\mathscr{X}^{*}$ , we begin by proving $\|\tilde{\mathscr{V}}\|_{F}\leq 1$ . If not, then the second condition in (35) holds, i.e.,

\displaystyle\left\langle\nabla f(\tilde{\mathscr{X}})-\nabla f(\mathscr{X}^{*}),\tilde{\mathscr{V}}\right\rangle\geq\alpha_{2}\|\tilde{\mathscr{V}}\|_{F}^{2}-\tau_{2}\sqrt{\log I^{\pi}/\|{\bm{\bm{\Omega}}}\|_{1}}\sum\nolimits_{i=1}^{M}\left\|\Delta_{{\left\langle i\right\rangle}}\right\|_{*}.

(73)

Since $\tilde{\mathscr{X}}$ is a first-order critical point, then

	$\displaystyle\left\langle\nabla f(\tilde{\mathscr{X}})+\partial r(\tilde{\mathscr{X}}),\mathscr{X}-\tilde{\mathscr{X}}\right\rangle\geq 0,$		(74)
	$\displaystyle\nabla f(\tilde{\mathscr{X}})+\partial r(\tilde{\mathscr{X}})\ni\bm{0}.$		(75)

Taking $\mathscr{X}=\mathscr{X}^{*}$ , from (74), we have

\displaystyle\left\langle\nabla f(\tilde{\mathscr{X}})+\partial r(\tilde{\mathscr{X}}),-\tilde{\mathscr{V}}\right\rangle\geq 0.

(76)

Combining (73) and (76), we have

\displaystyle\left\langle-\partial r(\tilde{\mathscr{X}})-\nabla f\left(\mathscr{X}^{*}\right),\tilde{\mathscr{V}}\right\rangle\geq\alpha_{2}\|\tilde{\mathscr{V}}\|_{F}^{2}-\tau_{2}\sqrt{\log I^{\pi}/\|{\bm{\bm{\Omega}}}\|_{1}}\sum\nolimits_{i=1}^{M}\left\|\Delta_{{\left\langle i\right\rangle}}\right\|_{*}.

(77)

Let $\tilde{v}_{i}=\|\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}}\|_{*}$ and $\tilde{v}=\sum\nolimits_{i=1}^{M}\tilde{v}_{i}$ . For the L.H.S of (77),

	$\displaystyle\left\langle\partial r(\tilde{\mathscr{X}})+\nabla f\left(\mathscr{X}^{*}\right),\tilde{\mathscr{V}}\right\rangle$	$\displaystyle=\left\langle\nabla f\left(\mathscr{X}^{*}\right),\tilde{\mathscr{V}}\right\rangle+\lambda\sum\nolimits_{i=1}^{M}\left\langle\partial\phi(\mathscr{X}_{{\left\langle i\right\rangle}}),\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}}\right\rangle$		(78)
		$\displaystyle\leq\max_{i}\left\\|[\nabla f\left(\mathscr{X}^{*}\right)]_{{\left\langle i\right\rangle}}\right\\|_{\infty}\tilde{v}_{i}+\lambda\sum\nolimits_{i=1}^{M}\left\\|\partial\phi(\mathscr{X}_{{\left\langle i\right\rangle}})\right\\|_{\infty}\tilde{v}_{i},$		(79)

Next, note that the following inequalities hold.

•

From the left part of (37) in Theorem 16, we have $\max_{i}\left\|[\nabla f\left(\mathscr{X}^{*}\right)]_{{\left\langle i\right\rangle}}\right\|_{\infty}\leq\frac{\lambda\kappa_{0}}{4}$ .
•

From Lemma 31, we have $\left\|\partial\phi({\bm{\bm{X}}})\right\|_{\infty}\leq\kappa_{0}$ .

Combining with (79), we have

\displaystyle\left\langle\partial r(\tilde{\mathscr{X}})+\nabla f\left(\mathscr{X}^{*}\right),\tilde{\mathscr{V}}\right\rangle\leq\frac{\lambda\kappa_{0}}{4}+3\lambda\kappa_{0}=\frac{13\lambda\kappa_{0}}{4}.

(80)

Combining (77) and (80), then rearranging terms, we have

\displaystyle\|\tilde{\mathscr{V}}\|_{F}\leq\frac{1}{\alpha_{2}}\left(\tau_{2}\sqrt{\log I^{\pi}/\|{\bm{\bm{\Omega}}}\|_{1}}+\lambda\kappa_{0}\right)\tilde{v}\leq\frac{1}{\alpha_{2}}\left(\tau_{2}\sqrt{\log I^{\pi}/\|{\bm{\bm{\Omega}}}\|_{1}}+\frac{13\lambda\kappa_{0}}{4}\right)R.

Finally, using assumptions on $\|{\bm{\bm{\Omega}}}\|_{1}$ and $\lambda$ , we have $\|\tilde{\mathscr{V}}\|_{F}\leq 1$ , which is in the contradiction with our assumption at the beginning of Part 1). Thus, $\|\tilde{\mathscr{V}}\|_{F}\leq 1$ must hold.

Part 2). Let $h_{i}(\mathscr{X})\!=\!\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ . Since the function $h_{i}(\mathscr{X})\!+\!\mu/2\left\|\mathscr{X}\right\|_{F}^{2}$ is convex (Lemma 32), we have

\displaystyle\left\langle\partial h_{i}(\tilde{\mathscr{X}}),\mathscr{X}^{*}-\tilde{\mathscr{X}}\right\rangle\leq\tilde{h}_{i}(\tilde{\mathscr{X}}).

(81)

where $\tilde{h}_{i}(\tilde{\mathscr{X}})=h_{i}(\mathscr{X}^{*})-h_{i}(\tilde{\mathscr{X}})+\frac{L}{2}\|\tilde{\mathscr{X}}-\mathscr{X}^{*}\|_{F}^{2}$ . From the first condition in (35), we have

\displaystyle\langle\nabla f(\tilde{\mathscr{V}})-\nabla f\left(\mathscr{X}^{*}\right),-\tilde{\mathscr{X}}\rangle\geq\alpha_{1}\|\tilde{\mathscr{V}}\|_{F}^{2}-\tau_{1}\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}\tilde{v}^{2}.

(82)

Combining (74) and (82), we have

	$\displaystyle\alpha_{1}\\|\tilde{\mathscr{V}}\\|_{F}^{2}-\tau_{1}\frac{\log I^{\pi}}{\\|{\bm{\bm{\Omega}}}\\|_{1}}\tilde{v}^{2}$	$\displaystyle\leq\left\langle\partial r(\tilde{\mathscr{X}}),\tilde{\mathscr{V}}\right\rangle-\left\langle\nabla f(\mathscr{X}^{*}),\tilde{\mathscr{V}}\right\rangle,$
		$\displaystyle=\lambda\sum\nolimits_{i=1}^{M}\left\langle\partial h_{i}(\tilde{\mathscr{X}}),\tilde{\mathscr{V}}\right\rangle-\left\langle\nabla f(\mathscr{X}^{*}),\tilde{\mathscr{V}}\right\rangle.$

Together with (81), we have

	$\displaystyle\alpha_{1}\\|\tilde{\mathscr{V}}\\|_{F}^{2}-\tau_{1}\frac{\log I^{\pi}}{\\|{\bm{\bm{\Omega}}}\\|_{1}}\tilde{v}^{2}$	$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})-\left\langle\nabla f(\mathscr{X}^{*}),\tilde{\mathscr{V}}\right\rangle,$
		$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})+\max_{i}\left\\|[\nabla f(\mathscr{X}^{*})]_{{\left\langle i\right\rangle}}\right\\|_{\infty}\tilde{v}_{i}$
		$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})+\max_{i}\left\\|[\nabla f(\mathscr{X}^{*})]_{{\left\langle i\right\rangle}}\right\\|_{\infty}\tilde{v},$

where the second inequality is from Lemma 28. Rearranging items in the above inequality, we have

\displaystyle\big{(}\alpha_{1}-\frac{\mu M}{2}\big{)}\|\tilde{\mathscr{V}}\|_{F}^{2}\!\leq\!\lambda\sum\nolimits_{i=1}^{M}\big{(}h_{i}(\mathscr{X}^{*})\!-\!h_{i}(\tilde{\mathscr{X}})\big{)}\!+\!\left(\max_{i}\left\|[\nabla f(\mathscr{X}^{*})]_{{\left\langle i\right\rangle}}\right\|_{\infty}\!+\!\tau_{1}\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}\tilde{v}\right)\tilde{v}.

(83)

Note that from the Assumption in Theorem 16, we have the following inequalities.

•

$\max_{i}\big{\|}\left[\nabla f(\mathscr{X}^{*})\right]_{{\left\langle i\right\rangle}}\big{\|}_{\infty}\leq\kappa_{0}\lambda/4$ .

•

Since $\|{\bm{\bm{\Omega}}}\|_{1}\geq 16R^{2}\max\left(\tau_{1}^{2},\tau_{2}^{2}\right)\log(I^{\pi})/\alpha_{2}^{2}$ and $\alpha_{2}\sqrt{\log I^{\pi}/\|{\bm{\bm{\Omega}}}\|_{1}}\leq\kappa_{0}\lambda/4$ , then

\displaystyle\frac{\tau_{1}\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}\tilde{v}\leq\frac{\tau_{1}}{\alpha_{2}}\sqrt{\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}}\tilde{v}\cdot\alpha_{2}\sqrt{\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}}\leq\frac{\tau_{1}}{\alpha_{2}}\sqrt{\frac{\alpha_{2}^{2}\log I^{\pi}}{16\tilde{v}^{2}\tau_{1}^{2}}}\tilde{v}\cdot\alpha_{2}\sqrt{\frac{\log I^{\pi}}{\|{\bm{\bm{\Omega}}}\|_{1}}}\leq\frac{\lambda\kappa_{0}}{4}.

Combing above inequalities into (83), we further have

\displaystyle\big{(}\alpha_{1}-\frac{\mu M}{2}\big{)}\|\tilde{\mathscr{V}}\|_{F}^{2}

\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\big{(}h_{i}(\mathscr{X}^{*})-h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\kappa_{0}}{2}\tilde{v}.

(84)

Part 3). Combining (84) and Lemma 27, as well as the subadditivity of $h_{i}$ , we have

	$\displaystyle\big{(}\alpha_{1}-\frac{LM}{2}\big{)}\\|\tilde{\mathscr{V}}\\|_{F}^{2}$	$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\big{(}h_{i}(\mathscr{X}^{*})-h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\kappa_{0}}{2}\big{(}\frac{\sum\nolimits_{i=1}^{M}h_{i}(\tilde{\mathscr{V}})}{LM}+\frac{LM}{2\lambda\kappa_{0}}\\|\tilde{\mathscr{V}}\\|_{F}^{2}\big{)},$
		$\displaystyle\leq\!\lambda\!\sum\nolimits_{i=1}^{M}\!\big{(}h_{i}(\mathscr{X}^{})\!-\!h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\sum\nolimits_{i=1}^{M}h_{i}(\mathscr{X}^{})\!+\!h_{i}(\tilde{\mathscr{X}})}{2D}+\frac{LM}{4}\\|\tilde{\mathscr{V}}\\|_{F}^{2}.$		(85)

Next, define

\displaystyle a_{v}=\alpha_{1}-\frac{3M}{4}\kappa_{0},\quad b_{v}=1+\frac{1}{2M},\quad c_{v}=1-\frac{1}{2M}.

Rearranging terms in (85), we have

\displaystyle a_{v}\|\tilde{\mathscr{V}}\|_{F}^{2}\leq\lambda\sum\nolimits_{i=1}^{M}b_{v}h_{i}(\mathscr{X}^{*})-c_{v}h_{i}(\tilde{\mathscr{X}}).

(86)

From Lemma 30, we have

\displaystyle b_{v}h_{i}(\mathscr{X}^{*})-c_{v}h_{i}(\tilde{\mathscr{X}})\leq L\big{(}b_{v}\left\|\varPhi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\|_{*}-c_{v}\left\|\varPsi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\|_{*}\big{)}.

(87)

Besides, we have the cone condition

\displaystyle\left\|\varPhi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\|_{*}\leq\frac{c_{v}}{b_{v}}\left\|\varPsi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\|_{*}.

(88)

Combining (86), (87) and (88), we have

	$\displaystyle a_{v}\\|\tilde{\mathscr{V}}\\|_{F}^{2}$	$\displaystyle\leq\lambda\kappa_{0}\sum\nolimits_{i=1}^{M}\big{(}b_{v}\left\\|\varPhi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\\|_{}-c_{v}\left\\|\varPsi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\\|_{}\big{)},$
		$\displaystyle\leq\lambda\kappa_{0}\sum\nolimits_{i=1}^{M}b_{v}\left\\|\varPhi_{k_{i}}(\tilde{\mathscr{V}}_{{\left\langle i\right\rangle}})\right\\|_{*}\leq\lambda\kappa_{0}\sum\nolimits_{i=1}^{M}c_{v}\sqrt{k_{i}}\\|\tilde{\mathscr{V}}\\|_{F}.$

where the last inequality comes from Lemma 29. Since $a_{v}>0$ as assumed, we conclude that

\displaystyle\|\tilde{\mathscr{V}}\|_{F}\leq\frac{\lambda\kappa_{0}c_{v}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}.

which proves the theorem.

B.10 Corollary 17

Proof When noisy level is sufficiently small, (37) reduces to

\displaystyle\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\leq\lambda\leq\frac{1}{4R\kappa_{0}}.

(89)

Let $\lambda=b_{1}\max_{i}\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}$ where $b_{1}\in\left[\frac{4}{\kappa_{0}},\frac{\alpha_{2}}{4R\kappa_{0}\max_{i}\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}}\right]$ . It is easy to check (89) holds. Then, from Theorem 16, we will have

\displaystyle\big{\|}\mathscr{X}^{*}-\tilde{\mathscr{X}}\big{\|}_{F}\leq b_{1}\max_{i}\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}\cdot\frac{\kappa_{0}c_{v}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}.

(90)

Next, note that

\displaystyle\mathbb{E}\left[\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{\infty}\right]\leq\mathbb{E}\left[\|\left[P_{{\bm{\bm{\Omega}}}}\left(\mathscr{E}\right)\right]_{{\left\langle i\right\rangle}}\|_{F}\right]=\mathbb{E}\left[\|\xi\cdot{\bm{\bm{\Omega}}}\|_{F}\right]=\sigma\|{\bm{\bm{\Omega}}}\|_{F}\leq\sigma\sqrt{I^{\pi}}.

(91)

Combining (90) and (91), we then have

\displaystyle\mathbb{E}\left[\big{\|}\mathscr{X}^{*}-\tilde{\mathscr{X}}\big{\|}_{F}\right]\leq\sigma\frac{\kappa_{0}c_{v}\sqrt{I^{\pi}}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}.

B.11 Corollary 18

Proof When $\left\|{\bm{\bm{\Omega}}}\right\|_{1}$ is sufficiently larger, (37) reduces to

\displaystyle 4\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}\leq\lambda\leq\frac{1}{4R}.

(92)

Let $\lambda=b_{3}\sqrt{\frac{\log I^{\pi}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}$ where $b_{3}\in\left[4,\frac{1}{4R\sqrt{\log I^{\pi}/\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\right]$ . It is easy to check (92) holds. Then, from Theorem 16, we will have

\displaystyle\big{\|}\mathscr{X}^{*}-\tilde{\mathscr{X}}\big{\|}_{F}\leq b_{3}\sqrt{\frac{\log I^{\pi}}{\left\|{\bm{\bm{\Omega}}}\right\|_{1}}}\cdot\frac{\kappa_{0}c_{v}}{a_{v}}\sum\nolimits_{i=1}^{M}\sqrt{k_{i}}.

B.12 Proposition 19

Proof First, from Proposition 1 in (Yao and Kwok, 2018), we know that the function $\kappa(|a|)-\kappa_{0}\cdot|a|$ is smooth. Since $\tilde{\ell}$ is also smooth, thus $\tilde{\kappa}_{\ell}$ is differentiable. Finally, note that $\lim\nolimits_{\delta\rightarrow 0}\ell(a;\delta)=|a|$ . Then, we have

	$\displaystyle\lim\nolimits_{\delta\rightarrow 0}\tilde{\kappa}_{\ell}(\|a\|;\delta)$	$\displaystyle=\lim\nolimits_{\delta\rightarrow 0}\big{[}\kappa_{0}\cdot\tilde{\ell}(\|a\|;\delta)+\left(\kappa_{\ell}(\|a\|)-\kappa_{0}\cdot\|a\|\right)\big{]},$
		$\displaystyle=\kappa_{0}\|a\|+\left(\kappa_{\ell}(\|a\|)-\kappa_{0}\|a\|\right)=\kappa_{\ell}(\|a\|).$

Thus, the Proposition holds.

B.13 Theorem 20

Proof First, by the definition of $\tilde{\kappa}_{\ell}$ in (41), when $|a|\leq\delta$ , we have

\displaystyle\lim\limits_{\delta\rightarrow 0}\partial\tilde{\kappa}_{\ell}(a;\delta)=\frac{a}{\delta}\kappa_{0}\in\begin{cases}[0,\kappa_{0})&\text{if}\;a\geq 0\\ (-\kappa_{0},0)&\text{otherwise}\end{cases}.

Thus,

\displaystyle\lim\nolimits_{\delta\rightarrow 0}\partial\tilde{\kappa}_{\ell}(a;\delta)=\partial\kappa_{\ell}(|a|).

(93)

Define $\tilde{F}_{\tau}(\mathscr{X};\delta)=\sum\nolimits_{(i_{1}...i_{M})\in\mathbf{\Omega}}\tilde{\ell}\left(\mathscr{X}_{i_{1}...i_{M}}-\mathscr{O}_{i_{1}...i_{M}};\delta\right)+\sum\nolimits_{i=1}^{D}\lambda_{i}\phi(\mathscr{X}_{{\left\langle i\right\rangle}})$ . Since $\mathscr{X}_{s}$ is obtained from solving (42) at step 4 of Algorithm 3, we have $\mathscr{X}_{s}\in\partial\tilde{F}_{\tau}(\mathscr{X};(\delta_{0})^{s})$ . Take $s\rightarrow\infty$ and use (93), we have $\lim\nolimits_{s\rightarrow\infty}\mathscr{X}_{s}\in\lim\nolimits_{s\rightarrow\infty}\partial\tilde{F}_{\tau}(\mathscr{X};(\delta_{0})^{s})=\lim\nolimits_{\delta\rightarrow 0}\partial\tilde{F}_{\tau}(\mathscr{X};\delta)=\partial\tilde{F}_{\tau}(\mathscr{X})$ . Thus, Theorem 20 holds.

References

Acar et al. (2011) E. Acar, D.M. Dunlavy, T. Kolda, and M. Mørup. Scalable tensor factorizations for incomplete data. Chemometrics and Intelligent Laboratory Systems, 106(1):41–56, 2011.
Agarwal et al. (2010) A. Agarwal, S. Negahban, and M. J. Wainwright. Fast global convergence rates of gradient methods for high-dimensional statistical recovery. In Advances in Neural Information Processing Systems, pages 37–45, 2010.
Attouch et al. (2013) H. Attouch, J. Bolte, and B. Svaiter. Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss-Seidel methods. Mathematical Programming, 137(1-2):91–129, 2013.
Bader and Kolda (2007) B. Bader and T. Kolda. Efficient MATLAB computations with sparse and factored tensors. SIAM Journal on Scientific Computing, 30(1):205–231, 2007.
Bahadori et al. (2014) M. Bahadori, Q. Yu, and Y. Liu. Fast multivariate spatio-temporal analysis via low rank tensor learning. In Advances in Neural Information Processing Systems, pages 3491–3499, 2014.
Balazevic et al. (2019) I. Balazevic, C. Allen, and T. Hospedales. TuckER: Tensor factorization for knowledge graph completion. In Conference on Empirical Methods in Natural Language Processing, pages 5188–5197, 2019.
Bauschke et al. (2008) H. Bauschke, R. Goebel, Y. Lucet, and X. Wang. The proximal average: Basic theory. SIAM Journal on Optimization, 19(2):766–785, 2008.
Belkin et al. (2006) M. Belkin, P. Niyogi, and V. Sindhwani. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. Journal of Machine Learning Research, 7(Nov):2399–2434, 2006.
Bengua et al. (2017) J. Bengua, H. Phien, H. Tuan, and M. Do. Efficient tensor completion for color image and video recovery: Low-rank tensor train. IEEE Transactions on Image Processing, 26(5):2466–2479, 2017.
Bollacker et al. (2008) K. Bollacker, C. Evans, P. Paritosh, T. Sturge, and J. Taylor. Freebase: A collaboratively created graph database for structuring human knowledge. In ACM SIGMOD International Conference on Management of Data, pages 1247–1250, 2008.
Bolte et al. (2010) J. Bolte, A. Daniilidis, O. Ley, and L. Mazet. Characterizations of lojasiewicz inequalities and applications. Transactions of the American Mathematical Society, 362(6):3319–3363, 2010.
Bolte et al. (2014) J. Bolte, S. Sabach, and M. Teboulle. Proximal alternating linearized minimization or nonconvex and nonsmooth problems. Mathematical Programming, 146(1-2):459–494, 2014.
Bordes et al. (2013) A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston, and O. Yakhnenko. Translating embeddings for modeling multi-relational data. In Advances in Neural Information Processing Systems, pages 2787–2795, 2013.
Boumal and Absil (2015) N. Boumal and P.-A. Absil. Low-rank matrix completion via preconditioned optimization on the grassmann manifold. Linear Algebra and its Applications, 475:200–239, 2015.
Boyd and Vandenberghe (2009) S. Boyd and L. Vandenberghe. Convex optimization. Cambridge University Press, 2009.
Boyd et al. (2011) S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 3(1):1–122, 2011.
Cai et al. (2010) J.-F. Cai, E. J. Candès, and Z. Shen. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 20(4):1956–1982, 2010.
Candès and Recht (2009) E. J. Candès and B. Recht. Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 9(6):717–772, 2009.
Candès and Tao (2005) E. J Candès and Terence Tao. Decoding by linear programming. IEEE Transactions on Information Theory, 51(12):4203–4215, 2005.
Candès et al. (2008) E. J. Candès, M. B. Wakin, and S. P. Boyd. Enhancing sparsity by reweighted $\ell_{1}$ minimization. Journal of Fourier Analysis and Applications, 14(5-6):877–905, 2008.
Candès et al. (2011) E. J. Candès, X. Li, Y. Ma, and J. Wright. Robust principal component analysis? Journal of the ACM, 58(3):11, 2011.
Chen et al. (2019) X. Chen, S. Liu, K. Xu, X. Li, X. Lin, M. Hong, and D. Cox. ZO-AdaMM: Zeroth-order adaptive momentum method for black-box optimization. In Advances in Neural Information Processing Systems, pages 7204–7215, 2019.
Chen et al. (2020) X. Chen, J. Yang, and L. Sun. A nonconvex low-rank tensor completion model for spatiotemporal traffic data imputation. Transportation Research Part C: Emerging Technologies, 117:102673, 2020.
Cheng et al. (2016) H. Cheng, Y. Yu, X. Zhang, E. Xing, and D. Schuurmans. Scalable and sound low-rank tensor learning. In International Conference on Artificial Intelligence and Statistics, pages 1114–1123, 2016.
Cichocki et al. (2015) A. Cichocki, D. Mandic, L. De Lathauwer, G. Zhou, Q. Zhao, C. Caiafa, and H. Phan. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Processing Magazine, 32(2):145–163, 2015.
Davis et al. (2011) D. Davis, R. Lichtenwalter, and N. V. Chawla. Multi-relational link prediction in heterogeneous information networks. In International Conference on Advances in Social Networks Analysis and Mining, pages 281–288, 2011.
Dettmers et al. (2018) T. Dettmers, P. Minervini, P. Stenetorp, and S. Riedel. Convolutional 2D knowledge graph embeddings. In AAAI Conference on Artificial Intelligence, 2018.
Duchi et al. (2011) J. Duchi, E. Hazan, and Y. Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul):2121–2159, 2011.
Efron et al. (2004) B. Efron, T. Hastie, I. Johnstone, and R. Tibshirani. Least angle regression. Annals of Statistics, 32(2):407–499, 2004.
Fan and Li (2001) J. Fan and R. Li. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 96(456):1348–1360, 2001.
Gandy et al. (2011) S. Gandy, B. Recht, and I. Yamada. Tensor completion and low-n-rank tensor recovery via convex optimization. Inverse Problems & Imaging, 27(2):025010, 2011.
Ghadimi and Lan (2016) S. Ghadimi and G. Lan. Accelerated gradient methods for nonconvex nonlinear and stochastic programming. Mathematical Programming, 156(1-2):59–99, 2016.
Gu et al. (2014) Q. Gu, H. Gui, and J. Han. Robust tensor decomposition with gross corruption. In Advances in Neural Information Processing Systems, pages 1422–1430, 2014.
Gu et al. (2017) S. Gu, Q. Xie, D. Meng, W. Zuo, X. Feng, and L. Zhang. Weighted nuclear norm minimization and its applications to low level vision. International Journal of Computer Vision, 121(2):183–208, 2017.
Gui et al. (2016) H. Gui, J. Han, and Q. Gu. Towards faster rates and oracle property for low-rank matrix estimation. In International Conference on Machine Learning, pages 2300–2309, 2016.
Guo et al. (2017) X. Guo, Q. Yao, and J. Kwok. Efficient sparse low-rank tensor completion using the Frank-Wolfe algorithm. In AAAI Conference on Artificial Intelligence, pages 1948–1954, 2017.
Han et al. (2018) X. Han, S. Cao, X. Lv, Y. Lin, Z. Liu, M. Sun, and J. Li. OpenKE: An open toolkit for knowledge embedding. In Conference on Empirical Methods in Natural Language Processing, pages 139–144, 2018.
Hare and Sagastizábal (2009) W. Hare and C. Sagastizábal. Computing proximal points of nonconvex functions. Mathematical Programming, 116(1-2):221–258, 2009.
Hartman (1959) P. Hartman. On functions representable as a difference of convex functions. Pacific Journal of Mathematics, 9(3):707–713, 1959.
He et al. (2019) W. He, Q. Yao, C. C. Li, N. Yokoya, and Q. Zhao. Non-local meets global: An integrated paradigm for hyperspectral denoising. In IEEE Conference on Computer Vision and Pattern Recognition, pages 6861–6870, 2019.
Hillar and Lim (2013) C. J. Hillar and L.-H. Lim. Most tensor problems are NP-hard. Journal of the ACM, 60(6), 2013.
Hong et al. (2020) D. Hong, T. Kolda, and J. A. Duersch. Generalized canonical polyadic tensor decomposition. SIAM Review, 62(1):133–163, 2020.
Hong et al. (2016) M. Hong, Z.-Q. Luo, and Meisam R. Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM Journal on Optimization, 26(1):337–364, 2016.
Hsieh et al. (2015) C.-J. Hsieh, N. Natarajan, and I. Dhillon. PU learning for matrix completion. In International Conference on Machine Learning, pages 2445–2453, 2015.
Hu et al. (2013) Y. Hu, D. Zhang, J. Ye, X. Li, and X. He. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(9):2117–2130, 2013.
Huang et al. (2020) H. Huang, Y. Liu, J. Liu, and C. Zhu. Provable tensor ring completion. Signal Processing, 171:107486, 2020.
Huber (1964) P. Huber. Robust estimation of a location parameter. Annals of Mathematical Statistics, pages 73–101, 1964.
Indyk et al. (2019) P. Indyk, A. Vakilian, and Y. Yuan. Learning-based low-rank approximations. In Advances in Neural Information Processing Systems, pages 7402–7412, 2019.
Janzamin et al. (2020) M. Janzamin, R. Ge, J. Kossaifi, and A. Anandkumar. Spectral learning on matrices and tensors. Foundations and Trends in Machine Learning, 2020.
Jiang et al. (2015) W. Jiang, F. Nie, and H. Huang. Robust dictionary learning with capped $\ell_{1}$ -norm. In International Joint Conference on Artificial Intelligence, 2015.
Kasai and Mishra (2016) H. Kasai and B. Mishra. Low-rank tensor completion: A Riemannian manifold preconditioning approach. In International Conference on Machine Learning, pages 1012–1021, 2016.
Kingma and Ba (2014) D. Kingma and J. Ba. Adam: A method for stochastic optimization. In International Conference on Learning Representations, 2014.
Kolda and Bader (2009) T. Kolda and B. Bader. Tensor decompositions and applications. SIAM Review, 51(3):455–500, 2009.
Kressner et al. (2014) D. Kressner, M. Steinlechner, and B. Vandereycken. Low-rank tensor completion by Riemannian optimization. BIT Numerical Mathematics, 54(2):447–468, 2014.
Lacroix et al. (2018) T. Lacroix, N. Usunier, and G. Obozinski. Canonical tensor decomposition for knowledge base completion. In International Conference on Machine Learning, 2018.
Le Thi and Tao (2005) H. A. Le Thi and P. D. Tao. The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Annals of Operations Research, 133(1-4):23–46, 2005.
Lei et al. (2009) T. Lei, X. Wang, and H. Liu. Uncoverning groups via heterogeneous interaction analysis. In IEEE International Conference on Data Mining, pages 503–512, 2009.
Lewis and Sendov (2005) A. S. Lewis and H. S. Sendov. Nonsmooth analysis of singular values. Set-Valued Analysis, 13(3):243–264, 2005.
Li and Lin (2015) H. Li and Z. Lin. Accelerated proximal gradient methods for nonconvex programming. In Advances in Neural Information Processing Systems, pages 379–387, 2015.
Li et al. (2017) Q. Li, Y. Zhou, Y. Liang, and P. Varshney. Convergence analysis of proximal gradient with momentum for nonconvex optimization. In International Conference on Machine Learning, pages 2111–2119, 2017.
Liu et al. (2013) J. Liu, P. Musialski, P. Wonka, and J. Ye. Tensor completion for estimating missing values in visual data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(1):208–220, 2013.
Loh and Wainwright (2015) P. Loh and M. Wainwright. Regularized M-estimators with nonconvexity: Statistical and algorithmic theory for local optima. Journal of Machine Learning Research, 16:559–616, 2015.
Lu et al. (2013) C. Lu, J. Shi, and J. Jia. Online robust dictionary learning. In IEEE Conference on Computer Vision and Pattern Recognition, pages 415–422, 2013.
Lu et al. (2016a) C. Lu, J. Feng, Y. Chen, W. Liu, Z. Lin, and S. Yan. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In IEEE Conference on Computer Vision and Pattern Recognition, pages 5249–5257, 2016a.
Lu et al. (2016b) C. Lu, J. Tang, S. Yan, and Z. Lin. Nonconvex nonsmooth low rank minimization via iteratively reweighted nuclear norm. IEEE Transactions on Image Processing, 25(2):829–839, 2016b.
Mazumder et al. (2010) R. Mazumder, T. Hastie, and R. Tibshirani. Spectral regularization algorithms for learning large incomplete matrices. Journal of Machine Learning Research, 11:2287–2322, 2010.
Mazumder et al. (2020) R. Mazumder, D. F. Saldana, and H. Weng. Matrix completion with nonconvex regularization: Spectral operators and scalable algorithms. Statistics and Computing, 30:1113–1138, 2020.
Miller (1995) G. A. Miller. WordNet: A lexical database for english. Communications of the ACM, 38(11):39–41, 1995.
Mu et al. (2014) C. Mu, B. Huang, J. Wright, and D. Goldfarb. Square deal: Lower bounds and improved relaxations for tensor recovery. In International Conference on Machine Learning, pages 73–81, 2014.
Narita et al. (2012) A. Narita, K. Hayashi, R. Tomioka, and H. Kashima. Tensor factorization using auxiliary information. Data Mining and Knowledge Discovery, 25(2):298–324, 2012.
Negahban and Wainwright (2012) S. Negahban and M. J. Wainwright. Restricted strong convexity and weighted matrix completion: Optimal bounds with noise. Journal of Machine Learning Research, 13(May):1665–1697, 2012.
Negahban et al. (2012) S. Negahban, P. Ravikumar, M. Wainwright, and B. Yu. A unified framework for high-dimensional analysis of $M$ -estimators with decomposable regularizers. Statistical Science, 27(4):538–557, 2012.
Nesterov (2013) Y. Nesterov. Introductory Lectures on Convex Optimization: A Basic Course. Springer Science & Business Media, 2013.
Nickel et al. (2015) M. Nickel, K. Murphy, V. Tresp, and E. Gabrilovich. A review of relational machine learning for knowledge graphs. Proceedings of the IEEE, 104(1):11–33, 2015.
Nimishakavi et al. (2018) M. Nimishakavi, P. Jawanpuria, and B. Mishra. A dual framework for low-rank tensor completion. In Advances in Neural Information Processing Systems, 2018.
Oseledets (2011) I. Oseledets. Tensor-train decomposition. SIAM Journal on Scientific Computing, 33(5):2295–2317, 2011.
Papalexakis et al. (2017) E. Papalexakis, C. Faloutsos, and N. Sidiropoulos. Tensors for data mining and data fusion: Models, applications, and scalable algorithms. ACM Transactions on Intelligent Systems and Technology, 8(2):16, 2017.
Parikh and Boyd (2013) N. Parikh and S. P. Boyd. Proximal algorithms. Foundations and Trends in Optimization, 1(3):123–231, 2013.
Phipps and Kolda (2019) E. Phipps and T. Kolda. Software for sparse tensor decomposition on emerging computing architectures. SIAM Journal on Scientific Computing, 41:C269–C290, 2019.
Rauhut et al. (2017) H. Rauhut, R. Schneider, and Ž. Stojanac. Low rank tensor recovery via iterative hard thresholding. Linear Algebra and its Applications, 523:220–262, 2017.
Rendle and Schmidt-Thieme (2010) S. Rendle and L. Schmidt-Thieme. Pairwise interaction tensor factorization for personalized tag recommendation. In ACM International Conference on Web Search and Data Mining, pages 81–90, 2010.
Shen et al. (2017) L. Shen, W. Liu, J. Huang, Y.-G. Jiang, and S. Ma. Adaptive proximal average approximation for composite convex minimization. In AAAI Conference on Artificial Intelligence, 2017.
Signoretto et al. (2011) M. Signoretto, R. Van de Plas, B. De Moor, and J. Suykens. Tensor versus matrix completion: A comparison with application to spectral data. Signal Processing Letter, 18(7):403–406, 2011.
Song et al. (2017) Q. Song, H. Ge, J. Caverlee, and X. Hu. Tensor completion algorithms in big data analytics. ACM Transactions on Knowledge Discovery from Data, 2017.
Srebro et al. (2005) N. Srebro, J. Rennie, and T. Jaakkola. Maximum-margin matrix factorization. In Advances in Neural Information Processing Systems, pages 1329–1336, 2005.
Tomioka and Suzuki (2013) R. Tomioka and T. Suzuki. Convex tensor decomposition via structured schatten norm regularization. In Advances in Neural Information Processing Systems, pages 1331–1339, 2013.
Tomioka et al. (2010) R. Tomioka, K. Hayashi, and H. Kashima. Estimation of low-rank tensors via convex optimization. Technical report, arXiv preprint, 2010.
Tomioka et al. (2011) R. Tomioka, T. Suzuki, K. Hayashi, and H. Kashima. Statistical performance of convex tensor decomposition. In Advances in Neural Information Processing Systems, pages 972–980, 2011.
Toutanova et al. (2015) K. Toutanova, D. Chen, P. Pantel, H. Poon, P. Choudhury, and M. Gamon. Representing text for joint embedding of text and knowledge bases. In Conference on Empirical Methods in Natural Language Processing, pages 1499–1509, 2015.
Tu et al. (2016) S. Tu, R. Boczar, M. Simchowitz, M. Soltanolkotabi, and B. Recht. Low-rank solutions of linear matrix equations via procrustes flow. In International Conference on Machine Learning, 2016.
Tucker (1966) L. R. Tucker. Some mathematical notes on three-mode factor analysis. Psychometrika, 31(3):279–311, 1966.
Vandereycken (2013) Bart Vandereycken. Low-rank matrix completion by riemannian optimization. SIAM Journal on Optimization, 23(2):1214–1236, 2013.
Wang et al. (2017) L. Wang, X. Zhang, and Q. Gu. A unified computational and statistical framework for nonconvex low-rank matrix estimation. In International Conference on Artificial Intelligence and Statistics, 2017.
Wang et al. (2019) Y. Wang, W. Yin, and J. Zeng. Global convergence of ADMM in nonconvex nonsmooth optimization. Journal of Scientific Computing, 78(1):29–63, 2019.
Wang et al. (2020) Z. Wang, Y. Zhou, Y. Liang, and G. Lan. Cubic regularization with momentum for nonconvex optimization. In Uncertainty in Artificial Intelligence, pages 313–322, 2020.
Wimalawarne et al. (2018) K. Wimalawarne, M. Yamada, and H. Mamitsuka. Convex coupled matrix and tensor completion. Neural Computation, 30:3095–3127, 2018.
Xu et al. (2013) Y. Xu, R. Hao, W. Yin, and Z. Su. Parallel matrix factorization for low-rank tensor completion. Inverse Problems & Imaging, 9(2):601–624, 2013.
Xue et al. (2018) S. Xue, W. Qiu, F. Liu, and X. Jin. Low-rank tensor completion by truncated nuclear norm regularization. International Conference on Pattern Recognition, pages 2600–2605, 2018.
Yao and Kwok (2018) Q. Yao and J. Kwok. Efficient learning with a family of nonconvex regularizers by redistributing nonconvexity. Journal of Machine Learning Research, 18(1):6574–6625, 2018.
Yao et al. (2017) Q. Yao, J. Kwok, F. Gao, W. Chen, and T.-Y. Liu. Efficient inexact proximal gradient algorithm for nonconvex problems. In International Joint Conference on Artificial Intelligence, pages 3308–3314, 2017.
Yao et al. (2019a) Q. Yao, J. Kwok, and B. Han. Efficient nonconvex regularized tensor completion with structure-aware proximal iterations. In International Conference on Machine Learning, pages 7035–7044, 2019a.
Yao et al. (2019b) Q. Yao, J. Kwok, T. Wang, and T.-Y. Liu. Large-scale low-rank matrix learning with nonconvex regularizers. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019b.
Yu (2013) Y.-L. Yu. Better approximation and faster algorithm using the proximal average. In Advances in Neural Information Processing Systems, pages 458–466, 2013.
Yu et al. (2015) Y.-L. Yu, Z. Xun, M. Micol, and E. Xing. Minimizing nonconvex non-separable functions. In International Conference on Artificial Intelligence and Statistics, pages 1107–1115, 2015.
Yuan et al. (2019) L. Yuan, C. Li, D. Mandic, J. Cao, and Q. Zhao. Tensor ring decomposition with rank minimization on latent space: An efficient approach for tensor completion. AAAI Conference on Artificial Intelligence, 2019.
Yuan and Zhang (2016) M. Yuan and C.-H. Zhang. On tensor completion via nuclear norm minimization. Foundations of Computational Mathematics, 16(4):1031–1068, 2016.
Zhang (2010a) C. H. Zhang. Nearly unbiased variable selection under minimax concave penalty. Annals of Statistics, 38(2):894–942, 2010a.
Zhang (2010b) T. Zhang. Analysis of multi-stage convex relaxation for sparse regularization. Journal of Machine Learning Research, 11:1081–1107, 2010b.
Zhang and Aeron (2017) Z. Zhang and S. Aeron. Exact tensor completion using t-SVD. IEEE Transactions on Signal Processing, 65(6):1511–1526, 2017.
Zhao et al. (2016) Q. Zhao, G. Zhou, S. Xie, L. Zhang, and A. Cichocki. Tensor ring decomposition. Technical report, arXiv, 2016.
Zheng and Lafferty (2015) Q. Zheng and J. Lafferty. A convergent gradient descent algorithm for rank minimization and semidefinite programming from random linear measurements. In Advances in Neural Information Processing Systems, 2015.
Zheng et al. (2013) X. Zheng, H. Ding, H. Mamitsuka, and S. Zhu. Collaborative matrix factorization with multiple similarities for predicting drug-target interactions. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2013.
Zhong and Kwok (2014) W. Zhong and J. Kwok. Gradient descent with proximal average for nonconvex and composite regularization. In AAAI Conference on Artificial Intelligence, pages 2206–2212, 2014.
Zhu et al. (2018) Z. Zhu, Q. Li, G. Tang, and M. Wakin. Global optimality in low-rank matrix optimization. IEEE Transactions on Signal Processing, 66(13):3614–3628, 2018.

	$\displaystyle\sum\nolimits_{d=1}^{D}\min\nolimits_{{\bm{\bm{X}}}_{d}}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}-\mathscr{Z}_{{\left\langle d\right\rangle}}\right\\|_{F}^{2}+\bar{\lambda}_{d}\,\phi({\bm{\bm{X}}}_{d}),$
	$\displaystyle\!\!\!=\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}}\frac{D}{2}\left\\|\mathscr{Z}\right\\|_{F}^{2}-\big{<}\mathscr{Z},\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\big{>}+\frac{D}{2}\sum\nolimits_{d=1}^{D}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}+\sum\nolimits_{d=1}^{D}\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d}),$
	$\displaystyle\!\!\!=\min\nolimits_{\{{\bm{\bm{X}}}_{d}\}}\frac{D}{2}\left\\|\mathscr{Z}\!-\!\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}\!\!\!-\frac{D}{2}\left\\|\sum\nolimits_{d=1}^{D}{\bm{\bm{X}}}_{d}^{{\left\langle d\right\rangle}}\right\\|_{F}^{2}\!\!\!+\sum\nolimits_{d=1}^{D}\big{[}\frac{1}{2}\left\\|{\bm{\bm{X}}}_{d}\right\\|_{F}^{2}\!+\!\bar{\lambda}_{d}\phi({\bm{\bm{X}}}_{d})\big{]}.$		(52)

	$\displaystyle F_{\tau}(\mathscr{X}_{t+1})\leq F_{\tau}(\mathscr{V}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\mathscr{V}_{t}\right\\|_{F}^{2}$	$\displaystyle\leq F_{\tau}(\bar{\mathscr{X}}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\\|_{F}^{2},$
		$\displaystyle\leq F_{\tau}(\mathscr{X}_{t})-\frac{\eta}{2}\left\\|\mathscr{X}_{t+1}-\bar{\mathscr{X}}_{t}\right\\|_{F}^{2}.$		(61)

	$\displaystyle\alpha_{1}\\|\tilde{\mathscr{V}}\\|_{F}^{2}-\tau_{1}\frac{\log I^{\pi}}{\\|{\bm{\bm{\Omega}}}\\|_{1}}\tilde{v}^{2}$	$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})-\left\langle\nabla f(\mathscr{X}^{*}),\tilde{\mathscr{V}}\right\rangle,$
		$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})+\max_{i}\left\\|[\nabla f(\mathscr{X}^{*})]_{{\left\langle i\right\rangle}}\right\\|_{\infty}\tilde{v}_{i}$
		$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\tilde{h}_{i}(\tilde{\mathscr{X}})+\max_{i}\left\\|[\nabla f(\mathscr{X}^{*})]_{{\left\langle i\right\rangle}}\right\\|_{\infty}\tilde{v},$

	$\displaystyle\big{(}\alpha_{1}-\frac{LM}{2}\big{)}\\|\tilde{\mathscr{V}}\\|_{F}^{2}$	$\displaystyle\leq\lambda\sum\nolimits_{i=1}^{M}\big{(}h_{i}(\mathscr{X}^{*})-h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\kappa_{0}}{2}\big{(}\frac{\sum\nolimits_{i=1}^{M}h_{i}(\tilde{\mathscr{V}})}{LM}+\frac{LM}{2\lambda\kappa_{0}}\\|\tilde{\mathscr{V}}\\|_{F}^{2}\big{)},$
		$\displaystyle\leq\!\lambda\!\sum\nolimits_{i=1}^{M}\!\big{(}h_{i}(\mathscr{X}^{})\!-\!h_{i}(\tilde{\mathscr{X}})\big{)}+\frac{\lambda\sum\nolimits_{i=1}^{M}h_{i}(\mathscr{X}^{})\!+\!h_{i}(\tilde{\mathscr{X}})}{2D}+\frac{LM}{4}\\|\tilde{\mathscr{V}}\\|_{F}^{2}.$		(85)

Low-rank Tensor Learning with Nonconvex Overlapped Nuclear Norm Regularization

Abstract

1 Introduction

Difference with the Conference Version

Notation

2 Related Works

2.1 Low-Rank Matrix Learning

2.1.1 Nuclear Norm Minimization

Lemma 1

2.1.2 Nonconvex Low-Rank Regularizer

Assumption 1

Lemma 2

2.1.3 Matrix Factorization

2.2 Low-Rank Tensor Learning

Definition 3

2.3 Proximal Average (PA) Algorithm

3 Proposed Algorithm

3.1 Issues with Existing Solvers

3.2 Structure-aware Proximal Average Iterations

3.2.1 Efficient Computations of 𝒳t\mathscr{X}_{t} and 𝒵t\mathscr{Z}_{t} in (18), (19)

3.2.2 Efficient Computation of 𝒴t+1i\mathscr{Y}^{i}_{t+1} in (20)

Proposition 4

Remark 5

3.2.3 Time and Space Complexities

3.3 Use of Adaptive Momentum

3.4 Convergence Properties

Proposition 6

Proposition 7

Proposition 8

3.4.1 With Smoothness Assumption on Loss ff

Theorem 9

Corollary 10

Remark 11

3.4.2 With Kurdyka-Łojasiewicz Condition on Approximated Objective FτF_{\tau}

Definition 12

Theorem 13

3.5 Statistical Guarantees

3.5.1 Controlling the Spikiness and Rank

3.5.2 Restricted Strong Convexity (RSC)

Definition 14

Lemma 15

3.5.3 Main results

Theorem 16

3.5.4 Dependencies on Noise Level and Number of Observations

Corollary 17

Corollary 18

4 Extensions

4.1 Robust Tensor Completion

Proposition 19

Theorem 20

4.2 Tensor Completion with Graph Laplacian Regularization

5 Experiments

5.1 Synthetic Data

5.1.1 Recovery Performance Comparison

5.1.2 Ranks during Iteration

5.1.3 Quality of Critical Points

5.1.4 Effects of Noise Level and Number of Observations

5.1.5 Effects of Tensor Order and Rank

5.2 Tensor Completion Applications

5.2.1 Color Images

5.2.2 Remote Sensing Data

5.2.3 Social Networks

5.3 Link Prediction in Knowledge Graph

5.4 Robust Tensor Completion

5.5 Spatial-temporal Data

6 Conclusion

Acknowledgement

Appendix

Appendix A Comparison with Incoherence Condition

Appendix B Proofs

B.1 Proposition 4

B.2 Proposition 6

B.3 Proposition 7

B.3.1 Auxiliary Lemma

Lemma 21

B.3.2 Proof of Proposition 7

B.4 Proposition 8

B.5 Theorem 9

Lemma 22

Lemma 23

Low-rank Tensor Learning with
Nonconvex Overlapped Nuclear Norm Regularization

3.2.1 Efficient Computations of $\mathscr{X}_{t}$ and $\mathscr{Z}_{t}$ in (18), (19)

3.2.2 Efficient Computation of $\mathscr{Y}^{i}_{t+1}$ in (20)

3.4.1 With Smoothness Assumption on Loss $f$

3.4.2 With Kurdyka-Łojasiewicz Condition on Approximated Objective $F_{\tau}$