Low-energy scattering of ultracold atoms by a dielectric nanosphere

The precise form of atom-surface potential is sensitive to various parameters such as characteristic wavelengths of atomic transitions, as well as the shape, dielectric function, and polabizability of the material. The exact treatments of dispersion interaction between an atom and a spherical surface for an arbitrary distance in terms of macroscopic QED are found in Ref. Buhmann . In this paper, we nonetheless employ an approximate construction of the dispersion-force potential Arnecke for numerical simplicity and analytical transparency. The exact and approximate potentials will be quantitatively compared later in this section.

Let $R$, $r$, and $r^{\prime}=r-R$ be the radius of a nanosphere, the distance of the atom from the center of the sphere, and distance from the surface of sphere, respectively. In this paper, we denote all the relevant formula in the International System of Units (SI units) unless otherwise stated, while we perform all the numerical calculations in atomic units (a.u.).

When the atom-surface distance $r^{\prime}$ is much smaller than the radius $R$ of the sphere, the interaction potential is well approximated with the one $V_{\rm fw}(r^{\prime})$ between the atom and a semi-infinite flat wall. The expression for $V_{\rm fw}(r^{\prime})$ was introduced by Tikochinsky and Spruch Tikochinsky as

	$\displaystyle V_{\rm fw}(r^{\prime})$	$\displaystyle=-\frac{\hbar}{8\pi^{2}\epsilon_{0}c^{3}}\int_{0}^{\infty}d\xi\xi^{3}\alpha({\mathrm{i}}\xi)$
		$\displaystyle\qquad\qquad\times\int_{1}^{\infty}dp\,e^{-2\xi pr^{\prime}/c}H(p,\epsilon({\mathrm{i}}\xi)),$		(1)

where

	$\displaystyle H(p,\epsilon)=\frac{\sqrt{\epsilon-1+p^{2}}-p}{\sqrt{\epsilon-1+p^{2}}+p}$
	$\displaystyle\qquad\qquad\quad+(1-2p^{2})\frac{\sqrt{\epsilon-1+p^{2}}-\epsilon p}{\sqrt{\epsilon-1+p^{2}}+\epsilon p},$		(2)

and $\epsilon_{0}$ and $c$ are the permittivity of vacuum and the speed of light, respectively. The quantities $\alpha({\mathrm{i}}\xi)$ and $\epsilon({\mathrm{i}}\xi)$ denote the atomic polarizability and the dielectric function of the surface at imaginary frequencies, respectively.

When the atom is far from the spherical surface, $r^{\prime}\gg R$, on the other hand, the potential is described by the one $V_{\mathrm{pp}}(r)$ between the atom and a point particle Buhmann :

$\displaystyle V_{\mathrm{pp}}(r)=-\frac{\hbar}{16\pi^{3}\epsilon_{0}^{2}r^{6}}$

$\displaystyle\int_{0}^{\infty}d\xi\alpha({\mathrm{i}}\xi)\alpha_{\mathrm{sphere}}({\mathrm{i}}\xi)g(\xi r/c),$

(3)

where $g(x)=e^{-2x}(3+6x+5x^{2}+2x^{3}+x^{4})$, and

$\displaystyle\alpha_{\mathrm{sphere}}({\mathrm{i}}\xi)=4\pi\epsilon_{0}R^{3}\frac{\epsilon({\mathrm{i}}\xi)-1}{\epsilon({\mathrm{i}}\xi)+2}$

(4)

is the total polarizability of the dielectric sphere Jackson .

In addition to the radius $R$ of the nanosphere, the wavelength $\lambda$ of the dominant atomic transition is also an important length scale that characterizes the interaction potential. For rubidium and cesium atoms, the typical wavelength $\lambda$ is within a range of 700–900 nm. In a dispersion-force potential, the retardation effect of the electromagnetic field is significant when $r^{\prime}\gg\lambda$. This regime is thus called the retarded regime, as discussed by Casimir and Polder Casimir . The retardation effects in the atom-atom potential of the form Eq. (3) was studied in Ref. Marinescu . In contrast, the retardation plays no role when $r^{\prime}\ll\lambda$, which is called the non-retarded regime. Each potential behaves in the non-retarded and retarded limits as

	$\displaystyle V_{\rm fw}(r^{\prime})$	$\displaystyle\xrightarrow{r^{\prime}\ll\lambda}-\frac{C_{3}}{r^{\prime 3}},\quad V_{\rm fw}(r^{\prime})\xrightarrow{r^{\prime}\gg\lambda}-\frac{C_{4}}{r^{\prime 4}},$		(5)
	$\displaystyle V_{\mathrm{pp}}(r)$	$\displaystyle\xrightarrow{r^{\prime}\ll\lambda}-\frac{C_{6}}{r^{6}},\quad V_{\mathrm{pp}}(r)\xrightarrow{r^{\prime}\gg\lambda}-\frac{C_{7}}{r^{7}}.$		(6)

Taking these geometric and internal length scales into account, we employ the following form of the interaction potential between an atom and the spherical surface Arnecke :

$\displaystyle V(r)=-\frac{\hbar^{2}}{2\mu}\left.\left[\frac{r^{\prime 3}}{\beta_{3}}v\left(\frac{r^{\prime}}{L}\right)+\frac{r^{\prime 6}}{\beta_{6}^{4}}v\left(\frac{r^{\prime}}{L^{\prime}}\right)\right]^{-1}\right|_{r^{\prime}=r-R},$

(7)

where $\mu$ is the reduced mass that can always be replaced with the atomic mass, and

$\displaystyle\beta_{n}=\left(\frac{2\mu C_{n}}{\hbar^{2}}\right)^{1/(n-2)}\qquad(n=3,4,6,7)$

(8)

is a length parameter as a measure of the typical interaction range. The parameters

$\displaystyle\,L=\frac{\beta_{4}^{2}}{\beta_{3}},\quad L^{\prime}=\frac{\beta_{7}^{5}}{\beta_{6}^{4}}$

(9)

characterize the typical length scales at which the power law crosses over from non-retarded to retarded behaviors in $V_{\rm fw}$ and $V_{\rm pp}$, respectively. The function $v(x)$ is an arbitrary form that satisfies asymptotic behaviors

$\displaystyle\lim_{x\to 0}\frac{1}{v(x)}=1,\quad\lim_{x\to\infty}\frac{1}{v(x)}=\frac{1}{x},$

(10)

and smoothly connects different power-law dependencies in the potential. In this paper, we use an expression Shimizu2001

$\displaystyle v(x)=1+x.$

(11)

In the following analysis, we employ the form Eq. (7) with the shape function Eq. (11) as the interaction potential between an atom and spherical surface. By definition, the potential in the proximity of the surface and at a large distance from the surface, respectively, behaves as

$\displaystyle V(r)\xrightarrow{r\to R}-\frac{C_{3}}{(r-R)^{3}},\quad V(r)\xrightarrow{r\to\infty}-\frac{C_{7}}{r^{7}}.$

(12)

We next compute the coefficients $C_{n}\ (n=3,4,6,7)$ appearing in the atom-surface interaction potential $V(r)$. The coefficients $C_{n}$ are expressed in terms of the atomic polarizability $\alpha$ and dielectric function $\epsilon$ of the sphere as Buhmann

$\displaystyle\begin{aligned} C_{3}&=\frac{\hbar}{16\pi^{2}\epsilon_{0}}\int_{0}^{\infty}\alpha({\mathrm{i}}\xi)\frac{\epsilon({\mathrm{i}}\xi)-1}{\epsilon({\mathrm{i}}\xi)+1}d\xi\\ C_{4}&=\frac{3\hbar c}{32\pi^{2}\epsilon_{0}}\alpha(0)\frac{\epsilon(0)-1}{\epsilon(0)+1}\phi(\epsilon(0))\\ C_{6}&=\frac{3\hbar R^{3}}{4\pi^{2}\epsilon_{0}}\int_{0}^{\infty}\alpha({\mathrm{i}}\xi)\frac{\epsilon({\mathrm{i}}\xi)-1}{\epsilon({\mathrm{i}}\xi)+2}d\xi\\ C_{7}&=\frac{23\hbar cR^{3}}{16\pi^{2}\epsilon_{0}}\alpha(0)\frac{\epsilon(0)-1}{\epsilon(0)+2}.\end{aligned}$

(13)

The function $\phi(\epsilon)$ appearing in $C_{4}$ is defined as Yan

	$\displaystyle\phi(\epsilon)$	$\displaystyle=\frac{\epsilon+1}{2(\epsilon-1)}\int_{0}^{\infty}\frac{1}{p^{4}}H(p,\epsilon){\mathrm{d}}p$
		$\displaystyle=\frac{\epsilon+1}{\epsilon-1}\left[\frac{1}{3}+\epsilon+\frac{4-(\epsilon+1)\epsilon^{1/2}}{2(\epsilon-1)}+a(\epsilon)+b(\epsilon)\right],$		(14)

where

	$\displaystyle a(\epsilon)$	$\displaystyle=-\frac{\sinh^{-1}\left[(\epsilon-1)^{1/2}\right]}{2(\epsilon-1)^{3/2}}\left[1+\epsilon+2\epsilon(\epsilon-1)^{2}\right],$
	$\displaystyle b(\epsilon)$	$\displaystyle=\frac{\epsilon^{2}}{(\epsilon+1)^{1/2}}\left[\sinh^{-1}(\epsilon^{1/2})-\sinh^{-1}(\epsilon^{-1/2})\right].$		(15)

The coefficients $C_{4}$ and $C_{7}$, which describe the retarded behaviors of $V_{\rm fw}$ and $V_{\mathrm{pp}}$, respectively, are determined by the static polarizability $\alpha(0)$ of the atom and the static dielectric constant $\epsilon(0)$ of the sphere. The known values of the static polarizabilities of rubidium Miller and cesium atoms 2003Amini-Gould , and of the dielectric constant of silica glass CRC , are tabulated in Table 1.

For the integrals in $C_{3}$ and $C_{6}$, which describe the non-retarded behaviors of $V_{\rm fw}$ and $V_{\mathrm{pp}}$, respectively, we need the atomic polarizability and the dielectric function of silica glass at imaginary frequencies. These are evaluated by the one-oscillator model and Lorentz model as follows.

The atom is adsorbed at the surface when the incident energy $E$ is larger than the barrier height $V_{\rm max}^{\rm(cl)}[\rho v]$. For each incident velocity $v$, we thus define a classical capture range $\rho_{c}$ by

$\displaystyle\frac{1}{2}\mu v^{2}=V^{\rm(cl)}_{\rm max}[\rho_{c}v],$

(22)

so an incident atom with the impact parameter $\rho<\rho_{c}$ is adsorbed at the surface, while an atom with $\rho>\rho_{c}$ is not. The quantity $\pi\rho_{c}^{2}$ corresponds to the classical absorption cross section LandauM ; Friedrich2013 .

Figure 4 shows the classical capture range $\rho_{c}$ as a function of the incident velocity $v$. We find that the capture range in the experimentally achievable low-energy regime is more than ten times larger than the geometric radius of the nanosphere. The capture range approximately behaves as

$\displaystyle\rho_{c}=R+\zeta_{n}v^{-2/n},\quad\zeta_{n}=\frac{\sqrt{n}}{(n-2)^{\frac{n-2}{2n}}}\left(\frac{C_{n}}{\mu}\right)^{1/n},$

(23)

where the second term is the classical capture range for a single inverse power-law potential $-C_{n}/r^{n}~{}(n>2)$ between two point particles. The power $n$ corresponds to the long-range behavior of our potential, i.e., $n=7$. For slow atoms, the second term in Eq. (23) is dominant, and $\rho_{c}$ thus behaves as $\sim v^{-2/7}$. As $v$ increases, it starts to deviate from $v^{-2/7}$ around $v\sim$ a few cm/s, at which the capture range measured from the surface $\rho_{c}-R$ decreases to a few hundreds nanometer, since the potential starts to deviate from $r^{\prime-7}$, entering a crossover regime around this distance. In a high-energy limit, on the other hand, the capture range coincides with the geometric radius of the sphere, $\rho_{c}\to R$. In this limit we may regard the potential as an inverted hard-wall potential of radius $R$.

The results so far also hold in the quantum scattering theory, as we see in later sections. However, we note that in the classical theory the atoms of angular momentum $L=0$ are always captured at the surface for any incident velocity because of the absence of the centrifugal barrier. This is not the case in the quantum theory.

We show in the previous subsection that for a fixed energy, an atom of impact parameter $\rho$ smaller than $\rho_{c}$ is adsorbed onto the surface of the nanosphere and cannot be detected. For $\rho>\rho_{c}$, on the other hand, the motion of an atom is restricted in the outer region of the centrifugal barrier $r>r_{0}$, where $r_{0}$ is the classical turning point defined as $E=V^{\rm(cl)}_{\rm eff}(r_{0})$ (see, inset of Fig. 4). Figure 5 (a) shows the atomic trajectories for several impact parameters $\rho>\rho_{c}$ when an atom with the velocity $v=50~{}$mm/s is injected along the $z$ axis from minus infinity to the positive $z$ direction, subsequently deflected due to the atom-surface potential, and scattered to an angle $\theta$ asymptotically. The trajectory of the atomic motion is obtained by integrating the equation of motion in the relative polar coordinates,

$\displaystyle\dot{r}=v\sqrt{1-\frac{\rho^{2}}{r^{2}}-\frac{2V(r)}{mv^{2}}},\quad\dot{\phi}=\frac{\rho v}{r^{2}},$

(24)

with the initial condition $r=\infty,~{}\phi=\pi$. When the impact parameter is precisely equal to $\rho_{c}$, the atom eternally orbits around the nanosphere with radius $\rho_{c}$. For impact parameters slightly larger than $\rho_{c}$, the atom is largely deflected by the potential, orbiting around the nanosphere for a while, and eventually scattered to a certain angle $\theta$. For larger impact parameters, in contrast, the motion of the atom is less and less affected by the potential and the scattering angle $\theta$ is thus smaller.

In a typical scattering experiment, not a single atom but a beam consisting of many atoms with a certain velocity and various impact parameters is incident on a target, and a detector located at a solid angle $d\varOmega=2\pi\sin\theta d\theta$ sufficiently far from the scattering center, counts the number of the scattered atoms. The detector counts located at a solid angle $d\varOmega$ per unit time yield the differential cross section,

$\displaystyle\frac{d\sigma_{\rm el}^{\rm(cl)}}{d\varOmega}=\frac{\rho(\theta)}{\sin\theta}\left|\frac{d\rho}{d\theta}\right|\qquad(\rho>\rho_{c}),$

(25)

where we define the scattering angle within $0\leq\theta\leq\pi$, by summing up all the branches associated with the multi-valuedness of the impact parameter $\rho(\theta)$. In Fig. 5 (b), we show the angle dependence of the differential cross section for several velocities of the atomic beam. For a faster beam, the angular distribution is narrower and the forward scattering is more dominant. The sharp increase in the differential cross section near $\theta=\pi$ is the analogy of the glory appearing in the Brocken effect Friedrich2013 .

The classical differential cross section diverges as $\theta\to 0$ and hence the total elastic cross section obtained by integrating with respect to the solid angle also diverges for any incident velocity. This unphysical divergence arises because the infinite series of impact parameters are involved in the classical differential cross section Eq. (25) by definition, and all of these atoms are scattered to an infinitesimally small angle due to the potential tail no matter how large the impact parameter is. Realistically, the beam width is finite and thus the divergences of the forward scattering and total elastic cross section do not occur.

We consider the stationary state described by the Schrödinger equation for the relative motion,

$\displaystyle\left[-\frac{\hbar^{2}\nabla^{2}}{2\mu}+V(\bm{r})\right]\psi(\bm{r};k)=E\psi(\bm{r};k),$

(26)

when the plane wave of the wavenumber $k=\mu v/\hbar$ and the energy $E=\hbar^{2}k^{2}/(2\mu)$ is incident on the nanosphere, as shown in Fig. 1. The stationary state $\psi(\bm{r};k)$ is expanded in terms of the partial waves labeled by the angular-momentum quantum number $l$, and its asymptotic form is given by

	$\displaystyle\psi(\bm{r};k)$	$\displaystyle=\sum_{l=0}^{\infty}\frac{u_{l}(r;k)}{r}P_{l}(\cos\theta)$		(27)
		$\displaystyle\xrightarrow{r\to\infty}e^{{\mathrm{i}}kz}+\frac{f(\theta;k)}{r}e^{{\mathrm{i}}kr},$		(28)

where $u_{l}(r;k)$ denotes the $l$th radial function, $P_{l}(x)$ the Legendre functions, $\theta$ the scattering angle, and $f(\theta;k)$ the scattering amplitude, respectively.

The problem is now reduced to solve the equation of the radial function for each partial wave:

$\displaystyle\frac{d^{2}u_{l}(r;k)}{dr^{2}}=-k_{l}(r;k)^{2}u_{l}(r;k),$

(29)

where $k_{l}(r;k)$ is the local wave number of the $l$th partial wave defined as Friedrich2013

$\displaystyle k_{l}(r;k)=\sqrt{k^{2}-\frac{l(l+1)}{r^{2}}-\frac{2\mu V(r)}{\hbar^{2}}}.$

(30)

Equation (29) is equivalent to the one-dimensional Schrödinger equation with the effective potential

$\displaystyle V_{\rm eff}^{(l)}(r)=\frac{\hbar^{2}l(l+1)}{2\mu r^{2}}+V(r),$

(31)

where the first term corresponds to the centrifugal potential for the $l$th partial wave, and the second term is the dispersion-force potential obtained in Sec. II.

At large distances from the surface, the asymptotic form of the $l$th radial wavefunction is expressed in terms of the $l$th order spherical Bessel function $j_{l}(x)$ and the $l$th order spherical Neumann function $n_{l}(x)$ as

$\displaystyle u_{l}(r;k)$

$\displaystyle\xrightarrow{r\to\infty}kr\left[F_{l}(k)j_{l}(kr)-G_{l}(k)n_{l}(kr)\right],$

(32)

which is also expressed in terms of the diagonal elements $S_{l}(k)$ of the $S$ matrix,

$\displaystyle u_{l}(r;k)\xrightarrow{r\to\infty}\frac{(2l+1)(-1)^{l+1}}{2{\mathrm{i}}k}\left[e^{-{\mathrm{i}}kr}-(-1)^{l}S_{l}(k)e^{{\mathrm{i}}kr}\right].$

(33)

The diagonal elements $S_{l}(k)$ of the $S$ matrix are expressed in terms of the phase shift $\delta_{l}$ as $S_{l}(k)=e^{2{\mathrm{i}}\delta_{l}(k)}$. The asymptotic forms of the spherical Bessel functions $j_{l}(x)\xrightarrow{x\to\infty}\sin\left(x-l\pi/2\right)/x$ and the spherical Neumann functions $n_{l}(x)\xrightarrow{x\to\infty}-\cos\left(x-l\pi/2\right)/x$ yield the relation

$\displaystyle S_{l}(k)=\frac{F_{l}(k)+{\mathrm{i}}G_{l}(k)}{F_{l}(k)-{\mathrm{i}}G_{l}(k)}.$

(34)

If the $l$th partial wave is unaffected by the potential, the phase shift is zero and hence $S_{l}(k)=1$. The effects of the potential scattering on the $l$th partial wave are characterized by the deviation of the value $S_{l}(k)$ from unity.

If the incident wave is partially absorbed by the surface, which is the case we consider, the $S$ matrix is non-unitary $|S_{l}(k)|<1$, and the phase shift is complex LandauQ . As we discuss in the next subsection, the reflection of the $l$th partial wave can occur at a nonclassical region in the coordinate space, and the only portions that are transmitted through the nonclassical region are absorbed by the surface. The absorption probability of the $l$th partial wave is given by $1-|S_{l}(k)|^{2}$.

Scattering amplitude $f(\theta;k)$ in Eq. (28), which is written in terms of the $S$-matrix as

$\displaystyle f(\theta;k)$

$\displaystyle=\sum_{l=0}^{\infty}\frac{(2l+1)}{2{\mathrm{i}}k}(S_{l}(k)-1)P_{l}(\cos\theta),$

(35)

characterizes the angle dependence of the scattering. The elastic differential cross section is defined in terms of the scattering amplitude as

$\displaystyle\frac{d\sigma_{\mathrm{el}}}{d\varOmega}(\theta;k)=|f(\theta;k)|^{2},$

(36)

which involves interference between different $l$th partial waves. Summing over the entire solid angle eliminates the off-diagonal terms, and yields the total elastic cross section,

$\displaystyle\sigma_{\mathrm{el}}(k)=\sum_{l=0}^{\infty}\frac{(2l+1)\pi}{k^{2}}|S_{l}(k)-1|^{2}=\sum_{l=0}^{\infty}\sigma_{\mathrm{el}}^{(l)}(k).$

(37)

The scattering amplitude and the elastic cross section are defined solely by the elastically scattered wave under the influence of the potential, since the contribution of the unaffected wave is eliminated by subtracting 1 from $S_{l}$. On the other hand, the absorption cross section $\sigma_{\mathrm{abs}}(k)$ is written LandauQ as

$\displaystyle\sigma_{\mathrm{abs}}(k)=\sum_{l=0}^{\infty}\frac{(2l+1)\pi}{k^{2}}(1-|S_{l}(k)|^{2})=\sum_{l=0}^{\infty}\sigma_{\mathrm{abs}}^{(l)}(k).$

(38)

The elastic and absorption cross sections involve only diagonal terms of the $S$ matrix and satisfy the optical theorem:

$\displaystyle\sigma_{\rm el}(k)+\sigma_{\rm abs}(k)=\frac{4\pi}{k}{\rm Im}[f(\theta=0;k)].$

(39)

The atom-surface interaction is strongly attractive near the surface of the nanosphere, thereby the waves are destined to be absorbed once they approach very close to the surface. There are several ways to take the absorption into account. One of methods is to make the potential complex as introduced in the study of the reactive collisions of molecules Idziaszek . However, the atom-surface potential is nontrivial in the proximity to surface and it is thus too obscure to determine a concrete form of the potential. Alternatively, we impose the following boundary condition in the vicinity of the surface $r\to R+$ Effective-range ; Friedrich2013 ; Cote96 ; Cote97 ; Cote98 :

$\displaystyle u_{l}(r;k)\overset{r\to R+}{\propto}\frac{1}{\sqrt{k_{l}(r;k)}}\exp\left(-{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho\right).$

(40)

With this boundary condition, in other words, we make an ansatz so there is only an incoming wave and no outgoing wave in the vicinity of the surface. The form of the wavefunction Eq. (40) is based on the semiclassical Wentzel-Kramer-Brillouin (WKB) approximation, which is shown to be valid near the surface $r\to R+$ for the following reasons.

Here we revisit the essence of this boundary condition by referring the classical capture model. In the general WKB approximation, the exponential form of the wavefunction is retained but the exponent is replaced by the action integral as

$\displaystyle u_{\rm WKB}(r;k)\propto\exp\left(\pm{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho\right).$

(41)

This wavefunction is valid, or can be even exact, as long as the quantality function or badlands function

$\displaystyle Q_{l}(r;k)=k_{l}(r;k)^{-3/2}\frac{d^{2}}{dr^{2}}k_{l}(r;k)^{-1/2},$

(42)

satisfies $|Q_{l}(r;k)|\ll 1$. The quantality function $Q_{l}(r;k)$ is thus a measure of nonclassicality Friedrich2002 . In the regime where $|Q_{l}(r;k)|\ll 1$ is satisfied, the incoming wave $\propto\exp(-{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho)$ and outgoing wave $\propto\exp(+{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho)$ are unambiguously decomposed.

Now we go back to our specific problem. In the vicinity of the surface, the interaction potential dominates in Eq. (30), i.e., $k_{l}(r;k)\xrightarrow{r\to R}\sqrt{-2\mu V(r)/\hbar^{2}}$. For the potential obtained in Sec. II, the local wavenumber behaves as $k_{l}(r;k)\xrightarrow{r\to R}\sqrt{\beta_{3}}/(r-R)^{3/2}$, and the quantality function thus behaves as $Q_{l}(r;k)\overset{r\to R}{\propto}(r-R)/\beta_{3}$, which indicates that the WKB approximation is valid at small distances. At sufficiently large distances where the atom is essentially free from the interaction and the local wave number $k_{l}(r;k)$ behaves as $k$, the condition $|Q_{l}(r;k)|\ll 1$ is also satisfied. Thus the exact wavefunction for the $l$th partial wave is well described by the superposition of ingoing and outgoing waves $\propto\exp(\pm{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho)$ at large distances. At small distances from the surface, in contrast, it would be described by only incoming wave $\propto\exp(-{\mathrm{i}}\int^{r}k_{l}(\rho;k)d\rho)$ because the wave cannot go outward due to the strong attractive interaction. This ansatz implies that the reflection of the $l$th incoming wave occurs somewhere in the intermediate distances at which $|Q_{l}(r;k)|\gg 1$.

For $l\geq 1$, we can estimate a critical angular momentum $\hbar l_{c}$ for each velocity from the condition $\hbar^{2}k^{2}/(2\mu)\simeq\underset{r}{\rm max}\{V_{\rm eff}^{(l_{c})}(r)\}$, which is the quantum version of Eq. (22), such that the $l$th partial waves are absorbed if a quantum analog of the impact parameter $\hbar l/(\mu v)=l/k$ is smaller than $l_{c}/k$, while they are elastically scattered by the centrifugal barrier or unaffected by the potential if $l/k>l_{c}/k$. The quantality function for the $l$th partial wave $Q_{l>l_{c}}(r;k)$ diverges when $k_{l>l_{c}}(r_{0};k)=0$, thus we may infer that the elastic scattering occurs around $r_{0}$ as previously discussed in this subsection. We note that the equation $k_{l}(r_{0};k)=0$ is the quantum version of the condition that determines the classical turning point $E=V_{\rm eff}^{\rm(cl)}(r_{0})$. The elastic scattering for $l>l_{c}$ is thus regarded as a classically allowed reflection by the centrifugal barrier.

The partial wave of $l=0$ is of particular interest. Classically, atoms with zero angular momentum are totally adsorbed onto the surface for any incident velocity because of the absence of the centrifugal barrier. Quantum mechanically, on the other hand, $s$-wave can be reflected even though the potential is purely attractive. This is a classically forbidden reflection, namely, the quantum reflection Friedrich2013 . The quantum reflection is expected to occur in a coordinate space where $|Q_{0}(r;k)|\gg 1$ as if an effective mirror exists in there. Such a nonclassical spacial region is called badlands Friedrich2002 ; Segev ; Effective-range ; Friedrich2013 ; Cote96 ; Cote97 ; Cote98 .

Figure 6 shows the magnitude of the $s$-wave quantality function for a rubidium atom. For lower incident energies, the magnitude of the $s$-wave quantality function as well as the distance from the surface at which $|Q_{0}(r;k)|$ takes the maximal value are larger. This indicates that the position of the badlands, i.e., an effective mirror, moves outer and its reflectivity is larger for lower incident energies. The location of the effective mirror, defined here as the position $r$ at which $|Q_{0}(r;k)|$ takes the maximal value (a solid line in Fig. 6), behaves as $r\propto v^{-2/7}$ at low energies. For higher energies, the peak height of $|Q_{0}(r;k)|$ decreases, and is indiscernible in the high-energy limit.

Quantum reflection has been experimentally observed and studied in several systems. Experiments on quantum reflection on fluid surfaces have been carried out by measurements of the reflectivity or sticking probability of incident helium or hydrogen atoms scattered by a liquid helium surface Nayak ; Berkhout ; Doyle ; Yu . Quantum reflection on solid surfaces has also been observed: specular reflection of cold metastable neon atoms on a silicon and a BK7 glass surface Shimizu2001 ; Shimizu2002 , quantum reflection of helium atoms incident on a silicon surface Oberst , of Bose-Einstein condensates on a solid surfaces Pasquini2004 ; Pasquini2006 , and far from threshold Druzhinina .

In the previous section, we denoted that $s$-wave scattering is qualitatively different from the classical scattering of atoms with vanishing angular momentum. In this subsection, we show various $s$-wave scattering properties, including the scattering length, the differential cross section, the elastic, and the absorption cross sections in a sufficiently low-energy regime.

The top panel of Fig. 7 shows the landscapes of the interaction potential in atomic units, as well as the $s$-wave quantality function for the incoming atomic velocity $v=100$ µm/s (see also Fig. 6). In the vicinity of surface $r-R\to 0$, and at large distances $r\to\infty$, the magnitude of the quantality function $Q_{0}(r;k)$ is small but is significantly large at intermediate distances. As discussed in the previous section, a portion of the wave approaching the surface through the badlands region is lost due to the absorption, while the remaining portion that does not go through the badlands undergoes quantum reflection. In the middle and bottom panels of Fig. 7, we show the radial function $u_{0}(r;k)$ (solid curve), its asymptotic form Eq. (32) away from the surface (dashed-dotted curve), and the WKB wavefunction that has only an incoming wave (dotted curve). We find that the exact wavefunction is well described by the WKB wavefunction from the surface proximity up to an appreciable distance ($\approx$ 200 nm) from the surface. The badlands region is located at a considerably large distance ($\approx 1$ µm) from the surface, where the potential is weakly attractive and the wavefunction is described by the asymptotic form.

In the limit $k\to 0$, there is no scattering of the partial waves for $l\geq 1$, i.e., $S_{l\geq 1}(k)\approx 1$, and hence the $s$-wave contribution dominates all scattering properties. In terms of the complex $s$-wave scattering length $A_{0}$ Friedrich2013 , the asymptotic behavior of the $s$-wave wavefunction and the phase shift at $k\to 0$ are given by $u_{0}(r;0)\overset{r\to\infty}{\propto}r-A_{0}$, and $\delta_{0}(k)\xrightarrow{k\to 0}-kA_{0}$, respectively. We thus obtain the dominant element of the $S$ matrix in the extremely low-energy regime as

$\displaystyle S_{0}(k)\xrightarrow{k\to 0}e^{2k\mathrm{Im}[A_{0}]}e^{-2{\mathrm{i}}k\mathrm{Re}[A_{0}]}.$

(43)

The elastic differential cross section, the elastic cross section associated with the quantum reflection, and the absorption cross section in the zero-energy limit are written as Friedrich2013 ; LandauQ

	$\displaystyle\frac{d\sigma_{\mathrm{el}}}{d\varOmega}(\theta;k)\xrightarrow{k\to 0}|A_{0}|^{2},\quad\sigma_{\mathrm{el}}(k)\xrightarrow{k\to 0}4\pi|A_{0}|^{2},$		(44)
	$\displaystyle\sigma_{\mathrm{abs}}(k)\xrightarrow{k\to 0}-\frac{4\pi}{k}\mathrm{Im}[A_{0}],$		(45)

in consistent with the Wigner threshold law Wigner . The numerically obtained zero-energy wave function yields the value of $A_{0}$, and the results are summarized in Table 4.

We next investigate various cross sections when the incident velocity is varied while the radius of the sphere is fixed as $R=75$ nm. In the following we show results for cesium atoms unless otherwise stated, since we have qualitatively the same results for rubidium atoms.

Figure 8 shows the elastic differential cross sections $|f(\theta;k)|^{2}$ for several incident velocities. For faster atoms, the forward scattering is more dominant and the angular distribution of $|f(\theta;k)|^{2}$ is narrower, in a manner similar to the classical differential cross section (see also Fig. 5). At large velocities, the angular distributions of the quantum and classical differential cross sections agree well, as shown in the leftmost inset of Fig. 8. As the velocity decreases, the anisotropy of $|f(\theta;k)|^{2}$ is suppressed, and in the $s$-wave regime it is independent of angle, approaching a constant value $|A_{0}|^{2}$. The difference between the angular distributions of the quantum and classical differential cross sections starts to be evident around $v\approx O(10)$ mm/s, where the thermal de Broglie wavelength is comparable to the size of the nanosphere. In the regime $v\lesssim O(10)$ mm/s, the quantum-mechanical differential cross section Eq. (36) thus reveals the matter-wave diffractions involving interference between different partial waves. Classically, on the other hand, an incident atom is fully characterized by a single angular momentum and there is no interference between atoms with different impact parameters in an incident beam.

Figure 9 shows elastic and absorption cross sections versus incident atomic velocity. Contributions from low-lying $(l\leq 8)$ partial waves are also drawn with thin curves. The scattering involves various partial waves in the relatively high-energy regime, but the contributions from large $l$ gradually decrease as the energy is lowered, and eventually only the $s$-wave contribution remains when $v\lesssim 500$ µm/s ($2E/k_{B}\lesssim O(1)$ nK). In the $s$-wave regime, the elastic cross section $\sigma_{\rm el}$ approaches the constant value $4\pi|A_{0}|^{2}$. This behavior of $\sigma_{\rm el}$ reveals the occurrence of the quantum reflection for the $s$-wave in stark contrast to the classical elastic scattering of the vanishing angular momentum. As discussed in Sec. III, the classical elastic cross section shows a fictitious divergence for any velocity associated with the inclusion of infinite impact parameters. If this divergence is properly eliminated, e.g., by using a finite beam, there would be no contribution from the vanishing angular momentum in the classical elastic cross section.

As shown in Fig. 9 (b), the total absorption cross section $\sigma_{\rm abs}$ and classical absorption cross section $\pi\rho_{c}^{2}$ are almost equal, $\sigma_{\rm abs}\simeq\pi\rho_{c}^{2}\propto v^{-4/7}$, for a wide range of velocity $v\gtrsim 500$ µm/s and a difference is found only in the $s$-wave regime $v\lesssim 500$ µm/s, which is roughly two orders of magnitude smaller than the velocity at which the difference in the elastic differential cross sections starts to emerge. This is because the total cross sections are characterized only by diagonal terms of the $S$ matrix and quantum-mechanical interference terms are not involved. The enhanced absorption cross section $\sigma_{\rm abs}$ in the $s$-wave regime is regarded as the manifestation of the quantized impact parameter $l/k$.

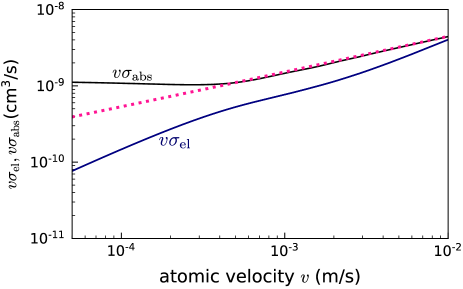
Another experimentally relevant quantity is the scattering rate, $v\sigma$. We show the elastic scattering rate and the loss rate in Fig. 10. As the energy is lowered, the loss rate associated with the absorption monotonically decreases in $v\gtrsim 500$ µm/s but is nearly constant in the $s$-wave regime, while the classical loss rate continues to monotonically decrease in that regime. The elastic scattering rate behaves monotonously for any velocity. The optical theorem Eq. (39) indicates that the sum of these rates $v(\sigma_{\rm el}+\sigma_{\rm abs})=v\sigma_{\rm tot}$ is independent of $v$, which can also be confirmed from Fig. 10.

Relatively high-energy regime — In a relatively high-energy regime, we find $S_{l}(k)\approx 0$ for the partial waves of $l\lesssim l_{c}\approx k\rho_{c}$. Hence the incoming partial waves of $l\lesssim l_{c}$ are absorbed onto the surface. In this case, the elastic and absorption cross sections have the same value $\sigma_{\mathrm{el}}^{(l)}(k)=\sigma_{\mathrm{abs}}^{(l)}(k)=(2l+1)\pi/k^{2}$, as we see from Eqs. (37) and (38). By summing partial cross sections up to $l=l_{c}$, the total elastic and absorption cross sections are obtained as $\sigma_{\rm el}(k)=\sigma_{\rm abs}(k)=\pi(l_{c}+1)^{2}/k^{2}$. The first term dominantly contributes at high energies, and it almost coincides with the classical absorption cross section $\pi\rho_{c}^{2}$.

In this subsection we investigate scattering properties as a function of radius $R$ of a nanosphere from 50 nm to 500 nm in the relatively low-energy regime. Figure 11 shows the complex $s$-wave scattering length $A_{0}$ of a cesium atom versus $R$. If the potential $V(r)$ depends only on $r^{\prime}=r-R$, the $s$-wave scattering length behaves as $A_{0}(R)=A_{0}(0)+R$. This is not the case for our potential, since the coefficients $C_{6}$ and $C_{7}$ depend on $R$. Nonetheless our scattering radius $|A_{0}(R)|$ also monotonically increases versus $R$. As compared with the scattering radius of the hard-sphere potential (dotted line in Fig. 11), that of our dispersion-force potential is found to be more than twice as long as $R$.