Lossless KV Cache Compression to 2%
Abstract
Large language models have revolutionized data processing in numerous domains, with their ability to handle extended context reasoning receiving notable recognition. To speed up inference, maintaining a key-value (KV) cache memory is essential. Nonetheless, the growing demands for KV cache memory create significant hurdles for efficient implementation. This work introduces a novel architecture, Cross-Layer Latent Attention (CLLA), aimed at compressing the KV cache to less than 2% of its original size while maintaining comparable performance levels. CLLA integrates multiple aspects of KV cache compression, including attention head/dimension reduction, layer sharing, and quantization techniques, into a cohesive framework. Our extensive experiments demonstrate that CLLA achieves lossless performance on most tasks while utilizing minimal KV cache, marking a significant advancement in practical KV cache compression.
Lossless KV Cache Compression to 2%
Zhen Yang*,1, J. N. Han*,1, Kan Wu1, Ruobing Xie+,1, An Wang 1,2, Xingwu Sun1, Zhanhui Kang1 1 Tencent Hunyuan 2 Tokyo Institute of Technology
1 Introduction
Large language models (LLMs) have been widely adopted and verified in various of fields, reshaping the way we collect and process information and impacting our daily lives Driess et al. (2023); Zhang et al. (2023); Zhu et al. (2023); Wang et al. (2024b). Recently, the long-context reasoning and understanding abilities of LLMs have gradually been acknowledged to be essential in reflecting LLMs’ capabilities and attracted more and more attention. Both closed-source and open-source LLMs are now striving to accommodate longer token lengths Achiam et al. (2023); DeepSeek-AI (2024). However, this rapid expansion in length introduces critical efficiency challenges into LLMs, particularly concerning the growing key-value (KV) cache memory issue, which poses a significant barrier to the practical deployment of more powerful LLMs. The KV cache technique, which involves caching and reusing previously computed key and value vectors from the classical multi-head attention (MHA) blocks Vaswani et al. (2017) in decoder-only Transformers, is broadly adopted to accelerate model inference speed. This approach, however, comes at the cost of increased GPU memory usage and is considered a default configuration in most decoder-only LLMs Bai et al. (2023); Touvron et al. (2023). Alleviating the increasing KV cache issue could free up GPU memory for other high-performing yet memory-intensive techniques, or alleviate constraints related to essential parameters such as batch size and token lengths, which are crucial for deploying more effective LLMs Sheng et al. (2023); Pope et al. (2023); Ainslie et al. (2023).
With the rapid growth of LLM sizes, numerous studies have raised concerns regarding the expanding KV cache and proposed various solutions. The overall KV cache size is associated with several factors, including the number of attention heads, the number of layers, the dimension of each head, and the sequence length. To enhance MHA efficiency in Transformers, methods such as multi-query attention (MQA) Shazeer (2019) and grouped-query attention (GQA) Ainslie et al. (2023) are proposed to reduce KV cache requirements by decreasing the number of KV heads. Additionally, multi-head latent attention (MLA) has been developed to mitigate performance degradation through low-rank KV joint compression DeepSeek-AI (2024). These methods concentrate more on the attention head and dimension aspects. Conversely, another set of methods focuses on reducing the number of layers involved in KV cache. YOCO Sun et al. (2024) proposes a decoder-decoder architecture with linear attention that compresses the cache to a single layer. Similarly, CLA Brandon et al. (2024) and MLKV Zuhri et al. (2024) share KV activation across adjacent layers, reusing KV cache of earlier layers. Furthermore, there has been considerable interests in KV quantization techniques Hooper et al. (2024); Liu et al. (2024b).
Despite these advancements, existing solutions often lead to non-negligible performance degradation in LLMs when subjected to significant KV cache compression ratios. Moreover, most research tends to concentrate on individual aspects of KV cache compression rather than effectively integrating multiple strategies into a cohesive architecture, which is efficient and non-trivial in practice.
In this work, we propose a novel Cross-Layer Latent Attention (CLLA) architecture for KV cache compression in LLM. Our objective is to reduce the KV cache to less than 2% of its original size of classical MHA while preserving comparable performance levels. In CLLA, we explore the potential for integrating various aspects of KV cache compression methods into a unified and stable framework. Specifically, we jointly address KV cache compression through attention head/dimension aspect, layer aspect, and quantization aspect, and explore various possible combinations to achieve lossless KV cache compression.
Extensive results demonstrate remarkable effectiveness of our CLLA-quant: LLMs can achieve lossless performance on most tasks while utilizing less than 2% of the original KV cache, with detailed analyses on our exploration on different CLLA variants. The primary contributions of this work are summarized as follows:
-
•
We introduce CLLA and CLLA-quant, a novel architecture for KV cache compression that intelligently integrates head/dimension, layer, and quantization aspects.
-
•
We explore diverse variants of CLLA for better performance. To our knowledge, CLLA is the first architecture to achieve a KV cache compression ratio below 2% with lossless performance.
-
•
We conduct extensive in-depth explorations and analyses on various ablations and possible combinations of KV cache compression methods, which could shed lights on future research and practical applications. We hope our simple and effective CLLA could facilitate LLM community.
2 Related Works
2.1 Large Language Models
Recently, transformer-based models have garnered significant attention due to their powerful performance in various fields, including NLP and multimodal tasks. Large language models such as GPT-4 OpenAI et al. (2023) and LLaMA3 AI@Meta (2024) have achieved remarkable results across a range of natural language processing tasks.
However, the traditional decoder-only architecture incurs substantial training and online inference costs. To address this issue, Palm Chowdhery et al. (2023) and StarCode Li et al. (2023b) utilize MQA Shazeer (2019), where all attention heads share a group of KV. This approach aims to reduce the computational overhead associated with the attention mechanism. LLaMA2 Touvron et al. (2023) employs a different strategy within its attention blocks by grouping keys and values (GQA) Ainslie et al. (2023) to minimize the KV cache during inference. Concurrently, it increases the feed-forward network hidden size to maintain model performance. FlashAttention Dao (2023) optimizes training and inference efficiency from the perspective of GPU I/O operations. This method specifically targets the bottlenecks in data movement and computation within the GPU architecture. Mixture-of-Experts models (Jiang et al., 2024; Muennighoff et al., 2024; Wang et al., 2024a) utilize sparse architectures to achieve improved performance.
2.2 KV Cache Compression
Previous research has utilized techniques such as reducing the dimensions of attention heads and employing low-rank matrix approximations to enhance model efficiency. Some recent work reduces the KV cache through the layer dimension(Wu and Tu, 2024; Zuhri et al., 2024; He and Wu, 2024; Liu et al., ). Notably, Yu effectively compressed models by minimizing errors in MHA-to-GQA transitions Yu et al. (2024), while maintaining compatibility with RoPE Su et al. (2023). Some research efforts concentrate on reducing KV cache requirements by decreasing the sequence length, using methods such as token dropping Zhang et al. (2024b); Li et al. (2024); Xiao et al. (2023); Shi et al. (2024) and prompt compression Jiang et al. (2023); Chuang et al. (2024). However, these methods often lead to a notable decline in performance.
Recently, many research efforts have employed quantization compression to reduce KV cache, thereby improving inference efficiency (Banner et al., 2018; Wu et al., 2020; Yang et al., 2024; He et al., 2024; Liu et al., 2024a). Gear Kang et al. (2024) utilizes low-rank matrices and low-precision quantization to achieve near-lossless 4-bit KV cache compression. Coupled Quantization Zhang et al. (2024a) encodes multiple KV channels into a low-bit code. KIVI Liu et al. (2024b) performs quantization on keys and values along the channel and token dimensions, respectively. These works have primarily focused on inference. In contrast, we propose CLLA-quant method to quantize the KV cache in 4-bit integers during training and deployment.

3 Methodology
3.1 Preliminary of KV Cache
Currently, transformer model is the most prevalent LLM architecture. It is composed of many blocks stacked together. Each block includes an attention layer and a MLP layer. Multi-head Attention (MHA) Vaswani et al. (2017) is a typical design for the attention layer. Given the sequence hidden states , the computations of MHA for each head are performed as follows:
| (1) | ||||
where , , and are weight matrices in for . denotes the number of heads. represents the calculation of scaled dot-product attention Vaswani et al. (2017).
To increase the speed of autoregressive decoding, it is necessary to store the key and value vectors ( and ) of previous input hidden states. In Transformer, the memory requirement for KV cache is influenced by multiple parameters: batch size (), number of layers (), sequence length (), number of attention heads (), and the dimension of each head (). This dependency can be formulated as:
| (2) |
Classical methods such as GQA Ainslie et al. (2023), MLA DeepSeek-AI (2024), and CLA Brandon et al. (2024) usually compress KV cache from , , and aspects as shown in Table 1. In this work, we strive to jointly consider all these aspects for performance-lossless KV cache compression.
| Method | KV Cache Memory |
|---|---|
| MHA | |
| GQA | |
| MLA | |
| CLA | |
| CLLA | |
| CLLA-quant |
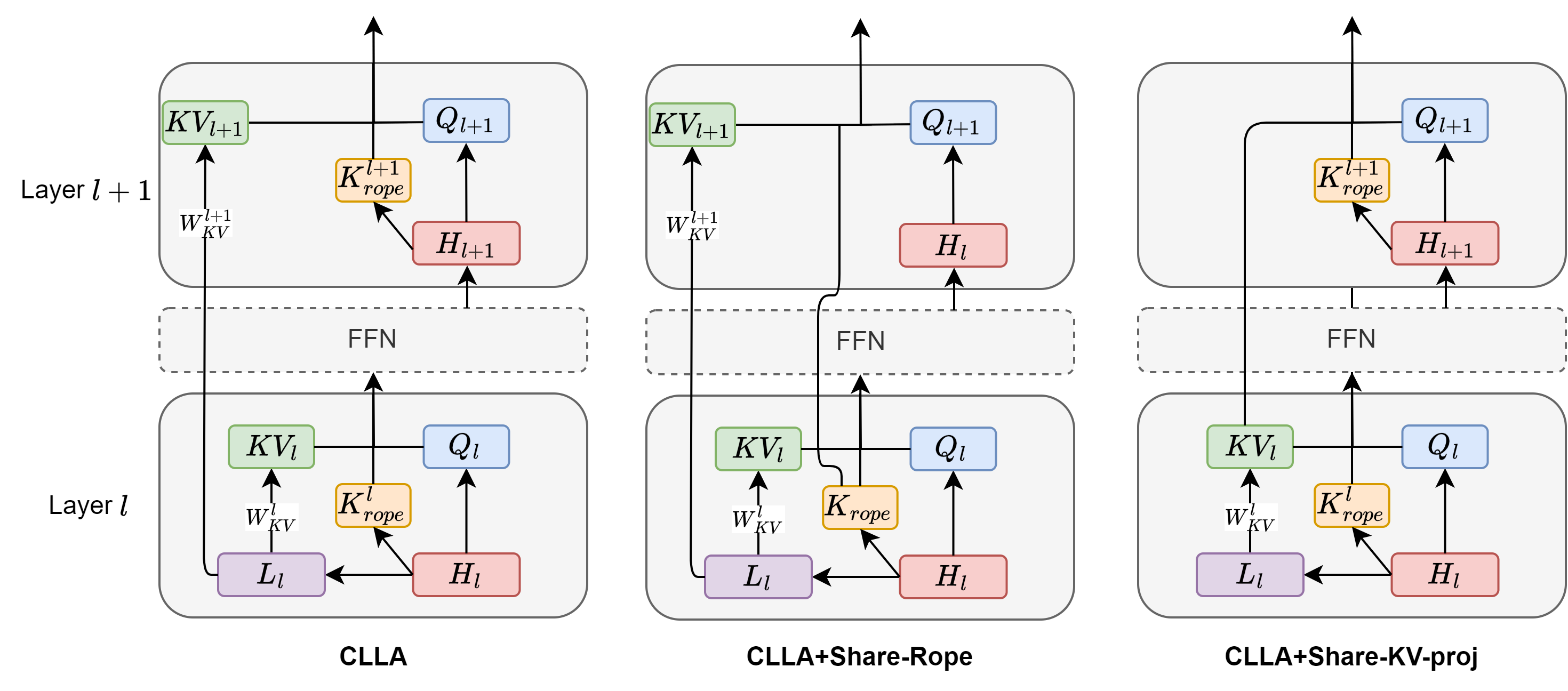
3.2 CLLA: CLA Meets MLA
CLLA involves compressing KV cache into low-rank latent states and subsequently allowing multiple layers to share these states. The key research point is how to effectively share compressed latent states across layers.
MLA basics. To begin with, we project the input hidden states of the attention layer into low-rank latent states denoted as :
| (3) |
This method enables significant compression since only the latent states need to be cached, rather than storing entire key and value vectors. During attention computation, we restore the latent states back to the standard key-value representations.
| (4) |
Subsequently, we compute the query vector to engage in attention calculation. To facilitate the use of RoPE, two additional small query vector and key vector are created as follows,
| (5) | ||||
Lastly, we incorporate vectors containing RoPE information into the query and value vectors and proceed with the attention calculation.
| (6) | ||||
where denotes the operation that implements the multi-head mechanism.
CLLA variants. When integrating MLA and CLA strategies, several variations and complexities must be considered. Compared to the naive CLA method (which shares KV activation directly across layers), we depict three variations in Figure 2. The left variation is adopted as our final CLLA architecture. It shares only latent vectors across layers while allowing each layer its own KV projection matrices to reconstruct KV activation. This variation demonstrated superior performance compared to others, and detailed experiments are presented in Section 5.2. Formally, for CLLA with a sharing factor of 2, the equation is defined as follows,
| (7) |
In this formulation, we share latent vectors while each layer utilizes its own RoPE vectors for keys. For layers employing latent vectors from previous layers, specific linear layers are used to project shared latent vectors back into and . Subsequently, is concatenated with for MHA calculations alongside and .
Explanation of the current CLLA selection. Although this approach requires more computational resources compared to variations that share both KV activation but not latent vector , we believe this trade-off is justified by its superior performance relative to other methods. We hypothesize that this improvement arises because each projection matrix can tailor latent vector projections into specific KV activation containing relevant information for that layer. Furthermore, we found that sharing only latent vectors significantly enhances performance when combined with quantization techniques due to quantization being applied at the latent vector level. Similar reasoning applies regarding specific projection layers mitigating quantization loss.
3.3 CLLA-quant: Latent Quantization
To further reduce memory overhead associated with KV cache, we implement low-bit quantization on latent states by converting them from 16-bit floating-point values into lower-bit integers using symmetric quantization Nagel et al. (2021). The quantization function can be expressed as follows:
| (8) |
| (9) |
| (10) |
Here represents the latent states, and represents their quantized version stored as -bit integers. denotes the rounding operator, while serves as the scaling factor. The latent states are scaled to the restricted range , which is set to . The quantized latent states are stored in cache and dequantized only when needed during computations. The dequantization function is defined as follows,
| (11) |
The recovered latent states are then utilized in computations. We adopt 4-bit for CLLA-quant.
Quantization recipe. To minimize quantization error further, we employ sub-channelwise quantization techniques Gholami et al. (2022), where every elements are grouped, with each group sharing a scaling factor. Additionally, prior to quantization, latent states are normalized using RMSNorm Zhang and Sennrich (2019). Both quantization and dequantization processes are applied during training and deployment phases. In training mode specifically, gradients associated with quantization are approximated using the straight-through estimator (STE) Bengio et al. (2013).
4 Experiments
4.1 Datasets and Experimental Settings
The training dataset was collected in-house and consists of a cleaned combination of Chinese and English datasets. We trained all models on 300 billion tokens. For evaluation, we aim to achieve robust conclusions across diverse domains in both English and Chinese. We conducted comprehensive evaluations involving 7 English tasks, including MMLU, Hellaswag, ARC-C, Winogrande, BoolQ, PIQA, and SIQA. For Chinese tasks, we evaluated models on 8 tasks: CMMLU, CEval, CLUEWSC2020, Thuc-news, OCNLI, C3, FewCLUE-CHID, and CMNLI. More details are noted in Appendix B.
In order to ensure equitable comparison, the intermediate dimensionality of the feed-forward neural network (FFN) was adjusted to maintain comparable activation parameters across all models. The Appendix elaborates on the implementation specifics of each model. The training process was executed utilizing 64 NVIDIA H800 GPUs, with the same hardware resources employed for the inference evaluations. Complete details of the training configurations are provided in the Appendix.
| Model | MMLU | Hellaswag | ARC-C | Winogrande | BoolQ | PIQA | SIQA | AVG |
|---|---|---|---|---|---|---|---|---|
| MHA | 38.61 | 54.78 | 48.10 | 55.31 | 70.60 | 73.76 | 55.94 | 56.73 |
| GQA | 37.59 | 54.10 | 51.51 | 56.91 | 69.67 | 74.70 | 53.33 | 56.83 |
| MLA | 40.51 | 54.23 | 48.83 | 55.56 | 70.83 | 73.94 | 56.19 | 57.16 |
| CLLA | 42.08 | 54.60 | 52.84 | 54.38 | 73.10 | 74.43 | 54.35 | 57.97 |
| CLLA-quant | 41.13 | 53.87 | 51.84 | 55.64 | 72.33 | 74.32 | 56.70 | 57.98 |
| Model | CMMLU | CEval | CLUEWSC2020 | Thuc-news | OCNLI | C3 | CHID | CMNLI | AVG |
|---|---|---|---|---|---|---|---|---|---|
| MHA | 36.88 | 42.78 | 69.42 | 96.14 | 55.61 | 60.43 | 79.20 | 52.79 | 61.66 |
| GQA | 36.79 | 39.99 | 70.19 | 95.47 | 56.14 | 60.40 | 78.71 | 54.55 | 61.53 |
| MLA | 39.20 | 44.29 | 69.23 | 96.27 | 54.07 | 61.20 | 78.71 | 50.78 | 61.72 |
| CLLA | 40.87 | 44.92 | 73.08 | 96.10 | 55.39 | 61.77 | 82.67 | 53.67 | 63.56 |
| CLLA-quant | 44.82 | 44.63 | 70.19 | 96.47 | 56.14 | 59.87 | 79.70 | 54.27 | 63.26 |
4.2 Competitors
For every competitor, we utilize the same 1.44 billion activation parameters with a Mixture of Experts (MoE) architecture Fedus et al. (2022); Lepikhin et al. (2020). Specifically, we employ a model with a 1Bx16 MoE configuration, comprising nearly 11 billion parameters in total, to ensure fair comparisons.The following methods were evaluated:
MHA: The foundational transformer architecture Vaswani et al. (2017); Radford et al. (2019) resembles that of the Llama2 model Touvron et al. (2023). It features SwiGLU Shazeer (2020) as the activation function for the feed-forward layer and utilizes RoPE Su et al. (2023) for the embedding of relative positions. All subsequent models are variations of this foundational model.
GQA: GQA Ainslie et al. (2023) groups query heads together, allowing each group to share keys and values. We set the number of KV heads to 8 out of a total of 16 query heads to reduce KV cache by half.
MLA: In MLA DeepSeek-AI (2024), the KV cache is mapped into a low-rank space. The latent dimension for this low-rank space is set at 512.
CLLA: Our method combines the settings from MLA and CLA Brandon et al. (2024) while adhering to the aforementioned sharing configurations.
CLLA-quant: We applied int4 scalar quantization to compress latent states with a quantization group size of 32 on the original CLLA.
In each model, the hidden size is configured to 1536, with 32 layers and 16 attention heads. We incorporated 17 experts in the MoE layer, consisting of one shared expert alongside 16 experts, from which the top-1 is selected for routing. To ensure the alignment of activation parameters and total parameters across various methods, we modified the expansion ratio of the feed-forward network (FFN) as needed for fair comparisons. Further details regarding training and model hyperparameters can be found in Appendix A.
4.3 Main Results
After pre-training on 300 billion tokens, we evaluated all models across 15 benchmarks that encompass a wide range of tasks. All models are compared in the same tokenizer and data. On English benchmarks shown in Table 2, MLA are comparable with GQA baseline. The proposed models CLLA and CLLA-quant achieve better results with higher compress ratio. We can achieve similar conclusion on Chinese benchmarks presented in Table 3. Additionally, theoretical KV cache memory bytes usages for each model are shown in Table 4. From these tables, several interesting observations emerge regarding the effectiveness of our methods in achieving high KV cache compression ratios without performance degradation:
| Method | KV Cache Memory | Compression Ratio |
|---|---|---|
| MHA | 6,144 Bytes | 100% |
| GQA | 3,072 Bytes | 50.0% |
| MLA | 576 Bytes | 9.4% |
| CLLA | 320 Bytes | 5.2% |
| CLLA-quant | 128 Bytes | 2.1% |
| Sharing Method | Model | Sharing Factor | Q Heads | KV Heads | KV Bytes/Token | Val PPL | |
|---|---|---|---|---|---|---|---|
| Intra-layer | GQA-Group8 | 96 | 1 | 16 | 8 | 49,152 | 8.93 |
| GQA-Group4 | 96 | 1 | 16 | 4 | 24,576 | 8.95 | |
| GQA-Group2 | 96 | 1 | 16 | 2 | 12,288 | 9.05 | |
| MQA | 96 | 1 | 16 | 1 | 6,144 | 9.11 | |
| Inter-layer | CLA-Share2 | 96 | 2 | 16 | 16 | 49,152 | 8.97 |
| CLA-Share4 | 96 | 4 | 16 | 16 | 24,576 | 9.07 | |
| CLA-Share8 | 96 | 8 | 16 | 16 | 12,288 | 9.47 | |
| Mixed | GQA-Group4+CLA-Share2 | 96 | 2 | 16 | 4 | 12,288 | 9.12 |
| GQA-Group2+CLA-Share2 | 96 | 2 | 16 | 2 | 6,144 | 9.19 | |
| MQA-Dim384-CLA-Share2 | 384 | 2 | 4 | 1 | 12,288 | 9.12 | |
| MQA-Dim192-CLA-Share2 | 192 | 2 | 8 | 1 | 6,144 | 9.16 |
First, CLLA notably surpassed MHA in performance while also achieving a significant reduction in memory usage of nearly 95%. For English tasks, CLLA’s performance was about 1.24 point higher than that of MHA, and it showed similar enhancements for Chinese tasks. This improvement is possibly attributed to our model design. Under the same amount of activated parameters, we were able to increase the FFN hidden size by utilizing parameters saved from the CLLA approach, which likely contributed to the improved outcomes.
Second, CLLA-quant exhibited results comparable to CLLA while further achieving a fourfold reduction in memory usage. These results verify the impressive conclusion that our CLLA-quant method compresses KV cache memory to 2% without performance loss generally on 15 benchmarks compared to MHA. We hypothesize that the minimal impact of quantization on performance is due to its application during pretraining, allowing the entire model to adapt to the quantized KV cache. The quantization likely enforces a form of robustness in the representations stored in the KV cache, ensuring that minor precision losses do not adversely affect the model’s ability.
5 In-depth Model Analyses on CLLA
It is nontrivial to compress KV cache from different aspects including layer, dimension, and bit levels. In this section, we conduct extensive explorations on different (successful or failed) strategies and report the insights found in our experiments, hoping to facilitate future research.
5.1 Intra-layer vs. Inter-layer Sharing
To gain a deeper understanding of the strategy for combining CLA and MLA, we conduct a thorough analysis of both intra-layer and inter-layer sharing methods. The superiority between inter-layer sharing methods, such as CLA, and intra-layer sharing strategies, such as MQA and GQA, has been a subject of contradictory conclusions in current studies. In Brandon et al. (2024), the authors claim that with proper design, the combination of intra-layer and inter-layer strategies can make inter-layer sharing better than intra-layer sharing in some situations. However, a later study Zuhri et al. (2024) found that intra-layer strategies are generally better than inter-layer strategies. To explore these design choices, a series of experiments were conducted. The experimental models are in the same setting with our main experiment, except we only train 50B tokens for a fast comparison on validation perplexity. The results are presented in Table 5:
(1) Intra-layer strategies consistently achieve lower validation perplexity compared to inter-layer strategies when using the same memory budget. Specifically, comparing GQA-Group8 with CLA-Share2, GQA-Group4 with CLA-Share4, and GQA-Group2 with CLA-Share8, intra-layer strategies consistently outperform inter-layer strategies in terms of validation perplexity. Furthermore, even with equivalent memory reductions, the performance loss associated with the CLA strategy is significantly greater than that of the GQA strategy. This conclusion is supported by comparisons between CLA configurations with varying share factors and GQA configurations with different group sizes.
(2) Neither the combination of GQA and CLA strategies nor adjustments to the head dimensions improved the performance. Specifically, when we combined both strategies, we observed that GQA-Group2+CLA-Share2 performed worse than MQA, while GQA-Group4+CLA-Share2 was inferior to GQA-Group2. Additionally, maintaining the total hidden dimension while adjusting head dimensions failed to surpass simple intra-layer sharing strategies. This is evident from comparisons between MQA-Dim192-CLA-Share2 and MQA as well as MQA-Dim384-CLA-Share2 and GQA-Group2.
Based on these observations, we can outline a design strategy for utilizing intra-layer and inter-layer sharing to conserve KV-cache memory. First, prioritize intra-layer strategies if the KV-cache memory budget can be met solely through intra-layer approaches. Second, resort to inter-layer strategies only after significantly compressing intra-layer memory strategies, such as MQA and MLA, when further reduction is necessary.
In addition to the aforementioned ablation studies, inspired by MLA, we explored the possibility of sharing input hidden states for attention blocks instead of KV heads. This approach necessitates caching input hidden states for inference while computing KV heads in real-time. We can view the MLA strategy as a LoRA variant of this concept. When applying CLA within this framework, we must determine whether to share KV projection weights as in Figure 3. Our findings indicate that allowing each layer its own KV projection weights yields slightly better performance than sharing KV projections, with validation perplexities of 8.97 versus 8.99. Although this decision is critical for CLLA, the difference is not substantial in this context.

5.2 CLLA Cross-layer Sharing Strategies
Upon decomposing the components eligible for cross-layer sharing within the MLA strategy, we identified three elements: KV latent vectors, K rope vectors, and KV projection matrices. These three configurations are illustrated in Figure 2. Our final design decision favors the first configuration due to its superior performance. The second configuration offers additional KV-cache savings but only marginally so because of the relatively small size of K rope vectors compared to KV latent vector sizes. The third configuration may reduce computation and model parameters.
We evaluated these three models based on downstream tasks under identical experimental settings as those used in the main experiments. The results are presented in Table 6, which displays average scores for both English and Chinese tasks. Detailed results for all English and Chinese task can be found in the Appendix C.
| Model | English | Chinese | AVG |
|---|---|---|---|
| CLLA | 57.97 | 63.56 | 60.77 |
| CLLA+share-krope | 56.24 | 61.71 | 58.98 |
| CLLA+share-kvproj | 59.47 | 61.40 | 60.44 |
Our analysis reveals that CLLA with exclusive sharing of KV latent vectors achieved the best performance. The strategy of sharing K rope vectors significantly detracted from performance with minimal benefits. While the KV projection sharing strategy yielded better results for English tasks, it was lower overall. Nevertheless, this approach can provide moderate improvements during training and inference by eliminating half of the KV projection calculations and matrices required. Given our primary focus on downstream performance, we opted for the first configuration as our CLLA strategy. Another reason for selecting this configuration is its favorable interaction with quantization techniques.
5.3 CLLA Quantization Strategies
Based on our previous findings, we selected CLLA and CLLA+share-kvproj for latent quantization training and compared their downstream performance as shown in Table 7. All experimental settings were consistent with those used in the main experiments. Our results indicate that the strategy without sharing KV projection matrices achieved significantly higher performance when combined with quantization techniques. The observed differences may be attributed to the fact that having multiple KV projections can better compensate for quantization loss compared to relying on a shared KV projection.
| Model | English | Chinese | AVG |
|---|---|---|---|
| CLLA-quant | 57.98 | 63.26 | 60.62 |
| CLLA-quant+share-kvproj | 58.44 | 61.45 | 59.95 |
6 Conclusion and Future Work
In this work, we introduce CLLA and CLLA-quant, two effective techniques for compressing KV caches. Both methods achieve substantial reductions in KV cache size without compromising performance, with CLLA-quant achieving memory usage as low as 2% while maintaining performance comparable to the baseline. We identify optimal design choices that effectively combine attention head/dimension reduction, layer sharing, and quantization techniques, which is verified by extensive experiments and analyses. Although CLLA is straightforward, it successfully confirms the feasibility of lossless large-ratio KV cache compression, which is promising to be the superior fundamental component for efficient LLM inference.
In the future, we will explore our CLLA series on larger scales of LLMs to verify its universality. Further experiments will also be conducted to discover more efficient parameter allocations on different components of LLM’s KV cache.
Limitations
Limitations of the current work are discussed below. Firstly, while the proposed CLLA-quant performs well in terms of achieving extreme KV cache savings, its structure is relatively complex. Streamlining this process while maintaining its effectiveness would greatly facilitate the practical application of this technology. Secondly, the experiments in this paper mainly focus on compressing and saving the KV cache. Further optimization of the framework is needed to reduce the time complexity in the Attention Block, ensuring high generation efficiency and throughput as the sequence length increases.
References
- Achiam et al. (2023) Josh Achiam, Steven Adler, Sandhini Agarwal, Lama Ahmad, Ilge Akkaya, Florencia Leoni Aleman, Diogo Almeida, Janko Altenschmidt, Sam Altman, Shyamal Anadkat, et al. 2023. Gpt-4 technical report. arXiv preprint arXiv:2303.08774.
- AI@Meta (2024) AI@Meta. 2024. Llama 3 model card.
- Ainslie et al. (2023) Joshua Ainslie, James Lee-Thorp, Michiel de Jong, Yury Zemlyanskiy, Federico Lebrón, and Sumit Sanghai. 2023. Gqa: Training generalized multi-query transformer models from multi-head checkpoints. arXiv preprint arXiv:2305.13245.
- Bai et al. (2023) Jinze Bai, Shuai Bai, Yunfei Chu, Zeyu Cui, Kai Dang, Xiaodong Deng, Yang Fan, Wenbin Ge, Yu Han, Fei Huang, et al. 2023. Qwen technical report. arXiv preprint arXiv:2309.16609.
- Banner et al. (2018) Ron Banner, Itay Hubara, Elad Hoffer, and Daniel Soudry. 2018. Scalable methods for 8-bit training of neural networks. Advances in neural information processing systems, 31.
- Bengio et al. (2013) Yoshua Bengio, Nicholas Léonard, and Aaron Courville. 2013. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv preprint arXiv:1308.3432.
- Bisk et al. (2020) Yonatan Bisk, Rowan Zellers, Jianfeng Gao, Yejin Choi, et al. 2020. Piqa: Reasoning about physical commonsense in natural language. In Proceedings of the AAAI conference on artificial intelligence, volume 34, pages 7432–7439.
- Brandon et al. (2024) William Brandon, Mayank Mishra, Aniruddha Nrusimha, Rameswar Panda, and Jonathan Ragan Kelly. 2024. Reducing transformer key-value cache size with cross-layer attention. arXiv preprint arXiv:2405.12981.
- Chowdhery et al. (2023) Aakanksha Chowdhery, Sharan Narang, Jacob Devlin, Maarten Bosma, Gaurav Mishra, Adam Roberts, Paul Barham, Hyung Won Chung, Charles Sutton, Sebastian Gehrmann, et al. 2023. Palm: Scaling language modeling with pathways. Journal of Machine Learning Research, 24(240):1–113.
- Chuang et al. (2024) Yu-Neng Chuang, Tianwei Xing, Chia-Yuan Chang, Zirui Liu, Xun Chen, and Xia Hu. 2024. Learning to compress prompt in natural language formats. arXiv preprint arXiv:2402.18700.
- Clark et al. (2019) Christopher Clark, Kenton Lee, Ming-Wei Chang, Tom Kwiatkowski, Michael Collins, and Kristina Toutanova. 2019. Boolq: Exploring the surprising difficulty of natural yes/no questions. arXiv preprint arXiv:1905.10044.
- Clark et al. (2018) Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. 2018. Think you have solved question answering? try arc, the ai2 reasoning challenge. arXiv preprint arXiv:1803.05457.
- Dao (2023) Tri Dao. 2023. Flashattention-2: Faster attention with better parallelism and work partitioning. arXiv preprint arXiv:2307.08691.
- DeepSeek-AI (2024) DeepSeek-AI. 2024. Deepseek-v2: A strong, economical, and efficient mixture-of-experts language model. arXiv preprint arXiv:2405.04434.
- Driess et al. (2023) Danny Driess, Fei Xia, Mehdi SM Sajjadi, Corey Lynch, Aakanksha Chowdhery, Brian Ichter, Ayzaan Wahid, Jonathan Tompson, Quan Vuong, Tianhe Yu, et al. 2023. Palm-e: An embodied multimodal language model. arXiv preprint arXiv:2303.03378.
- Fedus et al. (2022) William Fedus, Barret Zoph, and Noam Shazeer. 2022. Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. Journal of Machine Learning Research, 23(120):1–39.
- Gholami et al. (2022) Amir Gholami, Sehoon Kim, Zhen Dong, Zhewei Yao, Michael W Mahoney, and Kurt Keutzer. 2022. A survey of quantization methods for efficient neural network inference. In Low-Power Computer Vision, pages 291–326. Chapman and Hall/CRC.
- He and Wu (2024) Qiaozhi He and Zhihua Wu. 2024. Efficient llm inference with kcache. arXiv preprint arXiv:2404.18057.
- He et al. (2024) Yefei He, Luoming Zhang, Weijia Wu, Jing Liu, Hong Zhou, and Bohan Zhuang. 2024. Zipcache: Accurate and efficient kv cache quantization with salient token identification. arXiv preprint arXiv:2405.14256.
- Hendrycks et al. (2020) Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. 2020. Measuring massive multitask language understanding. arXiv preprint arXiv:2009.03300.
- Hooper et al. (2024) Coleman Hooper, Sehoon Kim, Hiva Mohammadzadeh, Michael W Mahoney, Yakun Sophia Shao, Kurt Keutzer, and Amir Gholami. 2024. Kvquant: Towards 10 million context length llm inference with kv cache quantization. arXiv preprint arXiv:2401.18079.
- Hu et al. (2020) Hai Hu, Kyle Richardson, Liang Xu, Lu Li, Sandra Kübler, and Lawrence S Moss. 2020. Ocnli: Original chinese natural language inference. arXiv preprint arXiv:2010.05444.
- Huang et al. (2024) Yuzhen Huang, Yuzhuo Bai, Zhihao Zhu, Junlei Zhang, Jinghan Zhang, Tangjun Su, Junteng Liu, Chuancheng Lv, Yikai Zhang, Yao Fu, et al. 2024. C-eval: A multi-level multi-discipline chinese evaluation suite for foundation models. Advances in Neural Information Processing Systems, 36.
- Jiang et al. (2024) Albert Q Jiang, Alexandre Sablayrolles, Antoine Roux, Arthur Mensch, Blanche Savary, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Emma Bou Hanna, Florian Bressand, et al. 2024. Mixtral of experts. arXiv preprint arXiv:2401.04088.
- Jiang et al. (2023) Huiqiang Jiang, Qianhui Wu, Chin-Yew Lin, Yuqing Yang, and Lili Qiu. 2023. Llmlingua: Compressing prompts for accelerated inference of large language models. arXiv preprint arXiv:2310.05736.
- Kang et al. (2024) Hao Kang, Qingru Zhang, Souvik Kundu, Geonhwa Jeong, Zaoxing Liu, Tushar Krishna, and Tuo Zhao. 2024. Gear: An efficient kv cache compression recipefor near-lossless generative inference of llm. arXiv preprint arXiv:2403.05527.
- Lepikhin et al. (2020) Dmitry Lepikhin, HyoukJoong Lee, Yuanzhong Xu, Dehao Chen, Orhan Firat, Yanping Huang, Maxim Krikun, Noam Shazeer, and Zhifeng Chen. 2020. Gshard: Scaling giant models with conditional computation and automatic sharding. arXiv preprint arXiv:2006.16668.
- Li et al. (2023a) Haonan Li, Yixuan Zhang, Fajri Koto, Yifei Yang, Hai Zhao, Yeyun Gong, Nan Duan, and Timothy Baldwin. 2023a. Cmmlu: Measuring massive multitask language understanding in chinese. arXiv preprint arXiv:2306.09212.
- Li et al. (2023b) Raymond Li, Loubna Ben Allal, Yangtian Zi, Niklas Muennighoff, Denis Kocetkov, Chenghao Mou, Marc Marone, Christopher Akiki, Jia Li, Jenny Chim, et al. 2023b. Starcoder: may the source be with you! arXiv preprint arXiv:2305.06161.
- Li et al. (2024) Yuhong Li, Yingbing Huang, Bowen Yang, Bharat Venkitesh, Acyr Locatelli, Hanchen Ye, Tianle Cai, Patrick Lewis, and Deming Chen. 2024. Snapkv: Llm knows what you are looking for before generation. arXiv preprint arXiv:2404.14469.
- (31) Akide Liu, Jing Liu, Zizheng Pan, Yefei He, Gholamreza Haffari, and Bohan Zhuang. Minicache: Kv cache compression in depth dimension for large language models, 2024b. URL https://arxiv. org/abs/2405.14366.
- Liu et al. (2024a) Peiyu Liu, Ze-Feng Gao, Wayne Xin Zhao, Yipeng Ma, Tao Wang, and Ji-Rong Wen. 2024a. Unlocking data-free low-bit quantization with matrix decomposition for kv cache compression. arXiv preprint arXiv:2405.12591.
- Liu et al. (2024b) Zirui Liu, Jiayi Yuan, Hongye Jin, Shaochen Zhong, Zhaozhuo Xu, Vladimir Braverman, Beidi Chen, and Xia Hu. 2024b. Kivi: A tuning-free asymmetric 2bit quantization for kv cache. arXiv preprint arXiv:2402.02750.
- Muennighoff et al. (2024) Niklas Muennighoff, Luca Soldaini, Dirk Groeneveld, Kyle Lo, Jacob Morrison, Sewon Min, Weijia Shi, Pete Walsh, Oyvind Tafjord, Nathan Lambert, et al. 2024. Olmoe: Open mixture-of-experts language models. arXiv preprint arXiv:2409.02060.
- Nagel et al. (2021) Markus Nagel, Marios Fournarakis, Rana Ali Amjad, Yelysei Bondarenko, Mart Van Baalen, and Tijmen Blankevoort. 2021. A white paper on neural network quantization. arXiv preprint arXiv:2106.08295.
- OpenAI et al. (2023) R OpenAI et al. 2023. Gpt-4 technical report. ArXiv, 2303:08774.
- Pope et al. (2023) Reiner Pope, Sholto Douglas, Aakanksha Chowdhery, Jacob Devlin, James Bradbury, Jonathan Heek, Kefan Xiao, Shivani Agrawal, and Jeff Dean. 2023. Efficiently scaling transformer inference. Proceedings of Machine Learning and Systems.
- Radford et al. (2019) Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever, et al. 2019. Language models are unsupervised multitask learners. OpenAI blog, 1(8):9.
- Sakaguchi et al. (2021) Keisuke Sakaguchi, Ronan Le Bras, Chandra Bhagavatula, and Yejin Choi. 2021. Winogrande: An adversarial winograd schema challenge at scale. Communications of the ACM, 64(9):99–106.
- Sap et al. (2019) Maarten Sap, Hannah Rashkin, Derek Chen, Ronan LeBras, and Yejin Choi. 2019. Socialiqa: Commonsense reasoning about social interactions. arXiv preprint arXiv:1904.09728.
- Shazeer (2019) Noam Shazeer. 2019. Fast transformer decoding: One write-head is all you need. arXiv preprint arXiv:1911.02150.
- Shazeer (2020) Noam Shazeer. 2020. Glu variants improve transformer. arXiv preprint arXiv:2002.05202.
- Sheng et al. (2023) Ying Sheng, Lianmin Zheng, Binhang Yuan, Zhuohan Li, Max Ryabinin, Beidi Chen, Percy Liang, Christopher Ré, Ion Stoica, and Ce Zhang. 2023. Flexgen: High-throughput generative inference of large language models with a single gpu. In Preceedings of ICML.
- Shi et al. (2024) Zhenmei Shi, Yifei Ming, Xuan-Phi Nguyen, Yingyu Liang, and Shafiq Joty. 2024. Discovering the gems in early layers: Accelerating long-context llms with 1000x input token reduction. arXiv preprint arXiv:2409.17422.
- Su et al. (2023) J Su, Y Lu, S Pan, A Murtadha, B Wen, and Y Liu Roformer. 2023. Enhanced transformer with rotary position embedding., 2021. DOI: https://doi. org/10.1016/j. neucom.
- Sun et al. (2020) Kai Sun, Dian Yu, Dong Yu, and Claire Cardie. 2020. Investigating prior knowledge for challenging chinese machine reading comprehension. Transactions of the Association for Computational Linguistics, 8:141–155.
- Sun et al. (2016) Maosong Sun, Jingyang Li, Zhipeng Guo, Z Yu, Y Zheng, X Si, and Z Liu. 2016. Thuctc: An efficient chinese text classifier. https://github.com/thunlp/THUCTC. GitHub Repository.
- Sun et al. (2024) Yutao Sun, Li Dong, Yi Zhu, Shaohan Huang, Wenhui Wang, Shuming Ma, Quanlu Zhang, Jianyong Wang, and Furu Wei. 2024. You only cache once: Decoder-decoder architectures for language models. arXiv preprint arXiv:2405.05254.
- Touvron et al. (2023) Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Proceedings of NIPS.
- Wang et al. (2024a) An Wang, Xingwu Sun, Ruobing Xie, Shuaipeng Li, Jiaqi Zhu, Zhen Yang, Pinxue Zhao, JN Han, Zhanhui Kang, Di Wang, et al. 2024a. Hmoe: Heterogeneous mixture of experts for language modeling. arXiv preprint arXiv:2408.10681.
- Wang et al. (2024b) Lei Wang, Chen Ma, Xueyang Feng, Zeyu Zhang, Hao Yang, Jingsen Zhang, Zhiyuan Chen, Jiakai Tang, Xu Chen, Yankai Lin, et al. 2024b. A survey on large language model based autonomous agents. Frontiers of Computer Science.
- Wu et al. (2020) Di Wu, Qi Tang, Yongle Zhao, Ming Zhang, Ying Fu, and Debing Zhang. 2020. Easyquant: Post-training quantization via scale optimization. arXiv preprint arXiv:2006.16669.
- Wu and Tu (2024) Haoyi Wu and Kewei Tu. 2024. Layer-condensed kv cache for efficient inference of large language models. arXiv preprint arXiv:2405.10637.
- Xiao et al. (2023) Guangxuan Xiao, Yuandong Tian, Beidi Chen, Song Han, and Mike Lewis. 2023. Efficient streaming language models with attention sinks. arXiv preprint arXiv:2309.17453.
- Xu et al. (2020) Liang Xu, Hai Hu, Xuanwei Zhang, Lu Li, Chenjie Cao, Yudong Li, Yechen Xu, Kai Sun, Dian Yu, Cong Yu, et al. 2020. Clue: A chinese language understanding evaluation benchmark. arXiv preprint arXiv:2004.05986.
- Xu et al. (2021) Liang Xu, Xiaojing Lu, Chenyang Yuan, Xuanwei Zhang, Huilin Xu, Hu Yuan, Guoao Wei, Xiang Pan, Xin Tian, Libo Qin, et al. 2021. Fewclue: A chinese few-shot learning evaluation benchmark. arXiv preprint arXiv:2107.07498.
- Yang et al. (2024) June Yong Yang, Byeongwook Kim, Jeongin Bae, Beomseok Kwon, Gunho Park, Eunho Yang, Se Jung Kwon, and Dongsoo Lee. 2024. No token left behind: Reliable kv cache compression via importance-aware mixed precision quantization. arXiv preprint arXiv:2402.18096.
- Yu et al. (2024) Hao Yu, Zelan Yang, Shen Li, Yong Li, and Jianxin Wu. 2024. Effectively compress kv heads for llm. arXiv preprint arXiv:2406.07056.
- Zellers et al. (2019) Rowan Zellers, Ari Holtzman, Yonatan Bisk, Ali Farhadi, and Yejin Choi. 2019. Hellaswag: Can a machine really finish your sentence? arXiv preprint arXiv:1905.07830.
- Zhang and Sennrich (2019) Biao Zhang and Rico Sennrich. 2019. Root mean square layer normalization. Advances in Neural Information Processing Systems, 32.
- Zhang et al. (2023) Junjie Zhang, Ruobing Xie, Yupeng Hou, Wayne Xin Zhao, Leyu Lin, and Ji-Rong Wen. 2023. Recommendation as instruction following: A large language model empowered recommendation approach. arXiv preprint arXiv:2305.07001.
- Zhang et al. (2024a) Tianyi Zhang, Jonah Yi, Zhaozhuo Xu, and Anshumali Shrivastava. 2024a. Kv cache is 1 bit per channel: Efficient large language model inference with coupled quantization. arXiv preprint arXiv:2405.03917.
- Zhang et al. (2024b) Zhenyu Zhang, Ying Sheng, Tianyi Zhou, Tianlong Chen, Lianmin Zheng, Ruisi Cai, Zhao Song, Yuandong Tian, Christopher Ré, Clark Barrett, et al. 2024b. H2o: Heavy-hitter oracle for efficient generative inference of large language models. Advances in Neural Information Processing Systems, 36.
- Zhu et al. (2023) Yutao Zhu, Huaying Yuan, Shuting Wang, Jiongnan Liu, Wenhan Liu, Chenlong Deng, Zhicheng Dou, and Ji-Rong Wen. 2023. Large language models for information retrieval: A survey. arXiv preprint arXiv:2308.07107.
- Zuhri et al. (2024) Zayd Muhammad Kawakibi Zuhri, Muhammad Farid Adilazuarda, Ayu Purwarianti, and Alham Fikri Aji. 2024. Mlkv: Multi-layer key-value heads for memory efficient transformer decoding. arXiv preprint arXiv:2406.09297.
Appendix A Implementation Details
To ensure a fair comparison, we primarily adjusted the intermediate size of the feed-forward neural network (FFN) to maintain similar activation parameters across models. The implementation details for each model are presented in Table 8. Aside from the parameters listed here, all other parameters are set to their default values. For instance, all models were configured with 32 layers and a vocabulary size of 128,256. In the MLA strategy, we established the KV LoRA rank at 512, the Q LoRA rank at 768, and the query-key rope head dimension at 64.
| Model | Intermediate Size | q heads | kv heads | head dim | topk/experts | Activation Parameters (B) | Total Parameters (B) |
|---|---|---|---|---|---|---|---|
| MHA | 3840 | 16 | 16 | 96 | 1+1 / 1+16 | 1.44 | 10.13 |
| GQA | 4096 | 16 | 8 | 96 | 1+1 / 1+16 | 1.44 | 10.69 |
| MLA | 3840 | 16 | 16 | 96 | 1+1 / 1+16 | 1.44 | 10.13 |
| CLLA | 4160 | 16 | 16 | 96 | 1+1 / 1+16 | 1.44 | 10.84 |
| CLLA-quant | 4160 | 16 | 16 | 96 | 1+1 / 1+16 | 1.44 | 10.84 |
All training runs were conducted using 64 NVIDIA H800 GPUs, with inference evaluations performed on the same hardware configuration. All the training settings as specified in Table 9.
| Hyper-parameters | Values |
|---|---|
| Optimizer | AdamW |
| Adam | (0.9, 0.95) |
| Adam | |
| Weight Decay | 0.1 |
| LR | |
| Min LR | |
| LR Decay Style | Cosine |
| Clip Grad | 1.0 |
| Batch Size | 4M Tokens |
| Warmup Steps | 2,000 |
| MoE Loss Coefficient | 0.005 |
| Moe Capacity Factor | 1.5 |
| Mixed Precision | BF16 |
Appendix B Evaluation Datasets Details
-
•
MMLU Hendrycks et al. (2020): A large-scale dataset for evaluating a model’s understanding across multiple languages and domains. Models are evaluated on the VAL split with 5 shot.
-
•
Hellaswag Zellers et al. (2019): A Greek-language variant of the SWAG dataset, assessing a model’s ability to reason about everyday situations.(zero shot)
-
•
ARC Clark et al. (2018): A dataset designed to test a model’s ability to answer questions that require complex reasoning and commonsense knowledge.(zero shot)
-
•
Winogrande Sakaguchi et al. (2021): An extension of the Winograd Schema Challenge, focusing on pronoun disambiguation in a large-scale setting.(zero shot)
-
•
BoolQ Clark et al. (2019): A dataset consisting of yes/no questions, where the answers can be inferred from a given passage.(zero shot)
-
•
PIQA Bisk et al. (2020): A dataset that combines visual and textual understanding, where models must answer questions about images based on a persona.(zero shot)
-
•
SIQA Sap et al. (2019): A dataset that evaluates a model’s ability to understand social scenarios and make appropriate inferences.(zero shot)
-
•
CMMLU Li et al. (2023a): A Chinese version of the MMLU dataset, focusing on multitask language understanding in Chinese. Models are evaluated on the VAL split with 5 shot.
-
•
CEval Huang et al. (2024): A benchmark for evaluating Chinese natural language processing tasks with 5 shot.
-
•
CLUEWSC2020 Xu et al. (2020): A Chinese dataset for named entity recognition in the financial domain.(zero shot)
-
•
Thuc-news Sun et al. (2016): A dataset containing Chinese news articles, used for text classification and other NLP tasks.(zero shot)
-
•
OCNLI Hu et al. (2020): A Chinese dataset for natural language inference tasks.(zero shot)
-
•
C3 Sun et al. (2020): A dataset designed to assess a model’s understanding of commonsense knowledge in Chinese.(zero shot)
-
•
FewCLUE-CHID Xu et al. (2021): Few-shot Chinese Language Understanding Evaluation - Chinese Health Information Dataset. A dataset for few-shot learning in the healthcare domain in Chinese.(zero shot)
-
•
CMNLI: Chinese multilingual natural language inference dataset in CLUE Xu et al. (2020), specifically designed for natural language inference tasks.(zero-shot)
Appendix C Results for Ablation Experiments
We provide detailed evaluation scores for the models discussed in Section 5, which include benchmarks for both English and Chinese tasks in Table 10 and Table 11.
| Model | MMLU | Hellaswag | ARC | Winogrande | BoolQ | PIQA | SIQA | AVG |
|---|---|---|---|---|---|---|---|---|
| CLLA+share-krope | 35.85 | 54.01 | 50.04 | 56.45 | 67.47 | 75.97 | 53.87 | 56.24 |
| CLLA+share-kvproj | 42.99 | 54.40 | 58.86 | 57.38 | 71.67 | 74.86 | 56.14 | 59.47 |
| CLLA-quant+share-kvproj | 42.15 | 54.53 | 57.86 | 56.99 | 68.23 | 74.54 | 54.76 | 58.44 |
| Model | CMMLU | CEval | CLUEWSC2020 | Thuc-news | OCNLI | C3 | CHID | CMNLI | AVG |
|---|---|---|---|---|---|---|---|---|---|
| CLLA+share-krope | 29.03 | 36.08 | 71.07 | 96.92 | 57.04 | 63.21 | 81.70 | 58.62 | 61.71 |
| CLLA+share-kvproj | 41.50 | 44.40 | 70.19 | 96.10 | 47.39 | 60.83 | 79.70 | 51.08 | 61.40 |
| CLLA-quant+share-kvproj | 39.17 | 41.70 | 71.15 | 96.80 | 48.78 | 60.97 | 78.22 | 54.83 | 61.45 |