Logic Embeddings for Complex Query Answering

Reasoning over knowledge bases is fundamental to Artificial Intelligence, but still challenging since most knowledge graphs (KGs) such as DBpedia (Bizer et al., 2009), Freebase (Bollacker et al., 2008), and NELL (Carlson et al., 2010) are often large and incomplete. Answering complex queries is an important use of KGs, but missing facts makes queries unanswerable under normal inference. Figure 1 shows an example of handling a logic query representing the natural language question “Which films star Golden Globe winners that have not also won an Oscar?”. Answering this query involves multiple steps of KG traversal and existential first-order logic (FOL) operations, each producing intermediate entities. We consider queries involving missing facts, which means there is uncertainty about these intermediates that complicates the task. Two main approaches to answering such multi-hop queries involving missing facts are (i) sequential path search and (ii) query embeddings. Sequential path search grows exponentially in the number of hops, and requires approaches like reinforcement learning (Das et al., 2017) or beam search (Arakelyan et al., 2020) that have to explicitly track intermediate entities. Query embeddings prefer composition over search, for fast (sublinear) inference and tractable scaling to more complex queries. While relation functions have to learn knowledge, composition can otherwise use inductive bias to model logic operators directly to alleviate learning difficulty.

Query embeddings need to (a) predict missing knowledge, (b) model logic operations, and (c) model answer uncertainty. Query2Box models conjunction as intersection of boxes, but is unable to model negation as the complement of a closed region is not closed (Ren et al., 2020). Beta embeddings of (Ren & Leskovec, 2020) model conjunction as weighted interpolation of Beta distributions and negation as inversion of density, but improvise logic and depend on neural versions of logic conjunction for better accuracy.

(Hamilton et al., 2018) models entities as points so are unable to naturally express uncertainty, while Query2Box uses poorly differentiable geometric shapes unsuited to uncertainty calculations. Beta embeddings naturally model uncertainty with densities and do support complex query embedding, although its densities have no closed form and entropy calculations are expensive.

Beta embeddings (Ren & Leskovec, 2020) are the first query embedding that supports negation and models uncertainty, however it (1) abruptly converts first-order logic to set logic, (2) only improvises set logic with densities, (3) requires expensive Beta distribution (no closed form), and (4) dissimilarity uses divergence that needs integration.

We present our logic embeddings to address these issues with (1) formulation of set logic in terms of first-order logic, (2) use of well-studied logic, (3) simple representation with truth bounds, and (4) fast, symmetric dissimilarity measure.

Logic embeddings are a compositional query embedding with inductive bias of real-valued logic, for answering (with uncertainty) existential ($\exists$) FOL multi-hop logical queries over incomplete KGs. It represents entity subsets with arrays of truth bounds on latent propositions that describe and compress their features and relations. This allows us to directly use real-valued logic to filter and identify answers. Truth bounds $[l,u]:0\!\leq\!l\!\leq\!u\!\leq\!1$ from (Riegel et al., 2020) express uncertainty about truths, stating it can be a value range (e.g. unknown $[0,1]$). Sum of bound widths model uncertainty, which correlates to answer size. Now intersection is simply conjunction ($\land$) of bounds to retain only shared propositions, union is disjunction ($\lor$) to retain all propositions, and complement is negation ($\neg$) of bounds to find subsets with opposing propositions.

The novelty of logic embeddings is that it (a) performs set logic with real-valued logic, (b) characterizes subsets with truth bounds, and (c) correlates bounds with uncertainty. Its benefits are (a) improved accuracy with well-studied t-norms, (b) faster, simplified calculations, and (c) improved prediction of answer size.

Our contributions of logic embeddings make several advances to address issues of poor logic and uncertainty modeling, and computational expense of current methods:

1. Direct logic. Defines Skolem set logic via maximal Skolemisation of first-order logic to embed queries, where proximity of logic embeddings directly evaluates logic satisfiability of first-order logic queries.

2. Improved logic. Performs set intersection as logic conjunction over latent propositions with t-norms, often used for intersection of fuzzy sets. (Mostert & Shields, 1957) decomposition provide weak, strong, and nilpotent conjunctions, which show higher accuracy than idempotent conjunction via density interpolation of (Ren & Leskovec, 2020).

3. Direct uncertainty. Truth bounds naturally model uncertainty and have fast entropy calculation. Both entropy and bounds width show superior correlation to answer size.

4. Improved measure. Measures dissimilarity with simple $L_{1}$-norm, which improves training speed and accuracy.

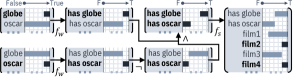
Our contributions also include (i) introduction of Skolem set logic in Section 2 to enable lifted inference, (ii) definition of logic embeddings in Section 3 to enable logic query composition, (iii) implementation details of method in Section 4, and (iv) detailed evaluation in Section 5 and new cardinality prediction experiment showing benefit of truth bounds.

We define an existential first-order language $\mathcal{L}$ whose signature contains a set of functional symbols $\mathcal{F}$ and a set of predicate symbols $\mathcal{R}$. The alphabet of $\mathcal{L}$ includes the logic symbols of conjunction ($\land$), disjunction ($\lor$), negation ($\neg$), and existential quantification ($\exists$). The semantics of $\mathcal{L}$ interprets the domain of discourse as a family of subsets $\mathcal{C}\subset 2^{\mathcal{V}}$, where $2^{\mathcal{V}}$ denotes the power set of a set of entities $\mathcal{V}$. This allows for lifted inference where variables and terms map to entity subsets, which are single elements in the discourse.

Sentences of $\mathcal{L}$ express relational knowledge, e.g. a binary predicate $r\!\in\!\mathcal{R}$ relates two unordered subsets via function $r\!:\!\mathcal{C}\!\times\!\mathcal{C}\!\mapsto\![0,1]$ that evaluates to a real truth value. However, the underlying knowledge is predicated under a different signature on domain of discourse $\mathcal{V}$, relating entities via $r^{\prime}\!:\!\mathcal{V}\!\times\!\mathcal{V}\!\mapsto\!\{\textit{False},\textit{True}\}$. Subsets $c,t\!\in\!\mathcal{C}$ are related via $r(c,t)$, with the union $t=\cup_{\forall v\in c}t^{\prime}$ over all underlying propositions $r^{\prime}(v,t^{\prime})$ for each entity $v\in c$ (see Figure 5).

Existential quantification in $\mathcal{L}$ results in sentences that are always true in the underlying interpretation¹¹1Universal quantification is not supported as interpretation in the underlying knowledge is contradictory, since useful relations cannot all be true for both empty and non-empty subsets. , because the nullset is present in $\mathcal{C}$. We introduce maximal quantification via a modified Skolem function to make $\mathcal{L}$ useful.

Definition 1 (Maximal Skolem function). A maximal Skolem function $f_{r}\in\mathcal{F}:\mathcal{C}\mapsto\mathcal{C}$ assigns the maximal subset $c$ to an existentially quantified variable $T$ so that $\exists T.r(a,T)\Leftrightarrow r(a,f_{r}(a))$ (equisatisfiable). The function receives input element $a\in\mathcal{C}$ and outputs the related subset $c$ over $\mathcal{V}$ with the largest cardinality, so that $f_{r}(a)=c:\;|c^{\prime}|\leq|c|,\;c,\forall c^{\prime}\in\mathcal{C}$. $\blacksquare$

Formulae in $\mathcal{L}$ such as $r(a,T)$ can thus convert to sentences $\exists T.r(a,T)$ by quantification over free variables, and the largest satisfying assignment to target variable $T:r(a,T)$ obtained via maximal Skolemisation $f_{r}(a)$ then subsumes all valid groundings in the underlying interpretation over $\mathcal{V}$. “Relation following” of (Cohen et al., 2020) is similar where $r(a,T)=\{t^{\prime}\;|\;\exists v\in a:r^{\prime}(v,t^{\prime})\}$. Normal Skolem functions are different as they only map to single entities.

Skolem set logic. This is set logic that involves Skolem functions that substitute related subsets. We introduce notation for maximal Skolemisation of sentences in $\mathcal{L}$ that represents set logic on Skolem terms in their underlying interpretation over $\mathcal{V}$. Evaluation in $\mathcal{L}$ of conjunction $\land$, disjunction $\lor$, and negation $\neg$ correspond to intersection, union, and complement in Skolem set logic, respectively.²²2Skolem set logic reuses operators $\land,\lor,\neg$ to signify that it performs direct real-valued logic on truth vectors of its terms. Skolem set logic usages are noted to avoid confusion with FOL.

Sentence forms and their Skolem set logic representations ($\land$, $\lor$ extends trivially to more inputs) for target variable $T$, given anchor elements $a$, $b$ (assigned subsets) and relation predicates ($r\!,\!\ldots\!,\!z$) include these conversion rules:

• •

  Relation: $\exists T.r(a,T)$ gives $f_{r}(a)$.

• •

  Negation: $\exists T.\neg r(a,T)$ gives $\neg f_{r}(a)$.

• •

  Conjunction: $\exists T.r(a,T)\land q(b,T)$ gives $f_{r}(a)\land f_{q}(b)$.

• •

  Disjunction: $\exists T.r(a,T)\lor q(b,T)$ gives $f_{r}(a)\lor f_{q}(b)$.

• •

  Multi-hop: $\exists T.r(a,V_{1})\land q(V_{1},V_{2})\land\ldots\land z(V_{n-1},T)$ has chain-like relations that give $f_{z}\cdots(f_{q}(f_{r}(a)))$.

Query formulae. We consider query formulae defined over $\mathcal{V}$ with $m$ anchor entities $a_{i}\in\mathcal{V}$, a single free target variable $T$, and $n$ bound variables $V_{j}$. Query answering assigns the subset $\{t\in\mathcal{V}\}\in\mathcal{C}$ of entities to $T$ that satisfy

We recast formulae into $\mathcal{C}$ by converting anchor entities to singleton subsets, we then quantify $T$ to maximally Skolemise the sentence and derive its Skolem set logic term $f(a_{1},a_{2},\ldots,a_{m})$ for $T$ given the anchor entities.

The dependency graph of formula (1) consists of vertices $\{a_{1},\ldots,a_{m},V_{1},\ldots,V_{n},T\}$ and a directed edge for each vertex pair $(x,y)$ related inside the formula, e.g. via $r(x,y)$. Queries are valid when the dependency graph is a single-sink acyclic graph with anchor entities as source nodes (Hamilton et al., 2018), and an equivalent to the original formula can then be recovered from Skolem set logic.

Our approach for positive inference on queries of form (1) require only Skolem set logic, but should also support:

1. 1.

   Lifted inference: Inference over subsets of entities, needing fewer actions than with single-entity inference;

2. 2.

   Knowledge integration: Underlying single-entity knowledge over $\mathcal{V}$ integrates over subsets from $\mathcal{C}$;

3. 3.

   Generalization: Use of subset similarities to predict absent knowledge with an uncertainty measure.

The powerset $\mathcal{C}$ over entities $\mathcal{V}$ from a typical KB is extremely large, so discrete approaches to achieve above with non-uniform subset representations are likely intractable.

Set embeddings. We consider set embeddings that map $\mathcal{C}$ to a continuous space $\mathcal{M}$, so these images of subsets approximately preserve their relationships from $\mathcal{C}$ (Sun & Nielsen, 2019). It has metric properties such as the volume of subsets, not usually considered by graph embeddings. Set embeddings have the following properties:

• •

  Uniform: Enables standard parameterization, simplifies memory structures and related computation;

• •

  Continuous: Differentiable, enables optimization;

• •

  Permutation-invariant: Subset elements unordered;

• •

  Uncertainty: Subset size corresponds to entropy;

• •

  Proximity: Relatively preserves subset dissimilarities.

Definition 2 (Logic embeddings). Logic embeddings are set embeddings that characterize subsets with latent propositions, and perform set logic on subsets via logic directly over their latent propositions. $\blacksquare$

Logic embeddings inherit the aforementioned properties and benefits of set embeddings, but are also:

• •

  Logical: Logic over truth values in embeddings performs set logic, and proximity correlates with satisfiability;

• •

  Contextual: Latent propositions integrate select knowledge depending on the subset;

• •

  Open-world: Accepts and integrates unknown or partially known knowledge and inferences.

Logic embeddings also share query embedding advantages of efficient answering, generalization, and full logic support:

• •

  Fast querying: Obtains answers closest to query embedding in sublinear time, unlike subgraph matching with exponential time in query size (Dalvi & Suciu, 2007).

• •

  General querying: Generalizes to unseen query forms.

• •

  Implicit prediction: Implicitly imputes missing relations, and avoids exhaustive link prediction (De Raedt, 2008) subgraph matching requires and scales poorly on.

• •

  Natural modeling: Supports intuitive set intersection, unlike point embeddings (Hamilton et al., 2018).

• •

  Uncertainty: Models answer size with embedding entropy (Ren & Leskovec, 2020) or truth bounds (ours).

• •

  Fundamental support: Handles negation (and disjunction via De Morgan’s law), unlike box embeddings where complements are not closed regions (and union resorts to disjunctive normal form) (Ren et al., 2020).

Latent propositions. A logic embedding keeps truth values with associate distribution $\mathbf{p}_{X}\in\mathcal{M}$ on latent propositions of features and properties that characterize and distinguish subset $X\subset\mathcal{V}$. Subset entities $x\in X$ may share a similar relation $r(x,Y)$ to a particular subset $Y$, where latent propositions can integrate such identifying relations. Logic embeddings need to be contextual given the limited embedding capacity, as only some relations may be relevant to define a particular subset.

Uncertainty. We represent volume in embedding space with lower and upper bounds $[l,u]$ on truth values, to express uncertainty and allow correlation of embedding entropy of a subset with its cardinality. We use truth bounds of (Riegel et al., 2020) that admit the open-world assumption and have probabilistic semantics to interpret known ($l\leq u$), unknown ($[0,1]$) and contradictory states ($l>u$, not considered here).

The logic embedding for $X\subset\mathcal{V}$ is an $n$-tuple $\mathbf{S}_{X}=([l_{i},u_{i}]:l_{i},u_{i}\in[0,1])_{i=1}^{n}$ of lower and upper bound pairs ($l_{i}\leq u_{i}$) that represents an $n$-tuple $\mathbf{p}_{X}=(P_{i})_{i=1}^{n}$ of uniform distributions $P_{i}=U(l_{i},u_{i})$, which omits contradiction $l_{i}>u_{i}$. The chain rule for differential entropy $H(\mathbf{p}_{X})=H(P_{1},\ldots,P_{n})$ of the embedding distribution applies and gives an upper-bound in terms of components $H(P_{i})=\log(u_{i}-l_{i})$, where

Condition 1 (Uncertainty axiom). Set embeddings should (approx.) satisfy $\forall X\in\mathcal{C}$: entropy $H(\mathbf{p}_{X})$ is a monotonically increasing function of $H(U_{X})$, where $U_{X}$ is a uniform distribution over elements of $X$ (Sun & Nielsen, 2019). $\blacksquare$

We measure adherence to the uncertainty axiom with correlation between subset size $|X|$ and entropy upper-bound $\sum_{i=1}^{n}H(P_{i})$ or total truth interval width $\sum_{i=1}^{n}(u_{i}-l_{i})$, and by predicting $|X|$ from $\mathbf{h}_{X}=[H(P_{i})]_{i=1}^{n}$.

Proximity. Subsets with high overlap should embed close by, whereas little to no overlap should result in relatively distant embeddings. We now review the proximity axiom.

Condition 2 (Proximity axiom). $\forall(X,X^{\prime})\in\mathcal{C}^{2}$: $D(\mathbf{p}_{X}\|\mathbf{p}_{X^{\prime}})$ should positively correlate with $D(U_{X}\|U_{X^{\prime}})$, given information divergence $D$ (Sun & Nielsen, 2019). $\blacksquare$

Relative entropy is an important divergence where the family of $f$-divergences $D_{f}(p|q)=\int p(x)f(q(x)/p(x))dx$ typically include $\log(p(x))$ or $p(x)^{-1}$ terms over finite support $x\in\mathcal{X}$. Uniform distributions $U(l,u)$ in logic embeddings may not cover a $[0,1]$ support, and may result in undefined divergence. Therefore, we measure dissimilarity $D(\mathbf{S}_{X},\mathbf{S}_{X^{\prime}})\in[0,1]$ between logic embeddings of subsets $(X,X^{\prime})$ with the expected mean of $L_{1}$-norms of truth bounds, where

Condition 3 (Satisfiability axiom). Substitution instance $q(X^{\prime})$ of first-order logic formula $q(T)$ has satisfiability $1-D(\mathbf{S}_{X},\mathbf{S}_{X^{\prime}})$, where target variable $T$ has answer $X$. $\blacksquare$

Query $q(T)$ is true for answer $X$, since $1-D(\mathbf{S}_{X},\mathbf{S}_{X})=1$, but candidate satisfiability $q(X^{\prime})$ can reduce to minimum 0 (false), depending on the dissimilarity between $X^{\prime}$ and $X$.

Set logic. Conjunction and disjunction of latent propositions of subsets perform their intersection and union, respectively, unlike information-geometric set embeddings that interpolate distributions. De Morgan’s law replaces disjunction $a\lor b$ with conjunction and negations $\neg(\neg a\!\land\!\neg b)$. Involute negation of $\mathbf{S}\!=\!\neg(\neg\mathbf{S})\!=\!([l_{i},u_{i}])_{i=1}^{n}$ describes complement³³3Truth bounds can share intervals with their negations, therefore complements can share latent propositions, which supports the diverse partitioning that complex queries require. $\neg\mathbf{S}=\left(\left[1\!-\!u_{i},1\!-\!l_{i}\right]\right)_{i=1}^{n}$. We use continuous t-norm $\top:[0,1]^{k}\mapsto[0,1]$ to perform generalized conjunction for real-valued logic, and calculate $\mathbf{S}^{\prime}=\bigwedge_{j=1}^{k}\mathbf{S}_{j}$ as

(Mostert & Shields, 1957) decompose any continuous t-norm into Archimedean t-norms, namely minimum/Gödel $\top_{\text{min}}(\mathbf{t})=\min(t_{1},\ldots,t_{k})$, product $\top_{\text{prod}}(\mathbf{t})=\prod_{j=1}^{k}t_{j}$, and Łukasiewicz $\top_{\text{luk}}(\mathbf{t})=\max(0,1-\sum_{j=1}^{k}(1-t_{j}))$, which we evaluate separately to consider all prime aspects.

Contextual. Limited capacity requires intersection to reintegrate latent propositions contextually via a weighted t-norm: 1) continuous function⁴⁴4We use non-monotonic smoothmin ($\alpha\!=\!-10$) for weighted minimum t-norm and set $l^{\prime}\!=\!u^{\prime}\!=\!(l+u)/2$ when $l\!>\!u$. $\top(\mathbf{w},\mathbf{t})$ of weights $\mathbf{w}$ and truths $\mathbf{t}$; 2) behaves equal to unweighted case if weights are 1; and 3) $w_{j}=0$ removes input $j$, and weights are in $[0,1]$.

Weight $w_{j}^{(v)}$ for $(l_{j}^{(v)},u_{j}^{(v)})$, the $j^{\text{th}}$ truth bounds in input $v$, depends on bounds of all conjunction inputs via attention, starting with function $g$ as

Softargmax over all the conjunction inputs yields a score $s_{j}^{(v)}=\exp(g_{j}^{(v)})/\sum_{h=1}^{k}\exp(g_{j}^{(h)})$ which normalizes after $w_{j}^{(v)}=s_{j}^{(v)}/\max(s_{j}^{(1)},\ldots,s_{j}^{(k)})$ to ensure max weight 1.

Query embedding. We calculate a logic embedding for a single-sink acyclic query with Skolem set logic over anchor entities. We keep vectors $\{\mathbf{r}\in\mathbb{R}^{d}\}$ for relation embeddings, and $\{\mathbf{x}\in[0,1]^{2d}\}$ for logic embeddings of all entities, where $\mathbf{x}=[l_{1},\ldots,l_{d},u_{1},\ldots,u_{d}]$. To measure the “cost” of modeling uncertainty by tracking bounds we also test point truth embeddings ($l=u$), where $\mathbf{x}=[t_{1},\ldots,t_{2d}]$.

We parameterize our Skolem function $f_{r}(\mathbf{x})=f(\mathbf{r},\mathbf{x})$ with $\mathbf{F}_{1}\in\mathbb{R}^{3d\times h}$, $\mathbf{F}_{2}\in\mathbb{R}^{h\times h}$, and $\mathbf{F}_{3}\in\mathbb{R}^{h\times 2d}$ to relate $\mathbf{x}$ to $\mathbf{y}=[\mathbf{y}_{l},\mathbf{y}_{l}+\mathbf{y}_{u}^{\prime}(1-\mathbf{y}_{l})]$, where $[\mathbf{y}_{l},\mathbf{y}_{u}^{\prime}]=f^{\prime}(\mathbf{r},\mathbf{x})=\sigma\left(\max\left(0,\max\left(0,[\mathbf{r},\mathbf{x}]\mathbf{F}_{1}\right)\mathbf{F}_{2}\right)\mathbf{F}_{3}\right)$ activates sigmoid.

Set logic has attention that uses $g(\mathbf{x})=\max\left(0,\mathbf{x}\mathbf{G}_{1}\right)\mathbf{G}_{2}$ with parameter matrices $\mathbf{G}_{1}\in\mathbb{R}^{2d\times 2d}$ and $\mathbf{G}_{2}\in\mathbb{R}^{2d\times d}$.

Cardinality prediction. We predict⁵⁵51:1 train:test, $\rho=10^{3}$, 250 epochs, Adam opt. ($lr=10^{-4}$). the cardinality $|X|$ of subset $X$ from the entropy vector $\mathbf{h}_{X}$ of its logic embedding with $\rho\cdot\sigma\left(\max\left(0,\max\left(0,\mathbf{h}_{X}\mathbf{H}_{1}\right)\mathbf{H}_{2}\right)\mathbf{H}_{3}\right)$ scaled by $\rho$, where $\mathbf{H}_{1}\in\mathbb{R}^{d\times\frac{d}{4}}$, $\mathbf{H}_{2}\in\mathbb{R}^{\frac{d}{4}\times\frac{d}{16}}$, and $\mathbf{H}_{3}\in\mathbb{R}^{\frac{d}{16}\times 1}$.

Query answering. Our objective is to embed a query $\mathbf{q}$ relatively close to its answers $\{\mathbf{y}\}$ and far from negative samples $\{\mathbf{z}\}$. We train model parameters⁶⁶6Hyperparameters include $d=400$, $h=1600$, $\gamma=0.375$, $k=128$ random negative samples, $512$ batch size, $450$k epochs, Adam optimizer ($lr=10^{-4}$). Pytorch on 1x NVIDIA Tesla V100. of 1) entity logic embeddings, 2) relation embeddings, 3) Skolem function, and 4) t-norm attention, to minimize query answering loss

We primarily compare against Beta embeddings (BetaE (Ren & Leskovec, 2020)) that also support arbitrary FOL queries and negation, where our logic embeddings (LogicE with Łukasiewicz t-norm) show improved 1) generalization, 2) reasoning, 3) uncertainty modeling, and 4) training speed.

Datasets. We use two complex logical query datasets from: q2b with 9 query structures (Ren et al., 2020), and BetaE that adds 5 for negation (Ren & Leskovec, 2020). They generate random queries separately over three standard KGs with official train/valid/test splits, namely FB15k (Bordes et al., 2013), FB15k-237 (Toutanova & Chen, 2015), NELL995 (Xiong et al., 2017). Table 1 shows the first-order logic and Skolem set logic forms of the 14 query templates.

We separately follow the evaluation procedures of above q2b and BetaE datasets.⁷⁷7https://github.com/francoisluus/KGReasoning Training omits ip/pi/2u/up (Table 1) to test handling of unseen query forms. Negation is challenging with 10x less queries than conjunctive ones.⁸⁸8Please see appendix for statistics of datasets.

Generalization. Queries have at least one link prediction task to test generalization, where withheld data contain goal answers. We measure Hits@k and mean reciprocal rank (MRR) of these non-trivial answers that do not appear in train/valid data. Table 4 tests both disjunctive normal form (DNF) and De Morgan’s form (DM) for unions (2u/up), but we only report DNF elsewhere as it outperforms DM.

LogicE with bounds generalizes better than BetaE, q2b, and gqe (Hamilton et al., 2018) on almost all query forms in Table 4, and further improves with point truths.⁹⁹9Please see appendix for full results on FB15k and NELL. LogicE also answers negation queries more accurately than BetaE for most query forms in Table 2. CQD-Beam does not handle negation nor uncertainty and is expensive as it grounds candidate entities explicitly, yet LogicE generalizes better and more efficiently in Table 5(a) on FB15k-237 and NELL.

Reasoning. Logical entailment on queries without missing links tests how faithful deductive reasoning is. We thus train on all splits and measure entailment accuracy in Table 5(b). LogicE on average reasons more faithfully than BetaE, q2b, and gqe baselines on all datasets.

EmQL is a query embedding that specifically optimises faithful reasoning (Sun et al., 2020), and thus outperforms all other methods in Table 5(b). However, EmQL without its sketch method has worse faithfulness than LogicE with point truths for FB15k and NELL, also EmQL does not support negation nor models uncertainty like LogicE.

Compare logics. LogicE can intersect via minimum, product, or Łukasiewicz t-norms, which perform similarly ($\pm$1%) in Table 3, while all outperform BetaE. Łukasiewicz provides superior uncertainty modeling, so is the default choice for LogicE. Attention via weighted t-norm improves LogicE accuracy (+9.6%), where one hypothesis is better use of limited embedding capacity through learning weighted combinations of latent propositions.

However, BetaE improves by avg. +12.3% with a similar attention mechanism so has greater dependence on it, possibly because it devises intersection as interpolation of densities, whereas LogicE uses established real-valued logic via t-norms. In particular, the BetaE intersect is idempotent while LogicE offers weak and strong conjunctions of which Łukasiewicz offers nilpotency.

Uncertainty modeling. Correlation between differential entropy $\sum_{i=1}^{n}H(P_{i})$ (upper-bound) and answer size (uncertainty, number of entities) is significantly higher in LogicE than BetaE using both Spearman’s rank correlation and Pearson’s correlation coefficient in Table 6. Both significantly outperform uncertainty of q2b with $L_{1}$ box size.

Total truth interval width $\sum_{i=1}^{n}(u_{i}-l_{i})$ of LogicE correlates better to answer size in most cases than BetaE, and offers direct use of the probabilistic semantics of truth bounds to simplify uncertainty modeling. Note that minimizing query answering loss in Eq. (8) does not directly optimize answer cardinality, so LogicE naturally models uncertainty only as by-product of learning to answer.

Cardinality prediction. Above evaluation aggregates entropy, but element-wise entropies $\mathbf{h}_{X}=[H(P_{i})]_{i=1}^{n}$ contain more information that we use for explicit answer size prediction. We train a regression classifier to map provided uncertainties $\mathbf{h}_{X}$ to answer size $|X|$, and measure mean absolute error $\|s-|X|\|/|X|$ of size prediction $s$.

Table 7 shows reduced cardinality prediction error of 83% with LogicE, compared to avg. 96% with BetaE, indicating more informative uncertainties with LogicE. However, these errors are still quite large, possibly because the main training objective does not directly optimize uncertainties for cardinality prediction.

Training speed. BetaE uses the Beta distribution with no closed form that requires integration to compute entropy and dissimilarity. In contrast, LogicE uses simple truth bounds with fast entropy and dissimilarity calculations. Figure 6 shows that LogicE with any t-norm trains 2-3x faster than BetaE, with the exact same compute resources, optimizer and learning rate. The LogicE training curve also appears smooth and monotonic, compared to disrupted learning progress with BetaE.

In addition to the overview of query embeddings in the Introduction, we also relate our work to 1) tensorized logic, 2) querying with t-norms, and 3) lifted inference.¹⁰¹⁰10Please see appendix for an extended related work section.

Tensorized logic. Distributed representations like embeddings can enable generalization and efficient inference that symbolic logic lacks. Logic tensors of (Grefenstette, 2013) express truths as specific tensors and map entities to one-hot vectors with full-rank matrices, but only memorize facts. Matrix factorization reduces one-hot vectors to low dimensions to enable generalization and efficiency while optimizing logic constraints, but can scale exponentially in the number of query variables (Rocktäschel et al., 2015).

Logic Tensor Networks learn a real vector per entity and even Skolem functions that map to entity features, but has weak inductive bias as it needs to learn predicates to perform logic (Serafini & Garcez, 2016). In contrast, logic embeddings support uncertainty and only has to learn Skolem functions to express knowledge and generalize, with direct logic on latent truths and logic satisfiability via distance.

Querying with t-norms. Triangular norms allow for differentiable composition of scores, often in the context of expensive search. (Guo et al., 2016) jointly embed KGs and logic rules via t-norm of scores, but only for simple rules. (Arakelyan et al., 2020) combine scores from a pretrained link predictor via t-norms repeatedly to search for an answer while tracking intermediaries, whereas logic embeddings perform vectorized t-norm to directly embed answers.

Lifted inference. Many probabilistic inference algorithms accept first-order specifications, but perform inference on a mostly propositional level by instantiating first-order constructs (Friedman et al., 1999; Richardson & Domingos, 2006). In contrast, lifted inference operates directly on first-order representations, manipulating not only individuals but also groups of individuals, which has the potential to significantly speed up inference (de Salvo Braz et al., 2007). We need to reason about entities we know about, as well as those we know exist but with unknown properties. Logic embeddings perform a type of lifted inference as it does not have to ground out the theory or reason separately for each entity, but can perform logic inference directly on subsets.

Embedding complex logic queries close to answers is efficient but presents several difficulties in set theoretic modeling of uncertainty and full existential FOL, where Euclidean geometry and probability density approaches suffer deficiency and computational expense. Our logic embeddings overcome these difficulties by converting set logic into direct real-valued logic. We execute FOL queries logically, and not through Venn diagram models like other embeddings, yet we achieve efficiency of lifted inference over subsets.

Main limitations include the need for more training data than search-based methods, although we have strong inductive bias of t-norm logic to reduce sample size dependence. Future work will consider negation attending to applied relations of its input to benefit from context like the t-norms.