Logic Distillation: Learning from Code Function by Function
for Planning and Decision-making
Abstract
Large language models (LLMs) have garnered increasing attention owing to their powerful logical reasoning capabilities. Generally, larger LLMs (L-LLMs) that require paid interfaces exhibit significantly superior performance compared to smaller LLMs (S-LLMs) that can be deployed on a variety of devices. Knowledge distillation (KD) aims to empower S-LLMs with the capabilities of L-LLMs, while S-LLMs merely mimic the outputs of L-LLMs, failing to get the powerful logical reasoning capabilities. Consequently, S-LLMs are helpless when it comes to planning and decision-making tasks that require logical reasoning capabilities. To tackle the identified challenges, we propose a novel framework called Logic Distillation (LD). Initially, LD employs L-LLMs to instantiate complex instructions into discrete functions and illustrates their usage to establish a function base. Subsequently, based on the function base, LD fine-tunes S-LLMs to learn the logic employed by L-LLMs in planning and decision-making. During testing, LD utilizes a retriever to identify the top- relevant functions based on instructions and current states, which will be selected and invoked by S-LLMs. Ultimately, S-LLMs yield planning and decision-making outcomes, function by function. Relevant experiments demonstrate that with the assistance of LD, S-LLMs can achieve outstanding results in planning and decision-making tasks, comparable to, or even surpassing, those of L-LLMs.
Introduction
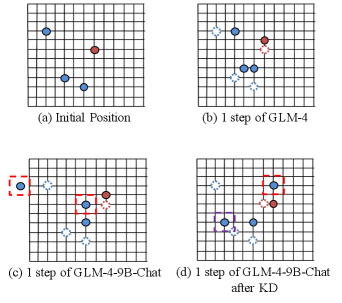
Large language models (LLMs) like GPT-3.5 (Ouyang et al. 2022) and GLM-4 (GLM et al. 2024) have been extensively applied owing to their robust capabilities in logical reasoning. Particularly, LLMs demonstrate superior performance in autonomous embodied agents, showcasing advanced planning and decision-making capabilities grounded in logical reasoning (Xi et al. 2023).
Despite the remarkable capabilities of LLMs such as GPT-3.5 and GLM-4, their substantial computational requirements render them impractical for deployment on most devices (Chen et al. 2024b, a). On the other hand, numerous companies have attempted to develop relatively smaller open-source LLMs, including GLM-4-9B (GLM et al. 2024) and LLaMA-7B (Touvron et al. 2023), which are compatible with consumer-grade GPUs like the RTX 4090 Ti. In this paper, we refer to LLMs that require invocation through a paid interface as Larger-LLMs (L-LLMs), in contrast to Smaller-LLMs (S-LLMs) deployable on consumer-grade GPUs. Generally, L-LLMs exhibit significantly superior performance across various domains, particularly in logical reasoning. Nonetheless, S-LLMs have garnered extensive attention owing to their convenient deployment and cost-free nature. Consequently, an increasing number of researchers are focusing on Knowledge Distillation (KD) of LLMs (Gou et al. 2021), where L-LLMs act as teachers imparting knowledge, while S-LLMs serve as students, mimicking the outputs of teachers (Xu et al. 2024).
While KD has been demonstrated to effectively enhance the capabilities of S-LLMs in numerous tasks, such as Natural Language Understanding (Dai et al. 2023; Gilardi, Alizadeh, and Kubli 2023), endowing S-LLMs with the planning and decision-making capabilities of L-LLMs through KD remains a challenge. We present the planning and decision-making outcome of a single step in a pursuit game, where LLMs control three blue dots in pursuit of an orange dot. Figure 1(a) displays the initial positions of four dots. Meanwhile, in Figure 1(b), it is evident that the L-LLM (GLM-4) effectively comprehends the game rules, enabling informed planning and decision-making based on the position of the orange dot at each step. In contrast, (c) reveals that the S-LLM (GLM-4-9B) lacks proficiency in following rules as the points enclosed by the red dashed line violate the rules of movement. Additionally, (d) highlights the issue with KD, where the student model simply mimics the output of the teacher model without comprehending the logic behind the teacher model’s planning and decision-making. Specifically, in (d), the orange dot moved one unit to the right, while the point enclosed by the purple dashed line moved one unit to the left. This stems from the KD process, where the S-LLM remembers the outputs the L-LLM has had in the past. Nevertheless, (d) demonstrates that the S-LLM is incapable of handling unseen circumstances, and fails to grasp the overall task objectives and rules. Based on the aforementioned analysis, we summarize the limitations of S-LLMs with KD as follows: 1. Ineffectiveness in following complex instructions: Despite extensive fine-tuning, S-LLMs continue to struggle with understanding intricate rules in planning and decision-making tasks. 2. Failure to comprehend the logic of L-LLMs: Fine-tuned S-LLMs simply mimic the outputs of L-LLMs and lose their planning and decision-making capabilities when encountering unknown scenarios.
Recently, there has been considerable work aimed at establishing the translation between natural language and code, where a sentence is a logical code line (Feng et al. 2020; Chen et al. 2021). Drawing inspiration from this, we suggest breaking down the planning and decision-making logic of L-LLMs into multiple stages, with each stage being represented by a specific code function. Subsequently, S-LLMs engage in planning and decision-making by learning and applying the pertinent functions. More specifically, we propose Logic Distillation (LD). First, we leverage the powerful comprehension and logical reasoning capabilities of L-LLMs to decompose the rules governing planning and decision-making tasks into multiple stages, forming different functions. Subsequently, we integrate these functions along with their comments, usage examples, etc., into a function base, and use it to fine-tune S-LLMs to enhance their ability to invoke relevant functions. Besides, to alleviate the issue of S-LLMs struggling to follow complex instructions, we propose transforming generation into selection. During each stage of planning and decision-making, LD employs a retriever to provide top- relevant functions based on the current state and instructions, enabling S-LLMs to select and execute functions from this set.
As depicted in Figure 2, both KD and LD require guidance from a teacher with superior capabilities. KD emphasizes the imparting of content, which involves students mimicking the teacher’s output. In contrast, the proposed LD concentrates on the underlying logic of task execution. The teacher decomposes a complex task into multiple basic logics, represented by functions, enabling the student to plan and make decision function by function.
The main contributions of this paper can be summarized as follows:
-
•
We analyzed the issues of Knowledge Distillation in the context of planning and decision-making in the LLMs era.
-
•
We propose Logic Distillation to enable S-LLMs to accomplish complex planning and decision-making tasks akin to L-LLMs.
-
•
We conducted experiments in different simulation scenarios to validate the effectiveness of the proposed method.


Related Work
Large language models (LLMs) (Chowdhery et al. 2022; Thoppilan et al. 2022; Zhao et al. 2023; Koundinya Gundavarapu et al. 2024) are trained on broad data and can be easily adapted to a wide range of tasks (Bommasani et al. 2021), which have been applied to education (Biswas 2023; Kasneci et al. 2023), healthcare (Thirunavukarasu et al. 2023; Peng et al. 2023; Guo et al. 2024), finance (Wu et al. 2023), etc. However, LLMs with impressive capabilities often suffer from size limitations, making them impractical to run on various devices and costly for invoking their interfaces (Chen et al. 2024b). In this paper, we refer to such LLMs as larger LLMs (L-LLMs). In contrast, we refer to LLMs with a smaller parameter scale that can be deployed on various devices as smaller LLMs (S-LLMs). Generally, S-LLMs are more flexible than L-LLMs, but their performance is significantly inferior to that of L-LLMs.
In order to endow S-LLMs with the superior capabilities of L-LLMs, Knowledge Distillation (KD) of LLMs has become a focal point of related research (Xu et al. 2024). In this context, L-LLMs like GPT-4 or GLM-4 are highly skilled teachers, while S-LLMs are students that learn to mimic the outputs of teachers (He et al. 2023; Gu et al. 2024; Agarwal et al. 2024; Liu et al. 2023). Besides, numerous works have also focused on the reasoning steps of LLMs. Distilling step-by-step (Hsieh et al. 2023) extracts L-LLM rationales as additional supervision for training S-LLMs within a multi-task framework. The Orca framework (Mukherjee et al. 2023) augments the prompt-response data pairs by incorporating a system message designed to facilitate student models’ comprehension of the reasoning process. Subsequently, Orca 2 (Mitra et al. 2023) advances this approach by training the student model to discern the most efficacious solution strategy for individual tasks, guided by the performance metrics established by Orca. However, these methods are essentially still making S-LLMs mimic the outputs of L-LLMs, rather than comprehending the reasoning logic.
Methodology
This paper investigates interactive planning and decision-making tasks, where interactions can be divided into multiple steps (each interaction counts as one step), and each step can be further divided into multiple stages (several stages collectively complete one planning and decision-making process).
As illustrated in Figure 3, we explore the Logic Distillation (LD) to empower S-LLMs to engage in planning and decision-making akin to L-LLMs. LD first decomposes rules (instructions) into multiple stages with L-LLMs and converts the execution logic into the corresponding code functions (such as calculating the distance between points). Then, LD will construct a function base containing functions and user manual of these functions. Besides, LD employs a retriever to find the top- functions that most relevant to the current stage and . Subsequently, S-LLMs will select functions one by one to plan and make decisions. Overall, in this context, LD consists of three components: (i) L-LLMs, (ii) retriever, (iii) S-LLMs.
L-LLMs
L-LLMs exhibit exceptional capabilities in planning and decision-making. To distill these capabilities into the S-LLMs, we propose instantiating the reasoning logic of L-LLMs through functions:
| (1) |
where L-LLMs parametrized by that generates a current token based on a context of the previous tokens, multiple constitute a function and user manual (includes rule explanations, code comments, corresponding invocation stages, and so on). In addition, a collection of and forms the function base .
Retriever
For the retriever , we have proposed two solutions tailored for function base of different scales. When the scale of the function base is large, we follow prior work (Lewis et al. 2020) to implement retrieval component based on DPR (Karpukhin et al. 2020), and retriever follows:
| (2) |
where is a dense representation of functions (including code comments and rule descriptions), and is a query representation. Retriever will return a top- list, where the functions with highest prior probability. As for small-scale function base, we will fine-tune S-LLMs so that S-LLMs can directly select and utilize the appropriate functions from base to plan and make decisions.
S-LLMs
We fine-tune S-LLMs to enable them to comprehend the functionality and the appropriate invocation timing of different functions. S-LLMs first select a function from or for stage :
| (3) |
Then, function will be executed to obtain the intermediate result of the -th stage.
| (4) |
If there are stages in a step of the task, then the S-LLMs will select functions, and the planning and decision-making outputs for that step will be:
| (5) |
If meets the requirements of the task, the planning and decision-making process will be halted. Otherwise, the will be regarded as input for the next step. The proposed LD is summarized in Algorithm 1.
Emergency handling of S-LLMs in LD
An advantage of LLMs is their ability to respond to various situations. When using LLMs to control embodied agents, they often can respond to unforeseen circumstances. For instance, when LLMs control unmanned vessels for maritime exploration, they might navigate from the open sea to archipelagos, and LLMs can analyze the specific terrain, enabling swift traversal of the archipelago.
Typically, emergency situations (such as avoiding whirlpools when controlling unmanned vessels) are simpler compared to the initial various instructions and rules. Therefore, in the LD framework, S-LLMs can be used to transform emergency into functions and add them to the function candidate list :
| (6) |
Through Equation 6, S-LLMs will possess stronger general capabilities.
It should be noted that, in contrast to KD, which necessitates S-LLMs to memorize massive L-LLMs’ outputs, LD merely requires S-LLMs to remember the usage rules of functions. Consequently, LD preserves more general capabilities of LLMs, including function generation.
Input: rules (instructions) .
Parameter: L-LLMs , S-LLMs , retriever .
Output: the planning and decision-making outcome .
Why Selection Is Better
For the aforementioned limitation of S-LLMs, ineffectiveness in following complex instructions, we propose change the function of S-LLMs from generation to selection. Specifically, S-LLMs are required to select the appropriate functions from a provided set, which are to be employed at various stages when confronting a particular problem. This section theoretically analyzes the advantages of selection over generation.

Assuming that the token list of LLMs contains a total of types of tokens, the retriever provides types of functions. For generation, the entropy of the prediction is:
| (7) | ||||
where is a token in the token list.
With Lagrange multiplier method, we get:
| (8) | ||||
then partially differentiating in Equation 8 with respect to and ,
| (9) |
When we perform selection, the number of candidates will be , and the maximum value of will be . As , , the maximum value of will be much smaller than that of , and the lower bound of selection will be much higher. Therefore, compared to generation, selection is more effective in maintaining stable outputs for S-LLMs.
| Success | Failure without Violation | Failure with Violation | Average Steps of Success | |
|---|---|---|---|---|
| S-LLM | — steps | |||
| L-LLM | steps | |||
| KD | steps | |||
| LD | steps |




Experiments
Our experiments aim to: (1) verify the effectiveness of LD in planning and decision-making task, (2) compare LD with baselines from both global and local perspectives, and discuss the reasons for the effectiveness of LD (3) verify that LD has a stronger ability to respond to emergencies111Code is included in the supplemental material and will be released upon the paper acceptance..
We conducted experiments based on the pursuit game to demonstrate that the proposed method can effectively enhance the planning and decision-making capabilities of S-LLMs. More specifically, the pursuit game involves two sides, each controlled by a different LLM. One LLM manages three blue dots, while the other LLM controls one orange dot. Each interaction between the two sides constitutes a step. In each iteration, the blue dots are constrained to move by two units, while the orange dot is restricted to a single unit of movement. The game concludes when the Manhattan distance between all three blue dots and the orange dot is less than 2 units.
In our experiments, the L-LLM is GLM-4, and the S-LLM is GLM4-9B-chat. The orange dot is consistently controlled by the L-LLM, while the blue dots are managed by the L-LLM, S-LLM, S-LLM with KD, and S-LLM with LD, respectively. Additional selection and judgment rules have been introduced to improve the success rate of the baselines. For selection, LLMs are provided with the next decision coordinates to choose from. Regarding judgment, if LLMs make more than seven illegal choices, the game is considered a failure. The upper limit for the number of moves in the game is capped at 100. We focus on utilizing LLMs to efficiently manage the blue dots to capture the orange dot. To perform KD, we initialize 221 sets of starting positions randomly and produce 103,355 sets of outputs with the L-LLM. Subsequently, we fine-tune the S-LLM with LoRA (Hu et al. 2021) based on these outputs. For a more details of the pursuit game, please refer to the Appendix.
For LD, as depicted in Figure 4, we initially establish a function base with the L-LLM, where L-LLM decomposes the rules and instantiating the planning and decision-making logic into multiple functions. Moreover, to assist the S-LLM in learning how to utilize various functions and decide when to invoke them, L-LLM creates a user manual for these functions. By fine-tuning the S-LLM with the user manual, it can comprehend the logic of the L-LLM and execute planning and decision-making processes function by function.
Better Performance with LD
The results of the pursuit game are presented in Table 1. It is evident that S-LLM struggles to comprehend complex instructions, as its failures consistently stem from rule violations. Conversely, the “Failure with Violation” rate of L-LLM is , demonstrating its superior comprehension and caability to follow instructions. By employing KD to mimic the L-LLM’s outputs, the S-LLM’s planning and decision-making capabilities significantly improve. Nonetheless, its success rate is notably lower than that of the L-LLM, and the number of steps in successful instances is higher. As for LD, the game’s success rate has reached , and the S-LLM completed the game with an average of fewer steps than the L-LLM. These results comprehensively demonstrate the effectiveness of LD in enhancing the S-LLM’s planning and decision-making capabilities.



Better Performance from a Local Perspective
We present the one-step planning and decision-making outcomes of different LLMs in Figure 5 (for the purpose of illustration, we have selected four scenarios where both the horizontal and vertical coordinates are within five units).
Figure 5(a) illustrates that while KD improves the alignment of S-LLM’s outputs with the rules, S-LLM still faces challenges in grasping the planning and decision-making logic of L-LLM. Consequently, the blue dots, controlled by S-LLM with KD, moves aimlessly, surpassing the maximum number of allowed movement steps, ultimately leading to the game’s failure. Figure 5(b) depicts that while S-LLM successfully completes the game, it still makes irrational decisions for the blue dots during specific moves, leading to a significantly higher number of steps compared to L-LLM. Regarding L-LLM and S-LLM with LD, as depicted in Figures 5(c) and 5(d), all LLMs demonstrate proficient control over the various blue dots, even as the blue dots approach the orange dots from different positions. These results indicate that, compared to KD, S-LLM with LD more effectively grasps the planning and decision-making logic of L-LLM.
| Success | Failure without Violation | Failure with Violation | Average Steps of Success | |
|---|---|---|---|---|
| S-LLM | — steps | |||
| L-LLM | steps | |||
| KD | steps | |||
| LD | steps |
Better Performance from a Global Perspective
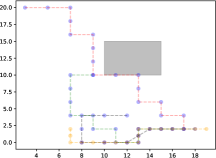
In Figure 6, we initialize different LLMs from identical starting positions: blue dots at , , and the orange dot at to enable a global comparison of the overall planning and decision-making capabilities among different LLMs.
In Figure 6(a), as S-LLM with KD merely mimics the outputs of L-LLM, blue dots may represent outputs from the L-LLM in different scenarios, resulting in behaviors such as repetitive circling. For instance, the point along the grey trajectory continuously shuttle back and forth, making it impossible to catch up with the orange point. In Figure 6(b), the point controlled by L-LLM appears to backtrack, mainly because of the orange point’s continuous back-and-forth movements in an attempt to escape encirclement. Besides, from Figure 6(c), it can be observed that S-LLM with LD enables the blue dots to approach the orange dot in a more direct manner. Contrasting with L-LLM, S-LLM with LD requires fewer steps to successfully capture the target. Such differences stem from different emphases: L-LLM employs a global perspective to design each function with rules. However, during each decision-making step, L-LLM was more susceptible to the influence of the current state, consequently neglecting global planning.
Pursuit Game with Emergencies
In order to assess the capacity of different LLMs to handle emergencies, we introduced a restricted area within the game plane. Related results are presented in Table 2.
In the more intricate scenario, L-LLM can still grasp the rules through simple textual descriptions and implement effective planning and decision-making, as the success rate achieve . Conversely, S-LLM with KD achieves a success rate of , with failures resulting from rule violations (accounting for ), indicating an inability of S-LLM with KD to comprehend the new rules. As for S-LLM with LD, the process involves S-LLM initially abstracting the restricted area as a coordinate filtering function. Then, this function will handle the output of from Figure 4, producing a list that excludes the coordinates of the restricted area. Subsequently, this list is utilized by to generate a suitable coordinate. The success rate of S-LLM with LD exceeds that of L-LLM by , and its average number of steps is approximately steps fewer than the baselines, demonstrating the powerful general capabilities of LD. It should be noted that, compared to KD, LD only uses few function usage examples to fine-tune S-LLM, which enable S-LLM to retain more general capabilities. More discussion please refer to the Appendix.
In Figure 7, we illustrate the comprehensive planning and decision-making processes of L-LLM and S-LLM with LD, which further validates the effectiveness of converting logic into functions.

Conclusion
LLMs have been widely applied across many different fields. However, larger LLMs (L-LLMs) with powerful capabilities in comprehension, planning, and decision-making are difficult to deploy on the vast majority of devices due to their parameter scale. In contrast to L-LLMs, smaller open-source LLMs (S-LLMs) are easier to deploy but fall significantly short in performance compared to their larger counterparts. To improve the performance of S-LLMs, researchers have proposed various Knowledge Distillation (KD) methods. Nevertheless, KD merely enables S-LLMs to mimic the outputs of L-LLMs, which is insufficient for addressing complex planning and decision-making problems. Thus, we propose Logic Distillation (LD), a method that instantiates the logic of L-LLMs by converting human-provided rules into functions, thereby establishing a function base. Subsequently, through fine-tuning, S-LLMs will comprehend the usage of each function, enabling S-LLMs to plan and make decisions function by function.
References
- Agarwal et al. (2024) Agarwal, R.; Vieillard, N.; Zhou, Y.; Stanczyk, P.; Garea, S. R.; Geist, M.; and Bachem, O. 2024. On-policy distillation of language models: Learning from self-generated mistakes. In The Twelfth International Conference on Learning Representations.
- Biswas (2023) Biswas, S. S. 2023. Role of chat gpt in public health. Annals of biomedical engineering, 51(5): 868–869.
- Bommasani et al. (2021) Bommasani, R.; Hudson, D. A.; Adeli, E.; Altman, R.; Arora, S.; von Arx, S.; Bernstein, M. S.; Bohg, J.; Bosselut, A.; Brunskill, E.; et al. 2021. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258.
- Chen et al. (2024a) Chen, D.; Zhang, S.; Zhuang, Y.; Tang, S.; Liu, Q.; Wang, H.; and Xu, M. 2024a. Improving Large Models with Small models: Lower Costs and Better Performance. arXiv preprint arXiv:2406.15471.
- Chen et al. (2024b) Chen, D.; Zhuang, Y.; Zhang, S.; Liu, J.; Dong, S.; and Tang, S. 2024b. Data Shunt: Collaboration of Small and Large Models for Lower Costs and Better Performance. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 38, 11249–11257.
- Chen et al. (2021) Chen, M.; Tworek, J.; Jun, H.; Yuan, Q.; Pinto, H. P. D. O.; Kaplan, J.; Edwards, H.; Burda, Y.; Joseph, N.; Brockman, G.; et al. 2021. Evaluating large language models trained on code. arXiv preprint arXiv:2107.03374.
- Chowdhery et al. (2022) Chowdhery, A.; Narang, S.; Devlin, J.; Bosma, M.; Mishra, G.; Roberts, A.; Barham, P.; Chung, H. W.; Sutton, C.; Gehrmann, S.; et al. 2022. Palm: Scaling language modeling with pathways. arXiv preprint arXiv:2204.02311.
- Dai et al. (2023) Dai, H.; Liu, Z.; Liao, W.; Huang, X.; Cao, Y.; Wu, Z.; Zhao, L.; Xu, S.; Liu, W.; Liu, N.; et al. 2023. Auggpt: Leveraging chatgpt for text data augmentation. arXiv preprint arXiv:2302.13007.
- Feng et al. (2020) Feng, Z.; Guo, D.; Tang, D.; Duan, N.; Feng, X.; Gong, M.; Shou, L.; Qin, B.; Liu, T.; Jiang, D.; et al. 2020. Codebert: A pre-trained model for programming and natural languages. arXiv preprint arXiv:2002.08155.
- Gilardi, Alizadeh, and Kubli (2023) Gilardi, F.; Alizadeh, M.; and Kubli, M. 2023. ChatGPT outperforms crowd workers for text-annotation tasks. Proceedings of the National Academy of Sciences, 120(30): e2305016120.
- GLM et al. (2024) GLM, T.; Zeng, A.; Xu, B.; Wang, B.; Zhang, C.; Yin, D.; Rojas, D.; Feng, G.; Zhao, H.; Lai, H.; Yu, H.; Wang, H.; Sun, J.; Zhang, J.; Cheng, J.; Gui, J.; Tang, J.; Zhang, J.; Li, J.; Zhao, L.; Wu, L.; Zhong, L.; Liu, M.; Huang, M.; Zhang, P.; Zheng, Q.; Lu, R.; Duan, S.; Zhang, S.; Cao, S.; Yang, S.; Tam, W. L.; Zhao, W.; Liu, X.; Xia, X.; Zhang, X.; Gu, X.; Lv, X.; Liu, X.; Liu, X.; Yang, X.; Song, X.; Zhang, X.; An, Y.; Xu, Y.; Niu, Y.; Yang, Y.; Li, Y.; Bai, Y.; Dong, Y.; Qi, Z.; Wang, Z.; Yang, Z.; Du, Z.; Hou, Z.; and Wang, Z. 2024. ChatGLM: A Family of Large Language Models from GLM-130B to GLM-4 All Tools. arXiv:2406.12793.
- Gou et al. (2021) Gou, J.; Yu, B.; Maybank, S. J.; and Tao, D. 2021. Knowledge distillation: A survey. International Journal of Computer Vision, 129(6): 1789–1819.
- Gu et al. (2024) Gu, Y.; Dong, L.; Wei, F.; and Huang, M. 2024. MiniLLM: Knowledge distillation of large language models. In The Twelfth International Conference on Learning Representations.
- Guo et al. (2024) Guo, J.; Shan, X.; Wang, G.; Chen, D.; Lu, R.; and Tang, S. 2024. HEART: Heart Expert Assistant with ReTrieval-augmented. In AAAI 2024 Spring Symposium on Clinical Foundation Models.
- He et al. (2023) He, X.; Lin, Z.; Gong, Y.; Jin, A.; Zhang, H.; Lin, C.; Jiao, J.; Yiu, S. M.; Duan, N.; Chen, W.; et al. 2023. Annollm: Making large language models to be better crowdsourced annotators. arXiv preprint arXiv:2303.16854.
- Hsieh et al. (2023) Hsieh, C.-Y.; Li, C.-L.; Yeh, C.-k.; Nakhost, H.; Fujii, Y.; Ratner, A.; Krishna, R.; Lee, C.-Y.; and Pfister, T. 2023. Distilling Step-by-Step! Outperforming Larger Language Models with Less Training Data and Smaller Model Sizes. In Findings of the Association for Computational Linguistics: ACL 2023, 8003–8017.
- Hu et al. (2021) Hu, E. J.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W.; et al. 2021. LoRA: Low-Rank Adaptation of Large Language Models. In International Conference on Learning Representations.
- Karpukhin et al. (2020) Karpukhin, V.; Oğuz, B.; Min, S.; Lewis, P.; Wu, L.; Edunov, S.; Chen, D.; and Yih, W. T. 2020. Dense passage retrieval for open-domain question answering. In 2020 Conference on Empirical Methods in Natural Language Processing, EMNLP 2020, 6769–6781. Association for Computational Linguistics (ACL).
- Kasneci et al. (2023) Kasneci, E.; Seßler, K.; Küchemann, S.; Bannert, M.; Dementieva, D.; Fischer, F.; Gasser, U.; Groh, G.; Günnemann, S.; Hüllermeier, E.; et al. 2023. ChatGPT for good? On opportunities and challenges of large language models for education. Learning and individual differences, 103: 102274.
- Koundinya Gundavarapu et al. (2024) Koundinya Gundavarapu, S.; Agarwal, S.; Arora, A.; and Thimmalapura Jagadeeshaiah, C. 2024. Machine Unlearning in Large Language Models. arXiv e-prints, arXiv–2405.
- Lewis et al. (2020) Lewis, P.; Perez, E.; Piktus, A.; Petroni, F.; Karpukhin, V.; Goyal, N.; Küttler, H.; Lewis, M.; Yih, W.-t.; Rocktäschel, T.; et al. 2020. Retrieval-augmented generation for knowledge-intensive nlp tasks. Advances in Neural Information Processing Systems, 33: 9459–9474.
- Liu et al. (2023) Liu, Z.; Oguz, B.; Zhao, C.; Chang, E.; Stock, P.; Mehdad, Y.; Shi, Y.; Krishnamoorthi, R.; and Chandra, V. 2023. Llm-qat: Data-free quantization aware training for large language models. arXiv preprint arXiv:2305.17888.
- Mitra et al. (2023) Mitra, A.; Del Corro, L.; Mahajan, S.; Codas, A.; Simoes, C.; Agarwal, S.; Chen, X.; Razdaibiedina, A.; Jones, E.; Aggarwal, K.; et al. 2023. Orca 2: Teaching small language models how to reason. arXiv preprint arXiv:2311.11045.
- Mukherjee et al. (2023) Mukherjee, S.; Mitra, A.; Jawahar, G.; Agarwal, S.; Palangi, H.; and Awadallah, A. 2023. Orca: Progressive learning from complex explanation traces of gpt-4. arXiv preprint arXiv:2306.02707.
- Ouyang et al. (2022) Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. 2022. Training language models to follow instructions with human feedback. Advances in neural information processing systems, 35: 27730–27744.
- Peng et al. (2023) Peng, C.; Yang, X.; Chen, A.; Smith, K. E.; PourNejatian, N.; Costa, A. B.; Martin, C.; Flores, M. G.; Zhang, Y.; Magoc, T.; et al. 2023. A study of generative large language model for medical research and healthcare. NPJ digital medicine, 6(1): 210.
- Thirunavukarasu et al. (2023) Thirunavukarasu, A. J.; Ting, D. S. J.; Elangovan, K.; Gutierrez, L.; Tan, T. F.; and Ting, D. S. W. 2023. Large language models in medicine. Nature medicine, 29(8): 1930–1940.
- Thoppilan et al. (2022) Thoppilan, R.; De Freitas, D.; Hall, J.; Shazeer, N.; Kulshreshtha, A.; Cheng, H.-T.; Jin, A.; Bos, T.; Baker, L.; Du, Y.; et al. 2022. Lamda: Language models for dialog applications. arXiv preprint arXiv:2201.08239.
- Touvron et al. (2023) Touvron, H.; Martin, L.; Stone, K.; Albert, P.; Almahairi, A.; Babaei, Y.; Bashlykov, N.; Batra, S.; Bhargava, P.; Bhosale, S.; et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
- Wu et al. (2023) Wu, S.; Irsoy, O.; Lu, S.; Dabravolski, V.; Dredze, M.; Gehrmann, S.; Kambadur, P.; Rosenberg, D.; and Mann, G. 2023. Bloomberggpt: A large language model for finance. arXiv preprint arXiv:2303.17564.
- Xi et al. (2023) Xi, Z.; Chen, W.; Guo, X.; He, W.; Ding, Y.; Hong, B.; Zhang, M.; Wang, J.; Jin, S.; Zhou, E.; et al. 2023. The rise and potential of large language model based agents: A survey. arXiv preprint arXiv:2309.07864.
- Xu et al. (2024) Xu, X.; Li, M.; Tao, C.; Shen, T.; Cheng, R.; Li, J.; Xu, C.; Tao, D.; and Zhou, T. 2024. A survey on knowledge distillation of large language models. arXiv preprint arXiv:2402.13116.
- Zhao et al. (2023) Zhao, W. X.; Zhou, K.; Li, J.; Tang, T.; Wang, X.; Hou, Y.; Min, Y.; Zhang, B.; Zhang, J.; Dong, Z.; et al. 2023. A survey of large language models. arXiv preprint arXiv:2303.18223.